The Connectivity of DVcube Networks: A Survey

Abstract

Analyzing network connectivity is important for evaluating the robustness, efficiency, and overall performance of various architectural designs. By examining the intricate interactions among nodes and their connections, researchers can determine a network’s resilience to failures, its capacity to support efficient information flow, and its adaptability to dynamic conditions. These insights are critical across multiple domains—such as telecommunications, computer science, biology, and social networks—where optimizing connectivity can significantly enhance functionality and reliability. In the literature, there are many variations of connectivity to measure network resilience and fault tolerance. In this survey, we focus on connectivity, tightly super connectivity, and h-extra connectivity within DVcube networks—a compound architecture combining disk-ring and hypercube-like topologies. Additionally, we identify several open problems to encourage further exploration in future research.

1. Introduction

Parallel computing plays an important role in significantly accelerating computational processes, making it an essential area of study in computer science. One of the fundamental aspects to be considered when designing a parallel computing system is the architecture of its interconnection network, as it determines the efficiency of communication between processors. The structure of the interconnection network greatly influences performance, scalability, and fault tolerance. In parallel computing, an interconnection network is typically represented using a graph-based model. In this model, each node (or vertex) corresponds to a processing element (such as a processor or computational unit), while each edge (or link) represents a communication pathway between two processing elements. This graph representation provides a mathematical framework for analyzing network topology, routing algorithms, and fault tolerance mechanisms. For the purposes of this survey, we will use the terms graph and network, vertex and node, as well as edge and link interchangeably. This interchangeable terminology will facilitate discussions about the structural properties and efficiency considerations of different interconnection network designs. The degree of a node in a network is the number of nodes adjacent to it. The order of a network is the number of nodes (vertices) in the network, while the size of the network is the number of links (edges) in this network. A Hamiltonian cycle in a network is a simple cycle that visits each node exactly once and returns to the starting node. A Hamiltonian decomposition of a network is a partition of its link (edge) set into Hamiltonian cycles such that each link belongs to exactly one Hamiltonian cycle, every node is included in each Hamiltonian cycle, and the union of all these Hamiltonian cycles covers all links (edges) of the network without overlap, i.e., the network is decomposed (divided) into link-disjoint (edge-disjoint) Hamiltonian cycles. Of course, Hamiltonian decomposition is only possible in certain types of networks (graphs).

Over the years, many interconnection network topologies have been proposed in the research literature [1,2,3,4,5,6,7,8]. A well-designed interconnection network should have several desirable properties, including symmetry, relatively small node degree, minimal network diameter, strong embedding capabilities, high scalability, efficient routing mechanisms, robust fault tolerance, Hamiltonian decomposition, and exceptional connectivity. These properties contribute to improving the performance, reliability, and adaptability of the network. In this survey, we focus on the diameter, connectivity, tightly super connectivity, and h-extra connectivity of networks. In the context of network topology, one of the most fundamental metrics is the order of a network, which refers to the total number of nodes present in the system. Another critical parameter is the diameter, which is defined as the length of the shortest path between the two most distantly separated nodes within the network. The diameter of a network plays a crucial role in determining communication efficiency, as a smaller diameter typically leads to shorter data transmission times and lower latency. Understanding the diameter of a network helps in optimizing routing algorithms and improving the overall performance of the network system. In addition to diameter, we also investigate network connectivity, which refers to the network’s ability to remain operational despite node or edge failures. One way to assess connectivity is by examining node cuts. A node cut is a subset of nodes whose removal disconnects the network, splitting it into at least two separate connected components. This means that if these specific nodes are removed, some nodes will no longer be able to communicate with others, leading to network fragmentation. A closely related concept is the edge cut, which consists of a subset of edges whose removal also results in the disconnection of the network. The (node) connectivity of a network is defined as the minimum number of nodes that must be removed to disconnect it, while edge connectivity is defined as the minimum number of edges that must be removed to achieve the same effect. Beyond basic connectivity, we also examine a more advanced metric known as h-extra connectivity. This parameter provides a deeper insight into network robustness by considering how many nodes need to be removed before every remaining connected component contains at least $h+1$ nodes. In other words, instead of simply disconnecting the network, this measure ensures that no remaining component is too small, which is crucial for maintaining system stability in large-scale distributed networks. The concept of h-extra connectivity is particularly useful in fault-tolerant network design, as it helps determine how well a network can withstand multiple node failures while still preserving a functional structure. Another significant metric in our study is the tightly super connectivity of a network, which provides further insight into the network’s resilience. The tightly super connectivity of a given network is the minimum number of nodes that must be removed so that the network splits into exactly two connected components, with one of these components being an isolated node. This measure is particularly relevant for analyzing network structures where single-node isolation must be avoided, such as in high-availability computing environments where every node must maintain at least some level of connectivity.

The connectivity of networks (graphs) can be applied to the following areas. In telecommunication networks, the connectivity between nodes (such as base stations and routers) determines the reliability and efficiency of data transmission. For example, in the design of 5G communication networks, it is necessary to ensure that even if some base stations fail, other nodes can still reroute data to maintain uninterrupted services. This “fault tolerance” is closely related to the high connectivity of the network (see [9]). In a data center or cloud computing platform, connectivity between servers affects data distribution and fault tolerance. For example, the hypercube structure is often used to design high-performance distributed computing systems because it has good symmetry and high connectivity, which can improve the efficiency of task dispatching and resource access (see [10]). In systems biology, studying the interactions between proteins allows the construction of a protein interaction network. Connectivity analysis of the network can be used to identify “key proteins” nodes that have a significant impact on overall biological function. If these key nodes fail, it may lead to overall system imbalance or disease (see [11]). On social platforms like Facebook and Twitter, connectivity affects the speed and reach of information dissemination. For example, a network with high connectivity can facilitate the rapid spread of information and make it easier for close-knit community structures to form. In addition, analyzing which nodes (users) are the “bridges” for information dissemination can help design marketing strategies or prevent the dissemination of false information (see [12]). For a more detailed discussion of the studied parameters and their real-world applications, we refer to the works presented in [13,14,15], which provide extensive background and theoretical foundations related to these connectivity measures.

The ring topology is a widely recognized and commonly utilized network architecture. It is particularly notable for its simplicity and ease of implementation. Over the years, many network protocols and algorithms have been specifically designed and implemented to function within a ring topology. However, despite its advantages, the ring topology suffers from a significant drawback—its capability for fault tolerance is quite poor. If there is a single node or a fault in any of the links, then the remaining network still is connected but its ring structure is destroyed. In addition, two faulty nodes or links possibly make the remaining network disconnected. This lack of robustness makes the ring topology less desirable for applications requiring high reliability and fault tolerance. One crucial metric used to evaluate network performance is the network’s diameter, which refers to the maximum shortest path between any two nodes in the network. In a ring topology with n nodes, the diameter is given by $\lceil {\displaystyle \frac{n}{2}}\rceil$. This means that as the number of nodes in the network increases, communication efficiency may decline because messages might have to travel through a large number of intermediate nodes before reaching their destination. Due to these limitations, researchers have explored various ways to enhance the fault tolerance and reduce the diameter of ring networks. One of the most straightforward approaches to achieving these improvements is by adding additional connections, or chords, between non-adjacent nodes in the ring. The resulting network structure, known as a chord ring, improves both fault tolerance and network efficiency. A chord ring can be viewed as a subclass of a broader category of network topologies known as circulant graphs. Circulant graphs have been extensively studied in the fields of graph theory and computer networking due to their desirable properties. These graphs are particularly useful in the design of multicomputer networks and distributed computing systems. When compared to traditional ring topologies, chord rings offer significant improvements in terms of fault tolerance. The additional chordal links provide alternative paths for data transmission, reducing the likelihood that a single node or link failure will disrupt communication. Furthermore, chord rings typically exhibit a smaller diameter than standard ring networks, leading to shorter message transmission times and improved overall performance. Despite these advantages, circulant graphs still have certain inherent limitations. The fundamental structure of a circulant graph remains a ring with additional chords. Because of this, running two parallel algorithms on a circulant topology simultaneously is not always efficient. It is often difficult to partition the node set of a circulant graph into two equal-sized subsets in such a way that both subsets can execute separate parallel algorithms independently. This issue arises because the added chordal connections do not necessarily facilitate independent execution of multiple tasks. Additionally, circulant graphs may retain some of the disadvantages of traditional rings, such as link congestion. As data flow through the network, specific links may experience heavy traffic, leading to bottlenecks and decreased performance. In [16], Opatrny et al. proposed DCC linear congruential graphs, which are similar to chord ring graphs, have smaller diameters, and hold higher classic diagnosability. However, they still have the disadvantages associated with circulant graphs. To address these challenges, researchers have proposed a more advanced and reliable network structure known as the dual-ring topology. A dual-ring structure, as the name suggests, consists of two interlinked rings rather than a single ring. In general, a dual-ring network is considered to be more reliable than a single-ring network because it provides additional redundancy. If one of the rings experiences a failure, the second ring can continue to maintain network connectivity, improving fault tolerance and overall system robustness. Building on this concept, we introduced an innovative and simplified architecture called the disc-ring network, first presented in [17]. The disc-ring network maintains a regular structure and is designed to enhance network reliability while keeping the construction process straightforward. The topology is formed by taking two rings with an equal number of nodes and introducing additional links between corresponding nodes in the two rings. These extra connections create a more interconnected network, enhancing both performance and fault tolerance. One of the key benefits of the disc-ring network is its lower diameter compared to both standard ring and dual-ring topologies. A smaller network diameter translates to faster data transmission, which is important for applications requiring real-time or high-speed communication. The simplicity of the disc-ring network’s structure also makes it easy to implement in practical systems. In Figure 1, a ring with six nodes is shown in Figure 1a, a chord ring with six nodes and six chords is depicted in Figure 1b, and Figure 1c shows the structure of a disc-ring network $D(6,3)$. As illustrated in Figure 1, disc-ring networks provide a clear and efficient framework for designing fault-tolerant and high-performance network architectures. Moreover, disc-ring networks possess additional desirable properties. They support Hamiltonian decomposition, which is a crucial feature for optimizing network routing and ensuring efficient data transmission. The routing algorithm for disc-ring networks can be executed in linear time, making them computationally efficient. This property ensures that data packets can be transmitted quickly with minimal computational overhead. Due to these advantages, disc-ring networks are gaining attention as a promising alternative to traditional ring-based architectures, particularly for applications in parallel computing, distributed systems, and high-reliability network environments.

Figure 1. (a) A ring with 6 nodes, (b) a chord ring with 6 nodes and 6 chords, and (c) a disc-ring network $D(6,3)$, where the black circles in $D(6,3)$ denote the outer ring nodes while solid circles denote the outer ring nodes [17].

Figure 1. (a) A ring with 6 nodes, (b) a chord ring with 6 nodes and 6 chords, and (c) a disc-ring network $D(6,3)$, where the black circles in $D(6,3)$ denote the outer ring nodes while solid circles denote the outer ring nodes [17].

In the literature, many interconnection networks have been introduced. Among the proposed interconnection network structures, the hypercube stands out as a particularly well-known and widely used topology because of its numerous advantageous characteristics. The hypercube is recognized for its high degree of regularity, inherent symmetry, small diameter, strong connectivity, recursive construction, natural partition ability, and relatively low link complexity [18]. These features make it a suitable candidate for parallel processing applications that require high-speed data exchange and fault resilience. In response to certain limitations of the traditional hypercube, various modifications and enhancements have been proposed to improve its performance. These notable variants of the hypercube include the twisted cube [5], locally twisted cube [19], crossed cube [20], augmented cube [1], Möbius cube [21], folded cube [22], shuffle cube [23,24], spined cube [25], divide-and-swap cube [26,27], Z-cube [28], etc. These modified topologies offer enhanced properties compared to the conventional hypercube. One of the key advantages of these hypercube variants is that they exhibit a significantly reduced diameter, approximately half the diameter of a comparable hypercube, while maintaining strong connectivity and efficient communication. A smaller network diameter means that messages can travel between nodes more quickly, improving overall performance.

In most of the existing fundamental interconnection networks, achieving an ideal balance between desirable network properties presents a significant challenge, as these properties often conflict with one another. Network designers must carefully consider trade-offs between various factors such as node degree, network diameter, scalability, and fault tolerance. For example, two commonly used network topologies, the $n\times n$ mesh and the torus, exhibit a fixed node degree, which is advantageous to maintain uniform network connectivity and simplify routing algorithms. However, these networks suffer from relatively large diameters. Specifically, the diameter of an $n\times n$ mesh is $2n$, while the diameter of a torus is n. A larger diameter means that data packets may have to travel through a greater number of intermediate nodes, leading to increased transmission delays and reduced network efficiency. On the other hand, the n-dimensional hypercube is another widely studied network topology that offers a significantly smaller diameter compared to mesh and torus networks. The diameter of a hypercube of n dimensions grows logarithmically with the number of nodes, making it highly efficient in terms of communication latency. However, this advantage comes at the cost of an increasing degree of nodes. As the network order expands, the degree of the node of a hypercube also increases logarithmically, which can introduce complexity in terms of hardware implementation and energy consumption. Due to these conflicting characteristics, researchers have explored alternative strategies to construct hybrid networks that can integrate the beneficial properties of different topologies while mitigating their limitations. To achieve this objective, many design schemes have been proposed to develop hybrid interconnection networks that combine two or more fundamental network structures. The goal is to construct a new network topology that retains the advantageous features of the underlying basic networks while minimizing their respective weaknesses. Several primary approaches have been identified to achieve such hybrid network designs. These include overlay networks, join operations, product graphs, composition techniques, and complete bipartite graphs [29]. Each of these schemes offers different advantages and trade-offs, depending on the specific application and performance requirements. Among these various hybridization techniques, compound networks have been recognized as particularly suitable for large-scale distributed computing systems. Compound networks are characterized by their good regularity, high expansibility, and modular design, making them an attractive choice for implementing efficient and scalable network infrastructures. Several well-known compound network architectures have been proposed in previous research, including CCC (Cube-Connected Cycles) [30,31], dBCube [32], and KCube (compound graph of Kautz digraph and hypercube) [33]. These networks are known for their excellent modularity, expandability, and regularity, which makes them ideal for applications that require high-performance parallel and distributed computing.

In 2013, we explored novel approaches to embedding hypercube-like networks, including hypercubes, twisted cubes, locally twisted cubes, and crossed cubes, into disc-ring networks to develop new compound architectures, referred to as the DVcube, that leverage the strengths of both network types [17]. The disc-ring network, as mentioned previously, is an improved topology derived from ring-based networks that incorporates additional links to enhance connectivity and reduce diameter. By embedding hypercube structures into disc-ring networks, we constructed a hybrid network topology that inherits the low-diameter property of hypercubes while maintaining the scalability and fault tolerance of disc-ring networks. A specific example of this hybrid approach involves replacing a single node within a disc-ring network with an entire hypercube structure. The resulting compound architecture effectively integrates multiple smaller hypercubes into the overall network framework, creating a system that is modular and efficient. This concept is illustrated in Figure 2, which depicts a compound network formed by embedding two-dimensional hypercubes into a disc-ring network. This hybridization approach allows for greater flexibility in network design, enabling the construction of large-scale distributed systems with optimized performance characteristics. One of the key advantages of this compound architecture is that it maintains a fixed node degree, number of links, and overall network size, ensuring that the network remains manageable and scalable. Furthermore, we analyzed and confirmed that the resulting hybrid structure has Hamiltonian properties [17]. Hamiltonian properties are crucial for optimizing routing algorithms, fault tolerance, and network traversal, as they ensure the existence of Hamiltonian paths and cycles within the network. These properties allow for efficient data transmission and improve the robustness of the network against node or link failures. In conclusion, the development of compound network architectures, such as those incorporating hypercube structures into disc-ring networks, represents a promising direction for advancing interconnection network design. By combining the strengths of different topologies, researchers can create scalable, fault-tolerant, and high-performance network architectures suitable for parallel computing, distributed systems, and high-speed data communication. Future research will likely continue to explore new hybrid network models that optimize various performance metrics while maintaining simplicity and practicality in real-world implementations.

Figure 2. The compound network DQcube constructed from hypercubes and disc-ring network [17].

Figure 2. The compound network DQcube constructed from hypercubes and disc-ring network [17].

Over the ten-year period from 2013 to 2024, many researchers have continued to investigate the compound architecture DVcube originally proposed by us. Over the years, various studies have explored different aspects of this architecture, including its structural properties, connectivity, and fault tolerance. Researchers have examined how this architecture can be utilized to improve network performance in distributed computing environments, parallel processing, and large-scale interconnection networks. In this survey, we aim to review existing results on various connectivity parameters, including diameter, connectivity, edge connectivity, h-extra connectivity, and tightly super connectivity, in the context of disc-ring networks and the compound architectures derived from disc-ring networks and hypercube-like topologies. By integrating hypercube structures into disc-ring networks, we seek to better understand how these combined architectures perform in terms of robustness, fault tolerance, and efficiency. Our survey will provide valuable insights into the theoretical and practical aspects of network design, helping to develop more resilient, scalable, and efficient interconnection networks for modern computing applications. These results will have potential applications in parallel computing, large-scale distributed systems, fault-tolerant computing architectures, and network optimization strategies. In addition, we provide some open problems related to the studied parameters in compound architectures constructed from disc-ring and hypercube-like networks.

We give a brief review on the diameter, (node and edge) connectivity, h-extra connectivity, tightly super connectivity, and other properties of the DVcube and hypercube-like networks. Details of the discussed network parameters are presented in the remaining sections. First, we review the properties of hypercube-like networks. The diameter and node connectivity of an n-dimensional hypercube is n [18]. Yang and Meng determined the extra connectivity of hypercubes [34]. In [35], Zhao et al. determined the component connectivity of the n-dimensional hypercube. They also computed the component edge connectivity of hypercubes [36]. Mane derived an upper bound of the structure connectivity of hypercubes [37]. In [38], Chelvam and Sivagami computed structure connectivity of hypercubes. Wang et al. studied the strong Menger (edge) connected property of hypercubes [39]. In [40], Zhu et al. investigated the h-extra r-component connectivity of hypercubes. In 2024, Chen et al. [41] proposed the new network parameter edge matroidal connectivity and studied it on hypercubes. Adams and Virk [42] provided a lower bound on the betti numbers of vietoris–rips complexes of hypercubes. Axenovich [43] decided the subclass of hypercubes with zero Turán density. In 2024, Janzer and Sudakov [44] provided a lower bound on the Turán number of the hypercube, and Tikhomirov [45] computed the Ramsey number of hypercubes, improving the previous result in [46]. Zhang et al. [47] computed cyclic diagnosability of an n-dimensional hypercube under the PMC model and the ${\mathrm{MM}}^{*}$ model as $5n-10$. Tapadia et al. [48] discussed graph theoretic properties of good sets including connectivity, node decomposition, domination, and identifying path covers, where a good set on k nodes is a node-induced subnetwork of the hypercube that has the maximum number of links. Recently, Jasim and Najim [49] studied the edges deletion problem of hypercubes, and Liu et al. [50] studied the g-good r-component edge connectivity of hypercubes. Very recently, Korže and Vesel [51] investigated the total, the outer, and the dual mutual-visibility number of hypercubes, and Wang [52] introduced and investigated a model of magnetic quantum walk on a hypercube. These recent studies demonstrate the continued relevance and rich combinatorial structure of hypercubes in modern graph theory and network design.

We now review important results concerning variants of hypercubes, including twisted cubes and locally twisted cubes. The diameter of an n-dimensional twisted cube is $\lceil {\displaystyle \frac{n+1}{2}}\rceil$ [5] and its node connectivity is n [53,54]. In [55], Yang et al. investigated how to embed cycles into twisted cubes with fault nodes or links. Fan et al. [56] studied the embedding of cycles in twisted cubes with fault edges. Xu [57] proved that twisted cubes are Hamiltonian connected. In 2010, Fan et al. [58] proposed a polynomial algorithm to check whether the faulty node set satisfies the condition that each node of the n-dimensional twisted cube has at least one fault-free neighbor. Yang [59] proposed algorithms to construct n edge-disjoint spanning trees and $\lceil {\displaystyle \frac{n}{2}}\rceil$ independent spanning trees in the n-dimensional twisted cube. Lai and their collaborators proved twisted cubes to be geodesic two-pancyclic [60], proposed two systematic methods to embed paths into twisted cubes [61], and studied the node identification problem in the twisted cube [62]. Chang et al. [63] gave a parallel algorithm to construct independent spanning trees in twisted cubes. Gou [64] determined the r-component (edge) connectivity of n-dimensional twisted cubes for small r. In [65], Zhang et al. proved that an n-dimensional twisted-like cube with $n-2$ fault nodes or links is Hamiltonian connected. Recently, Peter and Jeannette [66] computed the zero forcing number of twisted cubes. In the literature, there exists a variant of twisted cubes, namely, locally twisted cubes, which were first introduced in [67]. The diameter and node connectivity of an n-dimensional locally twisted cube are $\lceil {\displaystyle \frac{n+3}{2}}\rceil$ and n in [67,68], respectively. Shalini et al. [69] gave a linear time algorithm to embed a locally twisted cube into a grid network. Chang et al. [70] studied the extra and component connectivity of locally twisted cubes. In a series of works [19,71,72], Kung et al. investigated the exact neighborhood connectivity, structure connectivity, and two-disjoint-cycle-cover node/link-pancyclic properties of locally twisted cubes. Pan et al. [73] proposed a parallel algorithm to construct independent spanning trees on the line graph of a locally twisted cube. Kung et al. determined the structure connectivity of locally twisted cubes. In [74], Wang analyzed the three-connectivity of an n-dimensional locally twisted cube to be $n-1$. Recently, Hua and Zhao [75] computed the h-faulty-block connectivity of locally twisted cubes.

Crossed cubes are an important variant of hypercubes, and they have attracted significant attention due to their desirable topological properties. The diameter of an n-dimensional crossed cube is $\lceil {\displaystyle \frac{n+1}{2}}\rceil$ [4,76], and its node connectivity is n [77]. Efe et al. [78] studied some topological properties of crossed cubes in 1997. In [79], the wide diameter and fault diameter of an n-dimensional crossed cube were shown to be $\lceil {\displaystyle \frac{n}{2}}\rceil +2$. Fan et al. [80] proved that $\lceil {\displaystyle \frac{n+1}{2}}\rceil +1$ is the shortest possible length that can be embedded between any two distinct nodes with dilation 1 in the n-dimensional crossed cube, and they also verified the n-dimensional crossed cube to be node-pancyclic and edge-pancyclic for $n\ge 2$ in [81]. In [82], Fan and Jia embedded $4\times 2^{n-3}$ meshes into the n-dimensional crossed cube with dilation 1 and expansion 2. In [83,84,85], Hamiltonian cycles or a specific Hamiltonian cycle were considered to be embedded into crossed cubes. Dong et al. [86] embedded disjoint 3D meshes into crossed cubes. In [87], Chang and Wu determined that the conditional connectivity of an n-dimensional crossed cube is $2n-2$, where conditional connectivity refers to the network’s connectivity under the assumption that every node has at least one fault-free neighbor despite the presence of faults. Wang [88] gave an algorithm to construct a k-connected subnetwork of an n-dimensional crossed cube for $2\le k\le n-1$. In [89], the authors embedded an $N\times N$ mesh of trees into an n-dimensional crossed cube, where $N=2^{{\displaystyle \frac{n-2}{2}}}$. In [90], Chen et al. proved an n-dimensional crossed cube to be $(n-2)$-fault-tolerant Hamiltonian and $(n-3)$-fault-tolerant Hamiltonian connected for arbitrary faults. Hung et al. [91] investigated the strong fault-Hamiltonicity of crossed cubes. Guo [92] determined the r-component connectivity of crossed cubes for small r. In [93], Guo analyzed the k-restricted edge and node connectivity of crossed cubes for $1\le k\le 3$. Kung and Chen [94] proved an n-dimensional crossed cube to be Hamiltonian $(\lceil {\displaystyle \frac{n+1}{2}}\rceil +1)$-panconnected for $n\ge 4$. In [95], Cheng et al. constructed independent spanning trees with height n for an n-dimensional crossed cube. Pai et al. [96] developed a tree searching algorithm to find three completely independent spanning trees on an n-dimensional crossed cube for $n\ge 6$. Pan and Cheng [97] studied the structure connectivity and substructure connectivity of the crossed cubes. In [98], Jinyu et al. computed the fractional matching preclusion number and fractional strong matching preclusion number for the crossed cubes. Kung [99] determined the super path connectivity of the crossed cube. In [100], Pai et al. constructed three edge-disjoint Hamiltonian cycles in crossed cubes. Recently, Liu and Cheng [20] determined the generalized three-connectivity and the generalized four-connectivity of an n-dimensional crossed cube to be $n-1$. In addition, several variants of crossed cubes have been proposed. Wang et al. [101] introduced twisted crossed cubes, which combine properties of crossed and twisted cubes. The diameter and connectivity of an n-dimensional twisted crossed cube are $\lfloor {\displaystyle \frac{n+1}{2}}\rfloor$ and n, respectively. The folded crossed cube, proposed in [102], has diameter $\lceil {\displaystyle \frac{n}{2}}\rceil$ and connectivity $n+1$. Cei and Vumar [103] showed that the super connectivity and edge connectivity of an n-dimensional folded crossed cube are $2n$. Guo et al. [104] showed that the h-extra connectivity of an n-dimensional folded crossed cube is $(h+1)n-h-\left({\displaystyle \genfrac{}{}{0pt}{}{h}{2}}\right)+1$.

In addition to the variants of hypercubes discussed above, the augmented cube and Möbius cube are two notable extensions. The augmented cube was first introduced by Choudum and Sunitha [2]. The diameter of the n-dimensional augmented cube, denoted as $A{Q}_n$, is $\lceil {\displaystyle \frac{n}{2}}\rceil$, and its connectivity is $2n-1$ [2]. The connectivity-related properties of augmented cubes are summarized as follows. Zhang et al. [105] determined the component connectivity of augmented cubes. The super connectivity and super edge connectivity of $A{Q}_n$ are, respectively, $4n-8$ and $4n-4$ [106,107]. Cheng et al. [108] provided an upper bound and a lower bound of the g-extra connectivity for augmented cubes. Ba et al. [109] studied the star-structure connectivity of augmented cubes. Xu and Zhou [110] determined the h-extra edge connectivity of $A{Q}_n$ for $1\le h\le 2^{n-1}$ for improving the result in [111]. In [112], the structure connectivity and substructure connectivity of the augmented cubes are investigated. Shinde and Borse [113] analyzed the conditional h-edge connectivity of $A{Q}_n$. In 2024, Mane and Kandekar [114] demonstrated that the pendant three-tree connectivity of $A{Q}_n$ is $2n-3$, and Zhang et al. [8] studied the h-extra r-component edge connectivity of $A{Q}_n$. The diagnosability and super spanning connectivity of augmented cubes were studied in [115,116]. Other structural and topological properties of augmented cubes are reviewed below. Hsu et al. [117] studied the fault Hamiltonicity and the fault Hamiltonian connectivity of augmented cubes. The node-independent and edge-independent spanning trees in augmented cubes were constructed in [118] and [119,120]. In [121], Hung constructed two edge-disjoint Hamiltonian cycles and two-equal path cover in augmented cubes. Wang et al. [122] showed that $A{Q}_n$ remains pancyclic provided faulty vertices and/or edges do not exceed $2n-3$ and $n\ge 4$. In 2020, Kandekar et al. [123] decomposed $A{Q}_n$ into two spanning, regular, connected, and pancyclic subgraphs. Recently, Cheng proved that $A{Q}_n$ is two-disjoint-cycle-cover $[3,2^{n-1}]$-pancyclic [124]; however, this result was described in 2023 [125,126]. Next, we review the properties of the Möbius cube. The Möbius cube was first proposed by Cull and Larson [3]. The diameter of the n-dimensional Möbius cube $M{Q}_n$ is either $\lceil {\displaystyle \frac{n+2}{2}}\rceil$ or $\lceil {\displaystyle \frac{n+1}{2}}\rceil$, approximately half the diameter (n) of the equivalent hypercube $Q_n$, and the connectivity of $M{Q}_n$ is n [3]. In [127], Wang computed the h-extra connectivity of $M{Q}_n$ as $(n+1)(h+1)-{\displaystyle \frac{1}{2}}h(h+2)-1$. Recently, Zhao et al. [21] studied the structure connectivity and substructure connectivity of Möbius cubes. Other key properties of Möbius cubes include the following. Fan [128,129] studied the diagnosability of $M{Q}_n$ and proved that $M{Q}_n$ is Hamiltonian connected. Tsai [130] embedded meshes into Möbius cubes, and Cheng et al. [131] constructed independent spanning trees for Möbius cubes. In 2016, Liu et al. [132] proved that a complete binary tree can be embedded into $M{Q}_n$. Kocik et al. [133] solved the node-to-set disjoint paths problem in Möbius cubes, and Kocik and Kaneko [134] proposed an $O\left(n^2\right)$ time algorithm for the node-to-node disjoint paths problem in $M{Q}_n$. Ichida and Kaneko [135] further studied the set-to-set disjoint paths problem. Finally, Zhang et al. [136] investigated the fault-tolerant edge-pancyclicity of $M{Q}_n$.

In the last decade, several novel hypercube variants have been proposed, and many researchers have studied their structural and fault-tolerant properties. These variants include the shuffle cube, spined cube, divide-and-swap cube, and Z-cube. In 2001, Li et al. [23] introduced the shuffle cubes, proved that the diameter of n-dimensional shuffle cube $S{Q}_n$ is around ${\displaystyle \frac{n}{4}}$, and verified that the connectivity of $S{Q}_n$ is n. Xu et al. [137] determined that the super connectivity and the super edge connectivity of $S{Q}_n$ are $2n-4$ and $2n-2$, respectively, for $n\ge 6$. In [138], Xu et al. showed that $S{Q}_n$ has the conditional diagnosability of $4n-15$ for $n\equiv 2(mod 4)$ and $n\ge 10$. Lin et al. [139] determined the conditional diagnosability of $S{Q}_n$ as $3n-9$ and verified that $S{Q}_n$ is strongly n-diagnosable under the comparison model. Li et al. [140] computed the $(t,k)$-diagnosability of $S{Q}_n$ under PMC model. In 2020, Ding et al. [24] calculated the three-component and four-component connectivity of $S{Q}_n$ as $2n-4$ and $3n-8$, respectively. They also computed the three-component edge and four-component edge connectivity of $S{Q}_n$ as $2n-1$ and $3n-3$. Recently, Lu et al. [141] proposed two variants of shuffle cubes and analyzed their properties. In 2011, Zhou et al. [25] introduced the spined cube. The diameter of n-dimensional spined cube $SP{Q}_n$ is $\lceil {\displaystyle \frac{n}{3}}\rceil +3$ for $n\ge 14$ [25]. Cheng et al. [142] determined the one-extra edge connectivity of $SP{Q}_n$ as $2n-2$ for $n\ge 3$. In [143], Arockiaraj et al. proposed an algorithm to embed the spined cube into a grid. Yang et al. [144] proved that there exist two edge-disjoint Hamiltonian cycles in $SP{Q}_n$. In 2019, Kim et al. [26] introduced a new invariant of hypercubes, namely, divide-and-swap cube $DSC\left(n\right)$, with diameter $\le {\displaystyle \frac{5n}{4}}-1$ and with node degree ${log}_{2}n+1$. The connectivity of $DSC\left(n\right)$ is ${log}_2\left(n\right)+1$ and super connectivity of $DSC\left(n\right)$ is $2{log}_2\left(n\right)$ [27]. Zhou et al. [145] studied the structure and substructure connectivity of $DSC\left(n\right)$. In [146], the r-component connectivity and diagnosability of $DSC\left(n\right)$ are computed. More recently, the generalized connectivity on $DSC\left(n\right)$ was investigated in [147]. In 2024, Zhang et al. [148] constructed $d+1$ node-disjoint paths between any two distinct nodes in $DSC\left(n\right)$, where $n=2^d$ and $d\ge 1$, and Zhou et al. [149] computed the h-extra connectivity ($0\le h\le 10$) of $DSC\left(n\right)$ as $(d-2)(h+1)+4$ for $1\le h\le 10$. More recently, Zhang et al. [150] studied the node-to-set disjoint paths problem in a divide-and-swap cube. In the literature, Z-cubes (twisted hypercubes), which were first introduced by Zhu in [28], are considered to have the smallest diameter among hypercube-like networks. The diameter of n-dimensional Z-cube $Z{Q}_n$ is ${\displaystyle \frac{(1+o(1\left)\right)n}{{log}_{2}n}}$, and $Z{Q}_n$ is Hamiltonian connected for $n\ge 3$ [28]. However, its low-dimensional structure is not consistent with that of other hypercube variants, making its construction more complex. Several researchers have explored various properties of Z-cubes, including g-good neighbor conditional diagnosability [151], fault-diameter and wide-diameter [152], internally disjoint paths [153], structure connectivity and substructure connectivity [154], and g-extra conditional diagnosability [155].

In addition to the aforementioned hypercube variants, some researchers have explored the idea of combining two existing hypercube-like structures to create new variants. As a variant of the hypercube, exchanged hypercube $EH(s,t)$, proposed by Loh et al. [156], is a new interconnection network obtained by systematically removing links from a hypercube. It significantly reduces the number of links compared to a standard hypercube while preserving many topological and application support merits. It was proved that $EH(s,t)$ has connectivity $s+1$ [157] and super connectivity $2s$ [158]. In [159], Li et al. proposed a compounded network, called exchanged crossed cube $ECQ(s,t)$, which inherits desirable properties from both the crossed cube and the exchanged hypercube. This network achieves a more favorable balance between cost and performance in parallel computing systems. The connectivity and super connectivity of exchanged crossed cube $ECQ(s,t)$ are $s+1$ and $2s$, respectively [160,161]. Ning [162] computed the h-connectivity of exchanged crossed cube $ECQ(s,t)$ as $2^h(s-h+1)$. Recently, a number of studies have focused on the structural and fault-tolerant properties of the exchanged crossed cube $ECQ(s,t)$. Niu et al. [163] provided the upper and lower bounds of the $(s+1)$-wide diameter and s-fault diameter of $ECQ(s,t)$, Ning and Guo [164] computed the generalized three-connectivity of $ECQ(s,t)$ to be s, Wang et al. [165] computed the g-good-neighbor diagnosability of $ECQ(s,t)$ to be $2^g(s+2-g)-1$, Ning and Li [166] obtained the h-edge connectivity of $ECQ(s,t)$ to be $2^h(s-h+1)$, and Liu et al. [167] proved the two-restricted connectivity of $ECQ(s,t)$ to be $4s-4$. Although the exchanged crossed cube has been widely studied, its structure is more complex and challenging to construct compared to other hypercube-like networks. This paper provides a comprehensive survey of hypercube-like networks. The diameter and connectivity of these networks are summarized in

Table 1. The diameter and connectivity of hypercube-like networks.

Hypercube-Like Network	Diameter	(Node) Connectivity ($\mathit{\kappa }\left(\mathit{G}\right)$)
hypercube $Q_n$	n [18]	n [18]
twisted cube $T{Q}_n$	$\lceil {\displaystyle \frac{n+1}{2}}\rceil$ [5]	n [53,54]
locally twisted cube $LT{Q}_n$	$\lceil {\displaystyle \frac{n+3}{2}}\rceil$ [67]	n [68]
crossed cube $C{Q}_n$	$\lceil {\displaystyle \frac{n+1}{2}}\rceil$ [4,76]	n [77]
twisted crossed cube $TC{Q}_n$	$\lceil {\displaystyle \frac{n+1}{2}}\rceil$ [101]	n [101]
folded crossed cube $FC{Q}_n$	$\lceil {\displaystyle \frac{n}{2}}\rceil$ [102]	$n+1$ [102]
augmented cube $A{Q}_n$	$\lceil {\displaystyle \frac{n}{2}}\rceil$ [2]	$2n-1$ [2]
Möbius cube $M{Q}_n$	$\lceil {\displaystyle \frac{n+2}{2}}\rceil$ [3]	n [3]
shuffle cube $S{Q}_n$	$\lceil {\displaystyle \frac{n}{4}}\rceil$ [23]	n [23]
spined cube $SP{Q}_n$	$\lceil {\displaystyle \frac{n}{3}}\rceil +3$ [25]	n [25]
divide–swap cube $DSC\left(n\right)$	$\le {\displaystyle \frac{5n}{4}}-1$ [26]	${log}_2\left(n\right)+1$ [27]
Z-cube $Z{Q}_n$	${\displaystyle \frac{(1+o(1\left)\right)n}{{log}_{2}n}}$ [28]	n [28]

.

We next present a brief review of DVcube networks [17], a class of compound networks that integrate the structural characteristics of disc-ring networks and hypercube-like topologies. The hypercube-like networks considered in this context include the hypercube, twisted cube, locally twisted cube, and crossed cube. The DVcube is relatively simple to construct and exhibits many desirable topological properties. In 2018, Qin and Hao [168] conducted an in-depth study on fault Hamiltonicity of DVcube networks. Their research provided valuable insights into the fault tolerance and structural resilience of DVcube networks under different fault conditions. Lv et al. [169] carried out a detailed investigation of the fault diagnosability of DQcube networks, which embed hypercubes into disc-ring networks. Their study focused on the ability of DQcube networks to diagnose faulty nodes effectively. In addition, they examined the tightly super connectivity and three-extra connectivity of the DQcube, further expanding the understanding of its robustness and connectivity properties under various network failure scenarios. Zhang and Meng [170] explored the faulty diagnosability and h-extra connectivity of the DQcube. Their work analyzed how effectively faults could be diagnosed within the network, providing a deeper understanding of its fault tolerance mechanisms. Additionally, they computed the h-extra connectivity of the DQcube in their follow-up study [171], which helped in quantifying the network’s ability to maintain connectivity even in the presence of multiple node failures. Zhang et al. made significant contributions by computing the g-good neighbor connectivity and g-good neighbor diagnosability of the DQcube [172]. Their research shed light on the resilience of DQcube networks by considering connectivity constraints that require each connected component to have a minimum number of good neighbors, a property that enhances reliability in practical network applications. In [173], Liu studied the (r + 1)-component connectivity and diagnosability of the DQcube. This research expanded the existing knowledge on DQcube networks by examining their ability to maintain connectivity when multiple components are removed and analyzing their diagnostic capability under different failure conditions. The results provided a more comprehensive understanding of the robustness of the network. Recently, Zhou et al. [174] introduced the novel concepts of cluster connectivity and super cluster connectivity and computed these properties for the DQcube. These new connectivity measures provided fresh perspectives on how DQcube networks maintain structural integrity in the presence of failures, with potential implications for network design and optimization. In 2023, Zhang et al. [175] conducted an extensive study on DFcube networks, which are constructed by combining disc-ring networks and folded hypercube networks. Their work involved computing various connectivity parameters, including connectivity, edge connectivity, tightly super connectivity, and h-extra connectivity of the DFcube. The findings contributed to a better understanding of the structural robustness of the DFcube and provided valuable insights into its fault tolerance characteristics. This survey focuses on the connectivity, h-extra connectivity, and tightly super connectivity of DVcube networks constructed by integrating disc-ring structures with hypercube-like networks, including hypercubes, twisted cubes, locally twisted cubes, and crossed cubes.

The following is the organization of this paper. Section 2 introduces notation and definitions for the networks and problems studied. In Section 3, we give a survey on the previous established results. Section 4 lists possible future research. Finally, concluding remarks are provided in Section 5.

2. Terminology and Definitions

This section aims to introduce several terms and symbols along with presenting some definitions related to the studied problems and compound networks. To find the notations conveniently, the symbols used in this paper are listed in

Table 2. List of symbols used hereafter.

Symbol	Definition	Details
$diam\left(G\right)$	the diameter of network G	Equation (1)
$\kappa \left(G\right)$	the connectivity of G	the minimum number of nodes in G that must be removed to disconnect G
$\lambda \left(G\right)$	the edge connectivity of G	the minimum number of edges in G that must be removed to disconnect G
${\kappa }_h\left(G\right)$	the h-extra connectivity of G	the minimum number of nodes in G whose removal results in G being disconnected, and each remaining connected component has at least $h+1$ nodes
${\kappa }_t\left(G\right)$	the tightly super connectivity of G	the minimum number of nodes in G whose removal results in exactly two components, one of which is an isolated node
$D(m,d)$	a disc-ring network	Definition 1
$DV(m,d,n)$	a compound network constructed from $D(m,d)$ and n-dimensional hypercube-like network $H{L}_n$	Definition 1
$Q_n$	n-dimensional hypercube	Definition 2
$DQ(m,d,n)$	DQcube	a compound network built from $D(m,d)$ and $Q_n$, where Equation (2) satisfies and Figure 2 depicts $DQ(4,2,2)$ constructed from $D(4,2)$ and $Q_2$
$T{Q}_n$	n-dimensional twisted cube	Definition 4
$DT(m,d,n)$	DTcube	a compound network constructed from $D(m,d)$ and $T{Q}_n$, where Equation (2) satisfies, n is odd, and Figure 6 depicts a part of $DT(8,6,3)$ constructed from $D(8,6)$ and $T{Q}_3$
$LT{Q}_n$	n-dimensional locally twisted cube	Definition 5
$DL(m,d,n)$	DLcube	a compound network constructed from $D(m,d)$ and $LT{Q}_n$, where Equation (2) satisfies and Figure 8 depicts a part of $DL(8,6,3)$ constructed from $D(8,6)$ and $LT{Q}_3$
$C{Q}_n$	n-dimensional crossed cube	Definition 6
$DC(m,d,n)$	DCcube	a compound network constructed from $D(m,d)$ and $C{Q}_n$, where Equation (2) satisfies and Figure 10 depicts a part of $DC(8,6,3)$ constructed from $D(8,6)$ and $C{Q}_3$

and their detailed definitions are presented in the text of this section. If the reader encounters any graph-theoretic terminology not defined here, please refer to [176].

We usually use a graph to represent the topology of an interconnection network. In this survey, we use the terms “graph” and “network” interchangeably to describe the same concept. Throughout this survey, we only consider the finite, connected, and undirected networks. Let G be a network consisting of a set of nodes (vertices) and a set of links (edges). The node set of G, denoted as $V\left(G\right)$, is a finite collection of elements representing individual nodes, while the link set, denoted as $E\left(G\right)$, is a subset of all possible unordered pairs of nodes from $V\left(G\right)$. Specifically, a link in G is an element of the set $\left\{\right(u,v\left)\right|(u,v)$ is an unordered pair of $V\left(G\right)\}$. If there exists a link $(u,v)$ in the network G, we say that the node u is adjacent to the node v, and vice versa. In such a case, both u and v are said to be incident to the link $(u,v)$. The set of all nodes that are adjacent to a given node v in G is known as the neighborhood of v. This neighborhood of v in G is denoted by $N_G\left(v\right)$, and $de{g}_G\left(v\right)=\left|N_G\left(v\right)\right|$ is called the degree of v in G, where the subscript G is used to specify the graph being considered. However, when the context is clear, the subscript can be omitted for simplicity. A network G is called k-regular if each node in G has exactly k neighbors. In mathematical terms, this means that $|N_G\left(v\right)|=k$ for every node $v\in V\left(G\right)$. A path in a graph G is a sequence of nodes $v_1,v_2,\dots ,v_k$ such that each consecutive nodes $v_i$ and $v_{i+1}$ are adjacent for $1\le i<k$ and no node in it is repeated and is represented as $v_1\to v_2\to \dots \to v_k$. The shortest path between two nodes is the path with the minimum number of links (edges). Another fundamental property of a network G is the concept of distance, where G is finite and connected. The distance between two nodes u and v in G, denoted as $dist(u,v)$, is defined as the length of the shortest path between u and v. The diameter of a network G, denoted as $diam\left(G\right)$, is defined as the maximum value of $dist(u,v)$ on all pairs of nodes $u,v$ in $V\left(G\right)$, i.e.,

$$diam\left(G\right)=max\left\{dist\right(u,v\left)\right|u,v\in V\left(G\right)\},$$

(1)

where $V\left(G\right)$ is the set of nodes in the network G.

A fundamental concept in network robustness is the idea of a cut. A node cut (also known as a vertex cut) of a network G is a subset of nodes whose removal results in the disconnection of G. Similarly, an edge cut of G is a subset of edges whose removal leads to a disconnected network. The connectivity of G, denoted by $\kappa \left(G\right)$, is defined as the smallest number of nodes that must be removed to make G disconnected. Likewise, the edge connectivity of G, denoted by $\lambda \left(G\right)$, is the minimum number of edges that must be removed to disconnect G. Beyond basic connectivity, more advanced metrics are used to assess network resilience. One such measure is h-extra connectivity, denoted as ${\kappa }_h\left(G\right)$, which refers to the minimum number of nodes that need to be removed so that every remaining connected component of the network contains at least $h+1$ nodes. Another refined measure is the tightly super connectivity, denoted by ${\kappa }_t\left(G\right)$, which represents the minimum number of nodes that must be removed such that the resulting network consists of exactly two connected components, one of which is an isolated node.

In addition to connectivity and distance properties, modular arithmetic operations are used in this survey. For an integer z and a positive integer m, we define the function $z_{\parallel m}$ as follows: if $z\ge 0$, then $z_{\parallel m}=z$; otherwise, $z_{\parallel m}=z+m$. This function ensures that negative values are adjusted by adding m, effectively keeping results within a non-negative range. Furthermore, the notation $z_{\%m}$ represents the remainder when z is divided by m, which is a standard operation in modular arithmetic.

Next, we define the reviewed networks introduced in [17]. A disc-ring network, represented by $D(m,d)$, consists of two rings, where $1\le d\le m$ and each ring contains m nodes. One ring is called the inner ring, and the other is called the outer ring. Each node is labeled with a sequence $z_1{z}_2$ of two integers $z_1$, $z_2$, where $z_1$ is called the first index while $z_2$ is called the second index. If node $z_1{z}_2$ is in the outer ring, then $z_1=0$; otherwise, $z_1=1$. Within each individual ring, the nodes are sequentially labeled from 0 to $m-1$ in a counterclockwise direction. That is, for any node $z_1{z}_2$ belonging to either ring, its second index satisfies $0\le z_2\le m-1$. The link between nodes is defined according to two distinct sets of rules:

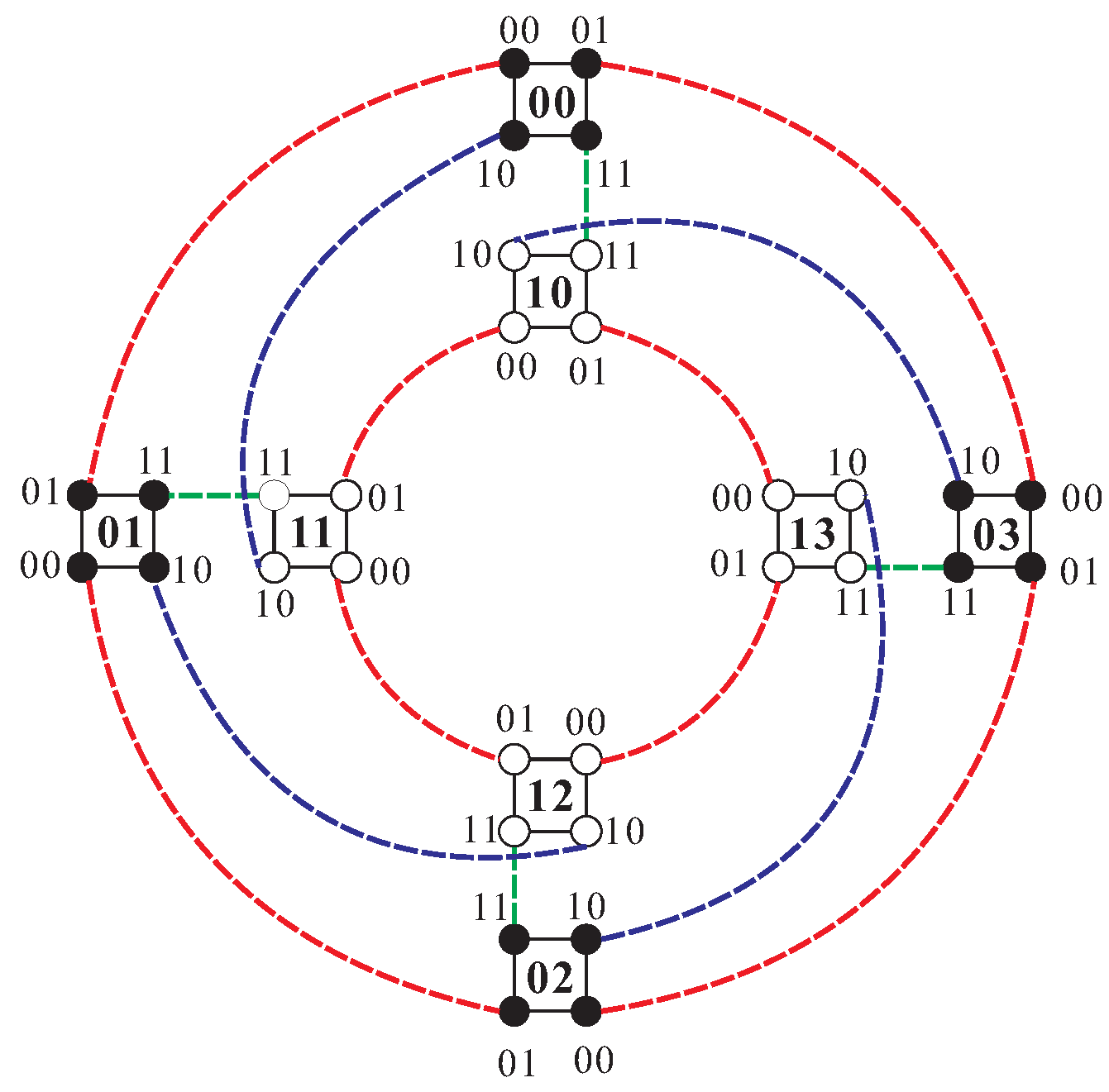
• Links between two nodes within the same ring: Each node $z_1{z}_2$ in a ring is directly connected to two adjacent nodes in the same ring. Specifically, it is adjacent to the node labeled $z_{1}x$, where $x\in \{{(z_2+1)}_{\%m},{(z_2-1)}_{\parallel m}\}$. This ensures that each node has exactly two connections to its immediate neighbors in the ring, maintaining the circular structure of the ring.
• Links between two nodes in different rings: Nodes in the outer ring establish links with nodes in the inner ring based on their second index. Specifically, for any node $0z_2$ in the outer ring, there exists a direct link connecting it to node $1y$ in the inner ring, where y is selected from the set $\{z_2,{(z_2+1)}_{\%m},\dots ,{(z_2+d-1)}_{\%m}\}$. This rule ensures that each outer ring node is linked to d consecutive nodes in the inner ring, creating inter-ring connections that provide additional paths for communication and connectivity within the network.

The formal mathematical definition of the disc-ring network follows from the above description, ensuring a structured and well-defined topology for further study and application.

Definition 1

(see [17]). The disc-ring graph, represented by $D(m,d)$, consists of outer and inner rings, where each ring contains m nodes and $1\le d\le m$. The node set of $D(m,d)$ is $\left\{z_1{z}_2\right|z_1=0$ or $1$, and $z_2\in \{0,1,\dots ,m-1\}\}$, where $z_1{z}_2$ is a sequence of two integers and is a label of a node, and $z_1$ indicates it is in inner or outer ring. Node $0z_2$ is in the outer ring while node $1z_2$ is in the inner ring. For any node $z_1{z}_2$, there is a link connecting it to node $z_{1}x$ for $x\in \{{(z_2+1)}_{\%m},{(z_2-1)}_{\parallel m}\}$. For any node $0z_2$, $0\le z_2\le m-1$, there is a link connecting it to node $1y$ for $y\in \{z_2,{(z_2+1)}_{\%m},\dots ,{(z_2+d-1)}_{\%m}\}$.

The DVcube $DV(m,d,n)$ is a compound network by replacing each node of $D(m,d)$ with an n-dimensional hypercube-like network $H{L}_n$ and linking each node of $H{L}_n$ with exactly one node of another hypercube-like network by a specific rule in [17], where $d+2=2^n$ and $H{L}_n$ is a hypercube, twisted cube, locally twisted cube, or crossed cube.

By the above definition, the disc-ring network $D(m,d)$ contains $2m$ nodes and is a $(d+2)$-regular undirected graph. Thus, $D(m,d)$ contains $m(d+2)$ links (edges). For example, Figure 1c depicts $D(6,3)$. We can easily verify that $D(m,1)$ is a prism graph (also called a circular ladder graph) [177], and $D(m,d)$ contains a Hamiltonian cycle which is a simple cycle passing through every node exactly once. A Hamiltonian decomposition of a graph G is a division of its edge set into disjoint Hamiltonian cycles, meaning the edges of G are grouped into separate Hamiltonian cycles without overlap. In [17], we demonstrated that $D(m,d)$ indeed admits a Hamiltonian decomposition. For example, Figure 3 shows two edge-disjoint Hamiltonian cycles of $D(5,2)$.

Theorem 1

(see [17]). The disc-ring network $D(m,d)$ possesses a Hamiltonian decomposition.

Figure 3. Two edge-disjoint Hamiltonian cycles of $D(5,2)$ are shown, where solid arrow lines represent one Hamiltonian cycle $C_1$ and dashed arrow lines represent the other cycle $C_2$ [17].

Figure 3. Two edge-disjoint Hamiltonian cycles of $D(5,2)$ are shown, where solid arrow lines represent one Hamiltonian cycle $C_1$ and dashed arrow lines represent the other cycle $C_2$ [17].

In Definition 1, we introduce a hybrid network combining a disc-ring network with hypercube-like networks, where a hypercube-like network refers to a variant of the hypercube, including the hypercube, twisted cube, locally twisted cube, and crossed cube. We first introduce a hybrid network DQcube constructed from a disc-ring network and hypercube networks. A binary string b of length n is represented as follows:

$$b=b_{n-1}{b}_{n-2}\dots b_1{b}_0,$$

(2)

where $b_{n-1}$ is the most significant bit and $b_0$ is the least significant bit. We denote the complement of bit $b_i$ by ${\overline{b}}_i=1-b_i$. Let b be a binary string. We denote as $b^k$ the new binary string obtained by repeating b string k times. For instance, ${\left(10\right)}^2=1010$ and $0^3=000$. We then define a hypercube as follows.

Definition 2

(See [18]). Let $Q_n$ be an n-dimensional hypercube. The node set $V\left(Q_n\right)$ is the set of all binary strings of length n, where each node is labeled as a binary string. There is a link between any two nodes of $Q_n$ if and only if their labels differ by exactly one bit. Generally, $Q_n$ can be constructed from two $Q_{n-1}$’s by adding $2^{n-1}$ links between the two $Q_{n-1}$’s. For example, Figure 4 shows $Q_2$ and $Q_3$, where $Q_3$ can be constructed from two $Q_2$’s.

Figure 4. (a) The 2-dimensional hypercube $Q_2$, and (b) the 3-dimensional hypercube $Q_3$ [17].

Figure 4. (a) The 2-dimensional hypercube $Q_2$, and (b) the 3-dimensional hypercube $Q_3$ [17].

By the definition of hypercube, $Q_n$ is a n-regular network with $|V\left(Q_n\right)|=2^n$ and $|E\left(Q_n\right)|=n\times 2^{n-1}$. The diameter of $Q_n$ has been computed as follows [18]:

$$diam\left(Q_n\right)=n.$$

(3)

In addition, it admits Hamiltonian decomposition [18,178]. Furthermore, disc-ring $D(4,1)$ is isomorphic to a 3-dimensional hypercube. In [33], Guo et al. constructed a compound network from two types of regular networks as follows.

Definition 3

(see [33]). Given two regular networks G and H, the compound network $G\left(H\right)$ is constructed by replacing each node of G by a copy of H and replacing each link of G by a link which connects two corresponding copies of H.

We construct compound networks by similar construction in [33]. A compound network DQcube [17] is constructed from a disc-ring and hypercubes as follows. The DQcube is the compound network of a disc-ring network G and hypercube H, where the disc-ring and hypercube networks are regular. It employs the hypercube topology as a unit cluster and connects many such clusters by means of a disc-ring structure. In the resultant network, the topology of disc-ring G is preserved, and only one link is inserted to connect two copies of hypercube H. There is an additional remote link associated with each node in a hypercube cluster. For each node in the resultant network, the degree is identical. A constraint must be satisfied for the two basic networks to constitute a compound network. That is, the degree of nodes in disc-ring network G must be equal to the number of nodes in hypercube H. Thus, if the DQcube, represented as $DQ(m,d,n)$, is constructed from disc-ring network $D(m,d)$ and hypercube $Q_n$, then it satisfies the following restriction [17]:

$$d+2=2^n.$$

(4)

For example, Figure 2 depicts a compound network $DQ(4,2,2)$ built from $D(4,2)$ and $Q_2$, where dashed lines indicate the remote links and the number inside the square is the label of this cluster.

For the various variants of the hypercube, these structures exhibit superior topological properties compared to the traditional hypercube network. These improved properties make them highly suitable for applications requiring efficient network communication and optimized connectivity. One significant advantage is that the diameter of these hypercube variants is approximately half of the network diameter of a comparable hypercube, leading to faster communication and lower latency in data transmission. This reduction in diameter results in an overall enhancement of network efficiency, making these variants highly advantageous in large-scale distributed computing. In [17], the construction of these hypercube variants was explored in depth. Specifically, the study utilized three distinct structures—twisted cubes, locally twisted cubes, and crossed cubes—as fundamental clusters in the development of DQcube variants. These clusters serve as building blocks that improve upon the traditional hypercube by introducing modifications in connectivity patterns, ultimately enhancing network performance while maintaining desirable properties such as regularity, symmetry, and fault tolerance. Now, we provide a detailed introduction and analysis of these hypercube variants, explaining their structural characteristics, their advantages over traditional hypercubes, and their applicability in advanced networking models.

Twisted cubes, a specialized variant of hypercubes, are introduced as follows. The node set of an n-dimensional twisted cube, denoted as $T{Q}_n$, consists of all binary strings of length n, where n is an odd integer. This means that each node in the twisted cube network corresponds to a unique binary string representation of length n, making it structurally similar to a hypercube but with distinct modifications that enhance its properties. To formally define $T{Q}_n$, an important function known as the i-th bit parity function ${\mathcal{P}}_i\left(b\right)$ is introduced. This function plays a crucial role in determining the connectivity of nodes in the twisted cube structure. Given a binary string $b=b_{n-1}{b}_{n-2}\dots b_1{b}_0$, the i-th bit parity function ${\mathcal{P}}_i\left(b\right)$ is defined for any index i satisfying $n-1\ge i\ge 0$ as follows: ${\mathcal{P}}_i\left(b\right)=b_i\oplus b_{i-1}\oplus \dots \oplus b_1\oplus b_0$, where ⊕ represents the exclusive-or (XOR) operation.

This function essentially determines a new bit value based on the cumulative XOR result of all bits from $b_i$ to $b_0$, thereby influencing how nodes are connected within the twisted cube topology.

To fully describe the structure of the n-dimensional twisted cube $T{Q}_n$, we present its recursive definition. For any odd integer $n\ge 1$, the twisted cube network is defined using a recursive construction that progressively builds higher-dimensional versions of $T{Q}_n$ by leveraging the structural properties of lower-dimensional twisted cubes. This recursive definition is fundamental in understanding how twisted cubes maintain their advantageous properties, such as reduced diameter, efficient routing, and enhanced fault tolerance, compared to standard hypercubes.

Definition 4

(see [5,179]). $T{Q}_1$ is the complete graph with two nodes labeled by 0 and 1, respectively. For an odd integer $n\ge 3$, $T{Q}_n$ consists of four copies of $T{Q}_{n-2}$. We use $T{Q}_{n-2}^{ij}$ to denote an $(n-2)$-dimensional twisted cube which is a subgraph of $T{Q}_n$ induced by the nodes labeled by $ij{b}_{n-3}{b}_{n-4}\dots b_1{b}_0$, where $i,j\in \{0,1\}$. Links that connect these four subtwisted cubes can be described as follows:

Each node $b=b_{n-1}{b}_{n-2}\dots b_1{b}_0 \in V\left(T{Q}_n\right)$ is adjacent to ${\overline{b}}_{n-1}{b}_{n-2}\dots b_1{b}_0$ and ${\overline{b}}_{n-1}{\overline{b}}_{n-2}\dots b_1{b}_0$ if ${\mathcal{P}}_{n-3}\left(b\right)=0$, and it is adjacent to ${\overline{b}}_{n-1}{b}_{n-2}\dots b_1{b}_0$ and $b_{n-1}{\overline{b}}_{n-2}\dots b_1{b}_0$ if ${\mathcal{P}}_{n-3}\left(b\right)=1$.

For example, Figure 5 shows $T{Q}_3$ and $T{Q}_5$ constructed from four $T{Q}_3$’s. By the above formal definition of the twisted cube, the n-dimensional twisted cube $T{Q}_n$ possesses regularity properties that make it a structured and predictable n-regular network. Specifically, it is characterized as an n-regular network, meaning that each node in $T{Q}_n$ has exactly n neighbors, ensuring uniform connectivity across the entire network. The total number of vertices (nodes) in the twisted cube network $T{Q}_n$ is $|V\left(T{Q}_n\right)|=2^n$, which follows directly from the fact that each node corresponds to a unique binary string of length n. Similarly, the total number of edges (connections between nodes) in $T{Q}_n$ is determined as $|E\left(T{Q}_n\right)|=n\times 2^{n-1}$, indicating that the network maintains a balanced and structured edge distribution. This structural regularity allows for efficient data routing, parallel processing, and fault-tolerant communication within the network. In addition to these fundamental properties, the diameter of the twisted cube network is given by

$$diam\left(T{Q}_n\right)=\lceil {\displaystyle \frac{n+1}{2}}\rceil ,$$

(5)

where it has been computed in [5] and $\lceil ·\rceil$ represents the ceiling function, ensuring that the diameter is always rounded up to the nearest integer. This means that, at most, any two nodes in $T{Q}_n$ are separated by approximately half the total number of dimensions, which is a significant improvement over standard hypercubes. Furthermore, the twisted cube is Hamiltonian connected, meaning that there exists a Hamiltonian path between any two nodes, allowing for highly efficient traversal and routing across the network [5,180].

Figure 5. (a) The 3-dimensional twisted cube $T{Q}_3$, and (b) the 5-dimensional twisted cube $T{Q}_5$ consisting of $T{Q}_3^{00}$, $T{Q}_3^{10}$, $T{Q}_3^{01}$, $T{Q}_3^{11}$, where the leading two bits of nodes are underlined [17].

Figure 5. (a) The 3-dimensional twisted cube $T{Q}_3$, and (b) the 5-dimensional twisted cube $T{Q}_5$ consisting of $T{Q}_3^{00}$, $T{Q}_3^{10}$, $T{Q}_3^{01}$, $T{Q}_3^{11}$, where the leading two bits of nodes are underlined [17].

Using the same construction principles applied to $DQ(m,d,n)$, we extend the compound network model to introduce a new variant, called the DTcube. This network is denoted as $DT(m,d,n)$ and is constructed by combining a disc-ring network $D(m,d)$ with a twisted cube $T{Q}_n$ following the conditions of Equation (2), and n is an odd integer. This constraint ensures that the degree of the disc-ring network aligns properly with the node number of the twisted cube, allowing for a seamless integration between the two structures. As an example, Figure 6 provides a visual representation of a partial DTcube network, specifically $DT(8,6,3)$. This figure illustrates how the disc-ring topology is connected to the twisted cube clusters, demonstrating the efficient and scalable design of the DTcube compound network.

Figure 6. The remote links of cluster 00 in DTcube $DT(8,6,3)$ [17].

Figure 6. The remote links of cluster 00 in DTcube $DT(8,6,3)$ [17].

The locally twisted cube is a variation of the twisted cube that incorporates local modifications to further optimize connectivity, reduce network diameter, and improve fault tolerance. It retains the fundamental structure of a hypercube but introduces localized twists in the connectivity pattern to achieve better network properties. The n-dimensional locally twisted cube $LT{Q}_n$ has the same number of nodes as a standard n-dimensional hypercube or twisted cube, meaning the node set consists of all possible binary strings of length n. However, the primary difference lies in how nodes are connected locally. The major difference is in the neighboring node connections, where local twists are introduced to reduce the longest shortest path between nodes (network diameter) while maintaining key structural properties such as symmetry and regularity. These local twists modify how nodes are connected at specific bit positions, ensuring that the network remains balanced and optimized for parallel processing. The formal definition of locally twisted cube is as follows.

Definition 5

(see [67,181]). The n-dimensional locally twisted cube $LT{Q}_n$ is defined recursively as follows:

(1) $LT{Q}_2$ is a network consisting of four nodes labeled with 00, 01, 10, and 11, respectively, connected by four links $(00,01)$, $(00,10)$, $(01,11)$, and $(10,11)$.

(2) For $n\ge 3$, $LT{Q}_n$ is built from two disjoint copies $LT{Q}_{n-1}$ according to the following steps. Let $LT{Q}_{n-1}^0$ denote the network obtained by prefixing the label of each node of one copy of $LT{Q}_{n-1}$ with 0, let $LT{Q}_{n-1}^1$ denote the network obtained by prefixing the label of each node of the other copy of $LT{Q}_{n-1}$ with 1, and connect each node $b=0b_{n-2}{b}_{n-3}\dots b_1{b}_0$ of $LT{Q}_{n-1}^0$ with the node $1(b_{n-2}\oplus b_0)b_{n-3}\dots b_1{b}_0$ of $LT{Q}_{n-1}^1$ by a link, where ‘⊕’ represents the modulo 2 addition. For example, Figure 7 depicts $LT{Q}_3$ and $LT{Q}_4$ constructed from two $LT{Q}_3$’s.

Figure 7. (a) The 3-dimensional locally twisted cube $LT{Q}_3$, and (b) the 4-dimensional locally twisted cube $LT{Q}_4$ consisting of sublocally twisted cubes $LT{Q}_3^0$ and $LT{Q}_3^1$, where the leading bits of nodes are underlined [17].

Figure 7. (a) The 3-dimensional locally twisted cube $LT{Q}_3$, and (b) the 4-dimensional locally twisted cube $LT{Q}_4$ consisting of sublocally twisted cubes $LT{Q}_3^0$ and $LT{Q}_3^1$, where the leading bits of nodes are underlined [17].

The diameter of $LT{Q}_n$ has been computed in [67] and is

$$diam\left(LT{Q}_n\right)=\lceil {\displaystyle \frac{n+3}{2}}\rceil .$$

(6)

Like a hypercube, $LT{Q}_n$ remains n-regular, meaning each node has exactly n links. Locally twisted cube $LT{Q}_n$ also provides more fault tolerance and admits Hamiltonian connected for $n\ge 3$, meaning there exists a Hamiltonian path between any two nodes, ensuring efficient routing. In addition, $LT{Q}_n$ contains two edge-disjoint Hamiltonian cycles for $n\ge 4$.

The locally twisted cube $LT{Q}_n$ can be used to construct compound networks like the DLcube, similar to the DQcube or DTcube, where it replaces the traditional hypercube or twisted cube as the unit cluster. The resultant network benefits from the enhanced properties of $LT{Q}_n$, such as lower diameter and improved connectivity. A compound network DLcube is constructed from disc-ring network $D(m,d)$ and locally twisted cube $LT{Q}_n$ and is characterized by $DL(m,d,n)$, where $d+2=2^n$ (Equation (2)). For example, Figure 8 depicts the remote links of cluster 00 in $DL(8,6,3)$.

Finally, we introduce another variant, crossed cubes, of hypercubes and the compound architecture constructed from them and disc-ring networks. A crossed cube, denoted as $C{Q}_n$, is an n-dimensional interconnection network that is constructed recursively [76]. This network serves as an alternative to traditional hypercubes, offering benefits in terms of reducing the average shortest path length while maintaining many of the connectivity and robustness features of hypercubes. Each node in the n-dimensional crossed cube $C{Q}_n$ is also labeled by a binary string of length n, i.e., $V\left(C{Q}_n\right)=V\left(Q_n\right)$. This means that for any given dimension n, there are exactly $2^n$ nodes in the structure, similar to a standard hypercube. Each node’s binary string representation determines its position in the network and its connections to other nodes. The recursive construction of $C{Q}_n$ is as follows. Initially, $C{Q}_1$ contains a link whose two end nodes are labeled with 0 and 1, respectively, and $C{Q}_2$ is isomorphic to a two-dimensional hypercube. For dimensions $n\ge 3$, the n-dimensional crossed cube $C{Q}_n$ is obtained by combining two copies of the $(n-1)$-dimensional crossed cube $C{Q}_{n-1}$. These two copies, referred to as $C{Q}_{n-1}^0$ and $C{Q}_{n-1}^0$, are structurally identical but are connected in a specific manner using $2^{n-1}$ additional links, where the labels of nodes in $C{Q}_{n-1}^0$ are preceded by 0, while the labels of nodes in $C{Q}_{n-1}^1$ are preceded by 1. There is a link joining a node $u=0u_{n-2}{u}_{n-3}\dots u_1{u}_0$ in $C{Q}_{n-1}^0$ with another node $v=1v_{n-2}{v}_{n-3}\dots v_1{v}_0$ in $C{Q}_{n-1}^1$ if and only if $\langle u_{2i+1}{u}_{2i},v_{2i+1}{v}_{2i}\rangle \in \{\langle 00,00\rangle ,\langle 10,10\rangle ,\langle 01,11\rangle ,\langle 11,01\rangle \}$ for all $\lfloor {\displaystyle \frac{n-1}{2}}\rfloor -1\ge i\ge 0$, and $u_{n-2}=v_{n-2}$ if n is even. The formally definition of $C{Q}_n$ is as follows.

Figure 8. The remote links of cluster 00 in DLcube $DL(8,6,3)$ [17].

Figure 8. The remote links of cluster 00 in DLcube $DL(8,6,3)$ [17].

Definition 6

(see [76]). The n-dimensional crossed cube $C{Q}_n$ is defined recursively as follows:

(1) $C{Q}_1$ contains a link whose two end nodes are labeled with 0 and 1, respectively, and $C{Q}_2$ is isomorphic to a two-dimensional hypercube.

(2) For $n\ge 3$, $C{Q}_n$ is built from two disjoint copies $C{Q}_{n-1}$ according to the following steps. Let $C{Q}_{n-1}^0$ denote the network obtained by prefixing the label of each node of one copy of $C{Q}_{n-1}$ with 0, and let $C{Q}_{n-1}^1$ denote the network obtained by prefixing the label of each node of the other copy of $C{Q}_{n-1}$ with 1. There is a link joining a node $u=0u_{n-2}{u}_{n-3}\dots u_1{u}_0$ in $C{Q}_{n-1}^0$ with another node $v=1v_{n-2}{v}_{n-3}\dots v_1{v}_0$ in $C{Q}_{n-1}^1$ if and only if $\langle u_{2i+1}{u}_{2i},v_{2i+1}{v}_{2i}\rangle \in \{\langle 00,00\rangle ,\langle 10,10\rangle ,\langle 01,11\rangle ,\langle 11,01\rangle \}$ for all $\lfloor {\displaystyle \frac{n-1}{2}}\rfloor -1\ge i\ge 0$ for all $\lfloor {\displaystyle \frac{n-1}{2}}\rfloor -1\ge i\ge 0$, and $u_{n-2}=v_{n-2}$ if n is even. For example, Figure 9 depicts $C{Q}_3$ and $C{Q}_4$.

Figure 9. (a) The 3-dimensional crossed cube $C{Q}_3$, and (b) the 4-dimensional crossed cube $C{Q}_4$ consisting of $C{Q}_3^0$ and $C{Q}_3^1$, where the leading bits of nodes are underlined [17].

Figure 9. (a) The 3-dimensional crossed cube $C{Q}_3$, and (b) the 4-dimensional crossed cube $C{Q}_4$ consisting of $C{Q}_3^0$ and $C{Q}_3^1$, where the leading bits of nodes are underlined [17].

The diameter of the crossed cube has been computed in [76] and is as follows:

$$diam\left(C{Q}_n\right)=\lceil {\displaystyle \frac{n+1}{2}}\rceil .$$

(7)

Furthermore, it has been observed that the same Hamiltonian properties hold for locally twisted cubes as well. These properties make both crossed cubes and locally twisted cubes highly useful in network topology designs. By following a similar construction methodology to that used for the development of the DQcube, we can design and construct a new type of compound network known as the DCcube [17]. The DCcube is fundamentally a compound network formed by integrating the disc-ring network $D(m,d)$ and the crossed cube $C{Q}_n$. The resulting structure is characterized by the notation $DC(m,d,n)$, where the relationship $d+2=2^n$ holds. This relationship defines the structural parameters of the DCcube and ensures a balanced and efficient network design. The construction constraints and methodological framework used for the DCcube remain consistent with those applied in the development of the DQcube, ensuring a structured and predictable network topology. Furthermore, the methodology for constructing remote links in the DCcube follows the same principles as that of the DQcube. These remote links play a crucial role in enhancing connectivity and reducing communication latency within the network. For instance, Figure 10 illustrates the remote links associated with cluster 00 in a specific instance of the DCcube, namely, $DC(8,6,3)$. This figure provides a visual representation of how remote links are established and highlights the structural similarities between the DCcube and DQcube. Through this approach, the DCcube emerges as a structured and well-defined compound network that inherits beneficial properties from both the disc-ring network and the crossed cube, making it a viable choice for efficient interconnection networks.

Figure 10. The remote links of cluster 00 in DCcube $DC(8,6,3)$ [17].

Figure 10. The remote links of cluster 00 in DCcube $DC(8,6,3)$ [17].

3. The Known Results for the Connectivity of the DVcube

This section aims to review the known results for the network parameters, including diameter, node connectivity, and h-extra connectivity, of the networks introduced in Section 2. In [17], we provided an upper bound of $diam\left(D\right(m,d\left)\right)$ as follows:

$$diam\left(D(m,d)\right)\le \lceil {\displaystyle \frac{m}{d-1}}\rceil +2.$$

(8)

It follows from the upper bound of $diam\left(D\right(m,d\left)\right)$; the upper bounds of $diam\left(DQ\right(m,d,$$n\left)\right)$, $diam\left(DT\right(m,d,n\left)\right)$, $diam\left(DL\right(m,d,n\left)\right)$, and $diam\left(DC\right(m,d,n\left)\right)$ were provided in [17].

By the definition of the studied networks in Section 2, their order (# of nodes), size (# of links), and node degree can be easily computed. In the past, many scholars [5,18,53,67,68,76,77] studied the network parameters, including diameter, node connectivity, edge connectivity, and h-extra connectivity, of $Q_n$, $T{Q}_n$, $LT{Q}_n$, and $C{Q}_n$. Yang and Meng [34] computed the h-extra connectivity of hypercube $Q_n$ to be $n(h+1)-2h-\left({\displaystyle \genfrac{}{}{0pt}{}{h}{2}}\right)$, where $\left({\displaystyle \genfrac{}{}{0pt}{}{h}{2}}\right)$ is the combination number. In [155], the h-extra connectivity of n-dimensional twisted hypercube is computed as $n(h+1)-{\displaystyle \frac{1}{2}}h(h+3)$. However, n-dimensional twisted hypercube is not $T{Q}_n$ defined here. Wang and Ren [68] computed the h-extra connectivity of locally twisted cube $LT{Q}_n$ to be $n-{\displaystyle \frac{1}{2}}h(h-2n+3)$. And the h-extra connectivity of crossed cube $C{Q}_n$ was computed to be $n(h+1)-{\displaystyle \frac{1}{2}}h(h+3)$ in [182]. For the compound network DQcube $DQ(m,d,n)$, Lv et al. [169] computed its node connectivity and tightly super connectivity to be $n+1$. The above related results are summarized in

Table 3. Known network parameters of the studied networks, where ‘?’ represents the unknown result.

Network G	Order (# of Nodes)	Size (# of Links)	Node Degree	Diameter	Node Connectivity ($\mathit{\kappa }\left(\mathit{G}\right)$)	h-Extra Connectivity (${\mathit{\kappa }}_{\mathit{h}}\left(\mathit{G}\right)$)
disc-ring $D(m,d)$	$2m$	$m(d+2)$	$d+2$	$\le \lfloor {\displaystyle \frac{m}{d-1}}\rfloor +2$ [17]	?	?
hypercube $Q_n$	$2^n$	$n{2}^{n-1}$	n	n [18]	n [18]	$n(h+1)-2h-\left({\displaystyle \genfrac{}{}{0pt}{}{h}{2}}\right)$ [34]
twisted cube $T{Q}_n$	$2^n$	$n{2}^{n-1}$	n	$\lceil {\displaystyle \frac{n+1}{2}}\rceil$ [5]	n [53,54]	?
locally twisted cube $LT{Q}_n$	$2^n$	$n{2}^{n-1}$	n	$\lceil {\displaystyle \frac{n+3}{2}}\rceil$ [67]	n [68]	$n-{\displaystyle \frac{1}{2}}h(h-2n+3)$ [68]
crossed cube $C{Q}_n$	$2^n$	$n{2}^{n-1}$	n	$\lceil {\displaystyle \frac{n+1}{2}}\rceil$ [4,76]	n [77]	$n(h+1)-{\displaystyle \frac{1}{2}}h(h+3)$ [182]
DQcube $DQ(m,d,n)$	$m{2}^{n+1}$	$(n+1)m{2}^n$	$n+1$	$\le (n+1)\lfloor {\displaystyle \frac{m}{d-1}}\rfloor +3n+2$ [17]	$n+1$ [169]	$(n+1)(h+1)-{\displaystyle \frac{1}{2}}h(h+2)$ [170]
DTcube $DT(m,d,n)$	$m{2}^{n+1}$	$(n+1)m{2}^n$	$n+1$	$\le \lceil {\displaystyle \frac{n+3}{2}}\rceil \lfloor {\displaystyle \frac{m}{d-1}}\rfloor +\lceil {\displaystyle \frac{3n+7}{2}}\rceil$ [17]	?	?
DLcube $DL(m,d,n)$	$m{2}^{n+1}$	$(n+1)m{2}^n$	$n+1$	$\le \lceil {\displaystyle \frac{n+5}{2}}\rceil \lfloor {\displaystyle \frac{m}{d-1}}\rfloor +\lceil {\displaystyle \frac{3n+13}{2}}\rceil$ [17]	?	?
DCcube $DC(m,d,n)$	$m{2}^{n+1}$	$(n+1)m{2}^n$	$n+1$	$\le \lceil {\displaystyle \frac{n+3}{2}}\rceil \lfloor {\displaystyle \frac{m}{d-1}}\rfloor +\lceil {\displaystyle \frac{3n+7}{2}}\rceil$ [17]	?	?

.

Since every above studied network G satisfies ${\Sigma }_{v\in V\left(G\right)}de{g}_G\left(v\right)=2\left|E\left(G\right)\right|$, where $de{g}_G\left(v\right)$ is the degree of node v in G, and it is regular and undirected, the number of links can be easily computed. It follows from Table 3 that many issues have not been resolved or only upper bounds of parameters in some studied networks are provided.

4. The Open Problems for the Connectivity of the DVcube

In Table 3, there are many unresolved problems for the connectivity and its variants of the DVcube, including the DTcube, DLcube, and DCcube. In this section, we provide some conjectures for them.

4.1. The Conjectures for the Diameter and Connectivity of Disc-Ring Networks

In [17], we provided an upper bound of diameter for disc-ring network $D(m,d)$. That is, $diam\left(D(m,d)\right)\le \lfloor {\displaystyle \frac{m}{d-1}}\rfloor +2$. In this subsection, we first attempt to compute $diam\left(D\right(m,d\left)\right)$. When $d=1$, it is easy to verify that $diam\left(D(m,1)\right)=\lfloor {\displaystyle \frac{m}{2}}\rfloor +1$. In the following, assume that $d\ge 2$. Based on the symmetry of the disc-ring network structure, we can select an outer ring node $v_0$ labeled by 00 as the reference point. According to the ring architecture, we know that the node furthest from $v_0$ is either $v_a=1\lfloor {\displaystyle \frac{m}{2}}\rfloor$ or $v_c=0\lfloor {\displaystyle \frac{m}{2}}\rfloor$, as shown in Figure 11. Then, starting from $v_0$, we follow a path $v_0\to 1(d-1)\to 0(d-1)\to \dots \to 1\left((k-1)(d-1)\right)\to 0\left((k-1)(d-1)\right)\to 1\left(k(d-1)\right)$ so that $v_a\in N\left(1\left(k(d-1)\right)\right)$ or $v_a\in N\left(0\left((k-1)(d-1)\right)\right)$, as shown in Figure 11. Consider the following two cases:

Case 1: $v_a\in N\left(1\left(k(d-1)\right)\right)$. Then, $dist(v_0,v_a)=2k$ and $dist(v_0,v_c)=2k+1$. Therefore, $diam\left(D\right(m,d\left)\right)=2k+1$. In this case, $k(d-1)+1=\lfloor {\displaystyle \frac{m}{2}}\rfloor$, and hence, $diam(D(m,d)=2k+1=2{\displaystyle \frac{\lfloor \frac{m}{2}\rfloor -1}{d-1}}+1$ (see Figure 11a). For example, $diam\left(D(6,3)\right)=2{\displaystyle \frac{\lfloor \frac{m}{2}\rfloor -1}{d-1}}+1=2{\displaystyle \frac{\lfloor \frac{6}{2}\rfloor -1}{3-1}}+1=3$ and $diam\left(D(5,2)\right)=2{\displaystyle \frac{\lfloor \frac{m}{2}\rfloor -1}{d-1}}+1=2{\displaystyle \frac{\lfloor \frac{5}{2}\rfloor -1}{2-1}}+1=3$ (see Figure 1).

Case 2: $v_a\in N\left(1\left((k-1)(d-1)\right)\right)$. Then, $dist(v_0,v_a)=2k-1$ and $dist(v_0,v_c)=2k$. Therefore, $diam\left(D\right(m,d\left)\right)=2k$. In this case, $k(d-1)\ge \lfloor {\displaystyle \frac{m}{2}}\rfloor$, and hence, $diam(D(m,d)=2k\ge 2{\displaystyle \frac{\lfloor \frac{m}{2}\rfloor }{d-1}}$. In this case, we can route a path from $v_0$ to $v_c$ with length $2{\displaystyle \frac{\lfloor \frac{m}{2}\rfloor }{d-1}}$, no path from $v_0$ to $v_c$ with length $2<{\displaystyle \frac{\lfloor \frac{m}{2}\rfloor }{d-1}}$, and, hence, $diam((D(m,d)=2{\displaystyle \frac{\lfloor \frac{m}{2}\rfloor }{d-1}}$ (see Figure 11b).

Figure 11. The diameter and routing of $D(m,d)$ for (a) $v_a(=0\lfloor {\displaystyle \frac{m}{2}}\rfloor )\in N\left(1\left(k(d-1)\right)\right)$ and (b) $v_a\in N\left(1\left((k-1)(d-1)\right)\right)$.

Figure 11. The diameter and routing of $D(m,d)$ for (a) $v_a(=0\lfloor {\displaystyle \frac{m}{2}}\rfloor )\in N\left(1\left(k(d-1)\right)\right)$ and (b) $v_a\in N\left(1\left((k-1)(d-1)\right)\right)$.

It follows from the above brief discussion that we make the following conjecture:

Conjecture 1.

Let $D(m,d)$ be a disc-ring network. If $d=1$, then $diam\left(D(m,d)\right)=\lfloor {\displaystyle \frac{m}{2}}\rfloor +1$; otherwise, $diam\left(D(m,d)\right)=2{\displaystyle \frac{\lfloor \frac{m}{2}\rfloor -1}{d-1}}+1$ or $2{\displaystyle \frac{\lfloor \frac{m}{2}\rfloor }{d-1}}$.

We now proceed to analyze in greater detail the (node) connectivity and edge connectivity characteristics of the disc-ring network $D(m,d)$. Our investigation begins with a preliminary observation regarding the fundamental connectivity properties of a basic ring network R. Specifically, if we remove any two vertices or any two links from such a ring structure, the result is the fragmentation of the ring into at least two disjoint subrings, thereby causing disconnection. This observation leads us to conclude that the node connectivity $\kappa \left(R\right)$ and the edge connectivity $\lambda \left(R\right)$ of the ring network R are both equal to 2. In other words, at least two nodes or edges must be removed to break the ring’s connectivity. Next, we extend this line of reasoning to more complex structures, namely, the network $D(m,d)$, which is derived from ring-based topologies but exhibits a higher degree of regularity and robustness. From their respective construction principles, it is evident that each of these networks is $(d+2)$-regular, meaning that every node is connected to exactly $d+2$ other nodes. This regularity plays a key role in determining the networks’ fault tolerance and resilience to disconnection. Given this $(d+2)$-regularity, removing $d+2$ edges will cause the network to be disconnected. Therefore, we can infer that the edge connectivity of $D(m,d)$ network satisfies the following inequality:

$$\lambda \left(D\right(m,d\left)\right)\le d+2.$$

(9)

Moreover, an analogous argument applies to node removal. The presence of a node cut of size $d+2$ that separates the network into disconnected components implies that the node connectivity satisfies the following inequality:

$$\kappa \left(D\right(m,d\left)\right)\le d+2.$$

(10)

Consider Figure 12 showing network $D(6,3)$. This figure shows a node cut of size $d+1$. The presence of such node cuts provides strong evidence for the network’s resilience while also posing interesting theoretical challenges. In light of these observations, the primary objective of this survey is to rigorously verify and potentially prove the conjecture regarding the exact values of the connectivity and edge connectivity of $D(m,d)$. This verification would contribute valuable insights into the structural robustness of these network topologies and their applicability in designing fault-tolerant systems. Then, we make the following conjecture.

Figure 12. (a) A disc-ring $D(6,3)$, and (b) the resultant network by removing 3 + 1 (=$d+1$) nodes from $D(6,3)$.

Figure 12. (a) A disc-ring $D(6,3)$, and (b) the resultant network by removing 3 + 1 (=$d+1$) nodes from $D(6,3)$.

Conjecture 2.

Let $D(m,d)$ be a disc-ring network. Then, $\kappa \left(D\right(m,d\left)\right)=d+1$ and $\gamma \left(D\right(m,d\left)\right)$$=d+2$.

In the next phase of our study, we shift our focus to analyzing the h-extra connectivity of the disc-ring network. The concept of h-extra connectivity provides a more refined measure of a network’s fault tolerance, not just capturing whether a network can be disconnected but also imposing additional conditions on the size of the remaining components after node failures. This makes it a useful metric for evaluating the robustness of networks in practical scenarios. To develop some foundational understanding, let us begin by examining a simple ring network $C_n$, which consists of n nodes connected in a closed loop, where each node is linked to exactly two neighbors. For such a ring, we can observe the behavior of its h-extra connectivity ${\kappa }_h\left(C_n\right)$. Specifically, if the number of nodes n in the ring is less than or equal to $2(h+1)+2$, then the network is so small and tightly connected that disconnecting it while meeting the h-extra condition requires removing all nodes, resulting in ${\kappa }_h\left(C_n\right)=n$. In contrast, if $n>2(h+1)+2$, the structure allows for more flexibility in how components can be separated, and the h-extra connectivity drops to a value of 2, i.e., ${\kappa }_h\left(C_n\right)=2$. This fundamental observation about the ring network forms the basis of our next objective. Motivated by the behavior of ${\kappa }_h\left(C_n\right)$, we aim to extend the analysis to more complex topology $D(m,d)$. In particular, our goal is to formally establish a conjecture that characterizes the h-extra connectivity for the disc-ring network, a structure that enhances the simple ring by introducing additional interconnections or layers. By doing so, we hope to gain deeper insight into how the network’s resilience scales with increasing size and complexity, and how it compares to the basic ring in terms of fault tolerance under the h-extra model. We then make the following conjecture for readers.

Conjecture 3.

Let $D(m,d)$ be a disc-ring network. Then,

$${\kappa }_h\left(D(m,d)\right)=\left\{\begin{array}{cc}2d\hfill & ,if2m\ge 2(h+1)+2d,i.e.,m-d\ge h+1;\hfill \\ 2m\hfill & ,otherwise.\hfill \end{array}\right.$$

For example, Figure 13 depicts two-extra connectivity of $D(6,3)$, where $m-d(=6-3)\ge h+1(=2+1)$.

Figure 13. (a) A disc-ring $D(6,3)$, and (b) the resultant network by removing $2\times 3(=2\times d)$ nodes from $D(6,3)$.

Figure 13. (a) A disc-ring $D(6,3)$, and (b) the resultant network by removing $2\times 3(=2\times d)$ nodes from $D(6,3)$.

We finally consider the tightly super connectivity of disc-ring network $D(m,d)$. By the definition of $D(m,d)$ network, it is $(d+2)$-regular. Thus, for each node u in $D(m,d)$ we must remove at least $d+2$ nodes which are the adjacent nodes of u from the network to obtain two connected components such that one component contains only the isolated node u. Thus, we can obtain the following lemma.

Lemma 1.

Let $D(m,d)$ be a disc-ring network. Then, ${\kappa }_t\left(D(m,d)\right)=d+2$.

4.2. The Conjectures for the Connectivity of DVcube Networks

In this subsection of our study, we delve into a comprehensive analysis of several key structural properties of a class of compound interconnection networks collectively referred to as DVcubes. These include four specific variants: the DQcube, DTcube, DLcube, and DCcube. The properties under investigation are crucial indicators of a network’s efficiency, fault tolerance, and robustness. Specifically, we focus on examining the diameter, connectivity, tightly super connectivity, and h-extra connectivity of these DVcube networks. The diameter of a network, which is defined as the greatest distance between any pair of nodes (in terms of the shortest path), is a critical metric in evaluating communication delay and overall performance. In our earlier work, referenced as [17], we established upper bounds for the diameters of each of the DVcube variants. That is, we provided maximum values for the diameter of the networks $DQ(m,d,n)$, $DT(m,d,n)$, $DL(m,d,n)$, and $DC(m,d,n)$, based on their structural configurations and parameter settings. Now, building upon that foundation, we move toward the next logical step in our investigation. Assuming that Conjecture 1 is valid, we aim to determine the lower bounds for the diameters of these same networks. By finding both upper and lower bounds, we can more precisely characterize the tightness and range of the network diameters and better understand how they scale with different parameters. Furthermore, our analysis extends beyond just diameter to include connectivity and tightly super connectivity, which reflect the network’s resilience against node failures, as well as h-extra connectivity, which offers a stricter measure of fault tolerance by requiring the remaining components after node removal to satisfy additional size conditions. Through these studies, we anticipate formulating a new conjecture that summarizes our findings and potentially guides future exploration of these DVcube topologies. This upcoming conjecture, if validated, will contribute to the theoretical foundation of compound network design and optimization, providing valuable insights for both academic research and practical applications in distributed systems, parallel computing, and communication networks.

Conjecture 4.

Let $DQ(m,d,n)$, $DT(m,d,n)$, $DL(m,d,n)$, and $DC(m,d,n)$ be a DQcube, DTcube, DLcube, and DCcube, respectively. Then, $diam\left(DQ(m,d,n)\right)=(n+1)\lfloor {\displaystyle \frac{m}{d-1}}\rfloor +3n+2$, $diam\left(DT(m,d,n)\right)=\lceil {\displaystyle \frac{n+3}{2}}\rceil \lfloor {\displaystyle \frac{m}{d-1}}\rfloor +\lceil {\displaystyle \frac{3n+7}{2}}\rceil$, $diam\left(DL(m,d,n)\right)=\lceil {\displaystyle \frac{n+5}{2}}\rceil \lfloor {\displaystyle \frac{m}{d-1}}\rfloor +\lceil {\displaystyle \frac{3n+13}{2}}\rceil$, and $diam\left(DC(m,d,n)\right)=\lceil {\displaystyle \frac{n+3}{2}}\rceil \lfloor {\displaystyle \frac{m}{d-1}}\rfloor +\lceil {\displaystyle \frac{3n+7}{2}}\rceil$.

Next, we study the node and edge connectivity of $DT(m,d,n)$, $DL(m,d,n)$, and $DC(m,d,n)$. By similar arguments in computing $\kappa \left(DQ(m,d,n)\right)=n+1=de{g}_{DQ(m,d,n)}\left(v\right)$ for $v\in DQ(m,d,n)$ [169], we conjecture that $\kappa \left(\right(DT(m,d,n))=\kappa (\left(DL\right(m,d,n)=\kappa (\left(DC\right(m,$$d,n\left)\right)=n+1$. In addition, their edge connectivity is also conjectured as $\gamma \left(\right(DT(m,d,n))=\gamma (\left(DL\right(m,d,n\left)\right)=\gamma \left(\right(DC(m,d,n))=n+1$. We then make the following conjecture:

Conjecture 5.

Let $DQ(m,d,n)$, $DT(m,d,n)$, $DL(m,d,n)$, and $DC(m,d,n)$ be a DQcube, DTcube, DLcube, and DCcube, respectively. Then, $\kappa \left(DQ\right(m,d,n\left)\right)=\kappa \left(DT\right(m,d,n\left)\right)=\kappa \left(DL\right(m,$$d,n\left)\right)=\kappa \left(DC\right(m,d,n\left)\right)=n+1$ and $\lambda \left(DQ\right(m,d,n\left)\right)=\lambda \left(DT\right(m,d,n\left)\right)=\lambda \left(DL\right(m,d,n\left)\right)=\lambda \left(DC\right(m,d,n\left)\right)=n+1$.

We then study the tightly super connectivity of the DVcube. Recall that a tightly super connectivity of a network G is the minimum size of a node cut F such that $G-F$ contains exactly two connected components and one of which is an isolated node. In Table 3, every compound architecture $DQ(m,d,n)$, $DT(m,d,n)$, $DL(m,d,n)$, and $DC(m,d,n)$ is $(n+1)$-regular. Let v be a node in a DVcube G. By removing $N_G\left(v\right)$ from G, we can obtain two connected components such that v is an isolated node in the one remaining component. Thus, we make the following conjecture:

Conjecture 6.

Let $DQ(m,d,n)$, $DT(m,d,n)$, $DL(m,d,n)$, and $DC(m,d,n)$ be a DQcube, DTcube, DLcube, and DCcube, respectively. Then, ${\kappa }_t\left(DQ(m,d,n)\right)={\kappa }_t\left(DT(m,d,n)\right)={\kappa }_t\left(DL(m,d,n)\right)={\kappa }_t\left(DC(m,d,n)\right)=n+1$.

Finally, we study the h-extra connectivity of DVcube G. We conjecture that ${\kappa }_h\left(DQ(m,d,n)\right)={\kappa }_h\left(DT(m,d,n)\right)={\kappa }_h\left(DL(m,d,n)\right)={\kappa }_h\left(DC(m,d,n)\right)=(n+1)(h+1)-{\displaystyle \frac{1}{2}}h(h+2)$.

Conjecture 7.

Let $DT(m,d,n)$, $DL(m,d,n)$, and $DC(m,d,n)$ be a DTcube, DLcube, and DCcube, respectively. Then, ${\kappa }_h\left(DT(m,d,n)\right)={\kappa }_h\left(DL(m,d,n)\right)={\kappa }_h\left(DC(m,d,n)\right)=(n+1)(h+1)-{\displaystyle \frac{1}{2}}h(h+2)$.

In summary, we conclude the reviewed network parameters and their conjectures of disc-ring, hypercube-like networks, and the DVcube in

Table 4. The network parameters of the studied networks, where ‘??’ indicates our conjecture and is an open problem.

Network G	Diameter $\mathbf{diam}\left(\mathit{G}\right)$	Node Connectivity $\mathit{\kappa }\left(\mathit{G}\right)$	Edge Connectivity $\mathit{\gamma }\left(\mathit{G}\right)$	Tightly Super Connectivity ${\mathit{\kappa }}_{\mathit{t}}\left(\mathit{G}\right)$	h-Extra Connectivity ${\mathit{\kappa }}_{\mathit{h}}\left(\mathit{G}\right)$
disc-ring $D(m,d)$	$2{\displaystyle \frac{\lfloor \frac{m}{2}\rfloor -1}{d-1}}+1$ or $2{\displaystyle \frac{\lfloor \frac{m}{2}\rfloor }{d-1}}$(??)	$d+1$ (??)	$d+2$ (??)	$d+2$ (??)	$2d$ (??)
hypercube $Q_n$	n [18]	n	n	n	$n(h+1)-2h-\left({\displaystyle \genfrac{}{}{0pt}{}{h}{2}}\right)$ [34]
twisted cube $T{Q}_n$	$\lceil {\displaystyle \frac{n+1}{2}}\rceil$ [5]	n [53,54]	n [53]	n	$n(h+1)-{\displaystyle \frac{1}{2}}h(h+3)$??
locally twisted cube $LT{Q}_n$	$\lceil {\displaystyle \frac{n+3}{2}}\rceil$ [67]	n [68]	n	n	$n-{\displaystyle \frac{1}{2}}h(h-2n+3)$ [68]
crossed cube $C{Q}_n$	$\lceil {\displaystyle \frac{n+1}{2}}\rceil$ [4,76]	n [77]	n	n	$n(h+1)-{\displaystyle \frac{1}{2}}h(h+3)$ [182]
DQcube $DQ(m,d,n)$	$(n+1)\lfloor {\displaystyle \frac{m}{d-1}}\rfloor +3n+2$ (??)	$n+1$ [169]	$n+1$ (??)	$n+1$ [169]	$(n+1)(h+1)-{\displaystyle \frac{1}{2}}h(h+2)$ [170]
DTcube $DT(m,d,n)$	$\lceil {\displaystyle \frac{n+3}{2}}\rceil \lfloor {\displaystyle \frac{m}{d-1}}\rfloor +\lceil {\displaystyle \frac{3n+7}{2}}\rceil$ (??)	$n+1$ (??)	$n+1$ (??)	$n+1$ (??)	$(n+1)(h+1)-{\displaystyle \frac{1}{2}}h(h+2)$ (??)
DLcube $DL(m,d,n)$	$\lceil {\displaystyle \frac{n+5}{2}}\rceil \lfloor {\displaystyle \frac{m}{d-1}}\rfloor +\lceil {\displaystyle \frac{3n+13}{2}}\rceil$ (??)	$n+1$ (??)	$n+1$ (??)	$n+1$ (??)	$(n+1)(h+1)-{\displaystyle \frac{1}{2}}h(h+2)$ (??)
DCcube $DC(m,d,n)$	$\lceil {\displaystyle \frac{n+3}{2}}\rceil \lfloor {\displaystyle \frac{m}{d-1}}\rfloor +\lceil {\displaystyle \frac{3n+7}{2}}\rceil$ (??)	$n+1$ (??)	$n+1$ (??)	$n+1$ (??)	$(n+1)(h+1)-{\displaystyle \frac{1}{2}}h(h+2)$ (??)

.

4.3. The Future Trends for the Connectivity of the DVcube

If the DVcube has node connectivity k, then at least k nodes must fail simultaneously to disrupt the network. A higher value of k indicates stronger fault recovery capability, greater communication stability, and improved support for critical applications such as HPC, AI, and data centers. The key future trends regarding the connectivity of the DVcube in terms of topology robustness and network resilience are listed as follows:

• Resolve related connectivity open in Table 4: There are many open problems for the related connectivity of the DVcube except the DQcube. In the future, the first important work is to solve these open issues to enhance the usability of the DVcube.
• Increased fault tolerance: Future DVcube designs aim to maximize node or edge connectivity, making the network more resilient to node or edge failures. Under this premise, we can first study the node or link fault tolerance of the DVcube. The hybrid fault model design of the DVcube network, which combines node and link failures, will make the DVcube more robust.
• Topology-aware algorithms: Routing, scheduling, and load-balancing algorithms will increasingly exploit the structural properties of the DVcube to enhance connectivity-aware performance. This work will be another future work in improving the practicality of the DVcube.
• Self-healing and reconfigurable architectures: In the future, we could modify the DVcube network to incorporate a self-reconfiguration mechanism, allowing the system to reorganize itself if a critical node is lost, thereby mitigating the impact of disconnections.
• Enhanced structural analysis and construction: Future research can analyze and optimize connectivity properties (e.g., edge and node connectivity) to improve the design-time and runtime reliability of the DVcube. Furthermore, we can use the hypercube variants with better diameter to combine with the disc-ring network to build a compound architecture. These invariants of the hypercube include shuffle cube, spined cube, and Z-cube (see Table 2). The efficiency of the composite network built may be better than the current DVcube. This is one of the possible future works.

In summary, the future of DVcube connectivity lies in enhancing its robustness, supporting dynamic reconfiguration, and applying connection-aware optimization to ensure high availability and performance of its applications on modern computing systems. These works will be open for interested readers.

5. Concluding Remarks

The compound architecture of disc-ring and hypercube-like networks combines features of these two topologies to exploit their strengths, such as scalability, fault tolerance, and efficient communication. The compound architecture can be applied to high-performance computing data centers, telecommunication networks, and so on. The connectivity of a network has many practical applications across various fields. It can be applied to network design and analysis, transportation and logistics, social networks, electrical networks, biological networks, computer science, robotics and AI, security and resilience, and so on. When the connectivity of a network is greater, its reliability and fault tolerance are stronger. In this survey, we study the connectivity and its variants of a compound architecture which is constructed from disc-ring and hypercube-like networks. We make some conjectures on the diameter, connectivity, edge connectivity, tightly super connectivity, and h-extra connectivity of the disc-ring network and DVcube including the DQcube, DTcube, DLcube, and DCcube. These conjectures are still open for interested readers.