Gene Selection Algorithms in a Single-Cell Gene Decision Space Based on Self-Information
Abstract
1. Introduction
1.1. Research Background
1.2. Related Work
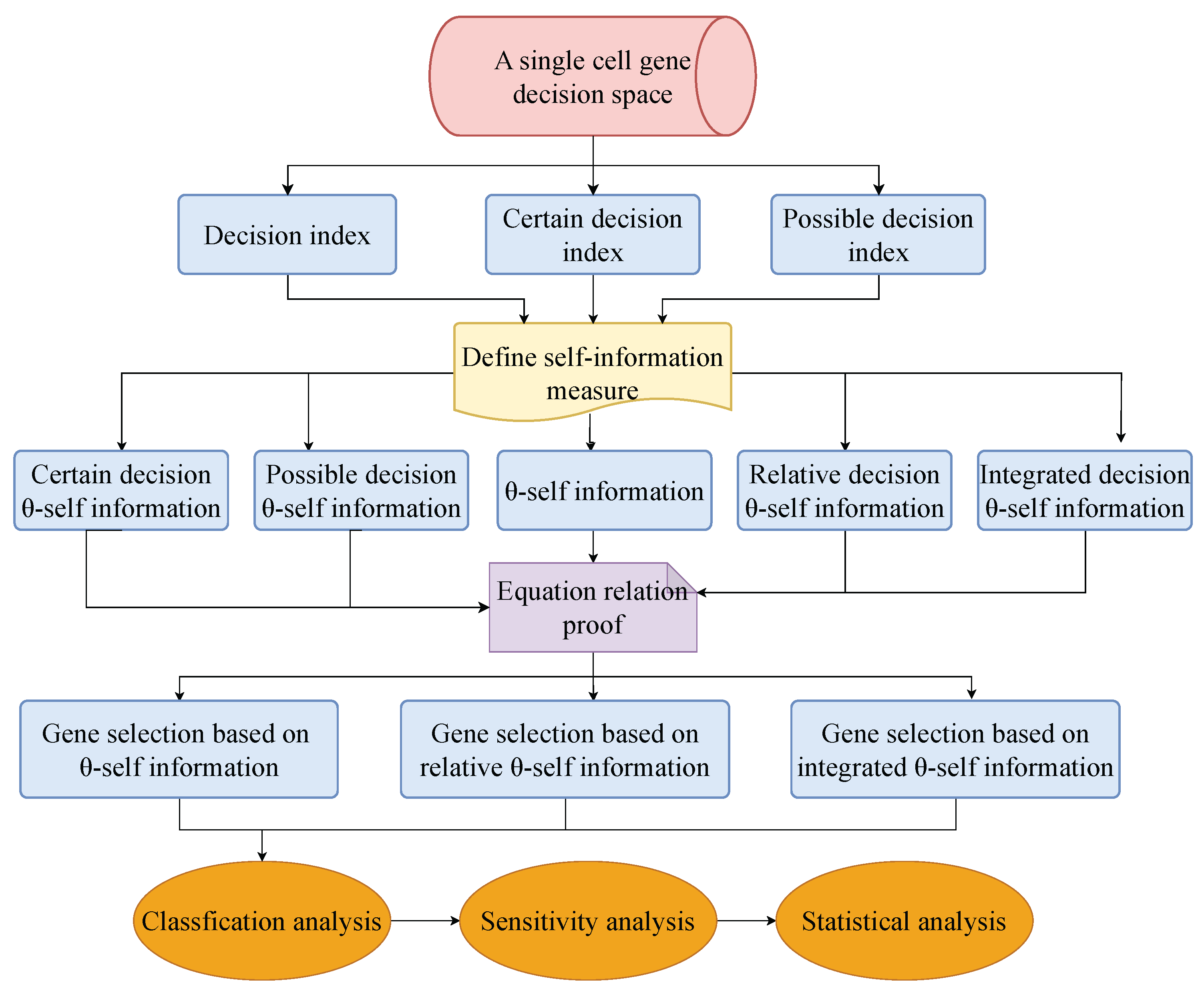
1.3. Motivation and Contributions
- (1)
- Given a subspace in the -space, the tolerance relation on the cell set is defined by introducing a variable parameter to control the distance between two gene expression values, which leads to the tolerance class. Rough approximations of this subspace are constructed. This overcomes the shortcomings of the traditional rough set model.
- (2)
- Five types of decision self-information measures as feature evaluation functions are proposed. The three feature evaluation functions with superior performance, self-information, relative self-information, and integrated self-information are chosen to design gene selection algorithms. The reason why they have superior performance is because they consider the classification information provided by both the upper and the lower approximations of the decision.
- (3)
- Three gene selection algorithms in an -space are put forward using the chosen self-information. These algorithms are demonstrated in several publicly available datasets for scRNA-seq. The experimental results show that these algorithms can effectively select gene subsets and outperform the existing algorithms.
1.4. Organization and Structure
2. A Single-Cell Gene Decision Space and Rough Set Model
- (1)
- If , then , ,
- (2)
- If , then , ,
- (1)
- If , then , ,
- (2)
- If , then ,
- (3)
- If , then , ,
3. Self-Information of a Subspace in an -Space
- (1)
- Non-negative: ;
- (2)
- If , then ;
- (3)
- If , then .
- (4)
- Strict monotonic: If , then .
- (1)
- -positive region of G with respect to d is known as
- (2)
- -dependence of G with respect to d is known as
- (1)
- If , then
- (2)
- If , then
- (3)
4. Gene Selection Algorithms in an -Space Based on Self-Information
4.1. Preliminaries
| Algorithm 1: An algorithm for selecting genes in an -space based on Fisher’s score |
 |
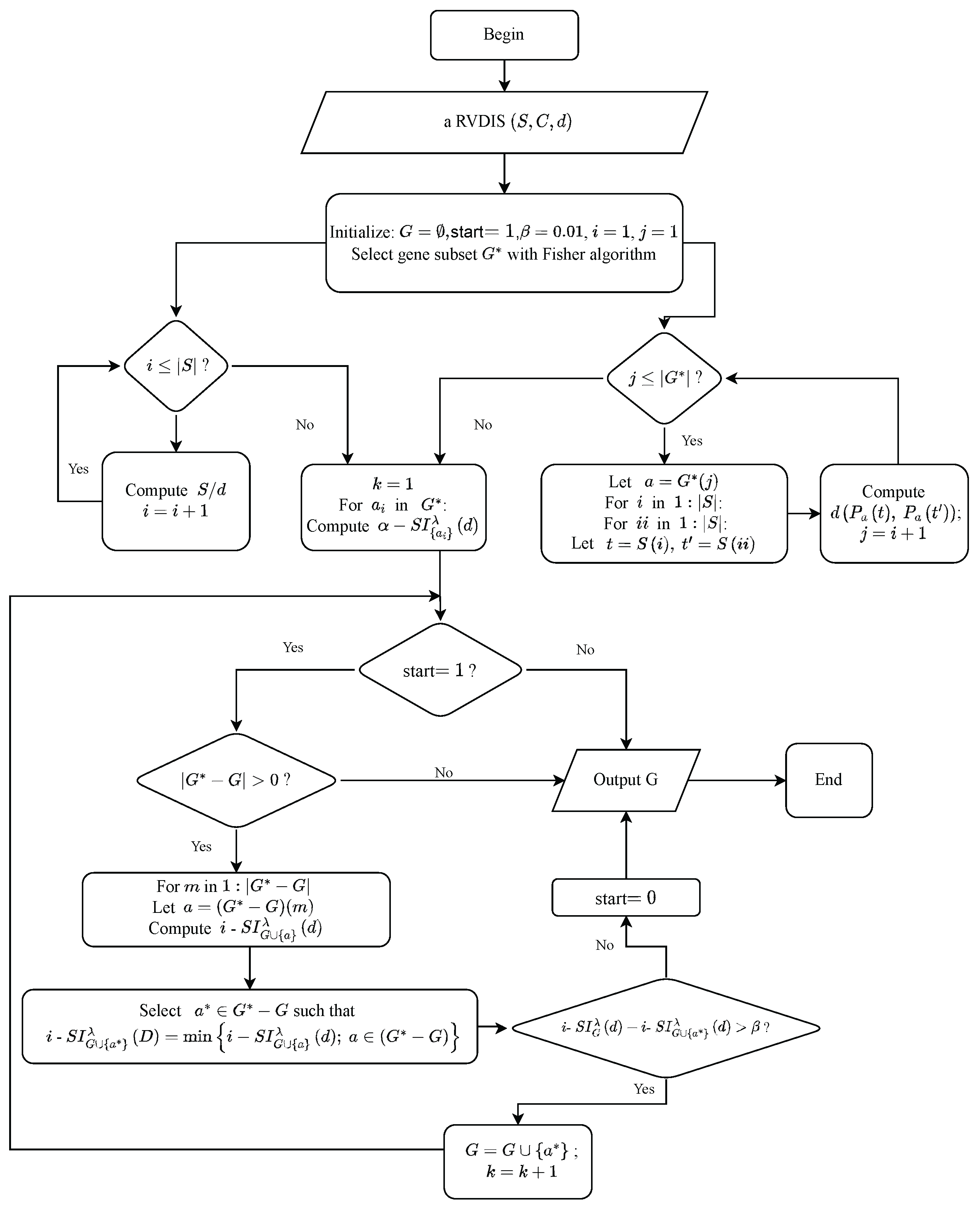
4.2. Gene Selection Algorithms
| Algorithm 2: A gene selection algorithm based on -self-information (F-) in an -space |
 |
| Algorithm 3: A gene selection algorithm based on relative -self-information (Fr-) in an -space |
 |
| Algorithm 4: A gene selection algorithm based on the integrated--self-information (Fi-) in an -space |
 |
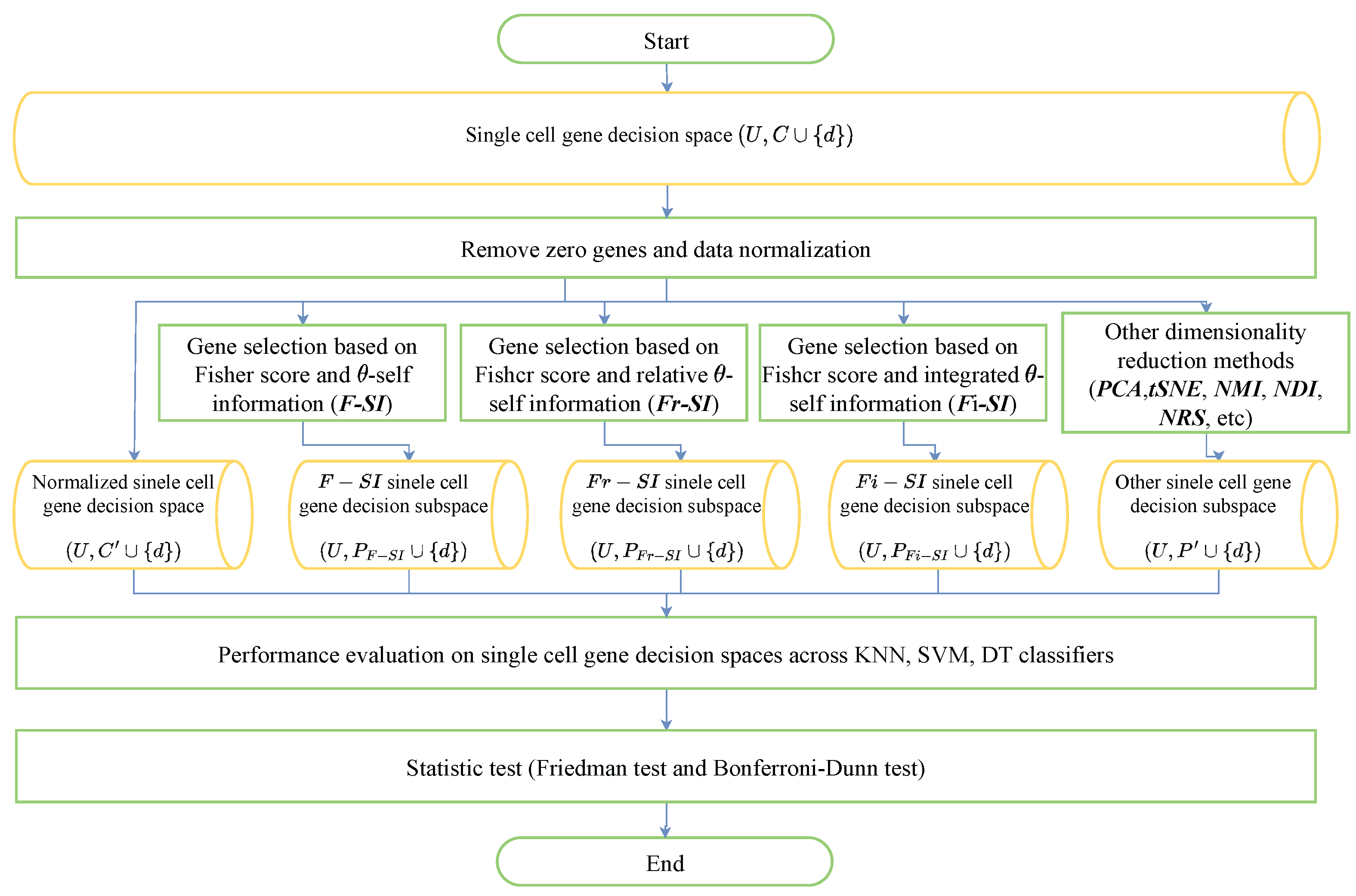
5. Experimental Analysis
5.1. Dataset and Preprocess
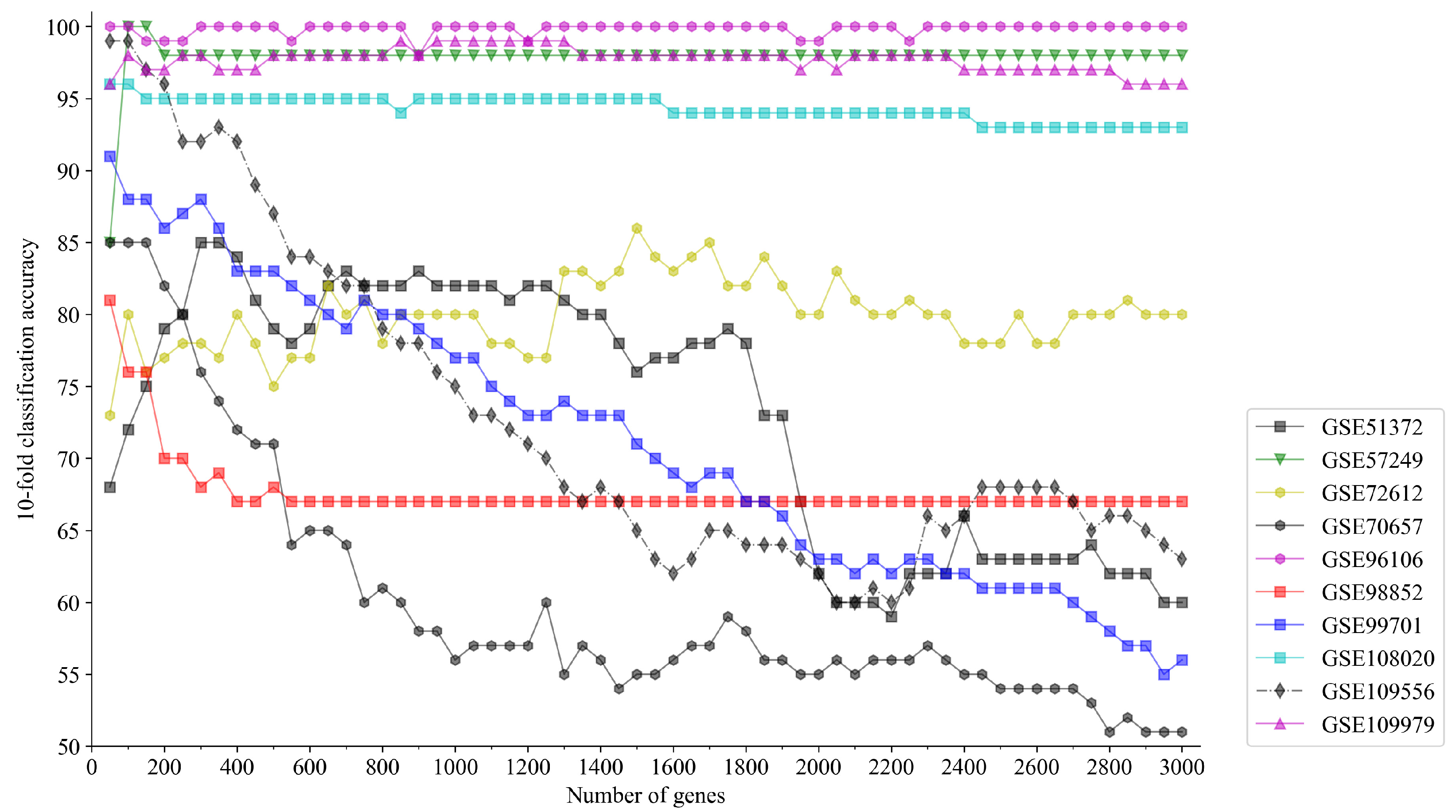
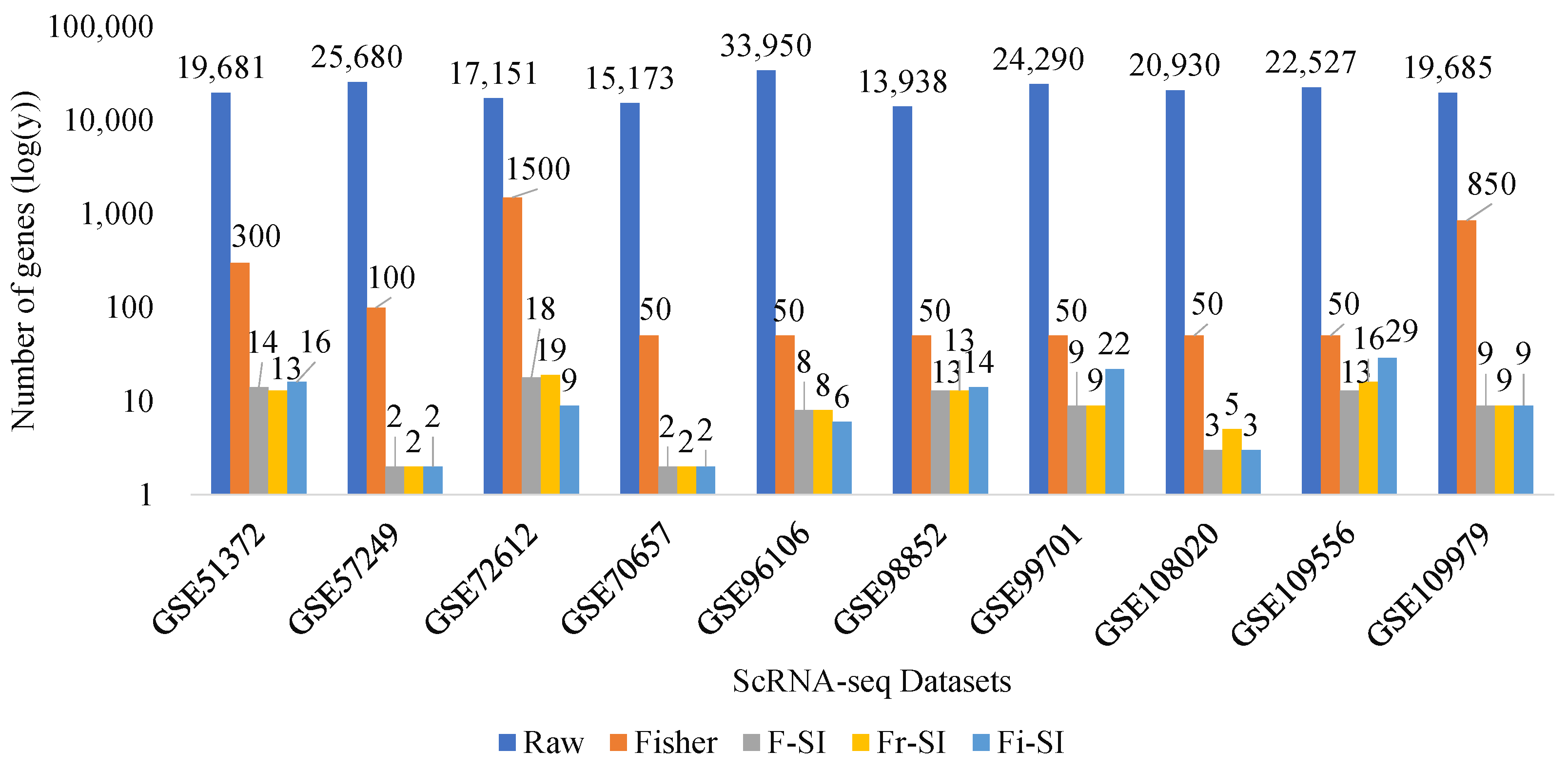
5.2. Preliminary Number of Genes
5.3. Benchmarking Compared with Raw Data and Fisher Data
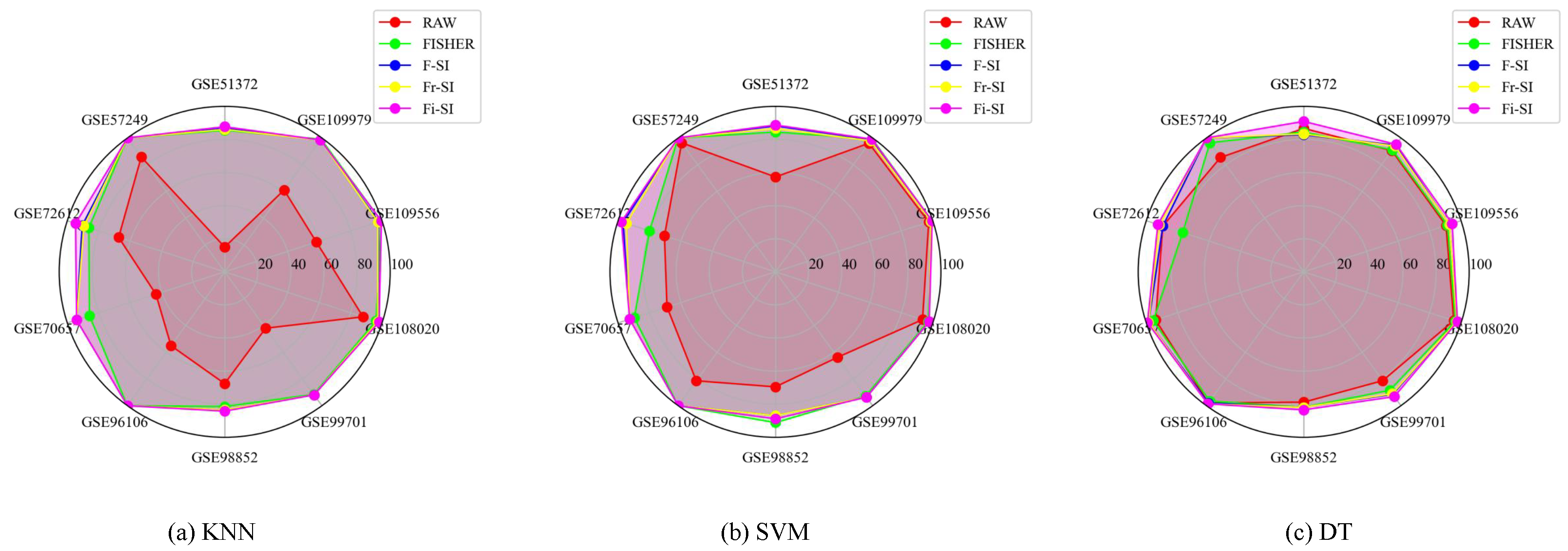
5.4. Performance Comparisons with PCA and tSNE
5.5. Comparisons with Other Algorithms
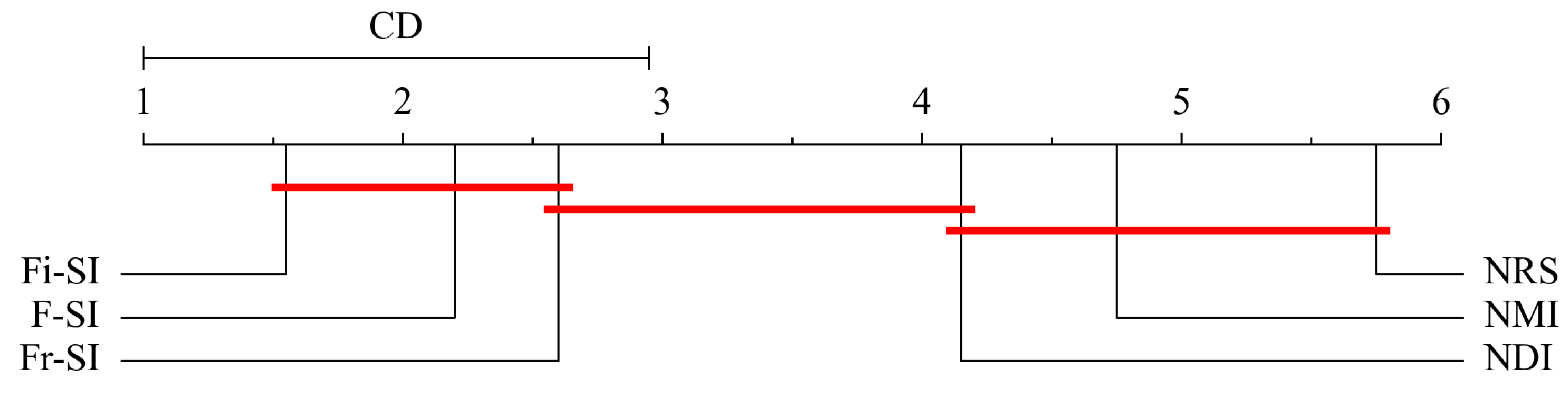
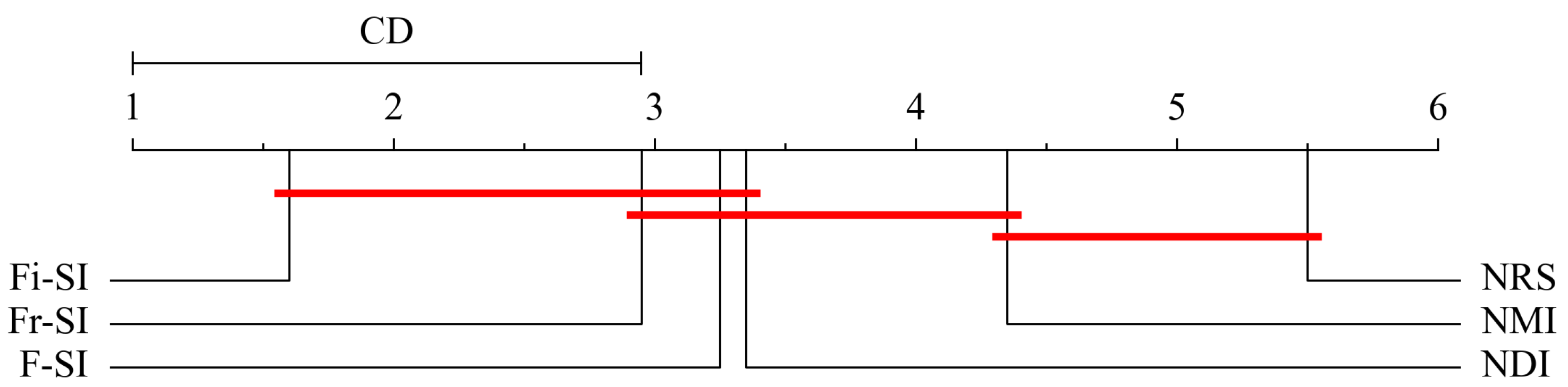
5.6. Statistical Analysis
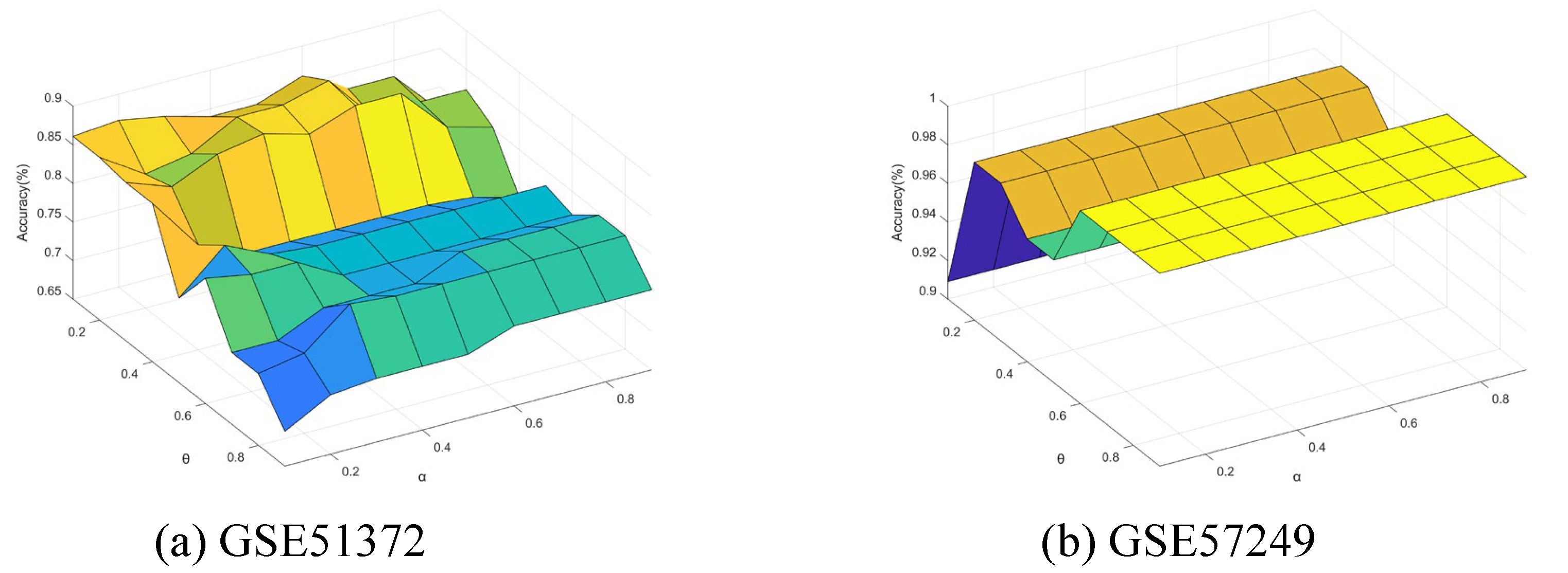
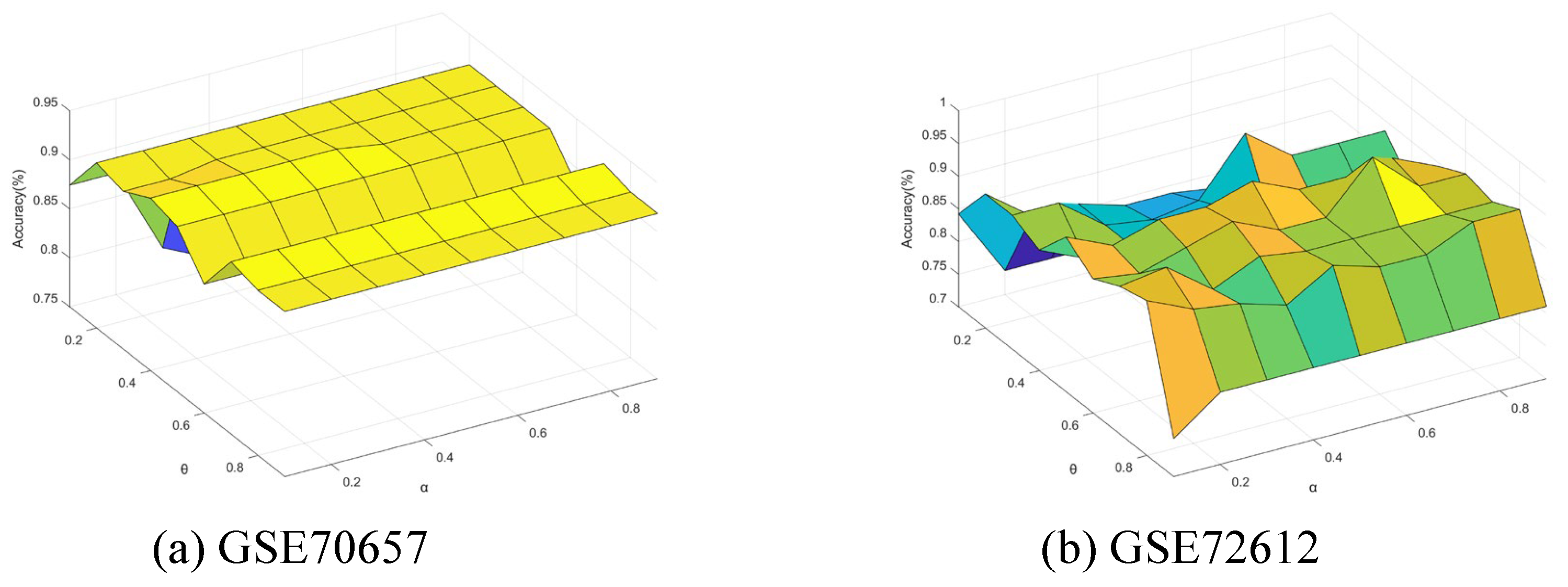
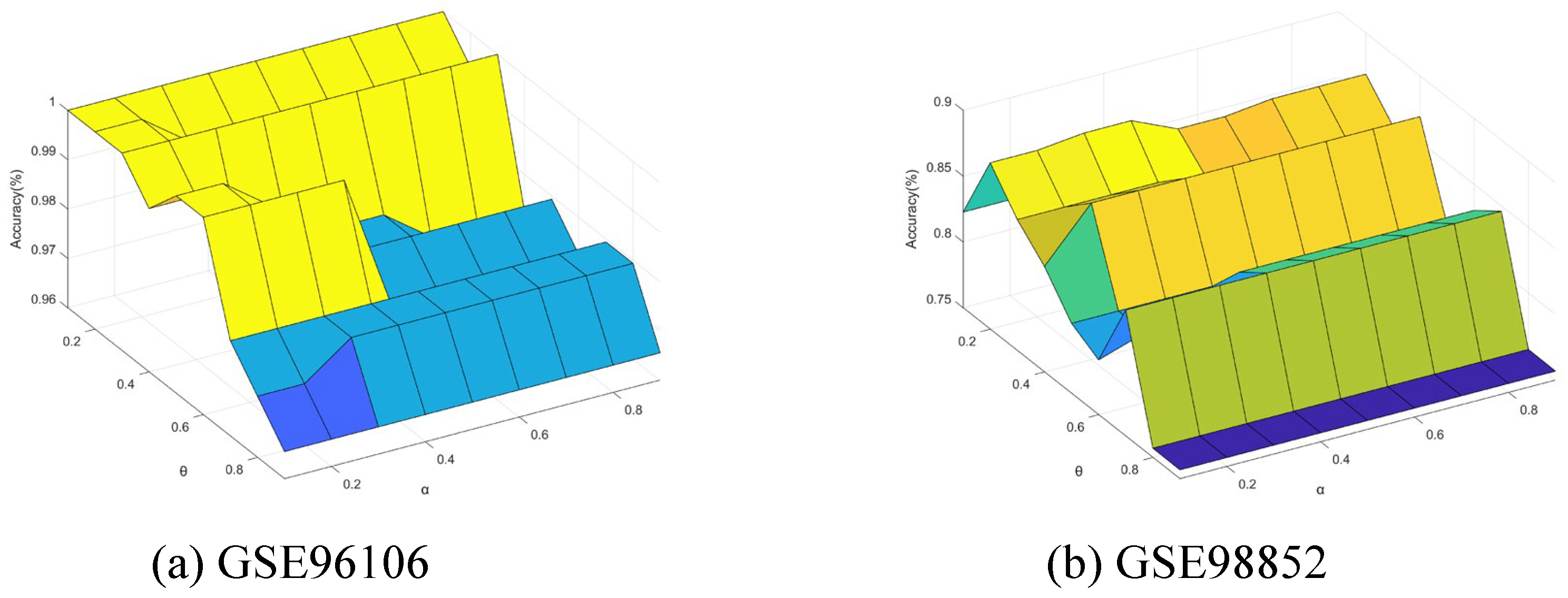
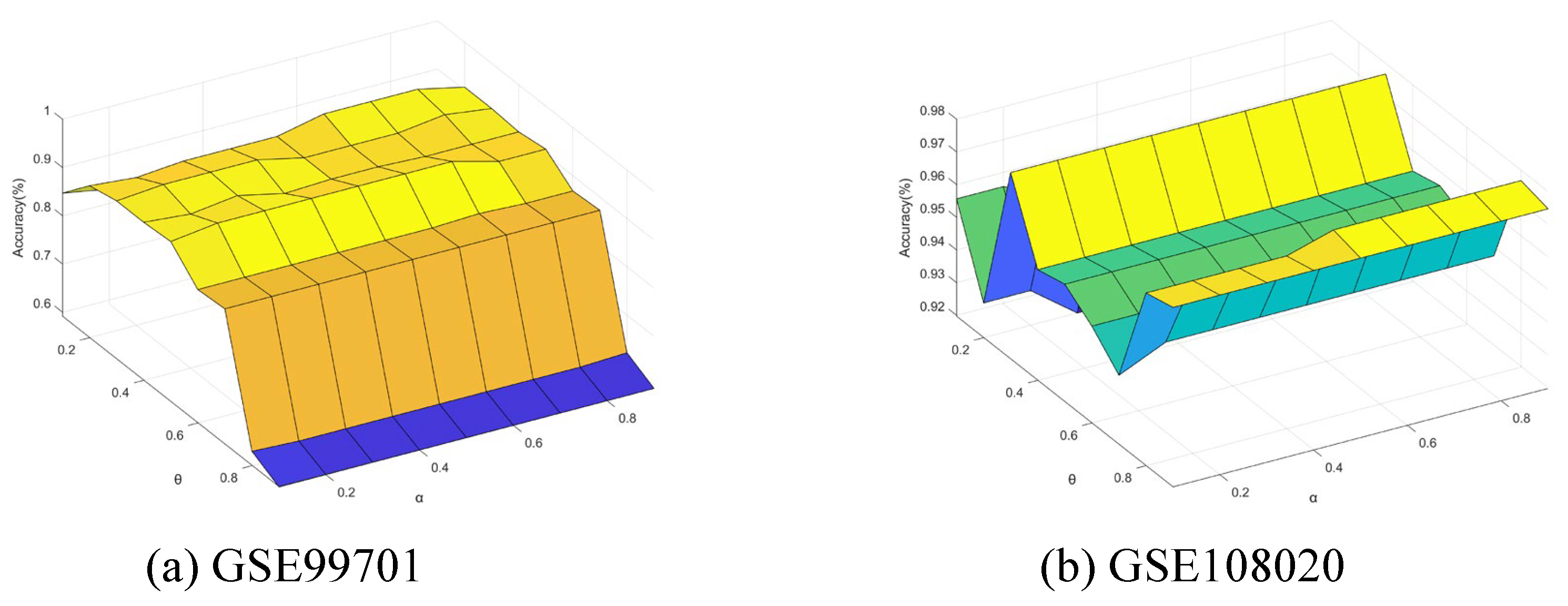
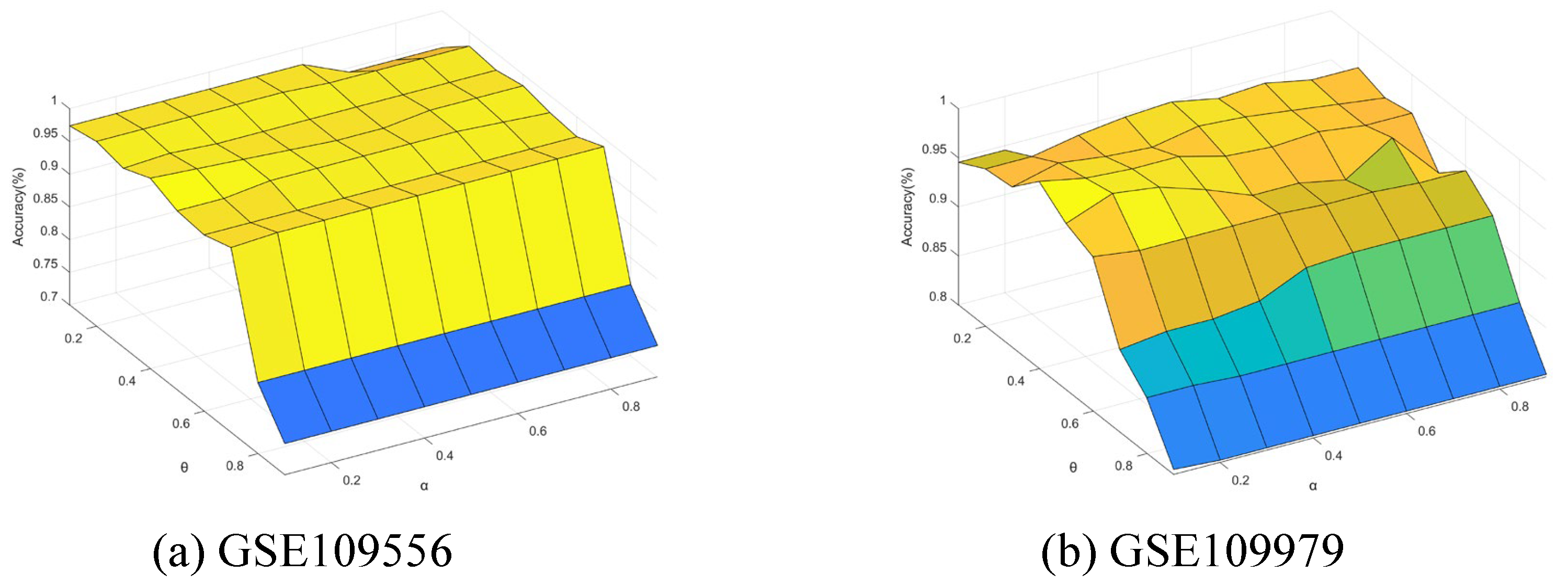
5.7. Sensitivity Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ayub, S.; Shabir, M.; Riaz, M.; Karaaslan, F.; Marinkovic, D.; Vranjes, D. Linear Diophantine Fuzzy Rough Sets on Paired Universes with Multi Stage Decision Analysis. Axioms 2022, 11, 686. [Google Scholar] [CrossRef]
- Ayub, S.; Shabir, M.; Riaz, M.; Mahmood, W.; Bozanic, D.; Marinkovic, D. Linear Diophantine Fuzzy Rough Sets: A New Rough Set Approach with Decision Making. Symmetry 2022, 14, 525. [Google Scholar] [CrossRef]
- Pawlak, Z. Rough sets. Int. J. Comput. Inf. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Wang, C.; Huang, Y.; Shao, M.; Hu, Q.; Chen, D. Feature selection based on neighborhood self-information. IEEE Trans. Cybern. 2019, 50, 4031–4042. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Chen, Y.; Zhang, G.; Li, Z.; Chen, L.; Wen, C.F. New uncertainty measurement for categorical data based on fuzzy information structures: An application in attribute reduction. Inf. Sci. 2021, 580, 541–577. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, P.; Ge, X.; Xie, N.; Zhang, G.; Wen, C.F. Uncertainty measurement for a fuzzy relation information system. IEEE Trans. Fuzzy Syst. 2019, 27, 2338–2352. [Google Scholar] [CrossRef]
- Navarrete, J.; Viejo, D.; Cazorla, M. Color smoothing for RGB-D data using entropy information. Appl. Soft Comput. 2016, 46, 361–380. [Google Scholar] [CrossRef]
- Hempelmann, C.F.; Sakoglu, U.; Gurupur, V.P.; Jampana, S. An entropy-based evaluation method for knowledge bases of medical information systems. Expert Syst. Appl. 2016, 46, 262–273. [Google Scholar] [CrossRef]
- Delgado, A.; Romero, I. Environmental conflict analysis using an integrated grey clustering and entropy-weight method: A case study of a mining project in Peru. Environ. Model. Softw. 2016, 77, 108–121. [Google Scholar] [CrossRef]
- Zeng, A.; Li, T.; Liu, D.; Zhang, J.; Chen, H. A fuzzy rough set approach for incremental feature selection on hybrid information systems. Fuzzy Sets Syst. 2015, 258, 39–60. [Google Scholar] [CrossRef]
- Kim, K.J.; Jun, C.H. Rough set model based feature selection for mixed-type data with feature space decomposition. Expert Syst. Appl. 2018, 103, 196–205. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Y.; Shao, M.; Qian, Y.; Chen, D. Fuzzy rough attribute reduction for categorical data. IEEE Trans. Fuzzy Syst. 2019, 28, 818–830. [Google Scholar] [CrossRef]
- Dai, J.H.; Hu, H.; Zheng, G.J.; Hu, Q.H.; Han, H.F.; Shi, H. Attribute reduction in interval-valued information systems based on information entropies. Front. Inf. Technol. Electron. Eng. 2016, 17, 919–928. [Google Scholar] [CrossRef]
- Singh, S.; Shreevastava, S.; Som, T.; Somani, G. A fuzzy similarity-based rough set approach for attribute selection in set-valued information systems. Soft Comput. 2020, 24, 4675–4691. [Google Scholar] [CrossRef]
- Sang, B.; Chen, H.; Yang, L.; Li, T.; Xu, W. Incremental feature selection using a conditional entropy based on fuzzy dominance neighborhood rough sets. IEEE Trans. Fuzzy Syst. 2021, 30, 1683–1697. [Google Scholar] [CrossRef]
- Huang, Z.; Li, J. Discernibility Measures for Fuzzy β Covering and Their Application. IEEE Trans. Cybern. 2022, 52, 9722–9735. [Google Scholar] [CrossRef]
- Jia, X.; Rao, Y.; Shang, L.; Li, T. Similarity-based attribute reduction in rough set theory: A clustering perspective. Int. J. Mach. Learn. Cybern. 2020, 11, 1047–1060. [Google Scholar] [CrossRef]
- Li, Z.; Qu, L.; Zhang, G.; Xie, N. Attribute selection for heterogeneous data based on information entropy. Int. J. Gen. Syst. 2021, 50, 548–566. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, X.; Dong, K. Attribute reduction via local conditional entropy. Int. J. Mach. Learn. Cybern. 2019, 10, 3619–3634. [Google Scholar] [CrossRef]
- Yuan, Z.; Chen, H.; Zhang, P.; Wan, J.; Li, T. A novel unsupervised approach to heterogeneous feature selection based on fuzzy mutual information. IEEE Trans. Fuzzy Syst. 2021, 30, 3395–3409. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, K.; Yang, X.; Fujita, H. Random sampling accelerator for attribute reduction. Int. J. Approx. Reason. 2022, 140, 75–91. [Google Scholar] [CrossRef]
- Jiang, Z.; Liu, K.; Yang, X.; Yu, H.; Fujita, H.; Qian, Y. Accelerator for supervised neighborhood based attribute reduction. Int. J. Approx. Reason. 2020, 119, 122–150. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, K.; Song, J.; Fujita, H.; Yang, X.; Qian, Y. Attribute group for attribute reduction. Inf. Sci. 2020, 535, 64–80. [Google Scholar] [CrossRef]
- Buettner, F.; Natarajan, K.N.; Casale, F.P.; Proserpio, V.; Scialdone, A.; Theis, F.J.; Teichmann, S.A.; Marioni, J.C.; Stegle, O. Computational analysis of cell-to-cell heterogeneity in single-cell RNA-sequencing data reveals hidden subpopulations of cells. Nat. Biotechnol. 2015, 33, 155–160. [Google Scholar] [CrossRef]
- Chung, W.; Eum, H.H.; Lee, H.O.; Lee, K.M.; Lee, H.B.; Kim, K.T.; Ryu, H.S.; Kim, S.; Lee, J.E.; Park, Y.H.; et al. Single-cell RNA-seq enables comprehensive tumour and immune cell profiling in primary breast cancer. Nat. Commun. 2017, 8, 15081. [Google Scholar] [CrossRef]
- Bommert, A.; Welchowski, T.; Schmid, M.; Rahnenführer, J. Benchmark of filter methods for feature selection in high-dimensional gene expression survival data. Briefings Bioinform. 2021, 23, bbab354. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, J.; Liu, F.; Wen, C.F. Uncertainty measurement for single cell RNA-seq data via Gaussian kernel: Application to unsupervised gene selection. Eng. Appl. Artif. Intell. 2024, 130, 107707. [Google Scholar] [CrossRef]
- Sharma, A.; Rani, R. C-HMOSHSSA: Gene selection for cancer classification using multi-objective meta-heuristic and machine learning methods. Comput. Methods Programs Biomed. 2019, 178, 219–235. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhao, Z.; Liu, F.; Li, Z. Uncertainty measurement for single cell RNA-seq data based on class-consistent technology with application to semi-supervised gene selection. Appl. Soft Comput. 2023, 146, 110645. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, X.Y.; Qian, Y.H.; Xu, J.C.; Zhang, S.G.; Tian, Y. Joint neighborhood entropy-based gene selection method with fisher score for tumor classification. Appl. Intell. 2019, 49, 1245–1259. [Google Scholar] [CrossRef]
- Sheng, J.; Li, W.V. Selecting gene features for unsupervised analysis of single-cell gene expression data. Briefings Bioinform. 2021, 22, bbab295. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, G.; Li, Z.; Qu, L.; Wen, C.F. Feature selection in a neighborhood decision information system with application to single cell RNA data classification. Appl. Soft Comput. 2021, 113, 107876. [Google Scholar] [CrossRef]
- Li, Z.; Feng, J.; Zhang, J.; Liu, F.; Wang, P.; Wen, C.F. Gaussian kernel based gene selection in a single cell gene decision space. Inf. Sci. 2022, 610, 1029–1057. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, G.; Huang, D.; Wang, Y. Gene selection in a single cell gene decision space based on class-consistent technology and fuzzy rough iterative computation model. Appl. Intell. 2023, 53, 30113–30132. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, P.; Pedrycz, W.; Li, Z. Neighborhood entropy guided by a decision attribute and its applications in multi-source information fusion and attribute selection. Appl. Soft Comput. 2024, 167, 112380. [Google Scholar] [CrossRef]
- Ma, X.; Liu, J.; Wang, P.; Yu, W.; Hu, H. Feature selection for hybrid information systems based on fuzzy ß covering and fuzzy evidence theory. J. Intell. Fuzzy Syst. 2024, 46, 4219–4242. [Google Scholar]
- Yu, W.; Ma, X.; Zhang, Z.; Zhang, Q. A Method for Fast Feature Selection Utilizing Cross-Similarity within the Context of Fuzzy Relations. cmc-Comput. Mater. Contin. 2025, 83, 1195–1218. [Google Scholar] [CrossRef]
- Ting, D.T.; Wittner, B.S.; Ligorio, M.; Jordan, N.V.; Shah, A.M.; Miyamoto, D.T.; Aceto, N.; Bersani, F.; Brannigan, B.W.; Xega, K. et al. Single-cell rna sequencing identifies extracellular matrix gene expression by pancreatic circulating tumor cells. Cell Rep. 2014, 8, 1905–1918. [Google Scholar] [CrossRef]
- Biase, F.H.; Cao, X.; Zhong, S. Cell fate inclination within 2-cell and 4-cell mouse embryos revealed by single-cell rna sequencing. Genome Res. 2014, 24, 1787–1796. [Google Scholar] [CrossRef]
- Grover, A.; Sanjuan-Pla, A.; Thongjuea, S.; Carrelha, J.; Giustacchini, A.; Gambardella, A.; Macaulay, I.; Mancini, E.; Luis, T.C.; Mead, A. et al. Single-cell rna sequencing reveals molecular and functional platelet bias of aged haematopoietic stem cells. Nat. Commun. 2016, 7, 11075. [Google Scholar] [CrossRef] [PubMed]
- Hawkins, F.; Kramer, P.; Jacob, A.; Driver, I.; Thomas, D.C.; McCauley, K.B.; Skvir, N.; Crane, A.M.; Kurmann, A.A.; Hollenberg, A.N.; et al. Prospective isolation of nkx2-1–expressing human lung progenitors derived from pluripotent stem cells. J. Clin. Investig. 2017, 127, 2277–2294. [Google Scholar] [CrossRef] [PubMed]
- Chiang, D.; Chen, X.; Jones, S.M.; Wood, R.A.; Sicherer, S.H.; Burks, A.W.; Leung, D.Y.; Agashe, C.; Grishin, A.; Dawson, P.; et al. Single-cell profiling of peanut-responsive t cells in patients with peanut allergy reveals heterogeneous effector th2 subsets. J. Allergy And Clinical Immunol. 2018, 141, 2107–2120. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Lee, J.W.; Chou, C.-L.; Nair, A.V.; Battistone, M.A.; Păunescu, T.G.; Merkulova, M.; Breton, S.; Verlander, J.W.; Wall, S.M.; et al. Transcriptomes of major renal collecting duct cell types in mouse identified by single-cell rna-seq. Proc. Natl. Acad. Sci. USA 2017, 114, E9989–E9998. [Google Scholar] [CrossRef]
- Hook, P.W.; McClymont, S.A.; Cannon, G.H.; Law, W.D.; Morton, A.J.; Goff, L.A.; McCallion, A.S. Single-cell rna-seq of dopaminergic neurons informs candidate gene selection for sporadic parkinson’s disease. bioRxiv 2017, 148049. [Google Scholar]
- Donega, V.; Marcy, G.; Giudice, Q.L.; Zweifel, S.; Angonin, D.; Fiorelli, R.; Abrous, D.N.; Rival-Gervier, S.; Koehl, M.; Jabaudon, D.; et al. Transcriptional dysregulation in postnatal glutamatergic progenitors contributes to closure of the cortical neurogenic period. Cell Rep. 2018, 22, 2567–2574. [Google Scholar] [CrossRef]
- Lu, J.; Baccei, A.; da Rocha, E.L.; Guillermier, C.; McManus, S.; Finney, L.A.; Zhang, C.; Steinhauser, M.L.; Li, H.; Lerou, P.H. Single-cell rna sequencing reveals metallothionein heterogeneity during hesc differentiation to definitive endoderm. Stem Cell Res. 2018, 28, 48–55. [Google Scholar] [CrossRef]

| d | ||||
|---|---|---|---|---|
| 0 | 0 | 0.1429 | 1 | |
| 0.2857 | 1.0000 | 1.0000 | 1 | |
| 1.0000 | 0.2500 | 0 | 0 |
| 1 | 2 | |
| 0 | 1 | |
| 0 | 1 |
| 1 | 2 | |
| 2 | 3 | |
| 2 | 3 |
| B | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0.3466 | 0.1733 | 0.3466 | 0.2426 | 0.3466 | 0.1352 | 0.2409 | 0.7324 | 0.1986 | |
| 0 | 0.3466 | 0.1733 | 0.3466 | 0.2426 | 0.3466 | 0.1352 | 0.2409 | 0.7324 | 0.1986 |
| B | |||||
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | |
| 0.3466 | 0.4818 | 0.4142 | 1.0808 | 0.4412 | |
| 0.3466 | 0.4818 | 0.4142 | 1.0808 | 0.4412 |
| GSE ID | Contributor | # Cells | # Raw Genes | # Class | # Preliminary Genes | Reference |
|---|---|---|---|---|---|---|
| GSE51372 | Chen | 187 | 19,681 | 7 | 300 | Chen et al. (2014) [39] |
| GSE57249 | Biase | 56 | 25,680 | 4 | 100 | Biase et al. (2014) [40] |
| GSE72612 | Watanabe | 95 | 17,151 | 3 | 1500 | Watanabe et al. (2018) |
| GSE70657 | Grover | 135 | 15,173 | 2 | 50 | Grover et al. (2016) [41] |
| GSE96106 | Hawkins | 145 | 33,950 | 2 | 50 | Hawkins et al. (2017) [42] |
| GSE98852 | Chiang | 259 | 13,938 | 2 | 50 | Chiang et al. (2017) [43] |
| GSE99701 | Chen | 235 | 24,290 | 5 | 50 | Chen et al. (2017) [44] |
| GSE108020 | Hook | 473 | 20,930 | 2 | 50 | Hook et al. (2018) [45] |
| GSE109556 | Donega | 230 | 22,527 | 2 | 50 | Donega et al. (2018) [46] |
| GSE109979 | Lu | 329 | 19,685 | 4 | 850 | Lu et al. (2018) [47] |
| Datasets | Raw Data | Fisher Data | F-SI | Fr-SI | Fi-SI |
|---|---|---|---|---|---|
| GSE51372 | 19,681 | 300 | 14 | 13 | 16 |
| GSE57249 | 25,680 | 100 | 2 | 2 | 2 |
| GSE72612 | 17,151 | 1500 | 18 | 19 | 9 |
| GSE70657 | 15,173 | 50 | 2 | 2 | 2 |
| GSE96106 | 33,950 | 50 | 8 | 8 | 6 |
| GSE98852 | 13,938 | 50 | 13 | 13 | 14 |
| GSE99701 | 24,290 | 50 | 9 | 9 | 22 |
| GSE108020 | 20,930 | 50 | 3 | 5 | 3 |
| GSE109556 | 22,527 | 50 | 13 | 16 | 29 |
| GSE109979 | 19,685 | 850 | 9 | 9 | 9 |
| Datasets | Raw | Fisher | PCA | tSNE | mRMR | ReliefF | NRS | NDI | NMI | F-SI | Fr-SI | Fi-SI |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GSE51372 | 14.98 | 85.53 | 75.97 | 55.6 | 86.91 | 86.35 | 76.5 | 78.09 | 73.34 | 86.61 | 86.07 | |
| GSE57249 | 85.76 | 98.18 | 87.58 | 97.61 | 96.81 | 80.3 | 94.55 | 80.3 | ||||
| GSE72612 | 67.37 | 86.32 | 76.84 | 71.58 | 91.65 | 89.71 | 66.32 | 83.16 | 77.89 | 90.53 | 89.47 | |
| GSE70657 | 43.7 | 85.93 | 70.37 | 56.3 | 90.74 | 88.63 | 71.85 | 85.19 | 82.22 | |||
| GSE96106 | 55.17 | 91.72 | 67.59 | 98.37 | 94.74 | 95.17 | 97.24 | |||||
| GSE98852 | 67.57 | 81.47 | 78.8 | 76.06 | 83.68 | 82.52 | 73.76 | 75.68 | 80.34 | 83.4 | 83.4 | |
| GSE99701 | 42.13 | 91.49 | 77.02 | 63.83 | 90.85 | 90.31 | 73.19 | 90.64 | 80 | |||
| GSE108020 | 87.95 | 96.2 | 93.87 | 93.45 | 97.18 | 97.06 | 97.25 | 95.99 | 97.68 | 97.46 | 97.26 | |
| GSE109556 | 58.26 | 98.26 | 80.43 | 96.63 | 96.46 | 93.48 | 96.96 | 96.52 | 97.83 | 97.39 | ||
| GSE109979 | 61.08 | 95.45 | 83.91 | 95.89 | 94.35 | 74.46 | 94.23 | 86.65 | 98.47 | 98.47 | 98.47 |
| Datasets | Raw | Fisher | PCA | tSNE | mRMR | ReliefF | NRS | NDI | NMI | F-SI | Fr-SI | Fi-SI |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GSE51372 | 57.31 | 84.47 | 69 | 63.68 | 83.25 | 81.33 | 73.27 | 84.98 | 73.83 | 88.22 | 86.63 | |
| GSE57249 | 96.36 | 98.18 | 91.06 | 98.91 | 97.18 | 75 | 96.36 | 75 | ||||
| GSE72612 | 70.53 | 80 | 71.58 | 65.26 | 96.15 | 95.11 | 62.11 | 84.21 | 80 | 96.84 | 94.74 | |
| GSE70657 | 68.89 | 89.63 | 78.52 | 57.78 | 91.58 | 91.39 | 74.81 | 91.85 | 85.93 | |||
| GSE96106 | 81.38 | 92.41 | 69.66 | 95.35 | 95.01 | 95.86 | 97.93 | |||||
| GSE98852 | 69.5 | 78.03 | 75.69 | 87.16 | 83.25 | 78.8 | 81.47 | 83.42 | 86.89 | 86.89 | 88.83 | |
| GSE99701 | 63.83 | 92.77 | 78.3 | 61.28 | 91.48 | 90.19 | 77.02 | 91.91 | 82.55 | |||
| GSE108020 | 93.45 | 97.05 | 90.92 | 94.08 | 97.29 | 96.37 | 97.47 | 96.41 | 97.46 | |||
| GSE109556 | 97.39 | 98.7 | 75.65 | 97.52 | 96.26 | 93.48 | 96.96 | 94.78 | 98.7 | 98.7 | ||
| GSE109979 | 96.06 | 95.45 | 80.25 | 97.93 | 98.31 | 78.41 | 95.74 | 87.56 | 98.79 | 97.86 | 99.09 |
| Datasets | Raw | Fisher | PCA | tSNE | mRMR | ReliefF | NRS | NDI | NMI | F-SI | Fr-SI | Fi-SI |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GSE51372 | 86.67 | 84.52 | 72.77 | 55.66 | 87.67 | 85.46 | 79.7 | 78.66 | 86.66 | 82.9 | 83.37 | |
| GSE57249 | 85.45 | 96.36 | 98.18 | 85.61 | 89.92 | 88.35 | 78.48 | 91.06 | 78.48 | |||
| GSE72612 | 89.47 | 76.84 | 76.84 | 81.05 | 91.08 | 89.63 | 69.47 | 82.11 | 77.89 | 89.47 | 91.58 | |
| GSE70657 | 94.07 | 95.56 | 73.33 | 56.3 | 97.82 | 93.27 | 90.37 | 95.56 | 97.04 | 98.52 | 98.52 | |
| GSE96106 | 97.93 | 96.55 | 93.1 | 61.38 | 97.95 | 96.83 | 94.48 | 97.24 | 97.93 | |||
| GSE98852 | 78.77 | 81.88 | 70.29 | 72.19 | 82.35 | 81.33 | 72.96 | 75.3 | 79.54 | 81.88 | 81.88 | |
| GSE99701 | 81.28 | 88.51 | 71.06 | 57.87 | 91.83 | 90.07 | 73.62 | 75.74 | 91.49 | 91.06 | ||
| GSE108020 | 95.35 | 96.41 | 93.24 | 94.3 | 96.35 | 97.13 | 97.68 | 97.89 | 97.25 | 97.25 | 97.68 | |
| GSE109556 | 90.43 | 91.3 | 76.09 | 93.38 | 93.61 | 91.74 | 95.22 | 91.3 | 92.61 | 92.61 | 94.35 | |
| GSE109979 | 90.55 | 91.17 | 92.72 | 91.49 | 93.49 | 92.57 | 71.42 | 88.75 | 82.39 | 94.54 | 93.92 |
| Datasets | KNN | SVM | DT | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F-SI | Fr-SI | Fi-SI | NRS | NDI | NMI | F-SI | Fr-SI | Fi-SI | NRS | NDI | NMI | F-SI | Fr-SI | Fi-SI | NRS | NDI | NMI | |
| GSE51372 | 2.0 | 3.0 | 1.0 | 5.0 | 4.0 | 6.0 | 2.0 | 3.0 | 1.0 | 6.0 | 4.0 | 5.0 | 4.0 | 3.0 | 1.0 | 5.0 | 6.0 | 2.0 |
| GSE57249 | 2.0 | 2.0 | 2.0 | 5.5 | 4.0 | 5.5 | 2.0 | 2.0 | 2.0 | 5.5 | 4.0 | 5.5 | 2.0 | 2.0 | 2.0 | 5.5 | 4.0 | 5.5 |
| GSE72612 | 2.0 | 3.0 | 1.0 | 6.0 | 4.0 | 5.0 | 2.0 | 3.0 | 1.0 | 6.0 | 4.0 | 5.0 | 3.0 | 2.0 | 1.0 | 6.0 | 4.0 | 5.0 |
| GSE70657 | 2.0 | 2.0 | 2.0 | 6.0 | 4.0 | 5.0 | 2.0 | 2.0 | 2.0 | 6.0 | 4.0 | 5.0 | 2.5 | 2.5 | 1.0 | 6.0 | 5.0 | 4.0 |
| GSE96106 | 2.5 | 2.5 | 2.5 | 6.0 | 2.5 | 5.0 | 2.5 | 2.5 | 2.5 | 6.0 | 2.5 | 5.0 | 4.0 | 2.0 | 2.0 | 6.0 | 2.0 | 5.0 |
| GSE98852 | 2.5 | 2.5 | 1.0 | 6.0 | 5.0 | 4.0 | 2.5 | 2.5 | 1.0 | 6.0 | 5.0 | 4.0 | 2.5 | 2.5 | 1.0 | 6.0 | 5.0 | 4.0 |
| GSE99701 | 2.0 | 2.0 | 2.0 | 6.0 | 4.0 | 5.0 | 2.0 | 2.0 | 2.0 | 6.0 | 4.0 | 5.0 | 3.0 | 4.0 | 1.5 | 6.0 | 1.5 | 5.0 |
| GSE108020 | 3.0 | 4.0 | 1.0 | 5.0 | 6.0 | 2.0 | 2.0 | 2.0 | 2.0 | 4.0 | 6.0 | 5.0 | 5.5 | 5.5 | 3.5 | 3.5 | 1.0 | 2.0 |
| GSE109556 | 2.0 | 3.0 | 1.0 | 6.0 | 4.0 | 5.0 | 2.5 | 2.5 | 1.0 | 6.0 | 4.0 | 5.0 | 4.0 | 3.0 | 2.0 | 5.0 | 1.0 | 6.0 |
| GSE109979 | 2.0 | 2.0 | 2.0 | 6.0 | 4.0 | 5.0 | 2.0 | 3.0 | 1.0 | 6.0 | 4.0 | 5.0 | 2.0 | 3.0 | 1.0 | 6.0 | 4.0 | 5.0 |
| FMR | 2.2 | 2.6 | 1.55 | 5.75 | 4.15 | 4.75 | 2.15 | 2.45 | 1.55 | 5.75 | 4.15 | 4.95 | 3.25 | 2.95 | 1.6 | 5.5 | 3.35 | 4.35 |
| Rank | 2.0 | 3.0 | 1.0 | 6.0 | 4.0 | 5.0 | 2.0 | 3.0 | 1.0 | 6.0 | 4.0 | 5.0 | 3.0 | 2.0 | 1.0 | 6.0 | 4.0 | 5.0 |
| Values | KNN | SVM | DT |
|---|---|---|---|
| 41.45 | 44.59 | 25.95 | |
| 43.69 | 74.25 | 9.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Y.; Lin, Y.; Huang, C.; Li, Z. Gene Selection Algorithms in a Single-Cell Gene Decision Space Based on Self-Information. Mathematics 2025, 13, 1829. https://doi.org/10.3390/math13111829
Fang Y, Lin Y, Huang C, Li Z. Gene Selection Algorithms in a Single-Cell Gene Decision Space Based on Self-Information. Mathematics. 2025; 13(11):1829. https://doi.org/10.3390/math13111829
Chicago/Turabian StyleFang, Yan, Yonghua Lin, Chuanbo Huang, and Zhaowen Li. 2025. "Gene Selection Algorithms in a Single-Cell Gene Decision Space Based on Self-Information" Mathematics 13, no. 11: 1829. https://doi.org/10.3390/math13111829
APA StyleFang, Y., Lin, Y., Huang, C., & Li, Z. (2025). Gene Selection Algorithms in a Single-Cell Gene Decision Space Based on Self-Information. Mathematics, 13(11), 1829. https://doi.org/10.3390/math13111829






