Abstract
Geometric image transformations are fundamental to image processing, computer vision and graphics, with critical applications to pattern recognition and facial identification. The splitting-integrating method (SIM) is well suited to the inverse transformation of digital images and patterns, but it encounters difficulties in nonlinear solutions for the forward transformation T. We propose improved techniques that entirely bypass nonlinear solutions for T, simplify numerical algorithms and reduce computational costs. Another significant advantage is the greater flexibility for general and complicated transformations T. In this paper, we apply the improved techniques to the harmonic, Poisson and blending models, which transform the original shapes of images and patterns into arbitrary target shapes. These models are, essentially, the Dirichlet boundary value problems of elliptic equations. In this paper, we choose the simple finite difference method (FDM) to seek their approximate transformations. We focus significantly on analyzing errors of image greyness. Under the improved techniques, we derive the greyness errors of images under T. We obtain the optimal convergence rates for the piecewise bilinear interpolations () and smooth images, where denotes the mesh resolution of an optical scanner, and N is the division number of a pixel split into sub-pixels. Beyond smooth images, we address practical challenges posed by discontinuous images. We also derive the error bounds , as . For piecewise continuous images with interior and exterior greyness jumps, we have . Compared with the error analysis in our previous study, where the image greyness is often assumed to be smooth enough, this error analysis is significant for geometric image transformations. Hence, the improved algorithms supported by rigorous error analysis of image greyness may enhance their wide applications in pattern recognition, facial identification and artificial intelligence (AI).
Keywords:
image geometric transformations; error analysis; splitting-integrating method; harmonic and Poisson models; finite difference method; pattern recognition; AI applications MSC:
65N15; 65D30; 68A45
1. Introduction
Graphics, pictures, computer images, computer vision and digital patterns are often distorted by linear or nonlinear transformations. The algorithms that correctly convert images and patterns under these transformations and restore their original images and patterns are essential for applications in image processing, pattern recognition and artificial intelligence (AI). We solicited numerical algorithms for image geometric transformations and proposed basic algorithms in a book [1] in 1989, which were developed from [2,3,4,5]. Since then, we have focused on refining existing numerical algorithms, with significant advancements reported in [1,6,7]. Geometric transformations heavily depend on shape boundaries, which are particularly important in applications like face fusion [8]. This paper extends the splitting algorithms of [9], with a focus on rigorous error analysis and broader applications. AI relies on three elements: data, models and algorithms. The new trend in AI is to significantly improve algorithmic efficiency, (see DeepSeek [10]); such a trend has guided our study for many years. A systematic summary of new numerical algorithms for image geometric transformations is provided in the new book [11].
Let us introduce the integral model of images and its basic algorithms (the model and algorithms as AI’s terminology). The digital image in 2D is denoted by a matrix with non-negative entries representing the pixel greyness. Each pixel greyness can also be regarded as the mean of a greyness function over a small pixel region, leading to a 2D integral. Hence, the image transformation can be reduced to numerical integration. Based on this idea, we develop the splitting-integrating method (SIM) in [1], which is, indeed, the composite centroid rule in numerical analysis (see Atkinson [12] and Davis and Rabinowitz [13]). The advantage of SIM is the simplicity of algorithms, in particular for the restoration of images because nonlinear solutions are not required. Although the smooth features of the piecewise integrand in the integral are different in different subregions, the same centroid rule is always chosen. In applications, we choose the simple piecewise constant interpolations as and the piecewise linear interpolations as . Our goal is to achieve the optimal convergence rates of sequential image greyness errors, where N is the division number of a pixel split into .
We may apply SIM for the forward transformation T, combine the SIM for , and develop a combination CIIM for a cycle transformation . A drawback of SIM for T is that nonlinear solutions may be involved. When the nonlinear transformations are not complicated, the Newton iteration method may be used to carry out the nonlinear solutions. In this case, the combination CIIM is studied in ([11], Chapters 4 and 5) to provide the optimal sequential convergence rates , . The CIIM can also be applied to n-dimensional image transformation reported in ([11], Chapter 2). However, for complicated nonlinear transformations T, solving the associated nonlinear equations becomes challenging, limiting the practicality of SIM and CIIM. For image conversion under a geometric transformation T, the splitting-shooting method (SSM) does not need nonlinear solutions. Hence, we may combine SSM for T and SIM for to develop a combination CSIM for . A strict analysis of the CSIM was given in Li and Bai [7], to reveal that only the low convergence rates of image greyness can be obtained for both and . Also, by probability analysis, a higher convergence rate as in probability can be reached in [7]. For 256 greyness-level images under a nonlinear transformation with a double enlargement, the division number N should be chosen as large as or 64 to provide satisfactory pictures (see [7]). For 256 real greyscale images, CSIM becomes impractical due to the prohibitively large number of pixels. In general, the original CSIM is suited well to a few (≤16) greyness level images. A sophisticated partition technique is also invented for CSIM, leading to the advanced combination and in ([11], Chapter 7), to reduce the division number N significantly.
Now, we recast CIIM and study new techniques embedded into the algorithm SIM for T to reduce and even bypass completely the nonlinear solutions. This is important to the wide application of CIIM. An interpolation technique is given in [6] to reduce the number of solutions to nonlinear equations from down to , where is the total number of image pixels. The piecewise bilinear interpolations are chosen in [6] based on the exact values of and at the semi-points . In this paper, we also solicit the interpolation to reduce the iteration number but based on the exact values of and at the pixel points . The algorithms in [6] are denoted as for T and for .
Moreover, since the values of and are unnecessary to be exact, we may also use the interpolation to obtain the approximate values of and to provide the improved algorithms for T and for without any nonlinear solutions. The improved algorithms are proposed in [9], but no error analysis exists so far. This is due to the improved techniques where the combination can be applied to the images under complicated transformations, e.g., those governed by partial differential equations (PDEs). In this paper, we also discuss the transformations of the Poisson and blending models by using the simple finite difference method (FDM) but apply the to image transformations undergone with these PDE models.
From the analysis in Section 4, the optimal convergence rates of greyness errors as can be maintained for continuous pictures by combination as well, where is the small image resolution. Another aspect of the analysis in this paper is to deal with image discontinuity. Real image greyness often has discontinuity. In this paper, we solicit the Sobolev norms and give an error analysis of the boundary discontinuity of image greyness. Using Sobolev norms, we derive the absolute errors , . This study is an important remedy for error analysis made for continuous images [7]. Geometric image transformations play a vital role in image processing, computer vision, computer graphics and AI. For pattern recognition and facial identification, finding and removing the geometric transformations involved are often a critical step. Hence, the improved algorithms with error analysis can be applied to enhance their performance in these areas.
The organization of this paper is as follows. In Section 2, the SIM is introduced for and T, and in Section 3, the interpolation techniques are proposed to reduce and even to bypass the nonlinear solutions. In Section 4, error analysis is made for both continuity and discontinuity of image greyness, and error bounds are derived. In Section 5, the PDE models of complicated transformations are approximated by the FDM, and then applied to image transformations by the new combination . In Section 6, some graphical and numerical experiments are provided to verify the theoretical analysis made, and to demonstrate the effectiveness of the proposed algorithms. Concluding remarks are given in Section 7, and a list of symbols used is provided in Appendix A.
2. The Splitting-Integrating Method and Its Combinations
2.1. Numerical Algorithms
Consider the cycle transformation : , where T is a nonlinear transformation defined by
In this paper, we assume that only the functions and are given explicitly, or implicitly governed by the PDE solutions. Denote by and the original and distorted images, where and are the image pixels located at and in the two Cartesian coordinates and , respectively:
and H is the mesh resolution of the optical scanner.
We solicit numerical algorithms shown in Figure 1 consisting of eight steps. Let denote the k-th level in the q-level system, where and are the whiteness and darkness, respectively. In steps 1 and 5, the pixel greyness is converted by
In steps 8 and 4, the conversions between the pixels and greyness in the q-level system are given by
Case II consists of all eight steps in Figure 1; Case I consists of steps 1–3 and 6–8, where the distorted image is converted from but with no feedback from to in step 5.
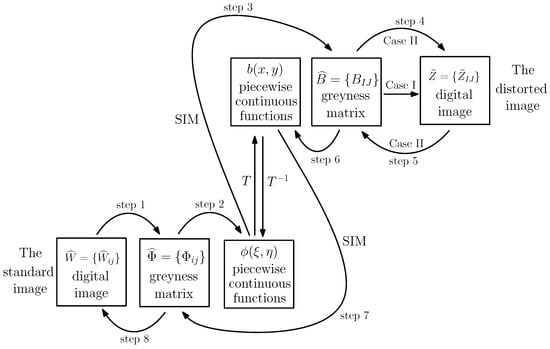
Figure 1.
Schematic steps of numerical methods for image transformations.
In steps 2 and 6, we choose the simple piecewise constant and the bilinear interpolations , and , defined by
where and are piecewise bilinear interpolations based on the and , respectively. In (6), the square small domains are defined by
Hence, the original and the distorted image domains are given by and .
2.2. A Splitting-Integrating Method for
The greyness and can be represented by the mean of continuous (or piecewise continuous) greyness functions and :
where . The linkage of digital images and integrals in (7) enables us to develop numerical algorithms for image transformations under T and easily. The greyness functions and can be formed by the cubic spline interpolations based on and , respectively (see [11], Chapter 5). Note that even is small, but not infinitesimal yet. In our previous analysis, we always assume that the piecewise cubic spline functions have
In this paper, we assume
where is the Sobolev space. Equation (7) is called the integral model of images, and numerical algorithms are developed based on (7) (see [1]).
First, consider the inverse transformation based on the known distorted image pixels , where the approximate functions . The composite centroid rule will be used to evaluate the integration values in (7). Let be split into uniform squares , i.e., , where
and h is the boundary length of , given by . For the small subpixels , the coordinates of the center of gravity are given by
By the composite centroid rule in Davis and Rabinowitz [13], we have
Hence, the normalized greyness of is obtained by
Note that the computational algorithms (11) do not involve any nonlinear solutions, and the sequential errors are proven to be as (see [11], Chapter 4).
2.3. A Splitting-Integrating Method for T
We now apply the splitting-integrating method to images under the forward transformation T based on the given . The piecewise interpolation functions are chosen, and . Let the pixel in be split into small sub-pixels with the boundary length , where
Also denote the coordinates of center of gravity of by
Similarly, we may evaluate pixel greyness by the composite centroid rule:
In (15), we do also need the inverse values and , which are unknown. Then, we need to solve the following nonlinear equations:
The Newton iteration method is suggested as
where is an initial approximation, and vectors and the Jacobian matrix are given by
For the given quadratic models of T, five to seven iterations may reduce the initial errors by a factor . Of course, other iteration methods may also be chosen (see Atkinson [12]). The combination CIIM is called when the SIM is used for images under both T and . Note that the nonlinear solutions are involved only for the forward transformation T.
3. Improved Algorithms of SIM for Images Under T
The nonlinear solutions for seeking from in (16) by the Newton iterations (17) may encounter some difficulties, e.g., choices of good initial values and multiple solutions. Below, we develop improved techniques to reduce and even to bypass the nonlinear solutions completely. Such improved techniques may also be incorporated with the PDE solutions in the harmonic, Poisson and blending models provided in Section 5.
Technique I: Reduction of nonlinear solutions.
In Li [6], the reduction technique was first used for evaluating and only at the center of gravity of in , i.e., at the mid-points . It is better to carry out (16) only at the pixel points . The number of solutions to (16) is only as in Li [6], where is the total pixel number of the image. The approximations of and in the quadrilateral in may be obtained by the piecewise bilinear approximations (see Figure 2), where the gravity center , and . Then, the values of at and can be evaluated by the bilinear approximation:
Moreover, the following linear approximations may be used (see Figure 3). If , we have
If ,
The formula for is similar. The advantage of (19) in Li [6] is that the greyness errors in the computation are smaller. The algorithms in [6] are denoted by for . Note that when , the using Technique I is just the original CIIM given in Section 2.3.
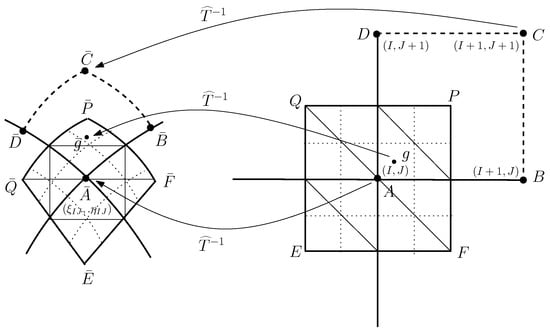
Figure 2.
The inverse transformations at the vertices of .
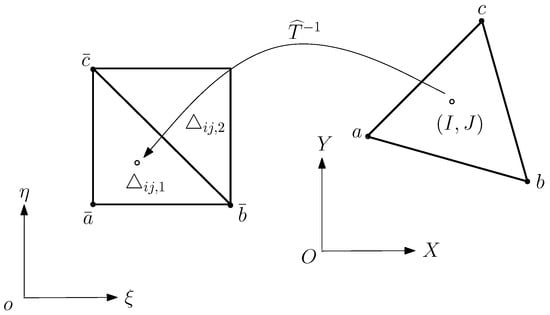
Figure 3.
The inverse transformation at in .
Technique II: Bypassing nonlinear solutions.
The values in (19)–(21) used in Technique I do not need to be exact, either, if their approximate values have small allowable errors. The nonlinear transformation T may also be approximated by a piecewise linear transformation on triangles , where in Figure 3. Hence, the values for can be evaluated approximately by those for . Note that the inverse transformation of is just a linear transformation locally. This avoids the nonlinear solutions in Algorithm SIM for T. The values and can be found using the following four steps.
- Step 1.
- Compute all and by and .
- Step 2.
- Find all potential in XOY, which can be determined by and , wherewhere is the largest integer . The definitions of and are the same.
- Step 3.
- Split into two triangles and as , where are also triangles, and find all possible such thatThe area coordinates , and are obtained from the following algebraic system:where are the vertices of triangles in Figure 3. The sufficient and necessary conditions for (22) are all nonnegative area coordinates .
- Step 4.
Note that Steps 1–4 above are easy to carry out. The computation complexity is also only , where is the total pixel number. More importantly, the computation for values, does not involve any nonlinear solutions. Based on the known , the bilinear approximations are formulated by
The improved SIM using Techniques I and II is given by
where given in (14). The computation complexity of (25) and (26) is , where . Hence, the CPU time by Techniques I and II is insignificant if comparing to . Note that no nonlinear solutions are needed in (26) either. To distinguish the algorithms using Techniques I and II from SIM and CIIM, we denote (26) by and the combination of (12) and (26) by . Technique I was proposed in [6] with a preliminary error analysis, but Technique II was proposed in [9] without error analysis. The error analysis is important and challenging for improved for T via both Techniques I and II.
Below, we will derive error bounds in the next section by Sobolev norms, which can be applied to discontinuous images.
4. Error Analysis
Algorithm analysis (such as error analysis) is essential to efficiency for numerical partial differential equations (PDEs). In this section, the new error analysis of image greyness by Techniques I and II is twofold.
I. Compared to error analysis in the original CIIM in Li [6], the inverse coordinates for and are not exact. First, the piecewise linear (or bilinear) interpolations and are used based on the exact values and in Technique I. We give a strict analysis (ref. [6], Section 6). Next, in Technique II, the inverse values and are approximated by and , also by using the piecewise linear interpolations. The linear (or bilinear) interpolations and on yield the same order of the errors, and the approximations and on also yield the same error for continuous images. The improvements in Section 3 will maintain the optimal convergence rates for as in [11] (Chapter 4). Therefore, Algorithms and circumvent the troublesome nonlinear solutions in the original CIIM in Section 2. For the rather complicated harmonic and blending models, the PDE solutions in Section 5 may be incorporated easily into the discrete algorithms proposed. Hence, the improved algorithms and may be applied to a wide scale of applications in digital images and patterns.
II. To estimate the errors of discontinuous images, we have to face the image discontinuity; this is a challenging task because discontinuity of image greyness always exists, and because the severe discontinuity may become useless for the continuous analysis of image transformations. In Section 4.2, we do not need the assumption (9) but still solicit the Sobolev norms for error analysis all the way. For the improved techniques in Section 3, the greyness errors, , are given in Corollary 1, where and . This is a significant development in error analysis for image transformations, noting that a high smooth greyness of images was often required in our previous papers [6,7]. New splitting techniques in this paper can also be applied to image processing, pattern recognition and AI under geometric transformation in [14,15,16,17].
4.1. Error Analysis for
Since the detailed analysis of the combinations for images under is given in Li [6], we only derive the distinct analysis for for T as . Let the division number , and then, we define the global greyness errors:
where are given in (26), and the sequential errors
and the pixel number . The Sobolev norms over are defined by
We consider the forward transformations T, and construct a cubic spline function passing over such that and . Define
where . The and denote the piecewise constant and bilinear functions, respectively. The transformation T is said to be regular if , and the Jacobian determinant J satisfies , where and are bounded constants. In this subsection, we assume that the image greyness is continuous to satisfy and as in (9), where is the Sobolev space. Such relaxed assumptions in the Sobolev space will be extended to the discontinuous greyness functions and in the sequential subsection. We have the following lemma.
Lemma 1.
Let T be regular, hold, and the interpolation functions with be used. There exists a bounded constant C independent of μ and h such that
where , and Case B denotes the whose inverse transformed shapes by fall across the boundary of in . For steps 2 and 3 in Figure 1, we have
where and .
Proof.
For simplicity, we consider only the case of and achieve the optimal convergence rates . For , the analysis may be carried out leading to and in probability in Li and Bai [7]. The difference in analysis between of Section 3 and SIM of Section 2 lies in the evaluation on the approximate errors resulting from , , and in (19) and (25), instead of the exact values, and . Now, we give the grayness errors from Technique I from Strang and Fix [18].
Lemma 2.
Let and in (19) be the piecewise bilinear interpolations of and on , based on the exact values of and satisfying the two equations and exactly. Suppose that and . There exists a bounded constant C independent of H such that
In Technique II, we obtain the approximations in (25) from the piecewise linear interpolations and (see Figure 3). Below we prove a lemma.
Lemma 3.
Let and be the piecewise linear interpolation based on the approximations: and , where and are the piecewise linear interpolations on in Lemma 2. Then, there exist the error bounds:
Proof.
Take the linear approximation (20) as an example. We have
where , , and . By using the affine transformation and , the triangle is transformed to a reference triangle . Then, we have
where the integrals are evaluated by calculus
Then, it follows that
Since all norms in finite dimensions are equivalent to each other, by noting , we obtain
where C is a bounded constant independent of H. Therefore, we obtain from (35) and (36)
This is the desired result (32), and Equation (33) holds similarly. □
Lemma 3 implies that the error order resulting from Technique II is no worse than that from Technique I. Now let us consider using Techniques I and II, and the absolute errors are defined by
where and are defined in (15) and (26), respectively. Denote
We have
To provide the error bounds for (39), we first give two lemmas.
Lemma 4.
Suppose that and . There exist the error bounds
Proof.
We have from and the Schwarz inequality
This is the first bound (40).
Next, we have from (43) and the Schwarz inequality
Third, from Lemma 3 we have similarly
This completes the proof of Lemma 4. □
The Jacobian determinant is given from (18). The nonsingular Jacobian determinant satisfies . Denote by the minimal singular value of Jacobian matrix . Then, we have , and give the following lemma.
Lemma 5.
Let the transformation T be regular. Then, under the inverse transformation , there exist the bounds
where is the maximal value of the Jacobian determinant, and is the minimal singular value of matrix in (18).
Proof.
We have
This is (45) for .
Now we prove a main theorem, which is not only important for error analysis of the improved algorithms in this paper, but also effective for error analysis of discontinuous greyness of images in Section 4.2.
Theorem 1.
Let and , and the conditions in Lemma 5 hold. Then, there exists the error bound for ,
Proof.
From Lemmas 1 and 5 for ,
where and are the original domains of and . Since can be regarded as piecewise bi-cubic spline functions, the following bounds hold due to finite-dimensional functions.
It follows that
Also we have from Lemmas 4 and 5
Remark 1.
For the regular transformation T, we have , and . Then, Equation (49) leads to
The error bounds (56) are the optimal estimates of the SIM via transformation in [11] (Chapters 3 and 4). The optimal convergence rates (56) remain for the improved via T without nonlinear solutions. Hence, the is beneficial for wide applications as in Section 5. Moreover, the error bounds (49) in Sobolev norms can be extended to discontinuous images below.
4.2. Error Analysis for Image Discontinuity
In our past study for image geometric transformations, the greyness functions were assumed to be continuous or even . However, since , we may study the discontinuity of digital images and patterns. In this subsection, we introduce the discontinuity degree. First, let us consider the binary images. If the entire image is either black or white, the discontinuity degree is zero. On the other hand, if the pixel is black when is even, and white when is odd, the discontinuity degree is one. Let be split into a partition of and denoted by . Denote by both the blacks and the whites existing at nine-pixel points (see Figure 4). Let the number . Hence, the discontinuity degree is defined by
There are four cases of an image in 2D of the image discontinuity with the discontinuity degree from (57).
Figure 4.
The square and in nodes.
- (1)
- There are only a few isolated pixels,
- (2)
- Greyness discontinuity exists only along the interior and exterior image boundary,
- (3)
- Greyness discontinuity is minor,
- (4)
- All are ,
The analysis below in this paper is well suited to Cases (1)–(3). For Case (4), the large, useless errors are obtained. Let us prove a new lemma.
Lemma 6.
For nonuniform binary images in , the error bounds of piecewise cubic-spline interpolant functions passing all are given by
Proof.
By the affine transformation: ,
the region is transformed to a unit square in Figure 4, where . Then, we have . Note that the same binary images at the nine-pixel points on as in . Let be the bi-quadratic Lagrange polynomial passing through all pixel points: . Based on the equivalence of finite dimensional norms, we can prove . Hence,
where is also a bi-quadratic Lagrange interpolant polynomial in .
For the q-greyness levels, we may define the greyness jumps of images as
The analysis of binary images can be extended to that of other multiple level images. From Theorem 1 and Lemma 6, we have the following theorem.
Theorem 2.
Let transformation T be regular and all conditions in Lemma 6 hold. When , there exist the bounds:
Proof.
From Theorem 1 and Lemma 6, we have
The regular transformation T implies , , . We have
This is the desired result (64) and completed the proof of Theorem 2. □
From Theorem 2, we have the following corollary.
Corollary 1.
Let all conditions in Theorem 1 hold. For the finite greyness jumps , the absolute errors are
When the images have with greyness jumps of interior and exterior boundaries ,
When with , denote . We have
Remark 2.
When the majority greyness of images is continuous, we have with . The errors are small due to small from (65). This is an important development from [6,7], where images are often assumed to be continuous. Note that the sequential errors as still hold. However for Case (4): the full discontinuous images, we have from (65) with and , which is meaningless. Another error analysis for greyness discontinuity is reported for other kinds of splitting algorithms in [11] (Chapter 8).
4.3. Summary of Six Combinations for the Cycle Transformation
Here let us give a summary of various combinations for the cycle transformation . There are six combinations with and in 2D images under : (1) , (2) and , (3) , (4) , (5) , and (6) in this paper. We list their characteristics, accuracy and convergence in Table 1 with only. The details of algorithms and rigor analysis are provided in a recent book [11]. Furthermore, a list of symbols used is listed in Appendix A.

Table 1.
Comparisons of six combinations for with in their characteristics, accuracy and convergence.
In summary, combination in [1,7] is the simplest, but suffers from low sequential errors and . Combination in [11] (Chapter 4) gains the better convergence rates, . When using the piecewise bilinear interpolations and , the sequential convergence rates are optimal. For using the piecewise constant interpolations and , the performance of is still satisfactory. However, suffers from nonlinear solutions during the forward transformation T. Consequently, for the inverse transformation , is recommended if the nonlinear solutions are easy using iteration methods. The original is suited well to low numbers of greyness-level images; but is suited to both low and high numbers of greyness level (≥256) images. The improved in [9] may completely bypass the nonlinear solutions, and its rigor analysis is explored in this paper. The improved are particularly beneficial for harmonic models with the finite element method, finite difference method and finite volume method because the approximate transformation obtained is already piecewise linear (see [8,9]).
To promote accurate images with no need for nonlinear solutions, for and for in [11] (Chapter 7) have been developed to have the optimal convergence rates . The sophisticated combinations in [11] (Chapter 8) may be easily carried out without sequential errors when . Moreover, an analysis in [11] (Chapter 8) reveals the better absolute error for all kinds of image discontinuity.
5. Applications to Harmonic, Poisson and Blending Models
5.1. Descriptions of the Models
Let us consider the arbitrary geometric shape transformations T by the given boundaries in both original and distorted images (see Figure 5). Assume , we may define the functions and by satisfying the Poisson equations
and the Dirichlet boundary conditions:
The transformation of (70)–(72) is called the Poisson model. When , Equations (70) and (71) are reduced to the harmonic equations:
Figure 5.
The transformation of arbitrary domains.
The transformation of (72) and (73) is called the harmonic model. The harmonic model was proposed in Li, et al. [1] and then in [9,11] for combinations CSIM and CIIM.
In this paper, we also propose blending models by assuming that the shapes can be blended as a thin elastic plate. This leads to the following two blending models.
- Simply supported blending models:
Since the white pixels can be added to images without any changes, the original image domains may be assumed to be rectangular or even square. The rectangular and square images have many applications, e.g., pictures, TV, etc. Below we will use the simple finite difference method (FDM) for harmonic, Poisson and blending models. The practical approximations and can be obtained and easily embedded into and . The error analysis for Poisson models in Section 5.3 shows that the optimal sequential errors will be maintained as well. Furthermore, the error analysis of the CSIM is made for harmonic, models by the FEM in [11] (Chapter 10).
5.2. The Finite Difference Method
Let be a unit square and the pixel points be chosen as the difference grid nodes. For the same partition , the standard five-node schemes of FDM for (70)–(72) are given by
and . The equations for are similar to (77) and (78). The successive over-relaxation iteration (SOR) may be chosen to solve (77) and (78) by
where w is the relaxation parameter. The iteration (79) is convergent when and optimal when (see Hageman and Young [19])
where is the spectral radius of the Jacobian iteration matrix. For the case of (77) and (78), . Since the iteration number is , the total CPU time for the FDM solutions is . For Dirichlet problems of PDE, the domain boundary must be given. The harmonic modes by using the FDM in (77)–(80) are used for face imaging resembling (face morphing) in a recent paper [8], where face boundary formulation is studied in detail.
Next, for the simply supported blending model (74)–(76), we may split into two Poisson models. Let and . We have two Poisson models.
- (I)
- Poisson Model A.
- (II)
- Poisson Model B.
We may also apply the same SOR to two models (81) and (82). As to the clamped blending models, we may obtain the FDM (see Figure 6a)
where the boundary conditions are given by
The difference equations for are similar. The block SOR can be used for solving (83) and (84) (see Hageman and Young [19]).
Figure 6.
Two partitions in the FDM.
When is an arbitrary bounded domain, the finite element method (FEM) may be chosen for the Poisson and the blending models. However, the programming of the FEM is more complicated than that of the FDM, in particular for the biharmonic equations in (74). Furthermore, the finite volume method (FVM) with Delaunay triangulation is used in [11] (Chapter 10). The FDM with SOR is easier to carry out for image transformations. It is worth pointing out that the FDM (77) is also a kind of FEM using linear elements of Figure 6b, or bilinear elements in Figure 6a.
Remark 3.
The standard five-node difference equations (77) are valid for uniform meshes as digital images. Rigor error analysis is given in Theorem 3 below for the improved by Techniques I and II to give the error . The Laplace operator can be used as a contour filter to test the edges of digital images; see Winnicki et al. [20]. The contour filter may be used for pre-processing to face boundary formulation for harmonic/Poisson models in [8]. Various difference schemes of nine-nodes: with , are discussed in [20]. Suppose the solutions . The best difference scheme is found in [20] ((16)–(18)) (called the fourth-order filter), to offer higher accuracy of the Laplace operator. The bounds of (87) can be improved to . Such a better difference scheme may also be used for harmonic/Poisson models. They are beneficial for the numerical algorithms by using piecewise-spline interpolations with in [11] (Chapter 10) due to the high errors requested.
5.3. Error Analysis for the FDM Solutions in
The FDM was used for harmonic transformations in [8,9], but no error analysis exists so far. In this subsection, we provide a new error analysis. In Section 2, and are exact. Since the values and can also be approximately obtained by FDM, and may be obtained approximately from and , which is similar to Section 3. To embed the FDM solutions and into SIM, we first give a lemma.
Lemma 7.
Let and be the piecewise bilinear interpolant on , and ξ and η be their inverse bilinear functions on , where by . Then, there exist the bounds,
where is the minimal value of matrix in (18), and the Jacobian determinant J satisfies .
Proof.
From the Lagrange mean theorem in calculus, we have
where is a mean value. Then, we have to lead to
This completes the proof of Lemma 7. □
Theorem 3.
Let all conditions in Theorem 1 hold. Suppose that and are the approximate solutions of the Poisson models by the FDM (or the linear FEM), there exist the error bounds of image errors for .
Proof.
We evaluate the greyness errors of the FDM. The FDM can be regarded as the linear FEM in the regular triangulation (see Figure 6b). The FDM solutions, and , have the error bounds for Poisson’s equation:
From (55), (87), Lemma 7 and Theorem 1, we obtain
This is the desired bound (86) and completes the proof of Theorem 3. □
Since Theorems 1 and 2 are similar to each other, all conclusions of error analysis for discontinuous images in Section 4.2 are valid.
6. Numerical and Graphical Experiments
6.1. Binary Images
Consider binary images with the conversion,
where and are used to display the greyness errors less than . We carry out combination for without nonlinear solutions. Choose the simple bi-quadratic model in [1] (p. 127). The greyness errors are listed in Table A1 and Table A2, and the graphical images are given in Figure A1 and Figure A2. In Table A1 and Table A2, E, , and are given in (27)–(29). Also , and denote the numbers of pixel errors for , and , respectively.
6.2. Harmonic and Poisson’s Models
Face recognition is an active research area due to wide applications, and we cite some recent reports [21,22,23,24,25,26]. Let us choose Lena’s images in [7,9], which consists of pixels with 256 greyness. Lena’s images were the standard model for testing in engineering. However, Lena’s images are no longer allowed in IEEE publications after 1 April 2024. Readers may refer to our original papers if necessary. We add a darkest square boundary for Lena’s images as in Figure A1 and choose the transformed boundary as that of the quadratic model, as in Figure A2. See Figures 12–18 in [7]. First, we use the for with the harmonic transformation T, with the same boundary of bi-quadratic transformation in [1] (p. 127). Next, consider the Poisson model (70)–(72), where the functions are given by
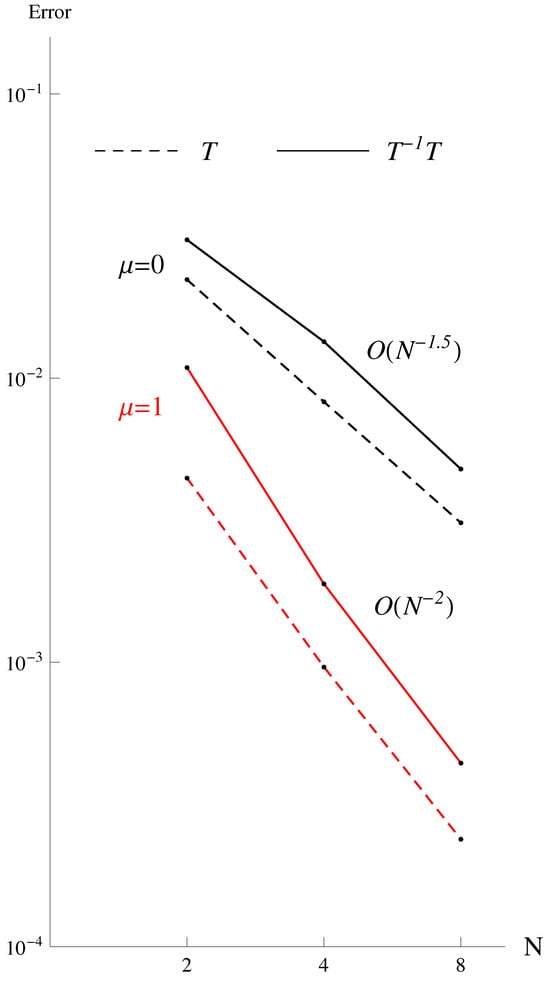
and is a smaller rectangle as . The exterior boundary is also chosen as that of the quadratic model. In this paper, we employ the FDM. The numerical results of greyness and pixel errors are listed in Table A3, Table A4, Table A5 and Table A6 for and . In Table A3, Table A4, Table A5 and Table A6, denotes the greyness-level errors in the 256 greyness-level system. Also, denotes the total number of non-empty pixels of the distorted images under T. In Table A5 and Table A6, the absolute errors of E and under the transformation T are computed from (27), and the sequential errors of and are computed from (28) and (29), respectively. For the cycle transformation , the sequential errors of and are defined similarly. The curves of under are drawn in Figure A3 from Table A5 and Table A6. We can see from Figure A3,
Equation (88) is consistent with (68) and Theorem 3 with by noting . Equation (89) is consistent with in probability in [7]. Note that the greyness discontinuity does happen, and the error analysis in Section 4.2 is valid and important in practical applications.
When the face boundary is changeable, the face images are also changeable [8]. The face transformations may be applied to the moving pictures as Sora. The harmonic models developed by using FDM in this paper may also be applied for face recognition and face morphing (see [8]). In addition, we also cited other reports [21,22,23,24,25,26,27,28] for this subject.
To close this section, let us give a remark.
Remark 4.
In this remark, we also apply the numerical algorithms to deep learning in AI. The numerical algorithms in Table 1 are the core of Chapters 2–8 of a new book [11]. The focus of this paper is error analysis for geometric transformations using Techniques I and II. The link between numerical algorithms and deep learning-based transformation may also be found in [11]. In [29,30,31], camera photos and the marine image videos are used; they may suffer from perspective transformations. The projective and perspective transformations are discussed in Chapter 1 of [11]. Moreover, in [32,33,34], the 3D videos and 3D geometric morphology are discussed, while the efficient numerical algorithms in 3D are explored in Chapter 9 of [11]. Feature-based approaches are discussed in [35,36,37], where line segments are basic features as handwritten characters. Their images are often found by cameras and X-rays. When geometric distortions and illumination effects are involved, the numerical algorithms in this paper and [11] can be used to remove them. Then, the correct pattern recognition can be made. Moreover, in [8,9] and Chapter 10 of [11], we provided more applicable examples in AI, such as handwriting recognition, hiding secret images, face image fusion, and morphing attack detection.
7. Concluding Remarks
Compared to our previous study of digital images under geometric transformations (see [1,6,7,9]), we address several novelties in this paper.
1. For the images under a nonlinear transformation T, the original SIM requires the nonlinear solutions, although the number of nonlinear equations may be reduced to in Li [6]. In Li, et al. [9], we proposed interpolation techniques that entirely bypass nonlinear solutions for the geometric images. The new numerical algorithms are called the improved for T and Combination under . This paper provides error analysis for the improved by using Techniques I and II.
2. The error bounds are given in Theorem 1 based on the Sobolev norms. The optimal convergence rates are obtained for the piecewise bilinear interpolations () and smooth images, where is the mesh resolution of an optical scanner, and N is the division number of a pixel split into sub-pixels.
3. For the images in which the portion of discontinuity is minor, the error bounds are given in Theorem 2. For general cases of discontinuous images, the error bounds are given in Corollary 1 as , when .
4. The combination can be applied to the harmonic, Poisson and blending models in Section 5 and their approximate solutions and may be obtained by the FDM using the SOR. The programming of the FDM is much easier than that of the FEM and the finite volume method (FVM), and the CPU time greatly reduced.
5. Numerical and graphical experiments are carried out in Section 6. The real images of (and ) pixels of 256 greyness-levels are carried out to show the importance of the improved algorithms. The numerical experiments in Section 6 also support the error analysis made.
6. New numerical algorithms for image geometric transformations in this paper are beneficial to computer vision, image processing and pattern recognition. Applications of numerical algorithms particularly to deep learning in AI are also given in Remark 4. Modern AI systems (e.g., ChatGPT, DeepSeek, Manus, Sora) rely on three core elements: data, models and algorithms. As emphasized in [8,10,11], efficient algorithms are critical for optimizing computational resources. Six combinations of numerical algorithms for the images under are summarized in Table 1.
Author Contributions
Conceptualization, Z.-C.L.; Methodology, H.-T.H., Y.W. and C.Y.S.; Writing—original draft, Z.-C.L.; Writing—review & editing, H.-T.H.; Funding acquisition, Y.W. and C.Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
We are grateful to the reviewers for valuable comments and suggestions. We also express our thanks to Yi-Chiung Lin for the numerical and graphical computations in this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Glossary of Symbols
- T: ; the nonlinear transformation.
- : the inverse transformation of T.
- : a cycle converse transformation of first T and then .
- I.
- Abbreviations of Numerical Algorithms
- (1)
- Single methods for T or :
- SSM: Splitting-shooting method for T.
- SIM: Splitting-integrating method for .
- : Advanced SSM for T having .
- : Advanced SSM for T without infinitesimal N.
- : Improved SIM reducing nonlinear equations for T.
- : Improved SIM bypassing nonlinear equations for T.
- (2)
- Combinations for (see Table 1):
- CIIM: Combination of splitting-integrating methods.
- : Combination of improved SIM reducing nonlinear solutions.
- : Combination of improved SIM bypassing nonlinear equations.
- CSIM: Combination of splitting-shooting-integrating methods.
- and : Advanced CSIM as having sequential errors.
- : CSIM without infinite N.
- CSSM: Combination of splitting-shooting methods.
- II.
- Regular Transformation Assumptions
- T: and , where is the Jacobian determinant of and . These conditions may lead to quasiuniform where .
- III.
- The integration representations of pixel greyness
- . .
- .
- and : the piecewise interpolation polynomials of order .
- IV.
- Greyness Errors
- (1)
- The absolute greyness errors:
- ..
- ,.
- : the numerical solutions.
- : the total number of nonempty pixels of .
- h: .
- (2)
- The sequential greyness errors for T:
- . .
- .
- (3)
- The absolute and sequential errors for :
- . .
- : the numerical solution.
- : , in particular and 2.
- : the total number of nonempty pixels of .
- : .
- V.
- Pixels, pixel regions and pixel errors
- . .
- .
- .
- .
- .
- .
- .
- , or ,or .
- , or .
- VI.
- Sobolev and other spaces with norms
- . .
- . .
- .
- : the Sobolev space of the functions with .
- : the space of the functions having k-order continuous derivatives.
- : the space of the functions having k-order bounded derivatives on ,where , and n is finite.
- VII.
- Other Notations
- The Jacobian matrix and determinant: .
- : the convergence rates.
- : the convergence rates in probability.
- H: the optimal resolution.
- h: the boundary length of and and .
- : the Laplace operator.
- : the floor function of x, i.e., the largest integer .

Table A1.
The greyness and pixel errors of binary images under by without nonlinear iterations for .
Table A1.
The greyness and pixel errors of binary images under by without nonlinear iterations for .
| T | ||||||||
| Sequential Errors | ||||||||
| N | Total | |||||||
| 1 | 687 | - | - | - | - | - | ||
| 2 | 824 | 80 | 57 | 0 | ||||
| 4 | 865 | 0 | 56 | 50 | ||||
| 8 | 862 | 0 | 25 | 21 | ||||
| 16 | 867 | 1 | 5 | 11 | ||||
| 32 | 867 | 0 | 2 | 2 | ||||
| 64 | 867 | 0 | 1 | 0 | ||||
| Sequential Errors | Absolute Errors | |||||||
| N | E | |||||||
| 1 | - | - | - | - | - | 2 | 0.5347127 | 0.07312 |
| 2 | 1 | 72 | 82 | 0.1801 | 0.2046 | 0 | 0.1801 | 0.2046 |
| 4 | 0 | 2 | 113 | 0.1026 | 0.1040 | 0 | 0.2067 | 0.1896 |
| 8 | 0 | 2 | 25 | 0 | 0.2142 | 0.1906 | ||
| 16 | 0 | 0 | 12 | 0 | 0.2152 | 0.1906 | ||
| 32 | 0 | 0 | 1 | 0 | 0.2156 | 0.1907 | ||
| 64 | 0 | 0 | 0 | 0 | 0.2156 | 0.1907 | ||

Table A2.
The greyness and pixel errors of binary images under by without nonlinear iterations for .
Table A2.
The greyness and pixel errors of binary images under by without nonlinear iterations for .
| T | ||||||||
| Sequential Errors | ||||||||
| N | Total | |||||||
| 1 | 903 | - | - | - | - | - | ||
| 2 | 957 | 1 | 5 | 54 | 0.2594(-1) | 0.4096(-1) | ||
| 4 | 961 | 1 | 9 | 4 | 0.592(-2) | 0.8293(-2) | ||
| 8 | 961 | 0 | 3 | 0 | 0.1440(-2) | 0.1816(-2) | ||
| 16 | 962 | 0 | 0 | 1 | 0.3611(-3) | 0.4303(-3) | ||
| 32 | 962 | 0 | 0 | 0 | 0.8800(-4) | 0.9834(-4) | ||
| 64 | 962 | 0 | 0 | 0 | 0.2256(-4) | 0.2472(-4) | ||
| Sequential Errors | Absolute Errors | |||||||
| N | E | |||||||
| 1 | - | - | - | - | - | 0 | 0.2134 | 0.1956 |
| 2 | 0 | 28 | 66 | 0.8706(-1) | 0.9920(-1) | 0 | 0.2964 | 0.2492 |
| 4 | 0 | 1 | 1 | 0.1603(-1) | 0.1473(-1) | 0 | 0.3121 | 0.2609 |
| 8 | 0 | 1 | 0 | 0.3762(-2) | 0.3226(-2) | 0 | 0.3158 | 0.2637 |
| 16 | 0 | 0 | 0 | 0.9333(-3) | 0.7585(-3) | 0 | 0.3168 | 0.2644 |
| 32 | 0 | 0 | 0 | 0.2316(-3) | 0.1843(-3) | 0 | 0.3170 | 0.2646 |
| 64 | 0 | 0 | 0 | 0.5829(-4) | 0.4552(-4) | 0 | 0.3170 | 0.2646 |

Table A3.
The greyness and pixel errors of Lena images under by for , where T is the harmonic model.
Table A3.
The greyness and pixel errors of Lena images under by for , where T is the harmonic model.
| T | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sequential Errors | Sequential Errors | Absolute Errors | ||||||||
| 1 | 64,324 | / | / | / | / | / | / | 0.58 | 0.2284(-2) | 0.4552(-1) |
| 2 | 65,641 | 6.01 | 0.2354(-1) | 0.7550(-1) | 6.20 | 0.2426(-1) | 0.6356(-1) | 5.94 | 0.2324(-1) | 0.5591(-1) |
| 4 | 66,264 | 2.34 | 0.8655(-1) | 0.2833(-1) | 3.16 | 0.1232(-1) | 0.2867(-1) | 6.35 | 0.2487(-1) | 0.5271(-1) |
| 8 | 66,512 | 0.95 | 0.3102(-2) | 0.1071(-1) | 1.18 | 0.4506(-2) | 0.1117(-1) | 6.47 | 0.2519(-1) | 0.5240(-1) |
| 16 | 66,576 | 0.38 | 0.1116(-2) | 0.4413(-2) | 0.41 | 0.1538(-2) | 0.4310(-2) | 6.49 | 0.2529(-1) | 0.5243(-1) |

Table A4.
The greyness and pixel errors of Lena images under by for , where T is the harmonic model.
Table A4.
The greyness and pixel errors of Lena images under by for , where T is the harmonic model.
| T | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sequential Errors | Sequential Errors | Absolute Errors | ||||||||
| 1 | 66,786 | / | / | / | / | / | / | 6.44 | 0.2508(-1) | 0.5398(-1) |
| 2 | 67,815 | 1.15 | 0.4474(-2) | 0.1561(-1) | 2.49 | 0.9690(-2) | 0.2499(-1) | 8.59 | 0.3349(-1) | 0.6628(-1) |
| 4 | 68,177 | 0.31 | 0.1090(-2) | 0.4358(-2) | 0.47 | 0.1847(-2) | 0.4183(-2) | 8.98 | 0.3504(-1) | 0.6907(-1) |
| 8 | 68,289 | 0.10 | 0.2377(-3) | 0.1805(-2) | 0.11 | 0.4428(-3) | 0.1223(-2) | 9.07 | 0.3539(-1) | 0.6969(-1) |

Table A5.
The greyness and pixel errors of Lena images under by for , where T is the Poisson model with on .
Table A5.
The greyness and pixel errors of Lena images under by for , where T is the Poisson model with on .
| T | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sequential Errors | Sequential Errors | Absolute Errors | ||||||||
| 1 | 69,284 | / | / | / | / | / | / | / | / | / |
| 2 | 70,558 | 5.67 | 0.2222(-1) | 0.7206(-1) | 7.84 | 0.3068(-1) | 0.9083(-1) | 8.08 | 0.3163(-1) | 0.9722(-1) |
| 4 | 71,145 | 2.26 | 0.8255(-2) | 0.2750(-1) | 3.45 | 0.1344(-1) | 0.3228(-1) | 8.18 | 0.3205(-1) | 0.9328(-1) |
| 8 | 71,366 | 0.98 | 0.3096(-2) | 0.1100(-1) | 1.25 | 0.4786(-2) | 0.1217(-1) | 8.28 | 0.3229(-1) | 0.9273(-1) |

Table A6.
The greyness and pixel errors of Lena images under by for , where T is the Poisson model with on .
Table A6.
The greyness and pixel errors of Lena images under by for , where T is the Poisson model with on .
| T | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sequential Errors | Sequential Errors | Absolute Errors | ||||||||
| 1 | 71,429 | / | / | / | / | / | / | 8.27 | 0.3225(-1) | 0.9324(-1) |
| 2 | 72,356 | 1.15 | 0.4449(-2) | 0.1713(-1) | 2.79 | 0.1089(-1) | 0.2734(-1) | 10.33 | 0.4033(-1) | 0.9884(-1) |
| 4 | 72,775 | 0.28 | 0.9620(-3) | 0.3144(-2) | 0.48 | 0.1887(-2) | 0.4070(-2) | 10.73 | 0.4189(-1) | 0.1005 |
| 8 | 72,880 | 0.10 | 0.2388(-3) | 0.7165(-3) | 0.11 | 0.4417(-3) | 0.8919(-3) | 10.83 | 0.4228(-1) | 0.1009 |

Figure A1.
The original binary image.
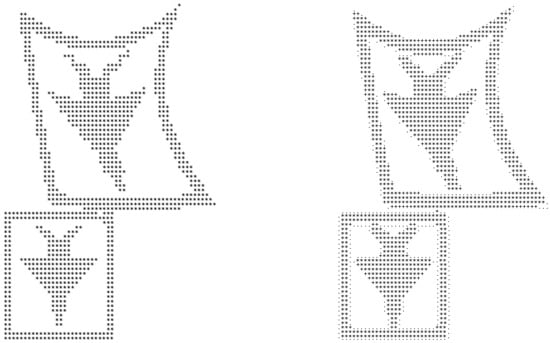
Figure A2.
The distorted and restored images under by for and (left) and for and (right).
References
- Li, Z.C.; Bui, T.D.; Tang, Y.Y.; Suen, C.Y. Computer Transformation of Digital Images and Patterns; World Scientific Publishing: Singapore; Hackensack, NJ, USA; London, UK, 1989. [Google Scholar]
- Farin, G. Curve and Surfaces for Computer-Aided Geometric Design: A Practical Guide, 3rd ed.; Academic Press: Boston, MA, USA, 1993. [Google Scholar]
- Foley, J.D.; van Dam, A.; Feiner, S.K.; Hughes, J.F. Computer Graphics: Principles and Practice, 2nd ed.; Addison-Wesley: Reading, MA, USA, 1990. [Google Scholar]
- Rogers, D.F.; Adams, J.A. Mathematical Elements for Computer Graphics, 2nd ed.; McGraw Hill: New York, NY, USA, 1989. [Google Scholar]
- Su, B.Q.; Liu, D.Y. Computational Geometry: Curve and Surface Modeling; Academic Press: Boston, MA, USA, 1989. [Google Scholar]
- Li, Z.C. Splitting-integrating method for the image transformations T and T−1T. Comput. Math. Applic. 1996, 32, 39–60. [Google Scholar] [CrossRef]
- Li, Z.C.; Bai, Z.D. Probabilistic analysis on the splitting-shooting method for image transformations. J. Comp. Appl. Math. 1998, 94, 69–121. [Google Scholar] [CrossRef]
- Huang, H.T.; Li, Z.C.; Wei, Y.; Suen, C.Y. Face boundary formulation for harmonic models: Face image resembling. J. Imaging 2025, 11, 14. [Google Scholar] [CrossRef]
- Li, Z.C.; Wang, H.; Liao, S. Numerical algorithms for image geometric transformation and applications. IEEE Trans. Sys. Man Cybern Part B-Cybern. 2004, 34, 132–149. [Google Scholar] [CrossRef] [PubMed]
- DeepSeek-AI Group. DeepSeek-R1: Incentivizing Reasoning Capability in LLMs via Reinforcement Learning. arXiv 2025, arXiv:2501.12948v1. [Google Scholar] [CrossRef]
- Li, Z.C.; Huang, H.T.; Wei, Y.; Suen, C.Y. Algorithms for Geometric Image Transformations. World Sci. 2025; in press. [Google Scholar]
- Atkinson, K.E. An Introduction to Numerical Analysis, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1989. [Google Scholar]
- Davis, P.J.; Rabinowitz, P. Methods of Numerical Integration, 2nd ed.; Academic Press Inc.: San Diego, CA, USA; New York, NY, USA, 1984. [Google Scholar]
- Castleman, K.R. Geometric transformations. In Microscope Image Processing, 2nd ed.; Merchant, F.A., Castlema, K.R., Eds.; Academic Press: London, UK; Elsevier: London, UK, 2023; pp. 47–54. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 4th ed.; Pearson: New York, NY, YSA, 2017. [Google Scholar]
- Lakemond, N.; Holmberg, G.; Pettersson, A. Digital transformation in complex systems. IEEE Trans. Eng. Manag. 2024, 71, 192–204. [Google Scholar] [CrossRef]
- Pang, Y.; Lin, J.; Qin, T.; Chen, Z. Image-to-image translation: Methods and applications. IEEE Trans. Multimed. 2021, 24, 3859–3881. [Google Scholar] [CrossRef]
- Strang, G.; Fix, G.J. An Analysis of the Finite Element Method; Prentice-Hall Inc.: Englewood Cliffs, NJ, USA, 1973. [Google Scholar]
- Hageman, L.A.; Young, D.M. Applied Iterative Method; Academic Press: New York, NY, YSA, 1981. [Google Scholar]
- Winnicki, I.; Jasinski, J.; Pietrek, S.; Kroszczynski, K. The mathematical characteristic of the Laplace contour filters used in digital image processing. The third order filters. Adv. Geod. Geoinf. 2022, 71, e23. [Google Scholar] [CrossRef]
- Guo, G.; Zhang, N. A survey on deep learning based face recognition. Comput. Vis. Image Underst. 2019, 189, 102805. [Google Scholar] [CrossRef]
- Indrawal, D.; Sharma, A. Multi-module convolutional neural network based optimal face recognition with minibatch optimization. Int. J. Image Graph. Signal Process. 2022, 3, 32–46. [Google Scholar] [CrossRef]
- Scherhag, U.; Rathgeb, C.; Merkle, J.; Busch, C. Deep face representations for differential morphing attack detection. IEEE Trans. Inf. Forensics Secur. 2020, 15, 3625–3639. [Google Scholar] [CrossRef]
- You, M.; Han, X.; Xu, Y.; Li, L. Systematic evaluation of deep face recognition methods. Neurocomputing 2020, 388, 144–156. [Google Scholar] [CrossRef]
- Tuncer, T.; Dogan, S.; Subasi, A. Automated facial expression recognition using novel textural transformation. J. Ambient Intell. Human Comput. 2023, 14, 9439–9449. [Google Scholar] [CrossRef]
- Venkatesh, S.; Ramachandra, R.; Raja, K.; Busch, C. Face morphing attack generation and detection: A comprehensive survey. IEEE Trans. Technol. Soc. 2021, 2, 128–145. [Google Scholar] [CrossRef]
- Aloraibi, A.Q. Image morphing techniques: A review. Technium 2023, 9, 41–53. [Google Scholar] [CrossRef]
- Li, J.; Zhou, S.K.; Chellappa, R. Appearance modeling using a geometric transform. IEEE Trans. Image Process. 2009, 18, 889–902. [Google Scholar] [PubMed]
- Cai, J.; Ding, S.; Zhang, Q.; Liu, R.; Zeng, D.; Zhou, L. Broken ice circumferential crack estimation via image techniques. Ocean Eng. 2022, 259, 111735. [Google Scholar] [CrossRef]
- Yao, F.; Zhang, H.; Gong, Y.; Zhang, Q.; Xiao, P. A study of enhanced visual perception of marine biology images based on diffusion-GAN. Complex Intell. Syst. 2025, 11, 1–20. [Google Scholar] [CrossRef]
- Zhou, L.; Cai, J.; Ding, S. The identification of ice floes and calculation of sea ice concentration based on a deep learning method. Remote. Sens. 2023, 15, 2663. [Google Scholar] [CrossRef]
- Wang, B.; Chen, W.; Qian, J.; Feng, S.; Chen, Q.; Zuo, C. Single-shot super-resolved fringe projection profilometry (SSSR-FPP): 100,000 frames-persecond 3D imaging with deep learning. Light. Sci. Appl. 2025, 14, 1–13. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, F.; Gu, Y.; Zhang, Y.; Cui, C.; Liu, J.; Qiu, Z.; Wang, P. Optimization of 3D reconstruction of granular systems based on refractive index matching scanning. Opt. Laser Technol. 2025, 186, 112662. [Google Scholar] [CrossRef]
- Xu, X.; Fu, X.; Zhao, H.; Liu, M.; Xu, A.; Ma, Y. Three-dimensional reconstruction and geometric morphology analysis of lunar small craters within the patrol range of the Yutu-2 rover. Remote. Sens. 2023, 15, 4251. [Google Scholar] [CrossRef]
- Sun, Q.; Wang, H.; Liu, W.; Zou, J.; Ye, F.; Li, Y. An improved stereo visual-inertial SLAM algorithm based on point-and-line features for subterranean environments. IEEE Trans. Veh. Technol. 2025, 74, 3925–3940. [Google Scholar] [CrossRef]
- Zhao, D.; Zhou, H.; Chen, P.; Hu, Y.; Ge, W.; Dang, Y.; Liang, R. Design of forward-looking sonar system for real-time image segmentation with light multiscale attention net. IEEE Trans. Instrum. Meas. 2024, 73, 4501217. [Google Scholar] [CrossRef]
- Li, M.; Jia, T.; Wang, H.; Ma, B.; Lu, H.; Lin, S.; Cai, D.; Chen, D. AO-DETR: Anti-Overlapping DETR for X-Ray Prohibited Items Detection. IEEE Trans. Neural Netw. Learn. Syst. 2024; early access. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).