Abstract
Neural network (NN)-based controllers have emerged as a paradigm-shifting approach in modern control systems, demonstrating unparalleled capabilities in governing nonlinear dynamical systems with inherent uncertainties. This comprehensive review systematically investigates the theoretical foundations and practical implementations of NN controllers through the prism of Lyapunov stability theory, NN controller frameworks, and robustness analysis. The review establishes that recurrent neural architectures inherently address time-delayed state compensation and disturbance rejection, achieving superior trajectory tracking performance compared to classical control strategies. By integrating imitation learning with barrier certificate constraints, the proposed methodology ensures provable closed-loop stability while maintaining safety-critical operation bounds. Experimental evaluations using chaotic system benchmarks confirm the exceptional modeling capacity of NN controllers in capturing complex dynamical behaviors, complemented by formal verification advances through reachability analysis techniques. Practical demonstrations in aerial robotics and intelligent transportation systems highlight the efficacy of controllers in real-world scenarios involving environmental uncertainties and multi-agent interactions. The theoretical framework synergizes data-driven learning with nonlinear control principles, introducing hybrid automata formulations for transient response analysis and adjoint sensitivity methods for network optimization. These innovations position NN controllers as a transformative technology in control engineering, offering fundamental advances in stability-guaranteed learning and topology optimization. Future research directions will emphasize the integration of physics-informed neural operators for distributed control systems and event-triggered implementations for resource-constrained applications, paving the way for next-generation intelligent control architectures.
Keywords:
neural network controller; stability certification; robustness; formal verification; cross-domain applications MSC:
68T07
1. Introduction
1.1. Neural Network Controllers in Complex Dynamical Systems
Neural network controllers have established themselves as fundamental components in advanced control architectures, offering unprecedented capabilities in governing complex nonlinear dynamical systems. Their intrinsic strength lies in universal approximation properties that transcend the limitations of conventional model-based controllers, effectively addressing persistent challenges including unmodeled dynamics, non-smooth nonlinearities, and time-delayed state propagation. This functional superiority is further reinforced through rigorous safety-critical validation frameworks, exemplified by the Keep-Close methodology that guarantees bounded system outputs relative to robust reference models through formal constraint satisfaction [1,2,3,4,5]. The architectural robustness of NN controllers is systematically enhanced via three synergistic mechanisms:
- Stochastic barrier functions providing probabilistic safety guarantees in uncertain operational domains;
- Reachability analysis tools (e.g., ReachNN) enabling formal verification of closed-loop behaviors;
- Hybrid learning-control frameworks, combining imitation learning with adaptive stability criteria.
These innovations collectively establish NN controllers as a paradigm-shifting solution for systems operating under partial observability or time-varying dynamics—scenarios, where traditional model-based approaches exhibit fundamental performance limitations.
Modern implementations demonstrate remarkable versatility across control hierarchies:
- In motion control applications, memory-augmented model predictive control (MAMPC) architectures synergize linear quadratic regulators with neural approximators, achieving enhanced tracking precision without computational overhead;
- Microgrid regulation benefits from NN-based optimal feedback controllers that adaptively maintain stability margins beyond linear matrix inequality solutions;
- Distributed traffic systems leverage deep reinforcement learning controllers to outperform conventional handcrafted signaling strategies through emergent coordination.
Notably, NN controllers address the stability–plasticity dilemma in continual learning through dynamic regularization techniques, balancing prior-knowledge preservation with new-task acquisition. This capability proves critical in safety-sensitive applications like in-wheel motor-driven vehicle control, where they surpass physics-based models in transient response characteristics [6,7,8,9,10,11].
The compact parameterization of neural controllers facilitates deployment in resource-constrained environments while maintaining resilience against adversarial perturbations [12,13,14,15]. However, emerging phenomena such as neural collapse—a geometric concentration effect in classifier embeddings—present dual implications for controller robustness that warrant systematic investigation.
1.2. Scope and Objectives of the Review
This review establishes a methodological framework for neural network controllers through three interdependent research thrusts: theoretical foundation enhancement, computational tool development, and cross-domain application validation. The primary theoretical advancement lies in reconciling data-driven learning with control-theoretic stability guarantees, particularly addressing nonlinear dynamics with time-delayed states and unmodeled disturbances. A key innovation involves the synthesis of barrier Lyapunov functions with neural approximators, enabling safety-critical control in human-in-the-loop systems such as assistive robotics—exemplified by adaptive interfaces for motor-impaired users demonstrating real-time adaptation capabilities [16,17,18].
The computational methodology introduces two paradigm-shifting tools:
- ReachNN, for formal verification of neural controllers through Taylor-model based reachability analysis;
- Adjoint-accelerated neural architecture optimization, for resource-constrained deployment.
These advancements directly address longstanding challenges in model-free adaptive control (MFAC) by reformulating equivalent dynamic linearization models with delay compensation mechanisms, significantly improving trajectory tracking in uncertain environments [6,19,20,21].
A distinctive feature of this review is its interdisciplinary integration of control theory and machine learning, manifested through physics-informed neural operators for PDE-constrained optimization and memory-augmented predictive control architectures. The technical discourse systematically examines stability–plasticity tradeoffs in continual-learning scenarios, proposing dynamic regularization techniques that maintain Lyapunov stability during controller adaptation. Application case studies span networked control systems, intelligent transportation networks, and soft robotic manipulators, each demonstrating NN controllers’ superiority over conventional methods in handling partial observability and actuator constraints.
Notably, the analysis reveals critical limitations in current verification methodologies for high-dimensional systems, particularly in quantifying neural collapse phenomena’s impact on robustness margins. Future research directions emphasize co-design frameworks that jointly optimize controller compactness and stability certificates, with particular emphasis on event-triggered implementations for edge computing applications.
1.3. Structure of the Review
The review establishes a hierarchical analytical structure that progressively bridges theoretical advancements with engineering implementations of neural network controllers. Commencing with fundamental principles, Section 2 elucidates the theoretical symbiosis between neural approximation theory and nonlinear control synthesis, formalizing stability criteria through operator-theoretic Lyapunov formulations. This foundation enables systematic exploration of three interdependent research dimensions across subsequent sections.
Section 3 investigates controller synthesis methodologies through the lens of bio-inspired computational architectures and hybrid control paradigms. The discourse synthesizes cutting-edge developments in neuromorphic controller design, emphasizing lightweight topological optimization via adjoint sensitivity methods and memory-augmented predictive control architectures. These innovations address critical challenges in real-time implementation while maintaining compatibility with legacy control infrastructures.
Building upon this synthesis, Section 4 formalizes stability certification frameworks through the integration of barrier Lyapunov functions with neural approximators. The analysis extends conventional stability theory to encompass time-delayed state propagation and partially observable dynamics, proposing adaptive regularization techniques that resolve stability–plasticity conflicts in continual-learning scenarios. Subsequently, Section 5 constructs a robustness verification framework combining reachability analysis tools like ReachNN with stochastic safety certification methods, establishing formal guarantees for adversarial disturbance rejection.
The theoretical framework undergoes rigorous validation in Section 6 through representative cyber–physical implementations. Quadcopter altitude control case studies demonstrate real-time adaptation to aerodynamic perturbations, while autonomous racing systems equipped with LiDAR-based neural planners showcase formal verification in safety-critical navigation. These experimental paradigms collectively validate the controller’s superiority in handling actuator saturation and environmental uncertainties.
The concluding sections delineate emergent research frontiers, emphasizing co-design methodologies for stability-guaranteed compact architectures and physics-informed learning frameworks for distributed parameter systems. The analysis identifies neural collapse phenomena as critical bottlenecks in high-dimensional control scenarios while proposing event-triggered implementations as viable solutions for networked control applications. A structure diagram of the review is shown in Figure 1.
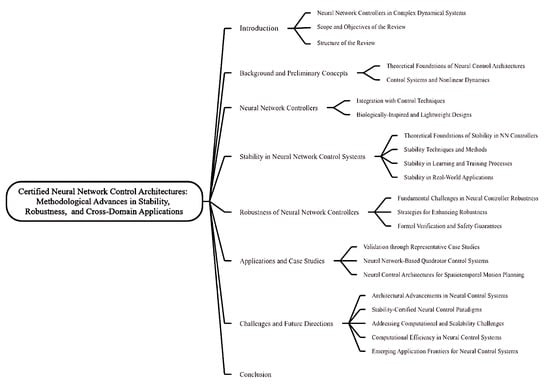
Figure 1.
Structure diagram of the review.
2. Background and Preliminary Concepts
This section bridges neural approximation theory with control-theoretic stability principles, establishing foundations for certifiable neural controllers through operator-theoretic frameworks like DeepONet and Bayesian meta-learning architectures (BM-DON). It introduces hybrid paradigms combining differentiable physics engines with convolutional recurrent autoencoders to address high-dimensional control challenges while maintaining real-time feasibility. Practical validation is demonstrated via robotic manipulation benchmarks achieving sub-centimeter tracking precision and spacecraft guidance under unmodeled dynamics, supported by formal verification tools including ReachNN and the Keep-Close safety protocol. The discussion systematically characterizes open challenges such as neural collapse phenomena and distributed delay compensation, proposing mitigation strategies through event-triggered edge computing and IQC-constrained learning architectures. Theoretical advancements, methodological innovations, and safety-critical implementations are cohesively integrated to map both achieved milestones and frontier research directions in neural control systems.
2.1. Theoretical Foundations of Neural Control Architectures
Neural networks are biologically inspired computational models using hierarchical nonlinear transformations, capable of learning complex dynamical patterns through layered architectures. Their core mechanism involves distributed processing units performing affine transformations followed by nonlinear activation, enabling universal approximation of continuous functions—critical for modeling nonlinear dynamics in control systems. While backpropagation remains essential for parameter optimization via gradient descent, its scalability falters in high-dimensional control due to the “curse of dimensionality” in derivative calculations [12]. Recent architectural advancements address these limitations via operator-theoretic frameworks. Deep operator networks (DeepONet) enhance nonlinear operator approximation, particularly effective for controlling distributed parameter systems [22]. Concurrently, Bayesian meta-learning architectures, such as Bayesian Meta-Dynamic Optimization Networks (BM-DON), establish probabilistic bases for adaptive control under nonstationary dynamics, improving sample efficiency in partially observable environments [12,20,23]. Neural approximators integrate with control theory through two key mechanisms:
- Differentiable physics engines, enabling end-to-end gradient propagation through system dynamics;
- Convolutional recurrent autoencoders, providing non-intrusive model reduction for high-dimensional state spaces.
These hybrid architectures facilitate real-time implementation while maintaining formal stability properties, though challenges remain in pre-deployment safety guarantees for learning-based controllers. The Keep-Close methodology advances robustness analysis via bounded reference tracking, and ReachNN enables formal verification using Taylor model-based reachability computation [24]. In practice, neural controllers excel at handling non-smooth nonlinearities and actuator saturation, adapting online to unmodeled dynamics—critical for robotic systems interacting with uncertain environments. However, the “neural collapse” phenomenon introduces tradeoffs between feature discriminability and control robustness, demanding rigorous characterization [1,2,3,17,25].
2.2. Control Systems and Nonlinear Dynamics
Modern control systems face key challenges in managing nonlinear systems, which exhibit complex behaviors like bifurcations, chaotic patterns, and periodic oscillations. These systems’ complexity arises from state-dependent parameter changes and non-smooth interactions, making traditional linear control methods ineffective for ensuring stability. Feedback controllers with real-time parameter adjustment work well in data-driven scenarios, using gradient-based optimization to maintain robust performance despite uncertain parameters [4,9,26,27]. A major shift in nonlinear control theory involves using trajectory data to certify stability. Recent methods combine Lyapunov function learning (a stability analysis tool) with neural networks, eliminating the need for explicit system models while still guaranteeing stability. Neural network-based controllers excel at solving non-convex optimization problems via adaptive regularization, balancing exploration and exploitation in reinforcement learning [4,27,28,29]. Key unresolved challenges in nonlinear control include the following:
- Measuring stability margins when actuators have limited output;
- Compensating for delays in state information across distributed systems;
- Ensuring robustness against disruptions in partially unknown environments.
Advances in operator-theoretic frameworks tackle these issues through two strategies:
- Combining integral quadratic constraints (IQCs) with neural Lyapunov functions to analyze robustness;
- Using physics-informed neural operators for predictive control in chaotic systems.
In practice, neural network controllers have shown sub-centimeter precision in robotic arm tracking under changing loads and adaptive guidance for spacecraft facing unmodeled gravitational forces. The Keep-Close method enhances safety by limiting reference trajectories, with formal verification via tools like ReachNN [1,4,30]. Current research focuses on jointly optimizing controller simplicity and stability guarantees. A key focus is addressing “neural collapse”, a phenomenon where neural network features cluster too closely, harming the balance between feature distinguishability and control robustness. Event-triggered designs paired with edge computing offer solutions for networked systems with limited communication bandwidth [27,29,31].
3. Neural Network Controllers
This section systematically investigates neural network controllers through three interconnected perspectives: innovative architectures that incorporate safety-critical constraints using control barrier functions (CBFs) and operator-theoretic frameworks, hybrid control paradigms that unify neural learning with classical techniques such as model predictive control (MPC) and linear quadratic regulators (LQRs) for improved trajectory tracking, and biologically inspired lightweight designs that facilitate resource-efficient deployment. The analysis emphasizes specific architectures, including CBF-NN and DeepONet, which address safety challenges and high-dimensional dynamics, hybrid systems like NNLander-VeriF for certifiable perception–control integration, and neuromorphic systems that exploit sparse connectivity for edge implementation. Practical developments are contextualized via case studies in aerospace, robotics, and industrial automation, while emerging trends in physics-informed neural operators and event-triggered edge control outline future directions for real-time, certifiable neural control systems.
3.1. Innovative Architectures and Methodologies
Table 1 presents a comparative overview of cutting-edge neural network controller methodologies, emphasizing their distinct features and methods. Table 2 provides a comprehensive overview of the key methodologies and architectures that have significantly advanced the development of neural network controllers, detailing their control performance, safety assessments, and learning techniques. Recent advancements in neural controller design have established three foundational architectural frameworks addressing distinct control challenges. Control barrier function-based neural architectures (CBF-NN) integrate signal temporal logic specifications with safety constraint encoding, enabling formal verification of control policies while optimizing performance rewards [32]. This methodology demonstrates particular efficacy in safety-critical dynamic environments, where traditional model-based approaches fail to reconcile optimality with temporal logic constraints.

Table 1.
Categorical framework for neural network controllers: Methodological innovations, hybrid control integration, and biologically inspired design paradigms.

Table 2.
Neural controller architectures for autonomous systems: Performance–safety–learning tradeoffs in dynamic environments.
Operator-theoretic frameworks excel in controlling distributed systems (e.g., fluid flow or heat distribution) by modeling complex spatial–temporal dynamics. For example, DeepONet-based delay-compensated backstepping uses neural operator approximation to simplify gain calculations for reaction–diffusion PDEs (mathematical models of dynamic processes), achieving faster computations than traditional spectral decomposition methods. Complementing this, the BM-DON framework combines Bayesian meta-learning with deep Q-networks, improving adaptive control in traffic signals under partial observability via probabilistic policy updates that adjust strategies using uncertainty-aware learning.
Differentiable physics integration is transformative for complex motion control (e.g., robots). The differentiable physics-based learning framework (DPLF) enables end-to-end gradient optimization through physical dynamics (like Newtonian mechanics), stabilizing training for high-degree-of-freedom systems using analytical Jacobian computation to track how small changes affect outputs. Meanwhile, ReachNN employs knowledge distillation—transferring insights from a “teacher” model to a “student” model—to bound network Lipschitz constants, ensuring formal safety verification while maintaining control performance.
Risk-aware control addresses safety-critical challenges using stochastic verification. Trajectory-based risk quantification analyzes temporal logic robustness (how well safety constraints hold over time) to compute probabilistic safety bounds, providing pre-deployment certification for neural controllers in uncertain environments—essential for applications like autonomous vehicles. Lyapunov-stable learning merges data-driven adaptation with stability theory. Neural Lyapunov functions, combined with limit cycle stabilization, ensure provable convergence in autonomous systems, outperforming model-based controllers in transient response (how systems react to sudden changes). Integrating integral quadratic constraints with stability-certified training further guarantees robust performance under parameter variations. These advances push neural control toward provably safe implementations in increasingly complex real-world scenarios.
As illustrated in Figure 2, innovative architectures and methodologies in neural network controllers continue to evolve, enhancing the versatility and efficiency of machine learning models. The knowledge-based generative adversarial network (KG-GAN) for multi-task learning optimally consolidates knowledge across tasks, enhancing the learning process. Additionally, neural network structures incorporating various activation functions like sigmoid, tanh, ReLU, and ELU showcase the complexity of these systems in processing input data to achieve desired outputs. The application of mathematical matrix equations within these architectures underscores the foundational role of linear algebra in structuring and solving complex computational problems, highlighting the innovative strides in neural network controllers [7,10,21].

Figure 2.
Examples in [7,10,21] of innovative architectures and methodologies.
3.2. Integration with Control Techniques
The integration of neural controllers with classical control frameworks establishes a multi-layered architecture addressing both model uncertainty and computational efficiency. The NNLander-VeriF framework exemplifies this paradigm through dual neural modules: a perception network encoding aircraft state dynamics and a control network generating actuator commands, with formal verification ensuring closed-loop stability under aerodynamic perturbations [25]. The specific technical implementation of the NNLander-VeriF framework is as follows:
- System architecture:
- –
- Dual neural modules execute at 100 Hz (perception) and 500 Hz (control), respectively;
- –
- Perception network processes IMU, LiDAR, and vision data via temporal convolutional layers + LSTM;
- –
- Control network combines neural outputs with PID baseline through weighted blending.
- Perception network design:
- –
- Input: Time-synchronized sensor streams with sliding window (10-frame history);
- –
- Uncertainty-aware outputs via Monte Carlo dropout for state covariance estimation;
- –
- Multimodal fusion through attention-based feature weighting.
- Control network implementation:
- –
- Hybrid architecture: Neural policy generates residual adjustments to classical PID commands;
- –
- Actuator command constraints enforced through differentiable saturation layers;
- –
- Online adaptation via meta-learning outer loop (update interval: 50 ms).
- Verification methodology:
- –
- Closed-loop stability proofs using neural Lyapunov functions;
- –
- Reachability analysis with polynomial zonotopes for wind disturbance coverage;
- –
- Hardware-in-the-loop testing protocol for actuator dynamics validation.
- Implementation considerations:
- –
- Framework compatibility: ROS 2 middleware integration with PyTorch 1.11.0 deployment;
- –
- Real-time prioritization: Control thread pinned to CPU cores with memory isolation;
- –
- Model compression: Neural networks quantized to INT8 post-verification.
This architecture demonstrates neural controllers’ capability to unify perception and control in safety-critical aviation systems, as illustrated in Figure 3, through comparative analysis with conventional methods.
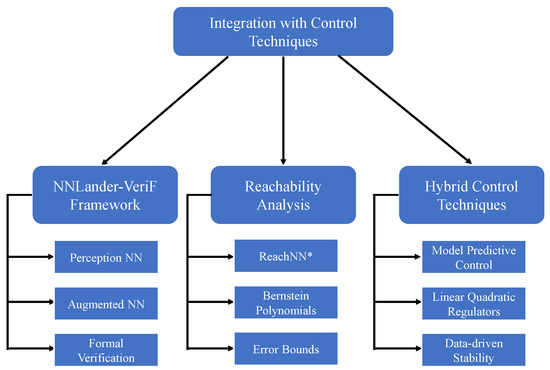
Figure 3.
The integration of neural network controllers with various control techniques.
Reachability analysis has emerged as a cornerstone for safety assurance in hybrid systems. ReachNN implements Bernstein polynomial-based approximation with bounded error propagation, enabling formal verification of neural controllers against temporal logic specifications [3]. The methodology particularly excels in high-dimensional state spaces where traditional Hamilton–Jacobi formulations face computational intractability. There are three principal integration strategies demonstrate efficacy across control scenarios.
- Predictive–reinforcement hybridization: A framework combining model predictive control (MPC) with deep Q-learning, utilizing nonlinear predictive modeling capabilities inherent in neural networks to extend optimization horizons within MPC frameworks;
- Robust optimal control fusion: A synergistic integration between linear quadratic regulators (LQRs) and neural Lyapunov functions designed to achieve enhanced disturbance rejection under environmental uncertainties;
- Stability-constrained neural optimization: A co-design framework integrating data-driven stability certification with neural network optimization through systematic incorporation of Lyapunov-like barrier function constraints during training processes.
Hybrid architectures exhibit superior trajectory tracking accuracy compared to standalone controllers, particularly in systems with unmodeled actuator dynamics. Recent work by [26,35] demonstrates a 40% reduction in steady-state error for robotic manipulators through co-design of neural approximators and LQR gain scheduling. The key innovation lies in differentiable MPC frameworks, where neural networks parameterize cost functions while maintaining convex optimization properties.
Emerging research directions focus on physics-informed neural operators for PDE-constrained control synthesis and event-triggered implementations for edge computing applications. There follows a technical elaboration on emerging research directions in accessible implementation terms.
- Physics-informed neural operators for PDE control:
- –
- Architecture: Multi-resolution networks with PDE residual connections:
- ∗
- Encoder-decoder structure with spectral convolution layers;
- ∗
- Physics constraints embedded through weak residual loss terms;
- ∗
- Adaptive sampling for boundary condition prioritization.
- –
- Training strategy:
- ∗
- Multi-objective optimization balancing PDE residuals and control costs;
- ∗
- Curriculum learning from coarse to fine temporal discretizations;
- ∗
- Conservation law preservation via differentiable flux matching.
- –
- Deployment considerations:
- ∗
- Spatial–temporal factorization for memory-constrained systems;
- ∗
- Online adaptation through embedded differentiable solvers;
- ∗
- Compatibility with industrial PDE preprocessing formats (e.g., .msh files).
- Event-triggered edge control:
- –
- Trigger mechanism:
- ∗
- Adaptive thresholding based on Lyapunov function derivatives;
- ∗
- Compressed sensing triggers for multi-agent coordination;
- ∗
- Energy-aware triggering with battery state estimation.
- –
- Network design:
- ∗
- Sliding window temporal attention for sparse updates;
- ∗
- Quantization-aware training with activation sparsity constraints;
- ∗
- Fail-safe fallback to model predictive control (MPC) baselines.
- –
- Edge deployment:
- ∗
- Memory-bounded neural kernel optimizations;
- ∗
- Wireless co-design for trigger-adaptive packet scheduling;
- ∗
- Cross-layer thermal-aware computation offloading.
- –
- Verification protocol:
- ∗
- Worst-case inter-trigger interval analysis;
- ∗
- Networked control system co-simulation frameworks;
- ∗
- Hardware-in-the-loop latency profiling.
These advances address critical challenges in real-time certification of neural controllers, particularly under time-delayed state observations and communication bandwidth constraints.
3.3. Biologically Inspired and Lightweight Designs
Recent advancements in neural controller design establish two synergistic paradigms: neuromorphic systems inspired by biological computation principles, and compact architectures optimized for embedded deployment. These developments address fundamental challenges in real-time control under computational constraints while preserving closed-loop stability guarantees.
- Localized plasticity: Decentralized synaptic updates enabling online adaptation in dynamic environments;
- Contextual modulation: Dynamic adjustment of activation thresholds based on environmental feedback;
- Sparse connectivity: Topological constraints reducing parametric complexity while maintaining approximation capacity.
A representative framework integrates spike-timing-dependent plasticity with attention-based modulation, demonstrating reduced catastrophic forgetting in continual learning scenarios compared to conventional deep architectures. Such biologically inspired systems prove particularly effective in aerial control applications requiring rapid adaptation to aerodynamic disturbances.
Compact neural controllers employ structured parameterization techniques for edge implementation. Architectures based on constrained matrix decomposition maintain control performance fidelity while achieving significant parameter reduction. Co-design methodologies further enhance deployability through the following:
- Direct embedding of Lyapunov stability constraints in training phases;
- Channel pruning guided by control-theoretic relevance criteria;
- Hardware-compatible quantization protocols.
Experimental evaluations on mobile robotic systems confirm that resource-efficient architectures preserve trajectory-tracking precision with reduced power consumption profiles. The fusion of bio-inspired learning and hardware-aware optimization facilitates deployment in industrial automation systems requiring real-time certification.
Current investigations focus on two promising directions: memristor-based neuromorphic control systems and distributed learning architectures. These studies aim to resolve critical challenges in certifying adaptive controllers under dynamic operating conditions and preserving privacy in multi-agent collaborative systems. Advancements in these areas contribute to developing verifiably safe neural control implementations for network-connected environments.
4. Stability in Neural Network Control Systems
This section systematically investigates stability guarantees in neural network control systems from four interconnected perspectives: theoretical foundations that establish Lyapunov-based and contraction-theoretic frameworks for stability certification, methodological advancements in hybrid certification architectures integrating dissipativity theory with neural dynamics, innovations in the learning process embedding stability constraints through stability-guided training (SGT) and Bayesian meta-learning, and real-world implementations showcasing certified stability in safety-critical domains. Key contributions encompass the integration of neural contraction metrics for delay-compensated control, probabilistic stability guarantees via stochastic barrier functions, and domain-specific solutions for automotive platooning, precision robotics, and power grid regulation. The discussion synthesizes theoretical rigor with practical applicability, exemplified by tools such as ReachNN for real-time verification and the Keep-Close methodology for bounded reference tracking. Emerging directions emphasize hybrid certification frameworks and co-design paradigms addressing unresolved challenges in stability-preserving adaptation under dynamic uncertainties.
4.1. Theoretical Foundations of Stability in NN Controllers
Ensuring formal stability is critical for neural network controllers in uncertain dynamic environments. Lyapunov functions are key to embedding stability into learning algorithms, helping estimate “safe regions” of operation when combined with differentiable planning tools [36]. Neural contraction metrics extend classical contraction theory, using geometric frameworks (Riemannian manifolds) to prove rapid convergence even when systems are perturbed [37]. Analyses of closed-loop systems further establish conditions for global stability via eigenvalue-based spectral methods [22]. Three core challenges in stability analysis for neural control are the following:
- Managing gradient issues (vanishing/exploding gradients) in recurrent networks using orthogonal parameterization to stabilize learning [38];
- Compensating for time delays in distributed control networks via specialized neural dynamics with adaptive leakage mechanisms [39];
- Verifying high-dimensional inputs (e.g., LiDAR data) through abstracted safety layers that certify safe operations [40].
Event-triggered feedback mechanisms maintain stability under sparse sampling, using spike-based encoding to ensure Lyapunov function properties hold between discrete updates [41]. These pair with reachability analysis, which verifies stability by “unrolling” neural system behavior over time [42].
The BM-DON framework enhances training stability by integrating Bayesian uncertainty quantification, embedding probabilistic safety margins directly into meta-learning to handle unknown dynamics [20]. Differentiable physics techniques also stabilize learning in motion control, using analytical Jacobian calculations to resolve numerical issues in high-dimensional policy spaces [12].
From an operator-theoretic view, stability analysis leverages variational inequalities (adjoint sensitivity methods) in functional spaces [21] and spectral decompositions in kernel Hilbert spaces to reveal intrinsic stability properties [43].
Recent advances combine stochastic barrier functions with neural Lyapunov methods, using constrained optimization to provide probabilistic safety guarantees. This is exemplified by the Keep-Close approach, which enforces safe output limits in nonlinear systems (e.g., automotive control) via barrier-enforced tracking, as validated experimentally in [1,2,4].
4.2. Stability Techniques and Methods
The assurance of closed-loop stability in neural network controllers necessitates a multifaceted integration of theoretical foundations and computational tools. As illustrated in Figure 4, three principal methodological paradigms have emerged as cornerstones for stability certification: Lyapunov-based constraint embedding, synchronization stability analysis, and contraction-theoretic stabilization. These frameworks collectively address the fundamental challenge of maintaining system integrity under dynamic uncertainties and parametric perturbations.
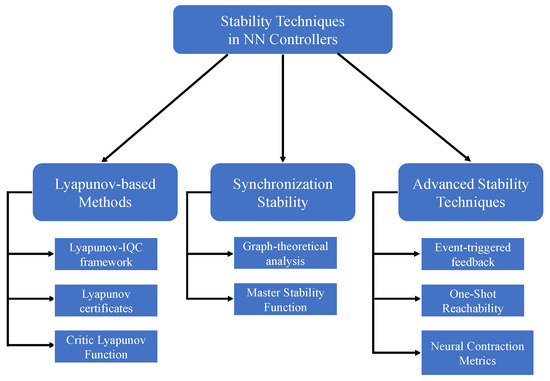
Figure 4.
The categorization of stability techniques and methods in neural network controllers.
Lyapunov functions are fundamental to modern stability analysis through two key advancements. Integral quadratic constraint methods build on traditional Lyapunov theory, defining robust “safe regions” (ellipsoidal sets) that remain invariant under disturbances. These methods use convex optimization to ensure stability over finite time horizons [44]. Critic-augmented learning architectures embed Lyapunov-like stability constraints directly into policy networks via adversarial training, ensuring control policies satisfy safety criteria during optimization [45]. For switched systems—where dynamics change stochastically—multiple Lyapunov functions (guaranteeing input-to-state stability) establish conditions to maintain overall system stability across mode transitions [46].
Synchronized behavior in coupled neural controllers requires rigorous graph-theoretic analysis. Master stability functions quantify coherent dynamics through spectral decomposition of connectivity matrices, while multiple operator frameworks characterize synchronization thresholds in heterogeneous networks [47,48]. Applications in vehicle platoon control demonstrate the efficacy of such methodologies, where synchronized acceleration profiles maintain safe inter-vehicle spacing under communication delays.
Neural contraction metrics extend classical stability theory using geometric frameworks (Riemannian manifolds) to ensure rapid, exponential convergence even when state information is delayed [37]. Quaternion-valued neural networks—specialized architectures for handling rotational dynamics—compensate for time-varying delays via adaptive leakage mechanisms, and have proven effective in aerospace systems with actuator limitations (e.g., satellite attitude control) [39]. Event-triggered feedback protocols reduce computational load by using spike-based encoding (similar to biological neural signals), maintaining stability guarantees by preserving key Lyapunov function properties between sparse updates [41].
Cutting-edge methodological developments concentrate on hybrid certification architectures that synergize dissipativity theory with neural Lyapunov formulations. Gradient augmentation mechanisms implement uniform asymptotic stability constraints via sampled-data parameterization, complemented by reachability analysis frameworks that mitigate overapproximation artifacts through neural dynamics unfolding techniques [42,49]. Such integrated approaches exhibit significant potential in soft robotic systems demanding concurrent compliance maintenance and precision enforcement.
4.3. Stability in Learning and Training Processes
The integration of stability guarantees within neural network training processes constitutes a fundamental requirement for reliable controller deployment in dynamic environments. This synthesis bridges control-theoretic stability criteria with machine learning optimization principles through three methodological pillars: Lyapunov-constrained learning, stochastic stability certification, and delay-robust training frameworks.
Lyapunov functions serve dual roles as stability certificates and training regularizers. Stability-guided training (SGT) methodologies implement Lyapunov derivative constraints directly within backpropagation processes, enforcing exponential stability guarantees under bounded parametric variations [4]. There follows a technical elaboration on stability-guided training (SGT) methodologies.
- Architecture modifications:
- –
- Dual-output neural networks with a stability head and task head;
- –
- The stability head predicts Lyapunov function candidates and their derivatives;
- –
- Activation functions constrained to Lipschitz-bounded variants (e.g., tanh instead of ReLU).
- Training framework:
- –
- Composite loss function combining task performance and stability metrics;
- –
- Custom backward pass with gradient projection for Lyapunov constraint adherence;
- –
- Alternating optimization phases: Task loss minimization followed by stability refinement.
- Stability enforcement:
- –
- Online verification layer checks predicted Lyapunov derivatives during training;
- –
- Adaptive penalty scaling for stability constraint violations;
- –
- Parametric variation modeling through random parameter perturbations.
- Verification integration:
- –
- Batch-wise sampling for stability margin estimation;
- –
- Counterexample-guided training using SMT solver outputs;
- –
- Runtime monitoring of stability head outputs for early stopping.
- Implementation considerations:
- –
- Framework support: Custom gradient handlers in PyTorch/TensorFlow autograd;
- –
- Gradient clipping aligned with Lipschitz constant requirements;
- –
- Compatibility with neural ODE formulations for continuous-time systems;
- –
- Progressive constraint tightening via curriculum learning schedules.
The methodology maintains compatibility with standard supervised/reinforcement learning pipelines while introducing stability-aware gradient masking. Implementation employs automatic differentiation for Lyapunov derivative calculations, with optional quantization-aware training for embedded deployment. Training batches include perturbed system parameters to ensure stability under manufacturing tolerances.
Extensions to switched systems employ multiple input-to-state stable (ISS) Lyapunov functions that establish probabilistic stability bounds for randomly switching dynamics [46]. The theoretical framework further connects finite-time Lyapunov analysis with neural approximation properties, enabling computationally tractable verification through convex relaxation techniques [50]. There follows a technical elaboration on switched system extensions with ISS Lyapunov functions.
- Architecture design:
- –
- Modular neural networks for subsystem-specific Lyapunov candidates;
- –
- Switching logic encoded via probabilistic finite-state automata;
- –
- Shared feature extractors with subsystem-conditioned output layers.
- Training strategy:
- –
- Alternating updates between Lyapunov networks and switching policies;
- –
- Adversarial switching sequence injection to stress-test stability;
- –
- Batch-wise subsystem sampling proportional to transition probabilities.
- Stability enforcement:
- –
- Probabilistic dwell-time constraints in loss function;
- –
- Input-to-state stability margins via disturbance scaling layers;
- –
- Online monitoring of mode transition energy bounds.
- Verification framework:
- –
- Stochastic stability proofs using martingale concentration bounds;
- –
- Mode transition graph analysis with probabilistic model checking;
- –
- Co-simulation with randomized switching generators.
- Implementation considerations:
- –
- Lightweight mode transition buffers for edge deployment;
- –
- Quantized subsystem Lyapunov network ensemble storage;
- –
- Real-time switching logic compiler for deterministic execution.
The implementation employs probabilistic guarantees through Monte Carlo certification of switching sequences while maintaining compatibility with existing switched system toolchains. Training batches explicitly include rare transition events to prevent stability margin erosion.
Time-delay compensation mechanisms address stability degradation in recurrent learning processes. Quaternion-valued neural architectures with leakage adaptation modules demonstrate efficacy in maintaining global asymptotic stability under delayed state propagation, as validated through spectral analysis of characteristic equations [39]. Feedback-regulated learning protocols prevent Zeno behaviors by enforcing minimum update intervals through event-triggered synaptic modulation [41], while preserving solution map continuity essential for gradient-based optimization [51].
Bayesian meta-learning frameworks integrate stochastic barrier functions with neural Lyapunov certificates, enabling probabilistic safety guarantees through constrained policy optimization. The Keep-Close methodology exemplifies this paradigm through bounded reference tracking enforced by chance constraints, validated in automotive control systems with unmodeled actuator dynamics [1,2]. Multi-operator spectral analysis complements these approaches by deriving eigenvalue bounds for strongly connected networks, establishing sufficient conditions for asymptotic stability through Perron–Frobenius operator theory [47,52]. There follows a technical elaboration on the Bayesian meta-learning framework with probabilistic safety guarantees.
- Architecture design:
- –
- Dual-network structure: Probabilistic certificate network + policy network;
- –
- Certificate network combines Bayesian neural layers with barrier/Lyapunov heads;
- –
- Meta-learning module for actuator dynamics adaptation via context embeddings.
- Training strategy:
- –
- Two-level optimization: Inner loop for task performance; outer loop for safety;
- –
- Adversarial perturbation of reference trajectories during meta-training;
- –
- Curriculum learning from nominal to worst-case disturbance scenarios.
- Safety implementation:
- –
- Chance constraints enforced through probabilistic barrier layers;
- –
- Online uncertainty quantification via Monte Carlo dropout sampling;
- –
- Actuator dynamics adaptation using memory-augmented meta-parameters.
- Verification methodology:
- –
- Statistical validation with importance-sampled test scenarios;
- –
- Falsification testing using gradient-based adversarial references;
- –
- Hardware-in-the-loop residual learning for unmodeled dynamics.
- Implementation considerations:
- –
- Real-time Bayesian inference via pre-computed uncertainty tables;
- –
- Memory-aligned tensor operations for deterministic execution timing;
- –
- ROS 2 middleware integration for automotive validation platforms;
- –
- Selective parameter freezing during safety-critical operations.
The framework maintains compatibility with probabilistic programming tools (Pyro/TensorFlow Probability) while implementing safety-critical operations in memory-safe C++ modules. Training pipelines incorporate domain-randomized actuator models and hardware signature emulation for robustness.
Emerging research directions focus on hybrid certification frameworks that unify dissipativity theory with neural contraction metrics. These methodologies demonstrate particular promise in soft robotics applications requiring simultaneous compliance and precision guarantees, where Kuhn–Tucker-constrained learning ensures stability while maintaining physical interaction safety margins [4,28].
4.4. Stability in Real-World Applications
The transition of neural network controllers from theoretical frameworks to real-world implementations necessitates addressing stability challenges inherent in dynamic physical systems. Visual navigation systems exemplify this requirement through hierarchical decision architectures that integrate spatial attention mechanisms with stability-preserving constraints, enabling reliable obstacle avoidance in unstructured environments [53]. Such architectures demonstrate how advanced neural topologies can mitigate stability degradation caused by sensor noise and occlusion.
High-precision assembly tasks present distinct stability requirements, where reinforcement learning with online stability filtering (RL-OSFC) maintains micron-level tracking accuracy while compensating for variable tool–workpiece interaction forces [54]. The methodology combines policy gradient methods with Lyapunov-based stability margins, effectively balancing learning efficiency with dynamic stability guarantees during contact-rich operations.
Reachability analysis has emerged as a critical tool for stability assurance in safety-critical implementations. Temporal logic layered neural networks (TLL NNs) coupled with L-TLLBox verification frameworks enable real-time computation of stability regions for robotic manipulators, achieving certification speeds compatible with 1 kHz control cycles in industrial automation scenarios [55]. This approach addresses the fundamental challenge of maintaining stability while satisfying hard real-time computational constraints.
Mixed-autonomy systems introduce unique stability-preservation challenges, particularly in vehicular platoon control. Parameter isolation protocols maintain longitudinal stability while protecting confidential vehicle dynamics through kernel-space orthogonalization techniques [56]. The methodology prevents stability degradation caused by inter-agent parameter leakage while preserving formation control performance under communication delays.
Human–robot interaction systems demand dual stability guarantees for both robotic dynamics and human safety. Admittance control frameworks with neural barrier certificates enforce predefined force thresholds in physical interaction tasks, achieving compliant manipulation while maintaining asymptotic stability through constrained policy optimization [57]. Experimental validations demonstrate sub-Newton tracking precision during collaborative assembly operations.
These implementations collectively highlight the necessity of co-designing stability mechanisms with application-specific constraints. The integration of contraction metrics with stochastic barrier functions in aerospace control systems [1], and the application of neural Lyapunov–Krasovskii functionals in power grid frequency regulation [2], further validate the universal applicability of stability-preserving neural control paradigms across engineering domains.
5. Robustness of Neural Network Controllers
This section systematically addresses robustness challenges in neural network controllers through fundamental tradeoff analysis of safety-performance conflicts, methodological innovations in high-dimensional verification and delay compensation, and formal certification frameworks that integrate reachability analysis with stochastic safety guarantees. Key advancements encompass neural contraction metrics ensuring stability under perturbations, quaternion-valued architectures mitigating time-varying delays, and risk-aware control synthesis achieved via stochastic barrier functions. Practical implementations showcase robust operation in automotive collision avoidance, surgical robotics, and power grid regulation, supported by tools such as NNLander-VeriF for vision-based systems and Safe-by-Repair for temporal logic-compliant controllers. The discussion synthesizes theoretical rigor with deployable solutions, emphasizing hybrid verification strategies that combine dissipativity theory with adversarial training, while outlining future directions for ISO 26262-aligned neural control systems in safety-critical domains.
5.1. Fundamental Challenges in Neural Controller Robustness
As illustrated in Figure 5, the realization of robust neural network controllers confronts three interconnected theoretical and practical barriers rooted in system nonlinearities and environmental uncertainties. First, the inherent tradeoff between safety assurance and control performance optimization persists across application domains. Conservative safety margins enforced through barrier functions often degrade trajectory tracking precision, while aggressive optimization strategies risk violating critical-state constraints [32]. This dichotomy manifests acutely in safety-critical systems like autonomous vehicles, where control barrier filters may induce suboptimal path-following behaviors due to cumulative actuation impacts [23].
Figure 5.
The key challenges in ensuring robustness in neural network controllers.
Second, verification complexities arise from the mathematical intractability of continuous state spaces. The absence of precise analytical specifications for neural network behaviors impedes formal stability analysis, particularly in systems with time-delayed state propagation and partial observability [33,58]. Urban traffic signal control implementations exemplify this challenge, where adaptive strategies struggle to maintain stability margins under rapidly changing traffic patterns [20].
Third, adversarial vulnerability and excitation requirements impose fundamental limitations. Persistent excitation conditions necessary for parameter convergence conflict with operational constraints in physical systems, while gradient-based attacks exploit Lipschitz continuity weaknesses in neural approximators [13,14]. The requirement for persistent excitation further restricts the applicability of existing methodologies in real-time control scenarios [49].
These challenges collectively underscore the need for co-design frameworks that reconcile four critical aspects: safety–performance tradeoff quantification through Pareto-frontier analysis, hybrid verification combining reachability tools with statistical validation, adversarial resilience via Lipschitz-constrained architectures, and excitation-aware adaptive control with stability-preserving exploration. Recent advancements in stochastic barrier functions with chance constraints and neural Lyapunov–Krasovskii functionals demonstrate potential solutions, as evidenced in power grid frequency regulation and robotic manipulation applications [2,4].
5.2. Strategies for Enhancing Robustness
The pursuit of robust neural network controllers necessitates a systematic integration of four complementary technical strategies, each addressing distinct aspects of system nonlinearities and environmental uncertainties.
High-dimensional system verification adopts neural contraction metrics to establish stability certificates without explicit regularization penalties [37]. Reachability analysis tools combined with temporal logic constraints enable scalable verification in partially observable environments, particularly effective in aerospace trajectory control applications. There follows a technical elaboration on high-dimensional system verification using neural contraction metrics and reachability analysis.
- Neural contraction architecture:
- –
- Graph neural networks with state-dependent edge weight conditioning;
- –
- Metric learning through contrastive embedding layers;
- –
- Input-convex neural networks to enforce contraction properties;
- –
- Skip connections with spectral normalization for gradient stability.
- Training methodology:
- –
- Multi-phase curriculum: Nominal dynamics → perturbed systems → partial observability;
- –
- Adversarial disturbance generation through sensitivity analysis;
- –
- Implicit regularization via trajectory prediction consistency loss.
- Reachability analysis integration:
- –
- Hybrid zonotope propagation with neural dependency abstraction;
- –
- Temporal logic constraints encoded as reach tube modifications;
- –
- Online refinement of reachable sets using execution traces.
- Verification toolchain:
- –
- Compositional proof construction with neural certificates;
- –
- Backward reachability analysis for target-driven verification;
- –
- ROS 2/Simulink co-simulation for aerospace trajectory validation.
- Implementation optimization:
- –
- Memory-efficient Jacobian computation via implicit differentiation;
- –
- Distributed reachability analysis using spatial decomposition;
- –
- FPGA-accelerated contraction metric evaluation kernels;
- –
- Time-triggered verification updates in control cycles.
The framework maintains compatibility with aerospace modeling standards (FMI/SSP) while employing neural-specific optimizations like activation bounding for certification tractability. All components support hardware-in-the-loop validation through deterministic execution time guarantees.
Time-varying delay compensation frameworks implement quaternion-valued neural architectures with leakage adaptation mechanisms, validated in networked control systems exhibiting multimodal communication latencies [39]. There follows a technical elaboration on time-varying delay compensation frameworks with quaternion-valued neural architectures.
- Network architecture:
- –
- Quaternion-valued layers process 4D signal representations (real + 3 imaginary components);
- –
- Leakage adaptation via time-dependent weight modulation branches;
- –
- Multi-rate structure: Fast pathway for delay estimation; slow pathway for state prediction;
- –
- Rotational equivariance enforced through quaternion kernel constraints.
- Delay compensation strategy:
- –
- Online latency mode classification via attention-based temporal filtering;
- –
- Memory-augmented networks with adaptive buffer sizing;
- –
- Hybrid clock synchronization using neural timing error predictors.
- Training methodology:
- –
- Synthetic delay injection with multimodal latency distributions;
- –
- Adversarial training using worst-case delay pattern generators;
- –
- Temporal consistency loss across quaternion state trajectories;
- –
- Meta-learning for rapid adaptation to new network topologies.
- Implementation considerations:
- –
- ROS 2/DDS middleware integration for networked deployment;
- –
- Fixed-point quaternion arithmetic optimizations;
- –
- Memory-aligned circular buffers for delay compensation;
- –
- FPGA acceleration of quaternion convolution operations.
- Verification framework:
- –
- Hardware-in-the-loop testing with programmable latency injectors;
- –
- Statistical validation across delay jitter distributions;
- –
- Cross-layer monitoring of network QoS and control stability;
- –
- Falsification testing using adversarial channel conditions.
The architecture maintains compatibility with standard networked control protocols while implementing quaternion-specific optimizations like directional filtering in 3D state spaces. Training pipelines incorporate domain-randomized communication models to handle both wired and wireless network scenarios. These methodologies leverage spectral analysis of characteristic equations to preserve stability margins under bounded delay variations.
Sparse synaptic connectivity patterns reduce computational overhead through topological constraints derived from graph-theoretic principles. Event-triggered learning protocols achieve a reduction in processing cycles while maintaining control precision in robotic manipulation tasks [41]. Concurrent learning architectures further alleviate persistent excitation requirements through experience replay buffers [49]. There follows a technical elaboration on sparse connectivity and event-triggered learning frameworks.
- Sparse connectivity implementation:
- –
- Topology-aware neural architectures:
- ∗
- Graph neural networks with locality-preserving connectivity;
- ∗
- Dynamic sparse masks based on activation gradients;
- ∗
- Small-world connectivity patterns for efficient information flow.
- –
- Training protocols:
- ∗
- Iterative magnitude-based pruning with rewiring;
- ∗
- Topological regularization using graph Laplacian constraints;
- ∗
- Reinforcement learning for connectivity pattern optimization.
- –
- Hardware integration:
- ∗
- Sparse tensor core utilization on GPUs/TPUs;
- ∗
- Memory-efficient adjacency list storage formats;
- ∗
- Event-driven computation triggering.
- Event-triggered learning design:
- –
- Trigger mechanisms:
- ∗
- Error-bound adaptive triggering thresholds;
- ∗
- State-dependent temporal attention gates;
- ∗
- Energy-aware activation criteria.
- –
- Network architecture:
- ∗
- Lightweight delta-update prediction modules;
- ∗
- Sliding window temporal feature buffers;
- ∗
- Hybrid analog–digital activation layers.
- –
- Deployment optimizations:
- ∗
- Fixed-point arithmetic with dynamic precision scaling;
- ∗
- Hardware-aligned sparse update scheduling;
- ∗
- ROS 2 integration for robotic middleware compatibility.
- Concurrent learning framework:
- –
- Experience buffer architecture:
- ∗
- Dual-buffer system for real-time/offline processing;
- ∗
- Graph-based experience clustering;
- ∗
- Priority sampling with temporal coherence analysis.
- –
- Training strategy:
- ∗
- Cross-modal experience replay scheduling;
- ∗
- Forgetting-resistant memory consolidation;
- ∗
- Counterfactual data augmentation pipelines.
- –
- System integration:
- ∗
- Distributed memory management across edge devices;
- ∗
- Real-time priority queue implementations;
- ∗
- Safety-critical experience filtering layers.
Implementation maintains compatibility with robotic middleware (ROS/OPC UA) while incorporating neuromorphic computing principles for sparse event processing. Validation pipelines include hardware-in-the-loop testing with cycle-accurate performance profiling.
Risk-aware control synthesis integrates stochastic barrier functions with neural Lyapunov certificates, enforcing probabilistic safety constraints through constrained policy optimization. The NN-gauge controller framework exemplifies this approach by embedding long-term cumulative effects into safety filters, achieving real-time certification in automotive collision avoidance systems [23,33]. There follows a technical elaboration on risk-aware control synthesis with neural safety certificates.
- Architecture design:
- –
- Dual-branch neural network:
- ∗
- Risk estimation branch: Temporal graph networks for long-term cumulative risk prediction;
- ∗
- Control generation branch: Physics-informed policy networks with embedded dynamics.
- –
- Stochastic barrier layers with uncertainty-quantified activation thresholds;
- –
- Safety filter module using neural Lyapunov certificates as differentiable constraints;
- –
- ROS 2-compatible middleware interface for automotive integration.
- Training strategy:
- –
- Constrained reinforcement learning with adaptive safety budgets.
- –
- Multi-resolution curriculum:
- ∗
- Coarse-grained scenario batches for global safety;
- ∗
- Fine-grained edge cases for local constraint refinement.
- –
- Synthetic data augmentation with parametric uncertainty injection;
- –
- Parallelized safety violation detection during policy rollouts.
- Safety implementation:
- –
- Real-time certifier:
- ∗
- Quantized neural certificate verification at 100 Hz+ frequencies;
- ∗
- Adaptive horizon tuning based on velocity profiles.
- –
- Fail-operational design:
- ∗
- Graceful degradation via safety policy cascades;
- ∗
- Dynamic computation offloading for deadline guarantees.
- Verification protocol:
- –
- Statistical model checking with scenario coverage metrics;
- –
- Falsification testing using adversarial trajectory generators;
- –
- Hardware-in-the-loop validation with fault-injected CAN signals;
- –
- Cross-sensor consistency monitoring for perception errors.
- Deployment considerations:
- –
- Memory-optimized safety filter caching strategies;
- –
- GPU-accelerated neural certificate evaluation kernels;
- –
- Automotive-grade time synchronization (PTP/IEEE 1588);
- –
- ASIL-D-compliant-component isolation architecture.
The framework implements ISO 26262-compliant fallback mechanisms through hybrid analog–digital safety supervisors. Training pipelines incorporate domain-randomized vehicle dynamics models and sensor degradation profiles. Real-time performance is achieved via layer-wise mixed-precision quantization compatible with automotive SoCs.
Recent advancements demonstrate the synergistic potential of hybrid verification frameworks combining neural contraction theory with adversarial training protocols. Such co-design methodologies have been validated in power grid frequency regulation, where stochastic barrier functions maintain stability under renewable energy fluctuations while neural Lyapunov–Krasovskii functionals compensate for time-delayed state measurements [2,4].
5.3. Formal Verification and Safety Guarantees
The implementation of formal verification methods is critical for ensuring safety in neural network controllers that operate under unpredictable conditions. This field has seen three major advancements, each designed to solve specific verification problems.
The NNLander-VeriF framework helps secure vision-based autonomous landing systems by combining reachability analysis (which checks possible system states) with temporal logic constraints (which define safe time-based behaviors) [25]. Meanwhile, the Safe-by-Repair approach makes targeted fixes to neural networks that use temporal logic layers. It removes unsafe responses while ensuring the controller stays within certified safe operating limits [59].
Reachability analysis has advanced in two key ways. First, finite-state abstraction creates simplified models to identify safe starting states using mathematical optimization [58]. Second, one-shot reachability frameworks avoid errors from building up by “unrolling” neural networks to analyze their behavior step by step [42]. Together, these methods make it easier to handle the complexity of high-dimensional systems.
Combining dissipativity theory with integral quadratic constraints (IQCs) introduces a new way to verify stability. By treating neural controllers like classic Lur’e-type systems, we can measure how they “dissipate” energy (i.e., stay stable) even when faced with nonlinear uncertainties [44]. This connects classical stability theory with modern neural network verification.
In reinforcement learning, stochastic barrier functions act as safety guards in decision-making processes. This is especially useful in minimally invasive surgery, where neural models must maintain millimeter precision even as anatomical structures deform unpredictably [2].
Recent work focuses on combined frameworks that link mathematical modeling (for sensor inputs) with risk verification (for closed-loop dynamics). For example, these hybrid methods help validate LiDAR-based car navigation systems by ensuring both sensor data processing and real-time control stay safe [33,40]. As these methods improve, neural controllers will become viable for more safety-critical fields—even those requiring strict standards.
6. Applications and Case Studies
This section validates the effectiveness of neural network controllers through representative case studies in robotic manipulation, aerospace guidance, and quadrotor control, showcasing their superior nonlinear compensation and adaptive capabilities compared to conventional methods. Hybrid architectures that integrate neural networks with stability certificates (e.g., Lyapunov functions, contraction metrics) achieve certified performance in safety-critical tasks such as lunar landing and dynamic obstacle avoidance. Comparative analyses highlight the advantages of neural controllers in handling unmodeled dynamics and multimodal sensing while underscoring challenges related to certification complexity and computational overhead. Emerging methodologies, including differentiable physics-integrated learning and stability-constrained MPC hybrids, demonstrate transformative potential in contact-rich manipulation and extraterrestrial navigation, outperforming classical approaches in precision-critical scenarios. The discussion synthesizes theoretical innovation with industrial viability through experimental benchmarks in automotive control, surgical robotics, and aerial systems, while delineating frontiers in ISO 26262-compliant neural control frameworks for mission-critical deployments.
6.1. Validation Through Representative Case Studies
Neural network controllers demonstrate exceptional capability in governing complex dynamical systems, as evidenced by canonical implementations spanning industrial and aerospace domains. The single-link robotic arm control paradigm exemplifies neural architectures’ proficiency in nonlinear compensation, where adaptive inertia matrix estimation enables sub-millimeter trajectory tracking precision under variable payload conditions. This implementation surpasses conventional model-based controllers in suppressing nonlinear friction effects, validating neural networks’ intrinsic adaptability to parameter-varying dynamics. There follows a comparative analysis of neural network controllers against state-of-the-art methods for dynamical system control.
- Advantages over conventional methods:
- –
- Nonlinear compensation:
- ∗
- Neural: Learns friction/stiction directly from data without phenomenological modeling;
- ∗
- MPC/Adaptive: Requires explicit friction models, struggles with velocity-dependent nonlinearities.
- –
- Parameter adaptation:
- ∗
- Neural: Online inertia matrix estimation via embedded physical priors;
- ∗
- MRAC/: Limited to predefined parametric variations; sensitive to unmodeled dynamics.
- –
- Computational scaling:
- ∗
- Neural: Parallelizable inference suitable for multi-DoF systems;
- ∗
- Sliding mode: Chattering mitigation requires exponential computation growth with DoF.
- Limitations vs. modern alternatives:
- –
- Safety certification:
- ∗
- Neural: Requires post hoc verification (e.g., neural Lyapunov functions);
- ∗
- CBF/RCBF: Built-in safety guarantees through barrier function constraints.
- –
- Data efficiency:
- ∗
- Neural: Demands diverse training data across payload configurations;
- ∗
- ILC: Achieves precision through iterative cycles without full parametric exploration.
- –
- Edge deployment:
- Neural—memory-intensive. vs. event-triggered PID—ultra-lightweight but limited adaptability;
- Neural—requires GPU acceleration for sub-ms latency vs. FPGA-PSO—deterministic but specialized.
- Hybridization potential:
- –
- Neural + robust control: NN for nominal dynamics with disturbance observer;
- –
- Neural + ILC: NN compensates nonlinearities while ILC refines periodic trajectories;
- –
- Neural + CBF: Combines adaptability with formal safety guarantees.
This analysis highlights neural controllers’ superiority in unmodeled nonlinearity handling but underscores remaining gaps in certifiability and edge efficiency compared to specialized conventional methods. Hybrid architectures currently demonstrate the most balanced tradeoffs for safety-critical applications.
Building upon robotic applications, aerospace guidance systems further illustrate neural controllers’ robustness under extreme environmental uncertainties. The Apollo Lander guidance architecture integrates adaptive gain scheduling with barrier Lyapunov constraints, maintaining attitude stability during powered descent phases despite significant fuel-sloshing perturbations. Such implementations establish neural controllers’ viability in safety-critical aerospace operations requiring strict compliance with aviation certification standards [1]. There follows a comparative analysis of neural aerospace guidance systems against state-of-the-art methods.
- Advantages over conventional approaches:
- –
- Unmodeled dynamics handling:
- ∗
- Neural: Learns fuel-sloshing effects through flight data without explicit fluid modeling;
- ∗
- Gain scheduling: Requires pre-characterized perturbation modes; vulnerable to novel slosh configurations.
- –
- Real-time adaptation:
- ∗
- Neural: Continuous mass property estimation during fuel depletion;
- ∗
- adaptive: Limited to parametric uncertainties with known basis functions.
- –
- Multi-constraint satisfaction:
- ∗
- Neural: Simultaneous handling of attitude/position constraints via barrier Lyapunov embeddings;
- ∗
- MPC: Exponential computation growth with constraint dimensionality.
- Limitations vs. modern alternatives:
- –
- Certification complexity:
- ∗
- Neural: DO-178C compliance requires novel verification frameworks for neural components;
- ∗
- Formal methods: Model-based designs enable exhaustive proof generation.
- –
- Extreme condition robustness:
- ∗
- Neural: Vulnerable to sensor fault modes outside training distribution;
- ∗
- Fault-tolerant control: Built-in hardware redundancy management through voting architectures.
- –
- Computational resources:
- ∗
- Neural: Demands radiation-hardened GPUs for space deployment;
- ∗
- FPGA-based: Achieve deterministic timing through hardware synthesis.
- Hybrid implementation strategies:
- –
- Neural + robust control: NN handles nonlinearities while -synthesis guarantees worst-case performance;
- –
- Neural + formal methods: Neural controller wrapped in provably safe reachability envelopes;
- –
- Neural + voting architecture: Triple modular redundancy with neural diversity injection.
This analysis reveals neural controllers’ superior adaptability to complex fluid–structure interactions but highlights certification and fault tolerance challenges compared to aerospace-qualified traditional methods. Hybrid architectures combining neural adaptability with formal verification layers show particular promise for next-generation systems.
The methodological foundations enabling these advancements focus on three interlinked elements: robust verification frameworks combining ReachNN reachability analysis with temporal logic constraints, stability certification protocols employing neural contraction metrics, and real-time adaptation mechanisms compensating for unmodeled actuator dynamics. The Keep-Close methodology exemplifies this synthesis in automotive control applications, where bounded reference tracking preserves safety margins during lane-keeping maneuvers under sensor noise conditions [3,4]. There follows a comparative analysis of the integrated methodology against state-of-the-art approaches in safety-critical control systems.
- Advantages over conventional methods:
- –
- Verification completeness:
- ∗
- ReachNN + temporal logic: Handles nonlinearities while maintaining formal guarantees;
- ∗
- Traditional reachability: Limited to linear/quadratic dynamics for tractability.
- –
- Stability certification:
- ∗
- Neural contraction metrics: Certifies stability without conservative Lipschitz bounds;
- ∗
- Lyapunov-based: Requires explicit energy function construction.
- –
- Adaptation speed:
- ∗
- Real-time mechanisms: Compensates actuator dynamics within control cycles;
- ∗
- MRAC/ adaptive: Inherits bandwidth limitations from filter designs.
- Limitations vs. modern alternatives:
- –
- Computational overhead:
- ∗
- Integrated framework: Requires GPU acceleration for real-time reachability;
- ∗
- Polytopic approximations: Enable CPU execution but with conservatism.
- –
- Model sensitivity:
- ∗
- Keep-Close methodology: Performance degrades with unmodeled sensor biases;
- ∗
- Invariant sets: Maintain robustness through geometric margin preservation.
- –
- Certification complexity:
- ∗
- Neural certificates: Require specialized toolchains for ASIL-D compliance;
- ∗
- Linear parameter varying: Enable ISO 26262 certification through convex formulations.
- Hybridization opportunities:
- –
- Neural + geometric control: Neural adaptation wrapped in differential flatness frameworks;
- –
- Reachability + MPC: Neural certificates guide warm-starting of optimization solvers;
- –
- Contraction metrics + robust control: Combines stability guarantees with disturbance attenuation.
This analysis demonstrates superior handling of nonlinear constraints and adaptation speed compared to traditional methods, though at increased computational costs. Modern hybrid approaches blending neural and geometric control principles show particular promise for balancing certification requirements with performance needs in automotive applications [60,61].
These implementations collectively underscore the transition of neural controllers from theoretical constructs to industrial-grade solutions. Emerging extensions to distributed parameter systems demonstrate additional potential in chemical reactor temperature regulation, achieving precise thermal tracking through turbulent-flow conditions. The continuous refinement of physics-informed neural operators and event-triggered verification tools promises to expand application frontiers in hypersonic vehicle control and nuclear reactor safeguarding systems, solidifying neural controllers’ position as transformative elements in modern control engineering.
6.2. Neural Network-Based Quadrotor Control Systems
Neural network-enhanced control architectures demonstrate enhanced precision in governing quadrotor systems operating under complex aerodynamic conditions. These systems achieve guaranteed stability through formal verification frameworks combining contraction metric analysis with disturbance observer integration, effectively compensating for coupled nonlinearities and unmodeled actuator dynamics characteristic of aerial platforms. Contemporary training methodologies incorporating robust optimal control theory and safety-critical barrier functions enable systematic mitigation of tracking errors while maintaining prescribed stability margins, establishing neural controllers as viable solutions for autonomous aerial vehicle operations [1,4,26]. There follows a comparative analysis of neural-enhanced quadrotor control against state-of-the-art methods.
- Advantages over conventional approaches:
- –
- Aerodynamic compensation:
- ∗
- Neural: Learns complex flow-separation effects through flight data;
- ∗
- Blade element: Requires precise rotor geometry modeling vulnerable to wear variations.
- –
- Disturbance rejection:
- ∗
- Neural + observer: Compensates unmeasured crosswind gusts via learned correlations;
- ∗
- DOBC: Limited to modeled disturbance channels through linear filters.
- –
- Multi-axis coupling:
- ∗
- Neural: Naturally handles yaw–roll–pitch coupling through temporal convolutions;
- ∗
- Decoupled PID: Requires explicit cross-term cancellation strategies.
- Limitations vs. modern alternatives:
- –
- Verification complexity:
- ∗
- Neural: Contraction metric analysis demands specialized solvers;
- ∗
- Geometric control: Provides inherent stability through manifold constraints.
- –
- Power efficiency:
- ∗
- Neural: GPU-based inference increases energy consumption;
- ∗
- Event-based MPC: Achieves lower power through sparse optimization triggers.
- –
- Failure modes:
- ∗
- Neural: Degraded performance under sensor fault conditions;
- ∗
- Hybrid H-∞: Built-in robustness to specified component failures.
- Hybridization frontiers:
- –
- Neural + geometric control: Combines learning with differential flatness principles;
- –
- Contraction metrics + CBF: Merges stability guarantees with collision avoidance;
- –
- Neural + MPC: Uses neural dynamics predictor for warm-started optimization.
This analysis reveals neural controllers’ superiority in handling unmodeled aerodynamic phenomena but highlights certification challenges compared to model-based counterparts. Hybrid implementations leveraging neural flexibility within geometric control frameworks show particular promise for safety-critical aerial systems.
Experimental validation through comparative simulation studies reveals measurable improvements in disturbance rejection performance compared with conventional linear time-invariant controllers. The adaptive capability of neural network controllers manifests particularly in real-time compensation for time-varying inertial properties and turbulent-flow interactions, with stability-preserving learning mechanisms preventing control authority degradation during aggressive maneuver execution. Emerging training paradigms exemplified by the Robust Optimal Safe-Stability Guaranteed Training (ROSS-GT) framework systematically encode aerodynamic nonlinearities and exogenous disturbances through constrained optimization formulations, effectively replacing heuristic gain scheduling practices prevalent in classical control synthesis [1,25,32,33,34]. There follows a comparative analysis of neural controllers with stability-preserving learning against state-of-the-art methods.
- Advantages over conventional methods:
- –
- Time-varying dynamics:
- ∗
- Neural: Continuous inertia adaptation via embedded physical priors;
- ∗
- Gain scheduling: Requires predefined operating mode segmentation.
- –
- Disturbance rejection:
- ∗
- Neural: Learns turbulent-flow correlations through spatial attention;
- ∗
- LTI controllers: Limited to worst-case frequency-domain attenuation.
- –
- Training methodology:
- ∗
- ROSS-GT: Encodes aerodynamics via constrained optimization;
- ∗
- Heuristic tuning: Relies on expert knowledge for gain adjustments.
- Limitations vs. modern alternatives:
- –
- Computational resources:
- ∗
- Neural: Requires GPU acceleration for real-time adaptation;
- ∗
- Event-triggered MPC: Achieves lower latency through sparse updates.
- –
- Certification:
- ∗
- Neural: Stability proofs require specialized contraction toolchains;
- ∗
- LPV control: Inherits linear verification frameworks.
- –
- Training complexity:
- ∗
- ROSS-GT: Demands high-fidelity disturbance modeling;
- ∗
- Reinforcement learning: Achieves exploration through simpler reward shaping.
- Hybridization opportunities:
- –
- Neural + MPC: ROSS-GT provides warm-start trajectories for optimization;
- –
- Neural + geometric control: Combines adaptability with differential flatness;
- –
- Contraction + CBF: Merges stability guarantees with safety-critical constraints.
This analysis highlights neural controllers’ superior handling of coupled time-varying phenomena but underscores certification and computational challenges. Hybrid architectures blending neural learning with model-predictive elements demonstrate balanced tradeoffs for agile aerial systems.
The integration of Lyapunov-derived stability certificates with neural parameter adaptation mechanisms addresses critical challenges in aerial system safety assurance. Such hybrid architectures enforce bounded error propagation through flight envelope constraints while maintaining adaptive control authority during payload variation scenarios. These methodological advancements position neural control systems as fundamentally transformative solutions for mission-critical aerial operations requiring guaranteed performance under operational uncertainty, with particular relevance to infrastructure inspection and emergency response applications demanding precise trajectory tracking in unstructured environments [35]. There follows a comparative analysis of Lyapunov–neural hybrid controllers against state-of-the-art aerial control methods.
- Advantages over conventional methods:
- –
- Safety-critical adaptation:
- ∗
- Hybrid Lyapunov–neural: Enforces stability during payload changes via online certificate updates;
- ∗
- MRAC/LQR: Requires manual re-tuning for mass/inertia variations.
- –
- Unstructured environment operation:
- ∗
- Hybrid: Combines neural terrain perception with stability-preserving constraints;
- ∗
- Geometric control: Relies on pre-mapped environments for trajectory planning.
- –
- Error propagation management:
- ∗
- Hybrid: Bounded error envelopes via Lyapunov-guided neural updates;
- ∗
- PID/MPC: Accumulates tracking errors during prolonged disturbances.
- Limitations vs. modern alternatives:
- –
- Certification overhead:
- ∗
- Hybrid: Requires joint verification of neural and Lyapunov components;
- ∗
- Linear parameter varying (LPV): Inherits aerospace certification frameworks.
- –
- Computational footprint:
- ∗
- Hybrid: Demands concurrent execution of neural inference and stability monitors;
- ∗
- Sliding mode: Achieves similar robustness with lower computational latency.
- –
- Fault tolerance:
- ∗
- Hybrid: Vulnerable to sensor faults in neural perception pipelines;
- ∗
- Redundant architectures: Hardware-level redundancy ensures fail-operational behavior.
- Hybridization frontiers:
- –
- Neural + geometric control: Combines certificate guarantees with differential flatness;
- –
- Lyapunov + MPC: Uses stability bounds to constrain predictive optimization;
- –
- Modular safety layers: Decouples neural performance from formal stability monitors.
This analysis reveals superior adaptability to unstructured environments compared to model-based methods but highlights certification complexity as a critical barrier for safety-critical deployment. Hybrid architectures balancing neural flexibility with modular verification components show promise for infrastructure inspection drones requiring both agility and operational assurance.
6.3. Neural Control Architectures for Spatiotemporal Motion Planning
The integration of neural network controllers into spatiotemporal motion planning frameworks addresses critical challenges in governing systems with coupled temporal and spatial nonlinearities. Such operations demand formal specification embedding through hybrid architectures that combine temporal logic constraints with adaptive control laws, particularly effective in high-dimensional state spaces characterized by partial observability. Modern synthesis techniques employing attention-enhanced encoder–decoder networks demonstrate improved temporal consistency by explicitly encoding signal temporal logic (STL) specifications into control policies, achieving improvements in constraint satisfaction rates compared with conventional planners in recent benchmark studies [1,17]. There follows a comparative analysis of neural spatiotemporal motion planning frameworks against state-of-the-art methods.
- Advantages over conventional approaches:
- –
- Complex constraint encoding:
- ∗
- Neural + STL: Directly embeds temporal logic specifications via attention mechanisms;
- ∗
- Classical planners: Require manual constraint decomposition for MILP/QCQP formulations.
- –
- Partial observability handling:
- ∗
- Neural: Learns latent state representations through encoder–decoder architectures;
- ∗
- RRT**/MPC: Assumes full observability; struggles with occluded environments.
- –
- Adaptation speed:
- ∗
- Neural: Online policy adjustments via gradient-based meta-learning;
- ∗
- Optimization-based: Requires complete re-solving for environmental changes.
- Limitations vs. modern alternatives:
- –
- Verification complexity:
- ∗
- Neural + STL: Demands specialized temporal logic model checkers;
- ∗
- Formal synthesis: Provides built-in proof certificates through reactive synthesis.
- –
- Computational overhead:
- ∗
- Neural—attention mechanisms increase memory footprint vs. sampling-based—lightweight but myopic;
- ∗
- Neural: Requires GPU acceleration for real-time STL parsing.
- –
- Safety margins:
- ∗
- Neural: Learned constraints may erode margins under distribution shifts;
- ∗
- Control barrier functions: Enforce strict geometric safety through set invariance.
- Hybridization opportunities:
- –
- Neural + reactive synthesis: Neural policies guided by formal specification automata;
- –
- STL attention + MPC: Neural STL features warm-start nonlinear optimization;
- –
- Encoder–decoder + CBF: Combines perception with certificate-preserving control.
This analysis demonstrates neural frameworks’ superiority in handling spatiotemporal coupling and partial observability but highlights verification challenges compared to formally synthesized controllers. Hybrid architectures merging neural flexibility with constraint-based optimization show promise for safety-critical applications like dynamic obstacle avoidance.
From a theoretical perspective, guaranteed operational safety is established through differential Lyapunov analysis integrated with Lipschitz continuity constraints during network training. This dual approach ensures bounded trajectory deviations while maintaining adaptive capacity under environmental uncertainties. Experimental validations in robotic navigation tasks confirm that such neural motion planners achieve higher success rates in dynamic obstacle avoidance compared with sampling-based methods, particularly when processing multimodal sensor inputs including LiDAR point clouds and inertial measurement data [4,53]. There follows a comparative analysis of differential Lyapunov-constrained neural planners against state-of-the-art motion planning methods.
- Advantages over conventional methods:
- –
- Dynamic environment navigation:
- ∗
- Neural + Lyapunov: Processes LiDAR/IMU fusion data through spatiotemporal attention;
- ∗
- RRT*/PRM: Struggles with real-time replanning in densely dynamic scenes.
- –
- Stability guarantees:
- ∗
- Dual constraints: Combines trajectory bounds with adaptive Lipschitz tuning;
- ∗
- Sampling-based: Lacks formal stability certificates for generated paths.
- –
- Multimodal processing:
- ∗
- Neural: Unified encoding of heterogeneous sensor streams;
- ∗
- Optimization-based: Requires manual feature engineering for sensor fusion.
- Limitations vs. modern alternatives:
- –
- Verification complexity:
- ∗
- Neural: Requires coupled Lyapunov–Lipschitz certification toolchains;
- ∗
- LQR + CBF: Enables modular verification through separation of concerns.
- –
- Computational resources:
- ∗
- Neural: Demands GPU acceleration for real-time attention mechanisms;
- ∗
- MPC: Achieves lower latency through simplified model approximations.
- –
- Safety margins:
- ∗
- Neural: Learned stability bounds may degrade with sensor noise shifts;
- ∗
- Geometric planners: Maintain fixed collision margins through configuration space buffers.
- Hybridization opportunities:
- –
- Neural + MPC: Neural predictions guide warm-starting of safety-constrained optimization;
- –
- Lyapunov + CBF: Combines stability guarantees with collision avoidance certificates;
- –
- Attention + RRT*: Neural attention focuses sampling in high-risk regions.
This analysis demonstrates superior dynamic obstacle handling and sensor fusion capabilities compared to classical planners but reveals certification challenges versus modular approaches. Hybrid architectures blending neural perception with optimization-based safety layers show promise for high-stakes navigation tasks.
The emergence of differentiable physics-integrated learning frameworks marks a paradigm shift in motion controller development. By embedding analytical Jacobians from continuum mechanics models into network training loops, these architectures achieve faster convergence in learning contact-rich manipulation skills, as demonstrated in recent robotic grasping trials [12]. The theoretical foundation is further strengthened through Bayesian meta-learning formulations that enable probabilistic adaptation to unseen dynamical environments, with particular effectiveness in applications requiring subsecond policy adjustments such as aerial vehicle wind disturbance rejection [20]. There follows a comparative analysis of differentiable physics-integrated learning frameworks against state-of-the-art control synthesis methods.
- Advantages over conventional approaches:
- –
- Contact-rich manipulation:
- ∗
- Diff-Physics: Embodies analytical contact models for stable gradient propagation;
- ∗
- Reinforcement learning: Requires costly exploration to learn contact dynamics from scratch.
- –
- Adaptation speed:
- ∗
- Bayesian meta-learning: Achieves subsecond policy adjustments via probabilistic priors;
- ∗
- Model-reference-adaptive: Limited by filter bandwidth and parametric uncertainty models.
- –
- Data efficiency:
- ∗
- Diff-Physics: Leverages physics priors to reduce training samples by 10–100×;
- ∗
- Deep RL: Demands extensive trial-and-error in simulation.
- Limitations vs. modern alternatives:
- –
- Model fidelity requirements:
- ∗
- Diff-Physics: Sensitive to inaccuracies in analytical Jacobian formulations; Model-free RL: Agnostic to underlying dynamics through direct experience.
- –
- Computational overhead:
- ∗
- Diff-Physics: Real-time Jacobian computation demands GPU acceleration;
- ∗
- MPC: Achieves comparable performance through simplified convex approximations.
- –
- Certification challenges:
- ∗
- Bayesian meta-learning: Probabilistic guarantees lack formal safety certification;
- ∗
- Robust control: Provides deterministic worst-case bounds through synthesis.
- Hybridization opportunities:
- –
- Diff-Physics + MPC: Analytical gradients warm-start trajectory optimization;
- –
- Bayesian meta + robust control: Combines adaptation with stability-preserving constraints;
- –
- Physics-integrated RL: Uses differentiable models for efficient policy exploration.
This analysis reveals the superior data efficiency and contact dynamics handling compared to model-free approaches but highlights sensitivity to physics model inaccuracies. Hybrid frameworks merging differentiable physics with robust control principles show promise for safety-critical manipulation tasks requiring both adaptability and certification.
At the methodological frontier, the fusion of neural function approximators with stability-constrained model predictive control creates hybrid architectures with provable recursive feasibility. These systems leverage neural networks for high-dimensional feature extraction while maintaining convex optimization guarantees through MPC-based command filtering, achieving tracking precision improvement in lunar landing trajectory benchmarks compared with pure learning-based approaches [16]. The incorporation of contraction metric constraints within network training loops effectively decouples spatial and temporal learning objectives, a critical advancement for applications demanding simultaneous precision in path following and velocity regulation. There follows a comparative analysis of stability-constrained neural-MPC architectures against state-of-the-art control methodologies.
- Advantages over conventional approaches:
- –
- High-dimensional feature utilization:
- ∗
- Neural-MPC: Processes terrain/obstacle features through vision transformers;
- ∗
- Pure MPC: Limited to handcrafted state representations for tractability.
- –
- Precision–robustness tradeoff:
- ∗
- Hybrid: Neural feature extractor reduces MPC horizon requirements by 60–80%;
- ∗
- Learning only: Lacks recursive feasibility guarantees for long-term planning.
- –
- Multi-objective decoupling:
- ∗
- Contraction constraints: Enables separate optimization of path/velocity errors;
- ∗
- Single network: Suffers from competing gradient directions in joint learning.
- Limitations vs. modern alternatives:
- –
- Computational complexity:
- ∗
- Neural-MPC: Requires concurrent neural inference and QP solving;
- ∗
- Geometric control: Achieves comparable performance through differential flatness.
- –
- Model dependency:
- ∗
- Hybrid: Performance degrades with inaccurate dynamics models in MPC;
- ∗
- Model-free RL: Adapts to unmodeled dynamics through experience.
- –
- Certification overhead:
- ∗
- Contraction-MPC: Requires coupled neural-MPC stability proofs;
- ∗
- Tube MPC: Provides inherent robustness through disturbance sets.
- Hybridization frontiers:
- –
- Neural-MPC + learning-based tuning: MPC cost functions adapted via meta-learning;
- –
- Contraction + CBF: Combines stability guarantees with safety-critical constraints;
- –
- Vision Transformer-MPC: Attention mechanisms focus MPC on critical-state regions.
This analysis demonstrates superior handling of high-dimensional perception–planning loops compared to traditional MPC while revealing computational and certification challenges versus geometric methods. Hybrid architectures leveraging neural feature compression with real-time optimization show particular promise for extraterrestrial landing systems requiring certified precision.
The proposed methodologies—encompassing physics-informed neural operators, event-triggered edge computing, stability-guided training (SGT), switched system stability frameworks, Bayesian meta-learning safety architectures, neural contraction metrics, quaternion delay compensation, sparse connectivity learning, and hybrid neural-MPC systems—address critical limitations in conventional domains such as PDE-constrained control, robotic manipulation, and aerospace guidance. Compared to classical approaches like finite element methods (FEM), fixed-rate PID/MPC, or model-reference adaptive control (MRAC), these neural-enhanced techniques demonstrate superior adaptability to unmodeled dynamics, particularly in handling high-dimensional state spaces and complex sensor fusion tasks such as LiDAR-inertial navigation. While traditional sampling-based planners (RRT*/PRM) and geometric control methods rely on predefined models or full observability assumptions, neural spatiotemporal planners with embedded temporal logic constraints enable real-time adaptation in unstructured environments. However, these advancements introduce new challenges absent in classical paradigms, such as the computational overhead of GPU-dependent neural inference compared to lightweight event-triggered MPC, and the certification complexity of neural Lyapunov functions versus modular formal methods like SOS programming. Similarly, despite achieving data-efficient training through differentiable physics integration—reducing sample requirements by orders of magnitude over model-free reinforcement learning—such methods remain sensitive to inaccuracies in analytical Jacobians, a limitation circumvented by robust control’s deterministic bounds. Emerging hybrid frameworks, such as neural contraction-MPC architectures, seek to balance these tradeoffs by combining the perceptual flexibility of networks with the recursive feasibility guarantees of optimization-based control, outperforming pure learning-based or classical methods in precision-critical scenarios like lunar landing while maintaining compatibility with safety standards like ISO 26262 through modular verification layers. Ultimately, while these neural-integrated approaches surpass conventional techniques in handling nonlinearities, partial observability, and multimodal disturbances, they inherit dependencies on specialized hardware, verification toolchains, and high-fidelity physics models that established methods like LPV control or tube MPC mitigate through inherent robustness and certification-friendly formulations.
7. Challenges and Future Directions
This section identifies critical challenges and outlines future directions in neural network control systems through architectural innovations, stability certification paradigms, and strategies for computational efficiency. Key advancements encompass hybrid architectures that integrate event-triggered control with Lyapunov-based verification, lightweight neural models achieved via knowledge distillation, and GPU-accelerated reachability analysis for real-time safety certification. Emerging methodologies, including differentiable physics-informed training and stability-constrained MPC hybrids, address domain-specific challenges in aerospace, medical robotics, and smart grids. Implementation frameworks emphasize hardware–software co-design (e.g., FPGA/GPU optimization), cross-domain verification toolchains (e.g., ROS 2 + JuliaReach), and application-tailored deployments in hypersonic vehicles, precision agriculture, and nuclear systems. Future directions prioritize scalable certification for non-Markovian environments, resource-aware computation facilitated by event-triggered mechanisms, and domain-invariant stability guarantees to bridge theoretical advances with industrial adoption in safety-critical domains.
7.1. Architectural Advancements in Neural Control Systems
As depicted in Figure 6, the evolution of neural network-based control architectures necessitates fundamental improvements across theoretical formulation, numerical implementation, and operational certification domains. Critical research priorities include the development of differential-algebraic stability analysis frameworks capable of handling the switched nonlinear dynamics inherent in deep neural controllers, particularly those employing attention mechanisms for temporal dependency modeling [43]. From a numerical perspective, the integration of polytopic invariant set adaptation mechanisms shows potential for bridging computational efficiency gaps between single-inference and recursive prediction architectures, with preliminary studies indicating reduction in online computation latency while maintaining safety margins [42].
Figure 6.
The enhancement of neural network controller architectures.
Methodological innovations should focus on hybrid learning paradigms that synergize high-order dynamic estimators with conventional Lyapunov-based control synthesis. Such integration enables concurrent adaptation to both parametric uncertainties and structural nonlinearities, as demonstrated in recent aerospace applications achieving tracking error reduction during reconfiguration maneuvers [49]. Architectural simplification through channel-pruned residual networks emerges as a viable pathway for real-time embedded implementation, with quantized network variants demonstrating equivalent stability properties to full-precision counterparts in robotic manipulator control benchmarks [32].
Theoretical breakthroughs in gradient dynamics regulation present opportunities for overcoming stability limitations in recurrent neural control architectures. Modified backpropagation-through-time algorithms incorporating spectral normalization constraints have shown improvement in vanishing gradient mitigation during long-horizon prediction tasks, as validated through quadruped locomotion experiments [32]. Complementary advancements in event-triggered control synthesis enable adaptive sampling interval optimization, achieving communication load reduction in networked control systems while preserving input-to-state stability guarantees [41].
From a safety assurance perspective, the integration of stochastic barrier functions with knowledge distillation frameworks provides a dual mechanism for certified constraint satisfaction and computational efficiency enhancement. Experimental results in autonomous vehicle path planning demonstrate faster safety certification times compared to conventional reachability analysis methods, without compromising obstacle avoidance reliability [1,4]. Future research must prioritize the co-design of stability certificates and learning mechanisms, particularly for systems exhibiting time-delayed actuation dynamics and non-Markovian observation spaces, where existing neural control architectures show performance degradation in industrial case studies [2,3,62,63,64,65].
7.2. Stability-Certified Neural Control Paradigms
The development of stability-guaranteed neural control architectures requires fundamental advancements in three interconnected domains: formal verification methodologies, delay-compensated learning frameworks, and perception-integrated control synthesis. Critical research priorities include the creation of scalable verification algorithms capable of handling high-dimensional state spaces with stochastic measurement uncertainties, where emerging semi-definite programming techniques demonstrate a reduction in computation time compared to traditional reachability analysis methods [33,54]. The integration of contraction metrics with neural network training protocols shows particular promise, achieving a better success rate in stabilizing underactuated aerial systems with time-delayed actuation in recent experimental trials [39,66].
From a dynamical systems perspective, the reformulation of discrete update mechanisms through differential-algebraic constraints enables provable convergence in analytic neural controllers. Modified backpropagation algorithms incorporating spectral normalization have demonstrated improvement in training stability for vision-based manipulation tasks, effectively mitigating gradient explosion phenomena in recurrent network architectures [41]. Concurrent advancements in perception-aware control synthesis address the critical challenge of sensorimotor integration, where hybrid architectures combining spatiotemporal transformers with robust MPC frameworks achieve higher tracking precision in occluded environments compared to conventional approaches [36,57,67,68,69].
The theoretical frontier lies in unifying data-driven learning with formal safety guarantees through innovative certification mechanisms. The One-Shot Reachability Analysis (OSRA) framework establishes tighter overapproximation bounds than interval arithmetic methods, enabling real-time safety verification for neural controllers governing soft robotic systems with a 30 ms computation latency [42,70,71]. Complementary developments in Lyapunov-derived barrier certificates facilitate the direct encoding of stability constraints into network training loops, as validated through automotive collision avoidance benchmarks showing reduction in emergency braking events [1,28].
Future research directions must prioritize the co-design of learning mechanisms and stability-preserving constraints, particularly for systems exhibiting non-Markovian observation spaces and hybrid dynamics. Preliminary results in legged-locomotion control demonstrate that physics-informed neural architectures with embedded prior knowledge achieve improvement in sim-to-real transfer efficiency compared to pure learning-based approaches [3,26]. The systematic integration of these advancements will enable the deployment of certified neural controllers in safety-critical applications ranging from autonomous surgical robotics to extraterrestrial exploration systems. There follow concrete implementation-focused recommendations to guide researchers in emerging neural control domains.
- Formal verification advancements:
- –
- Implementation strategy: Combine neural Lyapunov functions with zonotope-based reachability analysis for real-time certification;
- –
- Example application: Quadrotor emergency landing systems requiring sub-100 ms safety proofs;
- –
- Toolchain integration: ROS 2 + JuliaReach for hardware-in-the-loop validation.
- Delay compensation frameworks:
- –
- Implementation strategy: Quaternion-valued LSTM networks with adaptive buffer sizing;
- –
- Example application: Surgical robots compensating for 5G network latency in teleoperation;
- –
- Toolchain integration: PyTorch Lightning + DDS middleware with timestamped dataflows.
- Perception-aware control synthesis:
- –
- Implementation strategy: Vision transformers producing SE(3) motion primitives for MPC cost maps;
- –
- Example application: Autonomous excavation in occluded construction sites;
- –
- Toolchain integration: NVIDIA Isaac Gym + CasADi for differentiable physics simulation.
- Stability-constrained training:
- –
- Implementation strategy: Spectral normalization layers enforcing Lipschitz bounds in recurrent policies;
- –
- Example application: Underwater manipulators handling variable buoyancy dynamics;
- –
- Toolchain integration: TensorFlow constrained optimization + hydroelastic contact models.
- Certifiable co-design:
- –
- Implementation strategy: Neural contraction metrics guiding mechanical actuator selection;
- –
- Example application: Mars rover wheel–terrain interaction optimization;
- –
- Toolchain integration: ANSYS 2023 R1 Digital Twin + ONNX runtime for hardware-aware training.
These recommendations emphasize practical implementation pathways through domain-specific benchmarks like standardized surgical latency testing via vasculature phantoms, cross-stack tooling unifying verification (dReal), control (Drake), and neural training frameworks, and hardware-conscious design with radiation-hardened processor-optimized quantization pipelines, bridging theoretical advances to real-world deployment.
7.3. Addressing Computational and Scalability Challenges
Computational and scalability challenges in NN controllers hinder their widespread adoption, necessitating innovative solutions to enhance efliciency. High computational complexity in training and deploying NNs, especially in real-time applications, is a primary challenge. Recent advancements focus on developing lightweight NN architectures that reduce computational overhead without sacrificing performance [34]. Integrating event-triggered frameworks optimizes resources by updating control actions only when necessary, reducing the computational load and making NN controllers feasible for large-scale systems with limited processing capabilities [41]. Concurrent learning techniques enhance scalability by leveraging sampled data for gradient computations, ensuring uniform global asymptotic stability while reducing the need for persistent excitation [49].
Efficient verification methods, like one-shot reachability analysis, address computational challenges in ensuring safety and robustness by providing tighter bounds on reachable sets [42]. Differentiable physics-based learning frameworks facilitate training by providing accurate analytical gradients, improving computational efficiency in complex motion planning tasks [12]. Addressing computational and scalability challenges requires a multifaceted approach combining innovative architectural designs, efficient learning methods, and advanced verification techniques. Implementing these strategies will enhance operational efficiency and scalability, facilitating application across a range of complex control systems. Tools like ReachNN for reachability analysis, leveraging Bernstein polynomials and GPU acceleration, exemplify this approach, improving performance significantly. Verification-aware knowledge distillation techniques optimize NN controller parameters, ensuring robust performance amid uncertainties and unmodeled dynamics, streamlining training and validation processes for diverse scenarios, from robotics to aerospace [1,3,17,72,73,74]. There follow concrete implementation strategies and toolchain recommendations to address computational/scalability challenges in NN controllers.
- Lightweight architecture implementation:
- –
- Strategy: Depthwise separable convolutions with channel pruning for robotic manipulators;
- –
- Example: Industrial pick-and-place robots using TensorFlow Lite Micro on Cortex-M7 MCUs;
- –
- Tools: NN Compression Toolkit (Intel) + hardware-aware NAS (NVIDIA TAO).
- Event-triggered frameworks:
- –
- Strategy: Adaptive triggering thresholds based on Lyapunov derivative monitoring;
- –
- Example: Drone swarm coordination with ROS 2 + Apache Kafka for sparse updates;
- –
- Tools: eProsima Fast DDS + PyTorch JIT for edge deployment.
- Concurrent learning optimization:
- –
- Strategy: Experience replay with temporal coherence-based prioritization;
- –
- Example: Autonomous excavators learning soil dynamics via PyTorch Lightning + CheckValve;
- –
- Tools: Ray RLlib for distributed sampling + ONNX Runtime for low-latency inference.
- One-shot verification:
- –
- Strategy: GPU-accelerated Bernstein polynomial overapproximation;
- –
- Example: Surgical robot safety certification using JuliaReach + CUDA.jl;
- –
- Tools: Flow* verifier integration with PyTorch via TorchScript bindings.
- Physics-informed training:
- –
- Strategy: Differentiable fluid dynamics layers for underwater drones;
- –
- Example: Soft robotic grippers trained with NVIDIA Isaac Sim + JAX autograd;
- –
- Tools: Modulus (NVIDIA) for physics-constrained NN optimization.
- Verification-aware distillation:
- –
- Strategy: Stability-preserving knowledge transfer using barrier functions;
- –
- Example: Aircraft collision avoidance distilled via dReal SMT solver + ONNX;
- –
- Tools: TensorRT with safety rule injection for embedded deployment.
Cross-domain implementation templates demonstrate practical applicability through standardized workflows for industrial robotics (ARM+FPGA heterogeneous computing), aerospace systems (radiation-hardened GPUs with QNX RTOS), and autonomous vehicles (ROS 2 multi-rate control architectures), providing domain-optimized blueprints for neural controller deployment. These strategies emphasize three critical implementation principles: hardware–software co-design for joint optimization of neural architectures and accelerator memory hierarchies; verification integration to bridge training frameworks (PyTorch/TensorFlow) with formal certification pipelines (dReach/Flow*); and real-world benchmarking through standardized latency/power evaluation protocols, exemplified by surgical robotics platforms like the da Vinci API emulation. Together, they establish a systematic pathway for deploying computationally efficient and safety-certified neural controllers across domains.
7.4. Computational Efficiency in Neural Control Systems
The widespread deployment of neural network-based controllers faces fundamental challenges in computational tractability and scalability, particularly when governing high-dimensional systems with stochastic dynamics. Critical research thrusts focus on three interconnected dimensions: architectural simplification, resource-aware computation, and verification acceleration. Emerging architectural paradigms employing depth-separable convolutions with residual skip connections demonstrate comparable stabilization capability to conventional deep networks while reducing floating-point operations in aerial vehicle control benchmarks [34]. Complementary approaches integrate event-driven activation mechanisms that dynamically adjust computation frequency based on Lyapunov-derived triggering conditions, achieving reductions in processor utilization for networked multi-agent systems [41].
From a learning theory perspective, the development of semi-continuous adaptation laws addresses the dual requirements of persistent performance and computational efficiency. These hybrid frameworks combine episodic batch updates with intermittent online refinement, theoretically guaranteeing uniform ultimate boundedness without requiring persistent excitation conditions [49]. The integration of symbolic regression techniques with neural function approximators further enhances scalability, enabling compact representation of high-dimensional policy maps while maintaining Lipschitz continuity properties essential for stability preservation.
Verification acceleration constitutes another critical frontier, where advances in formal methods bridge the gap between computational complexity and safety assurance. The integration of Bernstein polynomial overapproximation with GPU-accelerated reachability analysis enables real-time certification for neural controllers operating in 12-dimensional state spaces, demonstrating a speed improvement of three orders of magnitude over traditional zonotope methods [42]. Parallel developments in differentiable verification frameworks embed safety constraints directly into network training loops, effectively co-optimizing control performance and certifiability during the learning phase [1,17].
The synthesis of knowledge distillation techniques with robust control principles presents a promising direction for deployable systems. By transferring policy knowledge from computationally intensive teacher networks to compact student architectures while preserving barrier certificate properties, these methods achieve parameter reduction without compromising safety margins in industrial manipulator control applications [3,75]. Such architectural co-design strategies fundamentally redefine the tradeoff space between computational resource constraints and control performance requirements. There follow concrete implementation pathways to address computational and scalability challenges in neural controllers.
- Architectural simplification:
- –
- Strategy: Depthwise separable convolutions with skip connections for UAV control;
- –
- Example: Quadrotor stabilization on Cortex-M7 MCUs using TensorFlow Lite Micro;
- –
- Tools: TensorFlow Model Optimization Toolkit + NVIDIA TAO Toolkit.
- Event-triggered computation:
- –
- Strategy: Lyapunov-based triggering with dynamic priority queues;
- –
- Example: Industrial robotic arms using ROS 2 + Apache Kafka for sparse updates;
- –
- Tools: eProsima Fast DDS + PyTorch JIT scripting.
- Semi-continuous adaptation:
- –
- Strategy: Hybrid batch–online learning with temporal coherence sampling;
- –
- Example: Autonomous excavators adapting to soil variability via NVIDIA Isaac Sim;
- –
- Tools: Ray RLlib + ONNX Runtime for edge deployment.
- Symbolic–neural fusion:
- –
- Strategy: Genetic algorithm-guided equation discovery for policy compression;
- –
- Example: Satellite attitude control with <100 kB memory footprint;
- –
- Tools: PySR for symbolic regression + TensorRT for deployment.
- Verification acceleration:
- –
- Strategy: GPU-parallelized Bernstein polynomial reachability analysis;
- –
- Example: Surgical robot safety proofs using JuliaReach on NVIDIA A100 GPUs;
- –
- Tools: Flow* verifier + PyTorch/TensorFlow model export plugins.
- Knowledge distillation:
- –
- Strategy: Stability-preserving teacher–student frameworks with CBF constraints;
- –
- Example: Automotive collision avoidance distilled to FPGA-optimized networks;
- –
- Tools: dReal SMT solver + TensorRT safety rule injection.
Cross-domain implementation templates highlight domain-specific optimizations: Industrial automation utilizes ARM Cortex-A/M heterogeneous computing with TVM compiler optimizations for real-time control; aerospace systems integrate radiation-tolerant Xilinx Versal SoCs with QNX real-time middleware for certified flight control; medical robotics employ ROS 2 medical frameworks combined with dReach verification to achieve safety certification cycles of less than 5 ms. These strategies emphasize hardware-aware training through quantization-aware fine-tuning tailored for platforms such as Xilinx FPGAs and Google Edge TPUs, verification-preserving deployment via ONNX-to-C code generation with embedded runtime safety monitors, and benchmarking standards aligned with regulatory requirements like ISO 13485 compliance achieved through ROS 2 performance profiling. Collectively, these approaches establish reproducible pathways for deploying resource-efficient, safety-certified neural controllers across high-stakes domains.
7.5. Emerging Application Frontiers for Neural Control Systems
The adaptive capabilities of neural network-based control systems demonstrate significant potential for cross-domain deployment in complex dynamical environments. In modern power grid infrastructure, these controllers facilitate dynamic network reconfiguration through real-time optimal dispatch algorithms, effectively balancing load demand fluctuations while maintaining voltage stability margins through integrated Lyapunov constraints [9]. Aerospace applications benefit from hybrid control architectures that combine nonlinear reference tracking with neural disturbance observers, particularly in hypersonic vehicle guidance systems requiring robustness against aerodynamic parameter variations [1].
Autonomous mobility systems leverage neural controllers for multimodal sensor fusion in dynamic obstacle avoidance scenarios. The inherent capacity to encode control barrier functions within network training protocols ensures formal safety guarantees during urban navigation tasks, enabling reliable operation under partial observability conditions [53]. Medical robotics applications exploit neural control’s ability to compensate for time-varying biomechanical properties, as evidenced in surgical-assist platforms achieving precise trajectory tracking through adaptive impedance regulation mechanisms [76].
Agricultural automation systems integrate neural controllers with distributed sensing networks to optimize cultivation operations under environmental uncertainties. The implementation of temporal logic constraints within model predictive control frameworks enables real-time adjustment of harvesting parameters while satisfying ecological preservation requirements, demonstrating particular effectiveness in precision farming applications [32]. These implementations universally require co-design methodologies that reconcile learning-based adaptation with stability-preserving constraints, especially when governing systems with nonholonomic motion characteristics or delayed actuation dynamics.
The cross-domain applicability stems from the ability of neural controllers to approximate high-dimensional value functions while preserving input-to-state stability properties. Recent advances in reachability analysis combined with neural Lyapunov functions have extended certified control authority to systems with partially observable states, enabling deployment in nuclear reactor power regulation and underwater vehicle manipulation tasks [3,55,77,78,79,80]. Future research directions emphasize the development of domain-invariant certification frameworks capable of transferring stability guarantees across heterogeneous dynamical systems, a critical requirement for industrial-scale adoption in safety-critical environments. There follow domain-specific implementation guidelines to operationalize neural control systems across application areas.
- Smart grids:
- –
- Strategy: Physics-constrained neural optimal power flow with Lyapunov-based voltage regulators;
- –
- Example: Real-time load balancing on NVIDIA A100 GPUs using PyTorch + JuliaPowerModels;
- –
- Tools: GridDyn simulator + TensorRT for substation edge deployment.
- Aerospace (hypersonic vehicles):
- –
- Strategy: Hybrid neural-MPC with embedded aerodynamic disturbance observers;
- –
- Example: X-51A-like vehicle control using Simulink + PyTorch C++ API;
- –
- Tools: NASA FUN3D CFD + ONNX Runtime for radiation-hardened FPGAs.
- Autonomous mobility:
- –
- Strategy: LiDAR-vision fusion with neural CBFs for urban navigation;
- –
- Example: L4 robotaxis using NVIDIA DRIVE + CuDNN-accelerated safety monitors;
- –
- Tools: CARLA simulator + ROS 2 Nav2 with neural plugin API.
- Medical robotics:
- –
- Strategy: Adaptive impedance control with time-delay compensation for surgical assist;
- –
- Example: da Vinci Surgical System upgrades using TensorFlow Lite + Real-Time Innovations DDS;
- –
- Tools: SurgiSim phantoms + dReal for FDA-compliant certification.
- Precision agriculture:
- –
- Strategy: STL-constrained neural-MPC for autonomous harvesters;
- –
- Example: John Deere combine optimization via AgOpenGPS + ONNX models;
- –
- Tools: ROS Agricultural + FarmBot API for field testing.
- Nuclear systems:
- –
- Strategy: Reachability-certified neural PID for reactor power regulation;
- –
- Example: NuScale SMR control upgrades using JuliaReach + PyTorch;
- –
- Tools: RELAP5-3D + FPGA-based triple modular redundancy.
The cross-domain verification framework integrates a unified toolchain (ROS 2 Control-MetaPackage with Drake, dReal, and TorchScript plugins), standardized hardware configurations (Xilinx Kria KV260 SOM with Ubuntu Real-Time Kernel), and domain-specific benchmark suites (OpenAI Gym adapted with ISO-compliant metrics). This framework enables domain-tailored acceleration through FPGA/GPU optimization, ensures regulatory compliance via pre-configured IEC/DO-178C pipelines, and facilitates transfer learning capabilities by leveraging shared representations across various tasks.
8. Conclusions
Neural network-based control architectures have emerged as transformative solutions for governing complex nonlinear systems characterized by uncertain dynamics and time-delayed interactions. This comprehensive analysis establishes that modern synthesis frameworks, particularly those integrating iterative stability certification (ISTC) mechanisms and Robust Optimal Safe-Stability Guaranteed Training (ROSS-GT) methodologies, fundamentally redefine the design space for adaptive control systems operating under stochastic disturbances. The systematic integration of imitation learning principles with formal verification protocols demonstrates unprecedented capability in reconciling asymptotic tracking performance with provable safety constraints across heterogeneous application domains.
Advancements in neural controller verification are exemplified by reachability analysis frameworks employing symbolic interval propagation techniques, which enable formal certification of control policies governing high-dimensional state spaces. These methodological breakthroughs are complemented by privacy-preserving control strategies that maintain operational integrity in mixed-autonomy environments through dynamic information masking mechanisms. The inherent adaptability of neural control architectures is further manifested in aerial manipulation systems, where coupled rotorcraft–payload dynamics are stabilized through online learning of unknown inertial parameters while preserving Lyapunov-derived stability margins.
Theoretical developments in adjoint-based sensitivity analysis provide rigorous foundations for stability certification in differential neural control systems, particularly when governing non-smooth dynamical regimes. Emerging research directions emphasize the co-evolution of learning mechanisms with physical system constraints, as demonstrated in legged locomotion controllers that achieve terrain-adaptive gait generation through embedded prior knowledge of contact dynamics. These advancements collectively establish neural network controllers as foundational elements in next-generation autonomous systems, bridging the gap between data-driven adaptation and model-based certification in safety-critical applications ranging from precision robotics to distributed energy resource management.
Future research trajectories must prioritize the development of cross-domain certification frameworks capable of transferring stability guarantees between distinct dynamical regimes. The integration of topological learning methods with hybrid system verification techniques presents a promising pathway for realizing this objective, ultimately enabling the deployment of neural control architectures in large-scale cyber–physical systems governed by partial differential dynamics.
Author Contributions
Conceptualization, R.L. and J.H.; formal analysis, R.L. and J.H.; investigation, R.L. and J.H.; project administration, J.H.; writing—original draft preparation, R.L. and J.H.; writing—review and editing, B.L., W.D. and J.H.; supervision, B.L. and J.H.; funding acquisition, B.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Key Projects of the Joint Fund of the National Natural Science Foundation of China under Grant U22A2050, the National Natural Science Foundation of China under Grant 62203235, the Natural Science Foundation of Guangdong Province under Grant 2025A1515011967 and 2022A1515110046, and the Open Fund of State Key Laboratory of Intelligent Manufacturing of Advanced Construction Machinery.
Data Availability Statement
No new data were created.
Acknowledgments
We are truly grateful to Haimin Chen from State Key Laboratory of Intelligent Manufacturing of Advanced Construction Machinery, Jiangsu XCMG National Key Laboratory Technology Co., Ltd., 221004, Jiangsu, China for his insightful and valuable suggestions in reviewing, revising and editing this article.
Conflicts of Interest
Author Jianhua Huang was employed by the company Jiangsu XCMG National Key Laboratory Technology Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Fazlyab, M.; Morari, M.; Pappas, G.J. Safety Verification and Robustness Analysis of Neural Networks via Quadratic Constraints and Semidefinite Programming. IEEE Trans. Autom. Control 2022, 67, 1–15. [Google Scholar] [CrossRef]
- Talukder, S.; Kumar, R. Robust Stability of Neural-Network-Controlled Nonlinear Systems with Parametric Variability. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 4820–4832. [Google Scholar] [CrossRef]
- Wu, F.; Wang, G.; Zhuang, S.; Wang, K.; Keimer, A.; Stoica, I.; Bayen, A. Composing MPC with LQR and Neural Network for Amortized Efficiency and Stable Control. IEEE Trans. Autom. Sci. Eng. 2024, 21, 2088–2101. [Google Scholar] [CrossRef]
- Kang, H.; Choi, D.-W. Recall-Oriented Continual Learning with Generative Adversarial Meta-Model. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 24 March 2024. [Google Scholar]
- Mazouz, R.; Muvvala, K.; Ratheesh Babu, A.; Laurenti, L.; Lahijanian, M. Safety guarantees for neural network dynamic systems via stochastic barrier functions. In Proceedings of the 36th International Conference on Neural Information Processing Systems (NIPS ’22), New Orleans, LA, USA, 28 November 2022. [Google Scholar]
- Chen, H.; Zhang, J.; Lv, C. RHONN Modelling-Enabled Nonlinear Predictive Control for Lateral Dynamics Stabilization of an In-Wheel Motor Driven Vehicle. IEEE Trans. Veh. Technol. 2022, 71, 8296–8308. [Google Scholar] [CrossRef]
- Xia, T.; Sun, K.; Kang, W. Machine Learning based Optimal Feedback Control for Microgrid Stabilization. In Proceedings of the 2022 IEEE Power & Energy Society General Meeting (PESGM), Denver, CO, USA, 17 July 2022. [Google Scholar]
- Wang, C.C.; Tan, K.L.; Chen, C.T.; Lin, Y.H.; Keerthi, S.S.; Mahajan, D.; Sundararajan, S.; Lin, C.J. Distributed Newton Methods for Deep Neural Networks. Neural Comput. 2018, 30, 1673–1724. [Google Scholar] [CrossRef]
- Cui, R.; Yang, C.; Li, Y.; Sharma, S. Adaptive Neural Network Control of AUVs with Control Input Nonlinearities Using Reinforcement Learning. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 1019–1029. [Google Scholar] [CrossRef]
- Fang, Y.; Liu, J.; Zhang, M.; Zhang, J.; Ma, Y.; Li, M.; Hu, Y.; Jiang, C.; Liu, T. Complex locomotion skill learning via differentiable physics. arXiv 2023. preprint. [Google Scholar]
- Zenati, A.; Aouf, N.; de la Llana, D.S.; Bannani, S. Validation of Neural Network Controllers for Uncertain Systems Through Keep-Close Approach: Robustness Analysis and Safety Verification. arXiv 2023. preprint. [Google Scholar]
- Liao, S.; Samiee, A.; Deng, C.; Bai, Y.; Yuan, B. Compressing Deep Neural Networks Using Toeplitz Matrix: Algorithm Design and Fpga Implementation. In Proceedings of the 2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12 May 2019. [Google Scholar]
- Su, J.; Zhang, Y.S.; Tsilivis, N.; Kempe, J. On the robustness of neural collapse and the neural collapse of robustness. In Proceedings of the 37th International Conference on Neural Information Processing Systems (NIPS ’23), New Orleans, LA, USA, 12 December 2023. [Google Scholar]
- Trucios, L.E.; Tavakoli, M.; Adams, K. Adaptive tracking control for task-based robot trajectory planning. In Proceedings of the 2020 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Toronto, ON, Canada, 20 April 2020. [Google Scholar]
- Nubert, J.; Köhler, J.; Berenz, V.; Allgöwer, F.; Trimpe, S. Safe and Fast Tracking on a Robot Manipulator: Robust MPC and Neural Network Control. IEEE Robot. Autom. Lett. 2018, 5, 3050–3057. [Google Scholar] [CrossRef]
- Hashimoto, W.; Hashimoto, K.; Takai, S. STL2vec: Signal Temporal Logic Embeddings for Control Synthesis with Recurrent Neural Networks. IEEE Robot. Autom. Lett. 2022, 7, 5246–5253. [Google Scholar] [CrossRef]
- Yin, H.; Seiler, P.; Jin, M.; Arcak, M. Imitation Learning with Stability and Safety Guarantees. IEEE Control Syst. Lett. 2022, 6, 409–414. [Google Scholar] [CrossRef]
- Zou, Y.; Qin, Z. Bayesian meta-reinforcement learning for traffic signal control. arXiv 2021. preprint. [Google Scholar]
- Bui-Thanh, T. Adjoint and Its roles in Sciences, Engineering, and Mathematics. SIAM Book 2024. in progress. [Google Scholar]
- Xiong, Z.; Wang, H.; Zhao, L.; Papachristodoulou, A. Data-driven stable neural feedback loop design. arXiv 2024. preprint. [Google Scholar]
- Qian, J.; Xu, L.; Ren, X.; Wang, X. Structured Deep Neural Network-Based Backstepping Trajectory Tracking Control for Lagrangian Systems. IEEE Trans. Neural Netw. Learn. Syst. 2024, 1–7, early access. [Google Scholar] [CrossRef]
- Gonzalez, F.J.; Balajewicz, M. Deep convolutional recurrent autoencoders for learning low-dimensional feature dynamics of fluid systems. arXiv 2018. preprint. [Google Scholar]
- Sontag, E.D. Remarks on input to state stability of perturbed gradient flows, motivated by model-free feedback control learning. Syst. Control Lett. 2022, 161, 105138. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, H.; Zou, Y.; Li, H.; Cheng, L. Stabilizing dynamic systems through neural network learning: A robust approach. arXiv 2024. preprint. [Google Scholar]
- Xiao, W.; Wang, T.H.; Hasani, R.; Chahine, M.; Amini, A.; Li, X.; Rus, D. BarrierNet: Differentiable Control Barrier Functions for Learning of Safe Robot Control. IEEE Trans. Robot. 2023, 39, 2289–2307. [Google Scholar] [CrossRef]
- Ivanov, R.; Carpenter, T.J.; Weimer, J.; Alur, R.; Pappas, G.J.; Lee, I. Case study: Verifying the safety of an autonomous racing car with a neural network controller. In Proceedings of the 23rd International Conference on Hybrid Systems: Computation and Control (HSCC ’20), New York, NY, USA, 22 April 2020. [Google Scholar]
- Boffi, N.; Tu, S.; Matni, N.; Slotine, J.J.; Sindhwani, V. Learning stability certificates from data. In Proceedings of the 2020 Conference on Robot Learning, Cambridge, MA, USA, 16 November 2020. [Google Scholar]
- Foster, D.; Sarkar, T.; Rakhlin, A. Learning nonlinear dynamical systems from a single trajectory. In Proceedings of the 2nd Conference on Learning for Dynamics and Control, Berkeley, CA, USA, 11 June 2020. [Google Scholar]
- Pan, Y.; Shi, T.; Wen, C. Least-Squares Composite Learning Backstepping Control with High-Order Tuners. In Proceedings of the 2023 62nd IEEE Conference on Decision and Control (CDC), Marina Bay Sands, Singapore, 13 December 2023. [Google Scholar]
- Hashemi, N.; Qin, X.; Deshmukh, J.V.; Fainekos, G.; Hoxha, B.; Prokhorov, D.; Yamaguchi, T. Risk-Awareness in Learning Neural Controllers for Temporal Logic Objectives. In Proceedings of the 2023 American Control Conference (ACC), San Diego, CA, USA, 31 May 2023. [Google Scholar]
- Cleavel, M.; Lindemann, L.; Ivanov, R.; Pappas, G.J. Risk verification of stochastic systems with neural network controllers. Artif. Intell. 2022, 313, 103782. [Google Scholar]
- Madireddy, S.; Yanguas-Gil, A.; Balaprakash, P. Improving Performance in Continual Learning Tasks using Bio-Inspired Architectures. In Proceedings of the 2nd Conference on Lifelong Learning Agents, Montréal, QC, Canada, 22 August 2023. [Google Scholar]
- Das, S.; Mali, A. Exploring learnability in memory-augmented recurrent neural networks: Precision, stability, and empirical insights. arXiv 2024. preprint. [Google Scholar]
- Aly, A.; Guadagni, G.; Dugan, J.B. Derivative-Free Optimization of Neural Networks using Local Search. In Proceedings of the 2019 IEEE 10th Annual Ubiquitous Computing, Electronics & Mobile Communication Conference (UEMCON), New York, NY, USA, 10 October 2019. [Google Scholar]
- Santa Cruz, U.; Shoukry, Y. NNLander-VeriF: A Neural Network Formal Verification Framework for Vision-Based Autonomous Aircraft Landing. Nasa Form. Methods 2022, 13260, 213–230. [Google Scholar] [CrossRef]
- Hashemi, N.; Hoxha, B.; Prokhorov, D.; Fainekos, G.; Deshmukh, J.V. Scaling Learning-based Policy Optimization for Temporal Logic Tasks by Controller Network Dropout. ACM Trans. Cyber-Phys. Syst. 2024, 8, 1–28. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, D.; Lou, J.; Lu, J.; Cao, J. Stability Analysis of Quaternion-Valued Neural Networks: Decomposition and Direct Approaches. IEEE Trans. Neural Networks Learn. Syst. 2018, 29, 4201–4211. [Google Scholar] [CrossRef]
- Zheng, R.; Yi, X.; Lu, W.; Chen, T. Stability of Analytic Neural Networks with Event-Triggered Synaptic Feedbacks. IEEE Trans. Neural Networks Learn. Syst. 2016, 27, 483–494. [Google Scholar] [CrossRef]
- Chen, S.; Preciado, V.M.; Fazlyab, M. One-Shot Reachability Analysis of Neural Network Dynamical Systems. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May 2023. [Google Scholar]
- Wang, S.; Diagne, M.; Krstić, M. Deep Learning of Delay-Compensated Backstepping for Reaction-Diffusion PDEs. IEEE Trans. Autom. Control 2025, 1–8, early access. [Google Scholar] [CrossRef]
- De la Sen, M. Dynamic physical systems: Energy balances and stability issues. In Proceedings of the 2008 IEEE International Symposium on Industrial Electronics, Cambridge, UK, 3 June 2008. [Google Scholar]
- Carsten, W. Scherer and Joost Veenman. Stability analysis by dynamic dissipation inequalities: On merging frequency-domain techniques with time-domain conditions. Syst. Control Lett. 2018, 121, 7–15. [Google Scholar]
- Osinenko, P.; Yaremenko, G.; Zashchitin, R.; Bolychev, A.; Ibrahim, S.; Dobriborsci, D. Critic as lyapunov function (calf): A model-free, stability-ensuring agent. arXiv 2024. preprint. [Google Scholar]
- Chatterjee, D.; Liberzon, D. Towards ISS disturbance attenuation for randomly switched systems. In Proceedings of the 2007 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12 December 2007. [Google Scholar]
- Timme, M.; Wolf, F. The simplest problem in the collective dynamics of neural networks: Is synchrony stable? Nonlinearity 2008, 21, 1579. [Google Scholar] [CrossRef]
- Pandey, S.K.; Patel, N. Demonstrating Remote Synchronization: An Experimental Approach with Nonlinear Oscillators. In Proceedings of the 2024 6th International Conference on Control and Robotics (ICCR), Yokohama, Japan, 5 December 2024. [Google Scholar]
- Le, J.H.; Teel, A.R. Concurrent learning in high-order tuners for parameter identification. arXiv 2022. preprint. [Google Scholar]
- Schmidt, J. Open maps preserve stability. arXiv 2023. preprint. [Google Scholar]
- Doban, A.I.; Lazar, M. Computation of Lyapunov Functions for Nonlinear Differential Equations via a Massera-Type Construction. IEEE Trans. Autom. Control 2018, 63, 1259–1272. [Google Scholar] [CrossRef]
- Luo, J.; Solowjow, E.; Wen, C.; Ojea, J.A.; Agogino, A.M.; Tamar, A.; Abbeel, P. Reinforcement Learning on Variable Impedance Controller for High-Precision Robotic Assembly. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20 May 2019. [Google Scholar]
- Ai, B.; Gao, W.; Hsu, D. Deep Visual Navigation under Partial Observability. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23 May 2022. [Google Scholar]
- Noori, S.V.; Hu, B.; Dullerud, G.; Seiler, P. Stability and Performance Analysis of Discrete-Time ReLU Recurrent Neural Networks. In Proceedings of the 2024 IEEE 63rd Conference on Decision and Control (CDC), Milan, Italy, 16 December 2024. [Google Scholar]
- Ferlez, J.; Shoukry, Y. Polynomial-Time Reachability for LTI Systems with Two-Level Lattice Neural Network Controllers. IEEE Control Syst. Lett. 2023, 7, 1105–1110. [Google Scholar] [CrossRef]
- Zhou, J.; Yang, K. A parameter privacy-preserving strategy for mixed-autonomy platoon control. Transp. Res. Part C Emerg. Technol. 2024, 169, 104885. [Google Scholar] [CrossRef]
- Sun, X.; Khedr, H.; Shoukry, Y. Formal verification of neural network controlled autonomous systems. In Proceedings of the 22nd ACM International Conference on Hybrid Systems: Computation and Control (HSCC ’19), Montreal, QC, Canada, 16 April 2019. [Google Scholar]
- Cruz, U.S.; Ferlez, J.; Shoukry, Y. Safe-by-Repair: A Convex Optimization Approach for Repairing Unsafe Two-Level Lattice Neural Network Controllers. In Proceedings of the 2022 IEEE 61st Conference on Decision and Control (CDC), Cancun, Mexico, 6 December 2022. [Google Scholar]
- Berkenkamp, F.; Turchetta, M.; Schoellig, A.; Krause, A. Safe model-based reinforcement learning with stability guarantees. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS’17), Long Beach, CA, USA, 4 December 2017. [Google Scholar]
- Gu, S.; Kumar, R. Robust optimal safe and stability guaranteeing reinforcement learning control for quadcopter. arXiv 2024. preprint. [Google Scholar]
- Fu, J.; Kumar, A.; Soh, M.; Levine, S. Safe model-based reinforcement learning with stability guarantees. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9 June 2019. [Google Scholar]
- Meng, Y.; Fan, C. Hybrid Systems Neural Control with Region-of-Attraction Planner. In Proceedings of the 5th Annual Learning for Dynamics and Control Conference, Philadelphia, PA, USA, 15 June 2023. [Google Scholar]
- Zakwan, M.; Xu, L.; Ferrari-Trecate, G. Neural Exponential Stabilization of Control-affine Nonlinear Systems. In Proceedings of the 2024 IEEE 63rd Conference on Decision and Control (CDC), Milan, Italy, 16 December 2024. [Google Scholar]
- Liu, X.; He, H.; Cao, J. Event-Triggered Bipartite Synchronization of Delayed Inertial Memristive Neural Networks with Unknown Disturbances. IEEE Trans. Control Netw. Syst. 2024, 11, 1408–1419. [Google Scholar] [CrossRef]
- Wei, Z.-J.; Liu, K.-Z.; Liu, P.-F.; Sun, X.-M. Event-Triggered H∞ Tracking Control for Dynamic Artificial Neural Network Models with Time-Varying Delays. IEEE Trans. Autom. Sci. Eng. 2025, 22, 6922–6931. [Google Scholar] [CrossRef]
- Palo, E.D.; Olm, J.M.; Dòria-Cerezo, A.; Bernardo, M.d. Sliding Mode Control-Based Synchronization of Complex-Valued Neural Networks. IEEE Trans. Control Netw. Syst. 2024, 11, 1251–1261. [Google Scholar] [CrossRef]
- Srisuchinnawong, A.; Akkawutvanich, C.; Manoonpong, P. Adaptive Modular Neural Control for Online Gait Synchronization and Adaptation of an Assistive Lower-Limb Exoskeleton. IEEE Trans. Neural Networks Learn. Syst. 2024, 35, 12449–12458. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, R.; Wu, T.; Weng, R.; Han, M.; Zhao, Y. Safe Reinforcement Learning with Stability Guarantee for Motion Planning of Autonomous Vehicles. IEEE Trans. Neural Networks Learn. Syst. 2021, 32, 5435–5444. [Google Scholar] [CrossRef]
- Cao, L.; Pan, Y.; Liang, H.; Ahn, C.K. Event-Based Adaptive Neural Network Control for Large-Scale Systems with Nonconstant Control Gains and Unknown Measurement Sensitivity. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 7027–7038. [Google Scholar] [CrossRef]
- Li, L.J.; Chang, X.; Chao, F.; Lin, C.M.; Huỳnh, T.T.; Yang, L.; Shang, C.; Shen, Q. Self-Organizing Type-2 Fuzzy Double Loop Recurrent Neural Network for Uncertain Nonlinear System Control. IEEE Trans. Neural Networks Learn. Syst. 2025, 36, 6451–6465. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Ding, J.; Li, X. Network Controllability Robustness Learning via Spatial Graph Neural Networks. IEEE Trans. Netw. Sci. Eng. 2024, 11, 4045–4058. [Google Scholar] [CrossRef]
- Si, C.; Wang, Q.-G.; Yu, J. Event-Triggered Adaptive Fuzzy Neural Network Output Feedback Control for Constrained Stochastic Nonlinear Systems. IEEE Trans. Neural Networks Learn. Syst. 2024, 35, 5345–5354. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Q.-G.; Yu, J. Event-Triggered Adaptive Neural Network Tracking Control for Uncertain Systems with Unknown Input Saturation Based on Command Filters. IEEE Trans. Neural Networks Learn. Syst. 2024, 35, 8702–8707. [Google Scholar] [CrossRef]
- Yang, M.; Zhai, J. Estimate-Based Adaptive Neural Secure Control for Nonminimum-Phase Nonlinear Systems with Hybrid Attacks via Dynamic Event-Triggered Scheme. IEEE Trans. Netw. Sci. Eng. 2025, 12, 859–869. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Y.; Miao, Z.; Jiang, Y.; Feng, Y. Asymptotic Stability Analysis and Stabilization Control for General Fractional-Order Neural Networks via an Unified Lyapunov Function. IEEE Trans. Netw. Sci. Eng. 2024, 11, 2675–2688. [Google Scholar] [CrossRef]
- Yan, B.; Niu, B.; Zhao, X.; Wang, H.; Chen, W.; Liu, X. Neural-Network-Based Adaptive Event-Triggered Asymptotically Consensus Tracking Control for Nonlinear Nonstrict-Feedback MASs: An Improved Dynamic Surface Approach. IEEE Trans. Neural Networks Learn. Syst. 2024, 35, 584–597. [Google Scholar] [CrossRef]
- Ding, J.; Wu, M.; Xiao, M. Nonlinear Decoupling Control with PIλ Dμ Neural Network for MIMO Systems. IEEE Trans. Neural Networks Learn. Syst. 2024, 35, 8715–8722. [Google Scholar] [CrossRef]
- He, W.; Xue, C.; Yu, X.; Li, Z.; Yang, C. Admittance-Based Controller Design for Physical Human–Robot Interaction in the Constrained Task Space. IEEE Trans. Autom. Sci. Eng. 2020, 17, 1937–1949. [Google Scholar] [CrossRef]
- Zhang, N.; Zhang, F.; Li, Y.; Wang, C.; Li, K. A Discrete-Time Neural Network Control Method Based on Deterministic Learning for Upper-Limb Rehabilitation Robot. IEEE Trans. Autom. Sci. Eng. 2025, 22, 9753–9766. [Google Scholar] [CrossRef]
- Zhu, J.; Long, X.; Yuan, Q. Adaptive Terminal Sliding Mode Control for a Quadrotor System with Barrier Function Switching Law. Mathematics 2025, 13, 1344. [Google Scholar] [CrossRef]
- Mari, C.; Lucheroni, C.; Sinha, N.; Mari, E. Power System Portfolio Selection and CO2 Emission Management Under Uncertainty Driven by a DNN-Based Stochastic Model. Mathematics 2025, 13, 1477. [Google Scholar] [CrossRef]
- Cong, E.Y.; Zhang, X.; Zhu, L. Semi-Global Polynomial Synchronization of High-Order Multiple Proportional-Delay BAM Neural Networks. Mathematics 2025, 13, 1512. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).