Economic Model Predictive Control for Wastewater Treatment Processes Based on Global Maximum Error POD-TPWL

Abstract

To address the challenge of low computational efficiency in nonlinear Economic Model Predictive Control (EMPC) for large-scale systems such as wastewater treatment plants (WWTPs), this paper proposes a Trajectory Piecewise Linearization (TPWL)-based EMPC framework integrated with global maximum error control (GMEC) and Proper Orthogonal Decomposition (POD). The TPWL method constructs a reduced-order model framework, while GMEC iteratively refines the linearization point selection process. A two-stage strategy is employed: first, coarse selection of candidate linearization points along the original nonlinear model’s state trajectory based on Euclidean distance, followed by refinement to determine optimal points that minimize global approximation errors. Simulation results demonstrate that the proposed method reduces computational time by at least 65% under identical weather conditions while maintaining effluent quality and total cost indices within acceptable thresholds. Compared with conventional TPWL-POD approaches, this framework achieves higher model accuracy and superior EMPC control performance. These advancements underscore the method’s potential for real-time implementation in complex industrial systems, balancing computational efficiency with control precision. Additionally, the framework’s modular design enables integration with existing optimization techniques to further reduce computational complexity without compromising effluent quality compliance.

1. Introduction

The intensification of industrialization and urbanization has exacerbated global water scarcity and pollution, positioning wastewater treatment and water quality optimization as pivotal challenges in environmental sustainability and resource recovery [1]. Internationally, water resource management has gained unprecedented policy emphasis, notably reflected in the United Nations Sustainable Development Goals (SDGs) that mandate urgent actions on clean water accessibility and aquatic ecosystem preservation [2,3].

Conventional control strategies in wastewater treatment, particularly Proportional-Integral-Derivative (PID) control, dominate industrial applications owing to their simplicity and cost-effectiveness for linear systems [4]. However, PID controllers are inherently limited in handling nonlinear dynamics, time-varying disturbances, and high-dimensional processes, often necessitating laborious parameter calibration to mitigate performance deterioration [5]. In contrast, Model Predictive Control (MPC) offers a systematic framework for handling multivariable nonlinear systems through receding horizon optimization, enabling global performance guarantees while explicitly accommodating constraints [6]. These advantages have spurred MPC’s adoption in wastewater treatment plants (WWTPs). For instance, Lin Yonggang et al. [7] applied MPC to optimize multipump station scheduling in sewage systems, effectively reducing complexity and costs. Martin M. et al. [8] implemented MPC in controlling cascaded bioreactors at wastewater treatment plants, achieving satisfactory performance with reduced steady-state errors. Economic Model Predictive Control (EMPC), an advanced variant of MPC, extends these benefits by directly incorporating economic objectives (e.g., energy minimization, operational cost reduction) into the optimization framework [9]. As evidenced by Zeng et al. [10], EMPC surpasses conventional PI and MPC in simultaneously enhancing effluent quality and lowering operational expenses. Nevertheless, deploying EMPC on high-fidelity models such as the Benchmark Simulation Model No. 1 (BSM1) entails solving computationally intensive nonlinear optimization problems at each sampling interval, posing prohibitive online computation demands for real-time implementation. Thus, reducing computation time is crucial for improving efficiency. To address this, scholars have proposed various methods to lower computational complexity. For example, Zhang et al. [11] introduced a distributed EMPC strategy, which enhanced effluent quality and energy efficiency through system-wide model design.

Model order reduction (MOR) techniques provide a systematic pathway to alleviate computational complexity. Among these, Trajectory Piecewise Linearization (TPWL) has emerged as a promising strategy that approximates nonlinear dynamics through locally linearized models along system trajectories [12]. By strategically selecting linearization points, TPWL enables tunable trade-offs between approximation accuracy and computational efficiency, making it particularly suited for real-time control of large-scale systems. For instance, Zhang et al. [13] applied TPWL to EMPC in wastewater treatment plants, demonstrating substantial improvements in computational efficiency through model approximation.

Proper Orthogonal Decomposition (POD), a common dimensionality reduction technique [14,15,16], has also been widely used in model simplification. By reducing the dimensionality of wastewater treatment plants (WWTPs) models and integrating TPWL, further simplification can be achieved.

The global maximum error control (GMEC) method iteratively refines approximate models by identifying and addressing the maximum error points during simulation until error thresholds are met.

Building on these advancements, this paper proposes a reduced-order TPWL-based EMPC framework integrated with GMEC for wastewater treatment plants. First, candidate linearization points are selected from the state trajectory of the original nonlinear model using TPWL. A reduced-order model is then constructed via POD, followed by TPWL simplification. During TPWL, linearization points are dynamically selected from the candidate pool using GMEC to ensure the maximum error of the simplified model meets predefined thresholds. Finally, the simplified model’s performance—including error magnitude, control efficacy, and computation time—is analyzed.

This study introduces a novel EMPC framework combining GMEC, TPWL, and POD (GMEC-POD-TPWL-EMPC), addressing the low computational efficiency of traditional EMPC in nonlinear wastewater treatment models. A two-stage linearization point selection strategy optimizes TPWL efficiency, overcoming the empirical limitations of traditional TPWL highlighted in [12,13]. Furthermore, by integrating POD, this work extends its application from fluid dynamics [14,15,16] to wastewater treatment control, offering new insights for real-time control of large-scale nonlinear systems.

An error feedback-based adaptive model simplification mechanism is developed, dynamically adjusting linearization point distribution via GMEC to balance computational efficiency and control accuracy. Compared with the single-point selection in [13], this paper’s dual-stage strategy combines state trajectory spacing with global error thresholds, minimizing redundant points and validating its applicability in complex industrial scenarios. Using BSM1 as a case study, the method’s effectiveness in high-dimensional nonlinear systems is demonstrated.

Additionally, this approach provides an efficient tool for real-time wastewater control. Experiments show that under controllable performance losses (e.g., effluent quality, energy consumption), the proposed method achieves optimization speeds meeting real-time requirements, outperforming traditional EMPC (e.g., the distributed strategy in [9,11] incurs extra communication costs). It quantifies the relationship between linearization points and computational efficiency, offering theoretical guidance for parameter tuning in industrial settings. Unlike intelligent control methods in [5,6], which rely on high-performance computing, this method reduces EMPC complexity, enabling deployment in resource-limited wastewater treatment plants.

2. Model Description

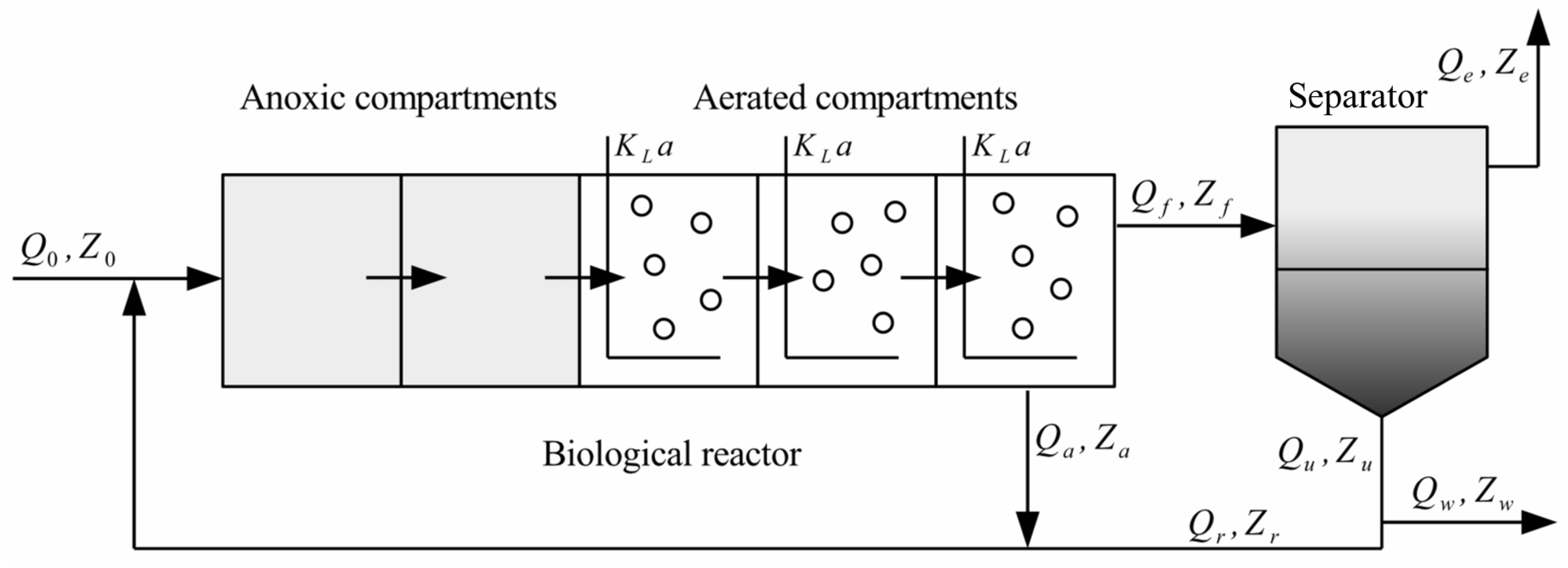
The wastewater treatment system analyzed in this study employs an enhanced configuration derived from the Benchmark Simulation Model No. 1 (BSM1), with schematic representation and parameter specifications provided in Figure 1 and

Table 1. WWTP model parameters.

${\mathit{V}}_1$ (Volume of Reactor 1)	1000 m3
$V_2$ (Volume of Reactor 2)	1000 m3
$V_3$ (Volume of Reactor 3)	1333 m3
$V_4$ (Volume of Reactor 4)	1333 m3
$V_5$ (Volume of Reactor 5)	1333 m3
$Q_w$ (Underflow rate)	385 m3/d
$Q_r$ (External recirculation rate)	18,446 m3/d
$V_s$ (Volume of Separator)	6000 m3
$K_L{a}_3$ (Oxygen transfer coefficient in Reactor 3)	240/d
$K_L{a}_4$ (Oxygen transfer coefficient in Reactor 4)	240/d

, respectively. The system integrates a five-compartment sludge reactor coupled with an ideal secondary clarifier [17]. Biochemical reactions within the reactor are spatially segregated: denitrification is facilitated in the first two anoxic compartments, where nitrate reduction generates nitrogen gas, while nitrification dominates the subsequent three aerobic compartments, enabling ammonia oxidation to nitrate.

Hydraulic inputs to the primary reactor compartment include three distinct streams: (1) raw influent with volumetric flow rate $Q_0$ and pollutant concentration $Z_0$; (2) internal recirculation flow ($Q_a$, $Z_a$) recycled from the terminal aerobic compartment; and (3) external recirculation flow ($Q_r$, $Z_r$) extracted from the clarifier underflow. The clarifier partitions the reactor effluent into two streams: purified overflow discharge ($Q_e$, $Z_e$) and underflow sludge withdrawal ($Q_w$, $Z_w$). A residual flow ($Q_f$, $Z_f$) from the final aerobic compartment directly feeds the clarifier. The process dynamics are governed by eight core biochemical reaction mechanisms [18].

The modified BSM1-based wastewater treatment process is mathematically represented by a system of 78 coupled ordinary differential equations (ODEs). Each reactor compartment and the ideal secondary clarifier [19] are governed by 13 interdependent state variables, each associated with a distinct differential equation. These variables, comprehensively detailed in

Table 2. Thirteen components of the modified BSM1 model.

Notation	Description	Unit
$S_I$	inert soluble organic matter	gCOD/m3
$S_S$	readily biodegradable and soluble substrate	gCOD/m3
$X_I$	inert particulate organic matter	gCOD/m3
$X_S$	slowly biodegradable and soluble substrate	gCOD/m3
$X_{B,H}$	biomass of active heterotrophs	gCOD/m3
$X_{B,A}$	biomass of active autotrophs	gCOD/m3
$X_P$	particulate generated from decay of organisms	gCOD/m3
$S_O$	dissolved oxygen	gCOD/m3
$S_{NO}$	nitrite nitrogen and nitrate	gN/m3
$S_{NH}$	free and saline ammonia	gN/m3
$S_{ND}$	biodegradable and soluble organic nitrogen	gN/m3
$X_{ND}$	particulate biodegradable organic nitrogen	gN/m3
$S_{ALK}$	alkalinity	mol/L

, encompass critical parameters such as substrate concentrations, biomass dynamics, and dissolved oxygen levels, collectively defining the system’s transient behavior.

For the first biological reaction chamber (k = 1):

$$\begin{array}{c}{\displaystyle \frac{d{Z}_1}{dt}}={\displaystyle \frac{1}{V_1}}(Q_a{Z}_a+Q_0{Z}_0+Q_r{Z}_r+r_1{V}_1-Q_1{Z}_1)\end{array}$$

(1)

$$\begin{array}{c}{Q}_1=Q_a+Q_r+Q_0\end{array}$$

(2)

For the second to fifth biological reaction chambers (k = 2, …, 5),

$$\begin{array}{c}{\displaystyle \frac{d{Z}_k}{dt}}={\displaystyle \frac{1}{V_k}}(Q_{k-1}{Z}_{k-1}+r_k{V}_k-Q_k{Z}_k)\end{array}$$

(3)

$$\begin{array}{c}{Q}_k=Q_{k-1}\end{array}$$

(4)

for which the conversion rate $r_k$ of each component is shown in [19]. The special case for the concentration of dissolved oxygen is as follows:

$${\displaystyle \frac{d{S}_{O,k}}{dt}}={\displaystyle \frac{1}{V_k}}(Q_{k-1}{S}_{O,k-1}+r_k{V}_k+K_L{a}_k{V}_k(S_O^{\ast }-S_{O,k})-Q_k{S}_{O,k})$$

(5)

Equations (1), (3), and (5) define key parameters governing the biological reactor dynamics: $S_{O,k}$ denotes the dissolved oxygen concentration in the k-th compartment, $Z_k$ corresponds to the compound concentration (as specified in Table 2) within the k-th reactor compartment, $V_k$ represents compartment volume, $r_k$ quantifies the compound-specific reaction rate, $s_O^{\ast }$ is the oxygen saturation constant (fixed at 8 $\mathrm{g}·{\mathrm{m}}^{-3}$), and $K_L{a}_k$ signifies the compartment-specific oxygen transfer coefficient. Notably, $K_L{a}_1$ and $K_L{a}_2$ are nullified ($0{\mathrm{d}}^{-1}$) in the anoxic compartments (Compartments 1–2) [19].

The ideal secondary clarifier [17] is modeled as a nonbiological membrane filtration unit. Soluble compounds are assumed fully homogenized within the clarifier, while particulate components undergo complete gravitational settling in its lower section [20].

In this case, the dynamic equation of the separator unit is as follows:

For soluble compounds:

$$\begin{array}{c}{\displaystyle \frac{d{Z}_k}{dt}}={\displaystyle \frac{1}{V_k}}(Q_f{Z}_f+Q_e{Z}_e+Q_r{Z}_r+Q_w{Z}_w)\end{array}$$

(6)

$$\begin{array}{c}{Z}_e=Z_r=Z_w=Z_k\end{array}$$

(7)

$$\begin{array}{c}{Z}_f=Z_{k-1}=Z_k\end{array}$$

(8)

For solid compounds:

$$\begin{array}{c}{\displaystyle \frac{d{Z}_k}{dt}}={\displaystyle \frac{1}{V_k}}(Qf{Z}_f+Q_r{Z}_r+Q_w{Z}_w)\end{array}$$

(9)

$$\begin{array}{c}{Z}_r=Z_w=Z_k\end{array}$$

(10)

$$\begin{array}{c}{Z}_f=Z_{k-1}=Z_k\end{array}$$

(11)

The following are some concentration and flow relationships in the process:

$$\begin{array}{c}{Z}_a=Z_5\end{array}$$

(12)

$$\begin{array}{c}{Q}_f=Q_5-Q_a=Q_e+Q_r+Q_w=Q_e+Q_u\end{array}$$

(13)

$$\begin{array}{c}{Z}_f=Z_5\end{array}$$

(14)

$$\begin{array}{c}{Z}_w=Z_r\end{array}$$

(15)

For the WWTP, the modified BSM1 model can be expressed in the following compact form:

$$\dot{x}\left(t\right)=f\left(x\left(t\right),u\left(t\right)\right)$$

(16)

where $\mathbf{x}\in {\mathbb{R}}^{78}$ denotes the state vector encapsulating all process variables, and $\mathbf{u}\in {\mathbb{R}}^3$ corresponds to the input vector comprising both manipulated and exogenous variables. The manipulated inputs include the internal recirculation flow rate $Q_a$ and the oxygen transfer coefficient $K_L{a}_5$ in the fifth bioreactor compartment, whereas the influent flow rate $Q_0$ is treated as an uncontrolled disturbance.

The economic control indicators for the model are defined as follows:

$$l_e={\omega }_{EQ}EQ\left(t\right)+{\omega }_{OCI}OCI\left(t\right)$$

(17)

where $EQ\left(t\right)$ represents the effluent quality, $OCI\left(t\right)$ denotes the overall cost index, which encompasses factors significantly affecting operational costs, ${\omega }_{EQ}$ and ${\omega }_{OCI}$ are the weighting coefficients for effluent quality and overall cost index. In this article, EQ $(\mathrm{kg}\mathrm{pollution}\mathrm{unit}·{\mathrm{day}}^{-1})$ is one of the important performance indicators. It represents the daily average value of the weighted sum of the emission concentrations of chemical substances. The concentrations of these compounds will affect the quality of treated water. EQ index can be described by the following:

$$\mathrm{EQ}={\displaystyle \frac{1}{T·1000}}{\int }_{t_0}^{t_f}\left(\begin{array}{c}{\beta }_{\mathrm{SS}}·{\mathrm{SS}}_e\left(t\right)+{\beta }_{\mathrm{COD}}·{\mathrm{COD}}_e\left(t\right)+{\beta }_{NKj}·S_{NKj,e}\left(t\right)\\ +{\beta }_{NO}·S_{NO,e}\left(t\right)+{\beta }_{\mathrm{BOD}}·{\mathrm{BOD}}_e\left(t\right)\end{array}\right)Q_e\left(t\right)dt$$

(18)

where

$$\begin{array}{c}{\mathrm{SS}}_e=0.75\left(X_{S,e}+X_{B_A,e}+X_{B_H,e}+X_{I,e}+X_{P,e}\right)\end{array}$$

(19)

$$\begin{array}{c}{\mathrm{COD}}_e=S_{I,e}+S_{S,e}+X_{S,e}+X_{I,e}+X_{B_H,e}+X_{B_A,e}+X_{P,e}\end{array}$$

(20)

$$\begin{array}{c}{\mathrm{BDO}}_e=0.25\left(S_{S,e}+X_{S,e}+\left(1-f_p\right)\left(X_{B_A,e}+X_{B_H,e}\right)\right)\end{array}$$

(21)

$$\begin{array}{c}{S}_{NKj,e}=S_{ND,e}+S_{NH,e}+X_{ND,e}+i_{XB}\left(X_{B_A,e}+X_{B_H,e}\right)+i_{XP}\left(X_{I,e}+X_{P,e}\right)\end{array}$$

(22)

Equation (18) defines key evaluation parameters: $t_0$ and $t_f$ denote the initial and terminal instants of the assessment interval, respectively, with $T=t_f-t_0$ representing the evaluation duration (typically $T=7\mathrm{days}$). The effluent quality index (EQ) incorporates constituent concentrations—suspended solids ($SS$), chemical oxygen demand ($COD$), biological oxygen demand ($BOD$), and Kjeldahl nitrogen ($S_{\mathrm{NKj}}$)—weighted by coefficients ${\beta }_{\mathrm{SS}}=2$, ${\beta }_{\mathrm{COD}}=1$, ${\beta }_{NKj}=30$, ${\beta }_{NO}=10$, and ${\beta }_{\mathrm{BOD}}=2$. Stoichiometric parameters $f_p=0.08$, $i_{XB}=0.08$, and $i_{XP}=0.06$ [21] further refine the model, where subscript e designates the secondary clarifier effluent.

Operational cost optimization is critical for ensuring the economic sustainability of wastewater treatment. The total operating cost, influenced by multiple factors (summarized in

Table 3. Factors that have a major impact on total operating costs.

Notation	Definition	Unit
SP	sludge production	$\mathrm{kg}·{\mathrm{day}}^{-1}$
AE	aeration energy	$\mathrm{kWh}·{\mathrm{day}}^{-1}$
PE	pumping energy	$\mathrm{kWh}·{\mathrm{day}}^{-1}$
ME	mixing energy	$\mathrm{kWh}·{\mathrm{day}}^{-1}$

), necessitates systematic control strategies to balance process efficiency and financial expenditures.

The sludge production rate, defined as the daily average mass of particulate solids generated during the operational evaluation period T, comprises two components: (1) particulate discharge via the secondary clarifier’s wastage flow $Q_w$ and (2) accumulated solids retained within the treatment facility. This metric is mathematically expressed as

$$\begin{array}{cc}\hfill \mathrm{SP}=& {\displaystyle \frac{0.75}{T·1000}}{\int }_{t_0}^{t_f}\left(X_{S,w}\left(t\right)+X_{I,w}\left(t\right)+X_{B_A,w}\left(t\right)+X_{B_H,w}\left(t\right)+X_{P,w}\left(t\right)\right)Q_w\left(t\right)dt\hfill \\ & +{\displaystyle \frac{1}{T·1000}}\left(\mathrm{SS}\left(t_f\right)-\mathrm{SS}\left(t_0\right)\right)\hfill \end{array}$$

(23)

where subscript w designates the wastage outlet of the secondary clarifier.

Aeration energy consumption (AE) is influenced by multiple operational and design parameters, including wastewater characteristics, microbial metabolic activity, sludge settling properties, aeration system efficiency, environmental conditions, process configuration, and advanced control strategies. AE is quantified using oxygen transfer rates ($K_L{a}_i$, $i=1,\dots ,5$) under a standardized immersion depth of 4 m, as defined by

$$\mathrm{AE}={\displaystyle \frac{S_o^{sat}}{T·1800}}{\int }_{t_0}^{t_f}\sum _{i=1}^5{V}_i·K_L{a}_i\left(t\right)dt$$

(24)

where $V_i$ represents the volume of the i-th reactor compartment ($i=1,\dots ,5$), $K_L{a}_i$ denotes the compartment-specific oxygen transfer coefficient, and $S_O^{\mathrm{sat}}$ is the oxygen saturation concentration (fixed at $8\mathrm{g}/{\mathrm{m}}^3$).

In the whole sewage treatment process, pumping energy is related to hydraulic characteristics, pumping equipment performance, sewage physical characteristics, process design, and operation strategy. Here, the energy consumed by the pump for internal circulation $Q_a$ and external circulation $Q_r$ is mainly considered, and its mathematical description is as follows:

$$\mathrm{PE}={\displaystyle \frac{1}{T}}{\int }_{t_0}^{t_f}\left(0.004Q_a\left(t\right)+0.05Q_w\left(t\right)+0,008Q_r\left(t\right)\right)dt$$

(25)

The mixing energy refers to the energy consumed by mixing compounds in an anoxic chamber to avoid precipitation. The calculation of me depends on the volume of each reaction chamber and the oxygen transfer rate. As shown in (26), it is positively correlated with the volume of the reaction chamber. Its mathematical expression is as follows:

$$\mathrm{ME}={\displaystyle \frac{24}{T}}{\int }_{t_0}^{t_f}\left(\sum _{i=1}^{5}0.005·V_i\right)dt$$

(26)

The overall cost index (OCI) approximates the total cost for WWTP operation by taking a weighted summation of the listed major factors as follows:

$$\mathrm{OCI}=5·\mathrm{SP}+\mathrm{AE}+\mathrm{PE}+\mathrm{ME}$$

(27)

3. Preliminary Selection of TPWL Linearization Points and Construction of Reduced-Order Models

3.1. TPWL Method

The fundamental principle of the Trajectory Piecewise Linearization (TPWL) method [22] is to approximate a nonlinear model through piecewise linearization at multiple selected linearization points, thereby overcoming the limitations of single-point linearization. TPWL’s trajectory-adaptive linearization fundamentally differs from other model order reduction methods. Key procedural stages of the TPWL method include the selection of linearization points [23], the approximation of nonlinear functions, the construction of weighting functions, and weighted summation.

For the nonlinear model:

$$\left\{\begin{array}{c}{\displaystyle \frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}}=f\left(x\left(t\right)\right)+Bu\left(t\right)\hfill \\ y\left(t\right)=C^{\top }x\left(t\right)\hfill \end{array}\right.$$

(28)

where $\mathbf{x}\left(\mathbf{t}\right)\in {\mathbb{R}}^n$ is the state vector of the system at time t, f(x) is a nonlinear function, $\mathbf{B}\in {\mathbb{R}}^{n\times p}$ is the input matrix, $\mathbf{u}\left(\mathbf{t}\right)\in {\mathbb{R}}^p$ is the control input, $\mathbf{C}\in {\mathbb{R}}^{n\times q}$ is the output matrix, and $\mathbf{y}\left(\mathbf{t}\right)\in {\mathbb{R}}^q$ is the output corresponding.

When the TPWL method is used to generate its approximate model, the original model is simulated with the given input U (T) in the time interval [$t_0$, $t_e$], the state trajectory is obtained, and the vector ($x_0$,…, $x_n$) on the state trajectory is obtained; Then, according to certain rules, several state vectors are selected as linearization points ($x_0^{lin}$,…, $x_{s-1}^{lin}$), where s is the number of linearization points. Then, the original nonlinear model is linearized at each linearization point to obtain a set of linearized models, such as

$$\left\{\begin{array}{c}{\displaystyle \frac{dx\left(t\right)}{dt}}=f\left(x_i^{lin}\right)+A_i\left(x-x_i^{lin}\right)+Bu\left(t\right)\hfill \\ y\left(t\right)=C^{T}x\left(t\right)\hfill \end{array}\right.,i=0,\dots ,s-1$$

(29)

where $A_i$ is the Jacobian matrix at the linearization point $x_i^{lin}$ of f(x), and then the weight function ${\omega }_i\left(x\right)$ is constructed. The construction method [24] is as follows:

• For each linearization point, calculate $d_i=\left|\right|x-x_i{\left|\right|}_2,i=0,\dots ,s-1$;
• Calculate $m=mi{n}_{i=0,\dots ,s-1}{d}_i$;
• Calculate ${\widehat{\omega }}_i=e^{-\beta d_i/m}$;
• Sum all ${\widehat{\omega }}_i$,$S\left(x\right)={\sum }_{i=0}^{s-1}{\widehat{\omega }}_i\left(x\right)$;
• Let ${\omega }_i\left(x\right)={\widehat{\omega }}_i\left(x\right)/S\left(x\right)$.

The weighting function ${\omega }_i\left(x\right)$ is parameterized by the normalized Euclidean distance $d_i$ (Equation (30)) and a scaling factor $\beta =25$, which governs the locality of linearized model dominance. The weighting coefficient ${\omega }_i\left(x\right)$ dynamically adapts as a function of the current state vector x within the state-space domain. When x exhibits geometric proximity to a linearization point $x_i$, the corresponding weight ${\omega }_i\left(x\right)$ asymptotically converges toward unity.

$$d_i=\sqrt{{\displaystyle \frac{{\sum }_{i=1}^n{(x_i-x_{i-1})}^2}{n}}}$$

(30)

The obtained linearized models are weighted and summed to obtain the piecewise linearized model:

$$\left\{\begin{array}{c}{\displaystyle \frac{dx\left(t\right)}{dt}}=\sum _{i=0}^{s-1}{\omega }_i\left(x\right)(f\left(x_i^{lin}\right)+A_i\left(x-x_i^{lin}\right)+Bu\left(t\right))\hfill \\ y\left(t\right)=C^{T}x\left(t\right)\hfill \end{array}\right.,i=0,\dots ,s-1$$

(31)

3.2. Preliminary Linearization Point Selection

The selection of linearization points is the most critical step in the TPWL method. The reasonable selection of linearization points is conducive to the construction of the approximate model. Considering that there are many state vectors on the state trajectory of Equation (16), the key linearization points cannot be directly obtained by one selection, so the strategy of two-point selection is adopted. First, the linearization points are preliminarily selected according to simple rules, and then the follow-up work is carried out to select the final linearization points from the initially selected points.

During primary selection, first select the first point $x_0$ on the state track as the first primary linearization point, and then calculate the distance between the subsequent linearization points and the previous linearization point. If the distance is greater than the set value d, select it as the primary linearization point until the number of points meeting the requirements or all state vectors are used up. Finally, these points form the primary point set $\{x_{00}^{lin},\dots ,x_{0k}^{lin}\}$ and record the position information of each point in the state track to form the set $\{a_0,\dots ,a_k\}$, where k is the number of primary points, d the form of root mean square error (RMSE) is the same as Equation (30),

• Set the threshold $d>0$ and give the input $u\left(t\right)$;
• Select the initial state as the first candidate linearization point and make $N=1$;
• Let $t=t_0+\Delta t$;
• The nonlinear full model Equation (28) is simulated, and the state vector $x\left(t\right)$ at time t is obtained;
• For the current state x, calculate:

  $$\delta =\Vert x-x_{N-1}\Vert$$

  (32)
• If $\delta <d$, it indicates that the current state x is close enough to the candidate linearization point just selected, then let $t=t+\Delta t$;
• If $\delta \ge d$, select x as the ($N+1$)-th candidate linearization point, add the point to the primary point set $\{x_{00}^{lin},\dots ,x_{0k}^{lin}\}$, record its corresponding position information a, and add the position information to the position information set $\{a_0,\dots ,a_k\}$; then, let $N=N+1$ and return to step 4;
• When $t\ge t_e$, the selection is terminated, and the primary point set $\{x_{00}^{lin},\dots ,x_{0k}^{lin}\}$ and the location information set $\{a_0,\dots ,a_k\}$ are saved.

The coarse selection phase employs a conventional distance-based criterion based on state distance. Its core advantage is that it is efficient in calculation and simple in implementation. It is suitable for the initial dimensionality reduction processing of large-scale nonlinear systems. The purpose is to select the dataset that can roughly represent the characteristics of the original nonlinear model on the state trajectory. Although this method has the risk of discarding a small part of key information and will be affected by the sensitivity of threshold d, it basically retains the data characteristics of the original model, reduces the amount of calculation, and reduces the relatively redundant solution process.

To mitigate potential omission of critical local dynamics and the sensitivity of threshold d while reducing the amount of calculation, we can consider introducing the method of dynamic threshold adjustment to dynamically adjust the threshold d according to the local curvature or gradient of the state trajectory. In addition to this method, we can also consider introducing an energy function, Lyapunov index, and other state points that have a significant impact on the stability of the system, or using reinforcement learning or active learning strategies to dynamically adjust the sampling position according to the current model error feedback. These methods need to be further studied.

3.3. Reduced-Order Model Construction

Proper Orthogonal Decomposition (POD) reduces the dimensionality of high-order models while preserving critical dynamic characteristics [25]. POD employs singular value decomposition (SVD) and is applicable to both linear and nonlinear systems [26].

For Equation (16), under a given input, the state $\mathbf{x}\in {\mathbb{R}}^n$ at sampled time instances can be represented as a state matrix X:

$$X=\left[\begin{array}{c}x\left(t_1\right)x\left(t_2\right)x\left(t_3\right)\dots x\left(t_N\right)\end{array}\right]$$

(33)

where $X\in {\mathbb{R}}^{n\times N}$ is termed the snapshot matrix, n is the number of state variables, and N is the number of sampling intervals ($N\gg n$). Performing SVD on X yields [27]:

$$X=U\Sigma V^T\in R^{n\times N}$$

(34)

where $U\in {\mathbb{R}}^{n\times n}$ (left singular vectors) and $V\in {\mathbb{R}}^{N\times N}$ (right singular vectors) are orthogonal matrices, and $\Sigma =\mathrm{diag}({\sigma }_1,\dots ,{\sigma }_n)\in {\mathbb{R}}^{n\times N}$ is a diagonal matrix of nonnegative singular values in descending order. Larger $\sigma$ values indicate greater importance of the corresponding basis vectors in capturing system dynamics [28].

$$X=U\Sigma V^T\approx U_k{\Sigma }_k{V}_k^T,k\ll n$$

(35)

Let $\mathbf{x}\left(t\right)\approx U_k\mathbf{z}\left(t\right)$, where $\mathbf{z}\left(t\right)\in {\mathbb{R}}^k$. The reduced-order model becomes

$$\dot{z}\left(t\right)=U_k^{T}f\left(U_{k}z\left(t\right),u\left(t\right)\right)$$

(36)

where $\mathbf{z}\left(t\right)$ is the approximation of $\mathbf{x}\left(t\right)$ in the low-dimensional subspace spanned by the first k left singular vectors of X. While POD alone does not significantly reduce the evaluation time for EMPC, combining POD with TPWL achieves substantial computational savings.

When the simplified model is constructed by the POD-TPWL method, the projection matrix V is generated by the POD method, in which the snapshot matrix is composed of the initially selected state vector, and then for each local linearized model in Equation (29), projection reduction is performed to obtain the following model:

$$\left\{\begin{array}{c}{\displaystyle \frac{dz\left(t\right)}{dt}}=f_{ir}+A_{ir}z+B_{r}u\left(t\right)\hfill \\ y\left(t\right)=C_r^{T}z\left(t\right)\hfill \end{array}\right.,i=0,\dots ,s-1$$

(37)

where $\mathbf{z}=V^{T}x$, r is the number of columns in V, $A_{i}r=V^T{A}_{i}V$, $f_{i}r=V^T\left[f\left({\mathbf{x}}_i^{\mathrm{lin}}\right)-A_i{\mathbf{x}}_i^{\mathrm{lin}}\right]$, $B_r=V^{T}B$, $C_r=V^{T}C$. At this time, the order of each local linearization model has been reduced from n to R, and $r\ll n$. Then, use the weight function to sum all the models in Equation (37) to obtain the model:

$$\left\{\begin{array}{c}{\displaystyle \frac{dz\left(t\right)}{dt}}=\sum _{i=0}^{s-1}{\omega }_i\left(z\right)[f_{ir}+A_{jr}z+B_{r}u\left(t\right)]\hfill \\ y\left(t\right)=C_r^{T}z\left(t\right)\hfill \end{array}\right.$$

(38)

4. Point Selection Method Based on Global Maximum Error Control Method

Since the computational overhead of the TPWL surrogate model is very small, it will not bring much additional computational overhead to establish a surrogate model by using the selected linearization points and selecting new linearization points by running the surrogate model. The GMEC framework requires co-simulation of the original and surrogate models under identical inputs to quantify trajectory deviations, select the state point with the largest deviation as the new linearization point, update the simplified model, and repeat the process until the maximum deviation is less than the set threshold. At this time, all the linearization points constituting this POD-TPWL model are the final linearization points required. Considering that the state trajectory of the original model contains many state points, the analysis is confined to the initially selected linearization points $\{x_{00}^{lin},\dots ,x_{0k}^{lin}\}$, thereby minimizing computational demands while retaining dominant dynamics. In this method, the global maximum error control is measured by RMSE, which is defined as follows:

$${\epsilon }_{RMSE}=\sqrt{{\displaystyle \frac{{\sum }_{i=1}^n{\epsilon }_i^2}{n}}}$$

(39)

Taking the nonlinear model given in Equation (28) as an example, the point selection process based on the global maximum error control method is as follows:

• Set the maximum error threshold $\alpha$ and input $U\left(t\right)$;
• By simulating the nonlinear model, the state information on all time steps is obtained, and these state vectors $\{x_0,\dots ,x_N\}$ are stored, where N + 1 is the number of state vectors;
• Select the initial state $x_0$ as the first linearization point $x_0^{lin}$, and let i = 1;
• The POD-TPWl method is used to establish a temporary model in the same form as Equation (38);
• Take the same time step as the nonlinear full model, simulate the model, and obtain the approximate state vector $\{{\tilde{x}}_0,\dots ,{\tilde{x}}_N\}$;
• In $\{{\tilde{x}}_0,\dots ,{\tilde{x}}_N\}$ and $\{x_0,\dots ,x_N\}$, K state points $\{{\tilde{x}}_{00},\dots ,{\tilde{x}}_{0k}\}$ and $\{x_{0}0,\dots ,x_{0}k\}$ with position information $\{a_0,\dots ,a_k\}$ are selected, and then the error of these points is calculated:

  $$e_j=\left|\right|{\tilde{x}}_j-x_j{\left|\right|}_{RMSE},j=0,\dots ,k;$$

  (40)
• Find the state ${\tilde{x}}_0$ that maximizes the error $e_j$ so that

  $$e_{max}=max{e}_j=e_m=\left|\right|{\tilde{x}}_m-x_m{\left|\right|}_{RMSE}$$

  (41)
  Record the maximum error $e_{m}ax$ and the position information of it;
• If $e_{max}\ge \alpha$, select the (i+1)-th linearization point $x_i^{lin}$ = $x_m$, make i = $i+1$, and return to step 4);
• If $e_{max}<\alpha$, the cycle ends, and the points in the linearization point set $\{x_0^{lin},x_1^{lin},\dots ,x_{i-1}^{lin}\}$ are the final linearization points. The simplified model based on these points is the reduced-order linearization model that meets the requirements. The selection process of linearization points is shown in Figure 2.

5. Design of EMPC Controller Based on Reduced-Order Linearized Model

In the above algorithm, the maximum error control limit $\mathrm{a}$ is a parameter that needs to be manually given, and its value is related to the approximate accuracy and scale of the final TPWL surrogate model, so it needs to be set according to the actual application requirements.

Unlike existing methods, the proposed GMEC dynamically incorporates new linearization points through a global maximum error feedback mechanism, iteratively refining the TPWL model to ensure balanced accuracy and efficiency. In addition, the existing linearization point selection algorithms are either based on the geometric distance between the state points, the error estimation between the local linearization reduced order model and the original nonlinear model, or the local approximation effect of the linearization function. Existing approaches primarily focus on local approximation accuracy (e.g., geometric proximity or Jacobian linearization fidelity), whereas the proposed GMEC method explicitly enforces global error bounds through iterative refinement.

EMPC extends the receding horizon optimization framework of MPC by embedding economic objectives (e.g., energy cost minimization, operational profit maximization) directly into the optimal control problem. This dual focus enables EMPC to simultaneously regulate dynamic performance (e.g., tracking accuracy, stability margins) and enhance economic efficiency.

MPC solves a finite-horizon optimal control problem iteratively, leveraging system predictions to compute control actions while explicitly handling constraints. Its defining feature—the receding horizon mechanism—applies only the immediate control input and recomputes the sequence at each sampling instant, thereby achieving closed-loop robustness. Economic optimization aims to minimize (or maximize) economic indicators of the system, such as energy consumption, operational costs, and revenue.

EMPC embeds economic optimization objectives directly into the MPC optimization problem, allowing the controller to consider both dynamic performance (e.g., tracking accuracy, stability) and economic performance (e.g., operating costs, energy efficiency).

The design of the EMPC controller based on the reduced-order linearized model, as described by Equation (38), is formulated as follows:

$$u^{\ast }\left(t\right|t_k)=\underset{u\left(t\right)\in S(\Delta )}{min}{\int }_{t_k}^{t_k+N}l\left(U_{k}z\left(t\right),u\left(t\right)\right)dt$$

(42)

$$\dot{z}\left(t\right)=\sum _{i=0}^{s-1}{\omega }_i\left(z\right)\left[f_{ir}+A_{jr}z+B_{r}u\left(t\right)\right]$$

(43)

$$z\left(t_k\right)=V^{T}x\left(t_k\right)$$

(44)

$$u\left(t\right)\in U$$

(45)

The EMPC objective function in Equation (42) minimizes the economic cost $l_e$ defined in Equation (17), where N denotes the prediction horizon, $\mathcal{S}(\Delta )$ is the set of piecewise-constant control policies with sampling interval $\Delta$, and U encodes input constraints. By solving Equation (42), the optimal control input $u^{\ast }(t\mid t_k)$ is obtained. The first element of the optimal control sequence is implemented, and the horizon is shifted forward at each sampling instant.

6. Experimental Simulation

6.1. Simulation Parameter Settings

The Trajectory Piecewise Linearization with Proper Orthogonal Decomposition (TPWL-POD) is applied to a wastewater treatment plant (WWTP) model. Based on the given input signals, the reduced-order basis and linearization points of the model are obtained, and the accuracy of the approximated model is compared with that of the original nonlinear model. Considering the influence of weather conditions on the model, this study focuses on evaluating control performance under sunny conditions, including effluent quality, operational costs, and computational efficiency.

The data files for sunny conditions are referenced from the BSM1 benchmark dataset, which is made publicly available by the International Water Association (IWA) [29]. These files contain the influent flow rate $Q_0$ and influent concentration $Z_0$. Under sunny conditions, static simulations of the WWTP are conducted using the average values of $Q_0$ and $Z_0$ to determine the optimal steady state, which serves as the initial condition for the wastewater treatment process.

The simulation spans 14 days, with the final 7-day period utilized for performance evaluation. The sampling time is defined as $\Delta =15$ min.

In the economic control objective function (Equation (17)), the weighting coefficients ${\omega }_{EQ}$ and ${\omega }_{OCI}$ are set to 1 and 0.3, respectively. For all EMPC controller designs, the control horizon is fixed at 25. The constraints on operational inputs in all control designs are as follows:

$$0[{\mathrm{m}}^3·{\mathrm{d}}^{-1}]\le Q_a\le 5Q_{0,stab}[{\mathrm{m}}^3·{\mathrm{d}}^{-1}]$$

(46)

$$0\left[{\mathrm{d}}^{-1}\right]\le K_L{a}_5\le 240\left[{\mathrm{d}}^{-1}\right]$$

(47)

where $Q_{0,\mathrm{stab}}$ represents the average influent flow rate under dry weather conditions, which is 18,446 m³ · d⁻¹.

The TPWL-POD framework initially selects 60 candidate linearization points. The reduced-order model (ROM) retains 30 dominant states via singular value truncation. Through preliminary simulations, the global maximum error threshold is set to 9 (RMSE), which balances accuracy and computational efficiency and determines the number of linearization points. A smaller threshold leads to more linearization points being selected. The threshold and reduced-order dimensionality are determined based on a trade-off between model accuracy and computational time. This process requires extensive simulations and empirical analysis.

The model’s accuracy increases as the threshold decreases and the reduced-order dimensionality increases. However, computational time also rises accordingly. Balancing model accuracy and computational efficiency is critical for establishing a reliable model. These parameters were carefully tuned to achieve an optimal compromise.

6.2. Model Validation

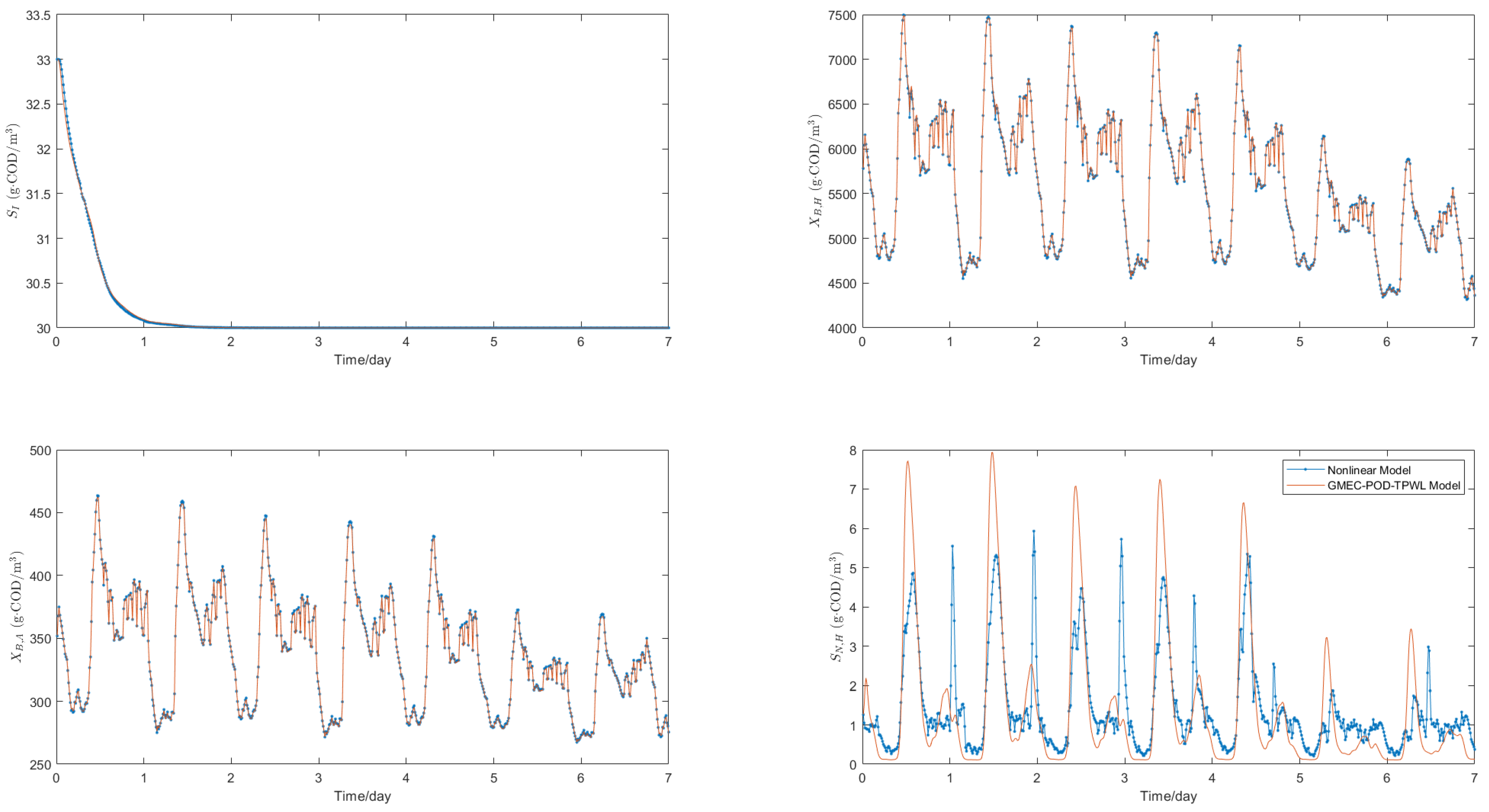
For both the original nonlinear model and the reduced-order linearized model, the state data generated under identical input signals during the first week are nearly identical. To illustrate this, this study selects four key state variables from the first reaction chamber for comparison: soluble nonbiodegradable organic matter ($S_I$), active heterotrophic bacteria ($X_{B,H}$), active autotrophic bacteria ($X_{B,A}$), and ammonia nitrogen ($S_{N,H}$). Figure 3 compares the temporal evolution of four critical states ($S_I$, $X_{B,H}$, $X_{B,A}$, $S_{N,H}$) between the original model and the GMEC-POD-TPWL model. The negligible deviations confirm the GMEC-POD-TPWL model’s fidelity in capturing dominant dynamics.

6.3. Model Comparison

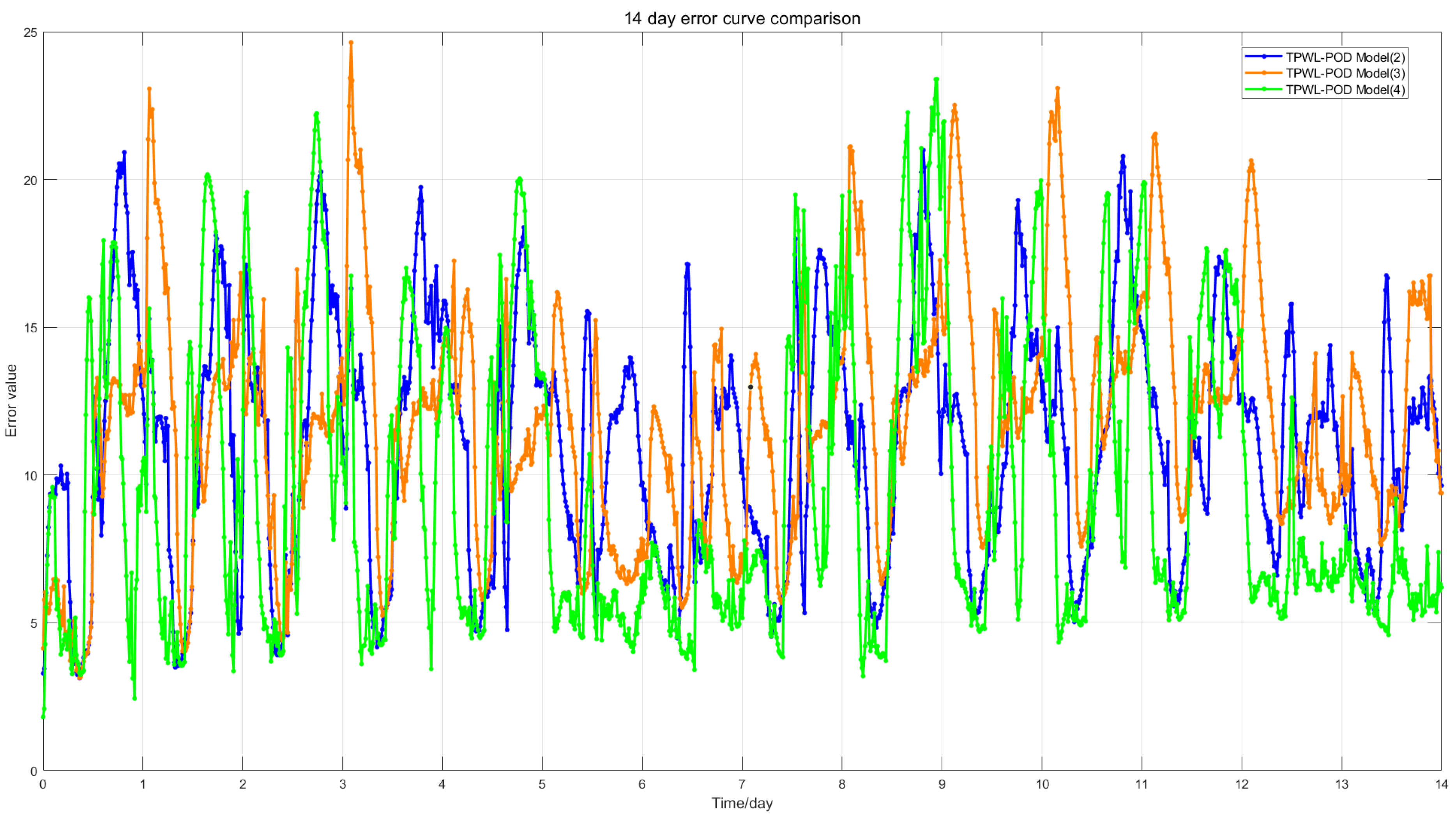
To validate the superiority of the proposed Global Maximum Error-based Secondary Point Selection (GMEC-POD-TPWL) modeling method over other TPWL approaches, this study compares its accuracy with the TPWL-POD method from reference [13] under varying numbers of linearization points (2, 3, and 4). A comparative analysis is conducted, and the results are presented in

Table 4. Comparison of RMSE of models with different linearization points.

Number of Linearization Points	RMSE of TPWL-POD Model	RMSE of GMEC-POD-TPWL Model
2	11.8574	10.2083
3	12.5110	9.9226
4	10.7056	5.9590

, Figure 4 and Figure 5. The error between the reduced-order models and the original model is quantified using the RMSE, calculated as in Equation (39).

Figure 4 illustrates the RMSE trajectories of the TPWL-POD model compared with the original model over the entire 14-day simulation period, while Figure 5 shows the corresponding error trajectories for the GMEC-POD-TPWL model.

As demonstrated, the proposed GMEC-POD-TPWL model achieves error reductions of 13.90%, 20.69%, and 44.34% for 2, 3, and 4 linearization points, respectively, compared with the TPWL-POD method. These results highlight a significant enhancement in model accuracy, confirming the effectiveness of the GMEC-based secondary point selection strategy.

The data in Table 4 indicate that as the linearization point increases, the errors of both models gradually decrease, and under the same linearization point, the error of the GMEC-POD-TPWL model is smaller than that of the TPWL-POD model.

6.4. EMPC Simulation Performance Metrics Comparison

Under dry weather conditions, this study compares the EMPC control computation time, effluent quality (EQ), overall cost index (OCI), and economic cost index between the original model, the GMEC-POD-TPWL model, and the TPWL-POD model under varying numbers of linearization points. The results are summarized in

Table 5. Control performance in dry weather condition under EMPC based on different models.

Model	Number of Linearization Points	Computation Time (s)	Effluent Quality (EQ) (kg Pollutant/Day)	Overall Cost Index (OCI)	Economic Cost Index (EQ + 0.3OCI)
Nonlinear Model	–	$1.10\times {10}^5$	3850.2729	12,759.1240	7678.0101
TPWL-POD Model	2	$2.43\times {10}^4$	5851.5064	12,802.0100	9692.1094
	3	$3.36\times {10}^4$	5543.9940	13,803.0061	9684.8958
	4	$3.94\times {10}^4$	5152.1915	14,164.0799	9401.4154
GMEC-POD-TPWL Model	2	$2.19\times {10}^4$	5295.0052	12,799.3666	9134.8152
	3	$3.29\times {10}^4$	4965.6642	13,632.7921	9055.5018
	4	$3.85\times {10}^4$	4564.7130	14,442.5203	8897.4691

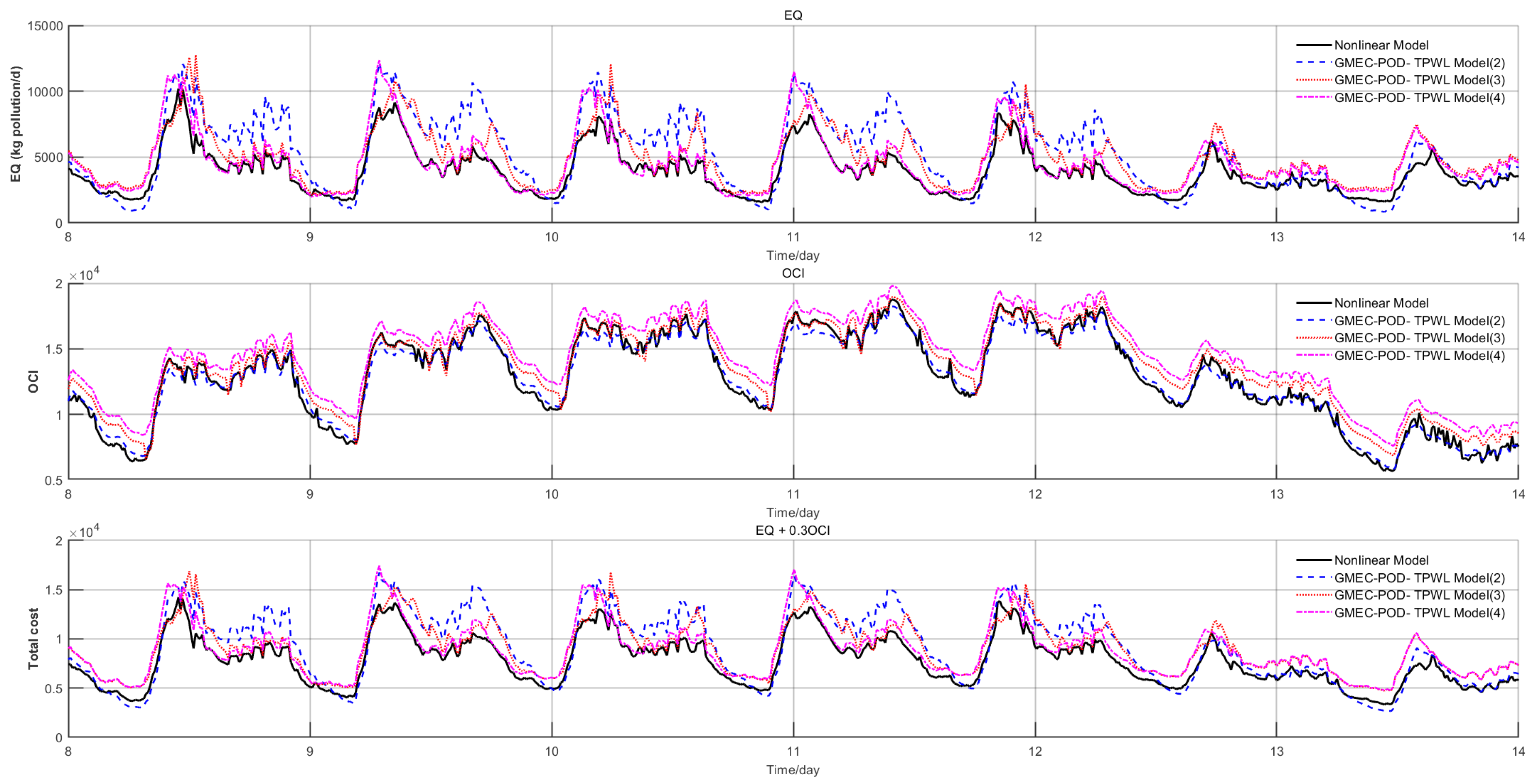
and illustrated in the figures below. Figure 6 displays the performance metric curves of the TPWL-POD model versus the original nonlinear model under different numbers of linearization points, while Figure 7 shows the corresponding curves for the GMEC-POD-TPWL model. As specified in Section 6.1, the comparison utilizes data from the last 7 days of the simulation period.

The experimental data demonstrate that both reduced-order models (TPWL-POD and GMEC-POD-TPWL) exhibit enhanced computational efficiency compared with the original nonlinear model. Specifically, increasing the number of linearization points improves model accuracy and control performance metrics for both approaches. The GMEC method ensures model accuracy through the implementation of a maximum error threshold, with its iterative process employing a maximum error prioritization strategy. Specifically, each iteration prioritizes the addition of linearization points that maximally reduce the peak approximation error in the simplified model, thereby guaranteeing progressive improvement in model fidelity. In contrast to conventional TPWL-POD approaches, which lack targeted error reduction mechanisms in their linearization point selection process and rely on increasing linearization point quantities to enhance accuracy—the GMEC-enhanced framework achieves superior model fidelity compared with conventional TPWL-POD implementations with equivalent numbers of linearization points. This accuracy advantage directly translates to enhanced EMPC control performance, as the refined model better preserves the dynamic characteristics of the original nonlinear system.

For the 4-linearization-point configuration, the GMEC-POD-TPWL model reduces computational time by 65.45% relative to the original nonlinear model (from $1.10\times {10}^5\mathrm{s}$ to $3.85\times {10}^4\mathrm{s}$), though this acceleration introduces performance trade-offs: effluent quality (EQ) decreases by 18.56% (from $4564.71\mathrm{kg}\mathrm{pollutant}/\mathrm{day}$ to $3850.27\mathrm{kg}\mathrm{pollutant}/\mathrm{day}$), while the overall cost index (OCI) and economic cost index increase by 13.19% and 15.88%, respectively. Compared with the TPWL-POD model [13], the proposed method achieves a 2.28% faster computation speed (from $3.85\times {10}^4\mathrm{s}$ to $3.94\times {10}^4\mathrm{s}$), coupled with a 44.34% reduction in model approximation error (from $\mathrm{RMSE}=5.96$ to $10.71$). Furthermore, it demonstrates superior control performance, evidenced by an 11.40% lower effluent pollutant concentration and a 5.36% reduction in economic costs, despite a marginal 1.97% increase in OCI.

The experimental results demonstrate conclusively that the GMEC-POD-TPWL framework provides statistically significant improvements in model accuracy, effluent quality regulation, and economic cost optimization compared with existing TPWL-POD methodologies.

7. Conclusions

This study proposes a reduced-order linearization framework for the modified wastewater treatment plant (WWTP) process, integrating a two-stage linearization point selection strategy: coarse selection based on state trajectory spacing, and refinement via global maximum error control (GMEC). The designed EMPC system demonstrates significant computational efficiency improvements compared with the original nonlinear model, albeit with controlled performance trade-offs. Experimental analyses reveal a critical accuracy–efficiency trade-off: increasing linearization points from 2 to 4 enhances model fidelity and control performance, but incurs a rise in computational load. Notably, the GMEC-POD-TPWL framework outperforms conventional TPWL-POD methods, achieving faster computation and lower economic costs at equivalent linearization points. The limitations of the proposed method include its suboptimal EMPC control performance relative to the original nonlinear model and preliminary validation under simplified operational scenarios. Additionally, the maximum error threshold in the GMEC framework requires manual specification, which restricts the adaptability of model construction. Future research should prioritize balancing computational acceleration with control performance preservation, conducting comparative simulations under more conditions, and integrating auxiliary strategies to dynamically adjust the GMEC threshold, thereby further enhancing model accuracy and control efficacy.