A Gain Scheduling Approach of Delayed Control with Application to Aircraft Wing in Wind Tunnel
Abstract
1. Introduction
2. Linear Mathematical Model Without Disturbances
2.1. Predictive Control Synthesis
2.2. Stability of the Mathematical Model Without Disturbances
3. Linear Mathematical Model with Disturbance
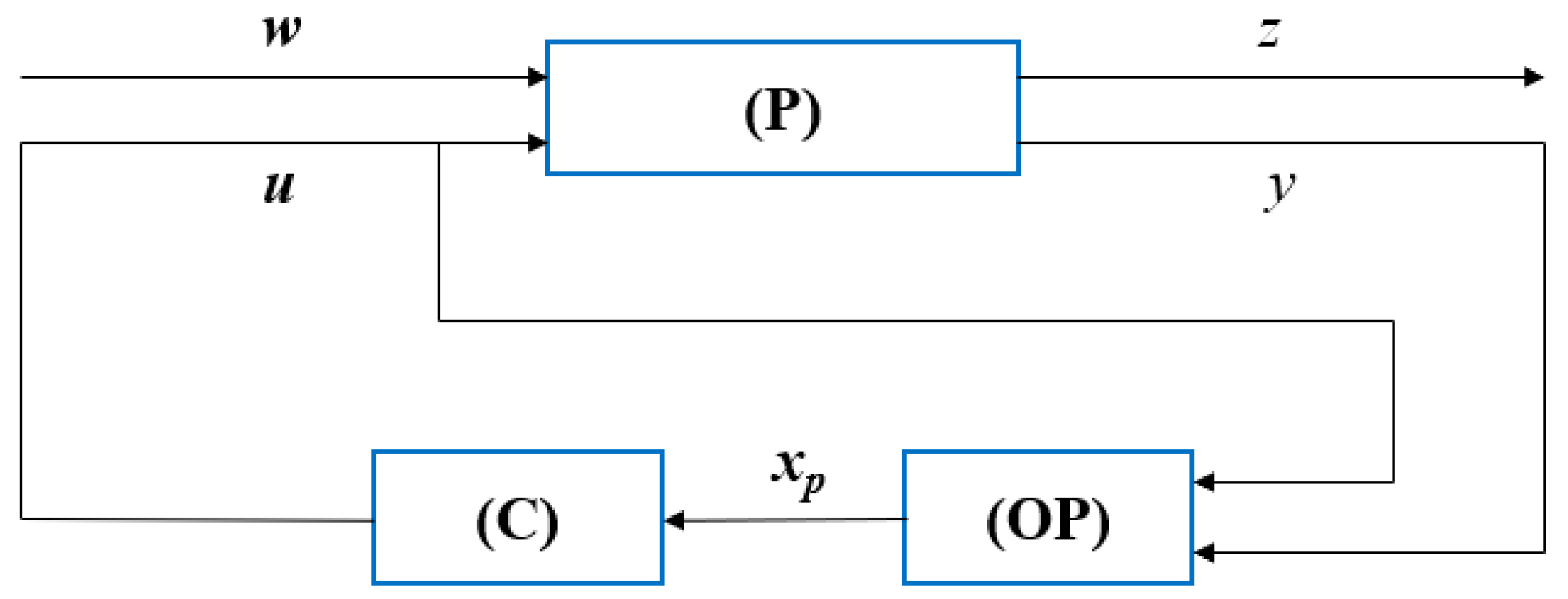
3.1. Using Predictive State Feedback with Observer to Eliminate Control Delay
3.2. BIBO Stability of the Mathematical Model with Disturbances
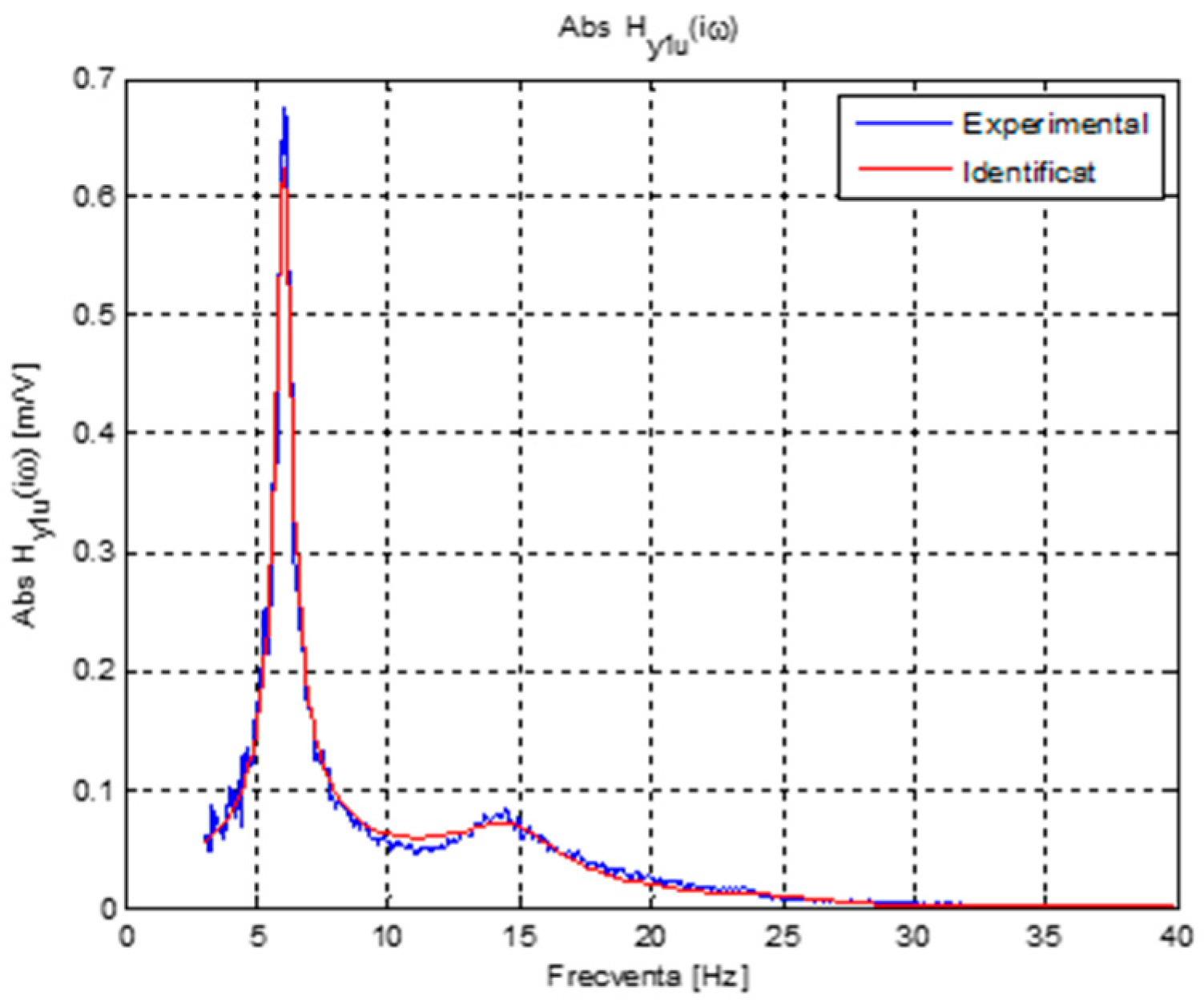
4. Physical Model and Experimental Identification of Mathematical Model
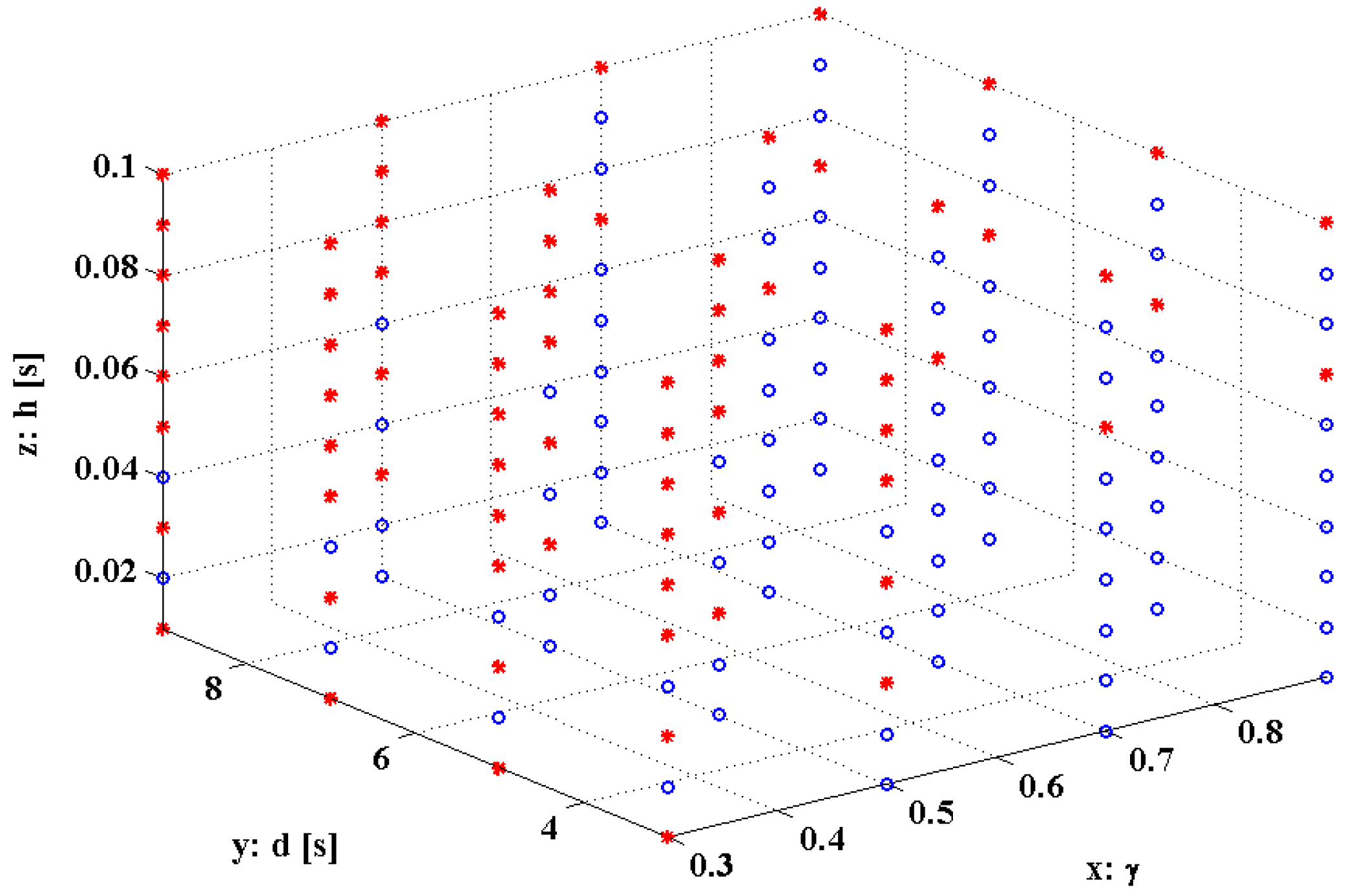
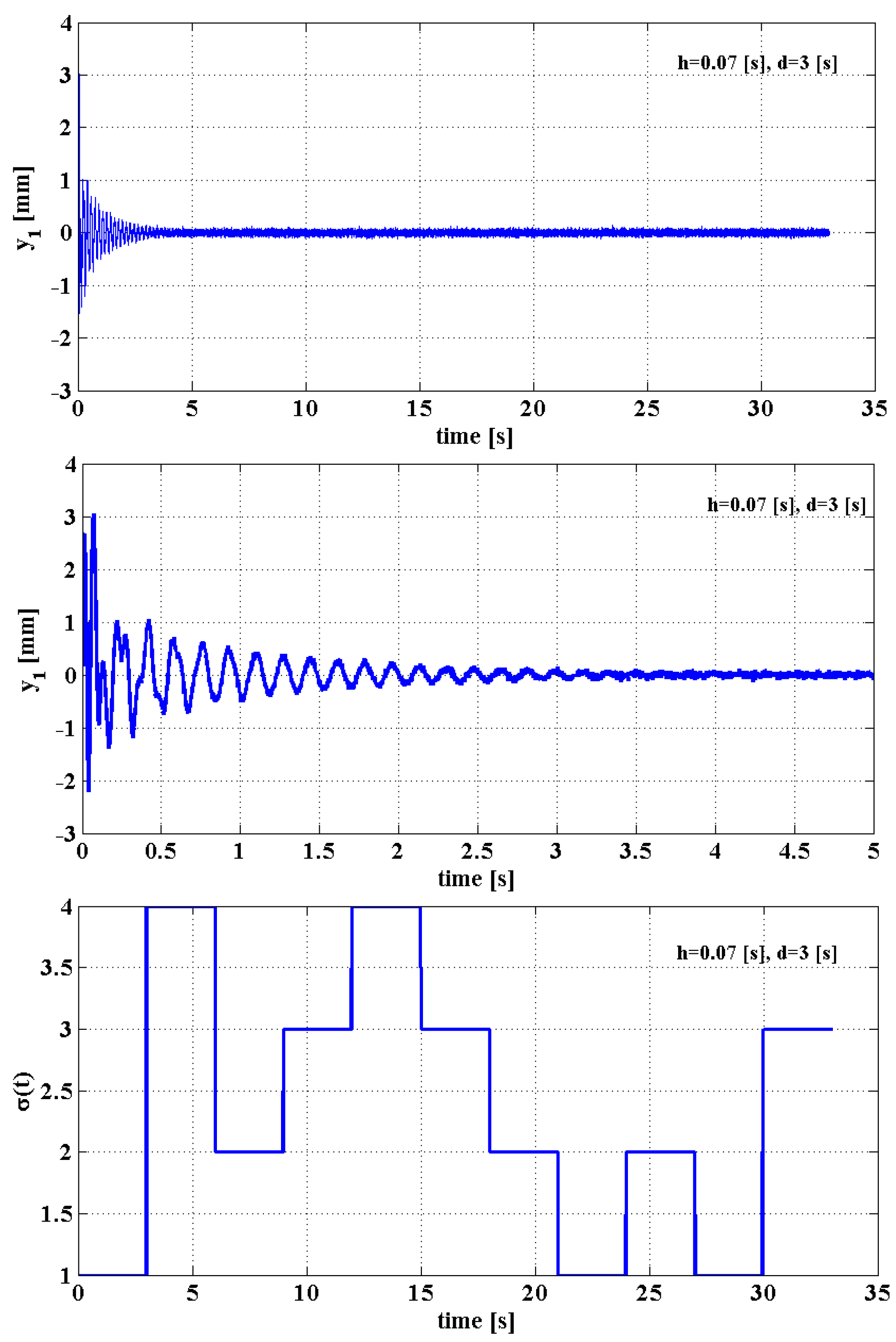
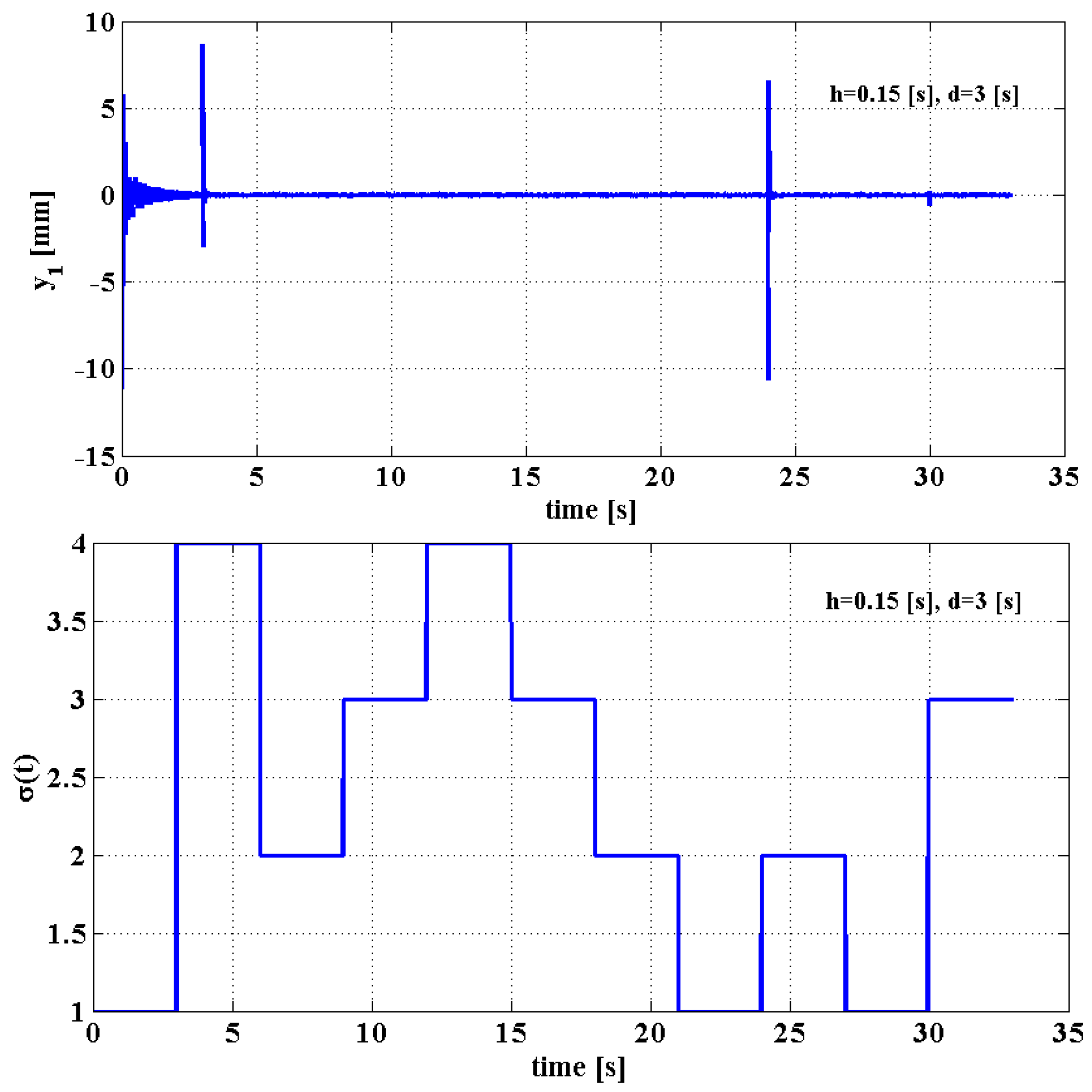
5. Stability Analysis and Numerical Simulations of Wing Model
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Briat, C. Linear Parameter-Varying and Time-Delay Systems—Analysis, Observation, Filtering & Control; Springer: Heidelberg, Germany, 2015. [Google Scholar]
- Lin, Z.; Khammash, M. Robust gain-scheduled aircraft longitudinal controller design using an H∞ approach. In Proceedings of the 2001 American Control Conference, Arlington, VA, USA, 25–27 June 2001; Volume 4, pp. 2729–2742. [Google Scholar]
- Newsom, R.J. Active Control of Aeroelastic Response; TM-83179; NASA: Washington, WA, USA, 1981.
- Kratochvíl, A.; Valenta, J. Active flutter suppression for light sport aircraft by a control surface split. CEAS Aeronaut. J. 2024, 15, 977–998. [Google Scholar] [CrossRef]
- Patartics, B.; Lipták, G.; Luspay, T.; Seiler, P.; Takarics, B.; Vanek, B. Application of Structured Robust Synthesis for Flexible Aircraft Flutter Suppression. IEEE Trans. Control. Syst. Technol. 2022, 30, 311. [Google Scholar] [CrossRef]
- Waitman, S.; Marcos, A. Active flutter suppression: Non-structured and structured H∞ design. IFAC PapersOnLine 2019, 52, 146–151. [Google Scholar] [CrossRef]
- Kwon, W.H.; Pearson, A.E. Feedback stabilization of linear systems with delayed control. IEEE Trans. Autom. Control 1980, 25, 266–269. [Google Scholar] [CrossRef]
- Sontag, E.D. Mathematical Control Theory. In Deterministic Finite Dimensional Systems, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Ursu, I.; Enciu, D.; Tecuceanu, G. Equilibrium stability of a nonlinear structural switching system with actuator delay. J. Frankl. Inst. 2020, 357, 3680–3701. [Google Scholar] [CrossRef]
- Bellman, R.; Cooke, K.L. Differential-Difference Equations; Academic Press: New York, NY, USA, 1963. [Google Scholar]
- Toader, A.; Ursu, I.; Enciu, D.; Tecuceanu, G. Towards nonconservative conditions for equilibrium stability. Applications to switching systems with control delay. Commun. Nonlinear Sci. 2023, 121, 107188. [Google Scholar] [CrossRef]
- Liberzon, D. Switching in Systems and Control; Birkhäuser: Boston, MA, USA, 2003. [Google Scholar]
- Colaneri, P. Dwell time analysis of deterministic and stochastic switched systems. Eur. J. Control 2009, 15, 228–248. [Google Scholar] [CrossRef]
- Geromel, J.C.; Colaneri, P. Stability and stabilization of continuous-time switched linear systems. SIAM J. Control Optim. 2006, 45, 1915–1930. [Google Scholar] [CrossRef]
- Chesi, G.; Colaneri, P.; Geromel, J.C.; Middleton, R.; Shorten, R. A Nonconservative LMI Condition for Stability of Switched Systems with Guaranteed Dwell Time. IEEE Trans. Autom. Control 2012, 57, 1297–1302. [Google Scholar] [CrossRef]
- Di Loreto, M.; Lafay, J.F.; Loiseau, J.J. Disturbance attenuation by dynamic output feedback for input-delay systems. In Proceedings of the 44th IEEE Conference on Decision and Control, and the European Control Conference, Seville, Spain, 12–15 December 2005. [Google Scholar]
- Hille, E.; Phillips, R.S. Functional Analysis and Semi-Groups; American Mathematical Soc.: Providence, RI, USA, 1957. [Google Scholar]
- Baker, R.A.; Vakharia, D.I. Input-output stability of linear time-invariant systems. IEEE Trans. Autom. Control 1970, 15, 316–319. [Google Scholar] [CrossRef]
- Desoer, C.A.; Vidyasagar, M. Feedback Systems: Input-Output Properties; SIAM: Philadelphia, PA, USA, 2009. [Google Scholar]
- Antsaklis, P.J.; Michel, A.N. Linear Systems; Birkhäuser: Boston, MA, USA, 2006. [Google Scholar]
- Geromel, J.; Colaneri, P. H∞ and dwell time specifications of continuous-time switched linear systems. IEEE Trans. Autom. Control 2010, 55, 207–212. [Google Scholar] [CrossRef]
- Margaliot, M.; Hespanha, J.P. Root-mean-square gains of switched linear systems: A variational approach. In Proceedings of the 2007 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007. [Google Scholar] [CrossRef]
- Hespanha, J.P. Root-mean-square gains of switched linear systems. IEEE Trans. Autom. Control 2003, 48, 2040–2045. [Google Scholar] [CrossRef]
- Chesi, G.; Colaneri, P. On the Synthesis of Static Output Feedback Controllers for Guaranteed RMS Gain of Switched Systems with Arbitrary Switching. In Proceedings of the 57th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), Nara, Japan, 11–14 September 2018. [Google Scholar] [CrossRef]
- Ursu, I.; Tecuceanu, G.; Toader, A.; Calinoiu, C. Switching neuro-fuzzy control with antisaturating logic. Experimental results for hydrostatic servoactuators. Proc. Rom. Acad. Math. Phys. Tech. Sci. Inf. Sci. 2011, 12, 231–238. [Google Scholar]
- Toader, A.; Ursu, I. Pilot modeling based on time delay synthesis. Proc. IME G J. Aero. Eng. 2014, 228, 740–754. [Google Scholar] [CrossRef]
- Ion-Guţă, D.D.; Ursu, I.; Toader, A.; Enciu, D.; Dancă, P.A.; Năstase, I.; Croitoru, C.V.; Bode, F.I.; Sandu, M. Advanced thermal manikin for thermal comfort assessment in vehicles and buildings. Appl. Sci. 2022, 12, 1826. [Google Scholar] [CrossRef]
- Ursu, I.; Ursu, F. An intelligent ABS control based on fuzzy logic. Aircraft application. In Proceedings of the ICTAMI 2003, International Conference on Theory and Applications of Mathematics and Informatics, Alba Iulia, Romania, 24–25 October 2003; pp. 355–368. [Google Scholar]
- Liu, G.-P. Predictive Control of High-Order Fully Actuated Nonlinear Systems with Time-Varying Delays. J. Syst. Sci. Complex 2022, 35, 457–470. [Google Scholar] [CrossRef]
- Zhuang, S.; Gao, H.; Shi, Y. Model Predictive Control of Switched Linear Systems with Persistent Dwell-Time Constraints: Recursive Feasibility and Stability. IEEE Trans. Autom. Control 2023, 68, 7887–7894. [Google Scholar] [CrossRef]
- Hassan, Y.F.; Zarkani, M.K.H.; Alali, M.J.; Daealhaq, H.; Chaoui, H. Guaranteed H∞ Performance of Switched Systems with State Delays: A Novel Low-Conservative Constrained Model Predictive Control Strategy. Mathematics 2024, 12, 246. [Google Scholar] [CrossRef]
- Darabseh, T.T.; Tarabulsi, A.; Mourad, A.-H. Active flutter suppression of a two-dimensional wing using quadratic Gaussian optimal control. Int. J. Struct. Stab. Dyn. 2022, 22, 2250157. [Google Scholar] [CrossRef]
- Ursu, I.; Ion Guta, D.D.; Enciu, D.; Tecuceanu, G.; Radu, A.A. Flight envelope expansion based on active mitigation of flutter via a V-stack piezoelectric actuator. IOP J. Phys. Conf. Ser. 2018, 1106, 012033. [Google Scholar] [CrossRef]
- Munteanu, F.; Oprean, C.; Stoica, C. INCAS Subsonic Wind Tunnel. INCAS Bull. 2009, 1, 12–14. [Google Scholar]
- Iorga, L.; Baruh, H.; Ursu, I. H∞ control with µ-analysis of a piezoelectric actuated plate. J. Vib. Control 2009, 15, 1143–1171. [Google Scholar] [CrossRef]
- Iorga, L.; Baruh, H.; Ursu, I. A review of robust control of piezoelectric smart structures. Trans. ASME Appl. Mech. Rev. 2008, 61, 17–31. [Google Scholar] [CrossRef]
- Ursu, I.; Tecuceanu, G.; Enciu, D.; Toader, A.; Nastase, I.; Arghir, M.; Calcea, M. A Smart Wing Model: From Design to Testing in a Wind Tunnel with a Turbulence Generator. Aerospace 2024, 11, 493. [Google Scholar] [CrossRef]
- Jones, P.W.; Smith, P. Stochastic processes. In An Introduction, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]


| Air Speed [m/s] | Poles | Zeros | Frequency [Hz] | Damping Ratio |
| 15 | −0.9 ± 36.66i | 74.93 | 5.84 | 0.02 |
| −3.37 ± 89.69i | −12.52 ± 72.99i | 14.30 | 0.04 | |
| −18.89 ± 1.15i | −43.53 | 18.61 | 0.16 | |
| 20 | −1.13 ± 37.19i | 294.2 | 5.92 | 0.03 |
| −7.70 ± 95.46i | 159.75 | 15.25 | 0.08 | |
| −80.95 ± 202.83i | −31.65 ± 51.2i | 34.71 | 0.37 | |
| 25 | −1.34 ± 37.55i | −3064.4 | 5.98 | 0.03 |
| −10.63 ± 94.90i | 99.4 | 15.21 | 0.11 | |
| −59.80 ± 184.28i | 63.4 ± 53.7i | 30.83 | 0.31 | |
| 30 | −1.69 ± 37.73i | 1643.3 | 6.01 | 0.05 |
| −13.92 ± 93.95i | −407.6 | 15.12 | 0.15 | |
| −81.45 ± 216.13i | 126.6; −58.3 | 36.78 | 0.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Enciu, D.; Toader, A.; Ursu, I. A Gain Scheduling Approach of Delayed Control with Application to Aircraft Wing in Wind Tunnel. Mathematics 2025, 13, 1614. https://doi.org/10.3390/math13101614
Enciu D, Toader A, Ursu I. A Gain Scheduling Approach of Delayed Control with Application to Aircraft Wing in Wind Tunnel. Mathematics. 2025; 13(10):1614. https://doi.org/10.3390/math13101614
Chicago/Turabian StyleEnciu, Daniela, Adrian Toader, and Ioan Ursu. 2025. "A Gain Scheduling Approach of Delayed Control with Application to Aircraft Wing in Wind Tunnel" Mathematics 13, no. 10: 1614. https://doi.org/10.3390/math13101614
APA StyleEnciu, D., Toader, A., & Ursu, I. (2025). A Gain Scheduling Approach of Delayed Control with Application to Aircraft Wing in Wind Tunnel. Mathematics, 13(10), 1614. https://doi.org/10.3390/math13101614







