Robust Stability of Switched Interconnected Systems with Switching Uncertainties
Abstract
1. Introduction
2. Model Description and Preliminaries
- is a nonsingular M-matrix.
- There exists a positive vector such that .
3. Main Result
3.1. Dynamical Behaviour Analysis of Modes
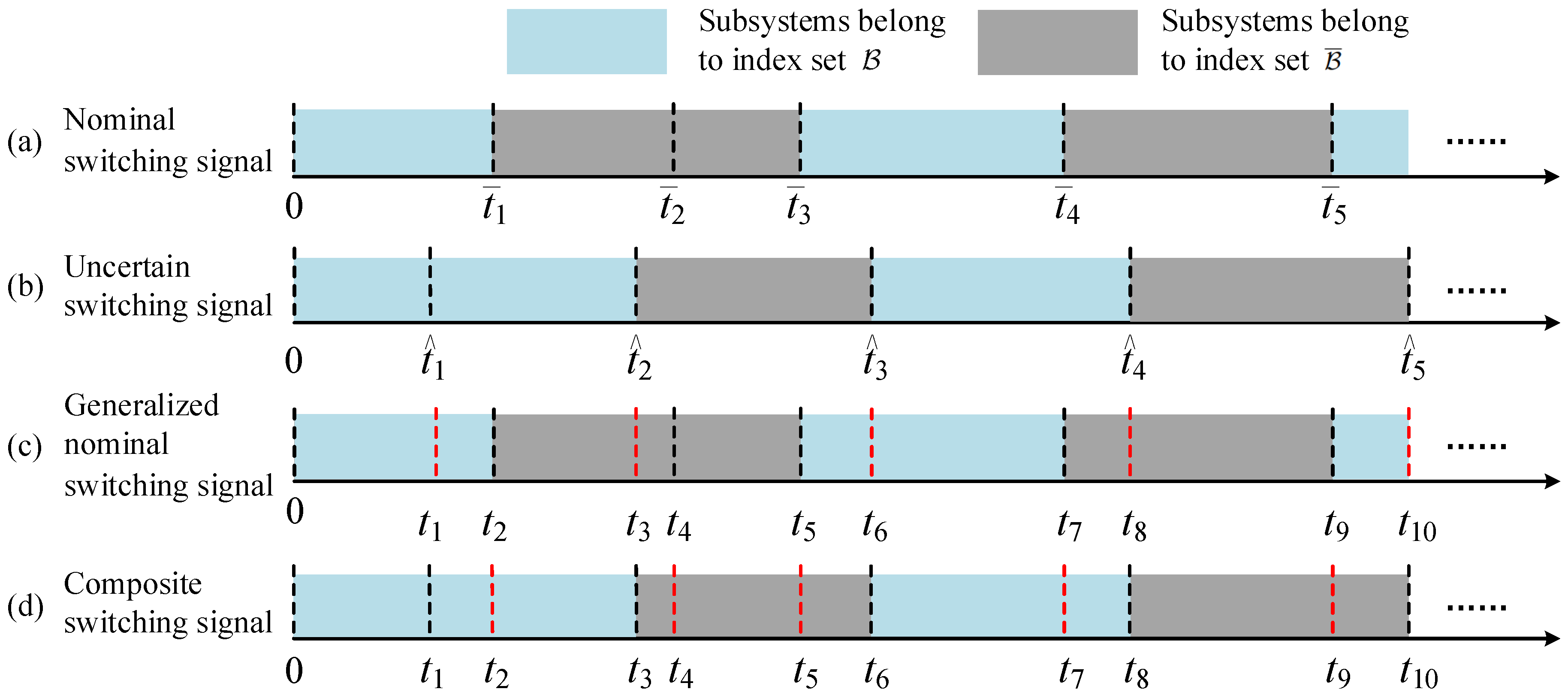
3.2. Stability Under Switching Sequence Uncertainties
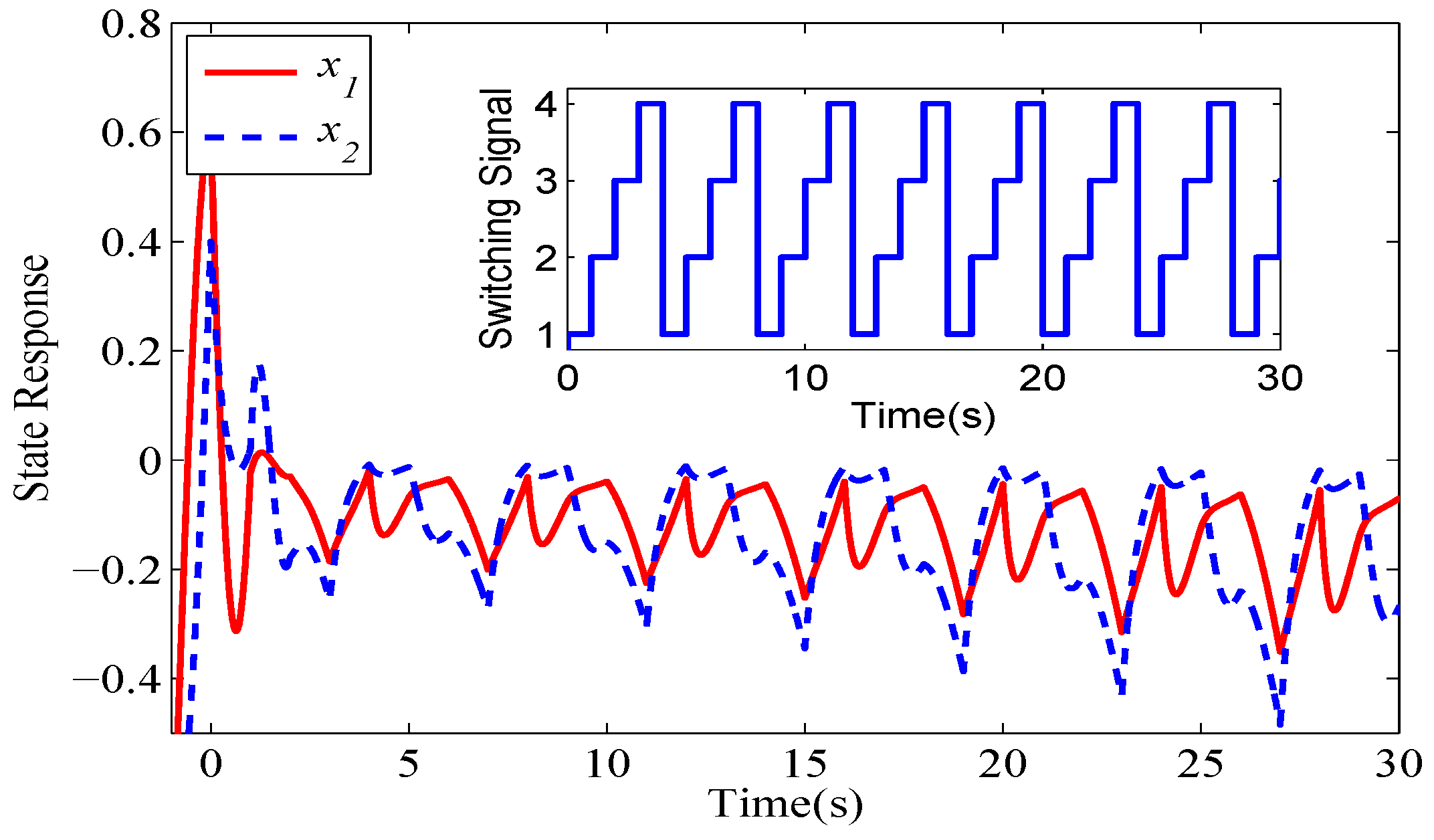
4. Numerical Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liberzon, D.; Morse, A.S. Basic problems in stability and design of switched systems. IEEE Control Syst. Mag. 1999, 19, 59–70. [Google Scholar]
- Daafouz, J.; Riedinger, P.; Iung, C. Stability analysis and control synthesis for switched systems: A switched Lyapunov function approach. IEEE Trans. Autom. Control 2002, 47, 1883–1887. [Google Scholar] [CrossRef]
- Xue, H.; Xu, X.; Zhang, J.; Yang, X. Robust stability of impulsive switched neural networks with multiple time delays. Appl. Math. Comput. 2019, 359, 456–475. [Google Scholar] [CrossRef]
- Xue, H.; Zhang, J. Robust exponential stability of interconnected switched systems with mixed delays and impulsive effect. Nonlinear Dynam. 2019, 97, 679–696. [Google Scholar] [CrossRef]
- Li, Y.; Xue, H. Robust stability analysis of switched neural networks with application in psychological counseling evaluation system. Mathematics 2024, 12, 2097. [Google Scholar] [CrossRef]
- Il’in, A.V.; Mosolova, Y.M.; Fomichev, V.V.; Fursov, A.S. On the problem of switched system stabilization. Moscow Univ. Comput. Math. Cybern. 2024, 48, 303–316. [Google Scholar] [CrossRef]
- Zhai, G.; Hu, B.; Yasuda, K.; Michel, A.N. Stability analysis of switched systems with stable and unstable subsystems: An average dwell time approach. Int. J. Syst. Sci. 2001, 32, 1055–1061. [Google Scholar] [CrossRef]
- Yang, H.; Jiang, B.; Cocquempot, V. A survey of results and perspectives on stabilization of switched nonlinear systems with unstable modes. Nonlinear Anal. Hybrid Syst. 2014, 13, 45–60. [Google Scholar] [CrossRef]
- Yang, H.; Cocquempot, V.; Jiang, B. On stabilization of switched nonlinear systems with unstable modes. Syst. Control Lett. 2009, 58, 703–708. [Google Scholar] [CrossRef]
- Zhang, M.; Gao, L. Input-to-state stability for impulsive switched nonlinear systems with unstable subsystems. Trans. Inst. Meas. Control 2018, 40, 2167–2177. [Google Scholar] [CrossRef]
- Xing, J.; Wu, B.; Wang, Y.; Liu, L. Exponential stability and non-weighted L2-gain analysis for switched neutral systems with unstable subsystems. Int. J. Syst. Sci. 2025, 56, 673–689. [Google Scholar] [CrossRef]
- Li, H.; Wei, Z. Stability analysis of discrete-time switched systems with all unstable subsystems. Discrete Contin. Dyn. Syst.-S 2024, 17, 2762–2777. [Google Scholar] [CrossRef]
- Zhang, N.; Sun, Y. Stabilization of switched positive linear delay system with all subsystems unstable. Int. J. Robust Nonlinear Control 2024, 34, 2441–2456. [Google Scholar] [CrossRef]
- Zhang, L.X.; Gao, H.J. Asynchronously switched control of switched linear systems with average dwell time. Automatica 2010, 46, 953–958. [Google Scholar] [CrossRef]
- Zong, G.; Wang, R.; Zheng, W.X.; Hou, L. Finite-time stabilization for a class of switched time-delay systems under asynchronous switching. Appl. Math. Comput. 2013, 219, 5757–5771. [Google Scholar] [CrossRef]
- Wu, X.; Tang, Y.; Cao, J.; Zhang, W. Distributed consensus of stochastic delayed multi-agent systems under asynchronous switching. IEEE Trans. Cybern. 2015, 46, 1817–1827. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Deng, F. Stability and stabilization of nonlinear stochastic systems with synchronous and asynchronous switching parameters to the states. IEEE Trans. Cybern. 2022, 53, 4894–4907. [Google Scholar] [CrossRef]
- Zhang, S.; Nie, A.B. Exponential stability of fractional-order uncertain systems with asynchronous switching and impulses. Int. J. Robust Nonlinear Control 2024, 34, 7285–7313. [Google Scholar] [CrossRef]
- Hu, B.; Xu, X.; Antsaklis, P.J.; Michel, A.N. Robust stabilizing control laws for a class of second-order switched systems. Syst. Control Lett. 1999, 38, 197–207. [Google Scholar] [CrossRef]
- Hetel, L.; Daafouz, J.; Iung, C. Stability analysis for discrete time switched systems with temporary uncertain switching signal. In Proceedings of the 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 5623–5628. [Google Scholar]
- Li, Z.G.; Soh, Y.C.; Wen, C.Y. Robust stability of quasi-periodic hybrid dynamic uncertain systems. IEEE Trans. Autom. Control 2001, 46, 107–111. [Google Scholar] [CrossRef]
- Sun, Z. Robust switching of discrete-time switched linear systems. Automatica 2012, 48, 239–242. [Google Scholar] [CrossRef]
- Han, T.-T.; Ge, S.S.; Lee, T.H. Adaptive neural control for a class of switched nonlinear systems. Syst. Control Lett. 2009, 58, 109–118. [Google Scholar] [CrossRef]
- Yang, H.; Jiang, B.; Tao, G.; Zhou, D. Robust stability of switched nonlinear systems with switching uncertainties. IEEE Trans. Autom. Control 2016, 61, 2531–2537. [Google Scholar] [CrossRef]
- Zhang, L.; Boukas, E. Stability and stabilization of Markovian jump linear systems with partly unknown transition probabilities. Automatica 2009, 45, 463–468. [Google Scholar] [CrossRef]
- Xiang, W.; Lam, J.; Li, P. On stability and H∞ control of switched systems with random switching signals. Automatica 2018, 95, 419–425. [Google Scholar] [CrossRef]
- Roy, S.; Baldi, S.; Ioannou, P.A. An adaptive control framework for underactuated switched Euler–Lagrange systems. IEEE Trans. Autom. Control 2021, 67, 4202–4209. [Google Scholar] [CrossRef]
- Brodtkorb, A.H.; Værnø, S.A.; Teel, A.R.; Sørensen, A.J.; Skjetne, R. Hybrid controller concept for dynamic positioning of marine vessels with experimental results. Automatica 2018, 93, 489–497. [Google Scholar] [CrossRef]
- Mahmoud, M.S.; AL-Sunni, F.M. Interconnected continuous-time switched systems: Robust stability and stabilization. Nonlinear Anal. Hybrid Syst. 2010, 4, 531–542. [Google Scholar] [CrossRef]
- Long, L.; Zhao, J. A small-gain theorem for switched interconnected nonlinear systems and its applications. IEEE Trans. Autom. Control 2013, 59, 1082–1088. [Google Scholar] [CrossRef]
- Long, L. Multiple Lyapunov functions-based small-gain theorems for switched interconnected nonlinear systems. IEEE Trans. Autom. Control 2017, 62, 3943–3958. [Google Scholar] [CrossRef]
- Hou, Y.; Liu, Y.-J.; Tong, S. Decentralized event-triggered fault-tolerant control for switched interconnected nonlinear systems with input saturation and time-varying full-state constraints. IEEE Trans. Fuzzy Syst. 2024, 32, 3850–3860. [Google Scholar] [CrossRef]
- Gurrala, G.; Sen, I. Power system stabilizers design for interconnected power systems. IEEE Trans. Power Syst. 2010, 25, 1042–1051. [Google Scholar] [CrossRef]
- Li, Y.M.; Tong, S.C. Adaptive neural networks prescribed performance control design for switched interconnected uncertain nonlinear systems. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 3059–3068. [Google Scholar] [CrossRef]
- Zhao, Y.W.; Zhang, H.Y.; Chen, Z.Y.; Wang, H.Q.; Zhao, X.D. Adaptive neural decentralised control for switched interconnected nonlinear systems with backlash-like hysteresis and output constraints. Int. J. Syst. Sci. 2022, 53, 1545–1561. [Google Scholar] [CrossRef]
- Zhai, D.; Liu, X.; Liu, Y.J. Adaptive decentralized controller design for a class of switched interconnected nonlinear systems. IEEE Trans. Cybern. 2020, 50, 1644–1654. [Google Scholar] [CrossRef]
- Zhang, J.; Li, S.; Ahn, C.K.; Xiang, Z.R. Adaptive fuzzy decentralized dynamic surface control for switched large-scale nonlinear systems with full-state constraints. IEEE Trans. Cybern. 2022, 52, 10761–10772. [Google Scholar] [CrossRef]
- Chen, Y. Fuzzy interactions compensation in adaptive control of switched interconnected systems. IEEE Trans. Autom. Sci. Eng. 2024, 21, 48–55. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Y.; Zhao, W. Approximately bi-similar symbolic model for discrete-time interconnected switched system. IEEE/CAA J. Autom. Sinica 2024, 11, 2185–2187. [Google Scholar] [CrossRef]
- Jonsson, U.T.; Kao, C.Y.; Fujioka, H. Low dimensional stability criteria for large-scale interconnected systems. In Proceedings of the 9th European Control Conference, Kos, Greece, 2–5 July 2007; pp. 2741–2747. [Google Scholar]
- Andersen, M.S.; Pakazad, S.K.; Hansson, A.; Rantzer, A. Robust stability analysis of sparsely interconnected uncertain systems. IEEE Trans. Autom. Control 2014, 59, 2151–2156. [Google Scholar] [CrossRef]
- Thanh, N.T.; Phat, V.N. Decentralized stability for switched nonlinear large-scale systems with interval time-varying delays in interconnections. Nonlinear Anal. Hybrid Syst. 2014, 11, 22–36. [Google Scholar] [CrossRef]
- Ren, H.; Zong, G.; Hou, L.; Yi, Y. Finite-time control of interconnected impulsive switched systems with time-varying delay. Appl. Math. Comput. 2016, 276, 143–157. [Google Scholar] [CrossRef]
- Malloci, I.; Lin, Z.; Yan, G. Stability of interconnected impulsive switched systems subject to state dimension variation. Nonlinear Anal. Hybrid Syst. 2012, 6, 960–971. [Google Scholar] [CrossRef]
- Yang, G.; Liberzon, D. A Lyapunov-based small-gain theorem for interconnected switched systems. Syst. Control Lett. 2015, 78, 47–54. [Google Scholar] [CrossRef]
- Cao, J.; Huang, D.; Qu, Y. Global robust stability of delayed recurrent neural networks. Chaos Solitons Fractals 2005, 23, 221–229. [Google Scholar] [CrossRef]
- Ensari, T.; Arik, S. New results for robust stability of dynamical neural networks with discrete time delays. Expert Syst. Appl. 2010, 37, 5925–5930. [Google Scholar] [CrossRef]
- Faydasicok, O.; Arik, S. A new upper bound for the norm of interval matrices with application to robust stability analysis of delayed neural networks. Neural Netw. 2013, 44, 64–71. [Google Scholar] [CrossRef] [PubMed]
- Siljak, D.D. Large Scale Dynamic Systems: Stability and Structure; IEEE: Amsterdam, The Netherlands, 1978. [Google Scholar]
- Li, X.; Cao, J.; Perc, M. Switching laws design for stability of finite and infinite delayed switched systems with stable and unstable modes. IEEE Access 2018, 6, 6677–6691. [Google Scholar] [CrossRef]
- Wang, Y.-E.; Karimi, H.R.; Wu, D. Conditions for the stability of switched systems containing unstable subsystems. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 653–657. [Google Scholar] [CrossRef]
- Xue, H.; Zhang, J.; Wang, H.; Jiang, B. Robust stability of switched interconnected systems with time-varying delays. J. Comput. Nonlinear Dyn. 2018, 13, 021004. [Google Scholar] [CrossRef]
- Qi, J.; Li, C.; Huang, T.; Zhang, W. Exponential stability of switched time-varying delayed neural networks with all modes being unstable. Neural Process. Lett. 2016, 43, 553–565. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, H.; Yang, X. Robust Stability of Switched Interconnected Systems with Switching Uncertainties. Mathematics 2025, 13, 1554. https://doi.org/10.3390/math13101554
Xue H, Yang X. Robust Stability of Switched Interconnected Systems with Switching Uncertainties. Mathematics. 2025; 13(10):1554. https://doi.org/10.3390/math13101554
Chicago/Turabian StyleXue, Huanbin, and Xiaopeng Yang. 2025. "Robust Stability of Switched Interconnected Systems with Switching Uncertainties" Mathematics 13, no. 10: 1554. https://doi.org/10.3390/math13101554
APA StyleXue, H., & Yang, X. (2025). Robust Stability of Switched Interconnected Systems with Switching Uncertainties. Mathematics, 13(10), 1554. https://doi.org/10.3390/math13101554





