A Heuristic Approach for Last-Mile Delivery with Consistent Considerations and Minimum Service for a Supply Chain
Abstract
:1. Introduction
2. Literature Review
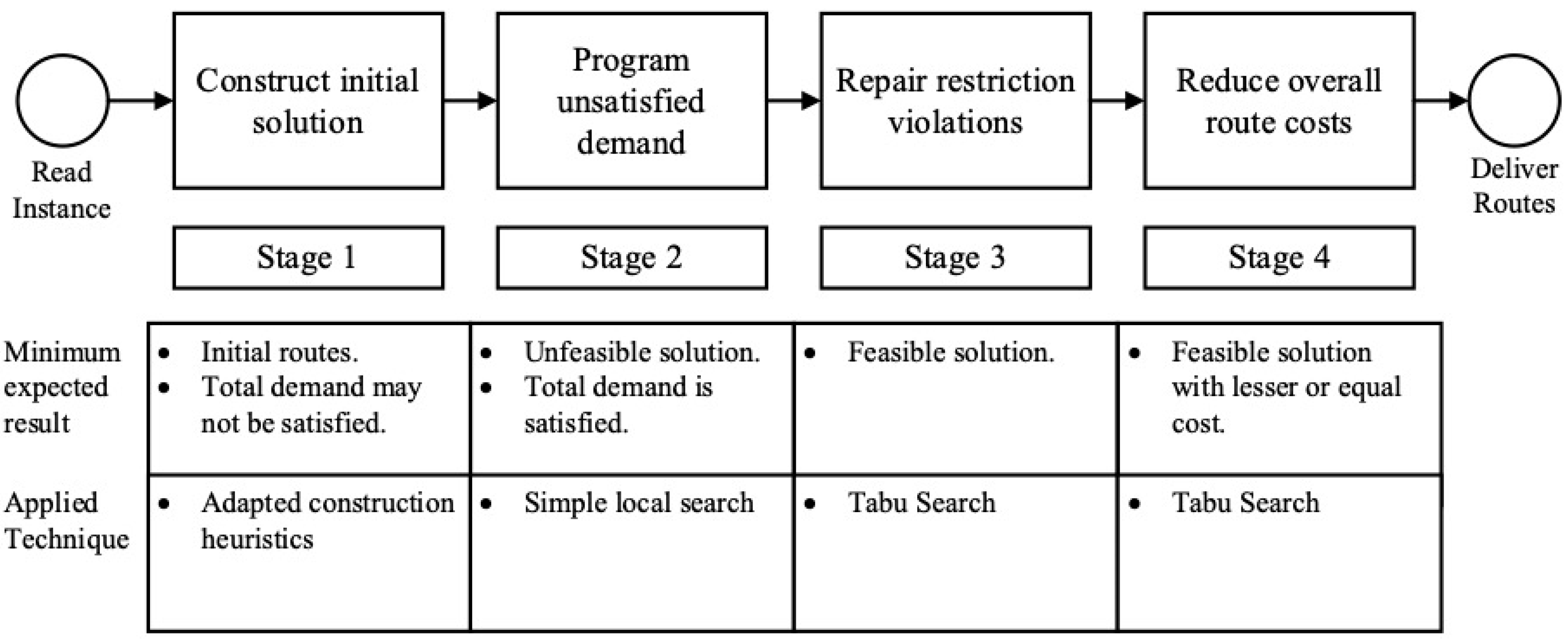
3. Proposed Approach
3.1. Description of the ConVRPms
- D: Planning horizon.
- K: Available vehicles.
- N: Customers.
- V: Nodes (the set N of customers plus the depot OR N0).
- A: Arc connecting nodes.
- T: Maximum operating time.
- L: Maximum difference for the accepted arrival times.
- Q: Load capacity of the vehicle.
- qid: Demand of customer i for day d.
- wid: Requested service by customer i for day d. This parameter takes a value of 1, indicating that customer i has a demand on day d.
- tij: Travel time from node to node j.
- sid: Service time of customer i for day d.
- .
- .
- i on the day d.
3.2. Proposed Solution Method
3.2.1. Description of the Proposed Algorithm
| Pseudocode 1. Proposed TSRI Algorithm |
| Procedure TSRI (, , , , ) Construct_solution(, , ) If then Schedule_unsatisfied_demand() If then Repair_solution() If then Improve_solution() Output: Feasible Solution Else Output: Infeasible Solution Return |
3.2.2. Stage 1: Constructing an Initial Solution
Savings Heuristic
- The route of vehicle l is inserted after the route of vehicle k
Route of the day Route of the day New route of day - The route of vehicle l is inserted before the route of vehicle k
Route of the day Route of the day New route of day - The inverse route of vehicle l is inserted after the route of vehicle k
Route of the day Inverse Route of the day New route of day - The route of vehicle l is inserted after the inverse route of vehicle k
Inverse Route of the day Route of the day New route of day
Parallel Insertion Heuristic
Sequential Insertion Heuristic
3.2.3. Stage 2: Scheduling Unsatisfied Demands
| Pseudocode 2. Proposed Completion Process Algorithm |
| Procedure completion (schedule with unsatisfied demand ) Unsatisfied customers in For Local_search(, ) Return Complete solution: |
3.2.4. Stage 3: Repairing the Solution
Repairing Empty or Overloaded Routes
Repair Routes with Excessive Duration
Repairing Inconsistent Arrival Times
| Pseudocode 3. Proposed repair procedure |
| Procedure Repair Procedure (Non-feasible solution, , ) 0 While ) do ← Local_search(, , ) ← ← While ) do ← Local_search(, , ) ← ← While ) do ← Local_search(, , ) ← ← Finalize Repair process If then Output: Feasible solution: Else Output: Infeasible solution: Return |
- The neighborhood NR1 is defined by DC repositioning and inter-route exchange operators and is focused on eliminating empty or overloaded routes.
- The neighborhood NR2 addresses violations related to excessive route durations, incorporating DC repositioning, 2-opt intraroute operators, and inter-route operators.
- The neighborhood NR3 is designed to correct inconsistencies in customer arrival times and includes DC repositioning, inter-route exchange, and 2-opt multiroute operators.
3.2.5. Stage 4: Improving the Solution
| Pseudocode 4. Proposed Improving Procedure |
| Procedure Improving Procedure (Feasible Solution, , ) 0 While do ← Local_search(, , ) If then ← Output: Feasible solution: Return |
4. Computational Experiments
4.1. Experimental Environment and Hardware
4.2. ConVRPM Test Instances
4.3. First Experiment
4.4. Second Experiment
- Feasibility of the solution:
- Completeness of the solution:
- Cost value of the solution:
- Total computing time:
5. Discussion of the Results
6. Concluding Remarks
- The adaptation of the TSRI algorithm for the solution of other variants of the ConVRP, its application for sets of instances of medium size, and the comparison of its performance concerning other heuristic methods.
- The incorporation of an initial phase for which multiple candidate solutions are evaluated and the incorporation of random elements within the improvement process on the basis of tabu search.
- A matheuristic solution method, which incorporates the TSRI algorithm as a higher bounding procedure, is developed prior to applying an optimization algorithm, such as branch-and-cut.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Id | Inst. | CPLEX Branch-and-Cut | TSRI—A | TSRI—P | TSRI—S | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| LB | z (BKS) | T.CPU [s] | z | T.CPU [s] | z | T.CPU [s] | z | T.CPU [s] | ||
| 1 | 10UC1 | 104.18 | 104.18 | 23.70 | 120.24 | 63.54 | 111.65 | 0.02 | 110.27 | 0.49 |
| 2 | 10CC1 | 61.69 | 61.69 | 8.94 | 91.38 | 2.34 | 79.14 | 0.54 | 79.25 | 0.28 |
| 3 | 15UC1 | 132.59 | 132.59 | 674.72 | - | - | 152.07 | 101.80 | 152.07 | 23.90 |
| 4 | 15CC1 | 60.07 | 82.56 | 3600.00 | 102.37 | 0.04 | 124.10 | 10.84 | 111.04 | 2.19 |
| 5 | 15CE1 | 122.20 | 146.47 | 3600.00 | 146.47 | 299.92 | 146.47 | 20.69 | 146.47 | 157.03 |
| 6 | 20UC1 | 109.84 | 159.07 | 3600.00 | 177.52 | 11.90 | 189.39 | 21.12 | 192.35 | 0.36 |
| 7 | 20UE1 | 138.54 | 221.45 | 3600.00 | 228.16 | 0.11 | 234.43 | 121.46 | 233.72 | 47.49 |
| 8 | 20CC1 | 70.43 | 98.93 | 3600.00 | 134.33 | 18.11 | 100.97 | 0.31 | 107.35 | 0.54 |
| 9 | 20CE1 | 135.23 | 165.47 | 3600.00 | 175.93 | 0.32 | 177.56 | 0.18 | 205.88 | 0.47 |
| 10 | 10UC3 | 81.35 | 81.35 | 1.20 | 81.38 | 0.00 | 84.97 | 0.01 | 120.18 | 0.02 |
| 11 | 10UE3 | 137.78 | 137.78 | 0.57 | 137.78 | 0.01 | 140.34 | 0.01 | 142.72 | 0.00 |
| 12 | 10CC3 | 54.47 | 54.47 | 2.68 | 55.81 | 0.00 | 60.82 | 0.01 | 84.04 | 0.00 |
| 13 | 10CE3 | 135.08 | 135.08 | 25.75 | 135.08 | 0.34 | 139.52 | 0.21 | 140.37 | 1.01 |
| 14 | 15UC3 | 120.70 | 120.70 | 84.62 | 134.41 | 0.14 | 133.22 | 0.34 | 158.09 | 103.79 |
| 15 | 15UE3 | 152.36 | 152.36 | 1299.71 | 171.76 | 5.63 | 161.84 | 6.77 | 159.02 | 4.77 |
| 16 | 15CC3 | 66.72 | 66.72 | 82.52 | 74.04 | 0.03 | 68.23 | 0.02 | 79.27 | 0.15 |
| 17 | 15CE3 | 126.81 | 126.81 | 60.81 | 142.76 | 0.15 | 141.94 | 0.02 | 143.75 | 0.23 |
| 18 | 20UC3 | 111.22 | 134.46 | 3600.00 | 148.64 | 0.06 | 181.10 | 0.32 | 185.07 | 0.59 |
| 19 | 20UE3 | 146.58 | 204.44 | 3600.00 | 228.61 | 0.35 | 244.03 | 22.95 | 252.04 | 0.44 |
| 20 | 20CC3 | 72.88 | 82.42 | 3600.00 | 96.79 | 0.27 | 92.54 | 0.25 | 119.35 | 0.54 |
| 21 | 20CE3 | 138.06 | 154.26 | 3600.00 | 165.55 | 0.27 | 178.32 | 0.11 | 177.70 | 0.56 |
| 22 | 10UCT | 81.29 | 81.29 | 1.15 | 81.37 | 0.00 | 81.74 | 0.00 | 108.67 | 0.00 |
| 23 | 10UET | 136.90 | 136.90 | 0.25 | 136.90 | 0.01 | 137.50 | 0.00 | 142.89 | 0.00 |
| 24 | 10CCT | 54.47 | 54.47 | 1.99 | 55.81 | 0.01 | 56.13 | 0.00 | 68.13 | 0.00 |
| 25 | 10CET | 135.08 | 135.08 | 143.88 | 135.08 | 0.07 | 138.61 | 0.89 | 138.61 | 0.72 |
| 26 | 15UCT | 112.02 | 112.02 | 5.28 | 112.66 | 0.02 | 113.85 | 0.04 | 131.10 | 0.09 |
| 27 | 15UET | 132.13 | 149.60 | 3600.00 | 163.58 | 3.14 | 156.28 | 0.03 | 163.58 | 0.13 |
| 28 | 15CCT | 64.96 | 64.96 | 22.62 | 71.69 | 0.02 | 71.80 | 0.02 | 78.32 | 0.28 |
| 29 | 15CET | 126.32 | 126.32 | 13.77 | 139.99 | 0.01 | 141.37 | 0.02 | 137.53 | 0.13 |
| 30 | 20UCT | 129.76 | 129.76 | 1289.33 | 140.23 | 1.65 | 142.73 | 0.14 | 180.08 | 0.46 |
| 31 | 20UET | 140.04 | 192.25 | 3600.00 | 218.99 | 2.16 | 220.54 | 0.11 | 249.36 | 0.48 |
| 32 | 20CCT | 79.68 | 79.68 | 141.38 | 90.32 | 0.04 | 85.58 | 0.21 | 111.51 | 0.48 |
| 33 | 20CET | 140.42 | 151.71 | 3600.00 | 164.27 | 3.51 | 165.39 | 0.08 | 171.06 | 0.59 |
| Average | 109.45 | 122.34 | 1535.91 | 133.12 | 12.94 | 134.97 | 9.38 | 144.87 | 10.55 | |
| Id | Inst. | CPLEX Branch-and-Cut | TSRI—A | TSRI—P | TSRI—S | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| LB | Z (BKS) | T.CPU [s] | z | T.CPU [s] | z | T.CPU [s] | z | T.CPU [s] | ||
| 1 | 10UC1 | 104.18 | 104.18 | 23.70 | 104.18 | 64.95 | 111.55 | 1.95 | 110.27 | 2.36 |
| 2 | 10CC1 | 61.69 | 61.69 | 8.94 | 81.03 | 3.82 | 75.59 | 2.28 | 75.59 | 1.64 |
| 3 | 15UC1 | 132.59 | 132.59 | 674.72 | - | - | 152.07 | 111.01 | 152.07 | 33.30 |
| 4 | 15CC1 | 60.07 | 82.56 | 3600.00 | 91.04 | 6.76 | 115.71 | 17.92 | 95.22 | 7.86 |
| 5 | 15CE1 | 122.20 | 146.47 | 3600.00 | 146.47 | 308.91 | 146.47 | 29.38 | 146.47 | 165.82 |
| 6 | 20UC1 | 109.84 | 159.07 | 3600.00 | 161.63 | 40.24 | 157.52 | 51.13 | 154.94 | 24.60 |
| 7 | 20UE1 | 138.54 | 221.45 | 3600.00 | 226.95 | 31.72 | 222.07 | 143.30 | 233.72 | 90.18 |
| 8 | 20CC1 | 70.43 | 98.93 | 3600.00 | 100.39 | 45.90 | 93.52 | 33.38 | 98.59 | 21.50 |
| 9 | 20CE1 | 135.23 | 165.47 | 3600.00 | 165.50 | 27.20 | 169.95 | 23.41 | 169.85 | 19.89 |
| 10 | 10UC3 | 81.35 | 81.35 | 1.20 | 81.35 | 1.54 | 81.35 | 1.35 | 86.37 | 1.08 |
| 11 | 10UE3 | 137.78 | 137.78 | 0.57 | 137.78 | 1.76 | 137.78 | 1.48 | 137.78 | 1.34 |
| 12 | 10CC3 | 54.47 | 54.47 | 2.68 | 54.47 | 1.50 | 54.47 | 1.00 | 54.47 | 0.56 |
| 13 | 10CE3 | 135.08 | 135.08 | 25.75 | 135.08 | 2.14 | 139.52 | 2.00 | 139.52 | 2.41 |
| 14 | 15UC3 | 120.70 | 120.70 | 84.62 | 131.86 | 8.17 | 122.15 | 4.94 | 137.29 | 110.40 |
| 15 | 15UE3 | 152.36 | 152.36 | 1299.71 | 171.76 | 14.80 | 153.58 | 11.91 | 152.36 | 8.68 |
| 16 | 15CC3 | 66.72 | 66.72 | 82.52 | 67.01 | 5.35 | 66.72 | 7.49 | 66.72 | 7.73 |
| 17 | 15CE3 | 126.81 | 126.81 | 60.81 | 126.81 | 4.86 | 126.81 | 3.77 | 126.81 | 3.16 |
| 18 | 20UC3 | 111.22 | 134.46 | 3600.00 | 136.52 | 35.02 | 145.78 | 17.42 | 150.13 | 19.11 |
| 19 | 20UE3 | 146.58 | 204.44 | 3600.00 | 217.71 | 34.57 | 227.18 | 37.88 | 232.32 | 19.38 |
| 20 | 20CC3 | 72.88 | 82.42 | 3600.00 | 94.64 | 32.11 | 90.33 | 30.91 | 88.26 | 12.97 |
| 21 | 20CE3 | 138.06 | 154.26 | 3600.00 | 160.83 | 26.90 | 161.32 | 7.40 | 156.27 | 8.77 |
| 22 | 10UCT | 81.29 | 81.29 | 1.15 | 81.29 | 1.74 | 81.29 | 1.27 | 81.29 | 1.06 |
| 23 | 10UET | 136.90 | 136.90 | 0.25 | 136.90 | 1.81 | 136.90 | 1.50 | 136.90 | 0.80 |
| 24 | 10CCT | 54.47 | 54.47 | 1.99 | 54.47 | 1.50 | 54.47 | 1.32 | 54.47 | 1.13 |
| 25 | 10CET | 135.08 | 135.08 | 143.88 | 135.08 | 1.89 | 135.44 | 2.58 | 135.44 | 2.42 |
| 26 | 15UCT | 112.02 | 112.02 | 5.28 | 112.02 | 7.70 | 113.19 | 8.39 | 113.78 | 3.94 |
| 27 | 15UET | 132.13 | 149.60 | 3600.00 | 149.74 | 5.36 | 149.63 | 4.84 | 149.63 | 3.25 |
| 28 | 15CCT | 64.96 | 64.96 | 22.62 | 64.96 | 6.12 | 64.96 | 4.54 | 64.96 | 4.84 |
| 29 | 15CET | 126.32 | 126.32 | 13.77 | 126.32 | 5.99 | 126.32 | 3.12 | 126.32 | 7.02 |
| 30 | 20UCT | 129.76 | 129.76 | 1289.33 | 129.76 | 21.58 | 135.99 | 35.11 | 141.46 | 12.68 |
| 31 | 20UET | 140.04 | 192.25 | 3600.00 | 210.19 | 44.92 | 208.93 | 17.37 | 225.31 | 21.90 |
| 32 | 20CCT | 79.68 | 79.68 | 141.38 | 79.68 | 19.76 | 83.08 | 28.83 | 82.93 | 8.82 |
| 33 | 20CET | 140.42 | 151.71 | 3600.00 | 151.71 | 16.09 | 156.50 | 15.73 | 154.76 | 9.46 |
| Average | 109.45 | 122.34 | 1535.91 | 125.79 | 26.02 | 127.22 | 20.18 | 128.25 | 19.40 | |
| Id | Inst. | CPLEX Branch-and-Cut | TSRI—A | TSRI—P | TSRI—S | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| LB | z (BKS) | T.CPU [s] | z | T.CPU [s] | z | T.CPU [s] | z | T.CPU [s] | ||
| 1 | 10UC1 | 104.18 | 104.18 | 23.70 | 104.18 | 72.44 | 104.18 | 8.67 | 110.27 | 10.11 |
| 2 | 10CC1 | 61.69 | 61.69 | 8.94 | 61.69 | 10.33 | 61.69 | 9.30 | 74.19 | 9.32 |
| 3 | 15UC1 | 132.59 | 132.59 | 674.72 | - | - | 147.67 | 148.09 | 147.67 | 69.83 |
| 4 | 15CC1 | 60.07 | 82.56 | 3600.00 | 91.04 | 52.12 | 102.02 | 49.49 | 91.04 | 52.26 |
| 5 | 15CE1 | 122.20 | 146.47 | 3600.00 | 146.47 | 344.83 | 146.47 | 64.86 | 146.47 | 201.42 |
| 6 | 20UC1 | 109.84 | 159.07 | 3600.00 | 156.50 | 211.14 | 152.62 | 214.44 | 154.94 | 208.57 |
| 7 | 20UE1 | 138.54 | 221.45 | 3600.00 | 223.76 | 189.83 | 222.07 | 322.39 | 225.93 | 249.93 |
| 8 | 20CC1 | 70.43 | 98.93 | 3600.00 | 100.39 | 216.08 | 93.52 | 208.41 | 93.52 | 182.41 |
| 9 | 20CE1 | 135.23 | 165.47 | 3600.00 | 165.50 | 225.36 | 165.07 | 182.30 | 168.62 | 185.05 |
| 10 | 10UC3 | 81.35 | 81.35 | 1.20 | 81.35 | 9.14 | 81.35 | 8.93 | 86.37 | 12.63 |
| 11 | 10UE3 | 137.78 | 137.78 | 0.57 | 137.78 | 9.00 | 137.78 | 8.63 | 137.78 | 8.59 |
| 12 | 10CC3 | 54.47 | 54.47 | 2.68 | 54.47 | 8.57 | 54.47 | 8.15 | 54.47 | 7.72 |
| 13 | 10CE3 | 135.08 | 135.08 | 25.75 | 135.08 | 9.73 | 135.08 | 8.88 | 135.08 | 9.18 |
| 14 | 15UC3 | 120.70 | 120.70 | 84.62 | 128.26 | 45.82 | 121.02 | 45.87 | 135.28 | 151.50 |
| 15 | 15UE3 | 152.36 | 152.36 | 1299.71 | 171.76 | 52.32 | 152.36 | 47.76 | 152.36 | 46.97 |
| 16 | 15CC3 | 66.72 | 66.72 | 82.52 | 67.01 | 41.58 | 66.72 | 43.98 | 66.72 | 43.96 |
| 17 | 15CE3 | 126.81 | 126.81 | 60.81 | 126.81 | 41.77 | 126.81 | 40.88 | 126.81 | 39.56 |
| 18 | 20UC3 | 111.22 | 134.46 | 3600.00 | 134.46 | 225.85 | 143.48 | 194.72 | 141.43 | 259.61 |
| 19 | 20UE3 | 146.58 | 204.44 | 3600.00 | 216.31 | 262.55 | 227.07 | 207.88 | 223.24 | 192.44 |
| 20 | 20CC3 | 72.88 | 82.42 | 3600.00 | 94.64 | 245.19 | 87.22 | 206.06 | 84.12 | 222.16 |
| 21 | 20CE3 | 138.06 | 154.26 | 3600.00 | 160.53 | 189.13 | 154.26 | 191.52 | 154.26 | 189.20 |
| 22 | 10UCT | 81.29 | 81.29 | 1.15 | 81.29 | 9.50 | 81.29 | 8.98 | 81.29 | 8.64 |
| 23 | 10UET | 136.90 | 136.90 | 0.25 | 136.90 | 9.27 | 136.90 | 8.75 | 136.90 | 7.90 |
| 24 | 10CCT | 54.47 | 54.47 | 1.99 | 54.47 | 8.79 | 54.47 | 8.63 | 54.47 | 8.35 |
| 25 | 10CET | 135.08 | 135.08 | 143.88 | 135.08 | 9.09 | 135.44 | 10.01 | 135.44 | 9.73 |
| 26 | 15UCT | 112.02 | 112.02 | 5.28 | 112.02 | 42.29 | 113.19 | 48.54 | 112.02 | 37.39 |
| 27 | 15UET | 132.13 | 149.60 | 3600.00 | 149.63 | 42.87 | 149.63 | 43.55 | 149.63 | 42.12 |
| 28 | 15CCT | 64.96 | 64.96 | 22.62 | 64.96 | 43.09 | 64.96 | 41.49 | 64.96 | 41.32 |
| 29 | 15CET | 126.32 | 126.32 | 13.77 | 126.32 | 43.16 | 126.32 | 40.01 | 126.32 | 44.20 |
| 30 | 20UCT | 129.76 | 129.76 | 1289.33 | 129.76 | 313.77 | 135.99 | 248.64 | 138.24 | 308.91 |
| 31 | 20UET | 140.04 | 192.25 | 3600.00 | 210.19 | 252.94 | 208.93 | 230.15 | 204.08 | 207.49 |
| 32 | 20CCT | 79.68 | 79.68 | 141.38 | 79.68 | 309.50 | 83.08 | 224.92 | 82.93 | 185.63 |
| 33 | 20CET | 140.42 | 151.71 | 3600.00 | 151.71 | 267.37 | 151.71 | 218.79 | 151.71 | 242.69 |
| Average | 109.45 | 122.34 | 1535.91 | 124.69 | 119.20 | 125.00 | 101.63 | 125.71 | 105.96 | |
| Graphic of the solutions: Instance 6 |
| Obtained routes of variant TSRIs—P and nMej = 50 |
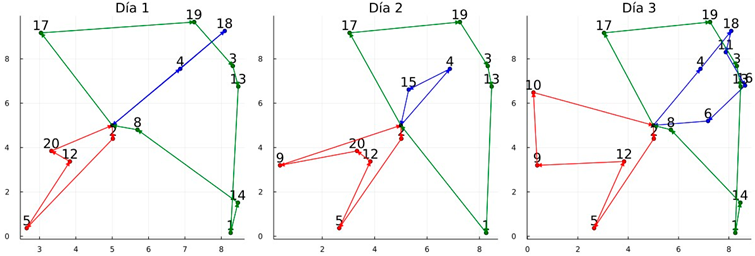 |
| Total cost (z) = 152.62, T.CPU = 214.44 s Lower_LB = 39.0%, Lower_BKS = −4.1% |
| Obtained routes with CPLEX Branch-and-Cut |
 |
| Total cost (z) = 159.07, T.CPU = 3600.00 s Lower_LB = 44.8%, Lower_BKS = 0.0% |
| Graphic of the solutions: Instance 8 |
| Obtained routes of variant TSRIs—P and nMej = 50 |
 |
| Total cost (z) = 93.52, T.CPU = 208.41 s (each route is determined by a color) Lower_LB = 32.8%, Lower_BKS = −5.5 p% |
| Obtained routes with CPLEX Branch-and-Cut |
 |
| Total cost (z) = 98.93, T.CPU = 3600.00 s (each route is determined by a color) Lower_LB = 40.5%, Lower_BKS = 0.0% |
| Graphic of the solutions: Instance 9 |
| Obtained routes of variant TSRIs—P and |
 |
| Total cost (z) = 165.07, T.CPU = 182.30 s (each route is determined by a color) Lower_LB = 22.1%, Lower_BKS = − 0.2% |
| Obtained routes with CPLEX Branch-and-Cut |
 |
| Total cost (z) = 165.47, T.CPU = 3600.00 s (each route is determined by a color) Lower_LB = 22.4%, Lower_BKS = 0.0% |
References
- Feillet, D.; Garaix, T.; Lehuédé, F.; Péton, O.; Quadri, D. A new consistent vehicle routing problem for the transportation of people with disabilities. Networks 2014, 63, 211–224. [Google Scholar] [CrossRef]
- Groër, C.; Golden, B.; Wasil, E. The consistent vehicle routing problem. Manuf. Serv. Oper. Manag. 2009, 11, 630–643. [Google Scholar] [CrossRef]
- Barros, L.; Linfati, R.; Escobar, J.W. An exact approach for the consistent vehicle routing problem (ConVRP). Adv. Prod. Eng. Manag. 2020, 15, 255–266. [Google Scholar] [CrossRef]
- Escobar, J.W.; Linfati, R.; Toth, P. A two-phase hybrid heuristic algorithm for the capacitated location-routing problem. Comput. Oper. Res. 2013, 40, 70–79. [Google Scholar] [CrossRef]
- Escobar, J.W.; Linfati, R.; Baldoquin, M.G.; Toth, P. A granular variable tabu neighborhood search for the capacitated location-routing problem. Transp. Res. Part B Methodol. 2014, 67, 344–356. [Google Scholar] [CrossRef]
- Tarantilis, C.D.; Stavropoulou, F.; Repoussis, P.P. A template-basedtabu search algorithm for the consistentvehicle routing problem. Expert Syst. Appl. 2012, 39, 4233–4239. [Google Scholar] [CrossRef]
- Kovacs, A.A.; Golden, B.L.; Hartl, R.F.; Parragh, S.N. The generalized consistent vehicle routing problem. Transp. Sci. 2015, 49, 796–816. [Google Scholar] [CrossRef]
- Xu, Z.; Cai, Y. Variable neighborhood search for consistent vehicle routing problem. Expert Syst. Appl. 2018, 113, 66–76. [Google Scholar] [CrossRef]
- Goeke, D.; Roberti, R.; Schneider, M. Exact and heuristic solution of the consistent vehicle-routing problem. Transp. Sci. 2019, 53, 1023–1042. [Google Scholar] [CrossRef]
- Rodríguez-Martín, I.; Salazar-González, J.J.; Yaman, H. The periodic vehicle routing problem with driver consistency. Eur. J. Oper. Res. 2019, 273, 575–584. [Google Scholar] [CrossRef]
- Stavropoulou, F.; Repoussis, P.P.; Tarantilis, C.D. The vehicle routing problem with profits and consistency constraints. Eur. J. Oper. Res. 2019, 274, 340–356. [Google Scholar] [CrossRef]
- Lespay, H.; Suchan, K. A case study of consistent vehicle routing problem with time windows. Int. Trans. Oper. Res. 2021, 28, 1135–1163. [Google Scholar] [CrossRef]
- Campelo, P.; Neves-Moreira, F.; Amorim, P.; Almada-Lobo, B. Consistent vehicle routing problem with service level agreements: A case study in the pharmaceutical distribution sector. Eur. J. Oper. Res. 2019, 273, 131–145. [Google Scholar] [CrossRef]
- Kulachenko, I.N.; Kononova, P.A. A Hybrid Local Search Algorithm for the Consistent Periodic Vehicle Routing Problem. J. Appl. Ind. Math. 2020, 14, 340–352. [Google Scholar] [CrossRef]
- Mancini, S.; Gansterer, M.; Hartl, R.F. The collaborative consistent vehicle routing problem with workload balance. Eur. J. Oper. Res. 2021, 293, 955–965. [Google Scholar] [CrossRef]
- Yao, Y.; Van Woensel, T.; Veelenturf, L.P.; Mo, P. The consistent vehicle routing problem considering path consistency in a road network. Transp. Res. Part B Methodol. 2021, 153, 21–44. [Google Scholar] [CrossRef]
- Yang, M.; Ni, Y.; Song, Q. Optimizing driver consistency in the vehicle routing problem under uncertain environment. Transp. Res. Part E Logist. Transp. Rev. 2022, 164, 102785. [Google Scholar] [CrossRef]
- Nolz, P.C.; Absi, N.; Feillet, D.; Seragiotto, C. The consistent electric-Vehicle routing problem with backhauls and charging management. Eur. J. Oper. Res. 2022, 302, 700–716. [Google Scholar] [CrossRef]
- Stavropoulou, F. The Consistent Vehicle Routing Problem with heterogeneous fleet. Comput. Oper. Res. 2022, 140, 105644. [Google Scholar] [CrossRef]
- Messaoudi, B.; Oulamara, A.; Salhi, S. A decomposition approach for the periodic consistent vehicle routeing problem with an application in the cleaning sector. Int. J. Prod. Res. 2023, 61, 7727–7748. [Google Scholar] [CrossRef]
- Kulachenko, I. Decomposition strategies for solving a large-scale consistent vehicle routing problem. In Proceedings of the 2023 19th International Asian School-Seminar on Optimization Problems of Complex Systems (OPCS), Novosibirsk, Russia, 14–22 August 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 48–52. [Google Scholar]
- Ackva, C.; Ulmer, M.W. Consistent routing for local same-day delivery via microo-hubs. OR Spectr. 2024, 46, 375–409. [Google Scholar] [CrossRef]
- Yu, X.P.; Hu, Y.S.; Wu, P. The consistent vehicle routing problem considering driver equity and flexible route consistency. Comput. Ind. Eng. 2024, 187, 109803. [Google Scholar] [CrossRef]
- Alvarez, A.; Cordeau, J.F.; Jans, R. The consistent vehicle routing problem with stochastic customers and demands. Transp. Res. Part B Methodol. 2024, 186, 102968. [Google Scholar] [CrossRef]
- Wu, S.; Jin, C.; Bo, H. Exact solution of workload consistent vehicle routing problem with priority distribution and demand uncertainty. Comput. Ind. Eng. 2025, 202, 110940. [Google Scholar] [CrossRef]
- Glover, F. Tabu search—Part I. ORSA J. Comput. 1989, 1, 190–206. [Google Scholar] [CrossRef]
- Clarke, G.; Wright, J.W. Scheduling of vehicles from a central depot to a Number of delivery points. Oper. Res. 1964, 12, 568–581. [Google Scholar] [CrossRef]
- Avdoshin, S.; Beresneva, E. Constructive heuristics for Capacitated Vehicle Routing Problem: A comparative study. Proc. Inst. System. Program. RAS 2019, 31, 145–156. [Google Scholar] [CrossRef]
- Kouider, T.O.; Cherif-Khettaf, W.R.; Oulamara, A. Constructive Heuristics for Periodic Electric Vehicle Routing Problem. In Proceedings of the 7th International Conference on Operations Research and Enterprise Systems (ICORES 2018), Funchal, Portugal, 24–26 January 2018; pp. 264–271. [Google Scholar]
- Bolanos, R.; Escobar, J.; Echeverri, M. A metaheuristic algorithm for the multi-depot vehicle routing problem with heterogeneous fleet. Int. J. Ind. Eng. Comput. 2018, 9, 461–478. [Google Scholar] [CrossRef]
- Bolaños, R.; Echeverry, M.; Escobar, J. A multiobjective non-dominated sorting genetic algorithm (NSGA-II) for the Multiple Traveling Salesman Problem. Decis. Sci. Lett. 2015, 4, 559–568. [Google Scholar] [CrossRef]
- Camilo-Velandia, R.; Alvarez-Martinez, D.; Escobar, J.W. A metaheuristic algorithm based on Ant Colony Based approach for the assigning tasks problem to a workforce with different skills. Decis. Sci. Lett. 2024, 13, 729–740. [Google Scholar] [CrossRef]
- Escobar-Falcón, L.; Alvarez-Martinez, D.; Wilmer-Escobar, J.; Granada-Echeverri, M. A specialized genetic algorithm for the fuel consumption heterogeneous fleet vehicle routing problem with bidimensional packing constraints. Int. J. Ind. Eng. Comput. 2021, 12, 191–204. [Google Scholar] [CrossRef]
- Londoño, A.A.; Gonzalez, W.G.; Giraldo, O.D.M.; Willmer, J. A new matheheuristic approach based on Chu-Beasley genetic approach for the multii-depot electric vehicle routing problem. Int. J. Ind. Eng. Comput. 2023, 14, 555–570. [Google Scholar]
- Wang, H.; Yu, X.; Lu, Y. A reinforcement learning-based ranking teaching-learning-based optimization algorithm for parameters estimation of photovoltaic models. Swarm Evol. Comput. 2025, 93, 101844. [Google Scholar] [CrossRef]









| Scenario | Population Parameters | Parameters of the Subset of Feasible Solutions | |||||
|---|---|---|---|---|---|---|---|
| Variant (Heuristic) | % Feasible Solutions | Average Lower-Bound BKS | Deviation Lower-Bound BKS | Average Lower Bound | Average CPU Time [s] | ||
| TSRI—A | 0 | 97.0% | 15.2% | 10.0% | 10.3% | 23.0% | 12.94 |
| TSRI—A | 10 | 97.0% | 51.5% | 3.3% | 6.5% | 15.3% | 26.02 |
| TSRI—A | 50 | 97.0% | 60.6% | 2.0% | 4.1% | 13.9% | 119.20 |
| TSRI—P | 0 | 100.0% | 3.0% | 10.5% | 10.5% | 23.4% | 9.38 |
| TSRI—P | 10 | 100.0% | 39.4% | 4.3% | 8.3% | 16.2% | 20.18 |
| TSRI—P | 50 | 100.0% | 60.6% | 2.1% | 5.2% | 13.7% | 101.63 |
| TSRI—S | 0 | 100.0% | 3.0% | 20.7% | 14.6% | 34.1% | 10.55 |
| TSRI—S | 10 | 100.0% | 39.4% | 4.7% | 6.3% | 16.6% | 19.40 |
| TSRI—S | 50 | 100.0% | 51.5% | 2.9% | 5.1% | 14.3% | 105.96 |
| Id | Inst. | CPLEX Branch-and-Cut | TSRI—A | TSRI—P | TSRI—S | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| LB | z (BKS) | T.CPU [s] | z | T.CPU [s] | z | T.CPU [s] | z | T.CPU [s] | ||
| 6 | 20UC1 | 109.84 | 159.07 | 3600.00 | 156.50 | 211.14 | 152.62 | 214.44 | 154.94 | 208.57 |
| 8 | 20CC1 | 70.43 | 98.93 | 3600.00 | 100.39 | 216.08 | 93.52 | 208.41 | 93.52 | 182.41 |
| 9 | 20CE1 | 135.23 | 165.47 | 3600.00 | 165.50 | 225.36 | 165.07 | 182.30 | 168.62 | 185.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santana Contreras, E.; Escobar, J.W.; Linfati, R. A Heuristic Approach for Last-Mile Delivery with Consistent Considerations and Minimum Service for a Supply Chain. Mathematics 2025, 13, 1553. https://doi.org/10.3390/math13101553
Santana Contreras E, Escobar JW, Linfati R. A Heuristic Approach for Last-Mile Delivery with Consistent Considerations and Minimum Service for a Supply Chain. Mathematics. 2025; 13(10):1553. https://doi.org/10.3390/math13101553
Chicago/Turabian StyleSantana Contreras, Esteban, John Willmer Escobar, and Rodrigo Linfati. 2025. "A Heuristic Approach for Last-Mile Delivery with Consistent Considerations and Minimum Service for a Supply Chain" Mathematics 13, no. 10: 1553. https://doi.org/10.3390/math13101553
APA StyleSantana Contreras, E., Escobar, J. W., & Linfati, R. (2025). A Heuristic Approach for Last-Mile Delivery with Consistent Considerations and Minimum Service for a Supply Chain. Mathematics, 13(10), 1553. https://doi.org/10.3390/math13101553







