Formal Verification of Multi-Thread Minimax Behavior Using mCRL2 in the Connect 4

Abstract

This study focuses on the formal verification of a parallel version of the minimax algorithm using the mCRL2 modeling language, applied to the game of Connect 4. The research aims to ensure that the algorithm behaves correctly in concurrent execution environments by providing a formal model and conducting rigorous verification. The parallel version of minimax distributes computations across multiple threads, with each thread evaluating different successor states concurrently. Using mCRL2, we specify the algorithm’s behavior, generate Labeled Transition Systems (LTSs), and verify critical properties such as the absence of deadlocks, liveness, and correctness of state transitions. The formal verification process demonstrates that the proposed model accurately represents the parallel minimax algorithm and ensures its reliability by verifying properties that guarantee unique and non-redundant actions throughout the execution. The findings highlight the value of formal methods in validating the correctness of parallel artificial intelligence algorithms, laying the foundation for future optimizations that focus on performance.

1. Introduction

The minimax algorithm is a fundamental technique in artificial intelligence and game theory, widely used for decision-making in adversarial settings such as chess and tic-tac-toe [1]. It works by minimizing the possible loss in the worst case, thus allowing optimal strategies against the opponent’s best play [2]. As computational demands increase in more complex games and deeper search trees, parallel versions of the minimax algorithm have been developed to improve performance by distributing the computations across multiple processors [3].

Formal verification of algorithms, especially in concurrent and parallel systems, is crucial to ensure their correctness and reliability [4]. Errors in such systems can have significant consequences, particularly in safety-critical applications. The mCRL2 toolkit is a formal modeling language designed to specify and analyze concurrent systems and protocols [5]. It provides facilities for the accurate modeling of system behaviors and supports verification through model checking, which allows for detecting problems such as deadlocks and violations of correctness properties [6].

Despite advances in the parallelization of the minimax algorithm, there is a notable gap in the existence of formal models that accurately capture the semantics of its parallel execution for rigorous verification. Existing research often focuses on performance improvements without thoroughly addressing correctness using formal methods. Closing this gap is essential to ensure that parallel implementations of the minimax algorithm are efficient and perform correctly under all circumstances.

This study presents a formal model of a parallel version of the minimax algorithm using mCRL2. Our approach allows for a detailed specification of the algorithm’s concurrent behaviors and facilitates the formal verification of its correctness properties. We employ model checking to verify that the parallel algorithm conforms to the expected results and is free of concurrency-induced errors. Our findings demonstrate that the formal model effectively represents the parallel minimax algorithm and that formal verification is a valuable tool to ensure its reliability.

The research’s innovation lies in applying formal methods, specifically mCRL2, to model and verify a parallel minimax algorithm in the context of Connect 4. While the use of concurrent process algebra, such as mCRL2, may not be entirely new in a global context, it is a field that is currently gaining traction in Colombia. This positions the research as a contribution to the local academic and technological landscape, where such formal methods are still in the early stages of exploration. By addressing the challenges of concurrency in AI algorithms—particularly in a game-theoretic setting—this research represents a step in advancing this field within the local context.

The comprehensive verification process, which includes properties like deadlock freedom, liveness, and correctness of state transitions, highlights an approach to ensuring the reliability of parallel minimax implementations. Moreover, this research improves the reliability of parallel minimax algorithms by providing unique and non-redundant evaluations during concurrent execution. This addresses practical challenges like duplicated computations or stale state analysis. This focus on correctness before performance optimization strengthens the foundation for future advancements.

Due to its nature, Connect 4 is especially useful as a teaching strategy to promote students’ computational thinking development. This game has been taken as an alternative to exploring the behavior of parallel algorithms. Due to the nature of the game and the implementation of the Minimax algorithm, resource competition situations are not presented, and the research is relevant in the sense of being applied in real scenarios where the game is used to motivate the development of computational thinking in educational environments.

Given the nature of our research versus formal verification with the mCRL2 toolset, prior knowledge about the mCRL2 toolset is highly suggested, whose official information is available at https://mcrl2.org/web/index.html (accessed on 21 June 2024).

2. Related Works

The literature has widely explored the formalization and verification of concurrent and distributed algorithms using mCRL2. Groote and Mousavi [5] introduce mCRL2 as a modeling language to describe and verify complex communicating computational systems, providing a solid foundation for its application in diverse domains.

Mathijssen [7] presents the specification and verification of an automated parking system using mCRL2, demonstrating the language’s capability to simultaneously model systems with multiple interacting components. Similarly, Mazzanti et al. [8] perform experiments on the formal modeling and verification of a deadlock avoidance algorithm for a CBTC system, using mCRL2 among other formal frameworks, highlighting its flexibility for analyzing critical algorithms in transportation systems.

In the software domain, van Beek and van den Brand [9] introduce a modular verification technique using mCRL2 to analyze the behavior of software product lines, addressing complexity in systems with variability. Later, van Beek et al. [10] present a family-based verification approach with mCRL2, allowing efficient analysis of software product lines by model checking.

Hojjat et al. [11] address the transformation and mapping of models to mCRL2. They describe a formal approach for design verification in SystemC by mapping it to the mCRL2 process algebra, facilitating the formal analysis of systems described in hardware and software design languages. Likewise, Kokash et al. [12,13] present a mapping from Reo to mCRL2 to enable the verification of service compositions and data flow modeling in service-oriented systems.

Oortwijn and Wijs [14] propose abstraction techniques for the automated verification of concurrent programs using message passing in concurrency and interprocess communication. They combine deductive and algorithmic verification to reason about concurrency. This approach is relevant for parallel algorithms, such as the parallel version of minimax.

Stappers [15] discusses techniques for transforming formal models, including mCRL2 models, to enable algorithm verification, which is relevant to our work on formalizing and verifying the minimax algorithm in its parallel version.

In this context, our work focuses on modeling and formally verifying a parallel version of the minimax algorithm using mCRL2. By addressing the challenges associated with concurrency and synchronization in artificial intelligence algorithms applied in competitive environments, we contribute to the existing literature.

3. Materials and Methods

3.1. mCRL2

The mCRL2 language was the primary tool used in this research. It is a formal language that allows the specification and analysis of concurrent systems. Its ability to model and verify systems using temporal logic makes mCRL2 an appropriate tool for analyzing the correctness and consistency of behaviors in complex systems. mCRL2 describes actions and transitions within a system and validates that the system complies with specific fundamental properties (absence of blockages, safety, and coherence, among others).

3.2. Labeled Transition Systems (LTSs)

A Labeled Transition System (LTS) is a graphical and formal representation of a system’s possible states and transitions. The nodes of the LTS represent the system’s different states, while the transitions between nodes show how the system progresses from one state to another. This representation allows the visualization and analysis of the system’s behavior in each state and validates that it complies with the defined properties.

3.3. Formal Specification Process

The formal specification of a system involves a detailed description of its behavior using algebraic equations and mathematical models. This process is divided into the following phases:

System modeling: The system’s behavior is defined using equations that describe how its state changes in response to actions or events. This mathematical description allows for an accurate understanding of how the system works.

Definition of Properties: In this phase, the fundamental properties that the system must satisfy are defined. These include the absence of deadlocks, the ability to reach terminal states (Liveness), ensuring no incorrect states are possible (Safety), and maintaining coherence in the growth of states (Successor Generation). These properties are expressed using mu-calculus.

Formal verification: Once the system has been specified and the properties defined, these properties are formally verified using mCRL2. The tool generates the Labeled Transition System (LTS), which allows for visual and mathematical verification of whether the system complies with the defined properties. Any violation of these properties can be identified at this stage, allowing adjustments or corrections to be made to the model.

3.4. Property Verification

The verification process checks that the system meets the properties formulated above. This includes checking the following:

No deadlocks: Ensures that the system is never stuck in a state from which it cannot move forward, which is critical to ensure the continued operation of the system.

Liveness: It verifies that a terminal state is unverifiably reachable during execution.

Safety is maintained: It verifies that the actions defined for the system are not repeated unnecessarily or at inappropriate times, ensuring that decisions within the system are unique and not redundant.

Consistency is maintained: By validating that the number of states generated at each depth level does not exceed the expected limit, thereby ensuring the system avoids generating unnecessary transitions or states.

3.5. Code and Model Availability

All models, codes, and scripts used to specify and verify the system will be available in a public repository, allowing other researchers to replicate and build upon the results presented. This repository can be found at https://github.com/difer19/Connect-4-mCRL2-Model (accessed on 21 June 2024).

3.6. Hardware Used

The model was run on a computer system with an AMD Ryzen 7 9700X processor, four cores, and 32 GB of RAM.

4. Results

4.1. Multi-Thread Minimax

Parallel algorithms provide significant advantages. “The parallel algorithms improve execution times by redistributing operations between processes and reducing interprocessor data exchange time” [16]. This approach is particularly advantageous for computationally intensive problems, where optimizing resource utilization can lead to substantial performance gains.

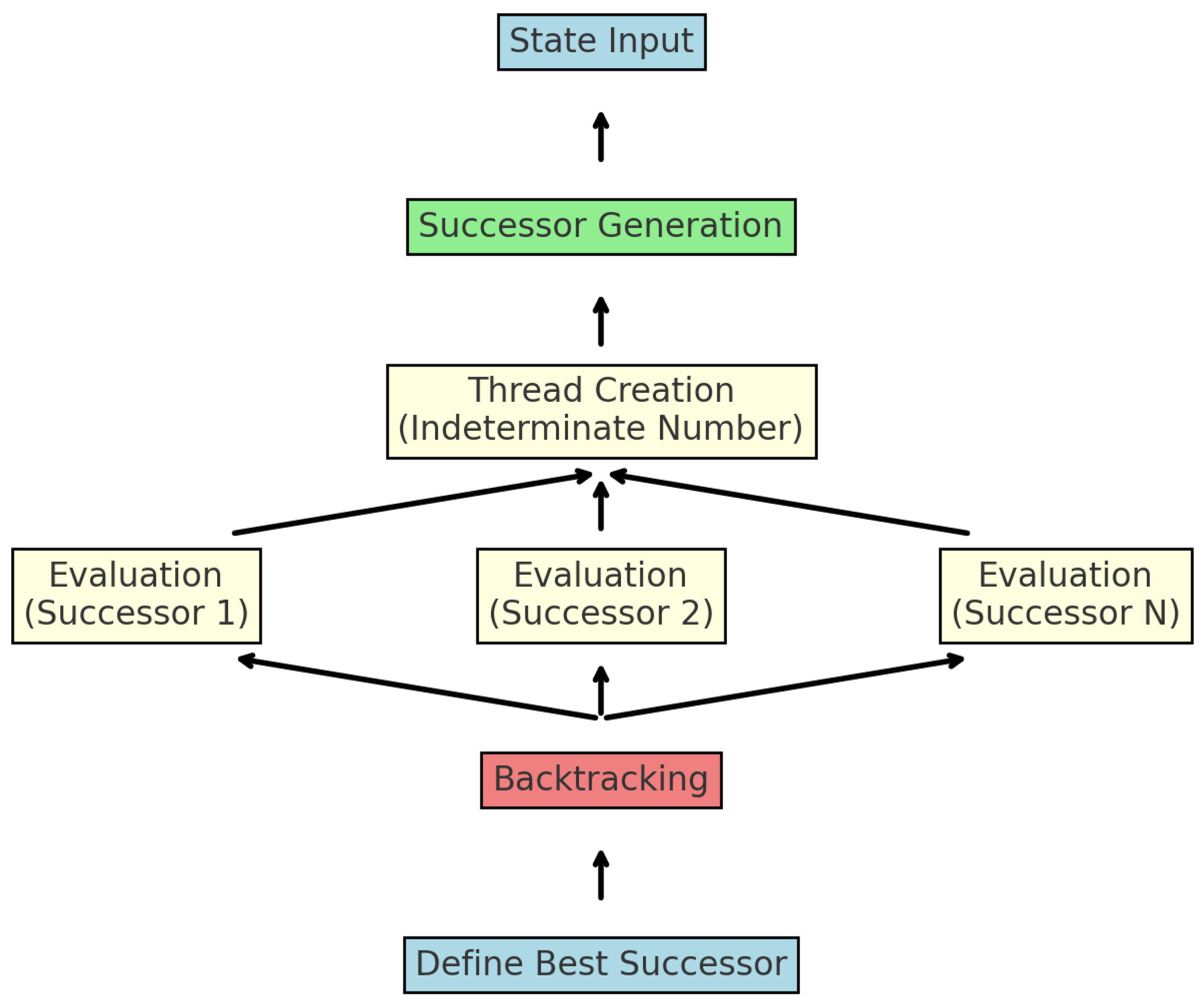
In this context, the minimax algorithm, widely used in artificial intelligence for two-player games, evaluates all possible future moves to determine the optimal move. Traditionally, this process is sequential and can become computationally expensive as the search depth and the number of possible states grow exponentially. Parallelization of the algorithm aims to reduce the computation time by taking advantage of available hardware resources, such as processing cores in a multi-core CPU. To address the parallelization of the minimax algorithm simply, both in terms of implementation and to be able to formalize the behavior, we propose to generate a thread for each of the immediate successor states of the current game state. Each thread executes the minimax algorithm independently to evaluate the value of the corresponding successor state. Once all threads have completed their execution, the results are collected, and the algorithm selects the best move based on the evaluations obtained in the backtracking process. This behavior can be observed in the following Figure 1.

This behavior is expressed by the following algorithms expressed in pseudocode for the maxValue (see Algorithm 1), minvalue (see Algorithm 2), and parallel minimax (see Algorithm 3) functions:

Algorithm 1 Max-value function

function MaxValue(state, currentDepth, maxDepth)     if $state.isFinal\left(\right)$ or $currentDepth>maxDepth$ then         return $state.value$     end if     $best\leftarrow -\infty$     for each successor in state.generateSuccessors(“X”) do           $best\leftarrow max(best,\mathrm{MinValue}(successor,currentDepth+1,maxDepth\left)\right)$     end for     return $best$ end function

Algorithm 2 Min-value function

function MinValue(state, currentDepth, maxDepth)     if $state.isFinal\left(\right)$ or $currentDepth>maxDepth$ then         return $state.value$     end if     $best\leftarrow \infty$     for each successor in state.generateSuccessors(“O”) do           $best\leftarrow min(best,\mathrm{MaxValue}(successor,currentDepth+1,maxDepth\left)\right)$     end for     return $best$ end function

Algorithm 3 Parallel MinMax function

Require: A state, $type\in \{“\max ”,“\min ”\}$

Ensure: The best or worst successor state based on the given type

function ParallelMinMax(state, type)     Initialize a pool of workers     $results\leftarrow \left[\right]$     $successors\leftarrow \mathrm{generateSuccessors}\left(\mathrm{state}\right)$     for each successor in successors do         if $type=“\max ”$ then              Add the result of evaluating MinValue(successor) to $results$         else if $type=“\min ”$ then              Add the result of evaluating MaxValue(successor) to $results$         end if     end for     Wait for all workers to finish     if $type=“\max ”$ then          $best\_value\leftarrow -\infty$          $best\_state\leftarrow \mathrm{None}$          for each result in results do                $value\leftarrow \mathrm{getResult}\left(\mathrm{result}\right)$                if $value>best\_value$ then                    $best\_value\leftarrow value$                    $best\_state\leftarrow \mathrm{corresponding}\mathrm{successor}$            end if         end for         return $best\_state$     else if $type=“\min ”$ then          $worst\_value\leftarrow \infty$          $worst\_state\leftarrow \mathrm{None}$          for each result in results do                $value\leftarrow \mathrm{getResult}\left(\mathrm{result}\right)$                if $value<worst\_value$ then                     $worst\_value\leftarrow value$                     $worst\_state\leftarrow \mathrm{corresponding}\mathrm{successor}$            end if         end for         return $worst\_state$     end if end function

4.2. Specifying Behavior Using mCRL2

We will use Connect 4 to represent the game state for the behavior specification because it represents a relatively simple behavior. Unlike more complex games, such as chess or Go, the rules of Connect 4 are straightforward, and the possible actions in each turn are delimited, facilitating the construction and understanding of the state model. This simplicity allows us to focus on implementing and evaluating the minimax algorithm without the complexity of the game interfering with our understanding of the process.

Furthermore, the Connect 4 game tree size is relatively small compared to other strategy games. Although the number of possible states in the game tree is still considerable, it is manageable enough to allow for the broadest exploration of potential moves to a reasonable depth. This is particularly important for representation, LTS generation, and property checking.

4.3. Data Representation Model

4.3.1. Turn Data Specification

A turn is an indicator that determines which player should make the next move in the game. It also represents an individual square on the game board and contains information about who occupies that square at a given position. It may be occupied by one of the players (X or O) or empty. To represent this information, we will use the struct keyword, which allows us to define a structured data type. The turn data type is defined as follows:

$$\begin{array}{cc}\hfill & \mathbf{sort}turn=void?isVoid|X?isX|O?isO;\hfill \\ \hfill & \mathbf{map}next:turn\to turn;\hfill \\ \hfill & \mathbf{eqn}next\left(X\right)=O;\hfill \\ \hfill & \mathbf{eqn}next\left(O\right)=X;\hfill \end{array}$$

In addition, recognizer functions are defined, which help determine whether data correspond to one of the specified values. Also, a function called next is defined to identify the next turn from the current turn.

4.3.2. Specification of Position Data

A position is the current state of the game board, which can be represented as follows:

$$\begin{array}{cc}\hfill & \mathbf{sort}position=List\left(List\right(token\left)\right);\hfill \end{array}$$

To manage the board’s behavior, functions are defined that allow information to be obtained from the board. In this case, we have functions to retrieve constants, such as the number of rows and columns, the maximum depth parameter arbitrarily defined for the specification, and the initial configuration of the board:

$$\begin{array}{cc}\hfill \mathbf{map}& Rows:\mathbb{N};\hfill \\ \hfill & Columns:\mathbb{N};\hfill \\ \hfill & initBoard:Position;\hfill \\ \hfill & maxDepth:\mathbb{N};\hfill \\ \hfill \mathbf{eqn}& \\ \hfill & Rows=6;\hfill \\ \hfill & Columns=7;\hfill \\ \hfill & maxDepth=4;\hfill \\ \hfill & initBoard=[\hfill \\ \hfill & [void,void,void,void,void,void,void],\hfill \\ \hfill & [void,void,void,void,void,void,void],\hfill \\ \hfill & [void,void,void,void,void,void,void],\hfill \\ \hfill & [void,void,void,void,void,void,void],\hfill \\ \hfill & [void,void,void,void,void,void,void],\hfill \\ \hfill & [void,void,void,void,void,void,void]\hfill \\ \hfill & ];\hfill \end{array}$$

Additionally, it is essential to establish specific functions for extracting information about a given state. This includes determining whether a specific position is a winning setup for a particular player. It is also crucial to identify whether a state represents a terminal condition of the game and obtain data from a specific column on the board. In addition, it must be possible to determine what the next empty position is in a given column if one exists:

$$\begin{array}{cc}\hfill \mathbf{map}& isWinner:Position\times Token\to \mathbb{B};\hfill \\ \hfill & isFinal:Position\to \mathbb{B};\hfill \\ \hfill & getCol:Board\times \mathbb{N}\to List\left(Token\right);\hfill \\ \hfill & getRowValue:List\left(Token\right)\to \mathbb{N};\hfill \\ \\ \hfill \mathbf{eqn}& isWinner(b,m)=\hfill \\ \hfill & (\exists row:\mathbb{N}.(row<Rows\wedge \hfill \\ \hfill & \left(\right(b.row.0\approx m\wedge b.row.1\approx m\wedge b.row.2\approx m\wedge b.row.3\approx m)\vee \hfill \\ \hfill & (b.row.1\approx m\wedge b.row.2\approx m\wedge b.row.3\approx m\wedge b.row.4\approx m)\vee \hfill \\ \hfill & (b.row.2\approx m\wedge b.row.3\approx m\wedge b.row.4\approx m\wedge b.row.5\approx m)\vee \hfill \\ \hfill & (b.row.3\approx m\wedge b.row.4\approx m\wedge b.row.5\approx m\wedge b.row.6\approx m)\left)\right))\vee \hfill \\ \hfill & (\exists col:\mathbb{N}.(col<Columns\wedge \hfill \\ \hfill & \left(\right(b.0.col\approx m\wedge b.1.col\approx m\wedge b.2.col\approx m\wedge b.3.col\approx m)\vee \hfill \\ \hfill & (b.1.col\approx m\wedge b.2.col\approx m\wedge b.3.col\approx m\wedge b.4.col\approx m)\vee \hfill \\ \hfill & (b.2.col\approx m\wedge b.3.col\approx m\wedge b.4.col\approx m\wedge b.5.col\approx m)\left)\right))\vee \hfill \\ \hfill & (b.0.0\approx m\wedge b.1.1\approx m\wedge b.2.2\approx m\wedge b.3.3\approx m)\vee \hfill \\ \hfill & (b.0.1\approx m\wedge b.1.2\approx m\wedge b.2.3\approx m\wedge b.3.4\approx m)\vee \hfill \\ \hfill & (b.0.2\approx m\wedge b.1.3\approx m\wedge b.2.4\approx m\wedge b.3.5\approx m)\vee \hfill \\ \hfill & (b.0.3\approx m\wedge b.1.4\approx m\wedge b.2.5\approx m\wedge b.3.6\approx m)\vee \hfill \\ \hfill & (b.1.0\approx m\wedge b.2.1\approx m\wedge b.3.2\approx m\wedge b.4.3\approx m)\vee \hfill \\ \hfill & (b.1.1\approx m\wedge b.2.2\approx m\wedge b.3.3\approx m\wedge b.4.4\approx m)\vee \hfill \\ \hfill & (b.1.2\approx m\wedge b.2.3\approx m\wedge b.3.4\approx m\wedge b.4.5\approx m)\vee \hfill \\ \hfill & (b.1.3\approx m\wedge b.2.4\approx m\wedge b.3.5\approx m\wedge b.4.6\approx m)\vee \hfill \\ \hfill & (b.2.0\approx m\wedge b.3.1\approx m\wedge b.4.2\approx m\wedge b.5.3\approx m)\vee \hfill \\ \hfill & (b.2.1\approx m\wedge b.3.2\approx m\wedge b.4.3\approx m\wedge b.5.4\approx m)\vee \hfill \\ \hfill & (b.2.2\approx m\wedge b.3.3\approx m\wedge b.4.4\approx m\wedge b.5.5\approx m)\vee \hfill \\ \hfill & (b.2.3\approx m\wedge b.3.4\approx m\wedge b.4.5\approx m\wedge b.5.6\approx m)\vee \hfill \\ \hfill & (b.0.3\approx m\wedge b.1.2\approx m\wedge b.2.1\approx m\wedge b.3.0\approx m)\vee \hfill \\ \hfill & (b.0.4\approx m\wedge b.1.3\approx m\wedge b.2.2\approx m\wedge b.3.1\approx m)\vee \hfill \\ \hfill & (b.0.5\approx m\wedge b.1.4\approx m\wedge b.2.3\approx m\wedge b.3.2\approx m)\vee \hfill \\ \hfill & (b.0.6\approx m\wedge b.1.5\approx m\wedge b.2.4\approx m\wedge b.3.3\approx m)\vee \hfill \\ \hfill & (b.1.3\approx m\wedge b.2.2\approx m\wedge b.3.1\approx m\wedge b.4.0\approx m)\vee \hfill \\ \hfill & (b.1.4\approx m\wedge b.2.3\approx m\wedge b.3.2\approx m\wedge b.4.1\approx m)\vee \hfill \\ \hfill & (b.1.5\approx m\wedge b.2.4\approx m\wedge b.3.3\approx m\wedge b.4.2\approx m)\vee \hfill \\ \hfill & (b.1.6\approx m\wedge b.2.5\approx m\wedge b.3.4\approx m\wedge b.4.3\approx m)\vee \hfill \\ \hfill & (b.2.3\approx m\wedge b.3.2\approx m\wedge b.4.1\approx m\wedge b.5.0\approx m)\vee \hfill \\ \hfill & (b.2.4\approx m\wedge b.3.3\approx m\wedge b.4.2\approx m\wedge b.5.1\approx m)\vee \hfill \\ \hfill & (b.2.5\approx m\wedge b.3.4\approx m\wedge b.4.3\approx m\wedge b.5.2\approx m)\vee \hfill \\ \hfill & (b.2.6\approx m\wedge b.3.5\approx m\wedge b.4.4\approx m\wedge b.5.3\approx m);\hfill \end{array}$$

$$\begin{array}{cc}\hfill & isFinal\left(b\right)=isWinner(b,X)\vee isWinner(b,O)\vee \hfill \\ \hfill & \neg {\exists }_{row,column:\mathbb{N}}.(row<Rows\wedge column<Columns\wedge b.row.column\approx void)\hfill \\ \hfill & getCol(b,columnIndex)=\hfill \\ \hfill & if(columnIndex<Columns,\hfill \\ \hfill & [b.0.columnIndex,b.1.columnIndex,b.2.columnIndex,b.3.columnIndex,\hfill \\ \hfill & b.4.columnIndex,b.5.columnIndex],[\left]\right);\hfill \\ \hfill & getRowValue\left(\right[\left]\right)=8;\hfill \\ \hfill & getRowValue\left(ls\right)=if\left(rhead\right(ls)\approx null,\#ls,getRowValue(rtail\left(ls\right)\left)\right);\hfill \end{array}$$

Finally, the functions that allow changing the state of the board and, thus, the evolution of a game include a function that will enable entering a token into the board and an auxiliary function to modify a particular column.

$$\begin{array}{cc}\hfill \mathbf{map}& replaceBoard:Position\times \mathbb{N}\times \mathbb{N}\times Token\to Position;\hfill \\ \hfill & replaceColumn:List\left(Token\right)\times \mathbb{N}\times Token\to List\left(Token\right);\hfill \\ \hfill \mathbf{eqn}& \\ \hfill & replaceBoard\left(\right[],i,j,n)=\left[\right];\hfill \\ \hfill & replaceBoard(ls▹,i,j,n)=if(i\approx 0,replaceColumn(ls,j,n)▹llst,\hfill \\ \hfill & ls▹replaceBoard(llst,Int2Nat(i-1),j,n));\hfill \\ \hfill & replaceColumn\left(\right[],j,n)=\left[\right];\hfill \\ \hfill & replaceColumn(e▹ls,j,n)=if(j\approx 0,n▹ls,\hfill \\ \hfill & e▹treplaceColumn(ls,Int2Nat(j-1),n));\hfill \\ \hfill & getCol(b,columnIndex)=\hfill \\ \hfill & if(columnIndex<Columns,\hfill \\ \hfill & [b.0.columnIndex,b.1.columnIndex,b.2.columnIndex,b.3.columnIndex,\hfill \\ \hfill & b.4.columnIndex,b.5.columnIndex],[\left]\right);\hfill \end{array}$$

In these equations, the mCRL2 operator ▹ is used to add an element to the beginning of a list, in the same way that the ◃ operator is used to add an element to the end of a list.

4.4. Behavior Model of the Minimax Algorithm

The minimax algorithm is a recursive procedure whose implementation can be broken down into three main phases: game tree generation, backtracking, and successor definition. These phases are explained in detail below:

Game tree generation is the first critical step in the minimax algorithm. This process involves building a tree representing all possible positions or states of the game up to a certain depth, starting from the current position. The parallel implementation of this stage would be completed by assigning each immediate successor of the current state to a process running in parallel.

Once the game tree has been generated, the minimax algorithm evaluates the nodes using a backtracking technique. This phase involves going back to the root, assigning each node a value that represents the best utility the player can secure from that state. For the states corresponding to the turns of the max player, the maximum value is selected among the utilities of its child nodes. On the other hand, the minimum value is chosen for the nodes corresponding to the min player’s turns. This logic can become excessively complex to specify algebraically, so in the context of this research, it will be encapsulated in a single action called backtracking.

Finally, the definition of the successor represents a return action in which the best successor would be returned according to the previous process, and this behavior is defined by the defSuccessor action.

4.5. Algorithm Model

Considering the behavior described above, the algorithm initially generates a parallel process to which it assigns a valid immediate successor derived from the game’s current state. Algebraically, this operation can be represented as follows:

$$\begin{array}{cc}\hfill Process& Pool(b:Position,m:Token,depth:\mathbb{N},c:\mathbb{N},thread:\mathbb{N})=\hfill \\ \hfill & \left(voidingetCol\right(b,c)\wedge depth<maxDepth)\to \hfill \\ \hfill & Minmax\left(replaceBoard\right(b,Int2Nat\left(\right(getRowValue\left(getCol\right(b,c\left)\right))-1),c,m),\hfill \\ \hfill & next\left(m\right),Int2Nat(depth+1),thread)\hfill \end{array}$$

The Minmax process represents the primary process in the algorithm’s execution. It includes invoking the procedure responsible for generating the successors from the current state. It also directs the transition to a successor state, selecting between a max or min state, depending on the player’s turn. Finally, the Minmax process also determines the moment to stop the generation of new successors, taking the depth condition as a reference.

$$\begin{array}{cc}\hfill Minmax& (b:List(Position),m:Token,depth:\mathbb{N},thread:\mathbb{N})=\hfill \\ \hfill & (depth\le maxDepth)\to \hfill \\ \hfill & (m\approx X)\to max(\#b,depth,thread,m)\hfill \\ \hfill & ·defSuc(b,0,0,[],next(m),Int2Nat(depth+1),thread)\hfill \\ \hfill & <>min(\#b,depth,thread,m)\hfill \\ \hfill & ·defSuc(b,0,0,[],next(m),Int2Nat(depth+1),thread)\hfill \\ \hfill & <>backtracking·defSuccessor·\delta \hfill \end{array}$$

Each level must carry the reference of all the successors corresponding to that level, and this is done by generating the list of successors for each of the states of the current level; this task is performed by the regList function, which is defined as follows:

$$\begin{array}{cc}\hfill & \mathbf{map}regList:List\left(Position\right)\times \mathbb{N}\times \mathbb{N}\times List\left(Position\right)\times Token\to List\left(Position\right);\hfill \\ \hfill & \mathbf{eqn}regList(lp,i,j,nl,m)=\hfill \\ \hfill & if(i\approx \#lp,nl,if(j<Columns,regList(lp,i,Int2Nat(j+1),\hfill \\ \hfill & nl◃replaceBoard(lp.i,Int2Nat(\left(getRowValue\right(getCol(lp.i,j)\left)\right)-1),j,m),m),\hfill \\ \hfill & regList(lp,Int2Nat(i+1),0,nl,m)\left)\right);\hfill \end{array}$$

This function, the defSuccessor process, sends the new list of successors to the primary process.

$$\begin{array}{cc}\hfill defSuc& (b:List(Position),i:\mathbb{N},j:\mathbb{N},nl:List(Position),m:Token,depth:\mathbb{N},thread:\mathbb{N})=\hfill \\ \hfill & Minmax\left(regList\right(b,i,j,nl,m),m,depth,thread)\hfill \end{array}$$

4.6. Model Restrictions

For a correct representation, the allow operator will be used to prevent the defSuccessor and backtracking actions that do not correspond to a multi-action appearing. This is done because the definition of successors is an action that must necessarily occur at the end. The communication operator will also be used to join the multi-actions. In addition, to reduce the model’s size, only the individual max and min actions and the parallel ones corresponding to the number of processes will be allowed. While it would be possible to have other types of processes, such as 4 min actions running simultaneously, these were deliberately blocked to prevent the model from growing excessively in the representation, which would cause issues when generating the LTS and verifying the properties. Finally, parallelism is implemented in the model, considering that given a state, it will have a maximum of seven successors.

$$\begin{array}{cc}\hfill & {\nabla }_{\{backtrackingParallel,defSucccessorGen,max,min,max|...|max,min|...\left|min\right\}}(\hfill \\ \hfill & {\Gamma }_{\left\{backtracking\right|...|backtracking\to backtrackingParallel,defSuccessor|...|defSuccessor\to defSucccessorGen\}}\hfill \\ \hfill & \left(processPool\right(initPosition,X,0,0,1\left)\right|\left|processPool\right(initPosition,X,0,1,2\left)\right||\hfill \\ \hfill & processPool(initPosition,X,0,2,3)\left|\right|processPool(initPosition,X,0,3,4)\left|\right|\hfill \\ \hfill & processPool(initPosition,X,0,4,5)\left|\right|processPool(initPosition,X,0,5,6)\left|\right|\hfill \\ \hfill & processPool(initPosition,X,0,6,7)\left)\right)\hfill \end{array}$$

Each call to the processPool operation represents each process executed according to the initial branches in the game tree.

4.7. Definition of Properties

4.7.1. Absence of Deadlocks

This property states that after any sequence of actions that does not contain defSuccessorGen, it is possible to execute another action; the following formula is intended to specify such a property. In this work, the following formalization is called “Deadlocks”:

$$\begin{array}{c}\hfill [\overline{defSuccessorGen}\ast ]\langle true\rangle true\end{array}$$

This property is intended to reflect a way of ensuring that an action can be performed in any state, which means that the behavior is not deadlocked.

4.7.2. Liveness

This property states that after executing a max or min action, as well as any multi-action composition of these, in a finite number of transitions, the defSuccessorGen action must inevitably occur. This condition is expressed by the formula, which in this article is called “Liveness”:

$$\begin{array}{cc}\hfill & {\forall }_{x,y,z:\mathbb{N},m:Token}\hfill \\ \hfill & \left[max\right(x,y,z,m)\cup min(x,y,z,m)\cup \hfill \\ \hfill & max(x,y,z,m)\left|max\right(x,y,z,m\left)\right|max(x,y,z,m)\left|max\right(x,y,z,m\left)\right|max(x,y,z,m)\hfill \\ & \left|max\right(x,y,z,m\left)\right|max(x,y,z,m)\cup \hfill \\ \hfill & min(x,y,z,m)\left|min\right(x,y,z,m\left)\right|min(x,y,z,m)\left|min\right(x,y,z,m\left)\right|min(x,y,z,m)\hfill \\ & \left|min\right(x,y,z,m\left)\right|min(x,y,z,m)]\hfill \\ \hfill & \mu X.\left[\overline{defSuccessorGen}\right]X\wedge \langle true\rangle true\hfill \end{array}$$

This expression defines a liveness condition, ensuring that the defSuccessorGen action must unavoidably occur within a finite number of steps, as stated by the formula. This guarantees that, regardless of the current state or the sequence of prior actions, the system will inevitably reach a point where this action is performed. In other words, after executing a single min/max step, the defSuccessorGen action is not merely possible or reachable—it is guaranteed to occur.

4.7.3. Safety

This property indicates that once a min or max action has been executed, associated with a specific process number and a certain depth. This action cannot be repeated in the future. In this paper, the following formalization is called “safety 1”. The formalization of this condition is detailed for the max action in the formula:

$$\begin{array}{cc}\hfill & [true\ast ]{\forall }_{x,y,z:\mathbb{N},m:Token}\left[max(x,y,z,m)\right]\hfill \\ & \mu Y.{\forall }_{x_2,:\mathbb{N},m_2:Token}.\langle \overline{max(x_2,y,z,m_2)}\rangle Y\vee \langle defSuccessorGen\rangle true\hfill \end{array}$$

In this paper, the following formalization is called “safety 2”. For the min action:

$$\begin{array}{cc}\hfill & [true\ast ]{\forall }_{x,y,z:\mathbb{N},m:Token}\left[min(x,y,z,m)\right]\hfill \\ & \mu Y.{\forall }_{x_2,:\mathbb{N},m_2:Token}.\langle \overline{min(x_2,y,z,m_2)}\rangle Y\vee \langle defSuccessorGen\rangle true\hfill \end{array}$$

In this paper, the following formalization is called “safety 3”, and for max multi-action:

$$\begin{array}{cc}\hfill & [true\ast ]{\forall }_{x,y,z:\mathbb{N},m:Token}\left[max(x,y,z,m)\right|...\left|max(x,y,z,m)\right]\hfill \\ & \mu Y.{\forall }_{x_2,:\mathbb{N},m_2:Token}.\langle \overline{max(x_2,y,z,m_2)|...|max(x_2,y,z,m_2)}\rangle Y\vee \langle defSuccessorGen\rangle true\hfill \end{array}$$

In this paper, the following formalization is called “safety 4”, and for the min multi-action:

$$\begin{array}{cc}\hfill & [true\ast ]{\forall }_{x,y,z:\mathbb{N},m:Token}\left[min(x,y,z,m)\right]|...|\left[min(x,y,z,m)\right]\hfill \\ & \mu Y.{\forall }_{x_2,:\mathbb{N},m_2:Token}.\langle \overline{min(x_2,y,z,m_2)|...|\left[min(x_2,y,z,m_2)\right]}\rangle Y\vee \langle defSuccessorGen\rangle true\hfill \end{array}$$

This statement establishes a safety constraint, ensuring that min or max actions, once performed under specific conditions linked to a particular process number and depth, are excluded from happening again. This property underlines the uniqueness and non-repetition of certain actions within the system once executed in a specific context. In other words, at any point, after performing max(x,y,z,m) or min(x,y,z,m), there is a trace consisting of different actions ending in defSuccessorGen.

4.7.4. Coherence in the Growth of States

A specific expression can approximate the increase in the number of states up to a certain depth in Connect 4.

$$\begin{array}{cc}\hfill & N_s\left(n\right)=\sum _{i=0}^n\left(7^n\right)\hfill \end{array}$$

Based on this approximation, the property in question states that, at a depth level n, the number of possible states cannot exceed the value determined by this expression. The corresponding formula formalizes and specifies this in detail. In this paper, the following formalization is called “Successor Generation”:

$$\begin{array}{cc}\hfill & [true\ast ]{\forall }_{x,y,z:\mathbb{N},m:Token}\hfill \\ \hfill & .[max(x,y,z,m)\cup min(x,y,z,m)](x\le 7^{y-1})\hfill \end{array}$$

This statement imposes an upper bound on the number of successor states that can arise at a given depth in the Connect 4 game tree, ensuring that the tree’s growth remains consistent within the parameters predicted by the expression.

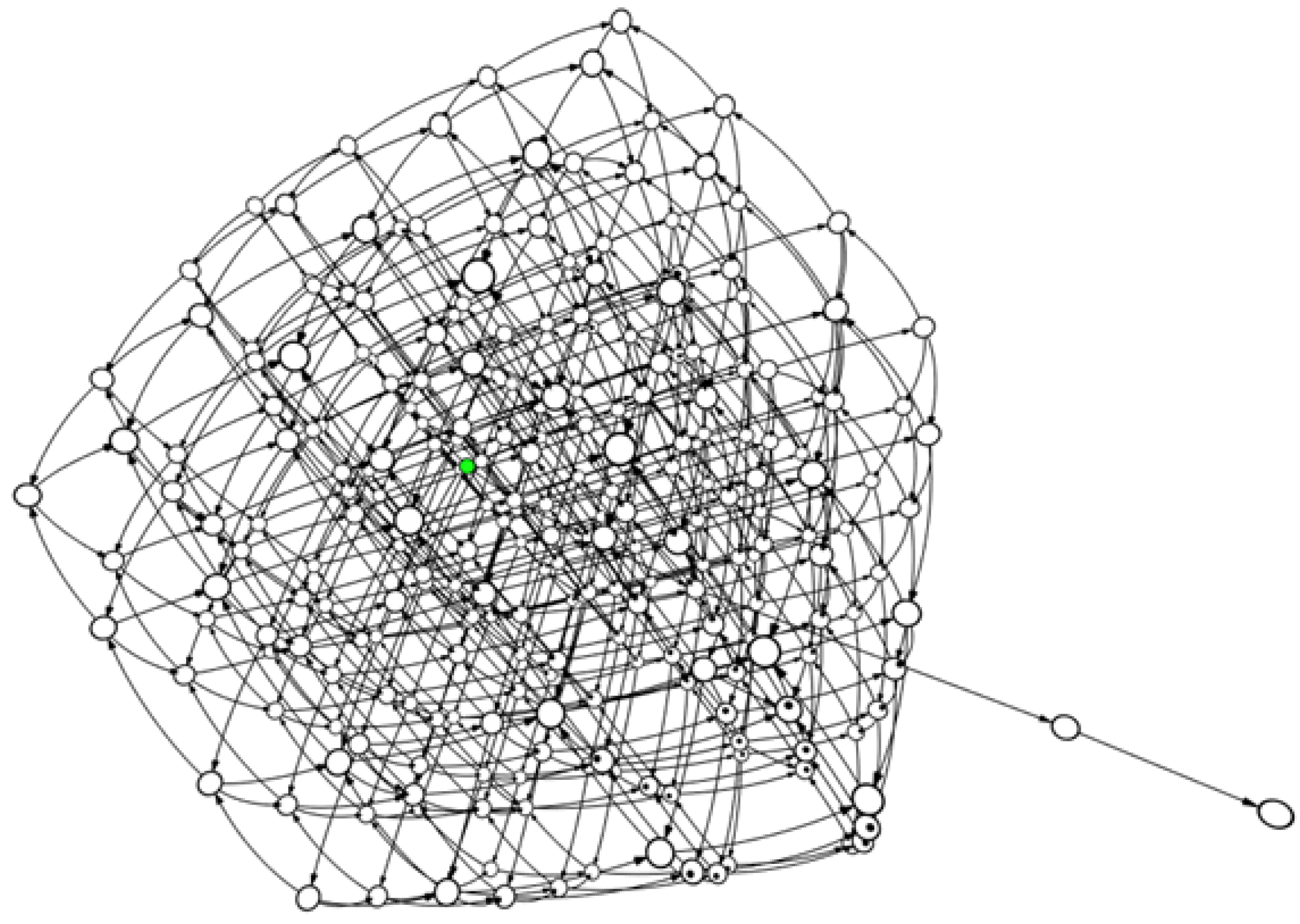
4.8. LTS of the Algorithm’s Behavior

The representation of the algorithm in a Labeled Transition System (LTS) was performed using four running processes and exploring up to three levels of depth. While it is technically possible to represent all the processes, doing so generates an excessively complex structure that is difficult to visualize. As the number of processes and the depth of analysis increases, the network expands exponentially, complicating the interpretation of states and transitions. For this reason, it was decided to limit the representation to a manageable number of processes and levels, which allows for a better understanding without sacrificing the essence of the system’s behavior, Figure 2 shows the partial LTS generated given the conditions mentioned above.

4.9. Property Verification Results

Property verification in the model involves several steps to ensure that the specified properties of the system are met; the process is shown below.

4.9.1. Obtaining LPS and LTS

Using the specification defined in the .mcrl2 file, the mcrl22lps tool is used to generate an .lps file, which provides a linear representation of the process. This step can be resource-intensive and time-consuming, so it is important to limit the maximum depth within the specification. To do this, the maxDepth value located on line 39 of the .mcrl2 file in the repository must be adjusted.

Once the .lps file is generated, the lps2lts tool is used to produce the .lts file. This file represents the labeled transition system derived from the linear process.

4.9.2. Generation of PBES

Using the .lts file and a modal formula, a parameterized Boolean equation system (PBES) is generated. The solution of this system determines whether the formula is satisfied. While it is possible to generate a PBES directly from the .lps file using the lps2pbes tool, this research opted to use the .lts file instead. This approach significantly reduced both the generation and solution time. For this purpose, the lts2pbes tool was utilized. This process is repeated for each formula proposed in the investigation.

4.9.3. Solution of PBES

Finally, using the .pbes file, the pbes2bool tool or other available tools in mCRL2, such as pbessolve, are used to determine whether the property is satisfied in the system. The result is presented as true if the property is satisfied or false otherwise.

The verification is performed using the proposed properties for the model, evaluating depths ranging from 1 to 7. The results of the specification property verification are presented below in

Table 1. Table of properties with depths 1 to 7.

Property	Depth 1	Depth 2	Depth 3	Depth 4	Depth 5	Depth 6	Depth 7
Deadlocks	true	true	true	true	true	true	true
Liveness	true	true	true	true	true	true	true
safety 1	true	true	true	true	true	true	true
safety 2	true	true	true	true	true	true	true
safety 3	true	true	true	true	true	true	true
safety 4	true	true	true	true	true	true	true
Successor Generation	true	true	true	true	true	true	true

.

5. Discussion

The central purpose of this research is to validate the correct behavior of the minimax algorithm in its formal implementation using mCRL2, a specialized language for the specification and verification of concurrent systems. The focus was to ensure that the algorithm, applied to the Connect 4 game, complies with critical properties, such as the absence of deadlocks, liveness, safety, and consistency in the growth of states within the game tree.

Specifying the algorithm’s behavior in a labeled transition model (LTS) allowed its operation to be decomposed into formal, verifiable actions. Throughout the model’s development, the minimax algorithm’s critical phases were implemented: game tree generation, backtracking, and optimal successor selection. This approach clearly represented each stage of the process, ensuring that successors were generated correctly at each level of the game and that the algorithm could determine the best move from the successor states.

One of the most relevant aspects of this research was the formal definition of the system’s properties. Verifying properties such as the absence of deadlocks ensured that there was always the possibility of performing a valid action in any state of the game. This is essential since, in complex concurrent systems, it is common for processes to become blocked if the interactions between them are not adequately managed. The validity of this property ensures that regardless of the game’s configuration at any given time, the system can continually advance to a successor state.

On the other hand, the liveness property is critical to ensuring that the algorithm is not only deadlock-free but also always reaches the state where the defSuccessorGen action can be executed. This implies that as the min or max actions are executed, a state will eventually be reached where the successor can be defined, ensuring that the system does not get caught in meaningless action loops.

Furthermore, the model’s safety was verified through the restrictions imposed on the min and max actions, which guarantee that they cannot be repeated once these actions have been executed under specific conditions (e.g., a certain number of processes and depth level). This verification ensures that the algorithm makes unique decisions and that there is no possibility of repeating the same action, which would be logically incorrect.

Another property verified was the consistency of state growth. This is particularly important in games like Connect 4, where the number of possible states increases with the depth of the game tree. Using a formal expression, it was verified that the number of states at each tree level does not exceed the expected value, ensuring that the tree’s growth is controlled and that the system does not generate more states than it should.

Regarding the formal implementation, using mCRL2 allowed the various actions and transitions of the minimax algorithm to be represented algebraically. The model’s structure faithfully reflected the algorithm’s expected behavior, ensuring that each action was executed at the right time and under the right conditions. In addition, the constraints implemented in the model (such as the allow operator to prevent incorrect actions) added a level of robustness, preventing the system from performing actions out of order or compromising the validity of the execution.

The model also correctly integrated the handling of successors at each level of the game tree. The regList function, responsible for generating the list of successors for each state, was crucial to ensure that the algorithm always had the right successors available for each level of the game. This function was also formally validated to ensure that it generated the correct successors, and these were adequately transmitted to the primary process via the defSuccessor action.

Finally, although not directly addressed in this research, it is essential to mention that the correct specification and verification of the behavior of the minimax algorithm constitute a solid foundation for future implementations that could benefit from parallelization. However, before addressing performance, priority was given to ensuring that the model’s behavior was correct and consistent in all critical aspects.

6. Conclusions

From the development and formal verification of the behavior of the minimax algorithm, the following key conclusions can be drawn:

Successful validation of algorithm behavior: The implementation of the minimax algorithm in mCRL2, applied to the Connect 4 game, was successfully validated, ensuring that the system meets critical properties such as the absence of deadlocks, liveness, and safety. This validation is essential to ensure that the algorithm makes correct decisions at each step of the search and backtracking process and that these decisions are unique and non-redundant.

Consistency in-state generation and evaluation: The representation of the game tree and the generation of successors were controlled and consistent, preventing the growth of the game tree from going beyond the expected parameters. This ensures that the number of states generated is manageable and suitable for the context of the game, ensuring the feasibility of the implementation.

Robust formal specification: Using mCRL2 to formally specify the behavior of the minimax algorithm allowed for a precise algebraic description of the system’s actions and transitions. This facilitated the verification of critical system properties and ensured the implementation was logical and consistent.

Preparation for future optimizations: Although the focus of this research was to ensure the system behavior’s validity, the model’s structure is prepared for future implementations that seek to optimize computation time through techniques such as parallelization. However, the priority was ensuring the algorithm’s basic behavior was correct before moving on to performance optimizations.

Applicability to other games and systems: While the model was implemented and validated specifically for the Connect 4 game, the methods and approaches could be adapted to other systems or games with similar structures. Validating critical properties, such as the absence of deadlocks and consistency in state growth, is applicable in various contexts, allowing this approach to be extended to other domains.