Active Obstacle Avoidance of Multi-Rotor UAV Swarm Based on Stress Matrix Formation Method
Abstract
1. Introduction
- (1)
- Consider the existence of unknown obstacles as external interference to increase the function of multi-rotor UAV swarm active obstacle avoidance. Multi-rotor UAV swarms in unknown environments and stress matrix-based multi-rotor UAV swarms use their detection ability to avoid unknown obstacles.
- (2)
- Design the virtual UAV as an auxiliary computational node to cooperate with the actual pilot UAV; the pilot UAV is only the first multi-rotor UAV swarm as the real UAV, and the other pilot UAVs are the virtual UAVs as the auxiliary computational nodes. This ensures the stability of the formation of the multi-rotor UAV swarm based on the stress matrix when encountering unknown obstacles.
2. Dynamic Model and Preliminary Knowledge
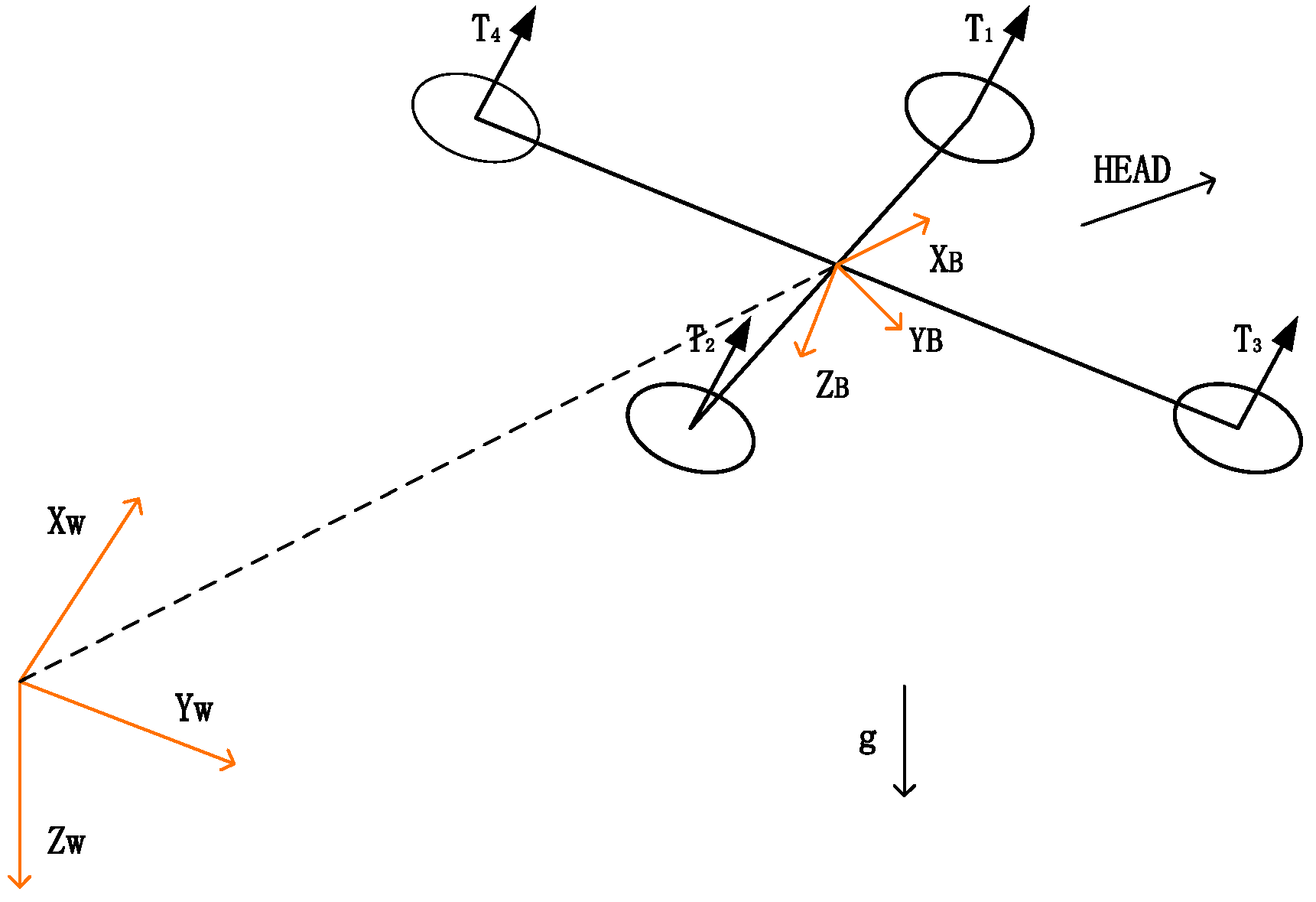
2.1. Dynamic Model
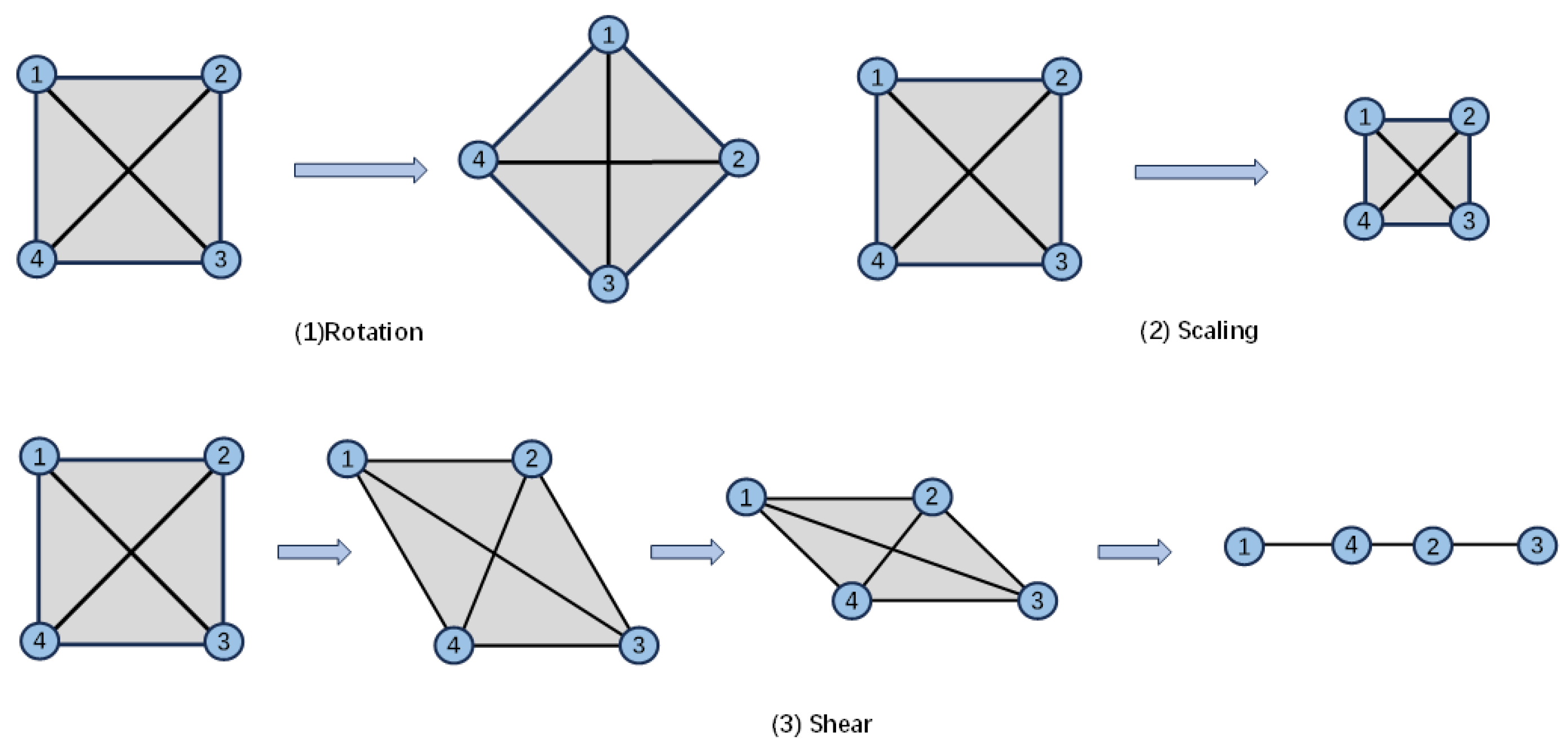
2.2. Preliminary Knowledge
3. Active UAV Obstacle Avoidance and Virtual UAV Design
3.1. Stress Matrix-Based Active Obstacle Avoidance
- (1)
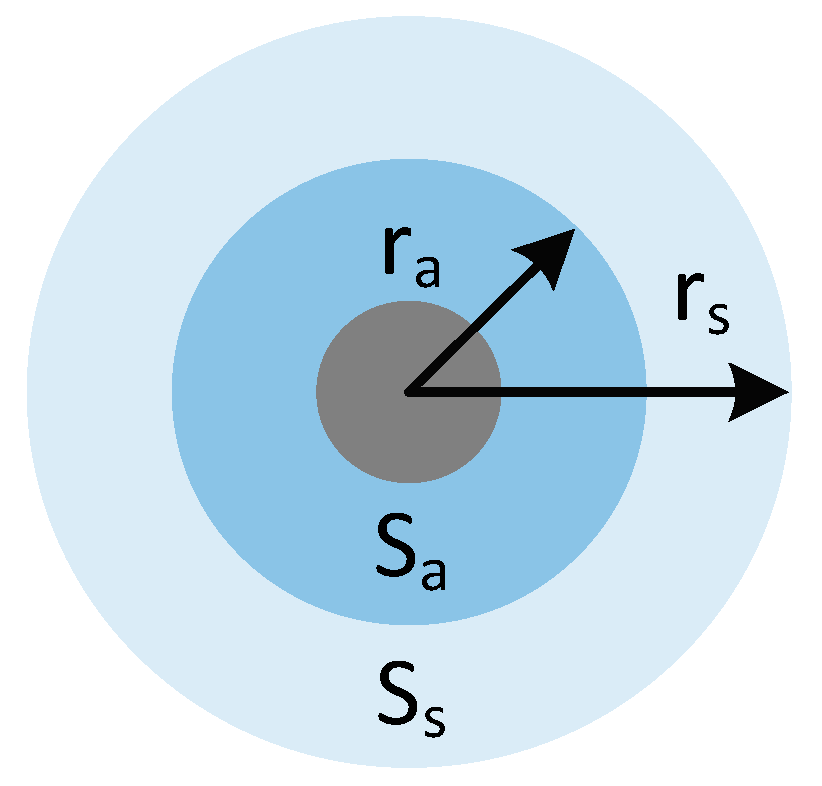
- Obstacle avoidance behavior: During operation, the formation must avoid environmental obstacles. Let be the closest point on the boundary of obstacle within the sensing range of the UAV. When the UAV senses an obstacle, it will generate a thrust to maneuver around it. The thrust direction is as follows:
- (2)
- Collision avoidance behavior: In addition to obstacle avoidance, the control algorithm also needs to adjust the positions of the UAVs to avoid collisions between them. To solve this problem, we propose to use UAVs and that are not on the same wing but within each other’s sensing area; that is, if the UAV enters the warning area , then the UAV will exert a repulsive force to prevent the drone from entering the warning area . Let . The collision avoidance behavior is determined as follows:
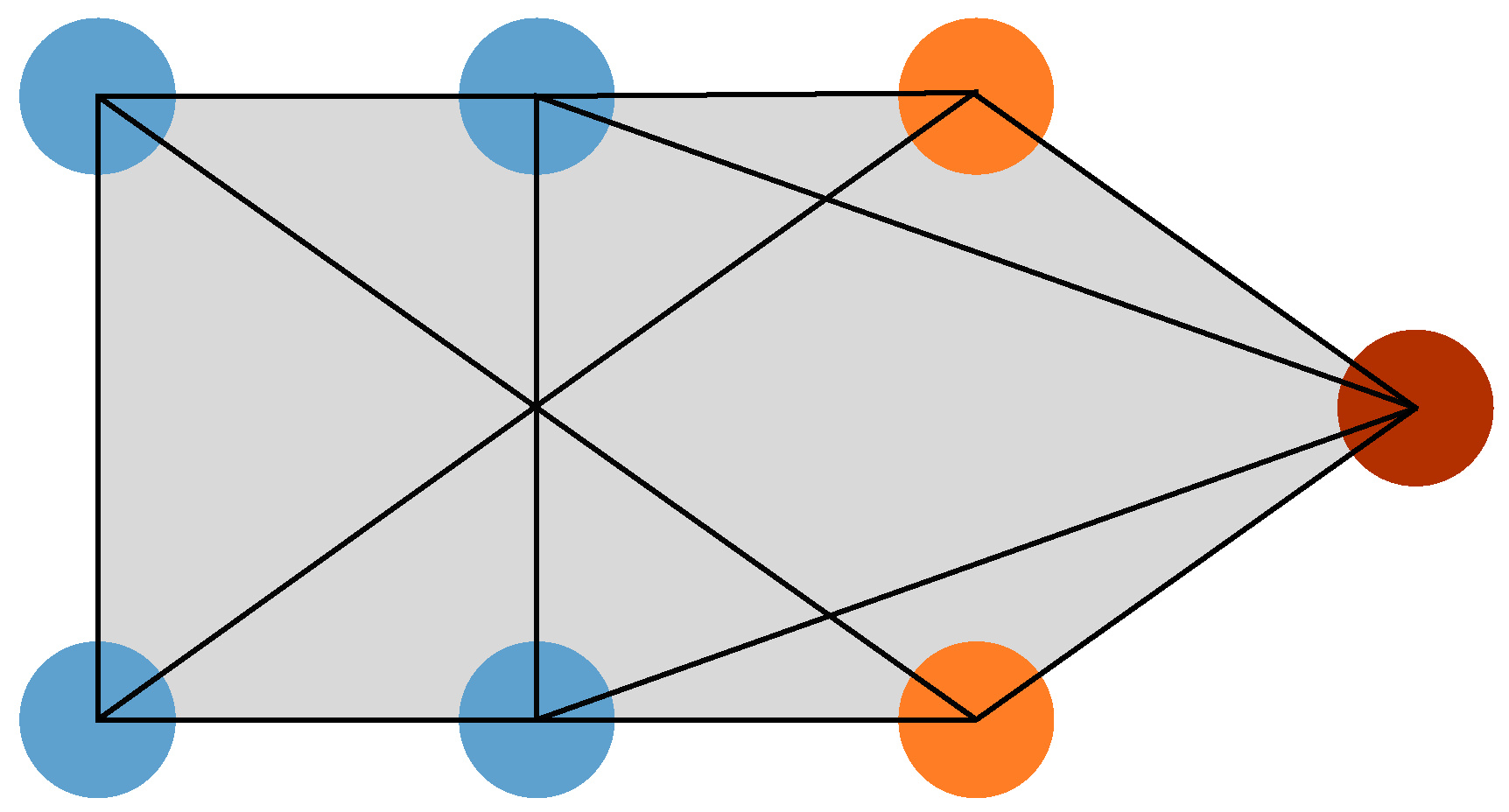
3.2. ‘Virtual UAV’ Design
4. Formation Control Law Design
4.1. Master–Leader Formation Control Laws
4.2. Leader–Slave Formation Control Laws
4.2.1. Leader Static
4.2.2. Leader Speed as a Constant Value
4.2.3. Time-Varying Leader Velocity
5. Simulation Verification
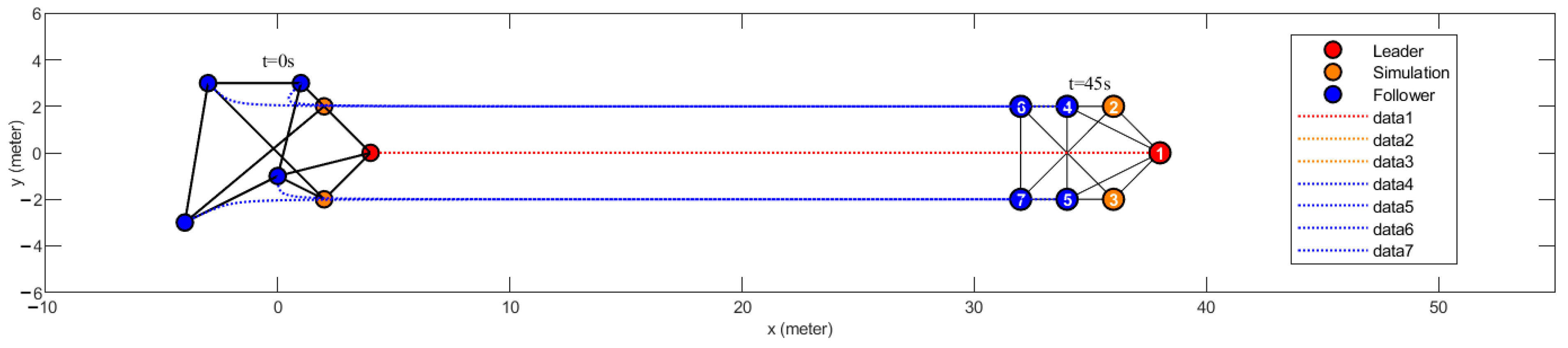
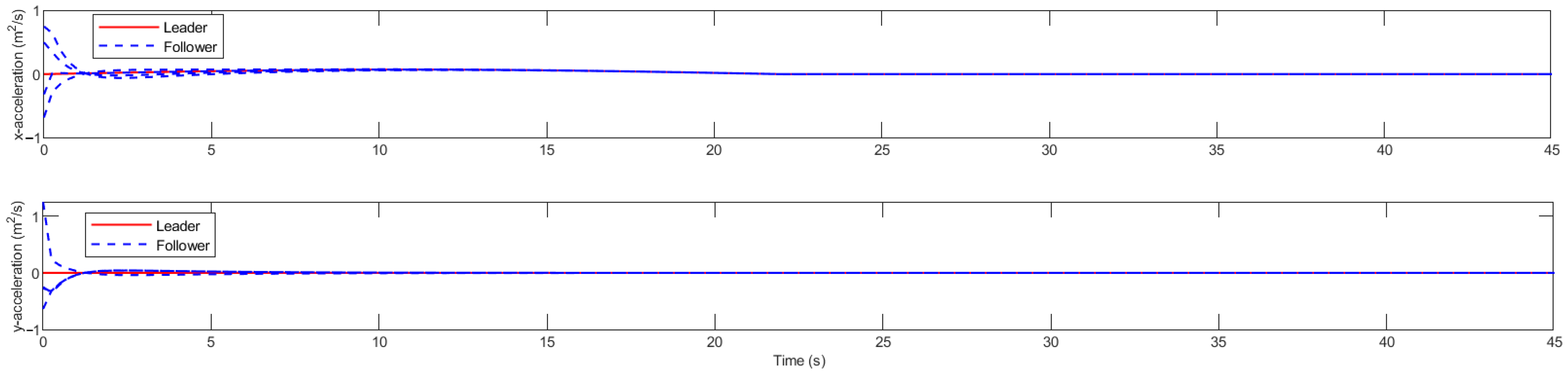
5.1. Multi-Rotor UAV Formation Verification Experiment in Obstacle-Free Environment
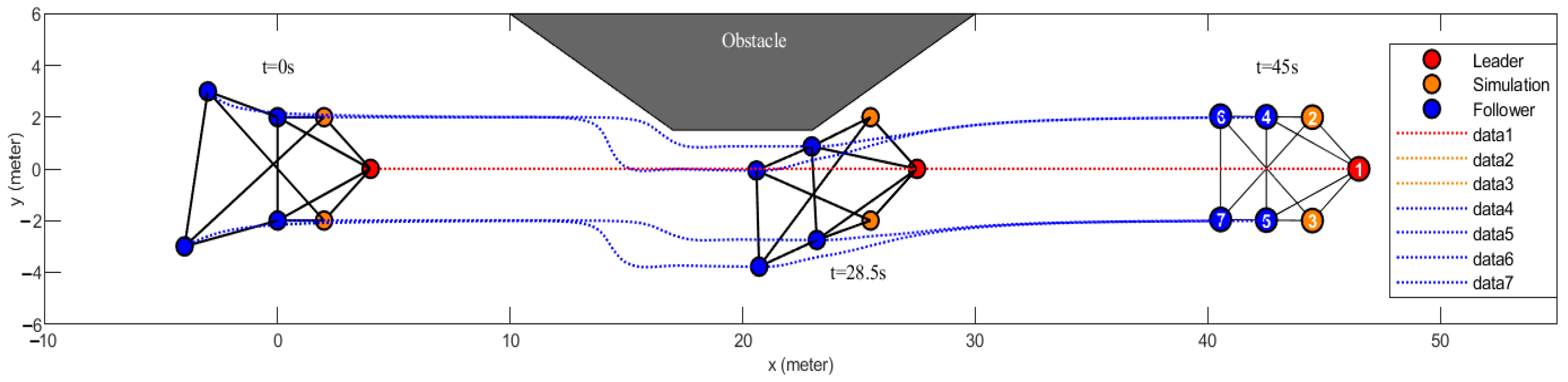
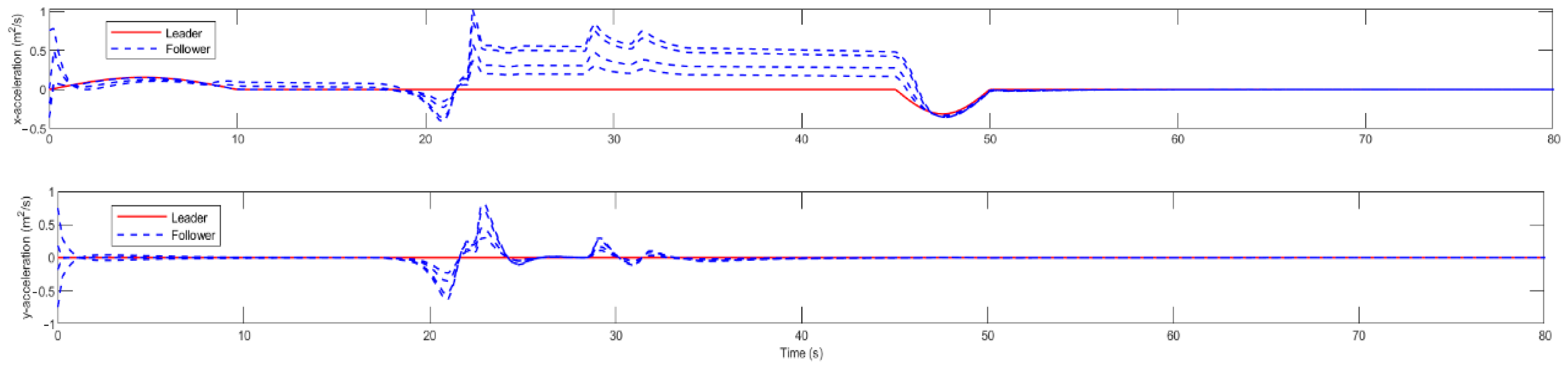
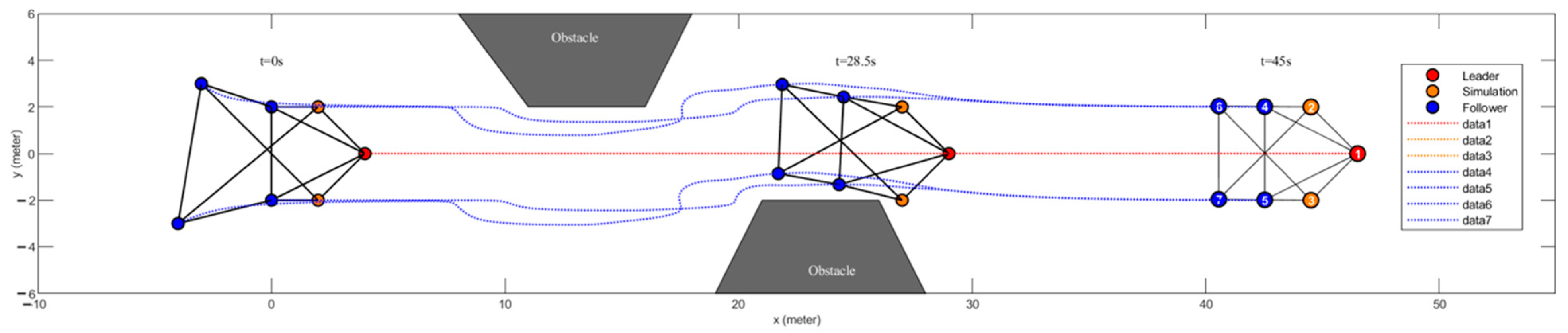
5.2. Multi-Rotor UAV Swarm Obstacle Avoidance Verification Experiment in a Unilateral Obstacle Environment
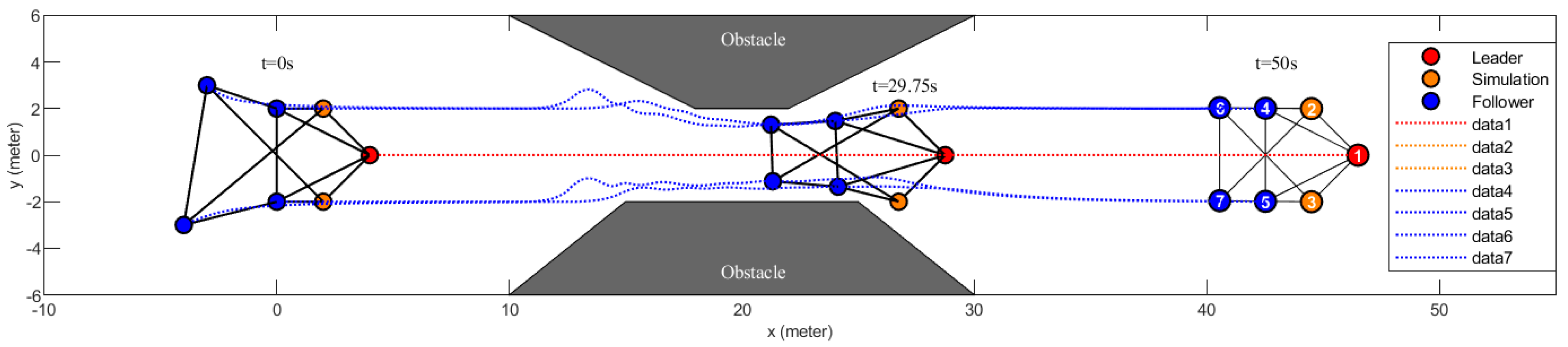
5.3. Multi-Rotor UAV Swarm Obstacle Avoidance Verification Experiment in a Bilateral Obstacle Environment
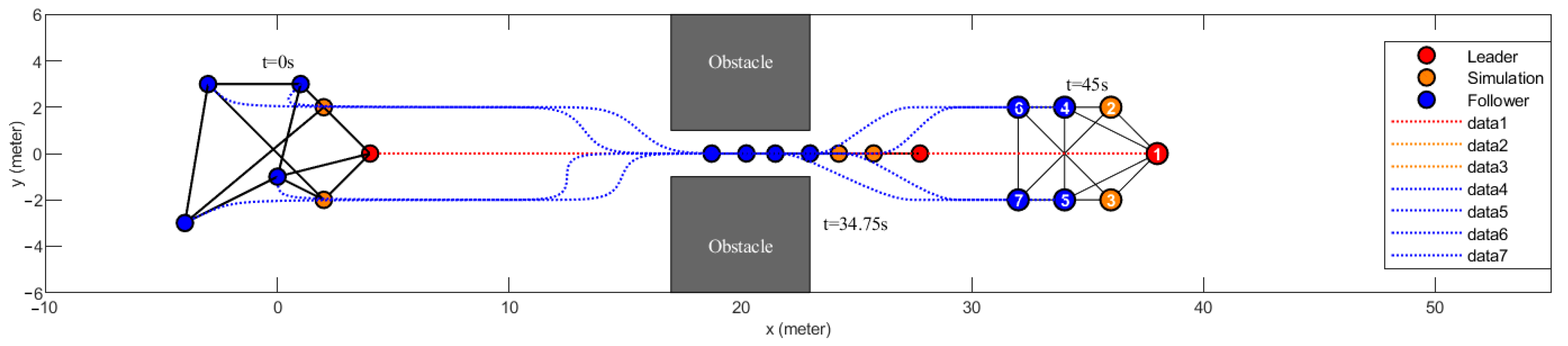
5.4. UAV Formation Verification Experiment Using Virtual UAVs
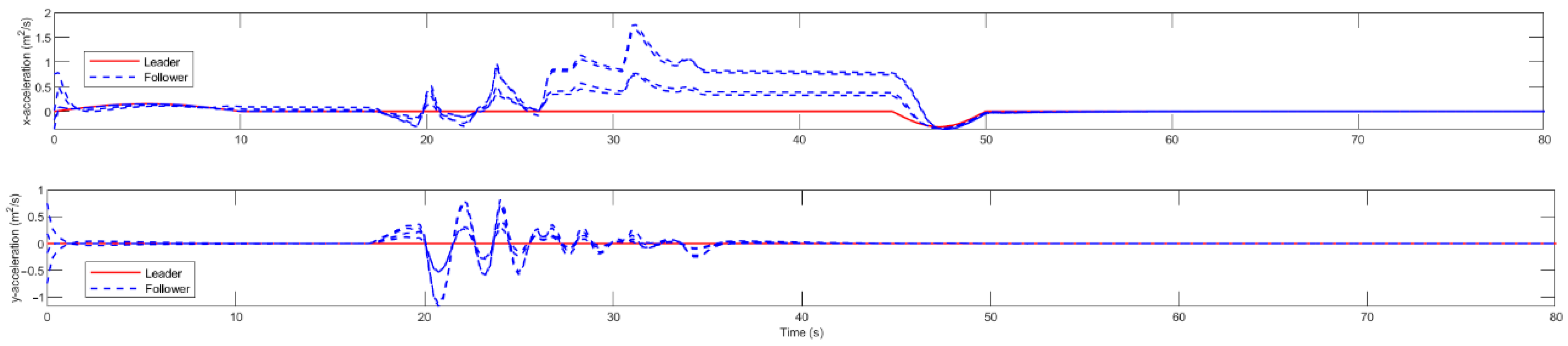
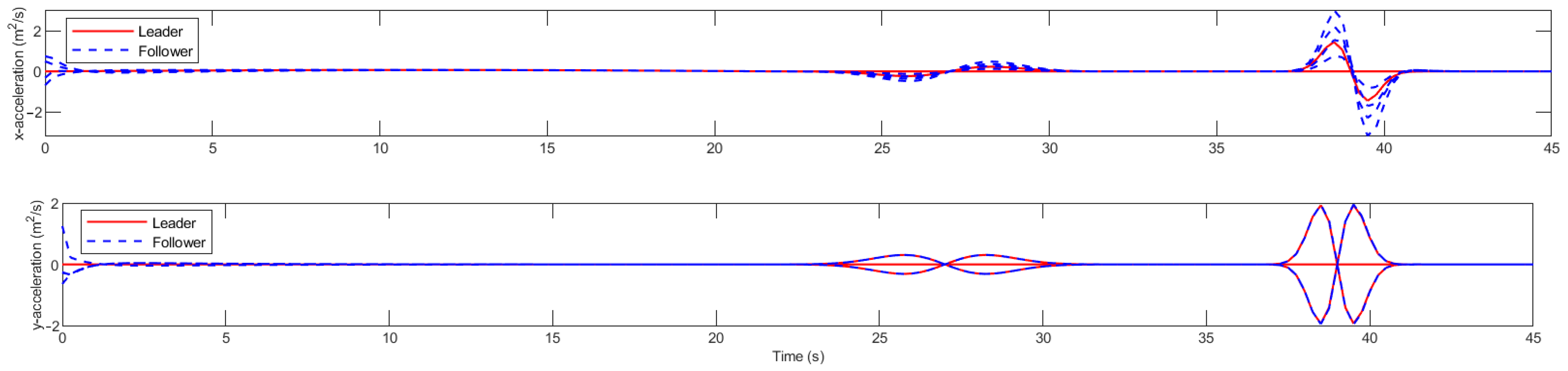
5.5. Drone Swarm Formation Obstacle Avoidance Simulation Experiment
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fahlstrom, P.G.; Gleason, T.J.; Sadraey, M.H. Introduction to UAV Systems; John Wiley & Sons: Hoboken, NJ, USA, 2022. [Google Scholar]
- Fan, B.; Li, Y.; Zhang, R.; Fu, Q. Review on the technological development and application of UAV systems. Chin. J. Electron. 2020, 29, 199–207. [Google Scholar] [CrossRef]
- Pan, Z.; Zhang, C.; Xia, Y.; Xiong, H.; Shao, X. An improved artificial potential field method for path planning and formation control of the multi-UAV systems. IEEE Trans. Circuits Syst. II Express Briefs 2021, 69, 1129–1133. [Google Scholar] [CrossRef]
- Fu, X.; Pan, J.; Wang, H.; Gao, X. A formation maintenance and reconstruction method of UAV swarm based on distributed control. Aerosp. Sci. Technol. 2020, 104, 105981. [Google Scholar] [CrossRef]
- Ali, Z.A.; Israr, A.; Alkhammash, E.H.; Hadjouni, M. A Leader-Follower Formation Control of Multi-UAVs via an Adaptive Hybrid Controller. Complexity 2021, 2021, 9231636. [Google Scholar] [CrossRef]
- Zhang, D.; Duan, H.; Zeng, Z. Leader–follower interactive potential for target enclosing of perception-limited UAV groups. IEEE Syst. J. 2021, 16, 856–867. [Google Scholar] [CrossRef]
- Jiang, C.; Fang, Y.; Zhao, P.; Panneerselvam, J. Intelligent UAV identity authentication and safety supervision based on behavior modeling and prediction. IEEE Trans. Ind. Inform. 2020, 16, 6652–6662. [Google Scholar] [CrossRef]
- Fina, L.; Smith, D.S.; Carnahan, J.; Sevil, H.E. Entropy-based distributed behavior modeling for multi-agent UAVs. Drones 2022, 6, 164. [Google Scholar] [CrossRef]
- Li, L.; Sheng, W.; Hu, C. Research on formation keeping of multi-rotor UAVs based on improved virtual structure method. J. Phys. Conf. Ser. 2020, 1631, 012106. [Google Scholar] [CrossRef]
- Wu, E.; Sun, Y.; Huang, J.; Zhang, C.; Li, Z. Multi UAV cluster control method based on virtual core in improved artificial potential field. IEEE Access 2020, 8, 131647–131661. [Google Scholar] [CrossRef]
- Jiang, Z.; Ge, J.; Xu, Q.; Yang, T. Terminal Distributed Cooperative Guidance Law for Multiple UAVs Based on Consistency Theory. Appl. Sci. 2021, 11, 8326. [Google Scholar] [CrossRef]
- Tao, C.; Zhang, R.; Song, Z.; Wang, B.; Jin, Y. Multi-UAV Formation Control in Complex Conditions Based on Improved Consistency Algorithm. Drones 2023, 7, 185. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, J.; Zhang, P. Multi-UAV formation control based on a novel back-stepping approach. IEEE Trans. Veh. Technol. 2020, 69, 2437–2448. [Google Scholar] [CrossRef]
- Justh, E.W.; Krishnaprasad, P.S. A Simple Control Law for UAV Formation Flying; Technical Report 2002-38; Institute for Systems Research: College Park, MD, USA, 2002. [Google Scholar]
- Ouyang, Q.; Wu, Z.; Cong, Y.; Wang, Z. Formation control of unmanned aerial vehicle swarms: A comprehensive review. Asian J. Control 2023, 25, 570–593. [Google Scholar] [CrossRef]
- Hu, Z.; Xu, X. Formation control for an UAV team with environment-aware dynamic constraints. IEEE Trans. Intell. Veh. 2023, 25, 570–593. [Google Scholar] [CrossRef]
- Azam, M.A.; Mittelmann, H.D.; Ragi, S. UAV formation shape control via decentralized markov decision processes. Algorithms 2021, 14, 91. [Google Scholar] [CrossRef]
- Zhang, J.-D.; Shi, Z.-Y.; Zhang, A.-L.; Yang, Q.-M.; Shi, G.-Q.; Wu, Y. UAV trajectory prediction based on flight state recognition. IEEE Trans. Aerosp. Electron. Syst. 2023, 60, 2629–2641. [Google Scholar] [CrossRef]
- Chung, W.; Son, H. Fault-tolerant control of multirotor UAVs by control variable elimination. IEEE/ASME Trans. Mechatron. 2020, 25, 2513–2522. [Google Scholar] [CrossRef]
- Ye, R.; Liu, P.; Shi, K.; Yan, B. State damping control: A novel simple method of rotor UAV with high performance. IEEE Access 2020, 8, 214346–214357. [Google Scholar] [CrossRef]
- Lin, Z.; Wang, L.; Chen, Z.; Fu, M.; Han, Z. Necessary and sufficient graphical conditions for affine formation control. IEEE Trans. Autom. Control 2015, 61, 2877–2891. [Google Scholar] [CrossRef]
- Zhao, S. Affine formation maneuver control of multiagent systems. IEEE Trans. Autom. Control 2018, 63, 4140–4155. [Google Scholar] [CrossRef]
- Xu, Y.; Zhao, S.; Luo, D.; You, Y. Affine formation maneuver control of high-order multi-agent systems over directed networks. Automatica 2020, 118, 109004. [Google Scholar] [CrossRef]
- Yang, Q.; Sun, Z.; Cao, M.; Fang, H.; Chen, J. Stress-matrix-based formation scaling control. Automatica 2019, 101, 120–127. [Google Scholar] [CrossRef]
- Asadi, D.; Bagherzadeh, S.A. Nonlinear adaptive sliding mode tracking control of an airplane with wing damage. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 232, 1405–1420. [Google Scholar] [CrossRef]
- Peng, P.; Dong, W.; Chen, G.; Zhu, X. Obstacle avoidance of resilient UAV swarm formation with active sensing system in the dense environment. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; IEEE: New York City, NY, USA, 2022; pp. 10529–10535. [Google Scholar]
- Wu, J.; Wang, H.; Liu, Y.; Zhang, M.; Wu, T. Learning-based fixed-wing UAV reactive maneuver control for obstacle avoidance. Aerosp. Sci. Technol. 2022, 126, 107623. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, S.; Fitch, R. Active SLAM for mobile robots with area coverage and obstacle avoidance. IEEE/ASME Trans. Mechatron. 2020, 25, 1182–1192. [Google Scholar] [CrossRef]
- Roghair, J.; Niaraki, A.; Ko, K.; Jannesari, A. A vision-based deep reinforcement learning algorithm for UAV obstacle avoidance. In Proceedings of the Intelligent Systems Applications: Proceedings of the 2021 Intelligent Systems Conference (IntelliSys), Virtual, 2–3 September 2021; Springer International Publishing: Cham, Switzerland, 2022; Volume 1. [Google Scholar]
- Bashir, N.; Boudjit, S.; Dauphin, G.; Zeadally, S. An obstacle avoidance approach for UAV path planning. Simul. Model. Pract. Theory 2023, 129, 102815. [Google Scholar] [CrossRef]
- Tai, J.J.; Phang, S.K.; Wong, Y.M.F. Optimized autonomous UAV design with obstacle avoidance capability. In Proceedings of the AIP Conference Proceedings 2020, Ekaterinburg, Russia, 18–22 May 2020; AIP Publishing: Melville, NY, USA; Volume 2233. [Google Scholar]
- Yasin, J.N.; Mohamed, S.A.S.; Haghbayan, M.-H.; Heikkonen, J.; Tenhunen, H.; Plosila, J. Unmanned aerial vehicles (UAVs): Collision avoidance systems and approaches. IEEE Access 2020, 8, 105139–105155. [Google Scholar] [CrossRef]
- Bui, D.N.; Phung, M.D.; Duy, H.P. Self-Reconfigurable V-shape Formation of Multiple UAVs in Narrow Space Environments. In Proceedings of the 2024 IEEE/SICE International Symposium on System Integration (SII), Ha Long, Vietnam, 8–11 January 2024; IEEE: New York City, NY, USA, 2024. [Google Scholar]
- Do, H.; Nguyen, H.; Nguyen, C.; Nguyen, M.; Nguyen, M. Formation control of multiple unmanned vehicles based on graph theory: A Comprehensive Review. EAI Endorsed Trans. Mob. Commun. Appl. 2022, 7, e3. [Google Scholar] [CrossRef]
- Xu, Y.; Zheng, W.; Luo, D.; Duan, H. Dynamic affine formation control of networked under-actuated quad-rotor UAVs with three-dimensional patterns. J. Syst. Eng. Electron. 2022, 33, 1269–1285. [Google Scholar]









| Number of Rotors | Layout Diagram | Structure and Characteristics |
| Three-rotor | 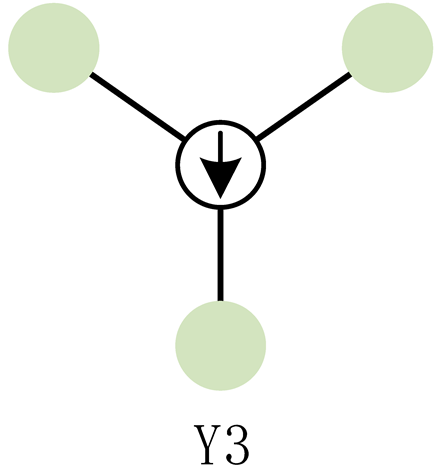 | It consists of three motors and propellers distributed in a triangle shape. It has a simple structure, high maneuverability, and is relatively small. |
| Quadcopter | 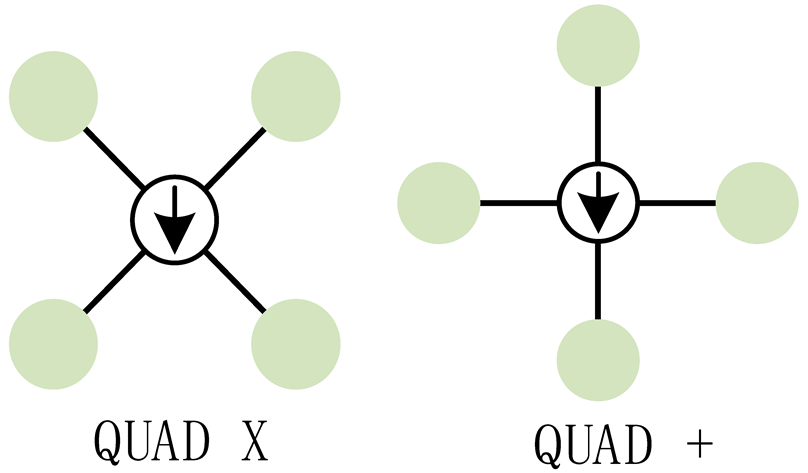 | It consists of 4 motors symmetrically distributed around the fuselage, and the adjacent motors rotate in opposite directions. It has simple control, high maneuverability, and low cost. |
| Hexacopter |  | It consists of 6 motors symmetrically distributed around the fuselage. The adjacent motors rotate in opposite directions. The structure is balanced, with good wind resistance and load-bearing capacity. |
| Octocopters |  | It consists of 8 motors symmetrically distributed around the fuselage, and the adjacent motors rotate in opposite directions. The structure is balanced, stable, and has good wind resistance and load-bearing capacity, but the cost is relatively high. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, Z.; Zhang, L.; Chi, Y.; Li, Z. Active Obstacle Avoidance of Multi-Rotor UAV Swarm Based on Stress Matrix Formation Method. Mathematics 2025, 13, 86. https://doi.org/10.3390/math13010086
Qiu Z, Zhang L, Chi Y, Li Z. Active Obstacle Avoidance of Multi-Rotor UAV Swarm Based on Stress Matrix Formation Method. Mathematics. 2025; 13(1):86. https://doi.org/10.3390/math13010086
Chicago/Turabian StyleQiu, Zhenyue, Lei Zhang, Yuan Chi, and Zequn Li. 2025. "Active Obstacle Avoidance of Multi-Rotor UAV Swarm Based on Stress Matrix Formation Method" Mathematics 13, no. 1: 86. https://doi.org/10.3390/math13010086
APA StyleQiu, Z., Zhang, L., Chi, Y., & Li, Z. (2025). Active Obstacle Avoidance of Multi-Rotor UAV Swarm Based on Stress Matrix Formation Method. Mathematics, 13(1), 86. https://doi.org/10.3390/math13010086





