On the Development of a Modified Timoshenko Beam Element for the Bending Analysis of Functionally Graded Beams
Abstract
1. Introduction
2. Functionally Graded Beams
3. Development of the Modified Timoshenko Beam Element
3.1. Displacement Field and Strain Energy
3.2. A New Modified Timoshenko Beam Element
4. Results and Discussion
4.1. Validation Study
4.2. Numerical Results
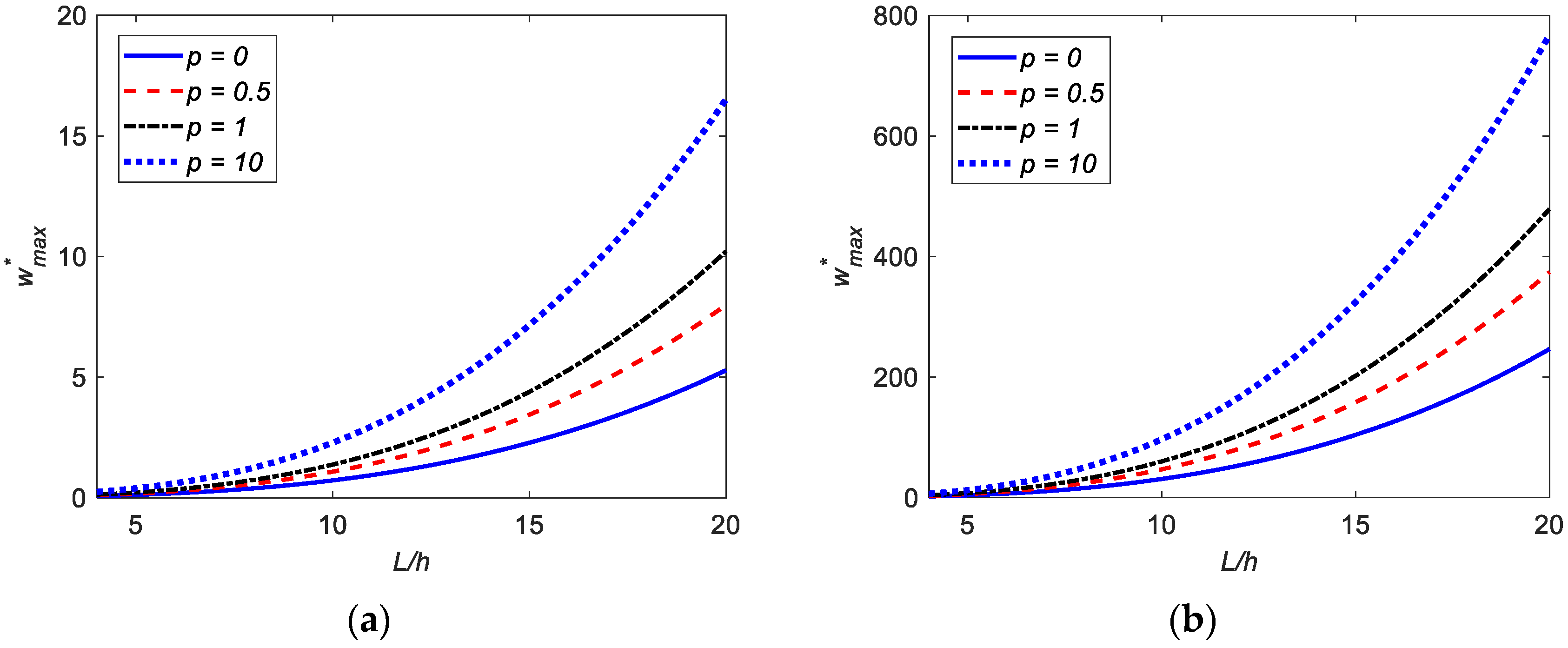
4.2.1. The Effects of the Length-to-Thickness Ratio on the Bending of FG Beams
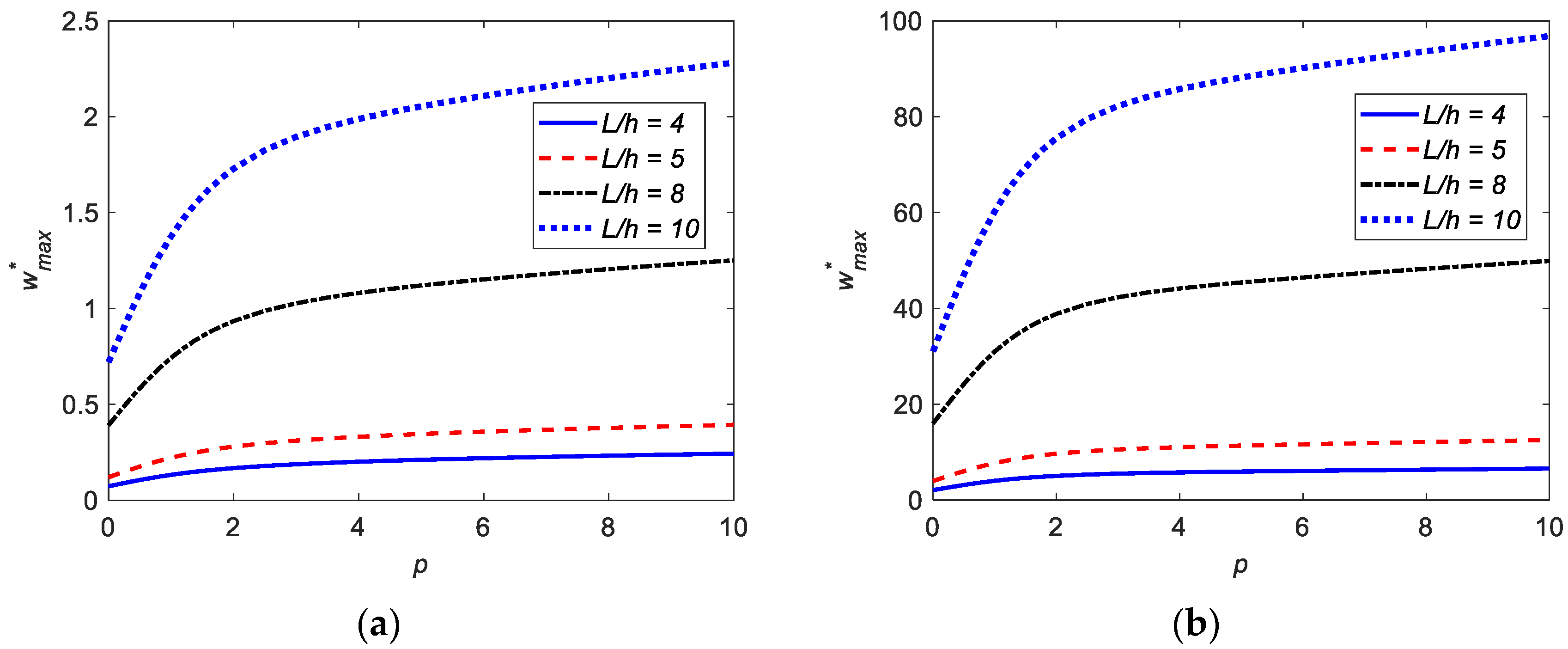
4.2.2. The Effects of the Power-Law Index on the Bending of FG Beams
5. Conclusions
- -
- When the length-to-thickness ratio increases, the deflections in the FG beams increase rapidly.
- -
- When the power-law index increases, the deflections in the FG beams increase.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Koizumi, M. FGM activities in Japan. Compos. Part B Eng. 1997, 28, 1–4. [Google Scholar] [CrossRef]
- Chakraborty, A.; Gopalakrishnan, S.; Reddy, J.N. A new beam finite element for the analysis of functionally graded materials. Int. J. Mech. Sci. 2003, 45, 519–539. [Google Scholar] [CrossRef]
- Reddy, J.N. A General Nonlinear Third-Order Theory of Functionally Graded Plates. Int. J. Aerosp. Light. Struct. 2011, 1, 1. [Google Scholar] [CrossRef]
- Reddy, J.N. Analysis of functionally graded plates. Int. J. Numer. Methods Eng. 2000, 47, 663–684. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Y.; Zhou, Y.; Yang, F. Static and dynamic analysis of thin functionally graded shell with in-plane material inhomogeneity. Int. J. Mech. Sci. 2021, 193, 106165. [Google Scholar] [CrossRef]
- Tian, X.; Zhou, Y.; Ding, S.; Wang, L. Exploring the effects of finite size and indenter shape on the contact behavior of functionally graded thermoelectric materials. Int. J. Solids Struct. 2024, 305, 113089. [Google Scholar] [CrossRef]
- Cheng, H.; He, W.; Zhang, J.; Cheng, Y. The dimension coupling method for 3D transient heat conduction problem with variable coefficients. Eng. Anal. Bound. Elem. 2024, 166, 105839. [Google Scholar] [CrossRef]
- Chen, W.Q.; Lü, C.F.; Bian, Z.G. A mixed method for bending and free vibration of beams resting on a Pasternak elastic foundation. Appl. Math. Model. 2004, 28, 877–890. [Google Scholar] [CrossRef]
- Pu, Y.; Jia, S.; Luo, Y.; Shi, S. Bending analysis of functionally graded sandwich beams with general boundary conditions using a modified Fourier series method. Arch. Appl. Mech. 2023, 93, 3741–3760. [Google Scholar] [CrossRef]
- Ghazwani, M.H. New Enriched Beam Element for Static Bending Analysis of Functionally Graded Porous Beams Resting on Elastic Foundations. Mech. Solids 2023, 58, 1878–1893. [Google Scholar] [CrossRef]
- Kapuria, S.; Bhattacharyya, M.; Kumar, A.N. Bending and free vibration response of layered functionally graded beams: A theoretical model and its experimental validation. Compos. Struct. 2008, 82, 390–402. [Google Scholar] [CrossRef]
- Kadoli, R.; Akhtar, K.; Ganesan, N. Static analysis of functionally graded beams using higher order shear deformation theory. Appl. Math. Model. 2008, 32, 2509–2525. [Google Scholar] [CrossRef]
- Giunta, G.; Belouettar, S.; Carrera, E. Analysis of FGM beams by means of classical and advanced theories. Mech. Adv. Mater. Struct. 2010, 17, 622–635. [Google Scholar] [CrossRef]
- Li, X.F.; Wang, B.L.; Han, J.C. A higher-order theory for static and dynamic analyses of functionally graded beams. Arch. Appl. Mech. 2010, 80, 1197–1212. [Google Scholar] [CrossRef]
- Ying, J.; Lü, C.F.; Chen, W.Q. Two-dimensional elasticity solutions for functionally graded beams resting on elastic foundations. Compos. Struct. 2008, 84, 209–219. [Google Scholar] [CrossRef]
- Şimşek, M. Static analysis of a functionally graded beam under a uniformly distributed load by Ritz method. Int. J. Eng. Appl. Sci. 2009, 1, 1–11. [Google Scholar]
- Thai, H.T.; Vo, T.P. Bending and free vibration of functionally graded beams using various higher-order shear deformation beam theories. Int. J. Mech. Sci. 2012, 62, 57–66. [Google Scholar] [CrossRef]
- Adiyaman, G.; Turan, M. Bending and Buckling Analysis of Porous 2D Functionally Graded Beams with Exponential Material Property Variation. Iran. J. Sci. Technol. Trans. Civ. Eng. 2024. [Google Scholar] [CrossRef]
- Nguyen, T.K.; Vo, T.P.; Thai, H.T. Static and free vibration of axially loaded functionally graded beams based on the first-order shear deformation theory. Compos. Part B Eng. 2013, 55, 147–157. [Google Scholar] [CrossRef]
- Mohammadi, H.; Kiani, Y. Isogeometric nonlinear free vibration analysis of FG-GRC laminated Timoshenko beams with temperature-dependent material properties. Structures 2024, 67, 106910. [Google Scholar] [CrossRef]
- Huang, Y.; Ouyang, Z.Y. Exact solution for bending analysis of two-directional functionally graded Timoshenko beams. Arch. Appl. Mech. 2020, 90, 1005–1023. [Google Scholar] [CrossRef]
- Tang, A.Y.; Wu, J.X.; Li, X.F.; Lee, K.Y. Exact frequency equations of free vibration of exponentially non-uniform functionally graded Timoshenko beams. Int. J. Mech. Sci. 2014, 89, 1–11. [Google Scholar] [CrossRef]
- Şimşek, M. Bi-directional functionally graded materials (BDFGMs) for free and forced vibration of Timoshenko beams with various boundary conditions. Compos. Struct. 2015, 133, 968–978. [Google Scholar] [CrossRef]
- Vo, T.P.; Thai, H.T.; Nguyen, T.K.; Inam, F.; Lee, J. Static behaviour of functionally graded sandwich beams using a quasi-3D theory. Compos. Part B Eng. 2015, 68, 59–74. [Google Scholar] [CrossRef]
- Chaabane, L.A. Analytical study of bending and free vibration responses of functionally graded beams resting on elastic foundation. Struct. Eng. Mech. 2019, 71, 185–196. [Google Scholar]
- Hadji, L.; Bernard, F. Bending and Free Vibration Analysis of Functionally Graded Beams on Elastic Foundations With Analytical Validation. Adv. Mater. Res. 2020, 9, 63–98. [Google Scholar] [CrossRef]
- Chen, D.; Yang, J.; Kitipornchai, S. Elastic buckling and static bending of shear deformable functionally graded porous beam. Compos. Struct. 2015, 133, 54–61. [Google Scholar] [CrossRef]
- Fouda, N.; El-midany, T.; Sadoun, A.M. Bending, buckling and vibration of a functionally graded porous beam using finite elements. J. Appl. Comput. Mech. 2017, 3, 274–282. [Google Scholar] [CrossRef]
- Vo, T.P.; Thai, H.T.; Nguyen, T.K.; Maheri, A.; Lee, J. Finite element model for vibration and buckling of functionally graded sandwich beams based on a refined shear deformation theory. Eng. Struct. 2014, 64, 12–22. [Google Scholar] [CrossRef]
- Glabisz, W.; Jarczewska, K.; Hołubowski, R. Stability of Timoshenko beams with frequency and initial stress dependent nonlocal parameters. Arch. Civ. Mech. Eng. 2019, 19, 1116–1126. [Google Scholar] [CrossRef]
- Fang, W.; Yu, T.; Van Lich, L.; Bui, T.Q. Analysis of thick porous beams by a quasi-3D theory and isogeometric analysis. Compos. Struct. 2019, 221, 110890. [Google Scholar] [CrossRef]
- Burlayenko, V.N.; Altenbach, H.; Dimitrova, S.D. Modal characteristics of functionally graded porous Timoshenko beams with variable cross-sections. Compos. Struct. 2024, 342, 118273. [Google Scholar] [CrossRef]
- Turan, M.; Adiyaman, G. Free Vibration and Buckling Analysis of Porous Two-Directional Functionally Graded Beams Using a Higher-Order Finite Element Model. J. Vib. Eng. Technol. 2024, 12, 1133–1152. [Google Scholar] [CrossRef]
- Ling, T.; Wu, X.; Huang, F.; Xiao, J.; Sun, Y.; Feng, W. Variable cross sections functionally grad beams on Pasternak foundations: An enhanced interaction theory for construction applications. Arch. Appl. Mech. 2024, 94, 1005–1020. [Google Scholar] [CrossRef]
- Aribas, U.N.; Atalay, M.; Omurtag, M.H. Warping included mixed finite elements for bending and stresses of functionally graded exact curved beams. Mech. Adv. Mater. Struct. 2024, 31, 5040–5056. [Google Scholar] [CrossRef]
- Benmalek, H.; Bouziane, S.; Bouzerd, H.; Suleiman, H. Innovative mixed finite element method for bending analysis of functionally graded beams: Modelling, validation, and applications. Eng. Res. Express 2024, 6, 15055. [Google Scholar] [CrossRef]
- Santos, H.; Mota Soares, C.M.; Mota Soares, C.A.; Reddy, J.N. A semi-analytical finite element model for the analysis of cylindrical shells made of functionally graded materials. Compos. Struct. 2009, 91, 427–432. [Google Scholar] [CrossRef]
- Li, L.; Li, X.; Hu, Y. Free vibration analysis of nonlocal strain gradient beams made of functionally graded material. Int. J. Eng. Sci. 2016, 102, 77–92. [Google Scholar] [CrossRef]


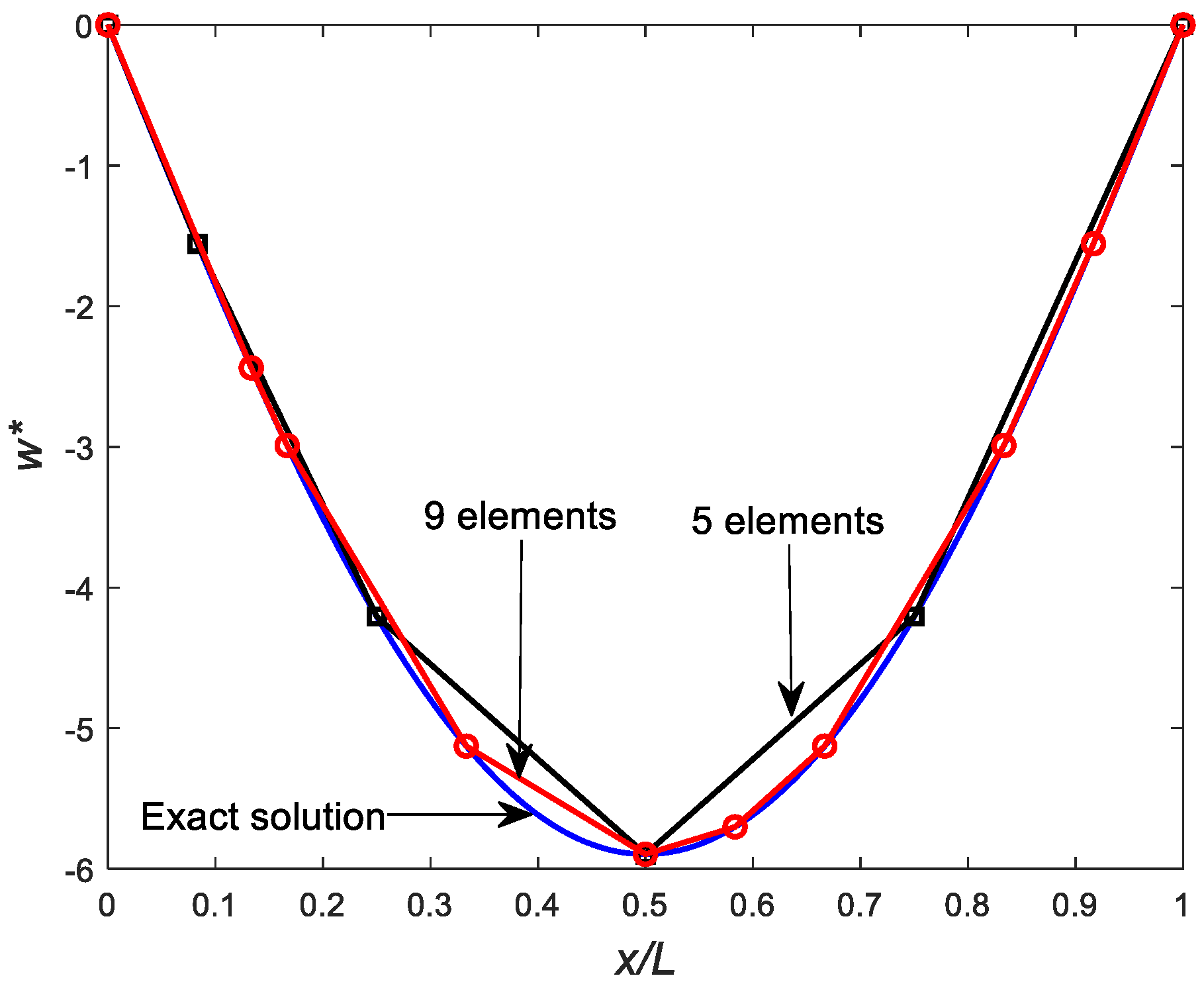

| Element Type | Number of Elements | Li et al. [14] | Thai et al. [17] | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 | 12 | 18 | 24 | 32 | |||||
| 5 | 0 | Proposed | 3.1657 | 3.1657 | 3.1657 | 3.1657 | 3.1657 | 3.1657 | 3.1654 |
| Timoshenko | 0.8624 | 2.9836 | 3.0823 | 3.1183 | 3.1388 | - | - | ||
| 1 | Proposed | 6.2599 | 6.2599 | 6.2599 | 6.2599 | 6.2599 | 6.2599 | 6.2594 | |
| Timoshenko | 1.5105 | 5.8417 | 6.0675 | 6.1503 | 6.1979 | - | - | ||
| 5 | Proposed | 9.6483 | 9.6483 | 9.6483 | 9.6483 | 9.6483 | 9.7802 | 9.8281 | |
| Timoshenko | 3.0362 | 9.3314 | 9.5914 | 9.6854 | 9.7391 | - | - | ||
| 10 | Proposed | 10.7195 | 10.7195 | 10.7195 | 10.7195 | 10.7195 | 10.8979 | 10.9381 | |
| Timoshenko | 3.6940 | 10.4678 | 10.7257 | 10.8187 | 10.8716 | - | - | ||
| 20 | 0 | Proposed | 2.8963 | 2.8963 | 2.8963 | 2.8963 | 2.8963 | 2.8962 | 2.8962 |
| Timoshenko | 0.0702 | 1.5237 | 2.0700 | 2.3657 | 2.5720 | - | - | ||
| 1 | Proposed | 5.8049 | 5.8049 | 5.8049 | 5.8049 | 5.8049 | 5.8049 | 5.8049 | |
| Timoshenko | 0.1190 | 2.8056 | 3.9391 | 4.5847 | 5.0495 | - | - | ||
| 5 | Proposed | 8.8069 | 8.8069 | 8.8069 | 8.8069 | 8.8069 | 8.8151 | 8.8182 | |
| Timoshenko | 0.2573 | 5.0532 | 6.6292 | 7.4377 | 7.9846 | - | - | ||
| 10 | Proposed | 9.6767 | 9.6767 | 9.6767 | 9.6767 | 9.6767 | 9.6879 | 9.6905 | |
| Timoshenko | 0.3229 | 5.8740 | 7.5244 | 8.3413 | 8.8829 | ||||
| 4 | 0.0730 | 0.0899 | 0.1057 | 0.1327 | 0.1678 | 0.2110 | 0.2429 |
| 5 | 0.1200 | 0.1488 | 0.1759 | 0.2218 | 0.2799 | 0.3456 | 0.3933 |
| 8 | 0.3919 | 0.4908 | 0.5847 | 0.7428 | 0.9341 | 1.1199 | 1.2511 |
| 10 | 0.7204 | 0.9052 | 1.0809 | 1.3762 | 1.7288 | 2.0540 | 2.2813 |
| 15 | 2.2815 | 2.8769 | 3.4441 | 4.3960 | 5.5159 | 6.4881 | 7.1588 |
| 20 | 5.2837 | 6.6714 | 7.9947 | 10.2137 | 12.8103 | 15.0106 | 16.5204 |
| 4 | 0.2369 | 0.2973 | 0.3546 | 0.4510 | 0.5668 | 0.6762 | 0.7531 |
| 5 | 0.4403 | 0.5539 | 0.6620 | 0.8435 | 1.0593 | 1.2541 | 1.3898 |
| 8 | 1.7036 | 2.1501 | 2.5757 | 3.2896 | 4.1265 | 4.8413 | 5.3327 |
| 10 | 3.2823 | 4.1459 | 4.9695 | 6.3504 | 7.9639 | 9.3224 | 10.2532 |
| 15 | 10.9280 | 13.8141 | 16.5681 | 21.1837 | 26.5592 | 31.0191 | 34.0639 |
| 20 | 25.7791 | 32.5966 | 39.1035 | 50.0069 | 62.6906 | 73.1583 | 80.2955 |
| 4 | 2.0954 | 2.6409 | 3.1604 | 4.0324 | 5.0606 | 5.9612 | 6.5837 |
| 5 | 4.0027 | 5.0511 | 6.0504 | 7.7266 | 9.6927 | 11.3764 | 12.5345 |
| 8 | 15.9962 | 20.2147 | 24.2395 | 30.9858 | 38.8524 | 45.4154 | 49.9019 |
| 10 | 31.0628 | 39.2680 | 47.0982 | 60.2206 | 75.5009 | 88.1690 | 96.8159 |
| 15 | 104.2373 | 131.8167 | 158.1407 | 202.2495 | 253.5398 | 295.7938 | 324.5911 |
| 20 | 246.5837 | 311.8631 | 374.1753 | 478.5807 | 599.9251 | 699.6670 | 767.6072 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghazwani, M.H.; Vinh, P.V.V. On the Development of a Modified Timoshenko Beam Element for the Bending Analysis of Functionally Graded Beams. Mathematics 2025, 13, 73. https://doi.org/10.3390/math13010073
Ghazwani MH, Vinh PVV. On the Development of a Modified Timoshenko Beam Element for the Bending Analysis of Functionally Graded Beams. Mathematics. 2025; 13(1):73. https://doi.org/10.3390/math13010073
Chicago/Turabian StyleGhazwani, Mofareh Hassan, and Pham V. V. Vinh. 2025. "On the Development of a Modified Timoshenko Beam Element for the Bending Analysis of Functionally Graded Beams" Mathematics 13, no. 1: 73. https://doi.org/10.3390/math13010073
APA StyleGhazwani, M. H., & Vinh, P. V. V. (2025). On the Development of a Modified Timoshenko Beam Element for the Bending Analysis of Functionally Graded Beams. Mathematics, 13(1), 73. https://doi.org/10.3390/math13010073







