Forecasting Influenza Trends Using Decomposition Technique and LightGBM Optimized by Grey Wolf Optimizer Algorithm
Abstract
1. Introduction
1.1. Literature Review
1.1.1. Prediction Models
1.1.2. Influence Factors
1.2. Gaps and Contributions
- Existing research in influenza forecasting often relies solely on historical time series data or a single Baidu Index, whereas this study innovatively integrates both the Baidu Index and historical autocorrelation data to construct a more comprehensive and accurate influenza prediction model. By merging these datasets, we can capture influenza trends more holistically, enhancing the precision and reliability of our forecasts and addressing the deficiencies in current research.
- In existing influenza prediction research using the Baidu Index, a significant gap is the neglect of feature selection. Spearman correlation analysis is essential for addressing this, as it allows for the careful screening and selection of input features, reducing dimensionality while preserving critical information, potentially enhancing model predictive accuracy.
- Existing research indicates that the application of decomposition techniques in the field of influenza prediction is not widespread. Despite the advancements achieved by machine learning models in predicting influenza trends, they still face challenges in avoiding overfitting and escaping local minima. Consequently, the incorporation of decomposition algorithms is expected to enhance the model’s capability to capture influenza trends by providing a multiscale analysis, while simultaneously reducing the risk of overfitting.
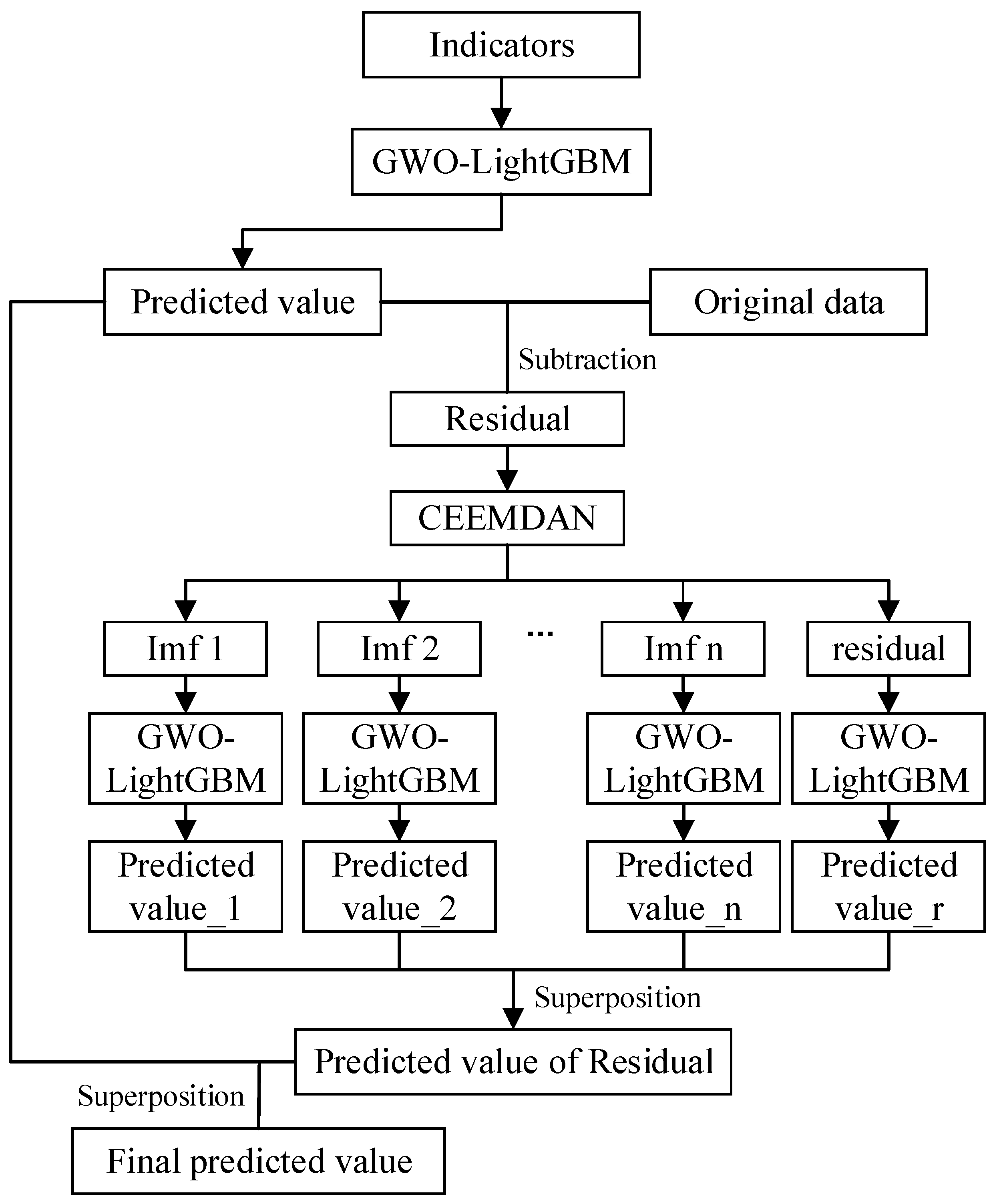
- In this study, we propose an innovative influenza trend prediction model, GWO-LightGBM-CEEMDAN, which integrates optimization algorithms with decomposition techniques. Unlike the conventional process of most existing models that proceed with decomposition before prediction, our model adopts a unique strategy of predicting first and then decomposing. Specifically, following the initial prediction, we apply the CEEMDAN algorithm to process the residual series, addressing potential instability issues. Ultimately, experimental results confirm the practicality and superiority of this approach.
- The Baidu Index is incorporated as an external influencing factor for prediction, realizing the application of big data in influenza prediction. This study adds Baidu Index as influencing factors on the basis of the original data and realizes the prediction with the help of internet search engine. In addition, compared to traditional big data, this study has updated the selection of the Baidu Index by adding new indices such as lymphocyte and nebulizer. The empirical analysis proves that the addition of the Baidu Index can improve the predictive ability of the model.
- Previous studies using the Baidu Index for influenza prediction often neglected the feature selection of input data; therefore, to compensate for this deficiency, this study uses Spearman correlation analysis to filter the input features in order to reduce the dimensionality of the data and retain the most important data information, which in turn improves the prediction performance of the model.
2. Materials and Methods
2.1. Data Collection and Preprocessing
2.1.1. Data Source
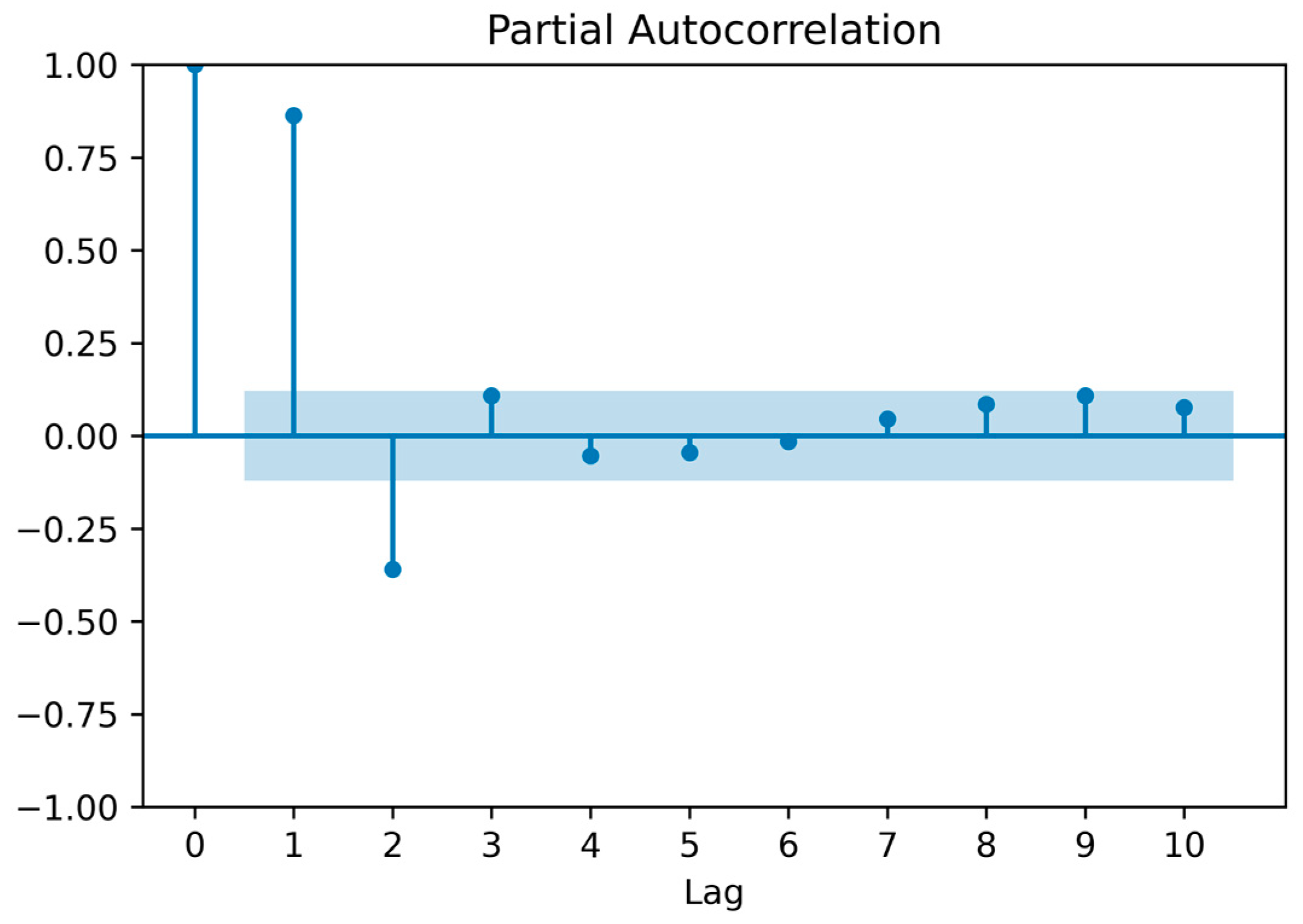
2.1.2. Data Analysis
2.1.3. Data Processing
2.2. Models
2.2.1. GWO Algorithm
- 1.
- Social class of grey wolf
- 2.
- Surrounding
- 3.
- Hunting
- 4.
- Attacking prey
| Algorithm 1. GWO algorithm pseudocode. |
| Inputs: Grey wolf population Xi; maximum number of iterations Imax |
| Output: The best agent position Xα |
| Process: |
| Initialize Xi, (i = 1, 2, …, n), a, A and C |
| Calculate the fitness of each Xi to choose the best three solutions Xα, Xβ and Xδ |
| While (t < Imax) |
| for each Xi |
| Update the position of the current search agent |
| end for |
| Update a, A and C |
| Calculate the fitness of all search agents |
| Update Xα, Xβ and Xδ |
| t = t + 1 |
| End while |
| Return Xα |
2.2.2. LightGBM Model
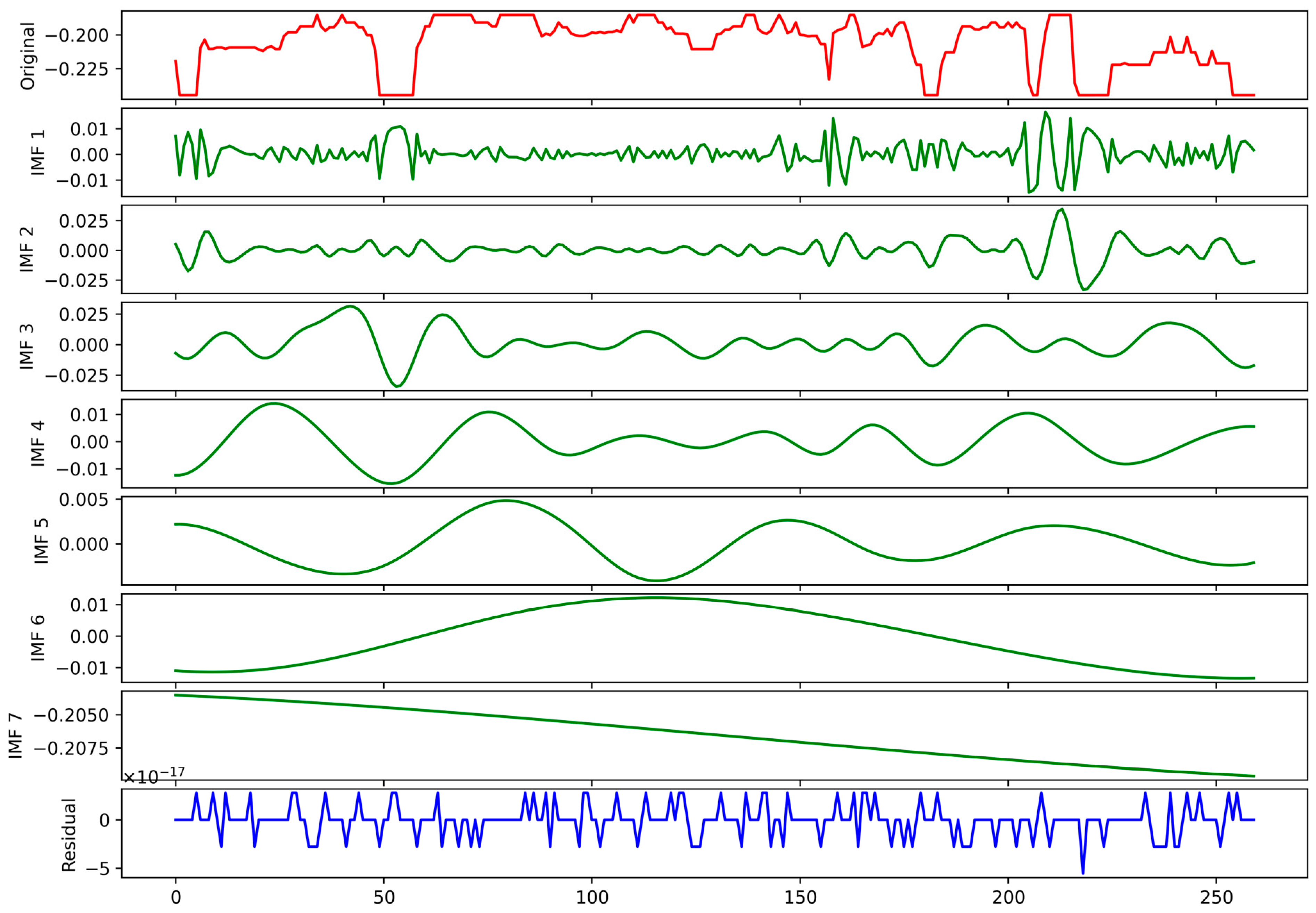
2.2.3. CEEMDAN Algorithm
2.2.4. GWO-LightGBM-CEEMDAN Model
2.3. Evaluation Indicators
3. Empirical Analysis and Results
3.1. Experimental Environment and Parameter Settings
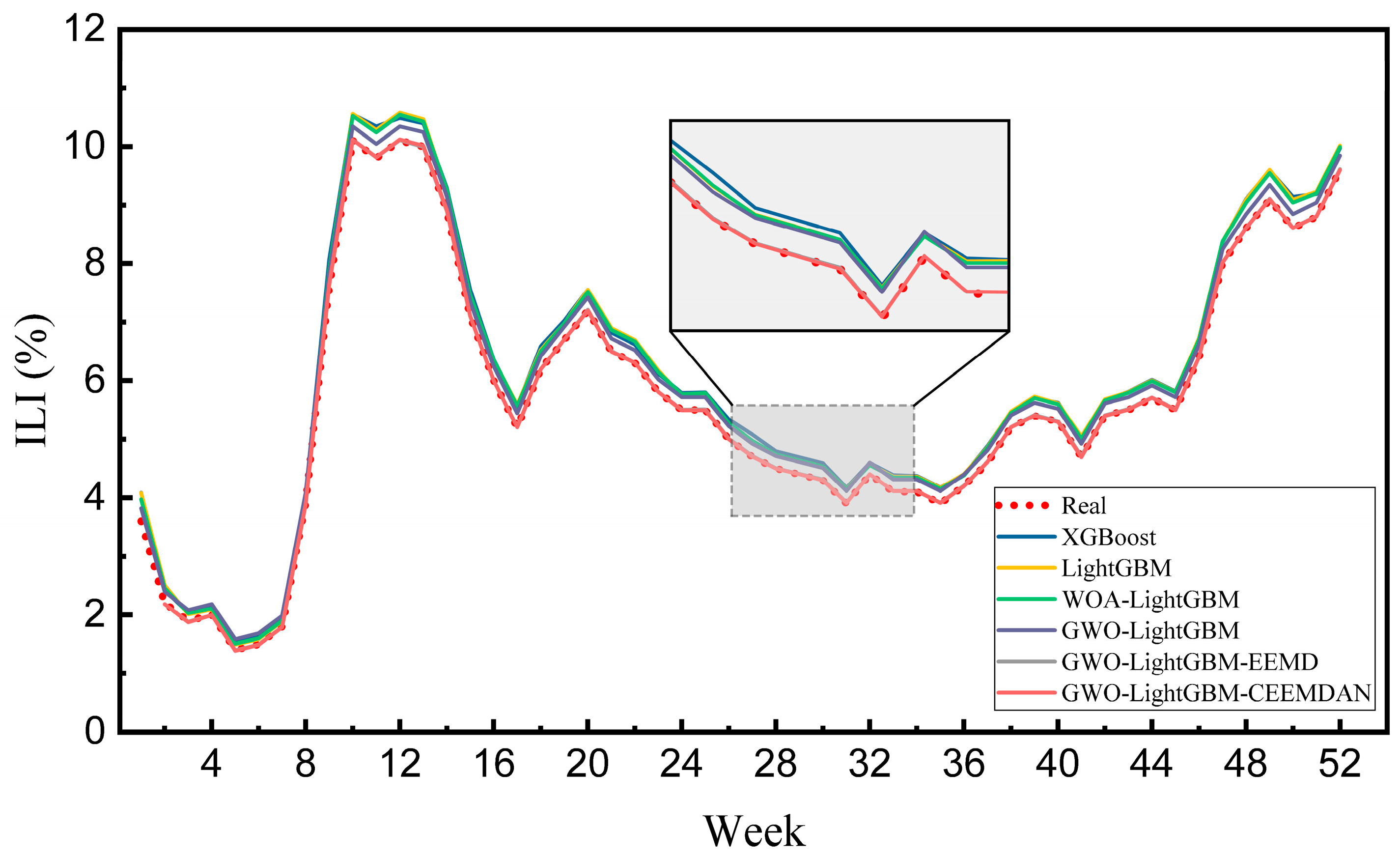
3.2. Experimental Results
3.3. Experiment II: Comparison of Model Proposed in This Paper with Different Input Indicators
4. Discussion
5. Conclusions
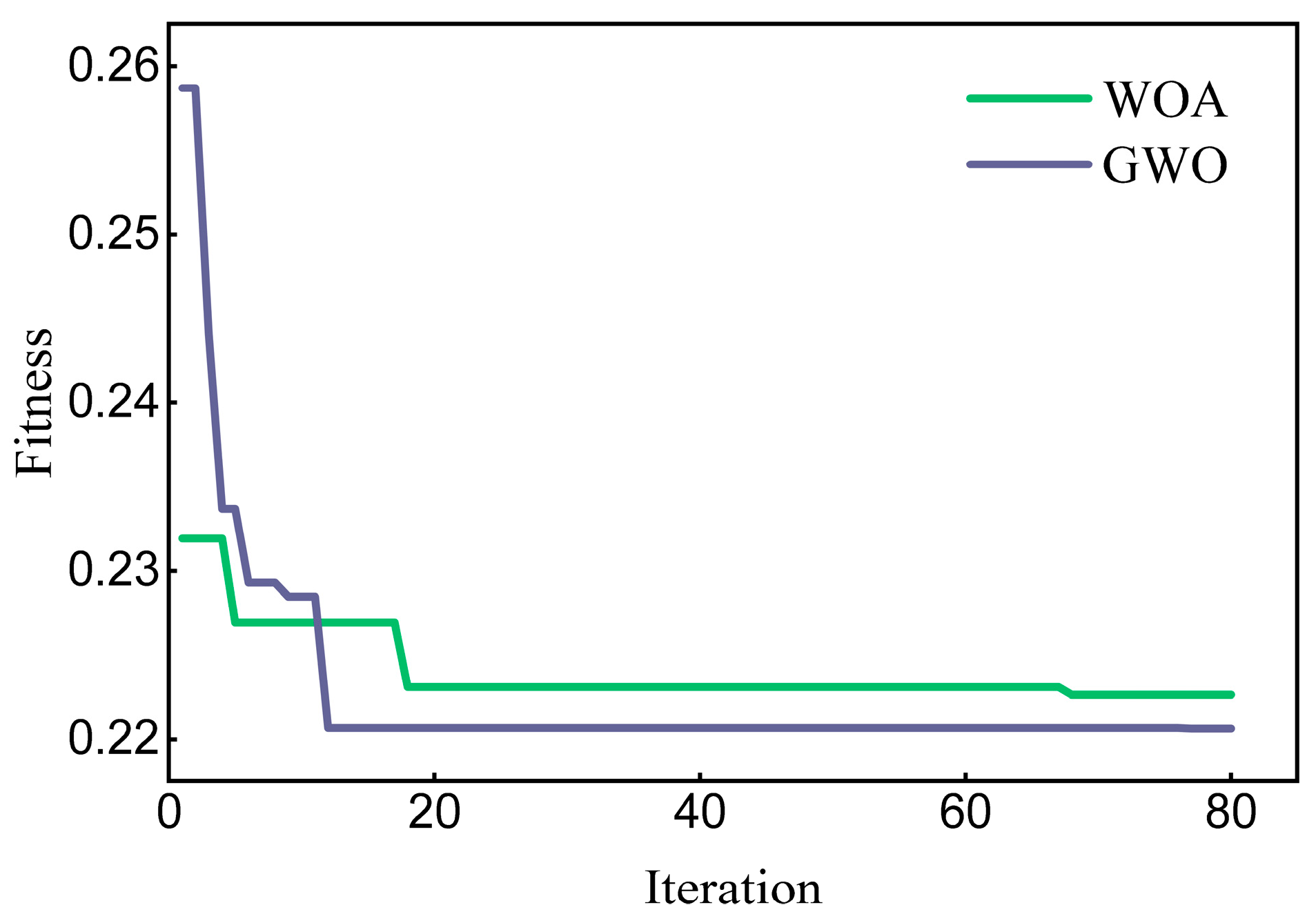
- Intelligent optimization algorithms help the base model find suitable parameters, reduce the trial-and-error time, and improve the efficiency of model operation. In this study, the GWO algorithm has demonstrated superiority over WOA in finding the optimal parameters for LightGBM, leading to more accurate prediction outcomes in the experimental set up.
- The residual term contains rich data signals, and decomposing the residual sequence can decompose the non-smooth, non-linear sequence into multiple regular subsequences, which in turn greatly improves the prediction degree of precision of the model. Compared to EEMD, CEEMDAN is more capable of decomposing residuals.
- Suitable input feature indicators are crucial for model prediction. As the internet develops, people today increasingly tend to seek help online after becoming ill. Thus, the Baidu Index can provide abundant information about a certain disease.
- Although multiple Baidu Index metrics influence the variability trends of influenza-like illness, it is inevitable in our research to subjectively select relevant Baidu Index metrics for analysis. However, in order to enhance objectivity and reliability in future studies, a more scientific and systematic approach to screening Baidu Index metrics can be explored in subsequent work, with the aim of refining the model and thereby providing more robust data support for influenza surveillance and early warning.
- This study introduces a model that is specifically tailored for predicting the percentage of influenza-like illness in the southern region of China. However, the limitation in obtaining detailed data from individual provinces and cities within Southern China impeded our ability to accurately evaluate the model’s performance at these more granular geographical levels. Hence, the applicability of the model across specific regions in Southern China remains an open question for further investigation. Future research should concentrate on this issue to determine whether the model possesses predictive accuracy at more detailed regional levels.
- Despite significant improvements with the proposed model, integrating GWO, LightGBM, and CEEMDAN, there is still ample room for further refinement. Future research endeavours could fruitfully investigate the incorporation of an ensemble learning strategy into the GWO-LightGBM model, followed by the application of a decomposition technique, to ascertain whether this approach can yield superior predictive outcomes.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Krammer, F.; Smith, G.J.D.; Fouchier, R.A.M.; Peiris, M.; Kedzierska, K.; Doherty, P.C.; Palese, P.; Shaw, M.L.; Treanor, J.; Webster, R.G.; et al. Influenza. Nat. Rev. Dis. Primers 2018, 4, 3. [Google Scholar] [CrossRef]
- Li, H.; Ge, M.; Wang, C. Spatio-temporal evolution patterns of influenza incidence and its nonlinear spatial correlation with environmental pollutants in China. BMC Public Health 2023, 23, 1685. [Google Scholar] [CrossRef]
- Lei, H.; Yang, L.; Wang, G.; Zhang, C.; Xin, Y.; Sun, Q.; Zhang, B.; Chen, T.; Yang, J.; Huang, W.; et al. Transmission Patterns of Seasonal Influenza in China between 2010 and 2018. Viruses 2022, 14, 2063. [Google Scholar] [CrossRef]
- World Health Organization. Influenza (Seasonal). Available online: https://www.who.int/news-room/fact-sheets/detail/influenza- (accessed on 6 March 2024).
- Qian, C.; Dai, Q.G.; Xu, K.; Deng, F.; Huo, X. Application of the moving epidemic interval method in assessing the intensity of influenza epidemics in Jiangsu Province, China. Chin. J. Health Stat. 2020, 37, 10–13+17. [Google Scholar]
- Xue, H.; Zhang, L.; Liang, H.; Kuang, L.; Han, H.; Yang, X.; Guo, L. Influenza trend prediction method combining Baidu index and support vector regression based on an improved particle swarm optimization algorithm. AIMS Math 2023, 8, 25528–25549. [Google Scholar] [CrossRef]
- Amendolara, A.B.; Sant, D.; Rotstein, H.G.; Fortune, E. LSTM-based recurrent neural network provides effective short term flu forecasting. BMC Public Health 2023, 23, 1788. [Google Scholar] [CrossRef]
- Hu, X.; Hu, X.j. Comparative study of forecasting models for H1N1 influenza A epidemic in Xinjiang. Chin. J. Health Stat. 2011, 28, 342–343. [Google Scholar]
- Dai, H.; Zhou, N.; Ren, X.; Luo, P.; Yi, S.; Quan, M.; Zha, W.; Lv, Y. Epidemiologic characteristics and prediction of incidence trend of all types of influenza based on ARIMA model. Dis. Surveill. 2022, 37, 1338–1345. [Google Scholar]
- He, Z.; Tao, H. Epidemiology and ARIMA model of positive-rate of influenza viruses among children in Wuhan, China: A nine-year retrospective study. Int. J. Infect. Dis. 2018, 74, 61–70. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Leng, K.; Lu, Y.; Wen, L.; Qi, Y.; Gao, W.; Chen, H.; Bai, L.; An, X.; Sun, B.; et al. Epidemiological features and time-series analysis of influenza incidence in urban and rural areas of Shenyang, China, 2010–2018. Epidemiol. Infect. 2020, 148, e29. [Google Scholar] [CrossRef]
- Qian, C.S.; Jiang, C.Y.; Xia, H.; Zheng, Y.X.; Liu, X.H.; Yang, M.; Xia, T. Time series analysis and prediction modeling of the percentage of influenza-like illness visits in Shanghai, China. Shanghai J. Prev. Med. 2023, 35, 116–121. [Google Scholar]
- Qin, S.; Zhao, J.; Deng, P.; Zhang, Y.; Jiang, Y. Application of Joinpoint regression analysis in the trend of influenza incidence in Qinghai Province from 2005 to 2023. Chin. J. Dis. Control. Prev. 2024, 28, 1295–1300+1307. [Google Scholar] [CrossRef]
- Chen, Y.; Chu, C.W.; Chen, M.I.C.; Cook, A.R. The utility of LASSO-based models for real time forecasts of endemic infectious diseases: A cross country comparison. J. Biomed. Inform. 2018, 81, 16–30. [Google Scholar] [CrossRef]
- Signorini, A.; Segre, A.M.; Polgreen, P.M. The Use of Twitter to Track Levels of Disease Activity and Public Concern in the U.S. during the Influenza A H1N1 Pandemic. PLoS ONE 2011, 6, e19467. [Google Scholar] [CrossRef] [PubMed]
- Tsan, Y.-T.; Chen, D.-Y.; Liu, P.-Y.; Kristiani, E.; Nguyen, K.L.P.; Yang, C.-T. The Prediction of Influenza-like Illness and Respiratory Disease Using LSTM and ARIMA. Int. J. Environ. Res. Public Health 2022, 19, 1858. [Google Scholar] [CrossRef] [PubMed]
- Manohar, B.; Das, R. Artificial Neural Networks for the Prediction of Monkeypox Outbreak. Trop. Med. Infect. Dis. 2022, 7, 424. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.L.; Hu, C.; Wang, P.; Hong, D.h.; Zhang, T.Z. Research on Multidimensional Credit Evaluation Model for Electricity Customers Based on Marketing Big Data. J. Southwest Univ. 2022, 44, 198–208. [Google Scholar] [CrossRef]
- Liang, Y.; Lin, Y.; Lu, Q. Forecasting gold price using a novel hybrid model with ICEEMDAN and LSTM-CNN-CBAM. Expert Syst. Appl. 2022, 206, 117847. [Google Scholar] [CrossRef]
- Liao, J.W. Research on Artificial Intelligence Forecasting of International Crude Oil Prices Based on VMD-LSTM-ELMAN Models. J. Chengdu Univ. Technol. 2024, 51, 164–180. [Google Scholar]
- Ginsberg, J.; Mohebbi, M.H.; Patel, R.S.; Brammer, L.; Smolinski, M.S.; Brilliant, L. Detecting influenza epidemics using search engine query data. Nature 2009, 457, 1012–1014. [Google Scholar] [CrossRef]
- Yuan, Q.; Nsoesie, E.O.; Lv, B.; Peng, G.; Chunara, R.; Brownstein, J.S. Monitoring Influenza Epidemics in China with Search Query from Baidu. PLoS ONE 2013, 8, e64323. [Google Scholar] [CrossRef]
- Li, Z.; Liu, T.; Zhu, G.; Lin, H.; Zhang, Y.; He, J.; Deng, A.; Peng, Z.; Xiao, J.; Rutherford, S.; et al. Dengue Baidu Search Index data can improve the prediction of local dengue epidemic: A case study in Guangzhou, China. PLoS Negl. Trop. Dis. 2017, 11, e0005354. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhou, H.; Zheng, L.; Li, M.; Hu, B. Using the Baidu index to predict trends in the incidence of tuberculosis in Jiangsu Province, China. Front. Public Health 2023, 11, 1203628. [Google Scholar] [CrossRef] [PubMed]
- Huang, R.; Luo, G.; Duan, Q.; Zhang, L.; Zhang, Q.; Tang, W.; Smith, M.K.; Li, J.; Zou, H. Using Baidu search index to monitor and predict newly diagnosed cases of HIV/AIDS, syphilis and gonorrhea in China: Estimates from a vector autoregressive (VAR) model. BMJ Open 2020, 10, e036098. [Google Scholar] [CrossRef] [PubMed]
- Dai, S.; Han, L. Influenza surveillance with Baidu index and attention-based long short-term memory model. PLoS ONE 2023, 18, e0280834. [Google Scholar] [CrossRef] [PubMed]
- Mestre, G.; Portela, J.; Rice, G.; Muñoz San Roque, A.; Alonso, E. Functional time series model identification and diagnosis by means of auto- and partial autocorrelation analysis. Comput. Stat. Data Anal. 2021, 155, 107108. [Google Scholar] [CrossRef]
- Gianfreda, A.; Maranzano, P.; Parisio, L.; Pelagatti, M. Testing for integration and cointegration when time series are observed with noise. Econ. Model. 2023, 125, 106352. [Google Scholar] [CrossRef]
- Duan, Y.; Zhang, J.; Wang, X.; Feng, M.; Ma, L. Forecasting carbon price using signal processing technology and extreme gradient boosting optimized by the whale optimization algorithm. Energy Sci Eng 2024, 12, 810–834. [Google Scholar] [CrossRef]
- Jiang, J.; Zhang, X.; Yuan, Z. Feature selection for classification with Spearman’s rank correlation coefficient-based self-information in divergence-based fuzzy rough sets. Expert Syst. Appl. 2024, 249, 123633. [Google Scholar] [CrossRef]
- Eden, S.K.; Li, C.; Shepherd, B.E. Nonparametric Estimation of Spearman’s Rank Correlation with Bivariate Survival Data. Biometrics 2022, 78, 421–434. [Google Scholar] [CrossRef] [PubMed]
- Zhong, M.X.; Xie, X.R. Clinical characterization of diabetic ketoacidosis combined with novel coronavirus pneumonia. Tianjin Med. J. 2023, 51, 1378–1381. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A highly efficient gradient boosting decision tree. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4 December 2017; pp. 3149–3157. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann Statist 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Cai, X.; Li, D.; Feng, L. Enhanced Carbon Price Forecasting Using Extended Sliding Window Decomposition with LSTM and SVR. Mathematics 2024, 12, 3713. [Google Scholar] [CrossRef]
- Hodson, T.O. Root-mean-square error (RMSE) or mean absolute error (MAE): When to use them or not. Geosci. Model Dev. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Zhang, X.-x.; Gu, L.-l.; Chen, H.; Jia, G.-z. Study on the influence of surrounding urban SO, NO, and CO on haze formation in Beijing based on MF-DCCA and boosting algorithms. Concurr. Comput. Pract. Exp. 2020, 32, e5921. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef] [PubMed]
- Shaik, N.B.; Jongkittinarukorn, K.; Bingi, K. XGBoost based enhanced predictive model for handling missing input parameters: A case study on gas turbine. Case Stud. Chem. Environ. Eng. 2024, 10, 100775. [Google Scholar] [CrossRef]
- Ihssan, S.; Shaik, N.B.; Belouaggadia, N.; Jammoukh, M.; Nasserddine, A. Enhancing PEHD pipes reliability prediction: Integrating ANN and FEM for tensile strength analysis. Appl. Surf. Sci. Adv. 2024, 23, 100630. [Google Scholar] [CrossRef]
- Tian, L.; Feng, L.; Yang, L.; Guo, Y. Stock price prediction based on LSTM and LightGBM hybrid model. J. Supercomput. 2022, 78, 11768–11793. [Google Scholar] [CrossRef]
- Guo, J.; Yun, S.; Meng, Y.; He, N.; Ye, D.; Zhao, Z.; Jia, L.; Yang, L. Prediction of heating and cooling loads based on light gradient boosting machine algorithms. Build. Environ. 2023, 236, 110252. [Google Scholar] [CrossRef]
- Duan, Y.; Zhang, J.; Wang, X. Henry Hub monthly natural gas price forecasting using CEEMDAN–Bagging–HHO–SVR. Front. Energy Res. 2023, 11, 1323073. [Google Scholar] [CrossRef]

| Count | Mean | Std | Min | 25% | 50% | 75% | Max | |
|---|---|---|---|---|---|---|---|---|
| Training set | 209 | 3.751 | 1.281 | 2.200 | 3.000 | 3.500 | 4.000 | 13.000 |
| Testing set | 52 | 5.706 | 2.335 | 1.400 | 4.275 | 5.450 | 7.125 | 10.100 |
| Category | Keywords |
|---|---|
| Common words | Cold(X1), influenza(X2), A influenza(X3), B influenza(X4), virus infection(X5), respiratory tract infection(X6), influenza virus(X7) |
| Prevention | Prevent the flu(X8), vaccination(X9), influenza vaccine(X10), mask(X11), alcohol(X12), disinfectant(X13), hand sanitizer(X14) |
| Symptoms | Fever(X15), high fever(X16), headache(X17), sore throat(X18), run at the nose(X19), sneeze(X20), nasal obstruction(X21), cough(X22), bronchitis(X23), diarrhea(X24), white lung(X25), leucocyte(X26), lymphocyte(X27) |
| Treatment | Nebulizer(X28), febrifuge(X29), ibuprofen(X30), Kuaike cold medication(X31), GanKang cold medication(X32), Tylenol(X33), oseltamivir(X34), ribavirin(X35), Suhuang Zhike Capsule(X36), antiviral oral liquid(X37) |
| Variable | Difference Order | t | p-Value | 1% | 5% | 10% |
|---|---|---|---|---|---|---|
| ILI% | 0 | −4.17 | 0.001 | −3.456 | −2.873 | −2.573 |
| 1 | −8.77 | 0.000 | −3.457 | −2.873 | −2.573 |
| Variable | Correlation Coefficient | p-Value | Variable | Correlation Coefficient | p-Value |
|---|---|---|---|---|---|
| X1 | 0.422 | 0.000 | X20 | 0.039 | 0.532 |
| X2 | 0.404 | 0.000 | X21 | 0.148 | 0.017 |
| X3 | 0.724 | 0.000 | X22 | 0.450 | 0.000 |
| X4 | 0.674 | 0.000 | X23 | 0.567 | 0.000 |
| X5 | 0.642 | 0.000 | X24 | −0.034 | 0.585 |
| X6 | 0.677 | 0.000 | X25 | 0.349 | 0.000 |
| X7 | 0.322 | 0.000 | X26 | 0.009 | 0.880 |
| X8 | 0.416 | 0.000 | X27 | 0.292 | 0.000 |
| X9 | −0.368 | 0.000 | X28 | 0.564 | 0.000 |
| X10 | 0.088 | 0.155 | X29 | 0.675 | 0.000 |
| X11 | −0.389 | 0.000 | X30 | 0.432 | 0.000 |
| X12 | −0.274 | 0.000 | X31 | 0.455 | 0.000 |
| X13 | −0.381 | 0.000 | X32 | 0.495 | 0.000 |
| X14 | −0.259 | 0.000 | X33 | 0.564 | 0.000 |
| X15 | 0.721 | 0.000 | X34 | 0.750 | 0.000 |
| X16 | 0.642 | 0.000 | X35 | 0.650 | 0.000 |
| X17 | −0.067 | 0.278 | X36 | 0.558 | 0.000 |
| X18 | 0.480 | 0.000 | X37 | 0.705 | 0.000 |
| X19 | 0.238 | 0.000 |
| Algorithm Name | Parameters Setting |
|---|---|
| XGBoost | Default |
| LightGBM | Default |
| WOA-LightGBM | Iterations = 30; noposs = 20; n_estimators = 38; num_leaves = 19; learning_rate = 0.082047; max_depth = 6 |
| GWO-LightGBM | Iterations = 30; noposs = 20; n_estimators = 10; num_leaves = 9; learning_rate = 0.020407; max_depth = 6 |
| Models | Parameter Optimization | Decomposition Technique |
|---|---|---|
| XGBoost (Model 1) | ||
| LightGBM (Model 2) | ||
| WOA-LightGBM (Model 3) | √ | |
| GWO-LightGBM (Model 4) | √ | |
| GWO-LightGBM-EEMD (Model 5) | √ | √ |
| GWO-LightGBM-CEEMDAN (Model 6) | √ | √ |
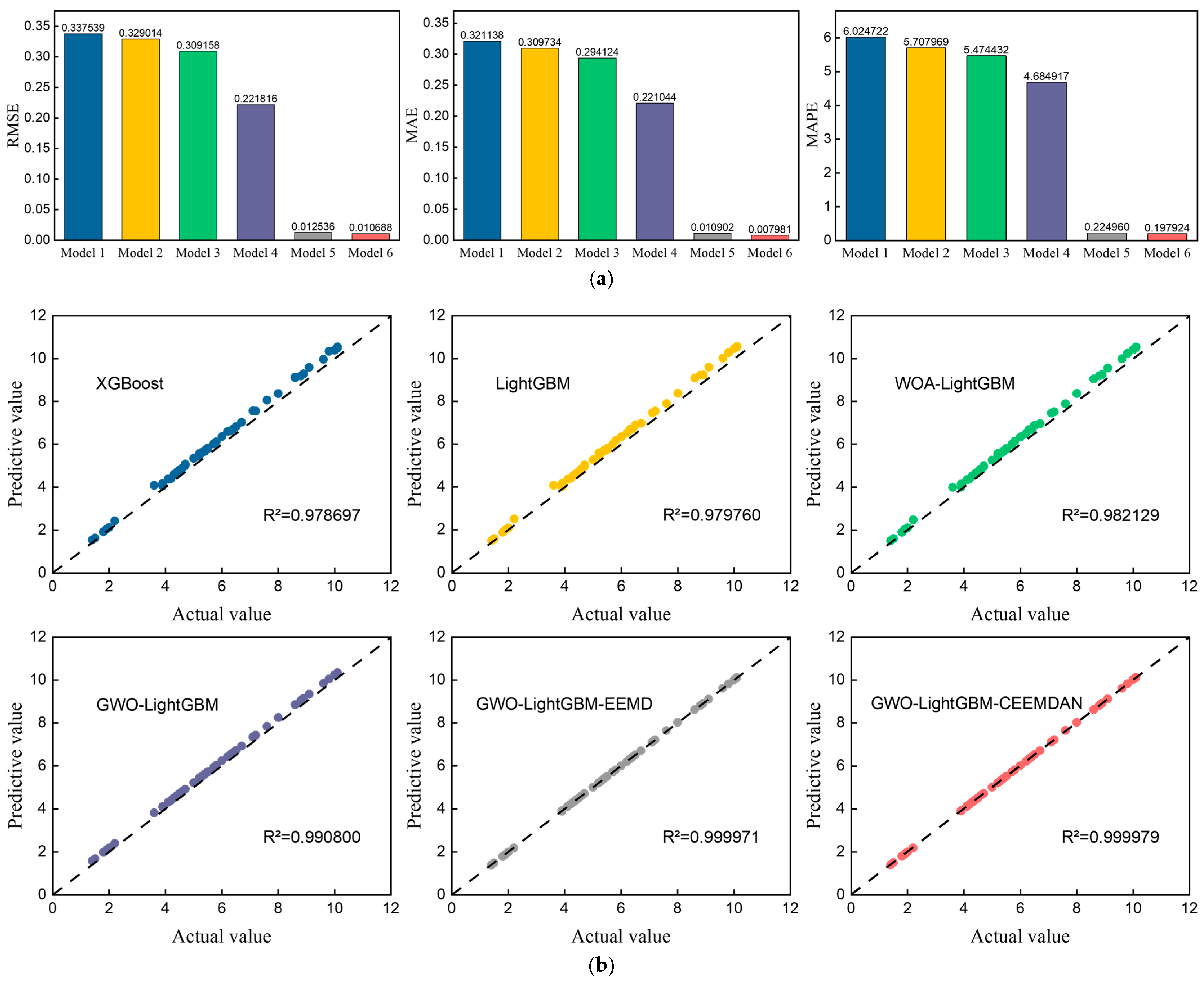
| Models | RMSE | MAE | MAPE | R2 |
|---|---|---|---|---|
| XGBoost | 0.337539 | 0.321138 | 6.024722 | 0.978697 |
| LightGBM | 0.329014 | 0.309734 | 5.707969 | 0.979760 |
| WOA-LightGBM | 0.309158 | 0.294124 | 5.474432 | 0.982129 |
| GWO-LightGBM | 0.221816 | 0.221044 | 4.684917 | 0.990800 |
| GWO-LightGBM-EEMD | 0.012536 | 0.010902 | 0.224960 | 0.999971 |
| GWO-LightGBM-CEEMDAN | 0.010688 | 0.007981 | 0.197924 | 0.999979 |
| Model | RMSE | MAE | MAPE | R2 |
|---|---|---|---|---|
| GWO-LightGBM-CEEMDAN (Model 6) | 0.010688 | 0.007981 | 0.197924 | 0.999979 |
| GWO-LightGBM-CEEMDAN’ (Model 7) | 0.012696 | 0.010001 | 0.213915 | 0.999970 |
| Benchmark Model | Comparative Model | RMSE | MAE | MAPE | ||
|---|---|---|---|---|---|---|
| 1 | LightGBM | VS. | GWO-LightGBM | 32.58% | 28.63% | 17.92% |
| 2 | GWO-LightGBM | VS. | GWO-LightGBM-EEMD | 94.35% | 95.07% | 95.20% |
| 3 | GWO-LightGBM-EEMD | VS. | GWO-LightGBM-CEEMDAN | 14.74% | 26.79% | 12.02% |
| 4 | GWO-LightGBM-CEEMDAN’ | VS. | GWO-LightGBM-CEEMDAN | 15.82% | 20.20% | 7.48% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, Y.; Li, C.; Wang, X.; Guo, Y.; Wang, H. Forecasting Influenza Trends Using Decomposition Technique and LightGBM Optimized by Grey Wolf Optimizer Algorithm. Mathematics 2025, 13, 24. https://doi.org/10.3390/math13010024
Duan Y, Li C, Wang X, Guo Y, Wang H. Forecasting Influenza Trends Using Decomposition Technique and LightGBM Optimized by Grey Wolf Optimizer Algorithm. Mathematics. 2025; 13(1):24. https://doi.org/10.3390/math13010024
Chicago/Turabian StyleDuan, Yonghui, Chen Li, Xiang Wang, Yibin Guo, and Hao Wang. 2025. "Forecasting Influenza Trends Using Decomposition Technique and LightGBM Optimized by Grey Wolf Optimizer Algorithm" Mathematics 13, no. 1: 24. https://doi.org/10.3390/math13010024
APA StyleDuan, Y., Li, C., Wang, X., Guo, Y., & Wang, H. (2025). Forecasting Influenza Trends Using Decomposition Technique and LightGBM Optimized by Grey Wolf Optimizer Algorithm. Mathematics, 13(1), 24. https://doi.org/10.3390/math13010024




