Study on Discrete Null-Field Equation Methods for Bounded Simply Connected Domains: Better Locations of Source Nodes

Abstract

The discrete null-field equation method (DNFEM) was proposed based on the null-field equation (NFE) of Green’s representation formulation, where only disk domains were discussed. However, the study of the DNFEM for bounded simply connected domains S is essential for practical applications. Since the source nodes must be located outside of a solution domain S, the first issue in computations is how to locate them. It includes two topics—Topic I: The source nodes must be located not only outside S but also outside the exterior boundary layers. The width of the exterior boundary layers is derived as $O(1/N)$, where N is the number of unknowns in the DNFEM. Topic II: There are numerous locations for source nodes outside the exterior boundary layers. Based on the sensitivity index, several better choices of pseudo-boundaries are studied for bounded simply connected domains. The advanced study of Topics I and II needs stability and error analysis. The bounds of condition numbers (Cond) are derived for bounded simply connected domains, and they are similar to those of the method of fundamental solutions (MFS). New error bounds are also provided for bounded simply connected domains. The thorough study of determining better locations of source nodes is also valid for the MFS and the discrete boundary integral equation method (DBIEM). The development of algorithms based on the NFE lags far behind that of the traditional boundary element method (BEM). Some progress has been made by following the MFS, and reported in this paper. From the theory and computations in this paper, the DNFEM may become a competent boundary method in scientific/engineering computing.

1. Introduction

Consider Laplace’s equation in 2D with the Dirichlet condition,

$$\begin{array}{ccc}\hfill & & \Delta u={\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}+{\displaystyle \frac{{\partial }^{2}u}{\partial y^2}}=0\mathrm{in}S,u=f\mathrm{on}\mathrm{\Gamma },\hfill \end{array}$$

(1)

where S is a bounded simply connected domain and $\mathrm{\Gamma }(=\partial S)$ is its smooth boundary. From the BEM theory (see [1,2]), Green’s representation formulas are given via different locations of the source nodes Q:

$$\begin{array}{ccc}\hfill & & {\int }_{\mathrm{\Gamma }}\{ln\left(\right|\overline{PQ}\left|\right){\displaystyle \frac{\partial u\left(\mathbf{y}\right)}{\partial \nu }}-u\left(\mathbf{y}\right){\displaystyle \frac{\partial ln\left(\right|\overline{PQ}\left|\right)}{\partial \nu }}\}d{s}_{\mathbf{y}}=\left\{\begin{array}{cc}-2\pi u\left(Q\right),\hfill & Q\in S,\hfill \\ -\pi u\left(Q\right),\hfill & Q\in \mathrm{\Gamma },\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \end{array}$$

(2)

where node $P=P\left(\mathbf{y}\right)\in \mathrm{\Gamma }$, and ${\displaystyle \frac{\partial }{\partial \nu }}$ denotes the outward normal derivative at $P\in \mathrm{\Gamma }$. We use the null-field equation (NFE) from the third equation of Equation (2):

$$\begin{array}{ccc}\hfill & & {\int }_{\mathrm{\Gamma }}ln\left(\right|\overline{PQ}\left|\right){\displaystyle \frac{\partial u\left(\mathbf{y}\right)}{\partial \nu }}d{s}_{\mathbf{y}}={\int }_{\mathrm{\Gamma }}u\left(\mathbf{y}\right){\displaystyle \frac{\partial ln\left(\right|\overline{PQ}\left|\right)}{\partial \nu }}d{s}_{\mathbf{y}},Q\in {\overline{S}}^c.\hfill \end{array}$$

(3)

Let $\mathrm{\Gamma }$ be divided into small ${\mathrm{\Gamma }}_j$ with the mesh spacings $h_j$, i.e., $\mathrm{\Gamma }={\cup }_{j=1}^N{\mathrm{\Gamma }}_j$. We assume that the mesh spacings $h_j$ are quasi-uniform satisfying ${\displaystyle \frac{{max}_j\left|h_j\right|}{{min}_j\left|h_j\right|}}\le C$, where C is a constant independent of N. Denote by $P_j$ the middle node of ${\mathrm{\Gamma }}_j$. By using the central rule to approximate Equation (3), we have the collocation equations

$$\begin{array}{ccc}\hfill & & \sum _{j=1}^N{h}_{j}ln\left(\right|\overline{P_j{Q}_i}\left|\right){\mu }_j=\sum _{j=1}^N{h}_j{u}_j{\displaystyle \frac{\partial ln\left(\right|\overline{P_j{Q}_i}\left|\right)}{\partial \nu }},i=1,2,...,M,M\ge N,\hfill \end{array}$$

(4)

where the unknown ${\mu }_j\approx {\displaystyle \frac{\partial u\left(P_j\right)}{\partial \nu }}$ at node $P=P_j\in {\mathrm{\Gamma }}_j$, $u_j=u\left(P_j\right)$ is known from the Dirichlet boundary condition in Equation (1), and ${\displaystyle \frac{\partial ln\left(\right|\overline{P_{j}Q}\left|\right)}{\partial \nu }}={\displaystyle \frac{\partial ln\left(\right|\overline{PQ}\left|\right)}{\partial \nu }}$ at $P_j\in {\mathrm{\Gamma }}_j$. Equation (4) is called the discrete null-field equation method (DNFEM). The traditional boundary element method (BEM) is based on the second equation of Equation (2):

$$\begin{array}{ccc}\hfill & & u\left(Q\right)=-{\displaystyle \frac{1}{\pi }}{\int }_{\mathrm{\Gamma }}\{ln\left(\right|\overline{PQ}\left|\right){\displaystyle \frac{\partial u\left(\mathbf{y}\right)}{\partial \nu }}-u\left(\mathbf{y}\right){\displaystyle \frac{\partial ln\left(\right|\overline{PQ}\left|\right)}{\partial \nu }}\}d{s}_{\mathbf{y}},Q\in \mathrm{\Gamma }.\hfill \end{array}$$

(5)

For $P\left(\mathbf{y}\right),Q\in \mathrm{\Gamma }$ in Equation (5), the troubles result from the singularity of the fundamental solution (FS) $ln\left(\right|\overline{PQ}\left|\right)$ when $Q\to P$.

Once the exterior normal derivatives ${\displaystyle \frac{\partial u\left(\mathbf{y}\right)}{\partial \nu }}$ on $\mathrm{\Gamma }$ have been obtained from Equations (4) and (5), the solutions at $Q\in S$ can be obtained from the first equation of Equation (2),

$$\begin{array}{ccc}\hfill & & u\left(Q\right)=-{\displaystyle \frac{1}{2\pi }}{\int }_{\mathrm{\Gamma }}\{ln\left(\right|\overline{PQ}\left|\right){\displaystyle \frac{\partial u\left(\mathbf{y}\right)}{\partial \nu }}-u\left(\mathbf{y}\right){\displaystyle \frac{\partial ln\left(\right|\overline{PQ}\left|\right)}{\partial \nu }}\}d{s}_{\mathbf{y}}.\hfill \end{array}$$

(6)

Similarly, by the central rule, from Equation (6), we have

$$\begin{array}{ccc}\hfill & & u\left(Q\right)=-{\displaystyle \frac{1}{2\pi }}\{\sum _{j=1}^N{h}_{j}ln\left(\right|\overline{P_{j}Q}\left|\right){\mu }_j-\sum _{j=1}^N{h}_j{\displaystyle \frac{\partial ln\left(\right|\overline{P_{j}Q}\left|\right)}{\partial \nu }}{u}_j\}.\hfill \end{array}$$

(7)

Equation (7) is also called the native scheme in Barnett [3], and it is accurate enough only for the solutions $u\left(Q\right)$ as $Q(\in S)$ outside the interior boundary layers. A further discussion is given in Section 3.

Equation (4) is denoted as

$$\begin{array}{ccc}\hfill & & \mathbf{A}\mathbf{x}=\mathbf{b},\hfill \end{array}$$

(8)

where the matrix $\mathbf{A}\in {\mathbf{R}}^{M\times N}(M\ge N)$, the vector $\mathbf{x}={\{{\mu }_1,{\mu }_2,...,{\mu }_N\}}^T\in {\mathbf{R}}^N$, and $\mathbf{b}\in {\mathbf{R}}^M$. The condition number and the effective condition number (Cond_eff) are given by

$$\begin{array}{ccc}\hfill & & \mathrm{Cond}={\displaystyle \frac{{\sigma }_{max}}{{\sigma }_{min}}},\mathrm{Cond}\_\mathrm{eff}={\displaystyle \frac{\parallel \mathbf{b}\parallel }{{\sigma }_{min}\parallel \mathbf{x}\parallel }},\hfill \end{array}$$

(9)

where $\parallel \mathbf{x}\parallel$ is the Euclidean norm, and ${\sigma }_{max}$ and ${\sigma }_{min}$ are the maximal and the minimal singular values of the matrix $\mathbf{A}$ in Equation (8), respectively.

In [4], the discussion for the DNFEM as Equation (4) was confined to disk domains. The early algorithms from the NFE were called the null-field equation method (NFEM) in [5,6,7]. In this paper, we will study the DNFEM for bounded simply connected domains S. More challenging problems arise: How do errors and ill-conditioning behave? How do we choose the source nodes outside S? In [4], the bounds of the condition number were derived only for disk domains, and only circular pseudo-boundaries were chosen. In fact, the main effort in [4] was devoted to dealing with the near singularity of Equation (6), and all numerical results were confined to disk domains.

The troubles from singularity in the integrals of Equation (5) hinder the BEM in practical applications. In contrast, no such troubles exist for Equations (3) and (4) because the derivatives of FS, such as ${\displaystyle \frac{\partial ln\left(\right|\overline{PQ}\left|\right)}{\partial \nu }}$, are highly smooth. The DNFEM and the BEM can be regarded as twins because they are based on Equations (3) and (4). It is expected that the DNFEM should be more advanced than the BEM. Unfortunately, little progress has been made for bounded simply connected domains in the existing literature. By following the method of fundamental solutions (MFS) in [8], some progress in the DNFEM has been made, and it is reported in this paper.

The source nodes are located not only outside S but also outside the exterior boundary layers to reach small numerical errors by the DNFEM, as in the MFS. This is the first topic to be studied in numerical computations. In this paper, the width $O\left({\displaystyle \frac{1}{N}}\right)$ of the exterior boundary layers is proved. The other topic is how to choose better pseudo-boundaries for the source nodes. The preliminary study of the MFS in [8] is valid for the DNFEM. To complete its study, we choose conformal mapping as in Katsurada and Okamoto [9], where the Fourier series in [4] was also used. Numerical comparisons are made for conformal mapping with other types of pseudo-boundaries, as in [8]. The sensitivity index is chosen as the criterion for better locations of source nodes, and it is closely related to the bounds of errors and condition numbers. A comprehensive study for better choices of source nodes is provided, and it is also valid for the MFS and the discrete boundary integral equation method (DBIEM). Hence, this paper is a continued study of the DNFEM in [4] but at an advanced level.

This paper is organized as follows. In the next section, a stability analysis is performed for bounded simply connected domains by linking the DNFEM to the MFS, and the error bounds are provided (proofs will appear elsewhere). In Section 3, the width of the exterior boundary layers is sought, and the conformal mapping using the Fourier series in [4] is employed for the pseudo-boundaries of source nodes. In Section 4, numerical experiments are carried out for peanut-like domains to support the algorithms proposed and the analysis performed. In Section 5, different types of pseudo-boundaries are tested numerically, and some comparisons are made for better numerical performance using the sensitivity index. In the last section, some concluding remarks are provided.

2. Stability and Error Analysis

2.1. Bounds of Conditions Between the DNFEM and MFS

The stability analysis performed in [4] was only for disk domains. In this section, the stability analysis is extended for bounded simply connected domains. We also link the DNFEM to the MFS and derive the bounds of the condition number (Cond). Below, we briefly describe the MFS. The solution is approximated by the linear combination of FS

$$\begin{array}{ccc}\hfill & & u_N=\sum _{i=1}^N{c}_{i}ln\left(\right|\overline{P{Q}_i}\left|\right),\hfill \end{array}$$

(10)

where the source nodes $Q_i\in {\mathrm{\Gamma }}_R$ and ${\mathrm{\Gamma }}_R$ is called the pseudo-boundary. Choose $P_j$ as the middle nodes of ${\mathrm{\Gamma }}_j$, and the mesh spacings $h_j$ are defined similarly as in Equation (4). We can obtain the collocation equations from the Dirichlet condition in Equation (1):

$$\begin{array}{ccc}\hfill & & {\displaystyle \sqrt{h_j}\sum _{i=1}^N{c}_{i}ln\left(\right|\overline{P_j{Q}_i}\left|\right)=\sqrt{h_j}f\left(P_j\right),j=1,2,...,M,M\ge N,}\hfill \end{array}$$

(11)

where $\sqrt{h_j}$ are weights. Equation (11) is called the MFS in [8,10,11] based on the collocation Trefftz method [11]. Once the coefficients $c_i$ have been obtained from Equation (11), the exterior normal derivatives on $\mathrm{\Gamma }$ are also obtained from Equation (10)

$$\begin{array}{ccc}\hfill & & {\displaystyle \frac{\partial u_N\left(P\right)}{\partial \nu }}=\sum _{i=1}^N{c}_i{\displaystyle \frac{\partial ln\left(\right|\overline{P{Q}_i}\left|\right)}{\partial \nu }},P\in \mathrm{\Gamma }.\hfill \end{array}$$

(12)

Since Equation (10) is valid in the entire solution domain S, it is simple to evaluate interior solutions in S using the MFS.

Equation (11) leads to an over-determined system:

$$\begin{array}{ccc}\hfill & & \mathbf{Fx}=\mathbf{d},\hfill \end{array}$$

(13)

where matrix $\mathbf{F}\in {\mathbf{R}}^{M\times N}(M\ge N)$, and vectors $\mathbf{x}={\{c_1,c_2,...,c_N\}}^T\in {\mathbf{R}}^N$ and $\mathbf{d}\in {\mathbf{R}}^M$. Similar to Equation (9), the condition number and the effective condition number are given by

$$\begin{array}{ccc}\hfill & & \mathrm{Cond}={\displaystyle \frac{{\sigma }_{max}}{{\sigma }_{min}}},\mathrm{Cond}\_\mathrm{eff}={\displaystyle \frac{\parallel \mathbf{d}\parallel }{{\sigma }_{min}\parallel \mathbf{x}\parallel }},\hfill \end{array}$$

(14)

where ${\sigma }_{max}$ and ${\sigma }_{min}$ are the maximal and the minimal singular values of the matrix $\mathbf{F}$ in Equation (13), respectively.

For disk domains S, we cite the results from [4] below.

Proposition 1. 

For disk domains, let the collocation and the source nodes be located uniformly on concentric circles. When $M\ge N$, the condition numbers of the DNFEM and the MFS are exactly the same.

We now study a bounded simply connected domain S. Let $M=N$ and the non-uniform partitions $\mathrm{\Gamma }={\cup }_{i=1}^N{\mathrm{\Gamma }}_i$, where $h_i$ is the boundary length of ${\mathrm{\Gamma }}_i$. Equation (11) in the MFS is rewritten as

$$\begin{array}{ccc}\hfill & & \sqrt{h_i}\sum _{j=1}^N{c}_{j}ln\left(\right|\overline{P_i{Q}_j}\left|\right)=\sqrt{h_i}f\left(P_i\right),i=1,2,...,N.\hfill \end{array}$$

(15)

Also, Equation (4) in the DNFEM is rewritten as

$$\begin{array}{ccc}\hfill & & \sum _{j=1}^N{h}_{j}ln\left(\right|\overline{P_j{Q}_i}\left|\right){\mu }_j=\sum _{j=1}^N{h}_j{u}_j{\displaystyle \frac{\partial ln\left(\right|\overline{P_j{Q}_i}\left|\right)}{\partial \nu }},i=1,2,...,N.\hfill \end{array}$$

(16)

Theorem 1. 

Let $M=N$, and suppose that the same $P(\in \mathrm{\Gamma }$) and Q outside Γ are chosen for both the DNFEM and the MFS. There exist the bounds

$$\begin{array}{ccc}& & {\left({\displaystyle \frac{{min}_i{h}_i}{{max}_i{h}_i}}\right)}^{{\displaystyle \frac{1}{2}}}\times \mathrm{Cond}\left(\mathbf{F}\right)\le \mathrm{Cond}\left(\mathbf{A}\right)\le {\left({\displaystyle \frac{{max}_i{h}_i}{{min}_i{h}_i}}\right)}^{{\displaystyle \frac{1}{2}}}\times \mathrm{Cond}\left(\mathbf{F}\right),\hfill \end{array}$$

(17)

where $\mathbf{A}$ and $\mathbf{F}$ are the coefficient matrices from Equations (16) and (15), respectively.

Proof. 

We find the entries of $\mathbf{A}=\left(A_{ij}\right)$ and $\mathbf{F}=\left(F_{ij}\right)$ from Equations (16) and (15):

$$\begin{array}{ccc}& & A_{ij}=h_{j}ln\left(\right|\overline{P_j{Q}_i}\left|\right)=\sqrt{h_j}(\sqrt{h_j}ln\left(\right|\overline{P_j{Q}_i}\left|\right)),F_{ij}=\sqrt{h_i}ln\left(\right|\overline{P_i{Q}_j}\left|\right).\hfill \end{array}$$

(18)

Define a diagonal matrix $\mathbf{D}=\mathrm{Diag}\{\sqrt{h_1},\sqrt{h_2},...,\sqrt{h_N}\}$. From Equation (18), we have $\mathbf{A}={\mathbf{F}}^T\mathbf{D}$ and $\mathbf{F}={\mathbf{D}}^{-1}{\mathbf{A}}^T$. Hence, we have

$$\begin{array}{ccc}& & \mathrm{Cond}\left(\mathbf{A}\right)\le \mathrm{Cond}\left(\mathbf{F}\right)\times \mathrm{Cond}\left(\mathbf{D}\right),\hfill \end{array}$$

(19)

$$\begin{array}{cc}& \mathrm{Cond}\left(\mathbf{F}\right)\le \mathrm{Cond}\left({\mathbf{D}}^{-1}\right)\times \mathrm{Cond}\left(\mathbf{A}\right)=\mathrm{Cond}\left(\mathbf{D}\right)\times \mathrm{Cond}\left(\mathbf{A}\right).\hfill \end{array}$$

(20)

For the diagonal matrix $\mathbf{D}$, we have

$$\begin{array}{ccc}& & \mathrm{Cond}\left(\mathbf{D}\right)={\displaystyle \frac{{max}_i\sqrt{h_i}}{{min}_i\sqrt{h_i}}}={\left({\displaystyle \frac{{max}_i{h}_i}{{min}_i{h}_i}}\right)}^{{\displaystyle \frac{1}{2}}}.\hfill \end{array}$$

(21)

Combining Equations (19)–(21) gives the desired result of Equation (17). □

Corollary 1. 

Let the conditions in Theorem 1 hold. For quasi-uniform partitions $\mathrm{\Gamma }={\cup }_{i=1}^N{\mathrm{\Gamma }}_i$, there exist the bounds

$$\begin{array}{ccc}& & c_0\mathrm{Cond}\left(\mathbf{F}\right)\le \mathrm{Cond}\left(\mathbf{A}\right)\le C\mathrm{Cond}\left(\mathbf{F}\right),\hfill \end{array}$$

(22)

where $c_0$ and C are two constants independent of N.

Below, we review the bounds of the condition number for the MFS, which are valid for the DNFEM as well. First, consider a circular boundary $\mathrm{\Gamma }$ with radius $\rho$, and choose a circular pseudo-boundary ${\mathrm{\Gamma }}_R$ with radius $R>\rho$. There exists the bound from [8] (p. 59),

$$\begin{array}{ccc}\hfill & & \mathrm{Cond}\le {\displaystyle \frac{N|lnR|}{2}}{\left({\displaystyle \frac{R}{\rho }}\right)}^{{\displaystyle \frac{N}{2}}},R\ne 1.\hfill \end{array}$$

(23)

For a non-circular boundary $\mathrm{\Gamma }$, denote $r_{min}{=max\rho |}_{\mathrm{\Gamma }}$. Suppose that there exists a positive constant $\gamma (\ge 1)$ independent of N such that

$$\begin{array}{ccc}\hfill & & {\parallel v\parallel }_{1,\mathrm{\Gamma }}\le C{N}^{\gamma }{\parallel v\parallel }_{0,\mathrm{\Gamma }},v\in V_N,\hfill \end{array}$$

(24)

where $V_N$ is the set from Equation (10) and C is a constant independent of N. The following bounds are derived in [8] (Chapter 6) as

$$\begin{array}{ccc}\hfill & & \mathrm{Cond}\le {\displaystyle \frac{N^{(1+\frac{\gamma }{2})}|lnR|}{2}}{\left({\displaystyle \frac{R}{r_{min}}}\right)}^{{\displaystyle \frac{N}{2}}},R\ne 1,\hfill \end{array}$$

(25)

where $\gamma \in [1,2]$ is a constant independent of N. For circular pseudo-boundaries, the condition $R\ne 1$ is given from Equations (23) and (25) for the discrete matrix $\mathbf{F}$ from the MFS. Otherwise, multiple solutions occur, and the degenerate scales are called.

For the non-circular/non-elliptic pseudo-boundary ${\mathrm{\Gamma }}_R$, the stability analysis is given in [8] (Chapter 15). Suppose that the domain boundary $\mathrm{\Gamma }$ is star-like, which can be denoted by a single-valued function $\rho =\rho \left(\theta \right)$, where $(\rho ,\theta )$ are polar coordinates. The outside pseudo-boundary ${\mathrm{\Gamma }}_R$ can also be chosen as the other single-valued function $\overline{\rho }=\overline{\rho }\left(\theta \right)$ ($>\rho \left(\theta \right))$. Denote ${\rho }_{min}\le \rho \le {\rho }_{max}$ and ${\overline{\rho }}_{min}\le \overline{\rho }\le {\overline{\rho }}_{max}$. Suppose that for the pseudo-boundary ${\mathrm{\Gamma }}_R$, no degenerate scales occur. Then, we have the following bounds of the MFS from [8] (Theorem 15.3.2):

$$\begin{array}{cc}& \mathrm{Cond}(\mathbf{F})=O\left(N^{(1+\frac{\gamma }{2})}{\left(\frac{{\overline{\rho }}_{max}+{\overline{\rho }}_{min}}{{\rho }_{max}+{\rho }_{min}}\right)}^{\beta N}\right),\hfill \end{array}$$

(26)

where $\beta \in [{\displaystyle \frac{1}{2}},1]$ and $\gamma (\ge 0)$ is also a constant independent of N.

Proposition 2. 

Let $u_{\nu }\in H^0\left(\mathrm{\Gamma }\right)$. Suppose that the quasi-uniform partition $\mathrm{\Gamma }={\cup }_{j=1}^N{\mathrm{\Gamma }}_j$ is chosen. For the DNFEM, the numerical solutions ${\mu }_j$ are small, to have

$$\begin{array}{ccc}\hfill & & \parallel \mathbf{x}\parallel =\sqrt{\sum _{j=1}^N{\mu }_j^2}=O\left(\sqrt{N}\right).\hfill \end{array}$$

(27)

Proof. 

Since ${\displaystyle \frac{h}{{min}_j{h}_j}}\le C$, where $h={max}_j{h}_j$, we have

$$\begin{array}{ccc}\hfill & & {\parallel \mathbf{x}\parallel }^2=\sum _{j=1}^N{\mu }_j^2\le \left(\underset{j}{max}{\displaystyle \frac{1}{h_j}}\right)\sum _{j=1}^N{h}_j{\mu }_j^2\approx \left({\displaystyle \frac{1}{{min}_j{h}_j}}\right)\sum _{j=1}^N{h}_j{\left({\displaystyle \frac{\partial u}{\partial \nu }}{|}_{P_j}\right)}^2\hfill \\ \hfill & & \le C{\displaystyle \frac{1}{h}}{\int }_{\mathrm{\Gamma }}{({\displaystyle \frac{\partial u}{\partial \nu }})}^{2}d\ell \le CN{\parallel u_{\nu }\parallel }_{0,\mathrm{\Gamma }}^2,\hfill \end{array}$$

(28)

which gives $\parallel \mathbf{x}\parallel \le C\sqrt{N}{\parallel u_{\nu }\parallel }_{0,\mathrm{\Gamma }}\le C\sqrt{N}$ and completes the proof of Proposition 2. □

2.2. Error Bounds of DNFEM

To differentiate from the stability analysis, the analytical approaches of the error analysis of the MFS in the existing literature are invalid for the DNFEM. A new error analysis for the DNFEM is explored by following the BEM using Galerkin approaches. Some key results are addressed. First, consider the pseudo-boundaries ${\mathrm{\Gamma }}_R$ outside $\overline{S}$, but not very close to its boundary $\mathrm{\Gamma }$, called the exterior boundary layers. We use piecewise polynomials of low degree, as in the BEM [2], and propose new algorithms called the discrete NFE method (DNFEM). The error bounds are derived, leading to polynomial convergence rates with low orders, as in the BEM. We may restate the algorithms from the DNFEM as the Galerkin approaches, as in [2] (p. 193). The Galerkin problem states the following: Let $u\in H^{{\displaystyle \frac{1}{2}}}\left(\mathrm{\Gamma }\right)$ and seek the solution $\mu \left(\mathbf{y}\right)\in H^{-{\displaystyle \frac{1}{2}}}\left(\mathrm{\Gamma }\right)$ such that

$$\begin{array}{ccc}\hfill & & b(\mu ,{\mu }^{\prime })=f(u,{\mu }^{\prime }),\forall {\mu }^{\prime }\in H^{-{\displaystyle \frac{1}{2}}}\left({\mathrm{\Gamma }}_R\right),\hfill \end{array}$$

(29)

where $H^{\pm {\displaystyle \frac{1}{2}}}\left(\mathrm{\Gamma }\right)$ is the Sobolev norm and

$$\begin{array}{ccc}\hfill & & b(\mu ,{\mu }^{\prime })={\int }_{{\mathrm{\Gamma }}_R}\left\{{\int }_{\mathrm{\Gamma }}ln\left(\mathbf{x},\mathbf{y}\right)\mu \left(\mathbf{y}\right)d{\sigma }_{\mathbf{y}}\right\}{\mu }^{\prime }\left(\mathbf{x}\right)d{\sigma }_{\mathbf{x}},\hfill \end{array}$$

(30)

$$\begin{array}{ccc}\hfill & & f(u,{\mu }^{\prime })={\int }_{{\mathrm{\Gamma }}_R}\left\{{\int }_{\mathrm{\Gamma }}u\left(\mathbf{y}\right){\displaystyle \frac{\partial ln\left(\mathbf{x},\mathbf{y}\right)}{\partial {\nu }_{\mathbf{y}}}}d{\sigma }_{\mathbf{y}}\right\}{\mu }^{\prime }\left(\mathbf{x}\right)d{\sigma }_{\mathbf{x}}.\hfill \end{array}$$

(31)

For simplicity, assume that S and $S_R$ are polygons with $S\subset S_R$, and ${\mathrm{\Gamma }}_R(=\partial S_R)$ is outside $\overline{S}$ but not very close to $\mathrm{\Gamma }$. Let $M=N$ and $\mathrm{\Gamma }={\cup }_{j=1}^N{\mathrm{\Gamma }}_j:={\mathrm{\Gamma }}^h$, where the subsections ${\mathrm{\Gamma }}_j$ are quasi-uniform with the maximal length $h={max}_j\left|{\mathrm{\Gamma }}_j\right|$. There exists the bound, ${\displaystyle \frac{h}{{min}_j\left|{\mathrm{\Gamma }}_j\right|}}\le C$, where C is a constant independent of N. Define by $V_h^p\left(\mathrm{\Gamma }\right)$ the collection of piecewise p-degree interpolation polynomials, as in the finite-element method (FEM) in Ciarlet [12]. For $p=0$, the constant is chosen on each ${\mathrm{\Gamma }}_j$; for $p=1$, the linear interpolation polynomial is given by the values at two boundary nodes of ${\mathrm{\Gamma }}_j$, and for $p=2,3$, the simple interpolation formulas can be found in [12] (p. 69) for uniform nodes on each ${\mathrm{\Gamma }}_j$. Since the construction of high p-degree interpolation polynomials is complicated, low-degree $p(\le 3)$ is then confined, as in the FEM in [12] and the BEM in Sauter and Schwab [2]. We choose $u_h(\in V_h^p\left(\mathrm{\Gamma }\right))$ as the piecewise p-degree polynomials, but ${\mu }_h(\in V_h^{p-1}\left(\mathrm{\Gamma }\right))$ and $v_{\overline{h}}\in V_{\overline{h}}^{p-1}\left({\mathrm{\Gamma }}_R\right)$ as the piecewise $(p-1)$-degree polynomials. Note that in each ${\mathrm{\Gamma }}_j$, the functions ${\mu }_h,u_h\in H^{\infty }\left({\mathrm{\Gamma }}_j\right)$ are highly smooth. Consider the Dirichlet problem with the known u on $\mathrm{\Gamma }$. For the DNFEM, the Galerkin problem states the following: Seek ${\mu }_h\in V_h^{p-1}\left(\mathrm{\Gamma }\right)$ such that

$$\begin{array}{ccc}\hfill & & b({\mu }_h,{\mu }^{\prime })=f(u_h,{\mu }^{\prime }),\forall {\mu }^{\prime }\in V_{\overline{h}}^{p-1}\left({\mathrm{\Gamma }}_R\right),\hfill \end{array}$$

(32)

where $u_h\in V_h^p\left(\mathrm{\Gamma }\right)$ denotes the piecewise p-degree interpolation polynomials from the known Dirichlet values. When the integrals involve numerical approximations, Equation (32) restates the following: Seek ${\widehat{\mu }}_h\left(\mathbf{y}\right)\in V_h^{p-1}\left(\mathrm{\Gamma }\right)$ such that

$$\begin{array}{ccc}\hfill & & \widehat{b}({\widehat{\mu }}_h,w_{\overline{h}})=\widehat{f}(u_h,w_{\overline{h}}),\forall w_{\overline{h}}\in V_{\overline{h}}^{p-1}\left({\mathrm{\Gamma }}_R\right),\hfill \end{array}$$

(33)

where

$$\begin{array}{ccc}\hfill & & \widehat{b}({\widehat{\mu }}_h,w_{\overline{h}})={\widehat{\int }}_{{\mathrm{\Gamma }}_R}\left\{{\widehat{\int }}_{\mathrm{\Gamma }}ln\left(\mathbf{x},\mathbf{y}\right){\widehat{\mu }}_h\left(\mathbf{y}\right)d{\sigma }_{\mathbf{y}}\right\}{w}_{\overline{h}}\left(\mathbf{x}\right)d{\sigma }_{\mathbf{x}},\hfill \end{array}$$

(34)

$$\begin{array}{ccc}\hfill & & \widehat{f}(u_h,w_{\overline{h}})={\widehat{\int }}_{{\mathrm{\Gamma }}_R}\left\{{\widehat{\int }}_{\mathrm{\Gamma }}{u}_h\left(\mathbf{y}\right){\displaystyle \frac{\partial ln\left(\mathbf{x},\mathbf{y}\right)}{\partial {\nu }_{\mathbf{y}}}}d{\sigma }_{\mathbf{y}}\right\}{w}_{\overline{h}}\left(\mathbf{x}\right)d{\sigma }_{\mathbf{x}},\forall w_{\overline{h}}\left(\mathbf{x}\right)\in V_{\overline{h}}^{p-1}\left({\mathrm{\Gamma }}_R\right),\hfill \end{array}$$

(35)

where ${\widehat{\int }}_{\mathrm{\Gamma }}$ and ${\widehat{\int }}_{{\mathrm{\Gamma }}_R}$ are the numerical approximations of ${\int }_{\mathrm{\Gamma }}$ and ${\int }_{{\mathrm{\Gamma }}_R}$, respectively.

For the bilinear form $b(·,·)$ in Equation (29), suppose that the inf-sup conditions hold:

$$\begin{array}{ccc}\hfill & & \underset{\mu \in H^{-{\displaystyle \frac{1}{2}}}\left(\mathrm{\Gamma }\right)\setminus \left\{0\right\}}{inf}\underset{{\mu }^{\prime }\in H^{-{\displaystyle \frac{1}{2}}}\left({\mathrm{\Gamma }}_R\right)\setminus \left\{0\right\}}{sup}{\displaystyle \frac{\left|b\right(\mu ,{\mu }^{\prime }\left)\right|}{{\parallel \mu \parallel }_{-\frac{1}{2},\mathrm{\Gamma }}{\parallel {\mu }^{\prime }\parallel }_{-\frac{1}{2},{\mathrm{\Gamma }}_R}}}\ge c_0>0,\hfill \end{array}$$

(36)

and

$$\begin{array}{ccc}\hfill & & \underset{\mu \in H^{-{\displaystyle \frac{1}{2}}}\left(\mathrm{\Gamma }\right)\setminus \left\{0\right\}}{sup}\left|b(\mu ,{\mu }^{\prime })\right|>0,\forall {\mu }^{\prime }\in H^{-{\displaystyle \frac{1}{2}}}\left({\mathrm{\Gamma }}_R\right)\setminus \left\{0\right\}.\hfill \end{array}$$

(37)

From Babuška and Aziz [13] and Sauter and Schwab [2] (p. 40), under Equations (36) and (37), there exists the unique solution $\mu \in H^{-{\displaystyle \frac{1}{2}}}\left(\mathrm{\Gamma }\right)$,

$$\begin{array}{ccc}\hfill & & {\parallel \mu \parallel }_{-{\displaystyle \frac{1}{2}},\mathrm{\Gamma }}\le {\displaystyle \frac{1}{c_0}}sup{\displaystyle \frac{\left|f\right(u,{\mu }^{\prime }\left)\right|}{\parallel {\mu }^{\prime }{\parallel }_{-\frac{1}{2},{\mathrm{\Gamma }}_R}}}\le C{\parallel u\parallel }_{{\displaystyle \frac{1}{2}},\mathrm{\Gamma }},\hfill \end{array}$$

(38)

where $c_0(>0)$ and C are two constants. Note that when ${\mathrm{\Gamma }}_R=\mathrm{\Gamma }$, Equations (29)–(38) lead to the corresponding equations of the BEM in [2] (p. 151).

The new inf-sup condition is proved and error bounds are derived elsewhere. Assume that $u\in H^{p+{\displaystyle \frac{3}{2}}}\left(S\right)(p=1,2,3)$. The optimal convergence rates are obtained:

$$\begin{array}{ccc}& & \parallel \mu -{\mu }_h{\parallel }_{-{\displaystyle \frac{1}{2}},\mathrm{\Gamma }}\le C{h}^{p+{\displaystyle \frac{1}{2}}}{\parallel u\parallel }_{p+{\displaystyle \frac{3}{2}},S},\parallel \mu -{\mu }_h{\parallel }_{0,\mathrm{\Gamma }}\le C{h}^p{\parallel u\parallel }_{p+{\displaystyle \frac{3}{2}},S},\hfill \end{array}$$

(39)

when h is the maximal boundary length of the quasi-uniform partition of $\mathrm{\Gamma }={\cup }_j{\mathrm{\Gamma }}_j$. Moreover, when numerical integrations are involved, we choose the quadrature rules with an accuracy of order p. The numerical solutions ${\widehat{\mu }}_h$ also have the optimal convergence rates:

$$\begin{array}{ccc}\hfill & & \parallel \mu -{\widehat{\mu }}_h{\parallel }_{-{\displaystyle \frac{1}{2}},\mathrm{\Gamma }}\le C{h}^{p+{\displaystyle \frac{1}{2}}}{\parallel u\parallel }_{p+{\displaystyle \frac{3}{2}},S},\parallel \mu -{\widehat{\mu }}_h{\parallel }_{0,\mathrm{\Gamma }}\le C{h}^p{\parallel u\parallel }_{p+{\displaystyle \frac{3}{2}},S}.\hfill \end{array}$$

(40)

In computation, we choose the central rule (or the trapezoidal rule), which can be regarded as the linear element (i.e., $p=1$). Then, from Equation (40), we have

$$\begin{array}{ccc}\hfill & & \parallel \mu -{\widehat{\mu }}_h{\parallel }_{-{\displaystyle \frac{1}{2}},\mathrm{\Gamma }}\le C{h}^{p+{\displaystyle \frac{1}{2}}}{\parallel u\parallel }_{p+{\displaystyle \frac{3}{2}},S}=C{h}^{{\displaystyle \frac{3}{2}}}{\parallel u\parallel }_{{\displaystyle \frac{5}{2}},S}=O(h^{{\displaystyle \frac{3}{2}}})=O(N^{-{\displaystyle \frac{3}{2}}}),\hfill \end{array}$$

(41)

$$\begin{array}{ccc}\hfill & & \parallel \mu -{\widehat{\mu }}_h{\parallel }_{0,\mathrm{\Gamma }}=O\left(h\right)=\left(N^{-1}\right).\hfill \end{array}$$

(42)

Numerical results are provided in Section 5 to verify the error bounds in Equation (42).

Consider disk domains with radius a, and choose larger circular pseudo-boundaries with radius $R>a$. Also, the trapezoidal rule is used. Based on [8] (Chapter 2), finite terms of Fourier expansions of degree n are used:

$$\begin{array}{ccc}\hfill & & {\mu }_n={\mu }_n\left(\theta \right)=p_0+\sum _{k=1}^n(p_{k}cosk\theta +q_{k}sink\theta )\mathrm{on}\mathrm{\Gamma },\hfill \end{array}$$

(43)

where $\mu ={\displaystyle \frac{\partial u}{\partial \nu }}={\displaystyle \frac{\partial u}{\partial \rho }}$, and $p_k$ and $q_k$ are expansion coefficients. Denote by $V_n\left(\mathrm{\Gamma }\right)$ the collection of functions defined by Equation (43). For u and ${\mu }^{\prime }$, we also choose finite terms of Fourier expansions of degree n, and denote by $U_n\left(\mathrm{\Gamma }\right)$ and $W_n\left({\mathrm{\Gamma }}_R\right)$ their respective collections. The Galerkin problem from Equation (33) involving numerical integration is rewritten as follows: Let $u_n\in U_n\left(\mathrm{\Gamma }\right)$ and seek ${\widehat{\mu }}_n\in V_n\left(\mathrm{\Gamma }\right)$ such that

$$\begin{array}{ccc}\hfill & & \widehat{b}({\widehat{\mu }}_n,{\mu }^{\prime })=\widehat{f}(u_n,{\mu }^{\prime }),\forall {\mu }^{\prime }\in W_n\left({\mathrm{\Gamma }}_R\right).\hfill \end{array}$$

(44)

Suppose that the trapezoidal rule is used to approximate the NFE. For the solutions ${\widehat{\mu }}_n$ from Equation (44), the following error bounds can be derived:

$$\begin{array}{ccc}\hfill & & \parallel \mu -{\widehat{\mu }}_n{\parallel }_{-{\displaystyle \frac{1}{2}},\mathrm{\Gamma }}\le C\{{\displaystyle \frac{1}{n^{p+\frac{1}{2}}}}{\parallel u\parallel }_{p+{\displaystyle \frac{3}{2}},S}+\sqrt{n}{({\displaystyle \frac{a}{R}})}^{N-n}\}.\hfill \end{array}$$

(45)

When N is chosen to satisfy

$$\begin{array}{ccc}\hfill & & N\ge max\{2n+1,n+{\displaystyle \frac{(p+1)lnn}{ln\frac{R}{a}}}\},\hfill \end{array}$$

(46)

the optimal convergence rates can be achieved:

$$\begin{array}{ccc}\hfill & & \parallel \mu -{\widehat{\mu }}_n{\parallel }_{-{\displaystyle \frac{1}{2}},\mathrm{\Gamma }}=O\left({\displaystyle \frac{1}{n^{p+\frac{1}{2}}}}{\parallel u\parallel }_{p+{\displaystyle \frac{3}{2}},S}\right).\hfill \end{array}$$

(47)

For the error in the zero-norm, we have

$$\begin{array}{ccc}\hfill & & \parallel \mu -{\widehat{\mu }}_n{\parallel }_{0,\mathrm{\Gamma }}\le C\{{\displaystyle \frac{1}{n^p}}{\parallel u\parallel }_{p+{\displaystyle \frac{3}{2}},S}+n{({\displaystyle \frac{a}{R}})}^{N-n}\}.\hfill \end{array}$$

(48)

Under Equation (46), Equation (48) leads to

$$\begin{array}{ccc}\hfill & & \parallel \mu -{\widehat{\mu }}_n{\parallel }_{0,\mathrm{\Gamma }}=O\left({\displaystyle \frac{1}{n^p}}{\parallel u\parallel }_{p+{\displaystyle \frac{3}{2}},S}\right).\hfill \end{array}$$

(49)

3. Locations of Source Nodes

3.1. Width of Exterior Boundary Layers

In the DNFEM and the MFS, the source nodes are located not only outside S but also outside the exterior boundary layers $S_{\delta }^{+}$, which are similar to the interior boundary layers for the boundary layer computation in Section 4.4. One may ask, what is the width of the boundary layers ${\delta }_{ext}$ of $S_{\delta }^{+}$? It is shown below that ${\delta }_{ext}=O\left({\displaystyle \frac{1}{N}}\right)$. Since the maximal N in numerical computations is still finite, the source nodes $Q_i$ must be located at a larger distance of $O\left({\displaystyle \frac{1}{N}}\right)$ to $\mathrm{\Gamma }$. In Section 4.4, the solutions in the interior boundary layers can only be computed after the ${\mu }_j$ in Equation (4) with a given N are obtained. Since the widths of the interior and exterior boundary layers are similar, the width study in this subsection is more important for the DNFEM.

To explore the width of the exterior boundary layers, we need the error analysis in Section 2.2. For simplicity, we consider a disk domain with radius a and choose an outside circle ${\mathrm{\Gamma }}_R$ with radius $R=a(1+{\displaystyle \frac{1}{N}})\ne 1$. The radius $R\ne 1$ is given to bypass the degenerate scales (see Equations (23) and (25)). Suppose that the solution $u\in H^{p+{\displaystyle \frac{3}{2}}}\left(S\right)$ is highly smooth with large p. In the error bounds of Equation (48), the second term is dominant:

$$\begin{array}{ccc}\hfill & & \parallel \mu -{\widehat{\mu }}_n{\parallel }_{0,\mathrm{\Gamma }}=O\left(n{({\displaystyle \frac{a}{R}})}^{N-n}\right)=O\left(N{({\displaystyle \frac{1}{1+\frac{1}{N}}})}^{{\displaystyle \frac{N}{2}}}\right)=O\left(Ny\right),\hfill \end{array}$$

(50)

where we choose $N=2n+1$ and denote $y={({\displaystyle \frac{1}{1+\frac{1}{N}}})}^{{\displaystyle \frac{N}{2}}}$. For large N, we have

$$\begin{array}{ccc}\hfill & & lny=-{\displaystyle \frac{N}{2}}ln(1+{\displaystyle \frac{1}{N}})\approx -{\displaystyle \frac{N}{2}}{\displaystyle \frac{1}{N}}=-{\displaystyle \frac{1}{2}},y\approx exp(-{\displaystyle \frac{1}{2}})={\displaystyle \frac{1}{\sqrt{e}}}=O\left(1\right).\hfill \end{array}$$

(51)

From Equations (50) and (51), we find large errors, as $\parallel \mu -{\widehat{\mu }}_n{\parallel }_{0,\mathrm{\Gamma }}=O\left(N\right)$.

Next, suppose that small errors of $O\left(\epsilon \right)$, where $\epsilon \ll 1$, are required for precision. Then, we may choose a slightly larger circle ${\mathrm{\Gamma }}_R$ with radius $R=a(1+{\displaystyle \frac{2}{N}}ln({\displaystyle \frac{N}{\epsilon }}))\ne 1$. We have

$$\begin{array}{ccc}& & \parallel \mu -{\widehat{\mu }}_n{\parallel }_{0,\mathrm{\Gamma }}=O\left(n{({\displaystyle \frac{a}{R}})}^{N-n}\right)=O\left(N{\left({\displaystyle \frac{1}{1+\frac{2}{N}ln\left(\frac{N}{\epsilon }\right)}}\right)}^{{\displaystyle \frac{N}{2}}}\right)=O(N{y}^{+}),\hfill \end{array}$$

(52)

where $y^{+}={\left({\displaystyle \frac{1}{1+\frac{2}{N}ln(\frac{N}{\epsilon })}}\right)}^{{\displaystyle \frac{N}{2}}}$. Hence, we have

$$\begin{array}{ccc}\hfill & & ln\left(y^{+}\right)=-{\displaystyle \frac{N}{2}}ln\left(1+{\displaystyle \frac{2}{N}}ln({\displaystyle \frac{N}{\epsilon }})\right)\approx -{\displaystyle \frac{N}{2}}\left({\displaystyle \frac{2}{N}}ln({\displaystyle \frac{N}{\epsilon }})\right)=ln({\displaystyle \frac{\epsilon }{N}}),y^{+}\approx {\displaystyle \frac{\epsilon }{N}}.\hfill \end{array}$$

(53)

In contrast, from Equations (52) and (53), we obtain small errors, as $\parallel \mu -{\widehat{\mu }}_n{\parallel }_{0,\mathrm{\Gamma }}=O\left(\epsilon \right)\ll 1$.

We summarize the above results as a proposition.

Proposition 3. 

Consider disk domains with radius a and use the circular pseudo-boundaries with radius $R(>a)$ in the DNFEM. Suppose that the solution $u\in H^{p+{\displaystyle \frac{3}{2}}}\left(S\right)$ is highly smooth with large p. When choosing the circular pseudo-boundaries with radius $R=a(1+{\displaystyle \frac{1}{N}})\ne 1$, large errors of $\parallel \mu -{\widehat{\mu }}_n{\parallel }_{0,\mathrm{\Gamma }}=O\left(N\right)$ may occur. However, when choosing circular pseudo-boundaries with a slightly larger radius $R=a(1+{\displaystyle \frac{2}{N}})ln\left({\displaystyle \frac{N}{\epsilon }}\right)\ne 1$, small errors of $\parallel \mu -{\widehat{\mu }}_n{\parallel }_{0,\mathrm{\Gamma }}=O\left(\epsilon \right)$, where $\epsilon \ll 1$, can be achieved. Hence, the width of the exterior boundary layers is determined as ${\delta }_{ext}={\displaystyle \frac{a}{N}}$.

Consider the MFS, where the solution $u_N$ in Equation (10) is given from Equation (11). From [8] (Chapter 2), we have the error bounds:

$$\begin{array}{ccc}\hfill & & \parallel u-u_N{\parallel }_{0,\mathrm{\Gamma }}\le C\left({\displaystyle \frac{1}{N^p}}{\parallel u\parallel }_{p+{\displaystyle \frac{1}{2}},S}+{({\displaystyle \frac{a}{R}})}^{N-n}\right).\hfill \end{array}$$

(54)

When $N=2n+1$, the second dominant term leads to

$$\begin{array}{ccc}& & \parallel u-u_N{\parallel }_{0,\mathrm{\Gamma }}=O\left({({\displaystyle \frac{a}{R}})}^{N-n}\right).\hfill \end{array}$$

(55)

Based on Equation (55), we can similarly prove the following corollary for the MFS.

Corollary 2. 

Consider disk domains with radius a and use the circular pseudo-boundaries with radius $R>a$ in the MFS. When radius $R=a(1+{\displaystyle \frac{1}{N}})\ne 1$, we have $\parallel u-u_N{\parallel }_{0,\mathrm{\Gamma }}=O\left(1\right)$. When radius $R=a(1+{\displaystyle \frac{2}{N}}ln\left({\displaystyle \frac{1}{\epsilon }}\right))\ne 1$, we have $\parallel u-u_N{\parallel }_{0,\mathrm{\Gamma }}=O\left(\epsilon \right)$. The same width ${\delta }_{ext}={\displaystyle \frac{a}{N}}$ of the exterior boundary layers is also found for the MFS.

Define the boundary and domain errors for the DNFEM and the MFS by

$$\begin{array}{ccc}& & {\parallel ▵\mu \parallel }_{\infty ,\mathrm{\Gamma }}=\underset{\mathrm{\Gamma }}{max}{|▵\mu |,\parallel ▵\mu \parallel }_{0,\mathrm{\Gamma }}={\left\{{\int }_{\mathrm{\Gamma }}{(▵\mu )}^{2}d\ell \right\}}^{1/2},▵\mu =\mu -{\mu }_N,\hfill \\ & & {\parallel ϵ\parallel }_{\infty ,\mathrm{\Gamma }}=\underset{\mathrm{\Gamma }}{max}{\left|ϵ\right|,\parallel ϵ\parallel }_{0,\mathrm{\Gamma }}={\left\{{\int }_{\mathrm{\Gamma }}{ϵ}^{2}d\ell \right\}}^{1/2},\hfill \\ & & \parallel {ϵ}_{\nu }{\parallel }_{0,\mathrm{\Gamma }}={\left\{{\int }_{\mathrm{\Gamma }}{ϵ}_{\nu }^{2}d\ell \right\}}^{1/2},{\parallel ϵ\parallel }_{0,S}={\left\{{\int }_S{ϵ}^{2}ds\right\}}^{1/2},\hfill \end{array}$$

where $ϵ=u-u_N$, ${ϵ}_{\nu }=u_{\nu }-{\left(u_N\right)}_{\nu }$, and ${\mu }_N$ and $u_N$ are obtained from the DNFEM and the MFS, respectively.

To evaluate the width of the exterior boundary layers, we choose the solution $u(x,y)=cos\left(y\right)e^x$. The results are given in Table 1 and Table 2. The curves based on the results in Table 1 and Table 2 are given in Figure 1 and Figure 2. For $N=58$, we have ${\delta }_{ext}={\displaystyle \frac{1}{N}}=0.0172$. In Table 1 and Table 2, the large errors of $O\left(1\right)$ are given for $R=1.02\approx 1+{\delta }_{ext}$ in agreement with Proposition 3 and Corollary 2. Next, for the errors ${\parallel ▵\mu \parallel }_{0,\mathrm{\Gamma }}$, from Proposition 3, we use $R=a(1+d)$, where the theoretical width $d={\displaystyle \frac{2}{N}}ln\left({\displaystyle \frac{N}{\epsilon }}\right)$. Hence, when $N=58$ and $\epsilon =0.01,{10}^{-4}$, we have

$$\begin{array}{ccc}\hfill & & d={\displaystyle \frac{2}{N}}ln({\displaystyle \frac{N}{\epsilon }})=0.299,0.458.\hfill \end{array}$$

(56)

Table 1. The errors and condition numbers for the DNFEM using the circular pseudo-boundaries with radius $R=1+d$ and $M=2N$ for $N=58$ in the unit disk domain.

N	$\mathit{R}=1+\mathit{d}$	${\parallel \mathbf{▵}\mathit{\mu }\parallel }_{\mathit{\infty },\mathit{\Gamma }}$	${\parallel \mathbf{▵}\mathit{\mu }\parallel }_{0,\mathit{\Gamma }}$	Cond	Cond_eff	$\parallel \mathit{x}\parallel$	${\mathit{\sigma }}_{min}$
	1.001	$3.71\times {10}^2$	$8.18\times {10}^2$	$1.46\times {10}^1$	$1.33\times {10}^0$	$2.49\times {10}^3$	$3.15\times {10}^{-1}$
	1.002	$2.25\times {10}^2$	$5.11\times {10}^2$	$1.89\times {10}^1$	$1.37\times {10}^0$	$1.55\times {10}^3$	$2.41\times {10}^{-1}$
58	1.005	$1.17\times {10}^2$	$2.75\times {10}^2$	$2.99\times {10}^1$	$1.57\times {10}^0$	$8.36\times {10}^2$	$1.50\times {10}^{-1}$
	1.010	$3.85\times {10}^1$	$8.99\times {10}^1$	$3.89\times {10}^1$	$2.99\times {10}^0$	$2.74\times {10}^2$	$1.14\times {10}^{-1}$
	1.020	$5.08\times {10}^{-1}$	$9.86\times {10}^{-1}$	$3.16\times {10}^1$	$3.17\times {10}^1$	$1.03\times {10}^1$	$1.38\times {10}^{-1}$
	1.050	$5.34\times {10}^{-2}$	$1.18\times {10}^{-1}$	$7.88\times {10}^1$	$5.94\times {10}^1$	$8.20\times {10}^0$	$5.37\times {10}^{-2}$
	1.1	$1.72\times {10}^{-4}$	$3.57\times {10}^{-4}$	$2.95\times {10}^2$	$2.17\times {10}^2$	$8.13\times {10}^0$	$1.37\times {10}^{-2}$
58	1.3	$8.31\times {10}^{-12}$	$9.48\times {10}^{-12}$	$3.18\times {10}^4$	$2.27\times {10}^4$	$8.13\times {10}^0$	$1.08\times {10}^{-4}$
	1.5	$1.92\times {10}^{-10}$	$2.51\times {10}^{-10}$	$2.13\times {10}^6$	$1.22\times {10}^6$	$8.13\times {10}^0$	$1.69\times {10}^{-6}$
	2.0	$1.91\times {10}^{-7}$	$3.07\times {10}^{-7}$	$1.53\times {10}^{10}$	$3.76\times {10}^9$	$8.13\times {10}^0$	$4.04\times {10}^{-10}$

Table 2. The errors and condition numbers for the MFS using circular pseudo-boundaries with radius $R=1+d$ and $N=2M$ for $M=58$ in the unit disk domain.

M	$\mathit{R}=1+\mathit{d}$	${\parallel \mathit{ϵ}\parallel }_{\mathit{\infty },\mathit{\Gamma }}$	${\parallel \mathit{ϵ}\parallel }_{0,\mathit{\Gamma }}$	$\parallel {\mathit{ϵ}}_{\mathit{\nu }}{\parallel }_{0,\mathit{\Gamma }}$	${\parallel \mathit{ϵ}\parallel }_{0,\mathit{S}}$	Cond	Cond_eff	$\parallel \mathit{x}\parallel$	${\mathit{\sigma }}_{min}$
	1.001	$1.35\times {10}^0$	$2.59\times {10}^0$	$7.33\times {10}^1$	$1.81\times {10}^0$	$1.46\times {10}^1$	$2.49\times {10}^0$	$1.90\times {10}^0$	$6.77\times {10}^{-1}$
	1.002	$1.34\times {10}^0$	$2.63\times {10}^0$	$5.50\times {10}^1$	$1.84\times {10}^0$	$1.89\times {10}^1$	$2.98\times {10}^0$	$2.08\times {10}^0$	$5.18\times {10}^{-1}$
58	1.005	$1.20\times {10}^0$	$2.61\times {10}^0$	$1.54\times {10}^1$	$1.84\times {10}^0$	$2.99\times {10}^1$	$9.87\times {10}^0$	$1.01\times {10}^0$	$3.22\times {10}^{-1}$
	1.010	$1.19\times {10}^0$	$1.66\times {10}^0$	$4.89\times {10}^1$	$1.06\times {10}^0$	$3.89\times {10}^1$	$2.45\times {10}^0$	$5.34\times {10}^0$	$2.45\times {10}^{-1}$
	1.020	$3.67\times {10}^{-1}$	$4.87\times {10}^{-1}$	$2.88\times {10}^1$	$7.71\times {10}^{-2}$	$3.16\times {10}^1$	$1.69\times {10}^0$	$6.38\times {10}^0$	$2.97\times {10}^{-1}$
	1.050	$2.32\times {10}^{-2}$	$3.72\times {10}^{-2}$	$2.16\times {10}^0$	$3.01\times {10}^{-3}$	$7.88\times {10}^1$	$1.03\times {10}^1$	$2.71\times {10}^0$	$1.15\times {10}^{-1}$
	1.1	$8.67\times {10}^{-4}$	$1.31\times {10}^{-3}$	$7.62\times {10}^{-2}$	$1.06\times {10}^{-4}$	$2.95\times {10}^2$	$7.71\times {10}^1$	$1.42\times {10}^0$	$2.94\times {10}^{-2}$
58	1.3	$3.58\times {10}^{-8}$	$4.60\times {10}^{-8}$	$2.61\times {10}^{-6}$	$4.15\times {10}^{-9}$	$3.18\times {10}^4$	$2.05\times {10}^4$	$6.76\times {10}^{-1}$	$2.31\times {10}^{-4}$
	1.5	$2.40\times {10}^{-11}$	$1.93\times {10}^{-11}$	$1.07\times {10}^{-9}$	$1.99\times {10}^{-12}$	$2.13\times {10}^6$	$1.27\times {10}^6$	$6.95\times {10}^{-1}$	$3.64\times {10}^{-6}$
	2.0	$1.29\times {10}^{-14}$	$1.47\times {10}^{-14}$	$2.57\times {10}^{-14}$	$7.37\times {10}^{-15}$	$1.53\times {10}^{10}$	$2.93\times {10}^9$	$1.26\times {10}^0$	$8.67\times {10}^{-10}$

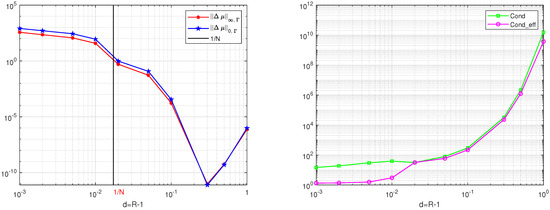
Figure 1. The curves via R from the results in Table 1 for $N=58$ for the DNFEM, for ${\parallel ▵\mu \parallel }_{0,\mathrm{\Gamma }}$, ${\parallel ▵\mu \parallel }_{\infty ,\mathrm{\Gamma }}$ (L), and for the Cond and the Cond_eff (R).

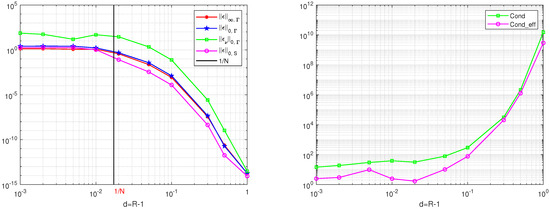
Figure 2. The curves via R from the results in Table 2 for $N=58$ for the MFS, for ${\parallel ϵ\parallel }_{\infty ,\mathrm{\Gamma }}$, ${\parallel ϵ\parallel }_{0,\mathrm{\Gamma }}$, $\parallel {ϵ}_{\nu }{\parallel }_{0,\mathrm{\Gamma }}$ and ${\parallel ϵ\parallel }_{0,S}$ (L), and for the Cond and the Cond_eff (R).

Since $h={\displaystyle \frac{2\pi }{N}}=0.108$ on $\mathrm{\Gamma }$, we find $d=2.8h,4.2h$ from Equation (56). In Table 1, small errors of $O\left({10}^{-3}\right)$ are shown for $R=1.1\approx 1+h$, which also supports the convergence results in Proposition 3. To achieve higher accuracy, the $5h$ rule was proposed by Barnett [3]. Later, more computations were carried out for the source nodes outside the exterior boundary layers (i.e., at least at a distance larger than $O\left({\displaystyle \frac{1}{maxN}}\right)$).

Next, for the DNFEM, when the source nodes are as far as $R\ge 1.5$, the errors become larger (see Table 1 and Figure 1) due to ill-conditioning. Hence, for the DNFEM, the source nodes should be chosen not too far from $\mathrm{\Gamma }$ (i.e., $R\in [1.1,1.3]$). However, for the MFS, source nodes far from $\mathrm{\Gamma }$ for $R=1.5,2.0$ are beneficial (see Table 2 and Figure 2). The locations of source nodes relative to $\mathrm{\Gamma }$ in the DNFEM are more sensitive than those in the MFS.

The term “boundary layers" originated from fluid mechanics, and the thickness (i.e., width) has been studied. In this paper, we also use the “boundary layers" resulting from the singularity of the FS: $ln\left(\right|\overline{PQ}\left|\right)$ as $Q\to P$. The exterior boundary layers occur for both the DNFEM and the MFS, but the interior boundary layers occur only for the DNFEM. In [3], the width of the interior boundary layers was studied for the boundary integral equation method (BIEM). In this paper, we explore the width of the exterior boundary layers for the DNFEM and the MFS, which is consistent with [3].

3.2. Pseudo-Boundaries from Conformal Mapping

For Jordan domains, conformal mapping was employed by Katsurada and Okamoto [9] to transform both the domain boundary and the pseudo-boundary into concentric circles. Then, exponential convergence rates were obtained for analytic solutions using the MFS. We use conformal mapping for the DNFEM (as well as the MFS) to find suitable pseudo-boundaries. We can express the coordinate functions using the Fourier series, as shown in [4]:

$$\begin{array}{ccc}\hfill & & x_n\left(\theta \right)=a_0+\sum _{k=1}^n{\rho }^k(a_{k}cosk\theta +b_{k}sink\theta ),y_n\left(\theta \right)={\overline{a}}_0+\sum _{k=1}^n{\rho }^k({\overline{a}}_{k}cosk\theta +{\overline{b}}_{k}sink\theta ),\hfill \end{array}$$

(57)

Let $L=2n+1$ and denote the uniform nodes on the unit circle $P_i^{\circ }=(cosih,sinih)$ with $h={\displaystyle \frac{2\pi }{L}}$. Also, denote the boundary nodes $P_i(x_i,y_i)\in \mathrm{\Gamma }$. The conformal mapping T from the unit circle to $\mathrm{\Gamma }$ in Equation (57) at $\rho =1$ can be defined, where the coefficients $a_k,b_k,{\overline{a}}_k$${\overline{b}}_k$ were obtained from [4]:

$$\begin{array}{ccc}\hfill & & a_0={\displaystyle \frac{1}{L}}\sum _{j=1}^L{x}_j,a_k={\displaystyle \frac{2}{L}}\sum _{j=1}^L{x}_{j}cos\left(k{\theta }_j\right),b_k={\displaystyle \frac{2}{L}}\sum _{j=1}^L{x}_{j}sin\left(k{\theta }_j\right),\hfill \end{array}$$

(58)

$$\begin{array}{ccc}\hfill & & {\overline{a}}_0={\displaystyle \frac{1}{L}}\sum _{j=1}^L{y}_j,{\overline{a}}_k={\displaystyle \frac{2}{L}}\sum _{j=1}^L{y}_{j}cos\left(k{\theta }_j\right),{\overline{b}}_k={\displaystyle \frac{2}{L}}\sum _{j=1}^L{y}_{j}sin\left(k{\theta }_j\right).\hfill \end{array}$$

(59)

Let the boundary $\mathrm{\Gamma }$ be defined by $(x,y)=\left(r\right(\theta )cos\theta ,r(\theta )sin\theta )$, where $r\left(\theta \right)$ is a function in polar coordinates. In Equations (58) and (59), we choose $x_j=r\left({\theta }_j\right)cos{\theta }_j$ and $y_j=r\left({\theta }_j\right)sin{\theta }_j$ with ${\theta }_j=jh$. The pseudo-boundary ${\mathrm{\Gamma }}_R$ of the source nodes can be determined using Equation (57) with small $\rho (>1)$. For $L=2n+2$, we choose the Fourier series:

$$\begin{array}{ccc}\hfill & & x_n\left(\theta \right)=a_0+\sum _{i=1}^n{\rho }^k(a_{k}cosk\theta +b_{k}sink\theta )+a_{n+1}{\rho }^{k+1}cos(n+1)\theta ,\hfill \end{array}$$

(60)

$$\begin{array}{ccc}\hfill & & y_n\left(\theta \right)={\overline{a}}_0+\sum _{i=1}^n{\rho }^k({\overline{a}}_{k}cosk\theta +{\overline{b}}_{k}sink\theta )+{\overline{a}}_{n+1}{\rho }^{k+1}cos(n+1)\theta .\hfill \end{array}$$

(61)

The conformal mapping T from $P_i^{\circ }$ to $P_i(x_i,y_i)$ with $i=1,2,\dots ,L$, is given by Equations (60) and (61) for $\rho =1$, where the Fourier coefficients are

$$\begin{array}{ccc}\hfill & & a_0={\displaystyle \frac{1}{L}}\sum _{j=1}^L{x}_j,a_{n+1}={\displaystyle \frac{1}{L}}\sum _{j=1}^L{x}_{j}cos(n+1){\theta }_j,\hfill \end{array}$$

(62)

$$\begin{array}{ccc}\hfill & & a_k={\displaystyle \frac{2}{L}}\sum _{j=1}^L{x}_{j}cos\left(k{\theta }_j\right),b_k={\displaystyle \frac{2}{L}}\sum _{j=1}^L{x}_{j}sin\left(k{\theta }_j\right),k=1,2,...,n,\hfill \end{array}$$

(63)

and

$$\begin{array}{ccc}\hfill & & {\overline{a}}_0={\displaystyle \frac{1}{L}}\sum _{j=1}^L{y}_j,{\overline{a}}_{n+1}={\displaystyle \frac{1}{L}}\sum _{j=1}^L{y}_{j}cos(n+1){\theta }_j,\hfill \end{array}$$

(64)

$$\begin{array}{ccc}\hfill & & {\overline{a}}_k={\displaystyle \frac{2}{L}}\sum _{j=1}^L{y}_{j}cos\left(k{\theta }_j\right),{\overline{b}}_k={\displaystyle \frac{2}{L}}\sum _{j=1}^L{y}_{j}sin\left(k{\theta }_j\right),k=1,2,...,n,\hfill \end{array}$$

(65)

where $x_j=r\left({\theta }_j\right)cos{\theta }_j$ and $y_j=r\left({\theta }_j\right)sin{\theta }_j$ with ${\theta }_j=jh$.

For disk domains S with radius a, the conformal mapping from a unit circle to a circle with radius a is given in Equations (57), (60) and (61) for $\rho =1$, where $a_1={\overline{b}}_1=a$, while all other coefficients $a_k,b_k,{\overline{a}}_k,{\overline{b}}_k$ are zero. In the general case, where $\mathrm{\Gamma }$ is defined by $(x,y)=\left(r\right(\theta )cos\theta ,r(\theta )sin\theta )$, nonzero coefficients $a_n,b_n,{\overline{a}}_n,{\overline{b}}_n$ arise. The conformal mappings in Equations (57), (60) and (61) are valid only for small values of $(\rho -1)$ and not for large values of L.

Proposition 4. 

Let $r=r\left(\theta \right)$ denote the conformal mapping, and suppose that the $2\pi$-periodic function $r\left(\theta \right)\in H^q(0,2\pi )$ with $q\ge 1$. For Fourier expansions in Equation (57), small values of $(\rho -1)$ and not large values of n (i.e., not large L) are required in applications. One necessary condition is

$$\begin{array}{ccc}\hfill & & {\displaystyle \frac{{\rho }^n}{n^q}}\le c_1,L=2n+1,\hfill \end{array}$$

(66)

where $c_1(>0)$ is a bounded constant independent of ρ and n. For the given n, the condition in Equation (66) leads to

$$\begin{array}{ccc}\hfill & & ln\rho \le {\displaystyle \frac{qlnn+ln{c}_1}{n}}.\hfill \end{array}$$

(67)

Proof. 

To find the conditions for the conformal mapping, we consider $x=r\left(\theta \right)cos\theta$ as an example. The function $r\left(\theta \right)$ can be expressed using a Fourier series as follows:

$$\begin{array}{ccc}\hfill & & r\left(\theta \right)={\alpha }_0+\sum _{k=1}^{\infty }({\alpha }_{k}cosk\theta +{\beta }_{k}sink\theta ),\hfill \end{array}$$

(68)

where ${\alpha }_k$ and ${\beta }_k$ are the true expansion coefficients. Then, we have

$$\begin{array}{ccc}\hfill & & r\left(\theta \right)cos\theta ={\alpha }_{0}cos\theta +\sum _{k=1}^{\infty }\left({\alpha }_{k}cosk\theta cos\theta +{\beta }_{k}sink\theta cos\theta \right)\hfill \\ \hfill & & ={\alpha }_{0}cos\theta +{\displaystyle \frac{1}{2}}\sum _{k=1}^{\infty }\left({\alpha }_k(cos(k+1)\theta +cos(k-1)\theta )+{\beta }_k(sin(k+1)\theta +sin(k-1)\theta )\right)\hfill \\ \hfill & & =a_0+\sum _{k=1}^{\infty }(a_{k}cosk\theta +b_{k}sink\theta ),\hfill \end{array}$$

(69)

where the coefficients in Equation (58) are determined by

$$\begin{array}{ccc}\hfill & & a_0={\displaystyle \frac{1}{2}}{\alpha }_1,a_1={\alpha }_0+{\displaystyle \frac{1}{2}}{\alpha }_2,b_1={\displaystyle \frac{1}{2}}{\beta }_2,\hfill \\ \hfill & & a_k={\displaystyle \frac{1}{2}}({\alpha }_{k-1}+{\alpha }_{k+1}),b_k={\displaystyle \frac{1}{2}}({\beta }_{k-1}+{\beta }_{k+1}),k=2,3,....\hfill \end{array}$$

(70)

Under the assumption $r\left(\theta \right)\in H^q(0,2\pi )$ with $q\ge 1$, we have the bounds for the coefficients in Equations (68) and (70):

$$\begin{array}{ccc}\hfill & & |{\alpha }_k|=O({\displaystyle \frac{1}{k^q}}),|{\beta }_k|=O({\displaystyle \frac{1}{k^q}}),|a_k|=O({\displaystyle \frac{1}{k^q}}),\left|b_k\right|=O({\displaystyle \frac{1}{k^q}}).\hfill \end{array}$$

(71)

From Equation (71), we have

$$\begin{array}{ccc}\hfill & & |x_n\left(\theta \right)|\le |a_0|+\sum _{k=1}^n{\rho }^k\left(\right|a_k\left|\right|cosk\theta |+|b_k\left|\right|sink\theta \left|\right)\hfill \\ \hfill & & \le |a_0|+\sum _{k=1}^n{\rho }^k\left(\right|a_k|+|b_k\left|\right)\le |a_0|+C\sum _{k=1}^n{\displaystyle \frac{{\rho }^k}{k^q}}.\hfill \end{array}$$

(72)

Since $|x_n\left(\theta \right)|$ is bounded, the last term, ${\displaystyle \frac{{\rho }^n}{n^q}}$, in the series ${\sum }_{k=1}^n{\displaystyle \frac{{\rho }^k}{k^q}}$ from Equation (72) must also be bounded, which leads to the necessary condition in Equation (66). Hence, small vallues of $(\rho -1)$ and not large values of n are required in applications. For a given n, the condition in Equation (67) follows directly from Equation (66). This completes the proof of Proposition 4. □

When $L=2n+2$, the Fourier expansions in Equations (60) and (61) are used. We take the peanut-like domain in Equation (85) below for testing purposes. Equations (60) and (61) work well when $L(=2n+2)\le 74$ and $\rho \le 1.32$, as shown in Figure 3, where only $M(=L)$ source nodes on ${\mathrm{\Gamma }}_R$ are shown. Other $M(>L)$ source nodes can also be obtained from the same pseudo-boundary ${\mathrm{\Gamma }}_R$ defined by Equations (60) and (61). When $\rho =1.64$, the source nodes at $L=26,74,150$ are illustrated in Figure 4. The source nodes at $L=150$ are useless, and some of them at $L=26,74$ are unacceptable. Several source nodes are too close to each other at $L=26$ and even located inside $\mathrm{\Gamma }$ at $L=74$. Figure 4 displays a failure of the conformal mapping for $\rho \ge 1.64$. To test the failure of the conformal mapping for large $L=2n+1$, we choose the same $\rho =1.13$ as shown in Figure 3. In Figure 5, failure occurs for $L\ge 640$, thus verifying the necessary condition in Proposition 4.

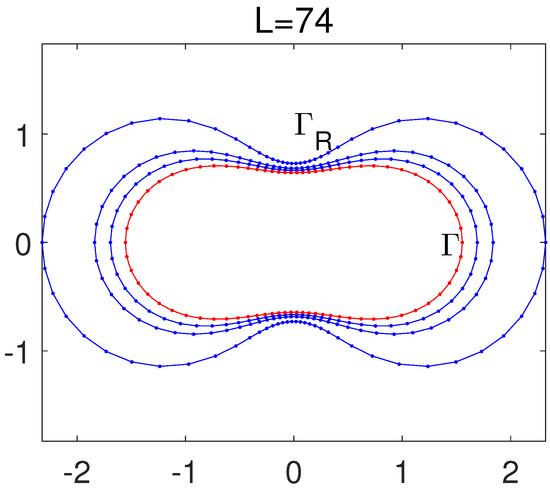
Figure 3. The boundary $\mathrm{\Gamma }$ of Equation (85) and the pseudo-boundaries ${\mathrm{\Gamma }}_R$ are plotted in Cartesian coordinates, with L source nodes given by the conformal mapping when $\rho =1.06,1.13,1.32$, and $L=74$.

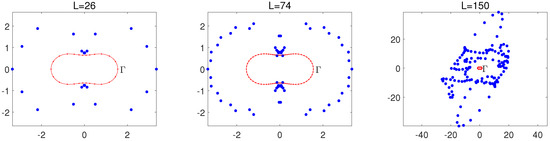
Figure 4. The boundary $\mathrm{\Gamma }$ of Equation (85) is plotted in Cartesian coordinates, with L source nodes given by the conformal mapping when $\rho =1.64$ and $L=26,74,150$.

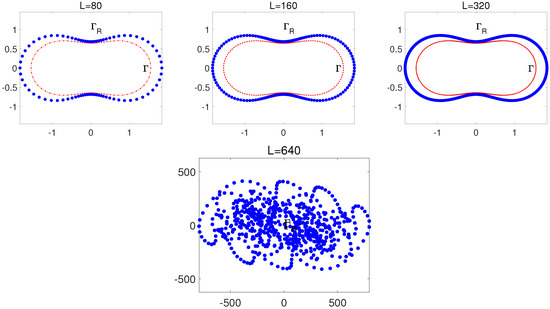
Figure 5. The boundary $\mathrm{\Gamma }$ of Equation (85) is plotted in Cartesian coordinates, with L source nodes given by the conformal mapping when $\rho =1.13$ and $L=80,160,320,640$.

In [9], the conformal mapping was carried out using complex functions. Let $N=2n+1$, and choose the complex transformation

$$\begin{array}{ccc}\hfill & & f\left(z\right)=\sum _{k=-n}^n{\alpha }_k{z}^k,\hfill \end{array}$$

(73)

where the complex function $f\left(z\right)=x\left(\theta \right)+\mathbf{i}y\left(\theta \right)$ with $x\left(\theta \right),y\left(\theta \right)\in \mathbf{R}$ and $\mathbf{i}=\sqrt{-1}$. The complex coefficients ${\alpha }_k={\beta }_k+\mathbf{i}{\gamma }_k$ with ${\alpha }_k,{\gamma }_k\in \mathbf{R}$. Choose the complex variable $z=\rho e^{\mathbf{i}\theta }$. From Equation (73), we have

$$\begin{array}{c}x\left(\theta \right)+\mathbf{i}y\left(\theta \right)=\sum _{k=-n}^n({\beta }_k+\mathbf{i}{\gamma }_k){\rho }^k{e}^{k\mathbf{i}\theta }=\sum _{k=-n}^n({\beta }_k+\mathbf{i}{\gamma }_k){\rho }^k(cosk\theta +\mathbf{i}sink\theta )\hfill \\ =\sum _{k=-n}^n{\rho }^k({\beta }_{k}cosk\theta -{\gamma }_{k}sink\theta )+\mathbf{i}\sum _{k=-n}^n{\rho }^k({\gamma }_{k}cosk\theta +{\beta }_{k}sink\theta )\hfill \\ ={\beta }_0+\sum _{k=1}^n\left\{({\rho }^k{\beta }_k+{\rho }^{-k}{\beta }_{-k})cosk\theta +(-{\rho }^k{\gamma }_k+{\rho }^{-k}{\gamma }_{-k})sink\theta )\right\}\hfill \\ +{\gamma }_0\mathbf{i}+\mathbf{i}\sum _{k=1}^n\left\{({\rho }^k{\gamma }_k+{\rho }^{-k}{\gamma }_{-k})cosk\theta +({\rho }^k{\beta }_k-{\rho }^{-k}{\beta }_{-k})sink\theta \right\}.\hfill \end{array}$$

(74)

Then, from Equation (74), we have

$$\begin{array}{ccc}\hfill & & x\left(\theta \right)=a_0+\sum _{k=1}^n{\rho }^k(a_{k}cosk\theta +b_{k}sink\theta ),y\left(\theta \right)={\overline{a}}_0+\sum _{k=1}^n{\rho }^k({\overline{a}}_{k}cosk\theta +{\overline{b}}_{k}sink\theta ),\hfill \end{array}$$

(75)

where the coefficients are given by

$$\begin{array}{ccc}\hfill & & a_0={\beta }_0,a_k={\beta }_k+{\rho }^{-2k}{\beta }_{-k},b_k=-{\gamma }_k+{\rho }^{-2k}{\gamma }_{-k},\hfill \\ \hfill & & {\overline{a}}_0={\gamma }_0,{\overline{a}}_k={\gamma }_k+{\rho }^{-2k}{\gamma }_{-k},{\overline{b}}_k={\beta }_k-{\rho }^{-2k}{\beta }_{-k}.\hfill \end{array}$$

(76)

When $\rho =1$, the conformal mapping in Equation (75) from [9] is equivalent to Equation (57) using the Fourier series (see [14], p.178). However, for $\rho \ne 1$, the two algorithms are slightly different. Hence, the pseudo-boundaries from [9] are also slightly different. Under some stronger analytic assumptions for the boundary $\mathrm{\Gamma }$ and the function f in Equation (1) (i.e., the analytic Jordan curve $\mathrm{\Gamma }$ and the analytic function f), the distance $|\rho -1|$ must be small but N may be large. Then, the fast Fourier transformation (FFT) can be used for large $N=2^{\ell }$ to save CPU time. The algorithms are given in [9] (p. 128).

Remark 1. 

In this paper, the number L is different from N, which is used in the DNFEM and the MFS. The L is confined to not be large (e.g., $L\le 74$ for $\rho =1.32$ or $L\le 320$ for $\rho =1.13$ for the peanut-like domain in Equation (85)), which may be smaller than N (even $L\ll N$) for some applications. For large N, we can use the known continuous curve in Figure 3 with $\rho \le 1.32$ and $L=72$. The source nodes $Q_i$ can be obtained directly from Equations (60) and (61) by ${\theta }_i=i{\displaystyle \frac{2\pi }{N}}$ (e.g., $N=10\times 2^k$) (see Section 5.2). Such algorithms are simple since the FFT in [9] can be bypassed. Hence, the small $(\rho -1)$ is only one key necessary condition of Proposition 4. Let us check the condition in Equation (66) again. If the boundary Γ is highly smooth with $r\left(\theta \right)\in H^q(0,2\pi )$, where q is large, both ρ and n in Equation (66) could be larger. When Γ is polygons or piecewise smooth curves, we have $r\left(\theta \right)\in H^0(0,2\pi )$ only. The conformal mapping fails because only $\rho =1$ is allowed from Equation (66) at $q=0$.

Remark 2. 

In Section 3.1, the width of the exterior boundary layers is studied for disk domains with circular pseudo-boundaries. In this remark, we seek the width of the exterior boundary layers for smooth domains when the pseudo-boundaries are obtained from the conformal mapping. For the conformal mapping, the width ${\delta }_{ext}$ of the exterior boundary layers can also be determined using the error estimates of the DNFEM. Consider both Γ and ${\mathrm{\Gamma }}_R$ to be highly smooth Jordan curves. By a one-by-one conformal mapping $g^{*}:\mathbf{R}\to \mathbf{C}$, Γ and ${\mathrm{\Gamma }}_R$ are, respectively, converted to a real axis and a parallel line in the complex plane (see Barnett ([3], Figure 2.1):

$$\begin{array}{ccc}& & {\mathrm{\Gamma }}_{{\alpha }^{*}}:=Z\{s=t+\mathbf{i}{\alpha }^{*},t\in [0,2\pi ],{\alpha }^{*}>0\}.\hfill \end{array}$$

(77)

For the analytic solutions from the DNFEM, using the trapezoidal rule, we have the following error bounds:

$$\begin{array}{ccc}& & \parallel \mu -{\widehat{\mu }}_n{\parallel }_{-{\displaystyle \frac{1}{2}},\mathrm{\Gamma }}\le C\sqrt{n}{e}^{-{\alpha }^{*}N}=O\left(\sqrt{N}{e}^{-{\alpha }^{*}N}\right),N=2n+1,\hfill \end{array}$$

(78)

$$\begin{array}{ccc}& & \parallel \mu -{\widehat{\mu }}_n{\parallel }_{0,\mathrm{\Gamma }}\le Cn{e}^{-{\alpha }^{*}N}=O\left(N{e}^{-{\alpha }^{*}N}\right),N=2n+1.\hfill \end{array}$$

(79)

When ${\alpha }^{*}={\displaystyle \frac{1}{N}}$, $\parallel \mu -{\widehat{\mu }}_n{\parallel }_{0,\mathrm{\Gamma }}=O\left(N\right)\gg 1$ from Equation (79). Thus, the DNFEM diverges. To achieve small $\parallel \mu -{\widehat{\mu }}_n{\parallel }_{0,\mathrm{\Gamma }}=O(\epsilon )$, a slightly larger ${\alpha }^{*}$ may be required to satisfy $N{e}^{-{\alpha }^{*}N}\le \epsilon \ll 1$. This yields

$$\begin{array}{ccc}& & {\alpha }^{*}\ge {\displaystyle \frac{1}{N}}(lnN-ln\epsilon )={\displaystyle \frac{1}{N}}ln({\displaystyle \frac{N}{\epsilon }}).\hfill \end{array}$$

(80)

The width ${\delta }_{ext}={\displaystyle \frac{1}{N}}$ is again found to coincide with Proposition 3 and Corollary 2 at $a=1$.

The conformal mapping $g^{*}:\mathbf{R}\to \mathbf{C}$ in Equation (77) is based on the Schwarz function in Davis [15]. In the complex plane, let $z=x+\mathbf{i}y$ and $\overline{z}=x-\mathbf{i}y$, and we have $x={\displaystyle \frac{z+\overline{z}}{2}}$ and $y={\displaystyle \frac{z-\overline{z}}{2\mathbf{i}}}$. A closed highly smooth contour $f(x,y)=0$ can be denoted by the analytic function $g(z,\overline{z})=g({\displaystyle \frac{z+\overline{z}}{2}},{\displaystyle \frac{z-\overline{z}}{2\mathbf{i}}})=0$, where g can be also regarded as a $2\pi$-periodical function in $z\in \mathbf{R}$. Thus, the boundary Γ of S is denoted by $g(z,0)=0$ with $z\in [0,2\pi ]$ and $\overline{z}=0$ (see [15], Chapters 2 and 5). We can relate the above mapping to the conformal mapping used here. Denote the other one-to-one conformal mapping $h^{*}:\mathbf{C}\to \mathbf{C}$ by $w=exp(-\mathbf{i}s)$. From Equation (77), we have

$$\begin{array}{ccc}\hfill & & w\left({\alpha }^{*}\right)=exp(-\mathbf{i}s)=exp(-\mathbf{i}(t+\mathbf{i}{\alpha }^{*}))=exp({\alpha }^{*}-\mathbf{i}t)=exp\left({\alpha }^{*}\right)\{cost-\mathbf{i}sint\}.\hfill \end{array}$$

(81)

Equation (81) also denotes circles with radii $e^{{\alpha }^{*}}$. When ${\alpha }^{*}={\displaystyle \frac{1}{N}}\ll 1$, we have $exp\left({\alpha }^{*}\right)\approx 1+{\alpha }^{*}$. By the composite conformal transformation $g^{*}\circ h^{*}$, the boundary Γ and the pseudo-boundary ${\mathrm{\Gamma }}_R$ are converted to a unit circle and a concentric circle with radius $1+{\alpha }^{*}$, as shown in this section. Hence, the width, ${\delta }_{ext}={\displaystyle \frac{1}{N}}$, of the exterior boundary layer is again confirmed. Hence, by using $\rho =e^{{\alpha }^{*}}$, Equation (57) is rewritten as

$$\begin{array}{ccc}& & x_n\left(\theta \right)=a_0+\sum _{k=1}^n{e}^{k{\alpha }^{*}}(a_{k}cosk\theta +b_{k}sink\theta ),y_n\left(\theta \right)={\overline{a}}_0+\sum _{k=1}^n{e}^{k{\alpha }^{*}}({\overline{a}}_{k}cosk\theta +{\overline{b}}_{k}sink\theta ).\hfill \end{array}$$

Remark 3. 

The study in this paper can be extended to n-dimensional (nD) Laplace’s equation in Equation (1). First, consider the 3D case. Since the FS is ${\displaystyle \frac{1}{|\overline{PQ}|}}$, the Green’s representation formula in Equation (2) is modified as follows (see Atkinson [16], p.430):

$$\begin{array}{ccc}\hfill & & {\int }_{\mathrm{\Gamma }}\left\{{\displaystyle \frac{1}{|\overline{PQ}|}}{\displaystyle \frac{\partial u\left(\mathbf{y}\right)}{\partial \nu }}-u\left(\mathbf{y}\right){\displaystyle \frac{\partial }{\partial \nu }}({\displaystyle \frac{1}{|\overline{PQ}|}})\right\}d{s}_{\mathbf{y}}=\left\{\begin{array}{cc}-4\pi u\left(Q\right),\hfill & Q\in S,\hfill \\ -2\pi u\left(Q\right),\hfill & Q\in \mathrm{\Gamma },\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \end{array}$$

(82)

where the node $P=P\left(\mathbf{y}\right)\in \mathrm{\Gamma }$. The NFE from the third equation of Equation (82) is given by

$$\begin{array}{ccc}\hfill & & {\int }_{\mathrm{\Gamma }}{\displaystyle \frac{1}{|\overline{PQ}|}}{\displaystyle \frac{\partial u\left(\mathbf{y}\right)}{\partial \nu }}d{s}_{\mathbf{y}}={\int }_{\mathrm{\Gamma }}u\left(\mathbf{y}\right){\displaystyle \frac{\partial }{\partial \nu }}({\displaystyle \frac{1}{|\overline{PQ}|}})d{s}_{\mathbf{y}},Q\in {\overline{S}}^c.\hfill \end{array}$$

(83)

For $n(\ge 3)$D, since the FS is given by ${\displaystyle \frac{1}{|\overline{PQ}{|}^{n-2}}}$ (see Chen and Zhou [17], p.214), the NFE is given by

$$\begin{array}{ccc}\hfill & & {\int }_{\mathrm{\Gamma }}{\displaystyle \frac{1}{|\overline{PQ}{|}^{n-2}}}{\displaystyle \frac{\partial u\left(\mathbf{y}\right)}{\partial \nu }}d{s}_{\mathbf{y}}={\int }_{\mathrm{\Gamma }}u\left(\mathbf{y}\right){\displaystyle \frac{\partial }{\partial \nu }}({\displaystyle \frac{1}{|\overline{PQ}{|}^{n-2}}})d{s}_{\mathbf{y}},Q\in {\overline{S}}^c.\hfill \end{array}$$

(84)

The algorithms of the DNFEM can be formulated similarly, where the source nodes $Q\in {\mathrm{\Gamma }}_R$ are located outside the boundary Γ. Since the conformal mapping in Section 3.2 can be extended to nD, the techniques for locating $Q\in {\mathrm{\Gamma }}_R$ in this paper can be developed further. Let us take the 3D case as an example. The conformal mapping in 3D is given in [8] (Section 13.2). The smooth surface Γ is converted using the conformal mapping T into a unit sphere with radius $\rho =1$. Then, the pseudo-surface ${\mathrm{\Gamma }}_R$ is obtained from the larger sphere with radius $\rho >1$ by applying its inverse transformation $T^{-1}$. For spheres, a distribution of good nodes is illustrated in ([8], p. 326). The collocation nodes on Γ and the source nodes on ${\mathrm{\Gamma }}_R$ can be found using $T^{-1}$. For the conformal mapping in Section 3.2, the techniques are simple and straightforward without solving linear algebraic equations. Such a remarkable advantage remains for the conformal mapping in 3D. For the DNFEM in 3D, the stability and error analysis in Section 2 needs to explored, and the width of the boundary layers in Section 3.1 can then be discussed similarly.

4. Numerical Experiments for Non-Disk Domains

4.1. Peanut-like Domains

Denote a peanut-like domain with the boundary $\mathrm{\Gamma }$ in polar coordinates by

$$\begin{array}{ccc}\hfill & & r\left(\theta \right)=\sqrt{cos\left(2\theta \right)+\sqrt{2-{sin}^2\left(2\theta \right)}},0\le \theta \le 2\pi .\hfill \end{array}$$

(85)

We have $r^{\prime }\left(\theta \right)=-{\displaystyle \frac{1}{2r\left(\theta \right)}}\{2sin\left(2\theta \right)+{\displaystyle \frac{sin4\theta }{\sqrt{1+{cos}^2\left(2\theta \right)}}}\}$, which yields $ds=\sqrt{r^2\left(\theta \right)+{\left(r^{\prime }\left(\theta \right)\right)}^2}d\theta$. Denote $h_j=\sqrt{r^2\left({\theta }_j\right)+{\left(r^{\prime }\left({\theta }_j\right)\right)}^2}▵\theta$, $▵\theta ={\displaystyle \frac{2\pi }{N}}$ and ${\theta }_j=j▵\theta$. The DNFEM solution ${\mu }_j$ and the MFS solution $c_i$ can be obtained from Equations (4) and (11), respectively. Suppose that the errors and the condition have exponential rates:

$$\begin{array}{ccc}\hfill & & {\parallel ▵\mu \parallel }_{0,\mathrm{\Gamma }},{\parallel {ϵ}_{\nu }\parallel }_{0,\mathrm{\Gamma }}=O\left(a^N\right),a<1;\mathrm{Cond}=O\left(b^N\right),b\ge 1.\hfill \end{array}$$

(86)

Define the sensitivity index $\alpha$ of the condition via errors by [8] (p. 345):

$$\begin{array}{ccc}\hfill & & \alpha =-{\displaystyle \frac{lnb}{lna}}>0,a<1\le b.\hfill \end{array}$$

(87)

The index $\alpha$ indicates the severity of the ill-conditioning. The smaller $\alpha$ is, the better the stability and numerical performance are achieved.

4.2. Numerical Results from the DNFEM and the MFS

We choose the source function in [8] (p. 376)

$$\begin{array}{ccc}\hfill & & u^{*}=u(x^{*},y^{*})=ln\left(\right|\overline{P{Q}^{*}}\left|\right),\hfill \end{array}$$

(88)

where the far node $Q^{*}=Q_{far}^{*}$ is outside $\mathrm{\Gamma }$ as $Q^{*}=Q_{far}^{*}=(x^{*},y^{*})=(0,3)$. The solution is highly smooth due to $Q^{*}(0,3)$ being far from $\mathrm{\Gamma }$ (see Figure 6). We choose the conformal mapping for the pseudo-boundaries, as shown in Figure 3, and list the results from the DNFEM in Table 3. In Table 3, we can see that for $\rho =1.06$,

$$\begin{array}{ccc}\hfill & & {\parallel ▵\mu \parallel }_{\infty ,\mathrm{\Gamma }}=O\left(N^{-1.66}\right)=O(0.{94}^N),{\parallel ▵\mu \parallel }_{0,\mathrm{\Gamma }}=O\left(N^{-1.80}\right)=O(0.{936}^N),\hfill \end{array}$$

(89)

$$\begin{array}{ccc}\hfill & & \mathrm{Cond}=O\left(N^{0.849}\right)=O(1.{03}^N),\alpha =0.447.\hfill \end{array}$$

(90)

For $\rho =1.13$,

$$\begin{array}{ccc}\hfill & & {\parallel ▵\mu \parallel }_{\infty ,\mathrm{\Gamma }}=O\left(N^{-2.12}\right)=O(0.{925}^N),{\parallel ▵\mu \parallel }_{0,\mathrm{\Gamma }}=O\left(N^{-2.40}\right)=O(0.{915}^N),\hfill \end{array}$$

(91)

$$\begin{array}{ccc}\hfill & & \mathrm{Cond}=O\left(N^{2.92}\right)=O(1.{11}^N),\alpha =1.17.\hfill \end{array}$$

(92)

For $\rho =1.32$,

$$\begin{array}{ccc}\hfill & & {\parallel ▵\mu \parallel }_{\infty ,\mathrm{\Gamma }}=O\left(N^{-2.56}\right)=O(0.{91}^N),{\parallel ▵\mu \parallel }_{0,\mathrm{\Gamma }}=O\left(N^{-3.19}\right)=O(0.{889}^N),\hfill \end{array}$$

(93)

$$\begin{array}{ccc}\hfill & & \mathrm{Cond}=O\left(N^{5.86}\right)=O(1.{24}^N),\alpha =1.83.\hfill \end{array}$$

(94)

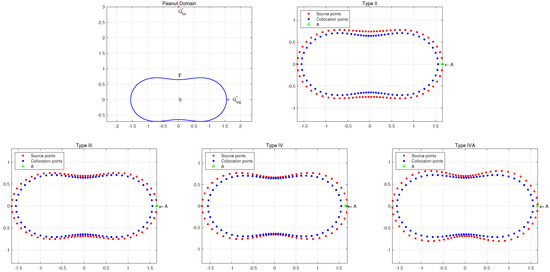
Figure 6. The boundary $\mathrm{\Gamma }$ with node $Q^{*}=Q_{far}^{*}=(x^{*},y^{*})=(0,3)$ and $Q_{sig}^{*}=(r_{max}+0.05,0)$ in Equation (88), and four pseudo-boundaries of Types II-IV and IVA with $N=74$, bypassing $A=(r_{max}+0.1,0)$. All boundaries are plotted in Cartesian coordinates.

Table 3. The errors and condition numbers for the DNFEM with $M=N$ using the pseudo-boundaries $\rho (>1)$ from Equations (60) and (61) at $L=M$ for the peanut-like domain, where $\rho ={\displaystyle \frac{r_{max}+d}{r_{max}}}$ with $d=0.1,0.2,0.5$, and the solution given by Equation (88) with $Q^{*}=(0,3)$ is chosen.

$\mathit{\rho }$	N	${\parallel \mathbf{▵}\mathit{\mu }\parallel }_{\mathit{\infty },\mathit{\Gamma }}$	${\parallel \mathbf{▵}\mathit{\mu }\parallel }_{0,\mathit{\Gamma }}$	Cond	Cond_eff	$\parallel \mathit{x}\parallel$	${\mathit{\sigma }}_{min}$
	6	$2.00\times {10}^{-1}$	$2.93\times {10}^{-1}$	$3.92\times {10}^1$	$3.44\times {10}^1$	$5.29\times {10}^{-1}$	$1.11\times {10}^{-1}$
	34	$2.03\times {10}^{-2}$	$2.48\times {10}^{-2}$	$2.78\times {10}^1$	$2.35\times {10}^1$	$1.97\times {10}^0$	$1.04\times {10}^{-1}$
1.06	50	$9.07\times {10}^{-3}$	$9.67\times {10}^{-3}$	$8.06\times {10}^1$	$6.83\times {10}^1$	$2.42\times {10}^0$	$3.52\times {10}^{-2}$
	58	$5.99\times {10}^{-3}$	$6.50\times {10}^{-3}$	$1.31\times {10}^2$	$1.11\times {10}^2$	$2.61\times {10}^0$	$2.16\times {10}^{-2}$
	74	$3.12\times {10}^{-3}$	$3.18\times {10}^{-3}$	$3.31\times {10}^2$	$2.80\times {10}^2$	$2.96\times {10}^0$	$8.54\times {10}^{-3}$
	6	$1.18\times {10}^{-1}$	$2.41\times {10}^{-1}$	$3.68\times {10}^0$	$3.59\times {10}^0$	$5.49\times {10}^{-1}$	$1.00\times {10}^0$
	26	$1.46\times {10}^{-2}$	$1.87\times {10}^{-2}$	$3.65\times {10}^1$	$3.06\times {10}^1$	$1.73\times {10}^0$	$7.67\times {10}^{-2}$
1.13	34	$9.26\times {10}^{-3}$	$9.55\times {10}^{-3}$	$9.11\times {10}^1$	$7.63\times {10}^1$	$2.00\times {10}^0$	$3.05\times {10}^{-2}$
	50	$3.00\times {10}^{-3}$	$3.02\times {10}^{-3}$	$4.97\times {10}^2$	$4.17\times {10}^2$	$2.43\times {10}^0$	$5.56\times {10}^{-3}$
	58	$1.59\times {10}^{-3}$	$1.73\times {10}^{-3}$	$1.12\times {10}^3$	$9.42\times {10}^2$	$2.62\times {10}^0$	$2.46\times {10}^{-3}$
	74	$5.80\times {10}^{-4}$	$5.77\times {10}^{-4}$	$5.61\times {10}^3$	$4.70\times {10}^3$	$2.96\times {10}^0$	$4.92\times {10}^{-4}$
	6	$6.46\times {10}^{-2}$	$1.66\times {10}^{-1}$	$3.13\times {10}^0$	$3.06\times {10}^0$	$6.55\times {10}^{-1}$	$9.15\times {10}^{-1}$
	26	$5.76\times {10}^{-3}$	$6.30\times {10}^{-3}$	$3.69\times {10}^2$	$2.71\times {10}^2$	$1.75\times {10}^0$	$7.99\times {10}^{-3}$
1.32	34	$3.66\times {10}^{-3}$	$2.81\times {10}^{-3}$	$2.04\times {10}^3$	$1.50\times {10}^3$	$2.01\times {10}^0$	$1.44\times {10}^{-3}$
	50	$9.11\times {10}^{-4}$	$5.13\times {10}^{-4}$	$5.60\times {10}^4$	$4.11\times {10}^4$	$2.43\times {10}^0$	$5.26\times {10}^{-5}$
	58	$4.35\times {10}^{-4}$	$2.44\times {10}^{-4}$	$2.88\times {10}^5$	$2.11\times {10}^5$	$2.62\times {10}^0$	$1.02\times {10}^{-5}$
	74	$1.03\times {10}^{-4}$	$5.54\times {10}^{-5}$	$7.68\times {10}^6$	$5.64\times {10}^6$	$2.96\times {10}^0$	$3.84\times {10}^{-7}$

Table 3. The errors and condition numbers for the DNFEM with $M=N$ using the pseudo-boundaries $\rho (>1)$ from Equations (60) and (61) at $L=M$ for the peanut-like domain, where $\rho ={\displaystyle \frac{r_{max}+d}{r_{max}}}$ with $d=0.1,0.2,0.5$, and the solution given by Equation (88) with $Q^{*}=(0,3)$ is chosen.

$\mathit{\rho }$	N	${\parallel \mathbf{▵}\mathit{\mu }\parallel }_{\mathit{\infty },\mathit{\Gamma }}$	${\parallel \mathbf{▵}\mathit{\mu }\parallel }_{0,\mathit{\Gamma }}$	Cond	Cond_eff	$\parallel \mathit{x}\parallel$	${\mathit{\sigma }}_{min}$
	6	$2.00\times {10}^{-1}$	$2.93\times {10}^{-1}$	$3.92\times {10}^1$	$3.44\times {10}^1$	$5.29\times {10}^{-1}$	$1.11\times {10}^{-1}$
	34	$2.03\times {10}^{-2}$	$2.48\times {10}^{-2}$	$2.78\times {10}^1$	$2.35\times {10}^1$	$1.97\times {10}^0$	$1.04\times {10}^{-1}$
1.06	50	$9.07\times {10}^{-3}$	$9.67\times {10}^{-3}$	$8.06\times {10}^1$	$6.83\times {10}^1$	$2.42\times {10}^0$	$3.52\times {10}^{-2}$
	58	$5.99\times {10}^{-3}$	$6.50\times {10}^{-3}$	$1.31\times {10}^2$	$1.11\times {10}^2$	$2.61\times {10}^0$	$2.16\times {10}^{-2}$
	74	$3.12\times {10}^{-3}$	$3.18\times {10}^{-3}$	$3.31\times {10}^2$	$2.80\times {10}^2$	$2.96\times {10}^0$	$8.54\times {10}^{-3}$
	6	$1.18\times {10}^{-1}$	$2.41\times {10}^{-1}$	$3.68\times {10}^0$	$3.59\times {10}^0$	$5.49\times {10}^{-1}$	$1.00\times {10}^0$
	26	$1.46\times {10}^{-2}$	$1.87\times {10}^{-2}$	$3.65\times {10}^1$	$3.06\times {10}^1$	$1.73\times {10}^0$	$7.67\times {10}^{-2}$
1.13	34	$9.26\times {10}^{-3}$	$9.55\times {10}^{-3}$	$9.11\times {10}^1$	$7.63\times {10}^1$	$2.00\times {10}^0$	$3.05\times {10}^{-2}$
	50	$3.00\times {10}^{-3}$	$3.02\times {10}^{-3}$	$4.97\times {10}^2$	$4.17\times {10}^2$	$2.43\times {10}^0$	$5.56\times {10}^{-3}$
	58	$1.59\times {10}^{-3}$	$1.73\times {10}^{-3}$	$1.12\times {10}^3$	$9.42\times {10}^2$	$2.62\times {10}^0$	$2.46\times {10}^{-3}$
	74	$5.80\times {10}^{-4}$	$5.77\times {10}^{-4}$	$5.61\times {10}^3$	$4.70\times {10}^3$	$2.96\times {10}^0$	$4.92\times {10}^{-4}$
	6	$6.46\times {10}^{-2}$	$1.66\times {10}^{-1}$	$3.13\times {10}^0$	$3.06\times {10}^0$	$6.55\times {10}^{-1}$	$9.15\times {10}^{-1}$
	26	$5.76\times {10}^{-3}$	$6.30\times {10}^{-3}$	$3.69\times {10}^2$	$2.71\times {10}^2$	$1.75\times {10}^0$	$7.99\times {10}^{-3}$
1.32	34	$3.66\times {10}^{-3}$	$2.81\times {10}^{-3}$	$2.04\times {10}^3$	$1.50\times {10}^3$	$2.01\times {10}^0$	$1.44\times {10}^{-3}$
	50	$9.11\times {10}^{-4}$	$5.13\times {10}^{-4}$	$5.60\times {10}^4$	$4.11\times {10}^4$	$2.43\times {10}^0$	$5.26\times {10}^{-5}$
	58	$4.35\times {10}^{-4}$	$2.44\times {10}^{-4}$	$2.88\times {10}^5$	$2.11\times {10}^5$	$2.62\times {10}^0$	$1.02\times {10}^{-5}$
	74	$1.03\times {10}^{-4}$	$5.54\times {10}^{-5}$	$7.68\times {10}^6$	$5.64\times {10}^6$	$2.96\times {10}^0$	$3.84\times {10}^{-7}$

We can see the errors ${\parallel ▵\mu \parallel }_{0,\mathrm{\Gamma }}=O\left(N^{-1.5}\right),O\left(N^{-2}\right),O\left(N^{-3}\right)$, at $\rho =1.06,1.13,1.32$, respectively, and they coincide with the error estimate in Equation (40). The polynomial convergence rates of low degree are confirmed numerically, thus supporting the error analysis. Moreover, the errors ${\parallel ▵\mu \parallel }_{0,\mathrm{\Gamma }}=O(0.{936}^N),O(0.{915}^N),O(0.{889}^N)$, at $\rho =1.06,1.13,1.32$, respectively, and they are consistent with the exponential convergence rates in Equation (79), where larger values of $\rho$ result in smaller errors ${\parallel ▵\mu \parallel }_{0,\mathrm{\Gamma }}$.

For the MFS, the results are listed in Table 4. In Table 4, we can see that for $\rho =1.06$,

$$\begin{array}{ccc}\hfill & & {\parallel ϵ\parallel }_{\infty ,\mathrm{\Gamma }}=O\left(N^{-3.12}\right)=O(0.{891}^N),{\parallel ϵ\parallel }_{0,\mathrm{\Gamma }}=O\left(N^{-3.48}\right)=O(0.{879}^N),\hfill \end{array}$$

(95)

$$\begin{array}{ccc}\hfill & & \parallel {ϵ}_{\nu }{\parallel }_{0,\mathrm{\Gamma }}=O\left(N^{-2.35}\right)=O(0.{917}^N),{\parallel ϵ\parallel }_{0,S}=O\left(N^{-3.61}\right)=O(0.{875}^N),\hfill \end{array}$$

(96)

$$\begin{array}{ccc}\hfill & & \mathrm{Cond}=O\left(N^{0.870}\right)=O(1.{03}^N),\alpha =0.341.\hfill \end{array}$$

(97)

For $\rho =1.13$,

$$\begin{array}{ccc}\hfill & & {\parallel ϵ\parallel }_{\infty ,\mathrm{\Gamma }}=O\left(N^{-3.09}\right)=O(0.{892}^N),{\parallel ϵ\parallel }_{0,\mathrm{\Gamma }}=O\left(N^{-3.51}\right)=O(0.{878}^N),\hfill \end{array}$$

(98)

$$\begin{array}{ccc}\hfill & & \parallel {ϵ}_{\nu }{\parallel }_{0,\mathrm{\Gamma }}=O\left(N^{-2.35}\right)=O(0.{917}^N),{\parallel ϵ\parallel }_{0,S}=O\left(N^{-3.78}\right)=O(0.{870}^N),\hfill \end{array}$$

(99)

$$\begin{array}{ccc}\hfill & & \mathrm{Cond}=O\left(N^{2.92}\right)=O(1.{11}^N),\alpha =1.20.\hfill \end{array}$$

(100)

For $\rho =1.32$,

$$\begin{array}{ccc}\hfill & & {\parallel ϵ\parallel }_{\infty ,\mathrm{\Gamma }}=O\left(N^{-4.30}\right)=O(0.{853}^N),{\parallel ϵ\parallel }_{0,\mathrm{\Gamma }}=O\left(N^{-4.60}\right)=O(0.{844}^N),\hfill \end{array}$$

(101)

$$\begin{array}{ccc}\hfill & & \parallel {ϵ}_{\nu }{\parallel }_{0,\mathrm{\Gamma }}=O\left(N^{-3.48}\right)=O(0.{879}^N),{\parallel ϵ\parallel }_{0,S}=O\left(N^{-5.26}\right)=O(0.{824}^N),\hfill \end{array}$$

(102)

$$\begin{array}{ccc}\hfill & & \mathrm{Cond}=O\left(N^{5.81}\right)=O(1.{24}^N),\alpha =1.67.\hfill \end{array}$$

(103)

The DNFEM and the MFS exhibit similar numerical performance due to similar sensitivity index $\alpha$. The key errors in Table 3 and Table 4 for $N=74$ are as follows:

$$\begin{array}{ccc}\hfill & & \mathrm{DNFEM}:{\parallel ▵\mu \parallel }_{0,\mathrm{\Gamma }}=3.18(-3),\mathrm{MFS}:{\parallel {ϵ}_{\nu }\parallel }_{0,\mathrm{\Gamma }}=2.40(-1),\mathrm{at}\rho =1.06,\hfill \end{array}$$

(104)

$$\begin{array}{ccc}\hfill & & \mathrm{DNFEM}:{\parallel ▵\mu \parallel }_{0,\mathrm{\Gamma }}=5.77(-4),\mathrm{MFS}:{\parallel {ϵ}_{\nu }\parallel }_{0,\mathrm{\Gamma }}=1.51(-2),\mathrm{at}\rho =1.13,\hfill \end{array}$$

(105)

$$\begin{array}{ccc}\hfill & & \mathrm{DNFEM}:{\parallel ▵\mu \parallel }_{0,\mathrm{\Gamma }}=5.54(-5),\mathrm{MFS}:{\parallel {ϵ}_{\nu }\parallel }_{0,\mathrm{\Gamma }}=1.62(-4),\mathrm{at}\rho =1.32.\hfill \end{array}$$

(106)

The DNFEM yields better accuracy for normal derivatives than the MFS. The same numerical conclusion was drawn in [4].

Table 4. The errors and condition numbers for the MFS with $N=M$ using the pseudo-boundaries $\rho (>1)$ from Equations (60) and (61) at $L=74$ for the peanut-like domain, where $\rho ={\displaystyle \frac{r_{max}+d}{r_{max}}}$ with $d=0.1,0.2,0.5$, and the solution given by Equation (88) with $Q^{*}=(0,3)$ is chosen.

$\mathit{\rho }$	M	${\parallel \mathit{ϵ}\parallel }_{\mathit{\infty },\mathit{\Gamma }}$	${\parallel \mathit{ϵ}\parallel }_{0,\mathit{\Gamma }}$	$\parallel {\mathit{ϵ}}_{\mathit{\nu }}{\parallel }_{0,\mathit{\Gamma }}$	${\parallel \mathit{ϵ}\parallel }_{0,\mathit{S}}$	Cond	Cond_eff	$\parallel \mathit{x}\parallel$	${\mathit{\sigma }}_{min}$
	6	$1.98\times {10}^1$	$3.81\times {10}^1$	$8.77\times {10}^1$	$2.34\times {10}^1$	$3.43\times {10}^1$	$1.03\times {10}^0$	$2.41\times {10}^1$	$1.27\times {10}^{-1}$
	34	$7.93\times {10}^{-2}$	$8.41\times {10}^{-2}$	$1.26\times {10}^0$	$4.56\times {10}^{-2}$	$2.53\times {10}^1$	$1.18\times {10}^1$	$8.99\times {10}^{-1}$	$3.02\times {10}^{-1}$
1.06	50	$2.94\times {10}^{-2}$	$2.54\times {10}^{-2}$	$6.20\times {10}^{-1}$	$1.28\times {10}^{-2}$	$7.40\times {10}^1$	$3.53\times {10}^1$	$7.32\times {10}^{-1}$	$1.24\times {10}^{-1}$
	58	$1.86\times {10}^{-2}$	$1.52\times {10}^{-2}$	$4.48\times {10}^{-1}$	$7.37\times {10}^{-3}$	$1.21\times {10}^2$	$5.77\times {10}^1$	$6.78\times {10}^{-1}$	$8.21\times {10}^{-2}$
	74	$7.86\times {10}^{-3}$	$6.04\times {10}^{-3}$	$2.40\times {10}^{-1}$	$2.72\times {10}^{-3}$	$3.05\times {10}^2$	$1.46\times {10}^2$	$6.00\times {10}^{-1}$	$3.67\times {10}^{-2}$
	6	$1.52\times {10}^0$	$2.55\times {10}^0$	$5.60\times {10}^0$	$1.50\times {10}^0$	$3.11\times {10}^0$	$1.03\times {10}^0$	$2.65\times {10}^0$	$1.16\times {10}^0$
	26	$4.67\times {10}^{-2}$	$4.00\times {10}^{-2}$	$4.68\times {10}^{-1}$	$1.91\times {10}^{-2}$	$3.11\times {10}^1$	$2.08\times {10}^1$	$7.91\times {10}^{-1}$	$1.96\times {10}^{-1}$
1.13	34	$2.15\times {10}^{-2}$	$1.58\times {10}^{-2}$	$2.54\times {10}^{-1}$	$6.82\times {10}^{-3}$	$7.81\times {10}^1$	$5.25\times {10}^1$	$6.89\times {10}^{-1}$	$8.88\times {10}^{-2}$
	50	$4.84\times {10}^{-3}$	$3.18\times {10}^{-3}$	$8.01\times {10}^{-2}$	$1.15\times {10}^{-3}$	$4.28\times {10}^2$	$2.88\times {10}^2$	$5.67\times {10}^{-1}$	$1.96\times {10}^{-2}$
	58	$2.30\times {10}^{-3}$	$1.53\times {10}^{-3}$	$4.57\times {10}^{-2}$	$5.16\times {10}^{-4}$	$9.66\times {10}^2$	$6.51\times {10}^2$	$5.27\times {10}^{-1}$	$9.37\times {10}^{-3}$
	74	$6.50\times {10}^{-4}$	$3.79\times {10}^{-4}$	$1.51\times {10}^{-2}$	$1.13\times {10}^{-4}$	$4.82\times {10}^3$	$3.25\times {10}^3$	$4.66\times {10}^{-1}$	$2.12\times {10}^{-3}$
	6	$3.49\times {10}^{-1}$	$4.61\times {10}^{-1}$	$1.02\times {10}^0$	$2.33\times {10}^{-1}$	$3.12\times {10}^0$	$3.11\times {10}^0$	$1.09\times {10}^0$	$9.29\times {10}^{-1}$
	26	$5.55\times {10}^{-3}$	$4.07\times {10}^{-3}$	$4.74\times {10}^{-2}$	$9.30\times {10}^{-4}$	$3.28\times {10}^2$	$2.97\times {10}^2$	$5.31\times {10}^{-1}$	$2.04\times {10}^{-2}$
1.32	34	$1.74\times {10}^{-3}$	$1.19\times {10}^{-3}$	$1.77\times {10}^{-2}$	$2.24\times {10}^{-4}$	$1.81\times {10}^3$	$1.63\times {10}^3$	$4.68\times {10}^{-1}$	$4.21\times {10}^{-3}$
	50	$1.87\times {10}^{-4}$	$1.18\times {10}^{-4}$	$2.57\times {10}^{-3}$	$1.65\times {10}^{-5}$	$4.97\times {10}^4$	$4.33\times {10}^4$	$3.99\times {10}^{-1}$	$1.86\times {10}^{-4}$
	58	$6.27\times {10}^{-5}$	$3.85\times {10}^{-5}$	$1.01\times {10}^{-3}$	$4.70\times {10}^{-6}$	$2.56\times {10}^5$	$2.14\times {10}^5$	$3.85\times {10}^{-1}$	$3.90\times {10}^{-5}$
	74	$7.16\times {10}^{-6}$	$4.38\times {10}^{-6}$	$1.62\times {10}^{-4}$	$4.30\times {10}^{-7}$	$6.83\times {10}^6$	$5.48\times {10}^6$	$3.55\times {10}^{-1}$	$1.65\times {10}^{-6}$

Let us discuss the width of the exterior boundaries in the DNFEM. For the conformal mapping, we find the width of the boundary layers as ${\displaystyle \frac{1}{N}}$ in Remark 2. Hence, for $N=74$, we need $\rho >1+{\displaystyle \frac{1}{N}}=1+{\displaystyle \frac{1}{74}}=1.0135.$ We cite Equation (80) as

$$\begin{array}{ccc}\hfill & & {\alpha }^{*}\ge {\displaystyle \frac{1}{N}}ln({\displaystyle \frac{N}{\epsilon }}).\hfill \end{array}$$

(107)

From Equation (104), we have $\epsilon ={\parallel ▵\mu \parallel }_{0,\mathrm{\Gamma }}=3.18(-3)$ at $N=74$. Equation (107) leads to

$$\begin{array}{ccc}\hfill & & {\alpha }^{*}\ge {\displaystyle \frac{1}{N}}ln({\displaystyle \frac{N}{\epsilon }})={\displaystyle \frac{1}{74}}ln({\displaystyle \frac{74}{3.18(-3)}})=0.136:=\delta \rho .\hfill \end{array}$$

(108)

Then, we require the pseudo-boundaries from the conformal mapping at $\rho \ge 1+\delta \rho =1.136$. When $\rho =1.13$, the numerical errors in Equation (105) are smaller, noting that $\epsilon ={\parallel ▵\mu \parallel }_{0,\mathrm{\Gamma }}=5.77(-4)<3.18(-3)$. This examination supports the width study of the exterior boundary layers in Remark 2. For the pseudo-boundaries outside the exterior boundary layers, we must choose $\rho$ to be larger than $1+{\displaystyle \frac{1}{maxN}}$. Note that the width of the exterior boundary layers depends on $maxN$. In computations, for the given pseudo-boundaries outside $\mathrm{\Gamma }$, a large N will be tested to achieve small errors. If such a goal can be fulfilled, the pseudo-boundaries are already outside the exterior boundary layers.

4.3. Verification of Proposition 2 and Theorem 1

First, let us examine the norm of $\parallel \mathbf{x}\parallel$ of the coefficients ${\mu }_i$ and $c_i$ from Table 3 and Table 4. By using $N=34$ and $N=74$, we have the following growth rates for $\rho =1.06,1.13,1.32$:

$$\begin{array}{ccc}\hfill & & \mathrm{DNFEM}:\parallel \mathbf{x}\parallel =O\left(N^{0.52}\right),O\left(N^{0.50}\right),O\left(N^{0.50}\right),\hfill \end{array}$$

(109)

$$\begin{array}{ccc}\hfill & & \mathrm{MFS}:\parallel \mathbf{x}\parallel =O\left(N^{-0.52}\right),O\left(N^{-0.50}\right),O\left(N^{-0.36}\right).\hfill \end{array}$$

(110)

The results in Equation (109) verify that $\parallel \mathbf{x}\parallel =O\left(\sqrt{N}\right)$ from the DNFEM in Proposition 2. Note that from Equation (110), $\parallel \mathbf{x}\parallel =O({\displaystyle \frac{1}{\sqrt{N}}})$ from the MFS is even smaller. However, for singularity solutions, such as in Motz’s problem, the $\parallel \mathbf{x}\parallel$ from the MFS is large (even huge) (see [8], Chapter 1).

Second, let us scrutinize the constants in Theorem 1. The non-uniform $h_i$ is given by

$$\begin{array}{ccc}\hfill & & h_i=\sqrt{r^2\left({\theta }_i\right)+{\left(r^{\prime }\left({\theta }_i\right)\right)}^2}▵\theta ,\hfill \end{array}$$

(111)

where $▵\theta ={\displaystyle \frac{2\pi }{N}}$. Since $maxr\left(\theta \right)=1.5538$ and $minr\left(\theta \right)=0.6436$, there exist the bounds

$$\begin{array}{ccc}& & max|r^{\prime }\left(\theta \right)|=max\left|{\displaystyle \frac{1}{2r\left(\theta \right)}}\left\{2sin\left(2\theta \right)+{\displaystyle \frac{sin4\theta }{\sqrt{1+{cos}^2\left(2\theta \right)}}}\right\}\right|\hfill \\ \hfill & & \le max{\displaystyle \frac{1}{2r\left(\theta \right)}}\left\{2|sin\left(2\theta \right)|+{\displaystyle \frac{|sin4\theta |}{\sqrt{1+{cos}^2\left(2\theta \right)}}}\right\}\le {\displaystyle \frac{3}{2}}{\displaystyle \frac{1}{minr\left(\theta \right)}}\le {\displaystyle \frac{3}{2}}{\displaystyle \frac{1}{0.6436}}=2.331.\hfill \end{array}$$

Then, we have

$$\begin{array}{ccc}& & {\displaystyle \frac{{max}_i{h}_i}{{min}_i{h}_i}}\le {\displaystyle \frac{max\sqrt{r^2\left(\theta \right)+{\left(r^{\prime }\left(\theta \right)\right)}^2}}{minr\left(\theta \right)}}\le {\displaystyle \frac{maxr\left(\theta \right)+max|r^{\prime }\left(\theta \right)|}{minr\left(\theta \right)}}\le {\displaystyle \frac{1.5538+2.331}{0.6436}}=6.04.\hfill \end{array}$$

Hence, from Theorem 1, we have

$$\begin{array}{ccc}\hfill & & 0.407\times \mathrm{Cond}\left(\mathbf{F}\right)\le \mathrm{Cond}\left(\mathbf{A}\right)\le 2.46\times \mathrm{Cond}\left(\mathbf{F}\right).\hfill \end{array}$$

(112)

On the other hand, we find from Table 5, that numerically,

$$\begin{array}{ccc}& & 1.00\times \mathrm{Cond}\left(\mathbf{F}\right)\le \mathrm{Cond}\left(\mathbf{A}\right)\le 1.18\times \mathrm{Cond}\left(\mathbf{F}\right).\hfill \end{array}$$

(113)

Equation (113) coincides perfectly with Equation (112), thus verifying Theorem 1.

Table 5. Ratios of the condition numbers for the pseudo-boundaries by the conformal mapping at $\rho =1.06,1.13,1.32$ for the peanut-like domain, where $\mathrm{Cond}\left(\mathbf{A}\right)$ and $\mathrm{Cond}\left(\mathbf{F}\right)$ are cited from Table 3 and Table 4, respectively.

$\mathit{\rho }$	N	6	26	34	50	58	74
1.06	DNFEM $\mathrm{Cond}\left(\mathbf{A}\right)$	3.92(1)	/	2.78(1)	8.06(1)	1.31(2)	3.31(2)
	MFS $\mathrm{Cond}\left(\mathbf{F}\right)$	3.43(1)	/	2.53(1)	7.40(1)	1.21(2)	3.05(2)
	Ratio : ${\displaystyle \frac{\mathrm{Cond}\left(\mathbf{A}\right)}{\mathrm{Cond}\left(\mathbf{F}\right)}}$	1.14	/	1.10	1.09	1.08	1.09
1.13	DNFEM $\mathrm{Cond}\left(\mathbf{A}\right)$	3.68	3.65(1)	9.11(1)	4.97(2)	1.12(3)	5.61(3)
	MFS $\mathrm{Cond}\left(\mathbf{F}\right)$	3.11	3.11(1)	7.81(1)	4.28(2)	9.66(2)	4.82(3)
	Ratio : ${\displaystyle \frac{\mathrm{Cond}\left(\mathbf{A}\right)}{\mathrm{Cond}\left(\mathbf{F}\right)}}$	1.18	1.17	1.17	1.16	1.16	1.16
1.32	DNFEM $\mathrm{Cond}\left(\mathbf{A}\right)$	3.13	3.69(2)	2.04(3)	5.60(4)	2.88(5)	7.68(6)
	MFS $\mathrm{Cond}\left(\mathbf{F}\right)$	3.12	3.28(2)	1.81(3)	4.97(4)	2.56(5)	6.83(6)
	Ratio : ${\displaystyle \frac{\mathrm{Cond}\left(\mathbf{A}\right)}{\mathrm{Cond}\left(\mathbf{F}\right)}}$	1.00	1.13	1.13	1.13	1.13	1.12

4.4. Computations for Solutions in the Interior Boundary Layers

The DNFEM suffers from difficulties in evaluating the solutions in the boundary layers, similar to the BEM. Note that the native algorithm in Equation (7) is ineffective for the solutions in the interior boundary layers. More efforts were made in [4] to seek simple algorithms for satisfactory solutions in the interior boundary layers. We briefly introduce them below.

Let $P\in \mathrm{\Gamma }$ and suppose that the solution $u\left(P\right)$ and the derivatives ${\mu }_k(\approx u_{\nu }\left(P_k\right))$ from Equation (4) are known, where $\nu$ is the exterior normal to $\mathrm{\Gamma }$ at $P_k$. Let $Q\in S$, and denote by $\overrightarrow{PQ}$ the interior normal of $\mathrm{\Gamma }$. Also, denote the distance $\delta =|\overline{PQ}|\ll 1$. From Taylor’s formula with first-order expansion at the center $P\in \mathrm{\Gamma }$, we choose the interpolation solutions in the interior boundary layers from [4]:

$$\begin{array}{ccc}\hfill & & {\tilde{u}}_N\left(Q\right)=u\left(P\right)-\delta {\widehat{\mu }}_k^{\left(q\right)}\left(\theta \right),\hfill \end{array}$$

(114)

where $q(=1,2,3)$ degree interpolations ${\widehat{\mu }}_k^{\left(q\right)}\left(\theta \right)$ are obtained from the known solutions ${\mu }_j$ in Equation (4). Denote the errors of ${\mu }_k$ from Equation (4) by

$$\begin{array}{ccc}\hfill & & |u_{\nu }\left(P_k\right)-{\mu }_k|\le C{N}^{-p},p\ge 1.\hfill \end{array}$$

(115)

Let $u\in C^2\left(S\right)$, $u_{\nu }\in C^{q+1}\left(\mathrm{\Gamma }\right)$, and Equation (115) be given. For Equation (114), we have the bound from [4]:

$$\begin{array}{ccc}\hfill & & |{\tilde{u}}_N\left(Q\right)-u\left(Q\right)|\le C\left\{\delta (N^{-(q+1)}+N^{-p})+{\delta }^2\right\},\hfill \end{array}$$

(116)

where C is a bounded constant independent of N and $\delta$.

Moreover, for high accuracy of the interpolation solutions in the interior boundary layers, we can employ the Fourier expansions, as in [4]:

$${\widehat{\mu }}_n^F\left(\theta \right)={\widehat{p}}_0+\sum _{i=1}^n({\widehat{p}}_{k}cosk\theta +{\widehat{q}}_{k}sink\theta ),0\le \theta <2\pi ,N=2n+1,$$

(117)

$${\widehat{\mu }}_n^{FB}\left(\theta \right)={\widehat{p}}_0+\sum _{i=1}^n({\widehat{p}}_{k}cosk\theta +{\widehat{q}}_{k}sink\theta )+{\widehat{p}}_{n+1}cos(n+1)\theta ,0\le \theta <2\pi ,N=2n+2,$$

(118)

where the Fourier coefficients

$$\begin{array}{ccc}\hfill & & {\widehat{p}}_0={\displaystyle \frac{1}{N}}\sum _{j=1}^N{\mu }_j,{\widehat{p}}_{n+1}={\displaystyle \frac{1}{N}}\sum _{j=1}^N{\mu }_{j}cos(n+1){\theta }_j,\hfill \end{array}$$

(119)

$$\begin{array}{ccc}\hfill & & {\widehat{p}}_k={\displaystyle \frac{2}{N}}\sum _{j=1}^N{\mu }_{j}cos\left(k{\theta }_j\right),{\widehat{q}}_k={\displaystyle \frac{2}{N}}\sum _{j=1}^N{\mu }_{j}sin\left(k{\theta }_j\right),k=1,2,...,n,\hfill \end{array}$$

(120)

with ${\theta }_j={\displaystyle \frac{2\pi }{N}}j$, and ${\mu }_j$ are given from Equation (4). The interpolation in Equation (114) is modified by

$$\begin{array}{ccc}& & {\tilde{u}}_N^F\left(Q\right)=u\left(P\right)-\delta {\widehat{\mu }}_n^F\left(\theta \right),{\tilde{u}}_N^{FB}\left(Q\right)=u\left(P\right)-\delta {\widehat{\mu }}_n^{FB}\left(\theta \right).\hfill \end{array}$$

(121)

Let $u\in C^2\left(S\right)$, $u_{\nu }\in H^{q+1}\left(\mathrm{\Gamma }\right)$, and Equations (117)–(120) be given. From the solutions ${\mu }_j$ from the DNFEM, suppose that

$$\begin{array}{ccc}\hfill & & \parallel \widehat{\mu }{-\mu \parallel }_0\le C{\displaystyle \frac{1}{N^p}},p\ge 3.\hfill \end{array}$$

(122)

For Equation (121), we have the bound (see [4])

$$\begin{array}{ccc}& & {\parallel {\tilde{u}}_N^F\left(Q\right)-u\left(Q\right)\parallel }_0=O\left(\delta \{N^{-(q+1)}+N^{-p}\}+O\left({\delta }^2\right)\right),N=2n+1,\hfill \\ & & {\parallel {\tilde{u}}_N^{FB}\left(Q\right)-u\left(Q\right)\parallel }_0=O\left(\delta \{N^{-(q+1)}+N^{-p}\}+O\left({\delta }^2\right)\right),N=2n+2.\hfill \end{array}$$

Remark 4. 

We can also replace $u\left(P\right)$ in Equation (114) with the piecewise interpolation polynomials based on $u_j$ at $P_j$ to give the second-kind approximation

$$\begin{array}{ccc}\hfill & & {\tilde{u}}_N^{*}\left(Q\right)={\widehat{u}}^{\left(q\right)}\left(\theta \right)-\delta {\widehat{\mu }}^{\left(q\right)}\left(\theta \right),\hfill \end{array}$$

(123)

where ${\widehat{u}}^{\left(q\right)}\left(\theta \right)$ are the piecewise q-degree interpolation polynomials. Also, we apply the Fourier series for both the solutions and their derivatives and modify Equation (121) as

$$\begin{array}{ccc}\hfill & & {\tilde{u}}_N^F\left(Q\right)=u_n^F\left(\theta \right)-\delta {\widehat{\mu }}_n^F\left(\theta \right),N=2n+1,\hfill \end{array}$$

(124)

$$\begin{array}{ccc}\hfill & & {\tilde{u}}_N^{FB}\left(Q\right)=u_n^{FB}\left(\theta \right)-\delta {\widehat{\mu }}_n^{FB}\left(\theta \right),N=2n+2.\hfill \end{array}$$

(125)

The error bounds are given in [4].

We first consider the simple algorithm in Equation (7), where the nodes Q may be located on the conformal mapping in Equations (60) and (61). We do not list the outputs in detail but provide only the errors of $u\left(Q\right)$ via Q in S in Figure 7. For the interior and exterior boundaries, the width of the interior boundaries was also given as ${\displaystyle \frac{1}{N}}$ in Remark 2. From Figure 7, the errors of the solutions in the interior boundary layers given by the native algorithms in Equation (7) are too large. On the other hand, the interpolation techniques in Section 4.4 for the computation of the interior boundary layers can be employed to give good solutions with small errors. In Figure 7, a few blue curves display higher accuracy in the numerical solutions. Unfortunately, we cannot explain the exact reasons for these outcomes (maybe due to the cancellation of rounding errors).

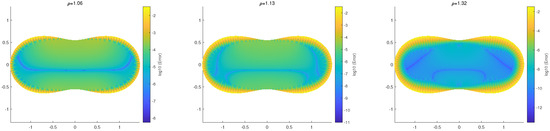
Figure 7. The errors $|u_N^S(\rho ,{\theta }_k)-u(\rho ,{\theta }_k)|$ in S using the simple algorithm in Equation (7) are shown, with colors based on u and $u_{\nu }$ on $\mathrm{\Gamma }$ from the DNFEM for $N=74$, for the peanut-like domain with $\rho =1.06$ (L), $\rho =1.13$ (M), and $\rho =1.32$ (R). The three boundaries $\mathrm{\Gamma }$ are plotted in Cartesian coordinates.

The normal direction is given by (see [18])

$$\begin{array}{ccc}\hfill & & \overrightarrow{n}={\displaystyle \frac{1}{\sqrt{r^2\left(\theta \right)+{\left(r^{\prime }\left(\theta \right)\right)}^2}}}\left\{(r^{\prime }\left(\theta \right)sin\theta +r\left(\theta \right)cos\theta )\overrightarrow{i}+(r\left(\theta \right)sin\theta -r^{\prime }\left(\theta \right)cos\theta )\overrightarrow{j}\right\},\hfill \end{array}$$

(126)

where $\overrightarrow{i}$ and $\overrightarrow{j}$ are the unit vectors along the X and the Y axes, respectively. For the peanut-like domain, the interior boundary ${\mathrm{\Gamma }}_{\delta }$ is given by

$$\begin{array}{ccc}& & {\mathrm{\Gamma }}_{\delta }=\left\{(x,y)\right|x=r\left(\theta \right)cos\theta -{\displaystyle \frac{\delta }{\sqrt{r^2\left(\theta \right)+{\left(r^{\prime }\left(\theta \right)\right)}^2}}}\left(r^{\prime }\left({\theta }_i\right)sin\theta +r\left(\theta \right)cos\theta \right),\hfill \\ \hfill & & y=r\left(\theta \right)sin\theta -{\displaystyle \frac{\delta }{\sqrt{r^2\left(\theta \right)+{\left(r^{\prime }\left(\theta \right)\right)}^2}}}\left(r\left(\theta \right)sin\theta -r^{\prime }\left({\theta }_i\right)cos\theta \right)\}.\hfill \end{array}$$

Piecewise interpolation polynomials with low degrees and Fourier series, as presented in [4], are also used to approximate $u\left(P\right)$ by using $u_j$ at $P_j$. The results are given in Table 6, where the second-kind approximations in Equation (123) and FOURIER B in Equation (125) from [4] are used. The error curves are shown in Figure 8, based on Table 6. When $\delta \ll 1$, the additional errors $O\left({\displaystyle \frac{1}{N^{q+1}}}\right)$ are dominant, as shown in [4]. Since $q\ge 4$, the Fourier series in Equation (125) yields better numerical performance. Figure 8 illustrates the importance of using Fourier series for solutions in the interior boundary layers. The numerical results of the techniques obtained with the Fourier series are consistent with the error analysis. Note that Table 6 and Figure 7 are based on Table 3 for $N=74$. Hence, the width of the interior boundary layers is more important than that of the exterior boundary layers in the DNFEM.

Table 6. The errors for different $\delta$ using the interpolation techniques in Equation (123) with degree $q=1,2,3$, and using FOURIER B with Equations (118)–(120) and (125), based on Table 3 at $\rho =1.32$ and $N=74$, where the q-degree interpolation and FOURIER B are used for both $\mu$ and u.

Interpolation	$\mathit{q}=1$		$\mathit{q}=2$		$\mathit{q}=3$		FOURIER B
$\mathbf{\delta }$	${\parallel \mathbf{ϵ}\parallel }_{\infty ,{\mathrm{\Gamma }}_{\mathbf{\delta }}}$	${\parallel \mathbf{ϵ}\parallel }_{\mathbf{0},{\mathrm{\Gamma }}_{\mathbf{\delta }}}$	${\parallel \mathbf{ϵ}\parallel }_{\infty ,{\mathrm{\Gamma }}_{\mathbf{\delta }}}$	${\parallel \mathbf{ϵ}\parallel }_{\mathbf{0},{\mathrm{\Gamma }}_{\mathbf{\delta }}}$	${\parallel \mathbf{ϵ}\parallel }_{\infty ,{\mathrm{\Gamma }}_{\mathbf{\delta }}}$	${\parallel \mathbf{ϵ}\parallel }_{\mathbf{0},{\mathrm{\Gamma }}_{\mathbf{\delta }}}$	${\parallel \mathbf{ϵ}\parallel }_{\infty ,{\mathrm{\Gamma }}_{\mathbf{\delta }}}$	${\parallel \mathbf{ϵ}\parallel }_{\mathbf{0},{\mathrm{\Gamma }}_{\mathbf{\delta }}}$
$1\times {10}^{-8}$	$1.03\times {10}^{-3}$	$1.05\times {10}^{-3}$	$1.62\times {10}^{-4}$	$1.50\times {10}^{-4}$	$3.40\times {10}^{-5}$	$2.35\times {10}^{-5}$	$7.80\times {10}^{-10}$	$7.87\times {10}^{-10}$
$1\times {10}^{-7}$	$1.03\times {10}^{-3}$	$1.05\times {10}^{-3}$	$1.62\times {10}^{-4}$	$1.50\times {10}^{-4}$	$3.40\times {10}^{-5}$	$2.35\times {10}^{-5}$	$7.78\times {10}^{-10}$	$7.87\times {10}^{-10}$
$1\times {10}^{-6}$	$1.03\times {10}^{-3}$	$1.05\times {10}^{-3}$	$1.62\times {10}^{-4}$	$1.50\times {10}^{-4}$	$3.40\times {10}^{-5}$	$2.35\times {10}^{-5}$	$7.70\times {10}^{-10}$	$7.85\times {10}^{-10}$
$1\times {10}^{-5}$	$1.03\times {10}^{-3}$	$1.05\times {10}^{-3}$	$1.62\times {10}^{-4}$	$1.50\times {10}^{-4}$	$3.40\times {10}^{-5}$	$2.35\times {10}^{-5}$	$1.14\times {10}^{-9}$	$9.71\times {10}^{-10}$
$1\times {10}^{-4}$	$1.03\times {10}^{-3}$	$1.05\times {10}^{-3}$	$1.62\times {10}^{-4}$	$1.50\times {10}^{-4}$	$3.40\times {10}^{-5}$	$2.35\times {10}^{-5}$	$1.52\times {10}^{-8}$	$6.39\times {10}^{-9}$
$1\times {10}^{-3}$	$1.02\times {10}^{-3}$	$1.04\times {10}^{-3}$	$1.61\times {10}^{-4}$	$1.50\times {10}^{-4}$	$3.38\times {10}^{-5}$	$2.34\times {10}^{-5}$	$2.02\times {10}^{-7}$	$1.50\times {10}^{-7}$
$3\times {10}^{-3}$	$1.02\times {10}^{-3}$	$1.04\times {10}^{-3}$	$1.60\times {10}^{-4}$	$1.49\times {10}^{-4}$	$3.39\times {10}^{-5}$	$2.34\times {10}^{-5}$	$1.15\times {10}^{-6}$	$1.24\times {10}^{-6}$
$1\times {10}^{-2}$	$9.97\times {10}^{-4}$	$1.02\times {10}^{-3}$	$1.58\times {10}^{-4}$	$1.46\times {10}^{-4}$	$3.77\times {10}^{-5}$	$2.83\times {10}^{-5}$	$1.01\times {10}^{-5}$	$1.36\times {10}^{-5}$
$3\times {10}^{-2}$	$9.71\times {10}^{-4}$	$1.00\times {10}^{-3}$	$1.84\times {10}^{-4}$	$1.83\times {10}^{-4}$	$8.33\times {10}^{-5}$	$1.27\times {10}^{-4}$	$8.37\times {10}^{-5}$	$1.21\times {10}^{-4}$
$1\times {10}^{-1}$	$1.31\times {10}^{-3}$	$1.67\times {10}^{-3}$	$9.20\times {10}^{-4}$	$1.30\times {10}^{-3}$	$8.86\times {10}^{-4}$	$1.30\times {10}^{-3}$	$8.87\times {10}^{-4}$	$1.29\times {10}^{-3}$
$3\times {10}^{-1}$	$8.02\times {10}^{-3}$	$1.04\times {10}^{-2}$	$7.54\times {10}^{-3}$	$1.04\times {10}^{-2}$	$7.52\times {10}^{-3}$	$1.04\times {10}^{-2}$	$7.52\times {10}^{-3}$	$1.04\times {10}^{-2}$

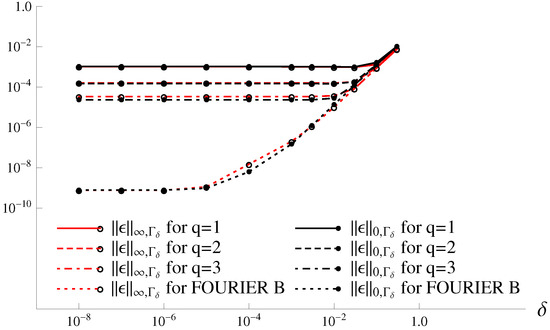
Figure 8. The error curves based on the results in Table 6.

5. Numerical Results for Different Pseudo-Boundaries Using the DNFEM

For bounded simply connected domains, choosing optimal pseudo-boundaries is an important computational topic. We refer readers to the study of the MFS in [8]. There are two kinds of pseudo-boundaries outside of S: Case A is a closed contour, and Case B consists of two radial lines [8] (Chapter 17). In this paper, we only choose the closed contour. In this section, we re-examine the conformal mapping in Section 3.2 and employ the pseudo-boundaries with equal distances/ratios discussed in [8] (Part III). Numerical comparisons are provided for both smooth and singular solutions.

By following [8] (Chapter 15), we choose the pseudo-boundaries with equal distances/ratios to $\mathrm{\Gamma }$ via the radial direction:

$$\begin{array}{ccc}\hfill & & r_1\left(\theta \right)=r\left(\theta \right)+\tau ,0\le \theta \le 2\pi ,\tau >0,\hfill \end{array}$$

(127)

$$\begin{array}{ccc}\hfill & & {\overline{r}}_1\left(\theta \right)={\tau }^{*}r\left(\theta \right),0\le \theta \le 2\pi ,{\tau }^{*}>1,\hfill \end{array}$$

(128)

where $r\left(\theta \right)$ is given in Equation (85). We consider four types of pseudo-boundaries via ${\theta }_i=i{\displaystyle \frac{2\pi }{N}}$:

Type I.

Circular pseudo-boundary with radius R.

Type II.

Equal distance to $\mathrm{\Gamma }$ in Equation (127).

Type III.

Equal ratio to $\mathrm{\Gamma }$ in Equation (128).

Type IV.

The conformal mapping in Equations (60)–(65).

Type IVA.

The conformal mapping by Katsurada and Okamoto [9] (p. 127) for $N=2n+2$ by

$$\begin{array}{ccc}\hfill & & x\left(\theta \right)+\mathbf{i}y\left(\theta \right)=\sum _{k=-n}^{n+1}({\beta }_k+\mathbf{i}{\gamma }_k){\rho }^k{e}^{\mathbf{i}k\theta },\hfill \end{array}$$

(129)

where the real function $x\left(\theta \right),y\left(\theta \right)\in \mathbf{R}$ and the real coefficients ${\alpha }_k,{\gamma }_k\in \mathbf{R}$.

The angles ${\theta }_i$ may be chosen uniformly via the arc length, and the numerical results did not show better numerical performance as that for amoeba-like domains in [8] (Chapter 16), where the boundary $\mathrm{\Gamma }$ has sharp changes of curvature. The details are omitted here. We only report the results for the DNFEM via equal angles as ${\theta }_i=i{\displaystyle \frac{2\pi }{N}}$.

5.1. Numerical Results for Smooth Solutions

Choose the highly smooth solution in Equation (88) with $Q_{far}^{*}=(0,3)$. Since Type I of the circular pseudo-boundary is less efficient, we only choose Types II-IV and IVA to pass through the same node $A=(x,y)=(r_{max}+0.1,0)$ (see Figure 6). For comparison, in this paper, we restrict node $A=(r_{max}+0.1,0)$ to remain relatively close to the boundary $\mathrm{\Gamma }$ because the DNFEM is more sensitive to ill-conditioning than the MFS (see Remark 5). To evaluate the numerical performance using the sensitivity index, we only evaluate the key results of the errors and Cond. The results of the DNFEM are given in Table 7. In Table 7, we can see that for Type II (equal distance) with $\tau =0.1$,

$$\begin{array}{ccc}\hfill & & \mathrm{Type}\mathrm{II}:{\parallel ▵\mu \parallel }_{0,\mathrm{\Gamma }}=O(0.{937}^N),\mathrm{Cond}=O(1.{10}^N),\alpha =1.46.\hfill \end{array}$$

(130)

For Type III (equal ratio) with ${\tau }^{*}={\displaystyle \frac{r_{max}+0.1}{r_{max}}}$,

$$\begin{array}{ccc}\hfill & & \mathrm{Type}\mathrm{III}:{\parallel ▵\mu \parallel }_{0,\mathrm{\Gamma }}=O(0.{933}^N),\mathrm{Cond}=O(1.{02}^N),\alpha =0.286.\hfill \end{array}$$

(131)

For Type IV (conformal mapping) with $\rho ={\displaystyle \frac{r_{max}+0.1}{r_{max}}}$,

$$\begin{array}{ccc}\hfill & & \mathrm{Type}\mathrm{IV}:{\parallel ▵\mu \parallel }_{0,\mathrm{\Gamma }}=O(0.{936}^N),\mathrm{Cond}=O(1.{03}^N),\alpha =0.447,\hfill \end{array}$$

(132)

$$\begin{array}{ccc}\hfill & & \mathrm{Type}\mathrm{IVA}:{\parallel ▵\mu \parallel }_{0,\mathrm{\Gamma }}=O(0.{851}^N),\mathrm{Cond}=O(1.{07}^N),\alpha =0.419.\hfill \end{array}$$

(133)

Type III (equal ratio) exhibits the best numerical performance due to the smallest sensitivity index $\alpha =0.286$. However, Type IVA [9] yields the smallest errors with ${\parallel ▵\mu \parallel }_{0,\mathrm{\Gamma }}=O(0.{851}^N)$. The key errors and conditions from Table 7 with $N=76$ are as follows:

$$\begin{array}{ccc}\hfill & & \mathrm{Type}\mathrm{II}:{\parallel ▵\mu \parallel }_{0,\mathrm{\Gamma }}=3.86(-3),\mathrm{Cond}=1260,\hfill \end{array}$$

(134)

$$\begin{array}{ccc}\hfill & & \mathrm{Type}\mathrm{III}:{\parallel ▵\mu \parallel }_{0,\mathrm{\Gamma }}=5.17(-3),\mathrm{Cond}=163,\hfill \end{array}$$

(135)

$$\begin{array}{ccc}\hfill & & \mathrm{Type}\mathrm{IV}:{\parallel ▵\mu \parallel }_{0,\mathrm{\Gamma }}=3.18(-3),\mathrm{Cond}=331,\hfill \end{array}$$

(136)

$$\begin{array}{ccc}& & \mathrm{Type}\mathrm{IVA}:{\parallel ▵\mu \parallel }_{0,\mathrm{\Gamma }}=1.67(-4),\mathrm{Cond}=233.\hfill \end{array}$$

(137)

Type IVA yields the smallest error ${\parallel ▵\mu \parallel }_{0,\mathrm{\Gamma }}=1.67(-4)$; the other three types yield similar errors ${\parallel ▵\mu \parallel }_{0,\mathrm{\Gamma }}\approx 3(-3)\sim 5(-3)$. For stability, Type II yields the largest $\mathrm{Cond}=1260$, but Type III yields the smallest $\mathrm{Cond}=163$.

Table 7. The errors and condition numbers for the DNFEM using Types II-IV and IVA [9] with $M=N$ for the peanut-like domain, where the smooth solution in Equation (88) with $Q_{far}^{*}=(0,3)$ is chosen.

	N	${\parallel \mathbf{▵}\mathit{\mu }\parallel }_{\mathit{\infty },\mathit{\Gamma }}$	${\parallel \mathbf{▵}\mathit{\mu }\parallel }_{0,\mathit{\Gamma }}$	Cond	Cond_eff	$\parallel \mathit{x}\parallel$	${\mathit{\sigma }}_{min}$
Type II	6	$2.08\times {10}^{-1}$	$3.22\times {10}^{-1}$	$1.87\times {10}^1$	$1.42\times {10}^1$	$6.64\times {10}^{-1}$	$2.09\times {10}^{-1}$
Equal distance	42	$1.17\times {10}^{-2}$	$1.71\times {10}^{-2}$	$1.60\times {10}^2$	$1.35\times {10}^2$	$2.24\times {10}^0$	$1.71\times {10}^{-2}$
$\tau =0.1$	58	$7.06\times {10}^{-3}$	$8.42\times {10}^{-3}$	$8.88\times {10}^2$	$7.51\times {10}^2$	$2.63\times {10}^0$	$3.08\times {10}^{-3}$
	74	$3.14\times {10}^{-3}$	$3.86\times {10}^{-3}$	$1.26\times {10}^4$	$1.07\times {10}^4$	$2.96\times {10}^0$	$2.17\times {10}^{-4}$
Type III	6	$2.32\times {10}^{-1}$	$5.83\times {10}^{-1}$	$3.98\times {10}^1$	$3.24\times {10}^1$	$5.93\times {10}^{-1}$	$1.06\times {10}^{-1}$
Equal ratio	50	$4.27\times {10}^{-3}$	$6.65\times {10}^{-3}$	$4.81\times {10}^1$	$4.16\times {10}^1$	$2.43\times {10}^0$	$5.73\times {10}^{-2}$
${\tau }^{*}={\displaystyle \frac{r_{max}+0.1}{r_{max}}}$	58	$4.55\times {10}^{-3}$	$6.34\times {10}^{-3}$	$7.28\times {10}^1$	$6.30\times {10}^1$	$2.63\times {10}^0$	$3.78\times {10}^{-2}$
	74	$4.05\times {10}^{-3}$	$5.17\times {10}^{-3}$	$1.63\times {10}^2$	$1.41\times {10}^2$	$2.97\times {10}^0$	$1.69\times {10}^{-2}$
Type IV	6	$2.00\times {10}^{-1}$	$2.93\times {10}^{-1}$	$3.92\times {10}^1$	$3.44\times {10}^1$	$5.29\times {10}^{-1}$	$1.11\times {10}^{-1}$
Conformal	50	$9.07\times {10}^{-3}$	$9.67\times {10}^{-3}$	$8.06\times {10}^1$	$6.83\times {10}^1$	$2.42\times {10}^0$	$3.52\times {10}^{-2}$
$\rho ={\displaystyle \frac{r_{max}+0.1}{r_{max}}}$	58	$5.99\times {10}^{-3}$	$6.50\times {10}^{-3}$	$1.31\times {10}^2$	$1.11\times {10}^2$	$2.61\times {10}^0$	$2.16\times {10}^{-2}$
	74	$3.12\times {10}^{-3}$	$3.18\times {10}^{-3}$	$3.31\times {10}^2$	$2.80\times {10}^2$	$2.96\times {10}^0$	$8.54\times {10}^{-3}$
Type IVA	6	$6.42\times {10}^0$	$9.68\times {10}^0$	$3.04\times {10}^0$	$1.31\times {10}^0$	$9.46\times {10}^0$	$8.57\times {10}^{-1}$
Conformal [9]	50	$1.08\times {10}^{-3}$	$1.27\times {10}^{-3}$	$7.52\times {10}^1$	$6.43\times {10}^1$	$2.43\times {10}^0$	$3.70\times {10}^{-2}$
$\rho ={\displaystyle \frac{r_{max}+0.1}{r_{max}}}$	58	$5.15\times {10}^{-4}$	$6.27\times {10}^{-4}$	$1.11\times {10}^2$	$9.51\times {10}^1$	$2.62\times {10}^0$	$2.50\times {10}^{-2}$
	74	$1.30\times {10}^{-4}$	$1.67\times {10}^{-4}$	$2.33\times {10}^2$	$1.99\times {10}^2$	$2.96\times {10}^0$	$1.20\times {10}^{-2}$

5.2. Numerical Results for Singular Solutions

Choose the singular solution in Equation (88) with $Q^{*}=Q_{sig}^{*}=(r_{max}+0.05,0)$ (see Figure 6). Since Type II is less effective, as seen in Section 5.1, we only use Types III, IV, and IVA passing through $A=(x,y)=(r_{max}+0.1,0)$. For singular solutions, the pseudo-boundaries should be chosen close to $\mathrm{\Gamma }$ (see [8], Part III). We carried out the computations with $M=N$ and $M=2N$. The results with $M=2N$ are slightly better than those with $M=N$. We only report the numerical performance with $M=2N$. The results are given in Table 8. In Table 8, $N=320$ is used for the conformal mapping. From Remark 1, we use the known continuous curve in Figure 3 with $\rho =1.06$ and $L=72$, and the source nodes can be obtained from Equations (60) and (61) when ${\theta }_i=i{\displaystyle \frac{2\pi }{N}}$ at $N=10\times 2^k$. For Type IVA [9], the same techniques as above are chosen for $N=10\times 2^k$ without using the FFT in [9]. In Table 8, we can see the following:

$$\begin{array}{ccc}\hfill & & \mathrm{Type}\mathrm{III}:{\parallel ▵\mu \parallel }_{0,\mathrm{\Gamma }}=O(0.{9825}^N),\mathrm{Cond}=O(1.{040}^N),\alpha =2.22,\hfill \end{array}$$

(138)

$$\begin{array}{ccc}\hfill & & \mathrm{Type}\mathrm{IV}:{\parallel ▵\mu \parallel }_{0,\mathrm{\Gamma }}=O(0.{9825}^N),\mathrm{Cond}=O(1.{048}^N),\alpha =2.66,\hfill \end{array}$$

(139)

$$\begin{array}{ccc}\hfill & & \mathrm{Type}\mathrm{IVA}:{\parallel ▵\mu \parallel }_{0,\mathrm{\Gamma }}=O(0.{9826}^N),\mathrm{Cond}=O(1.{039}^N),\alpha =2.18.\hfill \end{array}$$

(140)

A comparison of different pseudo-boundaries is given in Table 9. Types III, IV, and IVA [9] exhibit similar numerical performance. Note that the highly smooth domain boundary $\mathrm{\Gamma }$ is required for conformal mapping. For a polygonal $\mathrm{\Gamma }$ or a piecewise smooth curved boundary $\mathrm{\Gamma }$, however, the conformal mapping fails (see Remark 1), but Types II and III work well. Types IV and IVA (conformal mappings) are rather complicated; they are beneficial for the error analysis of the analytic solutions (see Equation (79)), thus enriching the DNFEM and the MFS in wide applications.

Table 9. Summary of the sensitivity index for the DNFEM using Types II-IV and IVA.

Type	II: Equal Distance	III: Equal Ratio	IV: Conformal	IVA: Conformal	Notes on Solutions
Parameter	$\tau =0.1$	${\tau }^{*}={\displaystyle \frac{r_{max}+0.1}{r_{max}}}$	$\rho ={\tau }^{*}$	$\rho ={\tau }^{*}$	smooth
$\alpha$	1.46	0.286	0.447	0.419	smooth
Parameter	/	${\tau }^{*}={\displaystyle \frac{r_{max}+0.1}{r_{max}}}$	$\rho ={\tau }^{*}$	$\rho ={\tau }^{*}$	singular
$\alpha$	/	2.22	2.66	2.18	singular

Table 8. The errors and the condition numbers for the DNFEM using Types III, IV, and IVA [9] with $M=2N$ for the peanut-like domain, where the singular solution in Equation (88) with $Q_{sig}^{*}=(r_{max}+0.05,0)$ is chosen.

	N	${\parallel \mathbf{▵}\mathit{\mu }\parallel }_{\mathit{\infty },\mathit{\Gamma }}$	${\parallel \mathbf{▵}\mathit{\mu }\parallel }_{0,\mathit{\Gamma }}$	Cond	Cond_eff	$\parallel \mathit{x}\parallel$	${\mathit{\sigma }}_{min}$
Type III	40	$1.13\times {10}^1$	$6.97\times {10}^0$	$3.87\times {10}^1$	$1.08\times {10}^1$	$1.39\times {10}^1$	$1.01\times {10}^{-1}$
Equal ratio	80	$6.07\times {10}^0$	$2.70\times {10}^0$	$2.85\times {10}^2$	$6.82\times {10}^1$	$2.30\times {10}^1$	$1.37\times {10}^{-2}$
${\tau }^{*}={\displaystyle \frac{r_{max}+0.1}{r_{max}}}$	160	$1.76\times {10}^0$	$6.30\times {10}^{-1}$	$7.37\times {10}^3$	$1.68\times {10}^3$	$3.40\times {10}^1$	$5.28\times {10}^{-4}$
	320	$1.47\times {10}^{-1}$	$5.02\times {10}^{-2}$	$2.50\times {10}^6$	$5.69\times {10}^5$	$4.83\times {10}^1$	$1.56\times {10}^{-6}$
Type IV	40	$1.12\times {10}^1$	$6.93\times {10}^0$	$5.12\times {10}^1$	$1.32\times {10}^1$	$1.40\times {10}^1$	$7.80\times {10}^{-2}$
Conformal	80	$6.04\times {10}^0$	$2.68\times {10}^0$	$4.96\times {10}^2$	$1.11\times {10}^2$	$2.30\times {10}^1$	$8.04\times {10}^{-3}$
$\rho ={\displaystyle \frac{r_{max}+0.1}{r_{max}}}$	160	$1.74\times {10}^0$	$6.23\times {10}^{-1}$	$2.35\times {10}^4$	$5.01\times {10}^3$	$3.40\times {10}^1$	$1.70\times {10}^{-4}$
	320	$1.45\times {10}^{-1}$	$4.95\times {10}^{-2}$	$2.71\times {10}^7$	$5.74\times {10}^6$	$4.83\times {10}^1$	$1.47\times {10}^{-7}$
Type IVA	40	$1.13\times {10}^1$	$6.95\times {10}^0$	$4.35\times {10}^1$	$1.16\times {10}^1$	$1.40\times {10}^1$	$9.06\times {10}^{-2}$
Conformal [9]	80	$6.09\times {10}^0$	$2.71\times {10}^0$	$3.04\times {10}^2$	$6.94\times {10}^1$	$2.29\times {10}^1$	$1.30\times {10}^{-2}$
$\rho ={\displaystyle \frac{r_{max}+0.1}{r_{max}}}$	160	$1.77\times {10}^0$	$6.38\times {10}^{-1}$	$7.37\times {10}^3$	$1.61\times {10}^3$	$3.40\times {10}^1$	$5.35\times {10}^{-4}$
	320	$1.49\times {10}^{-1}$	$5.17\times {10}^{-2}$	$2.17\times {10}^6$	$4.70\times {10}^5$	$4.83\times {10}^1$	$1.82\times {10}^{-6}$

Table 8. The errors and the condition numbers for the DNFEM using Types III, IV, and IVA [9] with $M=2N$ for the peanut-like domain, where the singular solution in Equation (88) with $Q_{sig}^{*}=(r_{max}+0.05,0)$ is chosen.

	N	${\parallel \mathbf{▵}\mathit{\mu }\parallel }_{\mathit{\infty },\mathit{\Gamma }}$	${\parallel \mathbf{▵}\mathit{\mu }\parallel }_{0,\mathit{\Gamma }}$	Cond	Cond_eff	$\parallel \mathit{x}\parallel$	${\mathit{\sigma }}_{min}$
Type III	40	$1.13\times {10}^1$	$6.97\times {10}^0$	$3.87\times {10}^1$	$1.08\times {10}^1$	$1.39\times {10}^1$	$1.01\times {10}^{-1}$
Equal ratio	80	$6.07\times {10}^0$	$2.70\times {10}^0$	$2.85\times {10}^2$	$6.82\times {10}^1$	$2.30\times {10}^1$	$1.37\times {10}^{-2}$
${\tau }^{*}={\displaystyle \frac{r_{max}+0.1}{r_{max}}}$	160	$1.76\times {10}^0$	$6.30\times {10}^{-1}$	$7.37\times {10}^3$	$1.68\times {10}^3$	$3.40\times {10}^1$	$5.28\times {10}^{-4}$
	320	$1.47\times {10}^{-1}$	$5.02\times {10}^{-2}$	$2.50\times {10}^6$	$5.69\times {10}^5$	$4.83\times {10}^1$	$1.56\times {10}^{-6}$
Type IV	40	$1.12\times {10}^1$	$6.93\times {10}^0$	$5.12\times {10}^1$	$1.32\times {10}^1$	$1.40\times {10}^1$	$7.80\times {10}^{-2}$
Conformal	80	$6.04\times {10}^0$	$2.68\times {10}^0$	$4.96\times {10}^2$	$1.11\times {10}^2$	$2.30\times {10}^1$	$8.04\times {10}^{-3}$
$\rho ={\displaystyle \frac{r_{max}+0.1}{r_{max}}}$	160	$1.74\times {10}^0$	$6.23\times {10}^{-1}$	$2.35\times {10}^4$	$5.01\times {10}^3$	$3.40\times {10}^1$	$1.70\times {10}^{-4}$
	320	$1.45\times {10}^{-1}$	$4.95\times {10}^{-2}$	$2.71\times {10}^7$	$5.74\times {10}^6$	$4.83\times {10}^1$	$1.47\times {10}^{-7}$
Type IVA	40	$1.13\times {10}^1$	$6.95\times {10}^0$	$4.35\times {10}^1$	$1.16\times {10}^1$	$1.40\times {10}^1$	$9.06\times {10}^{-2}$
Conformal [9]	80	$6.09\times {10}^0$	$2.71\times {10}^0$	$3.04\times {10}^2$	$6.94\times {10}^1$	$2.29\times {10}^1$	$1.30\times {10}^{-2}$
$\rho ={\displaystyle \frac{r_{max}+0.1}{r_{max}}}$	160	$1.77\times {10}^0$	$6.38\times {10}^{-1}$	$7.37\times {10}^3$	$1.61\times {10}^3$	$3.40\times {10}^1$	$5.35\times {10}^{-4}$
	320	$1.49\times {10}^{-1}$	$5.17\times {10}^{-2}$	$2.17\times {10}^6$	$4.70\times {10}^5$	$4.83\times {10}^1$	$1.82\times {10}^{-6}$

Remark 5. 

In Section 3.1, the DNFEM was more sensitive to ill-conditioning than the MFS. To achieve optimal convergence rates, regularization is often needed to remove severe ill-conditioning. In this paper, we do not use regularization and report numerical comparisons for the near node $A_1=(r_{max}+0.1,0)$ from Γ in this section. For far nodes $A_2=(r_{max}+0.3,0)$ and $A_3=(r_{max}+0.5,0)$, however, regularization (such as truncated singular-value decomposition (TSVD)) is needed for the DNFEM. The details are reported elsewhere. On the other hand, good numerical solutions are given in Table 3 for three nodes $A_1$, $A_2$, and $A_3$, where the DNFEM via the conformal mapping is chosen without regularization. The conformal mapping is more promising. The reason for this is that the ill-conditioning of the conformal mapping is similar to that in [4], where Γ and ${\mathrm{\Gamma }}_R$ are co-circles. Good numerical solutions are given in [4] for the DNFEM without regularization.

6. Concluding Remarks

Some novelties of this paper are as follows:

• The discrete null-field equation method (DNFEM) was proposed in [4], where the discussions and computations were confined only to disk domains. It is imperative to apply the DNFEM to bounded simply connected domains, which is the goal of this paper. A stability and error analysis is performed, and better locations of source nodes are studied thoroughly (see [8], Part III).
• For bounded simply connected domains, the bounds of the condition numbers are derived and given in Theorem 1. Both the DNFEM and the MFS share similar bounds of the condition numbers. The error analysis is performed using the Galerkin approaches of the BEM in [2]. Error bounds are provided in Section 2.2, while detailed proofs are given elsewhere. The stability and error analysis provides a theoretical foundation for the DNFEM.
• In the DNFEM and the MFS, the source nodes are located not only outside S but also outside the exterior boundary layers. The width of the exterior boundary layers is derived as $O\left({\displaystyle \frac{1}{N}}\right)$ in Section 3.1 for the disk domains and in Remark 2 for conformal mapping. The width of the exterior boundary layers is also valid for the interior boundary layers, as shown in Section 4.4. The width study of the exterior and interior boundary layers is imperative to the DNFEM.
• For smooth boundaries of Jordan domains, the conformal mapping in [9] is proposed to find the pseudo-boundaries, where the Fourier series in [4] is applied. The algorithms are provided and the necessary conditions are given in Proposition 4. The pseudo-boundaries from the conformal mapping must be near $\mathrm{\Gamma }$ (i.e., small $(\rho -1)$), and the number $L(=2n+1)$ of Fourier series terms in Equation (57) is also restricted from being large.
• For peanut-like domains, the pseudo-boundaries are formulated from the conformal mapping, and numerical experiments are carried out for the DNFEM and the MFS in Section 4. The stability and error analysis in Section 2 (as well as Equation (79)) is confirmed, and the new techniques in Section 4.4 are efficient for the solutions of the DNFEM in the interior boundary layers.
• Comparisons between the conformal mapping and other pseudo-boundaries are made in Section 5, as in [8] (Chapter 16). Numerical comparisons are reported for peanut-like domains, where all pseudo-boundaries ${\mathrm{\Gamma }}_R$ are passed through a near node $A=(r_{max}+0.1,0)$ to $\mathrm{\Gamma }$. Types IV and IVA offer similar numerical performance to Type III with equal ratios. The conformal mapping is beneficial for the error analysis of analytic solutions, and it can be extended to 3D (see Remark 3). Note that the conformal mapping fails for polygonal or piecewise curved boundaries, while Types II and III do not have such limitations.
• In summary, the algorithms of the DNFEM are much simpler than the traditional BEM. Based on the analysis, various choices of better locations of source nodes and good numerical computations, the DNFEM may become a new competent boundary method for scientific/engineering computing.