The Optimization of UAV-Assisted Downlink Transmission Based on RSMA

Abstract

Unmanned Aerial Vehicles (UAVs) provide exceptional flexibility, making them ideal for mitigating communication disruptions in disaster-affected or high-demand areas. When functioning as communication base stations, UAVs can adopt either orthogonal or non-orthogonal multiple access schemes. However, traditional Orthogonal Multiple Access (OMA) techniques are constrained by limited user access capacity and system throughput, necessitating the study of non-orthogonal access mechanisms for UAV-assisted communication systems. While much of the research on non-orthogonal multiple access focuses on Non-Orthogonal Multiple Access (NOMA), Rate-Splitting Multiple Access (RSMA), a novel non-orthogonal technique, offers superior throughput performance compared to NOMA. This paper, therefore, investigates the optimization of UAV-assisted downlink communication systems based on RSMA. We first develop a mathematical model of the system and decompose the primary optimization problem into multiple subproblems according to parameter types. To solve these subproblems, we propose an optimization algorithm that combines the Augmented Lagrange Method (ALM) with the Artificial Fish Swarm Algorithm (AFSA). The optimization algorithm is further enhanced by incorporating dynamic step size and visual strategies, as well as memory behaviors to improve convergence speed and optimization accuracy. To address linear equality constraints, we introduce a correction factor to modify the behavior of the artificial fish. The final optimization is achieved through cross-iterative solutions. Simulation results show that the system throughput under the RSMA strategy can be improved by 13.30% compared with NOMA, validating the effectiveness and superiority of RSMA in UAV-assisted communication systems.

1. Introduction

Compared to ground-based equipment such as communication vehicles and fixed base stations, Unmanned Aerial Vehicles (UAVs) offer a superior environment for signal transmission, as they experience less interference from external factors. In complex disaster scenarios, deploying ground equipment can be challenging and it is often difficult to find suitable locations. UAVs, on the other hand, can be easily deployed and positioned according to real-time demands, providing service to a wider range of users and overcoming coverage challenges in such environments.

One of the key challenges in UAV-assisted emergency communication is ensuring high Quality of Service (QoS). Enhancing QoS in emergency communication networks can be addressed at various levels, including network architecture [1], protocols at the network layer [2], and data link layer [3] designs. Previous studies [4] have explored routing protocols at the network layer for UAV-assisted emergency communication systems, while this paper focuses on improving QoS through a physical-layer-assisted Medium Access Control (MAC) design.

MAC protocols can be broadly categorized into orthogonal and non-orthogonal types. Traditional orthogonal MAC protocols, such as Time Division Multiple Access (TDMA) [5], Frequency Division Multiple Access (FDMA) [6], and Code Division Multiple Access (CDMA) [7], have been widely used in earlier generations of mobile communication systems (1G to 4G). However, these protocols struggle to meet the demands of large-scale user access and ultra-low latency scenarios, making them less suitable for modern communication needs. To address these limitations, the fifth generation (5G) of mobile communication systems has adopted non-orthogonal MAC protocols, such as Rate-Splitting Multiple Access (RSMA) [8], Sparse Code Multiple Access (SCMA) [9], and Non-Orthogonal Multiple Access (NOMA) [10], to manage user access.

This paper focuses on UAV-assisted emergency communication networks where UAVs serve as communication base stations. Specifically, we study the rate optimization problem in RSMA-based UAV communication networks. RSMA, as a non-orthogonal MAC protocol, differs from Spatial Division Multiple Access (SDMA) [11], which treats interference as noise, and from NOMA, which decodes all interference. RSMA partially decodes interference and treats part of it as noise, allowing users in the same group to share time-frequency resources. A key design aspect of non-orthogonal MAC protocols is beamforming, which, when optimized, can significantly enhance network throughput. Poor beamforming design, however, can lead to resource wastage and fail to meet rate requirements. Therefore, optimizing RSMA system parameters is crucial for achieving higher data transmission rates.

Additionally, both emergency communication systems and regular communication systems exhibit asymmetry between uplink and downlink communications, with the QoS demands typically higher for downlink. Therefore, optimizing the downlink system in RSMA-based UAV-assisted networks is of particular importance.

In this study, we address the rate optimization problem in the downlink of RSMA-based UAV communication systems, with the objective of maximizing transmission rates. We decompose the problem into three subproblems: UAV parameter optimization, RSMA parameter optimization, and user group parameter optimization. To solve these subproblems, we propose an optimization algorithm that combines the Augmented Lagrange Method (ALM) with the Artificial Fish Swarm Algorithm (AFSA) [12]. A ternary cross-iterative algorithm is designed to solve the original problem and achieve optimal performance in the downlink system.

2. Related Work

Since the proposal of RSMA, numerous researchers have investigated its application in various communication systems, including Cloud Radio Access Networks (C-RAN) [13], multibeam satellite systems [14], overloaded cellular Internet of Things (IoT) [15], and UAV communication systems [16]. The core concept of RSMA is to split messages into common and private parts, which are then decoded using Successive Interference Cancellation (SIC) [17].

Sidiropoulos [18] designed a full-duplex cooperative multicast mechanism based on RS. The authors developed specific beamforming methods for cooperative rate splitting and multicast beams, proposing an optimization scheme. They introduced a low-complexity iterative algorithm based on Successive Convex Approximation (SCA) to solve the problem. This approach effectively mitigates inter-group interference, improves resource utilization, and reduces system energy consumption. In reference [19], RS was introduced in an uplink NOMA system and its application in high-throughput satellite systems was examined. By modeling the channel, the authors derived a closed-form expression for the average system throughput. Numerical simulations demonstrated that the proposed scheme outperforms NOMA and SDMA in terms of throughput.

Further, Z. Yang [20] explored rate optimization in uplink communication systems using RSMA, focusing on optimizing user transmission power and the decoding order at the base station to maximize system throughput. In reference [21], RSMA was applied to an uplink cognitive radio system comprising a primary and secondary user, where the authors proposed an RSMA-based protocol and a SIC-based protocol for message decoding. Meanwhile, O. Dizdar [22] investigated RSMA in downlink multi-antenna cognitive radio systems, focusing on joint communication and interference cancellation for multicarrier waveforms. By employing RSMA, the authors aimed to communicate with secondary users while simultaneously mitigating interference to primary users.

Recent literature on RS/RSMA can be broadly categorized into studies of its applications in uplink systems [19,20,21] and downlink systems [22]. It is evident that most research focuses on RS/RSMA in uplink communication systems. However, RS/RSMA also holds significant potential for downlink systems. Therefore, further investigation into its application and performance in downlink systems is essential.

3. Mathematic Modeling

The location deployment of the base station as well as the resource allocation between and within user groups affect the overall transmission rate of the system. Therefore, it is important to study how to jointly deploy UAVs for rate optimization of RSMA downlink multi-user group systems under the uncertainty of UAV as a base station location. This section focuses on modeling and analyzing the UAV-assisted downlink RSMA system.

3.1. The Downlink RSMA System’s Modeling

The downlink RSMA system model studied in this paper is shown in Figure 1. Different groups of users use different communication channels, and users within the same group communicate using the RSMA mechanism, where users need to parse the public messages sent by the base station as well as the private messages sent to themselves.

The rate optimization problem for downlink RSMA systems can be described as Equation (1), where $n{u}_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}\left(i\right)$ is the number of users in the group $i$; $v_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}\left(i,j\right)$ is the downlink transmission rate of user $j$ in group $i$; $po{s}_u=\left(po{s}_u.x,po{s}_u.y,po{s}_u.z\right)$ is the location of the UAV base station; $x_{\mathrm{m}\mathrm{i}\mathrm{n}}$, $y_{\mathrm{m}\mathrm{i}\mathrm{n}}$, $z_{\mathrm{m}\mathrm{i}\mathrm{n}}$, $x_{\mathrm{m}\mathrm{a}\mathrm{x}}$, $y_{\mathrm{m}\mathrm{a}\mathrm{x}}$ and $z_{\mathrm{m}\mathrm{a}\mathrm{x}}$ are UAV position restrictions; $\alpha \left(i,j\right)$ is the rate proportion allocated to user j in the public message of the user group $i$; $p_c\left(i\right)$ is the public message downlink transmission power of the $i$-th group; $B_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}=\left\{B_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}\left(i\right),B_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}\left(2\right),...,B_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}\left(n{c}_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}\right)\right\}$ is the bandwidth allocation for each user group; $B_{da}$ is the total bandwidth of the system; $P_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}\_\mathrm{a}\mathrm{l}\mathrm{o}\mathrm{c}}$ is the power allocation for each user group and user member; $P_{\mathrm{B}\mathrm{S}}$ is the power limit of the base station; and $v{e}_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}\left(i,j\right)$ is the downlink rate requirement of the corresponding user.

$$\left\{\begin{array}{ll}\arg & {\max }_{po{s}_u,B_{\mathrm{down}},R,P_{\mathrm{down}\_\mathrm{aloc}}}{\displaystyle {\sum }_{i=1}^{n{c}_{\mathrm{down}}}{\displaystyle {\sum }_{j=1}^{n{u}_{\mathrm{down}}\left(i\right)}{v}_{\mathrm{down}}\left(i,j\right)}}\\ s.t.& x_{\min }\le po{s}_u.x\le x_{\max },y_{\min }\le po{s}_u.y\le y_{\max },z_{\min }\le po{s}_u.z\le z_{\max }\\ & {\displaystyle {\sum }_{i=1}^{n{c}_{down}}{B}_{\mathrm{down}}\left(i\right)=B_{da}},B_{\mathrm{down}}\left(i\right)\ge 0,1\le i\le n{c}_{\mathrm{down}}\\ & {\displaystyle {\sum }_{j=1}^{n{u}_{down}\left(i\right)}\alpha \left(i,j\right)=1,1\le i\le n{c}_{\mathrm{down}}}\\ & \alpha \left(i,j\right)\ge 0,1\le i\le n{c}_{\mathrm{down}},1\le j\le n{u}_{\mathrm{down}}\left(i\right)\\ & p_c\left(i\right)+{\displaystyle {\sum }_{j=1}^{n{u}_{\mathrm{down}}\left(i\right)}{p}_p\left(i,j\right)}=P_{\mathrm{down}}\left(i\right)\\ & {\displaystyle {\sum }_{i=1}^{n{c}_{\mathrm{down}}}{P}_{\mathrm{down}}\left(i\right)}\le P_{\mathrm{BS}}\\ & v_{\mathrm{down}}\left(i,j\right)\ge v{e}_{\mathrm{down}}\left(i,j\right),1\le i\le n{c}_{\mathrm{down}},1\le j\le n{u}_{\mathrm{down}}\left(i\right)\end{array}\right.$$

(1)

3.2. Model Solving Optimization

Due to the significant complexity of solving a problem directly (1), this paper decomposes it into three sub-problems: UAV position parameter optimization, user group parameter optimization and RSMA parameter optimization, and designs a ternary cross iterative optimization algorithm to complete the original problem solving. By grouping the UAV position $po{s}_u$ as the UAV parameter, the bandwidth allocation $B_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}$ as well as the inter-group power allocation in $P_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}\_\mathrm{a}\mathrm{l}\mathrm{o}\mathrm{c}}$ act as the user group resource parameter. The intra-group power allocation in $P_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}\_\mathrm{a}\mathrm{l}\mathrm{o}\mathrm{c}}$ is grouped into RSMA parameters, and the RSMA parameters of the downlink optimization system can still be solved independently for each user group.

• UAV parameter’s optimization problem

Optimizing UAV parameters such as position, altitude, and power is crucial for enhancing communication performance, especially when UAVs are used as flying base stations in areas with limited infrastructure. This improves coverage, reduces interference, and ensures efficient energy use, making it vital for applications like disaster recovery and remote connectivity. The optimization problem regarding the UAV position parameter can be abstracted into the following form:

$$\left\{\begin{array}{l}\arg {\min }_{po{s}_u}{V}_{\mathrm{target}}\\ \mathrm{subject} \mathrm{to} ua{v}_{lc}\\ \hspace{1em}{v}_{rc}\end{array}\right.$$

(2)

where $V_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}$ is the opposite number of the sum of downlink transmission rate. $ua{v}_{lc}$ is the location constraint of the UAV. $v_{rc}$ is the user’s downlink transmission rate constraint. In this case, the user group parameters as well as the RSMA parameters are treated as constants. In Equation (2), the first constraint determines the deployable region of the UAV, i.e., the search space of the solution, and the second constraint is the rate constraint, which corresponds to the rate demand constraint of Equation (1), which are inequality constraints. The Augmented Lagrange Method (ALM) is used in this paper to transform an inequality constrained optimization problem into an unconstrained optimization problem for further solution. We transform the rate requirement constraints of Equation (1) into the forms of Equation (3), then the left-hand side of the inequality is denoted as $g_{i,j}\left(X\right)$. The objective function of (2) is denoted as $f\left(X\right)$, where $X=\left(x,y,z\right)$ is the coordinates of the UAV. According to reference [10], the augmented Lagrange function of (2) is calculated as (4), where $nc$ is the number of user groups, $nu\left(i\right)$ is the number of users in group $i$, ${\lambda }^{i,j}$ is the Lagrange multiplier, and $\rho \left(\rho >0\right)$ is the penalty parameter. The Lagrange multiplier is updated by ${\lambda }_t^{i,j}=\min \left(\max \left(0,{\lambda }_{t-1}^{i,j}-\rho g_{i,j}\left(X_{t-1}\right)\right),{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}^{i,j}\right)$, where ${\lambda }_t^{i,j}$ represents the value of ${\lambda }^{i,j}$ when the number of iterations reaches $t$, ${\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}^{i,j}$ represents the upper limit of ${\lambda }^{i,j}$, and $X_{t-1}$ represents the value of solution obtained when the number of iterations reaches $t-1$. In this paper, we use dynamic penalty function; the penalty parameter $\rho$ is updated by ${\rho }_t=\rho t_{\mathrm{m}\mathrm{i}\mathrm{n}}+\left(\rho t_{\mathrm{m}\mathrm{a}\mathrm{x}}-\rho t_{\mathrm{m}\mathrm{i}\mathrm{n}}\right){\displaystyle \frac{t\sqrt{t}-1}{t_m\sqrt{t_m}-1}}$, where $t$ is the number of iterations, $\left[\rho t_{\mathrm{m}\mathrm{i}\mathrm{n}},\rho t_{\mathrm{m}\mathrm{a}\mathrm{x}}\right]$ is the range of values of $\rho$, and $t_m$ is the maximum number of iterations. As the number of iterations increases, the penalty parameter $\rho$ also increases.

$$v_{\mathrm{down}}\left(i,j\right)-v{e}_{\mathrm{down}}\left(i,j\right)\ge 0,1\le i\le n{c}_{\mathrm{down}},1\le j\le n{u}_{\mathrm{down}}\left(i\right)$$

(3)

$${\mathcal{L}}_{\rho }\left(X,\lambda \right)=f\left(X\right)+{\displaystyle \frac{1}{2\rho }}{\displaystyle {\sum }_{i=1}^{nc}{\displaystyle {\sum }_{j=1}^{nu\left(i\right)}\left\{{\left[\max \left(0,{\lambda }^{i,j}-\rho g_{i,j}\left(X\right)\right)\right]}^2-{\left({\lambda }^{i,j}\right)}^2\right\}}}$$

(4)

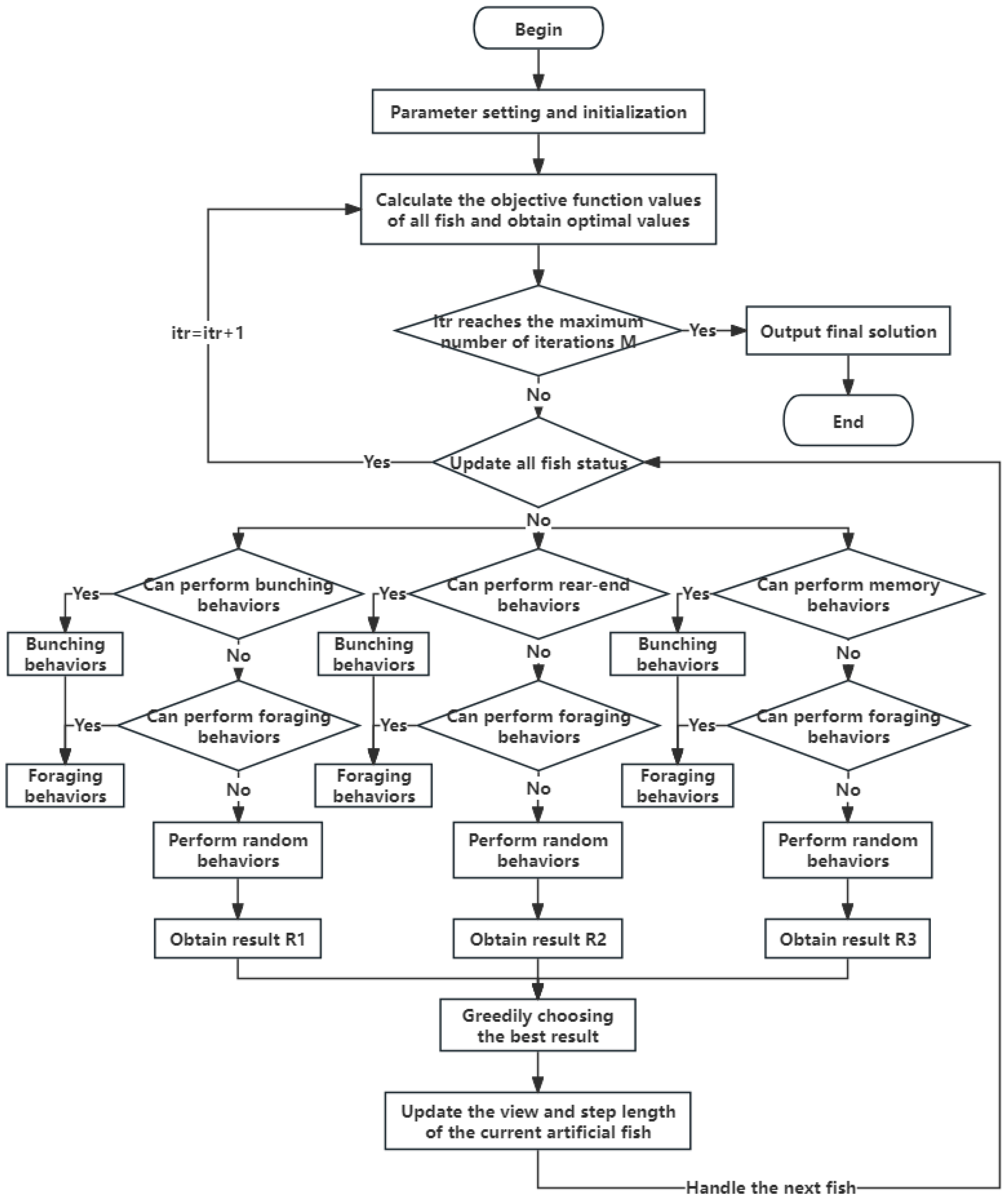
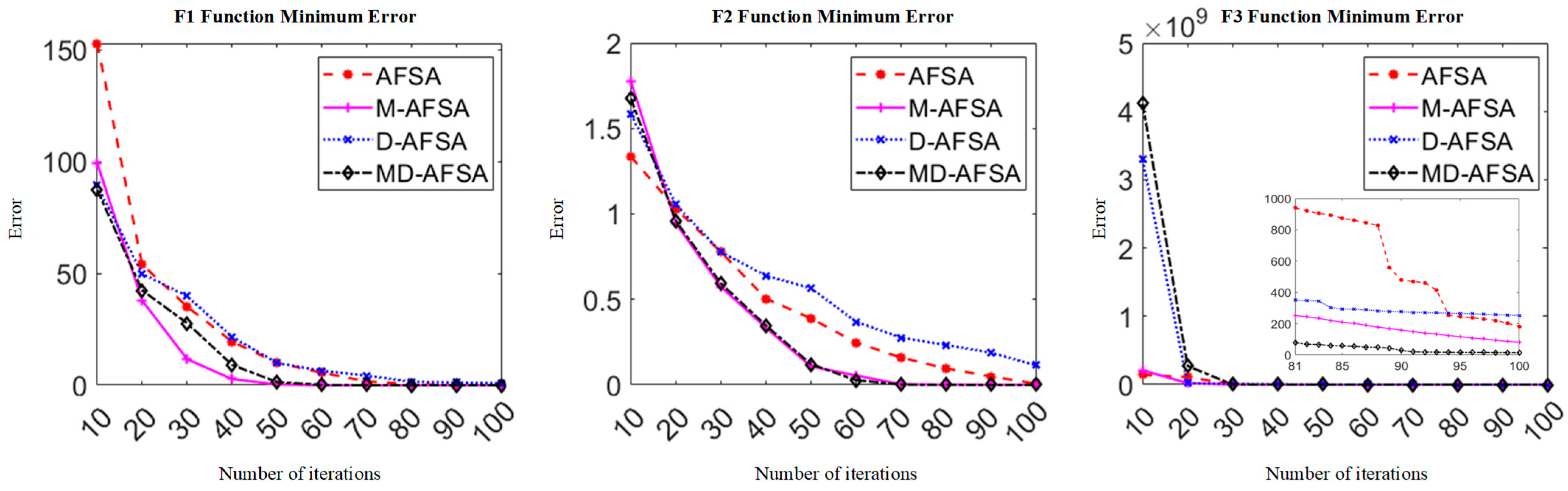
Eventually, the inequality constraint problem (2) is transformed into the unconstrained problem (4), which can be further solved using an unconstrained optimization algorithm. Considering the complexity of the problem and the shortcomings of traditional methods for solving this type of problems [11], this paper will use a heuristic algorithm to solve the problem and finally designs a dynamic memory fish swarm algorithm, which is described in Section 3.

• User group parameters’ optimization problem

Group parameters optimization involves managing resources such as power and bandwidth among multiple users in multicast or broadcast scenarios. It ensures efficient resource utilization, prevents service degradation, and balances power allocation, providing reliable service for all users in dense networks.

Firstly, the problem is abstractly modeled by considering the optimization of the user group parameters of the downlink system, whose optimization parameters include the bandwidth allocation ratio (5) and the power allocation ratio (6) between the groups, and thus the problem can be described as solving for the optimal downlink bandwidth allocation ratio as well as the power allocation ratio $P_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}^{\mathrm{S}\mathrm{P}}$ so that the downlink rate and the optimal and satisfy the user’s rate requirements.

$$\left\{\begin{array}{cc}\hfill \arg & {\min }_{B_{\mathrm{down}}^{\mathrm{sp}}}{V}_{\mathrm{target}}\hfill \\ \hfill s.t.& B_{\mathrm{down}}^{\mathrm{sp}}=\left(b{f}_{\mathrm{down}}^1,b{f}_{\mathrm{down}}^2,\dots ,b{f}_{\mathrm{down}}^{n{c}_{\mathrm{down}}}\right)\hfill \\ & {\displaystyle {\sum }_{i=1}^{n{c}_{\mathrm{down}}}b{f}_{\mathrm{down}}^i}=1\hfill \\ & b{f}_{\mathrm{down}}^i\ge 0,1\le i\le n{c}_{\mathrm{down}}\hfill \end{array}\right.$$

(5)

where $b{f}_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}^i$ represents the uplink bandwidth allocated to user group $i$, $p{f}_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}^i$ represents the proportion of power shared by the $i$-th user group.

$$\left\{\begin{array}{ll}\arg & {\min }_{P_{\mathrm{down}}^{\mathrm{sp}}}{V}_{\mathrm{target}}\\ s.t.& P_{\mathrm{down}}^{\mathrm{sp}}=\left(p{f}_{\mathrm{down}}^1,p{f}_{\mathrm{down}}^2,\dots ,p{f}_{\mathrm{down}}^{n{c}_{\mathrm{down}}}\right)\\ & {\displaystyle {\sum }_{i=1}^{n{c}_{\mathrm{down}}}p{f}_{\mathrm{down}}^i}=1\\ & p{f}_{\mathrm{down}}^i\ge 0,1\le i\le n{c}_{\mathrm{down}}\end{array}\right.$$

(6)

• RSMA parameters’ optimization problem

RSMA optimizes the splitting of user messages, power allocation, and bandwidth distribution to manage interference and enhance network efficiency. It enables better handling of user heterogeneity, improves spectral efficiency, and plays a key role in next-generation networks like 5G and 6G, particularly in UAV-assisted communications.

Consider the optimization of RSMA parameters for the downlink system, which consists of the common message splitting ratio $R_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}^{\mathrm{s}\mathrm{p}}$ and the power allocation ratio within the group $P{U}_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}^{\mathrm{s}\mathrm{p}}$. The problem can be described as solving for the optimal $R_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}^{\mathrm{s}\mathrm{p}}$ (as in Equation (7)) and $P{U}_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}^{\mathrm{s}\mathrm{p}}$ (as in Equation (8)) such that the transmission rate and is maximized while satisfying the user rate requirements.

$$\left\{\begin{array}{ll}\arg & {\min }_{R_{\mathrm{down}}^{\mathrm{sp}}}{V}_{\mathrm{target}}\\ s.t.& R_{\mathrm{down}}^{\mathrm{sp}}=\left(r{f}_{\mathrm{down}}^1,r{f}_{\mathrm{down}}^2,\dots ,r{f}_{\mathrm{down}}^{n{u}_{\mathrm{down}}}\right)\\ & {\displaystyle {\sum }_{i=1}^{n{u}_{\mathrm{down}}}r{f}_{\mathrm{down}}^i}=1\\ & r{f}_{\mathrm{down}}^i\ge 0,1\le i\le n{u}_{\mathrm{down}}\end{array}\right.$$

(7)

$$\left\{\begin{array}{ll}\arg & {\min }_{P{U}_{\mathrm{down}}^{s\mathrm{p}}}{V}_{\mathrm{target}}\\ s.t.& P{U}_{\mathrm{down}}^{\mathrm{sp}}=\left(pu{f}_{\mathrm{down}}^1,pu{f}_{\mathrm{down}}^2,\dots ,pu{f}_{\mathrm{down}}^{n{u}_{\mathrm{down}}+1}\right)\\ & {\displaystyle {\sum }_{i=1}^{n{u}_{\mathrm{down}}+1}pu{f}_{\mathrm{down}}^i}=1\\ & PU{f}_{\mathrm{down}}^i\ge 0,1\le i\le n{u}_{\mathrm{down}}+1\end{array}\right.$$

(8)

where $n{u}_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}$ is the number of users in the user group, $r{f}_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}^i$ represents the rate share of the $i$-th user in the user group in public messages, and $pu{f}_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}^i$ represents the proportion of power allocated to the $i$-th message in the group (the total number of messages is the number of users plus one). It can be transformed into a typical linear equation constrained optimization problem with the help of the augmented Lagrange function multiplier method [23], for which an algorithm is designed in this paper to optimize the solution algorithm of an artificial fish school under the constraints of linear equation, which is realized by adding constraints for each step of the operation of the artificial fish.

4. Optimization Problem Solving

4.1. Memory-Based Dynamic Artificial Fish Swarm Algorithm

This paper employs the improved Artificial Fish Swarm Algorithm to resolve the UAV parameter optimization problem presented in Section 3. The position of the artificial fish in AFSA provides a feasible solution to the optimization problem. AFSA’s optimization objective is to find the best position with the highest food concentration in the fish swarm, which represents the best solution [24]. Because the traditional Artificial Fish Swarm Algorithm (AFSA) is based on fixed step and fixed field of view for iteration, which may lead to relatively slow convergence or failure to reach the convergence point later. Therefore, this paper introduces a memory approach, dynamic step size, and dynamic field of view strategies. Finally, we design a Dynamic Memory Artificial Fish Swarm Algorithm (MD-AFSA) that can adjust the current movement strategy of the fish swarm according to the historical operation to achieve rapid convergence.

Figure 2 illustrates the improved model MD-AFSA proposed in this paper. Building upon the basic operations of the standard fish swarm algorithm, this model introduces a memory-based behavior operation, allowing the simultaneous execution of three search paths to locate the next state. After completing the state transition of the artificial fish, the step size and visual range are updated accordingly.

• First search path

Use $f\left(X_t\right)<f\left(X_{t-1}\right)$ to determine whether to perform the memory operation, indicating the artificial fish found a better position in the last iteration. If the condition is met, the Memory behavior is executed and the position of the artificial fish is updated by $X_i^{t+1}=X_i^t+rand\left[0,1\right]\times ste{p}_i^t\ast \left({\beta }_{1}di{r}_c+{\beta }_{2}di{r}_p\right)$, where $X_i^t$ denotes the position of the artificial fish $i$ after $t$ iterations. $ste{p}_i^t$ is the step size after iterating $t$ times. ${\beta }_1+{\beta }_2=$1, which is the constant coefficient factor. $di{r}_c$ and $di{r}_p$ are calculated as shown in (9), representing the current and historical direction. $X_t^{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}$ represents the optimal solution among all solutions after iterating for $t$ times. ${\mu }_t$ and ${\mu }_{t-1}$ represent the current and historical position validity, respectively.

• Second search path

Use ${\displaystyle \frac{f\left(X_c\right)}{n_{nb}}}<\vartheta f\left(X_i\right)$ to determine whether to perform Swarm behavior, where $X_c$ is the center position of the current artificial fish’s neighbors, $n_{nb}$ is the number of neighbors of the current artificial fish, and $\vartheta$ is the crowding factor. Satisfying this condition means that the partner center is not crowded, and thus Swarm behavior can be executed by $X_i^{t+1}=X_i^t+rand\left[0,1\right]\times ste{p}_i^t\ast {\displaystyle \frac{X_c-X_i^t}{\left|X_c-X_i^t\right|}}$. On the contrary, the artificial fish attempts to perform Foraging behavior. The prerequisite for performing Foraging behavior is that in the number of $tr{y}_{max}$ attempts, the presence of $X_n=X_i^t+visua{l}_i^t\times Rand\left[-1,1\right]$ and $f\left(X_n\right)<f\left(X_i^t\right)$. If the condition is met, the artificial fish will perform Foraging behavior by $X_i^{t+1}=X_i^t+rand\left[0,1\right]\times ste{p}_i^t\ast {\displaystyle \frac{X_n-X_i^t}{\left|X_n-X_i^t\right|}}$. Otherwise, it will execute Random behavior by $X_i^{t+1}=X_i^t+visua{l}_i^t\times Rand\left[-1,1\right]$.

• Third search path

Use ${\displaystyle \frac{f\left(X_j\right)}{n_{nb}}}<\vartheta f\left(X_i\right)$ to determine whether the artificial fish is capable of Rear-End behavior, where $X_j$ is the position of the optimal node between the current neighbor nodes.

$$\left\{\begin{array}{l}di{r}_c={\displaystyle \frac{{\mu }_t\left(X_t^{\mathrm{best}}-X_i^t\right)+{\mu }_{t-1}\left(X_t^{\mathrm{best}}-X_i^{t-1}\right)}{\left|{\mu }_t\left(X_t^{\mathrm{best}}-X_i^t\right)+{\mu }_{t-1}\left(X_t^{\mathrm{best}}-X_i^{t-1}\right)\right|}}\\ di{r}_p={\displaystyle \frac{{\mu }_t\left(X_{t-1}^{\mathrm{best}}-X_i^t\right)+{\mu }_{t-1}\left(X_{t-1}^{\mathrm{best}}-X_i^{t-1}\right)}{\left|{\mu }_t\left(X_{t-1}^{\mathrm{best}}-X_i^t\right)+{\mu }_{t-1}\left(X_{t-1}^{\mathrm{best}}-X_i^{t-1}\right)\right|}}\\ {\mu }_t={\displaystyle \frac{\left|f\left(X_i^t\right)-f\left(X_t^{\mathrm{best}}\right)\right|}{\left|f\left(X_i^t\right)-f\left(X_t^{\mathrm{best}}\right)\right|+\left|f\left(X_i^{t-1}\right)-f\left(X_t^{\mathrm{best}}\right)\right|}}\\ {\mu }_{t-1}={\displaystyle \frac{\left|f\left(X_i^{t-1}\right)-f\left(X_t^{\mathrm{best}}\right)\right|}{\left|f\left(X_i^t\right)-f\left(X_t^{\mathrm{best}}\right)\right|+\left|f\left(X_i^{t-1}\right)-f\left(X_t^{\mathrm{best}}\right)\right|}}\end{array}\right.$$

(9)

If condition is met, use $X_i^{t+1}=X_i^t+rand\left[0,1\right]\times ste{p}_i^t\ast {\displaystyle \frac{X_j-X_i^t}{\left|X_j-X_i^t\right|}}$ to execute Rear-End behavior. Conversely, trying to perform Foraging behavior.

In particular, the standard AFSA uses a fixed field of view and a step size, however, early in the algorithm iteration process, larger $visual$ and $step$ are required to enhance the search capability and the convergence speed, but later it need smaller $visual$ and $step$ to improve the search accuracy [25]. To address this problem, MD-AFSA designs a separate field of view as well as a step size for each artificial fish, and the field of view and step size of the artificial fish are updated after each iteration in the manner of (10) and (11), where $t_m$ is the algorithm’s maximum allowed number of iterations. $ste{p}_i^t$ is the step length after $t$ iterations. $visua{l}_i^t$ is the field of view after $t$ iterations. $st{h}_i^{\mathrm{m}\mathrm{i}\mathrm{n}}$ is the lower limit of the step size of artificial fish $i$ and $vt{h}_i^{\mathrm{m}\mathrm{i}\mathrm{n}}$ is the lower limit of the field of view of the artificial fish $i$. It is easy to prove that $ste{p}_i^t$ and $visua{l}_i^t$ are non-increasing and will eventually reach the lower limit.

$$ste{p}_i^{t+1}=\min \left(\cos \left({\displaystyle \frac{t\sqrt{t}}{t_m\sqrt{t_m}}}\ast {\displaystyle \frac{pi}{2}}\right)\ast ste{p}_i^t+st{h}_i^{\min },ste{p}_i^t\right)$$

(10)

$$visua{l}_i^{t+1}=\min \left(\cos \left({\displaystyle \frac{t\sqrt{t}}{t_m\sqrt{t_m}}}\ast {\displaystyle \frac{pi}{2}}\right)\ast visua{l}_i^t+vt{h}_i^{\min },visua{l}_i^t\right)$$

(11)

In addition, based on the behavioral performance of artificial fish, MD-AFSA provides an updated strategy for $st{h}_i^{\mathrm{m}\mathrm{i}\mathrm{n}}$ and $vt{h}_i^{\mathrm{m}\mathrm{i}\mathrm{n}}$:

• After consecutive $t_{th}$ iterations, if the current artificial fish view cannot capture the optimal solution after the previous iteration and no better position is found:

  $$\left\{\begin{array}{l}{\widetilde{sth}}_i^{\min }=\sqrt[4]{t_m}\ast st{h}_i^{\min }\\ {\widetilde{vth}}_i^{\min }=\sqrt[4]{t_m}\ast vt{h}_i^{\min }\end{array}\right.$$

  (12)
• After consecutive $t_{th}$ iterations, if the current artificial fish field of view captures the optimal solution after the previous iteration:

  $$\left\{\begin{array}{l}{\widetilde{sth}}_i^{\min }={\displaystyle \frac{st{h}_i^{\min }}{\sqrt[4]{t_m}}}\\ {\widetilde{vth}}_i^{\min }={\displaystyle \frac{vt{h}_i^{\min }}{\sqrt[4]{t_m}}}\end{array}\right.$$

  (13)

In this paper, the inequality problem of UAV position is transformed into an unconstrained problem by ALM in Section 3, which is solved by MD-AFSA in this section, and the complete algorithm flow is shown in Figure 2.

4.2. Memory-Based Dynamic AFSA Under Linear Equality Constraints

In this algorithm, user group parameters and RSMA parameters are optimized. Aiming at (7)and (8) in Section 3, this paper designs an artificial fish swarm optimization algorithm under linear equality constraints, which is realized by adding constraints to each step of the artificial fish. Let $P=I-A^T{\left(A{A}^T\right)}^{-1}A$. For $X_1$, satisfying $A{X}_1=b$. Denote $X_2=X_1+\alpha ·\ast P\ast X_r$, where $\alpha$ is the non-negative proportional control factor and $\ast$ represents the scalar multiplication by a vector and $X_r$ is an arbitrary vector. $A{X}_2=b+\alpha ·\ast \left(A\ast P\right)\ast X$ and because of $A\ast P=0$, $A{X}_2=b$, which satisfies the constraints of linear equality.

MD-AFSA in Section 3.1 is further optimized to obtain a Memory-based Dynamic Fish Swarm Algorithm Under Linear Equality Constraints (LEC-MD-AFSA). LEC-MD-AFSA modifies the relevant operational behavior of the artificial fish, so that the new solution obtained still satisfies the linear equality constraints.

Due to $X_1$ and $X_2$ satisfying the constraint $AX=b$, it is easy to prove that $A{X}_3=b$, where $X_3=X_1+k\ast \left(X_2-X_1\right)$, so the new solutions obtained from the Swarm and Rear-End behaviors of MD-AFSA still satisfy the constraint without correction. Similarly, the direction factor of the Memory behavior remains a linear combination of feasible solutions without correction. For the Foraging behavior, the artificial fish needs to try to find a new location within the field of view, and in order to make the found location satisfy the linear equality constraint, correct by $X_n=X_i^t+visua{l}_i^t\ast P\ast Rand\left[-1,1\right]$. For the random behavior, the correction is $X_i^{t+1}=X_i^t+P\ast Rand\left[-1,1\right]\ast visua{l}_i^t$. In the problem considered in this paper, the row vectors of matrix $A$ are orthogonal to each other and the values in $A$ only contain {0,1}. All elements in the vector $b$ are 1, therefore, several random numbers in the [0,1] interval can be randomly generated, and then divide each element by the sum of all numbers to get the initial solution of the artificial fish. The original user group and RSMA parameters’ optimization problems are turned into linear constraint problems in Section 3 using the augmented Lagrange function, and the solution algorithm is implemented based on MD-AFSA.

In conclusion, this paper decomposes the problem of UAV-assisted communication rate optimization based on RSMA into three sub-problems for solution. When solving a parameter optimization sub-problem, the parameters of other sub-problems are treated as constants; finally, the original optimization problem is solved by the ternary cross iteration method.

5. Simulation Analysis

Aiming at the downlink UAV-aided RSMA system designed in this paper, the proposed key algorithm and related systems are simulated and analyzed in MATLAB R2016a.

5.1. Simulation Analysis of MD-AFSA Algorithm Performance

In this study, the AFSA algorithm is improved and designed, and the MD-AFSA algorithm is proposed to improve the optimization ability and convergence speed of the algorithm, and realize the optimal solution of UAV deployment position. In the experiment, some test functions introduced in reference [26] are selected to analyze and compare the performance of the algorithm. The information of the selected test functions is shown in

Table 1. Single extremum test function.

Function	Function Expression	Range	Minimum Value
Step	$F_1\left(x\right)={\displaystyle \sum _{i=1}^D}{\left(x_i+0.5\right)}^2$	${\left[-100,100\right]}^D$	0
Schwefel 2.22	$F_2\left(x\right)={\displaystyle \sum _{i=1}^D}\left|x_i\right|+{\displaystyle \prod _{i=1}^D}\left|x_i\right|$	${\left[-10,10\right]}^D$	0
Cigar	$F_3\left(x\right)=x_1^2+{10}^6{\displaystyle \sum _{i=2}^D}{x}_i^6$	${\left[-100,100\right]}^D$	0

and

Table 2. Multi-extremum test function.

Function	Function Expression	Range	Minimum Value
Himmelblau	$F_4\left(x\right)={\displaystyle \frac{1}{D}}{\displaystyle \sum _{i=1}^D}\left(x_i^4-16x_i^2+5x_i\right)$	${\left[-5,5\right]}^D$	−78.3326
Schaffer	$F_5\left(x\right)=0.5+{\displaystyle \frac{{\left(sin\sqrt{{\displaystyle {\sum }_{i=1}^D}{x}_i^2}\right)}^2-0.5}{{\left(1+0.001\left({\displaystyle {\sum }_{i=1}^D}{x}_i^2\right)\right)}^2}}$	${\left[-100,100\right]}^D$	0
Alpine	$F_6\left(x\right)={\displaystyle \sum _{i=1}^D}\left|x_i\sin \left(x_i\right)+0.1x_i\right|$	${\left[-10,10\right]}^D$	0

.

The standard AFSA and the dynamic strategy and memory strategy proposed in this paper are tested on the test functions in Table 1 and Table 2, respectively. Figure 3 shows the test results of single extreme function.

In Figure 3, AFSA represents the standard artificial fish school algorithm, M-AFSA represents the memory strategy proposed in this paper to the standard artificial fish school algorithm, D-AFSA represents the dynamic step size and dynamic field strategy proposed in this paper to the standard artificial fish school algorithm, and MD-AFSA represents the dynamic memory fish school algorithm proposed in this paper. According to Figure 3, it can be seen that D-AFSA usually has a good convergence speed in the early stage of algorithm iteration, but the convergence speed is even lower than that of AFSA in the late stage of algorithm iteration; compared with D-AFSA and AFSA, M-AFSA can achieve faster convergence speed and lower error; the convergence speed of MD-AFSA in the iteration process of algorithm is close to that of M-AFSA (slightly lower in the early stage of F3), but it has a lower error. The final error of three single-extreme functions after 100 iterations using different optimization algorithms is shown in

Table 3. Error after 100 iterations of a single extremum function.

Function	F1	F2	F3
AFSA	1.71 × 10−4	7.51 × 10−3	1.82 × 102
M-AFSA	1.69 × 10−5	7.52 × 10−4	8.14 × 101
D-AFSA	8.46 × 10−1	1.15 × 10−1	2.53 × 102
MD-AFSA	6.40 × 10−7	9.91 × 10−5	1.50 × 101

. In this test, the error is defined as the difference between the sought objective function value and the actual minimum value. On the F1 function, the solution error of MD-AFSA is reduced by 99.63% compared with AFSA; on the F2 function, the solution error of MD-AFSA is reduced by 98.68% compared with AFSA; on the F3 function, the solution error of MD-AFSA is reduced by 91.76% compared with AFSA.

Figure 4 shows the test results of multi-extreme function, and the maximum iteration number of the algorithm is set to 100 times.

In Figure 4, the meaning of each curve is consistent with that of Figure 3. In the multi-extreme function test, D-AFSA still performs poorly, even lower than the standard AFSA algorithm; M-AFSA and MD-AFSA have better performance than AFSA and D-AFSA; On the basis of M-AFSA, MD-AFSA incorporates dynamic step size and dynamic field of view strategies, which is conducive to faster convergence and algorithm optimization.

The final errors of the three multi-extreme functions after 100 iterations using different optimization algorithms are shown in

Table 4. Error after 100 iterations of a multi extremum function.

Function	F4	F5	F6
AFSA	2.94 × 10−1	6.64 × 10−2	7.61 × 10−4
M-AFSA	8.36 × 10−4	1.91 × 10−2	2.29 × 10−4
D-AFSA	7.50 × 10−1	7.97 × 10−2	1.02 × 10−2
MD-AFSA	8.44 × 10−4	1.08 × 10−2	4.81 × 10−5

. The analysis shows that MD-AFSA has the lowest error only in all test functions. On the F4 function, the solution error of MD-AFSA is reduced by 99.71% compared with AFSA; on the F5 function, the solution error of MD-AFSA is reduced by 83.70% compared with AFSA; on the F6 function, the solution error of MD-AFSA is 93.67% lower than that of AFSA.

The optimization test of single extremum function and multi-extremum function shows that the MD-AFSA algorithm proposed in this paper has better convergence speed and optimization ability than the original algorithm, and can quickly find the optimal solution point of the objective function and solve the optimization problem.

Under the same experimental conditions (the hardware platform parameters and algorithm parameters are consistent), the time characteristics of different algorithms are tested, and the end condition of the algorithm is that the maximum number of iterations is reached or the difference between the optimization function value and the actual optimal value is less than 0.01. The test results are shown in Table 4.

According to

Table 5. Algorithm time characteristics (unit: s).

Function	AFSA	M-AFSA	D-AFSA	MD-AFSA
F1	1.72	1.51	1.65	1.50
F2	1.97	1.33	2.01	1.48
F3	3.24	2.61	3.52	2.43
F4	3.63	2.65	3.63	2.58
F5	4.06	3.74	4.14	4.22
F6	2.14	1.54	2.28	1.70

, when the optimization error is 0.01, D-AFSA can’t reduce the time consumption of the algorithm, while M-AFSA and MD-AFSA can effectively reduce the running time of the algorithm and improve the efficiency and practicability of the algorithm.

5.2. Simulation of Downlink RSMA System

This paper validates the UAV-assisted communication downlink transmission optimization based on RSMA by MATLAB. The key parameters of the simulation are in

Table 6. Key parameters of downlink RSMA system simulation.

Parameters	Value
System bandwidth	10 MHz
Area size	500 × 500 × 75 m3
UAV height	75 m
Noise power spectral density	−174 dBm/Hz
Range of Signal-to-noise ratio	0~30 dB
Number of users	10~130
Users Distribution	Random distribution

. Assume that the upstream transmission bandwidth allocated to a user group is 0.5 MHz, and the upper limit of transmit power for a single user is 10 dBm.

We first consider a scenario with a single user group (comprising two users) in the downlink system. In this case, the user group is allocated a bandwidth of 0.5 MHz and a total transmission power of 25 dBm. The rate curves for the users in the group are shown in Figure 5. As is illustrated, among the three mechanisms—OMA, NOMA, and RSMA—OMA achieves the smallest capacity region, while RSMA has the largest capacity region. This discrepancy arises because RSMA is equivalent to NOMA when no power is allocated to the common message for the user group. By allocating power to the common message appropriately, RSMA can achieve higher transmission rates than NOMA.

Next, we examine how varying the number of users and the system’s signal-to-noise ratio (SNR) impacts system throughput, as shown in Figure 6. All three access mechanisms utilize the optimization algorithm described in this paper to allocate power and bandwidth resources. The results indicate that as the number of users increases, the system throughput gradually approaches saturation. Additionally, higher system SNR results in increased throughput without any upper limit. Among the three approaches, the one presented in this paper demonstrates the best performance, with the RSMA strategy achieving 13.30% higher system throughput compared to the NOMA strategy.

By fixing the position of the UAV and allocating resources between and within user groups, we assess the downlink RSMA system throughput, as shown in Figure 7.

In Figure 7, RSMA-A represents the optimization strategy proposed in this paper. RSMA-SP denotes a scenario where the UAV base station position is fixed, followed by resource allocation using the described strategy for both inter-group and intra-group resources. RSMA-SA-1 and RSMA-SA-2 represent situations where the resource allocations between and within groups are fixed (matching the optimal solution derived by RSMA-A), followed by the random selection of two UAV deployment positions for base station deployment. The results show that changing the UAV deployment position significantly impacts system throughput in the downlink system. This trend aligns with findings in the uplink system: when the UAV position is fixed and the resource allocation strategy is optimized, throughput can be effectively enhanced.

6. Conclusions

This paper has investigated the application of UAVs as base stations in emergency communication scenarios. With their flexible deployment and excellent line-of-sight communication capabilities, UAVs can provide better QoS compared to ground-based stations. To enhance system access capacity and transmission rates, this study adopted RSMA as the access mechanism for UAV base stations and focused on optimizing the downlink rate of the RSMA system through joint UAV deployment strategies.

First, the downlink system was modeled, and the optimization parameters were divided into three categories: UAV positioning parameters, user group parameters, and RSMA parameters. The original optimization problem was decomposed into three subproblems, each solved using a ternary iterative approach. For the UAV positioning optimization subproblem, a solution algorithm combining the ALM and AFSA was proposed. Moreover, the AFSA was enhanced into the MD-AFSA algorithm, incorporating dynamic step size, vision, and memory strategies. For the optimization of user group and RSMA parameters, a detailed analysis was performed, followed by the design of a modified MD-AFSA algorithm under linear equality constraints—LEC-MD-AFSA. The effectiveness of both MD-AFSA and LEC-MD-AFSA algorithms was validated through simulations, and the performance of the downlink RSMA system was evaluated.

Simulation results showed that the MD-AFSA and LEC-MD-AFSA algorithms can reduce errors by more than 85% compared to the original algorithm, with error reductions exceeding 99% across multiple test functions. Additionally, in the downlink system, the RSMA scheme improved system throughput by 13.30% compared to NOMA.

Future research could focus on optimizing RSMA systems in more complex channel conditions to further enhance system throughput. Moreover, practical implementation of the proposed algorithms on hardware platforms could be considered for future validation and development.