Isolation Number of Transition Graphs
Abstract
1. Introduction
2. Main Results
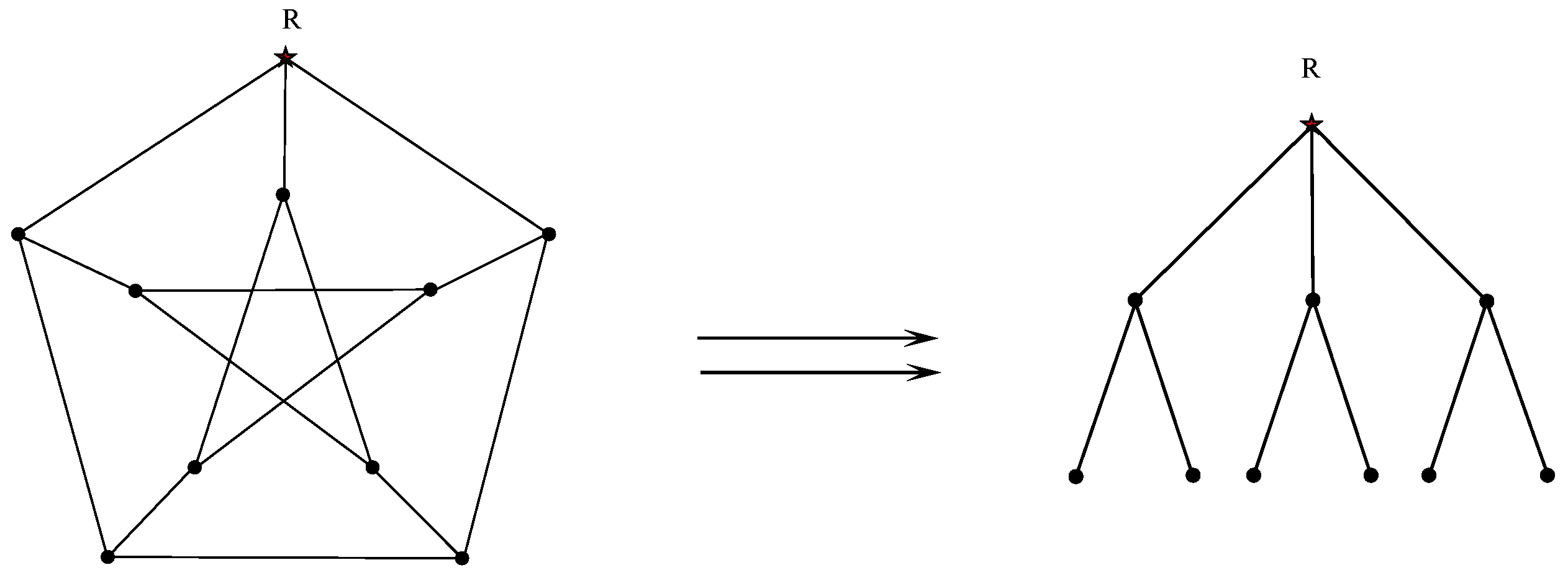
2.1. Isolation Number of a Graph
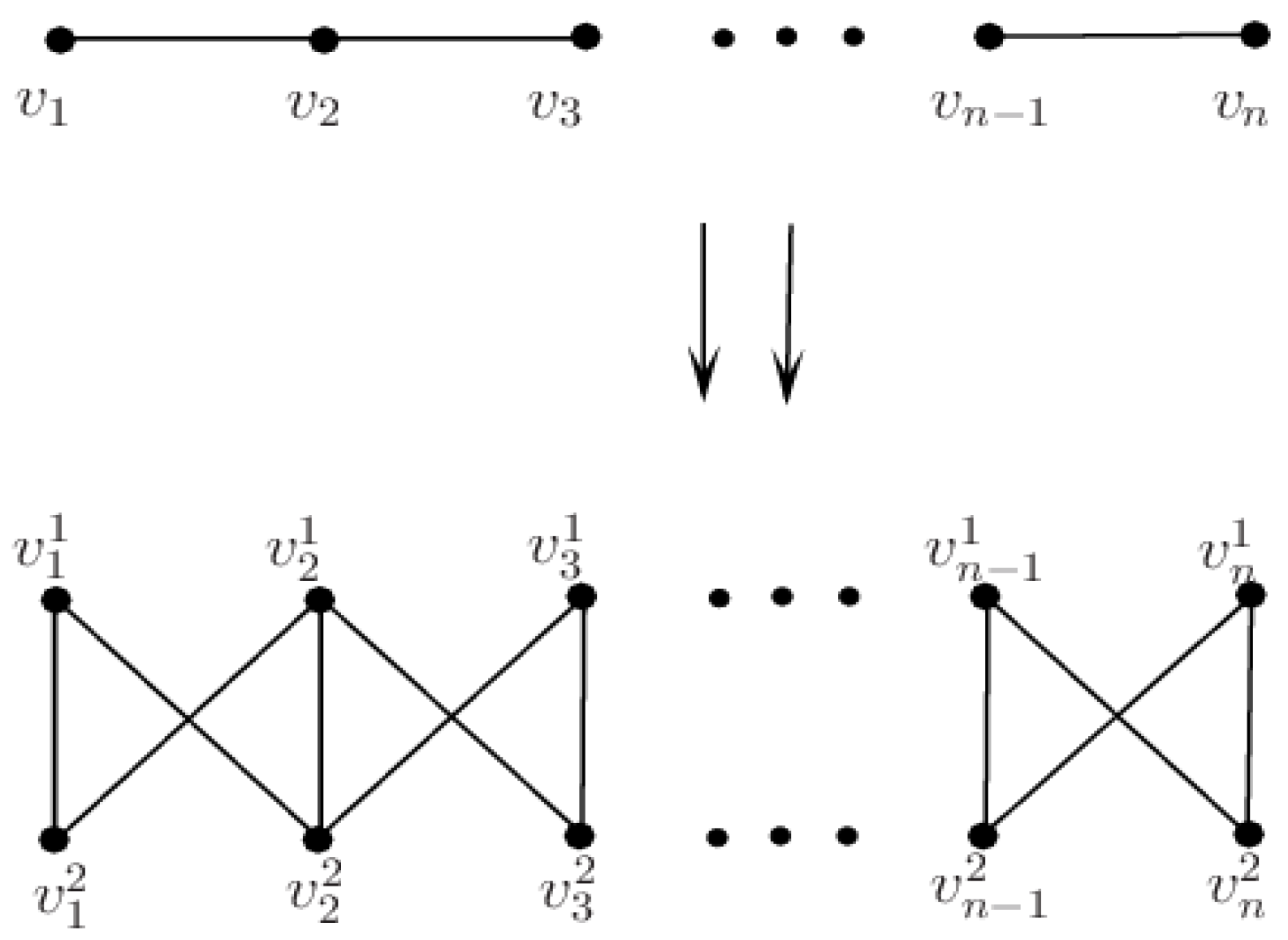
2.2. Isolation Number of the Total Graph
- (i)
- (ii)
- (iii)
- (i)
- (ii)
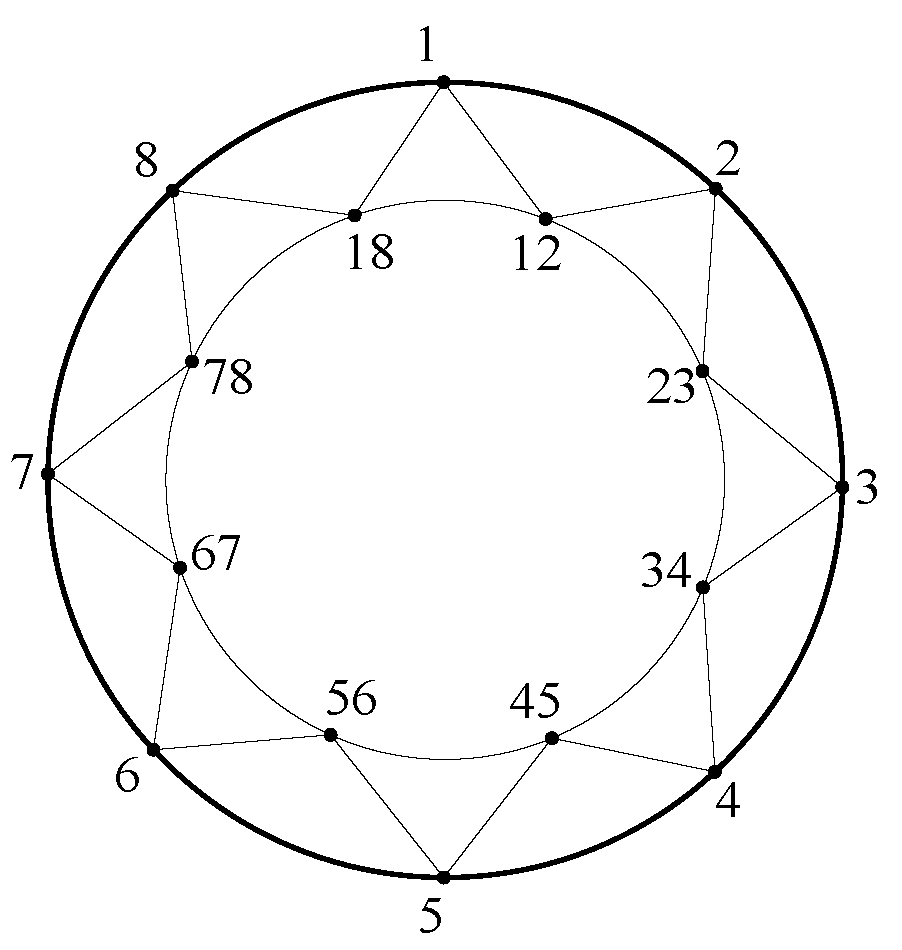
2.3. Isolation Number of Central Graph
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| The induced subgraph of vertex set X | |
| The number of neighbors of v in G | |
| The maximum degree of G | |
| The minimum degree of G | |
| The set of neighbors of v | |
| The set of neighbors of v and v | |
| The set of neighbors of all vertices in S | |
| The set of neighbors of all vertices in S and S | |
| set | A minimum dominating set |
| set | A minimum isolating set |
| removes the closed neighborhood of S | |
| The domination number of graph G | |
| The -isolation number of graph G | |
| The k-isolation number of graph G | |
| The 1-isolation number of graph G | |
| The isolation number of graph G |
References
- Berge, C. Theory of Graphs and Its Applications; Dunod: Paris, France, 1958. [Google Scholar]
- Hansberg, A.; Meierling, D.; Volkmann, L. A general method in the theory of domination in graphs. Int. J. Comput. Math. 2010, 87, 2915–2924. [Google Scholar] [CrossRef]
- Haynes, T.; Hedetniemi, S.; Slater, P. Fundamentals of Domination in Graphs; CRC Press: New York, NY, USA, 1998. [Google Scholar]
- West, D. Introduction to Graph Theory; Longman: London, UK, 1985. [Google Scholar]
- Hao, G.S.; Lim, M.H.; Ong, Y.S.; Huang, H.; Wang, G.G. Domination landscape in evolutionary algorithms and its applications. Soft Comput. 2019, 23, 3563–3570. [Google Scholar] [CrossRef]
- Stephen, S.; Rajan, B.; Ryan, J.; Grigorious, C.; William, A. Power domination in certain chemical structures. J. Discret. Algorithms 2015, 33, 10–18. [Google Scholar] [CrossRef]
- Rajan, R.S.; Anitha, J.; Rajasingh, I. 2-Power Domination in Certain Interconnection Networks. Procedia Comput. Sci. 2015, 57, 738–744. [Google Scholar] [CrossRef]
- Corcoran, P.; Gagarin, A. Heuristics for k-domination models of facility location problems in street networks. Comput. Oper. Res. 2021, 133, 53–68. [Google Scholar] [CrossRef]
- Zhu, X.; Yu, J.; Lee, W. New dominating sets in social networks. J. Glob. Optim. 2010, 48, 633–642. [Google Scholar] [CrossRef]
- Caroa, Y.; Hansbergb, A. Partial domination-the isolation number of a graph. Filomath 2017, 31, 3925–3944. [Google Scholar] [CrossRef]
- Favaron, O.; Kaemawichanurat, P. Inequalities between the Kk-isolation number and the independent Kk-isolation number of a graph. Discret. Appl. Math. 2021, 289, 93–97. [Google Scholar] [CrossRef]
- Peter, B.; Kurt, F.; Pawaton, K. Isolation of k-cliques. Discret. Math. 2020, 343, 111879. [Google Scholar]
- Shin-ichi, T.; Thiradet, J.; Pawaton, K. Isolation number of maximal outerplanar graphs. Discret. Appl. Math. 2019, 267, 215–218. [Google Scholar]
- Zhang, G.; Wu, B. K1,2-isolation in graphs. Discret. Appl. Math. 2021, 304, 365–374. [Google Scholar] [CrossRef]
- Magdalena, L.; María José, S.; Adriana, D.; Francisco, J.V. Isolation Number versus Domination number of trees. Mathematics 2021, 9, 1325. [Google Scholar] [CrossRef]
- Peter, B. Isolation of Cycles. Graphs Comb. 2020, 36, 631–637. [Google Scholar]
- Peter, B. Isolation of connected graphs. Discret. Appl. Math. 2023, 339, 154–165. [Google Scholar]
- Chen, J.; Xu, S. P5-isolation in graphs. Discret. Appl. Math. 2023, 340, 331–349. [Google Scholar] [CrossRef]
- Zhang, G.; Wu, B. A note on the Cycle Isolation Number of Graphs. Bull. Malays. Math. Sci. Soc. 2024, 47, 57. [Google Scholar] [CrossRef]
- Zhang, G.; Wu, B. Cycle Isolation of Graphs with Small Girth. Graphs Comb. 2024, 40, 38. [Google Scholar] [CrossRef]
- Yang, Z.; Arockiaraj, M.; Prabhu, S.; Arulperumjothi, M.; Liu, J.N. Second Zagreb and Sigma Indices of Semi and TotalTransformations of Graphs. Complexity 2021, 2021, 6828424. [Google Scholar] [CrossRef]
- Kalpana, M.; Vijayalakshmi, D. On b-coloring of central graph of some graphs. Commun. Fac. Sci. Univ. Ank. Ser. A1 Math. Stat. 2019, 68, 1229–1239. [Google Scholar] [CrossRef]
- Peter, B.; Kurt, F.; Pawaton, K. Isolation of k-cliques II. Discret. Appl. Math. 2022, 345, 112641. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, J.; Zhang, S. Isolation Number of Transition Graphs. Mathematics 2025, 13, 116. https://doi.org/10.3390/math13010116
Qu J, Zhang S. Isolation Number of Transition Graphs. Mathematics. 2025; 13(1):116. https://doi.org/10.3390/math13010116
Chicago/Turabian StyleQu, Junhao, and Shumin Zhang. 2025. "Isolation Number of Transition Graphs" Mathematics 13, no. 1: 116. https://doi.org/10.3390/math13010116
APA StyleQu, J., & Zhang, S. (2025). Isolation Number of Transition Graphs. Mathematics, 13(1), 116. https://doi.org/10.3390/math13010116




