1. Introduction
Stock market manipulation constitutes a deliberate attempt to distort the genuine prices of assets, thereby misleading investors and affecting their investment decisions. This manipulation not only triggers economic losses for investors but also compels the state to divert its limited resources towards monitoring and controlling such activities. Furthermore, companies targeted by manipulation efforts experience significant reputational damage, thus compounding the negative impact beyond mere financial loss [
1]. The U.S. Securities and Exchange Commission (SEC) succinctly defines stock market manipulation as intentional actions aimed at deceiving or defrauding investors through the control or artificial influence of asset prices. The study of stock market manipulation is crucial for maintaining market integrity, protecting investor interests, and ensuring the smooth functioning of financial markets. Understanding and combating such manipulative practices are essential for fostering a transparent, fair, and efficient market environment where investors can make decisions based on accurate and truthful information.
There is a prolific research stream seeking to understand the manipulation process [
2,
3]. For instance, Allen and Gale [
4] classified manipulation activities according to how they are performed into three categories: action-based, rumor-based, and trading. They also showed that an uninformed manipulator can benefit by mimicking the behavior of an informed trader with the help of information asymmetries. The work of the International Organization of Securities Commissions [
5] describes what methods manipulators use, with the main ones being wash sales, advancing the bid, pumping and dumping, marking the close, cornering the market, and squeezing the market. The work of Imisiker et al. [
6] analyzes the characteristics of manipulated shares, thereby concluding that companies that were previously manipulated and have high leverage ratios also have a high probability of being manipulated, while stocks with a high volume available for trading and high market capitalization are difficult to manipulate.
However, few studies seek to detect and predict manipulation, and even fewer use machine learning tools for detection [
2,
7]. The generally strong performance of supervised learning models can largely be attributed to their ability to learn from patterns explicitly presented to them. By employing labeled data, these models are trained to recognize and respond to the specific patterns they have been exposed to during the training process. This focused learning approach, however, introduces a significant limitation: the model’s difficulty in identifying novel manipulation patterns—those which it has not been previously taught [
8]. This inherent challenge emphasizes the need for models that can adapt to and detect emerging patterns of manipulation, thus extending beyond the confines of their initial training set.
Palshikar et al. [
9] performed one of the first investigations that allowed for detecting manipulation using fuzzy temporal logic; they identified the common trading patterns used by manipulators. Öğüt et al. [
2] used probabilistic neural networks (PNNs) and support vector machines (SVMs) to obtain better results in detecting manipulation cases than those obtained with traditional statistical models.
Diaz et al. [
10] used an unsupervised approach to identify manipulated hourly blocks, which were then used as labels for a supervised analysis. Using decision trees, they extracted different rules to identify manipulation patterns.
Cao et al. [
11] introduced a novel semisupervised learning methodology that employs a hidden Markov model (HMM) specifically designed for the task at hand. This approach, dubbed the Hidden Markov Model with Abnormal States (HMMAS), was strategically applied to analyze stock data from both the NASDAQ and London Stock Exchange, thereby aiming to uncover patterns indicative of market manipulation. In developing HMMAS, the authors posited certain assumptions about the underlying data distribution, thus creating a solid foundation for the targeted detection of manipulation within these major financial markets.
Yang et al. [
12] conducted a comparative analysis of various supervised learning algorithms with the objective of identifying suspected cases of market manipulation. Among the algorithms evaluated, the naive Bayes classifier emerged as the most effective, thus demonstrating superior performance in detecting potential manipulation instances.
Leangarun et al. [
13] used long short-term memory generative adversarial networks (LSTM-GANs) to achieve 68.1% accuracy when identifying manipulated cases. Wang et al. [
7] combined the characteristics derived from commercial records and those of listed companies and used recurrent neural networks (RNNs) to detect manipulation activities. Their results were, on average, 29.8% higher in terms of area under the ROC curve (AUC) than those observed in studies that used traditional statistical tools. Rizvi et al. [
14] proposed an unsupervised model based on the idea of learning the relationship between stock prices in the form of an affinity matrix; the characteristics extracted from this matrix were used to train an autoencoder. Finally, they used clustering based on kernel density estimation (MKDE) to detect manipulated operations, where nonclustered data were treated as manipulated. Rizvi et al. [
8] used kernel PCA to obtain vectors of characteristics delivered to MKDE to detect manipulations. To this end, they used a dataset with information on 13 stocks from NASDAQ and the London Stock Exchange (LSE), with the information of manipulations generated in synthetic form. Leangarun et al. [
15] compared the LSTM autoencoder (LSTM-AE) and LSTM-GANs, with both models identifying five of six manipulations and yielding a low false positive rate. Models based on deep learning show promising results. However, they are limited by high computational complexity [
16,
17].
From the studies reviewed, it is evident that employing a supervised learning approach carries the inherent risk of overfitting, where the algorithm might become excessively tailored to the labeled manipulation patterns at hand, thereby compromising its ability to generalize to new or unseen data. This risk is particularly pronounced in fields like stock market manipulation detection, where labeled data are scarce, thus making it crucial to mitigate overfitting to maintain model robustness. To address this challenge, our proposal advocates for the exploration of unsupervised learning techniques, which, by not relying on labeled data, naturally avoid the pitfalls of overfitting and potentially offer a more generalized and adaptable solution. Furthermore, a critical examination of the reported success rates and the transparency of false positive results, as emphasized by Rizvi et al. [
8], are essential steps to validate the effectiveness of these unsupervised approaches in real-world applications.
This study aims to detect manipulation activity using an unsupervised learning approach. To bolster the detection capabilities for anomalies, the dataset was augmented with new features derived from sophisticated statistical calculations. We performed manipulation detection using a voting ensemble composed of unsupervised anomaly detection models. We employed a real dataset to evaluate the performance of our proposal; this consists of annual data from eight stocks that have undergone manipulation activities.
This article centers on the transformative impact of the Isolation Forest (IF) algorithm in detecting stock market manipulation through an unsupervised learning approach. The isolation forest, distinguished by its innovative use of isolation rather than density or distance to identify anomalies, offers a unique advantage in the financial domain where manipulative activities are often subtle and masked within vast datasets. The unsupervised nature of this algorithm eliminates the need for a prelabeled dataset, thus addressing the challenge of scarce labeled data in the realm of financial fraud detection. Moreover, its efficiency in handling high-dimensional data and its scalability make it particularly suitable for the dynamic and complex environment of the stock market [
18,
19,
20]. By deploying this method, our study sheds light on its efficacy in uncovering manipulation patterns, thereby contributing to safer and more transparent financial markets.
The main contributions of this research are (1) proposing an unsupervised manipulation detection strategy that improves the task of identifying manipulated time blocks and (2) presenting the benefits of using a voting ensemble approach to detect manipulated blocks.
The remainder of this paper is organized as follows.
Section 2 describes the methodology used, the case study, the description of the voting ensemble model and the Isolation Forest algorithm, the performance measures used to evaluate the model, and ends with details of the model implementation.
Section 3 presents the results of the model in the search of manipulations; these are compared with the results of previous studies.
Section 4 discusses the results, in addition to making recommendations and observing weaknesses. Finally,
Section 5 summarizes the results and proposes future research directions.
2. Materials and Methods
This section details the methodology used to identify suspected manipulation cases using an unsupervised approach.
2.1. Methodology
Adopting the Cross-Industry Standard Process for Data Mining (CRISP-DM) methodology in our investigation into the capabilities of an isolation forest ensemble for detecting stock market manipulation offers a structured, iterative, and comprehensive framework that significantly enhances the study’s scientific rigor and practical applicability. The CRISP-DM methodology has been previously and successfully employed in other machine learning projects, as evidenced by the literature [
21,
22,
23]. By meticulously following CRISP-DM’s phases—from understanding the business problem and data to model evaluation and deployment—we ensure a deep alignment between our models and the real-world phenomenon of market manipulation. This approach not only guarantees the transparency and repeatability of our experiment but also ensures that our findings are directly applicable to real-world scenarios. The iterative nature of CRISP-DM allows for continuous model refinement, thus leading to optimized detection capabilities. Furthermore, the methodology’s emphasis on understanding business objectives and data intricacies ensures that our ensemble models are both effective in anomaly detection and relevant to the specific challenges of stock market manipulation, thereby providing a clear pathway for deploying these models in practical trading systems.
Figure 1 illustrates the distinct phases of the CRISP-DM methodology as implemented in our study.
2.2. Case Study
The dataset analyzed includes cases of manipulation identified during 2003 and pursued through litigation actions by the U.S. Securities and Exchange Commission (SEC). These data were used by [
10,
24] and consist of 12,748 instances with time information for the January–December period. Eight stocks were affected by manipulation activities during the analyzed period. There is certainty that these stocks were manipulated during 2003, but the total number of affected transactions is not known. In [
10], the authors manually labeled 55 cases containing manipulated transactions, which were used to evaluate the model performance.
Table 1 shows the number of manipulations per stock.
The 55 labeled manipulated transactions were identified by reviewing lawsuits filed by the SEC. Manipulated stocks are those that include words related to market manipulation in the lawsuits filed by the SEC, for example, “manipulation” and “marking the close”, or those referring to Sections 9(a) or 10(b) of the Securities and Exchange Act (1934), which are articles relating to market manipulation.
Initially, we selected variables commonly used in stock market analysis. These variables are price, return, volume, and number of transactions.
Figure 2 shows some selected stocks’ temporal distribution of manipulated blocks.
2.3. Ensemble Approach Using k-Partitioned Isolation Forests
In our investigation, we focus on harnessing the power of unsupervised learning to unearth fraudulent activities, thus utilizing the Isolation Forest algorithm across
k distinct partitions of the dataset. In this ensemble strategy and as shown in
Figure 3, the dataset is partitioned into distinct subsets by dividing it along its columns into
k random partitions. For each subset, the Isolation Forest algorithm is applied independently. The final determination of whether manipulation has occurred is made through a majority voting process among the outcomes of the Isolation Forest applications across all subsets. The assumption is that the ensemble approach enhances the robustness of fraud detection by aggregating multiple independent assessments, thus potentially capturing a broader range of manipulative activities within the dataset.
This study leverages the unsupervised learning capabilities of the Isolation Forest algorithm, thus deploying it across
k unique partitions of our dataset to detect fraudulent activities. By segmenting the dataset into
k random subsets, each defined by a division of the dataset’s columns, we apply the Isolation Forest algorithm to each subset independently. The collective judgement on the occurrence of manipulation is then derived from a majority vote across the results from these distinct isolation forest applications. This ensemble method is predicated on the notion that combining insights from multiple, independently assessed partitions increases the detection accuracy by capturing a wider spectrum of potential fraudulent behaviors. The dataset underpinning our analysis contains four fundamental variables central to stock market analytics, as recognized by prior research [
25,
26,
27]: price, return, volume, and trade count. A feature engineering process augments these variables with additional metrics that reveal the temporal dynamics of the market more comprehensively. This includes integrating moving averages to mitigate transient fluctuations, volatility indices to gauge price movements, calculations of abnormal returns to spotlight outliers, and standardizing these metrics into z scores and ratios for uniform assessment. After refining our dataset with these additional metrics, the features are randomly allocated into
k separate sets. This division paves the way for generating
k data subsets, with each offering a distinct lens for the anomaly detection task. Such an ensemble framework ensures that each instance is evaluated from multiple angles, with its classification as either anomalous or normal determined by the consensus from all analyses. The threshold for deeming an instance as manipulative is clearly established in Equation (
1), thus facilitating a detailed and precise mechanism for spotting manipulations.
In the described ensemble approach,
k represents the total number of classifiers deployed within each ensemble, with each classifier tasked with analyzing a specific partition of the data. The variable
denotes the vote cast by the anomaly detector for partition
i, thereby adopting a binary format where a vote of 1 signifies the classification of the instance as anomalous, and a vote of 0 indicates a normal classification. The decision threshold, a critical parameter in this setup, determines the minimum number of votes an instance must receive to be deemed manipulated. This threshold, along with the specific
k values utilized in our study, are detailed in
Table 2. This mechanism allows for a nuanced aggregation of classifier decisions, thereby ensuring that an instance is only classified as manipulated if it surpasses the predefined threshold of consensus among the ensemble’s classifiers, thereby enhancing the precision and reliability of the detection process.
Furthermore, we juxtaposed the outcomes from this ensemble strategy against results derived from applying the anomaly detection algorithm directly to the unpartitioned, original dataset. This comparison underscores the efficacy of the k-partitioned ensemble approach in enhancing fraud detection capabilities.
2.4. Performance Metrics
We evaluated the performance in terms of recall, precision, F1 Score (F1), and F2 Score (F2), which are commonly used metrics in this type of problem [
28,
29,
30,
31].
Precision in Equation (
2) is the ratio of correctly detected manipulations over the total manipulations identified by the model. In Equation (
3), the recall corresponds to the proportion of correctly identified manipulations out of the total number of manipulations. True Positives (TPs) represent the number of manipulations correctly identified by the model, False Positives (FPs) correspond to the number of nonmanipulated cases incorrectly identified as manipulated, and False Negatives (FNs) show the number of manipulated cases that are incorrectly classified as nonmanipulated. The F1 score, as defined in Equation (
4), serves as the harmonic mean between precision and recall, thus ensuring that both metrics contribute equally to the overall score. This balanced approach makes the F1 score particularly useful for scenarios where an even emphasis on precision and recall is desired. Conversely, the F2 score, outlined in Equation (
5), adjusts this balance by diminishing the weight of precision while amplifying that of recall. This modification is especially relevant in contexts where the cost of false negatives is higher than that of false positives, thereby making recall a more critical measure. For both the F1 and F2 scores, the optimal achievable value is 1, thereby indicating perfect precision and recall, while the least desirable score is 0, thus signifying the lowest performance in these metrics.
2.5. Anomaly Detection Algorithm
We employ Isolation Forest (IF) [
32] as the anomaly detection algorithm. IF is an unsupervised algorithm based on decision trees. The main idea behind using IF is that anomalous instances can be isolated from normal ones through the recursive partitioning of the dataset. This algorithm has been successfully used in different application fields, for example, to detect credit card fraud [
33] and health insurance fraud [
34], for software and UAV failure prediction [
35,
36], and in detecting unusual water consumption [
37]. Mendes et al. [
38] observed that IF outperformed more complex models in detecting anomalies.
Algorithm 1, known as Isolation Forest, is a novel approach specifically tailored for anomaly detection within datasets. This algorithm diverges from traditional methods by exploiting the inherent properties of anomalies being ’few and different’, thereby isolating them efficiently. At its core, the Isolation Forest algorithm utilizes a collection of Isolation Trees (iTrees), as described in Algorithm 2, to partition the data. Each iTree is constructed by recursively selecting a feature at random and then choosing a split value between the maximum and minimum values of the selected feature until instances are isolated or a predefined depth limit is reached. The crux of assessing an observation’s anomaly score lies in the PathLength method outlined in Algorithm 3. This method calculates the length of the path traversed in an iTree to isolate a sample, thus serving as a proxy for its anomaly score. Shorter paths indicate a higher likelihood of being anomalies, as they are easier to isolate. By averaging the path lengths over a forest of iTrees, the Isolation Forest algorithm provides a robust measure of an observation’s deviation from the norm, thus enabling effective and efficient anomaly detection in large datasets.
| Algorithm 1: iForest |
![Mathematics 12 01336 i001 Mathematics 12 01336 i001]() |
| Algorithm 2: iTree(X,e,l) |
![Mathematics 12 01336 i002 Mathematics 12 01336 i002]() |
| Algorithm 3: |
![Mathematics 12 01336 i003 Mathematics 12 01336 i003]() |
Equation (
6) presents the formula for calculating the anomaly score [
32], denoted as
, for an observation
x within a dataset by employing the Isolation Forest algorithm. This formula is crucial for assessing the anomaly degree of an instance in relation to the rest of the dataset. The equation is defined as
where:
represents the anomaly score of the observation x in a dataset of size n.
signifies the average path length (calculated by the PathLength method) from the root to the terminal node across all instances of Isolation Trees (iTrees) in the forest. This value reflects how quickly the observation x can be isolated in the iTrees forest.
is a normalization constant that depends on the dataset size n, thus ensuring that the score is independent of the dataset’s size and remains within a comparable range.
The factor normalizes the outcome so that scores fall within a range of 0 to 1, where values close to 1 indicate a high likelihood of being an anomaly, while values closer to 0 suggest the observation is normal.
The Isolation Forest algorithm requires the specification of two critical hyperparameters for its operation: the subsample size (
) and the number of trees (
t). As advised by the creators of the algorithm [
32], the recommended default values for these hyperparameters are set at 256 for the subsample size (
) and 100 for the number of trees (
). These default settings were empirically determined to provide a balance between computational efficiency and the algorithm’s effectiveness in isolating anomalies within a dataset.
2.6. Implementation
In this study, the experiments were meticulously carried out using Python. To identify anomalies within the dataset, we leveraged the Isolation Forest library (
https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.IsolationForest.html, accessed on 7 November 2023), an integral component of the scikit-learn toolkit. The selection of hyperparameter values was in strict accordance with the recommendations provided in [
32], thus ensuring an optimal configuration of the Isolation Forest algorithm for our specific use case. We defined an instance as anomalous if its anomaly score
S exceeded the threshold of 0.5, thereby allowing us to precisely target and investigate instances most likely indicative of manipulation within our analysis framework.
4. Discussion
The implementation of an unsupervised method for detecting stock manipulation, such as the Isolation Forest algorithm, offers significant advantages over supervised methods. Firstly, the unsupervised approach eliminates the need for previously labeling large datasets, which is a process that can be both costly and prone to errors, especially in dynamic and complex contexts like financial markets. Moreover, unsupervised methods are particularly skilled at identifying anomalies or atypical patterns without prior knowledge, which is crucial for uncovering new forms of stock manipulation that have not yet been documented. Another benefit is their ability to adapt and evolve with real-time data, thus providing more agile and accurate detections in an environment that is constantly changing. This adaptability contrasts with supervised systems, which may require frequent retraining and manual adjustments to maintain their effectiveness against new manipulation tactics. Therefore, an unsupervised approach not only offers a more efficient and less labor-intensive solution for fraud detection but also excels in its capacity to preempt emerging fraudulent strategies, thus strengthening the integrity of the stock market.
In the original dataset used in this research, each stock was represented through four distinct time series, thus posing a unique challenge when applying Isolation Forest for fraud detection. This algorithm, primarily designed for static datasets, necessitated an adaptation to handle time series data effectively. By converting the dynamic nature of time series into a static dataset enriched with statistical features across multiple columns, we were able to imbue the Isolation Forest algorithm with the ability to comprehend historical patterns within various transactions. This transformation is pivotal for a couple of reasons. Firstly, it addresses the inherent limitation of Isolation Forest in processing sequential data, which constitute a common characteristic of financial transactions. By aggregating time series into a set of descriptive statistics, we preserve essential temporal characteristics without compromising the algorithm’s integrity. Secondly, this approach allows for a more nuanced detection of anomalies. Traditional fraud detection mechanisms might struggle to differentiate between naturally occurring fluctuations and genuine instances of fraud. The enriched dataset provides a multidimensional view of each transaction, thus highlighting anomalies that would otherwise remain obscured in raw time series data.
In the ensemble method employing k isolation forests within our study, each classifier is trained on randomly selected columns, thereby forming k distinct partitions of the dataset. This design intentionally positions each isolation forest as a “weak classifier”, given that the random column selection limits the scope of data each classifier is exposed to. This limitation is strategic, as it diversifies the analytical perspectives across the ensemble, albeit at the cost of individual classifier robustness. Despite their designation as weak classifiers, the strength of the ensemble approach emerges from aggregating these diverse, partially informed classifiers through a majority voting mechanism. This integration of decisions from across the ensemble capitalizes on the varied insights each weak classifier contributes, based on its unique subset of features. Consequently, this method enhances the overall anomaly detection capability, thereby effectively compensating for the inherent limitations of individual classifiers. The ensemble’s collective intelligence, derived from amalgamating the outputs of multiple weak classifiers, significantly boosts the precision and reliability of stock market manipulation detection, thus demonstrating the efficacy of this approach in navigating complex datasets with nuanced patterns of fraud.
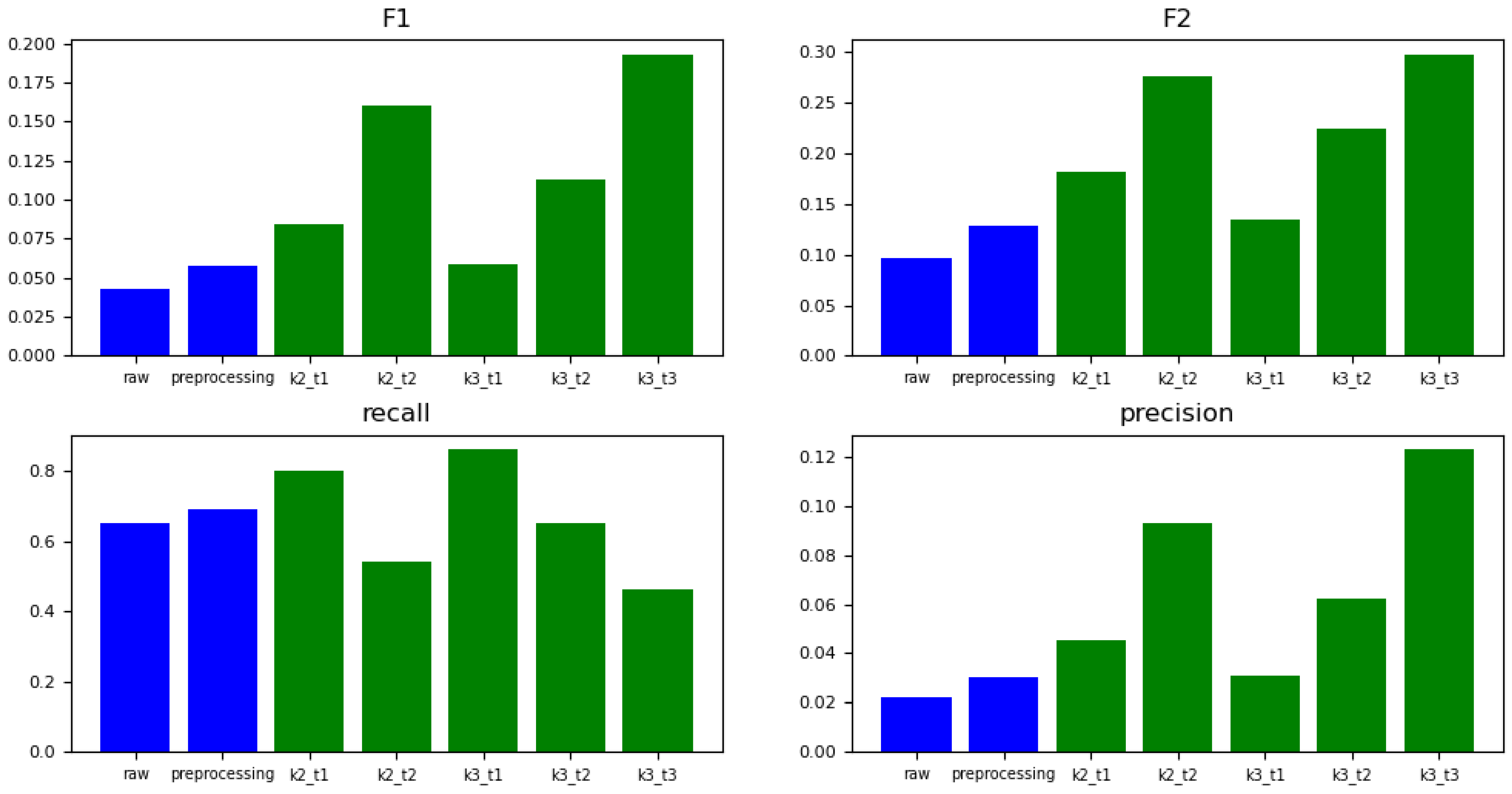
In the discussion of our findings, it is crucial to highlight the remarkable improvements facilitated by the adoption of a voting ensemble strategy. Our empirical analysis demonstrates that simply selecting two random feature sets significantly enhances performance metrics. Specifically, with and a voting threshold of 1, we observed a substantial uplift in the effectiveness of our approach: recall improved by an average of 14.3%, while precision saw a remarkable increase of 46.7% in comparison to the baseline performance of a singular classifier model. Moreover, when analyzing the top-performing configurations within our experiments, the enhancements become even more pronounced. The most effective ensemble setups yielded increases as notable as 28.9% in recall and an impressive 83.3% in precision. These findings underscore the potent capability of the voting ensemble strategy not just to outstrip the performance of individual classifiers, but to do so with considerable margins, thereby reinforcing the value of ensemble methods in complex anomaly detection scenarios such as stock market manipulation.
In the realm of fraud detection, the significance of recall is notably magnified, as highlighted in the literature [
39]. This emphasis stems from the understanding that the consequences of overlooking a genuine case of fraud carry far more weight than mistakenly flagging a legitimate transaction as suspicious. Within the context of our voting strategy, it was observed that for each
k value implemented, the optimal recall rate was achieved when the voting threshold was set to 1. Our experiments have meticulously explored scenarios with
k values of one, two, and three—relatively modest numbers. This naturally raises the intriguing question of the effects that an increased number of classifiers might have on performance metrics and, crucially, on determining the optimal voting threshold. While this line of inquiry is undoubtedly of interest to researchers and holds the potential to further refine fraud detection methodologies, it extends beyond the scope of our current study. Nonetheless, it underscores a promising avenue for future research, thereby inviting a deeper exploration into the scalability of the voting ensemble strategy and its implications for enhancing the detection of financial fraud.
Figure 5 elucidates the nuanced relationship between the threshold and various performance metrics: while recall demonstrated an inverse correlation with the threshold, precision, F1 score, and F2 score exhibited a direct correlation. This dynamic can be comprehended by observing that an increase in the threshold leads to a reduction in both true manipulated cases (TP) and suspected cases (TP + FP), with a more pronounced decrease in the latter. This trend primarily stems from a significant reduction in False Positives (FPs), as detailed in
Table 7. Consequently, the impact on recall was relatively modest compared to the more pronounced sensitivity of precision to threshold adjustments. In essence, precision exhibits a greater responsiveness to changes in the threshold compared to recall, thus highlighting the intricate balance between these metrics in optimizing fraud detection performance.
In our analysis, a crucial point of consideration is the inherent uncertainty surrounding the exact number of manipulated blocks within the dataset. This ambiguity introduces a potential for false positives—instances identified by our model as manipulations which do not match known cases of manipulation. However, it is important to acknowledge that these so-called false positives might, in reality, represent genuine instances of manipulation that have not been previously identified or documented. This scenario underscores a limitation in our validation process, where the benchmark for model accuracy is constrained by the completeness and reliability of the manipulation cases available for comparison.
Given this context, the presence of false positives in our results does not necessarily denote model inaccuracy but rather highlights the potential for our methodology to uncover new and unrecorded manipulations. This possibility emphasizes the dynamic and complex nature of stock market manipulation detection, where the discovery of new manipulation patterns can enhance the overall performance of the detection model.
5. Conclusions
This research aimed to detect stock market manipulation using an unsupervised approach. To this end, we proposed a voting ensemble strategy composed of k unsupervised anomaly detection models and evaluated the above on eight real datasets of stocks affected by manipulation activities. To assess the voting ensemble strategy’s performance, we used the ability to identify 55 manipulated time blocks.
To enhance the precision of our anomaly detection efforts, we engineered new features that facilitated the creation of data subsets. These subsets were then subjected to a collective decision-making process by the anomaly detection models, thus utilizing the Isolation Forest algorithm as our primary tool for identifying anomalies. An instance was classified as manipulated based on whether it garnered votes surpassing a predetermined threshold. Our findings compellingly demonstrate that the application of a voting ensemble strategy markedly boosted all measured performance metrics, thus surpassing outcomes reported in prior research. Remarkably, a mere division of the dataset into two subsets for voting, coupled with a threshold set to one, was sufficient to elevate performance indicators significantly. Notably, an increase in the voting threshold was found to substantially enhance precision, thus reducing the number of cases flagged for further investigation and, consequently, diminishing the resource expenditure required for audits. By employing this strategic voting mechanism, we achieved an identification of up to 89% of genuinely manipulated blocks, thus underscoring the profound potential of our approach in contributing to the integrity and surveillance of financial markets.
For future work, we aim to extend our investigation by assessing the effectiveness of the voting ensemble strategy in conjunction with an anomaly detection approach that focuses on the reconstruction error of time series. This exploration will delve into how discrepancies in reconstructed time series data can serve as a robust indicator of anomalies, as well as how the incorporation of a voting mechanism may further refine and improve the detection process. This direction promises to offer valuable insights into the nuanced dynamics of time series anomaly detection and the potential synergies with ensemble methodologies.