Abstract
Multi-objective evolutionary algorithms (MOEA) have attracted much attention because of their good global exploration ability; however, their local search ability near the optimal value is weak, and for large-scale decision-variable optimization problems the number of populations and iterations required by MOEA are very large, so the optimization efficiency is low. Gradient optimization algorithms can overcome these difficulties well, but gradient search methods are difficult to apply to multi-objective optimization problems (MOPs). To this end, this paper introduces a stochastic weighting function based on the weighted average gradient and proposes two multi-objective stochastic gradient operators. Further, two efficient evolutionary algorithms, MOGBA and HMOEA, are developed. Their local search capability has been greatly enhanced while retaining the good global exploration capability by using different offspring update strategies for different subpopulations. Numerical experiments show that HMOEA has excellent capture ability for various Pareto formations, and it can easily solve multi-objective optimization problems with many objectives, which improves the efficiency by a factor of 5–10 compared with typical multi-objective evolutionary algorithms. HMOEA is further applied to the multi-objective aerodynamic optimization design of the RAE2822 airfoil and the ideal Pareto front is obtained, which indicates that HMOEA is an efficient optimization algorithm with potential applications in aerodynamic optimization design.
Keywords:
aerodynamic optimization; multi-objective optimization; evolutionary algorithm; gradient optimization MSC:
68T20; 90C26
1. Introduction
Aircraft shape optimization is one of the key issues in aerodynamic layout design. The traditional aerodynamic optimization method that relies on experience and focuses on trial-and-error methods has high computational costs, long design cycles, and cannot guarantee the optimal aerodynamic shape [1]. With the rapid development of computer technology, aerodynamic optimization methods that combine optimization algorithms with computational fluid dynamics (CFD) technology can effectively and economically explore large design spaces to obtain the best solutions. This method has been used in aerodynamics in the past few decades. Optimization has played an important role in the design process [2,3,4]. From an engineering perspective, aerodynamic optimization can be regarded as MOPs, because researchers usually need to consider multiple objective functions, such as the performance of the aircraft at different altitudes and speeds. Ideally, researchers would prefer to obtain a solution that represents the best performance for a specific problem, but such a solution often does not exist in multi-objective situations. Obtaining the Pareto optimal set is a more preferable way because the decision maker can choose the solution that best suits their needs based on the Pareto optimal set [5]. Although many optimization algorithms have been developed and applied to aerodynamic optimization design, they often fail to provide satisfactory results for such problems. In general, optimization algorithms based on local gradient information (GBAs) and global evolutionary algorithms (EAs) are the two most widely used methods in aerodynamic optimization [1]. This is because, unlike other optimization problems, the evaluation function for aerodynamic optimization is generally CFD. It is well known that the time cost of CFD is very expensive. Moreover, aerodynamic optimization problems usually have large-scale design variables and the search of such spaces is not an easy task. Therefore, efficiency is a crucial issue in aerodynamic optimization, even beyond theoretical optimality. A large search space is good for evolutionary algorithms to find the global optimal solution, but it also means that a large population size is needed. In aerodynamic optimization, large populations often imply high CPU computational costs. Therefore, it is necessary to develop efficient multi-objective optimization algorithms.
GBAs can quickly converge to the vicinity of the extreme solution, and the optimization efficiency is very impressive. However, it depends on the initial value and gradient information; GBAs are essentially only local search algorithms and, thus, are difficult to converge to the global optimal solution [6]. In aerodynamic optimization, GBAs have been widely used due to the emergence of the adjoint method [7]. Unlike the finite difference method or the complex variable difference method, the adjoint method evaluates sensitivity information by solving the adjoint equation accompanying the flow equation and its computational complexity is independent of the number of design variables [8]. However, this technology still has shortcomings in dealing with MOPs and constrained optimization problems. Most of the existing optimization algorithms based on local gradient information focus on finding a single improvement direction. Using this method, it is difficult to evenly distribute the solution across the entire Pareto front, especially for a non-convex and discontinuous Pareto front.
EA is a population-based global optimization algorithm that uses the global structure of the search space to explore the objective function. It uses an evolutionary mechanism based on stochastic operations to provide perturbations to the population with genetic operators (selection, crossover, mutation, etc.) to find possible global optimal solutions, so they are particularly suitable for solving complex multimodal problems. It has good robustness because it does not require objectives and constraints to be continuous or differentiable. The population search mechanism of EAs can ultimately obtain a set of solutions instead of one solution. This characteristic determines that EAs are very suitable for solving MOPs [9]. The main advantage of EAs is their ability to optimally combine extraction and exploration [10]. Although this optimal combination may be suitable for EAs in theory, there are some problems in practical engineering applications. This is because, in theory, EAs assume that the population size is infinite, the fitness function accurately reflects the applicability of the solution, the interactions between genes are very small, etc. [11]. However, the actual population size is limited, which affects the sampling ability of EAs. Finite populations dictate that information about the local structure of the search space is often overlooked [12]. This leads to the fact that EAs require a lot of evaluation of the objective function, and the evaluation of the aerodynamic function is very time-consuming, making EA-based aerodynamic optimization methods very time-costly. Therefore, more attention should be paid to the number of function evaluations required by EAs when solving aerodynamic optimization problems. Optimization efficiency is a crucial issue faced by EAs when solving aerodynamic optimization problems. For this reason, it is essential to explore efficient aerodynamic optimization algorithms.
If different algorithms are combined into a hybrid algorithm, their deficiencies can be avoided as much as possible while retaining their respective favorable features; thus, adding local search methods to EAs not only helps to overcome the convergence difficulties due to the limited population size [13] but also avoids the dilemmas of GBAs in dealing with constrained problems and MOPs. Although EAs can quickly locate the region where the global optimum is located, they take a relatively long time to find the exact local optimum in the convergence region, and the combination of EAs and local search methods can improve the ability to accurately locate and accurately search for the global optimum solution [14]. With this hybridization, the local search helps direct the EAs to the globally optimal solution, thus improving the overall convergence efficiency. If a proper balance between global exploration and local exploitation capabilities can be further achieved, the algorithm can easily produce highly accurate solutions.
We know that in a single-objective case, additional use of gradient information can effectively improve the efficiency of the optimization algorithm. However, so far, there is no mature multi-objective optimization algorithm based on gradient information. Therefore, how to use gradient information to improve the efficiency of MOEA is an interesting question [15,16]. Based on this, our paper first proposes the multi-objective stochastic gradient operator, which uses a novel random weighted variable method to solve multi-objective problems, allocates new random weights in each iteration, and performs gradient optimization. This method is expected to make the solution diffuse in different directions during iteration so as to obtain a widely distributed Pareto-optimal solution. In addition, we also provide two modes for assigning random weights: single-weight and multi-weight modes. The single-weight mode generates a single random weight for each individual to perform gradient evolution, and the multi-weight mode generates multiple random weights for each individual to perform gradient evolution. Furthermore, based on the multi-objective gradient operator, the multi-objective gradient optimization algorithm (MOGBA) is proposed, which retains the main framework of MOEA while using the multi-objective gradient operator to replace the offspring generation mechanism based on crossover and mutation. Optimization can start with a random population, randomly assigning weights to each individual at each iteration, weighting the objective, and then performing gradient optimization. Theoretically, multi-weight search represents a multi-directional search, which can effectively explore the target space but also produces a lot of meaningless or inefficient searches. The computational cost is an important issue we need to consider. Therefore, we took advantage of the regularity of MOPs to divide the population with a clustering algorithm, conducted multi-weight searches for densely populated areas and degraded individuals, and performed single-weight searches for individuals in other areas to avoid wasting computing resources.
Although the use of gradient information does improve optimization efficiency to a certain extent, its local search characteristics make it difficult to handle complex problems, and excessive use of gradient information will quickly lose diversity and make the algorithm fall into local optimality [17]. Therefore, we propose a hybrid multi-objective evolutionary algorithm (HMOEA) based on MOGBA. HMOEA retains the genetic operator of MOEA as a global search operator and the multi-objective gradient operator as a local search operator. HMOEA evolves offspring populations by alternating between evolutionary operators and multi-objective gradient operators, which not only enhances the mining and convergence capabilities of the algorithm but also avoids the excessive use of gradient information, thereby ensuring the diversity of the population and the exploration capability of the algorithm. HMOEA combines the gradient-information-based multi-objective optimization algorithm of this paper, which is used to enhance mining capacity and speed up convergence, and the NSGA-III algorithm, which is used to enable the exploration of the optimal distribution of solutions. After successful validation in mathematical test cases, the method has been successfully applied to aerodynamic shape optimization, effectively reducing computational cycles.
2. Performance Analysis and Optimization Performance Comparison between EAs and GBAs
An optimization problem is a problem of finding the design variables that make the objective optimal, subject to constraints [1]. Optimization problems cover the fields of physics, chemistry, mathematics, biology, medicine, economics, aerospace, and other fields in the form of mathematical programming. Many problems in scientific research and engineering technology practice can be transformed into optimization problems. To solve the optimization problem, we must first abstract the specific problem into a mathematical model—that is, systematically analyze the problem and define the corresponding relationship between the decision variables and the objective function. After that, solving the mathematical model is another crucial task. Optimization methods can be divided into optimization algorithms based on gradient information and heuristic algorithms according to different orientations.
The gradient optimization method is a search method based on gradient information. The methods for obtaining gradient information mainly include the finite difference complex variable method, automatic differentiation method, and adjoint method, among which the adjoint method is the most efficient. Combining the adjoint method with the gradient-based optimization algorithm can significantly improve the efficiency of large-scale design variable optimization problems. However, the gradient-based optimization algorithms are essentially local optimization methods, which can easily fall into local optimality and make it difficult to obtain the global optimal aerodynamic shape. The heuristic algorithm has better global characteristics and can search for the global optimal solution with a greater probability. The natural parallelism of the algorithm is also very suitable for large-scale parallel computing. However, its optimization process may require a large number of calls to CFD analysis. What is more serious is that as the dimensionality of variables increases, a “curse of dimensionality” may occur.
In this section, we take the test function as an example to compare the performance of EAs and GBAs. Consider the following minimization problem of the Rosenbrock function:
where . This function is a unimodal function with the global minimum located in a narrow parabolic valley. The function graph is shown in Figure 1. However, even if this valley is easy to find, converging to the minimum is very difficult. Let D represent the variable dimension; we tested the 2-dimensional and 10-dimensional Rosenbrock functions. All parameters of the Genetic Algorithm (GA) [18] and L-BFGS-B [19] are set to default values. The GA population size is 20 times the decision variable dimension, and the iterations are 500 generations. Therefore, the number of fitness evaluations (FEs) is . L-BFGS-B performs the same number of fitness value evaluations, and the iterative process of each algorithm is shown in Figure 2.
Figure 1.
Rosenbrock function.
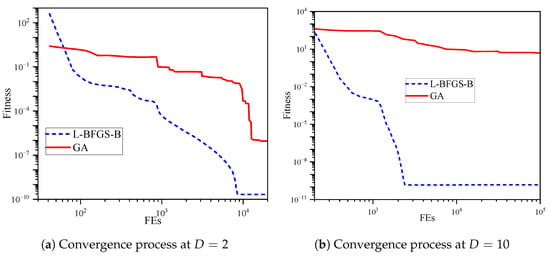
Figure 2.
Rosenbrock function optimization convergence process.
It can be seen from the figure that when , L-BFGS-B converges faster in the early stage, and the convergence speed does not decrease with the iteration, while GA performs stepwise descending convergence, which is relatively slow. The FEs required for GA and L-BFGS-B to achieve a convergence accuracy of are 12,320 and 1480, respectively, and the calculation amount required for GA is 8 times that of L-BFGS-B; when , L-BFGS-B can converge to near the optimal value very fast, but the convergence speed of GA is slower. To achieve a convergence accuracy of , GA and L-BFGS-B require FEs of 7600 and 400, respectively, which is nearly a 20-fold difference in computation. The convergence speed of GA at is significantly lower than that at , which shows that the increase in variable dimension brings great difficulties to the convergence of GA; however, L-BFGS-B does not encounter such problems. It can be seen that for continuous optimization problems, GBAs have unparalleled advantages in efficiency, and this advantage will gradually expand as the variable dimension increases, which is difficult for EAs to match.
Therefore, when solving engineering optimization problems, especially the optimization design problems of aerodynamic shape, we cannot just rely on evolutionary algorithms. It is best to integrate gradient information into the optimization design process to greatly improve the optimization efficiency.
3. Multi-Objective Deterministic Optimization Method Based on Stochastic Gradient Operator
It is well known that aerodynamic optimization problems usually have a high-dimensional design space in order to accurately describe the geometry of the vehicle, whereas evolutionary optimization in a high-dimensional space requires a large population size. In evolutionary algorithms, large population sizes are always accompanied by high CPU consumption [20]; efficiency is a crucial issue in aerodynamic optimization, even beyond the rigor of optimization theory.
Taking the 20-dimensional single-objective aerodynamic optimization problem as an example, we estimate the number of flow field calculations required for EAs and GBAs to conduct a simple efficiency evaluation. In general, the required population size for EAs is about 5–20 times the number of decision variables, and about 50 generations of evolution for aerodynamic optimization with EA methods will usually result in a relatively optimal solution, so the number of EA flow field calculations is about 5000–20,000; however, the computational cost of the gradient-based adjoint optimization method is independent of the number of design variables, and the computational cost of the adjoint equation is comparable to the computational cost of the flow field. Thus, it can be considered that the computational cost of solving one gradient is equivalent to the computational cost of solving two flow fields, and GBAs tend to converge after 50–100 iteration calculations, so it can be considered that the number of flow field calculations of GBAs is about 100–200 times. In addition, for multi-objective optimization problems, the number of populations required for EAs increases geometrically as the number of objectives increases, so the number of flow field calculations will also increase significantly, while GBAs based on weighted averages always have single-objective optimization properties, and the number of calculations will not increase as much as EAs. Thus, for continuous problems, gradient-based algorithms are always the fastest way to find optimization, although they may only find local optimal solutions.
Although the GBA method based on weighted average can efficiently solve multi-objective optimization problems with convex Pareto fronts, it cannot effectively solve multi-objective optimization problems with other types of Pareto fronts (concave, discrete, etc.) because it contains too much certainty and lacks randomness. In particular, it completely fails when solving discontinuous, discrete, and non-uniformly distributed Pareto front problems. Based on this, this section will introduce randomness based on the concept of weighted average and develop a multi-objective deterministic optimization algorithm based on stochastic gradient operators.
3.1. Stochastic Gradient Operator for Multi-Objective Optimization
Although the GBA method has high optimization efficiency, it is easy to fall into local optimality; more seriously, when facing multi-objective optimization problems, the GBA will not evenly distribute the solution across the entire Pareto front. Especially, when the Pareto front is non-convex, the optimization results will move toward the extreme point. When the objective function is weighted and averaged with a set of randomly given static weight functions, the optimization results will move to points A or B [21], as shown in Figure 3. In addition, when the objective function is complex, the GBA method may fall into a local optimum, like point C. Our analysis believes this is due to the fact that the GBA method based on static weights has more than enough certainty in the search direction but insufficient randomness when solving multi-objective optimization problems. Therefore, this paper tries to introduce uncertainty into the determinism in order to improve this kind of problem—that is, the random weights are reassigned to each objective function at each iteration, which makes the solution spread in different directions at each iteration but at the cost of slightly reducing the convergence speed due to the continuous change in direction.
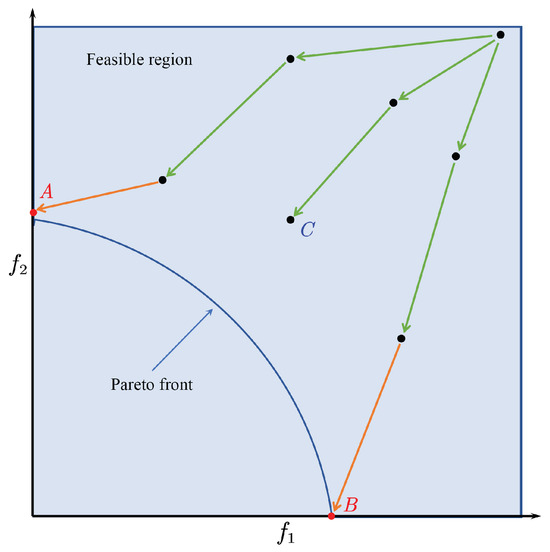
Figure 3.
Weighted function behavior in non-convex Pareto fronts.
Taking the minimization problem of multi-objective function with M objectives as an example, the group of random weights assigned to the individual in the parent population with population N is as follows:
where are random numbers and satisfy
So, multi-objective optimization is transformed into
In the single-weight mode, , in the multi-weight mode, —that is, in the single-weight mode, each individual corresponds to only one set of weights, and in the multi-weight mode, each individual corresponds to multiple sets of weights. Whether it is single-weight mode or multi-weight mode, each GBA optimization iteration regenerates a new random weight factor, which we call dynamic random weight factor. Figure 4 presents the search under single-weight and multi-weight modes. After that, each individual can be used as the initial value of the GBA. Gradient information can be obtained according to each objective function, and a local search can be performed to obtain the offspring population.
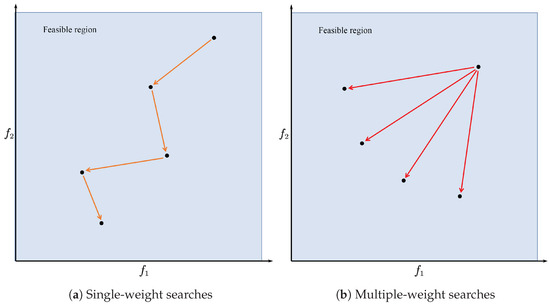
Figure 4.
Single-weight and multiple-weight searches.
The main reasons for developing the multi-weight model are as follows:
- Individual search in single-weight mode may be degraded; at this time, it is necessary to give more than one search direction for the individual to improve the search efficiency. In this case, although it will increase the computation by a small amount, it can improve the optimization efficiency of the algorithm.
- In practical engineering applications, it is possible to obtain one or a few initial values using engineering means, so iterative optimization using a small number of initial values (individuals) with a priori knowledge makes good engineering sense. The single-weight model in this case does not guarantee the diversity of solutions and is prone to fall into local optimality, in which case individuals need to be given multiple search directions for searching.
- If individuals in a certain area are very dense, then the location of this area may be very important, such as an inflection point or concave area, so individuals in this area should search in more directions [22].
3.2. Multi-Objective Gradient Optimization Algorithm (MOGBA) Based on Stochastic Gradient Operators
Based on the multi-objective gradient operator explained in Section 3.1, this paper develops the population-based multi-objective optimization algorithm MOGBA. The basic framework of MOGBA is similar to that of NSGA-III, but its offspring generation mechanism has undergone a significant change by introducing a multi-objective gradient operator to generate offspring. The main loop of MOGBA is described in Algorithm 1. First, an initial parent population P of size N is randomly generated based on the problem to be solved, including the number of decision variables V, the number of objectives M, and the constraints B. In this paper, B is the upper and lower bounds of the decision variables. Then, a multi-objective gradient operator is used to generate the offspring population Q. After that, we used fast non-dominated sorting to non-dominate the merged population and then used the reference point-based environmental selection mechanism in NSGA-III [23] to select N individuals as the next parent population. This process of offspring generation and selection is repeated until the termination condition is satisfied, and the final population P will be the solution set.
| Algorithm 1: Main loop of MOGBA |
 |
Different from existing research work, MOGBA uses a clustering algorithm to divide the population into subpopulations. MOGBA’s offspring generation mechanism first divides the current population P into K subpopulations through the AP clustering algorithm [24]; then, it performs a multi-weight search on the subpopulation containing the most individuals and performs a single-weight search on other subpopulations. It will judge the new solutions generated by the single-weight search. If degradation occurs—that is, the old solution dominates the new solution—then it performs a multi-weight search on the old solution again and merges all the new solutions generated into the descendant population Q. The offspring generation mechanism of MOGBA can be described as the following Algorithm 2.
| Algorithm 2: MOGBA local search offspring generation mechanism |
 |
3.3. Hybrid Multi-Objective Evolutionary Algorithm (HMOEA)
Although MOGBA can improve optimization efficiency to a certain extent, MOGBA is still essentially a local optimization algorithm. For optimization problems with complex Pareto fronts, MOGBA may fall into local optima due to the rapid loss of diversity, and gradient search for all individuals will greatly increase time costs and reduce optimization efficiency. The offspring generation mechanism of MOEA can be considered as a combination of two different search technologies: crossover and mutation. In generally, crossover and mutation in MOEA are simulated binary crossover (SBX) and polynomial mutation, respectively, and they will show different behaviors when searching the decision variable space. Crossover generates candidate solutions (offspring) through the combination of two parents, such that the solution obtained, independent of the way the parents are selected and combined, may be far from the initial solution. Therefore, the crossover operator is a powerful tool for searching the decision variable space and picking out the global optimal region. It is the core operator of MOEA but it lacks the ability to effectively re-find suboptimal solutions. Mutation has a more local impact because the probability of mutation is generally low and the changes in the decision variable space are usually small. Therefore, the mutation operator plays two important roles in MOEA [25]: 1—to provide the ability to efficiently regain suboptimal solutions; 2—to reintroduces alleles lost due to repeated application of the crossover operator in the population to maintain the population diversity. Although the mutation operator is beneficial to maintaining the diversity of the population, its local improvement of candidate solutions is unsatisfactory.
In summary, the multi-objective gradient operator and the cross-mutation operator are complementary to each other. We can combine these two operators to develop a hybrid multi-objective optimization algorithm (HMOEA) with balanced mining and exploration capabilities, making the algorithm efficient and robust. It is worth noting that the difference between HMOEA and MOGBA is not only the use of cross-mutation operators, which can spread excellent genes to other individuals, but also the fact that HMOEA only uses gradient search for representative individuals, which greatly reduces the frequency of the multi-objective gradient operator compared with MOGBA. The frequency of gradient search is reduced from every generation to every k generation, enabling better global search while reducing time cost.
The main loop of HMOEA is described in Algorithm 3. Similar to MOGBA, HMOEA first initializes the number of objectives M, the dimensions of the decision variables V, and the constraints B, and then generates the initial population P. Next, it is judged whether the current generation is divisible by k. If so, the multi-objective gradient operator is executed to generate the subpopulation Q (called local offspring generation). Otherwise, SBX and polynomial mutation are executed to generate the progeny population Q (called global offspring generation). The subsequent operations are the same as those mentioned in MOGBA.
| Algorithm 3: Main loop of HMOEA |
 |
In our design, the role of the multi-objective gradient operator in HMOEA is more to increase the mining capability of the algorithm and improve the optimization efficiency. Therefore, a different gradient search mechanism from MOGBA is used here. The mechanism for generating offspring using multi-objective gradient operators in HMOEA is given in Algorithm 4. HMOEA also uses a clustering algorithm to divide the population into subpopulations. In the HMOEA local offspring generation mechanism, the current population P is first divided into K subpopulations by the AP clustering algorithm; then, one individual is randomly selected to perform a multi-weight search in the subpopulation containing the most individuals, and for the other subpopulations, one individual is randomly selected to perform a single-weight search. Here, the same operation as in MOGBA is performed for the degraded individual—that is, the new solution generated by the single-weight search is judged. If degradation occurs—that is, the old solution dominates the new solution—then a multi-weight search is performed on the old solution again. Finally, all the new solutions generated are merged into the offspring population Q. It should be noted that the offspring population generation mechanism only performs a local search for random individuals in each subpopulation, so the size of the offspring population Q may be smaller or larger than N, but this does not hinder subsequent environmental selection.
| Algorithm 4: HMOEA local search offspring generation mechanism |
 |
It should be noted that the application object of the algorithm proposed in this paper is the aerodynamic shape optimization design; so, the acquisition of the gradient also takes a considerable amount of time, which is equivalent to the scale of solving the flow field control equations. Therefore, in this paper, each gradient solution is also regarded as a fitness value solution.
4. Numerical Experiments and Analysis
4.1. Experimental Settings and Performance Metrics
In order to verify the performance of the algorithm proposed in this paper, we used 12 benchmark multi-objective optimization problems for numerical experiments, including 5 two-objective functions ZDT1–ZDT4 and ZDT6 [26], and 7 three-objective functions DTLZ1–DTLZ7 [27]. These test functions provide sufficient tests for the algorithm’s search capabilities, convergence, and diversity of solution set distributions. The parameter settings of the test problem are shown in Table 1.

Table 1.
Test function parameter settings.
MOGBA and HMOEA were compared and analyzed with typical multi-objective optimization algorithms NSGA-II [28], NSGA-III, MOEA/D [29], and RVEA [30]. In order to evaluate the performance of the studied algorithm on MOPs, the following performance metrics are adopted.
- Inverted Generational Distance [31] (IGD). This metric is evaluated by calculating the average distance from the true Pareto-optimal solution set to the approximate non-dominated solution set. Suppose that P represents the approximate non-dominated solution set obtained by the algorithm and represents the true Pareto solution set. IGD can be defined as follows:where represents the minimum distance between the target point v and all points in the set P, and represents the number of points in . Obviously, if is large enough, it can represent the Pareto front well. The smaller IGD is, the closer the approximate non-dominated solution set is to the true front.
- Hypervolume [32] (HV). HV represents the evaluation of the volume enclosed by P using a reference point r and is defined as follows:where is the reference point dominated by any solution in the objective space and is Lebesgue measure. The larger HV is, the better the convergence and diversity of the approximate non-dominated solution set corresponding to P.
For the ZDT and DTLZ series problems tested in this paper, considering the fairness between all studied algorithms in the experiment, all comparison algorithms maintained their original designs. For example, all comparison algorithms use the same evolution operator, like SBX and polynomial mutation, etc. In addition, the upper limit of the number of evaluations for a single run of the test function is set to 10,000. The specific parameters of various algorithms are shown in Table 2.

Table 2.
Algorithm parameter settings.
4.2. Experimental Results and Analysis
Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 show the distribution of non-dominated solutions obtained by the six algorithms on ZDT1–ZDT4 and ZDT6, respectively. As can be seen from these figures, MOGBA has a performance second only to HMOEA in ZDT1–ZDT4, which verifies our expectations for multi-objective gradient operators. For the ZDT6 function, MOGBA did not obtain a non-dominated solution with good distribution and its performance was not as good as HMOEA and MOEA/D. This may be due to the rapid loss of diversity caused by the local optimization characteristics of MOGBA when processing complex functions. Compared with other algorithms, HMOEA obtains non-dominated solutions with higher quality and more uniform distribution on the ZDT functions, which demonstrates the effectiveness of the hybrid strategy we proposed.
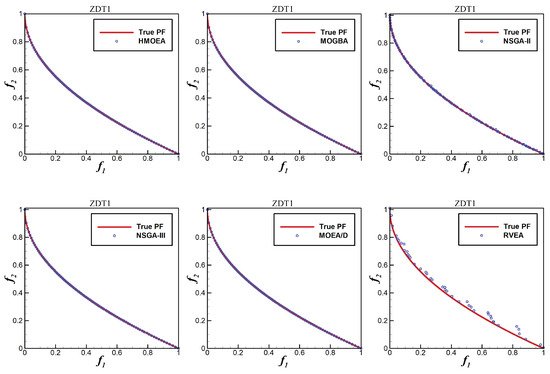
Figure 5.
ZDT1 non-dominated solution distribution.
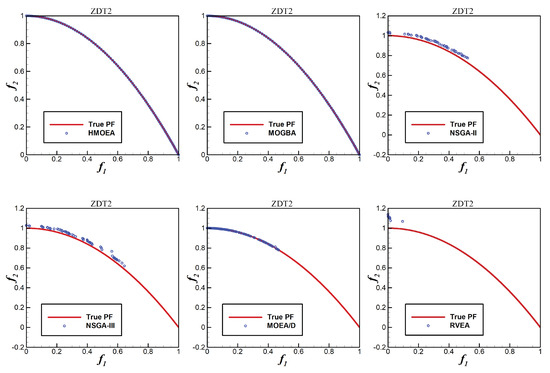
Figure 6.
ZDT2 non-dominated solution distribution.
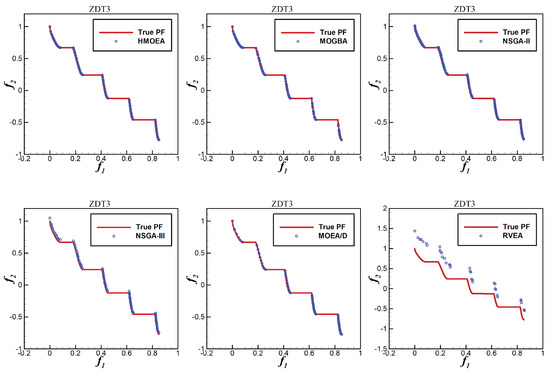
Figure 7.
ZDT3 non-dominated solution distribution.
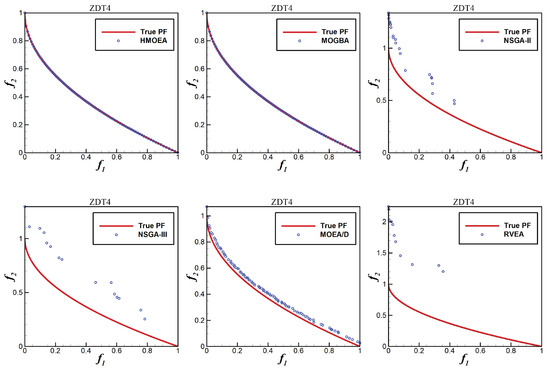
Figure 8.
ZDT4 non-dominated solution distribution.
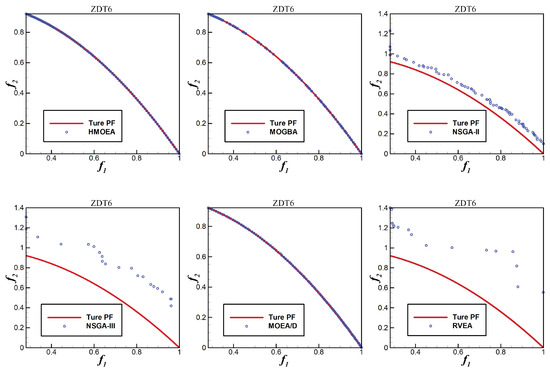
Figure 9.
ZDT6 non-dominated solution distribution.
To reduce the impact of algorithm randomness on the results, all algorithms were independently run 30 times on each problem, and the IGD and HV values of 30 runs were collected for comparison. All algorithms are terminated when a predetermined maximum number of evaluations is reached. The mean and standard deviation of IGD and HV are shown in Table 3 and Table 4. In order to obtain more reliable statistical conclusions, the Wilcoxon rank sum test is performed at the significance level of . The symbols “+, −, =” indicate that the result is significantly better, significantly worse, and statistically similar to those of HMOEA and MOGBA, respectively.

Table 3.
IGD metric. The first row in each cell represents the mean value , and its ranking in ascending order is listed in square brackets with the 1st place highlighted in bold. The second row is the standard deviation . The third row represents the results of the Wilcoxon rank sum test WR; the first bracket indicates the algorithm vs. HMOEA and the second indicates the algorithm vs. MOGBA.

Table 4.
HV metric. The first row in each cell represents the mean value , and its ranking in descending order is listed in square brackets with the 1st place highlighted in bold. The second row is the standard deviation . The third row represents the results of the Wilcoxon rank sum test WR; the first bracket indicates the algorithm vs. HMOEA and the second indicates the algorithm vs. MOGBA.
Finally, the mean value of the average index ranking of each algorithm on ZDT and DTLZ is calculated and counted separately, which is also called Mean ranking (MR). Further, the number of “+, −, =” obtained by each algorithm is counted to reflect the performance of the algorithm, as shown in Table 5. Among 120 () indicators, HMOEA received 118 “+” and 2 “=”, while MOGBA obtained 60 “+”.

Table 5.
Comprehensive performance metrics.
Based on various data, it can be seen that HMOEA and MOGBA have better performance. For the ZDT functions, the MR rankings from high to low are HMOEA, MOGBA, MOEA/D, NSGA-II, NSGA-III, and RVEA. For the DTLZ functions, the MR rankings are HMOEA, NSGA-II (NSGA-III), MOGBA, MOEA/D, and RVEA, as shown in Figure 10. It can be seen that although MOGBA’s comprehensive performance is second only to HMOEA, and MOGBA’s performance in ZDT functions is second only to HMOEA, its performance in DTLZ function is not as good as that of other algorithms. Its performance in DTLZ functions has declined significantly, indicating that MOGBA has certain deficiencies in processing complex functions. This can be attributed to MOGBA’s lack of global search capabilities and rapid loss of diversity, which is why we develop a hybrid strategy.
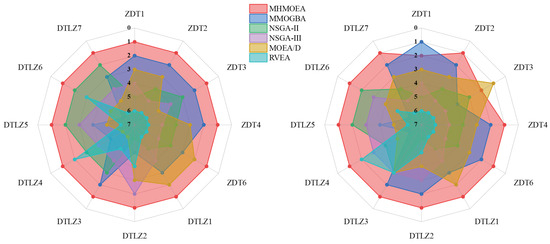
Figure 10.
Algorithm’s metrics ranking for different test functions (left: rank of the IGD mean value; right: rank of the HV mean value).
In general, our proposed MOGBA can perform well on some simple functions and can obtain Pareto solutions with better quality and distribution, showing higher efficiency, but its performance on complex functions slips significantly. HMOEA has the best performance on almost all test functions, and some non-dominated solutions with higher quality and better distribution can be obtained from these experiments. This verifies the effectiveness of our proposed solution that the hybrid of GBA and MOEA performs as we expected on MOPs. Therefore, we can conclude that the offspring generation mechanism based on multi-objective gradient operators contributes to the rapid convergence of the algorithm and enhances the algorithm mining capability. When dealing with complex problems, MOEA’s global search mechanism based on crossover and mutation plays an important role in improving the performance of the algorithm and determines the exploration capability of the algorithm. By combining these two complementary offspring generation methods, the proposed HMOEA performs efficiently and robustly on the studied problem.
5. HMOEA in Airfoil Aerodynamic Optimization
In the aerodynamic shape optimization design of aircraft, airfoil optimization design is a crucial step, and the fast and efficient design of airfoils to meet the engineering needs is the goal that researchers have been striving for. HMOEA has shown good performance in the optimization of benchmark functions. In this section, HMOEA is introduced into the optimal design of airfoils to complete the multi-objective optimization design and test the application value of HMOEA in engineering optimization.
5.1. Airfoil Optimization Framework
The airfoil aerodynamic optimization framework in this section is shown in Figure 11, which includes airfoil parameterization, structured mesh generation tools, flow, and adjoint solvers (SU2 [33]). For each iteration, the optimizer calls the components sequentially if necessary.
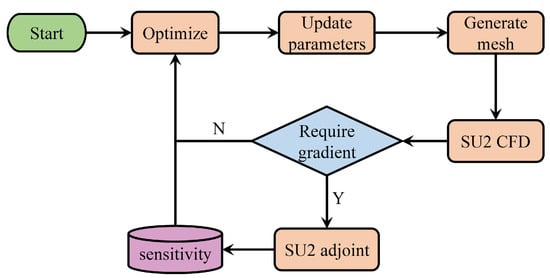
Figure 11.
Airfoil optimization framework.
In each iteration, the optimizer first updates the design variables and then converts them into the coordinate points of the airfoil through a parametric method. Then, a structured mesh is generated, and finally, the optimizer launches the flow field solver to evaluate the objective function. If necessary, it will drive the adjoint solver to obtain gradient information.
5.2. Airfoil Parameterization Method
Airfoil parameterization is a crucial step in aerodynamic optimization. Its accuracy determines the accuracy and reliability of the optimized airfoil. Many airfoil parameterization methods have been developed at home and abroad, such as FFD [34], Bezier [35]. CST [36], etc. This paper uses the fourth-order CST parametric method to control the airfoil shape. The parameter expression of the upper and lower surface curves of the airfoil is
where c is the airfoil chord. When , it represents the upper or lower surface of the airfoil. is the radius of the leading edge of the airfoil; and are the trailing edge inclination angles of the upper and lower surfaces of the airfoil, respectively; and are the shape parameters of the upper and lower surfaces. There are 9 optimization variables for the airfoil, and the benchmark airfoil is RAE2822. The design parameters and corresponding bounds are shown in Table 6.

Table 6.
Design parameter settings.
5.3. Airfoil Optimization Problem
Taking the RAE2822 airfoil as an example, multi-objective optimization design is performed on it. This section selects the lift-to-drag ratio of the airfoil in two states as the optimization objectives. The design states are
The optimization objectives are to maximize the lift-to-drag ratio in the two states. The constraint is that the airfoil area and lift coefficient do not decrease. The mathematical model can be described as follows:
where and are the lift and drag coefficients in the two states, respectively. The subscript represents the baseline airfoil RAE2822. The parameterization method adopts the CST method described in Section 5.2. The turbulence model uses , and the spatial discretization uses Roe scheme. Figure 12 shows a global and local zoomed-in view of the structured mesh used.

Figure 12.
Airfoil structured mesh.
In order to verify the accuracy of the aerodynamic characteristics analysis method, the calculation state is selected:
The pressure coefficient obtained from numerical solution is compared with the experimental value, as shown in Figure 13. It can be seen that the numerical simulation calculation results can closely approximate the experimental values and reflect the flow characteristics.
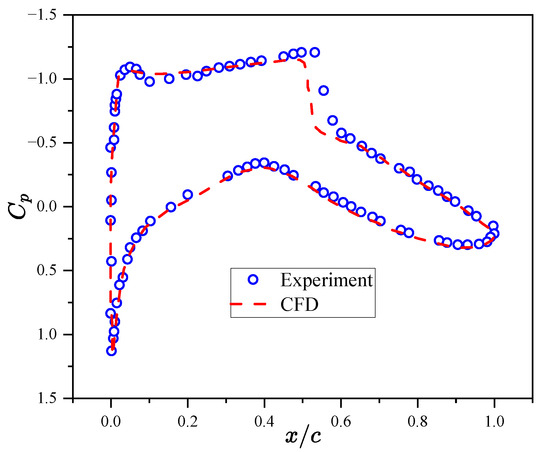
Figure 13.
Comparison of numerical simulation and experimental pressure coefficients.
5.4. Airfoil Optimization Results and Analysis
The optimization was performed using HMOEA, setting the population size to 50 and the maximum number of adaptive value evaluations to 4000, and the distribution of non-dominated solutions obtained is shown in Figure 14. Here, three non-dominant solutions are selected for analysis.
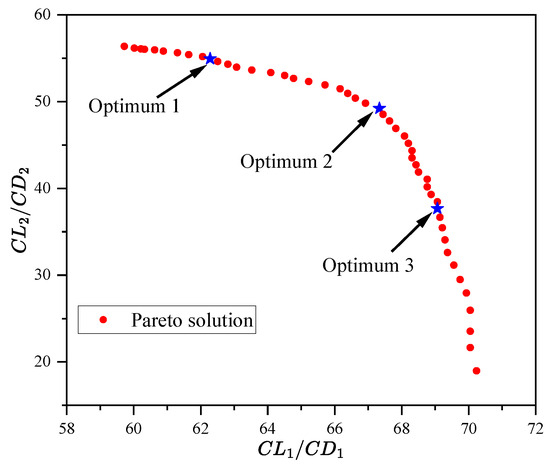
Figure 14.
Distribution of non-dominated solutions.
Table 7 lists the comparison of the aerodynamic characteristics of the airfoil before and after optimization in the two states. Optimized airfoil 1 improves by 10.91% and 47.72% in state 1 and state 2, respectively, which shows that the airfoil improves the state 1 lift-to-drag ratio by a small margin while greatly improving the state 2 lift-to-drag ratio. Optimized airfoil 2 improves 19.53% and 32.38% in state 1 and state 2, respectively, and simultaneously ensures an increase in lift-to-drag ratio in both states, making it a more comprehensive airfoil. Optimized airfoil 3 improves by 22.63% in state 1, and the lift-to-drag ratio almost remains unchanged in state 2.

Table 7.
Comparison of airfoil aerodynamic parameters.
Figure 15 shows the geometric shape comparison of the airfoil before and after optimization, and Figure 16 shows the comparison of pressure coefficient distribution before and after optimization. For state 1, the improvement in lift–drag ratio of the three optimized airfoils mainly comes from the increase in lift. For state 2, the lift of the three optimized airfoils increased slightly. The shock wave of optimized airfoil 1 was largely erased. The shock wave of optimized airfoil 2 was slightly weakened. The shock wave intensity of optimized airfoil 3 remained almost unchanged. In other words, for optimized airfoil 1 and optimized airfoil 2, the improvement in lift–drag ratio mainly comes from the reduction in drag caused by the weakening of shock waves and the increase in lift. It is possible that the lift–drag ratio of optimized airfoil 3 remained almost unchanged due to the simultaneous increases in lift and drag.
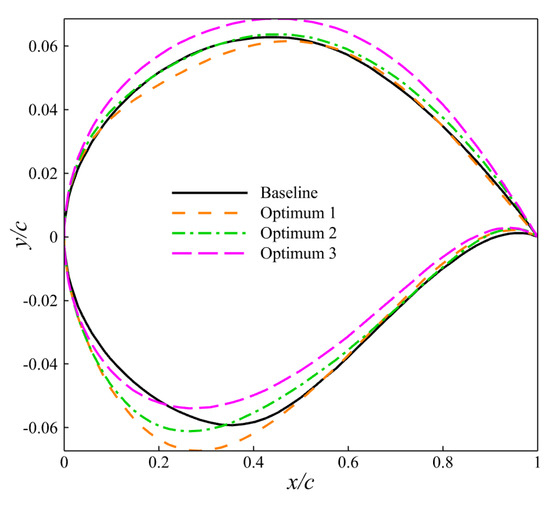
Figure 15.
Comparison of airfoil shape before and after optimization.
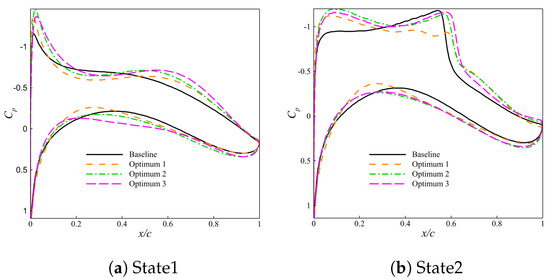
Figure 16.
Comparison of pressure coefficient distribution before and after optimization.
We give a series of Pareto-optimal solutions. For different Pareto-optimal solutions, the aerodynamic characteristics of the optimized airfoil in the two states also have different performances. Therefore, the Pareto-optimal solution suitable for specific problems can be selected according to needs.
5.5. Comparative Analysis of Algorithms
In order to better verify the value of the algorithm proposed in the paper in engineering applications, NSGA-II and MOPSO [37], which are commonly used in the field of engineering optimization, are selected for comparison. NSGA-II has the same parameter settings as the numerical experiment simulation case, and all parameters of the MOPSO algorithm are default parameters. In addition, the population size of these two calculations is set to 50, and the maximum number of fitness value evaluations is 4000. The comparison of optimization results is shown in Figure 17.
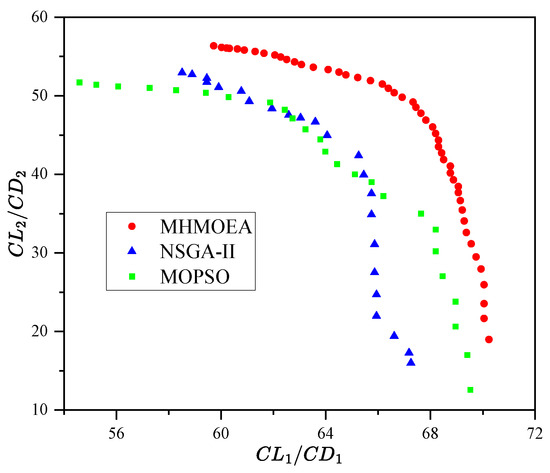
Figure 17.
Results of three algorithms in the airfoil optimization.
As can be seen from Figure 17, with the same number of fitness value evaluations, the distribution and convergence of the Pareto-optimal solution obtained by HMOEA are significantly better than NSGA-II and MOPSO. It can be seen that for aerodynamic optimization problems, HMOEA is obviously a more efficient algorithm. It can obtain a more ideal Pareto-optimal set with fewer flow field calculations, which greatly improves the efficiency of aerodynamic optimization.
6. Conclusions
- (1)
- This paper introduces a random weight function based on the weighted average gradient, proposes a multi-objective gradient operator, and develops two modes for assigning random weights: single-weight mode and multi-weight mode. Based on this, the multi-objective gradient algorithm (MOGBA) was developed and then combined with MOEA to develop the hybrid multi-objective evolutionary algorithm (HMOEA). HMOEA combines NSGA-III and L-BFGS-B to enhance exploration capabilities and speed up convergence, guide the development of optimal solutions, and explore the optimal distribution of solutions. Moreover, the hybrid and local search method developed can be extended to any stochastic and deterministic hybrid optimization method, and is not limited to NSGA-III and L-BFGS-B. In order to evaluate the comprehensive performance of the algorithm, it is compared with four classical multi-objective evolutionary algorithms, and 12 benchmarking functions are used to evaluate the performance of the proposed algorithm. The experimental results show that the algorithm proposed in this paper outperforms similar MOEAs on most of the test functions. It has faster convergence speed, higher convergence accuracy, and is able to obtain Pareto-optimal solutions with more uniform distribution.
- (2)
- The HMOEA is further applied to the aerodynamic multi-objective optimization design of the airfoil with the objective of maximizing the lift-to-drag ratio in two typical states, and the ideal Pareto front is finally obtained. This demonstrates the potential application of HMOEA in multi-objective aerodynamic optimization. Comparing HMOEA with NSGA-II and MOPSO, HMOEA obviously has higher optimization efficiency and obtains Pareto-optimal solutions with better distribution and convergence under the same number of flow field calculations, which proves that HMOEA can solve complex multi-objective aerodynamic optimization problems more effectively with less time. For more complex aerodynamic optimization problems, such as the complex shape optimization of the whole vehicle and the multi-objective optimization taking into account multiple states, the optimization algorithm will not make any difference in essence. In other words, HMOEA has the potential to be extended to complex aerodynamic optimization problems.
- (3)
- Of course, the current research is preliminary. First, further parametric analysis is needed to better realize the balance between optimal solution development and solution optimal distribution exploration. Secondly, gradient-based methods can significantly improve the efficiency of large-scale design variable optimization problems; so, the algorithm proposed in this paper should also have the potential to handle large-scale design variable optimization problems. This requires further experiments to verify the performance of HMOEA on such problems. Finally, the aerodynamic optimization example given in this paper is relatively simple, just a two-objective optimization problem under low-dimensional variables. Further testing is needed to evaluate the performance of HMOEA in engineering optimization. We will address these shortcomings in future work.
Author Contributions
Data curation, C.Z.; formal analysis, Z.T. and X.Z.; funding acquisition, Z.T.; investigation, C.Z.; methodology, C.Z. and Z.T.; project administration, C.Z.; resources, C.Z. and X.Z.; software, C.Z.; supervision, Z.T.; validation, X.H. and C.Z.; writing—original draft, C.Z.; writing—review and editing, C.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (12032011, 11772154), the Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD), and the Fundamental Research Funds for the Central Universities (NP2020102).
Data Availability Statement
The datasets generated and analyzed during the current study are available from the corresponding author on reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Tian, X.; Li, J. A novel improved fruit fly optimization algorithm for aerodynamic shape design optimization. Knowl.-Based Syst. 2019, 179, 77–91. [Google Scholar] [CrossRef]
- Lee, K.D.; Eyi, S. Aerodynamic design via optimization. J. Aircr. 1992, 29, 1012–1019. [Google Scholar] [CrossRef]
- Hajela, P. Nongradient methods in multidisciplinary design optimization-status and potential. J. Aircr. 1999, 36, 255–265. [Google Scholar] [CrossRef]
- Buckley, H.P.; Zingg, D.W. Approach to aerodynamic design through numerical optimization. AIAA J. 2013, 51, 1972–1981. [Google Scholar] [CrossRef]
- Mokarram, V.; Banan, M.R. A new PSO-based algorithm for multi-objective optimization with continuous and discrete design variables. Struct. Multidiscip. Optim. 2018, 57, 509–533. [Google Scholar] [CrossRef]
- Tang, Z.; Hu, X.; Périaux, J. Multi-level hybridized optimization methods coupling local search deterministic and global search evolutionary algorithms. Arch. Comput. Methods Eng. 2020, 27, 939–975. [Google Scholar] [CrossRef]
- Jameson, A. Aerodynamic design via control theory. J. Sci. Comput. 1988, 3, 233–260. [Google Scholar] [CrossRef]
- Jiaqi, L.; Juntao, X.; Feng, L. Aerodynamic design optimization by using a continuous adjoint method. Sci. China Phys. Mech. Astron. 2014, 57, 1363–1375. [Google Scholar]
- Lin, Q.; Liu, S.; Wong, K.C.; Gong, M.; Coello, C.A.C.; Chen, J.; Zhang, J. A clustering-based evolutionary algorithm for many-objective optimization problems. IEEE Trans. Evol. Comput. 2018, 23, 391–405. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Beasley, D.; Bull, D.R.; Martin, R.R. An overview of genetic algorithms: Part 1, fundamentals. Univ. Comput. 1993, 15, 56–69. [Google Scholar]
- Bosman, P.A.; de Jong, E.D. Exploiting gradient information in numerical multi–objective evolutionary optimization. In Proceedings of the 7th Annual Conference on Genetic and Evolutionary Computation, New York, NY, USA, 25–29 June 2005; pp. 755–762. [Google Scholar]
- Hu, X.; Huang, Z.; Wang, Z. Hybridization of the multi-objective evolutionary algorithms and the gradient-based algorithms. In Proceedings of the The 2003 Congress on Evolutionary Computation, Canberra, ACT, Australia, 8–12 December 2003; IEEE: New York, NY, USA, 2003; Volume 2, pp. 870–877. [Google Scholar]
- El-Mihoub, T.A.; Hopgood, A.A.; Nolle, L.; Battersby, A. Hybrid Genetic Algorithms: A Review. Eng. Lett. 2006, 13, 124–137. [Google Scholar]
- Bosman, P.A. On gradients and hybrid evolutionary algorithms for real-valued multiobjective optimization. IEEE Trans. Evol. Comput. 2011, 16, 51–69. [Google Scholar] [CrossRef]
- Bosman, P.A.; de Jong, E.D. Combining gradient techniques for numerical multi-objective evolutionary optimization. In Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation, New York, NY, USA, 8–12 July 2006; pp. 627–634. [Google Scholar]
- Lahanas, M.; Baltas, D.; Giannouli, S. Global convergence analysis of fast multiobjective gradient-based dose optimization algorithms for high-dose-rate brachytherapy. Phys. Med. Biol. 2003, 48, 599. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Blank, J.; Deb, K. pymoo: Multi-Objective Optimization in Python. IEEE Access 2020, 8, 89497–89509. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Tang, Z.; Luo, S.; Chen, Y.; Zhao, X.; Wu, P. Hierarchical variable fidelity evolutionary optimization methods and their applications in aerodynamic shape design. Appl. Soft Comput. 2022, 114, 108135. [Google Scholar] [CrossRef]
- Fletcher, R.; Reeves, C.M. Function minimization by conjugate gradients. Comput. J. 1964, 7, 149–154. [Google Scholar] [CrossRef]
- Hua, Y.; Jin, Y.; Hao, K. A clustering-based adaptive evolutionary algorithm for multiobjective optimization with irregular Pareto fronts. IEEE Trans. Cybern. 2018, 49, 2758–2770. [Google Scholar] [CrossRef] [PubMed]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2013, 18, 577–601. [Google Scholar] [CrossRef]
- Frey, B.J.; Dueck, D. Clustering by passing messages between data points. Science 2007, 315, 972–976. [Google Scholar] [CrossRef]
- Vicini, A.; Quagliarella, D. Airfoil and wing design through hybrid optimization strategies. AIAA J. 1999, 37, 634–641. [Google Scholar] [CrossRef]
- Deb, K.; Thiele, L.; Laumanns, M.; Zitzler, E. Scalable multi-objective optimization test problems. In Proceedings of the 2002 Congress on Evolutionary Computation, Honolulu, HI, USA, 12–17 May 2002; IEEE: New York, NY, USA, 2002; Volume 1, pp. 825–830. [Google Scholar]
- Deb, K.; Thiele, L.; Laumanns, M.; Zitzler, E. Scalable test problems for evolutionary multiobjective optimization. In Evolutionary Multiobjective Optimization: Theoretical Advances and Applications; Springer: Berlin/Heidelberg, Germany, 2005; pp. 105–145. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. A multiobjective evolutionary algorithm based on decomposition. In IEEE Transactions on Evolutionary Computation; IEEE Computational Intelligence Society: Piscataway, NJ, USA, 2006. [Google Scholar]
- Cheng, R.; Jin, Y.; Olhofer, M.; Sendhoff, B. A reference vector guided evolutionary algorithm for many-objective optimization. IEEE Trans. Evol. Comput. 2016, 20, 773–791. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L.; Laumanns, M.; Fonseca, C.M.; Da Fonseca, V.G. Performance assessment of multiobjective optimizers: An analysis and review. IEEE Trans. Evol. Comput. 2003, 7, 117–132. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Economon, T.D.; Palacios, F.; Copeland, S.R.; Lukaczyk, T.W.; Alonso, J.J. SU2: An open-source suite for multiphysics simulation and design. AIAA J. 2016, 54, 828–846. [Google Scholar] [CrossRef]
- Samareh, J. Aerodynamic shape optimization based on free-form deformation. In Proceedings of the 10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, New York, NY, USA, 30 August–30 September 2004; p. 4630. [Google Scholar]
- Andersson, F.; Kvernes, B. Bezier and B-Spline Technology. Ph.D. Thesis, Umea University, Umea, Sweden, 2003. [Google Scholar]
- Straathof, M.H.; van Tooren, M.J. Extension to the class-shape-transformation method based on B-splines. AIAA J. 2011, 49, 780–790. [Google Scholar] [CrossRef]
- Sierra, M.R.; Coello Coello, C.A. Improving PSO-based multi-objective optimization using crowding, mutation and ∈-dominance. In Proceedings of the International Conference on Evolutionary Multi-Criterion Optimization, Leiden, The Netherlands, 20–24 March 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 505–519. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).