Modeling and Structural Analysis of MEMS Shallow Arch Assuming Multimodal Initial Curvature Profiles
Abstract
1. Introduction
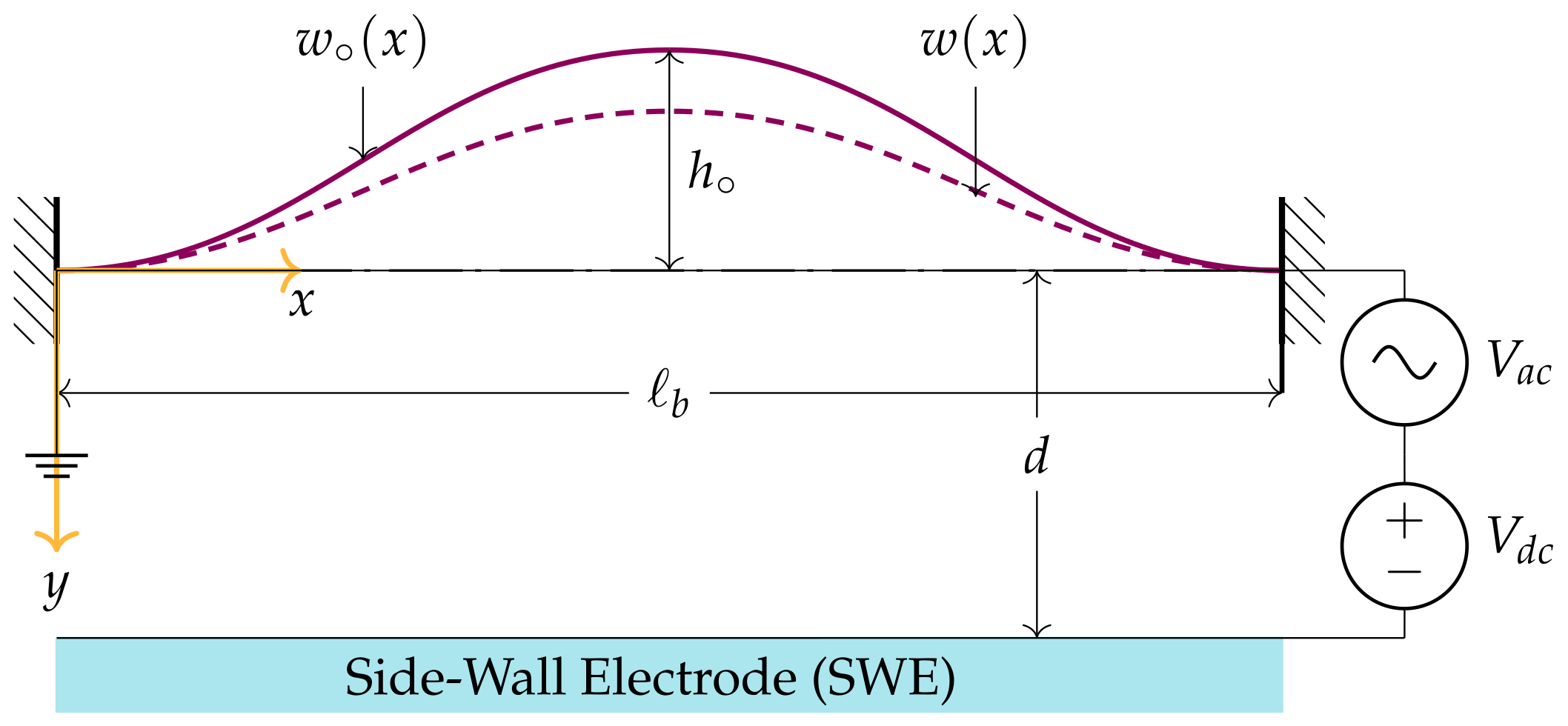
2. Mathematical Model
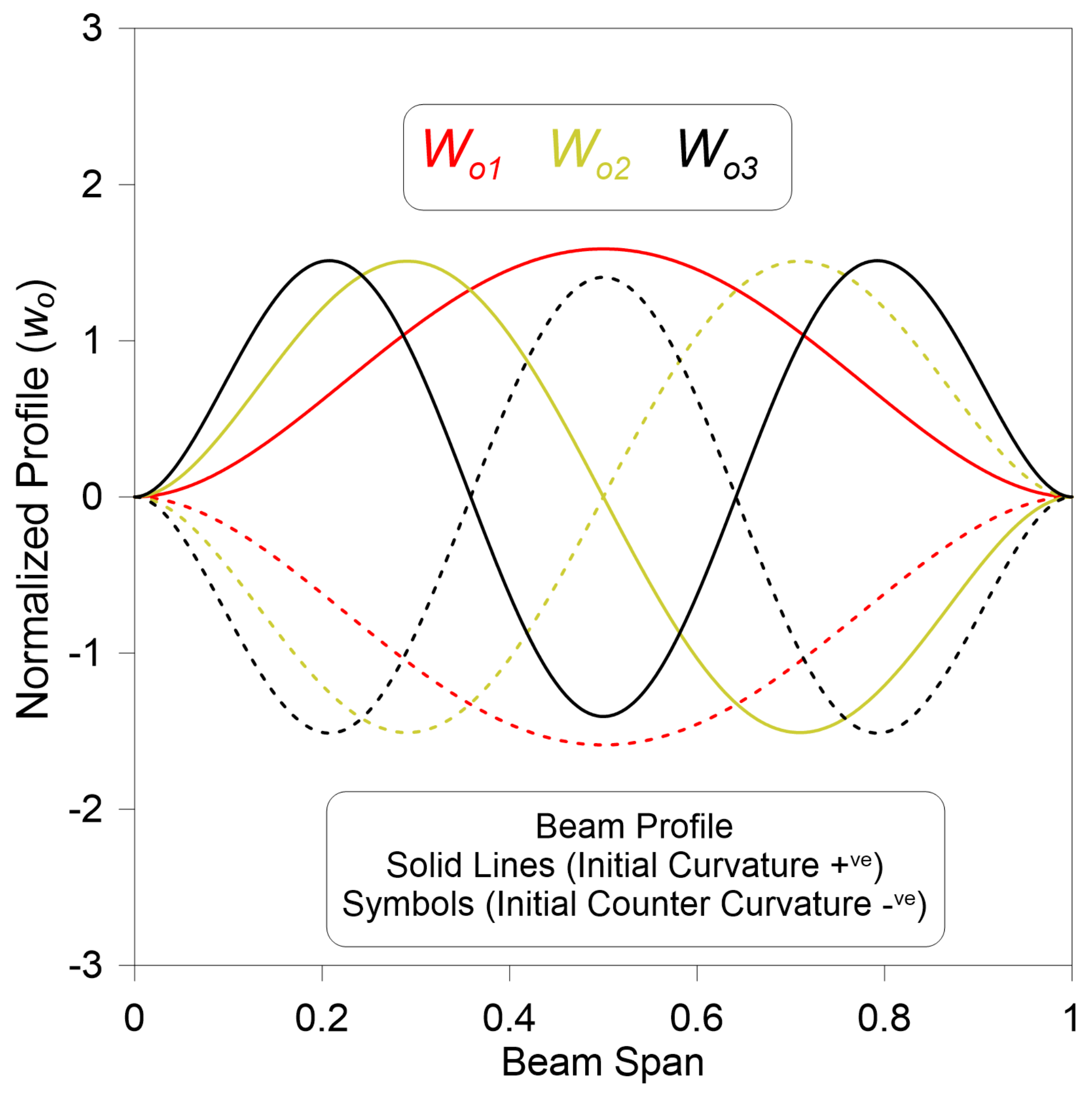
Reduced-Order Model (ROM)
3. Results and Discussion
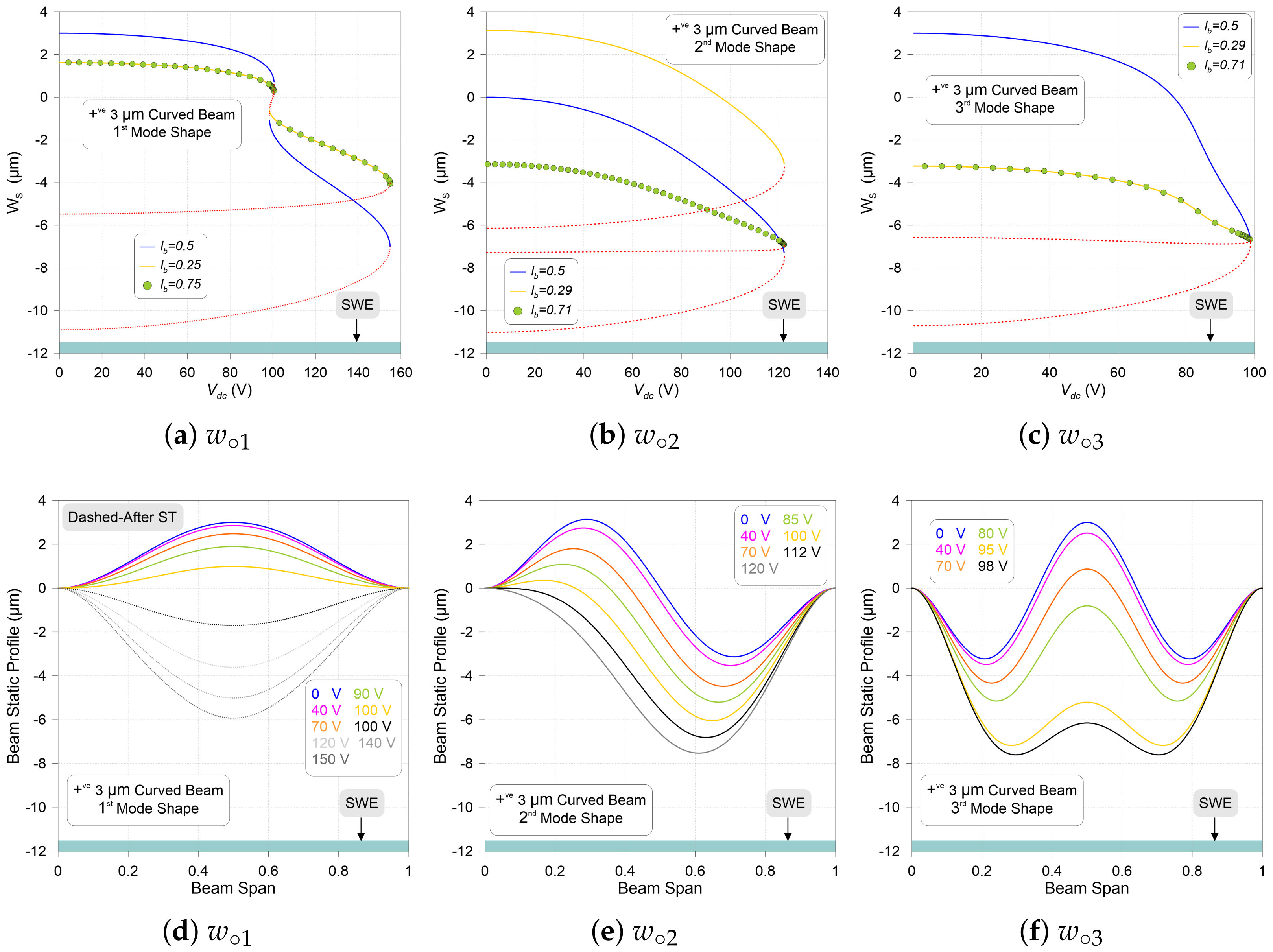
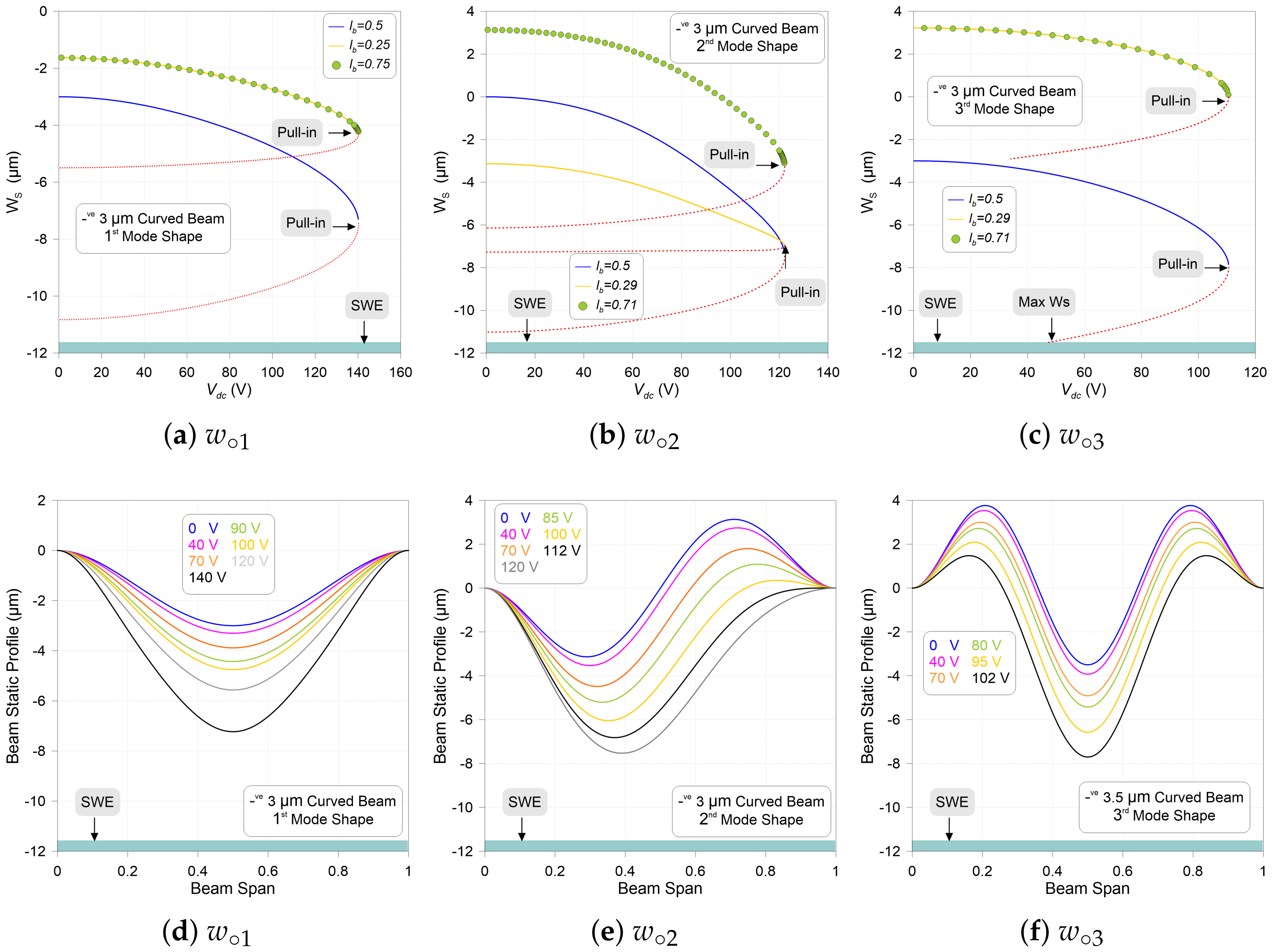
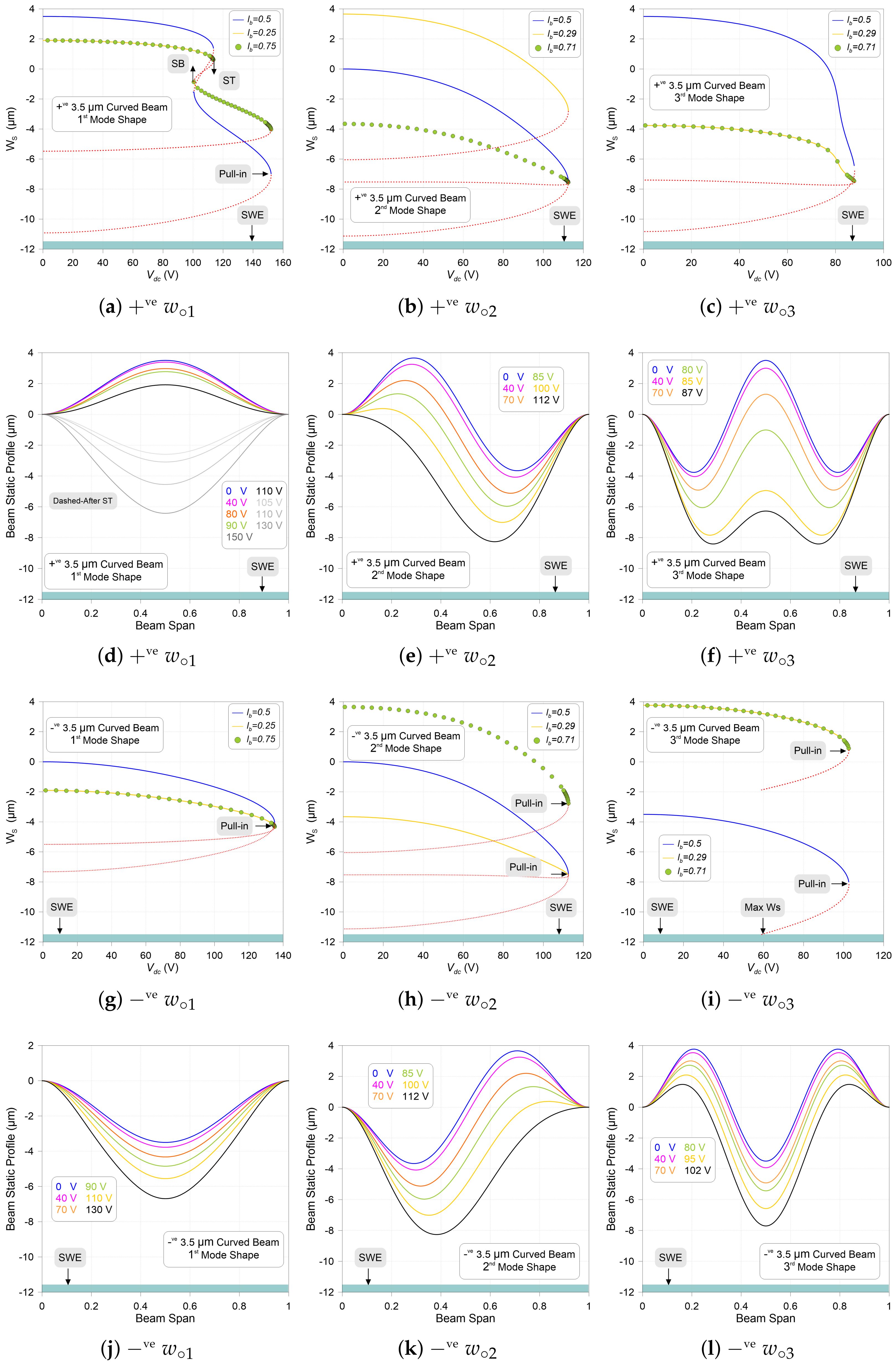
3.1. Static Behavior vs. dc Voltage
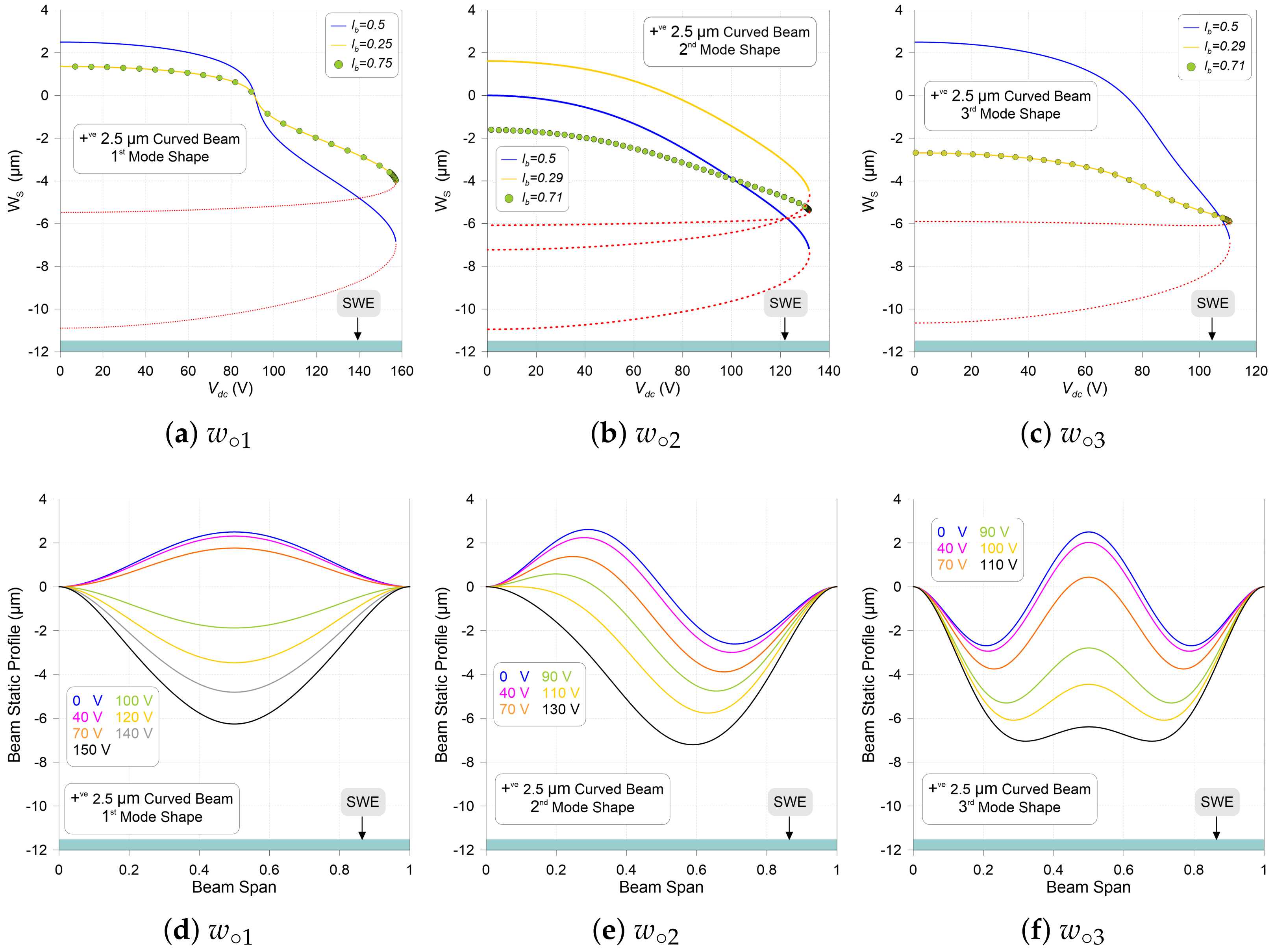
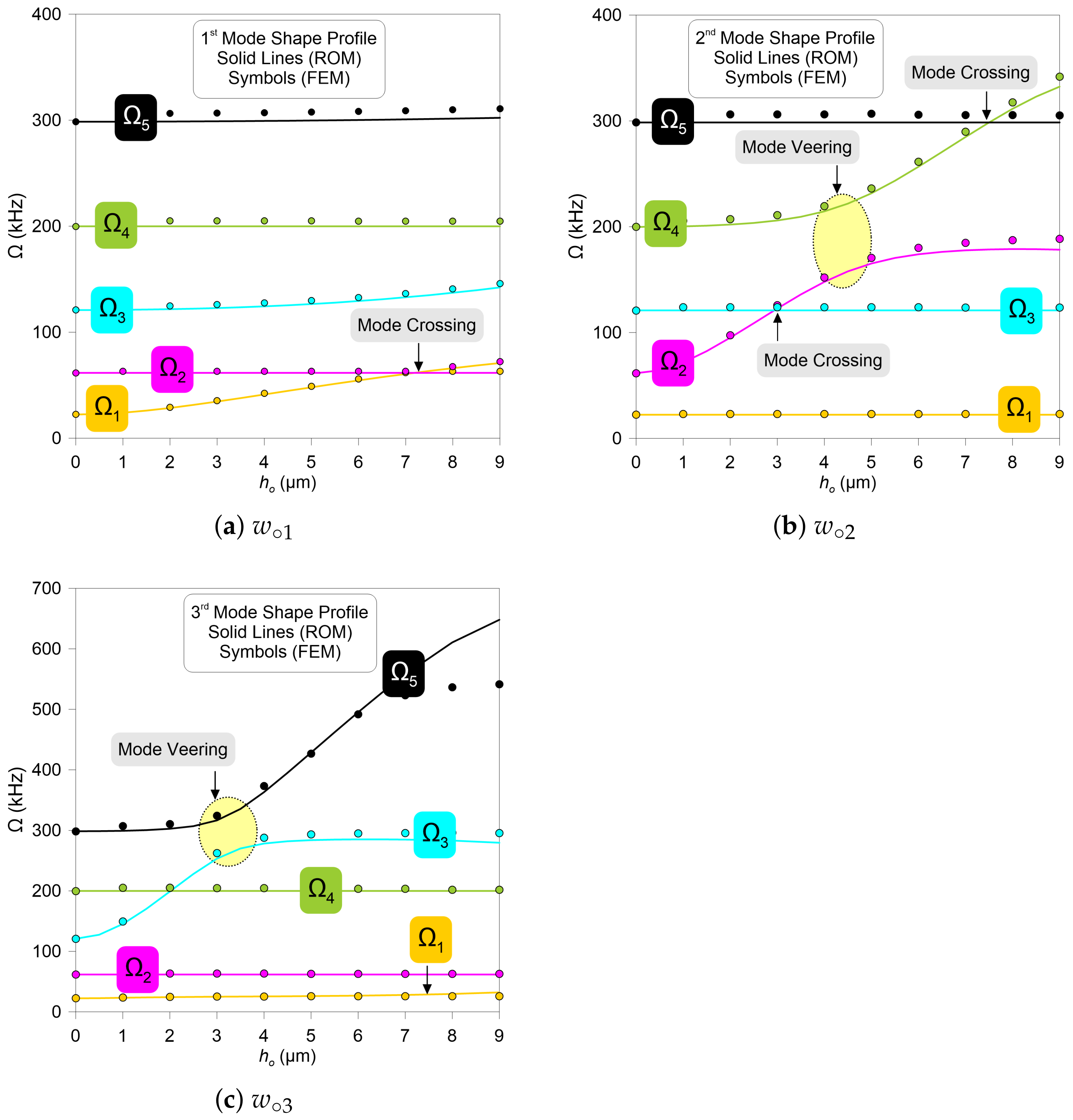
3.2. Eigenvalues vs. dc Voltage
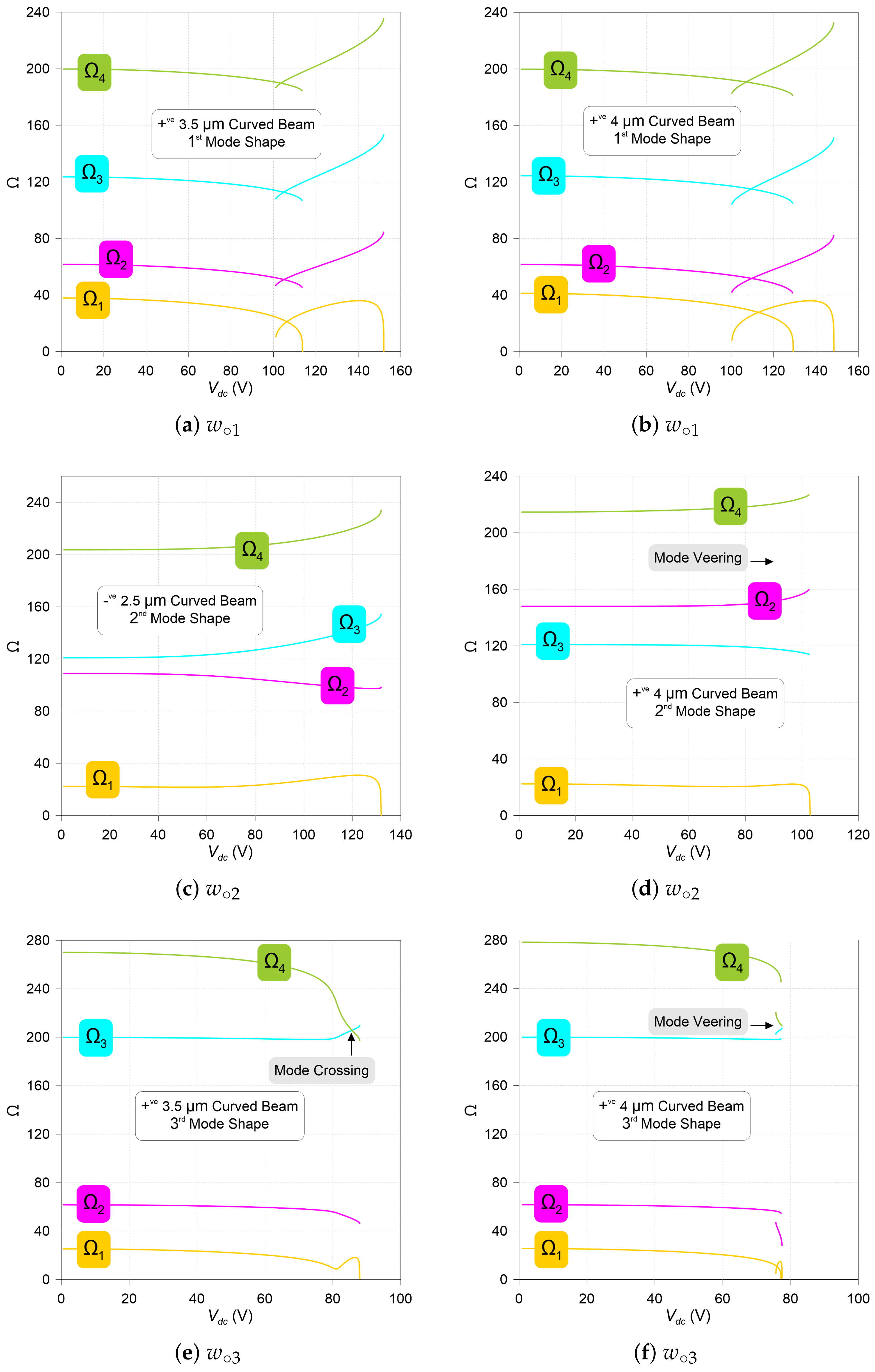
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
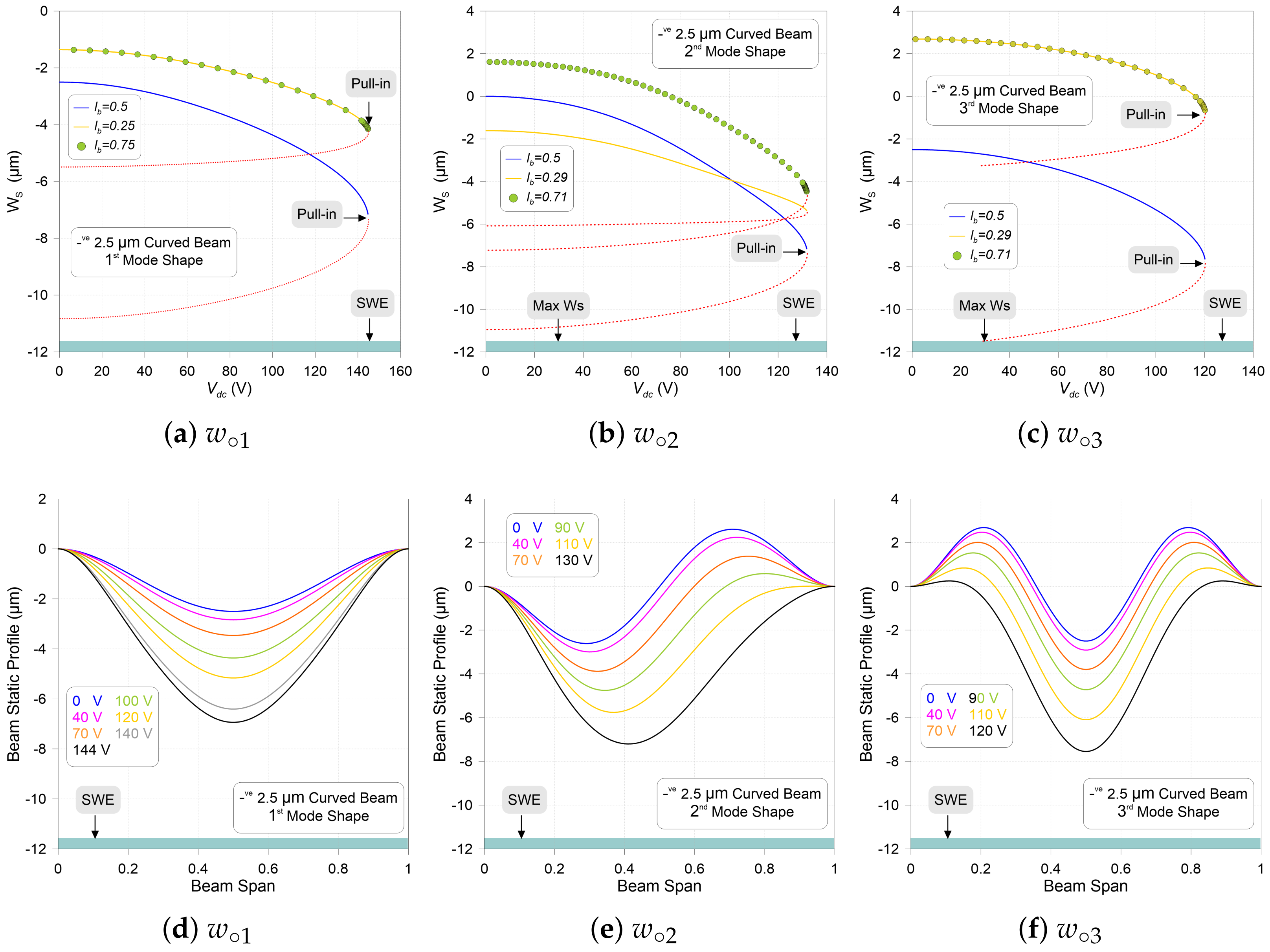
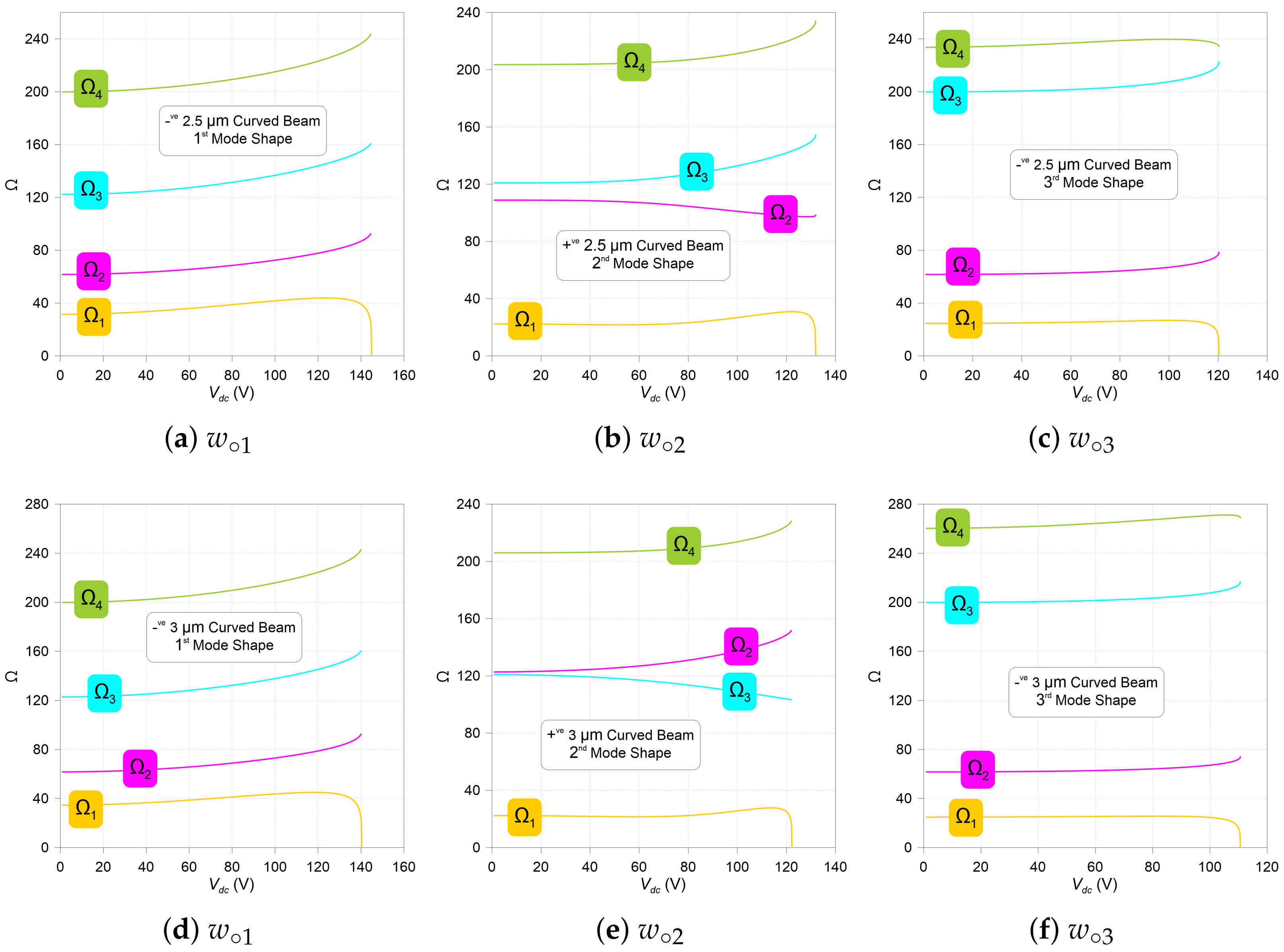

References
- Younis, M.I. MEMS Linear and Nonlinear Statics and Dynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; Volume 20. [Google Scholar]
- Haronian, D. A low-cost micromechanical accelerometer with integrated solid-state sensor. Sens. Actuators A Phys. 2000, 84, 149–155. [Google Scholar] [CrossRef]
- Morozov, N.F.; Indeitsev, D.A.; Igumnova, V.S.; Lukin, A.V.; Popov, I.A.; Shtukin, L.V. Nonlinear dynamics of mode-localized MEMS accelerometer with two electrostatically coupled microbeam sensing elements. Int. J.-Non-Linear Mech. 2022, 138, 103852. [Google Scholar]
- Pachkawade, V. State-of-the-art in mode-localized MEMS coupled resonant sensors: A comprehensive review. IEEE Sens. J. 2021, 21, 8751–8779. [Google Scholar] [CrossRef]
- Benjamin, E.; Lulinsky, S.; Krylov, S. Design and implementation of a bistable force/acceleration sensing device considering fabrication tolerances. J. Microelectromech. Syst. 2018, 27, 854–865. [Google Scholar] [CrossRef]
- Krakover, N.; Ilic, B.R.; Krylov, S. Displacement sensing based on resonant frequency monitoring of electrostatically actuated curved micro beams. J. Micromech. Microeng. 2016, 26, 115006. [Google Scholar] [CrossRef] [PubMed]
- Kessler, Y.; Liberzon, A.; Krylov, S. Flow velocity gradient sensing using a single curved bistable microbeam. J. Microelectromech. Syst. 2020, 29, 1020–1025. [Google Scholar] [CrossRef]
- Tang, X.; Liu, F. A novel benzene quantitative analysis method using miniaturized metal ionization gas sensor and non-linear bistable dynamic system. Bioengineered 2015, 6, 294–296. [Google Scholar] [CrossRef][Green Version]
- Ouakad, H.M.; Alneamy, A.M. Static and Eigenvalue Analysis of Electrostatically Coupled and Tunable Shallow Micro-Arches for Sensing-Based Applications. Micromachines 2023, 14, 903. [Google Scholar] [CrossRef]
- Alneamy, A.M.; Ouakad, H.M. Inertia mass bio-sensors based on snap-through phenomena in electrostatic MEMS shallow arch resonators. Int. J. Mech. Sci. 2023, 238, 107825. [Google Scholar] [CrossRef]
- Tella, S.A.; Younis, M.I. Toward cascadable MEMS logic device based on mode localization. Sens. Actuators A Phys. 2020, 315, 112367. [Google Scholar] [CrossRef]
- Medina, L. Unified dynamic bistability criteria in electrostatically actuated curved prestressed microbeams. Int. J. Mech. Sci. 2024, 263, 108765. [Google Scholar] [CrossRef]
- Mesbah, A.; Belabed, Z.; Tounsi, A.; Ghazwani, M.H.; Alnujaie, A.; Aldosari, S.M. Assessment of New Quasi-3D Finite Element Model for Free Vibration and Stability Behaviors of Thick Functionally Graded Beams. J. Vib. Eng. Technol. 2023, 12, 2231–2247. [Google Scholar] [CrossRef]
- Vlajic, N.; Fitzgerald, T.; Nguyen, V.; Balachandran, B. Geometrically exact planar beams with initial pre-stress and large curvature: Static configurations, natural frequencies, and mode shapes. Int. J. Solids Struct. 2014, 51, 3361–3371. [Google Scholar] [CrossRef]
- Zhou, Y.; Yi, Z.; Stanciulescu, I. Nonlinear buckling and postbuckling of shallow arches with vertical elastic supports. J. Appl. Mech. 2019, 86, 061001. [Google Scholar] [CrossRef]
- Nicoletti, R. On the natural frequencies of simply supported beams curved in mode shapes. J. Sound Vib. 2020, 485, 115597. [Google Scholar] [CrossRef]
- Karaagac, C.; Ozturk, H.; Sabuncu, M. Crack effects on the in-plane static and dynamic stabilities of a curved beam with an edge crack. J. Sound Vib. 2011, 330, 1718–1736. [Google Scholar] [CrossRef]
- Eisenberger, M.; Efraim, E. In-plane vibrations of shear deformable curved beams. Int. J. Numer. Methods Eng. 2001, 52, 1221–1234. [Google Scholar] [CrossRef]
- Yang, F.; Sedaghati, R.; Esmailzadeh, E. Free in-plane vibration of general curved beams using finite element method. J. Sound Vib. 2008, 318, 850–867. [Google Scholar] [CrossRef]
- Mohamed, S.A.; Assie, A.E.; Eltaher, M.A. Novel incremental procedure in solving nonlinear static response of 2D-FG porous plates. THin-Walled Struct. 2023, 189, 110779. [Google Scholar] [CrossRef]
- Medina, L.; Gilat, R.; Krylov, S. Symmetry breaking in an initially curved pre-stressed micro beam loaded by a distributed electrostatic force. Int. J. Solids Struct. 2014, 51, 2047–2061. [Google Scholar] [CrossRef]
- Alnujaie, A.; Akbas, S.D.; Eltaher, M.A.; Assie, A. Forced vibration of a functionally graded porous beam resting on viscoelastic foundation. Geomech. Eng. 2021, 24, 91–103. [Google Scholar]
- Sharma, A.K.; Godara, R.; Joglekar, M.M. Static and DC dynamic pull-in analysis of curled microcantilevers with a compliant support. Microsyst. Technol. 2019, 25, 965–975. [Google Scholar] [CrossRef]
- Medina, L.; Gilat, R.; Krylov, S. Latching in bistable electrostatically actuated curved micro beams. Int. J. Eng. Sci. 2017, 110, 15–34. [Google Scholar] [CrossRef]
- Shojaeian, M.; Beni, Y.T.; Ataei, H. Size-dependent snap-through and pull-in instabilities of initially curved pre-stressed electrostatic nano-bridges. J. Phys. D Appl. Phys. 2016, 49, 295303. [Google Scholar] [CrossRef]
- Alcheikh, N.; Ouakad, H.M.; Mbarek, S.B.; Younis, M.I. Crossover/veering in V-shaped MEMS resonators. J. Microelectromech. Syst. 2021, 31, 74–86. [Google Scholar] [CrossRef]
- Rosenberg, S.; Shoshani, O. Zero-dispersion point in curved micro-mechanical beams. Nonlinear Dyn. 2022, 107, 1–14. [Google Scholar] [CrossRef]
- Alneamy, A.; Khater, M.; Al-Ghamdi, M.; Abdel-Aziz, A.; Heppler, G.; Abdel-Rahman, E. Large oscillation of electrostatically actuated curved beams. J. Micromech. Microeng. 2020, 30, 095005. [Google Scholar] [CrossRef]
- Alfosail, F.K.; Hajjaj, A.Z.; Younis, M.I. Theoretical and experimental investigation of two-to-one internal resonance in MEMS arch resonators. J. Comput. Nonlinear Dyn. 2019, 14, 011001. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H. Bistable nonlinear response of MEMS resonators. Nonlinear Dyn. 2017, 90, 1627–1645. [Google Scholar] [CrossRef]
- Medina, L.; Gilat, R.; Ilic, B.R.; Krylov, S. Open-loop, self-excitation in a bistable micromechanical beam actuated by a DC electrostatic load. In Proceedings of the 2017 IEEE 30th International Conference on Micro Electro Mechanical Systems (MEMS), IEEE, Las Vegas, NV, USA, 22–26 January 2017; pp. 785–788. [Google Scholar]
- Rajaei, A.; Vahidi-Moghaddam, A.; Ayati, M.; Baghani, M. Integral sliding mode control for nonlinear damped model of arch microbeams. Microsyst. Technol. 2019, 25, 57–68. [Google Scholar] [CrossRef]
- Morozov, N.; Indeitsev, D.; Mozhgova, N.; Lukin, A.; Popov, I. Equilibrium Forms of an Initially Curved Bernoulli–Euler Beam in Electric and Thermal Fields; Doklady Physics; Springer: Berlin/Heidelberg, Germany, 2023; Volume 68, pp. 56–61. [Google Scholar]
- Indeitsev, D.; Mozhgova, N.; Lukin, A.; Popov, I. Model of a Micromechanical Mode-Localized Accelerometer with an Initially Curved Microbeam as a Sensitive Element. Mech. Solids 2023, 58, 779–792. [Google Scholar] [CrossRef]
- Younis, M.I.; Abdel-Rahman, E.M.; Nayfeh, A. A reduced-order model for electrically actuated microbeam-based MEMS. J. Microelectromech. Syst. 2003, 12, 672–680. [Google Scholar] [CrossRef]
- Ouakad, H.M.; Younis, M.I. The dynamic behavior of MEMS arch resonators actuated electrically. Int. J.-Non-Linear Mech. 2010, 45, 704–713. [Google Scholar] [CrossRef]
- Multiphysics, C. v. 5.2 a. COMSOL AB, Stockholm. Sweden, 2018. Available online: www.comsol.com (accessed on 4 March 2024).
- Hajjaj, A.Z.; Alcheikh, N.; Younis, M.I. The static and dynamic behavior of MEMS arch resonators near veering and the impact of initial shapes. Int. J.-Non-Linear Mech. 2017, 95, 277–286. [Google Scholar] [CrossRef]
- Alkharabsheh, S.A.; Younis, M.I. Statics and dynamics of MEMS arches under axial forces. J. Vib. Acoust. 2013, 135, 021007. [Google Scholar] [CrossRef]
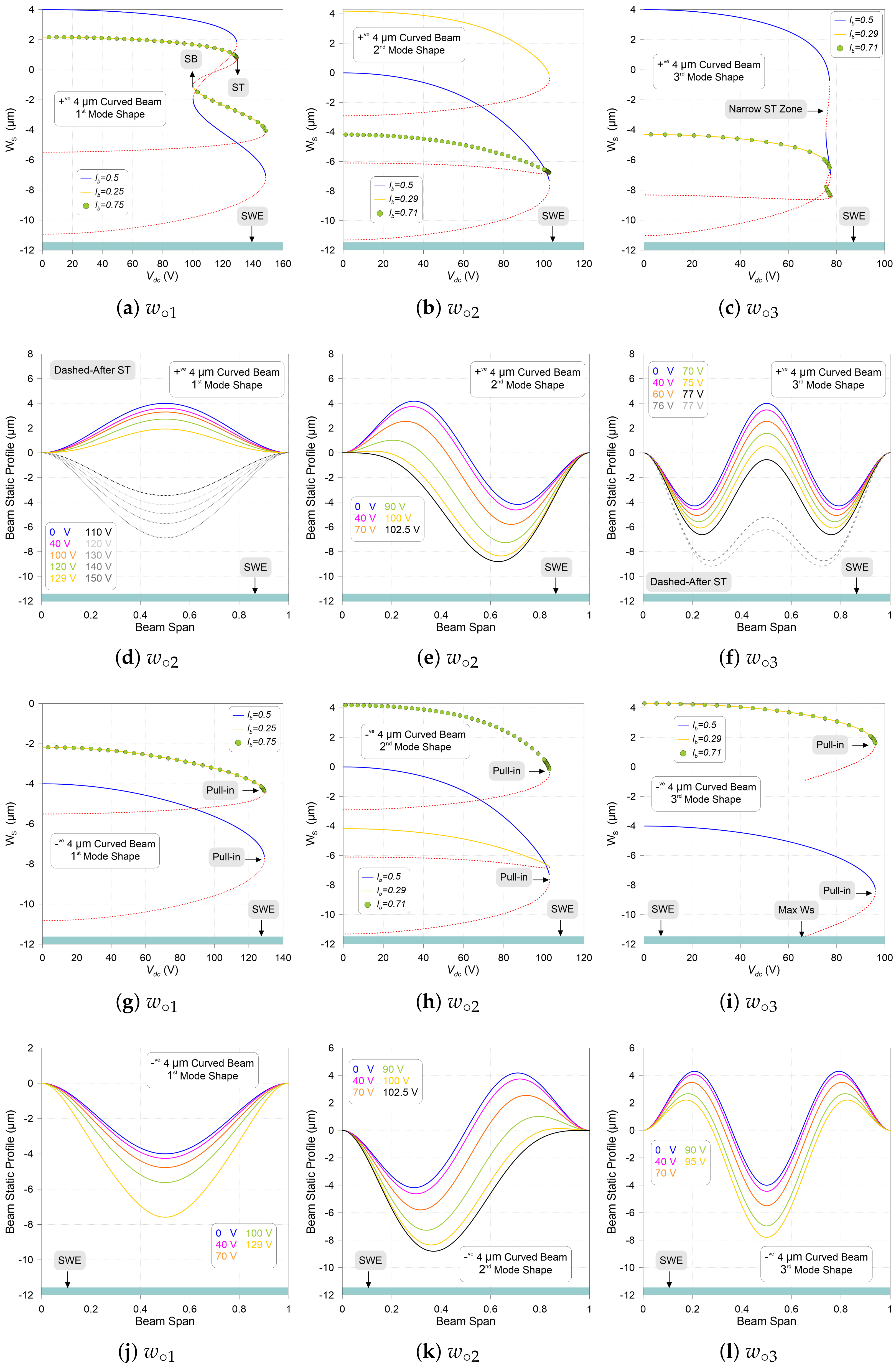

| Modes | ST | ST Error % | SB | SB Error % | PI | PI Error % |
|---|---|---|---|---|---|---|
| 2 | 112.6 | 0.09 | 100.2 | 0 | 165 | 7.7 |
| 3 | 113.6 | 0.8 | 100.09 | 0.1 | 151.99 | 0.8 |
| 5 | 112.71 | – | 100.2 | – | 153.2 | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alneamy, A.M.; Ouakad, H.M. Modeling and Structural Analysis of MEMS Shallow Arch Assuming Multimodal Initial Curvature Profiles. Mathematics 2024, 12, 970. https://doi.org/10.3390/math12070970
Alneamy AM, Ouakad HM. Modeling and Structural Analysis of MEMS Shallow Arch Assuming Multimodal Initial Curvature Profiles. Mathematics. 2024; 12(7):970. https://doi.org/10.3390/math12070970
Chicago/Turabian StyleAlneamy, Ayman M., and Hassen M. Ouakad. 2024. "Modeling and Structural Analysis of MEMS Shallow Arch Assuming Multimodal Initial Curvature Profiles" Mathematics 12, no. 7: 970. https://doi.org/10.3390/math12070970
APA StyleAlneamy, A. M., & Ouakad, H. M. (2024). Modeling and Structural Analysis of MEMS Shallow Arch Assuming Multimodal Initial Curvature Profiles. Mathematics, 12(7), 970. https://doi.org/10.3390/math12070970






