A New Class of Irregular Packing Problems Reducible to Sphere Packing in Arbitrary Norms
Abstract
1. Introduction
- The problem of Packing Objects Composed by Generalized Spheres (PCGS) is formulated for objects and containers represented by spheres in arbitrary norms.
- Non-overlapping and containment conditions considering allowable distances for irregular objects composed by generalized spheres are introduced. By means of a new composition condition, rotations and reflections of the irregular objects are enabled.
- The generalized balance, homothetic and sparse packing problems for objects composed by the generalized spheres are stated for various norms.
2. Mathematical Modeling
2.1. The Main Definitions
- (a)
- a containment condition ensures that all composed objects are completely in the container,
- (b)
- a non-overlapping condition states that there is no overlapping between any pair of the composed objects.
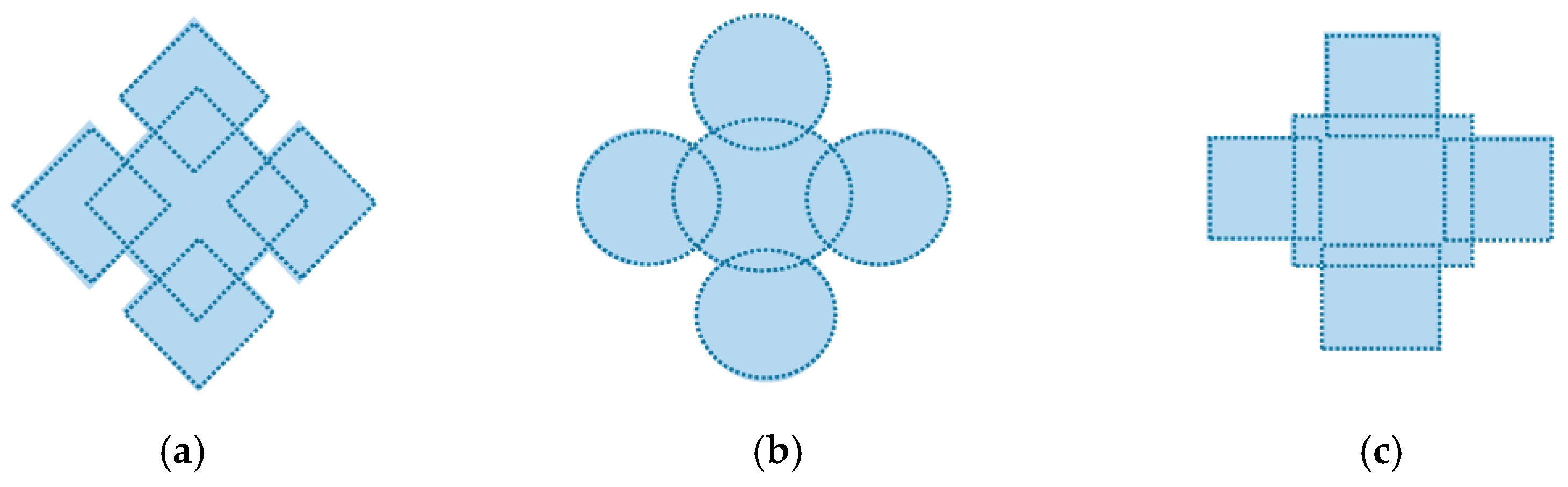
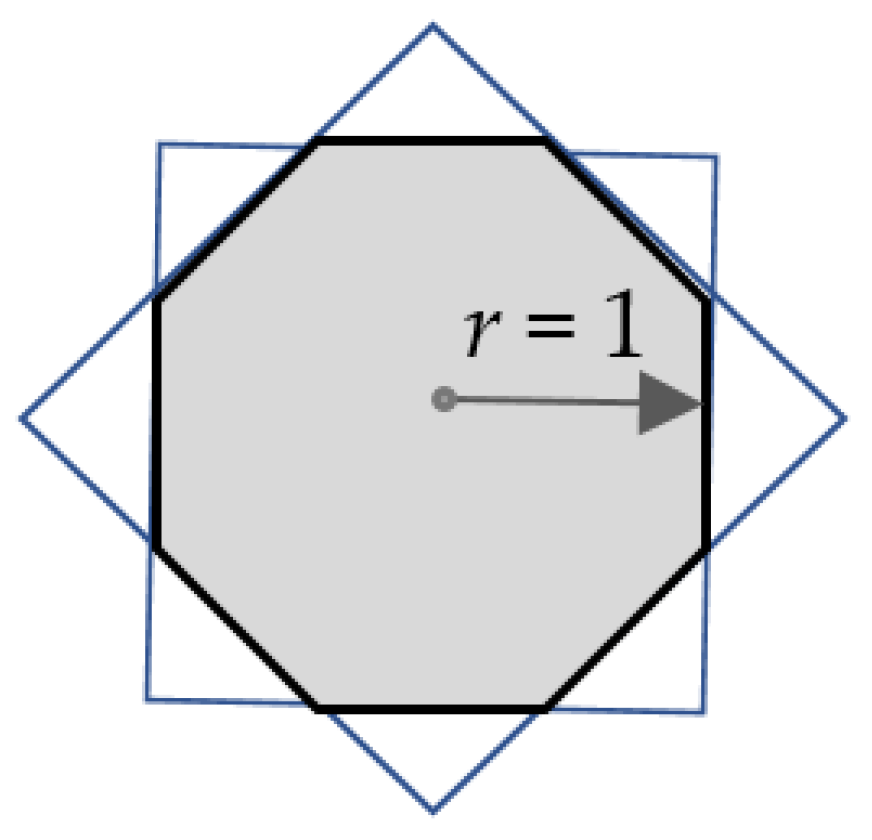
2.2. Useful Norms and Transformations
3. Some Cases of PCGS Problems
3.1. Generalized Balance Packing Problems (GBPP)
3.2. Generalized Homothetic Packing Problems (GHPP)
3.3. Generalized Sparse Packing Problems (GSPP)
4. Computational Results
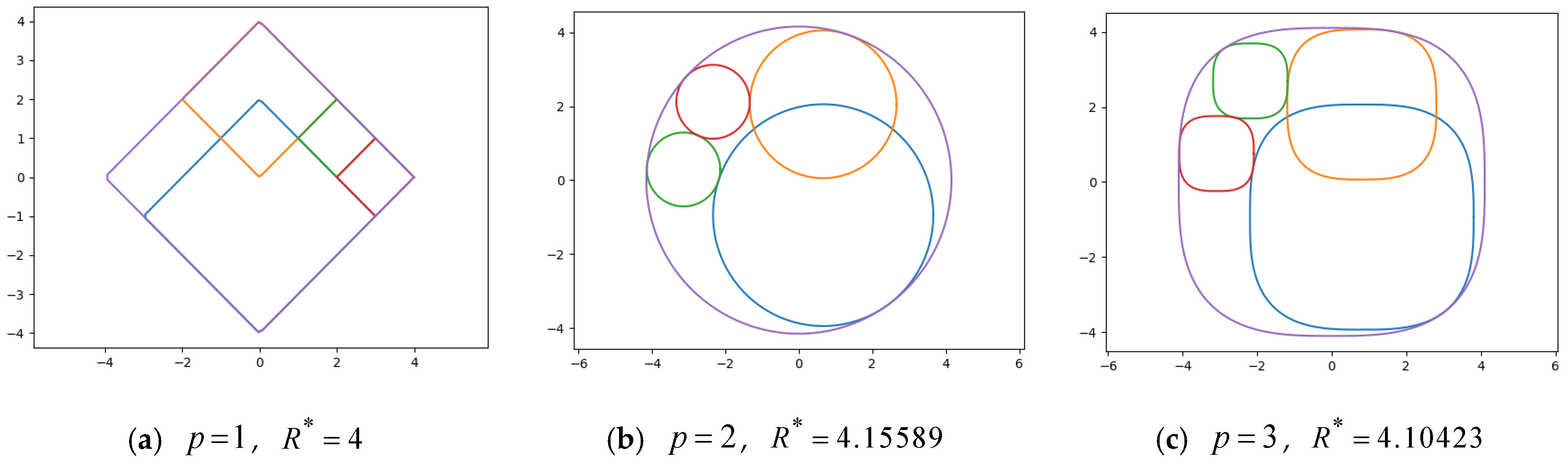
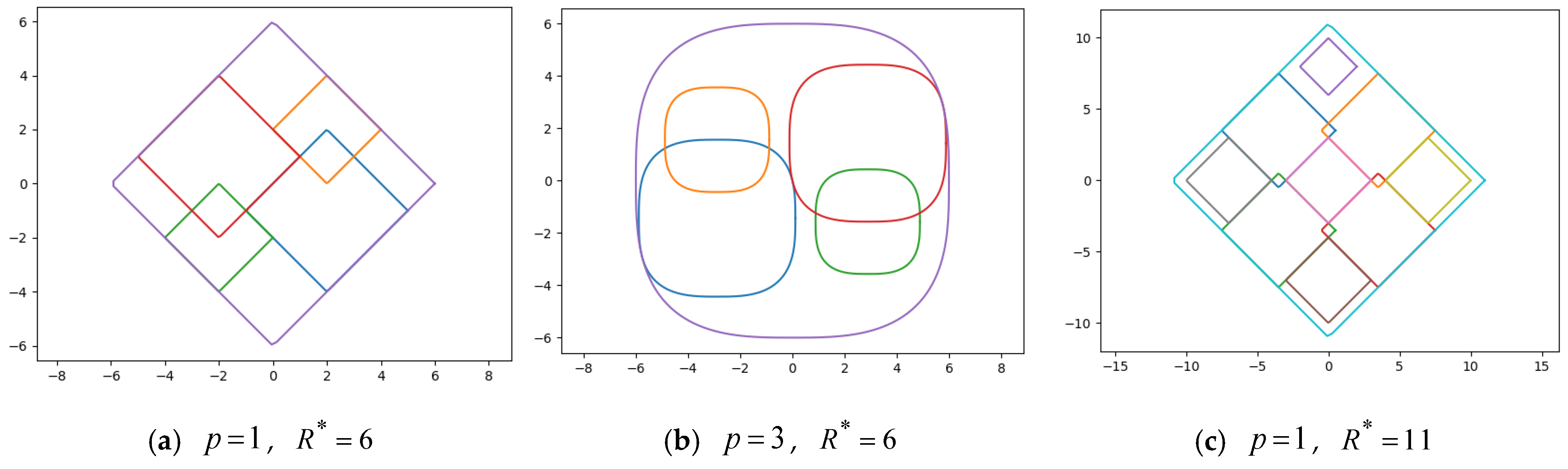
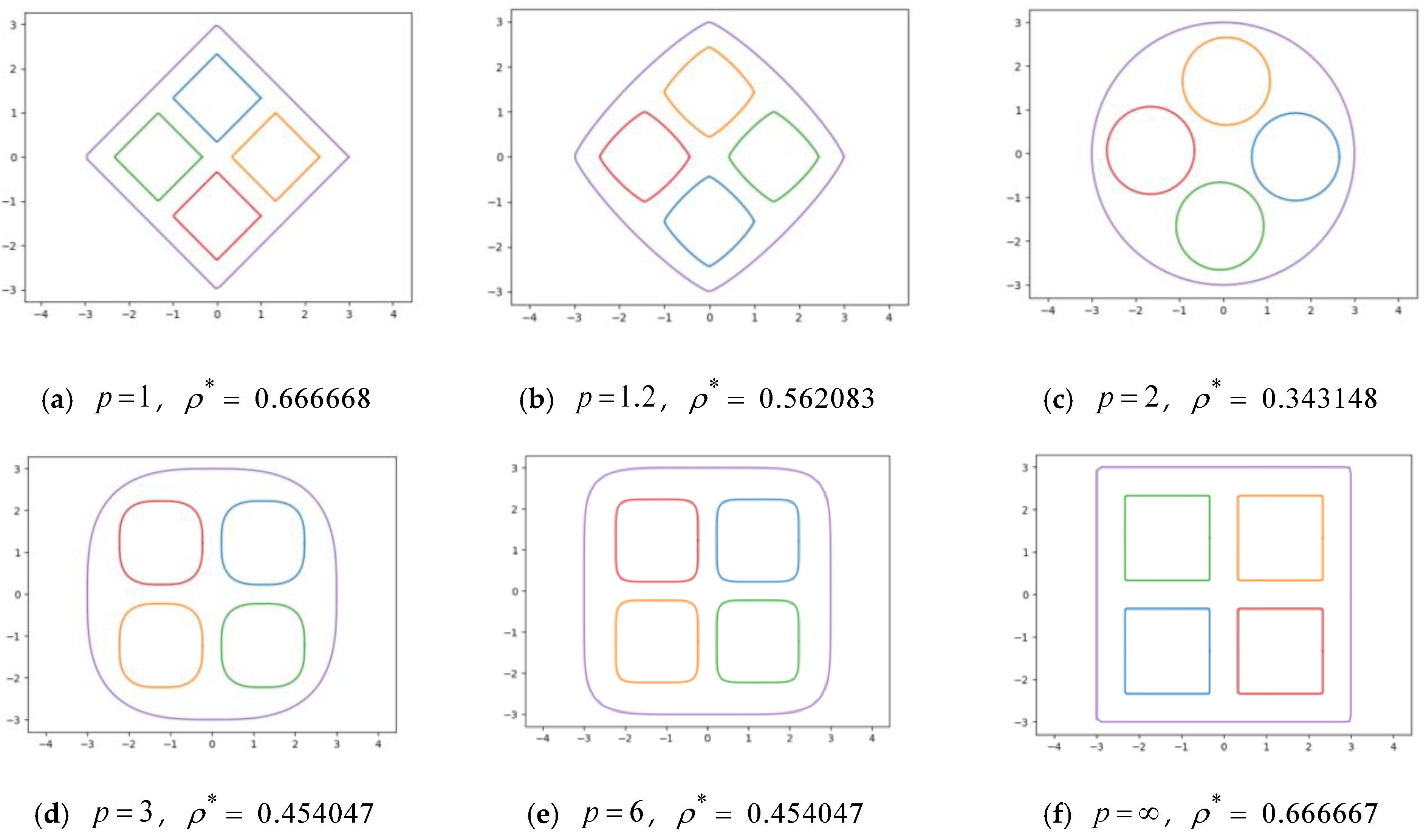
4.1. Computational Results for Generalized Balance Packing Problem (GBPP)
- (a)
- , , ;
- (b)
- , , ;
- (c)
- , , .
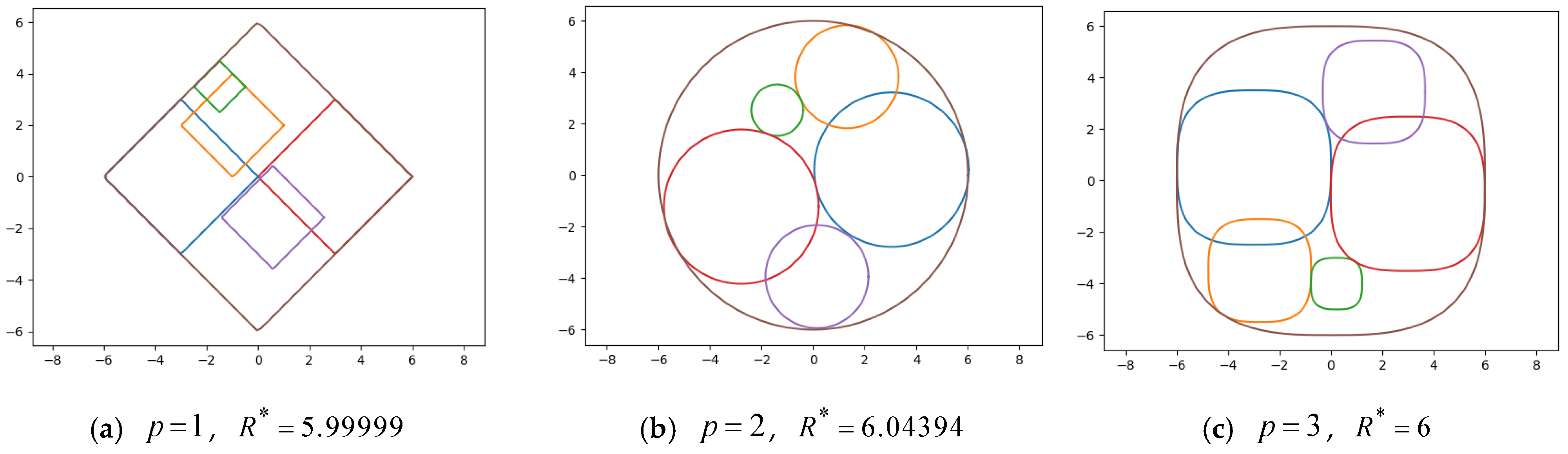
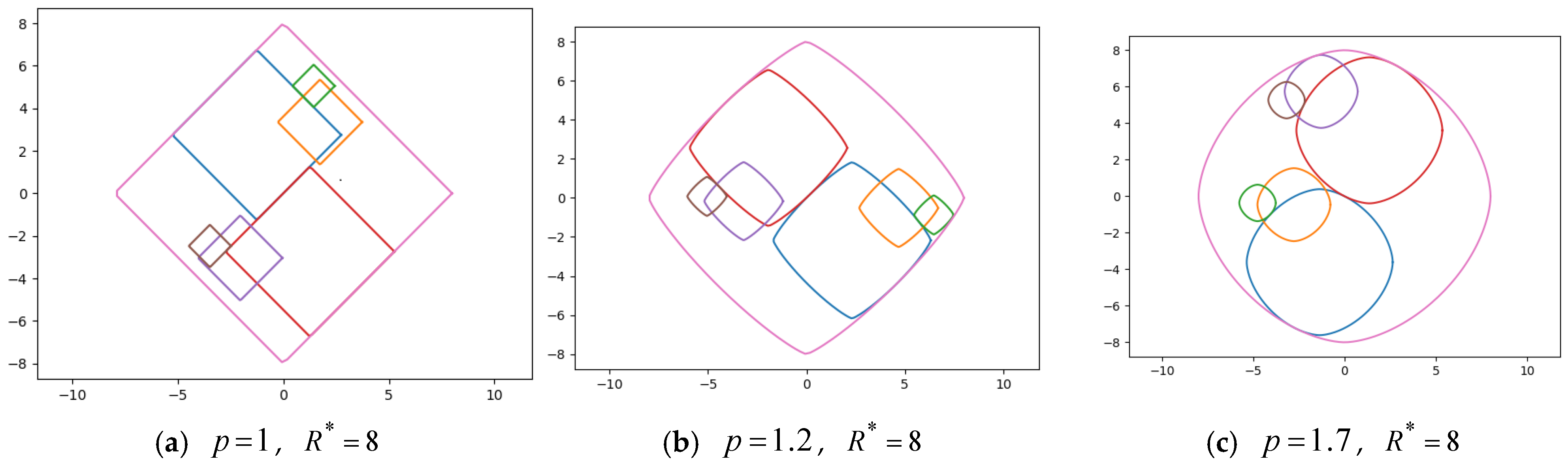
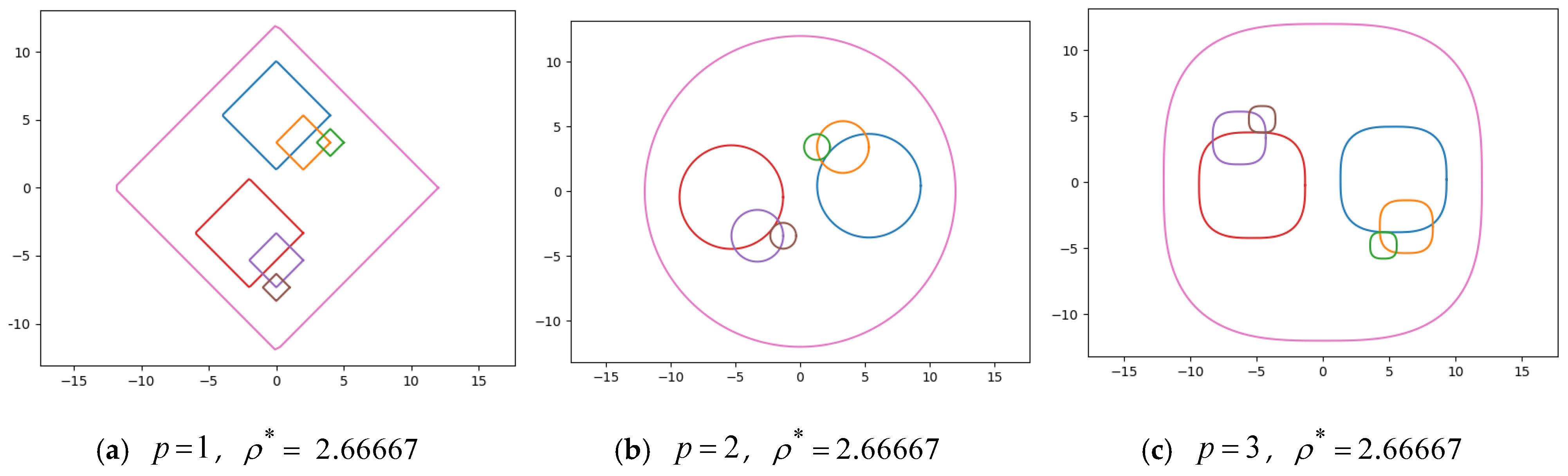
4.2. Computational Results for Generalized Homothetic Packing Problem (GHPP)
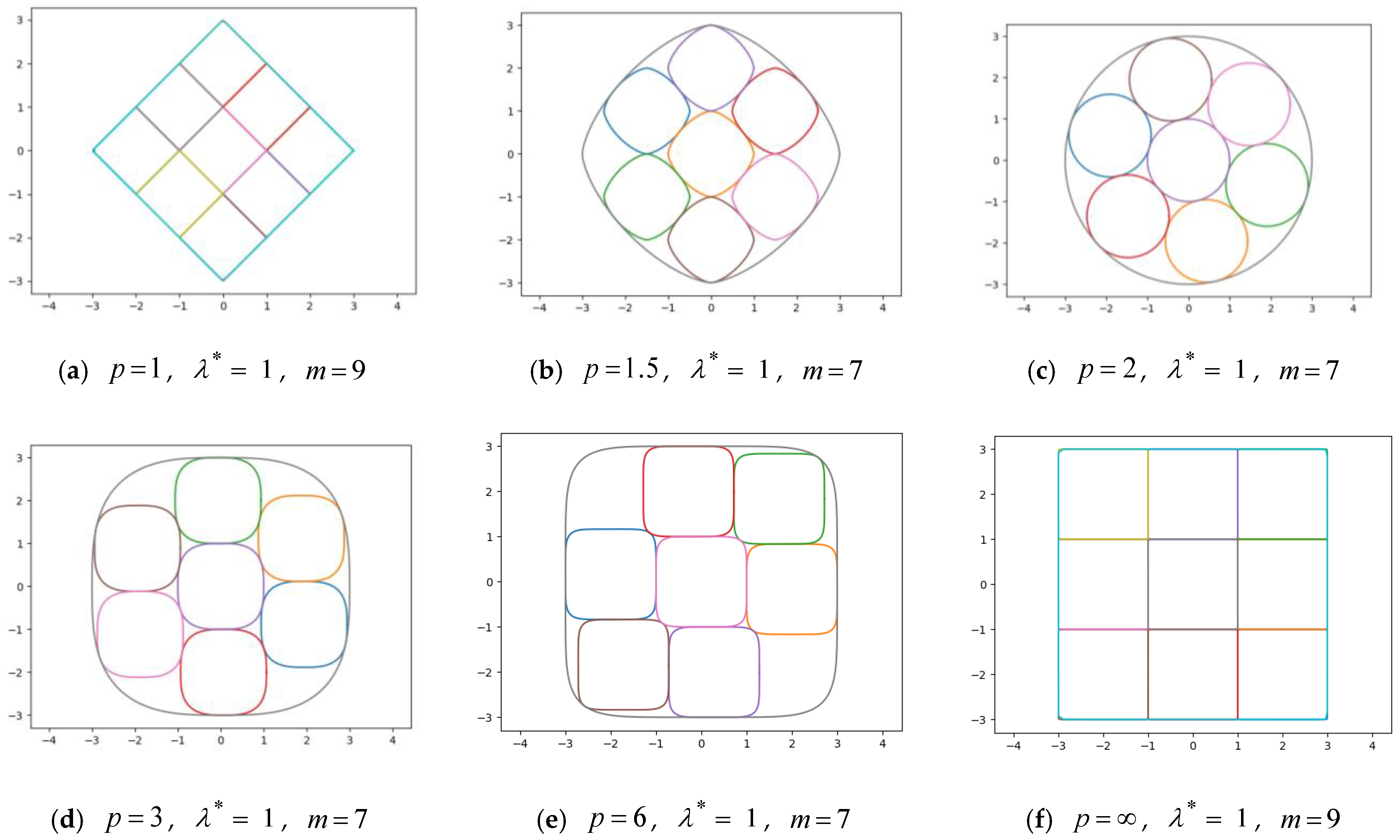
4.3. Computational Results for Generalized Sparse Packing Problem (GSPP)
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bennell, J.A.; Oliveira, J.F. The geometry of nesting problems: A tutorial. Eur. J. Oper. Res. 2008, 184, 397–415. [Google Scholar] [CrossRef]
- Bennell, J.A.; Oliveira, J.F. A tutorial in irregular shape packing problems. J. Oper. Res. Soc. 2009, 60 (Suppl. 1), 93–105. [Google Scholar] [CrossRef]
- Wang, J. Packing of unequal spheres and automated radiosurgical treatment planning. J. Comb. Optim. 1999, 3, 453–463. [Google Scholar] [CrossRef]
- Sutou, A.; Dai, Y. Global optimization approach to unequal sphere packing problems in 3D. J. Optim. Theory Appl. 2002, 114, 671–694. [Google Scholar] [CrossRef]
- Burtseva, L.; Valdez Salas, B.; Romero, R.; Werner, F. Recent advances on modelling of structures of multi-component mixtures using a sphere packing approach. Int. J. Nanotechnol. 2016, 13, 44–59. [Google Scholar] [CrossRef]
- Ma, P.; Chan, H.-K. Densest-Packed Columnar Structures of Hard Spheres: An Investigation of the Structural Dependence of Electrical Conductivity. Front. Phys. 2021, 9, 778001. [Google Scholar] [CrossRef]
- Marín-Aguilar, S.; Camerin, F.; van der Ham, S.; Feasson, A.; Vutukuri, H.R.; Dijkstra, M. A colloidal viewpoint on the sausage catastrophe and the finite sphere packing problem. Nat. Commun. 2023, 14, 7896. [Google Scholar] [CrossRef] [PubMed]
- Conway, J.H.; Sloane, N.J.A. Sphere Packings, Lattices and Groups; Springer: New York, NY, USA, 1999. [Google Scholar]
- Cullina, D.; Kiyavash, N. Generalized sphere-packing bounds on the size of codes for combinatorial channels. IEEE Trans. Inf. Theory 2016, 62, 4454–4465. [Google Scholar] [CrossRef]
- Duriagina, Z.; Lemishka, I.; Litvinchev, I.; Marmolejo, J.A.; Pankratov, A.; Romanova, T.; Yaskov, G. Optimized filling of a given cuboid with spherical powders for additive manufacturing. J. Oper. Res. Soc. China 2021, 9, 853–868. [Google Scholar] [CrossRef]
- Liu, F.; Chen, M.; Wang, L.; Luo, T.; Chen, G. Stress-field driven conformal lattice design using circle packing algorithm. Heliyon 2023, 9, e14448. [Google Scholar] [CrossRef] [PubMed]
- Castillo, I.; Kampas, F.J.; Pinter, J.D. Solving circle packing problems by global optimization: Numerical results and industrial applications. Eur. J. Oper. Res. 2008, 191, 786–802. [Google Scholar] [CrossRef]
- Chen, D. Sphere Packing Problem. In Encyclopedia of Algorithms; Kao, M.Y., Ed.; Springer: Boston, MA, USA, 2008. [Google Scholar] [CrossRef]
- Hifi, M.; M’Hallah, R. A literature review on circle and sphere packing problems: Models and methodologies. Adv. Oper. Res. 2009, 2009, 150624. [Google Scholar] [CrossRef]
- Fischer, A.; Scheithauer, G. Cutting and packing problems with placement constraints. In Optimized Packings with Applications; Fasano, G., Pintér, J.D., Eds.; Springer Optimization and Applications; Springer: Berlin/Heidelberg, Germany, 2015; Volume 105, pp. 119–156. [Google Scholar]
- Kampas, F.J.; Pintér, J.D.; Castillo, I. Packing ovals in optimized regular polygons. J. Glob. Optim. 2020, 77, 175–196. [Google Scholar] [CrossRef]
- Rao, Y.; Luo, Q. Intelligent Algorithms for Packing and Cutting Problem; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Dechant, P.-P.; Twarock, R. Models of viral capsid symmetry as a driver of discovery in virology and nanotechnology. Biochemist 2021, 43, 20–24. [Google Scholar] [CrossRef]
- Tetter, S.; Terasaka, N.; Steinauer, A.; Bingham, R.J.; Clark, S.; Scott, A.J.; Patel, N.; Leibundgut, M.; Wroblewski, E.; Ban, N.; et al. Evolution of a virus-like architecture and packaging mechanism in a repurposed bacterial protein. Science 2021, 372, 1220–1224. [Google Scholar] [CrossRef] [PubMed]
- Phua, A.; Smith, J.; Davies, C.H.J.; Cook, P.S.; Delaney, G.W. Understanding the structure and dynamics of local powder packing density variations in metal additive manufacturing using set Voronoi analysis. Powder Technol. 2023, 418, 118272. [Google Scholar] [CrossRef]
- Zhao, C.; Gao, Q.; Chen, Y.; Li, C. Application of parametric function in construction of particle shape and discrete element simulation. Powder Technol. 2021, 387, 481–493. [Google Scholar] [CrossRef]
- Soltanbeigi, B.; Podlozhnyuk, A.; Kloss, C.; Pirker, S.; Ooi, J.Y. Papanicolopulos, S.A. Influence of various DEM shape representation methods on packing and shearing of granular assemblies. Granul. Matter 2021, 23, 26. [Google Scholar] [CrossRef]
- Ma, H.; Xia, X.; Zhou, L.; Xu, C.; Liu, Z.; Song, T.; Zou, G.; Liu, Y.; Huang, Z.; Liao, X.; et al. A comparative study of the performance of different particle models in simulating particle charging and burden distribution in a blast furnace within the DEM framework. Energies 2023, 16, 3890. [Google Scholar] [CrossRef]
- Leao, A.A.S.; Toledo, F.M.B.; Oliveira, J.F.; Carravilla, M.A.; Alvarez-Valdes, R. Irregular packing problems: A review of mathematical models. Eur. J. Oper. Res. 2020, 282, 803–822. [Google Scholar] [CrossRef]
- Labrada-Nueva, Y.; Cruz-Rosales, M.H.; Rendón-Mancha, J.M.; Rivera-López, R.; Eraña-Díaz, M.L.; Cruz-Chávez, M.A. Overlap Detection in 2D Amorphous Shapes for Paper Optimization in Digital Printing Presses. Mathematics 2021, 9, 1033. [Google Scholar] [CrossRef]
- Guo, B.; Zhang, Y.; Hu, J.; Li, J.; Wu, F.; Peng, Q.; Zhang, Q. Two-dimensional irregular packing problems: A review. Front. Mech. Eng. 2022, 8, 966691. [Google Scholar] [CrossRef]
- Luo, Q.; Rao, Y. Improved Sliding Algorithm for Generating No-Fit Polygon in the 2D Irregular Packing Problem. Mathematics 2022, 10, 2941. [Google Scholar] [CrossRef]
- Fang, J.; Rao, Y.; Zhao, X.; Dum, B. A Hybrid Reinforcement Learning Algorithm for 2D Irregular Packing Problems. Mathematics 2023, 11, 327. [Google Scholar] [CrossRef]
- Fasano, G. Solving Non-Standard Packing Problems by Global Optimization and Heuristics; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Adler, J.R.; Schweikard, A.; Achkire, Y.; Blanck, O.; Bodduluri, M.; Ma, L.; Zhang, H. Treatment Planning for Self-Shielded Radiosurgery. Cureus 2017, 9, e1663. [Google Scholar] [CrossRef] [PubMed]
- Boles, M.A.; Talapin, D.V. Many-Body Effects in Nanocrystal Superlattices: Departure from Sphere Packing Explains Stability of Binary Phases. J. Am. Chem. Soc. 2015, 137, 4494–4502. [Google Scholar] [CrossRef]
- Banhelyi, B.; Palatinus, E.; Levai, B.L. Optimal circle covering problems and their applications. Cent. Eur. J. Oper. Res. 2015, 23, 815–832. [Google Scholar] [CrossRef]
- Romanova, T.; Litvinchev, I.; Pankratov, A. Packing ellipsoids in an optimized cylinder. Eur. J. Oper. Res. 2020, 285, 429–443. [Google Scholar] [CrossRef]
- Prvan, M.; Ozegovic, J.; Misura, A.B. On calculating the packing efficiency for embedding hexagonal and dodecagonal sensors in a circular container. Math. Probl. Eng. 2019, 2019, 9624751. [Google Scholar] [CrossRef]
- Arruda, V.P.R.; Mirisola, L.G.B.; Soma, N.Y. Almost squaring the square: Optimal packings for non-decomposable squares. Pesqui. Oper. 2022, 42, e262876. [Google Scholar] [CrossRef]
- Litvinchev, I.; Infante, L.; Ozuna, L. Approximate Packing: Integer Programming Models, Valid Inequalities and Nesting; Springer Optimization and Its Applications; Springer: Cham, Switzerland, 2015; Volume 105, pp. 117–135. [Google Scholar]
- Litvinchev, I.; Infante, L.; Ozuna, L. Packing circular-like objects in a rectangular container. J. Comput. Syst. Sci. Int. 2015, 54, 259–267. [Google Scholar] [CrossRef]
- Litvinchev, I.; Infante, L.; Ozuna, L. Using different norms in packing circular objects. In Intelligent Information and Database Systems; Nguyen, N.T., Trawineski, B., Kosala, R., Eds.; Springer: Cham, Switzerland, 2015; pp. 540–548. [Google Scholar]
- Narici, L.; Beckenstein, E. Topological Vector Spaces. In Pure and applied mathematics, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Khajavirad, A.; Sahinidis, N.V. A hybrid LP/NLP paradigm for global optimization relaxations. Math. Program. Comput. 2018, 10, 383–421. [Google Scholar] [CrossRef]
- Sahinidis, N. BARON User Manual v. 2024.3.10. Available online: https://minlp.com/downloads/docs/baron%20manual.pdf (accessed on 11 March 2024).
- Tawarmalani, M.; Sahinidis, N.V. A polyhedral branch-and-cut approach to global optimization. Math. Program. 2005, 103, 225–249. [Google Scholar] [CrossRef]
- Fourer, R.; Gay, D.M.; Kernighan, B. AMPL: A Modeling Language for Mathematical Programming, 2nd ed.; Duxbury: Thomson, Georgia, 2003. [Google Scholar]
- Stetsyuk, P.; Romanova, T.; Scheithauer, G. On the global minimum in a balanced circular packing problem. Optim. Lett. 2016, 10, 1347–1360. [Google Scholar] [CrossRef]
- Kallrath, J. Cutting and Packing Beyond and within Mathematical Programming. In Business Optimization Using Mathematical Programming; International Series in Operations Research & Management Science; Springer: Cham, Switzerland, 2021; Volume 307. [Google Scholar] [CrossRef]
- Yagiura, M.; Umetani, S.; Imahori, S. Cutting and Packing Problems: From the Perspective of Combinatorial Optimization; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Scheithauer, G. Introduction to Cutting and Packing Optimization: Problems, Modeling Approaches, Solution Methods; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Lai, X.; Hao, J.K.; Xiao, R.; Glover, F. Perturbation-based thresholding search for packing equal circles and spheres. INFORMS J. Comput. 2023, 35, 711–908. [Google Scholar] [CrossRef]
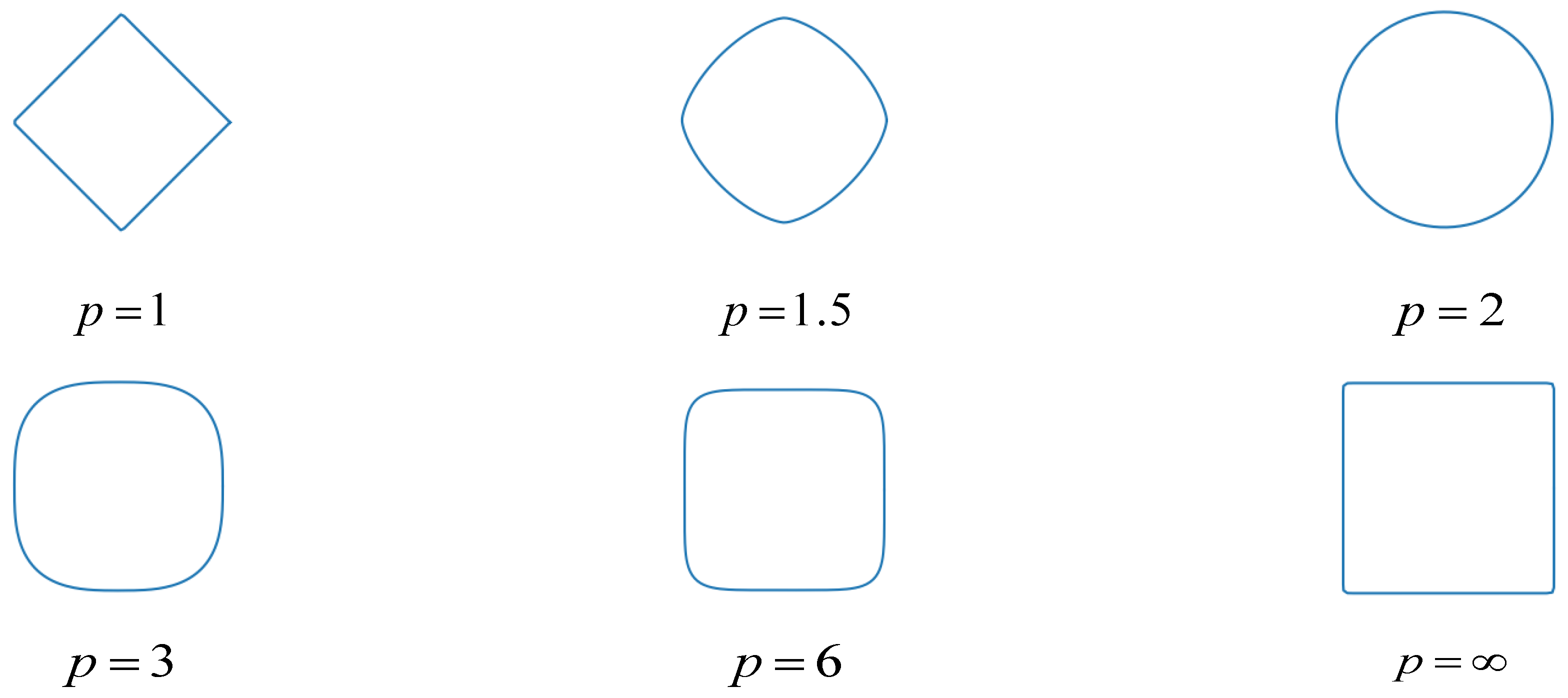

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Litvinchev, I.; Fischer, A.; Romanova, T.; Stetsyuk, P. A New Class of Irregular Packing Problems Reducible to Sphere Packing in Arbitrary Norms. Mathematics 2024, 12, 935. https://doi.org/10.3390/math12070935
Litvinchev I, Fischer A, Romanova T, Stetsyuk P. A New Class of Irregular Packing Problems Reducible to Sphere Packing in Arbitrary Norms. Mathematics. 2024; 12(7):935. https://doi.org/10.3390/math12070935
Chicago/Turabian StyleLitvinchev, Igor, Andreas Fischer, Tetyana Romanova, and Petro Stetsyuk. 2024. "A New Class of Irregular Packing Problems Reducible to Sphere Packing in Arbitrary Norms" Mathematics 12, no. 7: 935. https://doi.org/10.3390/math12070935
APA StyleLitvinchev, I., Fischer, A., Romanova, T., & Stetsyuk, P. (2024). A New Class of Irregular Packing Problems Reducible to Sphere Packing in Arbitrary Norms. Mathematics, 12(7), 935. https://doi.org/10.3390/math12070935








