Adaptive Fuzzy Backstepping Control for Itô-Type Nonlinear Switched Systems Subject to Unknown Hysteresis Input
Abstract
1. Introduction and Related Work
1.1. Introduction
1.2. Related Work
2. Problem Statement and Preliminaries
2.1. Problem Formulation
2.2. Problem Formulation
3. Adaptive Fuzzy Tracking Control Design
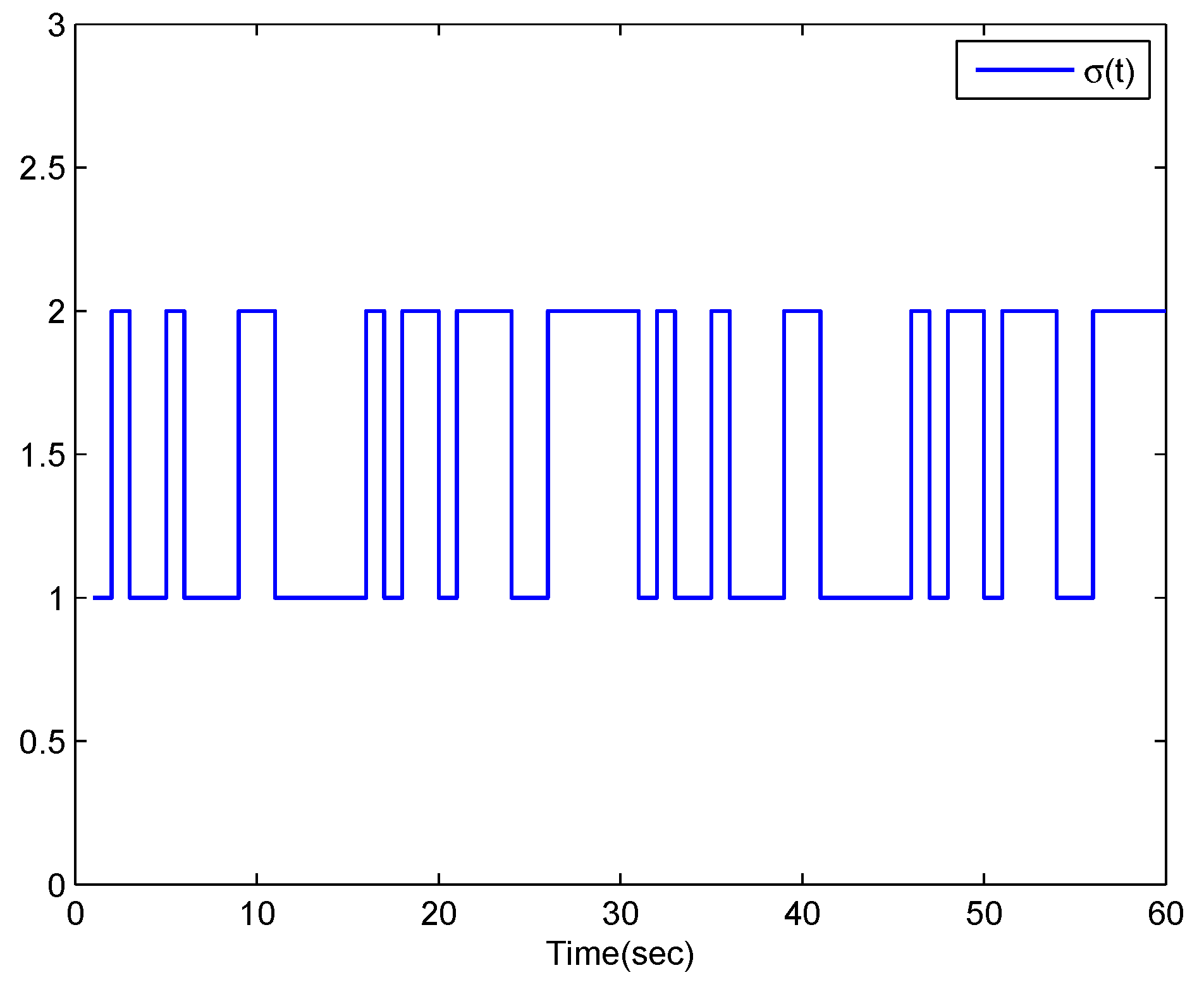
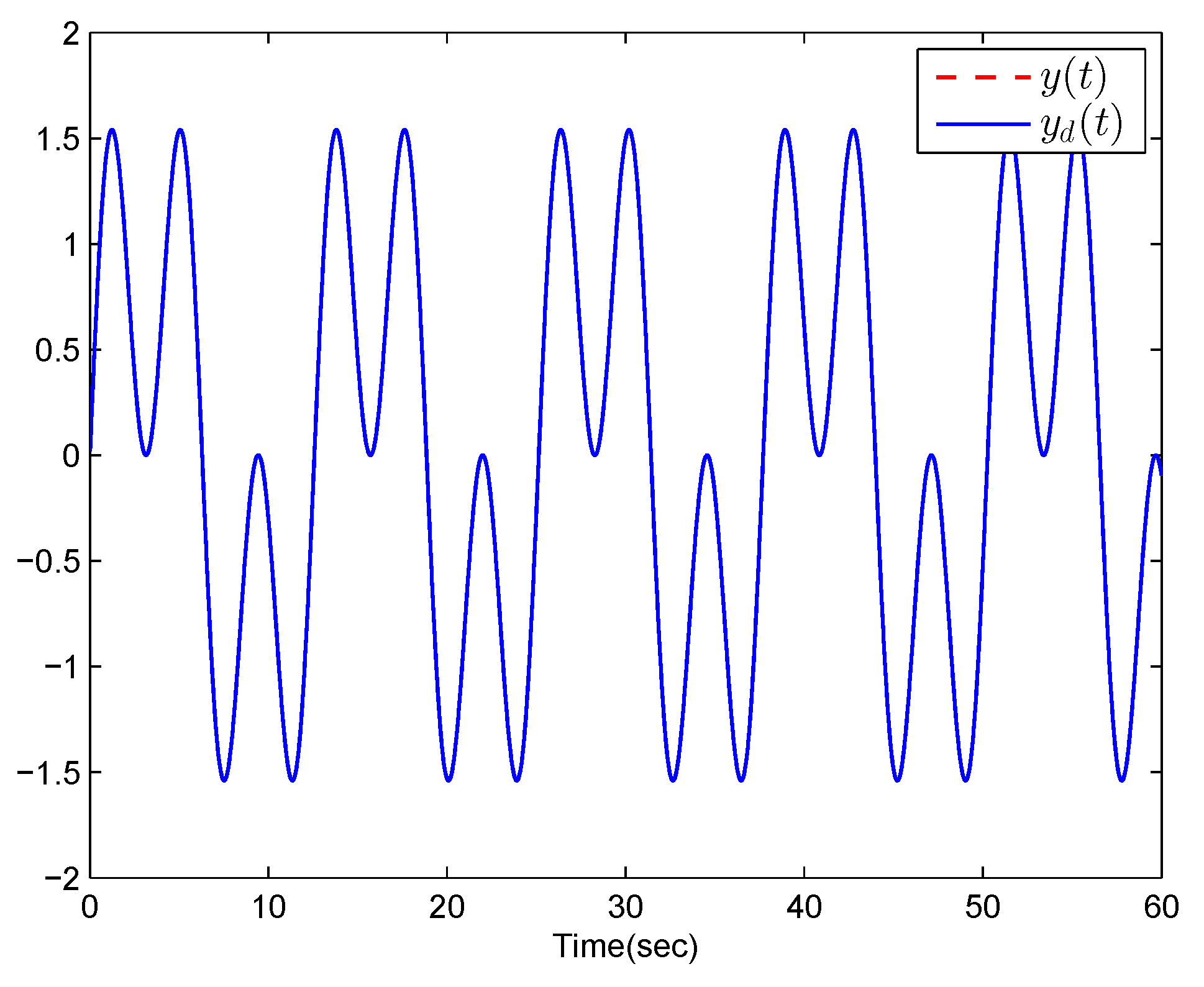
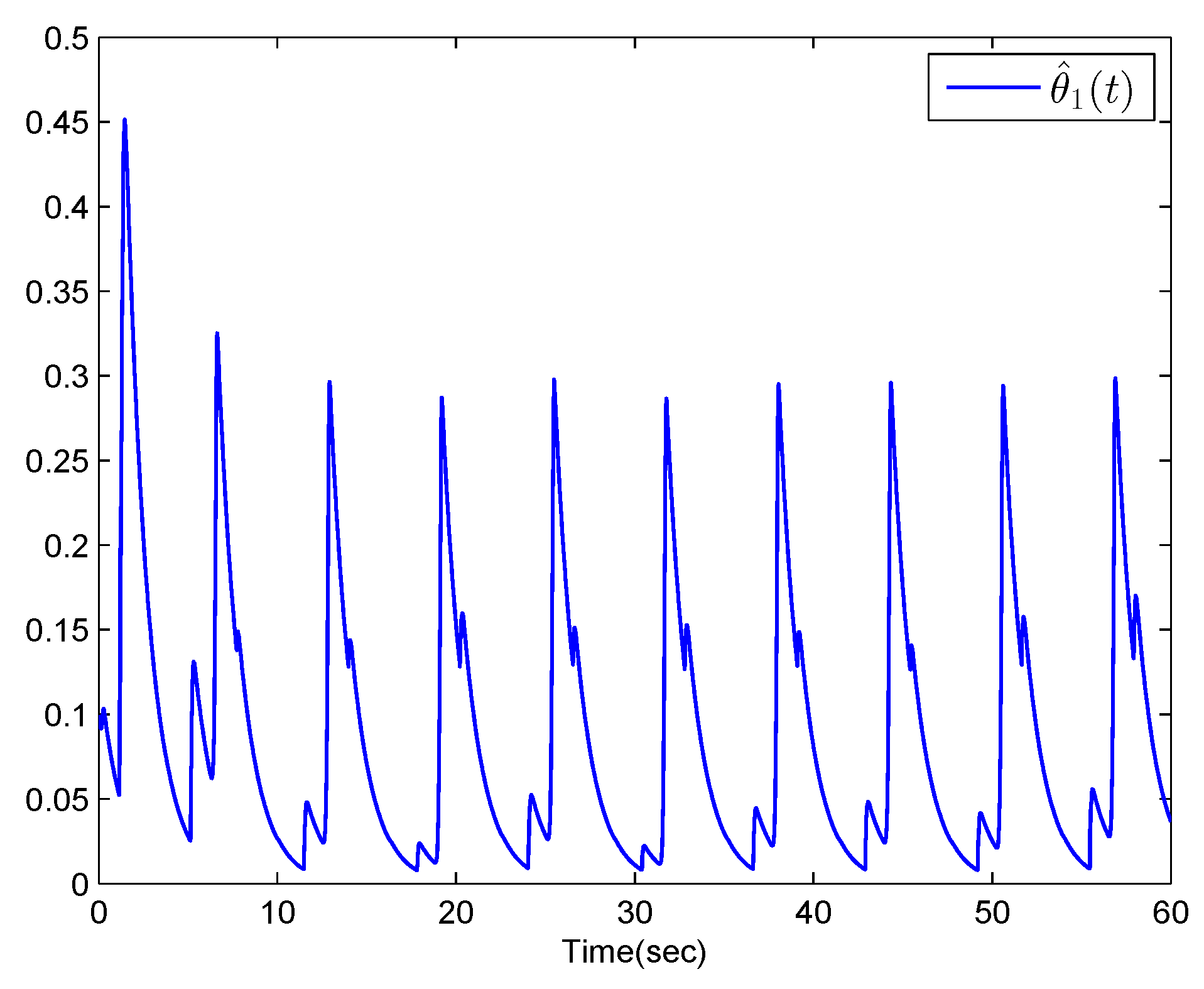
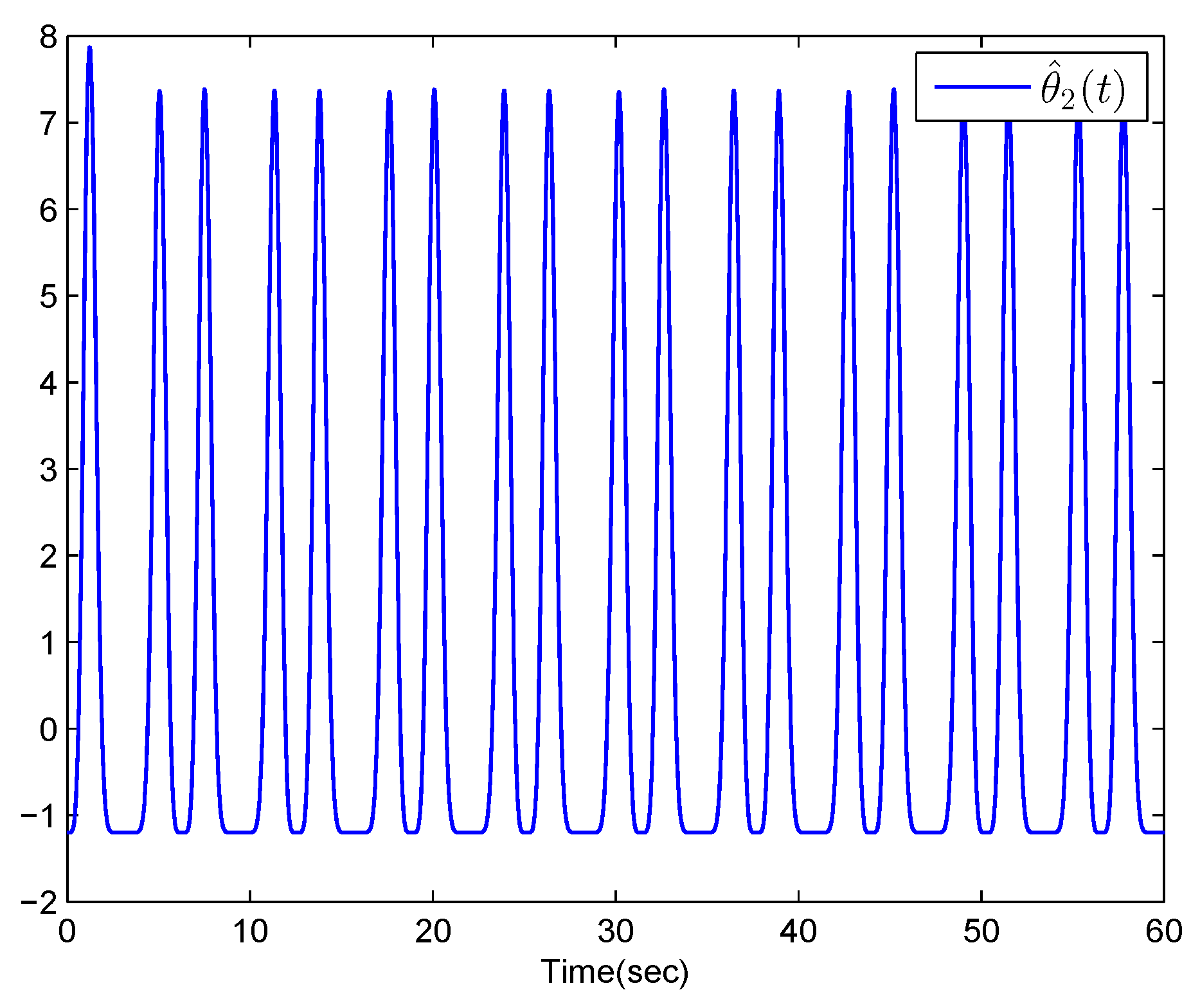
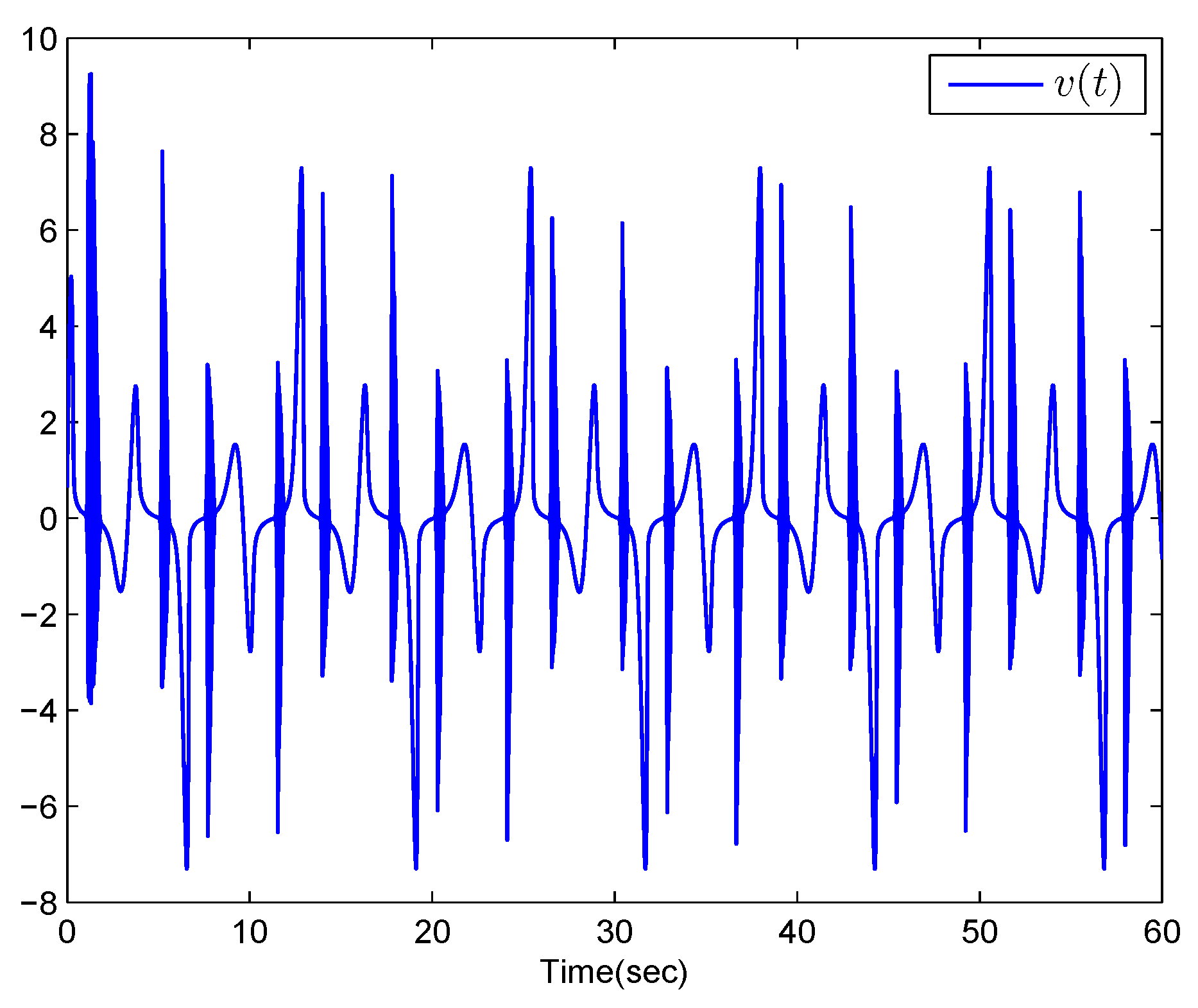
4. Numerical Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Z.; Wen, C.; Soh, Y. Switched controllers and their applications in bilinear systems. Automatica 2001, 37, 477–481. [Google Scholar] [CrossRef]
- Homaee, O.; Zakariazadeh, A.; Jadid, S. Real-time voltage control algorithm with switched capacitors in smart distribution system in presence of renewable generations. Int. J. Electr. Power 2014, 54, 187–197. [Google Scholar] [CrossRef]
- Jeon, D.; Tomizuka, M. Learning hybrid force and position control of robot manipulators. IEEE Trans. Robot. Autom. 1993, 9, 423–431. [Google Scholar] [CrossRef]
- Zhao, J.; Hill, D.; Liu, T. Synchronization of complex dynamical networks with switching topology: A switched system point of view. Automatica 2009, 45, 2502–2511. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, B.; Lin, C. Fuzzy adaptive fuzzy output-feedback tracking control for nonlinear strict-feedback systems in prescribed finite time. J. Frankl. Inst. 2021, 358, 7309–7332. [Google Scholar] [CrossRef]
- Zhao, D.; Ouyang, X.; Zhao, N.; Zhang, F. Event-triggered low-computation adaptive output-feedback fuzzy tracking control of uncertain nonlinear systems. ISA Trans. 2023, 144, 86–95. [Google Scholar] [CrossRef]
- Zhao, X.; Zheng, X.; Niu, B.; Liu, L. Adaptive tracking control for a class of uncertain switched nonlinear systems. Automatica 2015, 52, 185–191. [Google Scholar] [CrossRef]
- Xiong, Y.; Wu, Y.; Li, S.; Xiang, Z. Adaptive fuzzy output feedback fault-tolerant tracking control of switched uncertain nonlinear systems with sensor faults. J. Frankl. Inst. 2021, 358, 5771–5794. [Google Scholar] [CrossRef]
- Zhang, L.; Zhuang, S.; Shi, P. Non-weighted quasi-time-dependent H∞ filtering for switched linear systems with persistent dwell-time. Automatica 2015, 54, 201–209. [Google Scholar] [CrossRef]
- Zeng, D.; Liu, Z.; Chen, C.; Zhang, T. Event-triggered fuzzy adaptive control of nonlinear switched systems with predefined accuracy and mismatched switching. Fuzzy Set Syst. 2022, 443, 283–307. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, G.; Wu, L. Command filter-based adaptive fuzzy switching event-triggered control for non-affine nonlinear systems with actuator faults. Inf. Sci. 2023, 638, 118991. [Google Scholar] [CrossRef]
- Zhao, J.; Hill, D. On stability, L2-gain and H∞ control for switched systems. Automatica 2008, 44, 1220–1232. [Google Scholar] [CrossRef]
- Muller, M.; Liberzon, D. Input/output-to-state stability and state-norm estimators for switched nonlinear systems. Automatica 2012, 48, 2029–2039. [Google Scholar] [CrossRef]
- Lin, H.; Antsaklis, P. Stability and stabilizability of switched linear systems: A survey of recent results. IEEE Trans. Autom. Control 2009, 54, 308–322. [Google Scholar] [CrossRef]
- Komurcugil, H.; Ozdemir, S.; Sefa, I.; Altin, N.; Kukrer, O. Sliding-mode control for single-phase grid-connected LCL-filtered vsi with double-band hysteresis scheme. IEEE Trans. Ind. Electron. 2016, 63, 864–873. [Google Scholar] [CrossRef]
- Tan, X.; Baras, J. Modeling and control of hysteresis in magnestrictive actuators. Automatica 2004, 40, 1469–1480. [Google Scholar] [CrossRef]
- Wen, C.; Zhou, J. Decentralized adaptive stabilization in the presence of unknown backlash-like hysteresis. Automatica 2007, 43, 426–440. [Google Scholar] [CrossRef]
- Chen, G.; Dong, J. Approximate optimal adaptive prescribed performance control for uncertain nonlinear systems with feature information. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 2298–2308. [Google Scholar] [CrossRef]
- Ebeigbe, D.; Nguyen, T.; Richter, H.; Simon, D. Robust Regressor-free control of rigid robots using function approximations. IEEE Trans. Control Syst. Technol. 2020, 28, 1433–1446. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, G.; Li, Q.; Ahn, G. Multiple adaptive fuzzy Nussbaum-type functions design for stochastic nonlinear systems with fixed-time performance. Fuzzy Set Syst. 2024, 476, 108767. [Google Scholar] [CrossRef]
- Oksendal, B. Stochastic Differential Equations: An Introduction with Applications, 5th ed.; Springer: New York, NY, USA, 2000. [Google Scholar] [CrossRef]
- Yu, Z.; Li, S.; Yu, Z.; Li, F. Adaptive neural output feedback control for nonstrict-feedback stochastic nonlinear systems with unknown backlash-like hysteresis and unknown control directions. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 1147–1160. [Google Scholar] [CrossRef]
- Wang, F.; Liu, Z.; Zhang, Y.; Chen, C. Adaptive fuzzy control for a class of stochastic pure-feedback nonlinear systems with unknown hysteresis. IEEE Trans. Fuzzy. Syst. 2016, 24, 140–152. [Google Scholar] [CrossRef]
- Deng, H.; Krstic, M. Output-feedback stochastic nonlinear stabilization. IEEE Trans. Autom. Control 1999, 44, 328–333. [Google Scholar] [CrossRef]
- Deng, H.; Krstic, M. Output-feedback stabilization of stochastic nonlinear systems driven by noise of unknown covariance. Syst. Control Lett. 2000, 39, 173–182. [Google Scholar] [CrossRef]
- Feng, G. A survey on analysis and design of model-based fuzzy control systems. IEEE Trans. Fuzzy Syst. 2006, 14, 676–697. [Google Scholar] [CrossRef]
- Li, D.; Dong, J. Fuzzy control based on reinforcement learning and subsystem error derivatives for strict-feedback systems with an observer. IEEE Trans. Fuzzy Syst. 2023, 31, 2509–2521. [Google Scholar] [CrossRef]
- Namadchian, Z.; Rouhani, M. Adaptive prescribed performance neural network control for switched stochastic pure-feedback systems with unknown hysteresis. Neurocomputing 2021, 429, 151–165. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, L.; Niu, B.; Zhao, X.; Ahmad, A. Adaptive neural finite-time hierarchical sliding mode control of uncertain under-actuated switched nonlinear systems with backlash-like hysteresis. Inf. Sci. 2022, 599, 147–169. [Google Scholar] [CrossRef]
- Xu, S.; Wang, Z.; Fan, X.; Xiong, B. Experimental investigations of hypersonic inlet unstart/restart process and hysteresis phenomenon caused by angle of attack. Aerosp. Sci. Technol. 2023, 126, 107621. [Google Scholar] [CrossRef]
- Hao, S.; Pan, Y.; Zhu, Y.; Cao, L. Event-based adaptive tracking control for robotic systems with deferred position constraints and unknown backlash-like hysteresis. ISA Trans. 2023, 142, 289–298. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, M.; Nie, L.; Zhang, X.; Su, C. Prandtl-Ishlinskii model based event-triggered prescribed control: Design and application to piezoelectric-driven micropositioning stage. Mech. Syst. Signal Process. 2023, 200, 110562. [Google Scholar] [CrossRef]
- Mayergoyz, I. The Preisach Model for Hysteresis; Springer: Berlin, Germany, 1991. [Google Scholar]
- Wang, G.; Chen, G. Identification of piezoelectric hysteresis by a novel Duhem model based neural network. Sens. Actuators A Phys. 2017, 264, 282–288. [Google Scholar] [CrossRef]
- Ibrir, S.; Su, C. Adaptive stabilization of a class of feedforward nonlinear systems subject to unknown backlash-hysteresis inputs. IEEE Trans. Control Syst. Technol. 2017, 25, 1180–1192. [Google Scholar] [CrossRef]
- Chen, X.; Li, S.; Wang, R.; Xiang, Z. Event-Triggered output feedback adaptive control for nonlinear switched interconnected systems with unknown control coefficients. Appl. Math. Comput. 2023, 445, 127854. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, Z.; He, W.; Hong, K.; Li, H. Boundary adaptive fault-tolerant control for a flexible Timoshenko arm with backlash-like hysteresis. Automatica 2021, 130, 109690. [Google Scholar] [CrossRef]
- Zhu, Z.; Pan, Y.; Zhou, Q.; Lu, C. Event-triggered adaptive fuzzy control for stochastic nonlinear systems with unmeasured states and unknown backlash-like hysteresis. IEEE Trans. Fuzzy Syst. 2021, 29, 1273–1283. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, J.; Liu, Z.; Mu, C.; Hong, K. Adaptive neural network control of an uncertain 2-DOF helicopter with unknown backlash-like hysteresis and output constraints. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 10018–10027. [Google Scholar] [CrossRef]
- Fu, C.; Wang, Q.; Yu, J.; Lin, C. Neural network-based finite-time command filtering control for switched nonlinear systems with backlash-like hysteresis. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 3268–3273. [Google Scholar] [CrossRef] [PubMed]
- Ji, H.; Xi, H. Adaptive output-feedback tracking of stochastic nonlinear systems. IEEE Trans. Autom. Control 2006, 51, 355–360. [Google Scholar] [CrossRef]
- Deng, H.; Kristic, M. Stochastic nonlinear stabilization-I: A backstepping design. Syst. Control Lett. 1997, 32, 143–150. [Google Scholar] [CrossRef]
- Zhou, J.; Wen, C.; Li, T. Adaptive output feedback control of uncertain nonlinear systems with hysteresis nonlinearity. IEEE Trans. Autom. Control. 2012, 57, 2627–2633. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. 1985, 15, 116–132. [Google Scholar] [CrossRef]
- Niu, B.; Qin, T.; Fan, X. Adaptive neural network tracking control for a class of switched stochastic pure-feedback nonlinear systems with backlash-like hysteresis. Int. J. Syst. Sci. 2016, 47, 3378–3393. [Google Scholar] [CrossRef]










Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, X.; Li, Y. Adaptive Fuzzy Backstepping Control for Itô-Type Nonlinear Switched Systems Subject to Unknown Hysteresis Input. Mathematics 2024, 12, 1070. https://doi.org/10.3390/math12071070
Wan X, Li Y. Adaptive Fuzzy Backstepping Control for Itô-Type Nonlinear Switched Systems Subject to Unknown Hysteresis Input. Mathematics. 2024; 12(7):1070. https://doi.org/10.3390/math12071070
Chicago/Turabian StyleWan, Xiaohe, and Yan Li. 2024. "Adaptive Fuzzy Backstepping Control for Itô-Type Nonlinear Switched Systems Subject to Unknown Hysteresis Input" Mathematics 12, no. 7: 1070. https://doi.org/10.3390/math12071070
APA StyleWan, X., & Li, Y. (2024). Adaptive Fuzzy Backstepping Control for Itô-Type Nonlinear Switched Systems Subject to Unknown Hysteresis Input. Mathematics, 12(7), 1070. https://doi.org/10.3390/math12071070





