An IT2FS-ANP- and IT2FS-CM-Based Approach for Conducting Safety Risk Assessments of Nuclear Power Plant Building Projects
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Literature Review
1.3. Research Objective and Novel Contributions
2. Materials and Methods
2.1. Definitions of the IT2FS-ANP and IT2FS-CM Methods
2.1.1. IT2FS
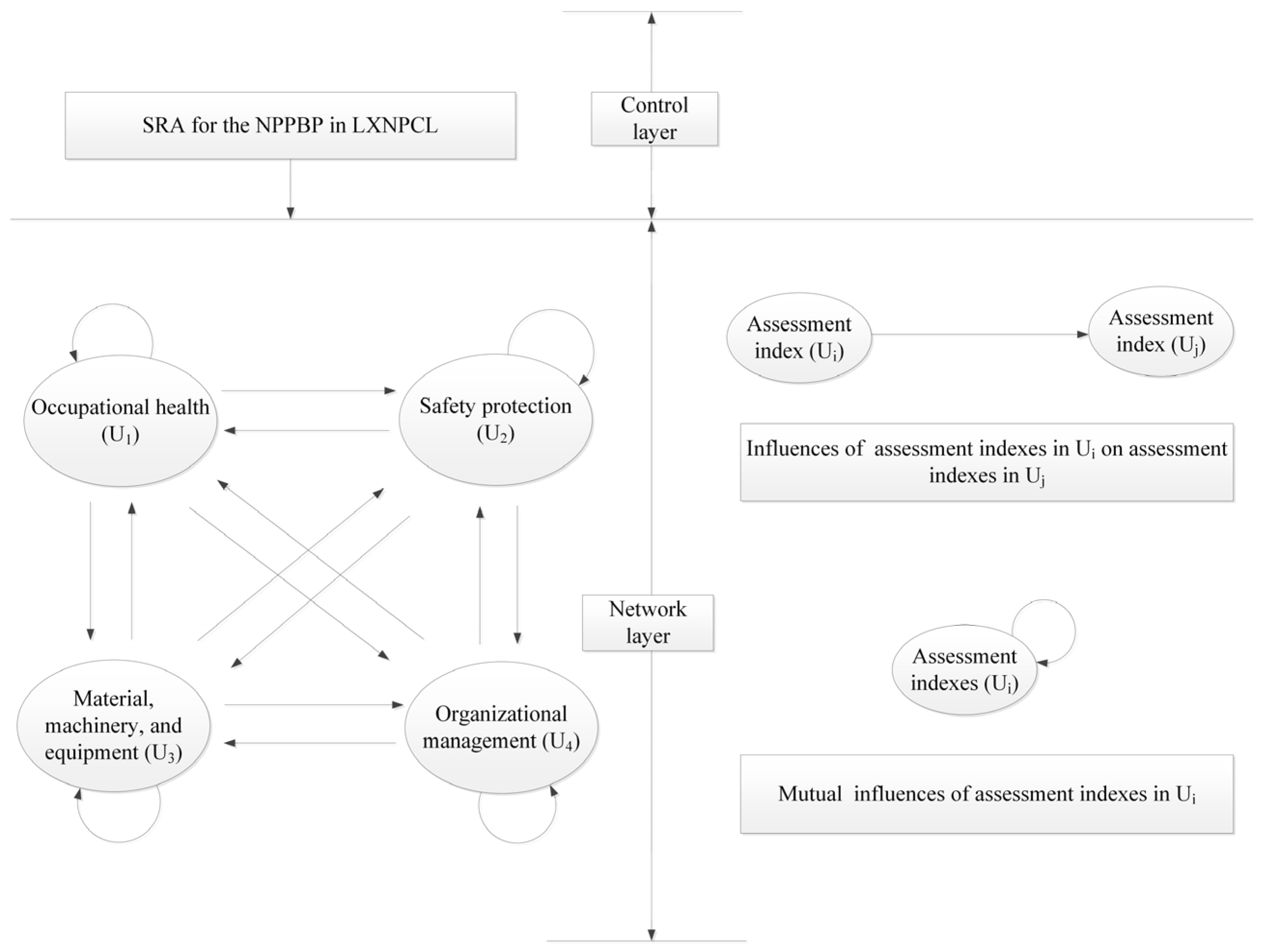
2.1.2. IT2FS-ANP
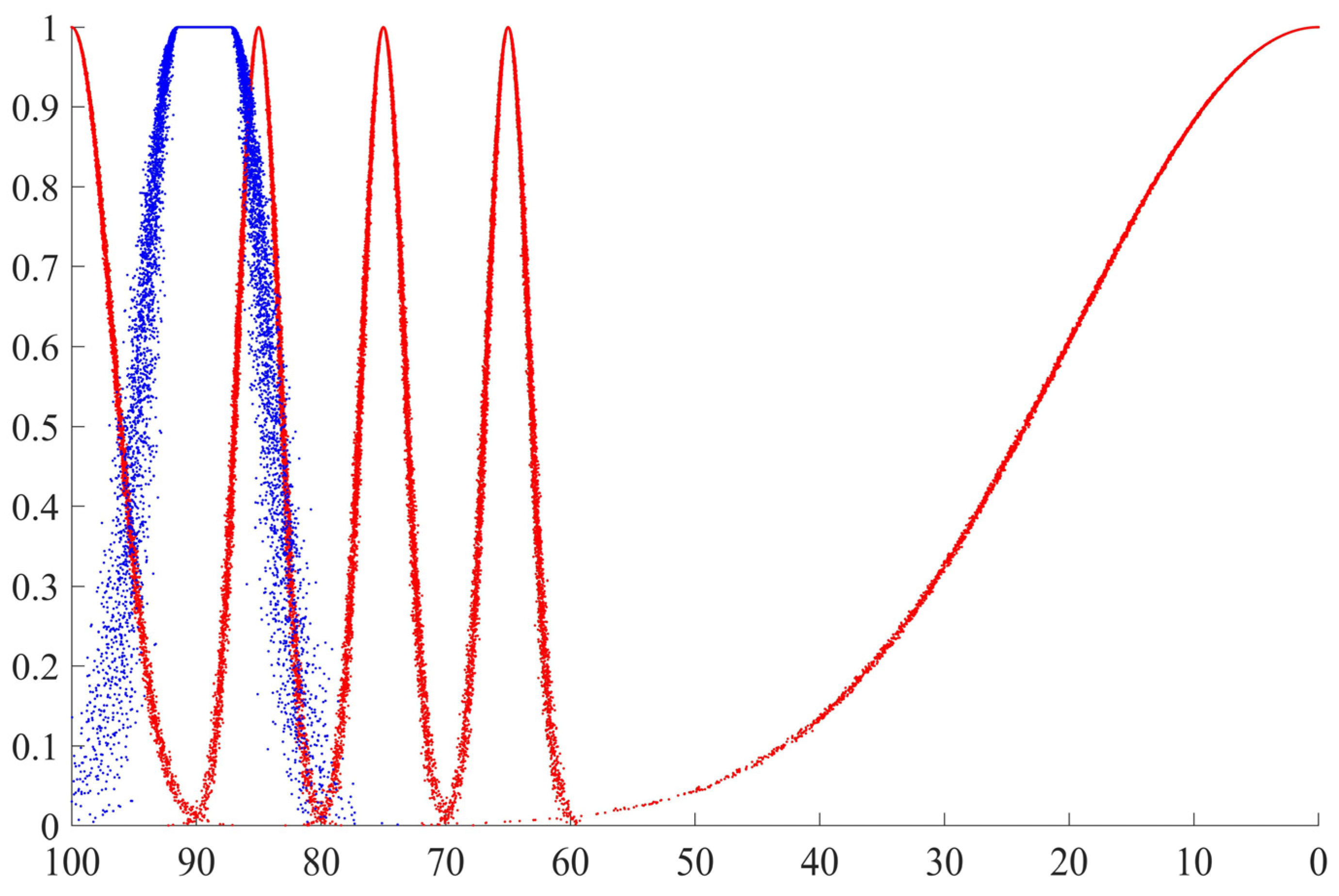
2.1.3. IT2FS-CM
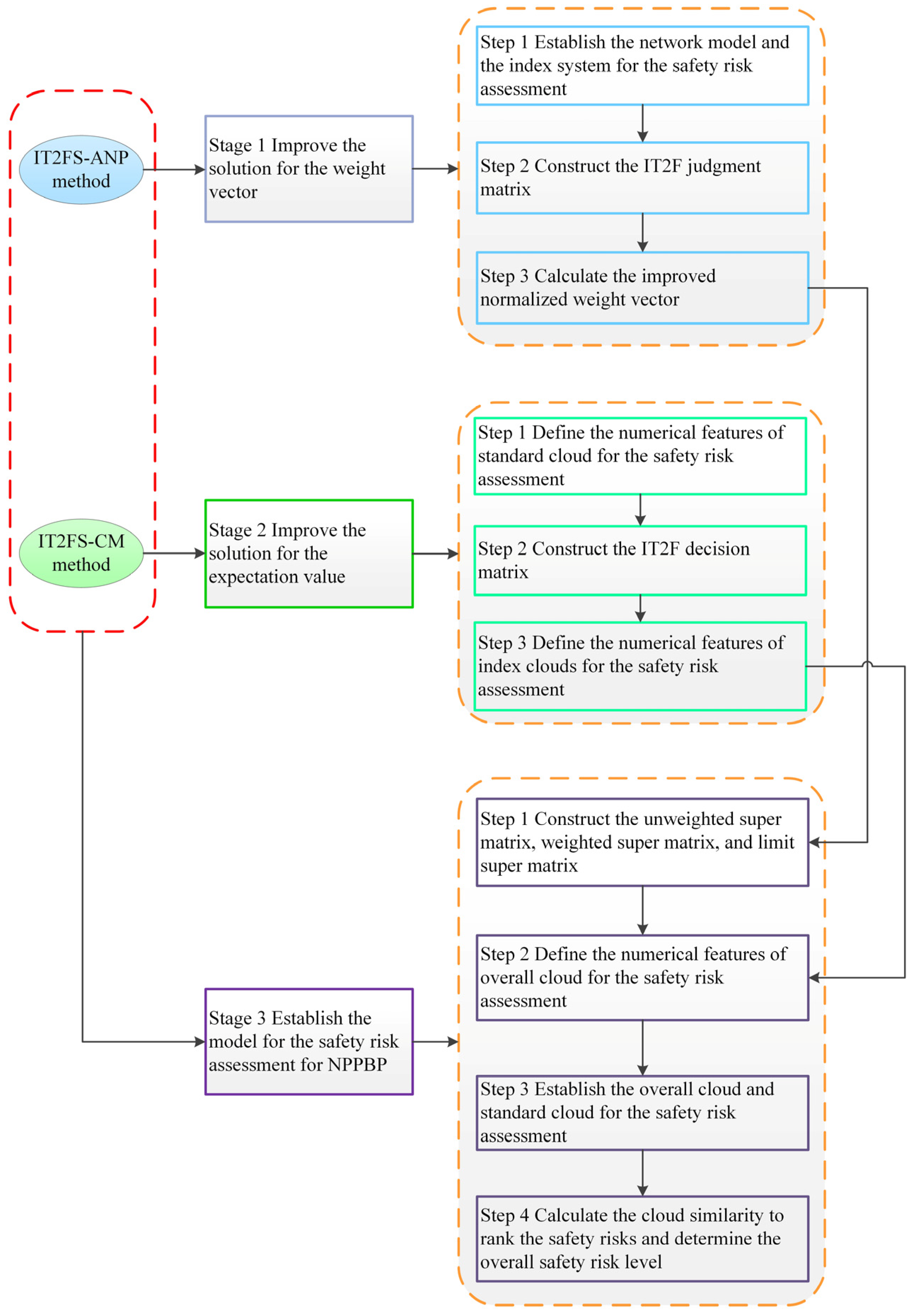
2.2. The IT2FS-ANP- and IT2FS-CM-Based Approach
2.2.1. Theoretical Framework
2.2.2. Stages of SRA
- (1)
- Use En0 as the mathematical expectation and He0 as the standard deviation in a normal distribution and calculate the normal random number yi.
- (2)
- Use as the mathematical expectation and yi as the standard deviation in a normal distribution and calculate the normal random number ai.
- (3)
- Calculate .
- (4)
- Repeat the above procedures (1)–(3) until N cloud droplets are generated.
- (1)
- Use as the mathematical expectation and as the variance in a normal distribution to calculate the normal random number zj.
- (2)
- Use as the mathematical expectation and as the variance in a normal distribution to calculate the normal random number kj.
- (3)
- Calculate .
- (4)
- Repeat the above procedures until N cloud droplets are generated.
- (5)
- Use to calculate the similarity between the overall cloud and the outstanding level cloud.
3. Application of the Approach
3.1. Case Description
3.2. Conducting the SRA
4. Results and Discussion
4.1. Comparison to the Traditional Method
- (1)
- The IT2FS-ANP method was compared with the traditional ANP method.
- (2)
- The IT2FS-CM method was compared with the traditional CM method.
4.2. Analysis of Assessment Results
4.3. Analysis of Assessment Results
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sui, Y.; Ding, R.; Wang, H. A novel approach for occupational health and safety and environment risk assessment for nuclear power plant construction project. J. Clean. Prod. 2020, 258, 120945. [Google Scholar] [CrossRef]
- Lu, W.; Huang, G.Q.; Li, H. Scenarios for applying RFID technology in construction project management. Autom. Constr. 2011, 20, 101–106. [Google Scholar] [CrossRef]
- Zou, P.X.W.; Zhang, G. Managing risks in construction projects: Life cycle and stakeholder perspectives. Int. J. Constr. Manag. 2009, 9, 61–77. [Google Scholar] [CrossRef]
- Ding, L.Y.; Zhou, C. Development of web-based system for safety risk early warning in urban metro construction. Autom. Constr. 2013, 34, 45–55. [Google Scholar] [CrossRef]
- Naghshbandi, S.N.; Varga, L.; Hu, Y. Technologies for safe and resilient earthmoving operations: A systematic literature review. Autom. Constr. 2021, 125, 103632. [Google Scholar] [CrossRef]
- Bavafa, A.; Mahdiyar, A.; Marsono, A.K. Identifying and assessing the critical factors for effective implementation of safety programs in construction projects. Saf. Sci. 2018, 106, 47–56. [Google Scholar] [CrossRef]
- Liu, R.; Mou, X.; Liu, H.C. Occupational health and safety risk assessment based on combination weighting and uncertain linguistic information: Method development and application to a construction project. IISE Trans. Occup. Ergon. Hum. Factors 2021, 8, 175–186. [Google Scholar] [CrossRef] [PubMed]
- Alkaissy, M.; Arashpour, M.; Rashidi, A.; Mohandes, S.R.; Farnood, P. Simulation-based analysis of occupational health and safety continuous improvement (OHSCI) in modern construction and infrastructure industries. Autom. Constr. 2021, 134, 104058. [Google Scholar] [CrossRef]
- Gul, M.; Ak, M.F.; Guneri, A.F. Occupational health and safety risk assessment in hospitals: A case study using two-stage fuzzy multi-criteria approach. Hum. Ecol. Risk Assess. Int. J. 2017, 23, 187–202. [Google Scholar] [CrossRef]
- Koc, K.; Ekmekcioğlu, Ö.; Gurgun, A.P. Accident prediction in construction using hybrid wavelet-machine learning. Autom. Constr. 2022, 133, 103987. [Google Scholar] [CrossRef]
- Yoon, S.J.; Lin, H.K.; Chen, G.; Yi, S.; Choi, J.; Rui, Z. Effect of occupational health and safety management system on work-related accident rate and differences of occupational health and safety management system awareness between managers in South Korea’s construction industry. Saf. Health Work. 2013, 4, 201–209. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.C.; Shariatfar, M.; Rashidi, A.; Lee, H.W. Evidence-driven sound detection for prenotification and identification of construction safety hazards and accidents. Autom. Constr. 2020, 113, 103127. [Google Scholar] [CrossRef]
- Gul, M.; Ak, M.F. A comparative outline for quantifying risk ratings in occupational health and safety risk assessment. J. Clean. Prod. 2018, 196, 653–664. [Google Scholar] [CrossRef]
- Sharma, R.K.; Gopalaswami, N.; Gurjar, B.R.; Agrawal, R. Assessment of failure and consequences analysis of an accident: A case study. Eng. Fail. Anal. 2020, 109, 104192. [Google Scholar] [CrossRef]
- Zhou, H.; Zhao, Y.; Shen, Q.; Yang, L.; Cai, H. Risk assessment and management via multi-source information fusion for undersea tunnel construction. Autom. Constr. 2020, 111, 103050. [Google Scholar] [CrossRef]
- Nieto-Morote, A.; Ruz-Vila, F. A fuzzy multi-criteria decision-making model for construction contractor prequalification. Autom. Constr. 2012, 25, 8–19. [Google Scholar] [CrossRef]
- Wu, Y.; Xu, C.; Li, L.; Wang, Y.; Chen, K.; Xu, R. A risk assessment framework of PPP waste-to-energy incineration projects in China under 2-dimension linguistic environment. J. Clean. Prod. 2018, 183, 602–617. [Google Scholar] [CrossRef]
- Beriha, G.S.; Patnaik, B.; Mahapatra, S.S. Assessment of occupational health practices in Indian industries: A neural network approach. J. Model. Manag. 2012, 7, 180–200. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, Z.; Kou, G.; Zhang, H.; Chao, X.; Li, C.C.; Dong, Y.; Herrera, F. Distributed linguistic representations in decision making: Taxonomy, key elements and applications, and challenges in data science and explainable artificial intelligence. Inf. Fusion. 2021, 65, 65–178. [Google Scholar] [CrossRef]
- Senesi, C.; Javernick-Will, A.; Molenaar, K.R. Benefits and barriers to applying probabilistic risk analysis on engineering and construction projects. EMJ—Eng. Manag. J. 2015, 27, 49–57. [Google Scholar] [CrossRef]
- Campos, A.C.S.M.; Mareschal, B.; De Almeida, A.T. Fuzzy flowSort: An integration of the flowSort method and fuzzy set theory for decision making on the basis of inaccurate quantitative data. Inf. Sci. 2015, 293, 115–124. [Google Scholar] [CrossRef]
- Mohammadfam, I.; Kamalinia, M.; Momeni, M.; Golmohammadi, R.; Hamidi, Y.; Soltanian, A. Developing an integrated decision making approach to assess and promote the effectiveness of occupational health and safety management systems. J. Clean. Prod. 2016, 127, 119–133. [Google Scholar] [CrossRef]
- Yu, K.; Zhou, L.; Hu, C.; Wang, L.; Jin, W. Analysis of influencing factors of occupational safety and health in coal chemical enterprises based on the analytic network process and system dynamics. Processes 2019, 7, 53. [Google Scholar] [CrossRef]
- Gong, X.; Yang, M.; Du, P. Renewable energy accommodation potential evaluation of distribution network: A hybrid decision-making framework under interval type-2 fuzzy environment. J. Clean. Prod. 2021, 286, 124918. [Google Scholar] [CrossRef]
- Bastida-Molina, P.; Ribó-Pérez, D.; Gómez-Navarro, T.; Hurtado-Pérez, E. What is the problem? The obstacles to the electrification of urban mobility in Mediterranean cities. Case study of Valencia, Spain. Renew. Sust. Energ. Rev. 2022, 166, 112649. [Google Scholar] [CrossRef]
- Akhtar, M.J.; Naseem, A.; Ahsan, F. A novel hybrid approach to explore the interaction among faults in production process with extended FMEA model using DEMATEL and cloud model theory. Eng. Fail. Anal. 2024, 157, 107876. [Google Scholar] [CrossRef]
- Ghosh, M.; Sing, J.K. Interval type-2 fuzzy set induced fuzzy rank-level fusion for face recognition. Appl. Soft Comput. 2023, 145, 110584. [Google Scholar] [CrossRef]
- Farman, H.; Javed, H.; Jan, B.; Ahmad, J.; Ali, S.; Khalil, F.N.; Khan, M. Analytical network process based optimum cluster head selection in wireless sensor network. PLoS ONE 2017, 12, e0180848. [Google Scholar] [CrossRef]
- Bobylev, N. Comparative analysis of environmental impacts of selected underground construction technologies using the analytic network process. Autom. Constr. 2011, 20, 1030–1040. [Google Scholar] [CrossRef]
- Zhang, X.; Hu, Z.; Zheng, M.; Li, J.; Liu, Y. A novel cloud model based data placement strategy for data-intensive application in clouds. Comput. Electr. Eng. 2019, 77, 445–456. [Google Scholar] [CrossRef]
- Afshar, M.R.; Alipouri, Y.; Sebt, M.H.; Chan, W.T. A type-2 fuzzy set model for contractor prequalification. Autom. Constr. 2017, 84, 356–366. [Google Scholar] [CrossRef]
- El-Sayegh, S.M.; Mansour, M.H. Risk assessment and allocation in highway construction projects in the UAE. J. Manag. Eng. 2015, 31, 04015004. [Google Scholar] [CrossRef]
- Hong, E.S.; Lee, I.M.; Shin, H.S.; Nam, S.W.; Kong, J.S. Quantitative risk evaluation based on event tree analysis technique: Application to the design of shield TBM. Tunn. Undergr. Sp. Technol. 2009, 24, 269–277. [Google Scholar] [CrossRef]
- Yeheyis, M.; Aguilar, G.; Hewage, K.; Sadiq, R. Exposure to crystalline silica inhalation among construction workers: A probabilistic risk analysis. Hum. Ecol. Risk Assess. 2012, 18, 1036–1050. [Google Scholar] [CrossRef]
- Choe, S.; Leite, F. Assessing safety risk among different construction trades: Quantitative approach. J. Constr. Eng. Manag. 2017, 143, 04016133. [Google Scholar] [CrossRef]
- Tong, R.; Cheng, M.; Zhang, L.; Liu, M.; Yang, X.; Li, X.; Yin, W. The construction dust-induced occupational health risk using Monte-Carlo simulation. J. Clean. Prod. 2018, 184, 598–608. [Google Scholar] [CrossRef]
- Bilir, S.; Gürcanli, G.E. A method for determination of accident probability in construction industry. Tek. Dergi. 2018, 8537–8562. [Google Scholar] [CrossRef]
- Aneziris, O.N.; Topali, E.; Papazoglou, I.A. Occupational risk of building construction. Reliab. Eng. Syst. Saf. 2012, 105, 36–46. [Google Scholar] [CrossRef]
- Bai, X.P.; Zhao, Y.H. A novel method for occupational safety risk analysis of high-altitude fall accident in architecture construction engineering. J. Asian Archit. Build. Eng. 2020, 20, 1–12. [Google Scholar] [CrossRef]
- Cebi, S. A New Risk assessment approach for occupational health and safety applications. In Proceedings of the INFUS 2020 Conference, Istanbul, Turkey, 21–23 July 2020; pp. 1345–1354. [Google Scholar] [CrossRef]
- Gul, M.; Celik, E. Fuzzy rule-based Fine–Kinney risk assessment approach for rail transportation systems. Hum. Ecol. Risk Assess. 2018, 24, 1786–1812. [Google Scholar] [CrossRef]
- Mohandes, S.R.; Zhang, X. Developing a holistic occupational health and safety risk assessment model: An application to a case of sustainable construction project. J. Clean. Prod. 2021, 291, 125934. [Google Scholar] [CrossRef]
- Pinto, A.; Nunes, I.L.; Ribeiro, R.A. Occupational risk assessment in construction industry—Overview and reflection. Saf. Sci. 2011, 49, 616–624. [Google Scholar] [CrossRef]
- Khan, M.W.; Ali, Y.; De Felice, F.; Petrillo, A. Occupational health and safety in construction industry in Pakistan using modified-SIRA method. Saf. Sci. 2019, 118, 109–118. [Google Scholar] [CrossRef]
- Aghaei, P.; Asadollahfardi, G.; Katabi, A. Safety risk assessment in shopping center construction projects using fuzzy fault tree analysis method. Qual. Quant. 2021, 1–17. [Google Scholar] [CrossRef]
- Pinto, A. QRAM a qualitative occupational safety risk assessment model for the construction industry that incorporate uncertainties by the use of fuzzy sets. Saf. Sci. 2014, 63, 57–76. [Google Scholar] [CrossRef]
- Liu, R.; Liu, Z.; Liu, H.C.; Shi, H. An improved alternative queuing method for occupational health and safety risk assessment and its application to construction excavation. Autom. Constr. 2021, 126, 103672. [Google Scholar] [CrossRef]
- Mohandes, S.R.; Zhang, X. Towards the development of a comprehensive hybrid fuzzy-based occupational risk assessment model for construction workers. Saf. Sci. 2019, 115, 294–309. [Google Scholar] [CrossRef]
- Amiri, M.; Ardeshir, A.; Fazel Zarandi, M.H. Fuzzy probabilistic expert system for occupational hazard assessment in construction. Saf. Sci. 2017, 93, 16–28. [Google Scholar] [CrossRef]
- Celik, E.; Gul, M. Hazard identification, risk assessment and control for dam construction safety using an integrated BWM and MARCOS approach under interval type-2 fuzzy sets environment. Autom. Constr. 2021, 127, 103699. [Google Scholar] [CrossRef]
- Wu, Z.Y.; Cao, J.; Ding, L. Structural state assessment based on similarity degree of membership cloud. In Proceedings of the 2010 Seventh International Conference on Fuzzy Systems and Knowledge Discovery, Yantai, China, 10–12 August 2010; pp. 1133–1137. [Google Scholar] [CrossRef]
- Lou, S.; Feng, Y.; Li, Z.; Zheng, H.; Tan, J. An integrated decision-making method for product design scheme evaluation based on cloud model and EEG data. Adv. Eng. Inform. 2020, 43, 101028. [Google Scholar] [CrossRef]
- Khedim, F.; Labraoui, N.; Abba Ari, A.A. A cognitive chronometry strategy associated with a revised cloud model to deal with the dishonest recommendations attacks in wireless sensor networks. J. Netw. Comput. Appl. 2018, 123, 42–56. [Google Scholar] [CrossRef]
- Zhao, Y.; Ma, Z.; Zheng, X.; Tu, X. An improved algorithm of nonlinear RED based on membership cloud theory. Chin. J. Electron. 2017, 26, 537–543. [Google Scholar] [CrossRef]
- Hosseini, F.; Safari, A.; Farrokhifar, M. Cloud theory-based multi-objective feeder reconfiguration problem considering wind power uncertainty. Renew. Energy 2020, 161, 1130–1139. [Google Scholar] [CrossRef]
- Chatterjee, K.; Bandyopadhyay, A.; Ghosh, A.; Kar, S. Assessment of environmental factors causing wetland degradation, using fuzzy analytic network process: A case study on Keoladeo National Park, India. Ecol. Modell. 2015, 316, 1–13. [Google Scholar] [CrossRef]
- Yao, K.; Lai, J.; Huang, W.; Tu, J. Utilize fuzzy Delphi and analytic network process to construct consumer product design evaluation indicators. Mathematics 2022, 10, 397. [Google Scholar] [CrossRef]
- Vinodh, S.; Anesh Ramiya, R.; Gautham, S.G. Application of fuzzy analytic network process for supplier selection in a manufacturing organization. Expert Syst. Appl. 2011, 38, 272–280. [Google Scholar] [CrossRef]
- Tan, T.; Mills, G.; Papadonikolaki, E.; Liu, Z. Combining multi-criteria decision making (MCDM) methods with building information modelling (BIM): A review. Autom. Constr. 2021, 121, 103451. [Google Scholar] [CrossRef]
- Asyraf, M.R.M.; Ishak, M.R.; Sapuan, S.M.; Yidris, N. Conceptual design of creep testing rig for full-scale cross arm using TRIZ-Morphological chart-analytic network process technique. J. Mater. Res. Technol. 2019, 8, 5647–5658. [Google Scholar] [CrossRef]
- Rohani, A.; Keramati, A.; Razmi, J. Presenting an innovative approach combining FA and ANP methods to identify and prioritize water pollutants in petroleum and petrochemical industries. Arch. Bus. Res. 2016, 4, 405–418. [Google Scholar] [CrossRef][Green Version]
- Asyraf, M.R.M.; Ishak, M.R.; Sapuan, S.M.; Yidris, N. Conceptual design of multi-operation outdoor flexural creep test rig using hybrid concurrent engineering approach. J. Mater. Res. Technol. 2020, 9, 2357–2368. [Google Scholar] [CrossRef]
- Martino, R.; Ventre, V. An analytic network process to support financial decision-making in the context of behavioural finance. Mathematics 2023, 11, 3994. [Google Scholar] [CrossRef]
- Asyraf, M.R.M.; Rafidah, M.; Ishak, M.R.; Sapuan, S.M.; Yidris, N.; Ilyas, R.A.; Razman, M.R. Integration of TRIZ, morphological chart and ANP method for development of FRP composite portable fire extinguisher. Polym. Compos. 2020, 41, 2917–2932. [Google Scholar] [CrossRef]
- Akyuz, E. A marine accident analysing model to evaluate potential operational causes in cargo ships. Saf. Sci. 2017, 92, 17–25. [Google Scholar] [CrossRef]
- Ayag, Z.; Gürcan Özdemir, R. Evaluating machine tool alternatives through modified TOPSIS and alpha-cut based fuzzy ANP. Int. J. Prod. Econ. 2012, 140, 630–636. [Google Scholar] [CrossRef]
- Lord, D.; Miranda-Moreno, L.F. Effects of low sample mean values and small sample size on the estimation of the fixed dispersion parameter of Poisson-gamma models for modeling motor vehicle crashes: A Bayesian perspective. Saf. Sci. 2008, 46, 751–770. [Google Scholar] [CrossRef]
- Wang, C.N.; Su, C.C.; Nguyen, V.T. Nuclear power plant location selection in Vietnam under fuzzy environment conditions. Symmetry 2018, 10, 548. [Google Scholar] [CrossRef]
- Wang, J.; Herricks, E.E. Risk assessment of bird–aircraft strikes at commercial airports submodel development. Transp. Res. Rec. 2012, 2266, 78–84. [Google Scholar] [CrossRef]
- Abdullah, L.; Zulkifli, N. A new DEMATEL method based on interval type-2 fuzzy sets for developing causal relationship of knowledge management criteria. Neural Comput. Appl. 2018, 31, 4095–4111. [Google Scholar] [CrossRef]
- Ghorabaee, M.K.; Zavadskas, E.K.; Amiri, M.; Esmaeili, A. Multi-criteria evaluation of green suppliers using an extended WASPAS method with interval type-2 fuzzy sets. J. Clean. Prod. 2016, 137, 213–229. [Google Scholar] [CrossRef]
- Yang, L.; Chen, C.; Jin, N.; Fu, X.; Shen, Q. Closed form fuzzy interpolation with Interval type-2 fuzzy sets. In Proceedings of the 2014 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Beijing, China, 6–11 July 2014; pp. 2184–2191. [Google Scholar] [CrossRef]
- Kahraman, C.; Öztayşi, B.; Uçal Sari, I.; Turanoǧlu, E. Fuzzy analytic hierarchy process with interval type-2 fuzzy sets. Knowledge-Based Syst. 2014, 59, 48–57. [Google Scholar] [CrossRef]
- Yazici, I.; Kahraman, C. VIKOR method using interval type two fuzzy sets. J. Intell. Fuzzy Syst. 2015, 29, 411–421. [Google Scholar] [CrossRef]
- Moharrer, M.; Tahayori, H.; Livi, L.; Sadeghian, A.; Rizzi, A. Interval type-2 fuzzy sets to model linguistic label perception in online services satisfaction. Soft Comput. 2015, 19, 237–250. [Google Scholar] [CrossRef]
- Sang, X.; Zhou, Y.; Yu, X. An uncertain possibility-probability information fusion method under interval type-2 fuzzy environment and its application in stock selection. Inf. Sci. 2019, 504, 546–560. [Google Scholar] [CrossRef]
- Ilbahar, E.; Kahraman, C.; Cebi, S. Location selection for waste-to-energy plants by using fuzzy linear programming. Energy 2021, 234, 121189. [Google Scholar] [CrossRef]
- Gölcük, İ. An interval type-2 fuzzy reasoning model for digital transformation project risk assessment. Expert Syst. Appl. 2020, 159, 113579. [Google Scholar] [CrossRef]
- Jana, D.K.; Ghosh, R. Novel interval type-2 fuzzy logic controller for improving risk assessment model of cyber security. J. Inf. Secur. Appl. 2018, 40, 173–182. [Google Scholar] [CrossRef]
- Kiracı, K.; Akan, E. Aircraft selection by applying AHP and TOPSIS in interval type-2 fuzzy sets. J. Air Transp. Manag. 2020, 89, 101924. [Google Scholar] [CrossRef]
- Dinçer, H.; Yüksel, S.; Martínez, L. Interval type 2-based hybrid fuzzy evaluation of financial services in E7 economies with DEMATEL-ANP and MOORA methods. Appl. Soft Comput. J. 2019, 79, 186–202. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, Y.; Chai, J.; Wang, L.; Wang, S.; Lev, B. Sustainable supply chain evaluation: A dynamic double frontier network DEA model with interval type-2 fuzzy data. Inf. Sci. 2019, 504, 394–421. [Google Scholar] [CrossRef]
- Sun, X.; Cai, C.; Pan, S.; Bao, N.; Liu, N. A university teachers’ teaching performance evaluation method based on type-II fuzzy sets. Mathematics 2021, 9, 2126. [Google Scholar] [CrossRef]
- Dey, A.; Pal, A.; Pal, T. Interval type 2 fuzzy set in fuzzy shortest path problem. Mathematics 2016, 4, 62. [Google Scholar] [CrossRef]
- Wu, T.; Liu, X.W.; Liu, S.L. A fuzzy ANP with interval type-2 fuzzy sets approach to evaluate enterprise technological innovation ability. In Proceedings of the 2015 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), İstanbul, Turkey, 2–5 August 2015; pp. 1–8. [Google Scholar] [CrossRef]
- Mendel, J.M.; Rajati, M.R.; Sussner, P. On clarifying some definitions and notations used for type-2 fuzzy sets as well as some recommended changes. Inf. Sci. 2016, 340–341, 337–345. [Google Scholar] [CrossRef]
- Celik, E.; Soner, O.; Akyuz, E.; Arslan, O. Evaluation of the potential sazards of ship-generated waste in maritime industry using a type-2 fuzzy analytical hierarchyprocess. Int. J. Marit. Eng. 2020, 162, 311–318. [Google Scholar] [CrossRef]
- Celik, E.; Akyuz, E. An interval type-2 fuzzy AHP and TOPSIS methods for decision-making problems in maritime transportation engineering: The case of ship loader. Ocean Eng. 2018, 155, 371–381. [Google Scholar] [CrossRef]
- Kiliҫ, M.; Kaya, I. Investment project evaluation by a decision making methodology based on type-2 fuzzy sets. Appl. Soft Comput. 2015, 27, 399–410. [Google Scholar] [CrossRef]
- Radziszewska-Zielina, E.; Śladowski, G.; Sibielak, M. Planning the reconstruction of a historical building by using a fuzzy stochastic network. Autom. Constr. 2017, 84, 242–257. [Google Scholar] [CrossRef]
- Senturk, S.; Binici, Y.; Erginel, N. The theoretical structure of fuzzy analytic network process (FANP) with interval type-2 fuzzy sets. IFAC-PapersOnLine 2016, 49, 1318–1322. [Google Scholar] [CrossRef]
- Ji, C.; Gao, F.; Liu, W. Dependence assessment in human reliability analysis based on cloud model and best-worst method. Reliab. Eng. Syst. Saf. 2024, 242, 109770. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, X.; Zhu, H.; AbouRizk, S.M. Perceiving safety risk of buildings adjacent to tunneling excavation: An information fusion approach. Autom. Constr. 2017, 73, 88–101. [Google Scholar] [CrossRef]
- Ayodele, T.R.; Ogunjuyigbe, A.S.O.; Odigie, O.; Munda, J.L. A multi-criteria GIS based model for wind farm site selection using interval type-2 fuzzy analytic hierarchy process: The case study of Nigeria. Appl. Energy 2018, 228, 1853–1869. [Google Scholar] [CrossRef]
- Wu, Y.; Xu, C.; Huang, Y.; Li, X. Green supplier selection of electric vehicle charging based on Choquet integral and type-2 fuzzy uncertainty. Soft Comput. 2020, 24, 3781–3795. [Google Scholar] [CrossRef]
- Abdullah, L.; Adawiyah, C.W.R.; Kamal, C.W. A decision making method based on interval type-2 fuzzy sets: An approach for ambulance location preference. Appl. Comput. Inform. 2018, 14, 65–72. [Google Scholar] [CrossRef]
- Li, L.; Kong, D.; Liu, Q.; Xiong, Y.; Chen, F.; Zhang, H.; Chu, Y. Comprehensive identification of surface subsidence evaluation grades of mines in southwest China. Mathematics 2022, 10, 2664. [Google Scholar] [CrossRef]
- Razmi, J.; Rafiei, H.; Hashemi, M. Designing a decision support system to evaluate and select suppliers using fuzzy analytic network process. Comput. Ind. Eng. 2009, 57, 1282–1290. [Google Scholar] [CrossRef]
- Parhoudeh, S.; Baziar, A.; Mazareie, A.; Kavousi-Fard, A. A novel stochastic framework based on fuzzy cloud theory for modeling uncertainty in the micro-grids. Int. J. Electr. Power Energy Syst. 2016, 80, 73–80. [Google Scholar] [CrossRef]
- Song, Q.; Jiang, P.; Zheng, S. The application of cloud model combined with nonlinear fuzzy analytic hierarchy process for the safety assessment of chemical plant production process. Process Saf. Environ. Prot. 2021, 145, 12–22. [Google Scholar] [CrossRef]
- Xu, J.; Ding, R.; Li, M.; Dai, T.; Zheng, M.; Yu, T.; Sui, Y. A new Bayesian network model for risk assessment based on cloud model, interval type-2 fuzzy sets and improved D-S evidence theory. Inf. Sci. 2022, 618, 336–355. [Google Scholar] [CrossRef]
- ISO/IEC/IEEE 15288; Systems and Software Engineering—System Life Cycle Processes. International Organization for Standardization (ISO)/International Electrotechnical Commission (IEC)/Institute of Electrical and Electronics Engineers (IEEE). ISO; IEC; IEEE: Geneva, Switzerland, 2015.

| Linguistic Scales for Importance | Trapezoidal IT2FS |
|---|---|
| Equally important | (1, 1, 1, 1; 1, 1), (1, 1, 1, 1; 1, 1) |
| Slightly more important | (1, 2, 4, 5; 1, 1), (1.2, 2.2, 3.8, 4.8; 0.8, 0.8) |
| Strongly more important | (3, 4, 6, 7; 1, 1), (3.2, 4.2, 5.8, 6.8; 0.8, 0.8) |
| Very strongly more important | (5, 6, 8, 9; 1, 1), (5.2, 6.2, 7.8, 8.8; 0.8, 0.8) |
| Absolutely more important | (7, 8, 9, 9; 1, 1), (7.2, 8.2, 8.8, 9; 0.8, 0.8) |
| No. | First Level Index | Second Level Index |
|---|---|---|
| 1 | Occupational health (U1) | Physical health status (U11) |
| 2 | Mental health status (U12) | |
| 3 | Occupational risk (U13) | |
| 4 | Safety protection (U2) | Safety protection facility (U21) |
| 5 | Personal protective equipment (U22) | |
| 6 | Safety mark (U23) | |
| 7 | Material, machinery, and equipment (U3) | Quality of material, machinery, and equipment (U31) |
| 8 | Installation and dismantling of machinery and equipment (U32) | |
| 9 | Maintenance of machinery and equipment (U33) | |
| 10 | Organizational management (U4) | Establishment of safety management system (U41) |
| 11 | Safety hazard identification, risk assessment, and control (U42) | |
| 12 | Education and training (U43) | |
| 13 | Emergency disposal and rescue (U44) |
| Index | U11 | U12 | U13 |
|---|---|---|---|
| U11 | 1 | (1/9, 1/8, 1/6, 1/5; 1, 1) (1/8.8, 1/7.8, 1/6.2, 1/5.2; 0.8, 0.8) | (5, 6, 8, 9; 1, 1), (5.2, 6.2, 7.8, 8.8; 0.8, 0.8) |
| U12 | (5, 6, 8, 9; 1, 1), (5.2, 6.2, 7.8, 8.8; 0.8, 0.8) | 1 | (1/9, 1/9, 1/8, 1/7; 1, 1) (1/9, 1/8.8, 1/8.2, 1/7.2; 0.8, 0.8) |
| U13 | (1/9, 1/8, 1/6, 1/5; 1, 1) (1/8.8, 1/7.8, 1/6.2, 1/5.2; 0.8, 0.8) | (7, 8, 9, 9; 1, 1), (7.2, 8.2, 8.8, 9; 0.8, 0.8) | 1 |
| Non-Normalized IT2F Weight Vector | Non-Normalized Weight Vector | Improved Normalized Weight Vector |
|---|---|---|
| (0.8221, 0.9086, 1.1006, 1.2164; 1, 1) (0.8392, 0.9263, 1.0795, 1.1917; 0.8, 0.8) | 0.9604 | 0.3341 |
| (0.8221, 0.8736, 1, 1.0874; 1, 1) (0.8329, 0.8898, 0.9835, 1.0692; 0.8, 0.8) | 0.8980 | 0.3124 |
| (0.9196, 1, 1.1447, 1.2164; 1, 1) (0.9353, 1.0168, 1.1238, 1.2006; 0.8, 0.8) | 1.0162 | 0.3535 |
| Assessment Level | Value Interval | Numerical Feature |
|---|---|---|
| Outstanding (I) | [90, 100] | (100, 3.333, 0.1) |
| Good (II) | [80, 90] | (85, 1.667, 0.1) |
| Moderate (III) | [70, 80] | (75, 1.667, 0.1) |
| General (IV) | [60, 70] | (65, 1.667, 0.1) |
| Unsatisfactory (V) | [0, 60] | (0, 20, 0.1) |
| No. | Assessment Index | Numerical Feature | Assessment Level | Similarity | Risk Ranking |
|---|---|---|---|---|---|
| 1 | U11 | (87.9, 91.8, 1.2533, 0.1235) | II | 0.9087 | 1 |
| 2 | U12 | (83.1, 88.2, 3.8602, 1.0268) | II | 0.5026 | 8 |
| 3 | U13 | (83.7, 88.7, 6.0159, 1.1681) | II | 0.3611 | 11 |
| 4 | U14 | (87.9, 92.0, 2.8074, 0.7576) | II | 0.7273 | 5 |
| 5 | U21 | (91.4, 95.3, 2.0053, 0.1523) | I | 0.4099 | 10 |
| 6 | U22 | (86.3, 90.2, 1.8800, 0.9898) | II | 0.7732 | 3 |
| 7 | U23 | (85.4, 89.9, 2.6320, 0.6795) | II | 0.7333 | 4 |
| 8 | U24 | (87.6, 92.5, 2.3562, 0.5200) | I | 0.7958 | 2 |
| 9 | U31 | (89.7, 93.6, 2.2560, 0.7677) | I | 0.6234 | 6 |
| 10 | U32 | (91.8, 95.6, 1.4037, 0.3043) | I | 0.3577 | 12 |
| 11 | U33 | (83.1, 88.1, 2.0053, 0.4483) | II | 0.4608 | 9 |
| 12 | U41 | (92.0, 95.8, 1.2533, 0.1709) | I | 0.3242 | 13 |
| 13 | U42 | (85.6, 90.0, 2.5066, 0.4886) | II | 0.5959 | 7 |
| No. | Assessment Level | Similarity |
|---|---|---|
| 1 | Outstanding | 0.3317 |
| 2 | Good | 0.1681 |
| 3 | Moderate | 2.0898 × 10−5 |
| 4 | General | 7.2700 × 10−25 |
| 5 | Unsatisfactory | 0.0141 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, R.; Liu, Z. An IT2FS-ANP- and IT2FS-CM-Based Approach for Conducting Safety Risk Assessments of Nuclear Power Plant Building Projects. Mathematics 2024, 12, 1038. https://doi.org/10.3390/math12071038
Ding R, Liu Z. An IT2FS-ANP- and IT2FS-CM-Based Approach for Conducting Safety Risk Assessments of Nuclear Power Plant Building Projects. Mathematics. 2024; 12(7):1038. https://doi.org/10.3390/math12071038
Chicago/Turabian StyleDing, Rui, and Zehua Liu. 2024. "An IT2FS-ANP- and IT2FS-CM-Based Approach for Conducting Safety Risk Assessments of Nuclear Power Plant Building Projects" Mathematics 12, no. 7: 1038. https://doi.org/10.3390/math12071038
APA StyleDing, R., & Liu, Z. (2024). An IT2FS-ANP- and IT2FS-CM-Based Approach for Conducting Safety Risk Assessments of Nuclear Power Plant Building Projects. Mathematics, 12(7), 1038. https://doi.org/10.3390/math12071038





