Abstract
In this paper, exact solutions of semilinear equations having exponential growth in the space variable x are found. Semilinear Schrödinger equation with logarithmic nonlinearity and third-order evolution equations arising in optics with logarithmic and power-logarithmic nonlinearities are investigated. In the parabolic case, the solution u is written as , , being real-valued functions. We are looking for the solutions u of Schrödinger-type equation of the form , respectively, for the third-order PDE, , where the amplitude b and the phase function a are complex-valued functions, , and is real-valued. In our proofs, the method of the first integral is used, not Hirota’s approach or the method of simplest equation.
Keywords:
semilinear parabolic equation; semilinear Schrödinger equation; logarithmic nonlinearity; parabolic equations with solutions of exponential growth; solutions into explicit form; special functions of Jacobi type; hyperbolic functions; Radhakrishnan–Kundu–Lakshmanan optic equation MSC:
35K58; 35Q51; 35Q55; 35K91; 35Q99
1. Introduction
This paper deals with exact (explicitly written) solutions of several semilinear evolution equations of mathematical physics. It concerns parabolic equations for which solutions with exponential growth in the space variable x are found, semilinear Schrödinger equation with logarithmic nonlinearity, and third-order evolution equations arising in optics with power and logarithmic-power nonlinearities. The latter are generalizations of the standard semilinear Schrödinger equation, which is of second order. We are looking for the solutions u of Schrödinger-type equations of the form , where A is the amplitude and is the phase function. are complex-valued. That ansatz is often used in mathematical physics and we shall mention only the classical paper [1] that stimulated in the middle of last century different applications of the asymptotical solutions in analysis, PDE, and certainly in physics. For the parabolic equation with , a and b are real-valued. Depending on the sign of some parameter , we can have dispersive and non-dispersive cases for the classical Schrödinger equation. Therefore, two different cases appear. In the first one, the phase is periodic in t, while in the general case, the amplitude is only bounded but not periodic in t. Its modulus is periodic. In the second case, the amplitude is bounded and tends to zero as a spiral for , while for fixed t, the phase is exponentially increasing in x. The "third order" Schrödinger-type equation possesses solutions of the type , being linear functions of . Under many restrictions, three types of solutions are constructed, namely solutions for which forms one-parametric family of periodic solutions, is a soliton, blows up at some , but and blows up at some point being periodic in t.
In proving our results, we use the method of the first integral from the theory of mechanical systems having one degree of freedom. For the sake of completeness, we shall say several words about the method of the first integral that possesses many applications to the theory of autonomous systems of ODE and to first-order quasilinear PDE [2,3]. The first integral appeared for the first time in the investigations of Newton and the proof of Kepler’s law and it relies on the construction into explicit form of the appropriate first integral. Assume that stands for the trajectory of some particle in the one-dimensional space with initial position and initial velocity . According to Newton’s second law, satisfies the ODE , where is the corresponding acting force. Denote by the kinetic energy of the particle. Then the full energy satisfies the relation . This is the classical energy conservation law. From a mathematical point of view, the function is the first integral of Newton’s second law, i.e., the phase trajectory is located on surface level , . Therefore, satisfies the first-order ODE with separate variables , and . If , we have that . By using different reference books on analysis as [4,5,6], we can express in some cases via elementary functions or some special functions (hyperbolic, Jacobi elliptic, Legendre elliptic function, etc.). As , the smooth mapping is invertible, i.e., there exists uniquely determined . So with . The above-mentioned results are usually local but it could happen that solutions global in t exist. The well-known approach of Hirota [7] and the method of the simplest equation [8] are not used here. Several historical notes are proposed below. The logarithmic Schrödinger equation was introduced in [9]. Applications of that equation in quantum optics, nuclear physics, transport and diffusion phenomena, theory of super fluidity, and Bose–Einstein condensation can be found, respectively, in the following papers: [10,11,12,13]. Numerical experiments in [14] show that the dynamical properties of the solutions in the logarithmic case are rather different from that for power-like nonlinearity. The strong superposition of two or finitely many Gaussians was studied in [15]. We rely here on [16,17,18] generalizing the dispersive case from [16]. In the last 10 years, many papers appeared on the cubic-quartic Fokas–Lenells equation with perturbation terms. The corresponding PDE of fourth order occurs in different systems in fluid mechanics, solid state physics and condensed matter, nonlinear optic and plasma physics. One can see [19] on the subject and the references therein.
Our aim here is to find out explicitly written solutions by using purely mathematical tools. So there are no numerical simulations. We give here a detailed study of the dispersive case of the logarithmic Schrödinger equation looking for solution , , being smooth complex-valued functions. is not periodic in general but we find a necessary and sufficient condition for its periodicity. It is interesting to mention that is always periodic. Our ODE are studied under Cauchy initial conditions. The situation is delicate if , , . The approach sketched above shows that its unique solution , . Certainly, at , . The Troesh boundary value problem , , is out of the scope of this paper but some aspect was studied in 2014 by H. Temini and H. Kurkcu (precise numerical solution for ).
The paper is organized as follows. In Section 2, we formulate our results, in Section 3, the proof of Theorem 1 is given, in Section 4, the detailed proof of Theorem 2 is proposed, geometrically illustrated, and mechanically interpreted, and Section 5 contains the proof of Theorem 3. References are given at the end of the paper. We point out that for logarithmic nonlinearities, technically the things differ from those for power nonlinearities.
2. Formulation of the Main Results
- We shall begin with the following nonlinear Cauchy problem:
The case of bounded real-valued solutions for parabolic equations is well-studied and we shall assume further on that and , , . Certainly, is not a solution of (1). Let . is a linear space. We shall look for a solution of (1) having the form
if , , .
This is our first result.
Theorem 1.
Uniqueness. Consider (1) with positive solution u such that
- (i)
- u , , ,
- (ii)
- , ,, .
Then u is uniquely determined for appropriate in .
Existence of solution for . Then there are three possible cases depending on the sign of λ, i.e.,
- -
- if , one can find
- -
- if
- -
- if , then , and a blows up for ; for .
The function in the first two cases.
- -
- if , again , but a blows up for .
According to the Granwall lemma, (ii) implies that for some , i.e., . Certainly, , , .
Our second model example is the Schrödinger equation with logarithmic nonlinearity:
Evidently, is not a solution of (3), while satisfies it .
Again we shall find a solution of (3) having the form
, , , . Otherwise will be bounded in x. (4) is called the Gaussian solution of (3). Below we present some historical remarks.
(3) possesses standing wave solutions called Gaussons: , . are not asymptotically stable for due to the Galilean invariance of (3). The latter means that if u is a solution of (3), then for each satisfies (3).
Introduce now the Sobolev-type space . T. Cazenave and A. Haraux proved in [20] in 1980 that for and the Cauchy problem for Equation (3) with initial data possesses a global solution such that
(conservation laws).
Below we formulate the logarithmic Sobolev inequality in [21]: For each and
There is equality in the previous estimate if and only if up to a translation , the function is a multiple of . Evidently, for .
This is our second result.
Theorem 2.
Consider (3) with , . Then exists and , is a periodic function for ( ). In the case (), is a bounded smooth closed curve located in the half plane tangential to the imaginary axes at the origin, . The function is defined everywhere and is written explicitly.
We point out that is not periodic in general for and we discuss this problem during the proof of Theorem 2, finding NSC . In the investigations for -periodic, the second Kepler law appears, i.e., and then the curve is either periodic or dense in the ring in , , , being a periodic function.
A. H. Ardila proved in 2016 in [22] that the Gaussons are orbitally stable in .
- 2.
- Our next step is to study two Schrödinger-type semilinear PDEs arising in optics, finding their special solutions that have appropriate physical interpretation. The first one is known as the Radhakrishnan–Kundu–Lakshmanan(RKL) equation (see [23]), namelywhere the constants are real and nonzero, (see, for example, [19]).The second equation has power-logarithmic nonlinearity:
The solutions are also known as dispersive optical ones. Concerning (5), presents the wave profile, describes the temporal evolution, a stands for the coefficient of chromatic dispersion, b is the coefficient of power law of self-phase modulation, is the coefficient of third-order dispersion, stands for the coefficient of self-steeping term of the short pulses, and n is the power law parameter (see [19]).
The solutions of (5) and (6) we are looking for will have the following form:
where is linear phase function:
, and amplitude . As usual, is the frequency, k is the wave number, and V is the velocity of the wave.
Putting (7) into (5) and (6) and separating the real and imaginary parts of the corresponding expressions, we come to the overdetermined system that should be satisfied by the real-valued positive function :
for Equation (5) and
for Equation (6).
We integrate the second equations in (8) and (9), and taking the constant of integration equal to 0, we obtain:
The first and second equations in (10) and (11) are identical iff
i.e.,
, .
This is our Theorem 3. Certainly we assume further on that condition (12) holds.
Theorem 3.
For appropriate values of the real coefficients , Equations (5) and (6) possess three different types of solutions having the form (7):
- -
- solutions for which φ forms a one parametric family of periodic functions;
- -
- φ is soliton, , ;
- -
- φ blows up at some and φ is periodic unbounded function ( for each , ).
The restrictions on the coefficients will be imposed during the proof of Theorem 3. The unbounded solutions are of two “qualitative” types: and . The non-periodic solutions of (5) will be found in explicit form when (10) under condition (12) is investigated. In fact, then they are , , and . Otherwise (say in the periodic case) the solutions up to the inverse mapping theorem are written into integral form. The solutions of (10) and (11) are written into integral form, but in general, the latter cannot be expressed via elementary or special functions (Jacobi ones, etc.).
3. Proof of Theorem 1
Consider the Cauchy problem (1) with , , . To prove the uniqueness of the classical solution u for arbitrary and in the same class, we take the second solution of the same equation admitting the initial condition . Then put ,
According to (i), (ii) , , i.e., . Moreover, . In a similar way, satisfies (13), , . Define . Evidently, , and
Certainly, , is a constant.
We apply to the linear equation with respect to w Theorem 10 from Chapter II of [24] and conclude that . For parabolic equations, see also [25].
To find a solution of (1) of the form (2), we find , , and from the Equation (1), we obtain
i.e., the system of ODE
, ; .
As everywhere in . It is easy to see that if there exists a solution global in of the ODE such that , , and , while . Thus, .
Having in mind that , we find
As
where .
In the case (uniqueness).
If , and but and blows up for .
If and the solution blows up.
The equation
can be rewritten as
and this is linear ODE with respect to .
Thus,
Evidently (see (16)),
So for ,
After easy computations, we conclude that
Remark 1.
, , in (20), i.e., and for .
If
Therefore, the solution of (1) for takes the form
4. Proof of Theorem 2
We repeat the same procedure as in the previous case. Things are more complicated, as the functions are complex-valued and the corresponding system ODE is in , not in .
Having in mind that
we obtain from (3) that
It is simpler to express from the first ODE. We are looking for
i.e., .
Certainly, is a complex-valued function, . Substituting (24) in the first equation of (23), we obtain
Splitting the real and imaginary parts of (25), we come to the system of ODE in the plane :
Thus,
One can rewrite applying the Fubini theorem in the triangle . So
(2), (27), and (29) imply that
i.e., with , we have
In the solvability of
we follow [16]. .
We shall find , , i.e., , (according to the equation).
Consequently,
Here we imitate the theory of Kepler’s law via Newton equation, i.e., we look for in polar coordinates:
-real-valued polar angle. As
from (32), we obtain
i.e.,
This way, we come to the area first integral of Kepler’s law. According to this law, the revolution of the Earth around the Sun is with constant area velocity. Then
To simplify things, we take
. Further on, .
Therefore,
Of course, , .
This is the main equation in our considerations here:
In a standard way, by multiplying (39) with r and integrating from 0 to t, we conclude that
Therefore, we shall concentrate on the following nonlinear ODE with separate variables:
Put . , , , for and for . Because of this, we must consider two different cases:
- (1)
- (2)
- .
Put . Then
In case (2), , i.e., U is strictly monotonically increasing and there exists a unique point such that , i.e., for , , and for . So .
In case (1), , for ; for , i.e., as .
The graph of is given in Figure 1.
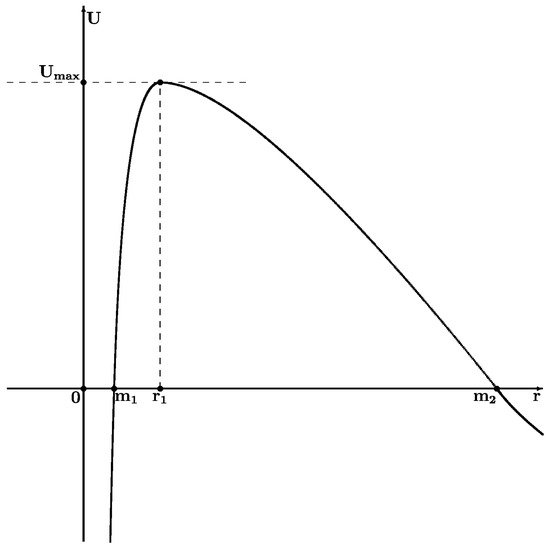
Figure 1.
Graph of the potential , .
It is obvious that there exist uniquely determined points and on , for and , , , , is strictly increasing for and strictly decreasing for . Evidently, .
In case (1), the unique solution of (41) is given by the formula
This is the graph of
for , , and are finite numbers as the integral is convergent at the end points (see Figure 2).
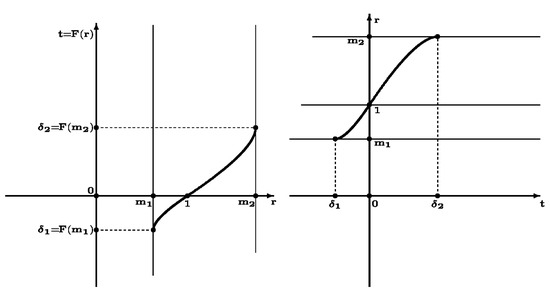
Figure 2.
Graph of the function for and its inverse function .
The inverse function is defined, and smooth in , for , . We continue smoothly in the interval in an even way, i.e., for each and then periodically on with period . Then satisfies (41) for each t. Obviously, , , , .
Then and is given by (31). is periodic with period but we do not know anything about . To find a better expression for , we compute:
Thus,
On the other hand, if is continuous periodic function with period T, its primitive is periodic with the same period if and only if .
One can easily see that
where the smooth periodic function vanishes at .
In fact, is periodic with period T as . Therefore, is periodic , i.e., (46) holds.
If , , K-real, then g is periodic with period T iff , being the set of the integers. The phase function of (45) can be written then as
being real-valued periodic functions with period T.
Put ,
is periodic with period T if and only if . In other words, it is very rare.
Certainly, is periodic as .
Remark 2.
The curve in is rather interesting. In fact, ω is smooth, , , .
Consequently the curve ω is located in the ring . It is periodic there if . If is an irrational number, then the curve ω is dense in the same ring [2,3]. ω can have infinitely many points of self-intersection.
Case (2) is absolutely different, as then is unbounded and is located in an angle: .
In case (2), we shall study (41) for but the integral exists for , , , , is a real number as the integral is convergent for .
On the other hand, for , ; for , implies that . This is the graph of (Figure 3).
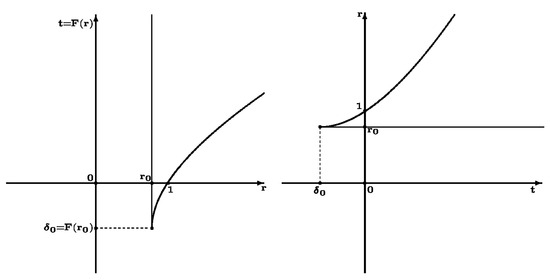
Figure 3.
Graph of , and its inverse function.
Its inverse function is such that for , , (see Figure 3). Again we continue in an even way with respect to , i.e., , ; satisfies (41) for each t.
We are interested in the behavior of at (asymptote) as . On the other hand, for ,
According to L’Hospital rule,
i.e., with , , , , .
Obviously, after the change ,
(L’Hospital is again applied). Our last step is to show that for .
This way we conclude that
i.e.,
(49) can be asymptotically inverted looking for , , . As , we find , i.e.,
Due to the definition of for
for , for ,
From (38), (51), and (52), it follows that , for each t,
i.e., .
As it concerns we know that , , . The integral is convergent for and , are finite numbers and the angle . This is the graph of , (see Figure 4).
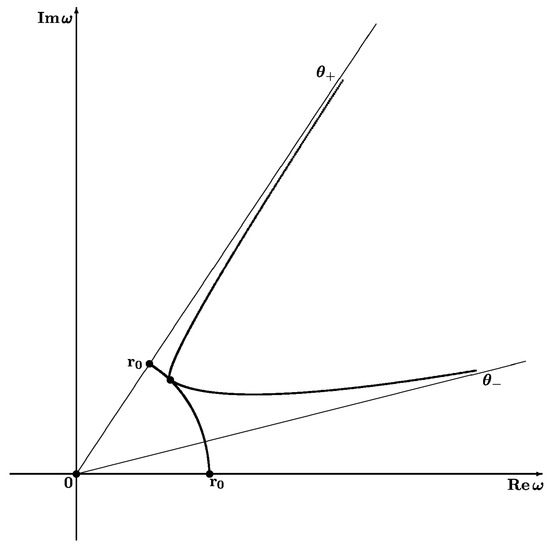
Figure 4.
Graph of .
Our last step is to illustrate geometrically the curve . As , , i.e., is rapidly increasing in function x for fixed t. Moreover, , , , , , , and , a is tangential to the imaginary axes at the origin, for , for , . is given in Figure 5.
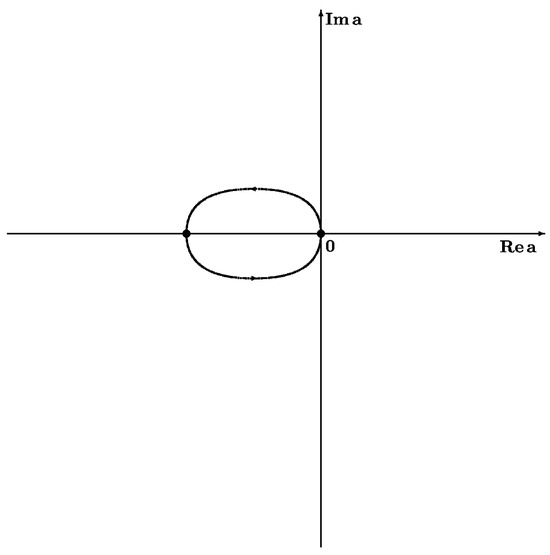
Figure 5.
Graph of .
Formula (45) shows that for . The phase function in t: is such that , and , .
In other words, the phase function in is superlinear for with growth . Last observation: describes a spiral in tending to 0, i.e., is a focus in the complex plane, . For each fixed t, is exponentially increasing in x. For fixed x: for :
The angle of rotation is bounded, , , .
5. Proof of Theorem 3
- We shall study first the ODE (11) under numberwhere , with , .
At the beginning, we observe that the smooth function , , has the following properties: , for and for , for , , , , for ; for . In a standard way, we obtain from (53) that
Certainly, and . So if we put
we come to the ODE
Thus,
We have four different cases for : , ; , ; , ; , . Evidently, , , , .
Moreover,
for some .
Assume (a) , . Then , , i.e., there exists a unique point with this property , for and for , as (see the graph of in Figure 6 and the graph of in Figure 7). is the unique point such that , .
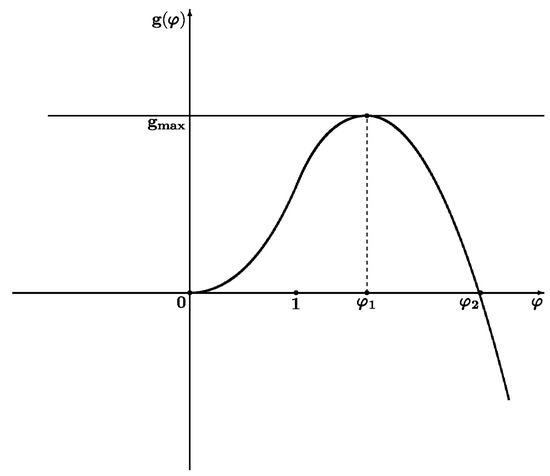
Figure 6.
Graph of , , .
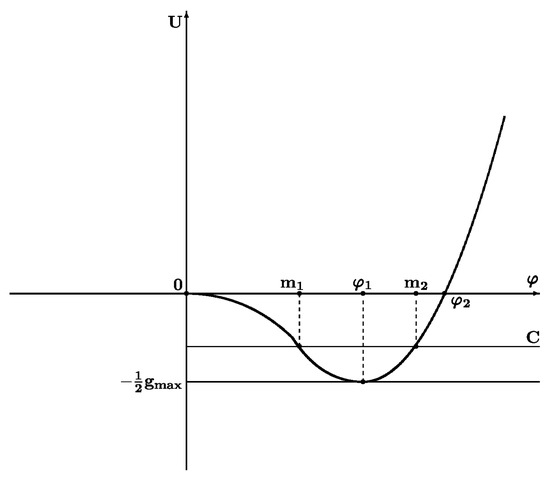
Figure 7.
Graph of .
Take and let be the unique points , with the properties , , . The initial data . As we know, formula (55) defines a periodic solution, (see Proof of Theorem 2, Figure 2 there, etc.). If , , , and the integral , has the following properties: , on , , is some number and . The inverse function is defined on , there, , for some A. We continue in an even way with respect to A, i.e., , obtaining this way a soliton solution of (11).
(b) Suppose that , , , i.e., . It follows that , ; , . We take the point as there are two numbers satisfying one of them less that and the other is .
Having in mind that for , we conclude that for , i.e., g is strictly monotonically increasing and for ,
i.e., if and only if . Assuming and having in mind that , we can construct a solution of (53) of the type , as for , the integral has the following properties: , , , . has a blow up for finite time, everywhere and . The latter result is rather implicit. So it is better to study the function , , , .
Evidently, , , , , , , .
Thus, . We are interested in the subcases of (b) ; for , . The integral is investigated for and the initial data . Then , for , , . The inverse function of , is positive in some interval , , , . We continue in an even way with respect to A the function and obtain a -type solution of (53).
The third subcase is and consequently there exists unique such that , for , . (55) will be considered on the interval , , , . Obviously, , , , . The inverse function has the behavior of (Figure 8).
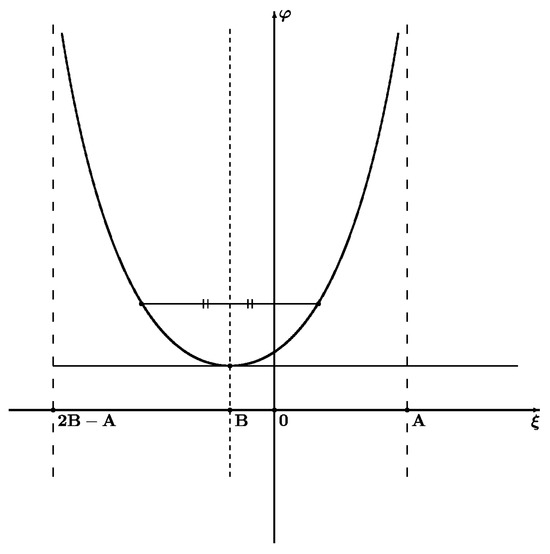
Figure 8.
Graph of the inverse function , , , , , .
The other two cases , or are omitted as they can be studied similarly to the previous cases (a) and (b).
- 2.
- We shall study now Equation (10) under condition (12), i.e.,In a standard way, we come to the first-order ODEwhereSo , .
In the special case , we conclude that
i.e., is any primitive of , , , .
There are four cases for the signs of in : , ; , - impossible; , and , .
Thus,
If , (56) possesses a one parametric family of periodic solutions. The proof repeats the proof of the similar results for (41), (1) and we omit it.
Suppose that
and , ; , ; , . Certainly, , .
The change in (59) gives us that
We shall study the cases
The case , is treated in a similar way as , and we omit the proof.
According to formulae 341.01, 281.01 from [4], we have that with ,
Therefore, (59) implies that
and , .
From (60), we obtain that
where , , .
(61) is a soliton-type solution, of course, and can be expressed via .
In the case , we have that
From trigonometry, it is known that for , :
Put , , . Put ; . So
Thus,
where , , . In other words,
The expression in the denominator can be expressed as .
Below we propose several useful identities from classical and hyperbolic trigonometries.
If , i.e., .
Assume that , . Then
where , .
Suppose that . Then
where , . Therefore, , .
Conclusion: The solution (61) can be rewritten as
where , . Formula (64) takes the form:
where , ; , , .
The function (71) is strictly positive and, being unbounded, is periodic with period .
Remark 3.
Suppose that in (56), i.e.,
Therefore,
If
Put , and assume that has three simple real roots . Then (72) possesses the special solution and stands for the Jacobi elliptic function with modulus [17].
The cubic equation , possesses three simple real roots if and only if has two simple real roots such that , . In our case , the coefficients of are , B, 0, C and the corresponding roots of are , . So and guarantee the existence of three simple real roots of . Certainly, .
Assume that in (56), i.e., the biquadratic polynomial
According to [17], the equation possesses the solution
where , and the simple real roots of are , , , the modulus , , .
As it concerns (73), there is a table for the solutions of (73) expressed by Jacobi elliptic functions for special values of the coefficients .
Example. Consider (73) with the following coefficients depending on the parameter : , , . Then it possesses the elliptic function solutions , .
Formulas (61) and (70) can be found directly, using the fact that , . Similarly, . So , . The second solution blows up for and .
6. Appendix on the Solvability of the Cauchy Problem for the Schrödinger Operator (3), u|t=0 = u0(x) in the Space W ∖ 0, λ < 0
For the sake of completeness, we shall prove unicity of (3) under the additional condition . Assume that , are two solutions of (3) having the same initial data and denote . Then
and we multiply both sides of (75) by and integrate in . Thus,
Taking the imaginary part of (76), we obtain that
In fact, . Having in mind that and implies that we conclude that for , :
Therefore,
Without loss of generality, we suppose that , i.e.,
The continuous function , satisfies the inequality
(Gronwall Lemma)
Unicity is verified.
We know that is not Lipschitz near 0. On the other hand, if , , then
7. Discussion and Open Problems
In optics, higher-order PDE of Schrödinger type could appear, namely
being polynomials of , .
A simple example is the Focas–Lenells equation (FLE)
where are real constants. We are looking for a solution of (80) having the form
-real, , all the coefficients being real-valued.
Taking (82) into (81) and splitting the real and imaginary parts, we obtain for a fourth-order ODE and third-order ODE with real coefficients. We take the coefficients of the third-order ODE to be zero and conclude that
In general, and these constants are real.
One can easily guess the validity of the following two propositions.
Proposition 1.
The soliton-type function
, -real, satisfies
if and only if , .
(84) does not verify (83).
Proposition 2.
- (1)
- , , , ; , , .
- (2)
- , , , ; , , , , where , .
Equation (86) does not satisfy (85).
In a similar way, one can find a blowing up solution of (83). We can reduce the order of (83) by two units, obtaining a non-autonomous second-order ODE for .
The open problem is to find soliton (blowing up)-type solutions of (80). One can try to construct soliton solutions by using the method of a priori estimates.
8. Conclusions
In this paper, we construct exact solutions of several model examples of semilinear PDE arising in mathematical physics. At first we study the parabolic PDE with nonlinearity and initial data , . The corresponding Cauchy problem possesses a unique solution for in the class of exponentially increasing functions u, , , . The solutions are either globally defined in t or the phase of blows up for some finite . Much more complicated is the case of the Schrödinger equation with nonlinearity , , . Here , , , , . If , there exists smooth periodic such that . It is interesting to note that is periodic but we find here a necessary and sufficient condition for periodicity of showing that is very rarely periodic.
For the first time, we investigate the case and prove that the smooth curve is bounded and located in the half plane being tangential to the imaginary axes at the origin, , for , for , while describes a focus in with center 0.
For the higher-order Schrödinger equations with power and power-logarithmic nonlinearities, we are looking for solutions of the type , -real, , , linear real-valued in . We split the corresponding real and imaginary parts and reduce the solvability of that semilinear PDE to the solvability of appropriate second-order autonomous ODE. By means of the method of first integral (used in mechanical processes of one degree of freedom), we obtain directly the solutions of type solitons, kinks, blowing up, etc. We propose here solutions of the type , , , , Jacobi elliptic functions that are found directly. In the higher-order case, things are complicated. If the appropriate autonomous semilinear ODEs are of even order by using the method of first integral and the change , we can reduce the order by (at least) two units, obtaining, for example, in the fourth-dimensional case, a second-order Emden–Fawler ODE.
Author Contributions
Conceptualization, P.P. and A.S.; methodology, P.P. and A.S.; investigation, P.P. and A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The second author acknowledge the project Machine learning through physics informed neural networks, KP06-H62/6.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lax, P. Asymptotic Solutions of Oscillatory Initial Value Problems. Duke Math. J. 1957, 24, 627–646. [Google Scholar] [CrossRef]
- Arnol’d, V. Ordinary Differential Equations; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Arnol’d, V. Mathematical Methods of Classical Mechanics; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Dwight, H. Tables of Integrals and Other Mathematical Data; The Mc Millan Co.: New York, NY, USA, 1961. [Google Scholar]
- Kamke, E. Differentialgleichungen; Lösungsmethoden und Lössungen: Leipzig, Germany, 1959. [Google Scholar]
- Whittaker, E.; Watson, G. A Course of Modern Analysis; Cambridge University Press: Cambridge, UK, 1927. [Google Scholar]
- Hirota, R. The Direct Method in Soliton Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Kudryashov, N. Simplest equation method to look for exact solutions of nonlinear differential equations. Chaos Solitons Fractals 2005, 24, 1217–1231. [Google Scholar] [CrossRef]
- Bialynicki-Birula, I.; Mycielski, J. Nonlinear wave mechanics. Ann. Phys. 1976, 100, 62–63. [Google Scholar] [CrossRef]
- Krolikowski, W.; Edmundson, D.; Bang, O. Unified model for partially coherent solitons in logarithmically nonlinear media. Phys. Rev. E 2000, 61, 3122–3126. [Google Scholar] [CrossRef]
- Hefter, E. Applications of the nonlinear Schrödinger equation with a logarithmic inhomogeneous term to nuclear physics. Phys. Rev. A 1985, 32, 1201–1204. [Google Scholar] [CrossRef] [PubMed]
- Hansson, T.; Anferson, D.; Lisak, M. Propagation of partially coherent solitons in saturable logarithmic media: A comparative analysis. Phys. Rev. A 2009, 80, 033819. [Google Scholar] [CrossRef]
- Avdeenkov, A.; Zloschchastiev, K. Quantum Bose liquids with logarithmic singularity. Self-sustainability and emergence of special extent. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 195303. [Google Scholar] [CrossRef]
- Bao, W.; Carles, R.; Su, C.; Tang, Q. Regularized numerical methors for logarithmic Schrödinger equation. Numer. Math. 2019, 143, 467–487. [Google Scholar] [CrossRef]
- Ferriere, G. The focusing logarithmic Schrödinger equation: Analysis of breathers and nonlinear superposition. Duscrete Cont. Dyn. Syst. 2020, 40, 6247–6274. [Google Scholar] [CrossRef]
- Carles, R. Logarithmic Schrödinger equation and isothermal fluids. Ems Math. Sci. 2022, 9, 99–134. [Google Scholar] [CrossRef]
- Popivanov, P.; Slavova, A. An Introduction. In Nonlinear Waves; Series on Analysis, Applications and Computation; World Scientific: Singapore, 2011; Volume 4. [Google Scholar]
- Popivanov, P.; Slavova, A. A geometrical approach. In Nonlinear Waves; Series on Analysis, Applications and Computation; World Scientific: Singapore, 2018; Volume 9. [Google Scholar]
- Zayed, E.; Shohib, R.; Alngar, M.; Biswas, A.; Yildirim, Y.; Dakova, A.; Moraru, L.; Alshehri, H. Dispersive optical solitons with Radhakrishnan-Kundu-Lakshmanan equation having multiplicative white noise by enhanced Kudryashov’s method and extended simplest equation. C. R. Acad. Bulg. Sci. 2023, 76, 849–862. [Google Scholar] [CrossRef]
- Cazenave, T.; Haraux, A. Equations d’evolution avec non-linearite logarithmique. Ann. Fac. Sci. Toulouse Math. 1980, 2, 21–51. [Google Scholar] [CrossRef]
- Lieb, E.; Loss, M. Analysis. In Graduate Studies in Mathematics, 2nd ed.; AMS: Providence, RI, USA, 2001; Volume 14. [Google Scholar]
- Ardila, A. Orbital stability of Gausson solutions to logarithmic Schrödinger equations. Electron. J. Differ. Equ. 2016, 2016, 335. [Google Scholar]
- Kutz, J. Model locked solution lasers. Siam Rev. 2006, 48, 629–678. [Google Scholar] [CrossRef]
- Friedman, A. Partial Differential Equations of Parabolic Type; Prentice Hall-Inc.: Englewood Cliffs, NY, USA, 1964. [Google Scholar]
- Evans, L. Partial Differential Equations. In Graduate Studies in Mathematics; AMS: Providence, RI, USA, 1998; Volume 19. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).