Deep Graph Learning-Based Surrogate Model for Inverse Modeling of Fractured Reservoirs
Abstract
1. Introduction
- (1)
- A novel deep graph learning-based feature learning method for the complex multi-scale fracture network is proposed. In this approach, the fracture network is represented as graph data, and the feature learning is performed based on parameters of each discrete fracture, which can effectively retain the discrete characteristics and geometric information of the fracture network. To the best of our knowledge, no work has reported using the deep graph learning method for the feature learning of a fracture network.
- (2)
- Based on the deep graph learning and multi-layer recurrent neural networks, a surrogate model for the embedded fracture numerical simulation was developed for the inversion of fracture distribution. This surrogate model can predict the production dynamics of wells under different fracture distribution conditions. Compared with EDFM simulation, the proposed surrogate model significantly reduces the computation cost of production prediction.
- (3)
- An effective surrogate-based inverse modeling framework was designed, which integrates the population-based differential evolution (DE) algorithm with the proposed surrogate model. Because of the cheap computational cost of the surrogate model, the search performance of the DE algorithm can be fully released and improve the solving efficiency of the inversion.
2. Methods
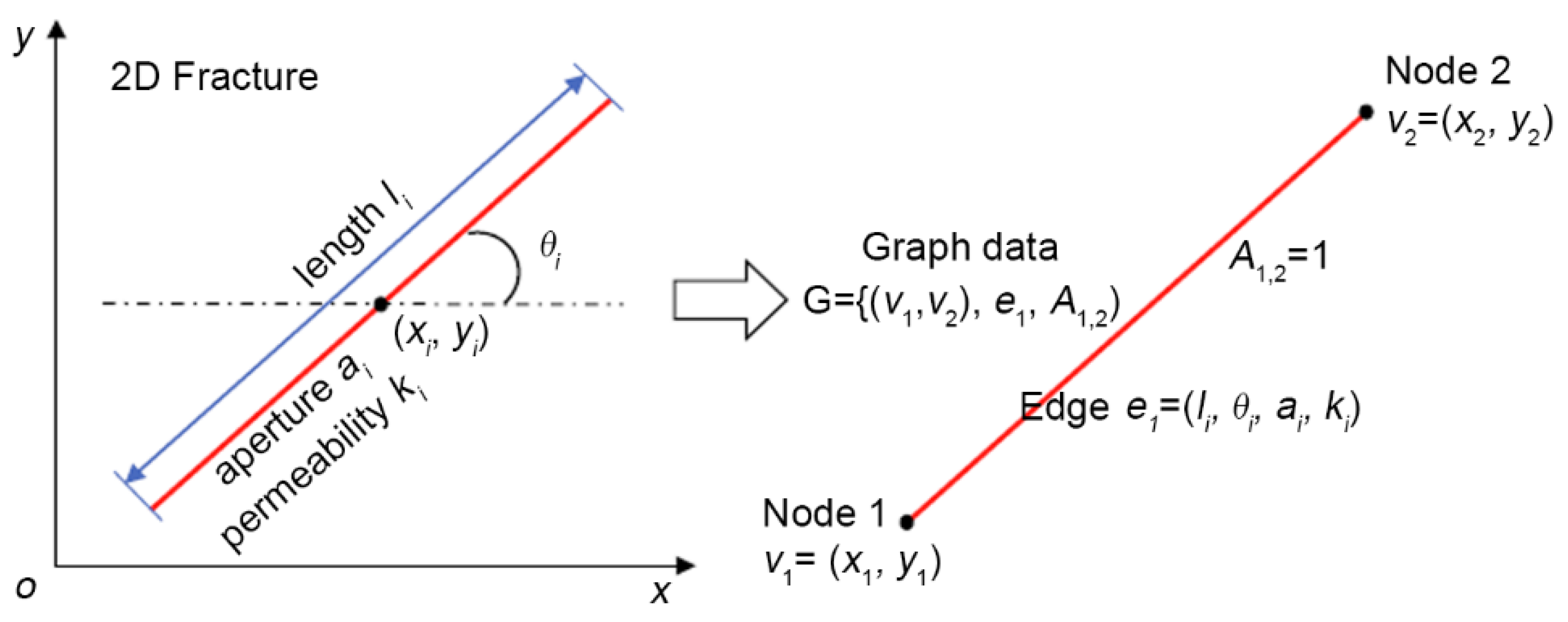
2.1. Generation of 2D Multi-Scale Fracture Network
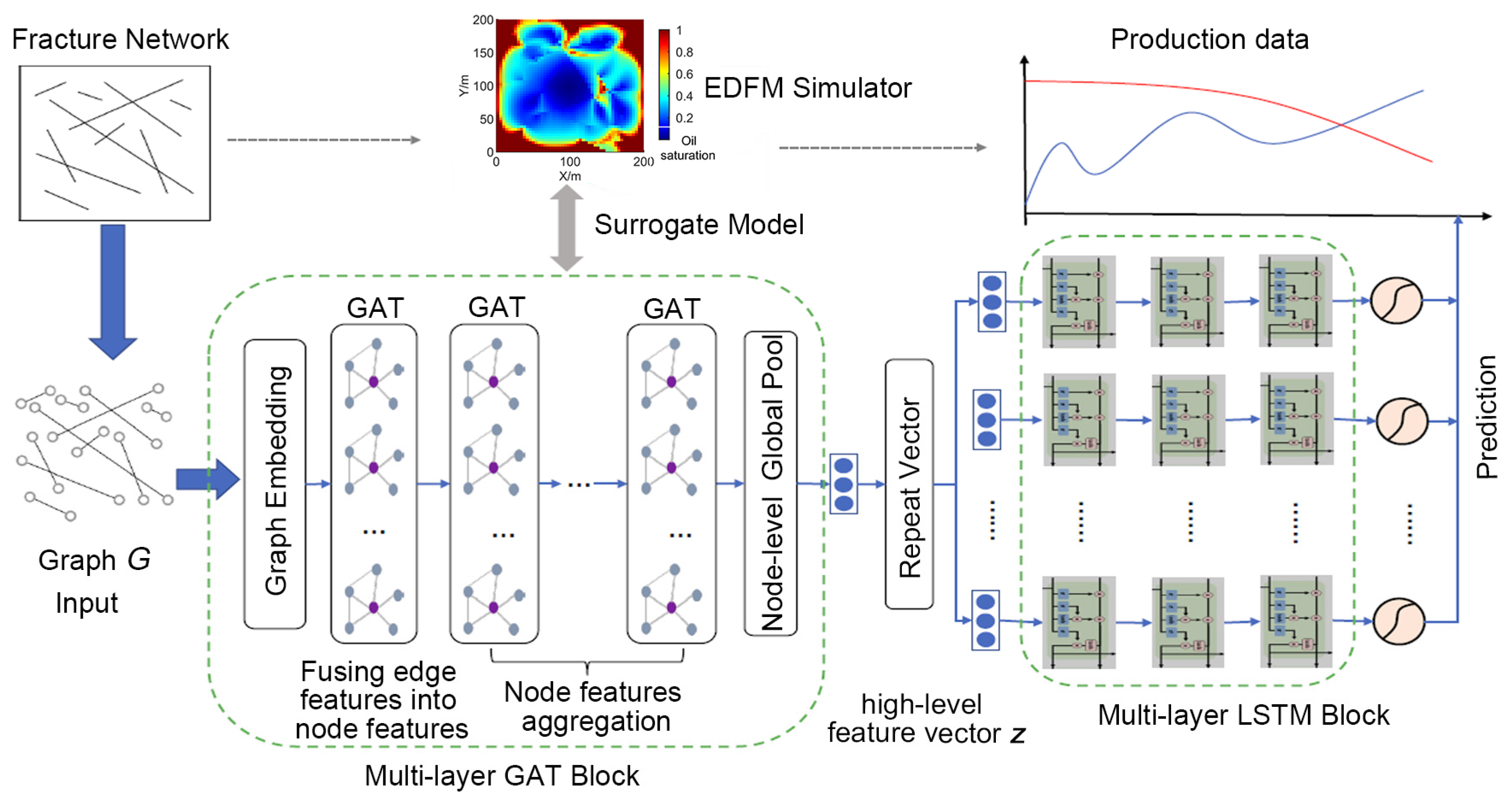
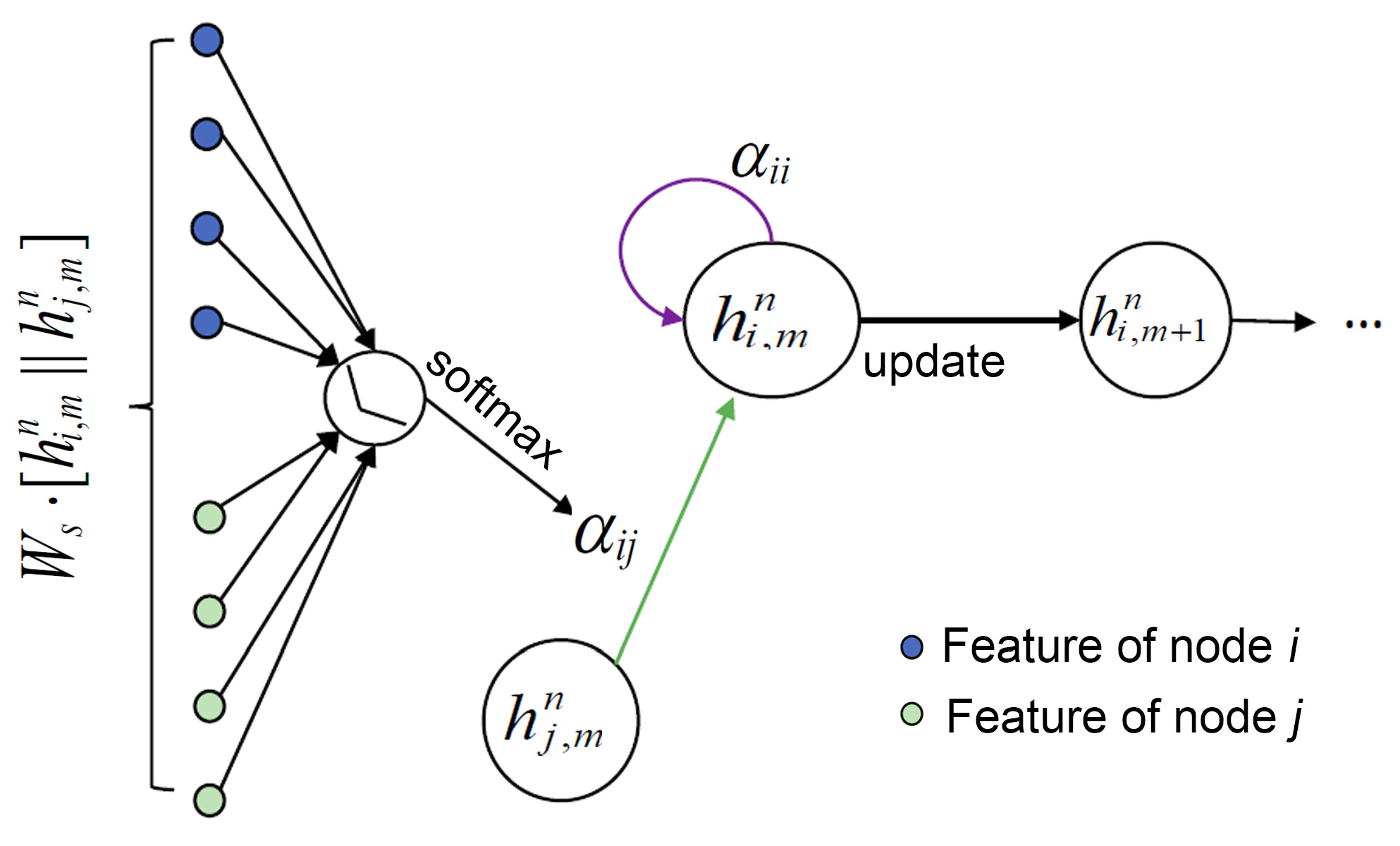
2.2. GAT-LSTM Surrogate Model
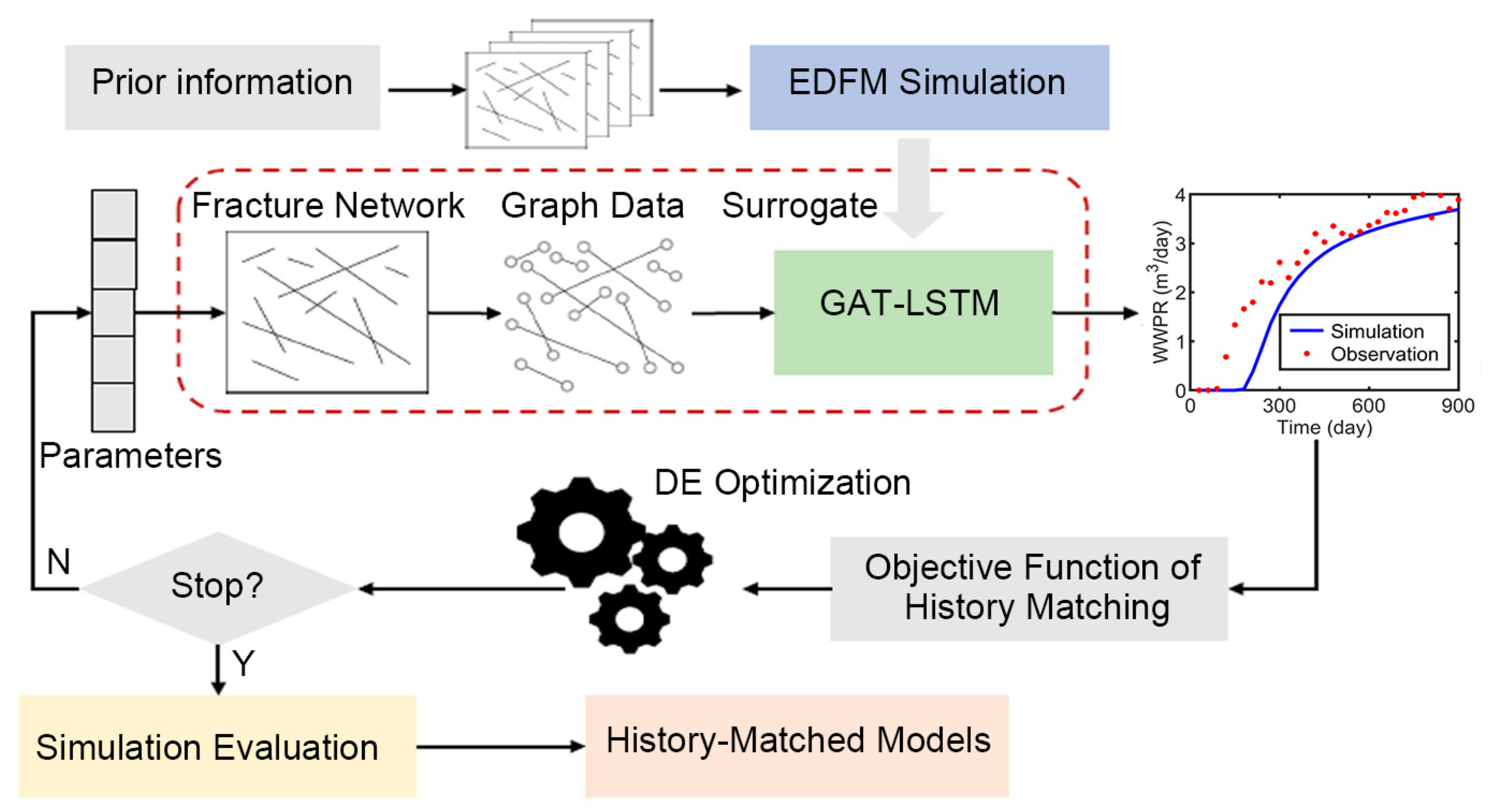
2.3. The GAT-LSTM Surrogate-Based Inverse Modeling Workflow
3. Case Studies
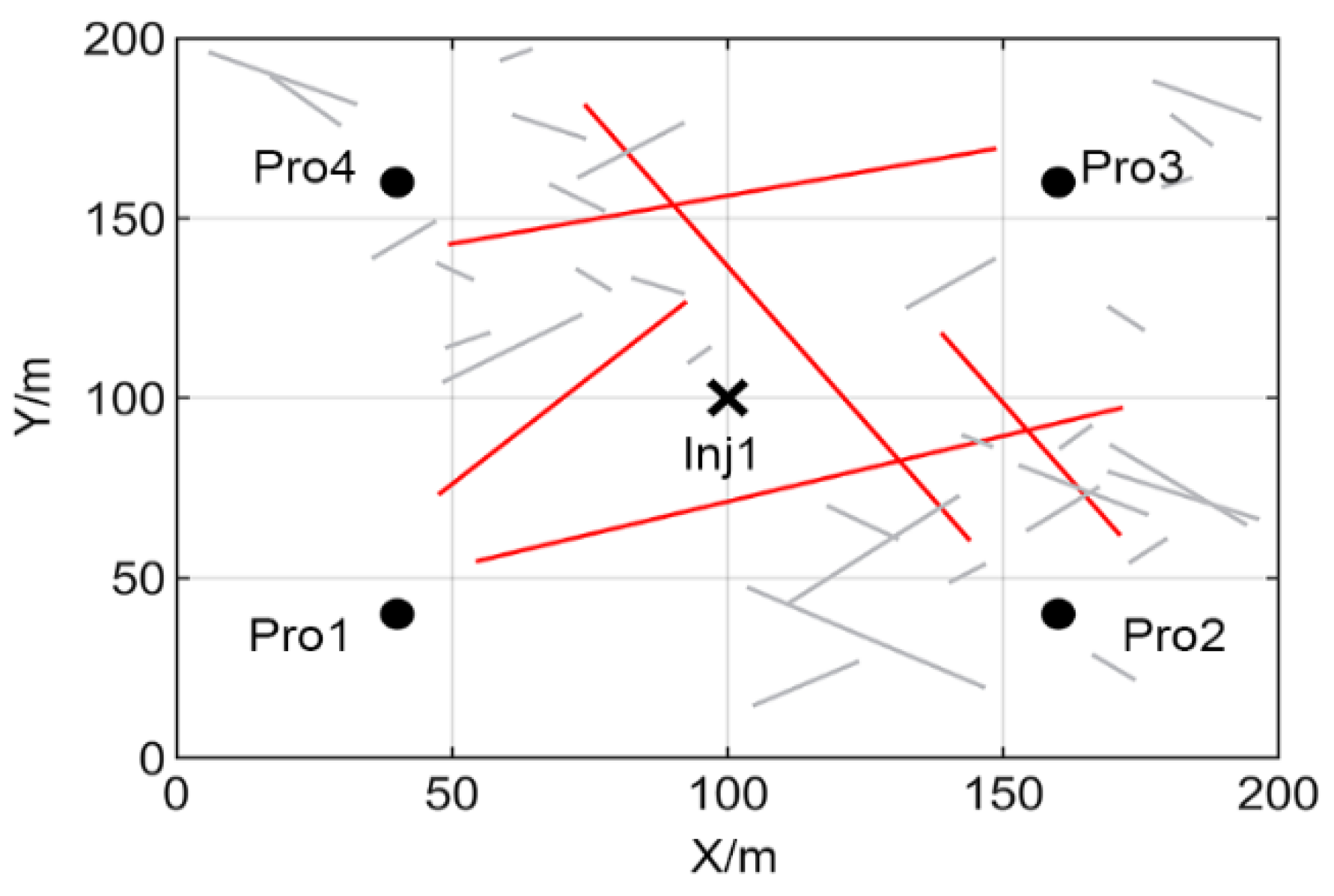
3.1. Two-Dimensional Fractured Reservoir Model
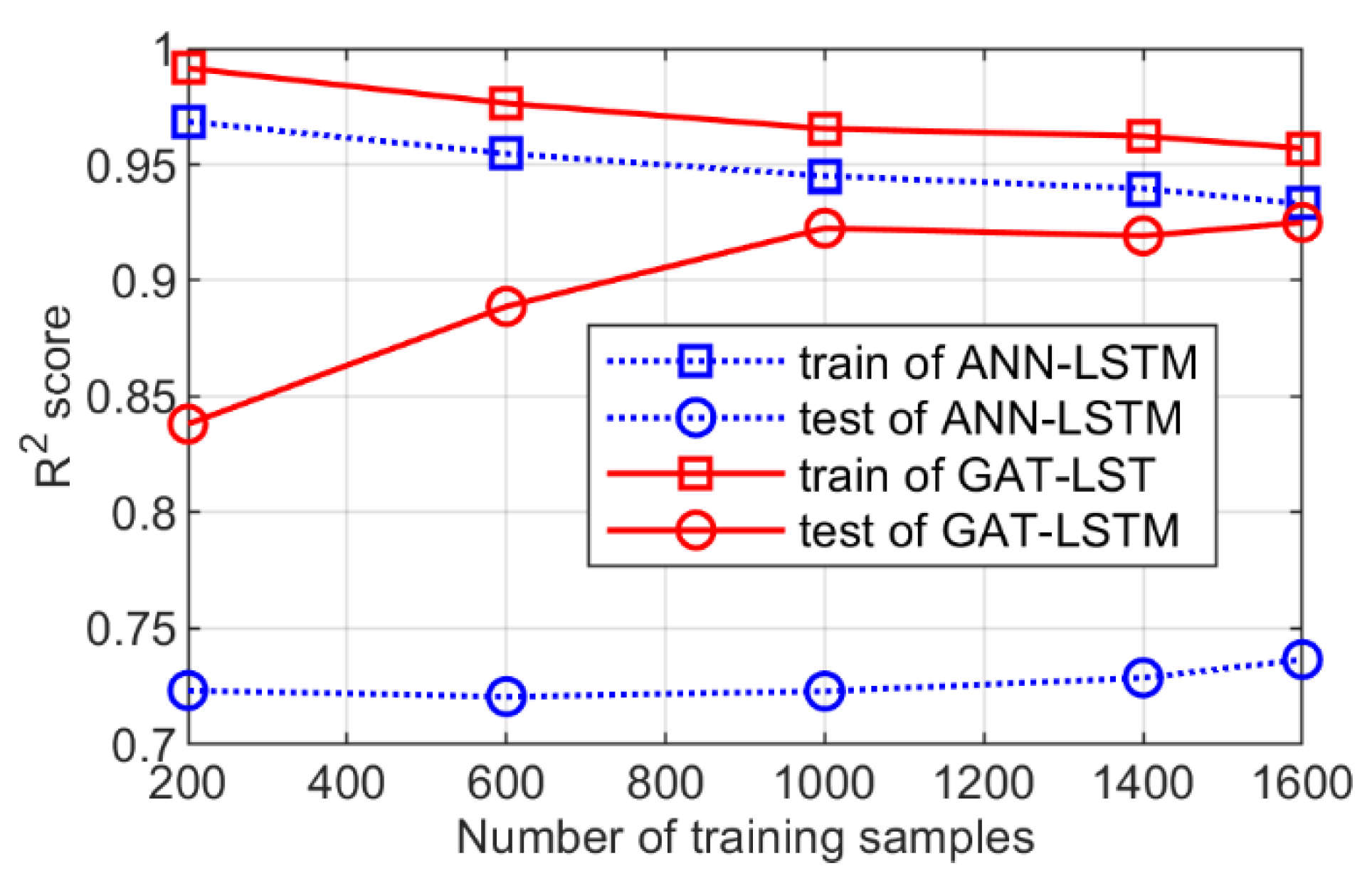
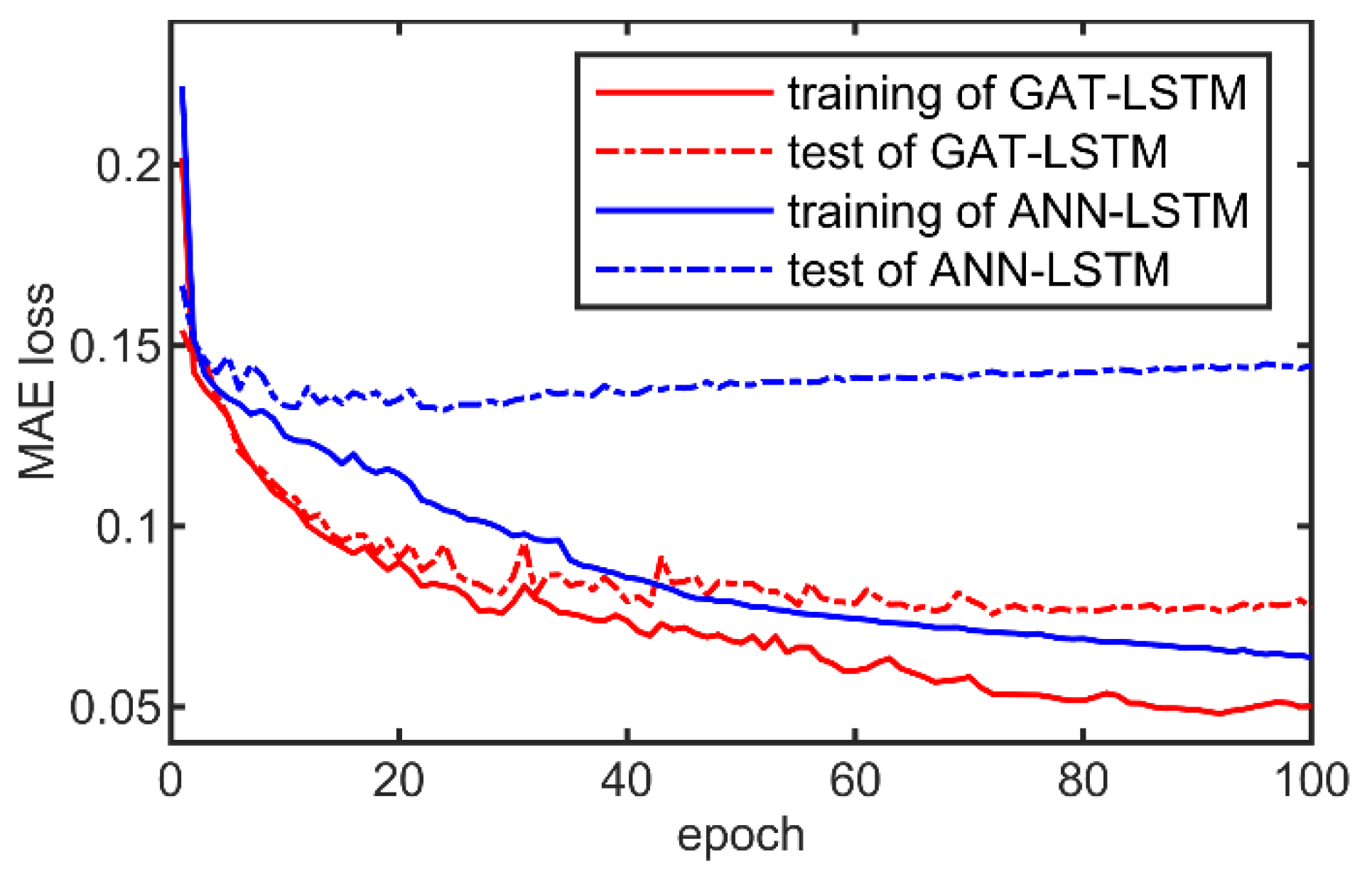
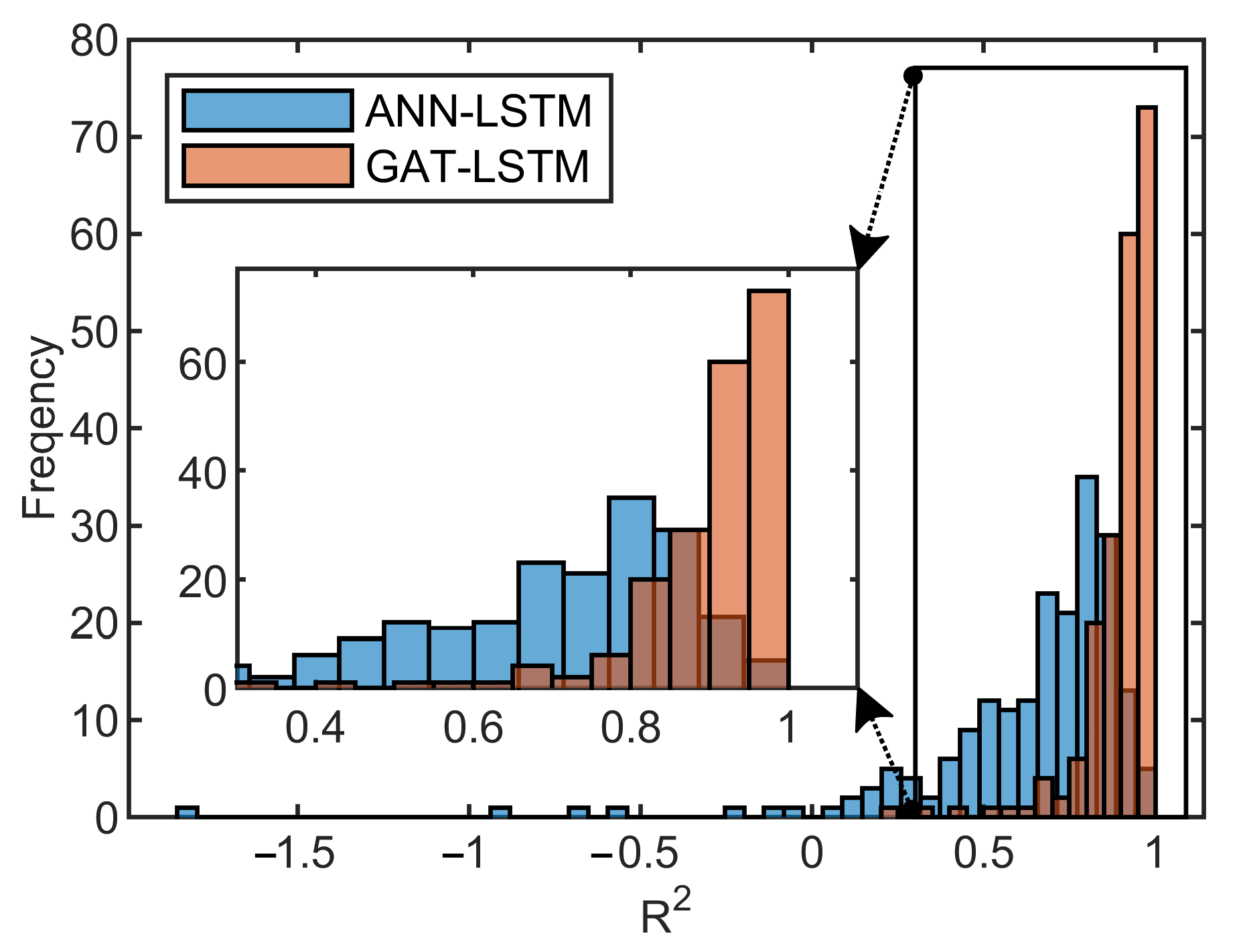
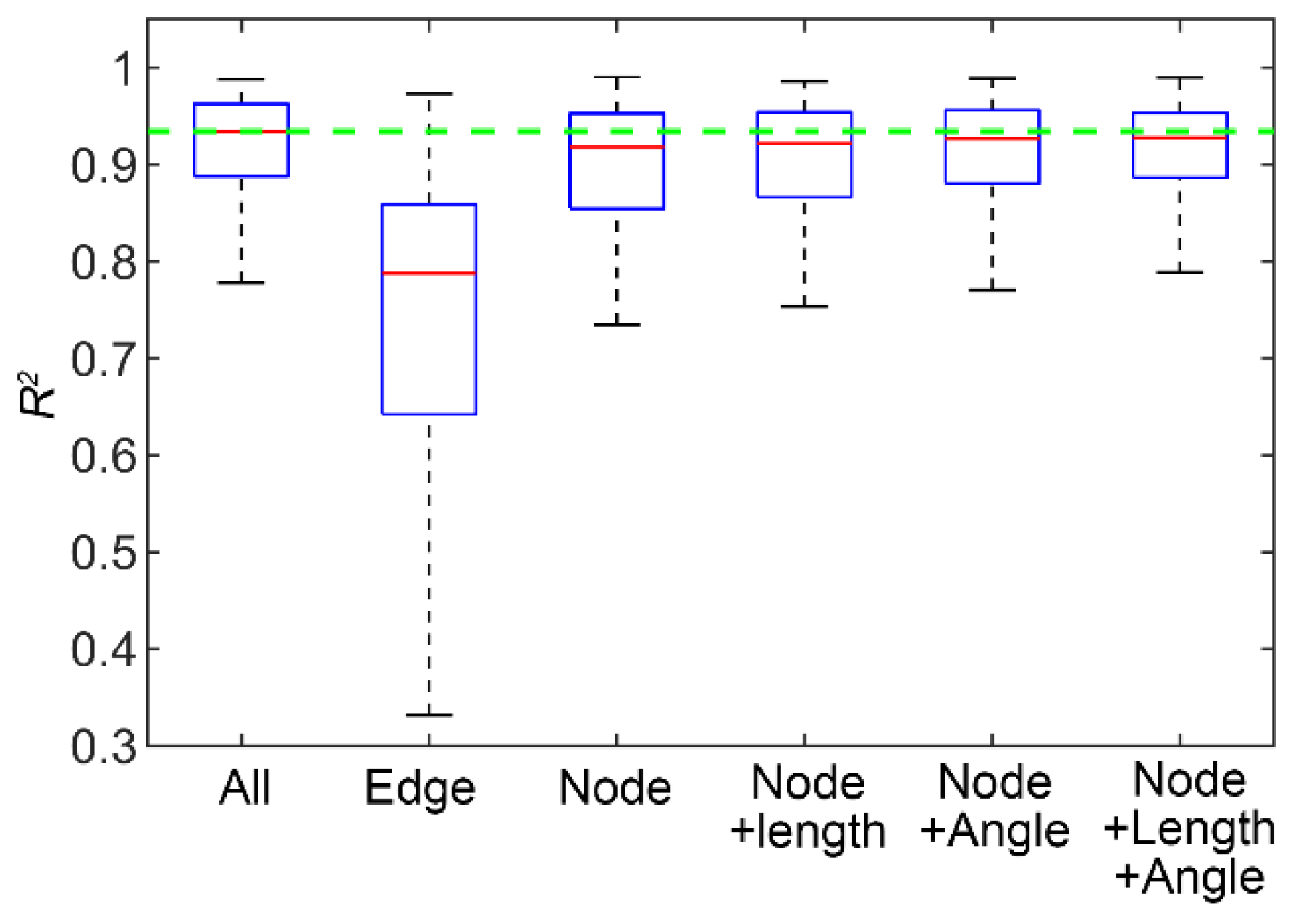
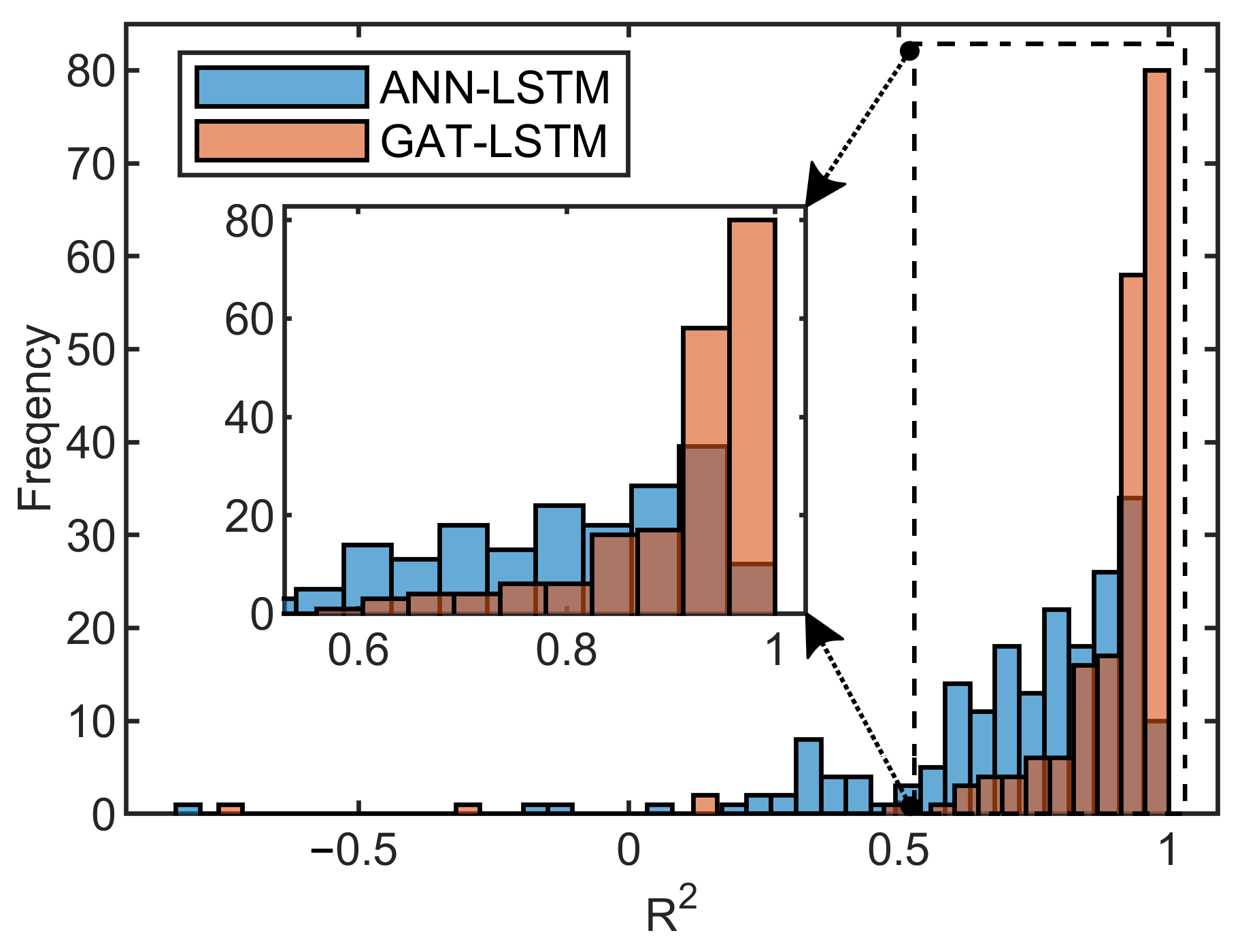
3.2. Analysis of the Surrogate Model Performance
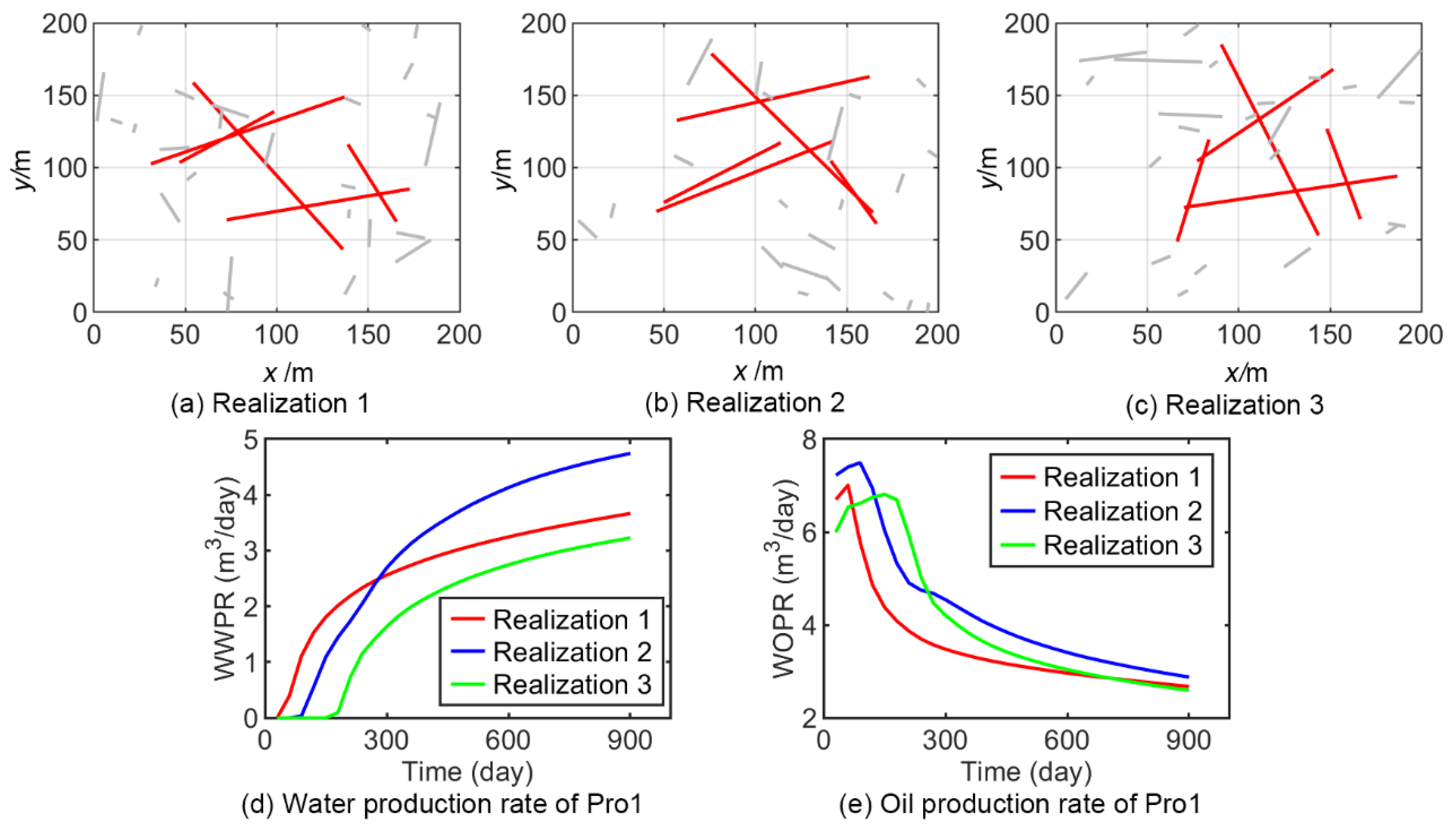
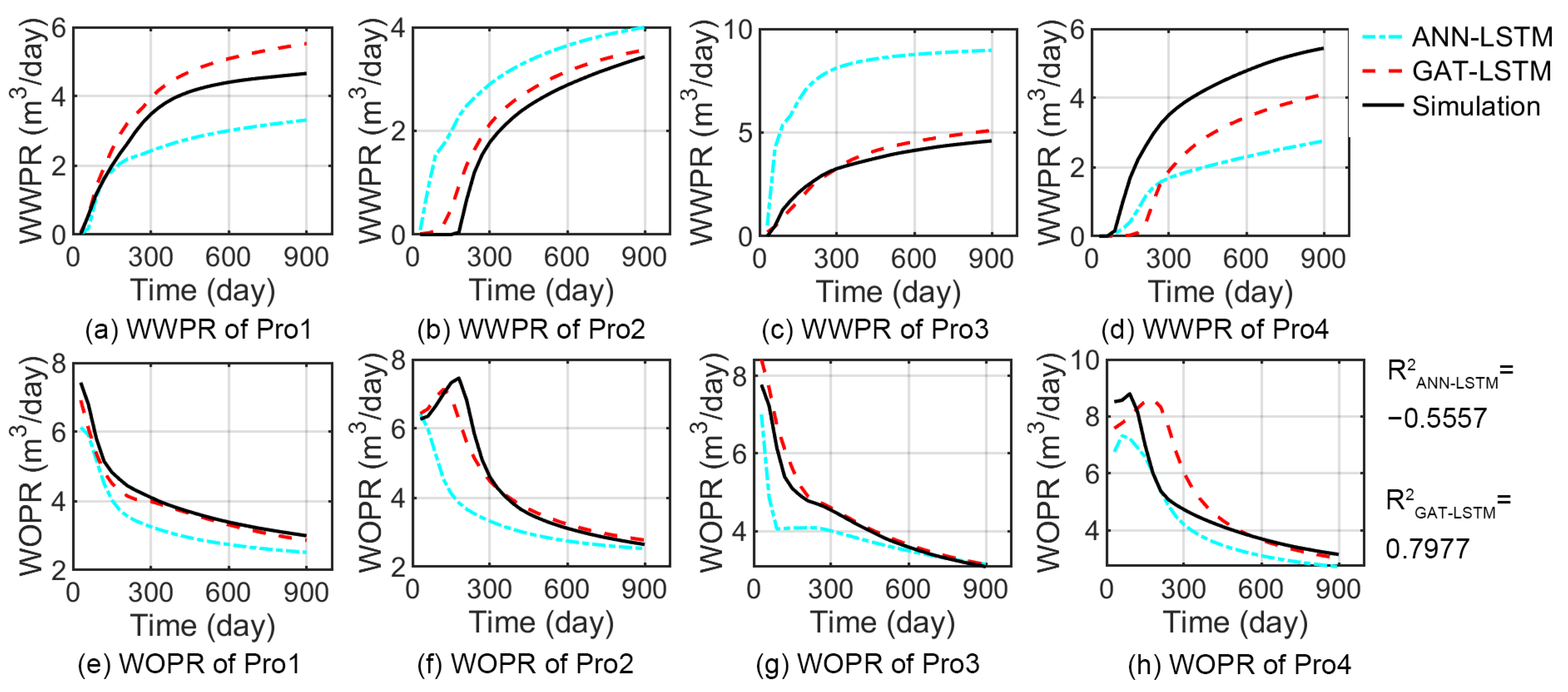
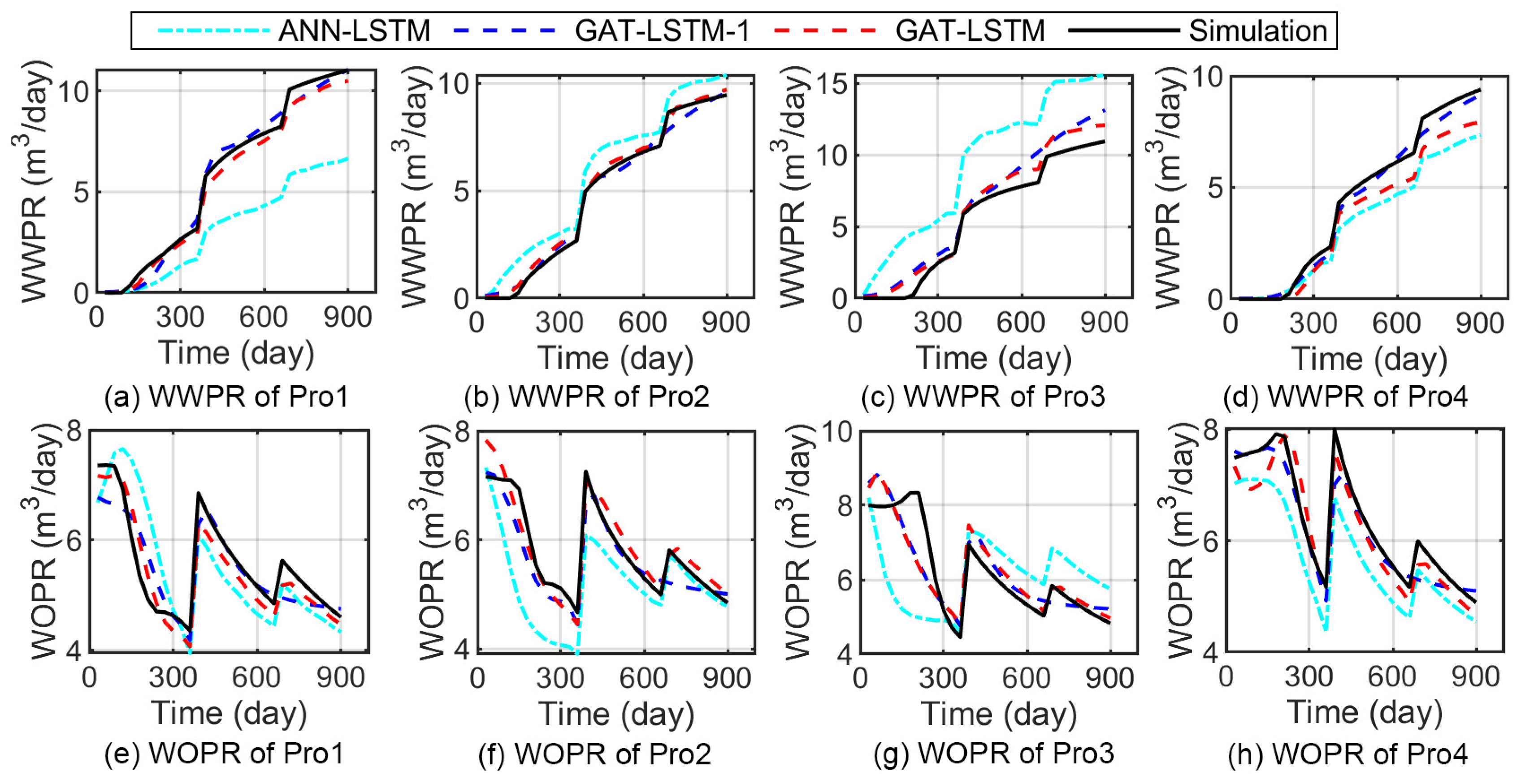
3.3. Test the Performance of the Model under Varying Operational Conditions
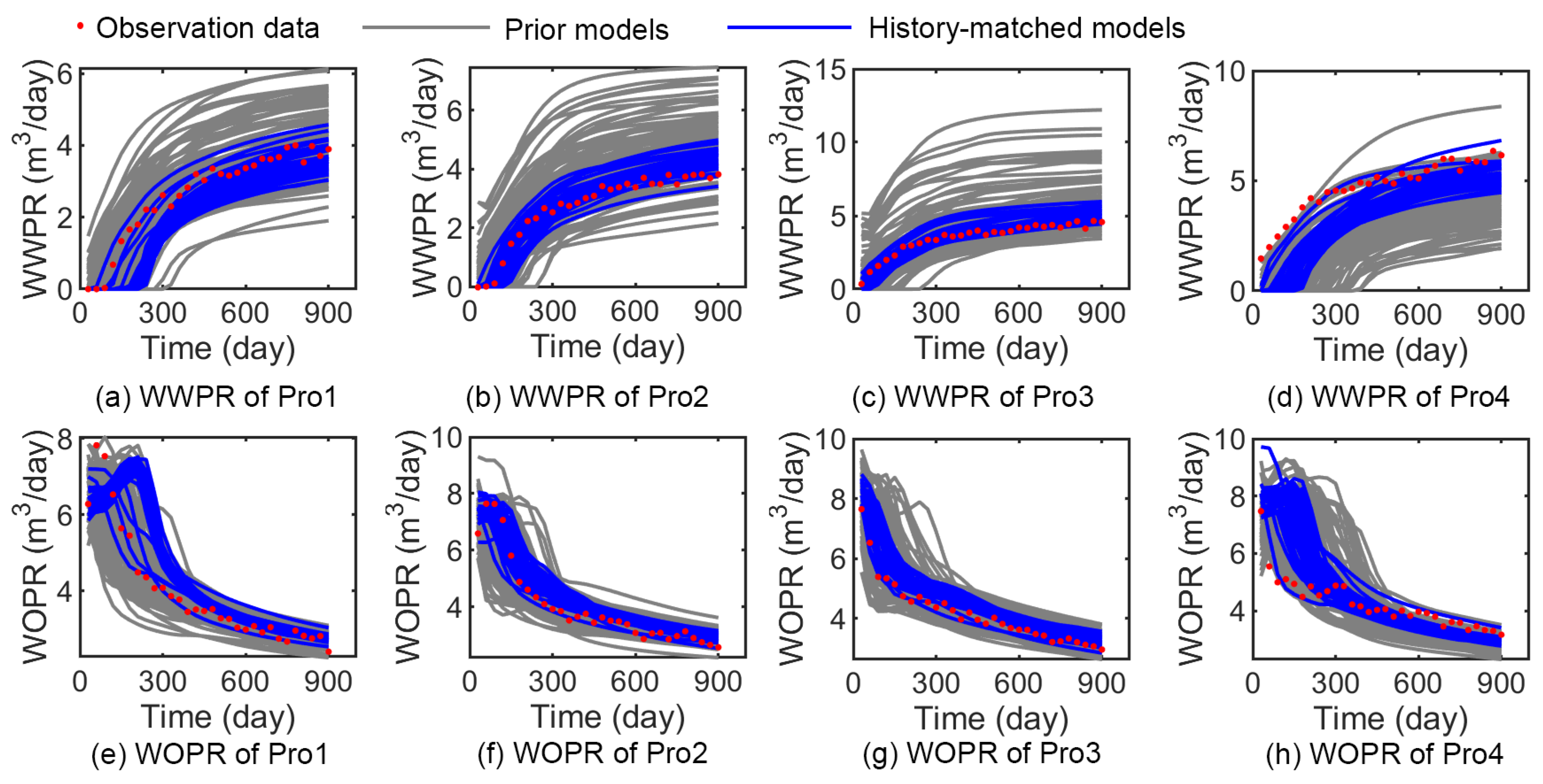
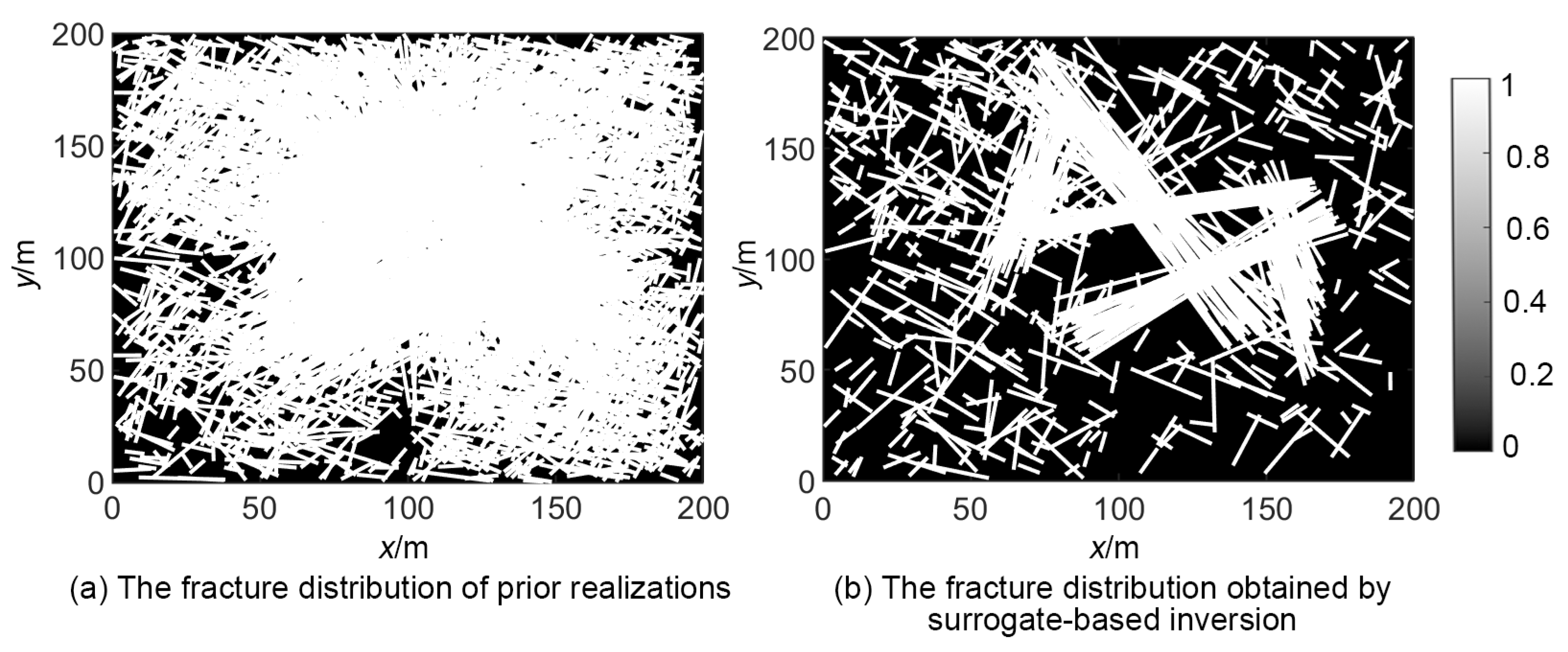
3.4. Results of Surrogate-Based Inverse Modeling
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abbasi, M.; Sharifi, M.; Kazemi, A. Fluid flow in fractured reservoirs: Estimation of fracture intensity distribution, capillary diffusion coefficient and shape factor from saturation data. J. Hydrol. 2020, 582, 124461. [Google Scholar] [CrossRef]
- Ghorbanidehno, H.; Kokkinaki, A.; Lee, J.; Darve, E. Recent developments in fast and scalable inverse modeling and data assimilation methods in hydrology. J. Hydrol. 2020, 591, 125266. [Google Scholar] [CrossRef]
- Tang, M.; Liu, Y.; Durlofsky, L.J. A deep-learning-based surrogate model for data assimilation in dynamic subsurface flow problems. J. Comput. Phys. 2020, 413, 109456. [Google Scholar] [CrossRef]
- Hamdi, H.; Couckuyt, I.; Sousa, M.C.; Dhaene, T. Gaussian Processes for history-matching: Application to an unconventional gas reservoir. Comput. Geosci. 2017, 21, 267–287. [Google Scholar] [CrossRef]
- Dachanuwattana, S.; Yu, W.; Sepehrnoori, K. An efficient MCMC history matching workflow using fit-for-purpose proxies applied in unconventional oil reservoirs. J. Pet. Sci. Eng. 2019, 176, 381–395. [Google Scholar] [CrossRef]
- Zhang, H.; Sheng, J.J. Surrogate-Assisted Multiobjective Optimization of a Hydraulically Fractured Well in a Naturally Fractured Shale Reservoir with Geological Uncertainty. SPE J. 2022, 27, 307–328. [Google Scholar] [CrossRef]
- Zhang, D.; Li, H. Efficient Surrogate Modeling Based on Improved Vision Transformer Neural Network for History Matching. SPE J. 2023, 28, 3046–3062. [Google Scholar] [CrossRef]
- Zhong, Z.; Sun, A.Y.; Ren, B.; Wang, Y. A Deep-Learning-Based Approach for Reservoir Production Forecast under Uncertainty. SPE J. 2021, 26, 1314–1340. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, J.; Ma, X.; Yao, C.; Zhang, L.; Yang, Y.; Wang, J.; Yao, J.; Zhao, H. History Matching of Naturally Fractured Reservoirs Using a Deep Sparse Autoencoder. SPE J. 2021, 26, 1700–1721. [Google Scholar] [CrossRef]
- Chen, G.; Luo, X.; Jiao, J.J.; Jiang, C. Fracture network characterization with deep generative model based stochastic inversion. Energy 2023, 273, 127302. [Google Scholar] [CrossRef]
- Yan, B.; Xu, Z.; Gudala, M.; Tariq, Z.; Finkbeiner, T. Reservoir Modeling and Optimization Based on Deep Learning with Application to Enhanced Geothermal Systems. In Proceedings of the SPE Reservoir Characterisation and Simulation Conference and Exhibition, Abu Dhabi, United Arab Emirates, 24–26 January 2023. [Google Scholar]
- Kim, Y.D.; Durlofsky, L.J. Neural network surrogate for flow prediction and robust optimization in fractured reservoir systems. Fuel 2023, 351, 128756. [Google Scholar] [CrossRef]
- Rao, X. A generic workflow of projection-based embedded discrete fracture model for flow simulation in porous media. Comput. Geosci. 2023, 27, 561–590. [Google Scholar] [CrossRef]
- Xu, Y.; Sepehrnoori, K. Modeling fracture transient flow using the Embedded Discrete Fracture Model with nested local grid refinement. J. Pet. Sci. Eng. 2022, 218, 110882. [Google Scholar] [CrossRef]
- Shaked, B.; Uri, A.; Eran, Y. How Attentive are Graph Attention Networks? In Proceedings of the International Conference on Learning Representations, Virtual Event, 25–29 April 2022.
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Youshua, B. Graph Attention Networks. In Proceedings of the 6th International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Yu, X.; Zhou, Y. Lstm and gru neural network performance comparison study: Taking yelp review dataset as an example. In Proceedings of the 2020 International Workshop on Electronic Communication and Artificial Intelligence (IWECAI), Shanghai, China, 12–14 June 2020; pp. 98–101. [Google Scholar]
- Wang, N.; Chang, H.; Kong, X.-Z.; Zhang, D. Deep learning based closed-loop well control optimization of geothermal reservoir with uncertain permeability. Renew. Energy 2023, 211, 379–394. [Google Scholar] [CrossRef]
- Bhatti, U.A.; Tang, H.; Wu, G.; Marjan, S.; Hussain, A. Deep learning with graph convolutional networks: An overview and latest applications in computational intelligence. Int. J. Intell. Syst. 2023, 2023, 8342104. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, L.; Zaki, M. Iterative deep graph learning for graph neural networks: Better and robust node embeddings. Adv. Neural Inf. Process. Syst. 2020, 33, 19314–19326. [Google Scholar]
- Xia, F.; Sun, K.; Yu, S.; Aziz, A.; Wan, L.; Pan, S.; Liu, H. Graph learning: A survey. IEEE Trans. Artif. Intell. 2021, 2, 109–127. [Google Scholar] [CrossRef]
- Mohamed, H.A.; Pilutti, D.; James, S.; Del Bue, A.; Pelillo, M.; Vascon, S. Locality-aware subgraphs for inductive link prediction in knowledge graphs. Pattern Recognit. Lett. 2023, 167, 90–97. [Google Scholar] [CrossRef]
- Ling, C.; Jiang, J.; Wang, J.; Thai, M.T.; Xue, R.; Song, J.; Qiu, M.; Zhao, L. Deep graph representation learning and optimization for influence maximization. In Proceedings of the International Conference on Machine Learning, Sanya, China, 27–29 December 2023; pp. 21350–21361. [Google Scholar]
- Gligorijević, V.; Renfrew, P.D.; Kosciolek, T.; Leman, J.K.; Berenberg, D.; Vatanen, T.; Chandler, C.; Taylor, B.C.; Fisk, I.M.; Vlamakis, H. Structure-based protein function prediction using graph convolutional networks. Nat. Commun. 2021, 12, 3168. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, K.; Yao, C.; Zhang, L.; Wang, J.; Yang, Y.; Yao, J. Multiscale-Network Structure Inversion of Fractured Media Based on a Hierarchical-Parameterization and Data-Driven Evolutionary-Optimization Method. SPE J. 2020, 25, 2729–2748. [Google Scholar] [CrossRef]
- Aghli, G.; Moussavi-Harami, R.; Mohammadian, R. Reservoir heterogeneity and fracture parameter determination using electrical image logs and petrophysical data (a case study, carbonate Asmari Formation, Zagros Basin, SW Iran). Pet. Sci. 2020, 17, 51–69. [Google Scholar] [CrossRef]
- Klimczak, C.; Schultz, R.; Parashar, R.; Reeves, D. Cubic law with aperture-length correlation: Implications for network scale fluid flow. Hydrogeol. J. 2010, 18, 851–862. [Google Scholar] [CrossRef]
- Xu, J.; Li, Z.; Du, B.; Zhang, M.; Liu, J. Reluplex made more practical: Leaky ReLU. In Proceedings of the 2020 IEEE Symposium on Computers and Communications (ISCC), Rennes, France, 7–10 July 2020; pp. 1–7. [Google Scholar]
- Ma, X.; Zhang, K.; Zhao, H.; Zhang, L.; Wang, J.; Zhang, H.; Liu, P.; Yan, X.; Yang, Y. A vector-to-sequence based multilayer recurrent network surrogate model for history matching of large-scale reservoir. J. Pet. Sci. Eng. 2022, 214, 110548. [Google Scholar] [CrossRef]
- Bao, K.; Lie, K.-A.; Møyner, O.; Liu, M. Fully implicit simulation of polymer flooding with MRST. Comput. Geosci. 2017, 21, 1219–1244. [Google Scholar] [CrossRef]
- Shah, S.; Møyner, O.; Tene, M.; Lie, K.-A.; Hajibeygi, H. The multiscale restriction smoothed basis method for fractured porous media (F-MsRSB). J. Comput. Phys. 2016, 318, 36–57. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Abadi, M.; Agarwal, A.; Barham, P.; Eugene, B. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]
- Ferludin, O.; Eigenwillig, A.; Blais, M.; Zelle, D.; Pfeifer, J.; Sanchez-Gonzalez, A.; Li, W.L.S.; Abu-El-Haija, S.; Battaglia, P.; Bulut, N. Tf-gnn: Graph neural networks in tensorflow. arXiv 2022, arXiv:2207.03522. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
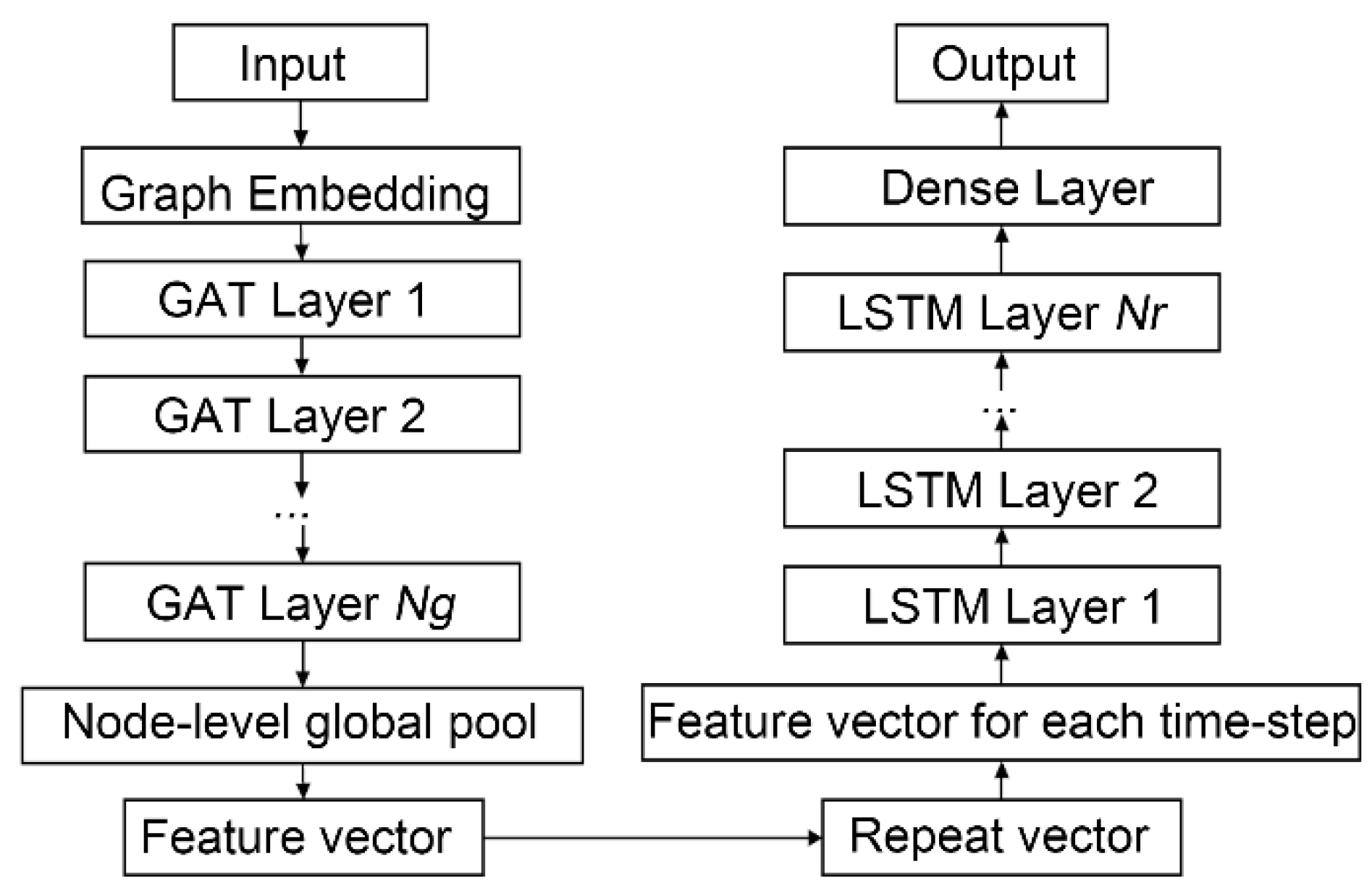



| Component | Layers | Hyper Parameters |
|---|---|---|
| Multi-layer GAT Block | Graph Embedding | d = 128, σ = ReLU |
| GAT Layer 1/2/3/4 | d = 128, w = 3, σ = ReLU | |
| Node-level Global Pool | Max pool | |
| Multi-layer ANN Block | Dense Layer 1 | d = 256, σ = ReLU |
| Dense Layer 2 | d = 128, σ = ReLU | |
| Dense Layer 3 | d = 100, σ = ReLU | |
| Multi-layer LSTM Block | Repeat Vector | t = 30 |
| LSTM Layer 1 | d = 100 | |
| LSTM Layer 2 | d = 100 | |
| Dense Layer 4 | d = 8, σ = tanh |
| x-Coordinate (m) | y-Coordinate (m) | Length (m) | Orientation (Degrees) | |||||
|---|---|---|---|---|---|---|---|---|
| Fracture | True | Initial Range | True | Initial Range | True | Initial Range | True | Initial Range |
| 1 | 109 | 90–130 | 121 | 100–140 | 140 | 130–150 | 120 | 80–130 |
| 2 | 113 | 90–130 | 76 | 70–100 | 125 | 100–130 | 20 | 10–40 |
| 3 | 99 | 80–120 | 156 | 120–160 | 103 | 90–120 | 15 | 10–50 |
| 4 | 70 | 60–100 | 100 | 80–130 | 70 | 60- 80 | 50 | 30–80 |
| 5 | 155 | 130–160 | 90 | 70–120 | 65 | 50–70 | 120 | 100–150 |
| Parameters | True Value | Initial Range |
|---|---|---|
| Fractal Dimension | 1.6 | 1.4–1.7 |
| Intensity D1 (Set 1) | 0.45 | 0.3–0.6 |
| Intensity D2 (Set 2) | 1−D1 | - |
| Mean of Orientation (Set 1) | 35 | 45–75 |
| Sd of Orientation (Set 1) | 10 | 8–15 |
| Mean of Orientation (Set 2) | 150 | 138–178 |
| Sd of Orientation (Set 2) | 10 | 8–15 |
| Proportion Score of Region 1 | 0.1 | 0.1–1 |
| Proportion Score of Region 2 | 0.3 | 0.1–1 |
| Proportion Score of Region 3 | 0.1 | 0.1–1 |
| Proportion Score of Region 4 | 0.3 | 0.1–1 |
| Surrogate Model | R2 > 0.8 | R2 > 0.85 | R2 > 0.9 |
|---|---|---|---|
| ANN-LSTM | 33% | 15.5% | 6% |
| GAT-LSTM | 91% | 81% | 66.5% |
| Inversion Method | Building the Data Set | Training the Model | DE Optimization | Evaluation of the Solutions | Total Time |
|---|---|---|---|---|---|
| Surrogate-based | 150 | 2 | 10 | 10 | 172 |
| Simulation Based | - | - | 2000 | - | 2000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Zhao, J.; Zhou, D.; Zhang, K.; Tian, Y. Deep Graph Learning-Based Surrogate Model for Inverse Modeling of Fractured Reservoirs. Mathematics 2024, 12, 754. https://doi.org/10.3390/math12050754
Ma X, Zhao J, Zhou D, Zhang K, Tian Y. Deep Graph Learning-Based Surrogate Model for Inverse Modeling of Fractured Reservoirs. Mathematics. 2024; 12(5):754. https://doi.org/10.3390/math12050754
Chicago/Turabian StyleMa, Xiaopeng, Jinsheng Zhao, Desheng Zhou, Kai Zhang, and Yapeng Tian. 2024. "Deep Graph Learning-Based Surrogate Model for Inverse Modeling of Fractured Reservoirs" Mathematics 12, no. 5: 754. https://doi.org/10.3390/math12050754
APA StyleMa, X., Zhao, J., Zhou, D., Zhang, K., & Tian, Y. (2024). Deep Graph Learning-Based Surrogate Model for Inverse Modeling of Fractured Reservoirs. Mathematics, 12(5), 754. https://doi.org/10.3390/math12050754








