Abstract
The solution of the nonlinear (NL) vibration problem of the interaction of laminated plates made of exponentially graded orthotropic layers (EGOLs) with elastic foundations within the Kirchhoff–Love theory (KLT) is developed using the modified Lindstedt–Poincaré method for the first time. Young’s modulus and the material density of the orthotropic layers of laminated plates are assumed to vary exponentially in the direction of thickness, and Poisson’s ratio is assumed to be constant. The governing equations are derived as equations of motion and compatibility using the stress–strain relationship within the framework of KLT and von Karman-type nonlinear theory. NL partial differential equations are reduced to NL ordinary differential equations by the Galerkin method and solved by using the modified Lindstedt–Poincaré method to obtain unique amplitude-dependent expressions for the NL frequency. The proposed solution is validated by comparing the results for laminated plates consisting of exponentially graded orthotropic layers with the results for laminated homogeneous orthotropic plates. Finally, a series of examples are presented to illustrate numerical results on the nonlinear frequency of rectangular plates composed of homogeneous and exponentially graded layers. The effects of the exponential change in the material gradient in the layers, the arrangement and number of the layers, the elastic foundations, the plate aspect ratio and the nonlinearity of the frequency are investigated.
Keywords:
composites; inhomogeneity; NL equations; NL vibration; plates; ground effect; NL frequencies MSC:
74B20; 74E05; 74E10; 74E30; 74F10; 74H10; 74H45; 74K20
1. Introduction
Laminated composite plates continue to be widely used in various fields of transportation, construction, aerospace, nuclear and fossil energy, chemistry and petrochemicals. The application of anisotropic and functionally graded materials increases the bearing capacity of structures. At the same time, using laminated plates in engineering design to reduce weight, increase durability and improve dynamic properties also provides economic advantages. For this reason, the use of laminated functionally graded orthotropic plates in aircraft, satellites, light alloy structures of automobiles and other engineering structures remains up to date. Additionally, depending on the application areas, laminated plates can be designed with different layer arrangements and numbers. Among the above factors affecting the dynamic properties of the plate structure, the functionally graded orthotropic material properties of the layers, as well as the layer arrangement and number, are also very important. All of these factors add additional complexity to the structural safety and reliability assessment. In the vibration analysis of plate structures, material and geometric properties should be taken into account as much as possible as a connection, which is one of the issues that make scientists think.
The natural evolution of plate theory, which is widely presented in the literature, has led to the formation and development of laminated plate theories [1]. Detailed information about the first studies on the laminated anisotropic plates and their development history is presented in monographs [2]. In this study, the main formulations of boundary value problems in laminated anisotropic plate theory were formulated, methods to solve them were developed, and practical applications were realized.
The use of structural elements consisting of layers with piecewise continuously changing material properties in different areas of contemporary technology necessitates the reconsideration of their nonlinear vibration calculations. One of the main reasons for this phenomenon lies in the exponentially graded anisotropic nature of the layers that form laminated structural elements. As is known, although efforts to create analytical models that reflect the reality of the mechanical properties of exponentially graded anisotropic materials are always on the agenda, the number of modeling studies is limited [3,4,5]. However, many studies have been conducted on linear [6,7,8,9,10,11] and nonlinear [12,13,14] vibrations of functionally or exponentially graded orthotropic single and laminated plates. Among these, Fazzolari and Carrera [6,7] studied vibration and thermo-mechanical buckling analysis of anisotropic multilayered composite and sandwich plates by using refined variable kinematic theories. Bacciocchi and Tarantino [8] analyzed the natural frequency behavior of functionally graded orthotropic cross-ply plates based on the finite element method. Zhang et al. [9] examined accurate linear free vibration solutions of orthotropic rectangular thin plates by straightforward finite integral transform method. Krysko et al. [10] presented the mathematical modeling of planar physically nonlinear inhomogeneous plates with rectangular cuts in the three-dimensional formulation, and the finite element method was employed to solve the problem. Hashemi [11] presented layer-wise solutions for variable stiffness laminated composite sandwich plates with curvilinear fibers using the p-version of the finite element method. Dat et al. [12] presented a vibration analysis of an auxetic laminated plate with magneto-electro-elastic face sheets subjected to blast loading. Singh et al. [13] presented the analytical solution of the viscoelastic free vibration problem of in-plane functionally graded orthotropic plates integrated with piezoelectric sensors. Simões et al. [14] studied the maximization of bending and membrane frequencies of vibration of variable stiffness laminated composite plates by a genetic algorithm. Ribeiro and Akhavan [15] developed a p-version finite element with hierarchic basis functions for the solution of nonlinear vibrations of variable stiffness laminated composite plates. Gupta and Pradyumna [16] studied geometrically nonlinear dynamic analysis of variable stiffness laminated composite and sandwich panels by formulating higher-order structural models and considering the effect of curvilinear fiber angles. Ribeiro et al. [17] investigated nonlinear forced vibrations of variable stiffness plates on elastic supports using Kirchhoff’s assumptions with von Karman’s strain–displacement relation. Alimoradzadeh et al. [18] presented the analysis of nonlinear axial–lateral combined vibration of functionally graded fiber-reinforced laminated composite beams under aero-thermal loads using multiple time scales.
Since multilayer heterogeneous plates are generally in contact with elastic environments during their operation, it has become a necessity to consider the effects of anisotropy, heterogeneity, arrangement and number of layers on their behavior, as well as the influences of elastic environments on the vibration characteristics. One of the most realistic elastic foundation models was proposed by Pasternak [19], and the simplest version of this model is known to be the Winkler model. There are some studies on linear and nonlinear vibrations of single-layer heterogeneous anisotropic structural elements in contact with elastic media. Among these studies, Tornabene [20] studied free vibrations of anisotropic doubly curved shells and panels of revolution with a free-form meridian resting on Winkler–Pasternak elastic foundations using the generalized differential quadrature (GDQ) method. Haciyev et al. [21] studied linear free bending vibration analysis of thin bidirectionally exponentially graded orthotropic rectangular plates resting on two-parameter elastic foundations. Zenkour and coauthors [22,23,24,25] studied bending and linear free vibration analyses of exponentially graded single-layer micro- and macro-plates in surrounding media using different theories and analytical methods. Sofiyev et al. [26] investigated the influences of two-parameter elastic foundations on the nonlinear free vibration of anisotropic shallow shell structures with variable parameters. Song et al. [27] proposed an analytical method for linear vibration analysis of arbitrarily shaped non-homogeneous orthotropic plates of variable thickness resting on the Winkler–Pasternak foundation. Melaibari et al. [28,29] examined the static response of 2D functionally graded porous plates resting on elastic foundations using midplane and neutral surfaces with movable constraints and differential quadrature method. Jena et al. [30,31] presented the free vibration of functionally graded beams and the stability of nanobeams resting on the Winkler–Pasternak elastic foundation using a novel numerical approach. Zaoui et al. [32] presented a mathematical approach for the mechanical behavior analysis of FGM plates on elastic foundations. Kumar et al. [33] investigated the linear vibration response of the exponential functionally graded material plate with variable thickness resting on the orthotropic Pasternak foundation. Tornabene et al. [34] applied general boundary conditions for the static analysis of anisotropic double-curved shells based on Winkler foundations using the GDQ method.
The literature review reveals that the nonlinear vibration problem of multilayer plates consisting of exponentially changing interaction of orthotropic layers with elastic foundations has not been studied sufficiently, and the problem has not yet been solved with the Lindstedt–Poincaré method. Among the analytical methods available for solving nonlinear ordinary differential equations, the Lindstedt–Poincaré method is one of the most effective methods. In this study, the nonlinear vibration behavior of plates consisting of exponentially graded orthotropic layers resting on elastic foundations is solved by the modified Lindstedt–Poincaré method. The Lindstedt–Poincaré method is an extension of perturbation methods used to find the periodic solution of NL-ODEs by eliminating secular terms.
The results of this theoretical study of the nonlinear vibration of laminated plates composed of EGOLs in elastic media have practical implications for optimizing structural design, material selection, and performance in aerospace, marine, automotive, and related fields. The knowledge gained can also contribute to nonlinear vibration control and structural health monitoring. In addition, the Lindstedt–Poincaré method used to solve this problem can be applied to other laminated structural systems.
This paper can be summarized as follows. The introduction is designed in accordance with the subject heading in Section 1. In Section 2, the mathematical modeling of mechanical properties of exponentially graded laminated composite plates and elastic foundations is presented. In Section 3, the nonlinear dynamic model of exponentially graded laminated composite plates is introduced. In Section 4, the nonlinear differential equations for laminated plates consisting of exponentially graded composite layers interaction with elastic foundations are solved using the modified Lindstedt–Poincaré method. In Section 5, after performing numerical simulations to verify the validity of the analytical expressions, numerical examples are presented to verify the specificity of NL vibrations of exponentially graded laminated composite plates. The analysis conducted in this study makes an innovative contribution to the existing literature by comprehensively assessing the linear and nonlinear oscillation behavior of laminated plates consisting of EGOLs in the elastic medium. Finally, Section 6 provides conclusions.
2. Modeling of Laminated Plates Composed of EGOLs
The schematic diagram of a laminated plate resting on a two-parameter elastic foundation composed of perfectly bonded exponentially graded orthotropic layers with total thickness, , and lengths and on the and axes, respectively, are shown in Figure 1. is the total number of layers, and each EGOL has a thickness of . The Cartesian coordinate system is used in the reference plane of the laminated plate, where the axis is taken along the length of the plate, the axis is taken along the width direction, and the axis is perpendicular to the reference plane. The origin is located at the left corner of the laminated EG orthotropic plate, as shown in Figure 1. The reference plane is located at the interface of the layers at even values of , while at odd values of , the reference plane is located at the reference plane of the middle layer. It is assumed that the main elasticity axes of all layers are parallel to the coordinate axes in the reference plane. The displacements in the and directions are indicated by and .
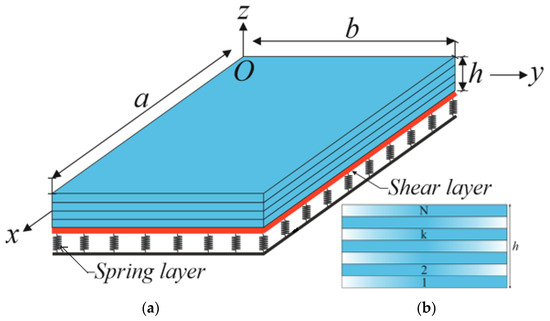
Figure 1.
(a) Geometry and coordinate system of laminated exponentially graded plate on the two-parameter elastic foundation and (b) cross-section of laminated plate.
Assuming that the elastic foundation is well connected to the laminated plate in the large deflection region, the load–displacement relationship of the elastic foundation is modeled as [18]
where is the force per unit area, is the hardness coefficient of the Winkler foundation, and is the hardness coefficient of the shear layer of the elastic foundation.
Let be the Airy stress function for the stress resultants so that [1,2,35]
In the following stages, will be used instead of .
The mechanical properties such as Young modulus , shear modulus and density of lamina kth are exponential functions of the thickness coordinate and are defined as follows [3,26]:
where are the material gradient parameters for the elasticity moduli and density, respectively, in the lamina kth, which varies in the range of [−1, 1]. Note that when , each layer of the plate is made of homogeneous orthotropic material.
3. Governing Equations
Based on the von Kármán-type nonlinear theory and the Kirchhoff–Love assumption, the motion and strain compatibility equations of exponentially graded orthotropic laminated plates, which includes the plate–foundation interaction, can be defined as [1,35]
where and are strains in the reference plane, and the forces , the moments and the density parameter are defined as follows [1,2,35]:
in which .
According to the generalized Hooke’s rule, the relationships between stresses () and strains of any point not located in the mid-plane ( and ) for the layers contained in laminated plates consisting of EGOLs can be constructed as follows [3]:
where
in which are Poisson ratios in the lamina kth and are considered constant and .
When Kirchhoff–Love plate theory and nonlinearity are applied together, the relationships between the strains at any point not in the mid-plane and the strains in the mid-plane of laminated plates consisting of EGOLs can be modeled as follows [35]:
where
Equation (9) is substituted into (7), and the resulting expressions are substituted into the integrals of (6), and considering Expression (2), the strains in the middle plane and the expressions of force and moment components based on and functions are derived. If those expressions are substituted into Equations (4) and (5), the nonlinear motion and deformation compatibility equations for laminated plates consisting of EGOLs, which includes the plate–foundation interaction within KLT, become as follows:
where
in which
4. Solution Method
The following simply supported boundary conditions are enjoined at the side edges of the laminated plate consisting of the EGOLs [1,35]:
Approximation functions that provide simply supported boundary conditions are sought as follows [35]:
where represents a time-dependent function, and and are the wave parameters in which (m, n) are mode numbers.
To find the Airy stress function from the particular solution of the non-homogeneous differential Equation (12), Relation (14) is substituted into the differential equation in question, and after some mathematical operations, the Airy stress function can be expressed with as follows:
The symbols in (17) are defined as follows:
The Galerkin method is applied to the nonlinear equation of motion; that is, Equation (11), in the region , is as follows:
After substituting Relations (16) and (17) into Equation (19) and performing the integration and taking into account , the following nonlinear ordinary differential equation is obtained for the nonlinear free vibration of laminated plates made of EGOLs which includes the plate–foundation interaction:
where , in which is the linear frequency of laminated plates made of EGOLs on the Pasternak elastic foundation and is defined as
Other symbols in (20) are
The basic idea of the modified method is introducing a new variable [36,37,38]:
where is the frequency, and is a small parameter. Equation (20) then becomes
where
To solve Equation (24), and are expanded by powers of as follows [36]:
where and are the unknown parameters.
By substituting (26) into Equation (24) and then collecting the coefficients of the same powers of , we obtain
Solving Equation (27) with the initial conditions , we obtain , and substituting the expression for the into (28) and after eliminating the secular terms, one obtains
Considering (30) and solving (28) with the initial conditions of yields
Substituting the expression for and into Equation (29) and solving with the initial conditions of , leading to the elimination of the secular term from the resulting equation, yields
When expressions for the and are substituted into the second equation of the set (26), the following algebraic equation for the nonlinear frequency is obtained:
where
The solution of the previous fourth-order algebraic equation gives the expression for the nonlinear frequency of laminated plates consisting of EGOLs, which includes the plate–foundation interaction:
The following expression is used for dimensionless values of nonlinear frequency:
The ratio of the nonlinear frequency to the linear frequency is expressed as
where denotes the linear frequency of laminated plates consisting of EGOLs without a ground and is defined as follows:
5. Results and Discussion
5.1. Comparative Examples
To validate the present formulations and results, some comparison examples are presented in this subsection, as shown in Table 1 and Table 2. In this section, the accuracy of the formulas is first confirmed by comparisons in the literature. Since it is seen that the smallest values of the frequency parameter occur at while making calculations in comparisons and numerical analyses, it is not included in the tables and figures.

Table 1.
The nonlinear frequency vs. linear frequency ratios of thin square single-layer and laminated homogeneous plates without elastic ground with simply supported boundary conditions (SS4).

Table 2.
Comparison of for single-layer square isotropic plates on the two-parameter elastic foundation.
Example 1.
The nonlinear frequency vs. linear frequency ratio () of thin square single-layer homogenous isotropic and laminated homogeneous orthotropic cross-ply plates without elastic groundwithin KLT for different nondimensional parameters f are compared with the results obtained in the study of Singha and Daripa [39], which used the finite element method (see
Table 1). In our calculations, the special case of Equation (37), that is, the case of , is considered. The material properties for the (0°/90°/0°/90°0°) array plate are taken from Singha and Daripa [39] and are as follows:
The isotropic material properties that make up the single-layer plate are as follows:
It is clearly seen in Table 1 that the numerical results obtained in this study for the ratio of both monolayer and laminated plates are in good agreement with the finite element results of Singha and Daripa [39].
Example 2.
In the second comparison, the accuracy in terms of dimensionless linear frequency for single-layer square isotropic plates resting on the Pasternak elastic foundation for , , and is ensured by comparing it with Wang et al. [40] and Zhong et al. [41]. In this example, relationship (21) is used for , , and the dimensionless linear frequency parameter on the Pasternak elastic foundation is taken into account as , with , as in Zhong et al. [41]. Table 2 reveals consistent agreement between our formulation and the findings presented in Wang et al. [40] and Zhong et al. [41], although based on different approaches.
5.2. Nonlinear Analysis in Elastic Media
In this subsection, the influences of two-parameter soil, non-homogeneity, and the number and arrangement of the layers on the nonlinear frequency of laminated plates consisting of exponentially graded layers are examined using the Maple 14 software program. In numerical examples, the Expressions (36) and (37) for the nonlinear vibration frequency of laminated plates consisting of exponentially graded layers interaction with elastic foundations are used. The exponentially graded orthotropic material types, i.e., EG(1,1), EG(1,0) and EG(−1,0) correspond to , and , respectively. Furthermore corresponds to a homogeneous case (H). The mechanical properties of a homogeneous carbon fiber-reinforced polymer in the layers are considered [2]: , , and . In the calculations, the coefficients of two-parameter soil are taken into account as , and , whereas corresponds to the example without soil. The sequence and number of layers forming the laminated plate used in the analyses are presented in Figure 2.
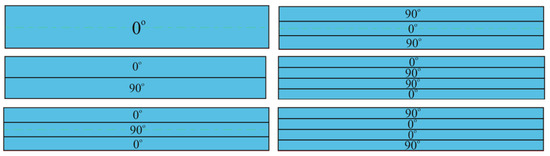
Figure 2.
Cross-sections of laminated plates with various layer sequences and numbers.
In Table 3 and Table 4, the variation in nonlinear vibration of multilayer plates with different arrangements and numbers, whose layers consist of the homogeneous orthotropic material (HOM) and layers of the exponentially graded orthotropic material (EGOM), respectively, according to the distribution of f, in cases with and without ground, for different a/b with a/h = 75 are presented. The NL frequency values increase when f and a/b ratios increase in cases with and without ground, in all alignments and layers, and in the EGOM profiles. In the HMO and EGOM cases, increasing f supports the increase in the NL frequency but also reveals that the ground effect makes the NL frequency values significant enough to be considered. Since each of the EG(1,1), EG(1,0) and EG(−1,0) profiles has their own unique effects on the NL frequency, separate evaluation and interpretation must be made for each profile. It is seen that the NL frequency values of laminated plates consisting of EG(−1.0)-profiled layers are higher than the values of the homogeneous case and are lower in other EGOM profiles.

Table 3.
Variation in NL frequency for single-layer and laminated plates consisting of HOM-profiled layers with and without elastic foundation against the f with different a/b.

Table 4.
Variation in NL frequency for single-layer and laminated plates consisting of EGOM-profiled layers with and without elastic foundation against the f with different a/b.
The effect of exponentially graded profiles on the NL frequency changes when the layer layout changes. As the laminated plates are compared with the (0°) single-layer plate, the most significant alignment influences on the NL frequency in the case without ground are 77.8% for the (90°/0°/90°) array plate consisting of layers with the EG(−1,0) profile at f = 0.25 and a/b = 1.5, while the lowest effect (−0.19%) is observed in the (90°/0°/90°) and (0°/90°/0°) array plates consisting of EG(−1.0) layers and it occurs for f = 1.5 and a/b = 1. In the absence of ground effect, the influence of the alignment on the NL frequency of laminated plates starting with (0°/…) in all EGOM profiles increases as f increment. In the grounded case, the strongest influence of the alignment on the NL frequency occurs in the (90°/0°/90°) array plate with EG(−1.0)-profiled layers, with 65.61% for f = 1.5 and a/b = 1.5, while the lowest effect is (−0.17%), which occurs in the (0°/90°/0°) and (90°/0°/90°) alignment plate with EG(1.0) and EG(1,1) profiles at f = 0.25 and a/b = 0.5. As can be seen, taking the ground into account reduces the influence of the layer arrangement on the NL frequency.
When the profile effect on NL frequency values of laminated plates consisting of layers with EGOM profiles is compared among themselves, the most significant influence occurs in the laminated plate with the EG(−1.0) profile. For example, at a/b = 0.5 and f = 1.5, the highest effects of the EG(−1,0) profile on the NL frequency occur with 27.02% and 40.92% for the (0°/90°) array plate with and without ground, respectively, while the highest effect occurs in the unconstrained (0°/90°/0°) array plate with 29.44% and in the (90°/0°/0°/90°) alignment plate on the elastic foundation with 26.57%, at a/b = 1.5 and f = 1.5. It is clearly seen that considering the ground weakens the effect of EG profiles on the NL frequency.
In laminated plates consisting of homogeneous orthotropic layers, the most significant ground effect on NL frequency values occurs with 51.3% in the (0°/90°)-aligned plate at a/b = 0.5 and f = 0.25, while the weakest effect occurs with 5.2% in the (90°/0°/90°)-aligned plate for a/b = 1.5 and f = 1.5. In laminated plates consisting of EGOM-profiled layers, the most significant ground effect on NL frequency values occurs in the (90°/0°/90°)-aligned plates consisting of EG(1,1) and EG(1,0) profiles with 139% for a/b = 0.5 and f = 0.25, while the weakest influence occurs with 3.15% in the (90°/0°/90°) plates with EG(−1,0) profiles for a/b = 1.5 and f = 1.5.
The distribution of the nonlinear frequency to linear frequency ratio (NLF/LF) for single-layer and laminated plates composed of H, EG(1,1), EG(1,0) and EG(−1,0) profiles with and without elastic ground against the f with different numbers and sequences of layers are plotted in Table 5 and Table 6 and in Figure 3, Figure 4, Figure 5 and Figure 6 for different a/h and when a/b = 0.5. Since the NLF/LF ratio is the same for EG(1,1) and EG(1,0) profiles, the same column is used in the tables. Although it is seen that the NLF/LF ratio increases when the f increases in plates starting from (0°/…) or (90°/…) array layers, in cases with and without ground, that ratio increases more clearly in some aligned plates in the case with ground.

Table 5.
Variation in NLF/LF frequency ratio for single-layer and laminated plates consisting of HOM-profiled layers with and without elastic foundation against the f with different a/h.

Table 6.
Variation in NLF/LF ratio for single-layer and laminated plates consisting of EGOM-profiled layers with and without elastic foundation against the f with different a/h.
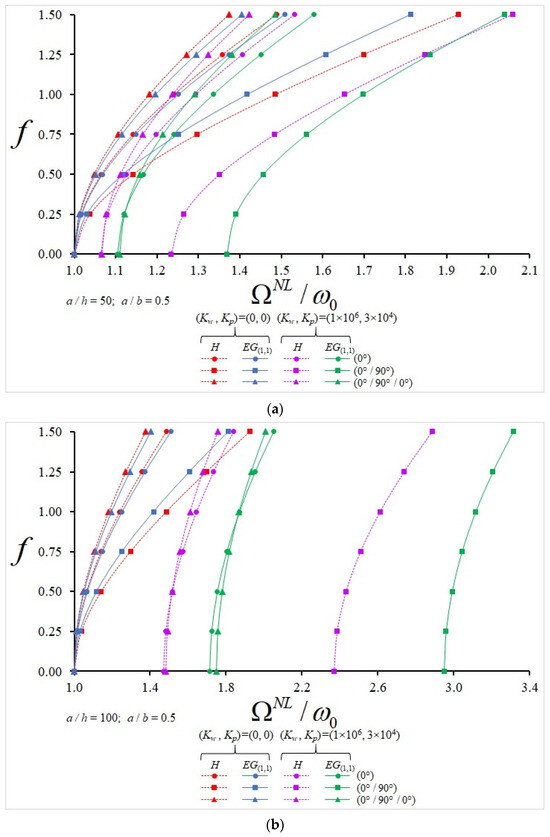
Figure 3.
Variation in NLF/LF for single-layer and (0°)-, (0°/90°)- and (0°/90°/0°)-aligned plates consisting of HOM- and EG(1,1)-profiled layers with and without elastic foundation against the f with (a) a/h = 50 and (b) a/h = 100.
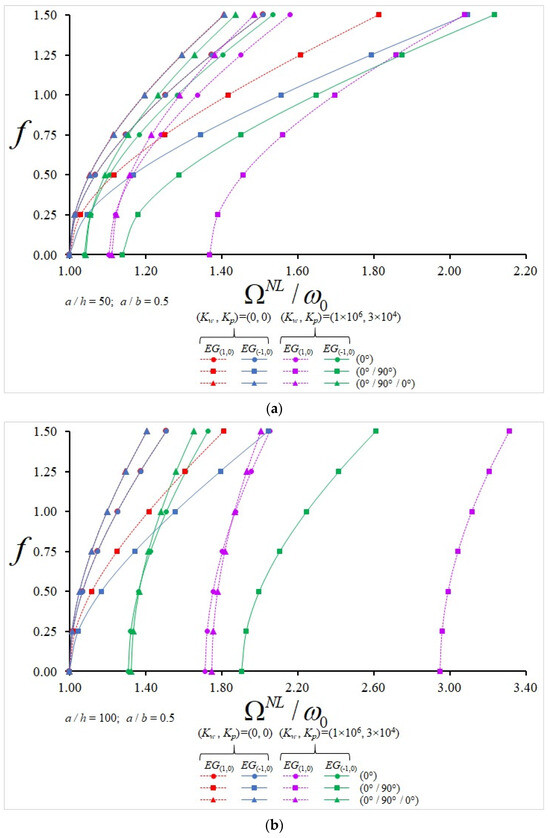
Figure 4.
Variation in NLF/LF for single-layer and (0°)-, (0°/90°)- and (0°/90°/0°)-aligned plates consisting of EG(1,0)- and EG(−1,0)-profiled layers with and without elastic foundation against the f with (a) a/h = 50 and (b) a/h = 100.
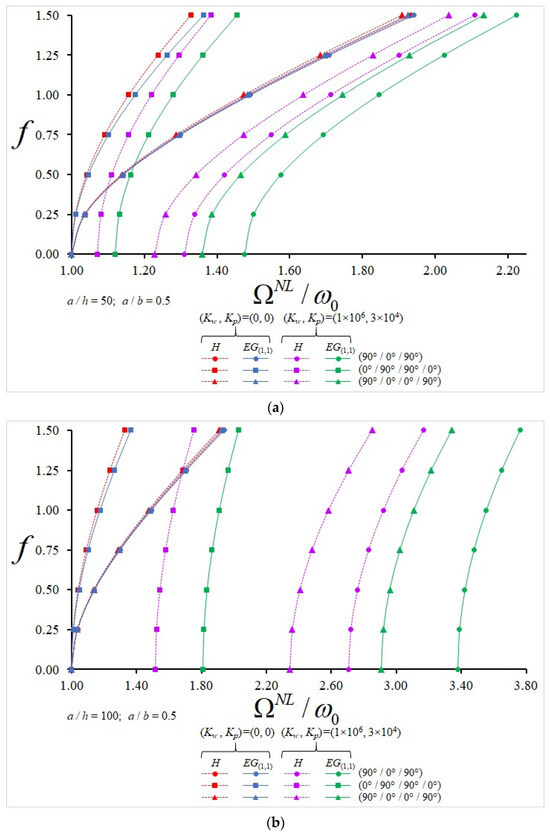
Figure 5.
Variation in NLF/LF for single-layer and (90°/0°/90°)-, (0°/90°/90°/0°)- and (90°/0°/0°/90°)-aligned plates consisting of HOM- and EG(1,1)-profiled layers with and without elastic foundation against the f with (a) a/h = 50 and (b) a/h = 100.
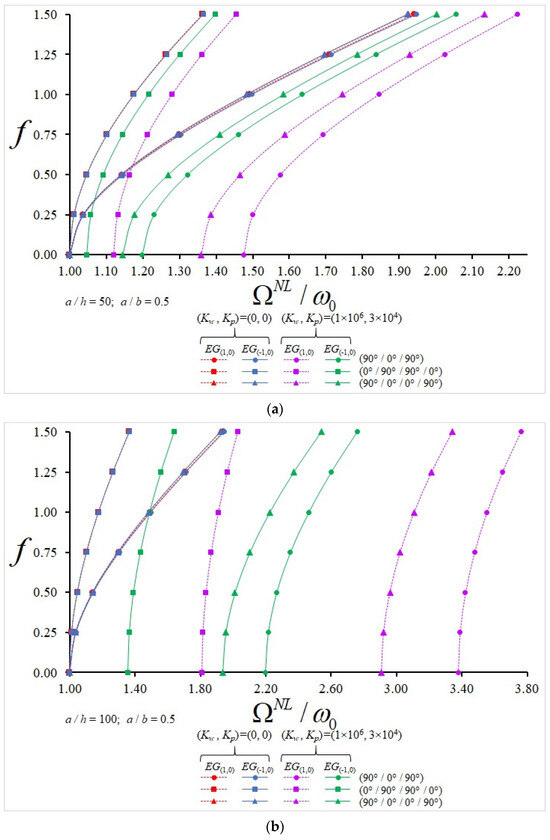
Figure 6.
Variation in NLF/LF for single-layer and (90°/0°/90°)-, (0°/90°/90°/0°)- and (90°/0°/0°/90°)-aligned plates consisting of EG(1,0)- and EG(−1,0)-profiled layers with and without elastic foundation against the f with (a) a/h = 50 and (b) a/h = 100.
In the case without ground, the influences of EGOM profiles on the NLF/LF ratio are weak at small values of f, while those effects increase for all alignments with the subsequent increase in f and show a more significant increase in plates with alignments starting with (0°/…) and are independent of the a/h ratio. In the presence of a ground effect, when the a/h ratio increases for the selected f, the effect of EGOM profiles on the NLF/LF ratio increases significantly depending on the layer arrangement and number and shows a more significant increase in plates with alignments starting with (90°/…). In the case of without ground, when f increases for the selected a/h, the influence of EGOM profiles on the NLF/LF ratio rises, whereas in the presence of the ground, those effects decrease, although they are much more pronounced.
For instance, in the ground case,
- (a)
- At a/h = 50 and f = 0.25, the influences of EG(1.0) and EG(−1.0) profiles on the NLF/LF ratio for plates with (0°/90°) alignment are 9.92% and (−6.75%); in the plates arranged in (0°/90°/0°), those effects are 4.17% and (−2.07%); in the plates arranged in (0°/90°/90°/0°), those influences are 4.64% and (−2.18%); in the plates arranged in (90°/0°/90°), those influences are 12.17% and (−8.1%); and in the plates arranged in (90°/0°/0°/90°), those effects are 10.15% and (−6.4%), respectively.
- (b)
- At a/h = 50 and f = 1.5, the influences of EG(1.0) and EG(−1.0) profiles on the NLF/LF ratio for plates with (0°/90°) alignment are (−0.96%) and 2.86%; in the plates arranged in (0°/90°/0°), those influences are 4.37% and 0.97%; in the plates arranged in (0°/90°/90°/0°), those influences are 5.17% and 1.11%; in the plates arranged in (90°/0°/90°), those effects are 5.4% and (−2.6%); and in the plates arranged in (90°/0°/0°/90°), those effects are 4.71% and (−1.65%), respectively.
- (c)
- At a/h = 100 and f = 0.25, the influences of EG(1.0) and EG(−1.0) profiles on the NLF/LF ratio for plates with (0°/90°) alignment are 24.1% and (−19.2%); in the plates arranged in (0°/90°/0°), those influences are 17.68% and (−10.5%); in the plates arranged in (0°/90°/90°/0°), those effects are 18.9% and (−10.6%); in the plates arranged in (90°/0°/90°), those influences are 24.65% and (−18.51%); and in the plates arranged in (90°/0°/0°/90°), those effects are 23.8% and (−17.2%), respectively.
- (d)
- At a/h = 100 and f = 1.5, the influences of EG(1.0) and EG(−1.0) profiles on the NLF/LF ratio for plates with (0°/90°) alignment are 14.85% and (−9.58%); in the plates arranged in (0°/90°/0°), those effects are 14.2% and (−5.93%); in the plates arranged in (0°/90°/90°/0°), those effects are 15.9% and (−6.3%); in the plates arranged in (90°/0°/90°), those effects are 18.75% and (−12.94%); and in the plates arranged in (90°/0°/0°/90°), those influences are 17.15% and (−11%), respectively (see Figure 3, Figure 4, Figure 5 and Figure 6).
When the NLF/LF ratio of EGOM-profiled plates with different alignments consisting of two, three and four layers on the ground is compared with the single-layer plate (0°), the alignment influences become evident with the increase in f at a/h = 50. While at a/h = 100, as f increases, the alignment effect reduces for the EG(1,0) profile, and that influence changes irregularly in the EG(−1,0) profile. Among all the arrays, the most significant influence on the NLF/LF ratio occurs in the (90°/0°/90°) array plate with EG(1,0) profile with 96.5% and 83.4% at f = 0.25 and f = 1.5, respectively, while those effects for the EG(−1,0) profile are 67.5% and 59.64% when f = 0.25 and f = 1.5, respectively, as a/h = 100 (also see Figure 3 and Figure 5).
In comparing the (0°)-monolayer plate with the layered plates in the case of without ground, the most significant alignment effect on the NLF/LF ratio occurs in the (0°/90°)-aligned plate and is approximately 35.61% at f = 1.5 for the EG(−1,0) profile and is independent of the a/h ratio. As the f ratio increases from 0.25 to 1.5 for all a/h, the alignment effect increases up to 29% in three-layer plates starting with (90°/…), while in aligned plates starting with (0°/…), that influence increases up to (−6.9%). In four-layer plates starting with (90°/…), it is observed that the alignment effect increases up to 27.55%, whereas starting with (0°/…)-aligned plates, it increases up to (−9.6%) as f rises from 0.25 to 1.5 for all a/h. In all layered plates, the effect of the soil on the NLF/LF ratio decreases significantly as f increases, while the increase in the a/h increases that effect significantly. The most significant ground effect on the NLF/LF ratio of all laminated plates occurs in the (/90°/0°/90°)-aligned plates for EG(1,0) and EG(1,1) profiles at a/h = 100 and f = 0.25, while for the EG(−1,0) profile, that effect would be about twice as low.
6. Conclusions
This study is devoted to solving the problem of the NL vibration of laminated plates consisting of EGOLs interacting with a two-parameter elastic foundation using the Lindstedt–Poincaré method. The NL fundamental relations and basic equations of laminated plates with EGOM profiles in an elastic medium were derived in this study. The amplitude-dependent expressions for the NL frequency are obtained using Galerkin and the modified Lindstedt–Poincaré method. The accuracy of the proposed solution is confirmed by comparing it with reliable results in the literature. The current analytical solution may be a valid option for comparison with finite element simulations. In addition, lamination schemes within the scope of two-dimensional theories in continuous environments enable fast and accurate solutions to the nonlinear vibration problem of cross-ply plates made of orthotropic materials. Therefore, compared with reliable numerical models, it can be applied to lattice and honeycomb plates without significant computational effort, as well as to plates composed of heterogeneous composite materials. The numerical results are interpreted and generalized as follows:
- (a)
- The NL frequency values increase when f and a/b ratios increase in cases with and without ground, in all alignments and layers and in exponentially graded orthotropic material profiles;
- (b)
- In the homogeneous orthotropic and exponentially graded orthotropic material cases, increasing f supports the increase in the NL frequency but also reveals that the ground effect makes the NL frequency values significant enough to be considered;
- (c)
- Since each of the EG(1,1), EG(1,0) and EG(−1,0) profiles has their own unique effects on the NL frequency, separate evaluation and interpretation must be made for each profile.
- (d)
- NL frequency values of laminated plates consisting of EG(−1.0) profile layers are higher than the values of the homogeneous case and are lower in other exponentially graded orthotropic material profiles;
- (e)
- The effect of exponential graduation profiles on the NL frequency changes when the layer layout or number of layers changes;
- (f)
- Taking the ground into account reduces the influence of the layer arrangement on the NL frequency;
- (g)
- As the model effect on NL frequency values of laminated plate consisting of layers with exponentially graded orthotropic material profiles is compared among themselves, the most significant effect occurs in the plate with the EG(−1.0) profile;
- (h)
- The ground weakens the influence of EG profiles and layer arrangement on the NL frequency;
- (i)
- Although the NLF/LF ratio increases when the f increases in plates starting from (0°/…) or (90°/…) array layers, in cases with and without ground, that ratio increases more clearly in some aligned plates in the case with a ground;
- (j)
- In the case without a ground, the influences of exponentially graded orthotropic material profiles on the NLF/LF ratio are weak at small values of f, while those effects increase for all alignments with the subsequent increase in f and show a more significant increase in plates with alignments starting with (0°/…), which are independent of the a/h ratio;
- (k)
- In the presence of ground effect, when the a/h ratio increases for the selected f, the effect of exponentially graded orthotropic material profiles on the NLF/LF ratio increases significantly depending on the layer arrangement and number and shows a more significant increase in plates with alignments starting with (90°/…);
- (l)
- In the case of without the ground, when f increases for the selected a/h, the influence of exponentially graded orthotropic material profiles on the NLF/LF ratio increases, whereas in the presence of the ground, those effects decrease, although they are much more pronounced;
- (m)
- When the NLF/LF ratio of exponentially graded orthotropic material-profiled plates with different alignments consisting of two, three and four layers on the ground is compared with the single-layer plate (0°), the alignment effects become evident with the increase in f;
- (n)
- In all layered plates, the influence of the soil on the NLF/LF ratio decreases significantly as f increases, while the increase in the a/h increases that effect significantly.
Author Contributions
Conceptualization, M.A.; methodology, M.A.; software, M.A.; validation, M.A. and F.T.; formal analysis, M.A.; investigation, M.A.; resources, M.A. and N.M.A.; writing—original draft preparation, M.A.; writing—review and editing, M.A., F.T., N.M.A. and A.H.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No data were reported in this study.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ambartsumian, S.A. Theory of Anisotropic Plates; Strength, Stability, Vibration; Technomic Publishing Company: Stamford, CT, USA, 1964. [Google Scholar]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis, 2nd ed.; CRC Press: New York, NY, USA, 2004. [Google Scholar]
- Pan, E. Exact solution for functionally graded anisotropic elastic composite laminates. J. Compos. Mater. 2003, 37, 1903–1920. [Google Scholar] [CrossRef]
- Ootao, Y.; Tanigawa, Y. Three-dimensional solution for transient thermal stresses of an orthotropic functionally graded rectangular plate. Compos. Struct. 2007, 80, 10–20. [Google Scholar] [CrossRef]
- Zenkour, A. Bending responses of an exponentially graded simply-supported elastic/viscoelastic/elastic sandwich plate. Acta Mech. Solida Sin. 2011, 24, 250–261. [Google Scholar] [CrossRef]
- Fazzolari, F.A.; Carrera, E. Advanced variable kinematics Ritz and Galerkin formulations for accurate buckling and vibration analysis of anisotropic laminated composite plates. Compos. Struct. 2011, 94, 50–67. [Google Scholar] [CrossRef]
- Fazzolari, F.A.; Carrera, E. Thermo-mechanical buckling analysis of anisotropic multilayered composite and sandwich plates by using refined variable-kinematics theories. J. Therm. Stresses 2013, 36, 321–350. [Google Scholar] [CrossRef]
- Bacciocchi, M.; Tarantino, A.M. Natural frequency analysis of functionally graded orthotropic cross-ply plates based on the finite element method. Math. Computat. Appl. 2019, 24, 52. [Google Scholar] [CrossRef]
- Zhang, J.H.; Ullah, S.; Zhong, Y. Accurate free vibration solutions of orthotropic rectangular thin plates by straightforward finite integral transform method. Arch. Appl. Mech. 2020, 90, 353–368. [Google Scholar] [CrossRef]
- Krysko, A.V.; Awrejcewicz, J.; Bodyagina, K.S.; Krysko, V.A. Mathematical modeling of planar physically nonlinear inhomogeneous plates with rectangular cuts in the three-dimensional formulation. Acta Mech. 2021, 232, 4933–4950. [Google Scholar] [CrossRef]
- Hachemi, M. Layer-wise solutions for variable stiffness composite laminated sandwich plate using curvilinear fibers. Mech. Adv. Mater. Struct. 2022, 29, 5460–5477. [Google Scholar] [CrossRef]
- Dat, N.D.; Quan, T.Q.; Duc, N.D. Vibration analysis of auxetic laminated plate with magneto-electro-elastic face sheets subjected to blast loading. Compos. Struct. 2022, 280, 114925. [Google Scholar]
- Singh, A.; Naskar, S.; Kumarı, P.; Mukhopadhyay, T. Viscoelastic free vibration analysis of in-plane functionally graded orthotropic plates integrated with piezoelectric sensors: Time-dependent 3D analytical solutions. Mech. Syst. Signal Process. 2023, 184, 109636. [Google Scholar] [CrossRef]
- Simões, T.M.; Ribeiro, P.; Conceição, A.C. Maximisation of bending and membrane frequencies of vibration of variable stiffness composite laminated plates by a genetic algorithm. J. Vib. Eng. Tech. 2023, in press. [Google Scholar] [CrossRef]
- Ribeiro, P.; Akhavan, H. Non-linear vibrations of variable stiffness composite laminated plates. Compos. Struct. 2012, 94, 2424–2432. [Google Scholar] [CrossRef]
- Gupta, A.; Pradyumna, S. Geometrically nonlinear dynamic analysis of variable stiffness composite laminated and sandwich shell panels. Thin Wall. Struct. 2022, 173, 109021. [Google Scholar] [CrossRef]
- Ribeiro, P.; Antunes, A.M.; Akhavan, H.; Rodrigues, J.D. Non-linear forced vibrations of variable stiffness plates on elastic supports. Mech. Adv. Mater. Struct. 2023, 30, 4246–4263. [Google Scholar] [CrossRef]
- Alimoradzadeh, M.; Tornabene, F.; Dimitri, R. Nonlinear axial-lateral coupled vibration of functionally graded-fiber reinforced composite laminated (FG-FRCL) beams subjected to aero-thermal loads. Int. J. Non-Lin. Mech. 2024, 159, 104612. [Google Scholar] [CrossRef]
- Pasternak, P.L. On a New Method of Analysis of an Elastic Foundation by Means of Two Foundation Constants; State Publishing House of Literature on Construction and Architecture: Moscow, Russia, 1954; Volume 1, pp. 1–56. (In Russian) [Google Scholar]
- Tornabene, F. Free vibrations of anisotropic doubly-curved shells and panels of revolution with a free-form meridian resting on Winkler-Pasternak elastic foundations. Compos. Struct. 2011, 94, 186–206. [Google Scholar] [CrossRef]
- Haciyev, V.C.; Sofiyev, A.H.; Kuruoglu, N. Free bending vibration analysis of thin bidirectionally exponentially graded orthotropic rectangular plates resting on two-parameter elastic foundations. Compos. Struct. 2018, 184, 372–377. [Google Scholar] [CrossRef]
- Zenkour, A.M. Trigonometric solution for an exponentially graded thick plate resting on elastic foundations. Arch. Mech. Eng. 2018, 65, 193–208. [Google Scholar]
- Zenkour, A.M.; Alghanmi, R.A. Bending of exponentially graded plates integrated with piezoelectric fiber-reinforced composite actuators resting on elastic foundations. Euro. J. Mech. A-Solids 2019, 75, 461–471. [Google Scholar] [CrossRef]
- Sobhy, M.; Zenkour, A.M. A comprehensive study on the size-dependent hygrothermal analysis of exponentially graded microplates on elastic foundations. Mech. Adv. Mater. Struct. 2020, 27, 816–830. [Google Scholar] [CrossRef]
- Alazwari, M.A.; Zenkour, A.M. A Quasi-3D refined theory for the vibration of functionally graded plates resting on visco-Winkler-Pasternak foundations. Mathematics 2022, 10, 716. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Turan, F.; Kadioglu, F.; Aksogan, O.; Hui, D. Influences of two-parameter elastic foundations on nonlinear free vibration of anisotropic shallow shell structures with variable parameters. Meccanica 2022, 57, 401–414. [Google Scholar] [CrossRef]
- Song, Y.Y.; Li, Q.H.; Xue, K. An analytical method for vibration analysis of arbitrarily shaped non-homogeneous orthotropic plates of variable thickness resting on Winkler-Pasternak foundation. Compos. Struct. 2022, 296, 115885. [Google Scholar] [CrossRef]
- Jena, S.K.; Chakraverty, S.; Manesh, V.; Harursampath, D. Free vibration of functionally graded beam embedded in Winkler-Pasternak elastic foundation with geometrical uncertainties using symmetric Gaussian fuzzy number. Euro. Phys. J. Plus 2022, 137, 399. [Google Scholar] [CrossRef]
- Jena, S.K.; Chakraverty, S.; Manesh, V.; Harursampath, D.; Sedighi, H.M. A novel numerical approach for the stability of nanobeam exposed to hygro-thermo-magnetic environment embedded in elastic foundation. ZAMM-J. Appl. Math. Mech. Z. Für Angew. Math. Und Mech. 2022, 102, e202100380. [Google Scholar] [CrossRef]
- Melaibari, A.; Mohamed, S.A.; Assie, A.E.; Shanab, R.A.; Eltaher, M.A. Static response of 2D FG porous plates resting on elastic foundation using midplane and neutral surfaces with movable constraints. Mathematics 2022, 10, 4784. [Google Scholar] [CrossRef]
- Melaibari, A.; Mohamed, S.A.; Assie, A.E.; Shanab, R.A.; Eltaher, M.A. Free vibration characteristics of bidirectional graded porous plates with elastic foundations using 2D-DQM. Mathematics 2023, 11, 46. [Google Scholar] [CrossRef]
- Zaoui, F.Z.; Ouinas, D.; Achour, B.; Touahmia, M.; Boukendakdji, M.; Latifee, E.R.; Enamur, R.R.; Al-Naghi, A.A.A.; Ahmed, A.A.; Olay, J.A.V. Mathematical approach for mechanical behaviour analysis of FGM plates on elastic foundation. Mathematics 2022, 10, 4764. [Google Scholar] [CrossRef]
- Kumar, V.; Singh, S.J.; Saran, V.H.; Harsha, S.P. Vibration response of the exponential functionally graded material plate with variable thickness resting on the orthotropic Pasternak foundation. Mech. Based Des. Struct. Mach. 2023, in press. [Google Scholar] [CrossRef]
- Tornabene, F.; Viscoti, M.; Dimitri, R. General boundary conditions implementation for the static analysis of anisotropic doubly-curved shells resting on a Winkler foundation. Compos. Struct. 2023, 322, 117198. [Google Scholar] [CrossRef]
- Volmir, A.S. The Nonlinear Dynamics of Plates and Shells; Science Edition: Moscow, Russia, 1972. [Google Scholar]
- He, J.H. Modified Lindstedt-Poincare methods for some strongly non-linear oscillations Part I: Expansion of a constant. Int. J. Non-Lin. Mech. 2002, 37, 309–314. [Google Scholar] [CrossRef]
- Hashemi, S.; Jafari, A.A. An analytical solution for nonlinear vibrations analysis of functionally graded plate using modified Lindstedt–Poincare method. Int. J. Appl. Mech. 2020, 1201, 2050003. [Google Scholar] [CrossRef]
- Althubiti, S. Nonlinear third-order differential equations with distributed delay: Some new oscillatory solutions. J. King Saud Univ.-Sci. 2023, 35, 102730. [Google Scholar] [CrossRef]
- Singha, M.K.; Daripa, R. Nonlinear vibration and dynamic stability analysis of composite plates. J. Sound Vib. 2009, 328, 541–554. [Google Scholar] [CrossRef]
- Wang, Q.; Shi, D.; Shi, X. A modified solution for the free vibration analysis of moderately thick orthotropic rectangular plates with general boundary conditions, internal line supports and resting on elastic foundation. Meccanica 2016, 51, 1985–2017. [Google Scholar] [CrossRef]
- Zhong, R.; Wang, Q.; Tang, J.; Shuai, C.; Liang, Q. Vibration characteristics of functionally graded carbon nanotube reinforced composite rectangular plates on Pasternak foundation with arbitrary boundary conditions and internal line supports. Curved Layer. Struct. 2018, 5, 10–34. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).