Halpern-Type Inertial Iteration Methods with Self-Adaptive Step Size for Split Common Null Point Problem

Abstract

In this paper, two Halpern-type inertial iteration methods with self-adaptive step size are proposed for estimating the solution of split common null point problems (${\mathrm{S}}_{\mathrm{p}}\mathrm{CNPP}$) in such a way that the Halpern iteration and inertial extrapolation are computed simultaneously in the beginning of each iteration. We prove the strong convergence of sequences driven by the suggested methods without estimating the norm of bounded linear operator when certain appropriate assumptions are made. We demonstrate the efficiency of our iterative methods and compare them with some related and well-known results using relevant numerical examples.

1. Introduction

The split feasibility problem $({\mathrm{S}}_{\mathrm{p}}\mathrm{FP})$ presented by Censor and Elfving [1] is the first split problem which has been studied intensively by researchers in applied sciences, see e.g., [2,3,4,5]. The split inverse problem $({\mathrm{S}}_{\mathrm{p}}\mathrm{IP})$ is the most prevalent split problem, due to Censor et al. [6]. Recently, various models of inverse problems have been developed and studied. Due to application oriented nature a growing interest has noticed in recent years in the study of split variational inequality/inclusion problems. Moudafi [7] studied a particular case of $({\mathrm{S}}_{\mathrm{p}}\mathrm{IP})$ called split monotone variational inclusion problem $({\mathrm{S}}_{\mathrm{p}}\mathrm{MVIP})$:

$$\begin{array}{c}\hfill \mathrm{Find}{\varphi }^{★}\in H_1\mathrm{such}\mathrm{that}{\varphi }^{★}\in {\mathrm{VI}}_{\mathrm{s}}\mathrm{P}(E_1;V_1;H_1)\mathrm{and}A({\varphi }^{★})\in {\mathrm{VI}}_{\mathrm{s}}\mathrm{P}(E_2;V_2;H_2),\end{array}$$

where $V_1:H_1\to 2^{H_1}$ and $V_2:H_2\to 2^{H_2}$ are set-valued mappings; $E_1:H_1\to H_1$ and $E_2:H_2\to H_2$ are single-valued mappings on Hilbert spaces $H_1$ and $H_2$, respectively; ${\mathrm{VI}}_{\mathrm{s}}\mathrm{P}(E_1,V_1;H_1)=\{{\varphi }^{★}\in H_1:0\in E_1({\varphi }^{★})+V_1({\varphi }^{★})\}$ and ${\mathrm{VI}}_{\mathrm{s}}\mathrm{P}(E_2,V_2;H_2)=\{A{\varphi }^{★}\in H_2:0\in E_2(A{\varphi }^{★})+V_2(A{\varphi }^{★})\}$. Moudafi [7] composed the following scheme for $({\mathrm{S}}_{\mathrm{p}}\mathrm{MVIP})$ . Let $\mu >0$, for arbitrary $z_0\in H_1$, compute

$$\begin{array}{c}\hfill z_{n+1}=X[z_n+\kappa A^{*}(Y-I)A{z}_n],\end{array}$$

where $A^{*}$ is an adjoint operator of A, $\kappa \in (0,1/L)$ with L being the spectral radius of operator $A^{*}A$, $X=R_{\mu }^{V_1}(I-\mu E_1)={(I+\mu V_1)}^{-1}(I-\mu E_1)$ and $Y=R_{\mu }^{V_2}(I-\mu E_2)={(I+\mu V_2)}^{-1}(I-\mu E_2)$. If $E_1=E_2=0$, then $({\mathrm{S}}_{\mathrm{p}}\mathrm{MVIP})$ turn into the split common null point problem (${\mathrm{S}}_{\mathrm{p}}\mathrm{CNPP})$, suggested by Byrne et al. [8]:

$$\begin{array}{c}\hfill \mathrm{Find}{\varphi }^{★}\in H_1\mathrm{such}\mathrm{that}{\varphi }^{★}\in {\mathrm{VI}}_{\mathrm{s}}\mathrm{P}(V_1;H_1)\mathrm{and}A({\varphi }^{★})\in {\mathrm{VI}}_{\mathrm{s}}\mathrm{P}(V_2;H_2),\end{array}$$

where ${\mathrm{VI}}_{\mathrm{s}}\mathrm{P}(V_1;H_1)=\{z\in H_1:0\in V_1(z)\}$ and ${\mathrm{VI}}_{\mathrm{s}}\mathrm{P}(V_2;H_2)=\{Az\in H_2:0\in V_2(Az)\}$. Also, Byrne et al. [8] composed the next scheme for $({\mathrm{S}}_{\mathrm{p}}\mathrm{CNPP})$. For arbitrary point $z_0\in H_1$, compute

$$\begin{array}{c}\hfill z_{n+1}=R_{\mu }^{V_1}[z_n+\kappa A^{*}(R_{\mu }^{V_2}-I)A{z}_n],\end{array}$$

where $L=\parallel A^{*}{A\parallel =\parallel A\parallel }^2$, $\tau \in (0,2/L)$. It is obvious to see that ${\varphi }^{★}$ solves $({\mathrm{S}}_{\mathrm{p}}\mathrm{CNPP})$ if and only if ${\varphi }^{★}=R_{\mu }^{V_1}[{\varphi }^{★}+\kappa A^{*}(R_{\mu }^{V_2}-I)A{\varphi }^{★}]$. Kazmi and Rizvi [9] investigated the solutions of $({\mathrm{S}}_{\mathrm{p}}{\mathrm{VI}}_{\mathrm{s}}\mathrm{P})$ and fixed point problem of a nonexpansive mapping T $(\mathrm{FPP})$ by using the following scheme. For  arbitrary $z_0\in H_1$, compute

$$\begin{array}{cc}\hfill y_n& =R_{\mu }^{V_1}[z_n+\kappa A^{*}(R_{\mu }^{V_2}-I)A{z}_n],\hfill \\ \hfill z_{n+1}& ={\zeta }_{n}h(z_n)+(1-{\zeta }_n)T{y}_n,\hfill \end{array}$$

where h is contraction and $\kappa \in (0,\frac{2}{{\parallel A\parallel }^2})$. Later, Dilshad et al. [10] investigated the common solution of $({\mathrm{S}}_{\mathrm{p}}{\mathrm{VI}}_{\mathrm{s}}\mathrm{P})$ and the fixed point of a finite collection of nonexpansive mappings. Recently, an alternative method was suggested by Akram et al. [11] to explore the common solution of $({\mathrm{S}}_{\mathrm{p}}{\mathrm{VI}}_{\mathrm{s}}\mathrm{P})$ and $(\mathrm{FPP})$ as follows:

$$\begin{array}{cc}\hfill y_n& =z_n-\kappa \left[(I-R_{{\mu }_1}^{V_1})z_n+A^{*}(I-R_{{\mu }_2}^{V_2})A{z}_n\right],\hfill \\ \hfill z_{n+1}& ={\zeta }_{n}h(z_n)+(1-{\zeta }_n)T(y_n),\hfill \end{array}$$

where $\kappa =\frac{1}{1+{\parallel A\parallel }^2}$. Later on many authors have shown their interest in solving $({\mathrm{S}}_{\mathrm{p}}{\mathrm{VI}}_{\mathrm{s}}\mathrm{P})$ and related problems, using innovative methods. Some interesting results can be found in [10,12,13,14,15,16] and references therein.

In the above-mentioned work and related literature, we found that the step size, which is under the control of norm $\parallel A^{*}A\parallel$, is required for the convergence of iterative schemes. To overcome this regulation, a new form of iterative schemes have been proposed, see, e.g., [16,17,18,19]. L$\acute{o}$pez  et al. [20] proposed a relaxed iterative scheme for $({\mathrm{S}}_{\mathrm{p}}\mathrm{FP})$:

$$\begin{array}{ccc}\hfill z_{n+1}& =& P_{Q_1}\left[I-{\tau }_n{A}^{*}(I-P_{Q_2})A]z_n\right],\hfill \end{array}$$

where $P_{Q_1}$ and $P_{Q_2}$ are the orthogonal projections on $Q_1$ and $Q_2$, respectively, and ${\tau }_n$ is calculated by

$$\begin{array}{ccc}\hfill {\tau }_n& :=& \frac{{ϵ}_{n}g(z_n)}{\parallel \nabla g(z_n){\parallel }^2},\hfill \end{array}$$

with $g(z)=\frac{1}{2}{\parallel (I-P_{Q_2})Az\parallel }^2$ and $\nabla g(z_n)=A^{*}(I-P_{Q_2})Az,n\ge 0$, and $0<{ϵ}_n<1$ and $inf{ϵ}_n(4-{ϵ}_n)>0$. Dilshad et al. [21], investigate the solution of $({\mathrm{S}}_{\mathrm{p}}\mathrm{CNPP})$ without using pre-calculated norm $\parallel A\parallel$. For arbitrary $\upsilon \in H_1$, compute

$$\begin{array}{cc}\hfill x_n& =(I-R_{\mu }^{V_1})z_n+A^{*}(I-R_{\mu }^{V_2})A{z}_n\\ \hfill z_{n+1}& ={\zeta }_n\upsilon +(1-{\zeta }_n)(z_n-{\tau }_n{x}_n)\end{array}$$

where ${\zeta }_n\in (0,1)$ and the ${\tau }_n$ is calculated by ${\tau }_n=\frac{\parallel (I-R_{{\mu }_1}^{V_1})(z_n){\parallel }^2+{\parallel A^{*}(I-R_{{\mu }_2}^{V_2})(A{z}_n)\parallel }^2}{\parallel (I-R_{{\mu }_1}^{V_1})(z_n)+A^{*}(I-R_{{\mu }_2}^{V_2})(A{z}_n){\parallel }^2}$.

Slow convergence of the suggested algorithms was the new problem for researchers. Therefore, many efforts have been made to accelerate the convergence. Several researchers have implemented the inertial term as one of the speed-up approaches. Recall that Alvarez and Attouch [22] established the inertial proximal point approach for the monotone mapping V utilising the notion of implicit descritization for derivatives

$$z_{n+1}={[I+\mu V]}^{-1}[z_n+{\alpha }_n(z_n-z_{n-1})],$$

where $\mu >0$, ${\alpha }_n\in [0,1)$ is the extrapolation coefficient and ${\alpha }_n(z_n-z_{n-1})$ composes the inertial term. It is found that this kind of scheme has an improved convergence rate and therefore this scheme was adopted, altered and implemented to solve various nonlinear problems, see, e.g., [23,24,25,26,27,28]. Very recently, Reich and Taiwo [29] studied some fast iterative methods for estimating the solution of variational inclusion problem in which they jointly compute the viscosity approximation and inertial extrapolation in the first step of iterations.

Inspired by the above-mentioned work, we suggest two Halpern-type inertial iteration methods with self adaptive step size for approaching the solution of $({\mathrm{S}}_{\mathrm{p}}\mathrm{CNPP})$ in the setting of Hilbert spaces. Our methods compute the Halpern iteration, inertial extrapolation simultaneously in the beginning of each iterations. We use the self-adaptive step-size such that the iteration process do not required the prior calculated norm of bounded linear operator. Our work can be seen as simple and accelerated modified methods for solving $({\mathrm{S}}_{\mathrm{p}}\mathrm{CNPP})$ .

We arrange this paper as follows. The following section recalls some definitions and results that are beneficial in the convergence analysis of the proposed methods. In Section 3, we propose our two Halpern-type, inertial and self-adaptive iteration methods and then we state and study the strong convergence results. Section 4 illustrates numerical examples in finite and infinite dimensional Hilbert spaces showing the behaviour and advantages of suggested iterative methods. We conclude our study and numerical experiment in Section 5.

2. Preliminaries

Assume that H is a real Hilbert space and D is a close and convex subset of H. If $\left\{z_n\right\}$ is a sequence in H, then $z_n\to z$ denotes strong convergence of $\left\{z_n\right\}$ to z and $z_n\rightharpoonup z$ denotes weak convergence. The weak $\omega$-limit of $\left\{z_n\right\}$ is defined by

$${\omega }_w(z_n)=\{z\in H:z_{n_j}\rightharpoonup z\mathrm{as}j\to \infty ,z_{n_j}\mathrm{is}\mathrm{a}\mathrm{subsequnce}\mathrm{of}{z}_n\}.$$

If $P_D\vartheta$ is the projection of $\vartheta$ onto $D\subset H$, then for some $\vartheta \in H$, there exists unique closest point in D indicate by $P_D\vartheta$ such that

$$\begin{array}{c}\hfill \parallel \vartheta -P_D\vartheta \parallel \le \parallel \vartheta -\omega \parallel ,forall\omega \in D,\end{array}$$

$P_D\vartheta$ also satisfies

$$\begin{array}{c}\hfill ⟨\omega -\vartheta ,P_D\omega -P_C\vartheta ⟩\ge {\parallel P_D\omega -P_D\vartheta \parallel }^2,forall\omega ,\vartheta \in H.\end{array}$$

Moreover, $P_D\omega$ is also identified by the fact

$$\begin{array}{c}\hfill P_D\omega =\eta \iff ⟨\omega -\eta ,\vartheta -\eta ⟩\ge 0,forall\vartheta \in D.\end{array}$$

For all $\eta ,\omega ,\vartheta$ in Hilbert space H, we have the following equality:

$$\begin{array}{c}\hfill {\parallel \eta \pm \vartheta \parallel }^2={\parallel \eta \parallel }^2\pm 2⟨\vartheta ,\eta +\vartheta ⟩.\end{array}$$

(1)

Definition 1.

A mapping $h:H\to H$ is called

(i) 

contraction, if $\parallel h(\eta )-\omega )\parallel \le \tau \parallel \eta -\omega \parallel ,forall\eta ,\omega \in H,\mathrm{and}\tau \in (0,1);$

(ii) 

nonexpansive, if $\parallel h(\eta )-h(\omega )\parallel \le \parallel \eta -\omega \parallel ,forall\eta ,\omega \in H;$

(iii) 

firmly nonexpansive, if ${\parallel h(\eta )-h(\omega )\parallel }^2\le ⟨\eta -\omega ,h(\eta )-h(\omega )⟩,forall\eta ,\omega \in H.$

Definition 2. 

Let $V:H\to 2^H$ be set-valued mapping. Then

(i) 

V is called monotone, if $⟨p-q,\eta -\omega ⟩\ge 0,forall\eta ,\omega \in H,p\in V(\eta ),q\in V(\omega )$;

(ii) 

$Graph(V)=\{(p,\omega )\in H\times H:\omega \in V(p)\}$;

(iii) 

V is called maximal monotone, if V is monotone and $(I+\mu V)(H)=H$, for $\mu >0$ and I is an identity mapping.

Lemma 1

([30]). If $\left\{z_n\right\}$ is a sequence of nonnegative real numbers such that

$$z_{n+1}\le (1-{\zeta }_n)z_n+{\beta }_n,n\ge 0,$$

where $\left\{{\zeta }_n\right\}$ is a sequence in $(0,1)$ and $\left\{{\beta }_n\right\}$ is a sequence in $\mathbb{R}$ such that

(i) 

${\sum }_{n=1}^{\infty }{\zeta }_n=\infty ;$

(ii) 

$lim\underset{n\to \infty }{sup}\frac{{\beta }_n}{{\zeta }_n}\le 0$ or ${\displaystyle \sum _{n=1}^{\infty }}\left|{\beta }_n\right|<\infty .$

Then $\underset{n\to \infty }{lim}{z}_n=0.$

Lemma 2

([31]). In a Hilbert space H,

(i) 

if $V:H\to 2^H$ is monotone and $R_{\mu }^V$ be the resolvent of V, then $R_{\mu }^V$ and $I-R_{\mu }^V$ are firmly nonexpansive for $\mu >0$.

(ii) 

if $V:H\to 2^H$ is nonexpansive, then $I-V$ is demiclosed at zero and if V is firmly nonexpansive then $I-V$ is firmly nonexpansive.

Lemma 3

([32]). For a bounded sequence $\left\{{\psi }_n\right\}$ in Hilbert space H. If there exists a subset $\varnothing \ne Q\subset H$ satisfying

(i) 

${lim}_{n\to \infty }\parallel {\psi }_n-\omega \parallel$ exists, $\forall \omega \in Q$,

(ii) 

${\omega }_w({\psi }_n)\subset Q.$

Then, there exists ${\varphi }^{★}\in Q$ such that ${\psi }_n\rightharpoonup {\varphi }^{★}$.

Lemma 4

([33]). Let $\left\{z_n\right\}$ be a sequence in $\mathbb{R}$ that does not decrease at infinity in the sense that there exists a subsequence $\left\{z_{n_k}\right\}$ of $\left\{z_n\right\}$ such that $z_{n_k}<z_{n_k+1}$ for all $k\ge 0$. Also consider the sequence of integers ${\left\{\rho (n)\right\}}_{n\ge n_0}$ defined by

$$\begin{array}{c}\hfill \rho (n)=max\{k\le n:z_k\le z_{k+1}\}.\end{array}$$

Then ${\left\{\rho (n)\right\}}_{n\ge n_0}$ is a nondecreasing sequence verifying ${lim}_{n\to \infty }\rho (n)=\infty$ and for all $n\ge n_0$, the following inequality holds:

$$\begin{array}{c}\hfill max\{z_{\rho (n)},z_{(n)}\}\le z_{\rho (n)+1}.\end{array}$$

3. Main Results

In this part, we describe our Halpern-type inertial iteration methods with self-adaptive step size for $({\mathrm{S}}_{\mathrm{p}}\mathrm{CNPP})$. We adopt the following assumptions to ensure the convergence of our methods:

$({\mathbf{S}}_{\mathbf{1}})$

$V_1:H_1\to 2^{H_1}$ and $V_2:H_2\to 2^{H_2}$ are maximal monotone operators;

$({\mathbf{S}}_{\mathbf{2}})$

$A:H_1\to H_2$ is a bounded linear operator;

$({\mathbf{S}}_{\mathbf{3}})$

$\left\{{\zeta }_n\right\}$ is a sequence in $(0,1)$ so that $\underset{n\to \infty }{lim}{\zeta }_n=0$ and ${\displaystyle \sum _{n=1}^{\infty }}{\zeta }_n=\infty$;

$({\mathbf{S}}_{\mathbf{4}})$

$\left\{{\delta }_n\right\}$ is a positive sequence so that ${\displaystyle \sum _{n=1}^{\infty }}{\delta }_n<\infty$ and $\underset{n\to \infty }{lim}\frac{{\delta }_n}{{\zeta }_n}=0$ ;

$({\mathbf{S}}_{\mathbf{5}})$

The solution set of $({\mathrm{S}}_{\mathrm{p}}\mathrm{CNPP})$ is express by $\mathsf{\Sigma }$ and $\mathsf{\Sigma }\ne \varnothing$.

Now, we can present our Halpern-type inertial iteration method for solving $({\mathrm{S}}_{\mathrm{p}}\mathrm{CNPP})$.

Remark 1.

From (3), we have ${\alpha }_n\le \frac{{\delta }_n}{\parallel z_n-z_{n-1}\parallel }$. By the choice of ${\alpha }_n>0$ and ${\delta }_n$ satisfying ${\displaystyle \sum _{n=1}^{\infty }}{\delta }_n<\infty$, we obtain $\underset{n\to \infty }{lim}{\alpha }_n\parallel z_n-z_{n-1}\parallel =0$ and by assumption $(\mathrm{S}4)$, we obtain $\underset{n\to \infty }{lim}\frac{{\alpha }_n\parallel z_n-z_{n-1}\parallel }{{\zeta }_n}\le \underset{n\to \infty }{lim}\frac{{\delta }_n}{{\zeta }_n}=0$.

Remark 2.

We can easily show that ${\varphi }^{★}\in \sum$ if and only if $R_{{\mu }_1}^{V_1}({\varphi }^{★})={\varphi }^{★}$ and $R_{{\mu }_2}^{V_2}(A{\varphi }^{★})=A({\varphi }^{★})$, by using the definition of resolvents of $V_1$ and $V_2$, respectively.

Lemma 5

([21]). If $w_n$ satisfies

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\frac{(\parallel (I-R_{{\mu }_1}^{V_1})(w_n){\parallel }^2+\parallel (I-R_{{\mu }_2}^{V_2})(A{w}_n){{\parallel }^2)}^2}{\parallel (I-R_{{\mu }_1}^{V_1})(w_n)+A^{*}(I-R_{{\mu }_2}^{V_2})(A{w}_n){\parallel }^2}=0,\end{array}$$

then

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel (I-R_{{\mu }_1}^{V_1})(w_n)\parallel =\underset{n\to \infty }{lim}\parallel (I-R_{{\mu }_2}^{V_2})(A{w}_n)\parallel =0.\end{array}$$

Remark 3.

If $z_{n+1}=w_n$, then from (5), we obtain

$$\begin{array}{c}\hfill {\tau }_n\parallel (I-R_{{\mu }_1}^{V_1})w_n+A^{*}(I-R_{{\mu }_2}^{V_2})A{w}_n\parallel =0.\end{array}$$

If $\parallel (I-R_{{\mu }_1}^{V_1})w_n+A^{*}(I-R_{{\mu }_2}^{V_2})A{w}_n\parallel =0$, we obtain that $w_n\in \sum$, otherwise by putting the value of ${\tau }_n$ and taking limit on both sides, we obtain

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\frac{\parallel (I-R_{{\mu }_1}^{V_1})(w_n){\parallel }^2+{\parallel (I-R_{{\mu }_2}^{V_2})(A{w}_n)\parallel }^2}{\parallel (I-R_{{\mu }_1}^{V_1})(w_n)+A^{*}(I-R_{{\mu }_2}^{V_2})(A{w}_n)\parallel }=0.\end{array}$$

(2)

By using Lemma 5, we conclude that

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel (I-R_{{\mu }_1}^{V_1})(w_n)\parallel =\underset{n\to \infty }{lim}\parallel (I-R_{{\mu }_2}^{V_2})(A{w}_n)\parallel =0,\end{array}$$

which implies that $w_n\in \sum$.

Theorem 1.

If the assumptions $({\mathbf{S}}_{\mathbf{1}})$–$({\mathbf{S}}_{\mathbf{5}})$ are satisfied. Then the sequence $\left\{z_n\right\}$ induced by Algorithm 1 converges strongly to a solution ${\varphi }^{★}$ of $({\mathrm{S}}_{\mathrm{p}}\mathrm{CNPP})$, where ${\mathrm{P}}_{\sum }(\upsilon )={\varphi }^{★}$.

Algorithm 1 Choose $\alpha \in [0,1)$ and ${\mu }_1>0,{\mu }_2>0$ are given. Choose arbitrary points $z_0$ and $z_1$ and set $n=0$.

Iterative Step: For iterates $z_n$, and  $z_{n-1}$,  $n\ge 1$, select $0<{\alpha }_n<{\overline{\alpha }}_n$, where $$\begin{array}{c}\hfill {\overline{\alpha }}_n=\left\{\begin{array}{c}min\left\{\frac{{\delta }_n}{\parallel z_n-z_{n-1}\parallel },\alpha \right\},\mathrm{if}{z}_n\ne z_{n-1},\hfill \\ \alpha ,\mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$ (3) Compute $$\begin{array}{ccc}\hfill w_n& =& {\zeta }_n\upsilon +(1-{\zeta }_n)\left[z_n+{\alpha }_n(z_n-z_{n-1})\right],\hfill \end{array}$$ (4) $$\begin{array}{ccc}\hfill z_{n+1}& =& w_n-{\tau }_n[(I-R_{{\mu }_1}^{V_1})w_n+A^{*}(I-R_{{\mu }_2}^{V_2})A{w}_n],\hfill \end{array}$$ (5) for some fixed element $\upsilon \in H_1$ and ${\tau }_n$ is defined as $$\begin{array}{ccc}\hfill {\tau }_n& =& \left\{\begin{array}{cc}\frac{\parallel (I-R_{{\mu }_1}^{V_1})(w_n){\parallel }^2+{\parallel (I-R_{{\mu }_2}^{V_2})(A{w}_n)\parallel }^2}{\parallel (I-R_{{\mu }_1}^{V_1})(w_n)+A^{*}(I-R_{{\mu }_2}^{V_2})(A{w}_n){\parallel }^2},\hfill & \mathrm{if}\parallel (I-R_{{\mu }_1}^{V_1})(w_n)+A^{*}(I-R_{{\mu }_2}^{V_2})(A{w}_n){\parallel }^2\ne 0\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\hfill \end{array}$$ (6) If $z_{n+1}=w_n$ then stop, if not, set $n=n+1$ and back to iterative step.

Proof. 

Let ${\varphi }^{★}\in \sum$ and using (1) and (5), we obtain

$$\begin{array}{cc}\hfill \parallel z_{n+1}-{\varphi }^{★}{\parallel }^2& =\parallel w_n-{\tau }_n[(I-R_{{\mu }_1}^{V_1})(w_n)+A^{*}(I-R_{{\mu }_2}^{V_2})(A{w}_n)]-{\varphi }^{★}{\parallel }^2\\ & \le \parallel w_n-{\varphi }^{★}{\parallel }^2+{\tau }_n^2{\parallel (I-R_{{\mu }_1}^{V_1})(w_n)+A^{*}(I-R_{{\mu }_2}^{V_2})(A{w}_n)\parallel }^2\\ & -2{\tau }_n⟨(I-R_{{\mu }_1}^{V_1})(w_n)+A^{*}(I-R_{{\mu }_2}^{V_2})(A{w}_n),w_n-{\varphi }^{★}⟩.\end{array}$$

(7)

For ${\varphi }^{★}\in \mathsf{\Sigma }$, by Remark 2, we have $R_{{\mu }_1}^{V_1}({\varphi }^{★})={\varphi }^{★}$ and $R_{{\mu }_2}^{V_2}(A{\varphi }^{★})=A{\varphi }^{★}$. Since $(I-R_{{\mu }_1}^{V_1})$ and $(I-R_{{\mu }_2}^{V_2})$ are firmly nonexpansive (Lemma 2), we have

$$\begin{array}{ccc}\hfill & & ⟨(I-R_{{\mu }_1}^{V_1})(w_n)+A^{*}(I-R_{{\mu }_1}^{V_2})(A{w}_n),w_n-{\varphi }^{★}⟩\hfill \\ & =& ⟨(I-R_{{\mu }_1}^{V_1})(w_n),w_n-{\varphi }^{★}⟩+⟨A^{*}(I-R_{{\mu }_2}^{V_2})(A{w}_n),w_n-{\varphi }^{★}⟩\hfill \\ & =& ⟨(I-R_{{\mu }_1}^{V_1})(w_n)-(I-R_{{\mu }_1}^{V_1})({\varphi }^{★}),w_n-{\varphi }^{★}⟩\hfill \\ & & +⟨A^{*}(I-R_{{\mu }_2}^{V_2})(A{w}_n)-A^{*}(I-R_{{\mu }_2}^{V_2})(A{\varphi }^{★}),w_n-{\varphi }^{★}⟩\hfill \\ & =& ⟨(I-R_{{\mu }_1}^{V_1})(w_n)-(I-R_{{\mu }_1}^{V_1})({\varphi }^{★}),w_n-{\varphi }^{★}⟩\hfill \\ & & +⟨(I-R_{{\mu }_2}^{V_2})(A{w}_n)-(I-R_{{\mu }_2}^{V_2})(A{\varphi }^{★}),A(w_n)-A({\varphi }^{★})⟩\hfill \\ & \ge & \parallel (I-R_{{\mu }_1}^{V_1})(w_n){\parallel }^2+{\parallel (I-R_{{\mu }_2}^{V_2})(A{w}_n)\parallel }^2\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\tau }_n^2{\parallel (I-R_{{\mu }_1}^{V_1})(w_n)+A^{*}(I-R_{{\mu }_2}^{V_2})(B{w}_n)\parallel }^2& -& 2⟨(I-R_{{\mu }_1}^{V_1})(w_n)+A^{*}(I-R_{{\mu }_2}^{V_2})(A{w}_n),w_n-{\varphi }^{★}⟩\hfill \\ & \le & \frac{(\parallel (I-R_{{\mu }_1}^{V_1})(w_n){\parallel }^2+\parallel (I-R_{{\mu }_2}^{V_2})(A{w}_n){{\parallel }^2)}^2}{\parallel (I-R_{{\mu }_1}^{V_1})(w_n)+A^{*}(I-R_{{\mu }_2}^{V_2})(A{w}_n){\parallel }^2}\hfill \\ & & -2\frac{(\parallel (I-R_{{\mu }_1}^{V_1})(w_n){\parallel }^2+\parallel (I-R_{{\mu }_2}^{V_2})(A{w}_n){{\parallel }^2)}^2}{\parallel (I-R_{{\mu }_1}^{V_1})(w_n)+A^{*}(I-R_{{\mu }_2}^{V_2})(A{w}_n){\parallel }^2}\hfill \\ & =& -\frac{(\parallel (I-R_{{\mu }_1}^{V_1})(w_n){\parallel }^2+\parallel (I-R_{{\mu }_2}^{V_2})(A{w}_n){{\parallel }^2)}^2}{\parallel (I-R_{{\mu }_1}^{V_1})(w_n)+A^{*}(I-R_{{\mu }_2}^{V_2})(A{w}_n){\parallel }^2}.\hfill \end{array}$$

(8)

From (7)–(8), we achieve

$$\begin{array}{ccc}\hfill \parallel z_{n+1}-{\varphi }^{★}{\parallel }^2& \le & \parallel w_n-{\varphi }^{★}{\parallel }^2-\frac{(\parallel (I-R_{{\mu }_1}^{V_1})(w_n){\parallel }^2+\parallel (I-R_{{\mu }_2}^{V_2})(A{w}_n){{\parallel }^2)}^2}{\parallel (I-R_{{\mu }_1}^{V_1})(w_n)+A^{*}(I-R_{{\mu }_2}^{V_2})(A{w}_n){\parallel }^2},\hfill \end{array}$$

(9)

or

$$\begin{array}{ccc}\hfill \parallel z_{n+1}-{\varphi }^{★}\parallel & \le & \parallel w_n-{\varphi }^{★}\parallel .\hfill \end{array}$$

(10)

Since $\underset{n\to \infty }{lim}{\alpha }_n\parallel z_n-z_{n-1}\parallel =0$, implies that ${\alpha }_n\parallel z_n-z_{n-1}\parallel$ is bounded, hence there exists a number $K_1$ such that ${\alpha }_n\parallel z_n-z_{n-1}\parallel \le K_1$. From  (4), it follows that  

$$\begin{array}{ccc}\hfill \parallel w_n-{\varphi }^{★}\parallel & =& \parallel {\zeta }_n\upsilon +(1-{\zeta }_n)\left[z_n+{\alpha }_n(z_n-z_{n-1}\parallel \right]-{\varphi }^{★}\parallel \hfill \\ & =& {\zeta }_n\parallel \upsilon -{\varphi }^{★}\parallel +(1-{\zeta }_n)\left[\parallel (z_n-{\varphi }^{★})+{\alpha }_n(z_n-z_{n-1})\parallel \right]\hfill \\ & \le & {\zeta }_n\parallel \upsilon -{\varphi }^{★}\parallel +(1-{\zeta }_n)\parallel \left[\parallel z_n-{\varphi }^{★}\parallel +{\alpha }_n\parallel z_n-z_{n-1}\parallel \right]\hfill \\ & \le & {\zeta }_n\parallel \upsilon -{\varphi }^{★}\parallel +(1-{\zeta }_n)\left[\parallel z_n-{\varphi }^{★}\parallel +K_1\right]\hfill \\ \hfill & \le & max\left\{\parallel \upsilon -{\varphi }^{★}\parallel ,\parallel z_n-{\varphi }^{★}\parallel +K_1\right\}\hfill \\ & \le & max\left\{\parallel \upsilon -{\varphi }^{★}\parallel ,\parallel w_{n-1}-{\varphi }^{★}\parallel +K_1\right\}\hfill \\ & & ⋮\hfill \\ & \le & max\left\{\parallel \upsilon -{\varphi }^{★}\parallel ,\parallel w_0-{\varphi }^{★}\parallel +K_1\right\},\hfill \end{array}$$

which implies that $\left\{w_n\right\}$ is bounded. By using (10), we conclude that $\left\{z_n\right\}$ is also bounded.

Let $v_n=z_n+{\alpha }_n(z_n-z_{n-1})$. The boundedness of $z_n$ implies that $v_n$ is also bounded. By using (4), we obtain

$$\begin{array}{ccc}\hfill \parallel w_n-{\varphi }^{★}{\parallel }^2& =& \parallel {\zeta }_n\upsilon +(1-{\zeta }_n)v_n-{\varphi }^{★}{\parallel }^2\hfill \\ & =& {\zeta }_n^2\parallel \upsilon -{\varphi }^{★}{\parallel }^2+{(1-{\zeta }_n)}^2{\parallel v_n-{\varphi }^{★}\parallel }^2+2{\zeta }_n(1-{\zeta }_n)⟨\upsilon -{\varphi }^{★},v_n-{\varphi }^{★}⟩,\hfill \end{array}$$

(11)

and

$$\begin{array}{ccc}\hfill \parallel v_n-{\varphi }^{★}{\parallel }^2& =& \parallel z_n+{\alpha }_n(z_n-z_{n-1})-{\varphi }^{★}{\parallel }^2\hfill \\ & =& \parallel z_n-{\varphi }^{★}{\parallel }^2+2{\alpha }_n⟨z_n-z_{n-1},v_n-{\varphi }^{★}⟩\hfill \\ & \le & \parallel z_n-{\varphi }^{★}{\parallel }^2+2{\alpha }_n\parallel z_n-z_{n-1}\parallel \parallel v_n-{\varphi }^{★}\parallel \hfill \\ & \le & \parallel z_n-{\varphi }^{★}{\parallel }^2+2{\psi }_n\parallel v_n-{\varphi }^{★}\parallel ,\hfill \end{array}$$

(12)

where ${\psi }_n={\alpha }_n\parallel z_n-z_{n-1}\parallel$. Therefore by using (11) and (12), we obtain

$$\begin{array}{ccc}\hfill \parallel w_n-{\varphi }^{★}{\parallel }^2& \le & {\zeta }_n^2{\parallel \upsilon -{\varphi }^{★}\parallel }^2+{(1-{\zeta }_n)}^2\left[\parallel z_n-{\varphi }^{★}{\parallel }^2+2{\psi }_n\parallel v_n-{\varphi }^{★}\parallel \right]\hfill \\ & & +2{\zeta }_n(1-{\zeta }_n)⟨\upsilon -{\varphi }^{★},v_n-{\varphi }^{★}⟩,\hfill \\ & \le & {(1-{\zeta }_n)}^2\parallel z_n-{\varphi }^{★}{\parallel }^2+2{\zeta }_n(1-{\zeta }_n)⟨\upsilon -{\varphi }^{★},v_n-{\varphi }^{★}⟩+{\zeta }_n^2{\parallel \upsilon -{\varphi }^{★}\parallel }^2\hfill \\ & & +2{\psi }_n\parallel v_n-{\varphi }^{★}\parallel .\hfill \end{array}$$

(13)

From (9) and (13), we get

$$\begin{array}{ccc}\hfill \parallel z_{n+1}-{\varphi }^{★}{\parallel }^2& \le & {(1-{\zeta }_n)}^2\parallel z_n-{\varphi }^{★}{\parallel }^2+2{\zeta }_n(1-{\zeta }_n)⟨\upsilon -{\varphi }^{★},v_n-{\varphi }^{★}⟩+{\zeta }_n^2{\parallel \upsilon -{\varphi }^{★}\parallel }^2\hfill \\ & & +2{\psi }_n\parallel v_n-{\varphi }^{★}\parallel -\frac{(\parallel (I-R_{{\mu }_1}^{V_1})(w_n){\parallel }^2+\parallel (I-R_{{\mu }_2}^{V_2})(A{w}_n){{\parallel }^2)}^2}{\parallel (I-R_{{\mu }_1}^{V_1})(w_n)+A^{*}(I-R_{{\mu }_2}^{V_2})(A{w}_n){\parallel }^2},\hfill \\ & \le & (1-{\zeta }_n)\parallel z_n-{\varphi }^{★}{\parallel }^2+{\zeta }_n\{2(1-{\zeta }_n)⟨\upsilon -{\varphi }^{★},v_n-{\varphi }^{★}⟩+{\zeta }_n{\parallel \upsilon -{\varphi }^{★}\parallel }^2\hfill \\ & & +2\frac{{\psi }_n}{{\zeta }_n}\parallel v_n-{\varphi }^{★}\parallel \}-\frac{(\parallel (I-R_{{\mu }_1}^{V_1})(w_n){\parallel }^2+\parallel (I-R_{{\mu }_2}^{V_2})(A{w}_n){{\parallel }^2)}^2}{\parallel (I-R_{{\mu }_1}^{V_1})(w_n)+A^{*}(I-R_{{\mu }_2}^{V_2})(A{w}_n){\parallel }^2}.\hfill \end{array}$$

(14)

Case I: Suppose that the sequence $\{\parallel z_n-{\varphi }^{★}\parallel \}$ is monotonically decreasing then there exists $m_0$ such that $\parallel z_{n+1}-{\varphi }^{★}\parallel \le \parallel z_n-{\varphi }^{★}\parallel$ for all $n\ge m_0$. Hence, the boundedness of $\{\parallel z_n-{\varphi }^{★}\parallel \}$ implies $\{\parallel z_n-{\varphi }^{★}\parallel \}$ is convergent. Therefore, using (14), we have

$$\begin{array}{c}\hfill \frac{(\parallel (I-R_{{\mu }_1}^{V_1})(w_n){\parallel }^2+\parallel (I-R_{{\mu }_2}^{V_2})(A{w}_n){{\parallel }^2)}^2}{\parallel (I-R_{{\mu }_1}^{V_1})(w_n)+A^{*}(I-R_{{\mu }_2}^{V_2})(A{w}_n){\parallel }^2}\le \parallel z_n-{\varphi }^{★}{\parallel }^2-\parallel z_{n+1}-{\varphi }^{★}{\parallel }^2-{\zeta }_n{\parallel z_n-{\varphi }^{★}\parallel }^2\\ \hfill +{\zeta }_n\left\{2(1-{\zeta }_n)⟨\upsilon -{\varphi }^{★},v_n-{\varphi }^{★}⟩+{\zeta }_n\parallel \upsilon -{\varphi }^{★}{\parallel }^2+2\frac{{\psi }_n}{{\zeta }_n}\parallel v_n-{\varphi }^{★}\parallel \right\}.\end{array}$$

(15)

Taking limit $n\to 0$, we obtain

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\frac{(\parallel (I-R_{{\mu }_1}^{V_1})(w_n){\parallel }^2+\parallel (I-R_{{\mu }_2}^{V_2})(A{w}_n){{\parallel }^2)}^2}{\parallel (I-R_{{\mu }_1}^{V_1})(w_n)+A^{*}(I-R_{{\mu }_2}^{V_2})(A{w}_n){\parallel }^2}=0.\end{array}$$

(16)

By using Lemma 5, we obtain

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel (I-R_{{\mu }_1}^{V_1})(w_n)\parallel =\underset{n\to \infty }{lim}\parallel (I-R_{{\mu }_2}^{V_2})(A{w}_n)\parallel =0.\end{array}$$

(17)

By using (5) and (16), we see that

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel z_{n+1}-w_n\parallel =0.\end{array}$$

(18)

Since $v_n=z_n+{\alpha }_n(z_n-z_{n-1})$ and using Remark 1, we obtain

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel z_n-v_n\parallel =\underset{n\to \infty }{lim}{\alpha }_n\parallel z_n-z_{n-1}\parallel =0.\end{array}$$

(19)

From (4), we have

$$\begin{array}{ccc}\hfill w_n-z_n& =& {\zeta }_n(\upsilon -z_n)+(1-{\zeta }_n){\alpha }_n(z_n-z_{n-1}),\hfill \\ \hfill \parallel w_n-z_n\parallel & \le & {\zeta }_n\parallel \upsilon -z_n\parallel +{\alpha }_n\parallel z_n-z_{n-1}\parallel ,\hfill \end{array}$$

taking limit $n\to \infty$, in  both the sides, using boundedness of $z_n$, Remark 1 and Assumption $({\mathrm{S}}_3)$, we get

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel w_n-z_n\parallel =0.\end{array}$$

(20)

Hence using (18) and (20), we conclude

$$\begin{array}{c}\hfill \parallel z_{n+1}-z_n\parallel \le \parallel z_{n+1}-w_n\parallel +\parallel w_n-z_n\parallel \to 0.\end{array}$$

(21)

Since $\left\{z_n\right\}$ is bounded, there exist a subsequence $\left\{z_{n_k}\right\}$ of $\left\{z_n\right\}$ so that $z_{n_k}\rightharpoonup \overline{\varphi }$ as $k\to \infty$. It follows from (19) and (20) that $v_{n_k}\rightharpoonup \overline{\varphi }$ and $w_{n_k}\rightharpoonup \overline{\varphi }$ as $k\to \infty$. We claim that $\overline{\varphi }\in \mathsf{\Sigma }$. From (5), it follows that

$$\begin{array}{ccc}\hfill \parallel z_{n_k+1}& -& w_{n_k}{\parallel }^2={\tau }_{n_k}^2{\parallel \left[(I-R_{{\mu }_1}^{V_1})w_{n_k+}{A}^{*}(I-R_{{\mu }_2}^{V_2})A{w}_{n_k}\right]\parallel }^2\hfill \\ & =& \frac{{\left(\parallel (I-R_{{\mu }_1}^{V_1})(w_{n_k}){\parallel }^2+{\parallel (I-R_{{\mu }_2}^{V_2})(A{w}_{n_k})\parallel }^2\right)}^2}{\parallel (I-R_{{\mu }_1}^{V_1})(w_{n_k})+A^{*}(I-R_{{\mu }_2}^{V_2})(A{w}_{n_k}){\parallel }^4}{\parallel (I-R_{{\mu }_1}^{V_1})w_{n_k+}{A}^{*}(I-R_{{\mu }_2}^{V_2})A{w}_{n_k}\parallel }^2\hfill \\ & =& \frac{{\left(\parallel (I-R_{{\mu }_1}^{V_1})(w_{n_k}){\parallel }^2+{\parallel (I-R_{{\mu }_2}^{V_2})(A{w}_{n_k})\parallel }^2\right)}^2}{\parallel (I-R_{{\mu }_1}^{V_1})(w_{n_k})+A^{*}(I-R_{{\mu }_2}^{V_2})(A{w}_{n_k}){\parallel }^2}.\hfill \end{array}$$

Taking $k\to \infty$ , and using Lemma 5, we obtain

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim}\parallel (I-R_{{\mu }_1}^{V_1})(w_{n_k})\parallel & =& \underset{n\to \infty }{lim}\parallel (I-R_{{\mu }_2}^{V_2})(A{w}_{n_k})\parallel =0.\hfill \end{array}$$

By the demiclosedness principle, we obtain

$$\begin{array}{c}\hfill (I-R_{{\mu }_1}^{V_1})(\overline{\varphi })=0,(I-R_{{\mu }_2}^{V_2})(A\overline{\varphi })=0.\end{array}$$

(22)

Remark 2 implies that $\overline{\varphi }\in \mathsf{\Sigma }$. Now, we exhibit that $\left\{z_n\right\}$ converge strongly to ${\varphi }^{★}$. From (14), we immediately see that

$$\begin{array}{ccc}\hfill \parallel z_{n+1}& -& {\varphi }^{★}{\parallel }^2\le (1-{\zeta }_n){\parallel z_n-{\varphi }^{★}\parallel }^2\hfill \\ & & +{\zeta }_n\left\{2(1-{\zeta }_n)⟨\upsilon -{\varphi }^{★},v_n-{\varphi }^{★}⟩+{\zeta }_n\parallel \upsilon -{\varphi }^{★}{\parallel }^2+2\frac{{\psi }_n}{{\zeta }_n}\parallel v_n-{\varphi }^{★}\parallel \right\}.\hfill \end{array}$$

(23)

Moreover, using $(S_2)$ and Remark 1, we get

$$\begin{array}{ccc}\hfill & & \underset{n\to \infty }{lim}\left\{2(1-{\zeta }_n)⟨\upsilon -{\varphi }^{★},v_n-{\varphi }^{★}⟩+{\zeta }_n\parallel \upsilon -{\varphi }^{★}{\parallel }^2+2\frac{{\psi }_n}{{\zeta }_n}\parallel v_n-{\varphi }^{★}\parallel \right\}\hfill \\ \hfill & =& \underset{k\to \infty }{lim}\left\{2(1-{\zeta }_{n_k})⟨\upsilon -{\varphi }^{★},v_{n_k}-{\varphi }^{★}⟩+{\zeta }_{n_k}\parallel \upsilon -{\varphi }^{★}{\parallel }^2+2\frac{{\psi }_{n_k}}{{\zeta }_{n_k}}\parallel v_{n_k}-{\varphi }^{★}\parallel \right\}\hfill \\ & =& 2⟨\upsilon -{\varphi }^{★},\overline{\varphi }-{\varphi }^{★}⟩\hfill \\ & \le & 0.\hfill \end{array}$$

(24)

By applying Lemma 1 to (23), we deduce that $z_n\to {\varphi }^{★}\in \mathsf{\Sigma }$ and ${\varphi }^{★}={\mathrm{P}}_{\mathsf{\Sigma }}\upsilon .$

• Case II: If the Case I is not true, then there exists a subsequence $\left\{z_{n_k}\right\}$ of $\left\{z_n\right\}$ such that $\parallel z_{n_k}-{\varphi }^{★}{\parallel }^2\le {\parallel z_{n_k+1}-{\varphi }^{★}\parallel }^2$ and the sequence defined by $\rho (n)=max\{m\le n:\parallel z_m-{\varphi }^{★}\parallel \le \parallel z_{m+1}-{\varphi }^{★}\parallel \}$ is an increasing sequence and $\rho (n)\to \infty$ as $n\to \infty$ and

  $$\begin{array}{c}\hfill 0\le \parallel z_{\rho (n)}-{\varphi }^{★}\parallel \le \parallel z_{\rho (n)+1}-{\varphi }^{★}\parallel ,\forall n\ge m.\end{array}$$

  (25)

Following the corresponding arguments as in the proof of Case I, we get

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel (I-R_{{\mu }_1}^{V_1})(w_{\rho (n)})\parallel =\underset{n\to \infty }{lim}\parallel (I-R_{{\mu }_2}^{V_2})(A{w}_{\rho (n)})\parallel =0,\end{array}$$

(26)

and

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel w_{\rho (n)}-v_{\rho (n)}\parallel =\underset{n\to \infty }{lim}\parallel z_{\rho (n)}-v_{\rho (n)}\parallel =0.\end{array}$$

(27)

From (23) and (16), we have

$$\begin{array}{ccc}\hfill 0\le \parallel z_{\rho (n)}& -& {\varphi }^{★}{\parallel }^2\le 2(1-{\zeta }_{\rho (n)})⟨\upsilon -{\varphi }^{★},v_{\rho (n)}-{\varphi }^{★}⟩+{\zeta }_{\rho (n)}{\parallel \upsilon -{\varphi }^{★}\parallel }^2\hfill \\ & & +2\frac{{\psi }_{\rho (n)}}{{\zeta }_{\rho (n)}}\parallel v_{\rho (n)}-{\varphi }^{★}\parallel \le 0.\hfill \end{array}$$

By taking limit $n\to \infty$, we obtain $\parallel z_{\rho (n)}-{\varphi }^{★}\parallel \to 0$ as $n\to \infty$. Invoking Lemma 4, we have

$$\begin{array}{c}\hfill 0\le \parallel z_n-{\varphi }^{★}\parallel \le max\left\{\parallel z_n-{\varphi }^{★}\parallel ,\parallel z_{\rho (n)}-{\varphi }^{★}\parallel \right\}\le \parallel z_{\rho (n)+1}-{\varphi }^{★}\parallel .\end{array}$$

(28)

Therefore from (28), it follows that $\parallel z_n-{\varphi }^{★}\parallel \to 0$ as $n\to \infty$. Hence, $z_n\to {\varphi }^{★}$ as $n\to \infty$ and we achieved the desired result.    □

Theorem 2.

Suppose that the assumptions $({\mathbf{S}}_{\mathbf{1}})$–$({\mathbf{S}}_{\mathbf{5}})$ are satisfied. Then the sequence $\left\{z_n\right\}$ induced by Algorithm 2 converge strongly to a solution ${\varphi }^{★}$ of $({\mathrm{S}}_{\mathrm{p}}\mathrm{CNPP})$, where ${\mathrm{P}}_{\sum }(\upsilon )={\varphi }^{★}$.

Algorithm 2 Choose $\alpha \in [0,1)$ and ${\mu }_1>0,{\mu }_2>0$ are given. Choose arbitrary points $z_0$ and $z_1$ and set $n=0$.

Iterative Step: Given the iterates $z_n$, and  $z_{n-1}$,  $n\ge 1$, choose $0<{\alpha }_n<{\overline{\alpha }}_n$, where $$\begin{array}{c}\hfill {\overline{\alpha }}_n=\left\{\begin{array}{c}min\left\{\frac{{\delta }_n}{\parallel z_n-z_{n-1}\parallel },\alpha \right\},\mathrm{if}{z}_n\ne z_{n-1},\hfill \\ \alpha ,\mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$ (29) Compute $$\begin{array}{ccc}\hfill w_n& =& {\zeta }_n\upsilon +(1-{\zeta }_n)z_n+{\alpha }_n(z_n-z_{n-1}),\hfill \end{array}$$ (30) $$\begin{array}{ccc}\hfill z_{n+1}& =& w_n-{\tau }_n[(I-R_{{\mu }_1}^{V_1})w_n+A^{*}(I-R_{{\mu }_2}^{V_2})A{w}_n],\hfill \end{array}$$ (31) for some fixed $\upsilon \in H_1$ and ${\tau }_n$ is defined as $$\begin{array}{ccc}\hfill {\tau }_n& =& \left\{\begin{array}{cc}\frac{\parallel (I-R_{{\mu }_1}^{V_1})(w_n){\parallel }^2+{\parallel (I-R_{{\mu }_2}^{V_2})(A{w}_n)\parallel }^2}{\parallel (I-R_{{\mu }_1}^{V_1})(w_n)+A^{*}(I-R_{{\mu }_2}^{V_2})(A{w}_n){\parallel }^2},\hfill & \mathrm{if}\parallel (I-R_{{\mu }_1}^{V_1})(w_n)+A^{*}(I-R_{{\mu }_2}^{V_2})(A{w}_n){\parallel }^2\ne 0\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\hfill \end{array}$$ (32) If $z_{n+1}=w_n$ then stop, if not, set $n=n+1$ and back to iterative step.

Proof. 

Let ${\varphi }^{★}\in \mathsf{\Sigma }$, and since $\underset{n\to \infty }{lim}\frac{{\alpha }_n\parallel z_n-z_{n-1}\parallel }{{\zeta }_n}=0$, implies that $\frac{{\alpha }_n\parallel z_n-z_{n-1}\parallel }{{\zeta }_n}$ is bounded, so there exists a number $K_2$ such that $\frac{{\alpha }_n\parallel z_n-z_{n-1}\parallel }{{\zeta }_n}\le K_2$. Then by using (30), we obtain

$$\begin{array}{ccc}\hfill \parallel w_n-{\varphi }^{★}\parallel & =& \parallel {\zeta }_n\upsilon +(1-{\zeta }_n)z_n+{\alpha }_n(z_n-z_{n-1})-{\varphi }^{★}\parallel \hfill \\ & \le & {\zeta }_n\parallel \upsilon -{\varphi }^{★}\parallel +(1-{\zeta }_n)\parallel z_n-{\varphi }^{★}\parallel +{\alpha }_n\parallel z_n-z_{n-1}\parallel \hfill \\ & =& {\zeta }_n\left[\parallel \upsilon -{\varphi }^{★}\parallel +\frac{{\alpha }_n}{{\zeta }_n}\parallel z_n-z_{n-1}\parallel \right]+(1-{\zeta }_n)\parallel z_n-{\varphi }^{★}\parallel \hfill \\ & =& {\zeta }_n\left[\parallel \upsilon -{\varphi }^{★}\parallel +K_2\right]+(1-{\zeta }_n)\parallel z_n-{\varphi }^{★}\parallel \hfill \\ & =& {\zeta }_n\left[\parallel \upsilon -{\varphi }^{★}\parallel +K_2\right]+(1-{\zeta }_n)\parallel w_{n-1}-{\varphi }^{★}\parallel \hfill \\ & \le & max\left\{\parallel \upsilon -{\varphi }^{★}\parallel +K_2,\parallel w_{n-1}-{\varphi }^{★}\parallel \right\}\hfill \\ & & ⋮\hfill \\ & \le & max\left\{\parallel \upsilon -{\varphi }^{★}\parallel +K_2,\parallel w_0-{\varphi }^{★}\parallel \right\}.\hfill \end{array}$$

By using (10), we obtain

$$\begin{array}{ccc}\hfill \parallel z_{n+1}-{\varphi }^{★}\parallel & \le & max\left\{\parallel \upsilon -{\varphi }^{★}\parallel +K_2,\parallel w_0-{\varphi }^{★}\parallel \right\},\hfill \end{array}$$

which implies that $\left\{z_n\right\}$ is bounded and so is $\left\{w_n\right\}$. Let $y_n={\zeta }_n\upsilon +(1-{\zeta }_n)z_n$, then by using (1), we obtain

$$\begin{array}{ccc}\hfill \parallel w_n-{\varphi }^{★}{\parallel }^2& =& \parallel y_n+{\alpha }_n(z_n-z_{n-1})-{\varphi }^{★}{\parallel }^2\hfill \\ & =& \parallel y_n-{\varphi }^{★}{\parallel }^2+2⟨y_n-{\varphi }^{★},{\alpha }_n(z_n-z_{n-1})⟩+{\alpha }_n^2{\parallel z_n-z_{n-1}\parallel }^2.\hfill \end{array}$$

(33)

Now, we estimate

$$\begin{array}{ccc}\hfill \parallel y_n-{\varphi }^{★}{\parallel }^2& =& \parallel {\zeta }_n\upsilon +(1-{\zeta }_n)z_n-{\varphi }^{★}{\parallel }^2\hfill \\ & =& {\zeta }_n^2\parallel \upsilon -{\varphi }^{★}{\parallel }^2+2{\zeta }_n(1-{\zeta }_n)⟨\upsilon -{\varphi }^{★},z_n-{\varphi }^{★}⟩+{(1-{\zeta }_n)}^2{\parallel z_n-{\varphi }^{★}\parallel }^2\hfill \end{array}$$

(34)

and

$$\begin{array}{ccc}\hfill ⟨y_n-{\varphi }^{★},{\alpha }_n(z_n-z_{n-1})⟩& =& ⟨{\zeta }_n\upsilon +(1-{\zeta }_n)z_n-{\varphi }^{★},{\alpha }_n(z_n-z_{n-1})⟩\hfill \\ & =& {\zeta }_n{\alpha }_n⟨\upsilon -{\varphi }^{★},(z_n-z_{n-1})⟩+(1-{\zeta }_n){\alpha }_n⟨z_n-{\varphi }^{★},z_n-z_{n-1}⟩\hfill \\ & \le & {\alpha }_n\parallel \upsilon -{\varphi }^{★}\parallel \parallel z_n-z_{n-1}\parallel +{\alpha }_n\parallel z_n-{\varphi }^{★}\parallel \parallel z_n-z_{n-1}\parallel \hfill \\ & \le & {\alpha }_n\parallel z_n-z_{n-1}\parallel \left\{\parallel \upsilon -{\varphi }^{★}\parallel +\parallel z_n-{\varphi }^{★}\parallel \right\}.\hfill \end{array}$$

(35)

From (33), (34), and (35), we obtain

$$\begin{array}{c}\hfill \parallel w_n-{\varphi }^{★}{\parallel }^2\le (1-{\zeta }_n)\parallel z_n-{\varphi }^{★}{\parallel }^2+{\zeta }_n\{{\zeta }_n\parallel \upsilon -{\varphi }^{★}{\parallel }^2+\frac{2{\alpha }_n}{{\zeta }_n}\parallel z_n-z_{n-1}\parallel \{\parallel \upsilon -{\varphi }^{★}\parallel \\ \hfill +\parallel z_n-{\varphi }^{★}\parallel \}\frac{2{\alpha }_n^2}{{\zeta }_n}{\parallel z_n-z_{n-1}\parallel }^2+2⟨\upsilon -{\varphi }^{★},z_n-{\varphi }^{★}⟩\}.\end{array}$$

(36)

Putting the value of $\parallel w_n-{\varphi }^{★}\parallel$ in (9), we have

$$\begin{array}{ccc}\hfill \parallel z_{n+1}-{\varphi }^{★}{\parallel }^2& \le & (1-{\zeta }_n){\parallel z_n-{\varphi }^{★}\parallel }^2\hfill \\ & & +{\zeta }_n\{{\zeta }_n\parallel \upsilon -{\varphi }^{★}{\parallel }^2+\frac{2{\alpha }_n}{{\zeta }_n}\parallel z_n-z_{n-1}\parallel \left\{\parallel \upsilon -{\varphi }^{★}\parallel +\parallel z_n-{\varphi }^{★}\parallel \right\}\hfill \\ & & +\frac{2{\alpha }_n^2}{{\zeta }_n}{\parallel z_n-z_{n-1}\parallel }^2+2⟨\upsilon -{\varphi }^{★},z_n-{\varphi }^{★}⟩\}\hfill \\ & & -\frac{(\parallel (I-R_{{\mu }_1}^{V_1})(w_n){\parallel }^2+\parallel (I-R_{{\mu }_2}^{V_2})(A{w}_n){{\parallel }^2)}^2}{\parallel (I-R_{{\mu }_1}^{V_1})(w_n)+A^{*}(I-R_{{\mu }_2}^{V_2})(A{w}_n){\parallel }^2}.\hfill \end{array}$$

(37)

Now, We can obtain the desired outcomes by following the corresponding steps as in the proof of Theorem 1. □

Remark 4.

Let ${\mathsf{{\rm Y}}}_1:H_1\to H_1$, ${\mathsf{{\rm Y}}}_2:H_2\to H_2$ be nonexpansive mappings and $A:H_1\to H_2$ is a bounded linear operator, then split common fixed point problem $({\mathrm{S}}_{\mathrm{p}}\mathrm{CFPP})$ is defined as:

$$\begin{array}{c}\hfill \mathrm{Find}{s}^{*}\in H_1\mathrm{such}\mathrm{that}{s}^{*}\in \mathrm{Fix}({\mathsf{{\rm Y}}}_1)\mathrm{and}A{s}^{*}\in H_2\mathrm{such}\mathrm{that}A{s}^{*}\in \mathrm{Fix}({\mathsf{{\rm Y}}}_2),\end{array}$$

(38)

where $\mathrm{Fix}({\mathsf{{\rm Y}}}_1)$ and $\mathrm{Fix}({\mathsf{{\rm Y}}}_2)$ denote the fixed point sets of mappings ${\mathsf{{\rm Y}}}_1$ and ${\mathsf{{\rm Y}}}_2$, respectively. By replacing $R_{{\mu }_1}^{V_1}$ and $R_{{\mu }_2}^{V_2}$ with nonexpansive mappings ${\mathsf{{\rm Y}}}_1$ and ${\mathsf{{\rm Y}}}_2$, respectively, in Algorithms 1 and 2, we can obtain the strong convergence theorems for $({\mathrm{S}}_{\mathrm{p}}\mathrm{CFPP})$.

4. Numerical Experiments

Example 1. 

Suppose $H_1=\mathbb{R}=H_2$. We define the monotone mappings $V_1$ and $V_2$ by $V_1(x)=\frac{x}{3}+1\mathrm{and}{V}_2(x)=x+1$. Let $A(x)=\frac{x}{3}$ is a bounded linear operator. It is obvious to see that $V_1$ and $V_2$ are monotone operators. The Resolvents of $V_1$ and $V_2$ are

$$\begin{array}{c}\hfill R_{{\mu }_1}^{V_1}(x)={[I+{\mu }_1{V}_1]}^{-1}(x)=\frac{3(x-{\mu }_1)}{3+{\mu }_1},{\mu }_1>0;\end{array}$$

$$\begin{array}{c}\hfill R_{{\mu }_2}^{V_2}(x)={[I+{\mu }_2{V}_2]}^{-1}(x)=\frac{x-{\mu }_2}{1+{\mu }_2},{\mu }_2>0.\end{array}$$

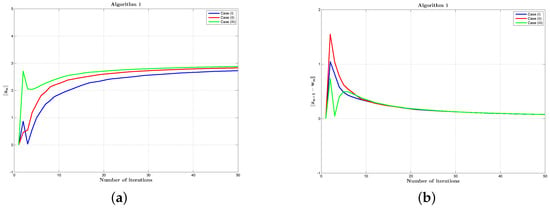
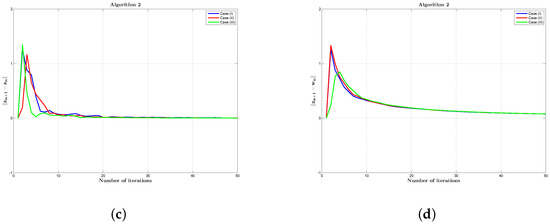
We choose ${\zeta }_n=\frac{1}{n+1}$ and ${\delta }_n=\frac{1}{1+n^2}$ satisfying the conditions $({\mathrm{S}}_3)$ and $({\mathrm{S}}_4)$. As a stopping condition, we set the maximum number of iterations at 50. The parameter ${\alpha }_n$ is created at random in the range $(0,{\overline{\alpha }}_n)$, where ${\overline{\alpha }}_n$ is computed by (3). It can easily seen that $\sum =\{-3\}$ and we select the fixed point $\upsilon =-3$. Figure 1 depicts the behaviour of the sequences derived from Algorithms 1 and 2 using three distinct cases, which are mentioned below:

Figure 1. Graphical behaviour of $\parallel z_n\parallel$, $\parallel z_{n+1}-w_n\parallel$ of Algorithm 1 are shown in figures (a,b) and graph of $\parallel z_{n+1}-z_n\parallel$ and $\parallel z_{n+1}-w_n\parallel$ of Algorithm 2 are displayed in figures (c,d) by choosing three distinct cases of parameters.

Case (I):

$z_0=0$, $z_1=2$, ${\mu }_1=0.5$, ${\mu }_2=0.8$.

Case (II):

$z_0=-3$, $z_1=1$, ${\mu }_1=1.2$, ${\mu }_2=0.9$.

Case (III):

$z_0=2$, $z_1=-4$, , ${\mu }_1=0.05$, ${\mu }_2=1$.

Comparison: Furthermore, we compare our proposed methods to the methods in Byrne et al. [8], Kazmi [9], Dilshad et al. [21] and Akram et al. [11]. We select $\kappa =0.15$ for Byrne et al. [8], Kazmi [9]; $\kappa =0.5$ for Akram et al. [11]; $\mu ={\mu }_1=1,{\mu }_2=2$ for Byrne et al. [8], Kazmi [9], Dilshad et al. [21] and Akram et al. [11]; $h(x)=\frac{x}{2}$, $T(x)=x$ for Kazmi [9] and Akram et al. [11]. We consider the following cases:

Case (A):

$z_0=2$, $z_1=0$, ${\zeta }_n=\frac{1}{1+n}$;

Case (B):

$z_0=-\sqrt{2}$, $z_1=11$, ${\zeta }_n=\frac{1}{{(1+n)}^{0.7}}$;

Case (C):

$z_0=5$, $z_1=-4$, ${\zeta }_n=\frac{1}{{(1+n)}^{0.7}}$;

Case (D):

$z_0=2/3$, $z_1=-\sqrt{3}$, ${\zeta }_n=\frac{1}{1+n}$;

It is noticed that our schemes are easy to implement and the choosing step size is free from the pre-calculation of $\parallel A\parallel$. The experiment results are presented in Table 1 and Figure 2.

Table 1. Numerical comparison of Algorithms 1 and 2 with the work studied in [8,9,11,21] for Example 1.

Methods	Iter (n)/Times (s)	Case (A)	Case (B)	Case (C)	Case (D)
Algorithm 1	Iteration	48	50	52	59
	Time/s	5.10 × ${10}^{-6}$	4.40 × ${10}^{-6}$	4.90 × ${10}^{-6}$	1.10 × ${10}^{-5}$
Algorithm 2	Iteration	41	50	41	50
	Time/s	4.70 × ${10}^{-6}$	3.00 × ${10}^{-6}$	1.16 × ${10}^{-5}$	3.00 × ${10}^{-6}$
Byrne et al. [8]	Iteration	102	108	100	101
	Time/s	1.93 × ${10}^{-4}$	1.63 × ${10}^{-4}$	2.17 × ${10}^{-4}$	1.73 × ${10}^{-4}$
Kazmi et al. [9]	Iteration	109	114	107	111
	Time/s	2.20 × ${10}^{-6}$	3.20 × ${10}^{-6}$	2.00 × ${10}^{-6}$	2.00 × ${10}^{-6}$
Dilshad et al. [21]	Iteration	126	128	109	120
	Time/s	5.20 × ${10}^{-6}$	3.10 × ${10}^{-6}$	2.30 × ${10}^{-6}$	3.00 × ${10}^{-6}$
Akram et al. [11]	Iteration	105	110	108	104
	Time/s	1.28 × ${10}^{-4}$	1.10 × ${10}^{-4}$	1.14 × ${10}^{-4}$	9.44 × ${10}^{-5}$

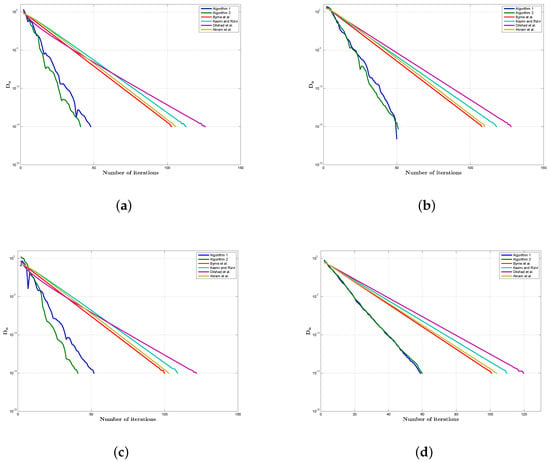
Figure 2. Graphical comparison of Algorithms 1 and 2 with Byrne et al. [8], Kazmi and Rizvi [9], Dilshad et al. [21] and Akram et al. [11] for Example 1 by using Case (A)–Case (D). (a) by Case (A), (b) by Case (B), (c) by case (C), (d) by Case (D).

Example 2. 

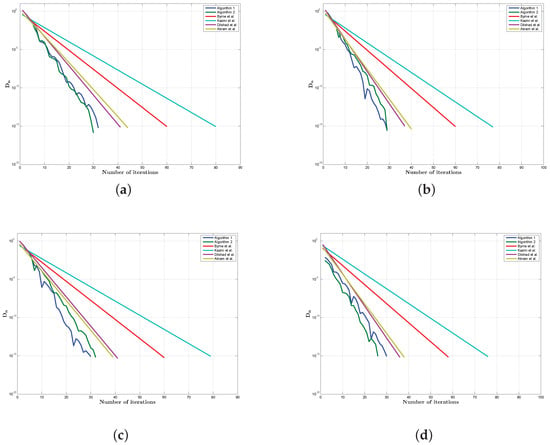
Let $H_1=H_2=l_2:=\{x:=(x_1,x_2,x_3,\cdots ,x_n,\cdots ),x_n\in \mathbb{R}:{\displaystyle \sum _{n=1}^{\infty }}\left|x_n\right|<\infty \}$ is a real Hilbert space with inner product $⟨x,y⟩={\displaystyle \sum _{n=1}^{\infty }}{x}_n{y}_n$ and the norm is given by $\parallel x\parallel ={\left({\displaystyle \sum _{n=1}^{\infty }}{\left|x_n\right|}^2\right)}^{1/2}$. We define the monotone mappings by $V_1(x)=x=(x_1,x_2,x_3,\cdots ,x_n,\cdots )$ and $V_2(x)=\frac{x}{3}=(\frac{x_1}{3},\frac{x_2}{3},\frac{x_3}{3},\cdots ,\frac{x_n}{3},\cdots )$. Let $A=I$, the identity operator hence so its adjoint $A^{*}$. The stopping criteria for our computation is $D_n<{10}^{-15}$, where $D_n=\parallel z_{n+1}-z_n\parallel$. We compare our proposed methods to the methods in Byrne et al. [8], Kazmi [9], Dilshad et al. [21] and Akram et al. [11].

We select $\kappa =0.25$ for Byrne et al. [8], and Kazmi [9]; $\kappa =0.5$ for Akram et al. [11]; ${\mu }_1=1.5$ and ${\mu }_2=0.5$ for Algorithms 1 and 2 and Akram et al. [11]; $\mu =1.5$ for Byrne et al. [8], Kazmi [9] and Dilshad et al. [21]; $h(x)=\frac{x}{2}=(\frac{x_1}{2},\frac{x_2}{2},\cdots ,\frac{x_n}{2},\cdots )$, $T(x)=x=(x_1,x_2,\cdots ,x_n,\cdots )$ for Kazmi [9] and Akram et al. [11]; $\nu =\mathbf{0}$ for Algorithms 1 and 2 and Dilshad et al. [21]; ${\delta }_n=\frac{1}{1+n^2}$, $\alpha =0.3$ and $\overline{\alpha }$ is selected randomly by (3). We take into consideration the following different cases:

Case(A′):

$z_0=(1,1/4,1/9,1/16,\cdots ),z_1=(1,1/8,1/27,1/256,\cdots )$ and ${\zeta }_n=\frac{1}{100+n}$;

Case(B′):

$z_0=(1,-1/2,1/3,-1/4,\cdots ),z_1=(1,0,1/3,0,\cdots )$ and ${\zeta }_n=\frac{1}{{(100+n)}^{0.25}}$;

Case(C′):

$z_0=(1,0,0,0,\cdots ),z_1=(2/3,2/9,2/27,2/54,\cdots )$ and ${\zeta }_n=\frac{1}{100+n}$;

Case(D′):

$z_0=(1/4,1/16,1/64,1/256,\cdots ),z_1=(0,1/2,0,1/4,\cdots )$ and ${\zeta }_n=\frac{1}{{(100+n)}^{0.25}}$;

The experiment results we have obtained are shown in Table 2 and Figure 3.

Table 2. Numerical comparison of Algorithms 1 and 2 with the work studied in [8,9,11,21] for Example 2.

Methods	Iter (n)/Times (s)	Case (A′)	Case (B′)	Case (C′)	Case (D′)
Algorithm 1	Iteration	34	28	30	30
	Time/s	1.36 × ${10}^{-5}$	1.93 × ${10}^{-5}$	1.36 × ${10}^{-5}$	1.39 × ${10}^{-5}$
Algorithm 2	Iteration	29	28	33	26
	Time/s	1.34 × ${10}^{-5}$	1.45 × ${10}^{-5}$	1.3× ${10}^{-5}$	1.24 × ${10}^{-5}$
Byrne et al. [8]	Iteration	60	60	59	57
	Time/s	1.54 × ${10}^{-5}$	1.06 × ${10}^{-5}$	1.78 × ${10}^{-5}$	1.03 × ${10}^{-5}$
Kazmi et al. [9]	Iteration	80	77	79	76
	Time/s	1.04 × ${10}^{-5}$	1.02 × ${10}^{-5}$	9.6 × ${10}^{-6}$	1.16 × ${10}^{-5}$
Dilshad et al. [21]	Iteration	41	37	41	37
	Time/s	3.23 × ${10}^{-5}$	4.49 × ${10}^{-5}$	3.14 × ${10}^{-5}$	3.97 × ${10}^{-5}$
Akram et al. [11]	Iteration	44	40	39	38
	Time/s	1.53 × ${10}^{-5}$	2.33 × ${10}^{-5}$	1.56 × ${10}^{-5}$	2.05 × ${10}^{-5}$

Figure 3. Graphical comparison of Algorithms 1 and 2 with Byrne et al. [8], Kazmi and Rizvi [9], Dilshad et al. [21] and Akram et al. [11] for Example 2 by using Case (A′)–Case (D′). (a) by Case (A′), (b) by Case (B′), (c) by Case (C′), (d) by Case (D′).

5. Conclusions

We have presented two Halpern-type inertial iteration methods with a self-adaptive step size to estimate the solution of $({\mathrm{S}}_{\mathrm{p}}\mathrm{CNPP})$ in such a way that the Halpern iteration and inertial term are computed simultaneously. We demonstrated the strong convergence of the suggested methods to approach the solution of $({\mathrm{S}}_{\mathrm{p}}\mathrm{CNPP})$ with some appropriate assumptions so that the calculation of $\parallel A\parallel$ is not necessary for the step size. Finally, we illustrate the proposed methods by choosing different parameters with suitable numerical examples. We show that our suggested schemes perform so well in the number of iterations as well as time taken by CPU. Note that the viscosity approximation is more general than the Halpern approximation method. Applying the viscosity-type inertial approximation to estimate the solution of $({\mathrm{S}}_{\mathrm{p}}\mathrm{CNPP})$ or $({\mathrm{S}}_{\mathrm{p}}\mathrm{MVIP})$ together with $(\mathrm{FPP})$ will be intriguing in the future.