Dynamic S-Box Construction Using Mordell Elliptic Curves over Galois Field and Its Applications in Image Encryption

Abstract

Elliptic curve cryptography has gained attention due to its strong resilience against current cryptanalysis methods. Inspired by the increasing demand for reliable and secure cryptographic methods, our research investigates the relationship between complex mathematical structures and image encryption. A substitution box (S-box) is the single non-linear component of several well-known security systems. Mordell elliptic curves are used because of their special characteristics and the immense computational capacity of Galois fields. These S-boxes are dynamic, which adds a layer of complexity that raises the encryption process’s security considerably. We suggest an effective technique for creating S-boxes based on a class of elliptic curves over $GF\left(2^n\right),n\ge 8$. We demonstrate our approach’s robustness against a range of cryptographic threats through thorough examination, highlighting its practical applicability. The assessment of resistance of the newly generated S-box to common attack methods including linear, differential, and algebraic attacks involves a thorough analysis. This analysis is conducted by quantifying various metrics such as non-linearity, linear approximation, strict avalanche, bit independence, and differential approximation to gauge the S-box’s robustness against these attacks. A recommended method for image encryption involves the use of built-in S-boxes to quickly perform pixel replacement and shuffling. To evaluate the efficiency of the proposed strategy, we employed various tests. The research holds relevance as it can provide alternative guidelines for image encryption, which could have wider consequences for the area of cryptography as a whole. We believe that our findings will contribute to the development of secure communication and data protection, as digital security is becoming increasingly important.

1. Introduction

Most individuals frequently want to keep their personal information confidential. There have been several occasions throughout history where it was necessary to keep important information hidden from intruders. In particular, it was still crucial to prevent enemies from intercepting communications between generals or rulers and their troops. In the past, simple strategies were used to obfuscate data. On the other hand, the world became more interconnected as society advanced. Due to the rising demand for electronic services, this resulted in an increasing reliance on electronic systems. It is a generally acknowledged activity to exchange private information online. As a result, the need for advanced techniques of data security has become more and more imperative every day. The basic goal of cryptography is the creation of techniques that guarantee safe communication over the networks. The word “cryptography” is derived from two Greek words: “Kryptos” which refers to something concealed or unrevealed and “graphein” which describes the process of learning or writing. The primary goal of cryptography is often regarded as safeguarding information security. The subjects of computer science, mathematics, communication science, physics, and electrical engineering play a significant role in the development of modern cryptography. Cryptography is useful in many real-world situations like protecting chip-based payment cards, allowing digital currencies, securing computer passwords, and simplifying electronic commerce. An S-box is the nonlinear component of cryptosystems employing block ciphers. These cryptosystems use two kinds of S-boxes, static and dynamic. Static S-boxes are fixed tables with substitution values that do not change during the encryption procedure. Even though they are easy to create and efficient, their fixed nature leaves them open to some kinds of assaults, such as differential cryptanalysis or algebraic attacks. Conversely, dynamic S-boxes provide unpredictability to the substitution procedure. They use functions or algorithms that, depending on certain variables or parameters, dynamically produce the substitution values. By increasing the complexity of the encryption scheme and making it harder for attackers to identify patterns in the substitution process, its security is strengthened.

Strong cryptosystems are also developed using elliptic curves. The most often used strategies for enhancing information security are those based on elliptic curves. We will specifically focus on elliptic curve cryptography (ECC) and the many approaches proposed by many experts in this field. The elliptic curve was initially used as a public key cryptosystem in 1985 by Miller [1]. Additionally, it was shown that the ECC cryptosystem is twenty percent more effective than the Diffie–Hellman algorithm. Koblatiz et al. in [2] presented the concept of a discrete logarithmic issue which is applied to construct a highly secure, quick, and effective security system. An effective method to multiply the elliptic curve points and their resources is provided in [3] and compared with binary and non-adjacent (NAF) forms. It has been found that ECC, which uses a shorter key length than RSA, is more secure overall. In [4], an elliptic curve is used over a prime field to generate elliptic curve points, and then, each point’s x and y coordinates are added. The modulo function is then used to construct various numbers of $4\times 4$ S-boxes. In [5], a procedure for creating prime field dependent $8\times 8$ (8 input bits, 8 output bits) S-boxes is described. In this work, the modulo operation is used after the x-coordinate of an elliptic curve to produce the various numbers of $8\times 8$ S-boxes dependent on the prime field. The authors in [6] presented novel approaches for creating S-boxes utilizing the total order on an elliptic curve (EC) over a prime field. A search method is used to efficiently construct an EC in place of the more traditional group rule, which is computationally expensive. The x-coordinates of the points of the order elliptic curve (OEC) are used in the construction method for the S-boxes. These methods can be used to create various numbers of $8\times 8$ S-boxes. Although they are independent of the underlying elliptic curve and may or may not generate an S-box for any input value, their result is still unpredictable. A $4\times 4$ S-box was developed in [7] by using elliptic curves over $GF\left(2^4\right)$. Shah et al. in [8] used the Mordell elliptic curves over finite fields with elements 256, 512, 2048. The authors designed three S-boxes with one S-box of nonlinearity 112 and with a very low score of strict avalanche criteria (SAC). The authors concluded that we can obtain good S-boxes over $GF\left(2^n\right),n\ge 9$. In this, study, we used the same idea and will show that over $GF\left(2^8\right)$, there are extremely good S-boxes as compared to S-boxes produced in [8] in terms of scores of strict avalanche criteria (SAC), bit independence criteria (BIC), linear approximation probability (LAP), and differential approximation probability (DAP) [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44].

The confidentiality, integrity, and validity of digital images depend on image encryption techniques, which also secure transmission, solve privacy issues, adhere to legal requirements, stop illegal changes, and safeguard intellectual property rights. Feng et al. in [45] developed a new fractional-order 3D Lorenz chaotic system and a 2D sinusoidally constrained polynomial hyper-chaotic map (2D-SCPM). The multi-image encryption technique outperforms several contemporary image encryption algorithms by utilizing multi-channel fusion, chaotic random substitution, dynamic diffusion, and quick scrambling. The authors in [46] used an image encryption method that employs two keys. The first key is generated by a 2D Logistic Sine map and a Linear Congruential Generator, while the second key is generated from the Tent map, the Bernoulli, and the KAA map. The study in [47] presents a Feistel cipher structure-based simplified picture encryption algorithm (SIEA) for picture security in cloud storage that makes use of the key generation and permutation approaches. For digital image encryption, the study [48] suggests ARHM (AES and Rossler Hyperchaotic Modeling) that combines AES with phantom transformation and the Rossler hyperchaotic system. This model conducts simulations and analyses including key space, key sensitivity, histogram, pixel correlation, entropy, and resistance to differential attacks. It makes use of chaotic system randomness and AES encryption speed. Ali et al. proposed an image encryption algorithm based on S-boxes using the direct product of cyclic groups and Galois fields [49]. The authors in [50] used Mobius transformation on a Galois field to generate robust S-boxes and presented a scheme that can protect medical images in a better way. The use of quantum theory in image encryption has been on the rise lately. The Quantum Chaotic Map and DNA Coding-based Image Encryption Algorithm (QCMDC-IEA) is susceptible to assaults on its DNA domain encryption and has intrinsic security weaknesses such as the presence of an equivalent key resulting from independent chaos-based sequences. A suggested technique of attack takes advantage of these flaws to achieve low complexity and full decipherment. The authors presented recommendations for security enhancements in similar cryptosystems to address the discovered weaknesses [51]. An image encryption algorithm utilizing Quantum Logistic and Lorenz Chaotic Map with DNA Coding, claims enhanced security, but a proposed chosen-plaintext attack exposes vulnerabilities in its permutation and diffusion key. Suggestions for improvement are offered to bolster the algorithm’s security and practicality in cryptographic design [52].

It is evident from the literature that there is a dire need to design robust S-boxes using algebraic structures to enhance the security of cryptosystems. The elliptic curves and Galois fields are used separately in the literature for designing image encryption schemes and S-boxes. The elliptic curves provide greater security due to the short key length, and its usage along with the Galois field can improve the strength of cryptosystems. The following are the motivations for the proposed work:

• The elliptic curves provide great resistance against linear and differential cryptanalysis due to their nonlinear nature.
• Compact S-box designs can be achieved by representing elliptic curves with smaller key sizes than conventional mathematical structures. In terms of efficiency, this can be helpful, particularly in settings with few resources.
• Hardware and software may both effectively implement elliptic curve operations. For real-world applications, such as embedded systems or gadgets with constrained processing power, this efficiency is essential.
• A further degree of protection is provided by the mathematical hardness of elliptic curve problems like the elliptic curve discrete logarithm problem. The cryptographic strength of elliptic curve-based designs is predicated on the difficulty of solving these complex mathematical problems.
• Due to the strong properties of elliptic curves and a highly nonlinear permutation of the Galois field, the proposed strategy for S-boxes and encryption has a greater ability to resist cryptanalysis.

The contributions of the proposed scheme are as follows.

• The generated S-boxes have nonlinearity greater than 105 with four optimal boxes of nonlinearity 112.
• As the degree of irreducible polynomials increases, the number of irreducible polynomials increases quickly, and we can produce millions of S-boxes with the proposed work in a short time.
• The entropy of the proposed cipher image is close to 8, confirming the efficacy of the effectiveness of the method.

The rest of the article is divided into five Sections. Section 2 deals with preliminaries. The proposed algorithm is described in Section 3. Analysis of S-boxes has been made in Section 4. We employed the proposed S-boxes in image encryption in Section 5. Section 6 concludes the study.

2. Preliminaries

In this section, we will present some basic definitions related to the Galois field and elliptic curves.

2.1. Irreducible Polynomial

If $(\mathbb{F},+,.)$ is a field, then a polynomial $f\left(x\right)\in \mathbb{F}\left[x\right]$ is called irreducible in $\mathbb{F}\left[x\right]$ whenever $f\left(x\right)=q\left(x\right)r\left(x\right)$ for $q\left(x\right),r\left(x\right)\in \mathbb{F}\left[x\right]$, then either $q\left(x\right)$ or $r\left(x\right)$ is a constant polynomial.

2.2. Maximal Ideal

Let M be an ideal of R and $M\ne R$, then M is called maximal if no proper ideal of R contains M.

2.3. Galois Field

For a prime number p and for an irreducible polynomial $f\left(x\right)$ of degree m in ${\mathbb{Z}}_p\left[x\right]$, the quotient ring ${\displaystyle \frac{{\mathbb{Z}}_p\left[x\right]}{<f\left(x\right)>}}=\left\{{\sum }_{k=0}^{m-1}{a}_k{t}^k\right|a_k\in {\mathbb{Z}}_p\forall 0\le k\le m-1\}$ is a finite field of order $p^m$ called Galois field and denoted by $GF\left(p^m\right)$, where t is a particular root of $f\left(x\right)$.

2.4. Elliptic Curve

Consider the field $\mathbb{F}$ with $\left|\mathbb{F}\right|=p^k$ for some prime p and natural number n, then the elliptic curve over F is defined as

$$E\left(\mathbb{F}\right)=\{(x,y)\in \mathbb{F}\times \mathbb{F}|(y^2=x^3+ax+b)\left(mod{p}^k\right);a,b\in \mathbb{F}\}\cup \left\{O\right\},\mathrm{with}4a^3+27b^2\not\equiv 0\left(\mathrm{mod}{p}^k\right),$$

where the point O is called the infinite point. This form is known as the Weierstrass form of an elliptic curve.

If char $\mathbb{F}\ne 2$ and $d\in \mathbb{F}-\{0,1\}$, then $x^2+y^2=1+d{x}^2{y}^2$ is known as Edward’s elliptic curve.

If $A,B\in \mathbb{F}$ and $B(A^2-4)\ne 0$, then the curve $B{y}^2=x^3+A{x}^2+x$ is known as the Montgomery form of an elliptic curve.

2.5. Mordell Elliptic Curve

The elliptic curve with $a=0$ is called a Mordell elliptic curve. If $p^k\equiv 2\left(\mathrm{mod}3\right)$, then there is randomness and distinctness in y-coordinates of points satisfying the elliptic curve.

3. Proposed Algorithm for the Construction of S-boxes

We used the x and y coordinates of points $(x,y)$ satisfying a Mordell elliptic curve that is interpreted over $GF\left(2^n\right)$ employing different irreducible polynomials of degree n.

3.1. S-Boxes Using Mordell Elliptic Curve over $GF\left(2^n\right),n=8,10,12$

An elliptic curve of the form $y^2=x^3+b,b\ne 0$ is called a Mordell elliptic curve. The number of points satisfying the curve other than infinity is exactly $p^n$, so we can use them to construct S-boxes. As there is no repetition in x-coordinates of point $(x,y)\in GF\left(2^n\right)\times GF\left(2^n\right)$, by defining a bijective map, we can obtain an S-box. We call an S-box-m the S-box generated by using an irreducible polynomial with decimal value m. The algorithm is described as follows.

(1)

Choose any irreducible polynomial of degree $8,10,12$ over the binary field.

(2)

Choose the Mordell elliptic curve $y^2=x^3+b,0\ne b\in GF\left(2^n\right)$.

(3)

Choose x-coordinates of points $(x,y)$ satisfying the Mordell curve.

(4)

Apply the multiplicative inverse of each non-zero element corresponding to a given irreducible polynomial.

(5)

For $GF\left(2^n\right),n=10,12$, apply modulo 256 and choose the 1st 256 unique values.

(6)

Reshape into $16\times 16$ matrix.

All 10 S-boxes are presented in Table 1, Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9 and Table 10. The table of comparison shows that S-boxes produced using these polynomials are better than the S-boxes designed in [8] in terms of scores of SAC, BIC SAC, LAP, and DAP.

Table 1. S-box-283.

0	116	58	44	29	237	22	121	131	222	251	12	11	122	177	91
1	180	110	69	254	92	94	183	126	106	124	224	40	7	13	35
141	170	90	146	55	5	175	151	127	50	46	31	47	174	214	56
246	75	241	108	103	202	211	133	128	109	195	239	163	99	235	52
203	153	85	243	45	76	73	16	150	216	143	17	218	197	198	104
82	43	77	57	49	36	166	181	115	138	184	117	212	219	14	70
123	96	168	102	245	135	54	186	190	132	101	120	228	226	207	3
209	95	201	66	105	191	67	60	86	114	72	113	15	234	173	140
232	88	193	242	167	24	244	182	155	42	38	165	169	148	8	221
79	63	10	53	100	62	71	112	158	20	200	142	39	139	78	156
41	253	152	32	171	34	145	208	149	159	18	118	83	196	215	125
192	204	21	111	19	240	223	6	217	136	74	61	4	213	227	160
176	255	48	119	84	81	51	161	247	249	206	189	27	157	93	205
225	64	68	187	37	236	147	250	2	220	231	188	252	248	80	26
229	238	162	89	233	97	33	129	185	137	210	134	172	144	30	65
199	178	194	25	9	23	59	130	164	154	98	87	230	107	179	28

Table 2. S-box-299.

0	116	171	43	192	25	128	213	96	170	153	167	64	188	255	238
1	39	145	184	244	87	57	242	56	33	30	53	245	175	37	168
149	215	134	40	221	14	92	165	122	210	190	159	137	146	121	113
230	248	232	29	68	104	150	6	236	183	23	108	181	182	246	212
223	100	254	166	67	201	20	70	251	231	7	136	46	243	199	65
187	89	225	177	220	11	88	253	9	2	114	195	60	112	74	193
115	191	124	77	116	24	155	45	34	99	52	211	75	249	3	227
164	163	17	63	252	81	26	203	233	93	176	147	228	18	148	120
250	86	50	129	127	101	83	247	180	31	241	49	10	204	148	19
133	80	28	97	143	21	15	226	194	160	239	42	84	107	35	214
200	103	185	140	229	59	205	130	110	27	144	222	44	79	135	8
85	154	48	90	198	141	217	237	94	102	32	5	119	156	235	132
172	41	202	197	62	98	179	38	58	219	12	208	216	69	234	71
206	51	118	47	54	151	158	16	91	78	207	174	106	66	123	117
82	161	196	76	157	139	138	142	126	109	189	162	13	186	240	36
105	152	61	55	218	111	95	72	73	178	209	22	173	4	169	224

Table 3. S-box-505.

0	227	141	246	186	82	123	248	93	255	41	25	193	77	124	153
1	148	46	133	175	213	90	211	237	102	165	20	192	244	235	135
252	28	74	88	23	80	190	31	171	214	150	109	45	249	149	78
168	38	188	219	201	212	26	223	217	230	54	172	101	113	16	228
126	177	14	205	37	6	44	139	247	17	40	204	95	83	243	209
207	24	68	181	15	73	195	250	49	226	161	53	71	81	79	76
84	200	19	163	94	159	145	184	152	162	106	61	13	146	147	48
72	66	29	151	197	143	254	233	241	55	220	110	43	231	215	132
63	21	164	9	7	50	154	203	238	134	3	118	22	170	185	112
56	176	160	62	85	218	11	156	59	240	253	232	67	131	119	210
155	99	12	239	34	97	166	91	116	104	216	64	157	89	125	117
105	191	199	137	189	122	221	96	47	10	130	174	120	51	225	138
42	18	100	111	245	236	173	224	32	121	179	35	180	167	92	2
198	39	194	182	208	128	178	234	158	202	108	75	52	107	129	169
36	222	33	57	242	70	183	4	87	142	187	98	127	30	136	103
69	114	140	8	229	196	60	206	233	86	65	27	5	115	58	144

Table 4. S-box-313.

0	143	219	146	241	153	73	255	228	85	208	158	184	160	227	119
1	162	19	107	118	34	171	190	61	246	54	100	93	55	94	64
156	218	81	91	149	138	169	57	59	48	17	187	201	235	95	52
232	33	152	137	124	206	230	198	13	106	142	253	197	202	224	30
78	22	109	242	180	247	177	6	214	125	69	68	200	213	128	110
88	151	205	31	164	144	159	175	43	66	181	165	195	212	60	173
116	20	140	161	76	222	216	65	62	23	103	25	115	132	99	145
174	150	8	209	127	14	166	240	155	21	217	28	56	42	168	84
39	29	11	199	170	5	121	238	90	35	231	192	196	102	3	189
141	182	45	114	96	79	239	238	51	80	98	92	194	167	157	237
44	221	215	12	250	136	147	104	82	63	72	252	211	18	203	74
40	123	133	130	46	50	49	220	82	135	97	178	234	32	210	47
58	183	10	229	70	185	204	27	38	2	111	236	108	122	188	186
131	24	41	129	76	193	36	67	9	233	245	248	37	26	249	179
87	243	75	134	126	225	244	148	163	176	7	113	83	86	120	191
223	53	251	154	4	226	172	77	16	101	117	254	139	15	105	112

Table 5. S-box-529.

126	170	84	93	21	125	187	246	134	205	148	51	227	208	218	185
47	210	39	20	234	197	157	95	252	158	11	203	98	32	115	37
58	103	90	86	28	94	27	44	165	217	77	167	76	102	36	189
0	207	195	141	160	179	194	49	202	110	80	200	222	213	29	19
81	199	113	232	132	38	240	2	74	151	9	149	53	123	52	223
253	55	43	153	237	70	254	99	245	114	69	54	196	154	143	116
46	104	112	128	78	224	140	173	137	41	122	129	190	162	88	60
71	87	5	225	42	83	244	144	233	239	120	65	229	169	6	72
209	214	146	101	7	155	216	238	100	174	181	61	164	212	4	92
67	220	97	79	236	82	221	241	235	127	176	150	152	182	18	171
59	145	230	14	249	24	142	228	250	63	105	117	31	193	172	89
188	243	180	109	13	133	159	124	161	25	204	68	12	147	85	96
186	3	168	34	206	183	219	107	40	139	35	8	231	163	198	30
201	33	56	91	119	108	177	255	17	22	248	184	135	15	192	175
226	23	131	211	121	73	111	26	57	1	251	45	136	247	191	10
106	166	118	138	178	75	215	16	50	242	156	130	66	62	64	48

Table 6. S-box-787.

199	149	74	169	137	82	29	152	20	132	130	205	16	18	209	14
176	196	15	43	91	253	214	165	60	200	102	23	171	131	151	250
46	219	123	188	85	236	12	154	246	138	220	44	11	39	239	104
0	231	241	38	142	215	47	177	167	26	179	180	71	90	136	57
191	124	226	126	65	115	254	184	141	222	193	206	235	19	42	233
119	150	129	147	31	52	182	160	8	114	213	156	120	158	53	243
7	245	216	208	50	61	159	207	75	24	225	204	202	56	83	81
127	2	105	99	107	72	210	240	9	170	98	144	36	232	201	221
155	101	28	247	63	5	103	10	146	238	96	25	203	32	173	4
181	67	224	164	197	1	153	112	183	77	139	185	248	13	33	118
108	35	198	3	88	122	212	249	86	234	187	22	76	95	121	134
51	97	37	178	70	162	166	230	228	34	113	186	218	69	195	106
116	94	172	27	251	157	41	66	211	223	255	163	6	190	135	229
79	58	128	59	244	168	161	140	92	84	227	62	109	48	80	30
125	55	73	133	217	54	100	145	21	64	89	40	237	252	87	148
78	242	110	117	189	93	49	143	68	194	175	17	174	111	192	45

Table 7. S-box-1315.

0	47	6	203	58	2	79	32	45	174	113	236	115	237	111	83
1	93	179	112	238	180	8	29	204	44	230	66	241	209	169	186
145	89	63	166	16	119	73	247	172	187	182	206	20	253	21	151
30	201	87	55	35	123	67	14	95	51	105	31	183	250	92	242
217	211	189	54	161	244	25	118	127	122	181	234	249	76	106	210
10	61	70	114	171	84	108	156	190	101	215	140	7	136	243	128
143	3	117	192	138	56	34	193	9	107	15	135	202	157	219	245
214	99	64	224	252	33	100	53	124	154	75	74	22	78	167	126
125	43	248	177	17	168	80	68	218	103	23	11	102	130	52	85
178	207	69	50	90	27	220	197	232	240	41	163	62	48	212	109
133	195	144	251	88	194	120	226	152	159	188	49	155	38	196	139
37	110	59	131	221	185	36	97	229	225	153	24	46	223	147	28
86	228	160	184	200	233	173	165	129	222	146	116	13	60	57	175
134	227	4	72	18	96	199	254	81	176	71	162	149	26	77	150
235	98	205	121	12	164	158	40	104	191	5	39	148	94	65	137
231	213	246	142	208	239	132	141	42	82	216	170	91	19	255	198

Table 8. S-box-1789.

0	174	7	200	185	119	106	56	16	123	13	248	157	142	181	171
1	165	172	15	178	152	226	173	4	132	44	55	175	81	189	65
126	240	100	111	182	2	224	235	208	155	113	99	244	228	28	229
84	76	120	251	188	12	159	74	207	219	225	186	245	78	109	103
191	115	18	168	68	252	20	34	210	146	49	195	51	190	30	82
204	158	166	196	137	144	150	217	220	197	83	206	98	80	88	101
42	127	205	62	234	37	61	91	69	243	10	70	238	38	17	35
218	66	71	213	211	179	117	60	45	96	255	86	8	167	5	147
161	52	193	27	162	54	125	94	97	3	138	64	43	92	183	222
29	214	79	122	24	75	247	36	129	77	85	156	130	216	41	233
230	227	25	39	221	6	110	58	141	163	139	40	232	19	199	241
254	11	249	250	93	121	116	21	134	26	203	145	153	246	14	73
149	136	32	33	143	187	148	23	215	53	46	31	176	124	104	231
59	170	154	180	89	201	135	102	194	63	118	47	105	67	212	90
237	9	108	253	184	50	128	209	72	140	192	160	223	22	198	202
239	87	107	112	114	131	57	169	236	151	133	95	164	48	177	242

Table 9. S-box-3441.

149	197	136	96	221	215	123	6	30	144	158	41	2	173	139	32
102	168	153	192	195	69	244	66	92	45	62	224	234	61	225	246
187	27	86	112	227	176	154	200	138	210	209	199	80	126	152	184
0	38	140	169	67	109	125	205	56	29	59	145	193	211	170	203
46	147	37	8	55	76	103	242	130	240	232	53	7	186	71	17
243	88	156	190	117	208	74	70	159	11	124	150	100	22	3	78
39	58	91	110	161	72	229	36	180	105	34	118	194	19	155	33
134	28	23	183	13	218	241	15	116	196	175	207	188	77	137	148
182	254	171	247	115	12	89	83	111	129	44	68	177	49	230	60
217	189	35	172	179	213	132	42	220	47	113	223	107	245	127	253
228	181	21	248	135	87	97	157	235	90	40	255	212	128	25	108
216	219	16	95	63	141	165	85	20	122	131	251	178	185	4	26
252	52	249	5	121	238	10	104	174	9	43	201	133	160	81	120
237	191	214	93	146	50	163	94	106	143	51	79	239	151	75	54
167	202	84	73	114	233	14	18	142	162	119	24	206	1	57	65
98	31	250	231	222	236	198	204	99	82	166	101	164	48	226	64

Table 10. S-box-7105.

0	188	251	4	58	82	164	231	117	104	76	237	41	128	78	203
1	12	6	137	191	110	48	88	129	225	163	19	31	245	73	91
224	214	126	178	34	42	89	161	255	193	32	172	238	186	147	62
64	90	235	55	21	194	201	11	121	175	95	229	92	119	60	199
240	143	192	254	211	205	57	29	116	35	252	140	25	93	239	226
127	81	45	152	96	135	66	24	18	70	124	79	198	249	227	241
160	14	134	69	246	74	166	158	77	37	33	132	253	159	23	3
118	105	167	141	123	54	180	145	236	234	113	173	242	87	151	244
120	40	72	133	195	52	179	115	59	27	83	53	181	155	208	144
109	107	217	102	184	22	183	106	146	233	185	43	153	38	5	85
223	61	7	207	51	138	17	170	65	47	247	228	68	49	71	112
28	100	220	111	216	149	215	9	243	139	202	200	8	46	171	98
80	75	84	250	36	2	15	248	136	165	162	212	86	13	20	196
122	10	154	157	67	190	125	168	209	197	103	177	206	94	156	114
187	204	148	176	230	63	218	108	219	30	26	182	189	44	210	232
213	222	169	131	99	130	174	221	50	150	39	142	16	101	97	56

3.2. S-Boxes Using Mordell Elliptic Curves over $GF\left(2^n\right),n=9,11$

Since 512, 2048 $\equiv 2\left(\mathrm{mod}3\right)$, the curve $y^2=x^3+b,0\ne b\in GF\left(2^n\right),n=9,11$ over $GF\left(2^n\right),n=9,11$ has exactly $p^n$ points in such a way that there is no repetition in x and y-coordinates with random values in y-coordinates. The proposed algorithm for the S-box is described as follows.

(1)

Choose any irreducible polynomial of degree $9,11$ over the binary field.

(2)

Choose the Mordell elliptic curve $y^2=x^3+b,0\ne b\in GF\left(2^n\right),n=9,11$.

(3)

Choose y-coordinates of points $(x,y)$ satisfying the Mordell curve.

(4)

Apply modulo 256 on y-coordinates to obtain answers in 0–255.

(5)

Select the 1st 256 unique values.

(6)

Reshape into a $16\times 16$ matrix.

4. Security Analysis of S-Boxes

This segment discusses the outcomes of security evaluations conducted on the proposed S-boxes to evaluate their resistance to cryptographic attacks. The S-box was evaluated through five different tests including Nonlinearity, Strict Avalanche Criteria (SAC), Bit Independence Criteria (BIC), Probability of Linear Approximation (LAP), and Probability of Differential Approximation (DAP). The results were compared to some popular S-boxes in Table 11.

Table 11. Algebraic analysis of proposed and some well-known S-boxes.

S-Boxes	Nonlinearity	SAC	BIC-NL	BIC-SAC	LAP	DAP
S-box-283	112	0.5032	112	0.5059	0.0625	0.0156
S-box-299	112	0.4998	112	0.5046	0.0625	0.0156
S-box-313	112	0.5032	112	0.5015	0.0625	0.0156
S-box-505	112	0.5022	112	0.5020	0.0625	0.0156
S-box-529	106	0.5020	102.5714	0.5056	0.1094	0.0391
S-box-787	106.25	0.5027	103.5	0.5036	0.0859	0.0391
S-box-1315	106	0.5039	105	0.5025	0.0859	0.0391
S-box-1789	105.75	0.5024	103.3571	0.5022	0.1016	0.0469
S-box-3441	105.75	0.4995	103.0714	0.5018	0.0859	0.0391
S-box-7105	105.25	0.5066	104.2143	0.4994	0.1016	0.0469
S-box over $GF\left(2^8\right)$ [8]	112	0.4871	112	-	0.0625	0.0156
S-box over $GF\left(2^9\right)$ [8]	106.25	0.4992	103.8	-	0.1328	0.0391
[49]	112	0.5034	112	0.5066	0.0625	0.0156
[50]	112	0.4988	112	0.5008	0.0625	0.0156
[53]	105.5	0.507	106	0.462	0.140	0.0242
[9]	106.75	0.5032	103.6429	0.5074	0.1484	0.0469
[54]	106	0.5051	98	-	0.148	0.039
Skipjack	105.75	0.503	104.14	0.499	0.109	0.0468
Residue prime	99.5	0.515	101.71	0.502	0.132	0.281
[16]	104.87	0.493	99	0.504	0.105	0.0390
[55]	96	0.4900	92	0.5100	0.23	0.050

4.1. Nonlinearity (NL)

The nonlinearity of a boolean function g is one of the most desirable characteristics of a strong S-box. It is defined as $N_g=2^{n-1}-{\displaystyle \frac{max|W\left(v\right)|}{2}}$, where $W\left(v\right)$ represents the Walsh spectrum of the polarity truth table of the boolean function g, and n is the number of input bits. The nonlinearity of a boolean function measures its difference from a set of all affine functions of n variables. We can calculate the Walsh spectrum in the following way; Walsh spectrum = Hadamard matrix of order $n\times n$ [polarity truth table of f].

4.2. Strict Avalanche Criteria (SAC)

To assess the cryptographic potency of substitution boxes (S-boxes) used in symmetric key algorithms, one property is known as strict avalanche criteria (SAC). A minor change in the input causes substantial changes in the output when using SAC, which quantifies how much changing a single bit of an S-box’s input impacts the output bits. The output bits of the S-box should change with a probability of 0.5 for each output bit when any one of its input bits is reversed. If all potential input bit changes are averaged, the amount of 0s and 1s in the output bits should be equal. By doing this, it is made sure that no particular output value is preferred by the S-box. Ideally, if k input bits are modified, at least $(k/2)$ output bits should also change. This characteristic makes sure that a minor change in the input spreads and results in a significant change in the result. A boolean function f satisfies the SAC if for every vector a of hamming weight 1, the function $f\left(x\right)\oplus f(x\oplus a)$ is balanced.

4.3. Bit Independence Criteria (BIC)

Let $f_a$ and $f_b$ be two-bit outputs of an S-box; if $f_a\oplus f_b(a\ne b,1\le a,b\le n)$ is highly nonlinear and satisfies the strict avalanche criteria, then S-box satisfies BIC. The bit independence criteria assesses the correlation between the input bits and the output bits of an S-box. An S-box should exhibit a high degree of bit independence, which means that the output bits should have as little correlation as possible with the input bits.

4.4. Linear Approximation Probability (LAP)

The probability of linear approximation for an S-box is the likelihood that its inputs will approach its outputs linearly given a certain number of input–output pairs. A weaker S-box would have a higher linear approximation probability because it would be more susceptible to linear attacks. On the other side, a smaller linear approximation probability indicates a stronger S-box. Due to this, the S-box exhibits greater resilience against linear attacks. The following formula can be used to calculate the linear approximation probability

$$L{P}_S=\underset{\alpha ,\beta \ne 0}{max}\left|\frac{|\{u\in GF\left(2^m\right)|\alpha .S\left(u\right)=\beta .S\left(v\right)\}|-2^{m-1}}{2^m}\right|$$

considering $u,v$ to be the input and output masks, respectively.

4.5. Differential Approximation Probability (DP)

The differential approximation probability for an S-box quantifies the probability that a particular input difference will result in a particular output difference, taking into account a specified number of rounds. It quantifies the probability of a particular differential characteristic occurring within the S-box. To calculate the differential approximation probability, one typically performs an exhaustive search over all possible input and output differences for a given number of rounds, counting the occurrences of each difference and calculating the probability as the ratio of the occurrences of the desired difference to the total number of input/output pairs tested. The lower the differential approximation probability, the more resistant the S-box is against differential cryptanalysis. A lower probability indicates that the S-box does not exhibit any strong differentials, making it more difficult for an attacker to exploit differential characteristics and break the cipher.

$$DP(\Delta u,\Delta v)=\frac{\left|\right\{u\in GF\left(2^m\right)|S\left(u\right)\oplus S(u\oplus \Delta u)=\Delta v\}|}{2^m},$$

where $\Delta u$ is the input, and $\Delta v$ is the output differential.

4.6. Discussion

• Large nonlinearity is required for the S-box to fend off linear attacks. Table 11 shows that there are four S-boxes with optimal nonlinearity, while the remaining also have considerable scores.
• The strict avalanche criterion is deemed to be met rather effectively by the SAC score that is close to the optimal value of 0.50. Table 11 shows that, in comparison to most recently created S-boxes with the avalanche effect, our best SAC score of $0.4998$ is quite near to the ideal value. As a result, the suggested S-box successfully satisfies the strict avalanche criteria.
• Under the bits independence requirement, the pair-wise disjoint boolean functions have demonstrated strong performance for both SAC and nonlinearity scores. Each of our proposed S-boxes has a sound score of nonlinearity and SAC.
• A lower DU score is indicative of a secure S-box. Among all generated S-boxes, none of the S-boxes has a score of DU greater than 10.
• The resistance of the S-box against linear cryptanalysis is likewise correlated with the likelihood of linear approximation. It is claimed that an S-box with a lower LAP score is more resistant to linear cryptanalysis. The LP values of our S-boxes are lower than many of the proposed S-boxes as shown in Table 11.

5. Image Encryption

In this section, we will examine an innovative approach for protecting digital images that makes use of a specially designed S-box. Our analysis included several distinct tests designed to assess the durability and effectiveness of our picture encryption approach while also testing its resistance to prospective attacks. After a thorough evaluation and analysis of our process, we compared the outcomes to those attained using well-known encryption methods. The results of our study showed that the suggested method for encrypting digital images performed the best overall. All the codings were completed in MATLAB R2023a using the CBC mode of AES with a random key of 256 bits. Figure 1a–k represents the plain and cipher image of a baboon, while Table 12 is the comparison of image encryption schemes.

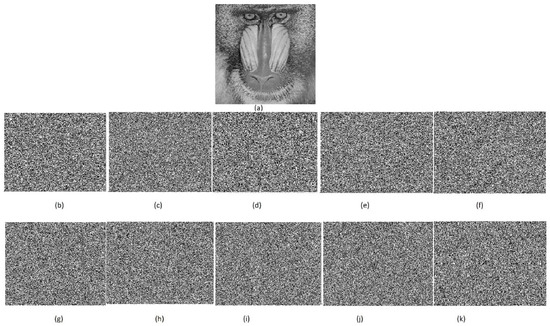
Figure 1. Plain image and cipher images using proposed S-boxes.

Table 12. Results of majority logic criteria and differential analysis of image encryption scheme.

S-Boxes	Entropy	Correlation	Contrast	Energy	Homogeneity	NPCR	UACI
S-box-283	7.9995	−0.0049	10.5706	0.0156	0.3882	99.61	33.52
S-box-299	7.9994	−0.0042	10.5556	0.0156	0.3884	99.59	33.48
S-box-505	7.9995	−0.0079	10.6160	0.0156	0.3882	99.61	33.43
S-box-313	7.9994	−0.0039	10.5683	0.0156	0.3885	99.62	33.53
S-box-529	7.9994	−0.0028	10.5213	0.0156	0.3917	99.64	33.39
S-box-787	7.9994	−0.0078	10.6421	0.0156	0.3885	99.62	33.62
S-box-1315	7.9993	−0.0061	10.5935	0.0156	0.3876	99.58	33.48
S-box-1789	7.9994	−0.0096	10.6143	0.0156	0.3881	99.63	33.46
S-box-3441	7.9994	−0.0001	10.5683	0.0156	0.3890	99.58	33.54
S-box-7105	7.9994	−0.0045	10.5679	0.0156	0.3888	99.61	33.49
[8]	7.9479	0.0036	9.9955	0.0158	0.3948	99.42	33.21
[49]	7.9994	−0.0079	10.6137	0.0156	0.3879	99.59	33.35

5.1. Entropy

Entropy is a metric that quantifies the degree of unpredictability or disorganization in the pixel values of an image. By utilizing Shannon’s entropy formula, which factors in the probability distribution of diverse pixel values present in the image, one can determine the entropy of an image. If all 256-pixel values within an 8-bit grayscale image occur with equal probability, then the image’s entropy value reaches its maximum possible value of 8. Scrambled illustrations with an entropy value that is near 8 have pixel values that are spread out as uniformly as possible. Therefore, it becomes difficult to predict the original image from the scrambled image.

$$H=-\sum _y\left(p\left(y\right){log}_2\left(p\left(y\right)\right)\right)$$

where $p\left(y\right)$ represents the probability of a pixel.

A strong image encryption scheme must have an entropy score close to 8.

5.2. Correlation

One method for evaluating the similarity between a filter and the corresponding pixels in an image is called correlation, which involves convolving the filter over the image using a mathematical operation. A way to assess the robustness of the confidentiality protocol is to examine the correlation between the original image and the scrambled image. A desirable property of an image encryption system is that the correlation statistic value amidst the original and scrambled images should be as close to 0 as possible. In practical image encryption scenarios, a correlation coefficient value approaching zero is considered ideal. A correlation coefficient value below 0.1 is generally considered a strong indicator of a high-quality encryption scheme. However, if the correlation coefficient value exceeds 0.1, it implies the existence of a weak encryption scheme with a risk of unveiling the original image from the scrambled image.

$$r=\frac{\sum ((a_i-{\mu }_a)·(b_i-{\mu }_b))}{\sqrt{\sum {(a_i-{\mu }_a)}^2}·\sqrt{\sum {(b_i-{\mu }_b)}^2}}$$

where ${\mu }_a$ and ${\mu }_b$ represent the means of their respective variables.

5.3. Contrast

The difference in brightness or intensity between various areas of an encrypted image is referred to as contrast in a cipher image. It specifies how distinct the dark and bright parts appear in the cipher image. Contrast is important for picture encryption because it influences the visual appeal and readability of the encrypted image. A stronger contrast indicates that there is a notable difference in brightness or intensity between various areas of the encrypted image. A high-contrast cipher image offers several advantages in an encryption scheme:

(1)

Enhanced Security: Higher contrast can make it more challenging for attackers to analyze or extract meaningful information from the cipher image. Well-defined edges and distinct intensity variations can make it harder to detect patterns or identify specific features within the image.

(2)

Robustness Against Attacks: A cipher image with higher contrast can exhibit greater resilience against common attacks, such as statistical analysis, pixel correlation, or known-plaintext attacks. The increased variability in intensity levels can make it more difficult to exploit statistical regularities and effectively break the encryption.

(3)

Improved Visual Quality: Although the primary goal of image encryption is security, maintaining a visually appealing and interpretable cipher image is also desirable. Higher contrast often leads to a more visually striking encrypted image, which may enhance the user experience and the overall acceptance of the encryption scheme.

$$Contrast=\sum _u\sum _v{(u-v)}^{2}p(u,v)$$

where $p(u,v)$ is the likelihood that two neighboring pixels in the image will have the same gray level, and $u,v$ are those intensities.

5.4. Homogeneity

The degree of uniformity or unpredictability of the cipher image created during the encryption process is referred to as homogeneity. In a homogeneous cipher image, each pixel value would be distinct from its surrounding pixels and the initial image’s general structure, exhibiting a high degree of randomness. On a scale from 0 to 1, the measure of homogeneity ranges from high heterogeneity or variety to high homogeneity or uniformity.

$$Homogeneity=\frac{1}{1+{\sum }_{u=1}^M{\sum }_{v=1}^M\frac{{(u-v)}^2}{M^2}},$$

where M is the number of gray levels in the image, and $(u,v)$ represents the position of a pixel in the GLCM.

5.5. Energy

Energy quantifies the overall contrast or level of activity in an image, and it is computed by summing the squared elements in the Gray-Level Co-occurrence Matrix (GLCM). A higher energy value indicates that the image contains more texture and contrast, while a lower energy value signifies a more homogeneous or uniform appearance.

$$Energy=\sum _{m=1}^N\sum _{n=1}^{N}GLCM{(m,n)}^2.$$

5.6. Number of Pixel Change Rate (NPCR)

The percentage of pixels between two dissimilar images is measured using this metric. NPCR examines the impact of a single-pixel alteration on the entire image encrypted using the suggested approach. It counts how many pixels in an encrypted image change every time a pixel in the original image changes. Consider two encrypted images C1 and C2 with dimensions M and N, corresponding to two plain images that have a one-pixel change. We can measure NPCR as

$$NPCR=\frac{{\sum }_{i,j}D(i,j)}{M\times N},$$

where $D(i,j)=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}C1(i,j)=C2(i,j)\hfill \\ 1,\hfill & \mathrm{if}C1(i,j)\ne C2(i,j)\hfill \end{array}\right.$.

5.7. Unified Average Changing Intensity (UACI)

The average intensity of the variations between the encrypted image and the original image is measured by the Unified Average Changing Intensity (UACI). We can measure UACI with the formula

$$UACI=\frac{1}{M\times N}\sum _{i,j}\frac{\left|C1\right(i,j)-C2(i,j\left)\right|}{255},$$

whereas $C1,C2,M,N$ are defined in NPCR.

5.8. Noise Attack Analysis

Even with noise from salt and pepper, the encryption approach should guarantee that the image’s actual content is kept private. Significant information about the underlying image content should not be revealed by the noise. The encryption plan might be made to adjust to different noise levels. Because of its versatility, the scheme can withstand variations in noise levels or types without losing its effectiveness. We used salt and pepper noise with different intensity levels to check the effectiveness of the proposed image encryption scheme. We can observe that the PSNR values are still greater than 30 after adding noise in the image (see Table 13). Figure 2 shows the results of the noise attack with an intensity of $0.1,0.3,0.5$, respectively.

Table 13. Noise attack analysis.

Intensity of Salt and Pepper Attack	PSNR
$0.001$	36.29
$0.1$	33.64
$0.3$	32.90
$0.5$	32.05

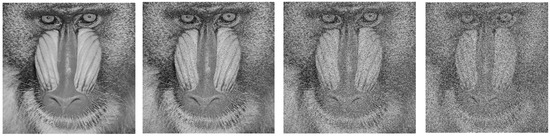
Figure 2. Salt and pepper noise attack on baboon with intensity of 0.1, 0.3, 0.5.

6. Conclusions and Future Study

Robust cryptographic solutions are extremely important as the digital landscape continues to change. Our study explores the complex field of image encryption, utilizing the strong characteristics of elliptic curve cryptography to improve security protocols. This paper utilizes the intricate configuration of elliptic curves within the binary Galois field extension $GF\left(2^n\right),n\ge 8$ to establish an effective approach for constructing S-boxes. There are a lot of existing schemes for designing S-boxes using the prime field, but we used $GF\left(2^n\right),n\ge 8$. We compared our results with existing schemes on prime fields and $GF\left(2^n\right),n\ge 8$. We concluded that for $n\ge 9$, the produced S-boxes are relatively weak as compared to the usage of $GF\left(2^8\right)$. Our conclusion contradicts the conclusion of [8] by producing a large number of S-boxes using $GF\left(2^8\right)$ and $GF\left(2^9\right)$. Our thorough analysis, which included measures, such as bit independence, strict avalanche, non-linearity, linear approximation, and differential approximation, highlighted the robustness of our suggested approach. Furthermore, we have employed S-boxes in the substitution process, yielding significantly superior results compared to various alternative methods. We demonstrated the effectiveness and efficiency of our method through extensive testing, providing a viable substitute for strengthening digital security protocols. Our research has the potential to advance data security and secure communication paradigms and advance the field of cryptography as a whole. Going ahead, our study offers insightful advice and suggestions for creating robust encryption systems, which are essential for protecting sensitive data in a world getting more digitally connected. In the future, we are interested in using some more elliptic and hyperelliptic curves over $GF\left(2^n\right),n\ge 8$ to design robust S-boxes.