Rational Involutions and an Application to Planar Systems of ODE
Abstract
1. Introduction
2. Preliminaries
3. Involutions in Family (1)
- vanish on these values.
- (1)
- (2)
- (3)
- (4)
- (5)
- (6)
4. Involutions with Quadratic Numerators
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
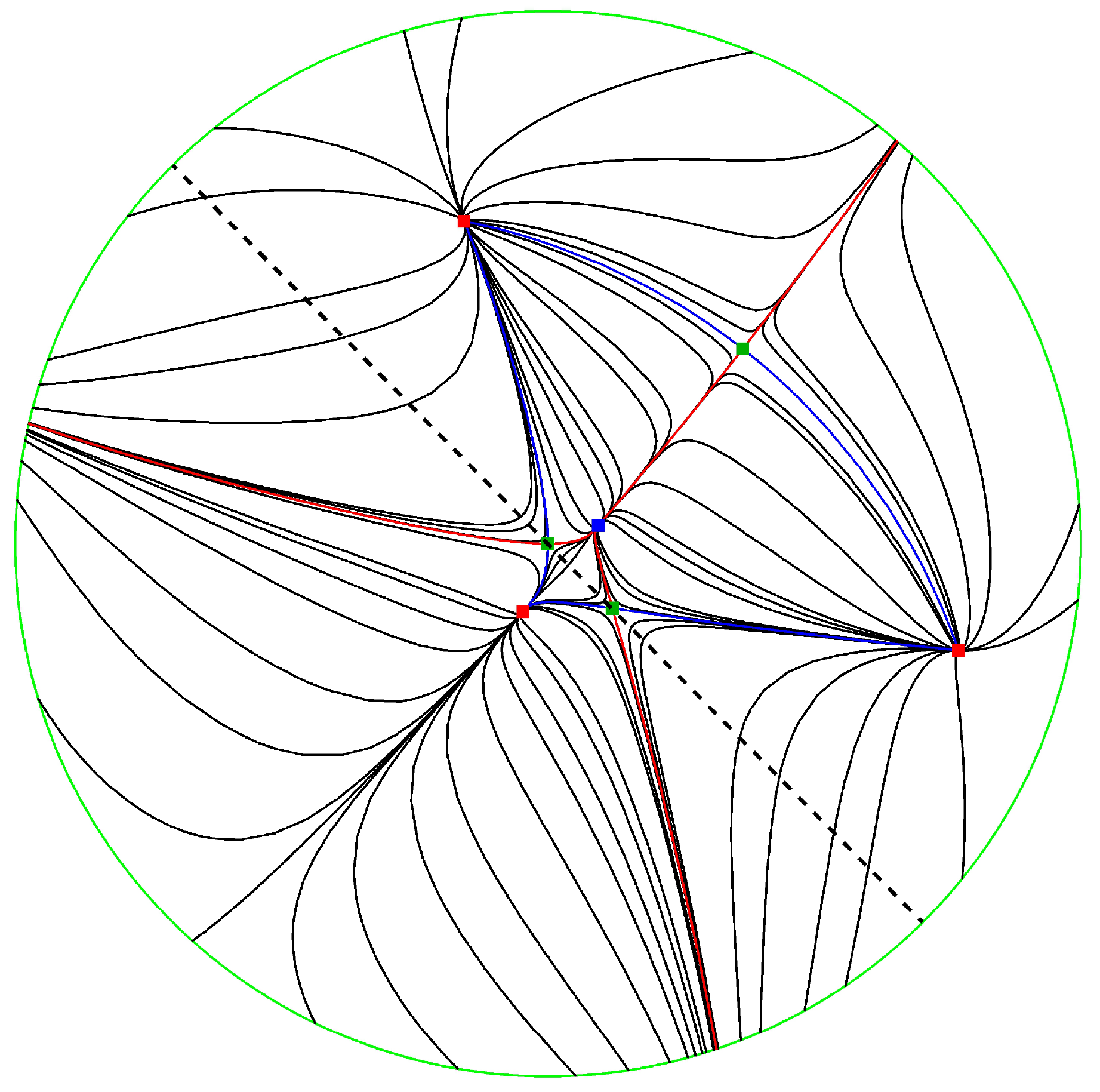
5. Reversible Systems
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
- (1)
- (2)
- (3)
- (4)
- (5)
- (6)
- (7)
- (8)
- (9)
- (10)
- (11)
- (12)
- (13)
- (14)
- (15)
- (16)
- (17)
References
- Cabada, A.; Tojo, F.A.F. Differential Equations with Involutions; Atlantis Press: Amsterdam, The Netherlands; Paris, France; Beijing, China, 2015. [Google Scholar]
- Arcet, B.; Romanovski, V.G. On Some Reversible Cubic Systems. Mathematics 2021, 9, 1446. [Google Scholar]
- Bastos, J.L.R.; Buzzi, C.A.; Torregrosa, J. Orbitally symmetric systems with application to planar centers. Commun. Pure Appl. Anal. 2021, 20, 3319–3346. [Google Scholar]
- Seiler, W.M. Involution and symmetry reductions. Math. Comput. Model. 1997, 25, 63–73. [Google Scholar]
- Lesniak, Z.; Shi, Y.-G. One class of planar rational involutions. Nonlinear Anal. Theory Methods Appl. 2011, 74, 6097–6104. [Google Scholar]
- Algaba, C.; García, J.; Giné, J. Nondegenerate and Nilpotent Centers for a Cubic System of Differential Equations. Qual. Theory Dyn. Syst. 2019, 18, 333–345. [Google Scholar]
- Dukarić, M. On integrability and cyclicity of cubic systems, Electron. J. Qual. Theory Differ. Equ. 2020. [Google Scholar] [CrossRef]
- Romanovski, V.G.; Shafer, D.S. The Center and Cyclicity Problems: A Computational Algebra Approach; Birkhäuser: Boston, MA, USA, 2009. [Google Scholar]
- Li, C.; Liu, C.; Yang, J. A cubic system with thirteen limit cycles. J. Differ. Equ. 2009, 246, 3609–3619. [Google Scholar]
- Li, J. Hilbert’s 16th problem and bifurcations of planar vector fields. Int. J. Bifurc. Chaos 2003, 13, 47–106. [Google Scholar]
- Li, J.; Liu, Y. New results on the study of Zq-equivariant planar polynomial vector fields. Qual. Theory Dyn. Syst. 2010, 9, 167–219. [Google Scholar]
- Cox, D.; Little, J.; O’Shea, D. Ideals, Varieties, and Algorithms; Springer: New York, NY, USA, 2007. [Google Scholar]
- Gianni, P.; Trager, B.; Zacharias, G. Gröbner bases and primary decomposition of polynomials. J. Symb. Comput. 1988, 6, 146–167. [Google Scholar]
- Shimoyama, T.; Yokoyama, K. Localization and primary decomposition of polynomial ideals. J. Symb. Comput. 1996, 22, 247–277. [Google Scholar]
- Decker, W.; Laplagne, S.; Pfister, G.; Shönemann, H. primedecGTZ—A Singular 4-3-1 Library for Computing the Prime Decomposition and Radical of Ideals. 2022. Available online: https://www.singular.uni-kl.de (accessed on 3 January 2024).
- Decker, W.; Greuel, G.-M.; Pfister, G.; Schönemann, H. Singular 4-3-1—A Computer Algebra System for Polynomial Computations. 2022. Available online: https://www.singular.uni-kl.de (accessed on 3 January 2024).
- Arnold, E.A. Modular algorithms for computing Gröbner bases. J. Symb. Comput. 2003, 35, 403–419. [Google Scholar]
- Romanovski, V.G.; Prešern, M. An approach to solving systems of polynomials via modular arithmetics with applications. J. Comput. Appl. Math. 2011, 236, 196–208. [Google Scholar]
- Wang, P.S.; Guy, M.J.T.; Davenport, J.H. P-adic reconstruction of rational numbers. SIGSAM Bull. 1982, 16, 2–3. [Google Scholar]
- Algaba, A.; García, C.; Giné, J. Orbital reversibility of planar vector fields. Mathematics 2021, 9, 14. [Google Scholar]
- Llibre, J.; Pantazi, C.; Walcher, S. First integrals of local analytic differential systems. Bull. Sci. Math. 2012, 136, 342–359. [Google Scholar]
- Artés, J.C.; Llibre, J.; Schlomiuk, D.; Vulpe, N. Geometric Configurations of Singularities of Planar Polynomial Differential Systems. A Global Classification in the Quadratic Case; Birkhäuser: Boston, MA, USA, 2021. [Google Scholar]
- Dumortier, F.; Llibre, J.; Artés, J.C. Qualitative Theory of Planar Differential Systems; Universitext; Springer: Berlin, Germangy, 2006. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mastev, I.; Romanovski, V.G.; Tian, Y. Rational Involutions and an Application to Planar Systems of ODE. Mathematics 2024, 12, 486. https://doi.org/10.3390/math12030486
Mastev I, Romanovski VG, Tian Y. Rational Involutions and an Application to Planar Systems of ODE. Mathematics. 2024; 12(3):486. https://doi.org/10.3390/math12030486
Chicago/Turabian StyleMastev, Ivan, Valery G. Romanovski, and Yun Tian. 2024. "Rational Involutions and an Application to Planar Systems of ODE" Mathematics 12, no. 3: 486. https://doi.org/10.3390/math12030486
APA StyleMastev, I., Romanovski, V. G., & Tian, Y. (2024). Rational Involutions and an Application to Planar Systems of ODE. Mathematics, 12(3), 486. https://doi.org/10.3390/math12030486






