A Comprehensive Multi-Strategy Enhanced Biogeography-Based Optimization Algorithm for High-Dimensional Optimization and Engineering Design Problems
Abstract
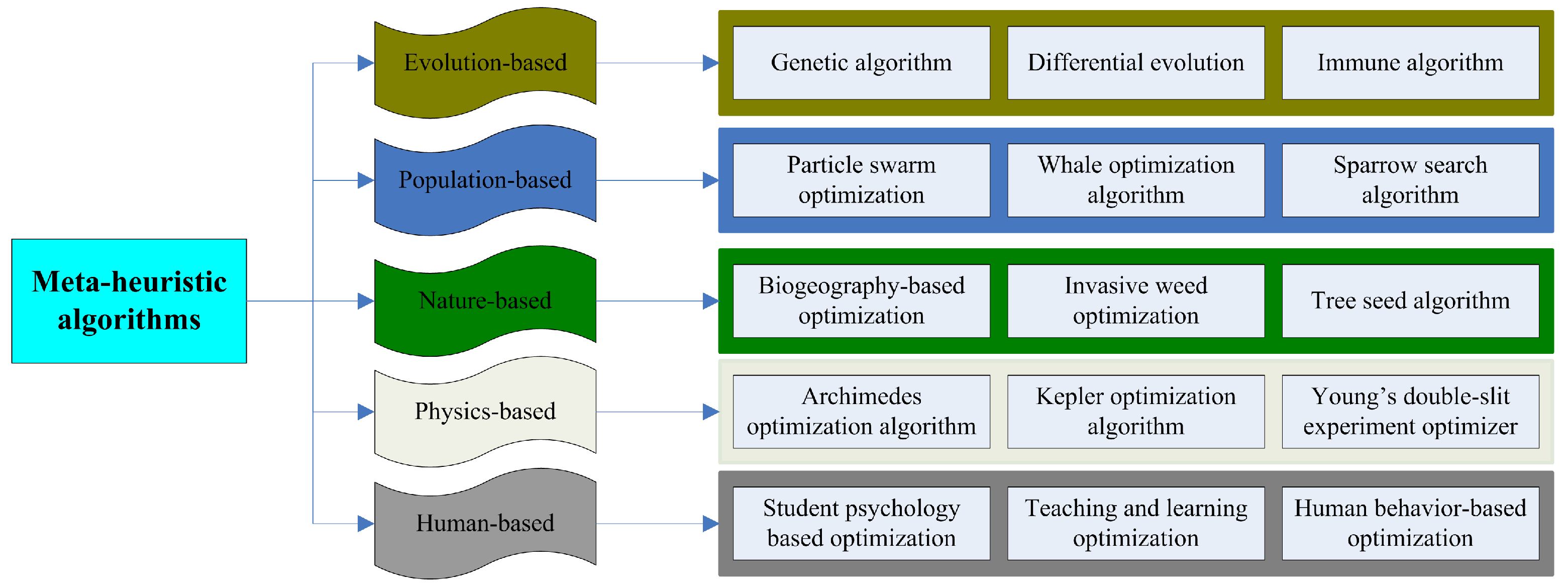
1. Introduction
- (1)
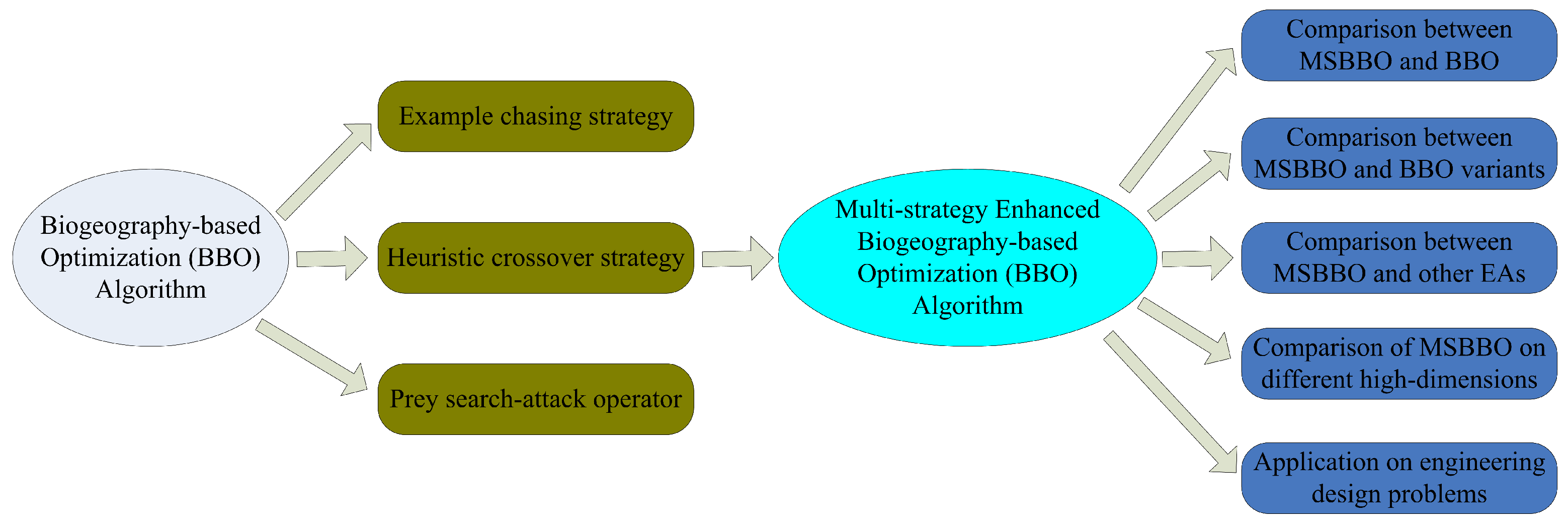
- A novel framework of BBO is proposed, which is simpler and more efficient than the original BBO algorithm. Meanwhile, MSBBO has lower computational complexity than BBO.
- (2)
- MSBBO uses the example chasing strategy to eliminate the misguidance of bad information in the population. Then, the heuristic crossover and prey search–attack strategies are used to balance the exploration and exploitation of the population. MSBBO makes BBO suitable for high-dimensional optimization environments.
- (3)
- MSBBO successfully challenges the 10,000-dimensional numerical optimization problem. Compared with other meta-heuristic algorithms, its convergence performance is basically not affected by dimensions and has good ductility.
2. Standard BBO
| Algorithm 1 Pseudo-code of the BBO. |
| initialize parameters: , I, E, N, and initialize the population by Equation (1) for t = 1 to T do calculate the and sort from best to worst calculate the by Equation (2), the and by Equation (3) calculate the by Equation (4), the by Equation (5) for i = 1 to N do % Migration for j = 1 to D do if rand(0,1) < do select the according to = end if end for % Mutation if rand(0,1) < do for j = 1 to D do end for end if end for end for output the optimal solution |
3. Proposed Algorithm: MSBBO
3.1. Motivation
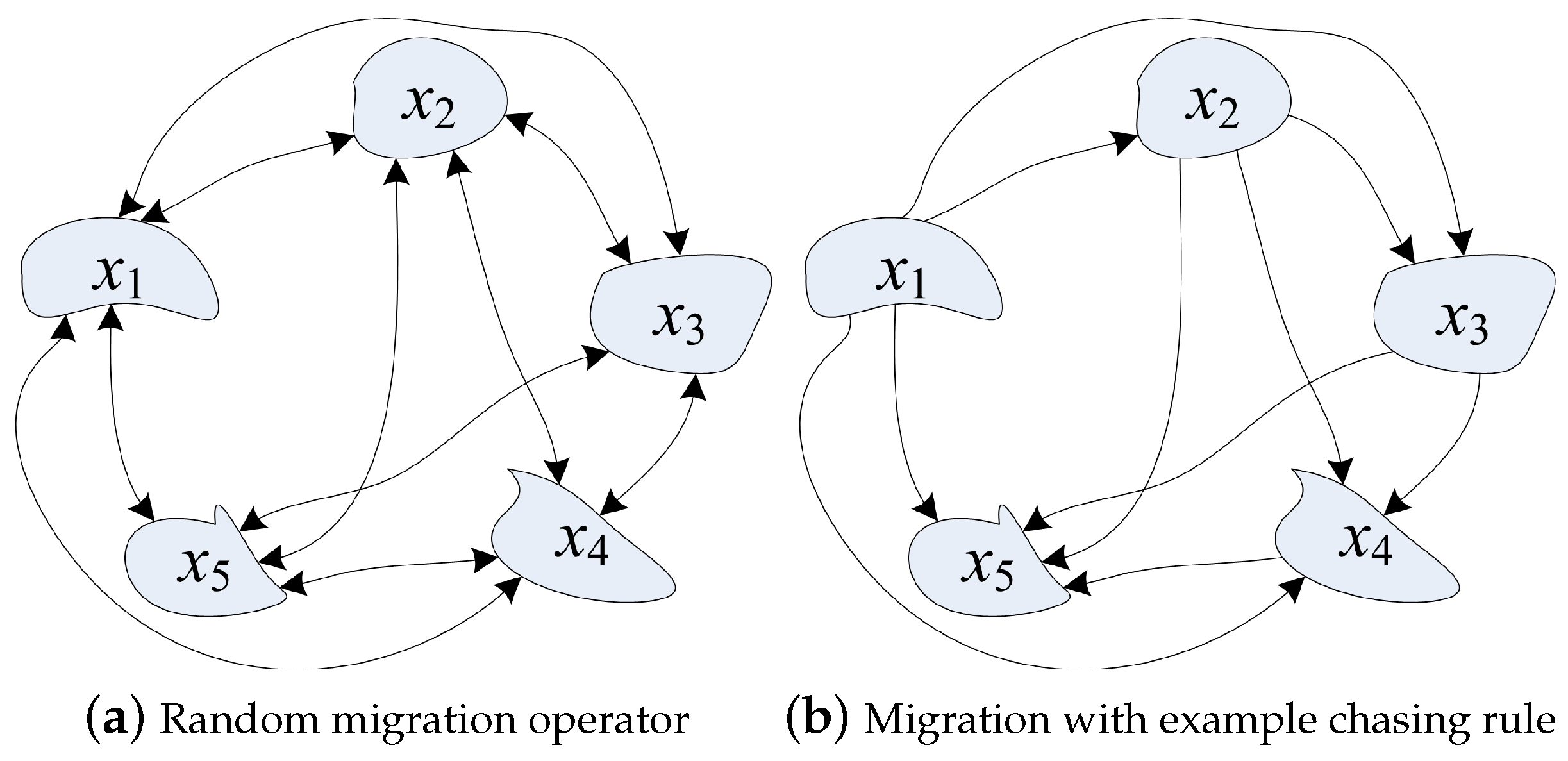
3.2. Example Chasing Strategy
3.3. Heuristic Crossover Strategy
3.4. Prey Search–Attack Operator
| Algorithm 2 Pseudo-code of the MSBBO. |
| initialize parameters: initialize the population by Equation (1) calculate the by Equation (2), the by Equation (3) calculate the HSI and sort from best to worst for t = 1 to T do for i = 1 to N do if rand(0,1) < do select the according to Equation (6) heuristic crossover of by Equations (7) and (8) end if calculate the by Equation (11), the by Equation (12) search the prey by Equation (9) attack the prey by Equation (10) end for calculate the HSI and sort from best to worst end for output the optimal solution |
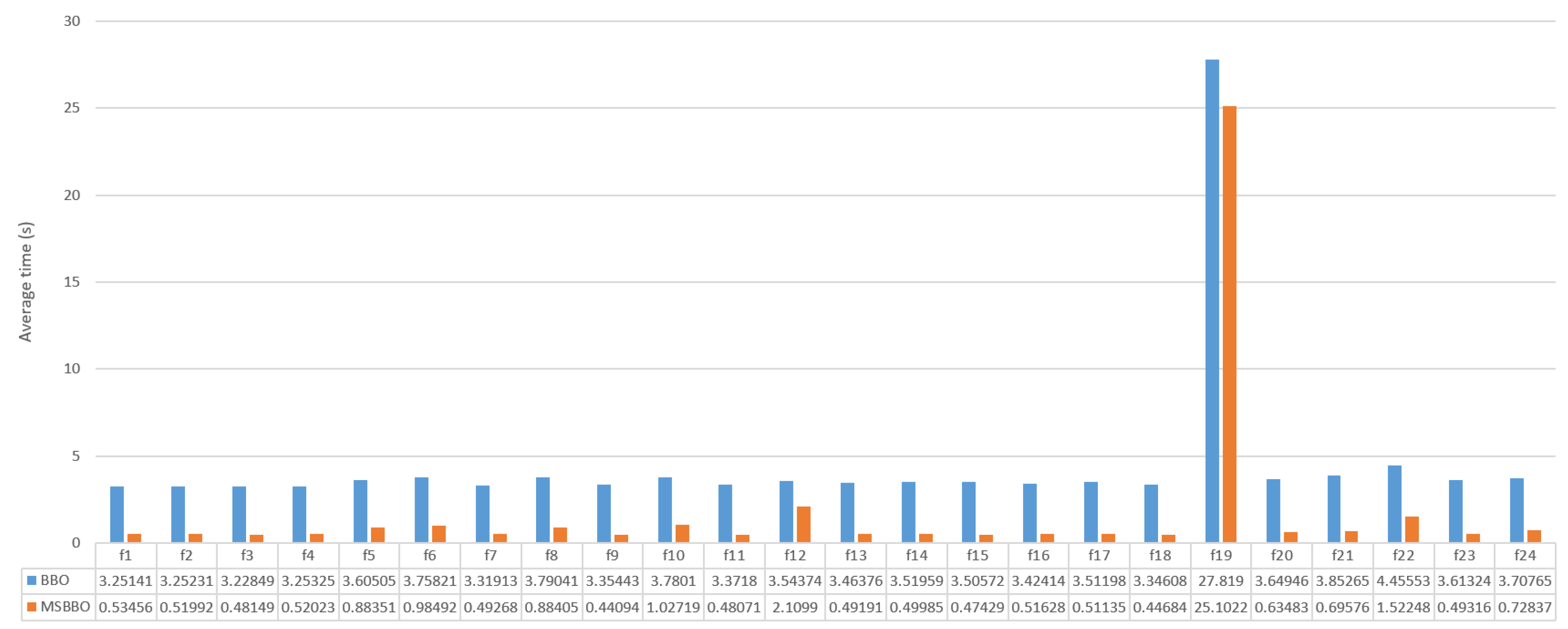
4. Complexity Analysis
5. Experimental Results and Analysis
5.1. Experiment Preparation
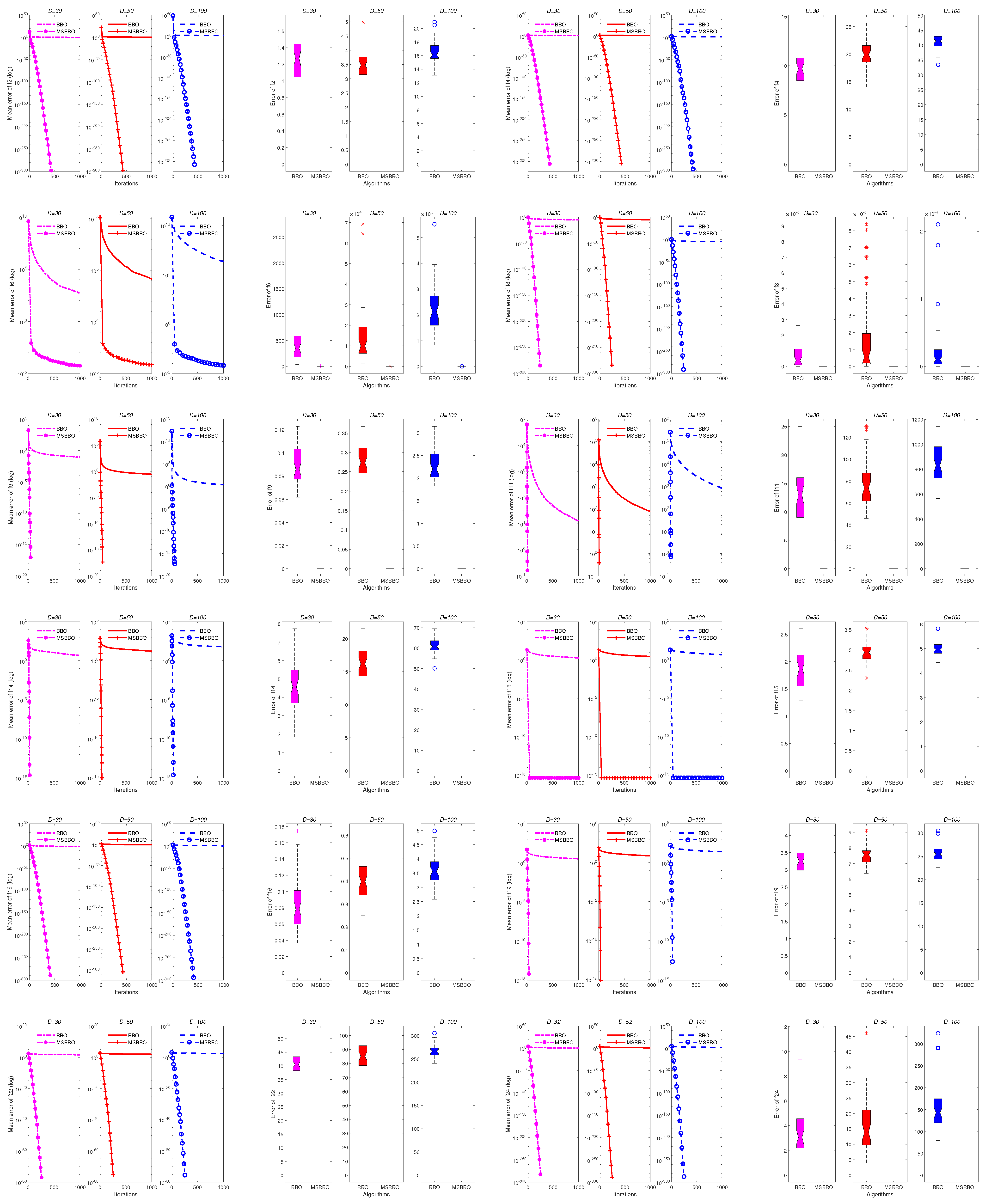
5.2. Comparison between MSBBO and Standard BBO
5.3. Comparison between MSBBO and BBO Variants
5.4. Comparison between MSBBO and Other Meta-Heuristic Algorithms
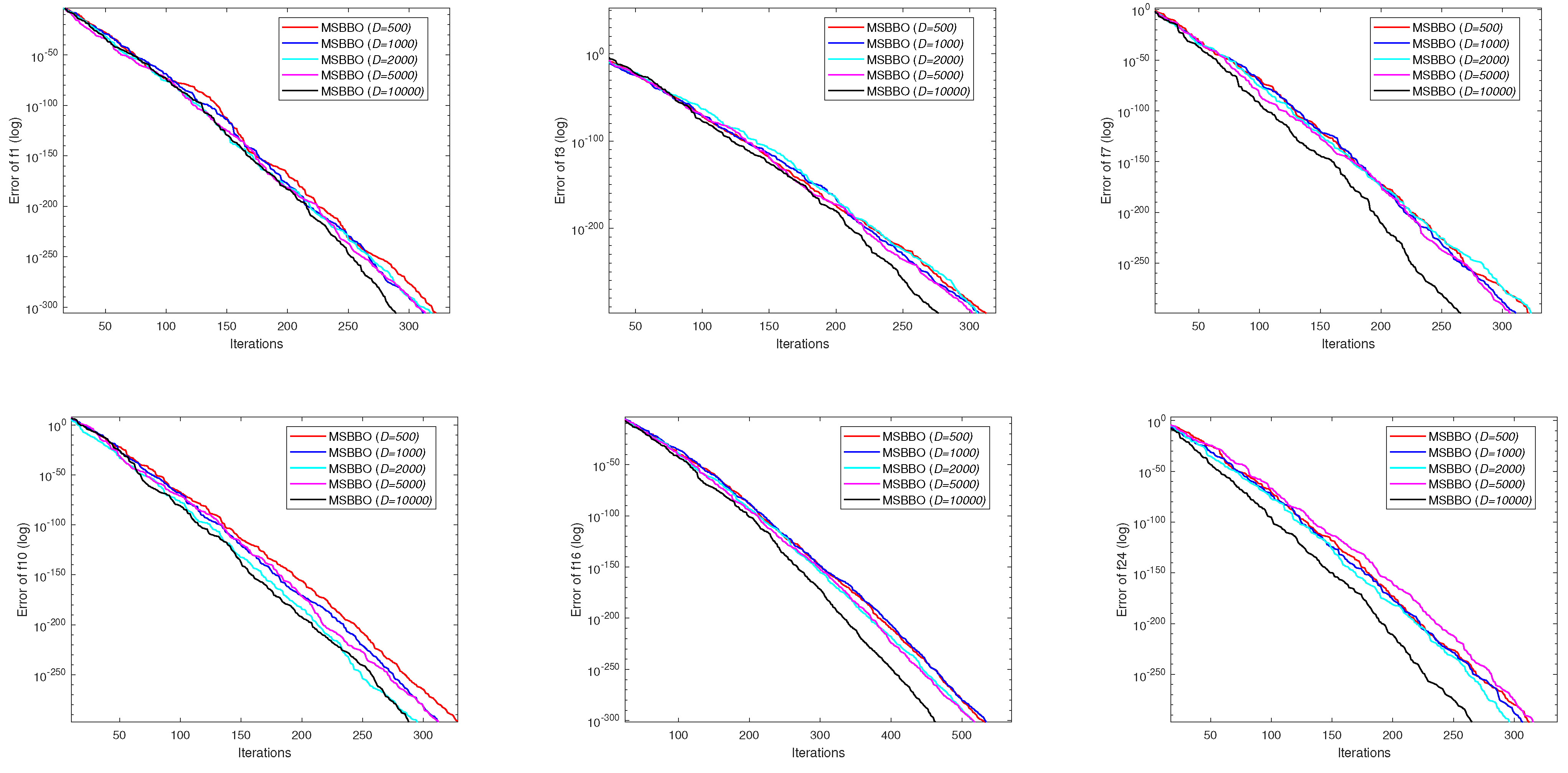
5.5. Comparison of MSBBO on Different High Dimensions
5.6. Application on Engineering Design Problems
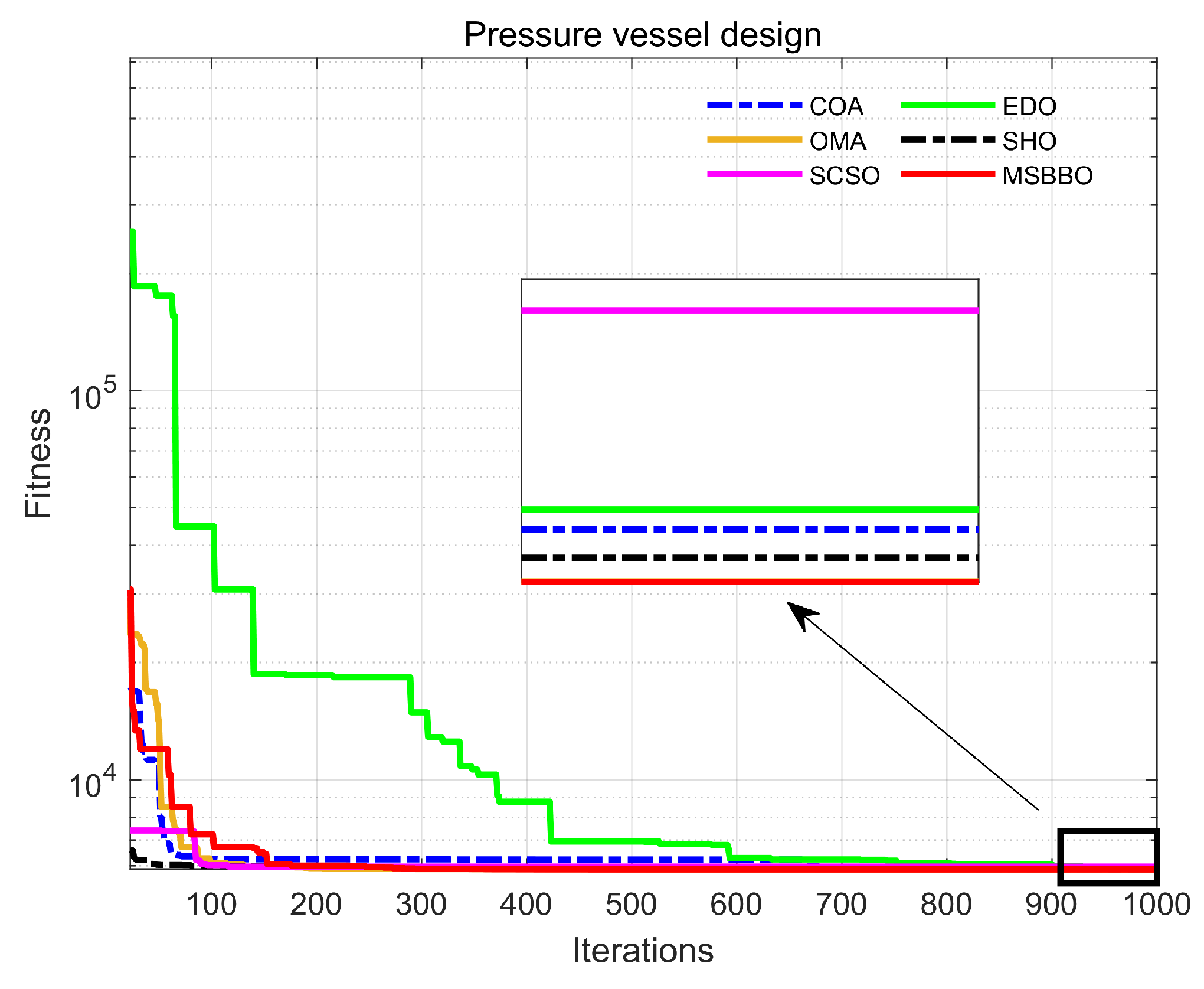
5.6.1. Pressure Vessel Design
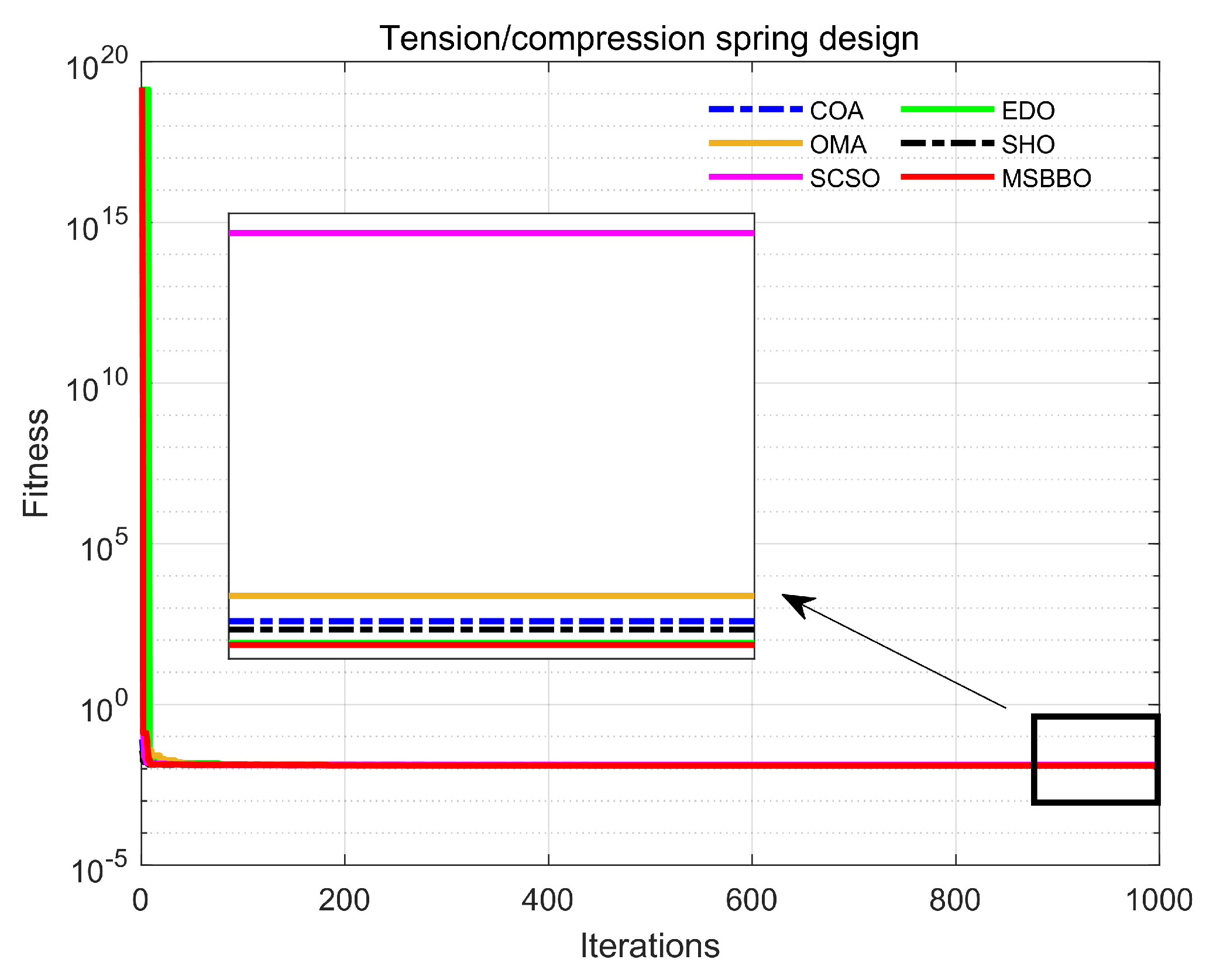
5.6.2. Tension/Compression Spring Design
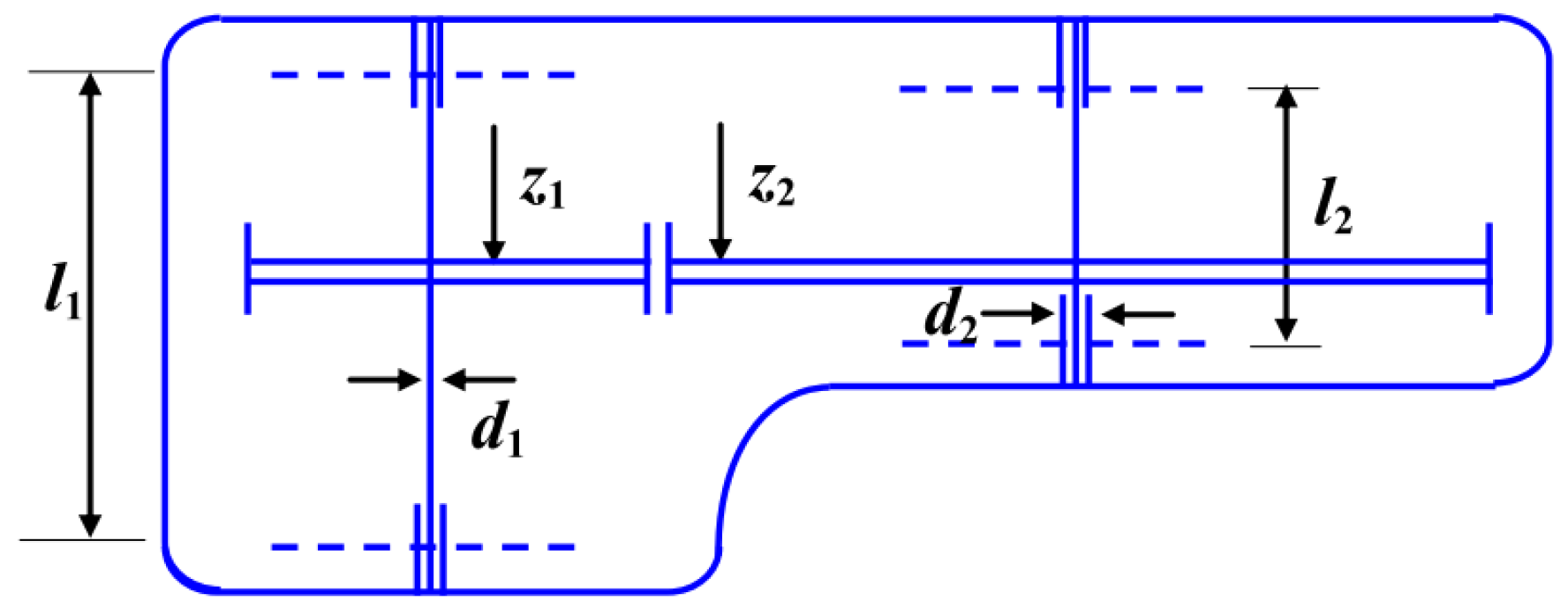
5.6.3. Welded Beam Design
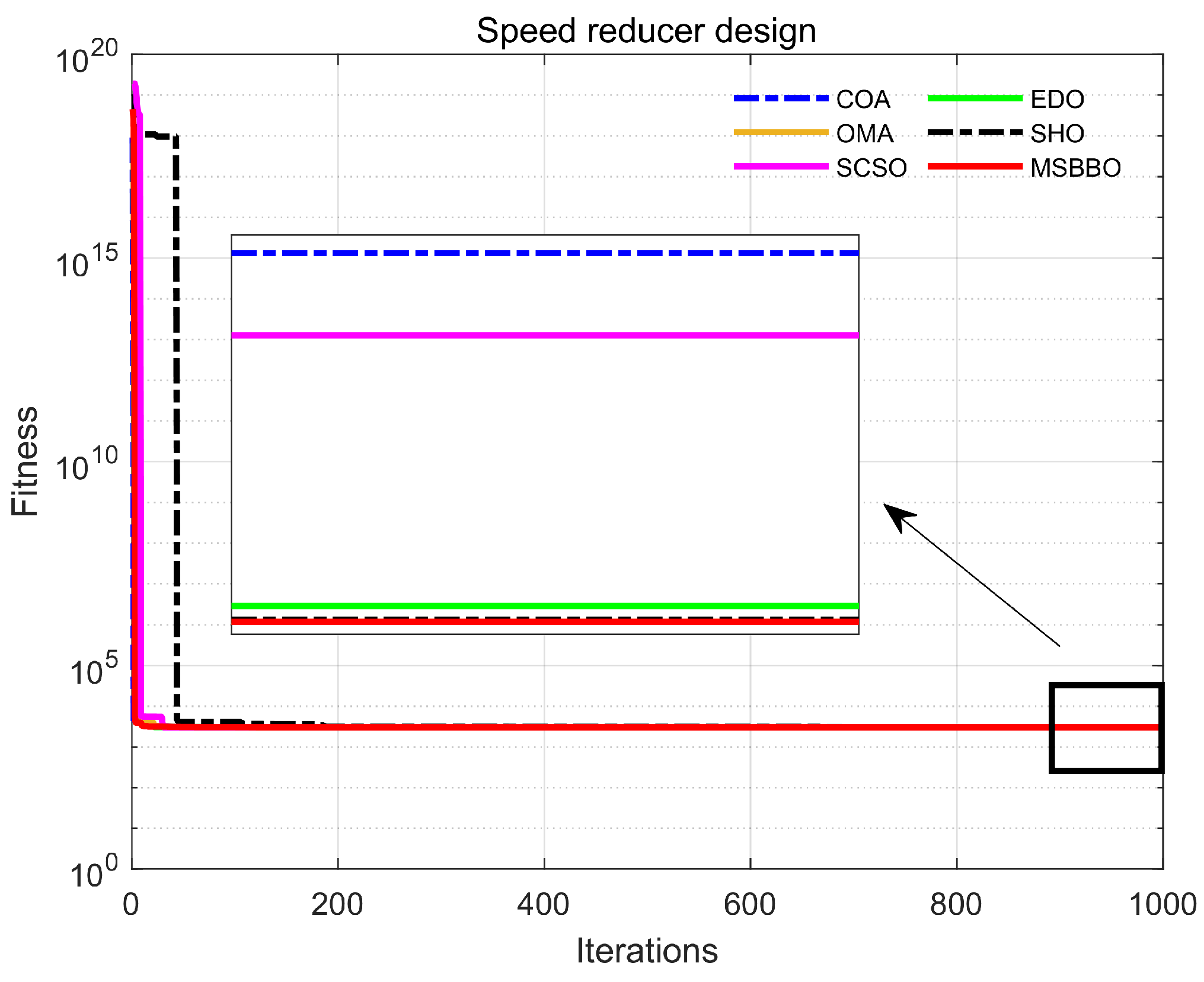
5.6.4. Speed Reducer Design
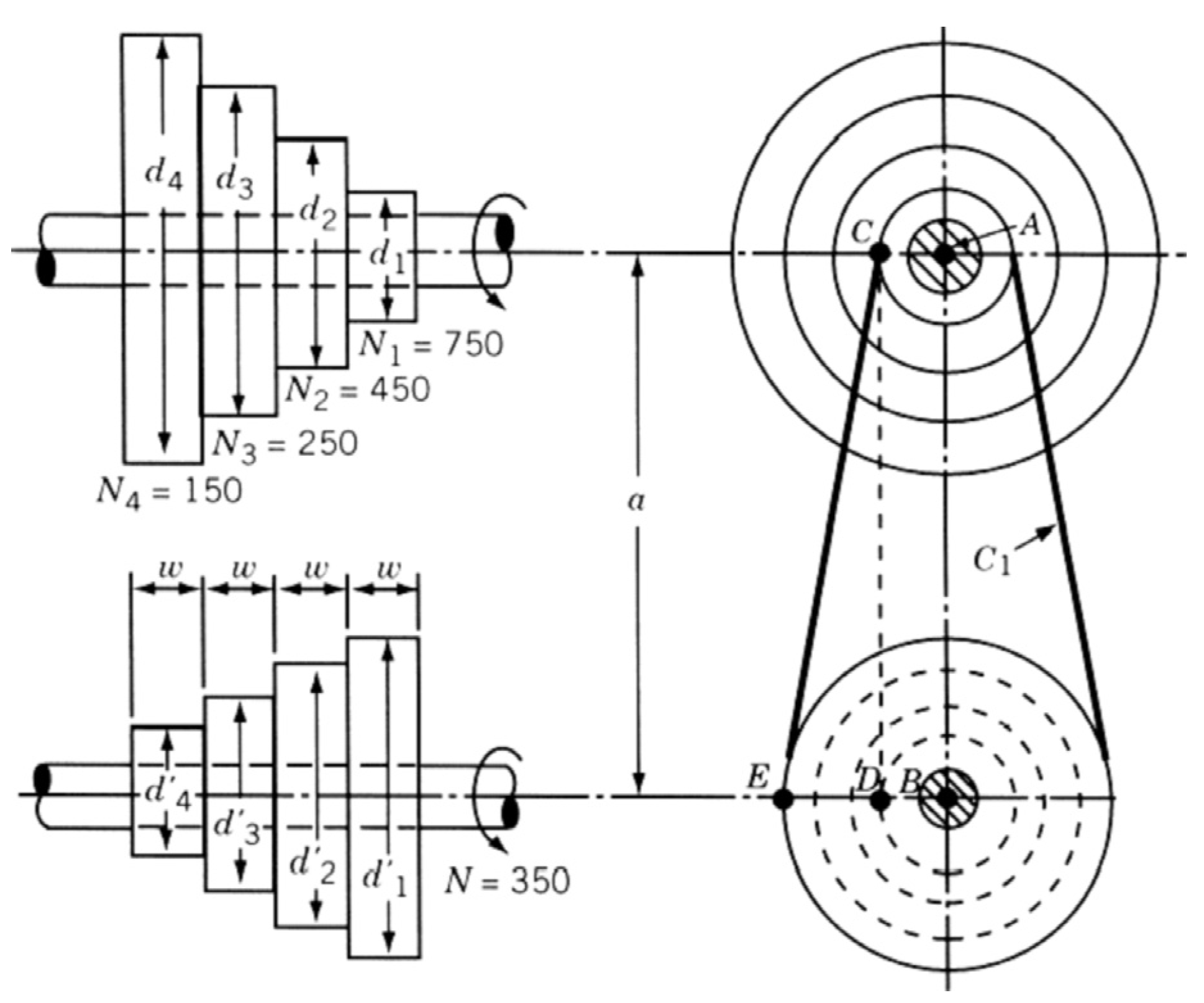
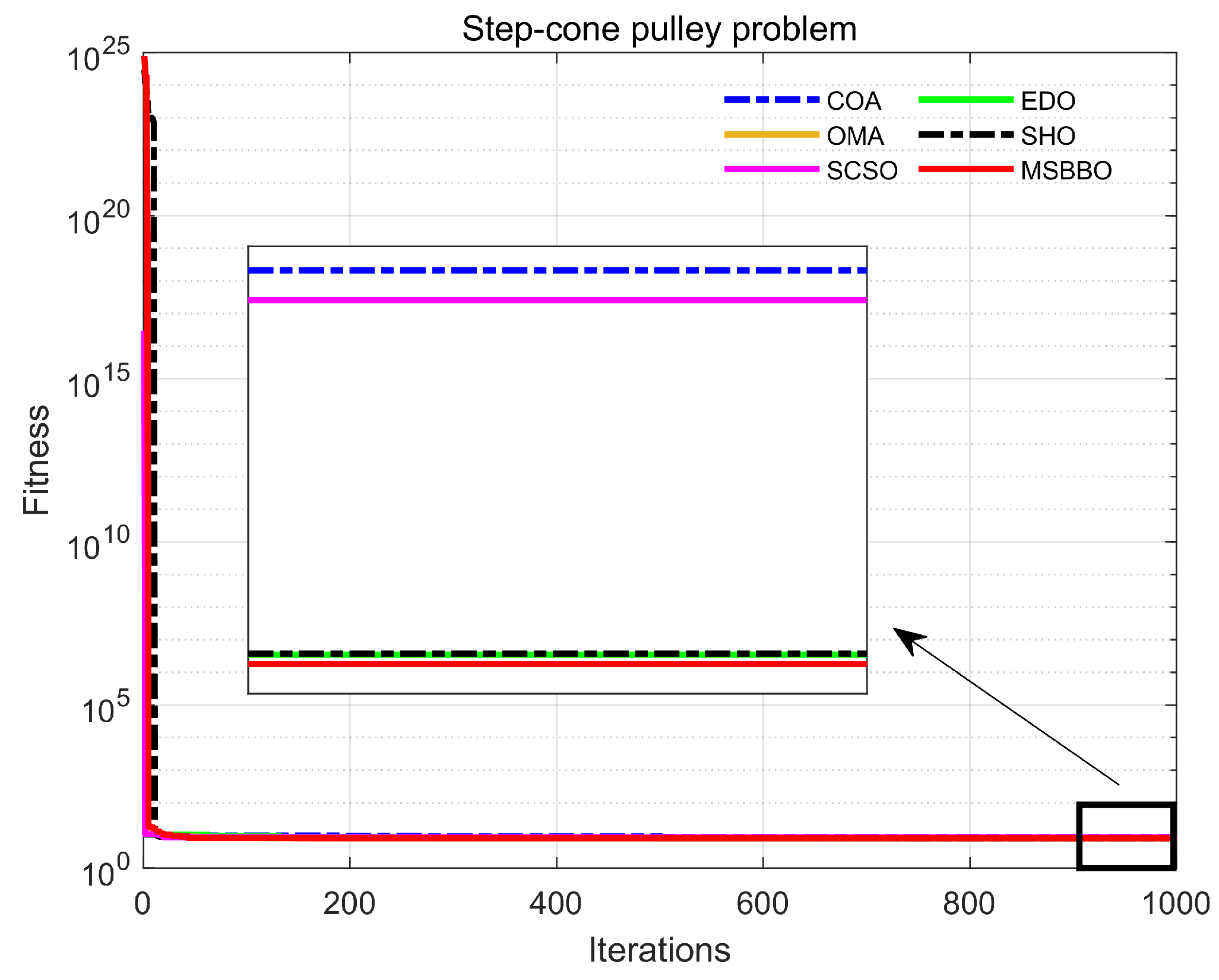
5.6.5. Step-Cone Pulley Problem
5.6.6. Robot Gripper Problem
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qian, K.; Liu, Y.; Tian, L.; Bao, J. Robot path planning optimization method based on heuristic multi-directional rapidly-exploring tree. Comput. Electr. Eng. 2020, 85, 106688. [Google Scholar] [CrossRef]
- Islam, M.A.; Gajpal, Y.; ElMekkawy, T.Y. Hybrid particle swarm optimization algorithm for solving the clustered vehicle routing problem. Appl. Soft Comput. 2021, 110, 107655. [Google Scholar] [CrossRef]
- Ertenlice, O.; Kalayci, C.B. A survey of swarm intelligence for portfolio optimization: Algorithms and applications. Swarm Evol. Comput. 2018, 39, 36–52. [Google Scholar] [CrossRef]
- Ding, H.; Gu, X. Hybrid of human learning optimization algorithm and particle swarm optimization algorithm with scheduling strategies for the flexible job-shop scheduling problem. Neurocomputing 2020, 414, 313–332. [Google Scholar] [CrossRef]
- Darvish, A.; Ebrahimzadeh, A. Improved fruit-fly optimization algorithm and its applications in antenna arrays synthesis. IEEE Trans. Antennas Propag. 2018, 66, 1756–1766. [Google Scholar] [CrossRef]
- Liu, Y.; Jin, S.; Zhou, J.; Hu, Q. A branch-and-bound algorithm for the unit-capacity resource constrained project scheduling problem with transfer times. Comput. Oper. Res. 2023, 151, 106097. [Google Scholar] [CrossRef]
- Babaie-Kafaki, S. A survey on the Dai–Liao family of nonlinear conjugate gradient methods. Rairo-Oper. Res. 2023, 57, 43–58. [Google Scholar] [CrossRef]
- Mittal, G.; Giri, A.K. A modified steepest descent method for solving non-smooth inverse problems. J. Comput. Appl. Math. 2023, 424, 114997. [Google Scholar] [CrossRef]
- Holland, J. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Application to Biology, Control and Artificial Intelligence; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341. [Google Scholar] [CrossRef]
- Dasgupta, D. An artificial immune system as a multi-agent decision support system. In Proceedings of the SMC’98 Conference Proceedings. 1998 IEEE International Conference on Systems, Man, and Cybernetics (Cat. No. 98CH36218), San Diego, CA, USA, 14 October 1998; Volume 4, pp. 3816–3820. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95 International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control. Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Xing, B.; Gao, W.J.; Xing, B.; Gao, W.J. Invasive weed optimization algorithm. In Innovative Computational Intelligence: A Rough Guide to 134 Clever Algorithms; Springer: Cham, Switzerland, 2014; pp. 177–181. [Google Scholar] [CrossRef]
- Kiran, M.S. TSA: Tree-seed algorithm for continuous optimization. Expert Syst. Appl. 2015, 42, 6686–6698. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussain, K.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W. Archimedes optimization algorithm: A new metaheuristic algorithm for solving optimization problems. Appl. Intell. 2021, 51, 1531–1551. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Azeem, S.A.A.; Jameel, M.; Abouhawwash, M. Kepler optimization algorithm: A new metaheuristic algorithm inspired by Kepler’s laws of planetary motion. Knowl.-Based Syst. 2023, 268, 110454. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; El-Shahat, D.; Jameel, M.; Abouhawwash, M. Young’s double-slit experiment optimizer: A novel metaheuristic optimization algorithm for global and constraint optimization problems. Comput. Methods Appl. Mech. Eng. 2023, 403, 115652. [Google Scholar] [CrossRef]
- Das, B.; Mukherjee, V.; Das, D. Student psychology based optimization algorithm: A new population based optimization algorithm for solving optimization problems. Adv. Eng. Softw. 2020, 146, 102804. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–learning-based optimization: An optimization method for continuous non-linear large scale problems. Inf. Sci. 2012, 183, 1–15. [Google Scholar] [CrossRef]
- Ahmadi, S.A. Human behavior-based optimization: A novel metaheuristic approach to solve complex optimization problems. Neural Comput. Appl. 2017, 28 (Suppl. S1), 233–244. [Google Scholar] [CrossRef]
- Chakraborty, S.; Saha, A.K.; Chakraborty, R.; Saha, M. An enhanced whale optimization algorithm for large scale optimization problems. Knowl.-Based Syst. 2021, 233, 107543. [Google Scholar] [CrossRef]
- Rivera, M.M.; Guerrero-Mendez, C.; Lopez-Betancur, D.; Saucedo-Anaya, T. Dynamical Sphere Regrouping Particle Swarm Optimization: A Proposed Algorithm for Dealing with PSO Premature Convergence in Large-Scale Global Optimization. Mathematics 2023, 11, 4339. [Google Scholar] [CrossRef]
- Long, W.; Wu, T.; Liang, X.; Xu, S. Solving high-dimensional global optimization problems using an improved sine cosine algorithm. Expert Syst. Appl. 2019, 123, 108–126. [Google Scholar] [CrossRef]
- Goel, L. A novel approach for face recognition using biogeography based optimization with extinction and evolution. Multimed. Tools Appl. 2022, 81, 10561–10588. [Google Scholar] [CrossRef]
- Jain, A.; Rai, S.; Srinivas, R.; Al-Raoush, R.I. Bioinspired modeling and biogeography-based optimization of electrocoagulation parameters for enhanced heavy metal removal. J. Clean. Prod. 2022, 338, 130622. [Google Scholar] [CrossRef]
- Zhang, Z.; Gao, Y.; Zuo, W. A dual biogeography-based optimization algorithm for solving high-dimensional global optimization problems and engineering design problems. IEEE Access 2022, 10, 55988–56016. [Google Scholar] [CrossRef]
- Zhang, Q.; Wei, L.; Yang, B. Research on Improved BBO Algorithm and Its Application in Optimal Scheduling of Micro-Grid. Mathematics 2022, 10, 2998. [Google Scholar] [CrossRef]
- Ma, H.; Simon, D.; Siarry, P.; Yang, Z.; Fei, M. Biogeography-based optimization: A 10-year review. IEEE Trans. Emerg. Top. Comput. Intell. 2017, 1, 391–407. [Google Scholar] [CrossRef]
- Ergezer, M.; Simon, D.; Du, D. Oppositional biogeography-based optimization. In Proceedings of the 2009 IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 11–14 October 2009; pp. 1009–1014. [Google Scholar] [CrossRef]
- Wang, G.G.; Gandomi, A.H.; Alavi, A.H. An effective krill herd algorithm with migration operator in biogeography-based optimization. Appl. Math. Model. 2014, 38, 2454–2462. [Google Scholar] [CrossRef]
- Lohokare, M.R.; Panigrahi, B.K.; Pattnaik, S.S.; Devi, S.; Mohapatra, A. Neighborhood search-driven accelerated biogeography-based optimization for optimal load dispatch. IEEE Trans. Syst. Man Cybern. Part Appl. Rev. 2012, 42, 641–652. [Google Scholar] [CrossRef]
- Chen, X.; Tianfield, H.; Du, W.; Liu, G. Biogeography-based optimization with covariance matrix based migration. Appl. Soft Comput. 2016, 45, 71–85. [Google Scholar] [CrossRef]
- Sang, X.; Liu, X.; Zhang, Z.; Wang, L. Improved biogeography-based optimization algorithm by hierarchical tissue-like P system with triggering ablation rules. Math. Probl. Eng. 2021, 2021, 6655614. [Google Scholar] [CrossRef]
- Zhang, Z.; Gao, Y.; Liu, Y.; Zuo, W. A hybrid biogeography-based optimization algorithm to solve high-dimensional optimization problems and real-world engineering problems. Appl. Soft Comput. 2023, 144, 110514. [Google Scholar] [CrossRef]
- Zhang, Z.; Gao, Y.; Guo, E. A supercomputing method for large-scale optimization: A feedback biogeography-based optimization with steepest descent method. J. Supercomput. 2023, 79, 1318–1373. [Google Scholar] [CrossRef]
- Garg, V.; Deep, K. Performance of Laplacian Biogeography-Based Optimization Algorithm on CEC 2014 continuous optimization benchmarks and camera calibration problem. Swarm Evol. Comput. 2016, 27, 132–144. [Google Scholar] [CrossRef]
- Zhao, F.; Qin, S.; Zhang, Y.; Ma, W.; Zhang, C.; Song, H. A two-stage differential biogeography-based optimization algorithm and its performance analysis. Expert Syst. Appl. 2019, 115, 329–345. [Google Scholar] [CrossRef]
- Khademi, G.; Mohammadi, H.; Simon, D. Hybrid invasive weed/biogeography-based optimization. Eng. Appl. Artif. Intell. 2017, 64, 213–231. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, D.; Fu, Z.; Liu, S.; Mao, W.; Liu, G.; Jiang, Y.; Li, S. Novel biogeography-based optimization algorithm with hybrid migration and global-best Gaussian mutation. Appl. Math. Model. 2020, 86, 74–91. [Google Scholar] [CrossRef]
- Zhang, X.; Kang, Q.; Tu, Q.; Cheng, J.; Wang, X. Efficient and merged biogeography-based optimization algorithm for global optimization problems. Soft Comput. 2019, 23, 4483–4502. [Google Scholar] [CrossRef]
- Reihanian, A.; Feizi-Derakhshi, M.R.; Aghdasi, H.S. NBBO: A new variant of biogeography-based optimization with a novel framework and a two-phase migration operator. Inf. Sci. 2019, 504, 178–201. [Google Scholar] [CrossRef]
- Gerton, J.L.; Hawley, R.S. Homologous chromosome interactions in meiosis: Diversity amidst conservation. Nat. Rev. Genet. 2005, 6, 477–487. [Google Scholar] [CrossRef]
- Dhiman, G.; Garg, M.; Nagar, A.; Kumar, V.; Dehghani, M. A novel algorithm for global optimization: Rat swarm optimizer. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 8457–8482. [Google Scholar] [CrossRef]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Atanassov, K.; Vassilev, P. Intuitionistic fuzzy sets and other fuzzy sets extensions representable by them. J. Intell. Fuzzy Syst. 2020, 38, 525–530. [Google Scholar] [CrossRef]
- Atanassov, K. Intuitionistic fuzzy modal topological structure. Mathematics 2022, 10, 3313. [Google Scholar] [CrossRef]
- Feng, Q.; Liu, S.; Zhang, J.; Yang, G.; Yong, L. Improved biogeography-based optimization with random ring topology and Powell’s method. Appl. Math. Model. 2017, 41, 630–649. [Google Scholar] [CrossRef]
- Xiong, G.; Shi, D. Hybrid biogeography-based optimization with brain storm optimization for non-convex dynamic economic dispatch with valve-point effects. Energy 2018, 157, 424–435. [Google Scholar] [CrossRef]
- Farrokh Ghatte, H. A hybrid of firefly and biogeography-based optimization algorithms for optimal design of steel frames. Arab. J. Sci. Eng. 2021, 46, 4703–4717. [Google Scholar] [CrossRef]
- Li, W.; Wang, G.G. Elephant herding optimization using dynamic topology and biogeography-based optimization based on learning for numerical optimization. Eng. Comput. 2022, 38 (Suppl. S2), 1585–1613. [Google Scholar] [CrossRef]
- Zhang, X.; Wen, S.; Wang, D. Multi-population biogeography-based optimization algorithm and its application to image segmentation. Appl. Soft Comput. 2022, 124, 109005. [Google Scholar] [CrossRef]
- Liang, S.; Fang, Z.; Sun, G.; Qu, G. Biogeography-based optimization with adaptive migration and adaptive mutation with its application in sidelobe reduction of antenna arrays. Appl. Soft Comput. 2022, 121, 108772. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Jain, M.; Singh, V.; Rani, A. A novel nature-inspired algorithm for optimization: Squirrel search algorithm. SWarm Evol. Comput. 2019, 44, 148–175. [Google Scholar] [CrossRef]
- Khishe, M.; Mosavi, M.R. Chimp optimization algorithm. Expert Syst. Appl. 2020, 149, 113338. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Chopra, N.; Ansari, M.M. Golden jackal optimization: A novel nature-inspired optimizer for engineering applications. Expert Syst. Appl. 2022, 198, 116924. [Google Scholar] [CrossRef]
- Zhong, C.; Li, G.; Meng, Z. Beluga whale optimization: A novel nature-inspired metaheuristic algorithm. Knowl.-Based Syst. 2022, 251, 109215. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Trojovská, E.; Trojovský, P. Coati Optimization Algorithm: A new bio-inspired metaheuristic algorithm for solving optimization problems. Knowl.-Based Syst. 2023, 259, 110011. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; El-Shahat, D.; Jameel, M.; Abouhawwash, M. Exponential distribution optimizer (EDO): A novel math-inspired algorithm for global optimization and engineering problems. Artif. Intell. Rev. 2023, 56, 9329–9400. [Google Scholar] [CrossRef]
- Cheng, M.Y.; Sholeh, M.N. Optical microscope algorithm: A new metaheuristic inspired by microscope magnification for solving engineering optimization problems. Knowl.-Based Syst. 2023, 279, 110939. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, T.; Ma, S.; Wang, M. Sea-horse optimizer: A novel nature-inspired meta-heuristic for global optimization problems. Appl. Intell. 2023, 53, 11833–11860. [Google Scholar] [CrossRef]
- Seyyedabbasi, A.; Kiani, F. Sand Cat swarm optimization: A nature-inspired algorithm to solve global optimization problems. Eng. Comput. 2023, 39, 2627–2651. [Google Scholar] [CrossRef]
- Wang, L.; Cao, Q.; Zhang, Z.; Mirjalili, S.; Zhao, W. Artificial rabbits optimization: A new bio-inspired meta-heuristic algorithm for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2022, 114, 105082. [Google Scholar] [CrossRef]
- Trojovská, E.; Dehghani, M.; Trojovský, P. Zebra optimization algorithm: A new bio-inspired optimization algorithm for solving optimization algorithm. IEEE Access 2022, 10, 49445–49473. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems. Math. Comput. Simul. 2022, 192, 84–110. [Google Scholar] [CrossRef]
- Yapici, H.; Cetinkaya, N. A new meta-heuristic optimizer: Pathfinder algorithm. Appl. Soft Comput. 2019, 78, 545–568. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, Z.; Wang, L. Manta ray foraging optimization: An effective bio-inspired optimizer for engineering applications. Eng. Appl. Artif. Intell. 2020, 87, 103300. [Google Scholar] [CrossRef]
- Savsani, P.; Savsani, V. Passing vehicle search (PVS): A novel metaheuristic algorithm. Appl. Math. Model. 2016, 40, 3951–3978. [Google Scholar] [CrossRef]
- Krenich, S.; Osyczka, A. Optimization of Robot Gripper Parameters Using Genetic Algorithms. In Romansy 13; Springer: Vienna, Austria, 2000. [Google Scholar] [CrossRef]



| Biogeography Theory | Biogeography-Based Optimization Algorithm |
|---|---|
| Habitats (Islands) | Individuals (candidate solutions) |
| Habitat suitability index () | Objective function value (fitness) |
| Suitability index variables () | Characteristic variables of solutions |
| Catastrophic events destroyed the habitat | Mutation |
| The number of habitats | Population size (the number of solutions) |
| Habitats with low HSI immigrate species | Inferior solutions accept variables |
| Habitats with high HSI emigrate species | Superior solutions share variables |
| Function | Search Space | |
|---|---|---|
| 0 | ||
| 0 | ||
| 0 | ||
| 0 | ||
| 0 | ||
| 0 | ||
| −450 | ||
| 0 | ||
| 0 | ||
| 0 | ||
| 0 | ||
| 0 | ||
| −330 | ||
| 0 | ||
| −140 | ||
| 0 | ||
| −180 | ||
| 0 | ||
| 0 | ||
, | 0 | |
| 0 | ||
| 0 | ||
| 0 | ||
| 0 |
| F | BBO (D = 30) | MSBBO (D = 30) | BBO (D = 50) | MSBBO (D = 50) | BBO (D = 100) | MSBBO (D = 100) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | |
| 1.74E+00 | 4.83E-01 | 0.00E+00 | 0.00E+00 | 1.47E+01 | 1.80E+01 | 0.00E+00 | 0.00E+00 | 3.56E+02 | 3.33E+03 | 0.00E+00 | 0.00E+00 | |
| 1.24E+00 | 6.40E-02 | 0.00E+00 | 0.00E+00 | 3.49E+00 | 2.53E-01 | 0.00E+00 | 0.00E+00 | 1.65E+01 | 2.82E+00 | 0.00E+00 | 0.00E+00 | |
| 6.89E+01 | 2.99E+02 | 0.00E+00 | 0.00E+00 | 2.12E+02 | 1.55E+03 | 0.00E+00 | 0.00E+00 | 7.91E+02 | 7.05E+03 | 0.00E+00 | 0.00E+00 | |
| 9.75E+00 | 3.53E+00 | 0.00E+00 | 0.00E+00 | 2.01E+01 | 5.39E+00 | 0.00E+00 | 0.00E+00 | 4.12E+01 | 6.70E+00 | 0.00E+00 | 0.00E+00 | |
| 1.88E+04 | 2.09E+07 | 0.00E+00 | 0.00E+00 | 5.51E+04 | 1.37E+08 | 0.00E+00 | 0.00E+00 | 2.11E+05 | 9.67E+08 | 0.00E+00 | 0.00E+00 | |
| 4.61E+02 | 1.88E+05 | 2.42E-05 | 2.47E-05 | 1.40E+04 | 1.73E+08 | 3.03E-05 | 4.05E-05 | 2.25E+06 | 8.81E+11 | 4.52E-05 | 4.41E-05 | |
| 1.29E+01 | 2.25E+01 | 0.00E+00 | 0.00E+00 | 6.61E+01 | 2.46E+02 | 0.00E+00 | 0.00E+00 | 8.55E+02 | 1.73E+04 | 0.00E+00 | 0.00E+00 | |
| 8.86E-06 | 2.13E-10 | 0.00E+00 | 0.00E+00 | 1.60E-05 | 5.24E-10 | 0.00E+00 | 0.00E+00 | 2.26E-05 | 1.56E-09 | 0.00E+00 | 0.00E+00 | |
| 8.93E-02 | 2.46E-04 | 0.00E+00 | 0.00E+00 | 2.78E-01 | 1.72E-03 | 0.00E+00 | 0.00E+00 | 2.30E+00 | 1.07E-01 | 0.00E+00 | 0.00E+00 | |
| 3.70E+05 | 8.62E+10 | 0.00E+00 | 0.00E+00 | 1.36E+06 | 6.38E+11 | 0.00E+00 | 0.00E+00 | 9.03E+06 | 9.35E+12 | 0.00E+00 | 0.00E+00 | |
| 1.29E+01 | 2.50E+01 | 0.00E+00 | 0.00E+00 | 7.63E+01 | 4.23E+02 | 0.00E+00 | 0.00E+00 | 8.49E+02 | 2.05E+04 | 0.00E+00 | 0.00E+00 | |
| 1.77E+03 | 5.33E+05 | 0.00E+00 | 0.00E+00 | 2.40E+04 | 6.00E+07 | 0.00E+00 | 0.00E+00 | 9.86E+05 | 4.18E+10 | 0.00E+00 | 0.00E+00 | |
| 4.76E+00 | 1.70E+00 | 0.00E+00 | 0.00E+00 | 1.73E+01 | 7.91E+00 | 0.00E+00 | 0.00E+00 | 8.17E+01 | 5.71E+01 | 0.00E+00 | 0.00E+00 | |
| 4.66E+00 | 2.02E+00 | 0.00E+00 | 0.00E+00 | 1.62E+01 | 6.40E+00 | 0.00E+00 | 0.00E+00 | 6.10E+01 | 1.37E+01 | 0.00E+00 | 0.00E+00 | |
| 1.85E+00 | 9.78E-02 | 4.44E-16 | 0.00E+00 | 2.93E+00 | 5.39E-02 | 4.44E-16 | 0.00E+00 | 4.98E+00 | 8.09E-02 | 4.44E-16 | 0.00E+00 | |
| 8.14E-02 | 9.15E-04 | 0.00E+00 | 0.00E+00 | 4.06E-01 | 8.68E-03 | 0.00E+00 | 0.00E+00 | 3.63E+00 | 2.76E-01 | 0.00E+00 | 0.00E+00 | |
| 1.10E+00 | 1.07E-03 | 0.00E+00 | 0.00E+00 | 1.60E+00 | 2.64E-02 | 0.00E+00 | 0.00E+00 | 8.29E+00 | 1.44E+00 | 0.00E+00 | 0.00E+00 | |
| 2.07E+00 | 5.86E-02 | 0.00E+00 | 0.00E+00 | 3.79E+00 | 1.73E-01 | 0.00E+00 | 0.00E+00 | 8.91E+00 | 4.75E-01 | 0.00E+00 | 0.00E+00 | |
| 3.22E+00 | 1.41E-01 | 0.00E+00 | 0.00E+00 | 7.51E+00 | 3.37E-01 | 0.00E+00 | 0.00E+00 | 2.56E+01 | 3.23E+00 | 0.00E+00 | 0.00E+00 | |
| 5.18E-01 | 1.38E-01 | 7.07E-02 | 2.90E-03 | 6.54E-01 | 1.32E-01 | 2.93E-01 | 2.07E-02 | 3.04E+00 | 4.73E-01 | 8.21E-01 | 9.38E-02 | |
| 3.54E+00 | 6.57E-01 | 5.95E-01 | 6.07E-02 | 6.62E+00 | 2.17E+00 | 3.54E+00 | 7.36E-01 | 3.81E+02 | 4.84E+05 | 1.53E+01 | 1.37E+00 | |
| 4.11E+01 | 2.09E+01 | 0.00E+00 | 0.00E+00 | 8.52E+01 | 6.65E+01 | 0.00E+00 | 0.00E+00 | 2.66E+02 | 1.65E+02 | 0.00E+00 | 0.00E+00 | |
| 4.43E+01 | 2.40E+02 | 0.00E+00 | 0.00E+00 | 2.23E+02 | 3.63E+03 | 0.00E+00 | 0.00E+00 | 2.53E+03 | 1.93E+05 | 0.00E+00 | 0.00E+00 | |
| 3.86E+00 | 6.75E+00 | 0.00E+00 | 0.00E+00 | 1.61E+01 | 7.63E+01 | 0.00E+00 | 0.00E+00 | 1.55E+02 | 2.71E+03 | 0.00E+00 | 0.00E+00 | |
| w/t/l | 0/0/24 | - | 0/0/24 | - | 0/0/24 | - | ||||||
| F | PRBBO (2017) | BBOSB (2018) | HGBBO (2020) | FABBO (2021) | BLEHO (2022) | MPBBO (2022) | BBOIMAM (2022) | MSBBO | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | |
| 1.43E-02 | 2.09E-05 | 2.01E+03 | 6.06E+04 | 2.13E-15 | 1.23E-30 | 1.47E-13 | 1.95E-27 | 1.80E+02 | 2.65E+03 | 7.93E-04 | 1.63E-07 | 1.29E+02 | 4.84E+02 | 0.00E+00 | 0.00E+00 | |
| 2.98E-02 | 3.18E-05 | 3.42E+01 | 1.25E+01 | 4.19E-11 | 1.56E-22 | 3.21E-07 | 6.91E-16 | 2.66E+01 | 2.54E+01 | 3.81E+02 | 7.19E+04 | 1.11E+01 | 5.55E-01 | 0.00E+00 | 0.00E+00 | |
| 2.08E+03 | 5.83E+04 | 2.97E+03 | 6.08E+04 | 3.78E+03 | 3.27E+04 | 2.54E+03 | 6.29E+04 | 1.46E+05 | 2.34E+10 | 2.61E+02 | 5.32E+03 | 1.55E+03 | 2.19E+04 | 0.00E+00 | 0.00E+00 | |
| 3.01E+01 | 1.99E+01 | 2.98E+01 | 7.53E+00 | 2.39E-02 | 7.06E-05 | 6.89E+01 | 1.20E+02 | 2.09E-02 | 1.67E-04 | 1.18E+01 | 3.09E+00 | 2.12E+01 | 3.17E+00 | 0.00E+00 | 0.00E+00 | |
| 4.05E+05 | 5.84E+09 | 5.09E+05 | 2.89E+09 | 6.95E+05 | 7.22E+10 | 4.68E+05 | 4.62E+09 | 1.87E+05 | 2.02E+09 | 2.18E+05 | 4.41E+09 | 1.78E+05 | 6.67E+08 | 0.00E+00 | 0.00E+00 | |
| 4.61E+01 | 1.68E+03 | 4.07E+03 | 1.46E+06 | 5.15E-02 | 1.35E-04 | 2.50E-01 | 3.86E-03 | 7.06E+03 | 4.18E+06 | 8.82E-01 | 3.27E-01 | 3.86E+04 | 8.48E+07 | 4.81E-05 | 4.41E-05 | |
| 1.98E-02 | 5.78E-05 | 2.20E+01 | 4.68E+00 | 1.28E-16 | 6.78E-33 | 1.02E-13 | 3.38E-28 | 3.04E+01 | 1.59E+01 | 3.51E-04 | 8.51E-08 | 1.41E+02 | 2.83E+02 | 0.00E+00 | 0.00E+00 | |
| 2.35E-21 | 1.17E-41 | 2.29E-05 | 6.36E-10 | 1.24E-109 | 2.68E-218 | 8.64E-01 | 3.33E-01 | 1.91E-23 | 7.38E-46 | 1.86E-19 | 8.30E-38 | 1.60E-06 | 4.63E-12 | 0.00E+00 | 0.00E+00 | |
| 1.40E-03 | 7.94E-08 | 2.31E+05 | 2.39E+10 | 4.94E-12 | 3.90E-24 | 1.99E-08 | 2.94E-18 | 4.69E+00 | 3.14E+00 | 1.65E-04 | 1.47E-09 | 1.74E+00 | 3.74E-02 | 0.00E+00 | 0.00E+00 | |
| 2.32E+01 | 9.02E+01 | 3.98E+05 | 6.59E+09 | 3.59E-10 | 2.85E-20 | 7.12E+01 | 6.03E+03 | 1.02E+07 | 5.47E+12 | 2.77E+04 | 1.42E+08 | 1.01E+06 | 6.47E+10 | 0.00E+00 | 0.00E+00 | |
| 0.00E+00 | 0.00E+00 | 4.75E+01 | 4.72E+01 | 0.00E+00 | 0.00E+00 | 4.54E+01 | 1.82E+02 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 1.52E+02 | 2.70E+02 | 0.00E+00 | 0.00E+00 | |
| 7.56E+01 | 7.15E+02 | 3.30E+05 | 1.82E+09 | 1.22E-11 | 8.06E-23 | 3.76E-09 | 4.10E-18 | 2.06E+06 | 6.25E+10 | 3.59E+01 | 6.74E+01 | 5.17E+05 | 2.37E+09 | 0.00E+00 | 0.00E+00 | |
| 6.63E+02 | 6.61E+02 | 7.12E+02 | 2.79E+03 | 1.31E-11 | 2.21E-22 | 1.14E+03 | 1.11E+04 | 3.34E+02 | 4.49E+03 | 3.99E+02 | 4.80E+03 | 1.02E+02 | 1.64E+02 | 0.00E+00 | 0.00E+00 | |
| 5.08E+02 | 7.19E+02 | 5.15E+02 | 2.58E+03 | 4.40E-04 | 2.96E-07 | 1.28E+03 | 1.76E+04 | 2.65E+02 | 2.27E+04 | 4.85E+02 | 3.67E+03 | 8.06E+01 | 3.05E+01 | 0.00E+00 | 0.00E+00 | |
| 1.26E-02 | 3.66E-06 | 3.11E+00 | 4.65E-02 | 1.99E+01 | 6.88E-04 | 1.60E+00 | 4.80E-01 | 3.63E+00 | 5.71E-02 | 6.84E+00 | 6.53E+01 | 2.26E+00 | 1.79E-02 | 4.44E-16 | 0.00E+00 | |
| 9.36E-01 | 6.22E-01 | 3.81E+01 | 1.74E+01 | 4.32E-02 | 3.99E-04 | 6.42E+00 | 8.08E+01 | 2.44E+01 | 2.45E+01 | 9.14E+00 | 8.52E+00 | 3.73E+00 | 5.73E-01 | 0.00E+00 | 0.00E+00 | |
| 5.28E-03 | 3.29E-06 | 1.78E-01 | 4.85E-04 | 1.11E-16 | 0.00E+00 | 3.84E-03 | 2.21E-05 | 1.26E+00 | 1.28E-03 | 2.79E-03 | 1.35E-05 | 2.31E+00 | 2.83E-02 | 0.00E+00 | 0.00E+00 | |
| 2.81E+00 | 3.55E-02 | 4.71E+00 | 8.88E-02 | 4.01E-01 | 3.98E-03 | 2.12E+00 | 2.09E-01 | 4.19E+00 | 7.28E-02 | 1.42E+00 | 2.51E-02 | 5.67E+00 | 4.96E-02 | 0.00E+00 | 0.00E+00 | |
| 9.38E-01 | 8.32E-03 | 1.88E+02 | 2.05E+01 | 6.87E-10 | 4.51E-20 | 6.35E+01 | 3.29E+01 | 1.26E+02 | 1.36E+02 | 8.27E-01 | 9.15E-03 | 4.10E+01 | 1.62E+00 | 0.00E+00 | 0.00E+00 | |
| 2.06E-02 | 3.31E-04 | 1.76E+00 | 2.49E-01 | 7.96E-06 | 3.26E-12 | 7.82E+00 | 1.06E+01 | 1.14E+01 | 4.55E+00 | 3.49E+00 | 2.35E+00 | 6.89E-02 | 1.59E-04 | 9.47E-01 | 7.06E-02 | |
| 2.73E-01 | 1.79E-02 | 1.84E+01 | 2.05E+01 | 8.71E-04 | 1.11E-07 | 1.09E+02 | 8.51E+03 | 5.11E+01 | 2.38E+02 | 2.52E-02 | 6.21E-04 | 6.59E+00 | 6.89E-01 | 3.21E+01 | 2.05E+00 | |
| 1.17E+02 | 1.02E+02 | 6.11E+02 | 2.38E+03 | 2.42E-03 | 5.70E-07 | 1.25E+03 | 7.29E+03 | 1.09E+03 | 5.35E+03 | 4.06E+02 | 7.15E+04 | 3.13E+02 | 1.75E+02 | 0.00E+00 | 0.00E+00 | |
| 7.21E-01 | 1.03E-01 | 1.22E+02 | 8.72E+01 | 4.34E-15 | 1.81E-29 | 4.16E+00 | 7.08E+00 | 1.70E+02 | 1.61E+02 | 2.11E-02 | 2.94E-04 | 4.70E+02 | 4.07E+03 | 0.00E+00 | 0.00E+00 | |
| 8.75E+00 | 8.98E+00 | 1.85E+03 | 8.66E+04 | 8.30E-01 | 5.30E-02 | 1.90E-01 | 5.15E-03 | 2.65E+01 | 4.97E+01 | 2.95E+00 | 2.06E+00 | 2.15E+01 | 3.55E+01 | 0.00E+00 | 0.00E+00 | |
| w/t/l | 2/1/21 | 1/0/23 | 2/1/21 | 0/0/24 | 0/1/23 | 1/1/22 | 2/0/22 | - | ||||||||
| F | GWO (2014) | WOA (2016) | SSA (2019) | ChOA (2019) | MPA (2020) | GJO (2022) | BWO (2022) | MSBBO | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | |
| 6.10E-56 | 5.02E-56 | 4.90E-103 | 2.03E-102 | 5.73E-05 | 1.32E-04 | 1.06E-12 | 9.06E-13 | 2.92E-125 | 7.86E-125 | 1.31E-16 | 1.49E-16 | 1.89E-04 | 1.51E-04 | 0.00E+00 | 0.00E+00 | |
| 1.00E-33 | 6.29E-34 | 1.15E-108 | 3.19E-108 | 6.69E-03 | 5.18E-03 | 2.18E-09 | 1.27E-09 | 1.63E-06 | 1.15E-05 | 4.44E-140 | 5.38E-140 | 1.83E-02 | 7.94E-03 | 0.00E+00 | 0.00E+00 | |
| 7.02E+03 | 5.32E+03 | 7.97E+03 | 3.52E+02 | 1.22E+00 | 3.08E+00 | 6.57E+02 | 4.06E+02 | 2.90E-02 | 2.01E-02 | 1.05E+04 | 1.05E+04 | 1.39E+00 | 1.26E+00 | 0.00E+00 | 0.00E+00 | |
| 9.94E+01 | 7.07E+01 | 9.89E+01 | 3.91E-01 | 1.05E-04 | 9.49E-05 | 2.63E+02 | 2.13E+02 | 6.28E-42 | 9.13E-42 | 2.13E+02 | 1.76E+02 | 3.50E-04 | 1.57E-04 | 0.00E+00 | 0.00E+00 | |
| 4.82E+05 | 2.99E+05 | 4.32E+07 | 2.83E+07 | 2.89E+00 | 2.67E+00 | 1.31E+06 | 6.79E+05 | 3.30E+02 | 6.46E+02 | 1.80E+07 | 1.12E+07 | 9.73E+00 | 7.54E+00 | 0.00E+00 | 0.00E+00 | |
| 6.84E-03 | 3.73E-03 | 2.00E+02 | 2.81E+02 | 3.52E-03 | 3.15E-03 | 6.51E-03 | 3.31E-03 | 2.59E-04 | 1.11E-04 | 2.74E+05 | 1.82E+05 | 2.31E-03 | 1.40E-03 | 4.98E-05 | 5.99E-05 | |
| 3.83E-56 | 3.73E-56 | 1.73E-102 | 1.13E-101 | 1.00E-05 | 1.75E-05 | 2.64E-13 | 1.89E-13 | 6.28E-126 | 1.02E-125 | 1.60E-15 | 2.02E-15 | 7.46E-05 | 6.95E-05 | 0.00E+00 | 0.00E+00 | |
| 5.65E-24 | 6.55E-24 | 1.40E-05 | 2.08E-05 | 2.60E-12 | 6.30E-12 | 2.61E+00 | 1.92E+00 | 0.00E+00 | 0.00E+00 | 2.15E-06 | 2.35E-06 | 1.20E-12 | 1.40E-12 | 0.00E+00 | 0.00E+00 | |
| 3.89E-15 | 3.31E-15 | 0.00E+00 | 0.00E+00 | 4.19E-04 | 3.59E-04 | 8.62E-11 | 5.33E-11 | 0.00E+00 | 0.00E+00 | 4.66E-16 | 2.54E-16 | 1.26E-03 | 4.90E-04 | 0.00E+00 | 0.00E+00 | |
| 2.56E-53 | 1.85E-53 | 2.51E-102 | 1.55E-101 | 1.05E+00 | 1.71E+00 | 6.21E-10 | 5.63E-10 | 1.01E-121 | 3.56E-121 | 4.16E-26 | 5.50E-26 | 5.85E+00 | 5.03E+00 | 0.00E+00 | 0.00E+00 | |
| 0.00E+00 | 0.00E+00 | 2.81E+01 | 3.49E+01 | 0.00E+00 | 0.00E+00 | 1.40E-01 | 3.51E-01 | 0.00E+00 | 0.00E+00 | 5.64E+02 | 4.66E+02 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |
| 4.23E-52 | 2.49E-52 | 1.34E-98 | 1.68E-98 | 1.39E+00 | 1.16E+00 | 8.24E-09 | 6.54E-09 | 8.73E-122 | 1.61E-121 | 9.39E-15 | 1.11E-14 | 2.95E+00 | 1.60E+00 | 0.00E+00 | 0.00E+00 | |
| 0.00E+00 | 0.00E+00 | 1.25E+02 | 5.98E+02 | 7.46E-06 | 1.48E-05 | 3.88E-06 | 4.23E-06 | 0.00E+00 | 0.00E+00 | 1.17E+03 | 1.50E+03 | 4.42E-05 | 4.06E-05 | 0.00E+00 | 0.00E+00 | |
| 1.24E+00 | 1.48E+00 | 7.29E+01 | 1.49E+02 | 1.34E-05 | 2.52E-05 | 2.82E-01 | 2.85E-01 | 0.00E+00 | 0.00E+00 | 8.99E+01 | 8.57E+01 | 3.69E-05 | 2.41E-05 | 0.00E+00 | 0.00E+00 | |
| 9.05E-14 | 7.37E-14 | 3.25E+00 | 7.11E+00 | 1.64E-04 | 1.58E-04 | 5.13E+01 | 4.48E+01 | 4.44E-15 | 0.00E+00 | 1.08E-10 | 1.21E-10 | 4.77E-04 | 2.40E-04 | 4.44E-16 | 0.00E+00 | |
| 2.01E-32 | 2.16E-32 | 3.13E+01 | 5.94E+01 | 2.32E-04 | 2.24E-04 | 1.83E-07 | 1.93E-07 | 2.77E-75 | 7.32E-75 | 2.55E+01 | 2.76E+01 | 1.85E-03 | 6.85E-04 | 0.00E+00 | 0.00E+00 | |
| 6.05E-04 | 2.99E-03 | 1.22E-03 | 5.39E-03 | 4.19E-06 | 1.12E-05 | 1.14E-02 | 1.34E-02 | 0.00E+00 | 0.00E+00 | 1.81E-02 | 2.12E-02 | 1.55E-05 | 1.48E-05 | 0.00E+00 | 0.00E+00 | |
| 2.69E-01 | 1.39E-01 | 1.22E+00 | 5.44E-01 | 6.06E-04 | 1.01E-03 | 2.20E-01 | 1.34E-01 | 1.60E-01 | 4.95E-02 | 4.27E+00 | 2.85E+00 | 1.93E-02 | 1.86E-02 | 0.00E+00 | 0.00E+00 | |
| 5.24E-14 | 7.35E-14 | 6.75E-14 | 8.46E-14 | 2.17E-01 | 1.51E-01 | 5.22E-08 | 4.40E-08 | 0.00E+00 | 0.00E+00 | 2.06E-13 | 1.69E-13 | 5.17E-01 | 2.59E-01 | 0.00E+00 | 0.00E+00 | |
| 1.22E+00 | 1.04E+00 | 2.34E+05 | 1.58E+05 | 1.19E-09 | 2.14E-09 | 2.45E+00 | 1.99E+00 | 2.66E-02 | 3.30E-03 | 4.80E+04 | 2.68E+04 | 1.86E-04 | 2.52E-04 | 1.09E+00 | 3.05E-02 | |
| 8.61E+01 | 5.98E+01 | 1.47E+05 | 9.36E+04 | 4.57E-07 | 1.31E-06 | 9.03E+01 | 4.26E+01 | 3.84E+01 | 1.08E+00 | 9.46E+04 | 6.91E+04 | 4.24E-06 | 3.10E-06 | 8.30E+01 | 4.75E+00 | |
| 2.27E-15 | 9.95E-16 | 4.51E-65 | 6.96E-65 | 6.88E+00 | 4.09E+00 | 3.72E-03 | 2.28E-03 | 1.63E-43 | 4.36E-43 | 9.25E-82 | 1.04E-81 | 1.57E+01 | 2.86E+00 | 0.00E+00 | 0.00E+00 | |
| 0.00E+00 | 0.00E+00 | 1.40E-16 | 4.57E-16 | 2.77E-04 | 5.38E-04 | 4.36E-11 | 4.60E-11 | 0.00E+00 | 0.00E+00 | 4.77E-15 | 3.19E-15 | 1.96E-03 | 1.86E-03 | 0.00E+00 | 0.00E+00 | |
| 4.10E-06 | 4.43E-06 | 1.60E-05 | 4.39E-05 | 7.55E-07 | 1.22E-06 | 1.50E-06 | 1.45E-06 | 2.27E-124 | 1.15E-123 | 1.55E-01 | 1.04E-01 | 4.66E-06 | 4.38E-06 | 0.00E+00 | 0.00E+00 | |
| w/t/l | 0/3/21 | 0/1/23 | 2/1/21 | 0/0/24 | 2/8/14 | 0/0/24 | 2/1/21 | - | ||||||||
| F | MSBBO (D = 500) | MSBBO (D = 1000) | MSBBO (D = 2000) | MSBBO (D = 5000) | MSBBO (D = 10,000) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | |
| 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |
| 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |
| 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |
| 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |
| 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |
| 4.98E-05 | 5.99E-05 | 5.10E-05 | 3.81E-05 | 5.37E-05 | 9.76E-05 | 5.87E-05 | 6.03E-05 | 6.02E-05 | 5.94E-05 | |
| 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |
| 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |
| 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |
| 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |
| 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |
| 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |
| 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |
| 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |
| 4.44E-16 | 0.00E+00 | 4.44E-16 | 0.00E+00 | 4.44E-16 | 0.00E+00 | 4.44E-16 | 0.00E+00 | 4.44E-16 | 0.00E+00 | |
| 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |
| 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |
| 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |
| 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |
| 1.09E+00 | 3.05E-02 | 1.13E+00 | 1.79E-02 | 1.16E+00 | 6.15E-02 | 1.16E+00 | 6.31E-02 | 1.17E+00 | 6.43E-02 | |
| 8.30E+01 | 4.75E+00 | 1.67E+02 | 9.49E+00 | 3.32E+02 | 1.97E+01 | 8.46E+02 | 3.09E+01 | 1.90E+03 | 4.12E+01 | |
| 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |
| 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |
| 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |
| Algorithm | Optimal Values for Variables | Optimal Cost | |||
|---|---|---|---|---|---|
| R | L | ||||
| COA | 0.78425309 | 0.38785440 | 40.63463345 | 195.95592683 | 5902.85656647 |
| EDO | 0.77997855 | 0.38558510 | 40.38924403 | 199.85289900 | 5909.44930611 |
| OMA | 0.77827133 | 0.38470014 | 40.32491200 | 199.92634333 | 5885.51298728 |
| SHO | 0.78255188 | 0.38700919 | 40.54668188 | 196.86310662 | 5893.43974421 |
| SCSO | 0.79522133 | 0.38960618 | 40.66736096 | 195.21548366 | 5976.11395352 |
| MSBBO | 0.77816864 | 0.38464916 | 40.31961873 | 200 | 5885.33277894 |
| Algorithm | Optimal Values for Variables | Optimal Cost | ||
|---|---|---|---|---|
| P | ||||
| COA | 0.05122526 | 0.34565821 | 12.14215544 | 0.01269823 |
| EDO | 0.05190445 | 0.36182344 | 11.22500450 | 0.01267212 |
| OMA | 0.05356063 | 0.40339534 | 8.53973118 | 0.01272961 |
| SHO | 0.05058048 | 0.33062883 | 13.22719241 | 0.01268814 |
| SCSO | 0.05718457 | 0.50390409 | 5.53685327 | 0.01318243 |
| MSBBO | 0.05120413 | 0.34516305 | 12.26044071 | 0.01266959 |
| Algorithm | Optimal Values for Variables | Optimal Cost | |||
|---|---|---|---|---|---|
| h | l | t | b | ||
| COA | 0.18479628 | 3.68381216 | 9.22577702 | 0.19867497 | 1.69837299 |
| EDO | 0.19793629 | 3.36058378 | 9.18941514 | 0.19902434 | 1.67299413 |
| OMA | 0.19883231 | 3.33736530 | 9.19202432 | 0.19883231 | 1.67021773 |
| SHO | 0.17440082 | 3.86323716 | 9.20290796 | 0.19878156 | 1.70196639 |
| SCSO | 0.17898507 | 3.68017384 | 9.47591891 | 0.19754191 | 1.72245954 |
| MSBBO | 0.19883231 | 3.33736530 | 9.19202432 | 0.19883231 | 1.67021773 |
| Algorithm | Optimal Values for Variables | Optimal Cost | ||||||
|---|---|---|---|---|---|---|---|---|
| b | m | z | ||||||
| COA | 3.50000068 | 0.7 | 17 | 7.3 | 8.007338125 | 3.354940375 | 5.286998297 | 3002.176768192 |
| EDO | 3.50025780 | 0.70000066 | 17 | 7.3 | 7.723941215 | 3.350658886 | 5.286670403 | 2994.758133972 |
| OMA | 3.5 | 0.7 | 17 | 7.3 | 7.715319911 | 3.350540949 | 5.286654465 | 2994.424465758 |
| SHO | 3.50004682 | 0.7 | 17 | 7.30178682 | 7.715591607 | 3.350558567 | 5.286654691 | 2994.469209053 |
| SCSO | 3.51205842 | 0.7 | 17 | 7.3 | 7.766370701 | 3.351151796 | 5.286672013 | 3000.448065947 |
| MSBBO | 3.50000001 | 0.7 | 17 | 7.30000014 | 7.715320035 | 3.350540986 | 5.286654467 | 2994.424489954 |
| Algorithm | Optimal Values for Variables | Optimal Cost | ||||
|---|---|---|---|---|---|---|
| COA | 17.43376313 | 29.03743308 | 50.95003894 | 89.57133620 | 89.72893135 | 8.80527504 |
| EDO | 17.00069596 | 28.33533123 | 50.82602160 | 84.55984091 | 89.95618331 | 8.19564986 |
| OMA | 16.96572313 | 28.25752810 | 50.79671071 | 84.49571607 | 90 | 8.18149598 |
| SHO | 17.12626161 | 28.25787354 | 50.79728294 | 84.49688761 | 89.99901887 | 8.19717274 |
| SCSO | 18.25834926 | 28.68767069 | 51.89516285 | 88.88993899 | 88.65129296 | 8.75660602 |
| MSBBO | 16.96572695 | 28.25753037 | 50.79673307 | 84.49572374 | 89.99999337 | 8.18149598 |
| Algorithm | Optimal Values for Variables | Optimal Cost | ||||||
|---|---|---|---|---|---|---|---|---|
| COA | 149.99754208 | 149.65008561 | 159.71207516 | 0.00198394 | 10.06515284 | 115.49379010 | 1.57052121 | 3.49048709 |
| EDO | 149.96736172 | 98.92864085 | 199.99158377 | 49.94588624 | 150 | 124.89353758 | 2.86707789 | 3.55150434 |
| OMA | 147.04217688 | 134.34472269 | 200 | 12.48032203 | 149.35062039 | 106.73574813 | 2.44307744 | 2.84065650 |
| SHO | 144.95148508 | 144.77644040 | 100.00021186 | 0.05032617 | 11.72681600 | 100.42656588 | 1.36167252 | 5.26168942 |
| SCSO | 149.14088858 | 148.88101175 | 148.11100725 | 0.04507554 | 60.56845351 | 108.40010554 | 1.99300044 | 3.63308379 |
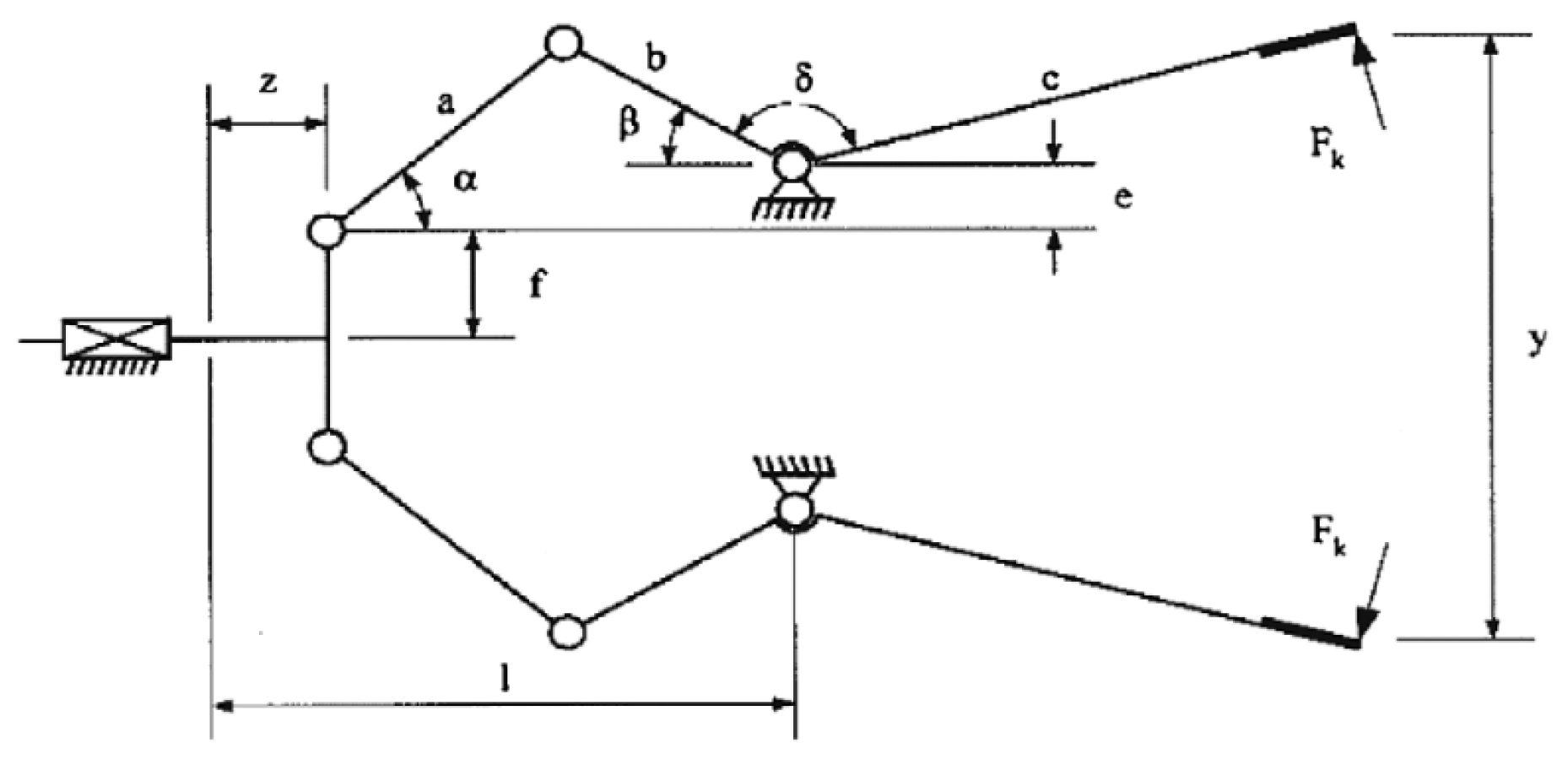
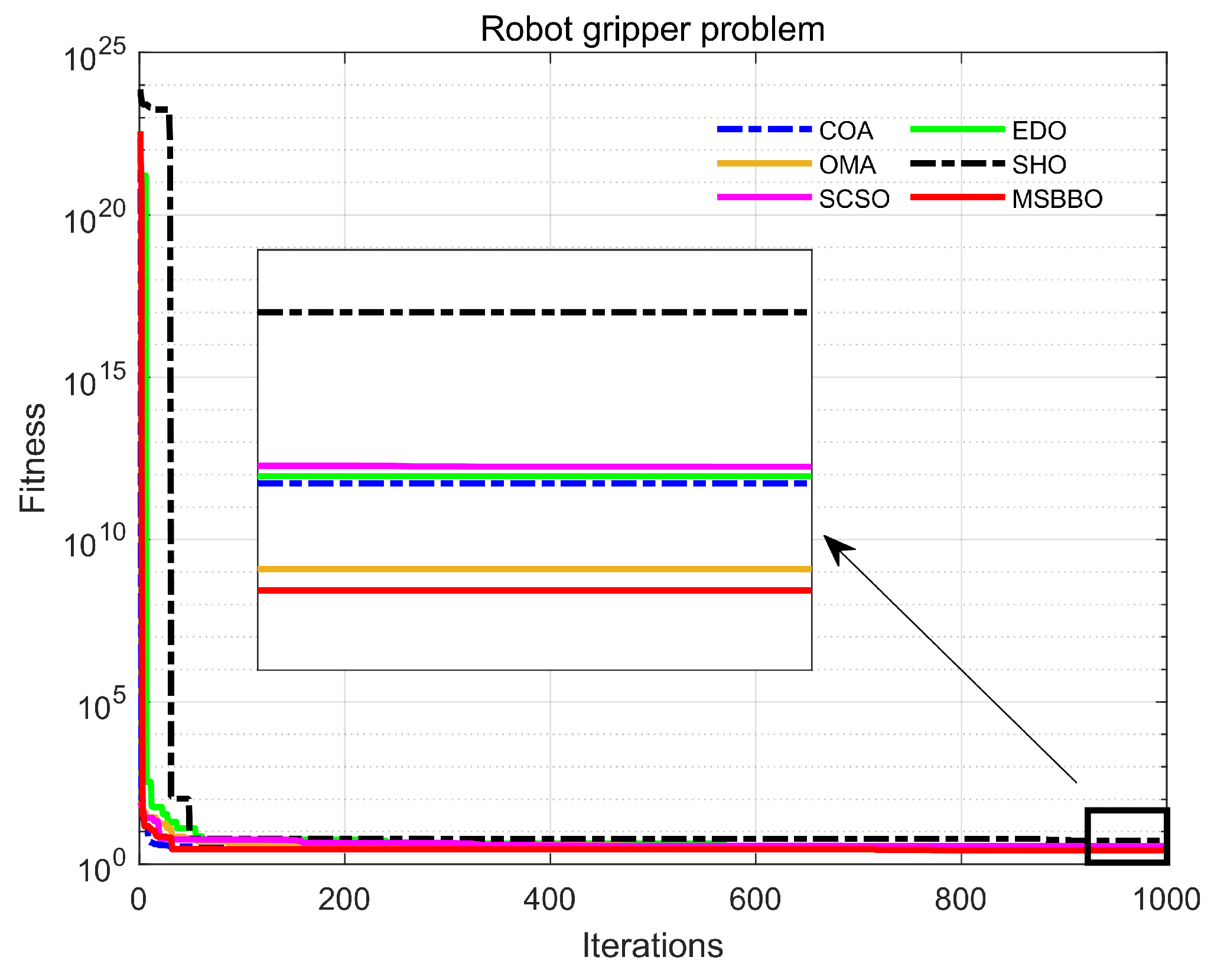
| MSBBO | 149.61527355 | 149.39619170 | 199.20669308 | 8.60E-16 | 149.63248094 | 108.80577404 | 2.42474600 | 2.69788610 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, C.; Li, T.; Gao, Y.; Zhang, Z. A Comprehensive Multi-Strategy Enhanced Biogeography-Based Optimization Algorithm for High-Dimensional Optimization and Engineering Design Problems. Mathematics 2024, 12, 435. https://doi.org/10.3390/math12030435
Gao C, Li T, Gao Y, Zhang Z. A Comprehensive Multi-Strategy Enhanced Biogeography-Based Optimization Algorithm for High-Dimensional Optimization and Engineering Design Problems. Mathematics. 2024; 12(3):435. https://doi.org/10.3390/math12030435
Chicago/Turabian StyleGao, Chenyang, Teng Li, Yuelin Gao, and Ziyu Zhang. 2024. "A Comprehensive Multi-Strategy Enhanced Biogeography-Based Optimization Algorithm for High-Dimensional Optimization and Engineering Design Problems" Mathematics 12, no. 3: 435. https://doi.org/10.3390/math12030435
APA StyleGao, C., Li, T., Gao, Y., & Zhang, Z. (2024). A Comprehensive Multi-Strategy Enhanced Biogeography-Based Optimization Algorithm for High-Dimensional Optimization and Engineering Design Problems. Mathematics, 12(3), 435. https://doi.org/10.3390/math12030435











