Asymptotic Tracking Control for Mismatched Uncertain Systems with Active Disturbance Rejection
Abstract
1. Introduction
- (1)
- A set of exact disturbance estimators (EDEs) with optimized design parameters which can acquire an asymptotic estimation performance is proposed;
- (2)
- Both mismatched and matched exogenous disturbances can be effectively compensated, and meanwhile an asymptotic tracking performance can be acquired.
2. Problem Formulation
3. Asymptotic Tracking Controller with Active Disturbance Rejection
3.1. Exact Disturbance Estimator
3.2. Controller Design
3.3. Main Theoretical Results
4. Illustration Example
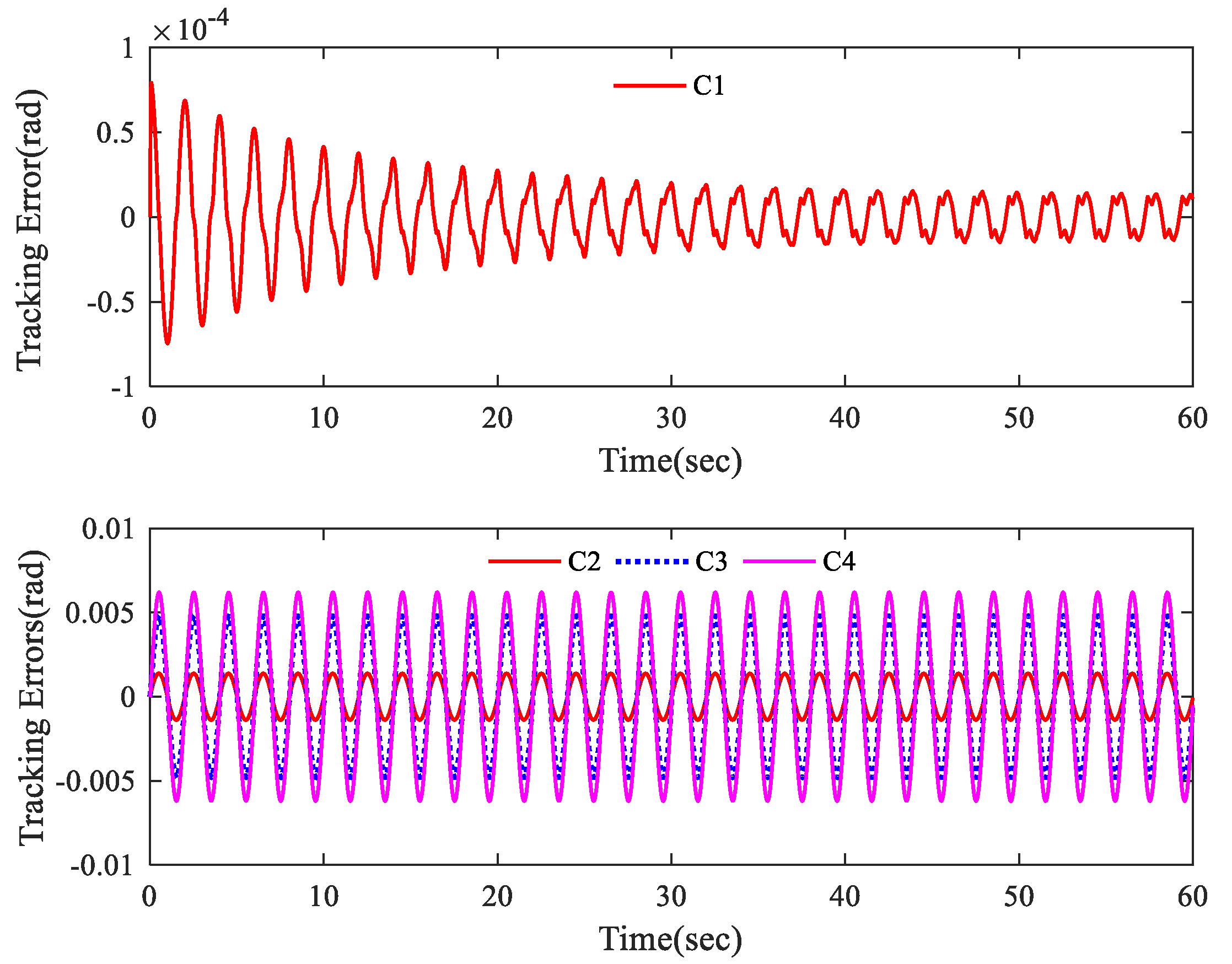
- (2)
- C2: It is same as C1 but without compensation of the mismatched external disturbances.
- (3)
- C3: It is same as C1 but without compensation of the matched external disturbances.
- (4)
- C4: It is same as C1 but without compensation of the mismatched and matched external disturbances simultaneously.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Yang, G.; Yao, J. Multilayer neurocontrol of high-order uncertain nonlinear systems with active disturbance rejection. Int. J. Robust Nonlinear Control. 2024. ahead of print. [Google Scholar] [CrossRef]
- Radke, A.; Gao, Z. A survey of state and disturbance observers for practitioners. In Proceedings of the American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; IEEE: New York, NY, USA, 2006; pp. 5183–5188. [Google Scholar]
- Deng, W.; Yao, J. Asymptotic tracking control of mechanical servosystems with mismatched uncertainties. IEEE/ASME Trans. Mechatron. 2020, 26, 2204–2214. [Google Scholar] [CrossRef]
- Yao, B.; Tomizuka, M. Adaptive robust control of SISO nonlinear systems in a semi-strict feedback form. Automatica 1997, 33, 893–900. [Google Scholar] [CrossRef]
- Ge, S.S.; Fan, H.; Tong, H.L. Robust adaptive control of nonlinear systems with unknown time delays. Automatica 2005, 41, 1181–1190. [Google Scholar] [CrossRef]
- Wen, C.; Jing, Z.; Liu, Z.; Su, H. Robust adaptive control of uncertain nonlinear systems in the presence of input saturation and external disturbance. IEEE Trans. Autom. Control 2011, 56, 1672–1678. [Google Scholar] [CrossRef]
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Springer: New York, NY, USA, 2014. [Google Scholar]
- Yong, F.; Han, F.; Yu, X. Chattering free full-order sliding-mode control. Automatica 2014, 50, 1310–1314. [Google Scholar]
- Chen, W.H.; Ballance, D.J.; Gawthrop, P.J.; O’Reilly, J. A nonlinear disturbance observer for robotic manipulators. IEEE Trans. Ind. Electron. 2000, 47, 932–938. [Google Scholar] [CrossRef]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Yang, G.; Yao, J.; Dong, Z. Neuroadaptive learning algorithm for constrained nonlinear systems with disturbance rejection. Int. J. Robust Nonlinear Control 2022, 32, 6127–6147. [Google Scholar] [CrossRef]
- Guo, B.Z.; Zhao, Z. On the convergence of an extended state observer for nonlinear systems with uncertainty. Syst. Control Lett. 2011, 60, 420–430. [Google Scholar] [CrossRef]
- Zheng, Q.; Gao, L.Q.; Gao, Z. On validation of extended state observer through analysis and experimentation. J. Dyn. Syst. Meas. Contr. 2012, 134, 024505. [Google Scholar] [CrossRef]
- Won, D.; Kim, W.; Shin, D.; Chung, C.C. High-gain disturbance observer-based backstepping control with output tracking error constraint for electro-hydraulic systems. IEEE Trans. Control Syst. Technol. 2014, 23, 787–795. [Google Scholar] [CrossRef]
- Chen, W.H.; Yang, J.; Guo, L.; Li, S. Disturbance-observer-based control and related methods—An overview. IEEE Trans. Ind. Electron. 2015, 63, 1083–1095. [Google Scholar] [CrossRef]
- Guo, B.Z.; Wu, Z.H.; Zhou, H.C. Active disturbance rejection control approach to output-feedback stabilization of a class of uncertain nonlinear systems subject to stochastic disturbance. IEEE Trans. Autom. Control 2015, 61, 1613–1618. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, X.; Xia, Y.; Zuo, Z.; Wang, Y. Disturbance observer-based integral sliding-mode control for systems with mismatched disturbances. IEEE Trans. Ind. Electron. 2016, 63, 7040–7048. [Google Scholar] [CrossRef]
- Han, J.; Zhang, H.; Wang, Y.; Liu, X. Anti-disturbance control for nonlinear system via adaptive disturbance observer. Int. J. Robust Nonlinear Control 2017, 27, 2121–2144. [Google Scholar] [CrossRef]
- Chen, W.H. Disturbance observer based control for nonlinear systems. IEEE/ASME Trans. Mechatron. 2004, 9, 706–710. [Google Scholar] [CrossRef]
- Yang, J.; Li, S.; Sun, C.; Guo, L. Nonlinear-disturbance-observer-based robust flight control for airbreathing hypersonic vehicles. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1263–1275. [Google Scholar] [CrossRef]
- Yang, G.; Yao, J.; Ullah, N. Neuroadaptive control of saturated nonlinear systems with disturbance compensation. ISA Trans. 2022, 122, 49–62. [Google Scholar] [CrossRef]
- Han, J. Active Disturbance Rejection Control Technique—The Technique for Estimating and Compensating the Uncertainties; National Defense Industry Press: Beijing, China, 2008. [Google Scholar]
- Gao, Z. Scaling and bandwidth-parameterization based controller tuning. In Proceedings of the American Control Conference, 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 4989–4996. [Google Scholar]
- Gao, Z. Active disturbance rejection control: A paradigm shift in feedback control system design. In Proceedings of the American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; IEEE: New York, NY, USA, 2006; pp. 2399–2405. [Google Scholar]
- Johnson, C. Accomodation of external disturbances in linear regulator and servomechanism problems. IEEE Trans. Autom. Control 1971, 16, 635–644. [Google Scholar] [CrossRef]
- Johnson, C. Optimal control of the linear regulator with constant disturbances. IEEE Trans. Autom. Control 1968, 13, 416–421. [Google Scholar] [CrossRef]
- Zhong, Q.C.; Kuperman, A.; Stobart, R.K. Design of UDE-based controllers from their two-degree-of-freedom nature. Int. J. Robust Nonlinear Control 2011, 21, 1994–2008. [Google Scholar] [CrossRef]
- Yang, J.; Li, S.; Su, J.; Yu, X. Continuous nonsingular terminal sliding mode control for systems with mismatched disturbances. Automatica 2013, 49, 2287–2291. [Google Scholar] [CrossRef]
- Yang, G. Asymptotic tracking with novel integral robust schemes for mismatched uncertain nonlinear systems. Int. J. Robust Nonlinear Control 2023, 33, 1988–2002. [Google Scholar] [CrossRef]
- Xian, B.; Dawson, D.M.; de Queiroz, M.S.; Chen, J. A continuous asymptotic tracking control strategy for uncertain nonlinear systems. IEEE Trans. Autom. Control 2004, 49, 1206–1211. [Google Scholar] [CrossRef]
- Xian, B.; de Queiroz, M.S.; Dawson, D.M.; McIntyre, M.L. A discontinuous output feedback controller and velocity observer for nonlinear mechanical systems. Automatica 2004, 40, 695–700. [Google Scholar] [CrossRef]
- Zou, X.; Yang, G.; Hong, R.; Dai, Y. Chattering-free terminal sliding-mode tracking control for uncertain nonlinear systems with disturbance compensation. J. Vib. Control 2023. [Google Scholar] [CrossRef]
- Farrell, J.A.; Polycarpou, M.; Sharma, M.; Dong, W. Command filtered backstepping. IEEE Trans. Autom. Control 2009, 54, 1391–1395. [Google Scholar] [CrossRef]
- Liu, Y.H. Adaptive dynamic surface asymptotic tracking for a class of uncertain nonlinear systems. Int. J. Robust Nonlinear Control 2018, 28, 1233–1245. [Google Scholar] [CrossRef]
- Guo, B.Z.; Jin, F.F. The active disturbance rejection and sliding mode control approach to the stabilization of the Euler–Bernoulli beam equation with boundary input disturbance. Automatica 2013, 49, 2911–2918. [Google Scholar] [CrossRef]
- Deng, W.; Yao, J.; Wang, Y.; Yang, X.; Chen, J. Output feedback backstepping control of hydraulic actuators with valve dynamics compensation. Mech. Syst. Signal Process. 2021, 158, 107769. [Google Scholar] [CrossRef]

| Variable | Implication | Value (Unit) |
|---|---|---|
| Jm | The rotational inertia of the load | 2.4 × 10−3 (kg·m2) |
| Bm | The viscous friction coefficient | 2.26 (N·m·s/rad) |
| Rm | The armature resistance | 3.0 (Ω) |
| Lm | The armature inductance | 0.08 (H) |
| Km | The torque constant | 1.85 (N·m/A) |
| Kv | The electrical gain | 2.26 |
| KE | The electromotive force coefficient | 1.25 (V·s/rad) |
| Δ2(t) | External disturbance | Sin (πt) |
| Δ3(t) | External disturbance | 15sin (πt) |
| Controller Parameter | Value | Controller Parameter | Value |
|---|---|---|---|
| k1 | 300 | λ2 | 1 × 107 |
| k2 | 100 | r1 | 150 |
| k3 | 100 | r2 | 150 |
| βo2 | 300 | Lc1 | 5 × 10−4 |
| βo3 | 500 | Lc2 | 5 × 10−4 |
| λ1 | 1.5 × 105 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, G.; Cui, L. Asymptotic Tracking Control for Mismatched Uncertain Systems with Active Disturbance Rejection. Mathematics 2024, 12, 411. https://doi.org/10.3390/math12030411
Yang G, Cui L. Asymptotic Tracking Control for Mismatched Uncertain Systems with Active Disturbance Rejection. Mathematics. 2024; 12(3):411. https://doi.org/10.3390/math12030411
Chicago/Turabian StyleYang, Guichao, and Longfei Cui. 2024. "Asymptotic Tracking Control for Mismatched Uncertain Systems with Active Disturbance Rejection" Mathematics 12, no. 3: 411. https://doi.org/10.3390/math12030411
APA StyleYang, G., & Cui, L. (2024). Asymptotic Tracking Control for Mismatched Uncertain Systems with Active Disturbance Rejection. Mathematics, 12(3), 411. https://doi.org/10.3390/math12030411







