Spatio-Temporal Dual Kriging with Adaptive Coefficient Drift Function
Abstract
1. Introduction
2. Methodological Framework of Spatio-Temporal Kriging Incorporating Auxiliary Variables
2.1. Spatio-Temporal Regression Kriging
2.2. Spatio-Temporal Kriging with External Drift
3. Methodology of Spatio-Temporal Dual Kriging
3.1. Spatio-Temporal Dual Kriging with Fixed Coefficient Drift Function
3.2. Spatio-Temporal Dual Kriging with Adaptive Coefficient Drift Function
4. Application of the Proposed ST-DK Techniques for Temperature and Air Pressure Interpolations in Thailand
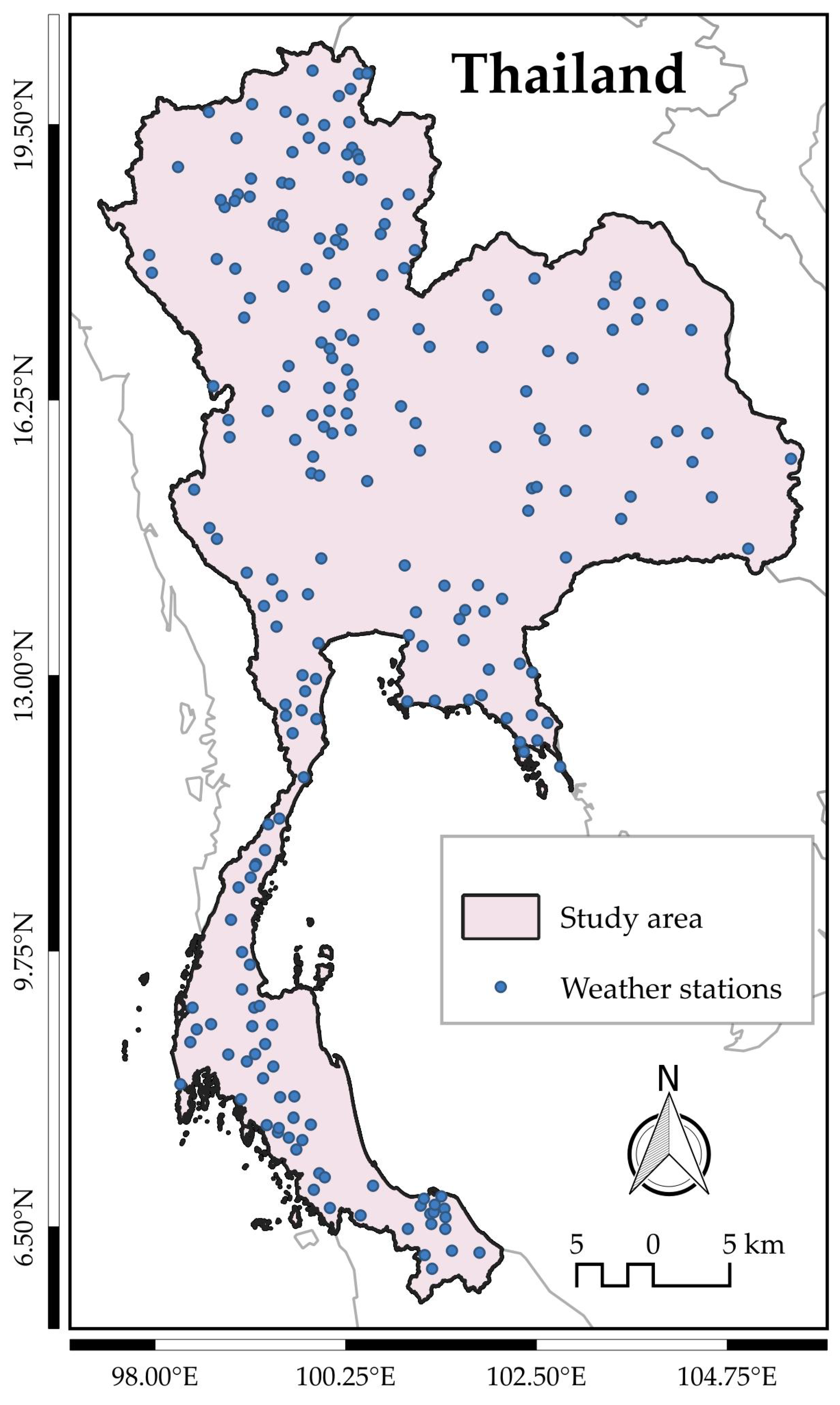
4.1. Study Area and Data Description
4.2. Selection of Auxiliary Variables
4.3. Accuracy Assessment
4.4. Results
4.4.1. Comparison of FST-DK with FST-RK
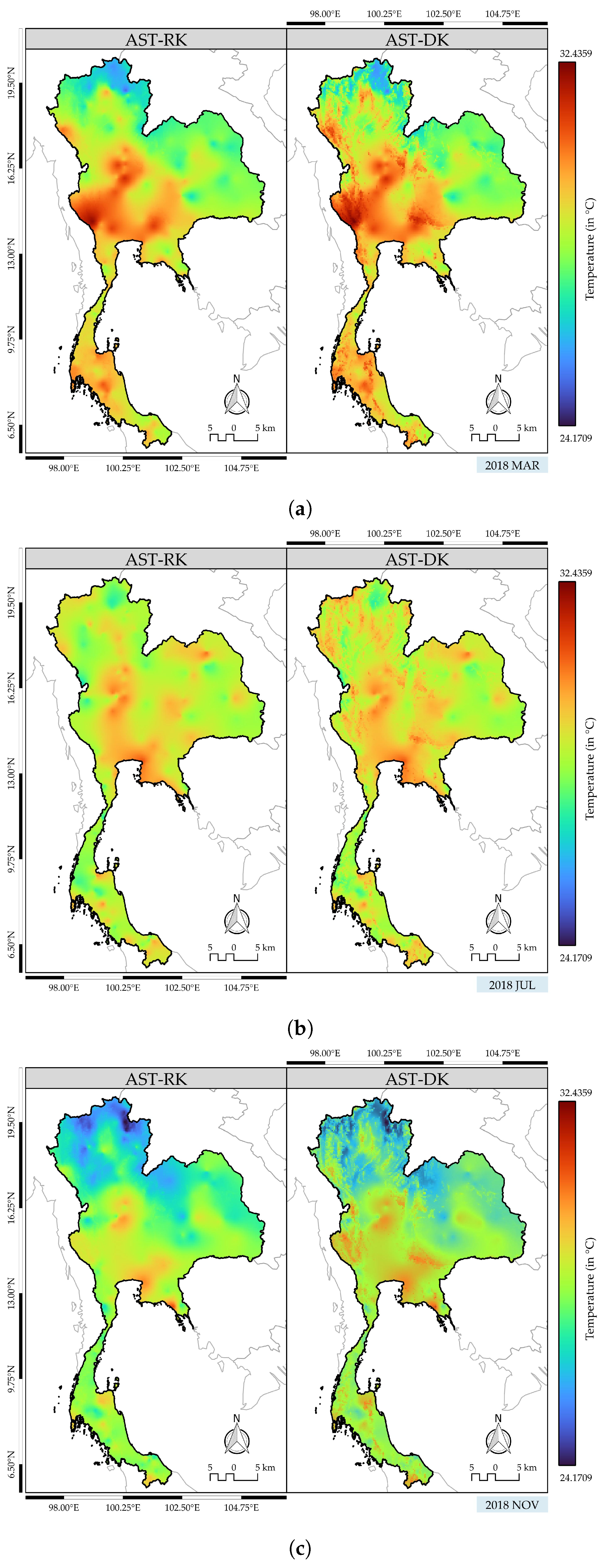
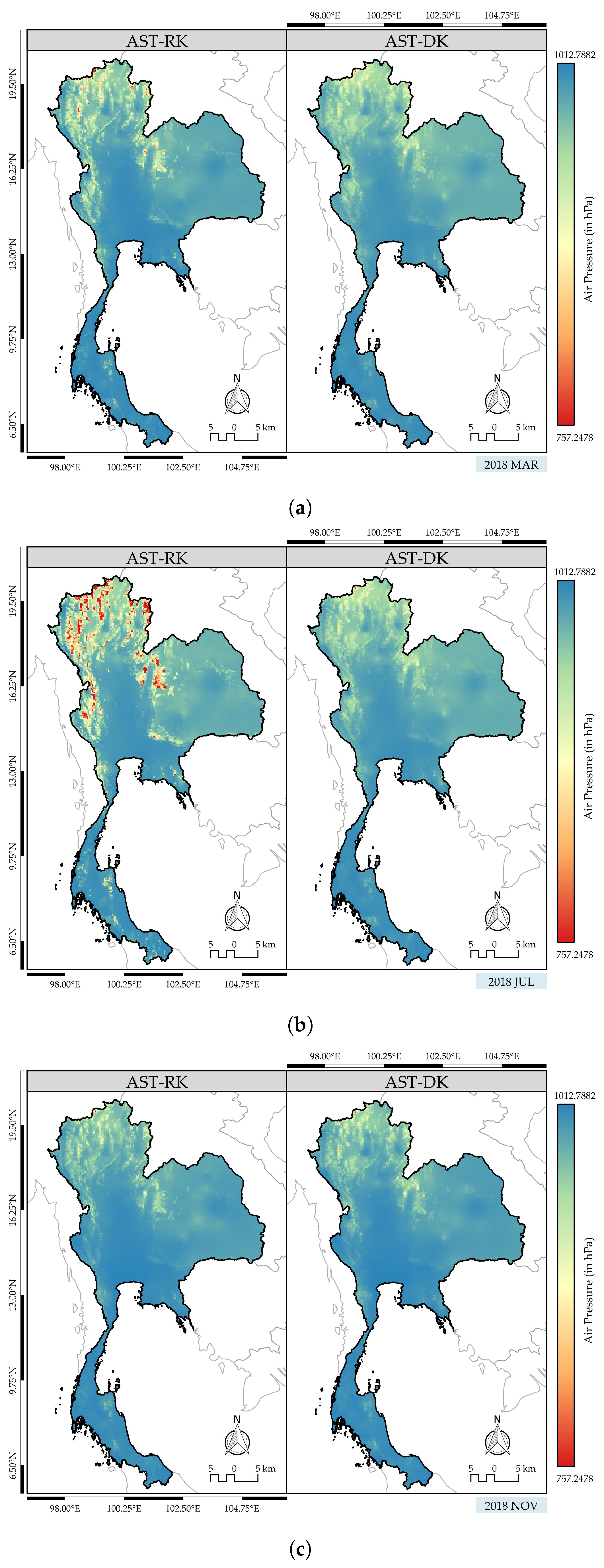
4.4.2. Comparison of AST-DK with AST-RK and GTWR
5. Conclusions and Discussions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AST-DK | Spatio-temporal dual kriging with adaptive coefficient drift function |
| AST-RK | Spatio-temporal regression kriging with adaptive coefficient drift function |
| DEM | Digital elevation model |
| DK | Dual kriging |
| FST-DK | Spatio-temporal dual kriging with fixed coefficient drift function |
| FST-RK | Spatio-temporal regression kriging with fixed coefficient drift function |
| GTWR | Geographically and temporally weighted regression |
| IDW | Inverse distance weighted |
| KED | Kriging with external drift |
| MAPE | Mean absolute percentage error |
| MLR | Multiple linear regression |
| NO2 | Nitrogen dioxide |
| OLS | Ordinary least squares |
| OK | Ordinary kriging |
| RMSE | Root mean square error |
| ST-DK | Spatio-temporal dual kriging |
| ST-KED | Spatio-temporal kriging with external drift |
| ST-OK | Spatio-temporal ordinary kriging |
| ST-RK | Spatio-temporal regression kriging |
| ST-SK | Spatio-temporal simple kriging |
Appendix A. The Formulation of the ST-KED System for Adaptive Coefficient Drift Function
Appendix A.1. Unbiasedness Condition
Appendix A.2. The Variance of the Estimation Error
Appendix A.3. Minimization Approach for ST-KED System Construction
References
- Liu, L.; Özsu, M.T. Encyclopedia of Database Systems; Springer: New York, NY, USA, 2009; Volume 6. [Google Scholar]
- Li, L.; Revesz, P. A comparison of spatiotemporal interpolation methods. In International Conference on Geographic Information Science; Springer: Berlin/Heidelberg, Germany, 2002; pp. 145–160. [Google Scholar]
- Li, L.; Revesz, P. Interpolation methods for spatiotemporal geographic data. Comput. Environ. Urban Syst. 2004, 28, 201–227. [Google Scholar] [CrossRef]
- Eldrandaly, K.; Abdelmouty, A. spatiotemporal interpolation: Current practices and future prospects. Int. J. Digit. Content Technol. Its Appl. 2017, 11, 2017. [Google Scholar]
- Li, J.; Heap, A.D. Spatial interpolation methods applied in the environmental sciences: A review. Environ. Model. Softw. 2014, 53, 173–189. [Google Scholar] [CrossRef]
- Xiao, Y.; Gu, X.; Yin, S.; Shao, J.; Cui, Y.; Zhang, Q.; Niu, Y. Geostatistical interpolation model selection based on ArcGIS and spatiotemporal variability analysis of groundwater level in piedmont plains, northwest China. SpringerPlus 2016, 5, 425. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Losser, T.; Yorke, C.; Piltner, R. Fast inverse distance weighting-based spatiotemporal interpolation: A web-based application of interpolating daily fine particulate matter PM2.5 in the contiguous US using parallel programming and kd tree. Int. J. Environ. Res. Public Health 2014, 11, 9101–9141. [Google Scholar] [CrossRef]
- Du, Z.; Wu, S.; Kwan, M.P.; Zhang, C.; Zhang, F.; Liu, R. A spatiotemporal regression-kriging model for space-time interpolation: A case study of chlorophyll-a prediction in the coastal areas of Zhejiang, China. Int. J. Geogr. Inf. Sci. 2018, 32, 1927–1947. [Google Scholar] [CrossRef]
- van Zoest, V.; Osei, F.B.; Hoek, G.; Stein, A. spatiotemporal regression kriging for modelling urban NO2 concentrations. Int. J. Geogr. Inf. Sci. 2020, 34, 851–865. [Google Scholar] [CrossRef]
- Adigi, J.A. Spatiotemporal Regression Kriging for Predicting Rainfall from Sparse Precipitation Data in Ghana. Master’s Thesis, University of Twente, Enschede, The Netherlands, 2019. [Google Scholar]
- Sekulić, A.; Kilibarda, M.; Protić, D.; Tadić, M.P.; Bajat, B. spatiotemporal regression kriging model of mean daily temperature for Croatia. Theor. Appl. Climatol. 2020, 140, 101–114. [Google Scholar] [CrossRef]
- Hu, D.; Shu, H.; Hu, H.; Xu, J. Spatiotemporal regression Kriging to predict precipitation using time-series MODIS data. Clust. Comput. 2017, 20, 347–357. [Google Scholar] [CrossRef]
- Subba Rao, T.; Terdik, G. On the frequency variogram and on frequency domain methods for the analysis of spatiotemporal data. J. Time Ser. Anal. 2017, 38, 308–325. [Google Scholar] [CrossRef]
- Mateu, J.; Giraldo, R. Introduction to Geostatistical Functional Data Analysis. In Geostatistical Functional Data Analysis; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2022; pp. 1–25. [Google Scholar]
- Idir, Y.M.; Orfila, O.; Judalet, V.; Sagot, B.; Chatellier, P. Mapping urban air quality from mobile sensors using spatiotemporal geostatistics. Sensors 2021, 21, 4717. [Google Scholar] [CrossRef] [PubMed]
- Snepvangers, J.; Heuvelink, G.; Huisman, J. Soil water content interpolation using spatiotemporal kriging with external drift. Geoderma 2003, 112, 253–271. [Google Scholar] [CrossRef]
- Bargaoui, Z.K.; Chebbi, A. Comparison of two kriging interpolation methods applied to spatiotemporal rainfall. J. Hydrol. 2009, 365, 56–73. [Google Scholar] [CrossRef]
- Carrera-Hernández, J.; Gaskin, S. Spatio temporal analysis of daily precipitation and temperature in the Basin of Mexico. J. Hydrol. 2007, 336, 231–249. [Google Scholar] [CrossRef]
- Trochu, F. A contouring program based on dual kriging interpolation. Eng. Comput. 1993, 9, 160–177. [Google Scholar] [CrossRef]
- Chaveesuk, R.; Smith, A.E. Dual Kriging: An exploratory use in economic metamodeling. Eng. Econ. 2005, 50, 247–271. [Google Scholar] [CrossRef]
- De Iaco, S.; Posa, D. Predicting spatiotemporal random fields: Some computational aspects. Comput. Geosci. 2012, 41, 12–24. [Google Scholar] [CrossRef]
- Montero, J.M.; Fernández-Avilés, G.; Mateu, J. Spatial and spatiotemporal Geostatistical Modeling and Kriging; John Wiley & Sons: Hoboken, NJ, USA, 2015; Volume 998. [Google Scholar]
- Weenink, P.L. Local spatiotemporal Regression Kriging for Property Price Predictions. Ph.D. Thesis, University Ofgroningen, Groningen, The Netherlands, 2022. [Google Scholar]
- Kyriakidis, P.C.; Journel, A.G. Geostatistical space–time models: A review. Math. Geol. 1999, 31, 651–684. [Google Scholar] [CrossRef]
- Rivoirard, J. Which models for collocated cokriging? Math. Geol. 2001, 33, 117–131. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, J.; Christakos, G. Prediction of soil heavy metal distribution using Spatiotemporal Kriging with trend model. Ecol. Indic. 2015, 56, 125–133. [Google Scholar] [CrossRef]
- Derakhshan, H.; Leuangthong, O. A Review of Separable Spatiotemporal Models of Regionalization; University of Alberta: Edmonton, AB, Canada, 2006. [Google Scholar]
- Wikle, C.K.; Zammit-Mangion, A.; Cressie, N. Spatiotemporal Statistics with R; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Rouhani, S.; Hall, T.J. Space-time kriging of groundwater data. In Proceedings of the Geostatistics: Proceedings of the Third International Geostatistics Congress, Avignon, France, 5–9 September 1988; Springer: Berlin/Heidelberg, Germany, 1989; pp. 639–650. [Google Scholar]
- Gräler, B.; Pebesma, E.J.; Heuvelink, G.B. spatiotemporal interpolation using gstat. R J. 2016, 8, 204. [Google Scholar] [CrossRef]
- De Cesare, L.; Myers, D.; Posa, D. Product-sum covariance for space-time modeling: An environmental application. Environ. Off. J. Int. Environ. Soc. 2001, 12, 11–23. [Google Scholar] [CrossRef]
- Cressie, N.; Wikle, C.K. Statistics for Spatiotemporal Data; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Cressie, N. Fitting variogram models by weighted least squares. J. Int. Assoc. Math. Geol. 1985, 17, 563–586. [Google Scholar] [CrossRef]
- Byrd, R.H.; Hribar, M.E.; Nocedal, J. An interior point algorithm for large-scale nonlinear programming. SIAM J. Optim. 1999, 9, 877–900. [Google Scholar] [CrossRef]
- Sideris, I.V.; Gabella, M.; Erdin, R.; Germann, U. Real-time radar–rain-gauge merging using spatiotemporal co-kriging with external drift in the alpine terrain of Switzerland. Q. J. R. Meteorol. Soc. 2014, 140, 1097–1111. [Google Scholar] [CrossRef]
- Wackernagel, H. Multivariate Geostatistics: An Introduction with Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Clasen, R.J. Numerical Methods for Inverting Positive Definite Matrices; RAND Corporation: Santa Monica, CA, USA, 1966. [Google Scholar]
- Xu, X.; Luo, X.; Ma, C.; Xiao, D. Spatial-temporal analysis of pedestrian injury severity with geographically and temporally weighted regression model in Hong Kong. Transp. Res. Part F Traffic Psychol. Behav. 2020, 69, 286–300. [Google Scholar] [CrossRef]
- Wu, S.; Wang, Z.; Du, Z.; Huang, B.; Zhang, F.; Liu, R. Geographically and temporally neural network weighted regression for modeling spatiotemporal non-stationary relationships. Int. J. Geogr. Inf. Sci. 2021, 35, 582–608. [Google Scholar] [CrossRef]
- Huang, B.; Wu, B.; Barry, M. Geographically and temporally weighted regression for modeling spatiotemporal variation in house prices. Int. J. Geogr. Inf. Sci. 2010, 24, 383–401. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Crespo, R.; Yao, J. Geographical and temporal weighted regression (GTWR). Geogr. Anal. 2015, 47, 431–452. [Google Scholar] [CrossRef]
- Chariyaphan, R. Thailand’s Country Profile 2012; Department of Disaster Prevention and Mitigation, Ministry of Interior: Bangkok, Thailand, 2012. [Google Scholar]
- Laonamsai, J.; Ichiyanagi, K.; Kamdee, K. Geographic effects on stable isotopic composition of precipitation across Thailand. Isot. Environ. Health Stud. 2020, 56, 111–121. [Google Scholar] [CrossRef]
- OpenData. Available online: https://data.hii.or.th (accessed on 14 October 2020).
- von Hippel, P.; Lynch, J. Efficiency gains from using auxiliary variables in imputation. arXiv 2013, arXiv:1311.5249. [Google Scholar]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Senthilnathan, S. Usefulness of Correlation Analysis. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3416918 (accessed on 24 August 2020).
- Du, K.L.; Swamy, M.N. Neural Networks and Statistical Learning; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Hodson, T.O. Root-mean-square error (RMSE) or mean absolute error (MAE): When to use them or not. Geosci. Model Dev. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Alsafadi, K.; Mohammed, S.; Mokhtar, A.; Sharaf, M.; He, H. Fine-resolution precipitation mapping over Syria using local regression and spatial interpolation. Atmos. Res. 2021, 256, 105524. [Google Scholar] [CrossRef]
- Craven, B.; Islam, S.M. Ordinary Least-Squares Regression. In The SAGE Dictionary of Quantitative Management Research; SAGE Publications Ltd.: Thousand Oaks, CA, USA, 2011; pp. 224–228. [Google Scholar]
- Bai, Y.; Wu, L.; Qin, K.; Zhang, Y.; Shen, Y.; Zhou, Y. A geographically and temporally weighted regression model for ground-level PM2. 5 estimation from satellite-derived 500 m resolution AOD. Remote Sens. 2016, 8, 262. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, M.; Huang, B.; Wu, C.; Shi, W. Modeling the spatiotemporal association between COVID-19 transmission and population mobility using geographically and temporally weighted regression. GeoHealth 2021, 5, e2021GH000402. [Google Scholar] [CrossRef] [PubMed]
- Chokngamwong, R.; Chiu, L.S. Thailand daily rainfall and comparison with TRMM products. J. Hydrometeorol. 2008, 9, 256–266. [Google Scholar] [CrossRef]
- Wongkoon, S.; Jaroensutasinee, M.; Jaroensutasinee, K. Distribution, seasonal variation & dengue transmission prediction in Sisaket, Thailand. Indian J. Med Res. 2013, 138, 347. [Google Scholar]
- Parlett, B.N. A new look at the Lanczos algorithm for solving symmetric systems of linear equations. Linear Algebra Its Appl. 1980, 29, 323–346. [Google Scholar] [CrossRef]
- Marcia, R.F. On solving sparse symmetric linear systems whose definiteness is unknown. Appl. Numer. Math. 2008, 58, 449–458. [Google Scholar] [CrossRef]
- Mele, G.; Ringh, E.; Ek, D.; Izzo, F.; Upadhyaya, P.; Jarlebring, E. Preconditioning for Linear Systems; KD Publishing: Seattle, WA, USA, 2020. [Google Scholar]
- Bertsekas, D.P. Constrained Optimization and Lagrange Multiplier Methods; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
| Variable | Temperature | Air Pressure |
|---|---|---|
| Temperature | 1.0000 | 0.5775 |
| Air Pressure | 0.5775 | 1.0000 |
| Relative Humidity | −0.2264 | 0.2204 |
| DEM | −0.4284 | −0.7577 |
| Target Variable | Auxiliary Variable | Error | FST-RK | FST-DK |
|---|---|---|---|---|
| Temperature | Air Pressure | RMSE MAPE | 0.8717 2.4435 | 0.8948 2.4940 |
| Air Pressure | Temperature, DEM | RMSE MAPE | 13.6485 0.7581 | 11.5184 0.7242 |
| Variable | Temperature | Air Pressure |
|---|---|---|
| Temperature | 1.0000 | 0.8021 |
| Air Pressure | 0.8021 | 1.0000 |
| Relative Humidity | −0.0710 | 0.3432 |
| DEM | −0.5907 | −0.7608 |
| Target Variable | Auxiliary Variable | Error | AST-RK | AST-DK | GTWR |
|---|---|---|---|---|---|
| Temperature | Air Pressure | RMSE MAPE | 0.8660 2.4302 | 0.8542 2.4099 | 1.4278 4.3972 |
| Temperature | Air Pressure, DEM | RMSE MAPE | 0.8955 2.4803 | 0.8336 2.3488 | 1.4211 4.3585 |
| Air Pressure | Temperature, DEM | RMSE MAPE | 11.9122 0.7121 | 10.5835 0.6799 | 12.2437 0.8044 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kongsanun, C.; Chutsagulprom, N.; Moonchai, S. Spatio-Temporal Dual Kriging with Adaptive Coefficient Drift Function. Mathematics 2024, 12, 400. https://doi.org/10.3390/math12030400
Kongsanun C, Chutsagulprom N, Moonchai S. Spatio-Temporal Dual Kriging with Adaptive Coefficient Drift Function. Mathematics. 2024; 12(3):400. https://doi.org/10.3390/math12030400
Chicago/Turabian StyleKongsanun, Chalida, Nawinda Chutsagulprom, and Sompop Moonchai. 2024. "Spatio-Temporal Dual Kriging with Adaptive Coefficient Drift Function" Mathematics 12, no. 3: 400. https://doi.org/10.3390/math12030400
APA StyleKongsanun, C., Chutsagulprom, N., & Moonchai, S. (2024). Spatio-Temporal Dual Kriging with Adaptive Coefficient Drift Function. Mathematics, 12(3), 400. https://doi.org/10.3390/math12030400






