An Efficient Quadrature Rule for Highly Oscillatory Integrals with Airy Function

Abstract

In this work, our primary focus is on the numerical computation of highly oscillatory integrals involving the Airy function. Specifically, we address integrals of the form ${\int }_0^b{x}^{\alpha }f\left(x\right)\mathrm{Ai}(-\omega x)dx$ over a finite or semi-infinite interval, where the integrand exhibits rapid oscillations when $\omega \gg 1$. The inherent high oscillation and algebraic singularity of the integrand make traditional quadrature rules impractical. In view of this, we strategically partition the interval into two segments: $[0,1]$ and $[1,b]$. For integrals over the interval $[0,1]$, we introduce a Filon-type method based on a two-point Taylor expansion. In contrast, for integrals over $[1,b]$, we transform the Airy function into the first kind of Bessel function. By applying Cauchy’s integration theorem, the integral is then reformulated into several non-oscillatory and exponentially decaying integrals over $[0,+\infty )$, which can be accurately approximated by the generalized Gaussian quadrature rule. The proposed methods are accompanied by rigorous error analyses to establish their reliability. Finally, we present a series of numerical examples that not only validate the theoretical results but also showcase the accuracy and efficacy of the proposed method.

1. Introduction

The numerical computation of highly oscillatory integrals arises in various scientific disciplines, ranging from physics to engineering and beyond [1,2,3,4,5,6]. Oscillatory integrals are characterized by rapidly oscillating integrands, and their accurate computation poses a formidable challenge due to the potential for high-frequency oscillations and significant cancellations. This challenge is particularly pronounced in integrals involving Airy functions, which are essential mathematical functions frequently encountered in the study of wave phenomena, quantum mechanics, and the analysis of asymptotic behavior [1,7,8,9,10].

The Airy function $\mathrm{Ai}(-\omega x)$, one of the solutions to the differential equation $y^{″}+{\omega }^{3}xy=0$, plays a significant role in applied mathematics and has been extensively studied for its oscillatory behavior when $\omega \gg 1$ and $x\ge 0$ (see, for instance, [11,12,13,14]). Figure 1 illustrates the rapid oscillation of $\mathrm{Ai}(-\omega x)$, with the oscillations becoming more pronounced as $\omega$ increases. As $x\to +\infty$, the following asymptotic formula is valid [13] [Equation (9.7.9)]:

$$\mathrm{Ai}(-x)\sim \frac{x^{-1/4}}{\sqrt{\pi }}\left(cos(\zeta -\pi /4)\sum _{k=0}^{\infty }{(-1)}^k\frac{u_{2k}}{{\zeta }^{2k}}+sin(\zeta -\pi /4)\sum _{k=0}^{\infty }{(-1)}^k\frac{u_{2k+1}}{{\zeta }^{2k+1}}\right),$$

(1)

where $\zeta =\frac{2}{3}{x}^{3/2}$, $u_0=1$ and

$$u_k=\frac{(2k+1)(2k+3)\cdots (6k-1)}{{\left(216\right)}^{k}k!},k=1,2,\dots .$$

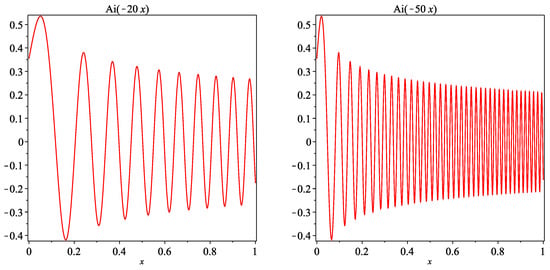
Figure 1. Plot of the Airy function $\mathrm{Ai}(-\omega x)$ for $\omega =20$ (left) and $\omega =50$ (right).

The numerical computation of integrals involving Airy functions is a difficult task, primarily due to their potential rapid oscillations over the interval. Standard numerical methods, such as Newton–Cotes and Gaussian quadrature rules, often struggle to handle the rapid oscillations in such integrals, necessitating the development of advanced techniques to ensure computational reliability.

This study aims to investigate numerical techniques for efficiently and accurately computing highly oscillatory integrals of the form

$$I\left[f\right]={\int }_0^b{x}^{\alpha }f\left(x\right)\mathrm{Ai}(-\omega x)dx,0<b\le +\infty ,$$

(2)

where $\alpha >-1$, and f is assumed to be smooth on $[0,b]$ and analytic in the complex plane $\left\{z\right|1\le \Re \left(z\right)\le b\}$. In particular, for the case $b=+\infty$, it is established from (1) that ensuring the existence of (2) requires the presence of constants $\sigma <-\alpha -3/4$ and C such that $f\left(x\right)\le C{x}^{\sigma }$ as $x\to +\infty$. In the past few years, many works have been devoted to the numerical treatment of the integrals in (2). The Levin-type method, developed by Levin [15] and later improved by Olver [12], transforms the solving of highly oscillatory integrals into an ordinary differential equation. Xiang and Wang (2010) introduced the Filon-type method for a more generalized integral ${\int }_0^{1}f\left(x\right)\mathrm{Ai}(-\omega g\left(x\right))dx$ with $g\left(x\right)>0$, employing a diffeomorphism transformation on the phase function $g\left(x\right)$ [16]. Xu and Xiang (2014) developed the Clenshaw-Curtis-Filon method specifically for the computation of (2) with $b=1$. Asymptotic expansions of ${\int }_0^{b}f\left(x\right)\mathrm{Ai}(-\omega x)dx$ with $b<+\infty$ have been explored by Olver (2007) and Kang (2018, 2020) [11,17,18]. All these methods share a remarkable advantage in that their accuracy improves rapidly as the frequency $\omega$ increases. However, each approach has limitations with effectiveness depending on the specific characteristics of the integral under consideration.

However, these existing numerical methods face limitations when directly applied to the integral (2), primarily due to the singularity at $x=0$ and the unbounded nature of the interval when $b=+\infty$. In order to avoid this defect, we divide the interval into two distinct segments and rewrite (2) as

$$I\left[f\right]={\int }_0^a{x}^{\alpha }f\left(x\right)\mathrm{Ai}(-\omega x)dx+{\int }_a^b{x}^{\alpha }f\left(x\right)\mathrm{Ai}(-\omega x)dx=:I_1\left[f\right]+I_2\left[f\right].$$

(3)

Without loss of generality, we assume $b>1$ and set $a=1$ in this paper. For $b\le 1$, the interval $[0,b]$ of (2) can be transformed to $[0,1]$ under a linear transformation. Then, the Filon-type method introduced in Section 2 will be applied to approximate (2). The algebraic singularity at $x=0$ is exclusively present in $I_1\left[f\right]$ and will be treated by the Filon-type method. For the evaluation of $I_2\left[f\right]$, a complex integration method is introduced by applying Cauchy’s integration theorem.

This work is organized as follows: In Section 2, we introduce the Filon-type method for computing $I_1\left[f\right]$ based on a two-point Taylor formula. Section 3 presents the complex integration method for approximating $I_2\left[f\right]$, where the highly oscillatory integrals are transformed into several non-oscillatory and exponentially decaying integrands on $[0,\infty )$. The application of a Gauss-Laguerre quadrature rule and its error estimates are discussed. Section 4 provides numerical examples to demonstrate the effectiveness of the proposed methods. Finally, we conclude this paper in Section 5.

2. The Filon-Type Method for ${\mathit{I}}_{\mathbf{1}}\left[\mathit{f}\right]$

The Filon method [19], named after the French mathematician L.N.G. Filon, stands out as an effective numerical technique designed specifically for a distinct class of highly oscillatory integrals ${\int }_a^{b}f\left(x\right){\mathrm{e}}^{\mathrm{i}\omega x}dx$. In this method, the non-oscillatory component $f\left(x\right)$ is approximated by a piecewise polynomial. This fundamental concept underwent further refinement by Iserles and Nørsett [5], who made a significant advancement by recognizing that the asymptotic expansion of ${\int }_a^{b}f\left(x\right){\mathrm{e}}^{\mathrm{i}\omega x}dx$ solely depends on the values and derivatives of $f\left(x\right)$ evaluated at the endpoints. Recently, this strategic approach has been extended to a broader spectrum of highly oscillatory integrals, including those with Bessel-type kernels [16,20].

In this section, the Filon-type method will be extended to the highly oscillatory integrals $I_1\left[f\right]$ with the Airy kernel. Let $m\ge 1$ be a positive integer. In order to obtain a higher asymptotic order, we seek a Hermite’s interpolation polynomial $P_{2m-1}\left(x\right)$ of $f\left(x\right)$ that satisfies

$$\begin{array}{cc}\hfill & P_{2m-1}\left(0\right)=f\left(0\right),P_{2m-1}^{\prime }\left(0\right)=f^{\prime }\left(0\right),\cdots ,P_{2m-1}^{(m-1)}\left(0\right)=f^{(m-1)}\left(0\right);\hfill \\ \hfill & P_{2m-1}\left(1\right)=f\left(1\right),P_{2m-1}^{\prime }\left(1\right)=f^{\prime }\left(1\right),\cdots ,P_{2m-1}^{(m-1)}\left(1\right)=f^{(m-1)}\left(1\right).\hfill \end{array}$$

(4)

Suppose that $f\left(x\right)$ is $(m-1)$-times differentiable on $[0,1]$, the unique polynomial of degree $2m-1$ that satisfies the condition (4) is the two-point Taylor formula, represented as

$$P_{2m-1}\left(x\right)=\sum _{k=0}^{m-1}{c}_k{x}^{k+1}{(x-1)}^k+\sum _{k=0}^{m-1}{d}_k{(x-1)}^{k+1}{x}^k,$$

(5)

where the coefficients are given by [21]

$$c_k=\left\{\begin{array}{ccc}f\left(1\right),\hfill & \hfill & k=0,\hfill \\ \sum _{j=0}^k\frac{(k+j-1)!}{j!(k-j)!}\frac{{(-1)}^{j}k{f}^{(k-j)}\left(1\right)-{(-1)}^{k}j{f}^{(k-j)}\left(0\right)}{k!},\hfill & \hfill & k\ge 1,\hfill \end{array}\right.$$

(6)

and

$$d_k=\left\{\begin{array}{ccc}-f\left(0\right),\hfill & \hfill & k=0,\hfill \\ \sum _{j=0}^k\frac{(k+j-1)!}{j!(k-j)!}\frac{{(-1)}^{j}j{f}^{(k-j)}\left(1\right)-{(-1)}^{k}k{f}^{(k-j)}\left(0\right)}{k!},\hfill & \hfill & k\ge 1.\hfill \end{array}\right.$$

(7)

As an approximation to $f\left(x\right)$, the two-point Taylor polynomial converges to $f\left(x\right)$ at the rate $o\left(x^m\right)$ as $x\to 0$, and at the rate $o\left({(x-1)}^m\right)$ as $x\to 1$. Here, $o\left(x^m\right)$ is defined in the sense that ${lim}_{x\to 0}\frac{f\left(x\right)-P_{2m-1}\left(x\right)}{x^m}=0$.

By substituting $P_{2m-1}\left(x\right)$ into $I_1\left[f\right]$, we obtain an approximation of $I_1\left[f\right]$ given by

$$I_1\left[f\right]\approx Q_m\left[I_1\right]:=\sum _{k=0}^{m-1}{c}_k{M}_k(k+1+\alpha ,\omega )+\sum _{k=0}^{m-1}{d}_k{M}_{k+1}(k+\alpha ,\omega ),$$

(8)

where $M_k(\rho ,\omega )$ are the moments defined by

$$M_k(\rho ,\omega )={\int }_0^1{x}^{\rho }{(x-1)}^k\mathrm{Ai}(-\omega x)dx.$$

(9)

An explicit formula for the moments is given by Xu [14] using the Meijer G-function.

Lemma 1 

([14]). When $\rho >-1$, the moments defined in (9) satisfy

$$\begin{array}{cc}\hfill M_k(\rho ,\omega )=\frac{{(-1)}^k\pi k!}{3^{k+2}}[& \sqrt[3]{3}{G}_{4,6}^{1,3}\left(\begin{array}{c}\frac{-\rho }{3},\frac{1-\rho }{3},\frac{2-\rho }{3},\frac{1}{2}\\ 0,\frac{1}{3},\frac{1}{2},\frac{-\rho -k-1}{3},\frac{-\rho -k}{3},\frac{-\rho -k+1}{3}\end{array}|-\frac{{\omega }^3}{9}\right)\hfill \\ \hfill & +\frac{\omega }{\sqrt[3]{3}}{G}_{4,6}^{1,3}\left(\begin{array}{c}\frac{-\rho -1}{3},\frac{-\rho }{3},\frac{1-\rho }{3},\frac{1}{2}\\ 0,-\frac{1}{3},\frac{1}{2},\frac{-\rho -k-2}{3},\frac{-\rho -k-1}{3},\frac{-\rho -k}{3}\end{array}|-\frac{{\omega }^3}{9}\right)],\hfill \end{array}$$

(10)

where the Meijer G-function involved is defined as (cf. [13])

$$\begin{array}{cc}\hfill & G_{p,q}^{m,n}\left(\genfrac{}{}{0pt}{}{a_1,\dots ,a_n,a_{n+1},\dots ,a_p}{b_1,\dots ,b_m,b_{m+1},\dots ,b_q}|z\right)\hfill \\ \hfill & =\frac{1}{2\pi \mathrm{i}}{\int }_L\frac{{\prod }_{k=1}^m\Gamma (b_k-s){\prod }_{j=1}^n\Gamma (1-a_j+s)}{{\prod }_{k=m+1}^q\Gamma (1-b_k+s){\prod }_{j=n+1}^p\Gamma (a_j-s)}{z}^{s}ds.\hfill \end{array}$$

(11)

Remark 1. 

The contour integration technique employed in (11) also offers an efficient and accurate implementation option for Meijer G-functions in software applications, including popular platforms like Matlab [22] and Mathematica.

Now, we turn our attention to the asymptotic properties of the errors in the Filon-type method. For simplicity, let $E_m\left(x\right):=f\left(x\right)-P_{2m-1}\left(x\right)$. It is evident that $E_m^{\left(k\right)}\left(0\right)=0$ and $E_m^{\left(k\right)}\left(1\right)=0$ for any $0\le k\le m-1$, defining

$${\sigma }_0\left(x\right)=x^{\alpha }{E}_m\left(x\right),{\sigma }_{k+1}={\left(\frac{{\sigma }_k\left(x\right)}{x}\right)}^{″},k\ge 0,$$

(12)

the asymptotic property of $I_1\left[f\right]-Q_m\left[I_1\right]$ is provided as follows.

Theorem 1. 

Let $\alpha >-1$ be real but not an integer. As $\omega \to \infty$, the Filon-type quadrature defined in (8) satisfies

$$I_1\left[f\right]-Q_m\left[I_1\right]=\mathcal{O}\left({\omega }^{-m-\alpha -1}\right).$$

(13)

Proof. 

Recalling Airy’s equation,

$$\frac{d^2}{d{x}^2}\mathrm{Ai}\left(x\right)-x\mathrm{Ai}\left(x\right)=0,$$

(14)

we have

$$\begin{array}{cc}\hfill I_1\left[f\right]-Q_m\left[I_1\right]=& {\int }_0^1{\sigma }_0\left(x\right)\mathrm{Ai}(-\omega x)dx\hfill \\ \hfill =& \frac{1}{{\omega }^3}{\int }_0^1\frac{{\sigma }_0\left(x\right)}{x}{\left(\mathrm{Ai}(-\omega x)\right)}^{″}dx\hfill \\ \hfill =& \frac{1}{{\omega }^3}\left[\frac{{\sigma }_0\left(x\right)}{x}{\left(\mathrm{Ai}(-\omega x)\right)}^{\prime }{|}_{x=0}^1-{\int }_0^1{\left(\frac{{\sigma }_0\left(x\right)}{x}\right)}^{\prime }{\left(\mathrm{Ai}(-\omega x)\right)}^{\prime }dx\right]\hfill \\ \hfill =& \frac{1}{{\omega }^3}{\left[\frac{{\sigma }_0\left(x\right)}{x}{\left(\mathrm{Ai}(-\omega x)\right)}^{\prime }-{\left(\frac{{\sigma }_0\left(x\right)}{x}\right)}^{\prime }\mathrm{Ai}(-\omega x)\right]}_{x=0}^1\hfill \\ \hfill & +\frac{1}{{\omega }^3}{\int }_0^1{\sigma }_1\left(x\right)\mathrm{Ai}(-\omega x)dx.\hfill \end{array}$$

(15)

Let $\kappa$ be the largest integer such that $\kappa <min\{\frac{m+\alpha }{3},\frac{m}{2}\}$. After an implementation of $\kappa$-times of integration (by parts), we obtain

$$\begin{array}{cc}\hfill I_1\left[f\right]-Q_m\left[I_1\right]=& \sum _{j=0}^{\kappa -1}\frac{1}{{\omega }^{3(j+1)}}{\left[\frac{{\sigma }_j}{x}{\left(\mathrm{Ai}(-\omega x)\right)}^{\prime }-{\left(\frac{{\sigma }_j}{x}\right)}^{\prime }\mathrm{Ai}(-\omega x)\right]}_{x=0}^1\hfill \\ \hfill & +\frac{1}{{\omega }^{3\kappa }}{\int }_0^1{\sigma }_{\kappa }\left(x\right)\mathrm{Ai}(-\omega x)dx.\hfill \end{array}$$

(16)

From $E_m^{\left(j\right)}\left(0\right)=E_m^{\left(j\right)}\left(1\right)=0$ for $j=0,1,\dots ,m-1$, we know that there exist functions $h_j\left(x\right)$ such that

$${\sigma }_j=x^{m+\alpha -3j}{(x-1)}^{m-2j}{h}_j\left(x\right),j=0,1,\cdots ,\kappa$$

(17)

where $h_j\left(x\right)$ is smooth with $h_j\left(0\right)\ne 0$ and $h_j\left(1\right)\ne 0$. Thus, the summation in the right-hand side of (16) vanishes. By substituting (17) into (16), we get

$$I_1\left[f\right]-Q_m\left[I_1\right]=\frac{1}{{\omega }^{3\kappa }}{\int }_0^1{x}^{m+\alpha -3\kappa }{(x-1)}^{m-2\kappa }{h}_{\kappa }\left(x\right)\mathrm{Ai}(-\omega x)dx.$$

(18)

In the following, we consider the asymptotic property of the integral in (18). By denoting

$${\Psi }_{\omega }\left(x\right)={\int }_0^x{t}^{m+\alpha -3\kappa }\mathrm{Ai}(-\omega t)dt,$$

(19)

we know from [14] (Theorem 3.1) that ${\Psi }_{\omega }\left(x\right)=\mathcal{O}\left({\omega }^{3\kappa -m-\alpha -1}\right)$ holds uniformly for all $x\in [0,1]$. As a result, it follows that

$$\begin{array}{cc}\hfill & I_1\left[f\right]-Q_m\left[I_1\right]\hfill \\ \hfill & =\frac{1}{{\omega }^{3\kappa }}{\int }_0^1{(x-1)}^{m-2\kappa }{h}_{\kappa }\left(x\right)d{\Psi }_{\omega }\left(x\right)\hfill \\ \hfill & =\frac{1}{{\omega }^{3\kappa }}{(x-1)}^{m-2\kappa }{h}_{\kappa }\left(x\right){\Psi }_{\omega }\left(x\right){|}_{x=0}^1-\frac{1}{{\omega }^{3\kappa }}{\int }_0^1{\Psi }_{\omega }\left(x\right)d\left\{{(x-1)}^{m-2\kappa }{h}_{\kappa }\left(x\right)\right\}\hfill \\ \hfill & =\mathcal{O}\left({\omega }^{-m-\alpha -1}\right).\hfill \end{array}$$

(20)

This completes the proof. □

In Figure 2, we demonstrate the asymptotic order of the error of the Filon-type method for $I_1\left[f\right]$, where $f\left(x\right)={\mathrm{e}}^{-1/x^2}\in C^{\infty }[0,1]$ is an infinitely differentiable function on $[0,1]$. The absolute errors of $Q_m\left[I_1\right]$ for various values of $\omega$ are displayed. It is evident that the accuracy of $Q_m\left[I_1\right]$ improves as $\omega$ increases and the decay rate is $\mathcal{O}\left({\omega }^{-m-\alpha -1}\right)$, which confirms the conclusion in Theorem 1.

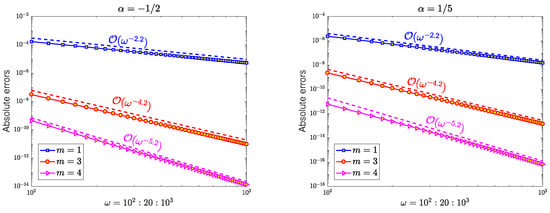
Figure 2. The absolute errors of $Q_m\left[I_1\right]$ with $f\left(x\right)={\mathrm{e}}^{-1/x^2}$ and varying $\omega ={10}^2:20:{10}^3$. The dashed lines depict the decay rates according to $\mathcal{O}\left({\omega }^{-m-\alpha -1}\right)$.

3. Complex Integration Method for ${\mathit{I}}_{\mathbf{2}}\left[\mathit{f}\right]$

This section is dedicated to the numerical computation of $I_2\left[f\right]$ defined in (3), where the function f is assumed to be analytic in the complex plane $\left\{z\right|1\le \Re \left(z\right)\le b\}$. The complex integration method will be applied to transform $I_2\left[f\right]$ into some non-oscillatory and exponentially decaying integrals.

By utilizing the identity derived from [13] [Equation (9.6.6)],

$$\mathrm{Ai}(-x)=\frac{\sqrt{x}}{3}\left[J_{1/3}\left(\frac{2}{3}{x}^{3/2}\right)+J_{-1/3}\left(\frac{2}{3}{x}^{3/2}\right)\right],$$

(21)

where $J_{\nu }\left(x\right)$ denotes the first kind of Bessel function of order $\nu$; we substitute (21) into $I_2\left[f\right]$, denoting $r=\frac{2}{3}{\omega }^{3/2}$ to obtain

$$\begin{array}{cc}\hfill I_2\left[f\right]=& \frac{1}{3}{\left(\frac{3}{2}r\right)}^{1/3}{\int }_1^b{x}^{\alpha +1/2}f\left(x\right)\left[J_{1/3}\left(r{x}^{3/2}\right)+J_{-1/3}\left(r{x}^{3/2}\right)\right]dx\hfill \\ \hfill =& \frac{2}{9}{\left(\frac{3}{2}r\right)}^{1/3}{\int }_1^{b^{3/2}}{x}^{2\alpha /3}f\left(x^{2/3}\right)\left[J_{1/3}\left(rx\right)+J_{-1/3}\left(rx\right)\right]dx.\hfill \end{array}$$

(22)

By recalling the integral representation of Bessel function, as given in [23] [Equation (8.411.10)], namely

$$J_{\nu }\left(x\right)=\frac{x^{\nu }}{2^{\nu }\sqrt{\pi }\Gamma (1/2+\nu )}{\int }_{-1}^1{(1-u^2)}^{\nu -1/2}{\mathrm{e}}^{\mathrm{i}xu}du,\Re \left(\nu \right)>-1/2,$$

(23)

where $\mathrm{i}=\sqrt{-1}$ is the imaginary unit, we apply Cauchy’s integral theorem [24] along with contributions from Chen [25] and Zaman et al. [26]. This allows us to express $I_2\left[f\right]$ as

$$\begin{array}{cc}\hfill I_2\left[f\right]=& \frac{\sqrt[3]{6}\mathrm{i}}{9\sqrt{\pi }\Gamma (5/6)}\left[{\int }_1^{b^{3/2}}{\Phi }_{1/3}^{+}\left(x\right){\mathrm{e}}^{-\mathrm{i}rx}dx-{\int }_1^{b^{3/2}}{\Phi }_{1/3}^{-}\left(x\right){\mathrm{e}}^{\mathrm{i}rx}dx\right]\hfill \\ \hfill & +\frac{2\sqrt[3]{3}\mathrm{i}}{9\sqrt{\pi }\Gamma (1/6)}{r}^{2/3}\left[{\int }_1^{b^{3/2}}{\Phi }_{-1/3}^{+}\left(x\right){\mathrm{e}}^{-\mathrm{i}rx}dx-{\int }_1^{b^{3/2}}{\Phi }_{-1/3}^{-}\left(x\right){\mathrm{e}}^{\mathrm{i}rx}dx\right],\hfill \end{array}$$

(24)

where ${\Phi }_{\nu }^{\pm }\left(x\right)$ is defined as

$${\Phi }_{\nu }^{\pm }\left(x\right)=x^{2\alpha /3-\nu }f\left(x^{2/3}\right){\int }_0^{+\infty }{y}^{\nu -1/2}{(y\pm 2\mathrm{i}rx)}^{\nu -1/2}{e}^{-y}dy.$$

(25)

3.1. Complex Integration Formulas

It is noteworthy that the integrands ${\Phi }_{\nu }^{\pm }\left(x\right)$ defined in (25) are non-oscillatory and analytic in the complex plane $\left\{z\right|\Re \left(z\right)\ge 1\}$. This characteristic makes the evaluation of the highly oscillatory integrals in (24) a typical problem and can be efficiently solved by the complex integration method [27,28].

Theorem 2. 

Let $f\left(z\right)$ be an analytic function in the complex plane $\Re \left(z\right)\ge 1$, and assume there exist some constants C and ${\omega }_0\in (0,\omega )$ such that $\left|f\left(z\right)\right|\le C{e}^{{\omega }_0\Im \left(z\right)}$. Then, we establish

$$\begin{array}{cc}\hfill I_2\left[f\right]=& \frac{\sqrt[3]{6}}{9\sqrt{\pi }\Gamma (5/6)}[\frac{{\mathrm{e}}^{-\mathrm{i}r}}{r}{\int }_0^{+\infty }{\Phi }_{1/3}^{+}\left(1-\frac{\mathrm{i}u}{r}\right){\mathrm{e}}^{-u}du+\frac{{\mathrm{e}}^{\mathrm{i}r}}{r}{\int }_0^{+\infty }{\Phi }_{1/3}^{-}\left(1+\frac{\mathrm{i}u}{r}\right){\mathrm{e}}^{-u}du\hfill \\ \hfill & -\frac{{\mathrm{e}}^{-\mathrm{i}r{b}^{3/2}}}{r}{\int }_0^{+\infty }{\Phi }_{1/3}^{+}\left(b^{3/2}-\frac{\mathrm{i}u}{r}\right){\mathrm{e}}^{-u}du-\frac{{\mathrm{e}}^{\mathrm{i}r{b}^{3/2}}}{r}{\int }_0^{+\infty }{\Phi }_{1/3}^{-}\left(b^{3/2}+\frac{\mathrm{i}u}{r}\right){\mathrm{e}}^{-u}du]\hfill \\ \hfill & +\frac{2\sqrt[3]{3}{r}^{2/3}}{9\sqrt{\pi }\Gamma (1/6)}[\frac{e^{-\mathrm{i}r}}{r}{\int }_0^{+\infty }{\Phi }_{-1/3}^{+}\left(1-\frac{\mathrm{i}u}{r}\right){\mathrm{e}}^{-u}du+\frac{{\mathrm{e}}^{\mathrm{i}r}}{r}{\int }_0^{+\infty }{\Phi }_{-1/3}^{-}\left(1+\frac{\mathrm{i}u}{r}\right){\mathrm{e}}^{-u}du\hfill \\ \hfill & -\frac{e^{-\mathrm{i}r{b}^{3/2}}}{r}{\int }_0^{+\infty }{\Phi }_{-1/3}^{+}\left(b^{3/2}-\frac{\mathrm{i}u}{r}\right){\mathrm{e}}^{-u}du-\frac{{\mathrm{e}}^{\mathrm{i}r{b}^{3/2}}}{r}{\int }_0^{+\infty }{\Phi }_{-1/3}^{-}\left(b^{3/2}+\frac{\mathrm{i}u}{r}\right){\mathrm{e}}^{-u}du],\hfill \end{array}$$

(26)

where $r=\frac{2}{3}{\omega }^{3/2}$ and ${\Phi }_{\nu }^{\pm }(·)$ are defined in (25).

Proof. 

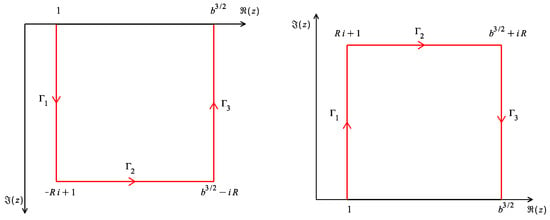
According to the assumption based on f, it is evident that ${\Phi }_{\nu }^{+}\left(z\right)$ is analytic in the complex region $\Re \left(z\right)\ge 1$. By using Cauchy’s integration theorem [24], we express the integral as

$${\int }_1^{b^{3/2}}{\Phi }_{\nu }^{+}\left(x\right){\mathrm{e}}^{-\mathrm{i}rx}dx={\int }_{{\Gamma }_1+{\Gamma }_2+{\Gamma }_3}{\Phi }_{\nu }^{+}\left(z\right){\mathrm{e}}^{-\mathrm{i}rz}dz,$$

(27)

where the integration paths ${\Gamma }_1$, ${\Gamma }_2$, and ${\Gamma }_3$ are shown in the left of Figure 3. In the following, we parameterize the integrals over these paths respectively.

Figure 3. The complex integration paths for the integrals in (24). The left one is for integrals with ${\Phi }_{\nu }^{+}\left(x\right)$, while the right one is for integrals with ${\Phi }_{\nu }^{-}\left(x\right)$.

For the path ${\Gamma }_1$, setting $z=1-\mathrm{i}u$ with $u\in [0,R]$ yields

$${\int }_{{\Gamma }_1}{\Phi }_{\nu }^{+}\left(z\right){\mathrm{e}}^{-\mathrm{i}rz}dz=-\mathrm{i}{\mathrm{e}}^{-\mathrm{i}r}{\int }_0^R{\Phi }_{\nu }^{+}(1-\mathrm{i}u){\mathrm{e}}^{-ru}du.$$

(28)

In the same way, for ${\Gamma }_3$, setting $z=b^{3/2}-\mathrm{i}u$ yields

$${\int }_{{\Gamma }_3}{\Phi }_{\nu }^{+}\left(z\right){\mathrm{e}}^{-\mathrm{i}rz}dz=\mathrm{i}{e}^{-\mathrm{i}r{b}^{3/2}}{\int }_0^R{\Phi }_{\nu }^{+}(b^{3/2}-\mathrm{i}u){\mathrm{e}}^{-ru}du.$$

(29)

For ${\Gamma }_2$, a change in the variable $z=u-\mathrm{i}R$ with $u\in [1,b^{3/2}]$ results in

$${\int }_{{\Gamma }_2}{\Phi }_{\nu }^{+}\left(z\right){\mathrm{e}}^{-\mathrm{i}rz}dz={\mathrm{e}}^{-rR}{\int }_1^{b^{3/2}}{\Phi }_{\nu }^{+}(u-\mathrm{i}R){\mathrm{e}}^{-\mathrm{i}ru}du.$$

(30)

Letting $R\to +\infty$, it is obvious that

$$\left|{\int }_{{\Gamma }_2}{\Phi }_{\nu }^{+}\left(z\right){\mathrm{e}}^{-\mathrm{i}rz}dz\right|\le {\mathrm{e}}^{-rR}{\int }_1^{b^{3/2}}\left|{\Phi }_{\nu }^{+}(u-\mathrm{i}ru)\right|du\to 0.$$

(31)

Combined with (27), (28), (31), and (29), we derive

$$\begin{array}{cc}\hfill {\int }_1^{b^{3/2}}{\Phi }_{\nu }^{+}\left(x\right){\mathrm{e}}^{-\mathrm{i}rx}dx=& -\frac{\mathrm{i}{\mathrm{e}}^{-\mathrm{i}r}}{r}{\int }_0^{+\infty }{\Phi }_{\nu }^{+}\left(1-\frac{\mathrm{i}u}{r}\right){\mathrm{e}}^{-u}du\hfill \\ \hfill & +\frac{\mathrm{i}{\mathrm{e}}^{-\mathrm{i}r{b}^{3/2}}}{r}{\int }_0^{+\infty }{\Phi }_{\nu }^{+}\left(b^{3/2}-\frac{\mathrm{i}u}{r}\right){\mathrm{e}}^{-u}du.\hfill \end{array}$$

(32)

After a similar argument and employing the integration paths depicted in the right of Figure 3, this leads to

$$\begin{array}{cc}\hfill {\int }_1^{b^{3/2}}{\Phi }_{\nu }^{-}\left(x\right){\mathrm{e}}^{\mathrm{i}rx}dx=& \frac{\mathrm{i}{\mathrm{e}}^{\mathrm{i}r}}{r}{\int }_0^{+\infty }{\Phi }_{\nu }^{-}\left(1+\frac{\mathrm{i}u}{r}\right){\mathrm{e}}^{-u}du\hfill \\ \hfill & +\frac{\mathrm{i}{\mathrm{e}}^{\mathrm{i}r{b}^{3/2}}}{r}{\int }_0^{+\infty }{\Phi }_{\nu }^{-}\left(b^{3/2}+\frac{\mathrm{i}u}{r}\right){\mathrm{e}}^{-u}du.\hfill \end{array}$$

(33)

This completes the proof by setting $\nu =1/3$ and $\nu =-1/3$, respectively. □

In particular, when $b=+\infty$, the complex integration method becomes particularly efficient by altering the integration paths of (24), as illustrated in Figure 4.

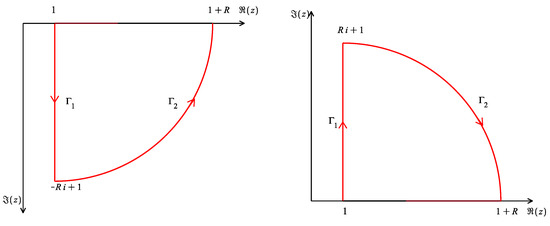
Figure 4. The complex integration paths for the integrals in (24) when $b=+\infty$. The left one is for integrals with ${\Phi }_{\nu }^{+}\left(x\right)$, while the right one is for integrals with ${\Phi }_{\nu }^{-}\left(x\right)$.

Theorem 3. 

Let $f\left(z\right)$ be an analytic function in the complex plane $\Re \left(z\right)\ge 1$, and assume that there exist some constants C and $\delta >0$ such that $\left|f\left(z\right)\right|\le {C\left|z\right|}^{-\delta }$ for all $\left|z\right|\ge 1$. For $b=+\infty$, we establish that

$$\begin{array}{cc}\hfill I_2\left[f\right]=& \frac{\sqrt[3]{6}}{9\sqrt{\pi }\Gamma (5/6)}\left[\frac{e^{-\mathrm{i}r}}{r}{\int }_0^{+\infty }{\Phi }_{1/3}^{+}\left(1-\frac{\mathrm{i}u}{r}\right)e^{-u}du+\frac{e^{\mathrm{i}r}}{r}{\int }_0^{+\infty }{\Phi }_{1/3}^{-}\left(1+\frac{\mathrm{i}u}{r}\right)e^{-u}du\right]\hfill \\ \hfill & +\frac{2\sqrt[3]{3}{r}^{2/3}}{9\sqrt{\pi }\Gamma (1/6)}\left[\frac{e^{-\mathrm{i}r}}{r}{\int }_0^{+\infty }{\Phi }_{-1/3}^{+}\left(1-\frac{\mathrm{i}u}{r}\right)e^{-u}du+\frac{e^{\mathrm{i}r}}{r}{\int }_0^{+\infty }{\Phi }_{-1/3}^{-}\left(1+\frac{\mathrm{i}u}{r}\right)e^{-u}du\right],\hfill \end{array}$$

(34)

where $r=\frac{2}{3}{\omega }^{3/2}$.

Proof. 

Applying Cauchy’s integral theorem [24], we have

$${\int }_1^{+\infty }{\Phi }_{\nu }^{+}\left(x\right){\mathrm{e}}^{-\mathrm{i}rx}dx={\int }_{{\Gamma }_1+{\Gamma }_2}{\Phi }_{\nu }^{+}\left(z\right){\mathrm{e}}^{-\mathrm{i}rz}dz,\mathrm{as}R\to +\infty ,$$

(35)

where ${\Gamma }_1$ and ${\Gamma }_2$ are complex paths shown in the left of Figure 4. We parameterize ${\Gamma }_1$ as $z=1-\mathrm{i}u,u\in [0,R]$, then

$${\int }_{{\Gamma }_1}{\Phi }_{\nu }^{+}\left(z\right){\mathrm{e}}^{-\mathrm{i}rz}dz={\mathrm{e}}^{-\mathrm{i}r}{\int }_0^R{\Phi }_{\nu }^{+}(1-\mathrm{i}u){\mathrm{e}}^{-ru}du.$$

(36)

For ${\Gamma }_2$, setting $z=1+R{\mathrm{e}}^{-\mathrm{i}\theta }$ with $\theta \in [0,\pi /2]$, we obatin

$${\int }_{{\Gamma }_2}{\Phi }_{\nu }^{+}\left(z\right){\mathrm{e}}^{-\mathrm{i}rz}dz=\mathrm{i}{\mathrm{e}}^{-\mathrm{i}r}R{\int }_0^{\pi /2}{\mathrm{e}}^{-\mathrm{i}(rRcos\theta +\theta )}{\mathrm{e}}^{-rRsin\theta }{\Phi }_{\nu }^{+}(1+R{\mathrm{e}}^{-\mathrm{i}\theta })d\theta .$$

(37)

As $R\to +\infty$, it follows that

$$\begin{array}{cc}\hfill \left|{\int }_{{\Gamma }_2}{\Phi }_{\nu }^{+}\left(z\right){\mathrm{e}}^{-\mathrm{i}rz}dz\right|\le & R{\int }_0^{\pi /2}{\mathrm{e}}^{-rRsin\theta }\left|{\Phi }_{\nu }^{+}(1+R{\mathrm{e}}^{-\mathrm{i}\theta })\right|d\theta \hfill \\ \hfill \le & C{R}^{1-\delta }{\int }_0^{\pi /2}{\mathrm{e}}^{-2rR\theta /\pi }d\theta \hfill \\ \hfill \le & C\pi R^{1-\delta }\frac{1-{\mathrm{e}}^{-rR}}{2rR}\to 0,\hfill \end{array}$$

(38)

where we used $sin\theta >2\theta /\pi$. As a result, we obtain that

$${\int }_1^{+\infty }{\Phi }_{\nu }^{+}{\mathrm{e}}^{-\mathrm{i}rx}dx={\mathrm{e}}^{-\mathrm{i}r}{\int }_0^{+\infty }{\Phi }_{\nu }^{+}(1-\mathrm{i}u){\mathrm{e}}^{-ru}du.$$

(39)

Similarly, by using the complex paths in the right of Figure 4, we get

$${\int }_0^{+\infty }{\Phi }_{\nu }^{-}\left(x\right){\mathrm{e}}^{\mathrm{i}rx}dx={\mathrm{e}}^{\mathrm{i}r}{\int }_0^{+\infty }{\Phi }_{\nu }^{-}(1+\mathrm{i}u){\mathrm{e}}^{-ru}du.$$

(40)

Substituting these into (24) leads to the desired result (34). □

3.2. Numerical Algorithms and Error Estimates

Apparently, the integrands in (26) are smooth and accompanied by the Laguerre weight function. This characteristic makes them amenable to be accurately approximated through the Gaussian quadrature rule. Consequently, employing the n-point Gauss-Laguerre quadrature rule provides a robust numerical method for evaluating $I_2\left[f\right]$:

$$\begin{array}{cc}\hfill Q_n\left[I_2\right]:=& \frac{\sqrt[3]{6}}{9\sqrt{\pi }\Gamma (5/6)}\sum _{k=1}^n{w}_k^{\left(0\right)}[\frac{{\mathrm{e}}^{-\mathrm{i}r}}{r}{\widehat{\Phi }}_{1/3}^{+}\left(1-\frac{\mathrm{i}}{r}{u}_k^{\left(0\right)}\right)+\frac{{\mathrm{e}}^{\mathrm{i}r}}{r}{\widehat{\Phi }}_{1/3}^{-}\left(1+\frac{\mathrm{i}}{r}{u}_k^{\left(0\right)}\right)\hfill \\ \hfill & -\frac{{\mathrm{e}}^{-\mathrm{i}r{b}^{3/2}}}{r}{\widehat{\Phi }}_{1/3}^{+}\left(b^{3/2}-\frac{\mathrm{i}}{r}{u}_k^{\left(0\right)}\right)-\frac{{\mathrm{e}}^{\mathrm{i}r{b}^{3/2}}}{r}{\widehat{\Phi }}_{1/3}^{-}\left(b^{3/2}+\frac{\mathrm{i}}{r}{u}_k^{\left(0\right)}\right)]\hfill \\ \hfill & +\frac{2\sqrt[3]{3}{r}^{2/3}}{9\sqrt{\pi }\Gamma (1/6)}\sum _{k=1}^n{w}_k^{\left(0\right)}[\frac{{\mathrm{e}}^{-\mathrm{i}r}}{r}{\widehat{\Phi }}_{-1/3}^{+}\left(1-\frac{\mathrm{i}}{r}{u}_k^{\left(0\right)}\right)+\frac{{\mathrm{e}}^{\mathrm{i}r}}{r}{\widehat{\Phi }}_{-1/3}^{-}\left(1+\frac{\mathrm{i}}{r}{u}_k^{\left(0\right)}\right)\hfill \\ \hfill & -\frac{{\mathrm{e}}^{-\mathrm{i}r{b}^{3/2}}}{r}{\widehat{\Phi }}_{-1/3}^{+}\left(b^{3/2}-\frac{\mathrm{i}}{r}{u}_k^{\left(0\right)}\right)-\frac{{\mathrm{e}}^{\mathrm{i}r{b}^{3/2}}}{r}{\widehat{\Phi }}_{-1/3}^{-}\left(b^{3/2}+\frac{\mathrm{i}}{r}{u}_k^{\left(0\right)}\right)],\hfill \end{array}$$

(41)

where ${\widehat{\Phi }}_{\nu }^{\pm }\left(x\right)$ is defined as a numerical approximation of ${\Phi }_{\nu }^{\pm }\left(x\right)$ by the Gaussian quadrature rule such that

$${\Phi }_{\nu }^{\pm }\left(x\right)\approx {\widehat{\Phi }}_{\nu }^{\pm }\left(x\right):=x^{2\alpha /3-\nu }f\left(x^{2/3}\right)\sum _{k=1}^n{w}_k^{(\nu -1/2)}{\left(u_k^{(\nu -1/2)}\pm 2\mathrm{i}rx\right)}^{\nu -1/2}.$$

(42)

Here, by using $\{u_k^{\left(\gamma \right)},w_k^{\left(\gamma \right)}\}$, we denote the quadrature nodes and weights of the generalized Laguerre quadrature rule corresponding to the weight function $u^{\gamma }{\mathrm{e}}^{-u}$ with $\gamma >-1$.

Remark 2. 

Algorithms for computing Gaussian quadrature nodes and weights have been extensively studied over the past several decades. The classic approach is the Golub-Welsch algorithm, which solves an eigenvalue problem and requires $\mathcal{O}\left(n^2\right)$ operations. However, when n is large, several fast algorithms have been presented by Glaser, Liu, and Rokhlin [29], as well as Hale and Trefethen [30]. These algorithms require only $\mathcal{O}\left(n\right)$ operations by leveraging the asymptotic properties of orthogonal polynomials.

Theorem 4. 

Suppose that $f\left(x\right)$ satisfies the condition in Theorem 2. Then, as $\omega \to +\infty$, the absolute errors of (41) satisfy that

$$|I_2\left[f\right]-Q_n\left[I_2\right]|=\mathcal{O}\left({\omega }^{-3n-7/4}\right).$$

(43)

Proof. 

As is known, the error of the n-point generalized Gaussian Laguerre quadrature rule to the integral [31]${\int }_0^{+\infty }{x}^{\gamma }{\mathrm{e}}^{-x}\phi \left(x\right)dx$ is

$$E_n\left[\phi \right]=\frac{n!\Gamma (n+\gamma +1)}{\left(2n\right)!}{\phi }^{\left(2n\right)}\left(\xi \right),\xi \in (0,+\infty ).$$

(44)

By substituting this into (26) and (41), it is not difficult to derive that

$$|I_2\left[f\right]-Q_n\left[I_2\right]|=\mathcal{O}\left(r^{-2n-1-1/6}\right)=\mathcal{O}\left({\omega }^{-3n-7/4}\right),$$

(45)

where we used $r=\frac{2}{3}{\omega }^{3/2}$. □

For the case $b=+\infty$, after applying the Gaussian quadrature rule to (34), we get the numerical algorithm for $I_2\left[f\right]$ such that

$$\begin{array}{cc}\hfill Q_n\left[I_2\right]:=& \frac{\sqrt[3]{6}}{9\sqrt{\pi }\Gamma (5/6)}\sum _{k=1}^n{w}_k^{\left(0\right)}\left[\frac{{\mathrm{e}}^{-\mathrm{i}r}}{r}{\widehat{\Phi }}_{1/3}^{+}\left(1-\frac{\mathrm{i}}{r}{u}_k^{\left(0\right)}\right)+\frac{{\mathrm{e}}^{\mathrm{i}r}}{r}{\widehat{\Phi }}_{1/3}^{-}\left(1+\frac{\mathrm{i}}{r}{u}_k^{\left(0\right)}\right)\right]\hfill \\ \hfill +& \frac{2\sqrt[3]{3}{r}^{2/3}}{9\sqrt{\pi }\Gamma (1/6)}\sum _{k=1}^n{w}_k^{\left(0\right)}\left[\frac{{\mathrm{e}}^{-\mathrm{i}r}}{r}{\widehat{\Phi }}_{-1/3}^{+}\left(1-\frac{\mathrm{i}}{r}{u}_k^{\left(0\right)}\right)+\frac{{\mathrm{e}}^{\mathrm{i}r}}{r}{\widehat{\Phi }}_{-1/3}^{-}\left(1+\frac{\mathrm{i}}{r}{u}_k^{\left(0\right)}\right)\right],\hfill \end{array}$$

(46)

where ${\Phi }_{\nu }^{\pm }\left(x\right)$ is defined in (42). As $\omega \to +\infty$, the error of the quadrature rule $Q_n\left[I_2\right]$ satisfies the estimate

$$|I_2\left[f\right]-Q_n\left[I_2\right]|=\mathcal{O}\left({\omega }^{-3n-7/4}\right).$$

(47)

In the following, we provide a numerical test of the error estimates of the complex integration method for $I_2\left[f\right]={\int }_1^b{x}^{\alpha }f\left(x\right)\mathrm{Ai}(-\omega x)dx$. We select $f\left(x\right)=1/(1+x^2)$ as the Runge function, which is analytic in the complex plane $\Re \left(z\right)\ge 1$ but has two poles at $z=\pm \mathrm{i}$. In Figure 5 and Figure 6, the absolute errors of $Q_n\left[I_2\right]$ for various values of $\omega$ are depicted in the left panel, while the absolute errors scaled by the factor ${\omega }^{3n+7/4}$ are presented in the right panel. It is evident that the accuracy of $Q_n\left[I_2\right]$ improves as $\omega$ increases, and the convergence rate is observed to be ${\omega }^{-3n-7/4}$. This observation aligns with the theoretical results stated in Theorem 4.

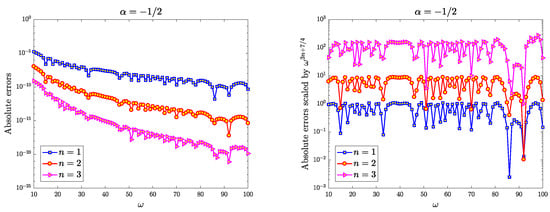
Figure 5. The absolute errors of $Q_n\left[I_2\right]$ (left) and the absolute errors scaled by ${\omega }^{3n+7/4}$ (right) for the integral $I_2\left[f\right]={\int }_1^2{x}^{\alpha }f\left(x\right)\mathrm{Ai}(-\omega x)dx$ with $f\left(x\right)=1/(1+x^2)$, where $\omega$ runs over $[10,100]$. The exact value of $I_2\left[f\right]$ is approximated by the software Mathematica 12.1 with high-precision arithmetic.

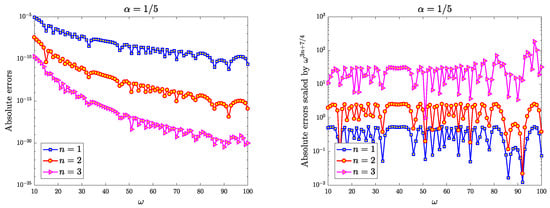
Figure 6. The absolute errors of $Q_n\left[I_2\right]$ (left) and the absolute errors scaled by ${\omega }^{3n+7/4}$ (right) for the integral $I_2\left[f\right]={\int }_1^{+\infty }{x}^{\alpha }f\left(x\right)\mathrm{Ai}(-\omega x)dx$ with $f\left(x\right)=1/(1+x^2)$, where $\omega$ runs over $[10,100]$. The exact value of $I_2\left[f\right]$ is approximated by the software Mathematica 12.1 with high-precision arithmetic.

4. Numerical Examples

This section is dedicated to presenting the efficiency and accuracy of the proposed method by several typical numerical examples. The exact values used were obtained from Mathematica 12.1 with high-precision arithmetic, whereas Matlab 2016 was used to compute the numerical results of the proposed method.

Example 1. 

We consider the highly oscillatory integral over a finite interval given by

$$I\left[f\right]={\int }_0^5{x}^{-1/2}sinx\mathrm{Ai}(-\omega x)dx.$$

(48)

After dividing the interval, we compute the integral over $[0,1]$ using the Filon-type method $Q_m\left[I_1\right]$ described in Section 2, and the integral over $[1,5]$ using the complex integration method $Q_n\left[I_2\right]$ described in Section 3. The exact values of $I\left[f\right]$ in the bottom row of Table 1 are computed by  Mathematica 12.1 with 16-digit precision. The absolute errors are displayed in Table 1, which shows the efficiency of the proposed method.

Table 1. Errors of the proposed numerical method for (48).

n ($=\mathit{m}$)	$\mathit{\omega }=1$	$\mathit{\omega }=10$	$\mathit{\omega }=20$	$\mathit{\omega }=40$	$\mathit{\omega }=80$	$\mathit{\omega }=160$
1	$3.2\times {10}^{-2}$	$2.3\times {10}^{-3}$	$8.2\times {10}^{-4}$	$2.9\times {10}^{-4}$	$1.0\times {10}^{-4}$	$3.6\times {10}^{-5}$
2	$5.9\times {10}^{-3}$	$5.7\times {10}^{-6}$	$5.4\times {10}^{-7}$	$4.9\times {10}^{-8}$	$4.3\times {10}^{-9}$	$3.8\times {10}^{-10}$
3	$1.5\times {10}^{-3}$	$6.4\times {10}^{-8}$	$9.3\times {10}^{-9}$	$9.8\times {10}^{-10}$	$9.4\times {10}^{-11}$	$8.6\times {10}^{-12}$
4	$3.1\times {10}^{-4}$	$3.9\times {10}^{-10}$	$2.3\times {10}^{-11}$	$1.1\times {10}^{-12}$	$4.9\times {10}^{-14}$	$2.2\times {10}^{-15}$
5	$1.3\times {10}^{-5}$	$2.9\times {10}^{-18}$	$1.1\times {10}^{-12}$	$1.8\times {10}^{-14}$	$2.6\times {10}^{-16}$	$1.2\times {10}^{-18}$
Exact values	0.5786450	0.0137262	0.0051914	0.0018297	0.0006740	0.0002367
(Mathematica)	00855307	61972158	39052109	30968546	91854124	76298767

Example 2. 

Now, let us consider the highly oscillatory integral over the semi-infinity interval

$$I\left[f\right]={\int }_0^{+\infty }{x}^{-1/2}\frac{1}{100+x^2}\mathrm{Ai}(-\omega x)dx.$$

(49)

Similarly, we compute the integral over $[0,1]$ by using the Filon-type method described in Section 2 and the integral over $[1,+\infty )$ by using the complex integration method described in Section 3. The absolute errors are displayed in Table 2. The bottom line of Table 2 gives the exact values of $I\left[f\right]$ obtained from the software  Mathematica  12.1 with 16-digit precision.

Table 2. Errors of the proposed numerical method for (49).

n ($=\mathit{m}$)	$\mathit{\omega }=1$	$\mathit{\omega }=10$	$\mathit{\omega }=20$	$\mathit{\omega }=40$	$\mathit{\omega }=80$	$\mathit{\omega }=160$
1	$4.3\times {10}^{-4}$	$1.6\times {10}^{-6}$	$5.2\times {10}^{-7}$	$1.8\times {10}^{-7}$	$6.4\times {10}^{-8}$	$2.2\times {10}^{-8}$
2	$4.0\times {10}^{-4}$	$5.5\times {10}^{-10}$	$3.6\times {10}^{-11}$	$3.9\times {10}^{-12}$	$2.5\times {10}^{-13}$	$2.8\times {10}^{-13}$
3	$1.9\times {10}^{-4}$	$6.1\times {10}^{-12}$	$1.2\times {10}^{-13}$	$1.4\times {10}^{-14}$	$1.7\times {10}^{-13}$	$5.9\times {10}^{-14}$
4	$6.0\times {10}^{-5}$	$2.2\times {10}^{-13}$	$1.9\times {10}^{-14}$	$2.1\times {10}^{-15}$	$2.7\times {10}^{-14}$	$5.8\times {10}^{-14}$
5	$4.3\times {10}^{-6}$	$2.8\times {10}^{-14}$	$1.9\times {10}^{-14}$	$2.1\times {10}^{-15}$	$2.7\times {10}^{-14}$	$5.8\times {10}^{-14}$
Exact values	0.0108855	0.0034428	0.0024344	0.0017214	0.0012172	0.0008607
(Mathematica)	10568092	84873791	87277255	42464043	43639445	21232015

From Table 1 and Table 2, it can be readily concluded that, for any fixed $\omega$, the accuracy of the proposed method improves significantly with an increase in n. The method requires only a small number of function evaluations to yield highly accurate approximations of $I\left[f\right]$. Furthermore, for a fixed value of n, the accuracy of the method improves with increasing values of $\omega$. The numerical examples presented in each section underscore the efficiency of our approach. For comparison, we provide the absolute errors of the proposed method for the non-oscillatory integrals ${\int }_0^b{x}^{\alpha }f\left(x\right)\mathrm{Ai}(-x)dx$ (see the second column of Table 1 and Table 2). The results illustrate the efficiency and accuracy of the proposed method.

5. Conclusions

In conclusion, this study addresses the numerical computation of highly oscillatory integrals involving the Airy function over both finite and semi-infinite intervals. The proposed method, which employs a partitioning strategy and complex integration techniques, demonstrates efficiency and accuracy in handling the challenges posed by the oscillatory nature of the integrands. This approach is easy to implement, and rigorous error analyses support its reliability. Numerical examples are provided to validate the theoretical results and highlight the accuracy of the methods. Furthermore, it is worth noting that the proposed method in this work achieves higher asymptotic rates concerning the frequency $\omega$ compared to those discussed in the previously mentioned references.

In the implementation of our methods, the function f is required to be analytic in the complex plane $\left\{z\right|1\le \Re \left(z\right)\le b\}$. However, this requirement may be overly restrictive. In situations where $f\left(x\right)$ is only differentiable but not analytic, it could be worthwhile to explore alternative approaches, such as employing suitably designed asymptotic methods or Filon-type methods. These considerations will be the focus of our future work.