Multi-Target Feature Selection with Adaptive Graph Learning and Target Correlations
Abstract
1. Introduction
- A novel MTFS method with low-rank constraint is designed to generate low redundancy yet informative feature subset for MTR by imposing a low-rank constraint on the regression matrix, to conduct subspace learning and thus decouple the inter-input as well as the inter-target relationships, which can reduce the influence of redundant or irrelevant features.
- Based on the nearest neighbors of the samples, the similarity-induced graph matrix is learned adaptively, and the local geometric structure of the data can be preserved during the feature selection process, thus mitigating the effects of noise and outliers.
- A manifold regularizer based on target correlation is designed by considering the statistical correlation information between multiple targets over the training set, which is beneficial to discover informative features that are associated with inter-target relationships.
- The alternative optimization algorithm is proposed to solve the proposed objective function, and the convergence of the algorithm is proved theoretically. Extensive experiments are conducted on a benchmark data sets to validate the feasibility and effectiveness of the proposed method.
2. Related Work
3. The Proposed Approaches
3.1. Notations
3.2. MTR Based on Low-Rank Constraint
3.3. Adaptive Graph-Learning Based on Local Sample Structure
3.4. Manifold Regularization of Global Target Correlations
3.5. Objective Function
4. Optimization Algorithm
4.1. Fix Update and
4.2. Fix and Update
| Algorithm 2 MTFS Method based on Alternating Optimization Algorithm |
 |
5. Convergence and Complexity Analysis
5.1. Convergence Analysis of Algorithm 2
5.2. Convergence Analysis of Algorithm 1
5.3. Complexity Analysis
6. Experiments
6.1. Datasets
6.2. Compared Methods
- MTFS [44]: The row sparsity constraint is imposed on the weight matrix by -norm regularization,where is the tuning parameter, we set the parameters to range as empirically.
- RFS [46]: By jointly imposing -norm regularization on the loss function and the weight matrix, the objective function of RFS is:where the parameter range as .
- SSFS [29]: The multi-layer regression structure is constructed by low-dimensional embedding, and the loss function, weight matrix and structure matrix are joint -norm regularized, and the objective function is:where , and are tuning parameters. All tuning parameters’ range as .
- HLMR-FS [47]: The method introduces a hyper-graph Laplacian regularization to maintain the correlation structure between samples and find the hidden correlation structure among different target variables via the low-rank constraint.where is the graph Laplacian matrix between the predicted output vectors of different training samples. and searched in the grid , and p searched in the grid .
- LFR-FS [30]: The method captures the correlation between different objectives through low-rank constraint, and by designing -norm regularization on the loss function and the regression matrix, the learning of the orthogonal subspace enables multiple outputs to share the same low-rank data structure to obtain the corresponding feature selection results.where searched in the grid , and p varied in .
- VMFS [26]: VMFS ranks each feature in MTR via the famous Multi-Criteria Decision-Making (MCDM) method called VIKOR.
- RSSFS [48]: RSSFS uses the mixed convex and non-convex -norm minimization on both regularization and loss function for joint sparse feature selection, and the objective function is:In the experiments, the regularization parameter and were set in , and p varied in .
6.3. Evaluation Metrics
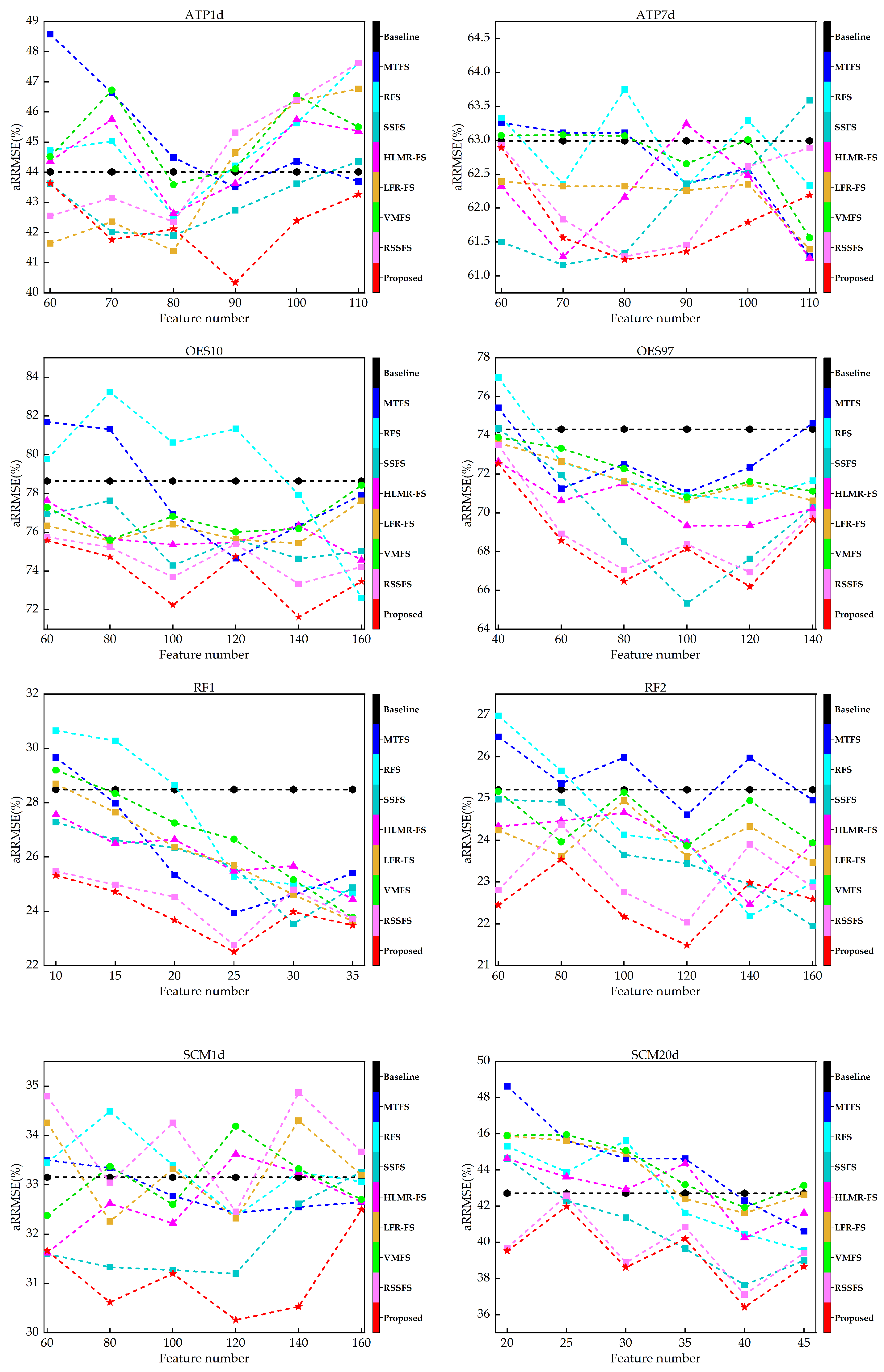
6.4. Results on the Data Sets
6.5. Effect of Low-Rank Constraint
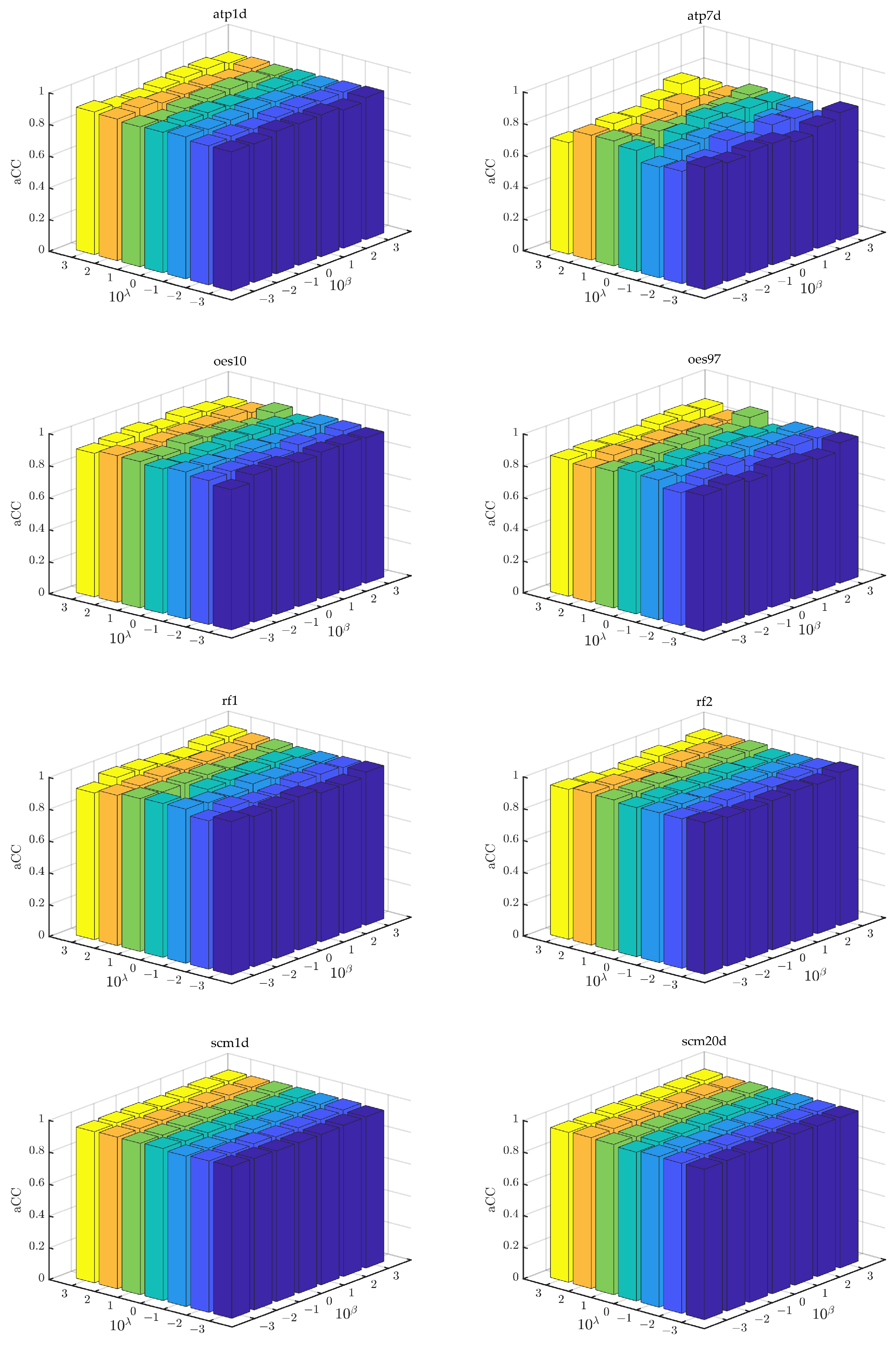
6.6. Parameter Sensitivity
6.7. Convergence Study
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, H.; Zhang, W.; Chen, Y.; Guo, Y.; Li, G.-Z.; Zhu, X. A novel multi-target regression framework for time-series prediction of drug efficacy. Sci. Rep. 2017, 7, 40652. [Google Scholar] [CrossRef] [PubMed]
- Kocev, D.; Džeroski, S.; White, M.D.; Newell, G.R.; Griffioen, P. Using single- and multi-target regression trees and ensembles to model a compound index of vegetation condition. Ecol. Model. 2009, 220, 1159–1168. [Google Scholar] [CrossRef]
- Sicki, D.M. Multi-target tracking using multiple passive bearings-only asynchronous sensors. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 1151–1160. [Google Scholar]
- He, D.; Sun, S.; Xie, L. Multi-Target Regression Based on Multi-Layer Sparse Structure and Its Application in Warships Scheduled Maintenance Cost Prediction. Appl. Sci. 2023, 13, 435. [Google Scholar] [CrossRef]
- Zhen, X.; Islam, A.; Bhaduri, M.; Chan, I.; Li, S. Descriptor Learning via Supervised Manifold Regularization for Multi-output Regression. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2035–2047. [Google Scholar] [PubMed]
- Wang, X.; Zhen, X.; Li, Q.; Shen, D.; Huang, H. Cognitive Assessment Prediction in Alzheimer’s Disease by Multi-Layer Multi-Target Regression. Neuroinformatics 2018, 16, 285–294. [Google Scholar] [CrossRef] [PubMed]
- Ghosn, J.; Bengio, Y. Multi-task learning for stock selection. In Proceedings of the 9th Advances in Neural Information Processing Systems, Denver, CO, USA, 2–5 December 1996; pp. 946–952. [Google Scholar]
- Chen, B.J.; Chang, M.W. Load forecasting using support vector Machines: A study on EUNITE competition 2001. IEEE Trans. Power Syst. 2004, 19, 1821–1830. [Google Scholar] [CrossRef]
- Cai, J.; Luo, J.; Wang, S.; Yang, S. Feature selection in machine learning: A new perspective. Neurocomputing 2018, 300, 70–79. [Google Scholar] [CrossRef]
- Dinov, I.D. Variable/feature selection. In Data Science and Predictive Analytics: Biomedical and Health Applications Using R; Springer International Publishing: Cham, Switzerland, 2018; pp. 557–572. [Google Scholar]
- Sechidis, K.; Spyromitros-Xioufis, E.; Vlahavas, I. Information Theoretic Multi-Target Feature Selection via Output Space Quantization. Entropy 2019, 21, 855. [Google Scholar] [CrossRef]
- He, X.; Deng, C.; Niyogi, P. Laplacian Score for Feature Selection. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 5–8 December 2005; Volume 18. [Google Scholar]
- Sechidis, K.; Brown, G. Simple strategies for semi-supervised feature selection. Mach. Learn. 2018, 107, 357–395. [Google Scholar] [CrossRef]
- Kohavi, R.; John, G.H. Wrappers for feature subset selection. Artif. Intell. 1997, 97, 273–324. [Google Scholar] [CrossRef]
- Tang, C.; Liu, X.; Li, M.; Wang, P.; Chen, J.; Wang, L.; Li, W. Robust unsupervised feature selection via dual self-representation and manifold regularization. Knowl.-Based Syst. 2018, 145, 109–120. [Google Scholar] [CrossRef]
- Nouri-Moghaddam, B.; Ghazanfari, M.; Fathian, M. A novel multi-objective forest optimization algorithm for wrapper feature selection. Expert Syst. Appl. 2021, 175, 114737. [Google Scholar] [CrossRef]
- Spyromitros-Xioufis, E.; Tsoumakas, G.; Groves, W.; Vlahavas, I. Multi-Label Classification Methods for Multi-Target Regression; Cornell University Library: Ithaca, NY, USA, 2014. [Google Scholar]
- Spyromitros-Xioufis, E.; Tsoumakas, G.; Groves, W.; Vlahavas, I. Multi-target regression via input space expansion: Treating targets as inputs. Mach. Learn. 2016, 104, 55–98. [Google Scholar] [CrossRef]
- Tsoumakas, G.; Spyromitros-Xioufis, E.; Vrekou, A.; Vlahavas, I. Multi-Target Regression via Random Linear Target Combinations; Springer: Berlin/Heidelberg, Germany, 2014; pp. 225–240. [Google Scholar]
- Zhu, Y.; Kwok, J.T.; Zhou, Z.H. Multi-Label Learning with Global and Local Label Correlation. IEEE Trans. Knowl. Data Eng. 2018, 30, 1081–1094. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, S.; Hu, R.; Zhu, Y.; Song, J. Local and Global Structure Preservation for Robust Unsupervised Spectral Feature Selection. IEEE Trans. Knowl. Data Eng. 2018, 30, 517–529. [Google Scholar] [CrossRef]
- Huang, Y.; Shen, Z.; Cai, F.; Li, T.; Lv, F. Adaptive graph-based generalized regression model for unsupervised feature selection. Knowl.-Based Syst. 2021, 227, 107156. [Google Scholar] [CrossRef]
- Zhen, X.; Yu, M.; He, X.; Li, S. Multi-Target Regression via Robust Low-Rank Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 497–504. [Google Scholar] [CrossRef]
- Zhen, X.; Yu, M.; Zheng, F.; Nachum, I.B.; Bhaduri, M.; Laidley, D.; Li, S. Multitarget Sparse Latent Regression. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 1575–1586. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, D.; Yang, J.Y.; Niu, B. Globally Maximizing, Locally Minimizing: Unsupervised Discriminant Projection with Applications to Face and Palm Biometrics. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 650–664. [Google Scholar] [CrossRef]
- Hashemi, A.; Dowlatshahi, M.B.; Nezamabadi-pour, H. VMFS: A VIKOR-based multi-target feature selection. Expert Syst. Appl. 2021, 182, 115224. [Google Scholar] [CrossRef]
- Petkovi, M.; Kocev, D.; Deroski, S. Feature ranking for multi-target regression. Mach. Learn. 2020, 109, 1179–1204. [Google Scholar] [CrossRef]
- Masmoudi, S.; Elghazel, H.; Taieb, D.; Yazar, O.; Kallel, A. A machine-learning framework for predicting multiple air pollutants’ concentrations via multi-target regression and feature selection. Sci. Total. Environ. 2020, 715, 136991. [Google Scholar] [CrossRef] [PubMed]
- Yuan, H.; Zheng, J.; Lai, L.L.; Tang, Y.Y. Sparse structural feature selection for multitarget regression. Knowl.-Based Syst. 2018, 160, 200–209. [Google Scholar] [CrossRef]
- Zhang, S.; Yang, L.; Li, Y.; Luo, Y.; Zhu, X. Low-Rank Feature Reduction and Sample Selection for Multi-output Regression; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Fan, Y.; Chen, B.; Huang, W.; Liu, J.; Weng, W.; Lan, W. Multi-label feature selection based on label correlations and feature redundancy. Knowl.-Based Syst. 2022, 241, 108256. [Google Scholar] [CrossRef]
- Xu, J.; Liu, J.; Yin, J.; Sun, C. A multi-label feature extraction algorithm via maximizing feature variance and feature-label dependence simultaneously. Knowl.-Based Syst. 2016, 98, 172–184. [Google Scholar] [CrossRef]
- Samareh-Jahani, M.; Saberi-Movahed, F.; Eftekhari, M.; Aghamollaei, G.; Tiwari, P. Low-Redundant Unsupervised Feature Selection based on Data Structure Learning and Feature Orthogonalization. Expert Syst. Appl. 2024, 240, 122556. [Google Scholar] [CrossRef]
- Ma, J.; Xu, F.; Rong, X. Discriminative multi-label feature selection with adaptive graph diffusion. Pattern Recognit. 2024, 148, 110154. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, Y.; Li, X. Unsupervised feature selection via adaptive graph learning and constraint. IEEE Trans. Neural Netw. Learn. Syst. 2020, 33, 1355–1362. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, S.; Zhu, Y.; Zhu, P.; Gao, Y. Unsupervised spectral feature selection with dynamic hyper-graph learning. IEEE Trans. Knowl. Data Eng. 2020, 34, 3016–3028. [Google Scholar] [CrossRef]
- You, M.; Yuan, A.; He, D.; Li, X. Unsupervised feature selection via neural networks and self-expression with adaptive graph constraint. Pattern Recognit. 2023, 135, 109173. [Google Scholar] [CrossRef]
- Acharya, D.B.; Zhang, H. Feature Selection and Extraction for Graph Neural Networks. In Proceedings of the 2020 ACM Southeast Conference (ACM SE ’20), Tampa, FL, USA, 2–4 April 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 252–255. [Google Scholar] [CrossRef]
- Chen, L.; Huang, J.Z. Sparse Reduced-Rank Regression for Simultaneous Dimension Reduction and Variable Selection. J. Am. Stat. Assoc. 2012, 107, 1533–1545. [Google Scholar] [CrossRef]
- Liu, G.; Lin, Z.; Yan, S.; Sun, J.; Yu, Y.; Ma, Y. Robust Recovery of Subspace Structures by Low-Rank Representation. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 171–184. [Google Scholar] [CrossRef] [PubMed]
- Doquire, G.; Verleysen, M. A graph Laplacian based approach to semi-supervised feature selection for regression problems. Neurocomputing 2013, 121, 5–13. [Google Scholar] [CrossRef]
- He, X.; Niyogi, P. Locality preserving projections. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, USA, 8–13 December 2003; Volume 16. [Google Scholar]
- Wang, H.; Yang, Y.; Liu, B. GMC: Graph-Based Multi-View Clustering. IEEE Trans. Knowl. Data Eng. 2020, 32, 1116–1129. [Google Scholar] [CrossRef]
- Liu, J.; Ji, S.; Ye, J. Multi-task feature learning via efficient ℓ2,1-norm minimization. In Proceedings of the Conference on Uncertainty in Artificial Intelligence, Montreal, QC, Canada, 18–21 June 2009; pp. 339–348. [Google Scholar]
- Tsoumakas, G.; Spyromitros-Xioufis, E.; Vilcek, J. MULAN: A Java library for multi-label learning. J. Mach. Learn. Res. 2011, 12, 2411–2414. [Google Scholar]
- Nie, F.; Huang, H.; Cai, X.; Ding, C. Efficient and Robust Feature Selection via Joint ℓ2,1-Norms Minimization. In Proceedings of the Neural Information Processing Systems (NIPS), Vancouver, BC, USA, 6–9 December 2010; pp. 1813–1821. [Google Scholar]
- Borchani, H.; Varando, G.; Bielza, C.; Larrañaga, P. A survey on multi-output regression. WIREs Data Min. Knowl. Discov. 2015, 5, 216–233. [Google Scholar] [CrossRef]
- Sheikhpour, R.; Gharaghani, S.; Nazarshodeh, E. Sparse feature selection in multi-target modeling of carbonic anhydrase isoforms by exploiting shared information among multiple targets. Chemom. Intell. Lab. Syst. 2020, 200, 104000. [Google Scholar] [CrossRef]
- Shawe-Taylor, J.; Cristianini, N. Kernel Methods for Pattern Analysis; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Demšar, J.; Schuurmans, D. Statistical comparisons of classifiers over multiple data sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]






| Datasets | Instances | Features | Targets | #-Fold | Domains |
|---|---|---|---|---|---|
| ATP1d | 337 | 411 | 6 | 10 | Price prediction |
| ATP7d | 296 | 411 | 6 | 10 | Price prediction |
| OES10 | 403 | 298 | 16 | 10 | Artificial |
| OES97 | 334 | 263 | 16 | 10 | Artificial |
| RF1 | 9125 | 64 | 8 | 2 | Environment |
| RF2 | 9125 | 576 | 8 | 2 | Environment |
| SCM1d | 9803 | 280 | 16 | 2 | Environment |
| SCM20d | 8966 | 61 | 16 | 2 | Environment |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; He, D. Multi-Target Feature Selection with Adaptive Graph Learning and Target Correlations. Mathematics 2024, 12, 372. https://doi.org/10.3390/math12030372
Zhou Y, He D. Multi-Target Feature Selection with Adaptive Graph Learning and Target Correlations. Mathematics. 2024; 12(3):372. https://doi.org/10.3390/math12030372
Chicago/Turabian StyleZhou, Yujing, and Dubo He. 2024. "Multi-Target Feature Selection with Adaptive Graph Learning and Target Correlations" Mathematics 12, no. 3: 372. https://doi.org/10.3390/math12030372
APA StyleZhou, Y., & He, D. (2024). Multi-Target Feature Selection with Adaptive Graph Learning and Target Correlations. Mathematics, 12(3), 372. https://doi.org/10.3390/math12030372








