Commutative Rings Behind Divisible Residuated Lattices

Abstract

Divisible residuated lattices are algebraic structures corresponding to a more comprehensive logic than Hajek’s basic logic with an important significance in the study of fuzzy logic. The purpose of this paper is to investigate commutative rings whose lattice of ideals can be equipped with a structure of divisible residuated lattice. We show that these rings are multiplication rings. A characterization, additional examples, and their connections to other classes of rings are established. Furthermore, we analyze the structure of divisible residuated lattices using finite commutative rings. From computational considerations, we present an explicit construction of isomorphism classes of divisible residuated lattices (that are not BL-algebras) of small size n ($2\le n\le 6$), and we give summarizing statistics.

1. Introduction

Nonclassical logics are strongly related to computer science, and they are represented as algebras.

Residuated lattices were introduced in [1,2], and the studies originated from the context of the theory of rings since the lattice of ideals of a commutative ring is a residuated lattice (see [3]).

Rings are important algebraic tools and many authors ([3,4,5,6,7,8,9], etc.) have studied algebras of logic connected with certain classes of rings.

Divisible residuated lattices (or residuated lattice-ordered monoids) were introduced in [10] as a unifying concept for Heyting algebras and Abelian lattice-ordered groups. These residuated lattices that satisfy the divisibility condition are connected with algebras in t-norm-based fuzzy logics as examples of BL-algebras.

It is known that BL-rings and MTL-rings are commutative unitary rings whose ideals form a BL-algebra and, respectively, an MTL-algebra.

Since BL-algebras are MTL-algebras satisfying the divisibility property, the question that one can ask is “what are commutative rings whose lattice of ideals satisfies the divisibility condition?”.

In this paper, we show that divisible residuated lattices are connected with multiplication rings, and using these algebras, we obtain a new description for multiplication rings (see Theorem 1 and Proposition 2). For other details, the readers are referred to [11].

We show that the class of multiplication rings contains other known classes of commutative rings: MV-rings, BL-rings, Von Neumann regular rings, rings which are principal ideal domains, and some types of finite unitary commutative rings (see Proposition 3 and Theorem 2).

We prove that a commutative ring which has at most five distinct ideals is principal, and its lattice of ideals is a divisible residuated lattice. Moreover, the ring $A=A_1\times \dots \times A_q$—such that the numbers of ideals of the rings $A_i$ are $n_{A_i}$, with $n_{A_i}\in \{2,3,5\},i\in \{1,2,\dots ,q\}$—is a principal ideal ring, and therefore, a multiplication ring; see Remark 7.

Using computer algorithms, in [12], isomorphism classes of divisible residuated lattices of size $n\le 12$ were counted. In this paper, using Theorem 4, we construct all (up to an isomorphism) divisible residuated lattices with $n\le 6$ elements (that are not BL-algebras) using the ordinal product BL-algebras. Also, we present summarizing statistics. This method can be used to construct finite divisible residuated lattices of larger size, with the inconvenience being the large number of algebras that should be generated (for example, there are 23 algebras with $n=6$ elements, and for $n=7$, there are 49 divisible residuated lattices).

2. Preliminaries

Definition 1

([1,2]). A (commutative) residuated lattice is an algebra $(L,\wedge ,\vee ,\odot ,\to ,0,1)$ equipped with an order ≤ such that the following are true:

(LR1) $(L,\wedge ,\vee ,0,1)$ is a bounded lattice;

(LR2) $(L,\odot ,1)$ is a commutative ordered monoid;

(LR3) $z\le x\to y$ iff $x\odot z\le y,$ for all $x,y,z\in L.$

In a residuated lattice for $x\in L,$ we denote $x^{*}=x\to 0.$

Example 1.

It is known that, for a commutative unitary ring $A,$ the lattice of ideals $\left(Id\right(A),\cap ,+,\otimes$ $\to ,0=\left\{0\right\},1=A)$ is a residuated lattice in which the order relation is ⊆ and

$$I+J=<I\cup J>=\{i+j,i\in I,j\in J\},$$

$$I\otimes J=\{\underset{k=1}{\sum ^n}{i}_k{j}_k,i_k\in I,j_k\in J\},$$

$$I\to J=(J:I)=\{x\in A,x·I\subseteq J\},$$

$$Ann\left(I\right)=\left(\mathbf{0}:I\right),where\mathbf{0}=<0>,$$

for every $I,J\in Id\left(A\right)$ (see [9]). $I+J,$ $I\otimes J,I\to J$ and $Ann\left(I\right)$ are ideals of $A,$ called sum, product, quotient. and annihilator (see [13]).

In a residuated lattice $(L,\wedge ,\vee ,\odot ,\to ,0,1)$, we consider the following identities:

$$\left(prel\right)(x\to y)\vee (y\to x)=1(\mathit{prelinearity});$$

$$\left(div\right)x\odot (x\to y)=x\wedge y(\mathit{divisibility}).$$

Definition 2

([14,15,16,17,18]). A residuated lattice L is called the following:

(i)

An MTL-algebra if L verifies $\left(prel\right)$ condition;

(ii)

Divisible if L verifies the $\left(div\right)$ condition;

(iii)

A BL-algebra if L verifies $\left(prel\right)+\left(div\right)$ conditions. A BL-chain is a totally ordered BL-algebra, i.e., a BL-algebra such that its lattice order is total.

(iv)

An MV-algebra if L is a BL-algebra in which $x^{**}=x,$ for every $x\in L$.

Proposition 1

([17]). Let $(L,\vee ,\wedge ,\odot ,\to ,0,1)$ be a residuated lattice. Then, we have the following equivalences:

(i)

L satisfies the $\left(\mathrm{div}\right)$ condition;

(ii)

For all $x,y\in L$, if $y\le x$, then there exists $z\in L$, such that $y=z\odot x.$

Example 2

([17]). We give an example of a divisible residuated lattice which is not a BL-algebra. Let $L=\{0,a,b,c,1\}$ with $0\le a,b\le c\le 1,$ but $a,b$ be incomparable, with the following operations:

$$\begin{array}{cccccc}\to & 0& a& b& c& 1\\ 0& 1& 1& 1& 1& 1\\ a& b& 1& b& 1& 1\\ b& a& a& 1& 1& 1\\ c& 0& a& b& 1& 1\\ 1& 0& a& b& c& 1\end{array},\begin{array}{cccccc}\odot & 0& a& b& c& 1\\ 0& 0& 0& 0& 0& 0\\ a& 0& a& 0& a& a\\ b& 0& 0& b& b& b\\ c& 0& a& b& c& c\\ 1& 0& a& b& c& 1\end{array}.$$

We remark that $(a\to b)\vee (b\to a)=c\ne 1.$

3. Divisible Residuated Lattices and Multiplication Rings

Lemma 1.

Let $(L,\vee ,\wedge ,\odot ,\to ,0,1)$ be a residuated lattice. The following assertions are equivalent:

(i) L is divisible;

(ii) For every $x,y,z\in L,$ $z\to (x\odot (x\to y\left)\right)=z\to (x\wedge y).$

Proof. 

$\left(i\right)\Rightarrow \left(ii\right),$ obviously.

$\left(ii\right)\Rightarrow \left(i\right).$ For $z=$ $x\wedge y$, we obtain $(x\wedge y)\to (x\odot (x\to y\left)\right)=1,$ so L is divisible since in a residuated lattice, $x\odot (x\to y)\le x\wedge y.$ □

Unitary commutative rings for which the lattice of ideals is an MV-algebra, a BL-algebra, or an MTL-algebra are called MV-rings, BL-rings, and, MTL-rings, respectively, and they were introduced in [4,5,6].

Definition 3

([19]). Let A be a commutative unitary ring. An ideal $I\in Id\left(A\right)$ is called a multiplication ideal if for every ideal $J\subseteq I$, there exists an ideal K such that $J=I\otimes K.$ The ring A is called a multiplication ring if all its ideals are multiplication ideals.

Multiplication rings have been studied in [20,21,22]. It is well known that a multiplication ring is a subring of a Cartesian product of Dedekind domains and special primary rings; see [22].

Using Proposition 1, we deduce the following.

Theorem 1.

A unitary commutative ring is a multiplication ring if and only if its lattice of ideals is a divisible residuated lattice.

Using Lemma 1, we obtain a new characterization for multiplication rings:

Proposition 2.

Let A be a commutative unitary ring. The following assertions are equivalent:

(i)

A is a multiplication ring;

(ii)

$I\otimes (J:I)=I\cap J,$ for every $I,J\in Id\left(A\right);$

(iii)

$\left(\right(I\otimes (J:I)):K)=\left(\right(I\cap J):K),$ for every $I,J,K\in Id\left(A\right).$

We recall that a residuated lattice $(L,\vee ,\wedge ,\odot ,\to ,0,1)$ in which $x^2=x,$ for all $x\in L,$ is called a Heyting algebra (see [17,18]).

In [23], it was proven that unitary commutative rings—for which the semiring of ideals under ideal sum and ideal product are Heyting algebras—are exactly Von Neumann regular rings, i.e., commutative rings A in which for every element $x\in A$, there exists an element $a\in A$, such that $x=a·x^2.$

Since MV-algebras, BL-algebras, and Heyting algebras are divisible residuated lattices, we have the following result:

Proposition 3.

MV-rings, BL-rings, and Von Neumann regular rings are multiplication rings.

Proposition 4.

A commutative unitary ring is

(i)

A BL-ring if and only if it is an MTL-ring and a multiplication ring;

(ii)

An MV-ring if and only if it is an multiplication MTL-ring and $Ann\left(Ann\right(I\left)\right)=I,$ for every $I\in Id\left(A\right).$

Proof. 

(i)

Obviously, a BL-algebra is an MTL-algebra satisfyng the divisibility property.

(ii)

MV-algebras are BL-algebras in which $x^{**}=x,$ for every x.

□

Theorem 2.

(i)

A commutative ring that is a principal ideal domain is a multiplication ring.

(ii)

A ring factor of a principal ideal domain is a multiplication ring.

(iii)

A finite commutative unitary ring of the form $A={\mathbb{Z}}_{k_1}\times {\mathbb{Z}}_{k_2}\times \dots \times {\mathbb{Z}}_{k_r}$ (direct product of rings, equipped with component-wise operations), where $k_i=p_i^{{\alpha }_i}$, $p_i$ is a prime number, is a multiplication ring.

Proof. 

$\left(i\right).$ Let A be a commutative ring that is a principal ideal domain, and $I=<i>$, $J=<j>,$ be the principal nonzero ideals generated by $i,j\in A$$\setminus \left\{0\right\}$.

If $d=$gcd$\{i,j\}$, then $i=i_{1}d$ and $j=j_{1}d$, with $1=$gcd$\{i_1,j_1\}$. We have $I\cap J=<ij/d>,$ $I\otimes J=<ij>$ and $\left(I:J\right)=$ $<i_1>.$

Thus, $J\otimes (I:J)=<j>\otimes <i_1>=<ij/d>=I\cap J$.

If $I=\left\{0\right\}$, since A is an integral domain, we have $J\otimes (\mathbf{0}:J)=J\otimes Ann\left(J\right)=\mathbf{0}=\mathbf{0}\cap J=$ $\mathbf{0}\otimes (J:\mathbf{0}),$ for every $J\in Id\left(A\right)\setminus \left\{0\right\}.$

$\left(ii\right).$ A ring factor of a principal ideal domain is an MV-ring (see [7]). Using Proposition 3, it is a multiplication ring.

$\left(iii\right).$ We apply $\left(ii\right)$ and Proposition 3 using the fact that BL-rings are closed under finite direct products (see [5]). Moreover, $\left(Id\left(A\right),\cap ,+,\otimes \to ,\left\{0\right\},A\right)$ is a divisible residuated lattice with ${\displaystyle \prod _{i=1}^r}\left({\alpha }_i+1\right)$ elements since it is an MV-algebra (see [7]). □

Example 3.

(1)

Following Theorem 2, the ring of integers $(\mathbb{Z},+,·)$ is a multiplication ring since $\mathbb{Z}$ is a principal ideal domain.

(2)

Let K be a field and $K\left[X\right]$ be the polynomial ring. For $f\in K\left[X\right]$, the quotient ring $A=K\left[X\right]/\left(f\right)$ is a multiplication ring since the lattice of ideals of this ring is an MV-algebra (see [7]).

Proposition 5.

If A is a multiplication ring, then for every $I,J,K\in Id\left(A\right)$, we have

(c₁)

$Ann\left(Ann\right(Ann\left(I\right))\to I)=\left\{0\right\};$

(c₂)

$Ann\left(Ann\right(I\to J\left)\right)=Ann\left(Ann\right(I\left)\right)\to Ann\left(Ann\right(J\left)\right);$

(c₃)

$Ann\left(Ann\right(I\otimes J\left)\right)=Ann\left(Ann\right(I\left)\right)\otimes Ann\left[Ann\right(Ann\left(I\right))\cap Ann(J\left)\right],$

(c₄)

$Ann\left(Ann\right(I\cap J\left)\right)=Ann\left(Ann\right(I\left)\right)\cap Ann\left(Ann\right(J\left)\right);$

(c₅)

$Ann\left(J\right)\subseteq I\Rightarrow I\to Ann\left(Ann\right(I\otimes J\left)\right)=Ann\left(Ann\right(J\left)\right);$

(c₆)

$I\otimes (J\cap K))=(I\otimes J)\cap (I\otimes K);$

(c₇)

$I\cap (J+K)=(I\cap J)+(I\cap K).$

Proof. 

$\left(c_1\right).$ From $Ann\left(I\right)\subseteq Ann\left(Ann\right(I\left)\right)\to I\Rightarrow Ann\left(Ann\right(Ann\left(I\right))\to I)\subseteq Ann\left(Ann\right(I\left)\right)$ $\Rightarrow Ann\left(Ann\right(Ann\left(I\right))\to I)=Ann\left(Ann\right(I\left)\right)\cap Ann\left(Ann\right(Ann\left(I\right))\to I)$ $\stackrel{\left(div\right)}{=}Ann\left(Ann\left(I\right)\right)$ $\otimes \left[Ann\right(Ann\left(I\right))\to Ann(Ann\left(Ann\right(I\left)\right)\to I\left)\right]=$ $Ann\left(Ann\left(I\right)\right)\otimes Ann\left[(Ann\left(Ann\left(I\right)\right)\to I)\right)\otimes Ann\left(Ann\left(I\right)\right)]\stackrel{\left(div\right)}{=}Ann(Ann\left(I\right)\otimes Ann(Ann\left(Ann\left(I\right)\right)\cap I)=Ann\left(Ann\left(I\right)\right)\otimes Ann\left(I\right)$ $=\mathbf{0}$,

$\left(c_2\right).$ We have $Ann\left(Ann\right(I\to J\left)\right)\subseteq Ann\left(Ann\right(I\left)\right)\to Ann\left(Ann\right(J\left)\right)=I\to Ann\left(Ann\right(J\left)\right).$ Also, $(I\to Ann(Ann\left(J\right)\left)\right)\to Ann\left(Ann\right(I\to J\left)\right)=$ $Ann\left(Ann\right(I\to Ann\left(Ann\right(J\left)\right)\left)\right)\to Ann\left(Ann\right(I\to J\left)\right)\supseteq$ $Ann\left(Ann[(I\otimes (I\to Ann\left(Ann\left(J\right)\right)))\to J]\right)\stackrel{\left(div\right)}{=}Ann\left(Ann[(I\cap Ann\left(Ann\left(J\right)\right))\to J]\right)\supseteq Ann\left(Ann[Ann\left(Ann\left(J\right)\right)\to J]\right)=A$

$\Rightarrow (I\to Ann(Ann\left(J\right)\left)\right)\to Ann\left(Ann\right(I\to J\left)\right)=A\Rightarrow I\to Ann\left(Ann\right(J\left)\right)\subseteq Ann\left(Ann\right(I\to J\left)\right)$$\Rightarrow Ann\left(Ann\right(I\to J\left)\right)=I\to Ann\left(Ann\right(J\left)\right)=Ann\left(Ann\right(I\left)\right)\to Ann\left(Ann\right(J\left)\right).$

$\left(c_3\right).$ From $Ann\left(Ann\right(I\otimes J\left)\right)\subseteq Ann\left(Ann\right(I\left)\right)\Rightarrow$ $Ann\left(Ann\right(I\otimes J\left)\right)=Ann\left(Ann\right(I\otimes J\left)\right)\cap Ann\left(Ann\right(I\left)\right)=Ann[J\to Ann(I\left)\right]\cap Ann\left(Ann\right(I\left)\right)=$ $Ann\left(Ann\right(I\left)\right)\otimes Ann\left[Ann\right(Ann\left(I\right))$ $\cap Ann\left(J\right)].$

$\left(c_4\right).$ Obviously, $Ann\left(Ann\right(I\cap J\left)\right)\subseteq Ann\left(Ann\right(I\left)\right),Ann\left(Ann\right(J\left)\right).$

Let $K\in Id\left(A\right)$ such that $K\subseteq Ann\left(Ann\right(I\left)\right),Ann\left(Ann\right(J\left)\right).$ Then, $Ann\left(Ann\right(K\left)\right)\subseteq Ann\left[Ann\right(I)+Ann(J\left)\right].$ But, $K\subseteq Ann\left(Ann\right(K\left)\right)$ and $Ann\left[Ann\right(I)+Ann(J\left)\right]=Ann\left(Ann\right(I\left)\right)$ $\cap Ann\left(Ann\right(J\left)\right)\Rightarrow K\subseteq Ann\left(Ann\right(I\left)\right)\cap Ann\left(Ann\right(J\left)\right).$

$\left(c_5\right).$ $I\to Ann\left(Ann\right(I\otimes J\left)\right)=Ann(I\otimes J)\to Ann\left(I\right)=Ann[I\otimes (I\to Ann\left(J\right)\left)\right]=Ann(I\cap Ann(J\left)\right)=Ann\left(Ann\right(J\left)\right).$

$\left(c_6\right).$ Clearly $I\otimes (J\cap K)\subseteq (I\otimes J)\cap (I\otimes K).$

Also, $(I\otimes J)\cap (I\otimes K)=(I\otimes J)\otimes \left[\right(I\otimes J)\to (I\otimes K\left)\right]=I\otimes [J\otimes (J\to (I\to (I\otimes K\left)\right)\left)\right]=$ $I\otimes [J\cap (I\to (I\otimes K)\left)\right]=$ $I\otimes \left[\right(I\to (I\otimes K))\otimes ((I\to (I\otimes K\left)\right)\to J\left)\right].$

But $K\subseteq I\to (I\otimes K)\Rightarrow (I\to (I\otimes K\left)\right)\to J\le K\to J,$ so $(I\otimes J)\cap (I\otimes K)\subseteq I\otimes (J\cap K)).$

$\left(c_7\right).$ Clearly, $I\cap (J+K)\supseteq (I\cap J)+(I\cap K).$ Also, we have $I\cap (J+K)=(J+K)\otimes \left[\right(J+K)\to I]=[J\otimes ((J+K)\to I\left)\right]+[K\otimes ((J+K)\to I\left)\right]\subseteq [J\otimes (J\to I\left)\right]+[K\otimes (K\to I\left)\right]=(I\cap J)+(I\cap K).$ □

4. Examples of Divisible Residuated Lattices Using Commutative Rings

In this section, we present ways to generate finite divisible residuated lattices using finite commutative rings.

In [17], Iorgulescu studied the influence of the condition $\left(div\right)$ on the ordinal product of two BL-algebras.

It is known that, if ${\mathcal{L}}_1=(L_1,{\wedge }_1,{\vee }_1,{\odot }_1,{\to }_1,0_1,1_1)$ and ${\mathcal{L}}_2=(L_2,{\wedge }_2,{\vee }_2,{\odot }_2,{\to }_2,$$0_2,1_2)$ are two BL-algebras such that $1_1=0_2$ and $(L_1\setminus \left\{1_1\right\})\cap (L_2\setminus \left\{0_2\right\})=\oslash ,$ then the ordinal product of ${\mathcal{L}}_1$ and ${\mathcal{L}}_2$ is the residuated lattice ${\mathcal{L}}_1⊠{\mathcal{L}}_2=(L_1\cup L_2,\wedge ,\vee ,\odot ,\to ,0,1)$, where

$$0=0_1\mathrm{and}1=1_2,$$

$$x\le y\mathrm{if}(x,y\in L_1\mathrm{and}x{\le }_{1}y)\mathrm{or}(x,y\in L_2\mathrm{and}x{\le }_{2}y)\mathrm{or}(x\in L_1\mathrm{and}y\in L_2),$$

$$x\to y=\left\{\begin{array}{c}1,\mathrm{if}x\le y,\\ x{\to }_{i}y,\mathrm{if}x\nleqq y,x,y\in L_i,i=1,2,\\ y,\mathrm{if}x\nleqq y,x\in L_2,y\in L_1\setminus \left\{1_1\right\}.\end{array}\right.$$

$$x\odot y=\left\{\begin{array}{c}x{\odot }_{1}y,\mathrm{if}x,y\in L_1,\\ x{\odot }_{2}y,\mathrm{if}x,y\in L_2,\\ x,\mathrm{if}x\in L_1\setminus \left\{1_1\right\}\mathrm{and}y\in L_2.\end{array}\right.$$

We recall that the ordinal product is associative, but is not commutative.

Proposition 6

([17], Corollary 3.5.10). Let ${\mathcal{L}}_1$ and ${\mathcal{L}}_2$ be BL-algebras.

(i)

If ${\mathcal{L}}_1$ is a chain, then the ordinal product ${\mathcal{L}}_1⊠{\mathcal{L}}_2$ is a BL-algebra (that is not an MV-algebra);

(ii)

If ${\mathcal{L}}_1$ is not a chain, then the ordinal product ${\mathcal{L}}_1⊠{\mathcal{L}}_2$ is only a residuated lattice satisfying the divisibility condition.

Remark 1.

An ordinal product of two BL-chains is a BL-chain.

In Table 1, we recall the structure of finite BL-algebras L with $2\le n\le 5$ elements; see [8].

Table 1. The structure of finite BL-algebras L with $2\le n\le 5$ elements.

$\left|\mathit{L}\right|=\mathbf{n}$	Nr of BL-alg	Structure
$n=2$	1	$\left\{Id\left({\mathbb{Z}}_2\right)(\mathrm{BL}-\mathrm{chain})\right.$
$n=3$	2	$\left\{\begin{array}{c}Id\left({\mathbb{Z}}_4\right)(\mathrm{BL}-\mathrm{chain})\\ Id\left({\mathbb{Z}}_2\right)⊡Id\left({\mathbb{Z}}_2\right)(\mathrm{BL}-\mathrm{chain})\end{array}\right.$
$n=4$	5	$\left\{\begin{array}{c}Id\left({\mathbb{Z}}_8\right)(\mathrm{BL}-\mathrm{chain})\\ Id({\mathbb{Z}}_2\times {\mathbb{Z}}_2)\left(\mathrm{BL}\right)\\ Id\left({\mathbb{Z}}_2\right)⊡Id\left({\mathbb{Z}}_4\right)(\mathrm{BL}-\mathrm{chain})\\ Id\left({\mathbb{Z}}_4\right)⊡Id\left({\mathbb{Z}}_2\right)(\mathrm{BL}-\mathrm{chain})\\ Id\left({\mathbb{Z}}_2\right)⊡(Id\left({\mathbb{Z}}_2\right)⊡Id\left({\mathbb{Z}}_2\right))(\mathrm{BL}-\mathrm{chain})\end{array}\right.$
$n=5$	9	$\left\{\begin{array}{c}Id\left({\mathbb{Z}}_{16}\right)(\mathrm{BL}-\mathrm{chain})\\ Id\left({\mathbb{Z}}_2\right)⊡Id\left({\mathbb{Z}}_8\right)(\mathrm{BL}-\mathrm{chain})\\ Id\left({\mathbb{Z}}_2\right)⊡Id({\mathbb{Z}}_2\times {\mathbb{Z}}_2)\left(\mathrm{BL}\right)\\ Id\left({\mathbb{Z}}_2\right)⊡(Id\left({\mathbb{Z}}_2\right)⊡Id\left({\mathbb{Z}}_4\right))(\mathrm{BL}-\mathrm{chain})\\ Id\left({\mathbb{Z}}_2\right)⊡(Id\left({\mathbb{Z}}_4\right)⊡Id\left({\mathbb{Z}}_2\right))(\mathrm{BL}-\mathrm{chain})\\ Id\left({\mathbb{Z}}_2\right)⊡(Id\left({\mathbb{Z}}_2\right)⊡(Id\left({\mathbb{Z}}_2\right)⊡Id\left({\mathbb{Z}}_2\right)))(\mathrm{BL}-\mathrm{chain})\\ Id\left({\mathbb{Z}}_8\right)⊡Id\left({\mathbb{Z}}_2\right)(\mathrm{BL}-\mathrm{chain})\\ (Id\left({\mathbb{Z}}_4\right)⊡Id\left({\mathbb{Z}}_2\right))⊡Id\left({\mathbb{Z}}_2\right)(\mathrm{BL}-\mathrm{chain})\\ Id\left({\mathbb{Z}}_4\right)⊡Id\left({\mathbb{Z}}_4\right)(\mathrm{BL}-\mathrm{chain})\end{array}\right.$

Using the construction of the ordinal products from Proposition 6, Remark 1, and Table 1, we can generate divisible residuated lattices (which are not BL-algebras) using commutative rings.

Example 4.

To generate the divisible residuated lattice with five elements from Example 2, we consider the commutative rings $({\mathbb{Z}}_2\times {\mathbb{Z}}_2,+,·)$ and $({\mathbb{Z}}_2,+,·).$ For ${\mathbb{Z}}_2\times {\mathbb{Z}}_2$, we obtain the lattice $Id\left({\mathbb{Z}}_2\times {\mathbb{Z}}_2\right)=\{\left(\widehat{0},\widehat{0}\right),\{\left(\widehat{0},\widehat{0}\right),\left(\widehat{0},\widehat{1}\right)\},\{\left(\widehat{0},\widehat{0}\right),\left(\widehat{1},\widehat{0}\right)\},{\mathbb{Z}}_2\times {\mathbb{Z}}_2\}=\{O,R,B,E\}$, which is an MV-algebra $(Id\left({\mathbb{Z}}_2\times {\mathbb{Z}}_2\right),\cap ,+,\otimes =\cap ,\to ,0=\left\{\left(\widehat{0},\widehat{0}\right)\right\},1={\mathbb{Z}}_2\times {\mathbb{Z}}_2)$ with the following operations:

$$\begin{array}{ccccc}\hfill \to & O& C\hfill & B& E\\ \hfill O& E& E\hfill & E& E\\ \hfill C& B& E\hfill & B& E\\ \hfill B& C& C\hfill & E& E\\ \hfill E& O& C\hfill & B& E\end{array}\mathit{and}\begin{array}{ccccc}\hfill \otimes & O& C\hfill & B& E\\ \hfill O& O& O\hfill & O& O\\ \hfill C& O& C\hfill & O& C\\ \hfill B& O& O\hfill & B& B\\ \hfill E& O& C\hfill & B& E\end{array}.$$

If we consider two BL-algebras isomorphic with $(Id\left({\mathbb{Z}}_2\times {\mathbb{Z}}_2\right),\cap ,+,\otimes \to ,0=\left\{\left(\widehat{0},\widehat{0}\right)\right\},$ $1={\mathbb{Z}}_2\times {\mathbb{Z}}_2)$ and $(Id\left({\mathbb{Z}}_2\right),\cap ,+,\otimes \to ,0=\left\{0\right\},1={\mathbb{Z}}_2)$ and denoted by ${\mathcal{L}}_1=(L_1=\{0,a,b,c\},{\wedge }_1,{\vee }_1,{\odot }_1,{\to }_1,0,c)$ and ${\mathcal{L}}_2=(L_2=\{c,1\},{\wedge }_2,{\vee }_2,{\odot }_2,{\to }_2,c,1),$ using Proposition 6, we generate the divisible residuated lattice ${\mathcal{L}}_1⊠{\mathcal{L}}_2=(L_1\cup L_2=\{0,a,b,c,1\},\wedge ,\vee ,\odot ,\to ,0,1)$ from Example 2.

Remark 2.

Using the model from Example 4, for two BL-algebras ${\mathcal{L}}_1$ and ${\mathcal{L}}_2$, we can denote these algebras to obtain two BL-algebras ${\mathcal{L}}_1^{\prime }$ and ${\mathcal{L}}_2^{\prime }$ isomorphic with ${\mathcal{L}}_1$ and ${\mathcal{L}}_2$, respectively, that satisfy the conditions imposed by the ordinal product.

We denote by ${\mathcal{L}}_1⊡{\mathcal{L}}_2$ the ordinal product ${\mathcal{L}}_1^{\prime }⊠{\mathcal{L}}_2^{\prime }.$

From Proposition 6, Remark 1, and Table 1, we deduce the following.

Theorem 3.

(i)

There are no divisible residuated lattices that are chains and are not BL-algebras;

(ii)

There are no divisible residuated lattices with $n\le 4$ elements that are not BL-algebras;

(iii)

To generate a divisible residuated lattice with $n\ge 5$ elements (which is not a BL-algebra) as the ordinal product ${\mathcal{L}}_1⊠{\mathcal{L}}_2$ of two BL-algebras ${\mathcal{L}}_1$ and ${\mathcal{L}}_2$, we have the following possibilities:

$$\begin{array}{ccc}& & {\mathcal{L}}_1\mathit{is}a\mathit{BL}-\mathit{algebra}\mathit{with}i\mathit{elements}(\mathit{that}\mathit{is}\mathit{not}a\mathit{chain})\mathit{and}\hfill \\ & & {\mathcal{L}}_2\mathit{is}a\mathit{BL}-\mathit{algebra}\mathit{with}j\mathit{elements},\hfill \end{array}$$

for $i,j\ge 2,i+j=n+1,$ $i\ne j$

or

$$\begin{array}{ccc}& & {\mathcal{L}}_1\mathit{is}a\mathit{BL}-\mathit{algebra}(\mathit{that}\mathit{is}\mathit{not}a\mathit{chain})\mathit{with}k\mathit{elements}\mathit{and}\hfill \\ & & {\mathcal{L}}_2\mathit{is}a\mathit{BL}-\mathit{algebra}\mathit{with}k\mathit{elements},\hfill \end{array}$$

for $k\ge 2,$ $k={\displaystyle \frac{n+1}{2}}$ $\in N.$

We make the following notations:

$${\mathcal{BL}}_n=\mathrm{the}\mathrm{set}\mathrm{of}\mathrm{BL}-\mathrm{algebras}\mathrm{with}n\mathrm{elements};$$

$${\mathcal{BL}}_n\left(c\right)=\mathrm{the}\mathrm{set}\mathrm{of}\mathrm{BL}-\mathrm{chains}\mathrm{with}n\mathrm{elements};$$

$${\mathcal{DIV}}_n=\mathrm{the}\mathrm{set}\mathrm{of}\mathrm{divisible}\mathrm{residuated}\mathrm{lattices}\mathrm{with}n\mathrm{elements};$$

$${\mathcal{DIV}}_n\left(c\right)=\mathrm{the}\mathrm{set}\mathrm{of}\mathrm{divisible}\mathrm{and}\mathrm{totally}\mathrm{ordered}\mathrm{residuated}\mathrm{lattices}\mathrm{with}n\mathrm{elements}.$$

Theorem 4.

(i)

All finite divisible residuated lattices (up to an isomorphism) with $2\le n\le 6$ elements can be generated using the ordinal product of BL-algebras.

(ii)

The number of non-isomorphic divisible residuated lattices with n elements ($2\le n\le 6$) is

$$\left|{\mathcal{DIV}}_2\right|=\left|{\mathcal{BL}}_2\right|=1,$$

$$\left|{\mathcal{DIV}}_3\right|=\left|{\mathcal{BL}}_3\right|=2,$$

$$\left|{\mathcal{DIV}}_4\right|=\left|{\mathcal{BL}}_4\right|=5,$$

$$\left|{\mathcal{DIV}}_5\right|=\left|{\mathcal{BL}}_5\right|+1=9+1=10,$$

$$\left|{\mathcal{DIV}}_6\right|=\left|{\mathcal{BL}}_6\right|+3=20+3=23,$$

(iii)

For every $n\ge$ $2,$

$$\left|{\mathcal{DIV}}_n\left(c\right)\right|=\left|{\mathcal{BL}}_n\left(c\right)\right|.$$

Proof. 

(i), (ii). We recall that $\left|{\mathcal{BL}}_2\right|=1,\left|{\mathcal{BL}}_3\right|=2,\left|{\mathcal{BL}}_4\right|=5,\left|{\mathcal{BL}}_5\right|=9$, and $\left|{\mathcal{BL}}_6\right|=20$ (see [8,12]). From Proposition 6, Remark 1, and Theorem 3, we remark that, using the ordinal product of two BL-algebras, we can generate divisible residuated lattices which are not BL-algebras only for $n\ge 5$.

Case $n=5.$

We obviously only have a divisible residuated lattice that is not a BL-algebra (up to an isomorphism) since we only have a BL-algebra with four elements (which is not a chain) isomorphic with $Id\left({\mathbb{Z}}_2\times {\mathbb{Z}}_2\right)$ and only a BL-algebra with two elements that are isomorphic with $Id\left({\mathbb{Z}}_2\right)$ (see Example 4).

Case $n=6.$

Using Theorem 3, to generate a divisible residuated lattice with six elements that is not a BL-algebra as an ordinal product ${\mathcal{L}}_1⊠{\mathcal{L}}_2$ of two BL-algebras ${\mathcal{L}}_1$ and ${\mathcal{L}}_2$, we consider the following:

$$\begin{array}{ccc}& & {\mathcal{L}}_1\mathrm{a}\mathrm{BL}-\mathrm{algebra}\mathrm{with}5\mathrm{elements}(\mathrm{which}\mathrm{is}\mathrm{not}\mathrm{a}\mathrm{chain})\mathrm{and}\hfill \\ & & {\mathcal{L}}_2\mathrm{a}\mathrm{BL}-\mathrm{algebra}\mathrm{with}2\mathrm{elements}\hfill \end{array}$$

and

$$\begin{array}{ccc}& & {\mathcal{L}}_1\mathrm{a}\mathrm{BL}-\mathrm{algebra}\mathrm{with}4\mathrm{elements}(\mathrm{which}\mathrm{is}\mathrm{not}\mathrm{a}\mathrm{chain})\mathrm{and}\hfill \\ & & {\mathcal{L}}_2\mathrm{a}\mathrm{BL}-\mathrm{algebra}\mathrm{with}3\mathrm{elements}.\hfill \end{array}$$

We obtain the following three algebras:

$$(Id\left({\mathbb{Z}}_2\right)⊡Id({\mathbb{Z}}_2\times {\mathbb{Z}}_2))⊡Id\left({\mathbb{Z}}_2\right),$$

$$Id({\mathbb{Z}}_2\times {\mathbb{Z}}_2)⊡(Id\left({\mathbb{Z}}_2\right)⊡Id\left({\mathbb{Z}}_2\right))$$

$$Id({\mathbb{Z}}_2\times {\mathbb{Z}}_2)⊡Id\left({\mathbb{Z}}_4\right).$$

We conclude that the structure of divisible residuated lattices L (that are not BL-algebras) with $2\le n\le 6$ is (up to an isomorphism) as follows:

$\left|L\right|=\mathbf{n}$	Nr of algebras	Structure
$n=2$	0	−
$n=3$	0	−
$n=4$	0	−
$n=5$	1	$Id({\mathbb{Z}}_2\times {\mathbb{Z}}_2))⊡Id\left({\mathbb{Z}}_2\right)$
$n=6$	3	$\left\{\begin{array}{c}(Id\left({\mathbb{Z}}_2\right)⊡Id({\mathbb{Z}}_2\times {\mathbb{Z}}_2))⊡Id\left({\mathbb{Z}}_2\right)\\ Id({\mathbb{Z}}_2\times {\mathbb{Z}}_2)⊡(Id\left({\mathbb{Z}}_2\right)⊡Id\left({\mathbb{Z}}_2\right))\\ Id({\mathbb{Z}}_2\times {\mathbb{Z}}_2)⊡Id\left({\mathbb{Z}}_4\right)\end{array}\right.$

$\left(iii\right).$ Clearly, a totally ordered divisible residuated lattice is a BL-algebra. □

Table 2 presents a summary of the number of BL-algebras and divisible residuated lattices with $n\le 6$ elements.

Table 2. The number of BL-algebras and divisible residuated lattices with $n\le 6$ elements.

	$\mathit{n}=2$	$\mathit{n}=3$	$\mathit{n}=4$	$\mathit{n}=5$	$\mathit{n}=6$
BL-algebras	1	2	5	9	20
divisible residuated lattices	1	2	5	10	23

5. Connections Between Commutative Rings and Residuated Lattices

For a commutative and unitary ring A, we have that $\left(Id\right(A),\cap ,+,\otimes \to ,0=\{0\},1=A)$ is a residuated lattice in which the order relation is ⊆, $I\to J=(J:I)$ and $I\odot J=I\otimes J,$ for every $I,J\in Id\left(A\right);$ see [9].

Definition 4.

Let A be a commutative unitary ring.

(i)

The ideal M of the ring A is maximal if it is maximal amongst all proper ideals of the ring A. From here, we have that there are no other ideals different from A containing M. The ideal J of the ring A is a minimal ideal if it is a nonzero ideal which contains no other nonzero ideals.

(ii)

A commutative local ring A is a ring with a unique maximal ideal.

(iii)

Let P $\ne A$ be an ideal in the ring A. Let $a,b\in A$ such that $ab\in P$. If we have $a\in P$ or $b\in P$, then P is called a prime ideal of A.

Definition 5.

(i)

([5]) A commutative ring A is called a Noetherian ring if the condition of the ascending chain is satisfied, which means that every increasing sequence of ideals $I_1\subseteq I_2\subseteq \dots \subseteq I_r\subseteq \dots$ is stationary, and that there is q, such that $I_q=I_{q+1}=\dots$.

(ii)

A commutative ring A is called an Artinian ring if the condition of descending chain is satisfied, which means that every decreasing sequence of ideals $I_1\supseteq I_2\supseteq \dots \supseteq I_r\supseteq \dots$ is stationary, and that there is q such that $I_q=I_{q+1}=\dots$.

Remark 3.

(i)

([24], Lemma 3.5) Let $A={\displaystyle \prod _{j\in J}}{A}_i$ be a direct product of rings. A is a multiplication ring if and only if $A_j$ is a multiplication ring for all $j\in J$.

(ii)

([24], Lemma 3.6) Let A be a multiplication ring and I be an ideal of A. Therefore, the quotient ring $A/I$ is a multiplication ring.

Remark 4.

([19], Corollary 6.1). Let A be a ring. The following conditions are equivalent:

(i)

$A\left[X\right]$ is a multiplication ring;

(ii)

A is a finite direct product of fields.

Remark 5.

([25,26]).

(1)

If A is a Noetherian ring, then the polynomial ring $A\left[X\right]$ is Noetherian and the quotient ring $A/I$ is also a Noetherian ring, for I is an ideal of A.

(2)

Any field and any principal ideal ring is a Noetherian ring.

(3)

Every ideal of the Noetherian ring A is finitely generated.

(4)

An integral domain A is an Artinian ring if and only if A is a field.

(5)

The ring $K\left[X\right]/\left(X^t\right)$ is an Artinian ring for a field K, and t is a positive integer.

(6)

A commutative Noetherian ring A is Artinian if and only if A is a product of local rings.

(7)

In an Artinian ring, every prime ideal is maximal.

(8)

An Artinian ring is a finite direct product of Artinian local rings.

Proposition 7

([27]). Let A be a commutative and unitary ring with a finite number of ideals. Let $n_m\left(A\right)$ be the number of maximal ideals in A; $n_p\left(A\right)$ be the number of prime ideals in A; and $n_I\left(A\right)$ be the number of all ideals in A. Therefore, $n_m\left(A\right)=n_p\left(A\right)=\alpha$ and $n_I\left(A\right)={\displaystyle \prod _{j=1}^{\alpha }}{\beta }_j,{\beta }_j$ are positive integers, ${\beta }_j\ge 2$.

Remark 6.

(1)

First, we must remark that $n_I\left(A_j\right)$ can be any positive integer ${\beta }_j\ge 2$. For example, the ring $K\left[X\right]/\left(X^{{\beta }_j}\right)$ has ${\beta }_j+1$ ideals, ${\beta }_j\ge 2$.

(2)

If $n_I\left(A\right)$ is finite, from the above proposition, we have only the following two possibilities:

-A is an integral domain; therefore, it is a field and, in this case, we have $n_m\left(A\right)=n_p\left(A\right)=1$ and $n_I\left(A\right)=2$ or

- A is not an integral domain and $n_m\left(A\right)=n_p\left(A\right)\ge 1$ and $n_I\left(A\right)>2$.

(3)

From the above proposition, it is clear that there are no finite commutative unitary rings such that $\left(n_m\left(A\right),n_p\left(A\right),n_I\left(A\right)\right)=\left(3,3,5\right)$ or $\left(n_m\left(A\right),n_p\left(A\right),n_I\left(A\right)\right)=\left(2,2,5\right)$, since 5 is a prime number. To find such an example, we must search in infinite rings or in noncommutative rings. Therefore, we have examples only in the case $\left(n_m\left(A\right),n_p\left(A\right),n_I\left(A\right)\right)=\left(1,1,5\right)$. Also, we can find examples of finite commutative unitary rings such that $\left(n_m\left(A\right),n_p\left(A\right),\right.$ $\left.n_I\left(A\right)\right)=\left(2,2,4\right)$ or finite commutative unitary rings such that $\left(n_m\left(A\right),n_p\left(A\right),n_I\left(A\right)\right)=\left(1,1,4\right)$.

Proposition 8.

Let A be a commutative ring which has at most five distinct ideals. Therefore, A is a principal ring.

Proof. 

Since the ring has a finite number of ideals, it is Noetherian; therefore, all ideals are finite-generated. If A has five ideals, let $a,b\in A$ be two distinct nonzero elements and $\left(a\right)$ and $\left(b\right)$ be the ideals generated by a and $\dot{b}$. We suppose that A is not a principal ideal. Therefore, we have $0,\left(a\right),\left(b\right),$ and A has four ideals. It is clear that $\left(a+b\right)$ and $\left(a,b\right)$ are also ideals of A. If we have $\left(a\right)=\left(a+b\right)$, then there is $q\in A$ such that $a+b=qa$, and then $b\in \left(a\right)$ is false. The same situation is if we suppose that $\left(b\right)=\left(a+b\right)$. It is clear that $\left(a+b\right)\ne A$, since we assume that A is not principal; therefore, $\left(a+b\right)=\left(a,b\right)$ and A is principal. □

Remark 7.

(i)

We remark that if A has $2,3$ or 5 ideals, it is therefore local, since it has only one maximal ideal. If A has 4 ideals, then it is not local, in general, since we can have two maximal ideals.

(ii)

Since a commutative ring, which is a principal ideal domain, is a multiplication ring, we have that for a ring with at most 5 ideals, the lattice of ideals $\left(Id\right(A),\cap ,+,\otimes \to ,0=\{0\},1=A)$ is a divisible residuated lattice.

(iii)

We know that if a ring A has a finite number of ideals, then it is Artinian and an Artinian ring is a finite direct product of Artinian local rings. Therefore, if $A=A_1\times \dots \times A_q,$ with $A_i$ local Artinian rings, we have that each ideal J in A is of the form $J=J_1\times \dots \times J_q$, with $J_i$ ideal in $A_i$. We obtain that the ring $A=A_1\times \dots \times A_q$—such that the numbers of ideals for the rings $A_i$ are $n_{A_i}$, with $n_{A_i}\in \{2,3,5\},i\in \{1,2,\dots ,q\}$—is a principal ideal ring, and therefore, a multiplication ring. For example, if $A=A_1\times A_2$, with $n_{A_1}=2$ and $n_{A_2}=5$, it is a principal ideal ring with 10 ideals, and therefore a multiplication ring, and the lattice $Id\left(A\right)$ is a divisible residuated lattice. If $A=A_1\times A_2\times A_3$, with $n_{A_1}=3,n_{A_2}=3$, and $n_{A_3}=5$, it is a principal ideal ring with 45 ideals, $Id\left(A\right)$ is a divisible residuated lattice, etc.

Remark 8.

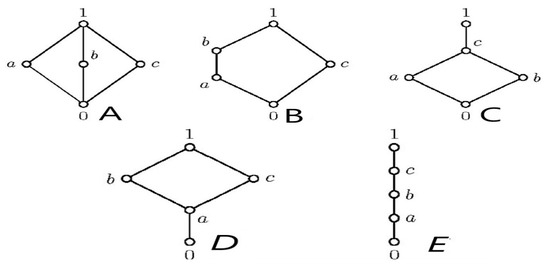
Since we have only five types of lattices with five elements (see Figure 1), from [27], to obtain divisible residuated lattices (DRLs), the lattice of ideals must be of the type $(Type\_A),(Type\_B)$, or $(Type\_C)$. $(Type\_B)$ is the pentagon lattice, which is not modular and can be excluded. Either only $(Type\_$$A)$ remains, the diamond lattice (which is not distributive but is modular), or $(Type\_C)$. But $(Type\_A)$ involves the existence of a ring with five ideals and three of them have to be maximal ideals, which is false, from Remark 8. Therefore, only $(Type\_C)$ remains. From here, we have that, to find an example of DRL, which comes from a multiplication ring, and an MTL ring, which is not a multiplication ring, we must search between infinite commutative and unitary rings and not between finite commutative and unitary rings.

Figure 1. The types of latices with five elements (A–E).

Definition 6

([28], p. 150). A unitary ring A is called an arithmetical ring if and only if for all ideals $I,J,$ and K, we have $I\cap \left(J+K\right)=(I\cap J)+(I\cap K)$, or, equivalently $I+\left(J\cap K\right)=\left(I+J\right)\cap \left(I+K\right)$, which means that the lattice of ideals is distributive.

Remark 9.

(1)

Using Proposition 5, the multiplication rings are arithmetical rings.

(2)

In the paper [6], the authors studied a class of commutative rings having the lattice of ideals of an MTL-algebra, which makes a BL-algebra not necessary.They proved that a local commutative ring with identity is an MTL-ring if and only if it is an arithmetical ring. Since an MTL-ring is an arithmetical ring and the converse is true if the ring is Noetherian, and since a unitary commutative Noetherian MTL-ring is also a BL-ring, therefore, to obtain a valid example of an MTL-ring which is not a BL-ring, we must search outside the Noetherian case.

(3)

From the above, to find an example of MTL-ring A of order 5 that is not a BL-ring, the lattice $Id\left(A\right)$ must be on $(Type\_C),$ since $(Type\_A)$ is not distributive.

In the following, we provide an example of a noncommutative ring A having lattice $Id\left(A\right)$, the diamond lattice.

Example 5.

We consider the noncommutative ring $A={\mathcal{M}}_2\left({\mathbb{Z}}_2\right)$, the set of quadratic matrices over the field ${\mathbb{Z}}_2$. We know that A is semisimple, and thus, all right or left ideals are principal and are generated by idempotents ([25], p. 150). If $e\in A$ is an idempotent, then $1-e$ is also an idempotent. We have the following idempotents: $\{\left(\begin{array}{cc}1& 0\\ 0& 0\end{array}\right),\left(\begin{array}{cc}0& 0\\ 0& 1\end{array}\right),\left(\begin{array}{cc}1& 1\\ 0& 0\end{array}\right),\left(\begin{array}{cc}0& 1\\ 0& 1\end{array}\right),\left(\begin{array}{cc}1& 0\\ 1& 0\end{array}\right),\left(\begin{array}{cc}0& 0\\ 1& 1\end{array}\right)\}$ and we have three proper left ideals: $a=A\left(\begin{array}{cc}1& 0\\ 0& 0\end{array}\right),b=A\left(\begin{array}{cc}0& 1\\ 0& 1\end{array}\right),c=A\left(\begin{array}{cc}1& 0\\ 1& 0\end{array}\right)$. The lattice $Id\left(A\right)$ is the diamond lattice, which is not a residuated lattice. The elements $a,b,c$ do not verify the condition 3 from the definition of residuated lattices. But the conditions $\left(prel\right)$ and $\left(div\right)$ are verified.

For other details, the readers are referred to [29].

6. Conclusions

In this paper, we studied commutative rings having on their lattice of ideals a structure of divisible residuated lattice. We proved that these rings are multiplication rings. Moreover, we gave a characterization and several examples, and we established some connections to other classes of rings. We also analyzed the structure of divisible residuated lattices by using finite commutative rings, presented an explicit construction of isomorphism classes of divisible residuated lattices of small size, and gave summarizing statistics.

These two areas, of commutative rings and residuated lattices, are usually studied independently and, for this reason, until now, connections between divisibility in residuated lattices and commutative rings have not been properly explored. Through the obtained results, we were focused on emphasizing how the properties of these specific rings can influence the structures of the lattices of their ideals. From here, a question arises: “who influences who?” The study of the commutative rings can allow us to find new applications and directions of research in the study of residuated lattices, or vice versa, the study of residuated lattices can bring us new ways to characterize the commutative rings.

As part of further research, our goal is to find other examples, especially examples of MTL residuated lattices that are not BL-algebras, that is, those which are not divisible residuated lattice. These examples are hard to find and this is also reinforced by the fact that such explicit examples are rare in the specialized literature. To find them, we must search far from the comfort area given by the finite commutative rings, where their structure is well known and clearly explained. For this purpose, we will study the arithmetical rings, trying to give new characterizations or classifications of these objects.