Application of a Hybrid of the Different Transform Method and Adomian Decomposition Method Algorithms to Solve the Troesch Problem
Abstract
1. Introduction
2. Different Transform Method
3. Adomian Decomposition Method
4. Solution Method
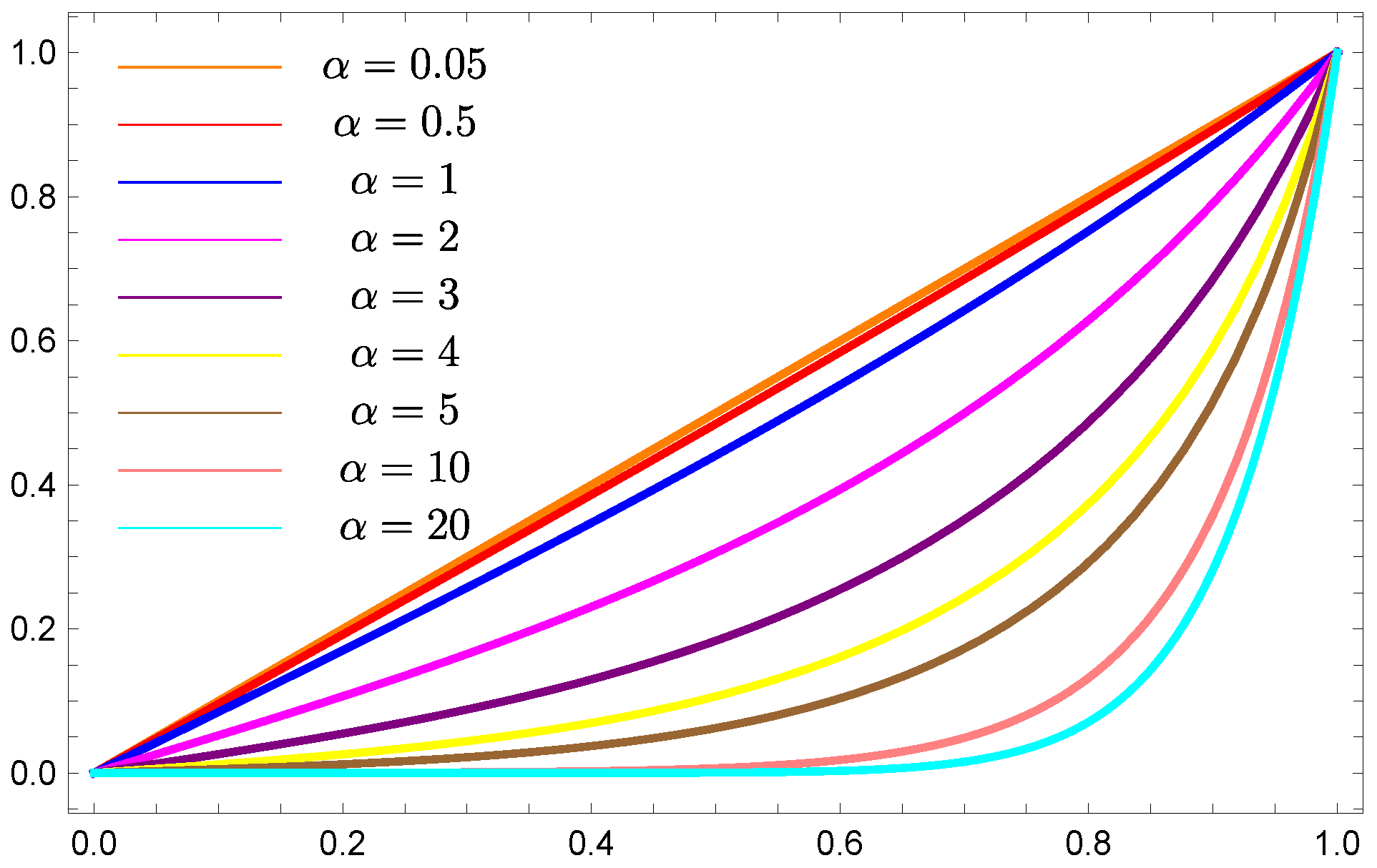
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Troesch, B.A. A simple approach to a sensitive two-point boundary value problem. J. Comput. Phys. 1976, 21, 279–290. [Google Scholar] [CrossRef]
- Feng, X.; Mei, L.; He, G. An efficient algorithm for solving Troesch’s problem. Appl. Math. Comput. 2007, 189, 500–507. [Google Scholar] [CrossRef]
- Mirmoradi, S.H.; Hosseinpour, I.; Ghanbarpour, S.; Barari, A. Application of an approximate analytical method to nonlinear Troesch’s problem. Appl. Math. Sci. 2009, 3, 1579–1585. [Google Scholar]
- Vazquez-Leal, H.; Khan, Y.; Fernandez-Anaya, G.; Herrera-May, A.; Sarmiento-Reyes, A.d.; Filobello-Nino, U.; Jimenez-Fernandez, V.-M.; Pereyra-Diaz, D. A general solution for Troesch’s problem. Math. Probl. Eng. 2012, 1, 208375. [Google Scholar] [CrossRef]
- Khuri, S.A.; Sayfy, A. Troesch’s problem: A B-spline collocation approach. Math. Comput. Model. 2011, 54, 9–10. [Google Scholar] [CrossRef]
- Chang, S.-H. A variational iteration method for solving Troesch’s problem. J. Comput. Appl. Math. 2010, 234, 3043–3047. [Google Scholar] [CrossRef]
- Izadi, M.; Yüzbaşi, Ş.; Noeiaghdam, S. Approximating solutions of non-linear Troesch’s problem via an efficient quasi-linearization Bessel approach. Mathematics 2021, 9, 1841. [Google Scholar] [CrossRef]
- Deeba, E.; Khuri, S.A.; Xie, S. An algorithm for solving boundary value problems. J. Comput. Phys. 2000, 159, 125–138. [Google Scholar] [CrossRef]
- Temimi, H. A discontinuous Galerkin finite element method for solving the Troesch’s problem. Appl. Math. Comput. 2012, 219, 521–529. [Google Scholar] [CrossRef]
- El-Gamel, M.; Sameeh, M. A Chebychev collocation method for solving Troesch’s problem. Int. J. Math. Comput. Appl. Res. 2013, 3, 23–32. [Google Scholar]
- Khuri, S.A. A numerical algorithm for solving Troesch’s problem. Int. J. Comput. Math. 2003, 80, 493–498. [Google Scholar] [CrossRef]
- Filali, D.; Ali, F.; Akram, M.; Dilshad, M. A Novel Fixed-Point Iteration Approach for Solving Troesch’s Problem. Symmetry 2024, 16, 856. [Google Scholar] [CrossRef]
- Kafri, H.Q.; Khuri, S.A.; Sayfy, A. A new approach based on embedding Green’s functions into fixed-point iterations for highly accurate solution to Troesch’s problem. Int. J. Comput. Methods Eng. Sci. Mech. 2016, 17, 93–105. [Google Scholar] [CrossRef]
- Mohyud-Din, S.T. Solution of Troesch’s problem using He’s polynomials. Rev. Un. Mat. Argentina 2011, 52, 143–148. [Google Scholar]
- Zhou, J.K. Differential Transformation and Its Applications for Electrical Circuits; Huazhong University Press: Wuhan, China, 1986. [Google Scholar]
- Ahmad, M.Z.; Alsarayreh, D.; Alsarayreh, A.; Qaralleh, I. Differential transformation method (DTM) for solving SIS and SI epidemic models. Sains Malays. 2017, 46, 2007–2017. [Google Scholar] [CrossRef]
- Hetmaniok, E.; Pleszczyński, M. Comparison of the selected methods used for solving the ordinary differential equations and their systems. Mathematics 2022, 10, 306. [Google Scholar] [CrossRef]
- Mohanty, M.; Jena, S.R. Differential transformation method (DTM) for approximate solution of ordinary differential equation (ODE). Adv. Model. Anal. B 2018, 61, 3. [Google Scholar] [CrossRef]
- Domairry, G.; Hatami, M. Squeezing Cu–water nanofluid flow analysis between parallel plates by DTM-Padé Method. J. Mol. Liq. 2014, 193, 37–44. [Google Scholar] [CrossRef]
- Sepasgozar, S.; Faraji, M.; Valipour, P. Application of differential transformation method (DTM) for heat and mass transfer in a porous channel. Propuls. Power Res. 2017, 6, 41–48. [Google Scholar] [CrossRef]
- Momani, S.; Odibat, Z. A novel method for nonlinear fractional partial differential equations: Combination of DTM and generalized Taylor’s formula. J. Comput. Appl. Math. 2008, 220, 85–95. [Google Scholar] [CrossRef]
- Merdan, M.; Gökdoğan, A.; Yıldırım, A.; Mohyud-Din, S.T. Numerical Simulation of Fractional Fornberg-Whitham Equation by Differential Transformation Method. Abstr. Appl. Anal. 2012, 2012, 965367. [Google Scholar] [CrossRef]
- Allahviranloo, T.; Kiani, N.A.; Motamedi, N. Solving fuzzy differential equations by differential transformation method. Inf. Sci. 2009, 179, 956–966. [Google Scholar] [CrossRef]
- Odibat, Z.M. Differential transform method for solving Volterra integral equation with separable kernels. Math. Comput. Model. 2008, 48, 1144–1149. [Google Scholar] [CrossRef]
- Hadizadeh, M.; Moatamedi, N. A new differential transformation approach for two-dimensional Volterra integral equations. Int. J. Comput. Math. 2007, 84, 515–526. [Google Scholar] [CrossRef]
- Brociek, R.; Pleszczyński, M. Comparison of Selected Numerical Methods for Solving Integro-Differential Equations with the Cauchy Kernel. Symmetry 2024, 16, 233. [Google Scholar] [CrossRef]
- Hetmaniok, E.; Pleszczyński, M.; Khan, Y. Solving the integral differential equations with delayed argument by using the DTM method. Sensors 2022, 22, 4124. [Google Scholar] [CrossRef]
- Yüzbaşı, Ş.; Ismailov, N. Solving systems of Volterra integral and integrodifferential equations with proportional delays by differential transformation method. J. Math. 2014, 2014, 725648. [Google Scholar] [CrossRef][Green Version]
- Brociek, R.; Pleszczyński, M. Differential Transform Method and Neural Network for Solving Variational Calculus Problems. Mathematics 2024, 12, 2182. [Google Scholar] [CrossRef]
- Nejatbakhsh, Y.; Allahviranloo, T.; Kiani, N.A. Solving Fuzzy Integral equations by Differential Transformation Method, First Joint Congress on Fuzzy and Intelligent Systems; Ferdowsi University of Mashhad: Mashhad, Iran, 2007. [Google Scholar]
- Liu, H.; Song, Y. Differential transform method applied to high index differential–algebraic equations. Appl. Math. Comput. 2007, 184, 748–753. [Google Scholar] [CrossRef]
- Ibis, B.; Bayram, M.; Agargun, A.G. Applications of fractional differential transform method to fractional differential-algebraic equations. Eur. J. Pure Appl. Math. 2011, 4, 129–141. [Google Scholar]
- Cockett, J.R.B.; Seely, R.A.G. The Faa di Bruno construction. Theory Appl. Categ. 2011, 25, 394–425. [Google Scholar]
- Mishkov, R.L. Generalization of the formula of Faa di Bruno for a composite function with a vector argument. Int. J. Math. Math. Sci. 2000, 24, 481–491. [Google Scholar] [CrossRef]
- Adomian, G. Nonlinear Stochastic Systems Theory and Applications to Physics; Springer Science and Business Media: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Adomian, G. A review of the decomposition method in applied mathematics. J. Math. Anal. Appl. 1988, 135, 501–544. [Google Scholar] [CrossRef]
- Chang, M.-H. A decomposition solution for fins with temperature dependent surface heat flux. Int. J. Heat Mass Transf. 2005, 48, 1819–1824. [Google Scholar] [CrossRef]
- Grzymkowski, R.; Pleszczyński, M.; Słota, D. Comparing the Adomian decomposition method and the Runge–Kutta method for solutions of the Stefan problem. Int. J. Comput. Math. 2006, 83, 409–417. [Google Scholar] [CrossRef]
- Grzymkowski, R.; Pleszczyński, M.; Słota, D. The two-phase Stefan problem solved by the Adomian decomposition method. In Proceedings of the 15th IASTED International Conference on Applied Simulation and Modelling, Rhodes, Greece, 26–28 June 2006; pp. 511–516. [Google Scholar]
- Lesnic, D.; Elliott, L. The decomposition approach to inverse heat conduction. J. Math. Anal. Appl. 1999, 232, 82–98. [Google Scholar] [CrossRef]
- Pamuk, S. An application for linear and nonlinear heat equations by Adomian’s decomposition method. Appl. Math. Comput. 2005, 163, 89–96. [Google Scholar] [CrossRef]
- Jafari, H.; Daftardar-Gejji, V. Solving linear and nonlinear fractional diffusion and wave equations by Adomian decomposition. Appl. Math. Comput. 2006, 180, 488–497. [Google Scholar] [CrossRef]
- Lesnic, D. The Cauchy problem for the wave equation using the decomposition method. Appl. Math. Lett. 2002, 15, 697–701. [Google Scholar] [CrossRef]
- Singla, R.K.; Das, R. Application of Adomian decomposition method and inverse solution for a fin with variable thermal conductivity and heat generation. Int. J. Heat Mass Transf. 2013, 66, 496–506. [Google Scholar] [CrossRef]
- Shahrezaee, A.M.; Hoseininia, M. Solution of some parabolic inverse problems by Adomian decomposition method. Appl. Math. Sci. 2011, 5, 3949–3958. [Google Scholar]
- Duan, J.-S.; Rach, R.; Baleanu, D.; Wazwaz, A.-M. A review of the Adomian decomposition method and its applications to fractional differential equations. Commun. Fract. Calc. 2012, 3, 73–99. [Google Scholar]
- Tatari, M.; Dehghan, M.; Razzaghi, M. Application of the Adomian decomposition method for the Fokker–Planck equation. Math. Comput. Model. 2007, 45, 639–650. [Google Scholar] [CrossRef]
- Wang, Q. Numerical solutions for fractional KdV–Burgers equation by Adomian decomposition method. Appl. Math. Comput. 2006, 182, 1048–1055. [Google Scholar] [CrossRef]
- Wazwaz, A.-M. A reliable modification of Adomian decomposition method. Appl. Math. Comput. 1999, 102, 77–86. [Google Scholar] [CrossRef]
- Behiry, S.H. Differential transform method for nonlinear initial-value problems by Adomian polynomials. J. Appl. Comput. Math. 2012, 1, 109–114. [Google Scholar] [CrossRef]
- Moon, S.D.; Bhosale, A.B.; Gajbhiye, P.P.; Lonare, G.G. Solution of non-linear Differential equations by using differential Transform Method. Int. J. Math. Stat. Invent. 2014, 2, 78–82. [Google Scholar] [CrossRef]
- Hastings, C.; Mischo, K.; Morrison, M. Hands-on Start to Wolfram Mathematica: And Programming with the Wolfram Language; Wolfram Media: Champaign, IL, USA, 2015. [Google Scholar]
- Wolfram, S. The Mathematica Book; Wolfram Research, Inc.: Champaign, IL, USA, 2003. [Google Scholar]

| x | |||||||
|---|---|---|---|---|---|---|---|
| 0.0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.1 | 0.09518 | 0.09604 | 0.00086 | 0.09594 | 0.09604 | 0.09594 | 0.00077 |
| 0.2 | 0.19063 | 0.19232 | 0.00169 | 0.19213 | 0.0015 | 0.19213 | 0.00149 |
| 0.3 | 0.28665 | 0.28908 | 0.00243 | 0.2888 | 0.00214 | 0.28879 | 0.00214 |
| 0.4 | 0.38352 | 0.38656 | 0.00304 | 0.38619 | 0.00266 | 0.38619 | 0.00266 |
| 0.5 | 0.48154 | 0.485 | 0.00346 | 0.48455 | 0.00301 | 0.48455 | 0.00301 |
| 0.6 | 0.581 | 0.58464 | 0.00364 | 0.58413 | 0.00313 | 0.58413 | 0.00313 |
| 0.7 | 0.68224 | 0.68572 | 0.00348 | 0.6852 | 0.00297 | 0.6852 | 0.00297 |
| 0.8 | 0.78557 | 0.78848 | 0.00291 | 0.78802 | 0.00245 | 0.78802 | 0.00244 |
| 0.9 | 0.89137 | 0.89316 | 0.00179 | 0.89286 | 0.00149 | 0.89285 | 0.00149 |
| 1.0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 |
| 0.0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.1 | 0.081797 | 0.084661 | 0.002864 | 0.027075 | 0.001129 | |
| 0.2 | 0.164531 | 0.170171 | 0.00564 | 0.056609 | 0.002361 | |
| 0.3 | 0.249167 | 0.257394 | 0.008227 | 0.091305 | 0.003811 | |
| 0.4 | 0.336732 | 0.347223 | 0.010491 | 0.134397 | 0.00561 | |
| 0.5 | 0.428347 | 0.4406 | 0.012253 | 0.190036 | 0.00797 | |
| 0.6 | 0.525274 | 0.538534 | 0.01326 | 0.263908 | 0.011161 | |
| 0.7 | 0.628971 | 0.642129 | 0.013158 | 0.364292 | 0.015487 | |
| 0.8 | 0.741168 | 0.752608 | 0.01144 | 0.504007 | 0.020869 | |
| 0.9 | 0.86397 | 0.871363 | 0.007393 | 0.704013 | 0.02385 | |
| 1.0 | 1 | 1.0 | 1 | 1.0 | ||
| 0.0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.1 | 0.081797 | 0.013276 | 0.001788 | 0.000118 | 0.000076 | |
| 0.2 | 0.164531 | 0.028707 | 0.003866 | 0.000365 | 0.000235 | |
| 0.3 | 0.249167 | 0.048805 | 0.006575 | 0.001009 | 0.00065 | |
| 0.4 | 0.336732 | 0.076875 | 0.01037 | 0.002749 | 0.001771 | |
| 0.5 | 0.428347 | 0.117628 | 0.01592 | 0.007472 | 0.004813 | |
| 0.6 | 0.525274 | 0.178181 | 0.024257 | 0.02028 | 0.013051 | |
| 0.7 | 0.628971 | 0.269837 | 0.036909 | 0.054827 | 0.035163 | |
| 0.8 | 0.741168 | 0.411406 | 0.055126 | 0.146913 | 0.093183 | |
| 0.9 | 0.86397 | 0.635472 | 0.072162 | 0.387611 | 0.235497 | |
| 1.0 | 1 | 1.0 | 1 | 1 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pleszczyński, M.; Kaczmarek, K.; Słota, D. Application of a Hybrid of the Different Transform Method and Adomian Decomposition Method Algorithms to Solve the Troesch Problem. Mathematics 2024, 12, 3858. https://doi.org/10.3390/math12233858
Pleszczyński M, Kaczmarek K, Słota D. Application of a Hybrid of the Different Transform Method and Adomian Decomposition Method Algorithms to Solve the Troesch Problem. Mathematics. 2024; 12(23):3858. https://doi.org/10.3390/math12233858
Chicago/Turabian StylePleszczyński, Mariusz, Konrad Kaczmarek, and Damian Słota. 2024. "Application of a Hybrid of the Different Transform Method and Adomian Decomposition Method Algorithms to Solve the Troesch Problem" Mathematics 12, no. 23: 3858. https://doi.org/10.3390/math12233858
APA StylePleszczyński, M., Kaczmarek, K., & Słota, D. (2024). Application of a Hybrid of the Different Transform Method and Adomian Decomposition Method Algorithms to Solve the Troesch Problem. Mathematics, 12(23), 3858. https://doi.org/10.3390/math12233858








