Dynamic Decisions of Quality and Goodwill in a Two-Echelon Supply Chain with Delay Effect

Abstract

Improving product quality is an effective way for a company to gain goodwill as well as to increase sales. In this paper, the focus is on a two-echelon supply chain consisting of a manufacturer and a retailer. Considering the delayed effect of quality improvement on product quality, the differential equations on the levels of quality and goodwill as the state variables are established to explore the impact of delay time on members’ strategy inputs, supply chain profits and performance under decentralized and centralized decision models. Additionally, in this paper, how different profit maximization scenarios affect supply chain revenue under decentralized models is examined. The equilibrium solutions are obtained by numerical simulation. The results show that both quality improvement efforts and marketing efforts are decreasing functions of delay time, and the delay effect affects the motivation of supply chain members’ strategic inputs. Importantly, supply chain profit under centralized decision is not always higher than that under decentralized decision when the manufacturer’s concern degree and delay time are taken into account. The Rubinstein bargaining model is then used to optimize the profit distribution between the manufacturer and the retailer under centralized decision. In this paper, it is also identified that the longer the delay time, the lower the levels of quality and goodwill. The dual effect of delay effect and concern degree will exacerbate the negative impact on the levels of quality and goodwill.

1. Introduction

As the economy moves forward at a rapid pace, the competitive pattern of the market has gradually changed, and product quality has become an effective way to improve the competitiveness of enterprises [1,2]. For example, a representative enterprise is Weichai Power Co., Ltd., whose self-developed Weichai engine with 1.8 million kilometers/30,000 h has set up the highest life standard for high-speed heavy-duty engines worldwide. In the past twenty years, this enterprise has gone from negative assets to an annual sale of CNY 213.96 billion by relying on high-quality products [3]. Therefore, quality level and brand goodwill as a comprehensive evaluation of the core competitiveness and performance of enterprises have received considerable attention in the supply chain management literature and have important research significance.

However, the improvement of product quality or brand goodwill does not immediately affect the profits of the supply chain during the implementation of enterprise decisions. On the contrary, there is a delay phenomenon [4]. In the promotional process of advertising, the advertising cost invested by enterprises will affect brand goodwill or sales after some time [5]. Manufacturers’ quality improvement behaviors also do not result in immediate quality improvement and take some time to materialize. In response, it takes time for consumers to perceive an improvement in product quality and to make a purchase decision. We refer to these phenomena above as the delay effect of strategy inputs [5]. When the delay effect exits, if the manufacturer ignores the phenomenon and blindly invests or terminates the investment, it will bring immeasurable losses to the enterprise. For example, despite Smartisan T1 hammer phone financing of as much as CNY 2 billion, the delay effect of production capacity and R&D of enterprise liabilities reached 99% in less than four years [6]. It follows that the delay effect in the behavior of upstream manufacturers impacts downstream retailers’ decisions, quality levels and brand goodwill. Therefore, the delay effect is crucial for the manufacturer and the retailer in the supply chain, especially since the length of delay time is key for enterprises to avoid unnecessary losses and create economic benefits.

In a decentralized supply chain, the pursuit of individual interests by each member often leads to conflicts and suboptimal outcomes among them [7,8], especially when the delay effect occurs. As the dominant player in the supply chain, the role of the manufacturer has endured some significant changes. The manufacturer has to guarantee the product quality while minimizing delay time in quality improvement to ensure stability in the downstream retail channel [9]. Henceforth, the manufacturer’s business objective changes from maximizing their profit to maximizing the relative profit, that is, maximizing the utility of the difference between their own profit and the degree of concern to the retailer’s profit, so as to ensure the overall competitiveness of the supply chain in the market. Therefore, the study of the degree of the manufacturer’s concern to the retailer and the determination of delay time is crucial to the economic efficiency of the whole supply chain system.

Based on the above analysis, in this paper, the intention is to examine the influence of delay effects on product quality, goodwill and strategic inputs in a two-echelon supply chain, and subsequently analyze the profits and decisions of the supply chain members under different decision models. The particular questions are outlined below, as follows:

(1)

How do the manufacturer and the retailer implement quality improvement decisions and marketing decisions when delay effects occur? What are the effects of delays in manufacturer quality improvement on product quality and goodwill? How do the levels of quality and goodwill change in comparison to the immediate effect?

(2)

What are the differences in investments and profits of the manufacturer and the retailer under decentralized and centralized models? In the relative profit decision model, what effect does the manufacturer’s concern degree have on the revenue of the retailer and the supply chain?

(3)

Is the supply chain profit under the centralized decision model necessarily better than those under the decentralized decision model? Which decision structure is more favorable to the economic efficiency of the supply chain and its members under the delay effect?

To solve the above questions, in this paper, a two-echelon supply chain is constructed consisting of the manufacturer and the retailer and the impact of the delayed effect of quality improvement on product quality and goodwill is considered. Using the delayed differential game theory, it investigates the quality decisions, marketing decisions and profits of supply chain members under decentralized and centralized models. Furthermore, in order to explore the impact of the manufacturer’s quality delay behavior downstream of the retailer, we designed decentralized decision models based on own profit and relative profit. It is found that the manufacturer’s profit is inversely proportional to the concern degree for the retailer’s profit. The higher the manufacturer’s concern, the lower their profit. This study further found that the delay effect is detrimental to the improvement of product quality and goodwill, and the length of the delay time directly affects the levels of quality and goodwill. Meanwhile, the delay time determines which cooperation mode the supply chain members choose to maximize their revenue. Unlike previous studies, the cooperation between members no longer optimizes the economic efficiency of the supply chain [10,11,12], which indicates that the study of the threshold of the delay time and the degree of concern is of great significance in the behavioral decision-making of supply chain members.

The rest of this paper is organized as follows: Section 2 is a review of the relevant literature. Section 3 presents the research problem of the supply chain and relevant assumptions. Section 4 and Section 5 construct different decision-making models and analyze the equilibrium results. The results analysis and managerial insights are conducted in Section 6. The final section summarizes the conclusions.

2. Literature Review

The relevant literature mainly includes the following five aspects: product quality in supply chain, goodwill in supply chain, product quality and goodwill in supply chain, supply chain with delay effect, and supply chain decision-making.

2.1. Product Quality in Supply Chain

The product quality in the supply chain has been the focus of scholars’ attention. The level of quality is not only one of the effective means for enterprises to compete but also can directly affect the purchase choice of consumers. However, the evaluation of quality is often subjective, leading to different measurement standards. Most studies have focused on the quality reference effect. Hardie et al. [13] put forward the concept of reference quality and analyzed the impact of quality on demand in terms of reference dependence and loss aversion. The verification results show that the gap between product quality and reference quality affects consumers’ choices. When the product quality exceeds the reference quality, the consumers’ purchasing rate increases. Zhou et al. [14] discussed the influence of the quality reference effect and service reference effect on the decisions of dual-channel supply chain members. In their study, four decision models were designed and obtained the optimal product quality and service quality to make the supply chain performance optimal. However, product quality is not only referable and testable; for the manufacturer, product quality is produced. Xu et al. [15] considered the effects of three subsidy strategies of the government, the manufacturer and the retailer on the green quality and profitability of products. They concluded that higher government subsidies could stimulate the manufacturer to improve the green quality of products, resulting in greater profitability for the entire supply chain. Chenavaz [16] studied the quality strategies of enterprises in static and dynamic environments, using Pontryagin’s maximum theory to obtain the optimal quality strategy input of monopoly enterprises, which provided important reference suggestions for enterprises’ quality inputs. Liu et al. [17] classified the quality behaviors of the manufacturer into myopic and far-sighted situations and discussed the product quality and pricing strategies under different decision models. They found that the level of product quality and price are lower under the manufacturer’s far-sighted decision making, while the manufacturer can provide higher quality products under the myopic decision making. In contrast to these studies, our study integrates the manufacturer’s quality strategy and the retailer’s marketing strategy and investigates how the level of product quality is affected by the delay effect of quality behavior.

2.2. Goodwill in Supply Chain

Retailers and distributors will enhance the level of brand goodwill through various marketing activities to drive demand. Numerous studies have shown that brand goodwill and advertising marketing can stimulate consumers’ buying inclination [18,19]. Gou et al. [20] believed that it was realistic to study the impact of advertising cooperation between enterprises on goodwill and sales. They designed three differential game models to describe the mode of advertising cooperation between two firms and found that advertising cooperation in the form of contract alliance is the choice model of most firms, and the level of advertising for products under a cooperative alliance is the optimum. Dai et al. [21] constructed two sales models of traditional channels and online retail channels and discussed the impact of advertising investment on manufacturer’s dynamic and static pricing. They suggested the dynamic pricing strategy of the manufacturer will limit advertising input, which is detrimental to supply chain efficiency. Yu et al. [22] also studied the advertising cooperation problem of horizontal enterprises, but they focused on the effect of the advertising threshold on the advertising level. The advertising threshold under monopoly and duopoly not only affects the level of advertising investment of enterprises, but also affects the advertising investment of the competitors. Taboubi [23] divided advertising investment into national and local, controlled by the manufacturer and the retailer, respectively. The proposed incentive mechanism can mitigate the problem of double marginalization and increase goodwill and demand.

2.3. Product Quality and Goodwill in Supply Chain

The above studies have examined the impact of supply chain members’ behavioral decisions on quality and goodwill, respectively. In practice, quality and goodwill interact with each other in the supply chain, which is affected by the behavioral decisions of enterprises. He et al. [24] designed two different sales functions offline and online to observe how reference quality effects affect consumer and enterprise decisions. It is found that when the offline shopping ratio is large, suppliers choose to increase quality improvement input; when the online consumer ratio is large, the enterprise should focus more on advertising input than on quality. Giovanni et al. [25] investigated the effects of quality improvement and advertising on goodwill in cooperative and non-cooperative situations. In their study, they elucidated that the manufacturer has an incentive to cooperate and achieve Pareto improvements when advertising is significantly beneficial to goodwill. Xu et al. [26] conducted a supply chain composed of two suppliers and manufacturers with competition and explored the effects of competition and brand halo on the quality strategies of the supply chain members. Their findings showed that the intensity of competition can influence members’ decisions to cooperate bilaterally, and brand halo is more conducive to product quality. Ni and Li [27] examined the relationship between price and product quality and goodwill. The results showed that product quality improvement has a direct impact on goodwill accumulation, and higher quality or goodwill can reduce the product price. In a study conducted by Reddy et al. [28], they combined quality with three classic dynamic advertising models to investigate the optimal decisions for quality inputs and advertising expenditures. They mainly focused on the effects of revenue parameters, pulse parameters and decay parameters on product quality, advertising inputs and goodwill. Liu et al. [29] surveyed the relationship between pay ware sales and product quality, goodwill and reference price, and analyzed product quality, advertising efforts and revenue under decentralized and centralized decisions. Similar to the above studies, in this paper, the impact of supply chain member decisions on quality and goodwill is also investigated. However, it differs by considering the concern degree of the manufacturer to affect the downstream retailer and the profitability of the supply chain.

2.4. Supply Chain with Delay Effect

Currently, the delay effect is widely studied in the field of supply chain management, which involves the delayed payment and decision equilibrium of supply chain members [30], the correlation effect between the delay effect of emission reduction technology and the level of carbon emission [31] and the impact of transportation lag on the inventory decision of upstream and downstream managers in the supply chain [32]. However, in terms of product quality or brand goodwill, most of the existing studies are about the effect of advertising and marketing on goodwill [18,19,20,21,22,23]. As early as 1977, Pauwels [33] generalized the Nerlove–Arrow model [18] of advertising by proposing that there is a delayed response of advertising expenditures to goodwill and sales. This delay is not conducive to advertising achieving its desired effects and also reduces the long-run equilibrium rate of advertising. Aravindakshan et al. [34] argued that consumers’ memory of advertisements appears to decline with conscious delay. The optimal advertising strategy is investigated by comparing the following three strategies: uniform expenditure, flash strategy and cyclic pulse. Their findings showed that impulse advertising is the optimal advertising strategy under the scalar delay differential equation. Chen et al. [35] studied the delay effect in advertising cooperation between the manufacturer and the retailer on the level of corporate social responsibility. The findings indicated that the time delay promotes the manufacturer’s social efforts and the retailer’s advertising campaigns, but damages the overall profitability of the supply chain. Yu et al. [36] examined the delay between advertising exposure and advertising effectiveness and discussed the advertising inputs and members’ profits under different cooperation scenarios. They designed a transfer payment contract to maximize the benefits of each member of the supply chain. Yu et al. [37] considered the effects of national and regional advertising input delays on brand goodwill and specifically analyzed the dynamic advertising decision problem of supply chain systems under the influence of stochastic factors. The results show that long advertising intervals will weaken the memorization effect of advertisements, which is not conducive to the establishment of brand goodwill. Wu et al. [38] demonstrated the dynamics of platform goodwill through the delay effect of advertising. Their proposed commission contract with bilateral participation can realize supply chain members’ profits at lower delay times. Zhou et al. [39] analyzed the delay effect of low carbon investment and low carbon effort on goodwill. Their findings showed that the length of delay determines the choice between decentralized and centralized decision-making options for supply chain members.

However, the above studies have mainly focused on the direct impact of advertising on goodwill, while ignoring the effects of product quality on goodwill under the changing competitive market. A limited number of scholars have studied the effect of quality delays on goodwill. Zhan et al. [40] investigated the effect of product quality and service quality delays on goodwill. They concluded that the delay time determines the decisions of the supply chain members, and the impact of quality on goodwill exists at different delay thresholds under decentralized and centralized decision-making. Peng and Ning [41] explored the delayed impact of quality improvement on goodwill in both decentralized and centralized decision-making models. They found that supply chain profits depend on the length of the delay time. Meanwhile, the competition coefficient of the two retailers affects the supply chain members’ decisions. Although the above literature examines the delayed effect of quality on goodwill, in practice, product quality is the most direct influence on the delay phenomenon of quality behavior. Compared with the above studies, we construct a delayed differential game model consisting of a manufacturer and a retailer and investigate the effect of quality behavior on two state variables, product quality and goodwill.

2.5. Supply Chain Decision-Making

Game theory has been widely used in supply chain decision-making, mainly through the Nash game, the Stackelberg game and the cooperative game [42,43,44,45]. Among them, the differential game describes the continuous process of the system state through differential equations, emphasizing the continuous game behavior and the strategic decisions of the members [46], which has been mentioned in the above literature on quality and goodwill. However, in the actual business activities, managers not only pay attention to their profits, but also pay attention to the profits of competitive enterprises or supply chain members. Therefore, some scholars have studied the decision-making of supply chain members under relative profits. Tanaka [47] constructed a two-stage game model and analyzed the strategy choices of duopoly enterprises under relative profit maximization in terms of price and output. Elsadany [48] studied duopoly enterprises with differentiated products and explored the dynamic game model of the enterprises under relative profit decision-making from the perspective of chaotic bifurcation. The results focused on the effects of the speed of strategy adjustment and parameter sensitivity on the stability of the game model. Hattori and Tanaka [49] surveyed the decision choices of duopoly enterprises with respect to new technologies under absolute and relative profit models. They pointed out that both enterprises would adopt the new technology in the relative profit maximization model, while the probability of both enterprises adopting the new technology would decrease in the absolute profit maximization model. Li and Ma [50] used the bifurcation theory to construct a dual-channel supply chain and analyzed the profits and decisions of the supply chain members under two utility functions of own profit maximization and relative profit maximization. Similar to the aforementioned studies, this paper also explores the decisions of supply chain members and supply chain profits under the relative profits model. It differs by using a delayed differential game supply chain to discuss the dynamic evolution of both product quality and goodwill.

2.6. Research Gap

Most of the studies on supply chains with the delay effect have focused on advertising and goodwill, with limited studies addressing product quality delay. In practice, the quality improvement of products is not instantaneous, as it takes some time for enterprises to improve quality from R&D to the finished product presented to consumers. In view of this, in this paper, the delayed impact of quality improvement on product quality is investigated. This work is closely related to the research of Zhan [40] and Ni [27], but there are still some distinctions between their studies. Firstly, the effect of product quality and service quality delays on goodwill was considered in the study of Zhan [40]; however, they only considered goodwill as a single state variable. Secondly, although Ni [27] constructed two state equations for the level of quality and goodwill, they neglected the impact of delay effect on quality goodwill in the supply chain. Therefore, in this study the dynamic levels of quality and goodwill as the state variables in a delayed environment are taken into account. Importantly, considering the influence of the delay effect on the upstream and downstream relationships, in this paper, a decision model of relative profit is designed, aiming to explore the impact of the manufacturer’s concern for the retailer’s profit on the supply chain members and the whole supply chain system under delay effect. Finally, some different conclusions are obtained. The profit of the supply chain is affected by delay time. The overall revenue of the supply chain is no longer optimal under centralized decision-making, which is different from the results of Zhan [40]. In particular, in this study, not only are the effects of different delay times on three decision-making models analyzed, but also the equilibrium strategies of supply chain members under the degree of the manufacturer’s concern for the retailer are investigated, as well as strategy choices. The differences between this study and the related literature are shown in

Table 1. Summary of the related literature.

Authors	Product Quality	Goodwill	Differential Game	Delay Effect	Decision Structure
Xu et al. [26]	×	√	√	×	Decentralized and integrated model, bilateral participation contract
Yang et al. [51]	√	×	√	×	Decentralized and overall alliance model
Taboubi [23]	×	√	√	×	Decentralized and coordination model, incentive mechanism
Ni et al. [27]	√	√	√	×	Price-quality and price-goodwill model
Li et al. [10]	√	×	√	×	Nash, Stackelberg and cooperation model
Zhan et al. [40]	√	×	√	√	Decentralized and centralized model
Yu et al. [36]	×	√	√	√	Non-cooperation, incomplete and complete cooperation model
Li [46]	×	×	√	×	Nash non-cooperative and Stackelberg model
Chen et al. [52]	√	×	√	×	Decentralized and centralized model
Li et al. [50]	×	×	×	×	Own profit and relative profit model
This paper	√	√	√	√	Decentralized and centralized model, bargaining model

×: not mentioned; √: mentioned.

.

3. Problem Description and Relevant Assumptions

The two-echelon supply chain constructed in this paper consists of a manufacturer and a retailer. The manufacturer improves product quality through quality behaviors such as R&D and updating technology. The manufacturer’s quality improvement behavior has a delayed effect on the product quality. The retailer is responsible for marketing and increasing the sales of the product through short- or long-term marketing activities. Brand goodwill is determined by a combination of product quality and marketing inputs. The cost of the entire supply chain system includes the cost of quality improvement inputs and investment in marketing efforts.

Assumption 1. 

The wholesale price is $w$, the retailer is $p$. The manufacturer’s quality input cost function is $C_m={\lambda }_m{E}_q^2(t)/2$, where $E_q(t)$ is the quality effort and ${\lambda }_m$ is the quality effort input cost coefficient. The retailer’s marketing input cost function is $C_R={\lambda }_R{E}_C^2(t)/2$, $E_C(t)$ is the retailer’s marketing effort and ${\lambda }_R$ is the marketing cost coefficient. When the manufacturer and the retailer make more quality and marketing efforts, they will pay more for their efforts.

Assumption 2. 

The level of product quality as a state variable is a dynamic process, and the improvement of product quality is related to the level of the manufacturer’s quality effort. On the basis of the Nerlover–Arrow [18] and Yu [36] goodwill models, a delay differential equation on product quality is constructed, as follows:

$$\dot{Q}(t)=\alpha E_q(t-h)-\beta Q(t),\hspace{1em}Q(0)=Q_0>0$$

(1)

where $\alpha >0$ is the influence coefficient of the manufacturer’s effort on product quality, $h$ is the delay time of the manufacturer’s product quality improvement, which indicates that it takes a certain period for the manufacturer’s quality improvement to improve the product quality, e.g., investment in product R&D and updating of technological knowledge. Due to the aging of production equipment and other uncontrollable factors, the product quality will naturally deteriorate, so $\beta >0$ represents the decay rate of product quality.

Assumption 3. 

Improvement in product quality can effectively increase brand goodwill, while the retailer’s marketing effort also affects the goodwill. In this study, the goodwill under the joint effect of quality and marketing effort is constructed and the dynamic evolution process is expressed as follows:

$$\dot{G}(t)=\gamma E_c(t)+\epsilon Q(t)-\delta G(t),\hspace{1em}G(0)=G_0>0$$

(2)

where $\gamma >0$ and $\epsilon >0$ refer to the influence coefficients of the marketing effort and product quality, respectively. Similarly, $\delta >0$ represents the natural reduction in goodwill over time without active marketing input.

Assumption 4. 

Consumers show a willingness to purchase high-quality products [20], so improvements in manufacturer’s product quality have a significant impact on market demand. Meanwhile, the retailer’s marketing methods greatly enhance the goodwill and inspire consumers to purchase. The demand function is as follows:

$$D(t)=(a-bp(t))(kQ(t)+mG(t))$$

(3)

where $a>0$denotes the potential market demand and satisfies $a-bp(t)>0$ to ensure non-negative and $b>0$ is the sensitivity to the product price. $k$ and $m$ signify the consumer’s preference for the quality and goodwill attribute of the product, indicating the pulling effect on market demand. As the levels of product quality and goodwill increase, consumers become less sensitive to price fluctuations.

Assumption 5. 

The manufacturer and the retailer are risk-neutral and rational, so decisions under different models are in a fully informative environment and follow profit or utility maximization. All supply chain members have a consistent discount rate $\rho$ with an infinite horizon $[0,\infty )$.

4. Model Framework

In this section, decentralized and centralized decision models are first constructed to explore the laws of supply chain quality and marketing decision-making under the delay effect. Secondly, we divided the decentralized game model into two scenarios, based on the own profit decision scenario and based on the relative profit decision scenario, and analyzed the impact of different decision structures on supply chain profits. Finally, the profits of the supply chain members in the centralized game models are coordinated to determine the effective range of revenue distribution. This provides valuable insights into the decision-making of supply chain members under the delay effect.

4.1. Decentralized Decision Model: Based on the Own Profit Decision Scenario (Model D)

In the decentralized decision model based on the own profit decision scenario (Model D), the manufacturer and the retailer act as independent individuals to pursue the maximization of profits. The manufacturer decides the level of the quality effort $E_q$ and the wholesale price $w$, and the retailer decides the level of the marketing effort $E_C$ and the retail price $p$ according to the manufacturer’s strategy. The profit functions of the manufacturer and the retailer are as follows:

$$J_M^D={\displaystyle {\int }_0^{\infty }{e}^{-\rho t}\left\{w(a-bp(t))(kQ(t)+mG(t))-\frac{{\lambda }_m}{2}{E}_q^2(t)\right\}}\mathrm{d}t$$

(4)

$$J_R^D={\displaystyle {\int }_0^{\infty }{e}^{-\rho t}\left\{(p(t)-w)(a-bp(t))(kQ(t)+mG(t))-\frac{{\lambda }_r}{2}{E}_c^2(t)\right\}}\mathrm{d}t$$

(5)

$$s.t.\left\{\begin{array}{l}\dot{Q}(t)=\alpha E_q(t-h)-\beta Q(t) \\ \dot{G}(t)=\gamma E_c(t)+\epsilon Q(t)-\delta G(t)\end{array}\right.$$

(6)

Proposition 1. 

(i) In Model D, the optimal quality and marketing efforts of the manufacturer and the retailer and the optimal retail price of products are as follows:

$$p^{D*}(t)={\displaystyle \frac{a+wb}{2b}},E_c^{D*}(t)={\displaystyle \frac{\gamma m{(a-wb)}^2{e}^{-\rho h}}{4b{\lambda }_r(\rho +\delta )}},$$

$$E_q^{D*}(t)={\displaystyle \frac{\alpha w(a-wb)(k(\rho +\delta )+\epsilon m)}{2{\lambda }_m(\rho +\beta )(\rho +\delta )}}{e}^{-\rho h}$$

(ii) The optimal trajectories of product quality and goodwill are the following:

$$Q^{D*}(t)=Q_0{e}^{-\beta t}+D_1(1-e^{-\beta t}),$$

$$G^{D*}(t)=e^{-\delta t}(G_0-{\displaystyle \frac{\epsilon D_1+D_2}{\delta }}-{\displaystyle \frac{\epsilon (Q_0-D_1)}{\delta -\beta }})+e^{-\beta t}{\displaystyle \frac{\epsilon (Q_0-D_1)}{\delta -\beta }}+{\displaystyle \frac{\epsilon D_1+D_2}{\delta }}$$

(iii) The profits of the manufacturer and the retailer and the system profit are as follows:

$$\begin{array}{ll}{J}_M^D& ={\displaystyle \frac{w(a-wb)k{Q}_0}{2(\rho +\beta )}}+{\displaystyle \frac{w(a-wb)m{G}_0}{2(\rho +\delta )}}+{\displaystyle \frac{m\epsilon Q_{0}w(a-wb)}{2(\rho +\beta )(\rho +\delta )}}+{\displaystyle \frac{{\gamma }^2{m}^{2}w{(a-wb)}^3{e}^{-\rho h}}{8b{\lambda }_r\rho {(\rho +\delta )}^2}}\\ & +{\displaystyle \frac{k{\alpha }^2{w}^2{(a-wb)}^2(k(\rho +\delta )+\epsilon m)}{4{\lambda }_m\rho {(\rho +\beta )}^2(\rho +\delta )}}{e}^{-\rho h}+{\displaystyle \frac{m\epsilon {\alpha }^2{w}^2{(a-wb)}^2(k(\rho +\delta )+\epsilon m)}{4{\lambda }_m\delta (\rho +\beta ){(\rho +\delta )}^2(\delta -\beta )}}{e}^{-\rho h}\\ & +{\displaystyle \frac{m\epsilon {\alpha }^2{w}^2{(a-wb)}^2(k(\rho +\delta )+\epsilon m)}{4{\lambda }_m\delta \beta \rho (\rho +\beta )(\rho +\delta )}}{e}^{-\rho h}-{\displaystyle \frac{m\epsilon {\alpha }^2{w}^2{(a-wb)}^2(k(\rho +\delta )+\epsilon m)}{4{\lambda }_m\beta {(\rho +\beta )}^2(\rho +\delta )(\delta -\beta )}}{e}^{-\rho h}\\ & -{\displaystyle \frac{{\alpha }^2{w}^2{(a-wb)}^2{(k(\rho +\delta )+\epsilon m)}^2}{8{\lambda }_m\rho {(\rho +\beta )}^2{(\rho +\delta )}^2}}{e}^{-2\rho h}\end{array}$$

$$\begin{array}{ll}{J}_R^D& ={\displaystyle \frac{{(a-wb)}^{2}k{Q}_0}{4b(\rho +\beta )}}+{\displaystyle \frac{{(a-wb)}^{2}m{G}_0}{4b(\rho +\delta )}}+{\displaystyle \frac{{(a-wb)}^{2}m\epsilon Q_0}{4b(\rho +\beta )(\rho +\delta )}}+{\displaystyle \frac{{\gamma }^2{m}^2{(a-wb)}^4}{16b^2{\lambda }_r\rho {(\rho +\delta )}^2}}{e}^{-\rho h}\\ & +{\displaystyle \frac{m\epsilon {\alpha }^{2}w{(a-wb)}^3(k(\rho +\delta )+\epsilon m)}{8b{\lambda }_m\delta (\rho +\beta ){(\rho +\delta )}^2(\delta -\beta )}}{e}^{-\rho h}-{\displaystyle \frac{m\epsilon {\alpha }^{2}w{(a-wb)}^3(k(\rho +\delta )+\epsilon m)}{8b{\lambda }_m\beta {(\rho +\beta )}^2(\rho +\delta )(\delta -\beta )}}{e}^{-\rho h}\\ & +{\displaystyle \frac{k{\alpha }^{2}w{(a-wb)}^3(k(\rho +\delta )+\epsilon m)}{8b{\lambda }_m\rho {(\rho +\beta )}^2(\rho +\delta )}}{e}^{-\rho h}+{\displaystyle \frac{m\epsilon {\alpha }^{2}w{(a-wb)}^3(k(\rho +\delta )+\epsilon m)}{8b{\lambda }_m\delta \beta \rho (\rho +\beta )(\rho +\delta )}}{e}^{-\rho h}\\ & -{\displaystyle \frac{{\gamma }^2{m}^2{(a-wb)}^4}{32b^2{\lambda }_r\rho {(\delta +\rho )}^2}}{e}^{-2\rho h}\end{array}$$

$$\begin{array}{ll}{J}^D& =J_M^D+J_R^D={\displaystyle \frac{k{Q}_0(a^2-w^2{b}^2)}{4b(\rho +\beta )}}+{\displaystyle \frac{m{G}_0(a^2-w^2{b}^2)}{4b(\rho +\delta )}}+{\displaystyle \frac{m\epsilon Q_0(a^2-w^2{b}^2)}{4b(\rho +\beta )(\rho +\delta )}}\\ & +{\displaystyle \frac{{\gamma }^2{m}^2{(a-wb)}^3(a+wb)}{16b^2{\lambda }_r\rho {(\rho +\delta )}^2}}{e}^{-\rho h}+{\displaystyle \frac{{\alpha }^{2}w{(a-wb)}^2(a+wb){(k(\rho +\delta )+\epsilon m)}^2}{8b{\lambda }_m\rho {(\rho +\beta )}^2{(\rho +\delta )}^2}}{e}^{-\rho h}\\ & -{\displaystyle \frac{{\gamma }^2{m}^2{(a-wb)}^4}{32b^2{\lambda }_r\rho {(\delta +\rho )}^2}}{e}^{-2\rho h}-{\displaystyle \frac{{\alpha }^2{w}^2{(a-wb)}^2{(k(\rho +\delta )+\epsilon m)}^2}{8{\lambda }_m\rho {(\rho +\beta )}^2{(\rho +\delta )}^2}}{e}^{-2\rho h}\end{array}$$

The proof of Proposition 1 is shown in Appendix A.

According to Proposition 1, the manufacturer’s quality improvement efforts and the retailer’s marketing efforts are decreasing functions with respect to the delay time. The length of the delay time affects the level of quality improvement and the level of marketing. When the delay time is longer, members’ efforts are lower. Conversely, the levels of members’ efforts are higher. This indicates that when the delay effect exists, the manufacturer’s quality improvement and the retailer’s marketing input cannot receive timely feedback within the expected time. Meanwhile, there is no significant improvement in the product quality recognized by the consumer. Therefore, as the delay time increases it greatly depletes the motivation of the supply chain members to produce and sell the products, further reducing the profitability of both the manufacturer and the retailer.

Corollary 1. 

In Model D, when there is no delay effect (immediate effect) on product quality, the optimal quality improvement effort and the optimal marketing effort, the optimal trajectories of product quality and goodwill are as follows:

$$E_c^{DI*}(t)={\displaystyle \frac{\gamma m{(a-wb)}^2}{4b{\lambda }_r(\rho +\delta )}},E_q^{DI*}(t)={\displaystyle \frac{\alpha w(a-wb)(k(\rho +\delta )+\epsilon m)}{2{\lambda }_m(\rho +\beta )(\rho +\delta )}},$$

$$Q^{DI*}(t)=Q_0{e}^{-\beta t}+{\displaystyle \frac{{\alpha }^{2}w(a-wb)(k(\rho +\delta )+\epsilon m)}{2{\lambda }_m\beta (\rho +\beta )(\rho +\delta )}}(1-e^{-\beta t}),$$

$$G^{DI*}(t)=e^{-\delta t}\left(G_0-D_4-{\displaystyle \frac{\epsilon Q_0}{\delta -\beta }}+{\displaystyle \frac{\epsilon D_3}{\delta (\delta -\beta )}}\right)+e^{-\beta t}\left({\displaystyle \frac{\epsilon (Q_0-D_3)}{\delta -\beta }}\right)+D_4+{\displaystyle \frac{\epsilon D_3}{\delta }}$$

From Corollary 1, when there is no delay effect (immediate effect, the delay time is zero) on the manufacturer’s quality improvement, the optimal quality improvement input and the marketing input are constant. That is, the production and operation inputs of the supply chain members are fixed in a certain period. However, both the quality improvement input and the marketing input under the delay effect are lower than the level of the strategies under the immediate effect, which indicates that the member strategies under the delay effect have damage to the supply chain performance.

4.2. Decentralized Decision Model: Based on the Relative Profit Decision Scenario (Model θ)

The vast majority of enterprises in the market are to maximize their profits as the business objective. However, in actual production and operation activities, enterprises will change the maximization business objective due to various external factors; they not only pursue their own profits, but also pay close attention to the profits of related competitors. Taking the delay effect as an example, since the delay effect of the quality improvement efforts on product quality enhancement occurs, this situation is a challenge for both the manufacturer and the retailer. On the one hand, the manufacturer will focus part of its efforts on the retailer’s revenue in order to stabilize the sales channel and reduce the risk of input delay effect in quality improvement. On the other hand, the retailer will formulate different marketing efforts based on the manufacturer’s delay. Therefore, the manufacturer’s business objective changes from focusing on its own profit to the relative profit of the retailer.

In general, the relative profit is the difference between the enterprise’s own profit and the concerned enterprise’s profit directly [53]. Some other scholars have measured relative profit through the business attitude between their own profit and the concerned enterprise’s profit and then deal with the interrelationship between the two enterprises in the form of the utility function [54]. In this paper, the above studies are combined to design a utility function based on the difference between own profit and concern for the retailer’s profit, expressed as follows:

$$U_M=J_M-\theta J_R$$

(7)

where $\theta \in (0,1)$ represents the degree of concern for the manufacturer. When $\theta =0$, it means that the manufacturer maximizes their profit as a business objective (Model D); when $\theta =1$, it means that the manufacturer will focus on the retailer’s operating profit in its quality improvement strategy. The larger $\theta$ is, the more sensitive the manufacturer is to the retailer’s profit, and as the retailer’s profit increases, the utility of the manufacturer decreases even though it continues to make profit through the retailer channel. While other factors remain the same, the increase in profit of the retailer in the supply chain indicates that sales of other products are more profitable for the retailer. At this time, the retail channel is no longer stable for the manufacturer, and the manufacturer is not satisfied with their quality improvement strategies and management methods.

Proposition 2. 

(i) In Model θ, the optimal quality improvement effort of the manufacturer, the optimal trajectories of product quality and goodwill are the following:

$$E_q^{\theta *}(t)=\left({\displaystyle \frac{\alpha Z_2}{{\lambda }_m}}-{\displaystyle \frac{((\rho +\delta )k+\epsilon m)\theta \alpha {(a-wb)}^2}{4b{\lambda }_m(\rho +\beta )(\rho +\delta )}}\right)e^{-\rho h},$$

$$Q^{\theta *}(t)=Q_0{e}^{-\beta t}+Z_3{e}^{-\rho h}(1-e^{-\beta t}),$$

$$G^{\theta *}(t)=e^{-\delta t}\left(G_0-Z_4\right)+e^{-\beta t}{\displaystyle \frac{\epsilon (Q_0-Z_3{e}^{-\rho h})}{\delta -\beta }}+Z_5.$$

(ii) The profits of the manufacturer and the retailer and the system profit are as follows:

$$J_R^{\theta }={\displaystyle \frac{{(a-wb)}^2}{4b}}\left({\displaystyle \frac{k{Q}_0-k{Z}_3}{\rho +\beta }}+{\displaystyle \frac{k{Z}_3+m{Z}_5}{\rho }}+{\displaystyle \frac{m\left(G_0-Z_4\right)}{\rho +\delta }}+{\displaystyle \frac{m\epsilon (Q_0-Z_3)}{(\delta -\beta )(\rho +\beta )}}\right)-{\displaystyle \frac{{\gamma }^2{m}^2{(a-wb)}^4{e}^{-2\rho h}}{32b^2{\lambda }_r\rho {(\delta +\rho )}^2}}$$

$$J_M^{\theta }={\displaystyle \frac{w(a-wb)}{2}}\left({\displaystyle \frac{k{Q}_0-k{Z}_3}{\rho +\beta }}+{\displaystyle \frac{k{Z}_3+m{Z}_5}{\rho }}+{\displaystyle \frac{m\left(G_0-Z_4\right)}{\rho +\delta }}+{\displaystyle \frac{m\epsilon (Q_0-Z_3)}{(\delta -\beta )(\rho +\beta )}}\right)-{\displaystyle \frac{{\lambda }_m}{2\rho }}{\left({\displaystyle \frac{\alpha Z_2}{{\lambda }_m}}-{\displaystyle \frac{\theta \alpha ((\rho +\delta )k+\epsilon m){(a-wb)}^2}{4b{\lambda }_m(\rho +\beta )(\rho +\delta )}}\right)}^2{e}^{-2\rho h}$$

The proof of Proposition 2 is shown in Appendix A.

In Model θ, the manufacturer changes their business objective from maximizing profit to the relative profit with reference to the retailer’s profit due to the uncertainty of product quality improvement caused by the delay effect. The retailer’s business objective remains unchanged, the marketing effort is still based on the principle of maximizing their profits, but their profits change with the levels of quality and goodwill. Proposition 2 shows that the quality improvement and marketing efforts decrease as the delay increases. The longer the delay time, the lower the strategic inputs of the supply chain members, until the manufacturer gives up the quality improvement effort and the retailer turns to investing in marketing other products. Therefore, the delay effect not only affects the motivation of both the manufacturer and the retailer, but also damages the profits of both sides.

Corollary 2. 

In Model θ, when there is no delay effect (immediate effect) on product quality, the optimal quality improvement effort, the optimal trajectories of product quality and goodwill are as follows:

$$E_q^{\theta I*}(t)={\displaystyle \frac{\alpha Z_2}{{\lambda }_m}}-{\displaystyle \frac{((\rho +\delta )k+\epsilon m)\theta \alpha {(a-wb)}^2}{4b{\lambda }_m(\rho +\beta )(\rho +\delta )}},$$

$$Q^{\theta I*}(t)=Q_0{e}^{-\beta t}+Z_3(1-e^{-\beta t}),$$

$$G^{\theta I*}(t)=e^{-\delta t}\left(G_0-Z_6\right)+e^{-\beta t}{\displaystyle \frac{\epsilon (Q_0-Z_3)}{\delta -\beta }}+Z_7.$$

According to Corollary 2, it can be seen that the manufacturer’s quality improvement is a constant value function varying with the parameter, which is consistent with the case in Corollary 1, that is, the quality improvement effort is fixed in the short term. In contrast, the quality level and goodwill level of products change with time and gradually stabilize. However, the product quality level and goodwill level show different evolutionary trends.

4.3. Centralized Decision Model (Model C)

The manufacturer and the retailer form a strategic partnership as a whole, and both parties will maximize the overall profit of the supply chain as the goal of joint decision-making behavior to achieve the optimal strategy. The decision-making model for the supply chain is as follows:

$$\begin{array}{ll}{J}^C=& {\displaystyle {\int }_0^{\infty }{e}^{-\rho t}\left\{(p(t)(a-bp(t))(kQ(t)+mG(t))-\frac{{\lambda }_m}{2}{E}_q^2(t)-\frac{{\lambda }_r}{2}{E}_c^2(t)\right\}}\mathrm{d}t\\ & s.t.\left\{\begin{array}{l}\dot{Q}(t)=\alpha E_q(t-h)-\beta Q(t) \\ \dot{G}(t)=\gamma E_c(t)+\epsilon Q(t)-\delta G(t)\end{array}\right.\end{array}$$

(8)

Proposition 3. 

(i) In Model C, the optimal quality and marketing efforts of the manufacturer and the retailer and the optimal retail price of products are as follows:

$$p^{C*}={\displaystyle \frac{a}{2b}}, E_c^{C*}(t)={\displaystyle \frac{a^{2}m\gamma e^{-\rho h}}{4b{\lambda }_r(\rho +\delta )}}, E_q^{C*}(t)={\displaystyle \frac{\alpha a^2(k(\rho +\delta )+\epsilon m)e^{-\rho h}}{4b{\lambda }_m(\rho +\beta )(\rho +\delta )}}.$$

(ii) The optimal trajectories of product quality and goodwill are as follows:

$$Q^{C*}(t)=Q_0{e}^{-\beta t}+Z_2(1-e^{-\beta t}),$$

$$G^{C*}(t)=e^{-\delta t}(G_0-{\displaystyle \frac{Z_1+\epsilon Z_2}{\delta }}-{\displaystyle \frac{\epsilon (Q_0-Z_2)}{\delta -\beta }})+{\displaystyle \frac{\epsilon (Q_0-Z_2)}{\delta -\beta }}{e}^{-\beta t}+{\displaystyle \frac{Z_1+\epsilon Z_2}{\delta }}.$$

(iii) The profit of the entire supply chain is as follows:

$$\begin{array}{ll}{J}^C& ={\displaystyle \frac{a^{2}k{Q}_0}{4b(\rho +\beta )}}+{\displaystyle \frac{a^{2}m{G}_0}{4b(\rho +\delta )}}+{\displaystyle \frac{a^{2}m\epsilon Q_0}{4b(\rho +\beta )(\rho +\delta )}}+{\displaystyle \frac{a^4{\gamma }^2{m}^2}{16b^2{\lambda }_r\rho {(\rho +\delta )}^2}}{e}^{-\rho h}\\ & +{\displaystyle \frac{{\alpha }^2{a}^4{(k(\rho +\delta )+\epsilon m)}^2}{16b^2{\lambda }_m\rho {(\rho +\beta )}^2{(\rho +\delta )}^2}}{e}^{-\rho h}-{\displaystyle \frac{{\alpha }^2{a}^4{(k(\rho +\delta )+\epsilon m)}^2}{32b^2{\lambda }_m\rho {(\rho +\beta )}^2{(\rho +\delta )}^2}}{e}^{-2\rho h}-{\displaystyle \frac{a^4{m}^2{\gamma }^2}{32b^2{\lambda }_r\rho {(\rho +\delta )}^2}}{e}^{-2\rho h}\end{array}$$

The proof of Proposition 3 is shown in Appendix A.

Proposition 3 shows that the quality improvement and marketing efforts are negatively correlated with the delay time under the centralized model, which is similar to the decentralized model. The retailer price is positively correlated with the underlying market demand while increasing in response to the decline in the price sensitivity coefficient. The optimal trajectory of product quality and goodwill exhibits the two distinct trends of gradually increasing to stability and remaining unchanged.

In Model C, the strategic inputs of supply chain members are all aimed at maximizing the overall profit of the supply chain. However, the maximum profit of the supply chain does not mean that the profit of each member in the supply chain is also optimal. The number of profits obtained by members is related to the distribution agreement. If the profit between the manufacturer and the retailer is not higher than the profits under the decentralized model, it is difficult to cooperate and carry out the centralized decision. Therefore, only the formulation of a scientific and reasonable distribution contract is the premise of cooperation between the manufacturer and the retailer, so as to achieve the coordination of the supply chain and realize the Pareto optimization.

In view of this, in this study, the Rubinstein bargaining model is used to allocate the overall profit of the supply chain, so that the manufacturer and the retailer can achieve the optimal performance of the supply chain under the premise of cooperation. This model involves the problem of time cost in the bargaining process between the parties of the game, which is typically resolved in the differential game model by using the discount factor in the differential equation. Suppose that the discount factors of the manufacturer and the retailer are ${\sigma }_M(0\le {\sigma }_M\le 1)$ and ${\sigma }_R(0\le {\sigma }_R\le 1)$, respectively. According to the Rubinstein bargaining model, the following conclusion can be obtained.

Proposition 4. 

In Model C, the optimal profits shared by the manufacturer and the retailer are as follows:

$$J_M^{CD}={\displaystyle \frac{1-{\sigma }_M}{1-{\sigma }_R{\sigma }_M}}(J^C-J_R^D-J_m^D)+J_m^D,J_R^{CD}={\displaystyle \frac{{\sigma }_M-{\sigma }_R{\sigma }_M}{1-{\sigma }_R{\sigma }_M}}(J^C-J_R^D-J_m^D)+J_m^D,$$

$$J_M^{C\theta }={\displaystyle \frac{1-{\sigma }_M}{1-{\sigma }_R{\sigma }_M}}(J^C-J_R^{\theta }-J_m^{\theta })+J_m^{\theta },J_R^{C\theta }={\displaystyle \frac{{\sigma }_M-{\sigma }_R{\sigma }_M}{1-{\sigma }_R{\sigma }_M}}(J^C-J_R^{\theta }-J_m^{\theta })+J_m^{\theta }.$$

The proof of Proposition 3 is shown in Appendix A.

Corollary 3. 

In Model C, when there is no delay effect (immediate effect) on product quality, the optimal quality improvement effort, the optimal trajectories of product quality and goodwill are as follows:

$$E_c^{CI*}(t)={\displaystyle \frac{a^{2}m\gamma }{4b{\lambda }_r(\rho +\delta )}},$$

$$E_q^{CI*}(t)={\displaystyle \frac{\alpha a^2(k(\rho +\delta )+\epsilon m)}{4b{\lambda }_m(\rho +\beta )(\rho +\delta )}},$$

$$Q^{CI*}(t)=Q_0{e}^{-\beta t}+{\displaystyle \frac{{\alpha }^2{a}^2(k(\rho +\delta )+\epsilon m)}{4b{\lambda }_m\beta (\rho +\beta )(\rho +\delta )}}(1-e^{-\beta t}),$$

$$\begin{array}{ll}{G}^{CI*}(t)& =e^{-\delta t}\left(G_0-{\displaystyle \frac{\epsilon Q_0}{\delta -\beta }}-{\displaystyle \frac{a^2{\gamma }^{2}m}{4b{\lambda }_r\delta (\rho +\delta )}}+{\displaystyle \frac{\epsilon {\alpha }^2{a}^2(k(\rho +\delta )+\epsilon m)}{4b{\lambda }_m\beta \delta (\rho +\beta )(\rho +\delta )}}+{\displaystyle \frac{\epsilon {\alpha }^2{a}^2(k(\rho +\delta )+\epsilon m)}{4b{\lambda }_m\beta (\rho +\beta )(\rho +\delta )(\delta -\beta )}}\right)\\ & +e^{-\beta t}\left({\displaystyle \frac{\epsilon Q_0}{\delta -\beta }}-{\displaystyle \frac{\epsilon {\alpha }^2{a}^2(k(\rho +\delta )+\epsilon m)}{4b{\lambda }_m\beta (\rho +\beta )(\rho +\delta )(\delta -\beta )}}\right)+{\displaystyle \frac{a^2{\gamma }^{2}m}{4b{\lambda }_r\delta (\rho +\delta )}}+{\displaystyle \frac{\epsilon {\alpha }^2{a}^2(k(\rho +\delta )+\epsilon m)}{4b{\lambda }_m\beta \delta (\rho +\beta )(\rho +\delta )}}\end{array}$$

Corollary 3 manifests that when there is no delay effect occurring, the quality improvement and marketing efforts under the centralized decision are constant value functions, which are both directly proportional to the quality improvement and goodwill coefficients and inversely proportional to the quality and goodwill decay parameters. The manufacturer focuses not only on product quality but also on goodwill when implementing a production plan, while the retailer only needs to focus on product goodwill when strategizing marketing activities. This is because the manufacturer’s production plan revolves around two main objectives. On the one hand, they need to reduce the decay rate of product quality through R&D efforts and technological improvements to obtain high- quality products. On the other hand, it is hoped that the high-quality products will be recognized by consumers to improve the goodwill level. The marketing objective of the retailer is to increase sales through higher product recognition, but product recognition is another form of consumer recognition of product quality.

5. Numerical Analysis

The equilibrium strategies and profit functions obtained from the above analysis are formally complex. In order to demonstrate more intuitively the levels of quality improvement and marketing strategies and product quality and goodwill under the delay effect, this section adopts the analytical method of numerical simulation to validate the conclusion of the propositions and to give the corresponding managerial insights. According to the relevant literature [36,38], the parameter values are as follows: $\alpha =0.4$, $\beta =0.5$, $\gamma =0.8$, $\epsilon =2$, $k=0.8$, $m=3$, $b=1.5$, ${\lambda }_m=1$, ${\lambda }_R=1$, $\delta =0.05$ and $\rho =0.1$. The results under the decentralized and centralized decision-making models are shown below.

5.1. The Impact of the Delay Effect on the Efforts of the Manufacture and the Retailer

Figure 1 shows the marketing effort of the retailer under decentralized and centralized decision models with the delay effect and the immediate effect. In the interval of the delay time of [0, 100], the level of marketing effort is a decreasing function of the delay time. The longer the delay time, the lower the marketing effort of the retailer, while the level of marketing effort is the highest under the immediate effect. This indicates that the delay effect is detrimental to the retailer’s strategic investment. With the increase in the delay time, the higher the cost of marketing effort, the lower the corresponding level of strategic investment. Regardless of whether the immediate or delayed effect occurs, the marketing effort under Model C is higher than that under Model D. However, as the delay time gradually increases, it is obvious from Figure 1 that the marketing level decreases rapidly under the centralized model, while the decentralized model decreases slowly. This is because the centralized model is more conducive to stimulating the enthusiasm of the retailer’s marketing investment. The retailer, as the main body in direct contact with consumers, has quick feedback on their publicity investment. At this time, due to the impact of the delay time of the upstream manufacturer, the retailer reduces marketing efforts in order to restrain consumers’ sensitivity to product quality. In Model D, the retailer takes the principle of maximizing their profits and adjusts the marketing strategies immediately according to the quality improvement strategies of the upstream manufacturer, so the level of strategic investment is relatively stable.

Figure 2 shows the quality improvement effort of the manufacturer under Model D, Model θ and Model C with the delay effect and immediate effect. Similar to the retailers, under three decision models, the impact of the delay effect on the level of strategic input of the manufacturer presents a similar rule. That is, the quality effort is negatively correlated with the delay time within the same delay interval. A longer delay will demotivate the manufacturer for the quality improvement strategy. In this section, the focus is on the impact of different degrees of the manufacturer’s concern on quality improvement input. When the manufacturer adopts relative profit as the business objective, the level of quality improvement investment decreases as the manufacturer’s concern for the retailer increases (when $\theta =0.5$ and $\theta =0.7$). This means that the increase in the concern degree for the retailer’s profit will reduce the quality effort of the manufacturer. Meanwhile, the manufacturer maintains the retail channel stability in a way that reduces some of the investment in quality improvement.

5.2. The Impact of the Delay Effect on Profits of the Manufacture and the Retailer

Figure 3 shows the impact of the manufacturer’s concern degree on their profit under Model θ. Set the degree of the manufacturer’s concern $\theta \in [0,1]$, while keeping the other parameters constant. The profit of the manufacturer is inversely related to the degree of the retailer. The more attention the manufacturer pays to the retailer’s earnings, the lower the profit and utility the manufacturer obtains. In the increasingly competitive market, delays in quality improvement undoubtedly create risk and uncertainty for downstream sale channels. Although the manufacturer will lose some of their revenue, it can effectively stabilize the upstream and downstream channels by adjusting their strategic inputs with a focus on the profitability of the retailer.

Figure 4 presents a comparison of the profits between the manufacturer and the retailer under centralized and decentralized decisions. Though numerical simulations, the distribution ranges of profits between the manufacturer and the retailer in centralized decision are ${\varphi }^D=[0.6361,0.7419]$ and ${\varphi }^{\theta }=[0.3763,0.9981]$. Further, we analyze the comparison from the following two perspectives. From the perspective of the decision structure, the profits of the manufacturer and the retailer in Figure 4a are obviously better under Model C than under Model D. In Figure 4b, the manufacturer’s profit structure remains unchanged, while the retailer’s profit is no longer optimal under Model C. When the delay time $h<38$, the retailer’s profit under Model θ is larger than that under Model C. As the delay time continues to increase, the retailer’s profit under Model C is superior to those under Model θ.

From the perspective of the supply chain members, due to the dominant role of the manufacturer in the supply chain, its profits are higher than those of the retailer in Model C and Model D. Specifically, in the centralized decision-making, the manufacturer dominates the degree of “patience” in the negotiation process and has the first bid which gives it a first-mover advantage. However, the decline in the manufacturer’s profit is not only lower than the profit of the retailer under Model θ, but also lower than the profit under Model D. On the other hand, the profit of the retailer increases sharply under Model θ. Obviously, the manufacturer is altruistic in Model θ, and the degree of the manufacturer’s concern brings a positive externality for the retailer.

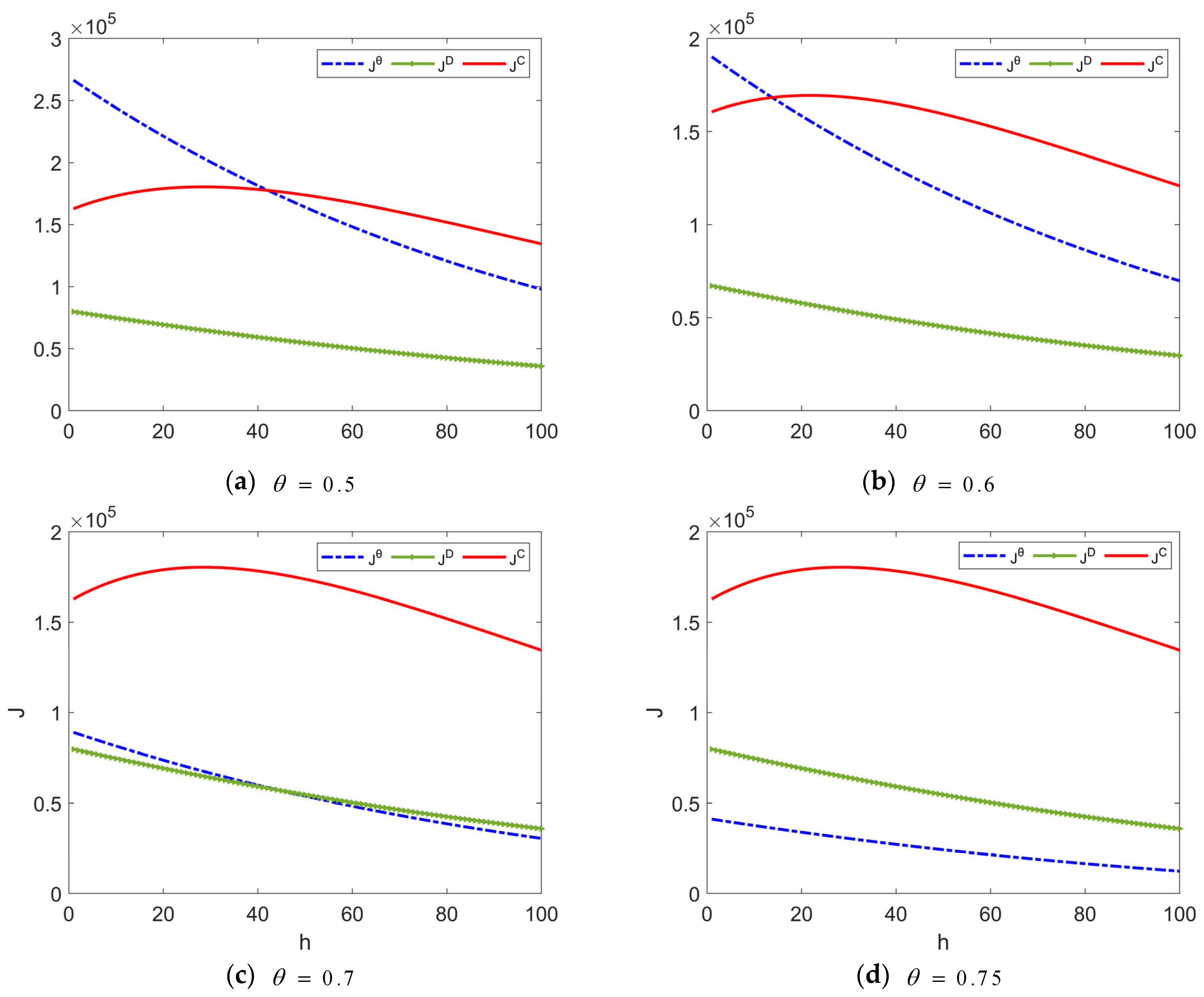
5.3. The Impact of the Delay Effect on the Profit of the Supply Chain in Different Decision Models

The interactions between the overall supply chain profit and the delay effect under different parameters $\theta$ are shown in Figure 5a–d. Figure 5a–d illustrate that with the increase in delay time, the overall profit of the supply chain decreases. In the decentralized decision model, the profits of the supply chain are always monotonically decreasing, while the profit of the supply chain in the centralized model shows a trend of increasing first and then decreasing. Taking the delay time $h=43$ as the critical point, when $h\in [0,43]$, the supply chain profit keeps rising with the increase in delay time, when $h\in (43,\infty )$, the supply chain revenue begins to decline gradually. This is because the manufacturer and the retailer have the highest level of strategic investment in Model C, and the combination of quality improvement and marketing strategies can bring high returns to the supply chain. However, due to the influence of delay time, the profit will not continue to increase but start to decline after reaching a certain extent. The manufacturer’s different concern degrees make supply chain profits under Model θ better than those under Model C, as shown in Figure 5a,b. At this point, the supply chain profit in Model C is no longer optimal, and the cooperation between the manufacturer and the retailer is not the optimal decision. As $\theta$ increases, the supply chain profit in Model θ decreases. In addition, in Figure 5a,b, when supply chain profits intersect in the two decision models, the length of the delay time becomes an important basis for judging which decision-making approach the members take. Different delay times correspond to different revenue options, the manufacturer and the retailer need to choose different cooperation ways in conjunction with their own needs. The impact of the manufacturer’s concern degree and delay time on strategic inputs as well as supply chain profit is shown in

Table 2. Impact of concern degree and delay time on strategic inputs and profits.

$\theta =0.5$		$\theta =0.7$
$E_q^C>E_q^{\theta }>E_q^D$		$E_q^C>E_q^D>E_q^{\theta }$
$h\le 46.713$	$h>46.713$	$h\le 42.8603$	$h>42.8603$
$J^{\theta }>J^C>J^D$	$J^C>J^{\theta }>J^D$	$J^C>J^{\theta }>J^D$	$J^C>J^D>J^{\theta }$

.

Combining Table 2 with Figure 5 shows that the profit of the supply chain under Model θ gradually decreases as the concern degree increases. This is because the manufacturer’s delay compensation to the retailer increases with the degree of concern. Correspondingly, the more profit they lose, the less investment is made in quality improvement. The manufacturer’s behavior is feasible in the short term; the retailer takes some marketing approach to increase sales through delay compensation. However, with the increase in the delay time, the profit loss of the manufacturer is escalated, and the delay in quality improvement does not allow for effective product quality improvement, which is detrimental to the manufacturer’s long-term development.

Thus, the decisions of supply chain members can be categorized into the two aspects of the manufacturer’s concern degree and the length of the delay time. When $h\le 46.713$, Model θ is the optimal choice for the supply chain members, in which case the manufacturer can optimize supply chain profit with a relatively low input of quality improvement. When $h>46.713$, the quality improvement of the manufacturer cannot obtain feedback within the expected time, so they will increase investment in research and development in order to obtain a quality breakthrough; therefore, Model C of the higher quality improvement inputs can meet the demands of the manufacturer, that is, high inputs bring high returns.

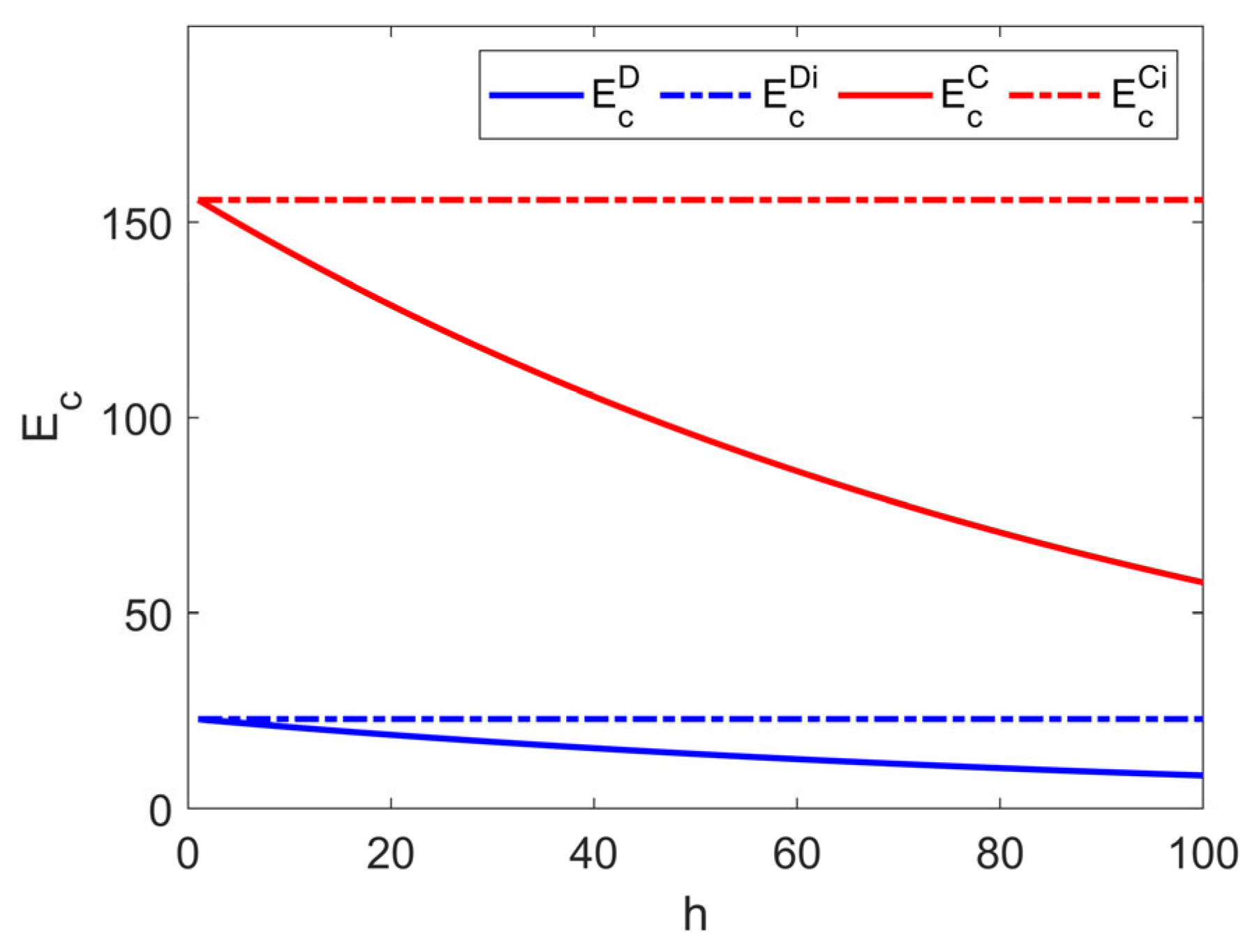
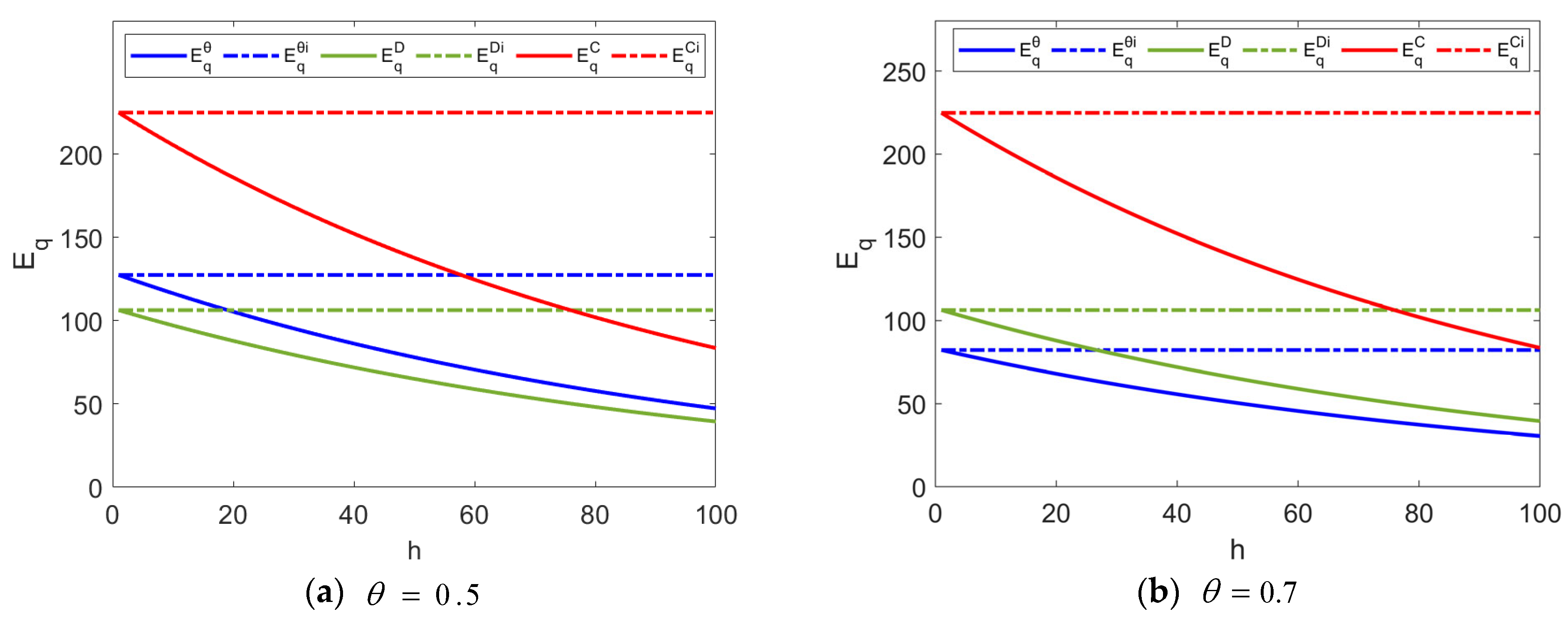
5.4. The Impact of the Delay Effect on Product Quality and Goodwill

The following shows the effects of different delay times and concern degrees on the levels of product quality and goodwill under three decision models, where Model C is represented by the red line, Model D by the green line and Model θ by the blue line. The delay times are selected as $h=0$ (dashed line), $h=10$ (solid line) and $h=40$ (triangular labeled line), as shown in Figure 6 and Figure 7.

According to Figure 6, in terms of the trajectory of product quality, when $h=0$ and $\theta =0.5$, there is $Q^{\theta }>Q^C>Q^D$; when $\theta =0.7$, there is $Q^C>Q^D>Q^{\theta }$. It indicates that when no delay effect exists, the manufacturer’s concern degree has a greater impact on product quality, and the centralized decision is no longer the best option for the members to integrate resources to improve the overall performance. Appropriate attention from the upstream manufacturer to the downstream retailer can lead to the optimization of product quality as well as total supply chain profits. In contrast, excessive attention from the manufacturer to the retailer’s profitability leads to a rapid decrease in the level of quality, which means that the manufacturer maintains downstream sales channels at the expense of some product quality inputs.

When the delay time is short ($h=10$), the trajectory of product quality under Model C and Model D shows a gradually increasing trend and converges to a steady state, while under Model θ it experiences a downward trend and eventually plateaus over time and the level of product quality goes from $Q^{\theta }>Q^C>Q^D$ in the initial period to $Q^C>Q^D>Q^{\theta }$ in the steady state. This is because the delay time is relatively short, the manufacturer optimizes the supply chain performance with lower quality improvement efforts than under Model C. The manufacturer’s focus on the retailer’s revenue creates a positive externality for the retailer, while the consumer’s perceived level of quality at this moment remains in the previous stage, so there is a $Q^{\theta }>Q^C$. When the delay time is relatively long ($h=40$), as shown in Propositions 1–3, it not only reduces the manufacturer’s quality improvement input and slows down the progress of quality improvement, but also reduces the retailer’s marketing level and the market share, which eventually leads to the loss of market competition and exit from the market. When $\theta =0.7$, regardless of the length of the delay time, the level of product quality maintains at $Q^C>Q^D>Q^{\theta }$, and it decreases significantly under Model θ. At this time, the manufacturer’s excessive concern has affected the quality improvement investment and improvement of product quality, which is not conducive to the manufacturer’s operation and development.

Figure 7 manifests that the trajectory of product goodwill depends on the delay time and concern degrees under three decision models. In both Model D and Model C ($\theta =0.5$), the levels of goodwill grow over time and gradually converge to a steady state, while in Model θ, the levels of goodwill decrease with time and converge to a stable state faster. When $\theta =0.7$, the levels of goodwill under Model D and Model C remain constant, while the level of goodwill decreases overall under Model θ. At this time, the decision of Model θ becomes less sensitive to the delay time. Although the manufacturer can obtain a higher level of goodwill by investing less in quality improvement input, the level of quality and the overall performance of the supply chain decrease, which is not conducive to the long-term development of member enterprises.

Comparing the delay and immediate effect, we can see that the level of goodwill under the immediate effect is higher than that under the delay effect. This is because the manufacturer’s quality improvement can quickly react to the product quality by consumer perception and thus improve the goodwill of the enterprise. The quality improvement input in decentralized decision-making that is lower than that of centralized decision-making can obtain higher quality levels and total returns, contributing to a higher level of goodwill, that is, the level of goodwill in the initial is $G^{\theta }>G^D>G^C$. As the delay effect increases, product quality cannot be improved immediately and effectively. Correspondingly, consumers cannot measure the improvement of product quality and also cannot have other feedback on the enterprise’s goodwill. The longer the delay time, the lower the level of goodwill. In Model θ, the retailer relies on the manufacturer’s delay subsidies to increase product sales in the short term through marketing, but when the subsidies are not a long-term behavior, they still cannot improve the demand in the long term, which makes the level of goodwill $G^C>G^{\theta }>G^D$ in the later stage.

6. Discussions

6.1. Results Analysis

Based on the above numerical modeling and simulation analysis, the following conclusions can be draw in this paper:

(1)

Both quality improvement efforts and marketing efforts are decreasing functions of delay time, and the length of delay time directly affects the motivation of decision-makers in strategy investment. In contrast to the decentralized model, the manufacturer and the retailer increase their strategic inputs under the centralized model. Centralization is more conducive to product quality and goodwill improvement.

(2)

In Model θ, the higher the manufacturer’s attention is to the retailer, the lower its level of quality improvement investment. The manufacturer maintains the downstream retail channel by reducing part of the quality improvement inputs.

(3)

The established Rubinstein bargaining model can ensure that the profits of the manufacturer and the retailer are not lower than the profits under decentralized decisions, and effectively motivate the supply chain members to participate in the cooperation.

(4)

When $\theta$ goes from 0.5 to 0.6, although the profit of the supply chain under Model θ begins to decrease, it is still higher than the profit of the supply chain under Model C for a relatively short delay time. As the delay time increases, the advantage of the centralized decision is prominent and the profit increases.

(5)

The longer the delay time, the lower the quality level and goodwill level. Compared with the delay effect, the levels of quality and goodwill are highest under the immediate effect, and when $\theta =0.5$, the level of product quality under the steady state in Model θ is always higher than that under Model C. However, the level of goodwill under Model θ is only higher than that under Model C within a certain time range.

(6)

Regardless of whether the delay effect occurs, the levels of quality and goodwill under Model D and Model C show an increase and tend to stabilize. On the contrary, the levels of quality and goodwill in Model θ show a decrease and tend to stabilize. Therefore, the dual effect of the delay effect and attention degree exacerbates the negative impact on product quality and goodwill.

The research in this paper improves the results of previous studies. Firstly, in contrast to previous studies, although some scholars have combined product quality and goodwill in recent years [19,20,22], few scholars have analyzed the delay effect in conjunction with these two factors. In this paper, the impact of the delay effect of quality improvement on product quality and goodwill is analyzed by considering the two factors of the manufacturer’s quality effort and the retailer’s marketing effort. In this paper, relevant decision suggestions and theoretical references are provided for supply chain members under different decision models. Secondly, in this study, a cooperative coordination mechanism is innovatively designed under the delay effect to improve the profits of the manufacturer and the retailer and promote cooperation among supply chain members. Different from the revenue sharing [17] and cost-sharing [12,14] in the cooperative coordination mechanism, the cooperative mechanism of Rubinstein bargaining is more suitable for the dynamic differential game model in this paper; the discount factor in the differential equation is regarded as the negotiation cost in the bargaining process, and the way to obtain the profit distribution through continuous negotiation is more in line with the reality. Finally, considering the influence of the delay effect on upstream and downstream relationships, in this paper, a relative profit decision model is constructed. Under the dual influence of delay effect and attention degree, the supply chain revenue is no longer optimal under the centralized decision model, which is different from the research results of [40]. This new perspective on the effects of delay time and attention degree on the dynamic decision-making of supply chain members aims to improve the performance of the entire supply chain system.

6.2. Managerial Insights

Our research has important theoretical and practical managerial insights. This study aims to help managers to better understand the impact of delay effect on decisions and provides a scientific basis for strategy inputs and decisions in dynamic supply chains.

(1)

The delay time is an important basis for the manufacturer’s decision. When the delay time $h\le 46.713$, the revenue of the supply chain under the relative profit decision is higher than that under the centralized decision. The manufacturer can make the supply chain more profitable with lower quality improvement inputs. When $h>46.713$, the supply chain revenue is optimal under the centralized decision. It can be seen that the length of the delay time determines in which way the manufacturer makes quality improvement inputs. Manufacturers can categorize product quality into long-term and short-term updates according to the short delay time to avoid excessive investment in the quality improvement process.

(2)

Maintaining channel stability is good for the long-term development of enterprises. The profit of the retailer under the relative profit decision is significantly increased. The manufacturer’s attention degree brings a positive externality to the retailer, which can stabilize the downstream retail channels to a certain extent. Therefore, when quality improvement takes a long time, the manufacturer’s marketing subsidy to downstream retailers can be divided into two parts. On the one hand, it can alleviate the delay loss caused by product updates; on the other hand, it can carry out advance marketing, promote and warm up for the launch of the new products, and increase the popularity and attention.

(3)

The bargaining approach to revenue distribution is more flexible. The optimal distribution interval of revenue between the manufacturer and the retailer under centralized decision is ${\varphi }^D=[0.6361,0.7419]$ and ${\varphi }^{\theta }=[0.3763,0.9981]$. In the face of the uncertainty of product quality replacement, the widening of the revenue distribution interval promotes the cooperation and mutual assistance between the manufacturer and the retailer, provides more choices for the cooperative alliance and finally realizes the Pareto improvement of both members. This also requires manufacturers not to focus on short-term revenue loss, but to establish long-term stable cooperative relationships with retailers to maximize profits.

(4)

The rational utilization of the concern degree and delay time are the keys to improving enterprise efficiency. When $\theta =0.5$ and the delay time is short, the manufacturer can obtain the product quality second only to the centralized decision with the lowest quality improvement input, while when the delay time is long, the manufacturer can obtain a quality level exceeding that of the Model C with the quality input of the Model θ. Therefore, a reasonable grasp of the relationship between the concern degree and the delay time could not only promote the close cooperation of the supply chain members, but also improve the operation efficiency of the entire supply chain system and reduce operating costs to create greater value for enterprises.

7. Conclusions

In this paper, the decision-making problem of the manufacturer and the retailer under the delay effect in a two-echelon supply chain is examined. Considering the impact of the delay effect on quality improvement behavior, in this paper, the strategic inputs and profits of supply chain members are investigated under three decision structures. In particular, in this paper, how the focus of the manufacturer on the retailer’s profitability affects the revenue of the supply chain members and the supply chain system is explored. In addition, we design a bargaining profit distribution mechanism to maximize the benefits of supply chain members. Finally, through numerical simulations, we discuss how concern degree and delay time affect product quality and goodwill as well as supply chain decisions, and provide an important direction for manufacturing enterprises and managers.

The main conclusions are as follows: (1) The delay time is inversely proportional to the strategic inputs of supply chain members, and the length of delay time directly affects the motivation of strategic inputs. However, the combination of the delay effect and the degree of manufacturer concern will have an unexpected result, that is, lower input under Model D could obtain the higher returns under Model C, which improves the overall profit and performance of the supply chain; (2) The bargaining profit distribution mechanism can significantly increase the profits of the manufacturer and the retailer. Compared with the profit distribution interval of the two profit maximization scenarios, the optimal distribution intervals of supply chain members under Model θ are larger, which is more conducive to the negotiation and cooperation between the manufacturer and the retailer; (3) In a competitive market environment, superior product quality can attract consumers to increase sales. Product upgrades and effective marketing strategies are critical to expanding market share. Manufacturers should actively improve product quality and enhance brand influence, combine breakthrough products with personalized and customized products according to the length of delay time, so as to alleviate the loss caused by the delay effect. Retailers should enhance their marketing efforts to promote the competitiveness of the supply chain.

There are also some limitations to this study. First, in this paper, the quality delay behavior of upstream manufacturers is studied. In reality, upstream and downstream members exhibit delayed behaviors. Therefore, it is necessary to incorporate retailer’s marketing delays into the dynamic environment. Second, the revenue allocation in this study adopts the Rubinstein bargaining model, the next step could explore other allocation methods. Lastly, in this paper, the stability of the supply chain is not considered. Future work could explore the impact of delays on the stability of the supply chain system and decision-making.