Infinite Dimensional Maximal Torus Revisited

Abstract

Let $T^m$ be the maximal torus of a set of $m\times m$ unitary diagonal matrices. Let $\mathcal{T}$ be a collection of all maps that rigidly rotate every circle of latitude of the sphere with a fixed angle. $\mathcal{T}$ is also a maximal torus, and we shall prove in this paper that $\mathcal{T}$ is the topological limit inf of $T^m$.

1. Introduction

There are at least two branches of mathematics where maximal tori of compact Lie groups play a crucial role. The first one is the representation theory of a finite-dimensional Lie group. The Lie algebra of a maximal torus that is a Cartan subalgebra determines the roots and all the irreducible representations of the Lie algebra.

The other area is symplectic geometry and dynamical systems. Indeed, if the action of a maximal abelian group of dimension n on a symplectic manifold M of dimension $2n$ is effective and Hamiltonian, the n component of the moment map $\mu =(f_1,f_2,\cdots f_n)$$:M⟶{\mathbb{R}}^n$ form a completely integrable system and the functions $f_i$ are constants of motion of the dynamical system.

In this paper, we are interested in the infinite-dimensional torus.

The first (known) maximal torus was described by D. Bao and T. Ratiu in their paper [1]. Later on, it was discovered in [2,3] that if $(\mathit{M},\omega ,\mathit{T},\mu )$ is a compact connected symplectic toric manifold, then the group of s-Sobolev equivariant symplectomorphisms ${\mathcal{D}}_{\omega }^s(\mathit{M},\mathit{T})$ is a maximal torus of the Lie group of the s-Sobolev symplectomorphism of $\mathit{M}$. ${\mathcal{D}}_{\omega }^s(\mathit{M},\mathit{T})$ is also equal to the stabilizer of the moment map under the action of the group, ${\mathcal{D}}_{\omega }^s\left(\mathit{M}\right)$ of Sobolev symplectomorphism of $\mathit{M}$.

In this paper, we will show that the infinite-dimensional torus of a sphere is induced by the maximal torus of the unitary group $\mathit{U}\left(m\right)$. This is not surprising, because in [2,4], the authors have shown similarities between $\mathit{U}\left(m\right)$ and the group of symplectomorphism of the annulus. Our results in this paper should reinforce the belief that $\mathit{SU}(\infty )$ is ${\mathcal{D}}_{\omega }^s\left(\mathit{M}\right)$.

Let us mention that the authors of [1] have pointed out that there are two ways to approximate ${\mathcal{D}}_{\omega }^s\left(\mathit{M}\right)$: either continuously, that is, at the Lie algebra level, or discretely, that is, using finite groups. The latter is what we did in this paper. We discretize the sphere using the moment map in a way similar to [5,6,7,8].

This paper is organized into four sections. In Section 2, we review facts about the unitary group $\mathit{U}\left(m\right)$. In Section 3, we prove that a unitary diagonal matrix defines an invertible measure-preserving transformation of the sphere and, consequently, that the infinite-dimensional torus is the limit of the finite-dimensional torus ${\mathit{T}}^{\mathit{m}}$. In Section 4, we compute the normalizer of the infinite-dimensional torus from the normalizer of ${\mathit{T}}^{\mathit{m}}$, and we show that the limit of the Weyl group of ${\mathit{T}}^{\mathit{m}}$ is nothing but the Weyl group of the infinite dimensional torus.

2. Special Unitary Matrices

The group of $m\times m$ unitary matrices is the set

$$\mathit{SU}\left(m\right)=\left\{\mathit{A},|\mathit{A}{\mathit{A}}^{*}=\mathit{I},det\left(A\right)=1\right\}$$

where ${\mathit{A}}^{*}$ is the conjugate of the matrix $\mathit{A}$ and $\mathit{I}$ is the identity matrix.

Let

$$diag({\theta }_1,{\theta }_2,\cdots ,{\theta }_m)=\left(\begin{array}{cccc}{e}^{i{\theta }_1}& 0& \cdots & 0\\ 0& e^{i{\theta }_2}& \cdots & 0\\ \cdots & \cdots & \cdots & 0\\ 0& 0& 0& e^{i{\theta }_m}\end{array}\right).$$

The subgroup ${\mathit{T}}^{\mathit{m}}$ of diagonal unitary matrices is a maximal abelian group:

$${\mathit{T}}^m=\left\{diag({\theta }_1,{\theta }_2,\cdots ,{\theta }_m),{\theta }_1+{\theta }_2+\cdots +{\theta }_m=0\right\}.$$

Let us review the computation of the normalizer of ${\mathit{T}}^m$. By definition, the group $\mathit{N}\left({\mathit{T}}^m\right)$ is calculated as follows:

$$\mathit{N}\left({\mathit{T}}^m\right)=\{g\in \mathit{U}\left(m\right),g·{\mathit{T}}^m{g}^{-1}={\mathit{T}}^m\}.$$

The normalizer of $T^m$ is the largest subgroup of $SU\left(m\right)$ that stabilizes $T^m$ under conjugation. Let $t\in {\mathit{T}}^m$. If $gt{g}^{-1}$ is a diagonal matrix, then it has the same eigenvalues as t, and therefore, the matrix $gt{g}^{-1}$ is just a permutation of the diagonal of t. Let ${\sum }_m$ be the symmetric group of m letters and let $\sigma \in {\sum }_m$. Let $P_{\sigma }$ be the matrix defined by ${\left(P_{\sigma }\right)}_{ij}={\left({\delta }_{\sigma \left(j\right)}^i\right)}_{i,j}$ where ${\delta }_j^i$ is the Kronecker symbol.

So if g is an element of the normalizer of ${\mathit{T}}^m$, then for $t\in {\mathit{T}}^m$, there exists $\sigma$ such that $gt{g}^{-1}=P_{\sigma }^{-1}t{P}_{\sigma }$. This leads to $P_{\sigma }g$ commuting with t, and since ${\mathit{T}}^m$ is maximal, this means that $P_{\sigma }g\in {\mathit{T}}^m$. In conclusion, we have found that the normalizer of ${\mathit{T}}^m$ is the subgroup

$$\mathit{N}\left({\mathit{T}}^m\right)=\{P_{\sigma }t,\sigma \in \sum _m,t\in {\mathit{T}}^m\}.$$

(1)

Therefore, the Weyl group is

$$W^m=\mathit{N}\left({\mathit{T}}^m\right)\setminus {\mathit{T}}^m=\sum _m.$$

(2)

Moreover, ${\mathit{T}}^m$ is a Lie group diffeomorphic with $\underset{mtimes}{\underbrace{S^1\times S^1\times \cdots S^1}}$, and its Lie algebra is isomorphic with ${\mathbb{R}}^m$. The exponential map is given by ${\mathbb{R}}^m⟶{\mathit{T}}^m$.

$$({\theta }_1,{\theta }_2,\cdots ,{\theta }_m)⟶\left(\begin{array}{cccc}{e}^{i{\theta }_1}& 0& \cdots & 0\\ 0& e^{i{\theta }_2}& \cdots & 0\\ \cdots & \cdots & \cdots & 0\\ 0& 0& 0& e^{i{\theta }_m}\end{array}\right).$$

3. Measure-Preserving Transformations of the Sphere

Think of $\mathbb{CP}\left(1\right)$ as the sphere in ${\mathbb{R}}^3$. Then the one-dimensional torus $S^1$ acts on it through rigid rotations about the vertical axis. This action is Hamiltonian concerning the Fubini–Study Symplectic form $\mathsf{\Omega }$ and has a moment map of J:

$$\begin{array}{cc}\hfill J:\mathbb{CP}\left(1\right)& ⟼[0,1]\hfill \\ \hfill {[1,re}^{2\pi i\theta }]& ⟼{\displaystyle \frac{1}{1+r^2}}.\hfill \end{array}$$

(3)

On the sphere, we have the Liouville measure, which, in this case, is just the symplectic form $\mathsf{\Omega }$ defined by $\mu \left(A\right)={\int }_A\mathsf{\Omega },$ where A is any Borel set of $\mathbb{CP}\left(1\right)$.

In all the sequels, we designate as $(\mathbb{X},\mu )$ either the sphere $\left(\mathbb{CP}\right(1),\mathsf{\Omega })$ or the unit interval $\left(\right[0,1],|·\left|\right)$ where $|·|$ is the Lebesgue measure.

A map $\varphi$ from $(\mathbb{X},\mu )$ to itself is a measure-preserving transformation if

$$\mu \left({\varphi }^{-1}\left(A\right)\right)=\mu \left(A\right),\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{B}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{l}\mathrm{s}\mathrm{e}\mathrm{t}\mathrm{A}.$$

For example, on the real line, translations of the form $x\to x+a$ preserve the length of segments. They are measure-preserving transformations.

Also, rotations by a fixed angle preserve areas and are also measure-preserving transformations on the plane $\mathbb{R}$.

A general example of measure-preserving transformation is symplectomorphisms. These are maps $\varphi$ from a symplectic manifold $(M,\omega )$ to $(M,\omega )$ such that ${\varphi }^{*}\omega =\omega$.

Let $Smeas\left(\mathbb{X}\right)$ be the semi-group of measure-preserving transformations of $(\mathbb{X},\mu )$, and let $Imeas\left(\mathbb{X}\right)$ the set of invertible measure-preserving transformations. On the open set $[1,w]$ of $\mathbb{CP}\left(1\right)$, if we set $z=1-J\left(w\right)$, the symplectic form $\omega$ can be written $dz\wedge d\theta$, and therefore, the map $\eta :\left(\mathbb{CP}\right(1),\mathsf{\Omega })⟶[0,1]\times [0,1]$ that sends $[1,w=r{e}^{2\pi i\theta }]$ to the point $(z,\theta )$ is a measure-preserving transformation. Thus, as far as measure theory is concerned, the sphere is just a square of $[0,1]\times [0,1]$. The outcome of this identification is that we can build many measure-preserving transformations of the sphere through measure-preserving transformations of the square. Indeed, if $\varphi :[0,1]\times [0,1]⟶[0,1]\times [0,1]$ is a measure-preserving transformation of the square, then the map $\tilde{\varphi }={\eta }^{-1}\circ \varphi \circ \eta$ is a measure-preserving transformation of the sphere. Afterwards, we will identify $\varphi$ and $\tilde{\varphi }$.

Each $S\in Smeas\left(\mathbb{X}\right)$ determines a bounded linear operator $P_S$ on $L^2\left(\mathbb{X}\right)$ using $P_S\left(f\right)=f\circ S$. The Strong Operator Topology induces a topology on $Smeas\left(\mathbb{X}\right)$.

Evidently, a sequence $S_n$ converges to S in the Strong Operator Topology if for every function $f,f\circ S_n$ converges to $f\circ S$ in $L^2\left(\mathbb{X}\right)$.

The collection of all sets of the form

$$N(S,f,ϵ):=\{T\in Imeas\left(\mathbb{X}\right),{\parallel f\circ T-f\circ S\parallel }_2\le ϵ\}.$$

constitute a sub-base for this topology on $Imeas\left(\mathbb{X}\right)$.

In particular, if ${\chi }_A$ denotes the characteristic function of a Borel set A, then $N(S,f,ϵ)$ becomes

$$N(S,{\chi }_A,ϵ)=\{T\in Imeas\left(\mathbb{X}\right):\mu (T^{-1}\left(A\right)▵S^{-1}\left(A\right))<ϵ\}$$

where $▵$ is the symmetric difference between two sets.

Another sub-base is the collection of sets of the form $N(S,{\chi }_A,ϵ)$; Halmos [9] uses it to define the neighborhood topology.

3.1. Measure-Preserving Transformations of the Unit Interval

Measure-preserving transformations of the unit interval, as we will see, play a very important role in constructing measure-preserving transformations of a sphere. A subset of Smeas(I) of great importance is the set of dyadic permutations.

Call an interval $\left[k\setminus 2^m,[k+1]\setminus 2^m\right),k=0,1,\cdots 2^m-1;m=0,1,\cdots$ a dyadic interval of rank m and a union of such intervals a dyadic set of rank m.

A dyadic permutation P of rank m is a one-to-one transformation of the interval which maps each dyadic interval of rank m onto itself or onto another one through an ordinary translation.

Theorem 1

(Density Of Dyadic Permutations). The set of dyadic permutations are dense in $Smeas\left(I\right)$ for the Strong Operator Topology.

Proof. 

It is shown in [9] that the set of dyadic transformations is dense in $Imeas\left(I\right)$ for the neighborhood topology.

Also, in [10] it is proven that $Smeas\left(I\right)$ is the closure of $Imeas\left(I\right)$ for the Strong Operator Topology.

This shows the density of the set of dyadic transformations in $Smeas\left(I\right)$ for the Strong Operator Topology.

Now, the interesting thing is that dyadic permutations come from permutations. □

Theorem 2.

Let ${\sum }_m$ be a symmetric group of $m+1$ letters. There exists a one-to-one group homomorphism from ${\sum }_m$ to Smeas(I).

Proof. 

Let $I_k^m=\left[{\displaystyle \frac{k}{m+1}},{\displaystyle \frac{k+1}{m+1}}\right)$ be a partition of the interval $[0,1]$. Define the map ${\mathsf{\Psi }}^m$$:{\sum }_m⟶Smeas\left(I\right)$ by associating with each $\sigma \in {\sum }_m,$ the invertible measure-preserving transformation $\widehat{\sigma }$ such that

$$\widehat{\sigma }\left(I_k^m\right)=I_{\sigma \left(k\right)}^m\mathrm{by}\mathrm{ordinary}\mathrm{translation}.$$

(4)

In other words if $\sigma$ permutes the elements $\{0,1,2,\cdots m\}$, then $\widehat{\sigma }$ permutes the intervals $I_0^m,I_1^m,\cdots I_m^m.$

We remark that if $ifm=2^n-1,$ then $\widehat{\sigma }$ is a dyadic transformation. Therefore we have our first main theorem. □

Theorem 3.

If $m=2^n-1$, the map ${\mathsf{\Psi }}^m$ identifies the symmetric group ${\sum }_m$ with a set of dyadic transformations of rank n, and the images of all these symmetric groups for all different values of n constitute a dense set in $Smeas\left(I\right)$ for the Strong Operator Topology.

3.2. Some Subgroups of $Imeas\left(\mathbb{CP}\right(1\left)\right)$

Now, let us look at some examples of measures that preserve the transformation of the sphere.

• The moment map J$:\left(\mathbb{CP}\right(1),\mathsf{\Omega })⟶\left(\right[0,1],|·\left|\right)$ is a measure-preserving transformation.
• Let $I_k^m=\left[{\displaystyle \frac{k}{m+1}},{\displaystyle \frac{k+1}{m+1}}\right[,k=0,1,\cdots ,m$ and let $S_k^m=J^{-1}\left(I_k^m\right)$ be a spherical segment. Let ${\sum }_m$ be a symmetric group of $m+1)$ letters. We have seen that every permutation $\sigma$ defines a map $\widehat{\sigma }$ that sends the interval $I_k^m$ to the interval $I_{\sigma \left(k\right)}^m$ through translation. $\widehat{\sigma }$ induces a measure-preserving transformation on $\mathbb{CP}\left(1\right)$ by permuting the spherical segments $S_k^m,k=0,1,\cdots ,m.$
  Therefore, for every natural number m, the symmetric group ${\sum }_m$ can be identified with a subgroup of $Imeas\left(\mathbb{CP}\right(1\left)\right)$.
• Let f be a differentiable function and let $X_f$ be the symplectic gradient of f. The flow of $X_f$ defines a family of invertible measure-preserving transformations of the sphere.
• The finite-dimensional torus ${\mathit{T}}^m$ can be identified with a subgroup of $Imeas\left(\mathbb{CP}\right(1\left)\right)$, as stated in the following Theorem:

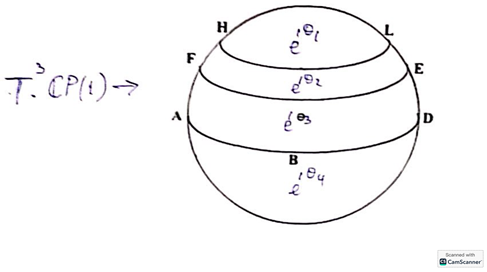
Theorem 4.

There is an action of the finite-dimensional torus:

$${\mathbb{T}}^m=\underset{m}{\underbrace{S^1\times S^1\times \cdots \times S^1}}onthesphere\mathbb{CP}\left(1\right).$$

Proof. 

Each element $t=(e^{i{\theta }_0},e^{i{\theta }_1},\cdots ,e^{i{\theta }_m})$ of the torus ${\mathbb{T}}^m$ acts on $\mathbb{CP}\left(1\right)$, by simply rotating every spherical segment $S_k^m$ by an angle of ${\theta }_k$ around the vertical axis.

Of course, this action is not differentiable if the angles ${\theta }_k$ are different.

But these spherical segments become thinner and thinner as m becomes bigger and bigger. Ultimately, they will shrink down to circles and the action of the tori ${\mathbb{T}}^m$ will just be rotating each circle of latitudes with a fixed angle The following picture illustrates how the torus $T^3=\left(\begin{array}{cccc}{e}^{i{\theta }_1}& 0& 0& 0\\ 0& e^{i{\theta }_2}& 0& 0\\ 0& 0& e^{i{\theta }_3}& 0\\ 0& 0& 0& e^{i{\theta }_4}\end{array}\right)$ acts on the sphere by rotating four spherical segments. □

There is nothing special about the choice of the intervals $I_k^m$. Any other partition of $[0,1]$ into m intervals is just fine:

Given a partition P of the interval $[0,1]$ into m subintervals,

$0=a_0<a_1<a_2<\cdots <a_{m-1}<a_m=1$, let $S_k^P=J^{-1}\left([a_k,a_{k+1})\right)$ be a spherical segment and let

$$(e^{i{\theta }_0},e^{i{\theta }_1},\cdots ,e^{i{\theta }_m})\in T^m.$$

Then, by rotating the spherical segment $S_k^P$ by an angle of ${\theta }_k$, we obtain an invertible measure preserving the transformation of the sphere.

So the intervals $I_k^m$ are just a particular partition.

We can generalize Theorem 4 as follows.

Theorem 5.

Let ${\mathcal{P}}^m$ be the set of partitions $P^m$ of the interval $[0,1]$ in exactly m intervals ${\left(I_k\right)}_k$. Let $J^{-1}\left(I_k\right)$ be a spherical segment.

Then, there exists a map

$$\mathsf{\Psi }:{\mathcal{P}}^m\times T^m\to Smeas\left(\mathbb{CP}\left(1\right)\right)$$

defined as follows: $\mathsf{\Psi }(P^m,{\left(e^{i{\theta }_k}\right)}_k)$ rotates each spherical segment $J^{-1}\left(I_k\right)$ by an angle ${\theta }_k$.

It was proven in [2,5] that the group

$$\mathcal{T}\left(\mathbb{CP}\right(1\left)\right)=\{\varphi \in Smeas(\mathbb{CP}\left(1\right)),\varphi (J,\theta )=(J,\theta +g\left(J\right)),g:[0,1]\to \mathbb{R}s-sobolev\}.$$

is a maximal torus of ${\mathcal{D}}_{\omega }^s\left(\mathbb{CP}\left(1\right)\right).$

Now, we can state one of our main results.

Theorem 6.

Let $\mathcal{T}\left(\mathbb{CP}\right(1\left)\right)$ be the subgroup of $Smeas\left(\mathbb{CP}\right(1\left)\right)$ that rotates every circle of latitude with a fixed angle. We have the following:

For every $\varphi \in \mathcal{T}\left(\mathbb{CP}\right(1\left)\right)$, there exists a sequence ${\left({\varphi }_m\right)}_m$ such that ${\varphi }_m\in {\mathbb{T}}^m$, and ${\left({\varphi }_m\right)}_m$ converges point-wise to ϕ.

Proof. 

Let $\varphi \in \mathcal{T}\left(\mathbb{CP}\right(1\left)\right)$ be defined by $\varphi (J,\theta )=(J,\theta +g(J\left)\right)$ in the local chart $[J,e^{i\theta }]$.

Since $g\left(J\right))$ is a measurable function on $[0,1]$, it can be approximated by step functions: there exists $g_m\left(J\right)={\sum }_{k=0}^{k=m}{\theta }_m^k{\chi }_{I_k}\left(J\right)$, which converges point-wise almost everywhere to $g\left(J\right)$ where ${\left(I_k\right)}_k$ is a partition of $[0,1]$ into m intervals.

It follows that ${\varphi }_m(J,\theta )=(J,\theta +g_m\left(J\right))$ is therefore an element of the torus ${\mathbb{T}}^m$ associated with the partition ${\left(I_k\right)}_k$. The convergence of the sequence ${\left({\varphi }_m\right)}_m$ is the consequence of the convergence of ${(\theta +g_m)}_m$ to $\theta +g\left(J\right)$. This complete the proof. □

4. Weyl Group

The Weyl group is, by definition, the group $W=\mathit{N}\left(\mathit{T}\right)\setminus \mathit{T}$, where $\mathit{T}$ is a maximal abelian group.

Theorem 7.

The normalizer $N\left(\mathcal{T}\right)$ of $\mathcal{T}$ is the group of maps

$$(r,\theta )\to \left(\varphi \right(r),j(r)\theta +k(r\left)\right)$$

with ϕ being an invertible measure-preserving transformation of $[0,\infty ],$ j measurable and equal to $\pm 1$ almost everywhere, and k being measurable. the “Weyl group” may be identified with a group of maps of the form

$$\{\varphi (r,\theta )=({\varphi }_1\left(r\right),j\left(r\right)\theta )\}.$$

The authors in [4] have shown that the Weyl group of the maximal torus of the annulus can be identified with a group of maps of the form

$$(z,\theta )\to \left(a\right(z),j(z\left)\theta \right)$$

where $z\to a\left(z\right)$ is an invertible measure-preserving transformation of the unit interval and $z\to j\left(z\right)$ is a measurable function equal to $\pm 1$ almost everywhere. Their proof applies word-by-word to the infinite-dimensional Lie group $\mathcal{T}\left(\mathbb{CP}\right(1\left)\right)$ of the sphere. For the sake of completeness, we reproduce the proof here.

Let $\varphi \in Smeas\left(\mathbb{CP}\right(1\left)\right)$ such that

$$\varphi \circ e^{if\left(r\right)}=e^{ih\left(r\right)}\circ \varphi$$

(5)

where $f\left(r\right)$ and $h\left(r\right)$ are measurable functions and $e^{ig\left(r\right)}(r,\theta )=(r,\theta +g\left(r\right))$ for any measurable function g. If

$$\varphi (r,\theta )=({\varphi }_1(r,\theta ),{\varphi }_2(r,\theta ))$$

then (5) becomes

$$({\varphi }_1(r,\theta +f\left(r\right)),{\varphi }_2(r,\theta +f\left(r\right)))=({\varphi }_1(r,\theta ),{\varphi }_2(r,\theta )+h\left({\varphi }_1(r,\theta )\right))$$

(6)

which translates to

$$\begin{array}{c}\hfill {\varphi }_1(r,\theta +f\left(r\right))={\varphi }_1(r,\theta )+f\left(r\right)\end{array}$$

(7)

$$\begin{array}{c}\hfill {\varphi }_2(r,\theta +f\left(r\right))={\varphi }_2(r,\theta )+h\left({\varphi }_1(r,\theta )\right).\end{array}$$

(8)

It follows from (7) that ${\varphi }_1$ is a function of r alone.

Rewrite (8) as

$${\varphi }_2(r,\theta +f\left(r\right))-{\varphi }_2(r,\theta )=h\left({\varphi }_1\left(r\right)\right)$$

The right hand side is independent of $\theta$, and therefore, ${\varphi }_2(r,\theta )$ must be linear in $\theta$, ${\varphi }_2(r,\theta )=j\left(r\right)\theta +k\left(r\right)$. Equation (8) then reads

$$j\left(r\right)f\left(r\right)=h\left({\varphi }_1\left(r\right)\right).$$

This equation should be verified for every measurable unction f, and this will happen only if the function ${\varphi }_1$ is one-to-one.

To summarize, the function $\varphi =({\varphi }_1,{\varphi }_2)$ is of the form $({\varphi }_1\left(r\right),j\left(r\right)\theta +k\left(r\right))$ with the function ${\varphi }_1$ being one-to-one.

Now, since $\varphi :\left(\mathbb{CP}\right(1),\mathsf{\Omega })\to \left(\mathbb{CP}\right(1),\mathsf{\Omega })$ is a measure-preserving transformation, the measure of strips

$$\{r\in E\}\times \{exp2\pi i\theta ,\theta \in [0,1\left]\right\},$$

($E\subset [0,1]$ measurable) is preserved; ${\varphi }_1$ then has to be a measure-preserving transformation. Also the measure of strips

$$\{r\in [0,\infty \left]\right\}\times \{exp2\pi i\theta ,\theta \in F\},$$

($F\subset [0,1]$ measurable) is preserved, and it follows that $j\left(r\right)=\pm 1$ almost everywhere. So $\varphi (r,\theta )=({\varphi }_1\left(r\right),\pm \theta +k\left(r\right))$.

Finally, if ${\psi }_i(r,\theta )=({\varphi }_i\left(r\right),j_i\left(r\right)\theta +k_i\left(r\right)),i=1,2$, and if ${\psi }_1={\psi }_2\circ e^{ih\left(r\right)},$ then ${\varphi }_1={\varphi }_2$ and $j_1\left(r\right)=j_2\left(r\right)$.

The quotient $N\left(\mathcal{T}\right)\setminus \mathcal{T}$ can be identified with

$$\{\varphi (r,\theta )=({\varphi }_1\left(r\right),j\left(r\right)\theta )\}.$$

as was claimed in the theorem.

N($\mathcal{T}$) versus $\mathit{N}\left({\mathit{T}}^m\right)$

In section, we have shown that the tori ${\left({\mathit{T}}^m\right)}_m$ converge to $\mathcal{T}$. In fact more is true.

Theorem 8.

The normalizers of ${\mathit{T}}^m$ also converge to N($\mathcal{T})$.

Proof 

• First of all, let us show that the normalizers of ${\mathit{T}}^m$ can be identified with a subgroup of N($\mathcal{T})$. We know from (1) that

  $$\mathit{N}\left({\mathit{T}}^m\right)=\left\{P_{\sigma }t,\sigma \in \sum _m,t\in {\mathit{T}}^m\right\}.$$
  With the element $P_{\sigma }t$ of the normalizer of ${\mathit{T}}^m$, we associate the map $\widehat{\sigma }$, which permutes the spherical segments $S_k^m$ followed by the action of t on these spherical segments.
• Theorem 7 tells us that a measure-preserving transformation $\psi$ is an element of the normalizer of $\mathcal{T}$ if it can be written as $\psi (r,\theta )=\left(\varphi \right(r),j(r)\theta +k(r\left)\right)$. In the local chart $z=1-J\left(r\right)$, $\psi$ can be written as

  $$\psi (z,\theta )=(\overline{\varphi }\left(z\right),\overline{j}\left(z\right)\theta +\overline{k}\left(z\right))$$

  where $\overline{\varphi }:[0,1]\to [0,1]$ is a measure-preserving transformation of the unit interval and $\overline{k}:[0,1]\to \mathbb{R}$ a measurable function. Now, we can use Theorem 3 to approximate $\overline{\varphi }$ via symmetric permutations and also approximate $\overline{k}$ via step functions. In other words, there exists a sequence of permutations ${\left({\sigma }_n\right)}_n$ and a sequence of step functions $k_n={\sum }_l{\theta }_l^n{\chi }_l^n$ such that ${\sigma }_n\to \overline{\varphi }$ and $k_n\to \overline{k}$.
  set $t_n=diag({\theta }_1^n,{\theta }_2^n,\cdots ,{\theta }_m^n)\in {\mathit{T}}^m$. It follows, then, that ${\left(P_{{\sigma }_n}{t}_n\right)}_n$ converges to $\psi .$

□

In conclusion, we think that these results can be extended to a maximal torus of symplectomorphisms on toric variety. Our next project will investigate how the Cartan subalgebra of the infinite-dimensional torus characterizes the adjoint representation defined by the Poisson bracket on functions.