Stability of the F^∗ Algorithm on Strong Pseudocontractive Mapping and Its Application

Abstract

This paper investigates the stability of the $F^{\ast }$ iterative algorithm applied to strongly pseudocontractive mappings within the context of uniformly convex Banach spaces. The study leverages both analytic and numerical methods to demonstrate the convergence and stability of the algorithm. In comparison to previous works, where weak-contraction mappings were utilized, the strongly pseudocontractive mappings used in this study preserve the convergence property, exhibit greater stability, and have broader applicability in optimization and fixed point theory. Additionally, this work shows that the type of mapping employed converges faster than those in earlier studies. The results are applied to a mixed-type Volterra–Fredholm nonlinear integral equation, and numerical examples are provided to validate the theoretical findings. Key contributions of this work include the following: (i) the use of strongly pseudocontractive mappings, which offer a more stable and efficient convergence rate compared to weak-contraction mappings; (ii) the application of the $F^{\ast }$ algorithm to a wider range of problems; and (iii) the proposal of future directions for improving convergence rates and exploring the algorithm’s behavior in Hilbert and reflexive Banach spaces.

1. Introduction

Throughout this work, X denotes a real Banach space, and Z represents the set of non-negative integers. $D\left(H\right)$ is the domain of the self-mapping H, while $F\left(X\right)$ refers to the fixed point set of H.

The mapping H is said to be as follows:

• Lipschitzian with constant L if for $L>0$, the following inequality holds for all $x,y\in D\left(H\right)$:

  $$\parallel H\left(x\right)-H\left(y\right)\parallel \le L\parallel x-y\parallel .$$

  (1)
  Here, L is a constant that satisfies $0<L<\infty$.
• Contractive if in inequality (1), $L\in (0,1)$.
• Nonexpansive if in inequality (1), $L=1$.

Definition 1

([1]). A mapping H is said to be k-strongly pseudocontractive if there exists a constant $k>1$ such that

$$\parallel x-y\parallel \le \parallel x-y+r\left(I-H\right)x-r\left(I-H\right)y\parallel ,$$

(2)

for all $x,y\in D\left(H\right)$ and for all $r<0$.

Remark 1.

From the result of Kato [2], inequality (1) is equivalent to inequality (2); then, there exists $j\left(x-y\right)\in J\left(x-y\right)$ such that

$$〈Hx-Hy,j\left(x-y\right)〉\le {\parallel x-y\parallel }^2,$$

(3)

for all $x,y\in D\left(H\right)$.

Remark 2.

From the inequality (1), Bogin [3] obtained the following inequality:

$$〈Hx-Hy,j\left(x-y\right)〉\le k{\parallel x-y\parallel }^2$$

or

$$〈Hx-Hy,j\left(x-y\right)〉\le (1-k){\parallel x-y\parallel }^2,$$

and the mapping H is said to be strongly pseudocontractive for some $k\in \left(0,1\right)$.

Remark 3.

A strongly pseudocontractive mapping is said to be a strongly ϕ-pseudocontractive mapping, given ϕ defined as $\varphi \left(s\right)=ks$ for $k\in (0,1)$ where the converse is not required to be true.

Definition 2.

A mapping H is said to be strongly ϕ-pseudocontractive ∀ $x,y\in Z$ where there exists $j(x-y)\in J(x-y)$ and there is a strictly increasing function $\varphi :[0,\infty )\to [0,\infty )$ with $\varphi \left(0\right)=0$ such that

$$〈Hx-Hy,j(x-y)〉\le {\parallel x-y\parallel }^2-\varphi \left(\parallel x-y\parallel \right)\parallel x-y\parallel .$$

Remark 4.

A strongly ϕ-pseudocontractive mapping is said to be generalized strongly Φ-pseudocontractive mapping with $\Phi :\left[0,\infty \right)\to \left[0,\infty \right)$ defined by $\Phi \left(s\right)=\varphi \left(s\right)$ where the converse is not needed to be true.

Definition 3.

A mapping H is said to be generalized strongly Φ-pseudocontractive ∀ $x,y\in Z$, having $j\left(x-y\right)\in J\left(x-y\right)$ and a strictly increasing function $\Phi :[0,\infty )\to [0,\infty )$ with $\Phi \left(0\right)=0$ such that

$$〈Hx-Hy,j(x-y)〉\le {\parallel x-y\parallel }^2-\Phi \left(\parallel x-y\parallel \right).$$

Definition 4

([4]). Let H be a self-mapping on a subset of a Banach space Z with a fixed point p and $\left\{t_n\right\}$ be an arbitrary sequence in K. Then, an iterative scheme $p_{n+1}=f(H,p_n)$ for some function f, converging to a fixed point p, is said to be H-stable or stable with respect to H if for

$${\vartheta }_n=\parallel t_{n+1}-f(H,t_n)\parallel (n\in {\mathbb{Z}}_{+}),$$

${\displaystyle \underset{n\to \infty }{lim}}{\vartheta }_n=0$ if and only if ${\displaystyle \underset{n\to \infty }{lim}}{t}_n=p$.

The stability results of various iterative schemes for several classes of nonlinear mappings have been identified and studied by many researchers. Among them is Ostrowski [4] who introduced the concept of stability for a fixed point iterative scheme and proved that Picard’s iterative scheme is stable with respect to contraction mappings. The theorem is as follows:

Theorem 1

([4]). Let $p_0$ be an arbitrary point in Z. Suppose $\left\{p_n\right\}$ is a sequence in Z which satisfies

$$\begin{array}{cc}\hfill & p_{n+1}=x_n^{\left(1\right)}H(x_n^{\left(2\right)}H(.....H(x_n^{\left(k\right)}H{p}_n+(1-x_n^{\left(k\right)})p_n+u_n^{\left(k\right)})+....)\hfill \\ & +(1-x_n^{\left(2\right)}{P}_n+u_n^{\left(2\right)})+(1-x_n^{\left(1\right)}{p}_n+u_n^{\left(1\right)})\hfill \end{array}$$

(4)

For $p_0\in Z$, $n=1,2,3,\dots$, $\left\{t_n\right\}$ is a sequence in Z; then,

$${\vartheta }_n=\parallel p_{n+1}-(1-x_n^{\left(1\right)})p_n-x_n^{\left(1\right)}H{p}_n^{\left(1\right)}-u_n^{\left(1\right)}\parallel ,n=0,1,\dots$$

where $\left(u_n^{\left(i\right)}\right)$ are sequences in a real Banach space Z and $\left(x_n^i\right)$, $i=1,k$ where k is a real sequence in $[0,1]$ satisfying the following conditions:

(c₁.)

${\sum }_{n=0}^{\infty }\parallel u_n^{\left(1\right)}\parallel \le \infty$;

(c₂.)

${\displaystyle \underset{n\to \infty }{lim}}\parallel u_n^{\left(i\right)}\parallel =0$, $i=2,k$;

(c₃.)

${\displaystyle \underset{n\to \infty }{lim}}{x}_n^{\left(1\right)}=0$, $i=1,k$;

(c₄.)

${\sum }_{n=1}^{\infty }{x}_n^{\left(1\right)}=\infty$.

Then,

(i) 

the sequence $\left\{p_n\right\}$ is almost H-stable

(ii) 

${\displaystyle \underset{n\to \infty }{lim}}{p}_{n+1}=p\in f\left(H\right)$ implies ${\displaystyle \underset{n\to \infty }{lim}}\vartheta =0$

Harder and Hicks [5] extended the work of Ostrowski [4] for more general iterative schemes with contractive conditions. In the process of estimating fixed points, the authors considered an estimated sequence $\left\{t_n\right\}$ instead of the theoretical sequence $\left\{p_n\right\}$ due to rounding errors and numerical estimation of functions. The authors stated the stability of an iterative scheme as follows:

Theorem 2

([5]). Let $(Z,d)$ be a complete metric space and $H:Z\to Z$ be a mapping. Then, given that $f_H=\{p\in Z:H_p=p\}$ is the set of fixed points of H, let ${\left\{t_n\right\}}_{n=0}^{\infty }\subset Z$ be the sequence generated by an iterative scheme which is defined by

$$t_{n+1}=f(H,t_n),forn=0,1,2,\dots ,t_0\in Z,$$

where $t_0\in Z$ is the first estimation and f is some function. Considering that the sequence ${\left\{t_n\right\}}_{n=0}^{\infty }$ converges to a fixed point p of H, then, setting ${\vartheta }_n=d\left(t_{n+1},f(H,t_n)\right)$ ∀ $n=0,1,2,\dots$ shows that the iterative scheme is H-stable if and only if

$$\underset{n\to \infty }{lim}{\vartheta }_n=0⟹\underset{n\to \infty }{lim}{t}_n=p.$$

Also, Ajibade et al [6] obtained the convergence and stability of the Ishikawa iterative process for a class of $\varphi$-quasinonexpansive mappings. Recently, Ali and Ali [7] constructed a new two-step iterative algorithm, known as $F^{\ast }$ iteration to estimate the fixed points of weak contractions in Banach spaces as given below:

$$\left\{\begin{array}{c}{p}_0\in Z\hfill \\ p_{n+1}=H{q}_n\hfill \\ q_n=H\left(\left(1-r_n\right)p_n+r_{n}H{p}_n\right).\hfill \end{array}\right.$$

(5)

The authors proved that the sequence of the proposed algorithm converges strongly to a fixed point of weak contractions. The $F^{\ast }$ iterative scheme is also shown to be almost stable for weak contractions and converges to a fixed point faster than Picard, Mann, Ishikawa, S, normal-S and Varat iterative schemes. A data dependence result was obtained using the $F^{\ast }$ iteration, and numerical examples were presented to validate the results. Furthermore, the results were also used to estimate the solution of the nonlinear quadratic Volterra integral equation. Finally, in the work, an open question arose thus—“can the sequence $\left\{p_n\right\}$ generated by $F^{\ast }$ iterative scheme converge to a fixed point of nonexpansive or pseudocontractive mappings?” In response to the question, Ajibade et al. [8] showed that the sequence generated by the $F^{\ast }$ iterative algorithm (5) converges strongly to a fixed point of a strongly pseudocontractive mapping in the framework of uniformly convex Banach spaces.

In addition, Gursoy [9] studied a mixed Volterra–Fredholm nonlinear integral equation and utilized it via a normal S-iterative scheme to show that the iterative sequence generated converges to a solution of its integral equation. Subsequently, Ali et al. [10] studied Picard’s three-step iterative scheme for the estimation of fixed points of Zamfirescu mappings in an arbitrary Banach space. The authors proved that Picard’s three-step iterative scheme was almost H-stable and converged faster than Picard, Mann, Ishikawa, Noor, S, normal S and other existing iterative schemes. Lastly, they applied the result to estimate the solution of a mixed Volterra–Fredholm nonlinear integral equation. More recently, Alshehri et al. [11] examined the $JF$ iterative scheme and estimated the fixed points of a nonlinear mapping which satisfies a condition in uniformly convex Banach spaces. Thereafter, weak and strong convergence results were obtained. The authors also highlighted that the $JF$ iterative scheme is weakly $w^{2}H$-stable with respect to most contractions, and at the end of their main results, a numerical example was given to show that the $JF$ iterative scheme is more effective in its convergence than some existing iterative schemes. As part of its application, the $JF$ iterative scheme was employed to approximate the solution of a mixed Volterra–Fredholm nonlinear integral equation (see also [12,13]). Several investigations were also conducted by researchers in the literature on the iterative scheme (see [14,15,16,17,18,19,20,21]). The mixed Volterra–Fredholm nonlinear integral equation which was first introduced by Cracium and Serban [22] is given as follows:

$$p\left(t\right)=F\left(t,p\left(t\right),{\int }_{a_1}^{t_1}....{\int }_{a_j}^{t_j}K\left(t,s,p\left(s\right)\right)ds{\int }_{a_1}^{b_1}....{\int }_{a_j}^{b_j}T\left(t,s,p\left(s\right)\right)ds\right).$$

(6)

Motivated by the works of [7,8,9], we investigate the stability of the $F^{\ast }$ iterative algorithm on a strongly pseudocontractive mapping in the framework of uniformly convex Banach space. The result is obtained via numerical and analytic methods (see [23,24,25,26,27,28,29,30,31]). The applicability of the result is shown on a mixed-type Volterra–Fredholm nonlinear integral equation. Finally, a numerical example is given. Some of the novel contributions of this work are as follows:

(i)

In [7], the authors used weak-contraction mapping to obtain the result, while in this work, we utilized strongly pseudocontractive mapping which preserves the convergence property, is more stable, and has wider applicability in optimization and fixed point theory.

(ii)

The type of map used in this work converges faster than the maps used in the previous works (see [7,8,9]).

In Section 1, an overview of previous works in this research direction is considered. Basic definitions, remarks, and results are given. In Section 2, useful lemmas necessary for proving our result are presented. In Section 3, the main results are presented. In Section 4, the applicability of our result is shown. Section 5 contains a numerical example that validates the main result. The last section contains concluding remarks and recommendations.

2. Preliminaries

Useful lemmas necessary to prove our main results are presented in this section as follows:

Lemma 1.

Let $J:Z\to 2^Z$ be the normalized duality mapping, then

$$\begin{array}{c}\hfill {\parallel a+b\parallel }^2\le {\parallel a\parallel }^2+2〈b,j(a+b)〉,\end{array}$$

(7)

for all $a,b\in Z$ where $j(a+b)\in J(a+b)$.

Lemma 2.

If ${\left\{{\mu }_n\right\}}_{n=0}^{\infty }$ is a non-negative real sequence satisfying

$${\mu }_{n+1}\le \left(1-{\gamma }_n\right){\mu }_n+{\sigma }_n,$$

(8)

where ${\gamma }_n\in \left[0,1\right]$, ${\sum }_{n=1}^{\infty }{\gamma }_n=\infty$, and ${\sigma }_n=o\left({\gamma }_n\right)$, then ${\mu }_n\to 0$ as $n\to \infty$.

3. Main Results

To show the stability of the $F^{\ast }$ iterative scheme using strongly pseudocontractive mapping in a uniformly convex Banach space, we prove the following theorem:

Theorem 3.

Let Z be a uniformly Banach space and $H:Z\to Z$ be a strongly pseudocontractive mapping with a bounded set and with $F\left(H\right)\ne \varnothing$. Let $\left\{r_n\right\}$ be a real sequence in $(0,1)$ satisfying the following conditions:

$$\underset{n\to \infty }{lim}{r}_n=0,\sum _{n=1}^{\infty }{r}_n=\infty .$$

Let $P_0$ be an arbitrary point in Z with $\left\{t_n\right\}$, a sequence in Z. Assume that $\left\{p_n\right\}$ is a sequence in Z which satisfies the iterative scheme

$$\left\{\begin{array}{c}{t}_{n+1}=H{c}_n\hfill \\ c_n=H{a}_n\hfill \\ a_n=\left(1-r_n\right)t_n+r_{n}H{t}_n.\hfill \end{array}\right.$$

Then,

(i) 

${lim}_{n\to \infty }{t}_n=p\in F\left(H\right)\Rightarrow {lim}_{n\to \infty }{\vartheta }_n=0$.

(ii) 

The sequence $\left\{p_n\right\}$ is almost H-stable.

Proof. 

(i) Let ${lim}_{n\to \infty }{t}_n=p\in F\left(H\right)$, where

$${\vartheta }_n=\parallel t_{n+1}-f(H,t_n)\parallel =\parallel t_{n+1}-(1-r_n)t_n-r_{n}H{t}_n\parallel .$$

Then, using some arithmetic and the conditions of the theorem, we obtain the following:

$$\begin{array}{cc}\hfill {\vartheta }_n=& \parallel t_{n+1}-(1-r_n)t_n-r_{n}H{t}_n\parallel \hfill \\ \hfill =& \parallel t_{n+1}-p-(1-r_n)t_n+(1-r_n)p+r_{n}p-r_{n}H{t}_n\parallel \hfill \\ \hfill =& \parallel t_{n+1}-p(1-r_n)(p-t_n)+r_n(p-H{t}_n)\parallel \hfill \\ \hfill \le & \left|\right|t_{n+1}-p\left|\right|+(1-r_n)\left|\right|p-t_n\left|\right|+r_n\left|\right|p-H{t}_n\left|\right|\hfill \\ \hfill {\vartheta }_n\le & \left|\right|t_{n+1}-p\left|\right|+(1-r_n)\left|\right|t_n-p\left|\right|+r_n\left|\right|H{t}_n-p\left|\right|⟶0asn⟶\infty .\hfill \end{array}$$

Thus, the theorem follows in the first part.

(ii) To show that the sequence $\left\{t_n\right\}$ is bounded, we have

$$\begin{array}{cc}\hfill \left|\right|t_{n+1}-p\left|\right|& =\parallel t_{n+1}-(1-r_n)t_n-r_{n}H{t}_n+(1-r_n)(t_n-p)+r_n(H{t}_n-Hp)\parallel \hfill \\ \hfill & \le \left|\right|t_{n+1}-(1-r_n)t_n-r_{n}H{t}_n\left|\right|+\left|\right|(1-r_n)(t_n-p)+r_n(H{t}_n-Hp)\left|\right|\hfill \\ \hfill & \le {\vartheta }_n+(1-r_n)\left|\right|(t_n-p)\left|\right|+r_n\left|\right|(H{t}_n-Hp)\left|\right|\hfill \\ \hfill & =(1-r_n)\left|\right|(t_n-p)\left|\right|+r_n{M}_1+{\vartheta }_n,\hfill \end{array}$$

where

$$M_1=\underset{n\in \mathbb{N}}{sup}\left|\right|H{t}_n-Hp\left|\right|.$$

$$\begin{array}{cc}\hfill \left|\right|t_{n+1}-p{\left|\right|}^2& =\left|\right|t_{n+1}-(1-r_n)t_n-r_{n}H{t}_n+(1-r_n)(t_n-p)+r_n(H{t}_n-Hp){\left|\right|}^2\hfill \\ \hfill & \le \left|\right|(1-r_n)(t_n-p)+r_n(H{t}_n-Hp){\left|\right|}^2+2\langle t_{n+1}-(1-r_n)t_n-r_{n}H{t}_n,\hfill \\ \hfill & j\left(t_{n+1}-p\right)\rangle \hfill \\ \hfill & \le {(1-r_n)}^2\left|\right|t_n-p{\left|\right|}^2+2\langle r_n(H{t}_n-Hp),j((1-r_n)(t_n-p)+r_n(H{t}_n-Hp))\rangle \hfill \\ \hfill & +2\langle t_{n+1}-(1-r_n)t_n-r_{n}H{t}_n,j\left(t_{n+1}-p\right)\rangle \hfill \\ \hfill & ={(1-r_n)}^2\left|\right|t_n-p{\left|\right|}^2+2r_n\langle (H{t}_n-Hp),j((1-r_n)(t_n-p)+r_n(H{t}_n-Hp))\rangle \hfill \\ \hfill & +2r_n\langle (H{t}_n-Hp),j(t_n-p)\rangle \hfill \\ \hfill & +2\langle t_{n+1}-(1-r_n)t_n-r_{n}H{t}_n,j\left(t_{n+1}-p\right)\rangle .\left(i\right).\hfill \end{array}$$

On the other hand,

$$\begin{array}{c}\hfill \left|\right|〈t_{n+1}-(1-r_n)t_n-r_{n}H{t}_n,j\left(t_{n+1}-p\right)〉\left|\right|\le M_1{\vartheta }_n.\left(ii\right).\end{array}$$

From (i) and (ii), we have

$$\begin{array}{c}\hfill \begin{array}{c}\left|\right|t_{n+1}-{p\left|\right|}^2\le {(1-r_n)}^2\left|\right|t_n-p{\left|\right|}^2+2r_n〈(H{t}_n-Hp),j\left((1-r_n)(t_n-p)+r_n(H{t}_n-Hp)-j(t_n-p)\right)〉\\ +2r_n〈(H{t}_n-Hp),j(t_n-p)〉+2M_1{\vartheta }_n.\left(iii\right)\end{array}\end{array}$$

Since H is strongly pseudocontractive,

$$\begin{array}{c}\hfill 〈H{t}_n-Hp,j(t_n,p)〉\le k\left|\right|t_n-p{\left|\right|}^2.\end{array}$$

Using the above inequality in (iii), we obtain

$$\begin{array}{c}\hfill \begin{array}{c}\left|\right|t_{n+1}-{p\left|\right|}^2\le {(1-r_n)}^2\left|\right|t_n-p{\left|\right|}^2+2r_n〈(H{t}_n-Hp),j\left((1-r_n)(t_n-p)+r_n(H{t}_n-Hp)-j(t_n-p)\right)〉\\ +2r_{n}k\left|\right|t_n-p{\left|\right|}^2+2M_1{\vartheta }_n.\left(iv\right)\end{array}\end{array}$$

Now, we show that the following sequence

$${\varrho }_n=〈H{t}_n-Hp,j((1-r_n)(t_n-p)+r_n(H{t}_n-Hp))-j(t_n-p)〉,$$

converges as $n⟶\infty .$ By the condition of the theorem and because $t_n$ and $H{t}_n$ are a bounded sequence in Z,

$$\begin{array}{c}\hfill (1-r_n)(t_n-p)+r_n(H{t}_n-Hp)-j(t_n-p)\\ \hfill \le t_n-p-r_n(t_n-p)+r_n(H{t}_n-Hp)-(t_n-p)\\ \hfill =r_{n}H{t}_n-r_n{t}_n+r_{n}p-r_{n}Hp⟶0asn⟶\infty .\end{array}$$

Z is a uniformly smooth Banach space and j is uniformly continuous on any bounded subset of Z. Thus, we have

$$j((1-r_n)(t_n-p)+r_n(H{t}_n-Hp))-j(t_n-p)⟶0asn⟶\infty$$

which makes ${\varrho }_n⟶0asn⟶\infty$. Using the above conditions in (iv), we have

$$\begin{array}{cc}\hfill \left|\right|t_{n+1}-p{\left|\right|}^2& \le {(1-r_n)}^2\left|\right|t_n-{p\left|\right|}^2+2r_n{\varrho }_n+2r_{n}k\left|\right|t_n-p{\left|\right|}^2+2M_1{\vartheta }_n\hfill \\ \hfill & \le [{(1-r_n)}^2+2r_{n}k]\left|\right|t_n-p{\left|\right|}^2+2r_n{\varrho }_n+2M_1{\vartheta }_n\hfill \\ \hfill & =[1-(2r_n-r_n^2-2r_{n}k)]\left|\right|t_n-p{\left|\right|}^2+2r_n{\varrho }_n+2M_1{\vartheta }_n\hfill \\ \hfill & =[1-r_n(2-r_n-2k)]\left|\right|t_n-p{\left|\right|}^2+2r_n{\varrho }_n+2M_1{\vartheta }_n,\left(v\right)\hfill \end{array}$$

by choosing a large positive N, such that for all $n\le N$ and ${\displaystyle \frac{1-rn}{2}}<k<{\displaystyle \frac{2-r_n}{2}}$, ${\sigma }_n=2r_n{\varrho }_n+2M_1{\vartheta }_n$, the inequality (v) above yields

$$\left|\right|t_{n+1}-{p\left|\right|}^2\le [1-r_n(2-r_n-2k)]\left|\right|t_n-p{\left|\right|}^2+{\sigma }_n$$

Therefore, by setting ${\mu }_n=\left|\right|t_n-p{\left|\right|}^2$ and ${\gamma }_n=r_n(2-r_n-2k)$,

$${\mu }_{n+1}\le (1-{\gamma }_n){\mu }_n+{\sigma }_n.$$

By using Lemma 2, we have ${\gamma }_n\in [0,1],$ ${\sum }_{n=1}^{\infty }{\gamma }_n=\infty$ and ${\sigma }_n=0\left(r_n\right)$. On taking the limit of both sides and ${\sum }_{n=1}^{\infty }{\vartheta }_n\le \infty$ thus, ${\mu }_n⟶0$ implies that $t_n⟶p$ as $n⟶\infty$. Hence, the sequence $\left\{p_n\right\}$ generated by the $F^{\ast }$ iterative scheme is almost H-stable. □

4. Application

In this aspect, the solution of a mixed Volterra–Fredholm nonlinear integral equation was approximated using the iterative scheme (6).

The mixed Volterra–Fredholm nonlinear integral equation is given as follows:

$$p\left(t\right)=F\left(t,p\left(t\right),{\int }_{a_1}^{t_1}....{\int }_{a_j}^{t_j}K\left(t,s,p\left(s\right)\right)ds{\int }_{a_1}^{b_1}....{\int }_{a_j}^{b_j}T\left(t,s,p\left(s\right)\right)ds\right),$$

(9)

where $\left[a_1;b_1\right]\times ....\times \left[a_j;b_j\right]$ is an interval in ${\mathbb{R}}^j$, $t=\left(t_1,t_2,\dots ,t_j\right)$, $s=\left(s_1,s_2,\dots ,s_j\right)\in \left[a_1,b_1\right]\times \dots \times \left[a_j,b_j\right]$, $K,T:\left[a_1;b_1\right]\times ....\times \left[a_j;b_j\right]\times \left[a_1;b_1\right]\times ....\times \left[a_j;b_j\right]\times \mathbb{R}\to \mathbb{R}$ continuous functions and $F:\left[a_1;b_1\right]\times ....\times \left[a_j;b_j\right]\times {\mathbb{R}}^3\to \mathbb{R}$.

Considering that the following conditions are satisfied:

$\left(M_1\right)$ $K,T:C\left(\left[a_1;b_1\right]\times ....\times \left[a_j;b_j\right]\times \left[a_1;b_1\right]\times ....\times \left[a_j;b_j\right]\times \mathbb{R}\right)$;

$\left(M_2\right)$ $F\in C\left(\left[a_1;b_1\right]\times ....\times \left[a_j;b_j\right]\times \left[a_1;b_1\right]\times ....\times \left[a_j;b_j\right]\times {\mathbb{R}}^3\right)$;

$\left(M_3\right)$ there exist non-negative constants $\alpha$, $\eta$, and $\gamma$ such that

$$|F\left(t,e_1,e_2,e_3\right)-F\left(t,f_1,f_2,f_3\right)|\le \alpha |e_1-f_1|+\eta |e_2-f_2|+\gamma |e_3-f_3|,$$

for all $t\in \left[a_1;b_1\right]\times ....\times \left[a_j;b_j\right]$, $e_j,f_j\in \mathbb{R}$, $j=1,2,3.$

$\left(M_4\right)$ there exist non-negative constants $L_K$ and $L_T$ such that

$$|K\left(t,s,u\right)-K\left(t,s,v\right)|\le L_K|u-v|$$

$$|T\left(t,s,u\right)-T\left(t,s,v\right)|\le L_T|u-v|,$$

for all $t,s\in \left[a_1;b_1\right]\times ....\times \left[a_j;b_j\right],u,v\in \mathbb{R}$.

$\left(M_5\right)$ $\alpha +\left(\eta L_K+\gamma L_T\right)$$\left(b_1-a_1\right)....\left(b_j-a_j\right)<1$. By the solution of problem $\left(4.2\right)$, we mean a function $p^{\ast }\in C\left(\left[a_1,b_1\right]\times \dots \times \left[a_j,b_j\right]\right)$.

Theorem 4.

Assume that conditions $\left(M_1\right)$–$\left(M_5\right)$ are satisfied. Then, a unique solution for Theorem 3 exists for $p^{\ast }\in C\left(\left[a_1,b_1\right]\times \dots \times \left[a_j,b_j\right]\right)$. Therefore, using the iterative Scheme in Equation (6), we prove the following main result.

Theorem 5.

Let $Y=C\left(\left[a_1,b_1\right]\times \dots \times \left[a_j,b_j\right],\parallel .\parallel \right)$ be a Banach space with Chebyshev’s norm. An operator $H:Y\to Y$ with $\left\{p_n\right\}$ as a sequence defined by the iterative scheme in Equation $\left(6\right)$ is given as

$$Hp\left(t\right)=F\left(t,p\left(t\right),{\int }_{a_1}^{t_1}....{\int }_{a_j}^{t_j}K\left(t,s,p\left(s\right)\right)ds{\int }_{a_1}^{b_1}....{\int }_{a_j}^{b_j}T\left(t,s,p\left(s\right)\right)ds\right),$$

(10)

where $F,K$ and T are defined as above. Considering that conditions $\left(M_1\right)$–$\left(M_5\right)$ are satisfied, Theorem 3 exists and the iterative scheme in Equation (6) converges to a unique solution $p^{\ast }\in C\left(\left[a_1,b_1\right]\times \dots \times \left[a_j,b_j\right]\right)$.

Proof. 

Firstly, we need to show the kind of mapping to be defined by H.

$$\begin{array}{c}{\parallel Hp-H{p}^{\ast }\parallel }^2={\parallel Hp-p^{\ast }\parallel }^2={|Hp\left(t\right)-H{p}^{\ast }\left(t\right)|}^2.\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\left|F\left(t,p\left(t\right),{\int }_{a_1}^{t_1}\dots {\int }_{a_j}^{t_j}K\left(t,s,p\left(s\right)\right)ds{\int }_{a_1}^{b_1}\dots {\int }_{a_j}^{b_j}T\left(t,s,p\left(s\right)\right)ds\right)\right.\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-{\left.F\left(t,p^{\ast }\left(t\right),{\int }_{a_1}^{t_1}\dots {\int }_{a_j}^{t_j}K\left(t,s,p^{\ast }\left(s\right)\right)ds{\int }_{a_1}^{b_1}\dots {\int }_{a_j}^{b_j}T\left(t,s,p^{\ast }\left(s\right)\right)ds\right)\right|}^2\hfill \end{array}$$

$$\begin{array}{c}\le \left[|p\left(t\right)-p^{\ast }\left(t\right)|+\eta |{\int }_{a_1}^{t_1}\dots {\int }_{a_j}^{t_j}K\left(t,s,p\left(s\right)\right)ds-{\int }_{a_1}^{t_1}\dots {\int }_{a_j}^{t_j}K\left(t,s,p^{\ast }\left(s\right)\right)ds|\right.\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\left.\gamma |{\int }_{a_1}^{b_1}\dots {\int }_{a_j}^{b_j}T\left(t,s,p\left(s\right)\right)ds-{\int }_{a_1}^{b_1}\dots {\int }_{a_j}^{b_j}T\left(t,s,p^{\ast }\left(s\right)\right)ds|\right]}^2\hfill \end{array}$$

$$\begin{array}{c}\le \left[\alpha |p\left(t\right)-p^{\ast }\left(t\right)|+\eta {\int }_{a_1}^{t_1}\dots {\int }_{a_j}^{t_j}|K\left(t,s,p\left(s\right)\right)-K\left(t,s,p^{\ast }\left(s\right)\right)|ds\right.\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\left.\gamma {\int }_{a_1}^{b_1}\dots {\int }_{a_j}^{b_j}|T\left(t,s,p\left(s\right)\right)-T\left(t,s,p^{\ast }\left(s\right)\right)|ds\right]}^2\hfill \end{array}$$

$$\begin{array}{c}\le \left[\alpha |p\left(t\right)-p^{\ast }\left(t\right)|+\eta {\int }_{a_1}^{t_1}\cdots {\int }_{a_j}^{t_j}{L}_K|p\left(s\right)-p^{\ast }\left(s\right)|ds\right.\hfill \\ {\left.\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\gamma {\int }_{a_1}^{b_1}\cdots {\int }_{a_j}^{b_j}{L}_T|p\left(s\right)-p^{\ast }\left(s\right)|ds\right]}^2\hfill \end{array}$$

$$\begin{array}{c}\\ ={\left[\alpha \parallel p-p^{\ast }\parallel +\eta {\int }_{a_1}^{t_1}\dots {\int }_{a_j}^{t_j}{L}_K\parallel p-p^{\ast }\parallel ds+\gamma {\int }_{a_1}^{b_1}\dots .{\int }_{a_j}^{b_j}{L}_T\parallel p-p^{\ast }\parallel ds\right]}^2\end{array}$$

$$\begin{array}{c}{\parallel Hp-H{p}^{\ast }\parallel }^2\le [\alpha \parallel p-p^{\ast }\parallel +\eta L_K\left(t_1-a_1\right)\left(t_2-a_2\right)\dots \left(t_j-a_j\right)\parallel p-p^{\ast }\parallel .\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\gamma L_T\left(b_1-a_1\right)\left(b_2-a_2\right)\dots \left(b_j-a_j\right)\parallel p-p^{\ast }\parallel {]}^2\hfill \end{array}$$

implying

$${\parallel Hp-H{p}^{\ast }\parallel }^2\le {\left[\left[\alpha +\left(\eta L_K+\gamma L_T\right)\left(b_1-a_1\right)\dots \left(b_j-a_j\right)\right]\parallel p-p^{\ast }\parallel \right]}^2.$$

(11)

Applying assumption $\left(M_5\right)$ we have

$$\alpha +\left(\eta L_K+\gamma L_H\right)\left(b_1-a_1\right)\dots \left(b_j-a_j\right)<1.$$

Moreover, Equation (10) can be written as follows:

$${\parallel Hp-H{p}^{\ast }\parallel }^2\le {\left[\left[\alpha +\left(\eta L_K+\gamma L_T\right)\left(b_1-a_1\right)\dots \left(b_j-a_j\right)\right]\right]}^2{\left[\parallel p-p^{\ast }\parallel \right]}^2,$$

(12)

by setting

$$k:={\left[\alpha +\left(\eta L_K+\gamma L_T\right)\left(b_1-a_1\right)\dots \left(b_j-a_j\right)\right]}^2<1.$$

Thus,

$${\parallel Hp-H{p}^{\ast }\parallel }^2=〈Hp-p^{\ast },j\left(Hp-p^{\ast }\right)〉\le k{\parallel p-p^{\ast }\parallel }^2.$$

Hence, this shows that the operator defined by H is a strongly pseudocontractive mapping. As stated in Theorem (3), we consider that $p^{\ast }$ is the fixed point of H. So, we show that $p_n\to p^{\ast }$ as $n\to \infty$. Inserting iterative scheme (6), Equation (10) and conditions $\left(M_1\right)$–$\left(M_4\right)$, we have

$$\begin{array}{c}\parallel z_n-p\parallel =\parallel \left(1-r_n\right)p_n+r_{n}H{p}_n\parallel \hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\parallel \left(1-r_n\right)p_n+r_{n}H{p}_n-r_{n}p+r_{n}p-p\parallel \hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\parallel \left(1-r_n\right)\left(p_n-p\right)+r_n\left(H{p}_n-p\right)\parallel \hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=|\left(1-r_n\right)\left(p_n\left(t\right)-p\left(t\right)\right)+r_n\left(H{p}_n\left(t\right)-p\left(t\right)\right)|\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\le \left(1-r_n\right)|p_n\left(t\right)-p\left(t\right)|+r_n|H{p}_n\left(t\right)-p\left(t\right)|.\hfill \end{array}$$

$$\begin{array}{c}=\left(1-r_n\right)|p_n\left(t\right)-p\left(t\right)|\hfill \\ \hspace{1em}\hspace{1em} +r_n|F\left(t,p_n\left(t\right),{\int }_{a_1}^{t_1}\cdots {\int }_{a_j}^{t_j}K\left(t,s,p_n\left(s\right)\right)ds,{\int }_{a_1}^{b_1}\cdots {\int }_{a_j}^{b_j}T\left(t,s,p_n\left(s\right)\right)ds\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-F\left(t,p\left(t\right),{\int }_{a_1}^{t_1}\cdots {\int }_{a_j}^{t_j}K\left(t,s,p\left(s\right)\right)ds,{\int }_{a_1}^{b_1}\cdots {\int }_{a_j}^{b_j}T\left(t,s,p\left(s\right)\right)ds\right)|.\hfill \end{array}$$

$$\begin{array}{c} \le \left(1-r_n\right)|p_n\left(t\right)-p^{\ast }\left(t\right)|+r_n\alpha |p_n\left(t\right)-p^{\ast }\left(t\right)|+r_n\eta |{\int }_{a_1}^{t_1}\cdots {\int }_{a_j}^{t_j}K\left(t,s,p_n\left(s\right)\right)ds\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} -{\int }_{a_1}^{t_1}\cdots {\int }_{a_j}^{t_j}K\left(t,s,p^{\ast }\left(s\right)\right)ds|+r_n\gamma |{\int }_{a_1}^{b_1}\cdots {\int }_{a_j}^{b_j}T\left(t,s,p_n\left(s\right)\right)ds\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-{\int }_{a_1}^{b_1}\cdots {\int }_{a_j}^{b_j}T\left(t,s,p^{\ast }\left(s\right)\right)ds|\hfill \\ \hspace{1em} \le \left(1-r_n\right)|p_n\left(t\right)-p^{\ast }\left(t\right)|+r_n\alpha |p_n\left(t\right)-p^{\ast }\left(t\right)|+r_n\eta {\int }_{a_1}^{t_1}\cdots {\int }_{a_j}^{t_j}|K\left(t,s,p_n\left(s\right)\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-K\left(t,s,p^{\ast }\left(s\right)\right)|ds+r_n\gamma {\int }_{a_1}^{b_1}\cdots {\int }_{a_j}^{b_j}|T\left(t,s,p_n\left(s\right)\right)-T\left(t,s,p^{\ast }\left(s\right)\right)|ds\hfill \\ \le \left(1-r_n\right)\parallel p_n\left(t\right)-p^{\ast }\left(t\right)\parallel +r_n\alpha \parallel p_n\left(t\right)-p^{\ast }\left(t\right)\parallel +r_n\eta {\int }_{a_1}^{t_1}\cdots {\int }_{a_j}^{t_j}{L}_K\parallel p_n\left(s\right)-p^{\ast }\left(s\right)\parallel ds\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+r_n\gamma {\int }_{a_1}^{b_1}\cdots {\int }_{a_j}^{b_j}{L}_T\parallel p_n\left(s\right)-p^{\ast }\left(s\right)\parallel ds.\hfill \end{array}$$

$$\begin{array}{c}\parallel z_n-p\parallel \le \alpha \parallel p_n-p\parallel +\eta L_K\left(t_1-a_1\right)\left(t_2-a_2\right)\dots \left(t_j-a_j\right)\parallel p_n-p\parallel \hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\gamma L_T\left(b_1-a_1\right)\left(b_2-a_2\right)\dots \left(b_j-a_j\right)\parallel p_n-p\parallel .\hfill \end{array}$$

This implies that

$$\parallel z_n-p^{\ast }\parallel \le \parallel p_n-p^{\ast }\parallel \left\{1-r_n\left(1-\left[\alpha +\left(\eta L_K+\gamma L_T\right)\left(b_1-a_1\right)\dots \left(b_j-a_j\right)\right)\right]\right\}.$$

(13)

Similarly, we have

$$\begin{array}{c}\parallel q_n-p^{\ast }\parallel =\parallel H{z}_n-p^{\ast }\parallel =|H{z}_n\left(t\right)-H{p}^{\ast }\left(t\right)|\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}=\left|F\left(t,z_n\left(t\right),{\int }_{a_1}^{t_1}\dots {\int }_{a_j}^{t_j}K\left(t,s,z_n\left(s\right)\right)ds{\int }_{a_1}^{b_1}\dots {\int }_{a_j}^{b_j}T\left(t,s,z_n\left(s\right)\right)ds\right)\right.\hfill \\ \left.\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-F\left(t,p^{\ast }\left(t\right),{\int }_{a_1}^{t_1}\dots {\int }_{a_j}^{t_j}K\left(t,s,p^{\ast }\left(s\right)\right)ds{\int }_{a_1}^{b_1}\dots {\int }_{a_j}^{b_j}T\left(t,s,p^{\ast }\left(s\right)\right)ds\right)\right|\hfill \end{array}$$

$$\begin{array}{c}\le \alpha |z_n\left(t\right)-p^{\ast }\left(t\right)|+\eta \left|{\int }_{a_1}^{t_1}\dots {\int }_{a_j}^{t_j}K\left(t,s,z_n\left(s\right)\right)ds-{\int }_{a_1}^{t_1}\dots {\int }_{a_j}^{t_j}K\left(t,s,p^{\ast }\left(s\right)\right)ds\right|\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +\gamma \left|{\int }_{a_1}^{b_1}\dots {\int }_{a_j}^{b_j}H\left(t,s,q_n\left(s\right)\right)ds-{\int }_{a_1}^{b_1}\dots {\int }_{a_j}^{b_j}H\left(t,s,p^{\ast }\left(s\right)\right)ds\right|\hfill \end{array}$$

$$\begin{array}{c}\le \alpha |z_n\left(t\right)-p^{\ast }\left(t\right)|+\eta {\int }_{a_1}^{t_1}\dots {\int }_{a_j}^{t_j}|K\left(t,s,z_n\left(s\right)\right)-K\left(t,s,p^{\ast }\left(s\right)\right)|ds\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\gamma {\int }_{a_1}^{b_1}\dots {\int }_{a_j}^{b_j}|T\left(t,s,z_n\left(s\right)\right)-T\left(t,s,p^{\ast }\left(s\right)\right)|ds\hfill \end{array}$$

$$\begin{array}{c}\le \alpha |z_n\left(t\right)-p^{\ast }\left(t\right)|+\eta {\int }_{a_1}^{t_1}\dots {\int }_{a_j}^{t_j}{L}_K|z_n\left(s\right)-p^{\ast }\left(s\right)|ds+\gamma {\int }_{a_1}^{b_1}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\dots {\int }_{a_j}^{b_j}{L}_T|z_n\left(s\right)-p^{\ast }\left(s\right)|ds\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\alpha \parallel z_n-p\parallel +\eta {\int }_{a_1}^{t_1}\dots {\int }_{a_j}^{t_j}{L}_K\parallel z_n-p^{\ast }\parallel ds+\gamma {\int }_{a_1}^{b_1}\dots {\int }_{a_j}^{b_j}{L}_T\parallel z_n-p^{\ast }\parallel ds\hfill \end{array}$$

$$\begin{array}{c}\parallel q_n-p\parallel \le \alpha \parallel z_n-p\parallel +\eta L_K\left(t_1-a_1\right)\left(t_2-a_2\right)\dots \left(t_j-a_j\right)\parallel z_n-p\parallel \hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\gamma L_T\left(b_1-a_1\right)\left(b_2-a_2\right)\dots \left(b_j-a_j\right)\parallel z_n-p\parallel .\hfill \end{array}$$

Thus, it implies that

$$\parallel q_n-p\parallel \le \left[\alpha +\left(\eta L_K+\gamma L_T\right)\left(b_1-a_1\right)\dots \left(b_j-a_j\right)\right]\parallel z_n-p\parallel .$$

(14)

$$\begin{array}{c}\parallel p_{n+1}-p^{\ast }\parallel =\parallel H{q}_n-p^{\ast }\parallel =|H{q}_n\left(t\right)-H{p}^{\ast }\left(t\right)|\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}=\left|F\left(t,q_n\left(t\right),{\int }_{a_1}^{t_1}\dots {\int }_{a_j}^{t_j}K\left(t,s,q_n\left(s\right)\right)ds{\int }_{a_1}^{b_1}\dots {\int }_{a_j}^{b_j}T\left(t,s,q_n\left(s\right)\right)ds\right)\right.\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\left.F\left(t,p^{\ast }\left(t\right),{\int }_{a_1}^{t_1}\dots {\int }_{a_j}^{t_j}K\left(t,s,p^{\ast }\left(s\right)\right)ds{\int }_{a_1}^{b_1}\dots {\int }_{a_j}^{b_j}T\left(t,s,p^{\ast }\left(s\right)\right)ds\right)\right|\hfill \end{array}$$

$$\begin{array}{c}\le \alpha |q_n\left(t\right)-p^{\ast }\left(t\right)|+\eta |{\int }_{a_1}^{t_1}\dots {\int }_{a_j}^{t_j}K\left(t,s,q_n\left(s\right)\right)ds-{\int }_{a_1}^{t_1}\dots {\int }_{a_j}^{t_j}K\left(t,s,p^{\ast }\left(s\right)\right)ds|\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\gamma |{\int }_{a_1}^{b_1}\dots {\int }_{a_j}^{b_j}T\left(t,s,q_n\left(s\right)\right)ds-{\int }_{a_1}^{b_1}\dots {\int }_{a_j}^{b_j}T\left(t,s,p^{\ast }\left(s\right)\right)ds|\hfill \end{array}$$

$$\begin{array}{c}\le \alpha |q_n\left(t\right)-p^{\ast }\left(t\right)|+\eta {\int }_{a_1}^{t_1}\dots {\int }_{a_j}^{t_j}|K\left(t,s,q_n\left(s\right)\right)-K\left(t,s,p^{\ast }\left(s\right)\right)|ds+\gamma {\int }_{a_1}^{b_1}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\dots {\int }_{a_j}^{b_j}|T\left(t,s,q_n\left(s\right)\right)-T\left(t,s,p^{\ast }\left(s\right)\right)|ds\hfill \end{array}$$

$$\begin{array}{c}\le \alpha |q_n\left(t\right)-p^{\ast }\left(t\right)|+\eta {\int }_{a_1}^{t_1}\dots {\int }_{a_j}^{t_j}{L}_K|q_n\left(s\right)-p^{\ast }\left(s\right)|ds+\gamma {\int }_{a_1}^{b_1}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\dots {\int }_{a_j}^{b_j}{L}_T|q_n\left(s\right)-p^{\ast }\left(s\right)|ds\hfill \end{array}$$

$$\begin{array}{c}\\ =\alpha |q_n-p^{\ast }|+\eta {\int }_{a_1}^{t_1}\dots {\int }_{a_j}^{t_j}{L}_K|q_n-p^{\ast }|ds+\gamma {\int }_{a_1}^{b_1}....{\int }_{a_j}^{b_j}{L}_T|q_n-p^{\ast }|ds\end{array}$$

$$\begin{array}{c}\parallel p_{n+1}-p^{\ast }\parallel \le \alpha \parallel q_n-p^{\ast }\parallel +\eta L_K\left(t_1-a_1\right)\left(t_2-a_2\right)\dots \left(t_j-a_j\right)\parallel q_n-p^{\ast }\parallel \hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\gamma L_T\left(b_1-a_1\right)\left(b_2-a_2\right)\dots \left(b_j-a_j\right)\parallel q_n-p^{\ast }\parallel .\hfill \end{array}$$

This implies that

$$\parallel p_{n+1}-p^{\ast }\parallel \le \left[\alpha +\left(\eta L_K+\gamma L_T\right)\left(b_1-a_1\right)\dots \left(b_j-a_j\right)\right]\parallel q_n-p^{\ast }\parallel .$$

(15)

Substituting (13) into (14) gives

$$\parallel p_{n+1}-p^{\ast }\parallel \le {\left[\alpha +\left(\eta L_K+\gamma L_T\right)\left(\left(b_1-a_1\right)\dots \left(b_j-a_j\right)\right)\right]}^2\parallel z_n-p^{\ast }\parallel .$$

(16)

Substituting (12) into (15),

$$\begin{array}{c}\parallel p_{n+1}-p^{\ast }\parallel \le {\left[\alpha +\left(\eta L_K+\gamma L_T\right)\left(\left(b_1-a_1\right)\dots \left(b_j-a_j\right)\right)\right]}^2\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\times \left\{1-r_n\left(1-\left[\alpha +\left(\eta L_K+\gamma L_H\right)\left(b_1-a_1\right)\dots \left(b_j-a_j\right)\right)\right]\right\}\times \parallel p_n-p^{\ast }\parallel .\hfill \end{array}$$

Applying assumption $\left(M_5\right)$, we have

$$\alpha +\left(\eta L_K+\gamma L_T\right)\left(b_1-a_1\right)\dots \left(b_j-a_j\right)<1.$$

Also,

$${\left[\alpha +\left(\eta L_K+\gamma L_T\right)\left(b_1-a_1\right)\dots \left(b_j-a_j\right)\right]}^2<1^2.$$

So,

$\parallel p_{n+1}-p^{\ast }\parallel \le \left\{1-r_n\left(1-\left[\alpha +\left(\eta L_K+\gamma L_T\right)\left(b_1-a_1\right)\dots \left(b_j-a_j\right)\right]\right)\right\}\times \parallel p_n-p^{\ast }\parallel .$

Thus, it follows by induction that

$$\parallel p_{n+1}-p^{\ast }\parallel \le \parallel p_0-p^{\ast }\parallel \times \prod _{k=0}^n\left\{1-r_k\left(1-\left[\alpha +\left(\eta L_K+\gamma L_T\right)\times \prod _{i=1}^j\left(b_i-a_i\right)\right]\right)\right\}.$$

(17)

Since $r_k\in \left(0,1\right)$ for all $k\in \mathbb{N}$, using assumption $\left(M_5\right)$ gives

$$1-r_k\left(1-\left[\alpha +\left(\eta L_K+\gamma L_T\right)\prod _{i=1}^j\left(b_i-a_i\right)\right]\right)<1.$$

Accepting the fact that $exp-y\ge 1-y$, ∀ $y\in \left(0,1\right)$ where Equation $\left(4.17\right)$ is rewritten as

$$\parallel p_{n+1}-p^{\ast }\parallel \le \parallel p_0-p^{\ast }\parallel exp-\left(1-\left[\alpha +\left(\eta L_K+\gamma L_T\right)\times \prod _{i=1}^j\left(b_i-a_i\right)\right]\right)\sum _{k=0}^n{r}_k.$$

Taking the $limasn\to \infty$ on both sides yields ${\displaystyle \underset{n\to \infty }{lim}}\parallel p_n-p^{\ast }\parallel =0$, which implies $p_n\to p^{\ast }$. Hence, (6) converges strongly to a unique solution of the mixed-type Volterra–Fredholm nonlinear integral Equation (9). □

5. Numerical Example

Example 1.

Let $Y=\left[0,1\right)$ and consider the mapping $Hx={\displaystyle \frac{x}{7\left(1+x\right)}}$. Now, $F_H=0$. Hence, we claim that the $F^{\ast }$ iteration algorithm is stable. Let us consider $r_n={\displaystyle \frac{1}{2}}$ and the control sequence $p_n=q_n={\displaystyle \frac{1}{n}}$, then ${lim}_{n\to \infty }{p}_n=0$.

• Solution:

$$\begin{array}{cc}\hfill {\vartheta }_n& =\parallel p_{n+1}-H{q}_n\parallel =\parallel p_{n+1}-H\left(H\left(\left(1-r_n\right)p_n+r_{n}H{p}_n\right)\right)\parallel \hfill \\ \hfill & =∥p_{n+1}-H\left(H\left({\displaystyle \frac{16n+14}{\left(2n\right)\left(14n+14\right)}}\right)\right)∥\hfill \\ & =∥p_{n+1}-H\left({\displaystyle \frac{16n+14}{7\left(\left(2n\right)\left(14n+14\right)+\left(16n+14\right)\right)}}\right)∥\hfill \\ \hfill & =∥p_{n+1}-{\displaystyle \frac{16n+14}{7\left(28n^2+60n+28\right)}}∥\hfill \\ \hfill & =\parallel {\displaystyle \frac{1}{n+1}}-{\displaystyle \frac{16n+14}{7\left(28n^2+60n+28\right)}}\parallel \hfill \\ \hfill & =∥{\displaystyle \frac{196n^2+404n+182}{\left(196n^2+420n+196\right)\left(n+1\right)}}∥\hfill \\ \hfill & =∥{\displaystyle \frac{196n^2+404n+182}{196n^3+616n^2+616n+196}}∥\hfill \end{array}$$

On taking the $limasn\to \infty$ on both sides, we have ${\displaystyle \underset{n\to \infty }{lim}}{\vartheta }_n=0$. Hence, the $F^{\ast }$ iterative algorithm is H-stable.

• Iterative Test:

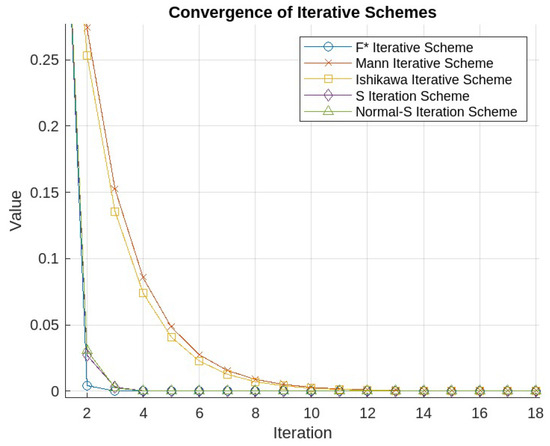
The $F^{\ast }$ iterative scheme converged in 4 iterations to 0.0000001. The Mann iterative scheme converged in 23 iterations to 0.000002. The Ishikawa iterative scheme converged in 23 iterations to 0.000001. The S iteration scheme converged in 7 iterations to 0.0000000. In

Table 1. A comparison of different iterative schemes.

Step Number	${\mathit{F}}^{\ast }$	Mann	Ishikawa	S	Normal S
1	0.5000000	0.5000000	0.5000000	0.5000000	0.5000000
2	0.0042561	0.2738100	0.2532500	0.0270560	0.0307080
3	0.0000495	0.1522600	0.1354500	0.0029657	0.0024545
4	0.0000006	0.0855680	0.0739820	0.0003622	0.0002000
5	0.0000000	0.0484140	0.0409030	0.0000462	0.0000163
6	0.0000000	0.0275060	0.0227900	0.0000060	0.0000013
7	0.0000000	0.0156650	0.0127630	0.0000008	0.0000001
8	0.0000000	0.0089341	0.0071723	0.0000000	0.0000000
9	0.0000000	0.0050995	0.0040406	0.0000000	0.0000000
10	0.0000000	0.0029122	0.0022805	0.0000000	0.0000000
11	0.0000000	0.0016635	0.0012888	0.0000000	0.0000000
12	0.0000000	0.0009504	0.0007292	0.0000000	0.0000000
13	0.0000000	0.0005430	0.0004129	0.0000000	0.0000000
14	0.0000000	0.0003103	0.0002340	0.0000000	0.0000000
15	0.0000000	0.0001773	0.0001327	0.0000000	0.0000000
16	0.0000000	0.0001013	0.0000753	0.0000000	0.0000000
17	0.0000000	0.0000579	0.0000427	0.0000000	0.0000000
18	0.0000000	0.0000331	0.0000243	0.0000000	0.0000000
19	0.0000000	0.0000189	0.0000138	0.0000000	0.0000000
20	0.0000000	0.0000108	0.0000078	0.0000000	0.0000000
21	0.0000000	0.0000062	0.0000045	0.0000000	0.0000000
22	0.0000000	0.0000035	0.0000025	0.0000000	0.0000000
23	0.0000000	0.0000020	0.0000014	0.0000000	0.0000000
24	0.0000000	0.0000000	0.0000000	0.0000000	0.0000000
25	0.0000000	0.0000000	0.0000000	0.0000000	0.0000000

, we present the different iterative schemes values for the first 25 steps and in Figure 1, we showed the convergence of the different iterative schemes.

6. Conclusions

In conclusion, $F^{\ast }$ iterative algorithm has been proved to be stable for a strongly pseudocontractive mapping on a uniformly convex Banach space. The applicability of the result is shown on a mixed-type Volterra–Fredholm nonlinear integral equation, and an example is also given which validates the result. Meanwhile, as an open problem, we pose the following questions:

(i)

Can the sequence $\left\{p_n\right\}$ generated by $F^{\ast }$ iterative algorithm converge to a fixed point of strictly pseudocontractive mapping under a suitable condition unlike the strongly pseudocontractive mapping proved in this work?

(ii)

Can a researcher construct an iterative algorithm that converges faster than $F^{\ast }$ iterative algorithm and also prove the stability of the algorithm?

(iii)

Can an investigation be carried out on both Hilbert and reflexive Banach spaces?