Competitive Elimination Improved Differential Evolution for Wind Farm Layout Optimization Problems

Abstract

The wind farm layout optimization problem (WFLOP) aims to maximize wind energy utilization efficiency under different wind conditions by optimizing the spatial layout of wind turbines to fully mitigate energy losses caused by wake effects. Some high-performance continuous optimization methods, such as differential evolution (DE) variants, exhibit limited performance when directly applied due to WFLOP’s discrete nature. Therefore, metaheuristic algorithms with inherent discrete characteristics like genetic algorithms (GAs) and particle swarm optimization (PSO) have been extensively developed into current state-of-the-art WFLOP optimizers. In this paper, we propose a novel DE optimizer based on a genetic learning-guided competitive elimination mechanism called CEDE. By designing specialized genetic learning and competitive elimination mechanisms, we effectively address the issue of DE variants failing in the WFLOP due to a lack of discrete optimization characteristics. This method retains the adaptive parameter adjustment capability of advanced DE variants and actively enhances population diversity during convergence through the proposed mechanism, preventing premature convergence caused by non-adaptiveness. Experimental results show that under 10 complex wind field conditions, CEDE significantly outperforms six state-of-the-art WFLOP optimizers, improving the upper limit of power generation efficiency while demonstrating robustness and effectiveness. Additionally, our experiments introduce more realistic wind condition data to enhance WFLOP modeling.

1. Introduction

In the past few decades, the global energy landscape has undergone profound changes, primarily due to increasing attention on climate change and the urgent need to reduce carbon emissions [1]. Fossil fuels have long been the cornerstone of global energy production, but they are also considered a major source of greenhouse gas emissions, exacerbating global warming [2,3]. This has prompted a shift towards cleaner and renewable energy sources worldwide to meet growing energy demands while reducing environmental impacts [4]. Among these alternative energies, wind power has emerged as one of the most viable solutions due to its scalability, reliability, and relatively low environmental footprint. Wind power not only possesses renewable characteristics but can also adapt to different geographical regions, giving it immense potential. Wind farms have the capability of generating substantial amounts of electricity without emitting harmful pollutants. However, despite its apparent environmental benefits, wind power’s dominance in the energy market is still not widely established [5]. This is mainly due to several economic challenges associated with deployment, including high initial construction costs and intermittent wind, leading to unstable output [6,7]. Therefore, improving wind power generation efficiency is a fundamental and important goal with respect to the promotion of its broader application. In this context, the Wind Farm Layout Optimization Problem (WFLOP) has become a key engineering challenge. The main objective of the WFLOP is to optimize turbine layout within a farm to maximize energy output while minimizing costs and mitigating adverse effects caused by wake effects. Wake effects refer to deceleration phenomena occurring behind turbines that significantly reduce farm efficiency and lead to decreased power generation. Thus, optimizing turbine layouts to minimize these effects is crucial for the enhancement of overall wind farm performance.

The WFLOP is a typical engineering optimization issue aimed at maximizing the utilization efficiency of wind energy by reasonably arranging the layout of wind turbines. The core of this problem lies in addressing the wind speed loss caused by wake effects. A wake effect refers to the phenomenon where, due to aerodynamic actions, the wind speed behind a working turbine decreases, affecting the power generation efficiency of downstream turbines. Jensen’swake model, as a classic wake effect model, is widely used to assess power losses in wind farms. Based on this model, researchers can more accurately predict the energy output of a wind farm and, thus, optimize the spatial arrangement of turbines. Since sufficient safety distances must be maintained between turbines to avoid mechanical failures or vortex interference, the WFLOP is typically described using discrete models. Although this discretized modeling approach simplifies real-world complexity to some extent, it also increases optimization difficulty. Traditional continuous optimization methods often perform poorly in this field due to mismatches with the solution space of discrete optimization problems. Therefore, research on solutions to the WFLOP mainly focuses on effectively applying discrete optimization algorithms. Due to their generality and ease of use, metaheuristic algorithms are currently the most widely employed global optimization methods for various complex engineering optimization problems [8]. In the latest research addressing the WFLOP, metaheuristic algorithms, particularly Genetic Algorithms (GAs) and Particle Swarm Optimization (PSO), have been extensively applied and have contributed to several of the current state-of-the-art WFLOP optimizers. Although PSO was initially designed for continuous optimization problems, through adjustments in encoding schemes and fitness evaluations, it has achieved outstanding performance on the WFLOP, alongside discretely encoded GAs. Initially, multiple optimization methods were proposed to address the WFLOP, including ant colony optimization, mixed integer programming, sequential convex optimization, simulated annealing, and random search, among other classical techniques [9,10,11,12,13].

As one of the most classical metaheuristic algorithms, GAs have long been widely applied to the WFLOP due to their effectiveness in handling multi-dimensional, nonlinear, and non-convex global optimization problems [14]. Early studies optimized various turbine layouts using GAs, improving power generation efficiency [15,16]. Statistical studies indicate that GAs the most extensively researched and applied metaheuristic algorithms [17]. This is because GAs can adapt to both binary and continuously encoded optimization problems. Additionally, due to their simple structure, GAs are more suitable for use in resource-constrained industrial areas or for reducing computational costs [18]. In recent years, GA and PSO variants for the WFLOP have been further developed and have achieved state-of-the-art performance. In the field of GAs, Ju et al. proposed an adaptive GA (AGA), which, combined with the Jensen wake model and land behavior constraints, demonstrated significant improvements on the WFLOP [19]. However, compared to other recent WFLOP optimizers, the simple adaptive method did not provide the AGA with sufficient computational resources to tackle the computational complexity of the problem. Moreover, the relatively simple core of GAs made the AGA vulnerable to challenges faced by other optimizers. Ju et al. also introduced a GA variant guided by support vector regression (SUGGA). As an efficient and widely applicable WFLOP optimizer, SUGGA was the first to establish and open-source a relevant benchmark library, promoting WFLOP research and technical reproducibility [20]. However, SUGGA inherits GAs’ simple computational processes and relies heavily on the generation of pre-existing layout data. When addressing a new WFLOP, it is difficult to obtain high-quality data to effectively support and guide SUGGA, which limits its performance and general applicability. In the PSO domain, Lei et al. tested and improved a genetic learning-based particle swarm optimization algorithm and proposed AGPSO through an adaptive replacement strategy. This algorithm performed outstandingly in several WFLOP benchmark tests [21]. However, despite incorporating PSO’s computational power into the GA structure, the frequent replacement of the worst solutions reduced the algorithm’s exploratory capability and made it prone to prematurely converging to local optima. Additionally, AGPSO requires greater computational resources for evaluation. Subsequently, a PSO variant incorporating chaotic search was proposed, achieving state-of-the-art performance in larger-scale WFLOP scenarios with 60 to 80 turbines [22]. However, the chaotic search still excessively consumes evaluation resources, leading to performance degradation under scenarios of limited computational capacity. In recent years, research based on other types of metaheuristic algorithms has also been attempted to challenge the advanced performance of GA variants on the WFLOP. Yang et al. proposed a WFLOP optimizer based on spherical evolution and demonstrated its effectiveness compared to GA variants [23,24]. However, its performance still could not compete with the most advanced WFLOP optimizers. Unlike this paper’s approach, which enhances exploratory behavior and solution diversity, Yu et al. attempted to address the failure of DE variants on the WFLOP caused by the lack of discrete features through the use of chaotic local mapping. They proposed CLSHADE and demonstrated some performance improvements [25]. However, CLSHADE did not achieve reliable results in more extensive WFLOP scenarios.

When using metaheuristic algorithms for optimization, the primary difference between discrete and continuous problems lies in the domain of the individuals’ genes within the population. Continuous optimization problems allow algorithms to exhibit infinite differentiability within the domain, enabling individuals to search, trial, and learn across an infinite number of points [26]. In contrast, in discrete optimization problems, the solution space is limited to a finite set of points [27]. Therefore, algorithms in discrete optimization often face greater challenges, such as learning failures and resource wastage due to repeated trial and error [28]. When metaheuristic algorithms are applied to continuous optimization problems, the algorithm gradually narrows the search space as it approaches a local optimum and may further improve precision by adjusting the step size [29,30]. However, in discrete optimization, local optima are usually more precise, and the difference in objective function values between neighboring feasible solutions is greater. Consequently, greedy strategies in metaheuristic algorithms may cause individuals to become more easily trapped in local optima, making escape difficult. This limitation is especially pronounced in the WFLOP. Due to the discrete nature of wind farm layouts, when the set turbine solution is far from the optimal layout, continuous optimization strategies are more likely to cause stagnation in solution quality. This characteristic makes the WFLOP particularly challenging to solve. Therefore, optimizing the WFLOP with metaheuristic algorithms requires not only the overcoming of the challenge of escaping local optima but also a focus on continuous rebalancing of the exploration and exploitation abilities of both the population and individuals during the search process to avoid premature convergence and resource wastage. Our research aims to improve metaheuristic algorithms to overcome and adapt to the optimization challenges inherent in the WFLOP. This research also provides insights into solving similar discrete optimization problems and offers perspectives on how to effectively apply continuous optimization algorithms to discrete problems, along with statistical experimental validation.

In continuous optimization problems, the Differential Evolution (DE) algorithm is widely used in single-objective, multi-objective, and large-scale optimization fields due to its strong exploitation capabilities and excellent local search performance [31,32,33]. Its outstanding performance has been proven in numerous prestigious international competitions, particularly in the IEEE CEC Numerical Optimization Competition [34,35,36,37]. However, due to the continuous optimization nature of DE variants [34,38], they have been shown to perform far worse than GA and PSO variants when directly applied to problems based on discrete characteristics. Therefore, DE fails to demonstrate its real performance on the WFLOP due to its tendency to fall into discrete local optima caused by its inherent search characteristics [21,22]. In order to overcome the non-adaptability of DE variants to the WFLOP and unlock the potential of high-performance WFLOP optimizers based on DE variants, which are likely to surpass the current state-of-the-art GA and PSO variants, we propose a genetic learning-based, competitive elimination mechanism-based differential evolution algorithm called CEDE, based on the well-known Linear population reduction-based Success History-based parameter Adaptation for Differential Evolution (LSHADE) [36], aiming to fully leverage DE’s inherent performance advantages. In our method, the classical continuous adaptive parameter adjustment capabilities of LSHADE are retained. By incorporating a genetic learning mechanism, individuals are enabled to perform large-scale exploration in the solution space, addressing the local optima issue caused by the discrete nature of the WFLOP. Furthermore, by crossing the genes of the current optimal solution with those of the elite solution set, effective large-scale exploration is achieved while ensuring the preservation of high-quality genes. This improvement not only effectively overcomes the bottleneck of traditional DE’s continuous adjustment strategy in discrete problems, where it tends to fall into local optima, but also enhances population diversity. Moreover, the introduction of a genetic learning mechanism helps mitigate the adverse effects of population size dynamics on optimization performance brought about by the DE search paradigm [39,40], allowing the algorithm to maintain stable performance when tackling complex WFLOPs. Experimental and statistical test results demonstrate that our improved method significantly enhances performance in the discrete optimization scenario of the WFLOP, showing stronger global search and local exploitation capabilities than the most advanced PSO, GA, and DE variants on the WFLOP. CEDE successfully solved 10 complex wind farm scenarios, achieving higher power generation efficiency than compared models. Statistical analysis and solution visualization validate the effectiveness and robustness of CEDE in wind farm layout optimization.

The originality and contributions of this paper are summarized as follows:

(1)

This paper conducts a in-depth analysis of the WFLOP based on the latest relevant research, enhancing the modeling of the WFLOP to incorporate more realistic wind conditions in experiments.

(2)

The proposed CEDE optimizer combines genetic learning and competitive elimination mechanisms, achieving a balance between exploitation and exploration for the first time in solving the WFLOP with the classical DE variant LSHADE.

(3)

Experimental and statistical test results demonstrate that the proposed CEDE performs excellently on the WFLOP, with significant performance improvement and robustness, outperforming the most advanced WFLOP algorithms.

(4)

The wind condition data discussed herein, wind condition files applicable to the code, and the code itself will be open-sourced to advance related research on the WFLOP.

In Section 2, we provide a detailed introduction to the methods related to the CEDE algorithm. Section 3 summarizes the experimental data and the comparative results with those achieve by other algorithms. Finally, Section 4 presents the conclusions of this paper and prospects for future research.

2. Methodology

In this section, we first model the wake effect for the WFLOP. Then, we propose a new optimization method and apply it to various simulated wind conditions in experiments using wind farm modeling.

2.1. Modeling

In this study, we use Jensen’s wake model [41,42]. This wake model has been widely used in both traditional and recent research on WFLOP algorithm development [19,20,21,22]. As one of the few wake models with open-source code, Jensen’s wake model is characterized by its relatively low computational complexity and widespread usage. These features facilitate extensive experiments and statistical validation on the WFLOP with more complex and realistic wind conditions without compromising the fair comparison of algorithm performance [43,44,45,46]. All state-of-the-art WFLOP algorithms compared in this paper’s experiments also utilized this classic wake model in their original studies.

As shown in Figure 1 Jensen’s wake model is based on the known wind speed ($V_0$);, the rotor radius ($L_W$) of the upstream turbine at position i; the output wind speed ($V_1$); and the covered area ($L_X$) of the downstream turbine group at position j, which is at a distance of d from position i. The momentum conservation equation for the wind speed ($V_2$) obtained by the downstream turbines at position j is given as follows:

$$\pi L_W^2{V}_1+\pi (L_X^2-L_W^2)V_0=\pi L_X^2{V}_2,$$

(1)

where the values of $L_X$ and $V_1$ are derived based on the trigonometric relationship (2) and Betz’s theory (3) [47].

$$L_X=L_W+X·tan\theta ,$$

(2)

$$V_1=(1-a)V_0,$$

(3)

where the dimensionless parameter ($\theta$) determines the angular range of the wake effect’s influence on wind speed. For most onshore scenarios, the value is approximately 0.075, while for offshore applications, a value of 0.04 is recommended [42]. It is determined by the hub height (h) of the turbine and the surface roughness ($z_0$) of the wind farm area as follows:

$$\theta ={\displaystyle \frac{0.5}{In\left(\frac{h}{z_0}\right)}},$$

(4)

where, on sandy ground, $z_0$ usually ranges between 0.2 mm and 0.3 mm.

Therefore, the downstream wind speed ($V_2$) under the influence of wake effects can be expressed as follows:

$$V_2={\displaystyle \frac{L_W^2(1-a)V_0+({(L_W+X·tan\frac{0.5}{In\left(\frac{z}{z_0}\right)})}^2-L_W^2)V_0}{{L_W+X·tan(\frac{0.5}{In\left(\frac{z}{z_0}\right)})}^2}}.$$

(5)

In wind condition modeling, recent related research has mostly been based on unidirectional, bidirectional, and symmetrical wind directions with uniform or relatively uniform wind speeds. However, monsoon variations often lead to atmospheric instability in the troposphere. Therefore, a more realistic wind condition model should randomly input non-uniform wind speeds from multiple directions (four or more). On the other hand, these studies model wind speeds based on normal distributions, with some even using integer values to represent wind speed distributions. Although certain distribution models may be more suitable in specific contexts, the Weibull distribution is currently widely used for wind speed modeling. The primary reason is its ability to better fit the characteristics of real wind speed data. In this study, based on the average wind speed in Japan and related research, we defined a wind speed distribution with a mean of 13 m/s using the Weibull distribution. A new wind speed sample was constructed by sampling 100,000 times [48]. Figure 2 presents a visual comparison between the normal distribution and the Weibull distribution used in this paper. Furthermore, in some past studies, there were instances where the model code failed to achieve the intended mean wind speed and, even after correction, still deviated from reality. Although such issues persist in the latest studies, based on the experimental results obtained in this paper, these differences in wind farm modeling have no fundamental impact on the effectiveness testing and performance comparison of advanced WFLOP optimizers. This paper aims to model a more realistic WFLOP problem based on publicly available wind condition data from meteorological agencies in the relevant region to validate the effectiveness of both state-of-the-art optimizers and the newly proposed optimizer, providing more realistic and reasonable comparative results.

2.2. State-of-the-Art Differential Evolution

As one of the most classic metaheuristic evolutionary algorithms, differential evolution (DE) has been widely validated for its effectiveness and efficiency in NP-hard problems since its inception [49]. Algorithms based on its variant, LSHADE, have won virtually all IEEE Congress on Evolutionary Computation (IEEE CEC) Numerical Optimization Competitions over the past decade [36,37,50,51,52,53]. First, the solution set is defined as follows:

$$P_x^{\left(k\right)}=\{x_1^{\left(k\right)},x_2^{\left(k\right)},\dots ,x_i^{\left(k\right)},\dots ,x_{N{P}^{\left(k\right)}}^{\left(k\right)}\}$$

(6)

where $x_{N{P}^{\left(k\right)}}^{\left(k\right)}$ represents the $NP$-th solution in the k-th generation and $P_x^{\left(k\right)}$ represents the set of populations in the k-th generation.

The genotype of each solution is represented as follows:

$$x_i^{\left(k\right)}=\{x_{i1}^{\left(k\right)},x_{i2}^{\left(k\right)},\dots ,x_{ij}^{\left(k\right)},\dots ,x_{iD}^{\left(k\right)}\}$$

(7)

where $x_{iD}^{\left(k\right)}$ represents the value of the D-th dimension of the i-th solution in the k-th generation.

The individual solutions in the initial solution set are defined as follows:

$$x_{ij}^{\left(1\right)}=x_{lj}+(x_{hj}-x_{lj})·rand(0,1]$$

(8)

where $x_{lj}$ and $x_{hj}$ represent the minimum and maximum possible values of the j-th dimension, respectively, and $rand(0,1]$ represents a random number in the range of $(0,1]$.

The mutation operation is performed based on the sum of two differences among four individuals in the population as follows:

$${y^{\prime }}_{ij}^{\left(k\right)}=x_{ij}^{\left(k\right)}+s_i·(x_{pbes{t}_{i}j}^{\left(k\right)}+x_{r_{1}j}^{\left(k\right)}-x_{r_{2}j}^{\left(k\right)}-x_{ij}^{\left(k\right)})$$

(9)

where $x_{pbes{t}_{i}j}^{\left(k\right)}$ represents one of the highest-quality $p·NP$ solutions randomly selected in the $k^{th}$ generation. $x_{r_{1}j}^{\left(k\right)}$ and $x_{r_{2}j}^{\left(k\right)}$ are two solutions taken from the solution set of the $k^{th}$ generation according to their indices by random integers of $r_1$ and $r_2$, respectively, falling in the range of $[1,NP]$. $s_i$ is a scale-factor parameter used to control the magnitude of differential terms. ${y^{\prime }}_{ij}^{\left(k\right)}$ denotes the new solution obtained after differential mutation.

After the mutation operation, a genetic crossover strategy is used. Some gene information of the mutated individual ($x_{ij}^{\left(k\right)}$) is crossed into the newly mutated individual (${y^{\prime }}_{ij}^{\left(k\right)}$). The expression is as follows:

$$y_{ij}^{\left(k\right)}=\left\{\begin{array}{cc}{y^{\prime }}_{ij}^{\left(k\right)}\hfill & ,j=j_{rand}\vee rand(0,1)<c_i\hfill \\ x_{ij}^{\left(k\right)}\hfill & ,\mathrm{otherwise}\hfill \end{array}\right.$$

(10)

where $c_i$ is a crossover parameter used to control the number of crossover genes.

Greedy selection is used for parent–child competition and elimination and is expressed as follows:

$$x_{ij}^{(k+1)}=\left\{\begin{array}{c}{y}_{ij}^{\left(k\right)},\mathrm{if}f\left(y_i^{\left(k\right)}\right)\le f\left(x_i^{\left(k\right)}\right)\hfill \\ x_{ij}^{\left(k\right)},\mathrm{otherwise}\hfill \end{array}\right.$$

(11)

where $x_{ij}^{(k+1)}$ represents the value of the j-th gene of the i-th individual in the new generation ($k+1$).

In order to adaptively adjust and optimize the two parameters ($s_i$ and $c_i$), probability sampling based on Cauchy distribution and normal distribution is used to guide the mutation and crossover operations of each solution in the population. The expression is as follows:

$$s_i^{\left(k\right)}=Cauchyrand(L_{1m},0.1)$$

(12)

$$c_i^{\left(k\right)}=Normrand(L_{2m},0.1)$$

(13)

where $Cauchyrand(L_{1m},0.1)$ and $Normrand(L_{2m},0.1)$ represent single-point sampling from a Cauchy distribution with a mean value of the h-th archive’s values of $L_1$ and a normal distribution with a mean value of the h-th archive’s values of $L_2$, respectively, both with a standard deviation of 0.1. The variable m is incremented by 1 in each iteration and reset to 1 when it exceeds the maximum value (M), that is, the memory capacity for archives $L_1$ and $L_2$ is equal to M.

In each generation, the individuals with successfully improved quality are averaged using a weighted matrix based on their progress in the evaluation function, as expressed below:

$$l_s^{\left(k\right)}={\displaystyle \frac{{\sum }_{h=1}^{|S_s^{\left(k\right)}|}{\omega }_h^{\left(k\right)}{s_h^{\left(k\right)}}^2}{{\sum }_{h=1}^{|S_s^{\left(k\right)}|}{\omega }_h^{\left(k\right)}{s}_h^{\left(k\right)}}}$$

(14)

$$l_c^{\left(k\right)}={\displaystyle \frac{{\sum }_{h=1}^{|S_c^{\left(k\right)}|}{\omega }_h^{\left(k\right)}{c_h^{\left(k\right)}}^2}{{\sum }_{h=1}^{|S_c^{\left(k\right)}|}{\omega }_h^{\left(k\right)}{c}_h^{\left(k\right)}}}$$

(15)

$${\omega }_h^{\left(k\right)}={\displaystyle \frac{f_h^{\left(k\right)}-f_h^{(k-1)}}{{\sum }_{g=1}^{|S^{\left(k\right)}|}{f}_g^{\left(k\right)}-f_g^{(k-1)}}}$$

(16)

where $l_s^{\left(k\right)}$ and $l_c^{\left(k\right)}$ represent the learning reference values of $s_i$ and $c_i$, respectively, derived from the weighted matrix average based on the progress of the evaluation function for the k-th generation population. They are sequentially stored in a memory archive of size M. ${\omega }_h^{\left(k\right)}$ represents the proportion of the latest progress achieved by solution h relative to the total progress of the solution set.

A widely used, efficient population-size linear reduction strategy is employed to preliminarily balance development and exploration in the early and late stages of optimization.

$$N{P}^{(k+1)}=round(N{P}_{init}-nfe{s}^{\left(k\right)}·{\displaystyle \frac{N{P}_{init}-N{P}_{min}}{maxFEs}})$$

(17)

where $maxFEs$ and $nfes$ represent the maximum number of evaluations available in a single optimization and the current evaluation count during the process, respectively, and $N{P}_{init}$ and $N{P}_{min}$ represent the population size at the beginning and end of the optimization process, respectively.

2.3. The Proposed CEDE

In order to enable LSHADE to adapt to WFLOPs with discrete optimization characteristics, this section proposes a competitive elimination mechanism based on genetic learning to avoid over-exploitation, reasonably escape local optimal regions, and effectively enhance solution diversity.

First, a mutation operation of the genetic algorithm over the entire domain is implemented, resulting in a new solution. This process is expressed as follows:

$$x_{mutation,j}^{\left(k\right)}=x_{lj}+(x_{hj}-x_{lj})·rand(0,1]$$

(18)

where $x_{mutation,j}^{\left(k\right)}$ represents the new individual generated by this mutation operation.

If the evaluation quality of $x_{mutation,j}^{\left(k\right)}$ is better than that of a randomly selected individual ($x_{pbest,j}^{\left(k\right)}$) from the high-quality solution set, then it undergoes real-number domain genetic learning crossover with $x_{gbest,j}^{\left(k\right)}$; otherwise, the randomly selected $x_{pbest,j}^{\left(k\right)}$ undergoes real-number domain genetic learning crossover with $x_{gbest,j}^{\left(k\right)}$.

$$e_{i,j}^{\left(k\right)}=\left\{\begin{array}{cc}rand(0,1)·x_{pbest,j}^{\left(k\right)}+(1-rand(0,1))·x_{gbest,j}^{\left(k\right)}\hfill & ,\mathrm{if}f\left(x_{pbest}\right)>f\left(x_{mutation}\right)\hfill \\ rand(0,1)·x_{mutation,j}^{\left(k\right)}+(1-rand(0,1))·x_{gbest,j}^{\left(k\right)}\hfill & ,\mathrm{otherwise}\hfill \end{array}\right.$$

(19)

where $rand(0,1)$ represents a random number selected within the range of $(0,1)$. $f\left(x_{pbest}\right)$ and $f\left(x_{mutation}\right)$ represent the evaluation function values of $x_{pbest}$ and $x_{mutation}$, respectively (i.e., the energy conversion efficiency of the wind farm in the WFLOP).

A small probability threshold ($p_m$) is set (0.01 in this study), and $e_{i,j}^{\left(k\right)}$ is initialized with a certain probability. This allows the population to obtain new solutions independent of the current gene-pool information with a certain probability, enabling periodic wide-range exploration for the population.

$$e_{i,j}^{\left(k\right)}=x_{lj}+(x_{hj}-x_{lj}),\mathrm{if}rand(0,1)<p_m$$

(20)

Finally, if the genetic learning operator obtains a solution superior to the current global optimum, it replaces the global optimal solution ($x_{gbest,j}$). This operation increases population diversity while allowing the global optimum brought about by genetic learning to broadly readjust LSHADE’s main optimization mechanism, i.e., differential mutation. This enables the proposed strategy to effectively intervene and adjust LSHADE when addressing WFLOPs, countering local optima stickiness caused by discrete characteristics of the solution space.

$$x_{gbest,j}^{\left(k\right)}=\left\{\begin{array}{cc}{e}_{i,j}^{\left(k\right)}\hfill & ,\mathrm{if}f(e_i^{\left(k\right)})>f(x_{gbest}^{\left(k\right)})\hfill \\ x_{gbest,j}^{\left(k\right)}\hfill & ,\mathrm{otherwise}\hfill \end{array}\right.$$

(21)

where $f(e_i^{\left(k\right)})$ represents the function evaluation value of $e_i^{\left(k\right)}$.

2.4. Decimal Encoding for CEDE

In order to adapt to solving WFLOPs, the feasibility detection algorithm for the latest solution includes both traditional boundary detection and duplicate wind turbine position detection. A simple example is used here for visual explanation. In a wind farm with $4\times 4$ turbine positions, 4 turbines are places along the diagonal (from top left to bottom right). First, through vector expansion, the field is expanded to a 16-dimensional binary code by rows. Then, each dimension is serialized, obtaining real-number encoding results ($\{1,6,11,16\}$). The length of this vector equals the maximum number of turbines that can be placed in the wind farm; each value represents a turbine position index. For a WFLOP where up to four turbines can be placed, the solution’s dimension is 4, and each gene’s domain is an integer in the range of $[1,16]$, as shown in Figure 3.

In addition, to avoid infeasible solutions caused by multiple genes taking repeated values, after rounding to integers, the duplicate individuals are updated sequentially using a proximity update detection method, as shown in Figure 4. The pseudocode and the flow chart of CEDE are shown in Algorithm 1 and Figure 5, respectively.

Algorithm 1: Pseudocode of CEDE.

3. Results

In this section, we set up wind conditions with 10 different numbers of wind sources and conducted experiments in a $12\times 12$ wind field. Based on the average wind speed in Japan and related studies, we defined a wind speed distribution with a mean value of 13 m/s using the Weibull distribution. Wind speed samples were obtained from 100,000 samplings [48]. WFLOPs with 10, 20, 30, 50, and 80 turbines were used for testing. The comparison algorithms include recently proposed state-of-the-art WFLOP optimizers: two GA variants, two PSO variants, one spherical evolution variant, and two DE variants. Among them, comparisons with LSHADE supported ablation experiments. To eliminate errors caused by randomness, each algorithm was implemented in 51 independent experiments for statistical testing. All tested algorithms used recommended parameters from their original papers; CEDE inherited all basic parameters from LSHADE. Consistent with the WFLOP optimizer settings, the maximum number of evaluations was set to 24,000. As the most widely used statistical method in recent relevant studies on engineering optimization [54,55,56] and wind farm layout optimization [21,22], we chose the Wilcoxon test as the statistical test method for this study.

In this study, we specifically selected the latest algorithms proposed for the WFLOP that have achieved the best performance, including AGA, SUGGA, LSE, AGPSO, CGPSO, and CLSHADE. AGA and SUGGA were successively proposed by Ju et al. in 2019 [19,20], achieving then state-of-the-art results. They were the first to publicly release the open-source code of the WFLOP, enabling researchers in the field of computer science to participate in related studies. Subsequently, using the open-source code base, Lei et al. achieved significantly better and highly generalizable experimental results in small- and large-scale WFLOPs compared to AGA and SUGGA. During this period, LSE, by introducing a novel spherical evolution algorithm, outperformed AGA and SUGGA. However, the performance of LSE was unable to compete with that of AGPSO and CGPSO. Later, Yu et al. applied LSHADE to the WFLOP for the first time through chaotic search and proposed CLSHADE. Although CLSHADE lacked performance stability, it achieved results on some WFLOP instances, even surpassing AGPSO and CGPSO. Due to LSHADE’s popularity and performance in metaheuristic algorithm competitions, it was also included in our comparative experiments to further illustrate the specificity of CEDE for WFLOPs. Among these state-of-the-art WFLOP optimizers, other metaheuristic algorithms have been repeatedly verified as non-competitive for WFLOPs. Therefore, in this paper, given the recent accumulation of multiple state-of-the-art metaheuristic WFLOP optimizers, we only used these specialized advanced algorithms to test whether CEDE can surpass the peak performance currently achievable by WFLOP optimizers.

3.1. Wind Condition Setting

We tested 10 different wind directions (labeled directions 1–10)and obtained 50 test groups with five different turbine placement combinations. Due to the use of non-uniform sampling under each wind direction, these experimental conditions can better simulate complex and real wind conditions according to their challenges. Figure 6 presents an example of a wind rose graph for wind conditions with an average wind speed of 13 m/s based on the Weibull distribution for directions 1, 2, 4, 6, 8, and 10.

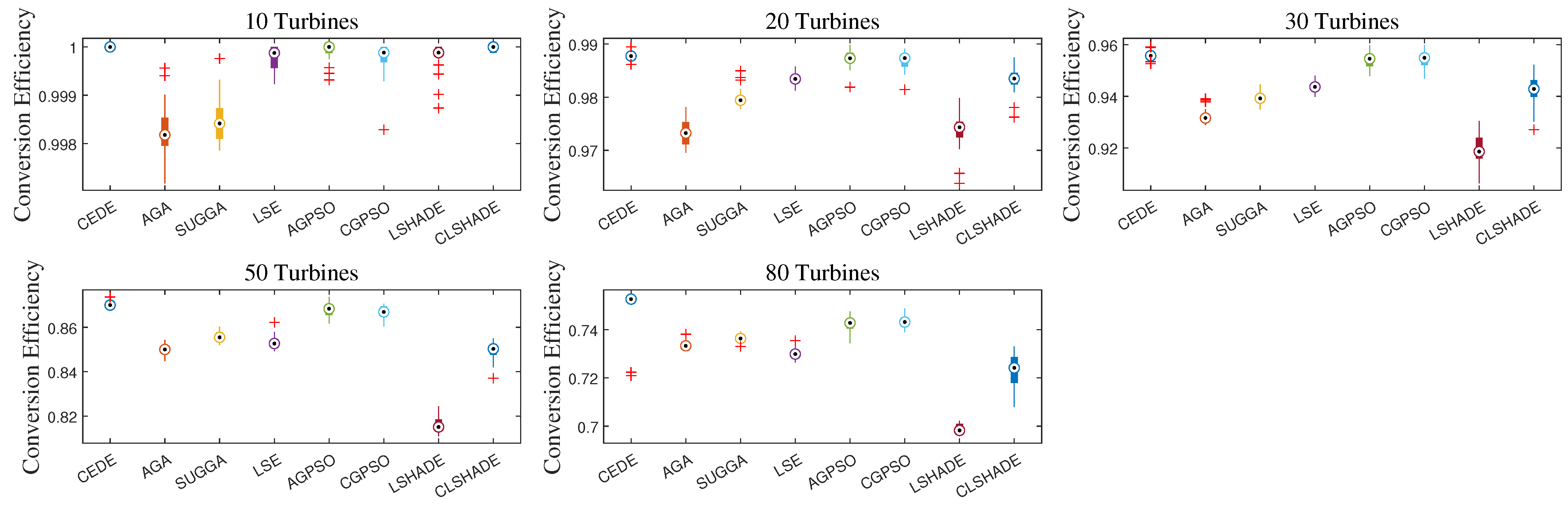
3.2. Comparison Results Between CEDE and State-of-the-Art WFLOP Optimizers

The results of statistical comparison of CEDE with other state-of-the-art WFLOP optimizers are shown in

Table 1. Experimental results of CEDE in comparison with other state-of-the-art WFLOP optimizers. Bold text indicates the best mean values among the comparison algorithms.

	CEDE		AGA		SUGGA		LSE		AGPSO
	Mean	Std	Mean	Std	Mean	Std	Mean	Std	Mean	Std
WS1tn10	100%	0%	100%	0%	100%	0%	100%	0%	100%	0%
WS1tn20	99.956%	0.063%	99.786%	0.077%	99.762%	0.063%	99.807%	0.083%	99.974%	0.063%
WS1tn30	98.812%	0.046%	98.444%	0.102%	98.494%	0.064%	98.295%	0.122%	98.839%	0.082%
WS1tn50	95.561%	0.128%	94.172%	0.223%	94.650%	0.209%	93.728%	0.246%	95.492%	0.315%
WS1tn80	88.544%	0.764%	84.863%	0.224%	85.494%	0.262%	85.326%	0.271%	87.128%	0.376%
WS2tn10	100%	0%	100%	0%	100%	0%	100%	0%	100%	0%
WS2tn20	99.516%	0.052%	99.018%	0.121%	98.851%	0.129%	99.041%	0.142%	99.601%	0.103%
WS2tn30	97.645%	0.084%	97.251%	0.196%	96.842%	0.222%	96.524%	0.216%	97.905%	0.270%
WS2tn50	92.622%	0.182%	91.814%	0.255%	91.446%	0.306%	90.356%	0.234%	92.451%	0.404%
WS2tn80	83.366%	0.820%	81.356%	0.249%	81.365%	0.246%	80.795%	0.125%	82.549%	0.361%
WS3tn10	100%	0%	99.926%	0.054%	99.943%	0.045%	100%	0%	100%	0%
WS3tn20	98.787%	0.123%	96.945%	0.300%	96.966%	0.259%	98.080%	0.228%	98.589%	0.256%
WS3tn30	95.148%	0.238%	92.134%	0.456%	92.142%	0.517%	93.497%	0.255%	94.739%	0.540%
WS3tn50	85.512%	0.196%	81.675%	0.455%	81.507%	0.393%	82.582%	0.399%	84.860%	0.424%
WS3tn80	69.594%	0.215%	66.483%	0.241%	66.464%	0.232%	67.030%	0.144%	68.440%	0.369%
WS4tn10	100%	0%	99.949%	0.037%	99.966%	0.023%	99.995%	0.011%	99.999%	0.006%
WS4tn20	98.567%	0.101%	98.055%	0.178%	98.170%	0.201%	97.736%	0.163%	98.892%	0.178%
WS4tn30	95.891%	0.134%	95.103%	0.209%	95.185%	0.220%	94.402%	0.210%	96.166%	0.266%
WS4tn50	89.097%	0.173%	88.062%	0.188%	88.160%	0.237%	86.992%	0.373%	88.957%	0.383%
WS4tn80	77.317%	0.581%	75.904%	0.238%	75.908%	0.208%	74.950%	0.288%	76.630%	0.328%
WS5tn10	100%	0%	99.827%	0.052%	99.850%	0.047%	99.977%	0.023%	99.990%	0.017%
WS5tn20	98.779%	0.066%	97.319%	0.243%	97.982%	0.174%	98.355%	0.110%	98.723%	0.153%
WS5tn30	95.579%	0.143%	93.221%	0.273%	93.935%	0.228%	94.394%	0.222%	95.387%	0.310%
WS5tn50	87.028%	0.127%	84.997%	0.246%	85.616%	0.206%	85.299%	0.262%	86.814%	0.319%
WS5tn80	75.053%	0.788%	73.351%	0.171%	73.632%	0.150%	73.000%	0.219%	74.251%	0.321%
WS6tn10	99.951%	0.034%	99.483%	0.166%	99.452%	0.128%	99.762%	0.092%	99.877%	0.089%
WS6tn20	95.845%	0.195%	93.807%	0.201%	94.046%	0.342%	94.845%	0.260%	95.947%	0.355%
WS6tn30	89.438%	0.158%	87.088%	0.249%	87.081%	0.267%	87.951%	0.308%	89.710%	0.400%
WS6tn50	76.694%	0.100%	74.949%	0.192%	74.912%	0.152%	75.125%	0.160%	76.646%	0.202%
WS6tn80	61.932%	0.393%	60.674%	0.112%	60.639%	0.101%	60.488%	0.127%	61.574%	0.125%
WS7tn10	99.992%	0.010%	99.697%	0.089%	99.707%	0.072%	99.903%	0.053%	99.957%	0.050%
WS7tn20	98.548%	0.110%	97.331%	0.216%	97.432%	0.221%	98.004%	0.181%	98.691%	0.314%
WS7tn30	96.529%	0.175%	94.224%	0.310%	94.252%	0.212%	94.964%	0.280%	96.557%	0.426%
WS7tn50	89.978%	0.195%	87.122%	0.328%	87.072%	0.283%	87.483%	0.348%	89.687%	0.418%
WS7tn80	78.325%	1.155%	76.214%	0.182%	76.400%	0.280%	76.016%	0.181%	77.505%	0.317%
WS8tn10	99.750%	0.046%	99.279%	0.088%	99.366%	0.100%	99.583%	0.083%	99.706%	0.079%
WS8tn20	97.100%	0.102%	95.527%	0.185%	95.729%	0.174%	96.356%	0.126%	97.111%	0.178%
WS8tn30	92.675%	0.107%	90.717%	0.270%	90.938%	0.197%	91.509%	0.170%	92.646%	0.269%
WS8tn50	83.400%	0.094%	81.649%	0.152%	81.979%	0.148%	81.990%	0.219%	83.275%	0.243%
WS8tn80	71.095%	0.417%	69.903%	0.124%	69.967%	0.112%	69.705%	0.120%	70.809%	0.146%
WS9tn10	99.924%	0.031%	99.424%	0.086%	99.496%	0.126%	99.784%	0.064%	99.839%	0.086%
WS9tn20	97.436%	0.099%	96.129%	0.212%	96.080%	0.261%	96.639%	0.181%	97.413%	0.270%
WS9tn30	93.288%	0.138%	91.310%	0.177%	91.445%	0.240%	91.917%	0.233%	93.189%	0.382%
WS9tn50	83.372%	0.533%	82.061%	0.126%	82.136%	0.141%	82.284%	0.144%	83.324%	0.197%
WS9tn80	71.363%	0.497%	70.427%	0.128%	70.501%	0.108%	70.119%	0.090%	71.034%	0.159%
WS10tn10	99.882%	0.043%	99.799%	0.058%	99.806%	0.046%	99.662%	0.084%	99.896%	0.066%
WS10tn20	97.924%	0.122%	98.118%	0.223%	98.261%	0.169%	96.578%	0.238%	98.481%	0.400%
WS10tn30	95.029%	0.317%	95.004%	0.262%	95.265%	0.239%	92.564%	0.262%	95.778%	0.711%
WS10tn50	87.589%	0.295%	86.885%	0.255%	87.188%	0.229%	84.804%	0.232%	87.578%	0.497%
WS10tn80	75.972%	0.246%	74.943%	0.179%	75.211%	0.172%	73.755%	0.147%	75.174%	0.236%
W/T/L	−/−/−		46/1/3		46/2/2		47/3/0		25/16/9

and

Table 2. Experimental results of CEDE in comparison with other state-of-the-art WFLOP optimizers. Bold text indicates the best mean values among the comparison algorithms.

	CEDE		CGPSO		LSHADE		CLSHADE
	Mean	Std	Mean	Std	Mean	Std	Mean	Std
WS1tn10	100%	0%	100%	0%	100%	0%	100%	0%
WS1tn20	99.956%	0.063%	99.942%	0.079%	99.643%	0.076%	99.939%	0.066%
WS1tn30	98.812%	0.046%	98.820%	0.087%	97.372%	0.280%	98.575%	0.079%
WS1tn50	95.561%	0.128%	95.368%	0.275%	90.627%	0.362%	93.952%	0.322%
WS1tn80	88.544%	0.764%	87.147%	0.308%	82.172%	0.237%	85.102%	0.608%
WS2tn10	100%	0%	100%	0%	100%	0%	100%	0%
WS2tn20	99.516%	0.052%	99.520%	0.117%	98.854%	0.115%	99.339%	0.106%
WS2tn30	97.645%	0.084%	97.855%	0.239%	95.436%	0.313%	97.102%	0.267%
WS2tn50	92.622%	0.182%	92.615%	0.382%	87.685%	0.233%	90.483%	0.794%
WS2tn80	83.366%	0.820%	82.637%	0.383%	78.495%	0.211%	80.417%	0.681%
WS3tn10	100%	0%	100%	0%	100%	0%	99.998%	0.009%
WS3tn20	98.787%	0.123%	98.547%	0.250%	96.963%	0.342%	97.889%	0.367%
WS3tn30	95.148%	0.238%	94.796%	0.523%	90.636%	0.253%	92.526%	0.670%
WS3tn50	85.512%	0.196%	84.821%	0.488%	78.659%	0.221%	81.163%	0.657%
WS3tn80	69.594%	0.215%	68.467%	0.402%	64.431%	0.137%	66.430%	0.640%
WS4tn10	100%	0%	100%	0%	100%	0%	99.997%	0.019%
WS4tn20	98.567%	0.101%	98.811%	0.162%	97.618%	0.151%	98.330%	0.140%
WS4tn30	95.891%	0.134%	96.310%	0.251%	93.341%	0.348%	95.112%	0.313%
WS4tn50	89.097%	0.173%	89.027%	0.318%	83.775%	0.312%	87.337%	0.656%
WS4tn80	77.317%	0.581%	76.592%	0.337%	72.072%	0.319%	74.958%	0.332%
WS5tn10	100%	0%	99.979%	0.034%	99.983%	0.029%	99.996%	0.006%
WS5tn20	98.779%	0.066%	98.689%	0.160%	97.368%	0.344%	98.333%	0.228%
WS5tn30	95.579%	0.143%	95.434%	0.308%	91.948%	0.596%	94.217%	0.572%
WS5tn50	87.028%	0.127%	86.685%	0.284%	81.605%	0.331%	84.955%	0.422%
WS5tn80	75.053%	0.788%	74.308%	0.232%	69.863%	0.200%	72.246%	0.773%
WS6tn10	99.951%	0.034%	99.886%	0.081%	99.854%	0.071%	99.914%	0.048%
WS6tn20	95.845%	0.195%	95.931%	0.286%	94.304%	0.242%	95.395%	0.339%
WS6tn30	89.438%	0.158%	89.697%	0.448%	86.093%	0.444%	88.502%	0.436%
WS6tn50	76.694%	0.100%	76.567%	0.213%	73.026%	0.239%	74.762%	0.408%
WS6tn80	61.932%	0.393%	61.592%	0.120%	58.672%	0.167%	60.086%	0.462%
WS7tn10	99.992%	0.010%	99.971%	0.037%	99.938%	0.027%	99.980%	0.018%
WS7tn20	98.548%	0.110%	98.574%	0.304%	97.246%	0.212%	98.271%	0.147%
WS7tn30	96.529%	0.175%	96.518%	0.455%	92.612%	0.299%	95.179%	0.420%
WS7tn50	89.978%	0.195%	89.651%	0.359%	83.638%	0.259%	87.125%	0.515%
WS7tn80	78.325%	1.155%	77.571%	0.309%	73.326%	0.250%	75.575%	0.609%
WS8tn10	99.750%	0.046%	99.678%	0.083%	99.630%	0.050%	99.720%	0.063%
WS8tn20	97.100%	0.102%	97.010%	0.212%	95.807%	0.336%	96.495%	0.324%
WS8tn30	92.675%	0.107%	92.653%	0.239%	89.898%	0.382%	91.661%	0.363%
WS8tn50	83.400%	0.094%	83.260%	0.187%	79.719%	0.190%	81.915%	0.380%
WS8tn80	71.095%	0.417%	70.834%	0.178%	67.826%	0.167%	69.472%	0.489%
WS9tn10	99.924%	0.031%	99.867%	0.089%	99.818%	0.049%	99.887%	0.046%
WS9tn20	97.436%	0.099%	97.446%	0.277%	95.768%	0.389%	96.739%	0.350%
WS9tn30	93.288%	0.138%	93.306%	0.375%	90.499%	0.328%	92.004%	0.306%
WS9tn50	83.372%	0.533%	83.400%	0.225%	80.840%	0.148%	81.858%	0.235%
WS9tn80	71.363%	0.497%	71.083%	0.137%	68.738%	0.122%	69.729%	0.168%
WS10tn10	99.882%	0.043%	99.884%	0.071%	99.762%	0.060%	99.877%	0.046%
WS10tn20	97.924%	0.122%	98.431%	0.405%	96.337%	0.180%	97.526%	0.282%
WS10tn30	95.029%	0.317%	95.520%	0.673%	91.432%	0.248%	93.573%	0.409%
WS10tn50	87.589%	0.295%	87.433%	0.553%	82.497%	0.289%	85.006%	0.419%
WS10tn80	75.972%	0.246%	75.160%	0.310%	71.640%	0.226%	73.326%	0.496%
W/T/L	−/−/−		26/17/7		46/4/0		44/6/0

. “WS1tn10” represents the WFLOP for a single wind direction with 10 turbines, and other naming rules follow this analogy. “Mean” and “Std” represent the mean and standard deviation of 51 optimization results, respectively. “W/T/L” stands for Win, Tie, and Lose; this result is based on whether there is a significant difference between CEDE and competitors according to the Wilcoxon rank-sum test. The data in the experiment indicate the total power generation efficiency of turbines within the wind farm.

CEDE achieved the best mean performance among all competitors in the vast majority of cases. This indicates that CEDE has a greater ability to find better wind farm layout solutions in a single optimization run and exhibits stronger generality and adaptability to different environments. Notably, CEDE obtained the best mean values in all 80-turbine WFLOPs (with the best mean in each scenario highlighted in bold). This demonstrates CEDE’s more stable performance when solving more complex WFLOPs. One of the objectives of CEDE is to leverage our proposed strategy to enable LSHADE to fully utilize its original performance in the WFLOP and to provide an efficient application and improvement approach for DE variants. Experimental results show that CEDE significantly improved LSHADE’s performance in 46 out of 50 problems and achieved comparable performance in 4 lower-complexity 10-turbine problems. This demonstrates that our proposed strategy effectively enhanced LSHADE’s performance on WFLOPs and delivered superior performance in comparison to other state-of-the-art WFLOP optimizers.

Figure 7 and Figure 8 illustrate the convergence process of each optimizer in a three-direction WFLOP and their box plots based on statistical results. From the convergence plots, it can be observed that CEDE improves the upper bound of solution quality to varying degrees for turbine counts of 10, 20, 30, 50, and 80. Furthermore, the more complex the WFLOP and the higher the number of turbines, the greater the advantage CEDE provides in solution quality. Compared to LSHADE, which exhibits the poorest convergence performance, our proposed strategy led to a substantial enhancement in its performance. It can be said that CEDE successfully recaptures the performance advantages demonstrated by DE variants in complex continuous optimization problems when applied to WFLOPs. In the box plots, CEDE shows high stability in optimization and the best mean values for optimal solutions, indicating that CEDE is more likely to achieve the highest quality solution in a single optimization run. Compared to LSHADE, CEDE also exhibits a clear performance advantage in the box plots. Moreover, although CLSHADE, a DE variant specifically designed for WFLOPs, shows some improvement over LSHADE, the magnitude of the improvement is significantly less than that of CEDE. This may be due to its chaotic local search strategy focusing too much on further exploiting local optima while neglecting the importance of global exploration behavior in discrete optimization. Thus, this partially proves that CEDE’s approach of strengthening exploration in DE variants is more reasonable than focusing on local optima. Similar phenomena are observed in the convergence plots and box plots of other scenarios, with some examples placed in the appendix for readers’ reference (Figure A1, Figure A2, Figure A3 and Figure A4).

Figure 9, Figure 10 and Figure 11 present visualizations of the optimal layouts obtained by the tested algorithms for WFLOPs under three different wind conditions and turbine numbers. In Figure 9, due to the relatively low complexity of the combination of 5 wind directions and 10 turbines, all tested optimizers achieved a perfect turbine layout across multiple optimizations, with an energy conversion rate of 100%. However, as shown by the results in Table 1 and Table 2, only CEDE was able to consistently find the perfect layout in every optimization run for the corresponding scenario. It can be seen from the figure that the perfect layout can be achieved through various different layout patterns. In Figure 10, it is evident that the algorithms that achieved higher energy conversion efficiency layouts (CEDE, AGPSO, and CGPSO) exhibit more regular turbine layout patterns. This also simplifies the difficulty of turbine construction and maintenance and leaves more regular open land available for other agricultural activities. Additionally, in the comparison of the optimal solutions obtained across multiple optimizations, CEDE’s layout still achieved the highest energy conversion rates. As shown in Figure 11, CEDE’s optimal solutions across multiple optimizations resulted in the most visibly regular turbine arrangement and the highest energy conversion rate. This demonstrates CEDE’s superiority, even in complex scenarios involving a large number of turbines.

3.3. Discussion

In this section, we further discuss CEDE, including its hyperparameter sensitivity, generalizability to other discrete problems, the significance of CEDE for WFLOPs, future developments in wind farm modeling, and the potential for testing larger-scale wind farms under dynamic wind conditions.

First, regarding the issue of hyperparameter sensitivity in the DE optimization paradigm, the scale factor and crossover rate are the most critical parameters affecting algorithm performance. Since the proposal of DE in 1997, numerous studies have explored the optimal settings and adaptive strategies for these two parameters [38]. Starting in 2013, the SHADE algorithm introduced a success–history-based adaptive mechanism (SHA), which designed an adaptive adjustment strategy for F and CR, significantly improving the robustness of DE [57]. Extensive research [58,59] has shown that the default initial values in the SHA mechanism (F = 0.5) exhibit high stability and generalizability across a wide range of engineering and benchmark problems [37,60,61,62]. Therefore, under the SHA mechanism, the sensitivity of the initial values of F and CR is no longer a major factor affecting the practical application of DE variants in engineering. In this paper, CEDE, SHADE, LSHADE, and CLSHADE all inherit this mechanism.

Secondly, the generalizability of CEDE to other discrete optimization problems primarily depends on whether the problem can be transformed into continuous encoding. For discrete optimization problems that can be described using continuous encoding, CEDE can be directly applied and demonstrate its efficient global search capabilities. However, when addressing specific problems, it remains necessary to select the most suitable optimizer based on the practical characteristics of the problem. In WFLOPs, although initial studies primarily adopted discrete encoding to optimize wind turbine layouts, we leveraged continuous encoding combined with the advantages of DE to push optimization performance to new heights.

Thirdly, as the WFLOP is a typical NP-hard problem, it is challenging to solve using mathematical methods or exhaustive search [63]. The uniqueness of the WFLOP lies in its complex requirements for wind farm layouts. Prior to optimization, wind farms typically lack a specific turbine arrangement, with layouts often relying on random settings, uniform distribution, or initial planning conducted by companies based on terrain and preferences. However, this approach is ineffective in addressing the significant impact of wake effects on power generation efficiency. The CEDE optimizer not only enhances the energy conversion efficiency of turbine layouts but also provides wind farm companies with a more scientific layout solution, reducing subjectivity and limitations in the planning process.

Finally, the construction and development of future wind farm models represent an important direction in WFLOP optimization research. Currently, mainstream wind farm modeling is largely based on static or regular wind conditions. These models assume uniform and stable wind speed and direction, neglecting the complex three-dimensional meteorological conditions present in real wind farms. However, real-world wind farm environments are often influenced by various dynamic factors, such as terrain undulations, seasonal changes, and random fluctuations in wind speed and direction, which place higher demands on existing optimization algorithms. Therefore, developing wind farm models that can adapt to three-dimensional modeling and dynamic wind conditions and testing them in large-scale wind farms are key research topics for the future. Specifically, three-dimensional wind farm modeling can integrate computational fluid dynamics with real terrain data to more accurately simulate localized wind speed enhancement effects and turbulence phenomena [64]. For instance, in mountainous wind farms, wind speed enhancement on windward slopes and turbulence formation on leeward slopes significantly impact turbine layout. Adopting three-dimensional modeling can capture these details, providing more reliable input conditions for optimization. Moreover, dynamic wind farm modeling is particularly significant for offshore wind farm applications. Taking the North Sea wind farms as an example, wind speed and direction exhibit notable temporal dynamics due to monsoons and tides. By introducing multi-scenario wind farm simulations and combining probabilistic distribution analysis to optimize year-round wind conditions, layout robustness and adaptability can be significantly improved. CEDE’s robustness in dynamic wind conditions enables it to effectively address complex variations, providing solid technical support for such dynamic optimization problems [65]. In ultra-large-scale wind farms, such as the Hami wind region in Xinjiang, China, or wind farms in Texas, USA, the number of turbines often reaches several hundred or even thousands. Three-dimensional modeling combined with dynamic wind farm simulations can comprehensively evaluate wake effects and environmental impacts, such as potential disturbances to local climate microcirculation. Leveraging CEDE’s global search capabilities and population diversity maintenance, layouts can be efficiently optimized in vast solution spaces, enhancing overall wind farm performance. At the same time, real-time changes in wind conditions during the operation of actual wind farms necessitate dynamic optimization strategies. Through high-precision real-time monitoring technologies (e.g., weather stations and drones), combined with CEDE for online optimization, turbine operating parameters (such as rotor speed or blade angle) can be dynamically adjusted to further improve power generation efficiency. Finally, multi-objective dynamic optimization offers more possibilities for wind farm development [66]. In certain scenarios, such as the Altamont wind farm in California, optimization must balance not only power generation efficiency but also environmental factors (e.g., bird protection or land-use efficiency). By integrating dynamic wind farm models with CEDE’s single-objective optimization capabilities, an optimal balance between energy utilization and environmental conservation can be achieved [67]. In summary, the combination of three-dimensional modeling and dynamic wind farm simulations will provide significant support for WFLOP research and practical applications. CEDE’s high level of robustness and exploration capabilities make it particularly advantageous in addressing environments with complex wind conditions. Future research directions could further explore the integration of dynamic wind farm models with real-time optimization frameworks to address even more complex practical problems.

4. Conclusions

The proposed CEDE significantly outperforms other state-of-the-art WFLOP optimizers under various real wind condition simulations and achieves more regular turbine layout patterns. Consequently, CEDE not only improves energy conversion efficiency but also facilitates agricultural planning and other economic activities in non-turbine areas of wind farms. Technically, CEDE introduces a novel genetic learning-based competitive elimination mechanism that successfully enhances the well-known LSHADE, which excels in complex continuous optimization, by moderately increasing population diversity and incorporating exploration operations. CEDE makes DE variants more adaptable to the discrete optimization characteristics of WFLOPs and fully leverages their efficient, continuous optimization strategies. Although CEDE has successfully surpassed current advanced WFLOP optimizers, the potential of DE variants to solve WFLOPs may still be underexplored, given their absolute advantages and stability in some complex optimization problems. Future research should thoroughly test the performance of other DE variants on WFLOPs, analyze them, and introduce this paper’s strategy or seek more optimal adaptation strategies in the most promising variants. Additionally, the difficulty of obtaining wind farm layout optimization codes in the past has hindered the progress of algorithm researchers to some extent. While we are making our code publicly available, we also call on more WFLOP researchers to open-source their work to advance more realistic WFLOP testing and research. This will significantly contribute to the growth of wind farm energy conversion efficiency.