Optimal Feedback Rate for Multi-Antenna Maximum Ratio Transmission in Single-User MIMO Systems with One-Bit Analog-to-Digital Converters in Dense Cellular Networks

Abstract

Stochastic geometry has emerged as a powerful tool for modeling cellular networks, especially in dense deployment scenarios where inter-cell interference is significant. Previous studies have extensively analyzed multi-antenna systems with partial channel state information at the transmitter (CSIT) using stochastic geometry models. However, most of these works assume the use of infinite-resolution analog-to-digital converters (ADCs) at the receivers. Recent advances in low-resolution ADCs, such as one-bit ADCs, offer an energy-efficient alternative for millimeter-wave systems, but the interplay between limited feedback and one-bit ADCs remains underexplored in such networks. This paper addresses this gap by analyzing the optimal feedback rate that maximizes net spectral efficiency in dense cellular networks, modeled using stochastic geometry, with both limited feedback and one-bit ADC receivers. We introduce an approximation of the achievable spectral efficiency to derive a differentiable expression of the optimal feedback rate. The results show that while the scaling behavior of the optimal feedback rate with respect to the channel coherence time remains unaffected by the ADC’s resolution, the absolute values are significantly lower for one-bit ADCs compared to infinite-resolution ADCs. Simulation results confirm the accuracy of our theoretical approximations and demonstrate the impact of ADC resolution on feedback rate optimization.

1. Introduction

Stochastic geometry has been widely utilized to model cellular networks in recent research [1,2,3,4,5,6,7]. For example, Ref. [1] proposed a mathematical framework that could compute the error probability of multiple-input and multiple-output (MIMO) systems in downlink cellular networks using stochastic geometry, while Ref. [2] applied an equivalent in-distribution-based approach for the performance evaluation of MIMO cellular networks. In [3], stochastic geometry was used to model a multi-user MIMO (MU-MIMO) heterogeneous network, where the probability of success and spectral efficiency area were analyzed. The authors in [4] modeled intelligent reflective surface (IRS)-assisted cellular networks using stochastic geometry and examined both their spectral and energy efficiency. Similarly, Ref. [5] modeled massive multicell MIMO networks using stochastic geometry, focusing on spectral efficiency and antenna correlations. Scalable cell-free massive MIMO systems were analyzed in [6] in terms of their secrecy performance, and Ref. [7] studied non-orthogonal multiple-access (NOMA) systems combined with reconfigurable intelligent surfaces (RISs), conducting performance evaluations within networks modeled by stochastic geometry.

In these studies, the Poisson Point Process (PPP) is often employed to model inter-cell interference from different base stations (BSs) in dense cellular networks. Additionally, several works have extended PPP-based models to examine the impact of limited channel state information at the transmitter (CSIT) on multi-antenna transmission, especially when downlink transmission is affected by multicell interference. For example, Ref. [8] modeled a dense cellular network using a homogeneous PPP, where each user’s received signal was heavily interfered with by signals from multiple BSs. Each user provided partial CSIT through limited feedback, and BSs performed multi-antenna transmission based on this partial information. The study analyzed the optimal feedback rate to maximize net spectral efficiency, utilizing maximum ratio transmission (MRT) and zero-forcing beamforming (ZFBF) for single-user and multi-user cases, respectively. This research has been extended to various applications. For instance, Ref. [9] explored the net secrecy rate rather than net spectral efficiency, and Refs. [10,11] examined scenarios where the number of receiving antennas is greater than one, analyzing the effect of this on system performance. Specifically, Ref. [10] focused on the single-user case, while Ref. [11] addressed the multi-user scenario.

These studies provide insights into optimizing feedback rates for multi-antenna transmission in dense cellular networks based on partial CSIT. However, most of the existing literature assumes the use of infinite-resolution analog-to-digital converters (ADCs) at the receivers. In contrast, recent research has explored the use of low-resolution ADCs, particularly as a solution that allows us to harness the wide-frequency resources in millimeter-wave bands while significantly reducing power consumption [12]. As a result, performance analyses have been conducted on systems using one-bit ADCs, investigating the performance achievable with a restriction on the resolution of ADCs [12,13,14,15,16]. For example, Ref. [13] identified the capacity of a one-bit quantized Gaussian channel, while Ref. [14] studied the achievable rate for multi-antenna systems with one-bit ADCs at the receivers. The exact capacity of multiple-input and single-output (MISO) channels was provided, and approximations for single-input and multiple-output (SIMO) and MIMO channels were derived, assuming perfect CSIT. In [15], hybrid architectures with few-bit ADC receivers were analyzed, and Ref. [16] explored limited feedback combined with finite-bit ADCs.

Although there has been extensive research on systems using one-bit ADCs, as discussed above, there is a lack of studies investigating scenarios where both limited feedback and one-bit ADC receivers are used in dense cellular networks, particularly those modeled with stochastic geometry. This study aims to fill this research gap by considering such a network scenario and analyzing the optimal feedback rate that maximizes net spectral efficiency. The main contributions of this study are as follows:

• We derive the optimal feedback rate that maximizes the net spectral efficiency. To derive the optimal feedback rate, we require a differentiable formula of the net spectral efficiency as a function of the number of feedback bits. However, obtaining the exact form of the maximum achievable spectral efficiency is challenging due to its dependence on symbol distributions from all BSs. Therefore, we first introduce an approximation of the achievable spectral efficiency, which allows for easier differentiation.
• Using this approximation, we derive the optimal feedback rate by identifying the critical point of the net spectral efficiency function. As a result, the scaling rate of the optimal feedback is shown to follow a logarithmic function of the channel coherence time, similar to the case with infinite-resolution ADCs. This result suggests that the optimal feedback rate is independent of the ADC resolution of the receiver. While the scaling rate remains unaffected by ADC resolution, the absolute value of the optimal number of feedback bits is lower with one-bit ADCs compared to infinite-resolution ADCs. The simulation results validate the accuracy of our approximations and the scaling behavior of the optimal feedback rate.

The remainder of this paper is structured as follows: Section 2 outlines the system model, including the network and channel models, the beamforming method, and the performance metrics used. Section 3 presents the analysis of the optimal feedback rate, while Section 4 discusses simulation results that validate the approximations used in the performance analysis and the key findings related to the optimal feedback rate. Finally, Section 5 concludes the paper.

Notations: Matrices are denoted by uppercase bold letters, while column vectors are represented by lowercase bold letters. The notation $\parallel ·\parallel$ represents the vector norm, and $|·|$ denotes the absolute value of a complex number. The expectation of an event is indicated by $\mathbb{E}(·)$. The sets $\mathbb{R}$ and $\mathbb{C}$ refer to the sets of real and complex numbers, respectively. For a complex number, Re[·] and Im[·] denote its real and imaginary parts, respectively. In addition, a list summarizing the variables and functions used in the manuscript has been included in the Notations section.

2. System Model

In this paper, we consider an optimized feedback rate that maximizes the net spectral efficiency achieved by each user in a cellular network. The network consists of BSs randomly located on a two-dimensional plane, where the BS locations follow a homogeneous PPP with the intensity $\lambda$. The distance of BS i from the origin is denoted by $d_i$, with the distances $d_1,d_2,\cdots$ sorted in ascending order, meaning that BS 1 is the nearest to the origin. Each BS is equipped with N transmit antennas, and each mobile user has a single receive antenna. The users are also randomly located according to an independent homogeneous PPP, separate from the BS distribution. We assume that the intensity of the user distribution is significantly greater than that of the BS distribution, ensuring that there is more than one user within the Voronoi region of each BS for any realization of the two independent PPPs.

Each BS selects one user at random (or using a round-robin scheme) from within its Voronoi region for downlink transmission. The primary performance metric is the net ergodic spectral efficiency achieved by each scheduled user. Due to the stationarity of the homogeneous PPP, the ergodic spectral efficiency of each user is equivalent, assuming the BSs employ the same transmission strategy. This allows us to select any user in the network as the target for performance analysis. Furthermore, by leveraging the stationarity of the homogeneous PPP, we can assume, without a loss of generality, that the target user is located at the origin through an appropriate parallel translation.

Figure 1 illustrates our network model, in which each base BS is associated with a user, located within its Voronoi region, for downlink transmission. Signals from other BSs interfere with the received signal of the target user.

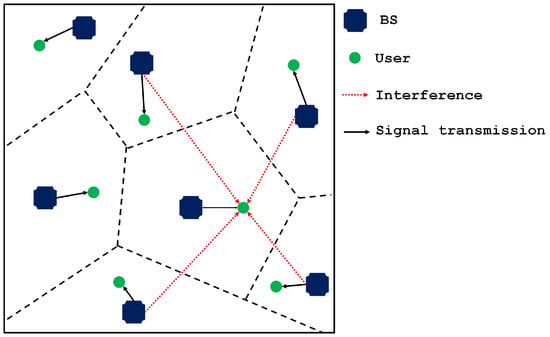
Figure 1. Cellular network modeled with BSs and scheduled users distributed by PPP.

2.1. Channel Model

Since BS 1 is the nearest BS to the target user, it serves as the user’s serving BS. The random channel between the target user and BS i is modeled by the vector ${\mathbf{h}}_i\in {\mathbb{C}}^{N\times 1}$. The signal received by the target user is described as follows:

$$\begin{array}{cc}\hfill y& =d_1^{-{\displaystyle \frac{\alpha }{2}}}{\mathbf{h}}_1^H{\mathbf{v}}_1{s}_1+\sum _{i=2}^{\infty }{d}_i^{-{\displaystyle \frac{\alpha }{2}}}{\mathbf{h}}_i^H{\mathbf{v}}_i{s}_i+z,\hfill \end{array}$$

(1)

where ${\mathbf{v}}_i$ denotes the beamforming vector of BS i and $s_i$ represents the information symbol transmitted by BS i. Additionally, z denotes circularly symmetric complex Gaussian noise with unit variance.

We assume Rayleigh fading for small-scale channel variations, meaning that the entries of ${\mathbf{h}}_i$ are independent and identically distributed (i.i.d.) and follow a circularly symmetric complex Gaussian distribution with unit variance. The path loss exponent is denoted by $\alpha >2$. The system’s transmit power is P and thus $\mathbb{E}\left[\right|s_i{|}^2]=P$. It is assumed that the target user can perfectly estimate their downlink channel ${\mathbf{h}}_1$.

The real and imaginary parts of the received signal y are processed by individual one-bit ADCs, such that the one-bit quantized received signal of the target user is given by

$$\begin{array}{c}\hfill r=\mathrm{sign}\left(\mathrm{Re}\right[y\left]\right)+\mathrm{sign}\left(\mathrm{Im}\right[y\left]\right)\mathbf{j},\end{array}$$

(2)

where $\mathrm{sign}(·)$ denotes the signum function and $\mathbf{j}$ is the imaginary unit.

For simplicity, in the remainder of this paper, we use d, $\mathbf{h}$, $\mathbf{v}$, and s to represent the distance between the target user and BS 1, the channel vector, the beamforming vector, and the information symbol of the target user, respectively. That is, the following notations will be used to simplify descriptions:

$$\begin{array}{c}\hfill d=d_1,\mathbf{h}={\mathbf{h}}_1,\mathbf{v}={\mathbf{v}}_1,s=s_1.\end{array}$$

(3)

2.2. Finite-Rate Feedback and Precoding

In this study, we consider a scenario in which each BS is unable to directly track its downlink channel, a common assumption in frequency division duplex (FDD)-based systems. In this case, to provide partial channel state information (CSI) to the transmitter, each user is required to quantize their channel and feedback the information to their associated BS, providing partial CSI to the transmitter. A widely used method for this is known as limited feedback [17], where each user employs a predefined codebook to quantize its channel direction vector. The channel direction vector of the target user is defined as

$$\begin{array}{c}\hfill \tilde{\mathbf{h}}\triangleq {\displaystyle \frac{\mathbf{h}}{\parallel \mathbf{h}\parallel }}.\end{array}$$

(4)

In this work, rather than using an explicit codebook, we adopt a well-known approximation called the quantization cell upper bound (QUB) model. This model provides an upper bound to the cumulative distribution function (CDF) of the quantization error and typically offers an upper-bound performance in terms of codebook construction. Let $\widehat{\mathbf{h}}$ represent the quantized channel vector of $\mathbf{h}$. In general, the channel direction vector of the target user can be expressed as

$$\begin{array}{c}\hfill \tilde{\mathbf{h}}=\left(\cos \theta \right)\widehat{\mathbf{h}}+\left(\sin \theta \right)\mathbf{g},\end{array}$$

(5)

where $\mathbf{g}$ is a vector isotropically distributed within the left null space of $\widehat{\mathbf{h}}$ and the term ${\sin }^2\theta$ is defined as the quantization error. The QUB model approximates and bounds the CDF of the quantization error as follows:

$$\begin{array}{c}\hfill F_{{\sin }^2\theta }\left(x\right)\le \left\{\begin{array}{cc}{2}^B{x}^{N-1},\hfill & 0\le x\le \delta ,\hfill \\ 1,\hfill & x\ge \delta ,\hfill \end{array}\right.\end{array}$$

(6)

where $\delta =2^{-{\displaystyle \frac{B}{N-1}}}$ and B represents the number of bits used for quantization and feedback. Consequently, the codebook’s size is typically given by $2^B$ when using an explicit codebook to obtain the quantized channel vector.

To illustrate this bound in (6), let us consider a realistic quantization based on the following explicit codebook:

$$\begin{array}{c}\hfill \mathcal{C}=\{{\mathbf{c}}_1,\cdots ,{\mathbf{c}}_{2^B}\},\end{array}$$

(7)

where each codeword is typically represented by a unit vector in ${\mathbb{C}}^{N\times 1}$. The quantized channel is then determined as follows, to minimize the quantization error:

$$\begin{array}{c}\hfill \widehat{\mathbf{h}}=\underset{\mathbf{c}\in \mathcal{C}}{argmin}(1-|{\tilde{\mathbf{h}}}^H\mathbf{c}{|}^2).\end{array}$$

(8)

Consequently, the quantization error ${\sin }^2\theta$ is expressed as

$$\begin{array}{c}\hfill {\sin }^2\theta =\underset{i=1,\cdots ,2^B}{min}(1-|{\tilde{\mathbf{h}}}^H{\mathbf{c}}_i{|}^2).\end{array}$$

(9)

Its CDF can be derived as follows:

$$\begin{array}{cc}\hfill F_{{\sin }^2\theta }\left(x\right)& =\mathrm{Pr}\left({\sin }^2\theta \le x\right)\hfill \\ \hfill & =\mathrm{Pr}\left((1-|{\tilde{\mathbf{h}}}^H{\mathbf{c}}_1{|}^2)\le x\mathrm{or}(1-|{\tilde{\mathbf{h}}}^H{\mathbf{c}}_2{|}^2)\le x\mathrm{or},\cdots ,\mathrm{or}(1-|{\tilde{\mathbf{h}}}^H{\mathbf{c}}_{2^B}{|}^2)\le x\right)\hfill \\ \hfill & \stackrel{\left(a\right)}{\le }\mathrm{Pr}\left((1-|{\tilde{\mathbf{h}}}^H{\mathbf{c}}_1{|}^2)\le x\right)+\mathrm{Pr}\left((1-|{\tilde{\mathbf{h}}}^H{\mathbf{c}}_2{|}^2)\le x\right)+\cdots +\mathrm{Pr}\left((1-|{\tilde{\mathbf{h}}}^H{\mathbf{c}}_{2^B}{|}^2)\le x\right)\hfill \\ \hfill & \stackrel{\left(b\right)}{=}{2}^B\mathrm{Pr}\left((1-|{\tilde{\mathbf{h}}}^H{\mathbf{c}}_1{|}^2)\le x\right)\hfill \\ \hfill & \stackrel{\left(c\right)}{=}{2}^B{x}^{N-1}.\hfill \end{array}$$

(10)

Here, (a) follows by applying the union bound and (b) uses the fact that $1-|{\tilde{\mathbf{h}}}^H{\mathbf{c}}_i{|}^2$ follows a beta distribution with the parameters $N-1$ and 1 (see Section C in [18]). To validate the QUB’s tightness, we provide simulation results using random vector quantization (RVQ), which provides a lower-bound performance. If the performance gap between the lower bound (RVQ) and the upper bound (QUB) is minimal, the QUB approximation can be considered accurate, and the corresponding verification is provided in Section 4.

By definition, the quantization error ${\sin }^2\theta$ satisfies

$$\begin{array}{c}\hfill {\sin }^2\theta =1-{|{\tilde{\mathbf{h}}}^H\widehat{\mathbf{h}}|}^2.\end{array}$$

(11)

As a beamforming strategy, we consider MRT. Since each BS only has access to the quantized channel, the beamforming vector is calculated based on the quantized channel. Therefore, the beamforming vector is obtained as

$$\begin{array}{c}\hfill \mathbf{v}=\widehat{\mathbf{h}}.\end{array}$$

(12)

Figure 2 presents a block diagram of the downlink transmission. The target user quantizes their channel direction vector and feeds back the quantized channel direction information (CDI) to the BS for beamforming. The BS associated with the target user employs MRT as a beamforming strategy using N transmit antennas. The real and imaginary components of the signal received by the target user are processed through individual one-bit ADCs prior to digital signal processing.

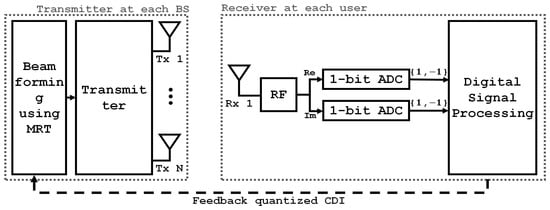
Figure 2. Block diagram of downlink transmission.

2.3. Perfomance Metric

The instantaneous rate achieved by the target user is upper-bounded by

$$\begin{array}{c}\hfill R(\mathcal{H},\mathcal{D})\triangleq \underset{F_s}{max}I(r;s),\end{array}$$

(13)

for given channel vectors and BS locations, where the maximum is taken over all possible distributions of s. In (13), $\mathcal{H}=\{{\mathbf{h}}_i:i\in \mathbf{N}\}$ and $\mathcal{D}=\{d_i:i\in \mathbf{N}\}$. Accordingly, in (13), $F_s$ represents an arbitrary CDF of s.

3. Performance Analysis

3.1. Approximation of the Spectral Efficiency

As discussed in Section 2.3, the achievable rate for the target user is bounded by the maximum mutual information relayed between the input and output of the channels with one-bit quantizers:

$$\begin{array}{c}\hfill R(\mathcal{H},\mathcal{D})\triangleq \underset{F_s}{max}I(r;s).\end{array}$$

(14)

In (1), the received signal of the target user is interfered with by the transmitted signals from other BSs, as denoted by $\mathsf{\Psi }$ in the following equation:

$$y=d_1^{-{\displaystyle \frac{\alpha }{2}}}{\mathbf{h}}_1^H{\mathbf{v}}_1{s}_1+\underset{\mathsf{\Psi }}{\underbrace{\sum _{i=2}^{\infty }{d}_i^{-{\displaystyle \frac{\alpha }{2}}}{\mathbf{h}}_i^H{\mathbf{v}}_i{s}_i}}+z.$$

(15)

The instantaneous rate of the target user, for given BS locations and channel values, is not only influenced by the distribution of $s_1$ but also by the information symbols from other BSs. As a result, obtaining an exact CDF for $\mathsf{\Psi }$ is challenging. Instead, we approximate the interference term $\mathsf{\Psi }$ as a Gaussian random variable, conditioned on the channel realizations. This approximation leverages the central limit theorem, which is commonly used to model small-scale fading channels in wireless environments. Given that $s_i$ has an identical distribution across BSs, $\mathsf{\Psi }$ is a weighted sum of identically distributed random variables for the given channel realizations. Such random variables can often be approximated by a normal distribution with the same variance. The variance of $\mathsf{\Psi }$ is given by ${\sum }_{i=2}^{\infty }{d}_i^{-\alpha }|{\mathbf{h}}_i^H{\mathbf{v}}_i{|}^2·\mathbb{E}\left[\right|s_i{|}^2]$. Figure 3 validates this approach by comparing the CDF of $\mathsf{\Psi }$ to that of a normal distribution with the same variance. The results in Figure 3 are obtained by carrying out the following procedures:

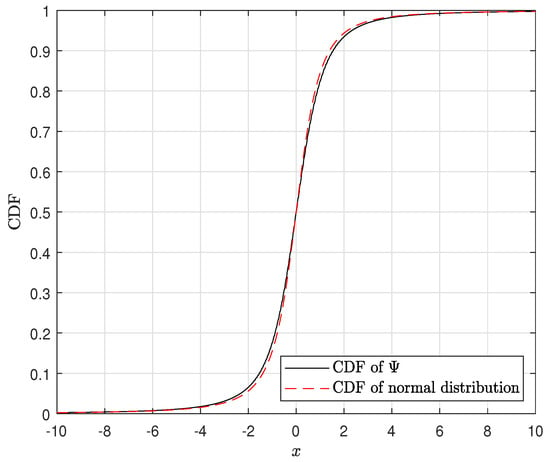
Figure 3. Verification of Gaussian approximation for $\mathsf{\Psi }$. $N=4$.

• For each realization of the channel distributions (${\mathbf{h}}_i$ and $d_i$), both the conditional CDF of $\mathsf{\Psi }$ and the CDF of a normal distribution with a variance equal to V are obtained
• They are averaged over the channel distributions to obtain the two graphs in Figure 3, respectively.

Assuming $\mathsf{\Psi }$ follows a Gaussian distribution, the real and imaginary parts of the target user’s input–output channel can be modeled as a one-bit quantized Gaussian channel, as described in [13]. In this case, the maximum mutual information is given as follows [13]:

$$\begin{array}{c}\hfill 2(1-H_b\left(Q\left(\mathrm{SINR}\right)\right)),\end{array}$$

(16)

where the maximum is achieved with QPSK modulation (quadrature phase shift keying: using two independent antipodal signals for both the real and imaginary components, respectively). In (16), $H_b(·)$ denotes the binary entropy function,

$$\begin{array}{c}\hfill H_b\left(p\right)=-p·logp-(1-p)·log(1-p),\end{array}$$

$Q(·)$ denotes the tail probability of the standard normal distribution,

$$\begin{array}{c}\hfill Q\left(x\right)={\int }_x^{\infty }{\displaystyle \frac{1}{\sqrt{2\pi }}}{e}^{{\displaystyle \frac{-t^2}{2}}}dt,\end{array}$$

(17)

and SINR denotes the signal-to-interference-and-noise ratio. Based on this discussion, and assuming $I_C$ is Gaussian, the instantaneous achievable rate can be approximated as

$$\begin{array}{cc}\hfill R(\mathcal{H},\mathcal{D})& \approx 2\left(1-H_b\left(Q\left(\sqrt{{\displaystyle \frac{{P{d}^{-\alpha }\left|{\mathbf{h}}^H\mathbf{v}\right|}^2}{P{\sum }_{i=2}^{\infty }{d}_i^{-\alpha }{\left|{\mathbf{h}}_i^H{\mathbf{v}}_i\right|}^2+1}}}\right)\right)\right)\hfill \\ \hfill & =2\left(1-H_b\left(Q\left(\sqrt{{\displaystyle \frac{{|{\mathbf{h}}^H\mathbf{v}|}^2}{I_C+d^{\alpha }/P}}}\right)\right)\right),\hfill \end{array}$$

(18)

where P is the power of the signal and $I_C$ is the term representing multicell interference, defined as

$$\begin{array}{c}\hfill I_C=d^{\alpha }\sum _{i=2}^{\infty }{d}_i^{-\alpha }{\left|{\mathbf{h}}_i^H{\mathbf{v}}_i\right|}^2.\end{array}$$

(19)

3.2. Derivation for the Optimal Feedback Rate

Using the approximation in (18) from the previous subsection, the ergodic rate achieved by the target user can be expressed as

$$\begin{array}{c}\hfill R_e=\mathbb{E}\left[2\left(1-H_b\left(Q\left(\sqrt{{\displaystyle \frac{{|{\mathbf{h}}^H\mathbf{v}|}^2}{I_C+d^{\alpha }/P}}}\right)\right)\right)\right],\end{array}$$

(20)

where the expectation is taken over the randomness of the channels and the BS locations. We then define the net ergodic rate, or ergodic net spectral efficiency, which serves as the main performance metric of this study, as follows:

$$\begin{array}{cc}\hfill R_{Net}& \triangleq R_e-{\displaystyle \frac{B}{T_c}}\hfill \\ \hfill & =2-2·\mathbb{E}\left[\left(H_b\left(Q\left(\sqrt{{\displaystyle \frac{{|{\mathbf{h}}^H\mathbf{v}|}^2}{I_C+d^{\alpha }/P}}}\right)\right)\right)\right]-{\displaystyle \frac{B}{T_c}},\hfill \end{array}$$

(21)

which incorporates the uplink’s resource consumption for feedback, similar to in previous studies [8]. Here, $T_c$ represents the channel coherence time. In this study, we employ a block fading channel model that is widely used in mobile communication systems, where the channel value remains constant within a block consisting of multiple downlink channel uses. The channel value randomly and independently fades across different blocks. Since the quantized CDI is treated as control information, it is assumed to be fed back to the BS at the start of each block, and the quantized CDI is utilized consistently for all downlink channel uses within that block. In this model, the number of channel uses sharing the same channel within each block is referred to as the channel coherence time $T_c$. In our analysis, we primarily focus on scenarios where $T_c$ is relatively large. In this case, the resource usage for downlink transmission is significantly greater than that for CSI feedback (via the uplink channel), which makes the impact of the number of feedback bits or the associated feedback delay marginal in our setup.

In this subsection, we analyze the optimal number of feedback bits for maximizing the net spectral efficiency $R_{Net}$. Since $R_{Net}$ is a real-valued function of B, its optimal value can be found by identifying its critical points. Although the number of feedback bits B must be a natural number in practical systems, the QUB model introduced in Section 2.2 allows us to assume that B is a real number. Simulations show that there exists a unique critical point corresponding to the maximum. For simplicity, we introduce the following notation:

$$\begin{array}{c}\hfill G\left(x\right)=2-H_b\left(Q\left(\sqrt{x}\right)\right).\end{array}$$

(22)

From [19], we know

$$\begin{array}{c}\hfill g\left(x\right)\triangleq {\displaystyle \frac{d}{dx}}G\left(x\right)=-{\displaystyle \frac{e^{-\frac{x}{2}}}{\sqrt{2\pi x}}}{log}_2\left({\displaystyle \frac{Q\left(\sqrt{x}\right)}{1-Q\left(\sqrt{x}\right)}}\right).\end{array}$$

(23)

Using (5) and (12), we obtain

$$\begin{array}{c}\hfill |{\mathbf{h}}^H{\mathbf{v}|}^2=\parallel \mathbf{h}\parallel {\cos }^2\theta .\end{array}$$

(24)

Furthermore, from (6), we have

$$\begin{array}{c}\hfill {\sin }^2\theta \sim \delta {\beta }_{N-1,1},\end{array}$$

(25)

where ${\beta }_{N-1,1}$ represents a random variable that follows a beta distribution with the parameters $N-1$ and 1.

The derivative of $R_e$ can then be calculated as

$$\begin{array}{cc}\hfill {\displaystyle \frac{d}{dB}}{R}_e& ={\displaystyle \frac{d}{dB}}\mathbb{E}\left[G\left({\displaystyle \frac{{\left|\right|\mathbf{h}\left|\right|}^2(1-\delta {\beta }_{N-1,1})}{I_C+d^{\alpha }{P}^{-1}}}\right)\right]\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill & =\mathbb{E}\left[{\displaystyle \frac{1}{I_C+d^{\alpha }{P}^{-1}}}·{\left|\right|\mathbf{h}\left|\right|}^2·ln2·{\displaystyle \frac{1}{N-1}}\delta ·{\beta }_{N-1,1}·g\left({\displaystyle \frac{{\left|\right|\mathbf{h}\left|\right|}^2(1-\delta {\beta }_{N-1,1})}{I_C+d^{\alpha }{P}^{-1}}}\right)\right]\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill & =\mathbb{E}\left[-{\displaystyle \frac{\gamma \delta {\beta }_{N-1,1}ln2}{N-1}}·{\displaystyle \frac{e^{-\frac{\gamma }{2}(1-\delta {\beta }_{N-1,1})}}{\sqrt{2\pi \gamma (1-\delta {\beta }_{N-1,1})}}}{log}_2\left({\displaystyle \frac{Q\left(\sqrt{\gamma (1-\delta ·\beta )}\right)}{1-Q\left(\sqrt{\gamma (1-\delta {\beta }_{N-1,1})}\right)}}\right)\right],\hfill \end{array}$$

(28)

where $\gamma$ is defined as

$$\begin{array}{c}\hfill \gamma ={\displaystyle \frac{{\parallel \mathbf{h}\parallel }^2}{I_C+d^{\alpha }{P}^{-1}}}.\end{array}$$

(29)

By approximating $1-\delta ·{\beta }_{N-1,1}$ as 1, which becomes more accurate for larger values of B, the derivative simplifies to

$$\begin{array}{c}\hfill {\displaystyle \frac{d}{dB}}{R}_e\approx \delta \mathbb{E}\left[-{\displaystyle \frac{\gamma {\beta }_{N-1,1}ln2}{N-1}}·{\displaystyle \frac{e^{-\frac{\gamma }{2}}}{\sqrt{2\pi \gamma }}}{log}_2\left({\displaystyle \frac{Q\left(\sqrt{\gamma }\right)}{1-Q\left(\sqrt{\gamma }\right)}}\right)\right]\triangleq \delta E_1,\end{array}$$

(30)

where

$$\begin{array}{cc}\hfill E_1& =\mathbb{E}\left[-{\displaystyle \frac{\gamma {\beta }_{N-1,1}ln2}{N-1}}·{\displaystyle \frac{e^{-\frac{\gamma }{2}}}{\sqrt{2\pi \gamma }}}{log}_2\left({\displaystyle \frac{Q\left(\sqrt{\gamma }\right)}{1-Q\left(\sqrt{\gamma }\right)}}\right)\right]\hfill \\ \hfill & \stackrel{\left(a\right)}{=}\mathbb{E}\left[-{\displaystyle \frac{\sqrt{\gamma }ln2}{N}}·{\displaystyle \frac{e^{-\frac{\gamma }{2}}}{\sqrt{2\pi }}}{log}_2\left({\displaystyle \frac{Q\left(\sqrt{\gamma }\right)}{1-Q\left(\sqrt{\gamma }\right)}}\right)\right],\hfill \end{array}$$

(31)

where $\mathbb{E}\left[{\beta }_{N-1,1}\right]={\displaystyle \frac{N-1}{N}}$ is used for $\left(a\right)$. This expectation is a function of the random variable $\sqrt{\gamma }$, but an explicit computation of the expectation is extremely difficult as $\sqrt{\gamma }$ is a mixture of a lot of random variables, as shown in (29). Thus, instead of directly calculating $E_1$, we consider an approximation of $\sqrt{\gamma }$ such that it can be represented by the single random variable d, which has the most dominant effect on the achievable rate. Specifically,

$$\begin{array}{cc}\hfill \sqrt{\gamma }={\displaystyle \frac{\sqrt{{\parallel \mathbf{h}\parallel }^2}}{\sqrt{I_C+d^{\alpha }{P}^{-1}}}}& \stackrel{\left(a\right)}{\approx }{\displaystyle \frac{\mathbb{E}\left[\sqrt{{\parallel \mathbf{h}\parallel }^2}\right]}{\sqrt{\mathbb{E}[\left[I_C\right]+d^{\alpha }{P}^{-1}]}}}\hfill \\ \hfill & \stackrel{\left(b\right)}{=}{\displaystyle \frac{\mathsf{\Gamma }(N+\frac{1}{2})}{\mathsf{\Gamma }\left(N\right)\sqrt{\frac{2}{\alpha -2}+d^{\alpha }{P}^{-1}}}}\triangleq \widehat{\gamma },\hfill \end{array}$$

(32)

where $\sqrt{{\parallel \mathbf{h}\parallel }^2}$ and $I_C$ are approximated by their expectations for $\left(a\right)$; here, $\mathsf{\Gamma }(·)$ denotes the gamma function. To obtain $\left(b\right)$, $\mathbb{E}\left[I_C\right]={\displaystyle \frac{2}{\alpha -2}}$ ([8], Appendix B) is used, along with following equality:

$$\begin{array}{c}\hfill \mathbb{E}\left[\sqrt{{\parallel \mathbf{h}\parallel }^2}\right]={\displaystyle \frac{1}{\mathsf{\Gamma }\left(N\right)}}{\int }_0^{\infty }{x}^{N+{\displaystyle \frac{1}{2}}-1}{e}^{-x}dx={\displaystyle \frac{\mathsf{\Gamma }(N+\frac{1}{2})}{\mathsf{\Gamma }\left(N\right)}},\end{array}$$

(33)

which is obtained based on the fact that ${\parallel \mathbf{h}\parallel }^2$ is a gamma-distributed random variable with the parameters N and 1. Based on the approximation in (32), $E_1$ can be approximated as

$$\begin{array}{cc}\hfill E_1& \approx \mathbb{E}\left[-{\displaystyle \frac{\widehat{\gamma }ln2}{N}}·{\displaystyle \frac{e^{-\frac{{\widehat{\gamma }}^2}{2}}}{\sqrt{2\pi }}}{log}_2\left({\displaystyle \frac{Q\left(\widehat{\gamma }\right)}{1-Q\left(\widehat{\gamma }\right)}}\right)\right]\hfill \\ \hfill & =-{\displaystyle \frac{ln2}{N\sqrt{2\pi }}}{\int }_0^{\infty }{f}_1\left({\displaystyle \frac{\mathsf{\Gamma }(N+\frac{1}{2})}{\mathsf{\Gamma }\left(N\right)\sqrt{2/(\alpha -2)+r^{\alpha }{P}^{-1}}}}\right)·\left(2\lambda \pi r\right)e^{-\lambda \pi r^2}dr\hfill \\ \hfill & =-{\displaystyle \frac{ln2}{N\sqrt{2\pi }}}{\int }_0^{\infty }{f}_1\left({\displaystyle \frac{\mathsf{\Gamma }(N+\frac{1}{2})}{\mathsf{\Gamma }\left(N\right)\sqrt{2/(\alpha -2)+P^{-1}{t}^{\alpha /2}·{\left(\lambda \pi \right)}^{-\alpha /2}}}}\right)e^{-t}dt\triangleq E_2,\hfill \end{array}$$

(34)

where

$$\begin{array}{c}\hfill f_1\left(x\right)=x{e}^{-{\displaystyle \frac{x^2}{2}}}{log}_2\left({\displaystyle \frac{Q\left(x\right)}{1-Q\left(x\right)}}\right).\end{array}$$

(35)

The value of $E_2$ can be calculated using numerical methods. Thus, although it is difficult to obtain an explicit form of the definite integral in (34), it can be numerically evaluated by calculating a Riemann sum, as there is a single variable for integration and the integrand is a smooth function.

Substituting this approximation into (30), we further approximate the derivative of $R_e$ as

$$\begin{array}{c}\hfill {\displaystyle \frac{d}{dB}}{R}_e\approx \delta E_2.\end{array}$$

(36)

Using the approximations in (30) and (36), we can estimate the critical point of $R_{Net}$ by solving the following equation:

$$\begin{array}{c}\hfill {\displaystyle \frac{d}{dB}}{R}_{Net}={\displaystyle \frac{d}{dB}}{R}_e-{\displaystyle \frac{1}{T_c}}\approx \delta E_i-{\displaystyle \frac{1}{T_c}}=0,\end{array}$$

(37)

where $i=1,2$. Since $E_1$ and $E_2$ are not dependent on B in (30) and (36), the solution to (37) is approximately

$$\begin{array}{c}\hfill B^{*}\approx (N-1){log}_2\left(T_c{E}_i\right)=(N-1){log}_2{T}_c+(N-1){log}_2{E}_i,\end{array}$$

(38)

for $i=1,2$, where $\delta =2^{-{\displaystyle \frac{B}{N-1}}}$ is used for the calculation. This result approximates the scaling rate of the optimal number of feedback bits as a function of the channel coherence time $T_c$.

The following table compares the proposed analysis with previous studies related to deriving the optimal feedback rate, which use various system models.

In Table 1, BD stands for block diagonalization and $N_r$ denotes the number of receiving antennas each user has. The scaling rate derived in this study is identical to that obtained with infinite-resolution ADCs [8], indicating that the rate of the increase in the optimal number is unaffected by the resolution of the ADCs. However, as shown in the following section, the absolute number of feedback bits is generally much lower than that required for infinite-resolution ADCs.

Table 1. Comparison of optimal feedback rates found in the literature with our results.

Transmit Scheme	Nr	ADC Type	Optimal Feedback Rate
MRT for single user [8]	$N_r=1$	Infinite-resolution ADCs	$(N-1){log}_2{T}_c$
ZFBF for multiple users [8]	$N_r=1$	Infinite-resolution ADCs	${\displaystyle \frac{\alpha (N-1)}{2}}{log}_2{T}_c$
MRT for single user [10]	$N_r>1$	Infinite-resolution ADCs	$N_r(N-N_r){log}_2{T}_c$
BD for multiple users [11]	$N_r>1$	Infinite-resolution ADCs	${\displaystyle \frac{\alpha N_r(N-N_r)}{2}}{log}_2{T}_c$
MRT for single user (this study)	$N_r=1$	One-bit ADCs	$(N-1){log}_2{T}_c$

4. Simulation Results and Discussion

In this section, we verify the analytical results from the previous section using Monte Carlo simulations. Unless otherwise specified, we assume $\alpha =4$ and $\lambda ={10}^{-5}/\pi$. For simplicity, the network size is limited to a circular area with a radius of 5 km.

In Figure 4, the net spectral efficiency $R_{Net}=R_e-{\displaystyle \frac{B}{T_c}}$, defined in (21), is plotted as a function of B, demonstrating that there is typically, at most, one maximum point. This is because the ergodic spectral efficiency $R_e$ is described by a concave function (since ${\mathcal{H}}_b\left(Q\left(\sqrt{x}\right)\right)$ is convex [13]) whose derivative is positive and converges to zero, while ${\displaystyle \frac{B}{T_c}}$ has a constant slope. Thus, if a critical point exists, there is at most one corresponding to the global maximum. If no critical point exists, the net spectral efficiency is maximized when $B=0$. Figure 4 also shows that this critical point can be identified by finding the zero-crossing of the derivative of $R_{Net}$, which is obtained in the figure by solving (26).

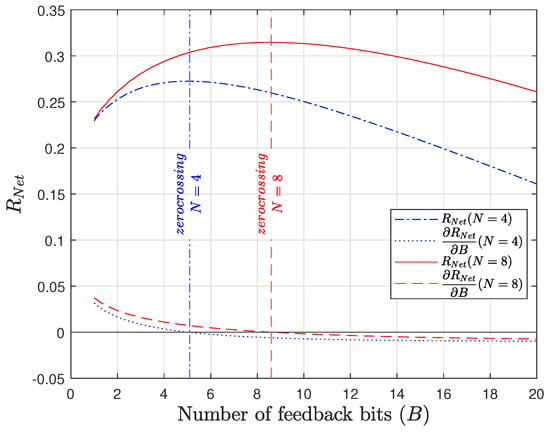
Figure 4. Net spectral efficiency vs. B.

In Figure 5 and Figure 6, we validate the scaling behavior of the number of feedback bits derived from (38). Figure 5 and Figure 6 represent the cases of $N=4$ and $N=8$, respectively. In each figure, both $E_1$ and $E_2$ serve as approximations of the true optimal number, with the true optimal values obtained through an exhaustive search. Although minor discrepancies exist between the approximations and the actual optimal values, the proposed approximations closely track the scaling behavior of the optimal numbers, which is the main focus of this study.

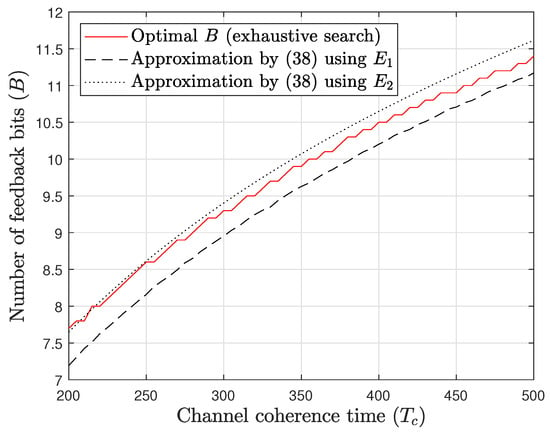
Figure 5. The optimal number of feedback bits vs. $T_c$. $N=4$.

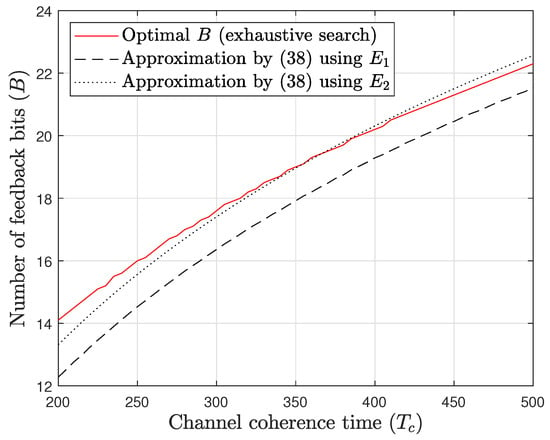
Figure 6. The optimal number of feedback bits vs. $T_c$. $N=8$.

Moreover, the discrepancies are nearly within 1 bit across all values of $T_c$ in the simulation. Given that the net spectral efficiency changes gradually, as shown in Figure 4, such discrepancies do not result in a significant gap between the net spectral efficiencies obtained using the true optimal number and the proposed approximation. This conjecture is further supported by Figure 7 and Figure 8, where the gap in the net spectral efficiencies between the true optimal values and the proposed approximations remains negligible, provided $T_c$ is sufficiently large.

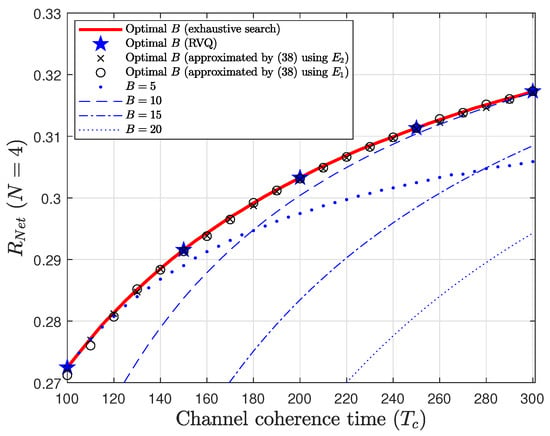
Figure 7. Net spectral efficiency obtained using $B=B^{*}$ vs. $T_c$ when $N=4$.

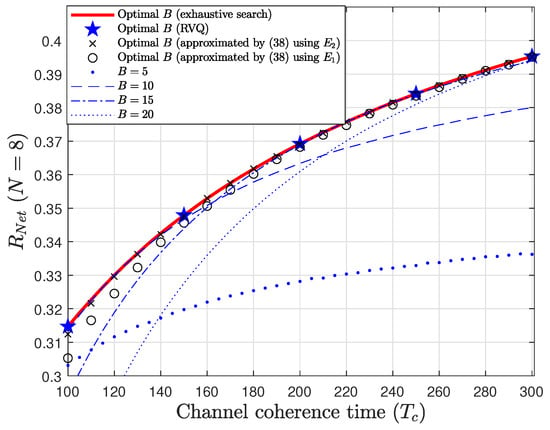
Figure 8. Net spectral efficiency obtained using $B=B^{*}$ vs. $T_c$ when $N=8$.

As predicted in the previous section, the scaling in Figure 5 and Figure 6 follows a logarithmic function of the channel coherence time $T_c$, with the logarithmic function scaled by $N-1$. This scaling behavior of the optimal number is equivalent to that of infinite-resolution ADCs [8], indicating that the optimal feedback rate is unaffected by the resolution of the ADCs at the receiver. While the scaling behavior is independent of the ADCs’ resolution, the absolute values of the optimal number are significantly lower than those obtained with infinite-resolution ADCs.

Figure 7 and Figure 8 compare the net spectral efficiency achieved with the optimal number of feedback bits to that obtained with fixed values of B. Since $B^{*}$ is the optimal number, the case where $B=B^{*}$ generally outperforms those with a fixed B, regardless of the specific fixed value chosen. When B is relatively small, e.g., $B=5$, good performance is observed at moderate values of $T_c$, but that performance deteriorates as $T_c$ increases. Conversely, when B is relatively large, e.g., $B=20$, good performance is seen at higher values of $T_c$, but poor performance is observed at lower values of $T_c$. Thus, as suggested by our analytical results in (38), the feedback rate must scale with $T_c$ to consistently achieve an optimal performance.

It should also be noted that our analysis in Section 3 does not impose any restrictions on the intensity $\lambda$ of the homogeneous PPP of BSs, making our results applicable to ultra-dense networks. Generally, as indicated in Equation (34) of this paper, the optimal number of feedback bits increases with $\lambda$, although the rate of increase eventually saturates as the term ${\displaystyle \frac{1}{\lambda }}$ in the denominator approaches zero. This observation is corroborated by Figure 9 and Figure 10. In Figure 9, the optimal feedback rate increases as the intensity $\lambda$ rises from ${\displaystyle \frac{{10}^{-5}}{\pi }}$ to $5\times {\displaystyle \frac{{10}^{-5}}{\pi }}$. However, in Figure 10, we see that the increase in the optimal feedback rate begins to saturate as $\lambda$ increases from $10\times {\displaystyle \frac{{10}^{-5}}{\pi }}$ to $50\times {\displaystyle \frac{{10}^{-5}}{\pi }}$.

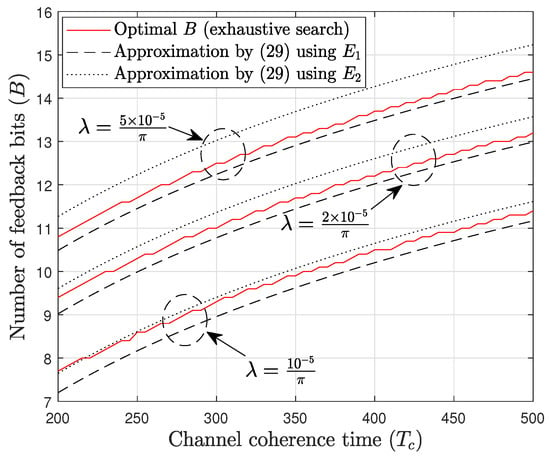
Figure 9. Optimal number of feedback bits versus $T_c$ for various values of $\lambda$.

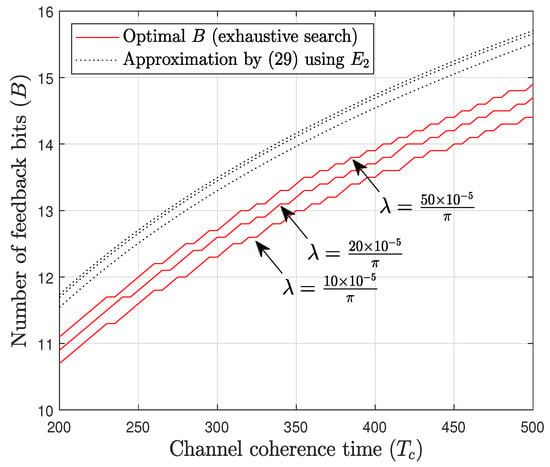
Figure 10. Optimal number of feedback bits versus $T_c$ for various values of $\lambda$.

5. Conclusions

In this paper, we investigated the optimal feedback rate in dense cellular networks where both limited feedback and one-bit ADC receivers are employed. Using stochastic geometry to model inter-cell interference, we introduced an approximation of the achievable spectral efficiency, enabling us to derive a differentiable expression of the optimal feedback rate. Our analysis revealed that while the scaling of the optimal feedback rate with respect to the channel coherence time is consistent with that of systems using infinite-resolution ADCs, the actual values are considerably lower when one-bit ADCs are employed. This indicates that the resolution of the ADCs plays a crucial role in determining the system’s overall performance, particularly in terms of the feedback rate. Our simulation results corroborated our theoretical findings, demonstrating that our approximation accurately captures the relationship between feedback rate and system performance. The insights gained from this study are instrumental for the design of limited-feedback-based beamforming systems, particularly in the context of energy-efficient deployments where power consumption is a critical factor.

Future work may extend these results in several directions. For instance, we could derive the optimal number of feedback bits when receivers use 2-bit or 3-bit ADCs, generalizing these cases to k-bit low-resolution ADCs. However, this would require deriving the optimal input signaling and the corresponding capacity. Our work can also be extended to scenarios where each base station simultaneously serves multiple users through spatial division multiple access (SDMA), such as a ZFBF. This extension could incorporate k-bit ADCs within the SDMA context. Another direction is to explore an alternative cellular interference model, employing a different random point process to more accurately capture practical wireless cellular network characteristics.