An Anonymous and Efficient Authentication Scheme with Conditional Privacy Preservation in Internet of Vehicles Networks

Abstract

The Internet of Vehicles (IoV) is an emerging technology that enables vehicles to communicate with their surroundings, provide convenient services, and enhance transportation systems. However, IoV networks can be vulnerable to security attacks because vehicles communicate with other IoV components through an open wireless channel. The recent related work suggested a two-factor-based lightweight authentication scheme for IoV networks. Unfortunately, we prove that the related work cannot prevent various security attacks, such as insider and ephemeral secret leakage (ESL) attacks, and fails to ensure perfect forward secrecy. To address these security weaknesses, we propose an anonymous and efficient authentication scheme with conditional privacy-preserving capabilities in IoV networks. The proposed scheme can ensure robustness against various security attacks and provide essential security features. The proposed scheme ensures conditional privacy to revoke malicious behavior in IoV networks. Moreover, our scheme uses only one-way hash functions and XOR operations, which are low-cost cryptographic operations suitable for IoV. We also prove the security of our scheme using the “Burrows–Abadi–Needham (BAN) logic”, “Real-or-Random (ROR) model”, and “Automated Validation of Internet Security Protocols and Applications (AVISPA) simulation tool”. We evaluate and compare the performance and security features of the proposed scheme with existing methods. Consequently, our scheme provides improved security and efficiency and is suitable for practical IoV networks.

1. Introduction

The Internet of Vehicles (IoV) is a technology that integrates vehicular ad hoc networks (VANETs) and the Internet of Things (IoT) [1]. In IoV networks, vehicles can communicate with other IoV components and access a lot of information over the Internet. In IoV networks, vehicles perform multiple tasks simultaneously, such as automated driving, multimedia services, traffic flow management, and battery management [2,3,4]. To handle these tasks, vehicles are equipped with on-board units (OBUs) that process large amounts of data in real time [5]. This enables vehicles to make intelligent decisions and enhance safety and efficiency in IoV systems. The vehicles equipped with OBU generate and transmit traffic data to nearby roadside units (RSUs) [6], and RSUs transmit wireless information from vehicles and pedestrians to a central server. As the number of vehicles increases significantly, researchers have proposed that RSUs process a part of the data processing to reduce the overload on the trusted authority (TA) [7,8,9]. This approach leverages the regional characteristics of IoV services and enhances efficiency because RSUs can process computational tasks at the network edge [10]. Thus, users can utilize advanced IoV services, including emergency vehicle preemption, intelligent traffic management systems, and multi-collision-avoidance assistance.

In IoV networks, wireless communication over an open channel is highly susceptible to various security threats [11]. Vehicles exchange sensitive information with RSUs, including the condition, location, travel route, and identity [12]. Thus, an adversary can guess an identity or password by capturing, modifying, and replaying messages. The data leakage can undermine IoV services, leading to significant security and privacy risks, including user impersonation and unauthorized tracking. Moreover, an adversary can attempt to perform various security attacks using these captured data, such as replay and man-in-the-middle (MitM) attacks. Therefore, vehicles and RSUs must authenticate each other to establish secure connections. Furthermore, the activities of malicious adversaries can disrupt normal communication and create network congestion by transmitting false information in IoV networks [13]. Thus, many researchers have proposed authentication schemes that revoke the adversary’s authority by applying conditional privacy [14,15].

In general, conditional privacy can be achieved using a public-key cryptosystem [16]. However, public-key cryptosystems may overload vehicles due to their constrained resources, such as limited memory, power, and communication capacity. A high amount of computational loads leads to a communication delay, critically damaging real-time responses. This delay can slow down the exchange of real-time information, which is crucial for addressing emergency situations and reducing accident risks. Moreover, these delays can hinder the real-time exchange of information, which is critical for responding to emergencies and minimizing the risk of accidents. Moreover, mobility is an essential consideration in IoV environments. Due to their high speeds, vehicles should establish frequent and rapid connections with RSUs within short intervals. Therefore, it is essential to design an authentication scheme that accounts for the lightweight nature of IoV networks.

In 2024, Sibahee et al. [17] suggested a two-factor-based privacy-preserving scheme for efficient authentication in IoV using lightweight primitives such as hash and XOR operations. They demonstrated security robustness against various attacks, such as impersonation and privileged insider attacks. Unfortunately, we found that Sibahee et al.’s scheme [17] is vulnerable to ephemeral secret leakage (ESL) and insider attacks. Furthermore, their scheme fails to ensure perfect forward secrecy. We propose an anonymous and efficient authentication scheme with conditional privacy preservation in IoV networks to improve these security weaknesses. We consider conditional privacy to keep the quality of information, which can exclude malicious vehicles. In the proposed scheme, the TA can trace the real identities of malicious vehicles from pseudo-identities. In addition, the proposed scheme incurs lower computational and communication costs compared with existing conditional privacy-preserving authentication (CPPA) schemes, as it uses only hash functions and XOR operations. Therefore, we demonstrate that our scheme is lightweight and practical, effectively addressing the privacy and security challenges in IoV networks.

1.1. Contributions

The following descriptions represent the main contributions of this research.

• We have identified and demonstrated the security vulnerabilities in Sibahee et al.’s scheme [17], particularly its susceptibility to insider attacks and its failure to ensure perfect forward secrecy. To mitigate these weaknesses, we propose an enhanced scheme that effectively addresses security concerns.
• The proposed scheme ensures essential security requirements and prevents various security attacks. Moreover, our scheme ensures conditional privacy, effectively countering malicious behavior while maintaining efficiency by utilizing only collision-resistant one-way hash functions and XOR operations.
• Moreover, formal security analysis is conducted using “Burrows–Abadi–Needham (BAN) logic” [18], the “Real-or-Random (ROR) model” [19], and the “Automated Validation of Internet Security Protocols and Applications (AVISPA) simulation tool” [20,21] to prove the security of the proposed scheme.
• We perform a performance evaluation to analyze the communication cost, computational cost, energy consumption, and security properties of the proposed scheme in comparison with the related schemes.

1.2. Organization

The rest of this paper is organized as follows: Section 2 provides a review of related studies, and Section 3 introduces the preliminaries. Section 4 and Section 5 present an analysis of Sibahee et al.’s scheme [17] and a demonstration of its security flaws, respectively. We propose a lightweight and conditional privacy-preserving authentication scheme for IoV networks in Section 6. In Section 7, we conduct the informal and formal security analysis and demonstrate the security of our scheme. In Section 8, we evaluate the performance of our scheme compared with the existing schemes. Toward the end of this article, Section 9 concludes with a summary of our paper.

2. Related Works

IoV has become a complex network, and researchers have proposed comprehensive directions to address dynamic characteristics such as high mobility, interoperability, scalability, and reliability. Qureshi et al. [22] proposed an IoV network model to support major network requirements, such as connectivity for safety and user infotainment services. They explained that IoV networks have suffered from various security vulnerabilities because networks are extended to connect numerous vehicles and infrastructures. Taslimasa et al. [23] suggested applications of IoV with security aspects. They introduced the various security threats in IoV, such as modification, eavesdropping, impersonation, and denial of service (DoS) attacks. Sharma et al. [24] introduced security requirements and threats for IoV networks. To overcome the drawbacks of existing schemes, they emphasized the importance of authentication, data integrity, and real-time communication for secure IoV networks. However, in the existing secure authentication schemes for IoV networks, TA cannot effectively trace the real identity of a malicious vehicle from a pseudo-identity.

To address the security and privacy issues, many researchers have proposed a secure authentication scheme with conditional privacy in IoV networks. A CPPA scheme implements an important function in which any other entity except the TA cannot reveal the real identity of a vehicle. In the last decade, many mutual authentications with conditional privacy have been proposed to secure vehicular environments. Xu et al. [25] designed a CPPA scheme in which the TA stores the tuples of the most recent successful session to resist desynchronization attacks. In their scheme, RSUs can authenticate with vehicles, which can reduce bottleneck problems and improve communication efficiency. However, Kumar et al. [26] argued that Xu et al.’s scheme [25] did not provide perfect forward secrecy or resistance against login verification, stolen verifier, privileged insider, and desynchronization attacks. Therefore, Kumar et al. [26] suggested a desynchronization-resistant CPPA scheme for VANETs that provides conditional privacy using a hash function and symmetric key cryptography. In their scheme, TA does not store secret parameters or compute shared keys using parameters received only from public channels. However, the existing CCPA schemes are still vulnerable to potential security threats and lack of security properties, such as stolen verifiers, privileged insiders, desynchronization, physically captured attacks, and perfect forward secrecy. These impose additional security challenges, considering illegal involvement through public communication channels.

Thus, many researchers designed public-key cryptography-based robust authentication schemes to improve the security level of the previous CCPA schemes. Zhong et al. [27] designed a practical ID-based CPPA scheme that uses ECC operations to improve the security of VANETs. They also use the registration list to shorten the retrieval time of the revocation list, which helps to prevent an adversary from attempting further malicious attacks. Similarly, Cui et al. [28] proposed an ECC-based CPPA scheme for VANETs where a vehicle is kept anonymous from cloud service providers. Their scheme allows entities to register only once, reducing the storage burden of redundant registration information for vehicles. Moreover, a cloud broker can choose a cloud service provider (CSP) that can provide suitable services to vehicle users. Thus, vehicle users can easily access vehicular services and reduce dependence on a single CSP. They focused on increasing various services, which resulted in additional costs and overheads. Awais et al. [29] proposed a three-factor authentication protocol for fog-based VANETs using ECC. In their scheme, the fog node acts as an intermediary node to establish a session key among all entities. Their scheme applied fuzzy-verifier techniques that use unclonable properties of biometric information to resist password-guessing attacks. Kumar et al.’s scheme [30] also used ECC and ensured security properties, such as conditional privacy, untraceability, and anonymity. Their scheme provided fog-node-assisted real-time communications in VANETs. While these authentication schemes [27,28,29,30] enhance security for vehicles, most of their authentication processes rely on public-key cryptographic operations. Since the public-key infrastructures are based on the complexity of mathematical computation, the excessive use of public-key cryptography can incur comparatively high computational and communication overheads in resource-constrained environments like IoV networks.

Due to performance requirements for IoV, many researchers have focused on the importance of lightweight properties for real-time communication of vehicles. They proposed authentication schemes that aim to use only low-cost cryptographic operations to efficiently validate the legitimacy of vehicles. Chen et al. [31] proposed an anonymous and lightweight authentication scheme based on smart card protocol for typical IoV authentication scenarios. Using hash and modular exponential operations, their scheme improved the existing scheme by addressing identified weaknesses. They demonstrated the robustness of their scheme compared with previous schemes in terms of security and performance. Chaudhry [32] presented an efficient authentication scheme for communication between vehicles and RSUs. Their scheme also builds on an existing scheme, improving security flaws and overloads. Their scheme focused on efficiency to lower communication and computational costs, using symmetric encryption, XOR operations, and hash functions. Most of the proposed lightweight schemes utilize various low-cost cryptographic operations, but they cannot provide some security properties and conditional privacy. Recently, Sibahee et al. [17] suggested a lightweight two-factor authentication scheme for secure communication between vehicles and RSUs. They argued that their scheme can resist various IoV attacks, such as MitM, impersonation, desynchronization, and message replay attacks. However, Sibahee et al.’s scheme has the weakness of insider and ESL attacks and cannot provide perfect forward secrecy. To resolve these security flaws of Sibahee et al.’s scheme [17], we propose an anonymous and efficient authentication scheme with conditional privacy preservation in IoV networks.

Table 1. The summary of related works.

Scheme	Communication	Contributions	Limitations
Xu et al. [25]	V2I	Proposed an authentication scheme for IoV designing storage forms of TA against desynchronization attacks Utilization of RSUs to reduce the load of TA Security demonstration using ROR model and simulation tool Proverif	Vulnerable to login verification, stolen verifier, privileged insider, and desynchronization attacks Cannot ensure perfect forward secrecy
Kumar et al. [26]	V2I	Proposed an authentication scheme using symmetric key cryptography for energy efficiency Using pseudo-identities updated in each session Provide conditional privacy preservation	Vulnerable to RSU captured attacks Cannot ensure perfect forward secrecy
Zhong et al. [27]	V2I	Proposed an authentication scheme using ECC, which prevents continuous attacks by shortening retrieval time Provide password change phase on offline Provide conditional privacy preservation	Vulnerable to smart card capture, offline password guessing, ESL, and MitM attacks High computational and communication overhead using ECC Large storage loads to registration list
Cui et al. [28]	V2I	Proposed a multi-cloud-based authentication scheme that uses only one registration process to reduce redundancy Provide conditional privacy preservation	High computational and communication cost using ECC Cannot ensure perfect forward secrecy
Awais et al. [29]	V2I	Proposed a mutual authentication scheme for VANET environments using fog computing Processing authentication and key agreement with three factors	High computational and communication cost using ECC Cannot ensure conditional privacy preservation
Kumar et al. [30]	V2I	Proposed the real-time communication scheme using fog computing Distribute entire traffic load through a group of controlled RSUs Provide conditional privacy preservation	High computational and communication cost using ECC Vulnerable to spoofing, repudiation, and DoS attacks
Chen et al. [31]	V2I	Proposed a lightweight authentication scheme for distribution of entire traffic load using modular exponential operation Provide conditional privacy	Vulnerable to identity guessing, ESL, and replay attacks Cannot ensure conditional privacy preservation
Chaudhry [32]	V2I	Proposed a lightweight authentication scheme using symmetric encryption Provide conditional privacy preservation	Vulnerable to identity guessing and ESL attacks Cannot ensure conditional privacy preservation and perfect forward secrecy
Sibahee et al. [17]	V2I	Proposed a lightweight authentication scheme using only hash and XOR operation model for distribution of entire traffic load Provide conditional privacy	Vulnerable to insider and ESL attacks Cannot ensure conditional privacy preservation and perfect forward secrecy
Proposed	V2I	Proposed a lightweight authentication scheme using only hash and XOR operation Secure mutual authentication against various security attacks Security analysis through BAN logic, ROR model, and AVISPA simulation Better computation, communication costs, and security properties compared with existing schemes

presents the summary of related works [17,25,26,27,28,29,30,31,32].

3. Preliminaries

This section introduces an adversary model, security goals, and the system model of our scheme.

3.1. Adversary Model

The proposed scheme utilizes the Dolev–Yao (DY) [33] and Canetti–Krawczyk (CK) [34] adversary models, which are widely used to depict the capabilities of an adversary $\mathcal{A}$. Based on the DY model, $\mathcal{A}$ can eavesdrop on the exchanged messages through an open channel. $\mathcal{A}$ can save, modify, and distort the messages illegally undetected. The CK model aims to define the severe capabilities of $\mathcal{A}$ for strong security. Under the CK model, $\mathcal{A}$ can control the communication between each entity and reveal secret information, such as a server’s master key and ephemeral random numbers generated in a session. Table 2 explains the adversary model classified as several attacker types [35], and the detailed assumptions are listed below:

• $\mathcal{A}$ can register as a legal user of the system and obtain communication messages.
• $\mathcal{A}$ can repudiate having sent or received messages and transmit fake messages to confuse the TA.
• $\mathcal{A}$ can capture OBUs to retrieve all the authentication parameters stored in it [36].
• $\mathcal{A}$ can disclose the long-term secret keys used in communication between IoV entities.
• $\mathcal{A}$ can attempt various attacks including replay, offline password guessing, and privileged insider attacks [37].

Table 2. The description of $\mathcal{A}$ based on attacker types.

Type	Description
Internal	$\mathcal{A}$ can access the network and interact with other entities as an authenticated user.
External	$\mathcal{A}$ can attack from outside the network, with limited capacity due to lack of internal access.
Malicious	$\mathcal{A}$ can use its abilities to pursue personal gain and disrupt the network’s functionality.
Active	$\mathcal{A}$ can inject malicious nodes into transmitted messages to gain unauthorized access.

Table 2. The description of $\mathcal{A}$ based on attacker types.

Type	Description
Internal	$\mathcal{A}$ can access the network and interact with other entities as an authenticated user.
External	$\mathcal{A}$ can attack from outside the network, with limited capacity due to lack of internal access.
Malicious	$\mathcal{A}$ can use its abilities to pursue personal gain and disrupt the network’s functionality.
Active	$\mathcal{A}$ can inject malicious nodes into transmitted messages to gain unauthorized access.

3.2. Security Goals

Security concerns in the IoV have significant implications for vehicles’ activities. To effectively counter the capabilities outlined in Section 3.1, our scheme should achieve security and performance requirements as follows:

• Mutual Authentication: All messages and communicating entities must be authenticated before being trusted. It is crucial to verify the authenticity of communication sources from the authentication messages. The system should be capable of distinguishing between legitimate nodes and potentially malicious ones.
• Data Integrity: The integrity of received data should be guaranteed, ensuring it remains unaltered in its original form. The system should be able to detect any tampering attempts to prevent unauthorized modifications during transmission.
• Anonymity: The real identities of entities must be protected from the adversary who may intercept transmitted messages. This ensures that the adversary cannot trace the mobilities of vehicles or track their activities.
• Conditional Privacy: All entities except for the TA should be unable to trace or extract the vehicle’s real identity from the exchanged messages. The TA can only track the vehicle’s real identity when malicious activity is detected.
• Attack Resilience: To ensure enhanced privacy and security in IoV networks, the proposed scheme should be resilient against various security attacks, including offline password guessing, MitM, insider, ESL, forgery, and so on.
• Low Overhead: Security protocols should not introduce significant delays in message transmission considering the real-time characteristics of the IoV. Therefore, security protocols for IoV networks should ensure low overhead to maintain real-time communication.

3.3. System Model

This section represents detailed descriptions of our system model. The proposed system model is composed of TA, RSUs, and vehicles, as shown in Figure 1, and the description of the entities is as follows:

• TA: TA is a fully trusted authority responsible for system initialization, parameter generation, and registration management of other components within the IoV network. TA has sufficient storage and computational resources for the IoV networks. After vehicle registration, the TA securely stores the pseudo-identity $PI{D}_i$ of the vehicle encrypted with a shared secret key x and a master key $K_{TA}$. The TA can only retrieve the vehicle’s real identity from $PI{D}_i$ if the vehicle is detected as malicious activity.
• RSU: Each RSU has a unique identity and interacts with the TA using its identity. RSUs are semi-trusted, which are honest but curious entities. Therefore, RSUs may collect received messages and can perform the correct functions. RSUs have sufficient abilities to communicate with vehicles via wireless channels, enabling traffic-related information and facilitating mutual authentication processes. They are placed physically near vehicles and in charge of real-time communication. Moreover, they keep the recent revocation list, which has been updated by the TA. If a malicious vehicle attempts to authenticate using a revoked $PI{D}_i$, the RSU performs a revocation process. To enhance security and privacy, RSUs play a crucial role in ensuring conditional privacy by maintaining vehicle anonymity during the authentication process.
• Vehicle: Vehicles collect useful information through sensors and interact with other components in IoV networks. Vehicles rely on OBUs to exchange messages with RSUs. OBUs facilitate wireless communication over an open channel but have limited computational resources.

Figure 1. System model of the proposed scheme.

Figure 1. System model of the proposed scheme.

4. Review of Sibahee et al.’s Scheme

In Sibahee et al.’s scheme [17], the TA communicates with vehicles indirectly, and a session key is shared among vehicles, RSUs, and the TA. Sibahee et al.’s authentication scheme is composed of two phases: registration and login and authentication phases. The notations of this paper are described in

Table 3. Notations and descriptions.

Notation	Description
$V_i$	i-th vehicle
$RS{U}_j$	j-th roadside unit
$TA$	Trusted authority
$I{D}_i,P{W}_i$	Unique identity and password of $V_i$
$I{D}_j$	Unique identity of $RS{U}_j$
$I{D}_{TA}$	Unique identity of $TA$
$PI{D}_i$	Pseudo-identity of $V_i$
$K_{TA}$	Master key only known to $TA$
$S{K}_V,S{K}_R,S{K}_T$	Session key calculated by the $V_i,RS{U}_j$, and $TA$
$K_{R_{j}TA}$	Shared secret key between $RS{U}_j$ and $TA$
$x,a,k_r$	Random number
$r_n$	Random nonce (n = 1, 2, 3, …)
$T_n$	Timestamp (n = 1, 2, 3, …)
$h(·)$	Collision-resistant cryptographic one-way hash function
$\left|\right|$	Concatenation operation
⊕	Exclusive-OR operation

.

4.1. Registration Phase

In Sibahee et al.’s scheme [17], RSUs and vehicles must register their identities and share secret parameters with the TA. Section 4.1.1 and Section 4.1.2 describe the registration process of $V_i$ and $RS{U}_j$, respectively.

4.1.1. $V_i$ Registration

During this phase, $V_i$ and TA exchange their identity and registration parameters over a secure channel. Figure 2 shows the process of $V_i$ registration, and the following steps explain it in detail.

Step 1:

$V_i$ inputs $I{D}_i$ and $P{W}_i$. Then, $V_i$ chooses a random number a. Using these parameters, $V_i$, equipped with an OBU, computes security parameters $A_1=h(I{D}_i\left|\right|P{W}_i\left|\right|a)$ and $A_2=h(I{D}_i\left|\right|a)$. Through a secure channel, $V_i$ constructs and sends a request $Req=\{I{D}_i,a,A_1,A_2\}$ to the TA.

Step 2:

Upon receiving $Req$, the TA firstly checks whether the parameter $A_2=h(I{D}_i\left|\right|a)$ exists in the TA’s repository. If $A_2$ is not in its repository, the TA stores $A_2$. Then, the TA computes $A_3=h(I{D}_{TA}\left|\right|K_{TA}\left|\right|A_2)\oplus A_1$, $A_4=h(A_2\left|\right|K_{TA})$, and $A_5=h(A_1\left|\right|A_2\left|\right|A_4)$, using its $I{D}_{TA}$ and $K_{TA}$. After that, the TA composes a registration request response $Res=\{A_3,A_4,A_5,I{D}_{TA}\}$ and sends it to $V_i$ over a secure channel.

Step 3:

When $V_i$ obtains $Res$, $V_i$ computes $B_1=h(I{D}_i\left|\right|P{W}_i)\oplus a$. Finally, $V_i$ stores $\{A_3,A_4,A_5,$$B_1,I{D}_{TA}\}$ in OBU’s memory.

Figure 2. Vehicle registration phase of Sibahee et al.’s scheme [17].

Figure 2. Vehicle registration phase of Sibahee et al.’s scheme [17].

4.1.2. $RS{U}_j$ Registration

$RS{U}_j$ must register in the TA to exchange information with vehicles. Figure 3 presents the RSU registration phase of Sibahee et al.’s scheme [17]. Detailed steps of the process are described as follows:

Step 1:

The TA chooses $I{D}_j$ for $RS{U}_j$ and selects $K_{TA}$ as its private parameter. Afterwards, the TA computes the shared secret key $K_{R_{j}TA}=h(I{D}_j\left|\right|K_{TA})$. The TA stores $\left\{I{D}_j\right\}$ in its secure database.

Step 2:

The TA deposits $\{I{D}_j,K_{R_{j}TA}\}$ in each $RS{U}_j$. Then, $RS{U}_j$ saves $\{I{D}_j,K_{R_{j}TA}\}$.

Figure 3. RSU registration phase of Sibahee et al.’s scheme [17].

Figure 3. RSU registration phase of Sibahee et al.’s scheme [17].

4.2. Login and Authentication Phase

After the successful registration process, $V_i$ needs complete mutual authentication with RSUs to establish the session key for secure communication. This phase is described in Figure 4, and the detailed descriptions are as follows:

Step 1:

$V_i$ inputs $I{D}_i$ and $P{W}_i$ and derives $a=B_1\oplus h(I{D}_i\left|\right|P{W}_i)$, $A_1=h(I{D}_i\left|\right|P{W}_i\left|\right|a)$, and $A_2=h(I{D}_i\left|\right|a)$. $V_i$ computes $A_5^{\ast }=h(A_1\left|\right|A_2\left|\right|A_4)$ and checks whether $A_5\stackrel{?}{=}{A}_5^{\ast }$. If $A_5$ and $A_5^{\ast }$ equal, $V_i$ generates a random nonce $r_1$ and a timestamp $T_1$. Otherwise, the login process is terminated. $V_i$ computes parameters $B_2=A_3\oplus A_1=h(I{D}_{TA}\left|\right|K_{TA}\left|\right|A_2)$, $B_3=B_2\oplus r_1$, and $B_4=h(I{D}_{TA}\left|\right|I{D}_j\left|\right|B_2\left|\right|A_2\left|\right|r_1\left|\right|T_1)$. To connect with $RS{U}_j$, $V_i$ constructs the login message $L_M=\{B_3,B_4,I{D}_{TA},A_2,I{D}_j,T_1\}$ and sends $L_M$ to the TA through a public channel.

Step 2:

After receiving $L_M$ from $V_i$, the TA verifies the legitimacy of $I{D}_{TA}$. Then, the TA selects the current timestamp $T_2$ and checks if $T_1$ is valid, comparing $|T_2-T_1|$ with the maximum value of the transfer waiting time $T_{Max}$. After the TA checks if $|T_2-T_1|\le T_{Max}$, it derives $B_2=h(I{D}_{TA}\left|\right|K_{TA}\left|\right|A_2)$ and $r_1^{\ast }=B_2\oplus B_3$. The TA derives the parameter $B_4^{\ast }=h(I{D}_{TA}\left|\right|I{D}_j\left|\right|B_2\left|\right|A_2\left|\right|r_1\left|\right|T_1)$ and verifies $B_4^{\ast }\stackrel{?}{=}{B}_4$. If the verification is legitimate, the TA retrieves $I{D}_j$ from its database and generates a random nonce $r_2$. The TA generates a timestamp $T_3$ and computes $K_{R_{j}TA}=h(I{D}_j\left|\right|K_{TA})$, $B_5=h(K_{R_{j}TA}\left|\right|I{D}_j\left|\right|I{D}_{TA})\oplus r_1$, $C_1=h(r_1)\oplus r_2$, and $C_2=h(K_{R_{j}TA}\left|\right|r_1\left|\right|r_2\left|\right|T_3)$. At last, the authentication message $AU{T}_1=\{I{D}_j,B_5,C_1,C_2,T_3\}$ is composed and sent to $RS{U}_j$.

Step 3:

$RS{U}_j$ receives $AU{T}_1$ and verifies the legitimacy of $I{D}_j$. Then, $RS{U}_j$ selects a timestamp $T_4$. On condition that $|T_4-T_3|>T_{Max}$, this message fails to authenticate, and the session is terminated. Otherwise, $I{D}_j$ and $T_3$ are now successfully validated. $RS{U}_j$ derives $r_1^{\ast }=B_5\oplus h(K_{R_{j}TA}\left|\right|I{D}_j\left|\right|I{D}_{TA})$, $r_2^{\ast }=C_1\oplus h(r_1)$, and $C_2^{\ast }=h(K_{R_{j}TA}\left|\right|r_1^{\ast }\left|\right|r_2^{\ast }\left|\right|T_3)$ and checks $C_2^{\ast }\stackrel{?}{=}{C}_2$. If equality holds, $RS{U}_j$ generates a random nonce $r_3$ and computes $S{K}_R=h(r_1\left|\right|r_2\left|\right|r_3)$. After calculating $C_3=h(K_{R_{j}TA}\left|\right|r_2)\oplus r_3$, $C_4=I{D}_j\oplus h(r_3\left|\right|C_3)$, and $C_5=h(S{K}_R\left|\right|I{D}_j\left|\right|I{D}_{TA}\left|\right|r_3\left|\right|T_4)$, $RS{U}_j$ constructs $AU{T}_2=\{C_3,C_4,C_5,T_4\}$ and transmits it to the TA.

Step 4:

When TA receives $AU{T}_2$, the TA generates a timestamp $T_5$ and verifies the received timestamp $T_4$ by checking $|T_5-T_4|\le T_{Max}$. The TA calculates $r_3^{\ast }=C_3\oplus h(K_{R_{j}TA}\left|\right|r_2)$, $I{D}_j^{\ast }=C_4\oplus h(r_3^{\ast }\left|\right|C_3)$, and verifies if there is $I{D}_j^{\ast }$ in its repository. If it is not, the session is terminated. Afterward, it computes $C_5^{\ast }=h(S{K}_R\left|\right|I{D}_j^{\ast }\left|\right|I{D}_{TA}$$\left|\right|r_3^{\ast }\left|\right|T_4)$ and verifies $C_5^{\ast }\stackrel{?}{=}{C}_5$. Then, the TA computes session key $S{K}_T=h(r_1\left|\right|r_2\left|\right|r_3)$ and parameters $D_1=h(r_1\left|\right|A_2)\oplus r_2$, $D_2=h(r_1\left|\right|r_2)\oplus r_3$, $D_3=h(S{K}_T\left|\right|A_2\left|\right|r_2\left|\right|r_3\left|\right|T_5)$. They are used to compose $AU{T}_3=\{D_1,D_2,D_3,T_5\}$ and the TA sends it to $V_i$.

Step 5:

Upon receiving $AU{T}_3$, $V_i$ selects a current timestamp $T_6$ to verify the freshness of $T_5$. $V_i$ calculates $r_2^{\ast }=D_1\oplus h(r_1\left|\right|A_2)$, $r_3^{\ast }=D_2\oplus h(r_1\left|\right|r_2)$, $S{K}_V=h(r_1\left|\right|r_2^{\ast }\left|\right|r_3^{\ast })$, and $D_3^{\ast }=h(S{K}_V\left|\right|A_2\left|\right|r_2^{\ast }\left|\right|r_3^{\ast }\left|\right|T_5)$. On condition that $D_3^{\ast }=D_3$, $V_i$ successfully establishes the session key as $S{K}_V=S{K}_T=S{K}_R$.

Figure 4. Login and authentication phase of Sibahee et al.’s scheme [17].

Figure 4. Login and authentication phase of Sibahee et al.’s scheme [17].

5. Security Analysis of Sibahee et al.’s Scheme [17]

In this section, we demonstrate that Sibahee et al.’s scheme [17] cannot prevent insider and ESL attacks. Concurrently, their scheme does not provide perfect forward secrecy.

5.1. Insider Attack

Assume $\mathcal{A}$ registers successfully as a legal user with the TA. Then, $\mathcal{A}$ can obtain authentication information by legitimate communications with RSUs and the TA. With these parameters, $\mathcal{A}$ can calculate other vehicles’ session keys. The detailed steps are below.

Step 1:

$\mathcal{A}$ can process the login and authentication phase. $\mathcal{A}$ inserts the identity $I{D}_A$ and the password $P{W}_A$ of $\mathcal{A}$. After completing the login phase, $\mathcal{A}$ sends a login request message $L_{MA}$ to the TA. Upon receiving $L_{MA}$, the TA and RSU proceed with the authentication phase, and the TA sends message $AU{T}_{3A}$ to $\mathcal{A}$.

Step 2:

Then, $\mathcal{A}$ captures message $AU{T}_{1A}=\{I{D}_j^{\prime },B_5^{\prime },C_1^{\prime },C_2^{\prime },T_3^{\prime }\}$ during the login and authentication phase. Finally, $\mathcal{A}$ computes the parameter $h(K_{R_{j}TA}\left|\right|I{D}_j\left|\right|I{D}_{TA})=B_5^{\prime }\oplus r_{2A}$, where $r_{2A}$ is a random nonce that $\mathcal{A}$ has already known and used for login. The parameter is always used between the TA and the RSU during the authentication process.

Step 3:

After getting $h(K_{R_{j}TA}|\left|I{D}_j\right||I{D}_{TA})$, $\mathcal{A}$ eavesdrops messages $L_M,AU{T}_1,AU{T}_2,$ and $AU{T}_3$ exchanged by other legitimate vehicles via a public channel. Then, $\mathcal{A}$ computes $r_1=B_5\oplus h(K_{R_{j}TA}\left|\right|I{D}_j\left|\right|I{D}_{TA})$ from the message $AU{T}_1=\{I{D}_j,B_5,C_1,C_2,T_3\}$. Using the obtained $r_1$, $\mathcal{A}$ can compute $r_2=C_1\oplus h(r_1)$.

Step 4:

Now, $\mathcal{A}$ obtains $r_1$ and $r_2$. Using parameter $D_2$ in $AU{T}_3$, $\mathcal{A}$ can compute $r_3=D_2\oplus h(r_1\left|\right|r_2)$. Finally, $\mathcal{A}$ can calculate $SK=h(r_1|\left|r_2\right||r_3)$.

Therefore, Sibahee et al.’s scheme [17] does not prevent insider attacks.

5.2. ESL Attack

In Sibahee et al.’s scheme, $SK$ consists of only random nonces. If all random nonces are leaked, $\mathcal{A}$ can directly calculate $SK$. Details are as follows:

Step 1:

$\mathcal{A}$ intercepts messages $L_M=\{B_3,B_4,I{D}_{TA},A_2,I{D}_j,T_1\}$ and $AU{T}_3=\{D_1,D_2,D_3,T_5\}$.

Step 2:

After getting parameters $A_2,D_1$, and $D_2$, $\mathcal{A}$ computes $r_2=D_1\oplus h(r_1\left|\right|A_2)$ and $r_3=D_2\oplus h(r_1\left|\right|r_2)$. Then, $\mathcal{A}$ has $r_1,r_2$, and $r_3$ to calculate $SK=h(r_1|\left|r_2\right||r_3)$.

Consequently, Sibahee et al.’s scheme [17] does not resist ESL attacks.

5.3. Perfect Forward Secrecy

If $\mathcal{A}$ obtains the long-term secret key $K_{TA}$ of the TA, the session keys can be disclosed. The following steps show the details:

Step 1:

If $\mathcal{A}$ obtains the master key $K_{TA}$, $\mathcal{A}$ can compute $K_{R_{j}TA}=h(I{D}_j\left|\right|K_{TA})$ by utilizing the login message $L_M=\{B_3,B_4,I{D}_{TA},A_2,I{D}_j,T_1\}$.

Step 2:

By intercepting the authentication message $AU{T}_1=\{I{D}_j,B_5,C_1,C_2,T_3\}$, $\mathcal{A}$ can compute $r_1=B_5\oplus h(K_{R_{j}TA}\left|\right|I{D}_j\left|\right|I{D}_{TA})$ and $r_2=C_1\oplus h(r_1)$.

Step 3:

After $\mathcal{A}$ obtains the message $AU{T}_2=\{C_3,C_4,C_5,T_4\}$, $\mathcal{A}$ can compute $r_3=C_3\oplus h(K_{R_{j}TA}\left|\right|r_2)$ and $SK=h(r_1|\left|r_2\right||r_3)$.

Thus, Sibahee et al.’s scheme does not ensure perfect forward secrecy.

6. Proposed Scheme

To resolve the security weakness of Sibahee et al.’s scheme [17], we propose an improved authentication scheme. The proposed scheme comprises three phases: vehicle and RSU registration, login and authentication, and revocation phases.

6.1. Registration Phase

Before the actual deployment in IoV networks, vehicles or RSUs must acquire legitimate credentials. Through a secure channel, they send their real identities to the TA, and the TA shares secret parameters for authentication. As shown in Figure 5 and Figure 6, we present detailed descriptions of the registration phase for vehicles and RSUs.

6.1.1. $V_i$ Registration

To authenticate with an RSU, $V_i$ has to be registered at TA. The TA generates $PI{D}_i$ for $V_i$ and stores it instead of $I{D}_i$ for anonymity.

Step 1:

$V_i$ inputs $I{D}_i$ and $P{W}_i$. After that, $V_i$ sends $\left\{I{D}_i\right\}$ to the TA over a secure channel.

Step 2:

The TA receives $\left\{I{D}_i\right\}$ and then generates random numbers a and x. Using the received registration request $\left\{I{D}_i\right\}$, the TA derives parameters $HI{D}_i=I{D}_i\oplus h(K_{TA}\left|\right|I{D}_{TA})$, $PI{D}_i=HI{D}_i\oplus x$, $X_i=h(HI{D}_i\left|\right|I{D}_{TA}\left|\right|K_{TA})$, and $S_x=x\oplus h(PI{D}_i\left|\right|$$K_{TA})$. Then, the TA stores $\left\{S_x\right\}$ with $PI{D}_i$ in its secure database and sends the message $\{PI{D}_i,X_i,x,a\}$ to $V_i$.

Step 3:

Upon receiving the message, $V_i$ computes $HI{D}_i=PI{D}_i\oplus x$, $A_i=(x||X_i)\oplus h(P{W}_i\left|\right|I{D}_i\left|\right|a)$, $C_i=h(I{D}_i\left|\right|A_i)\oplus a$, and $V_{Li}=h(P{W}_i\left|\right|HI{D}_i\left|\right|X_i)$. Finally, $V_i$ stores $\{PI{D}_i,V_{Li},A_i,C_i\}$ in OBU’s memory and discards the rest of the values.

Figure 5. Vehicle registration phase of the proposed scheme.

Figure 5. Vehicle registration phase of the proposed scheme.

6.1.2. $RS{U}_j$ Registration

$RS{U}_j$ sends its $I{D}_j$ and shares a secret parameter $K_{R_{j}TA}$ for secure communication.

Step 1:

$RS{U}_j$ selects $I{D}_j$ and transmits $\left\{I{D}_j\right\}$ to TA via a secure channel.

Step 2:

The TA receives $\left\{I{D}_j\right\}$, then generates a random number $k_r$ and derives $K_{R_{j}TA}=h(k_r\left|\right|I{D}_{TA}\left|\right|K_{TA})$. Afterward, the TA stores $\left\{k_r\right\}$ with $I{D}_j$ in its database and sends the message $\left\{K_{R_{j}TA}\right\}$ to $RS{U}_j$.

Step 3:

At last, $RS{U}_j$ receives and stores $\left\{K_{R_{j}TA}\right\}$ in its repository.

Figure 6. RSU registration phase of the proposed scheme.

Figure 6. RSU registration phase of the proposed scheme.

6.2. Login and Authentication Phase

$V_i$ has to complete the login phase before proceeding to the authentication phase. After the successful login, $V_i$ can authenticate mutually and establish a session key with $RS{U}_j$ through the assistance of the TA. In Figure 7, this phase is described by the following:

Step 1:

$V_i$ inputs $I{D}_i$ and $P{W}_i$ into the OBU of $V_i$. Next, $V_i$ computes the login parameters $a=C_i\oplus h(I{D}_i\left|\right|A_i)$, $(x||X_i)=A_i\oplus h(P{W}_i\left|\right|I{D}_i\left|\right|a)$ and $HI{D}_i=PI{D}_i\oplus x$. With the parameters, $V_i$ confirms whether $V_{Li}\stackrel{?}{=}h(P{W}_i\left|\right|$$HI{D}_i\left|\right|$ $X_i)$. If it is unequal, the login process is terminated. Otherwise, $V_i$ is ready to authenticate with RSUs. $V_i$ generates a random nonce $r_1$ and obtains a timestamp $T_V$. $V_i$ computes $M_1=r_1\oplus h(X_i\left|\right|x\left|\right|T_V)$, $V_1=h(PI{D}_i\left|\right|r_1\left|\right|X_i\left|\right|T_V)$. After that, the message $\{PI{D}_i,M_1,V_1,T_V\}$ is composed and sent to $RS{U}_j$ for mutual authentication.

Step 2:

Upon receiving the message $\{PI{D}_i,M_1,V_1,T_V\}$ from $V_i$, $RS{U}_j$ checks the revocation list with $PI{D}_i$. Then, $RS{U}_j$ generates a timestamp $T_R$ and checks the freshness of $T_V$. $RS{U}_j$ calculates $V_2=h(V_1\left|\right|M_1\left|\right|I{D}_j\left|\right|K_{R_{j}TA}\left|\right|T_R)$. With the received messages, $RS{U}_j$ sends $\{PI{D}_i,I{D}_j,M_1,V_2,T_V,T_R\}$ to the TA.

Step 3:

The TA checks a validation of timestamp $T_R$ and retrieves $S_x$ and $k_r$ from $PI{D}_i$ and $I{D}_j$ respectively. Then, the TA derives $x=S_x\oplus h(PI{D}_i\left|\right|K_{TA})$, $HI{D}_i=PI{D}_i\oplus x$, $X_i^{\prime }=h(HI{D}_i\left|\right|K_{TA})$, and ${K_{R_{j}TA}}^{\prime }=h(k_r\left|\right|I{D}_{TA}\left|\right|K_{TA})$. After that, the TA computes $r_1^{\prime }=M_1\oplus h(X_i^{\prime }\left|\right|x\left|\right|T_V)$, $V_1^{\prime }=h(PI{D}_i\left|\right|r_1^{\prime }\left|\right|X_i^{\prime }\left|\right|T_V)$, $V_2^{\prime }=h(V_1^{\prime }\left|\right|M_1\left|\right|I{D}_j\left|\right|{K_{R_{j}TA}}^{\prime }\left|\right|T_R)$ and verifies the equality of $V_2^{\prime }$ and $V_2$. If it is not equal, the authentication phase is terminated. Otherwise, the TA selects a random nonce $r_2$ and timestamp $T_{TA}$. The TA calculates $M_2=(r_2\left|\right|r_1\oplus x)\oplus h(I{D}_j\left|\right|K_{R_{j}TA}\left|\right|T_{TA})$, $V_R=h(r_2\left|\right|I{D}_j\left|\right|K_{R_{j}TA}\left|\right|T_{TA})$, and $V_V=h(r_2\left|\right|X_i\left|\right|r_1\left|\right|T_{TA})$. Finally, the TA sends $\{M_2,V_R,V_V,T_{TA}\}$ to $RS{U}_j$.

Step 4:

Upon receiving the message, $RS{U}_j$ checks a freshness of timestamp $T_{TA}$. If not, this session is terminated. Otherwise, $RS{U}_j$ derives $(r_2^{\prime }\left|\right|r_1\oplus x)=M_2\oplus h(I{D}_j\left|\right|K_{R_{j}TA}\left|\right|T_{TA})$ and checks the equality of $V_R^{\prime }=h(r_2^{\prime }\left|\right|I{D}_j\left|\right|K_{R_{j}TA}\left|\right|T_{TA})$ and $V_R$. If so, $RS{U}_j$ generates a random nonce $r_3$ and selects a timestamp $T_{RR}$. $RS{U}_j$ calculates $M_3=(r_2\left|\right|r_3)\oplus h(r_1\oplus x)$, the session key $SK=h(r_2|\left|r_3\right||r_1\oplus x)$, and $V_3=h(V_V\left|\right|SK\left|\right|r_3\left|\right|T_{RR})$. Then, $RS{U}_j$ sends $\{M_3,V_3,T_{TA},T_{RR}\}$ to $V_i$ over a public channel.

Step 5:

Upon getting the message, $V_i$ checks the timestamp $T_{RR}$. $V_i$ computes $(r_2^{\prime }\left|\right|r_3^{\prime })=M_3\oplus h(r_1\oplus x)$, the session key $S{K}^{\prime }=h(r_2^{\prime }\left|\right|r_3^{\prime }\left|\right|r_1\oplus x)$, and $V_V^{\prime }=h(r_2^{\prime }\left|\right|X_i\left|\right|r_1\left|\right|T_{TA})$. $V_i$ checks the equality of $V_3^{\prime }=h(V_V^{\prime }\left|\right|S{K}^{\prime }\left|\right|r_3^{\prime }\left|\right|T_{RR})$ and $V_3$. If $V_3^{\prime }\stackrel{?}{=}{V}_3$ is correct, $V_i$ succeeds the authentication and establishes $SK$ with $RS{U}_j$.

Step 6:

When authentication is achieved successfully, $V_i$ and the TA update their parameters. $V_i$ computes $PI{D}_i^{new}=PI{D}_i\oplus h(r_1\left|\right|HI{D}_i)$, $A_i^{new}=(x\oplus h(r_1\left|\right|HI{D}_i)||X_i)\oplus h(P{W}_i\left|\right|I{D}_i\left|\right|a)$, $C_i^{new}=a\oplus h(I{D}_i\left|\right|A_i^{new})$ and updates $\{PI{D}_i,A_i,C_i\}$ to $\{PI{D}_i^{new}$, $A_i^{new}$, $C_i^{new}\}$. On the other side, the TA computes $PI{D}_i^{new}=PI{D}_i\oplus h(r_1\left|\right|HI{D}_i)$, $S_x^{new}=x\oplus h(PI{D}_i^{new}\left|\right|K_{TA})\oplus h(r_1\left|\right|HI{D}_i)$ and updates $\{PI{D}_i,S_x\}$ to $\{PI{D}_i^{new},S_x^{new}\}$.

Figure 7. Login and authentication phase of the proposed scheme.

Figure 7. Login and authentication phase of the proposed scheme.

6.3. Revocation Phase

The TA can disclose the real identities of malicious vehicles and trace them. When a malicious vehicle is detected, an RSU sends its pseudo-identity to TA. TA adds this pseudonym and identity to the revocation list and notifies all RSUs about the update. The following steps and Figure 8 detail the revocation process of a malicious vehicle:

Step 1:

Once an RSU issues a $PI{D}_i$ used by a misbehaving vehicle, the TA receives it and traces the real $I{D}_i$ from $PI{D}_i$.

Step 2:

The TA retrieves $S_x$ from $PI{D}_i$. Then the TA derives $x=S_x\oplus h(PI{D}_i\left|\right|K_{TA})$ and $HI{D}_i=PI{D}_i\oplus x$. Using these parameters, the TA computes $I{D}_i=HI{D}_i\oplus h(K_{TA}\left|\right|I{D}_{TA})$ and can acquire the real identity.

Step 3:

After that, the malicious vehicle’s real $I{D}_i$ and $PI{D}_i$ are added to the revocation list, and the updated list is sent to all RSUs.

Figure 8. Revocation phase of the proposed scheme.

Figure 8. Revocation phase of the proposed scheme.

7. Security Analysis

We conduct various security analyses such as informal security, BAN logic, ROR model, and AVISPA simulation tool. Specific details regarding the proof process for each analysis are elaborated in the section below.

7.1. Informal Security Analysis

We perform an informal analysis to demonstrate that our scheme can prevent various attacks, such as insider, OBU captured, privileged insider, offline password guessing, vehicle impersonation, ESL, MitM, forgery, desynchronization, and replay attacks. Additionally, we show that our scheme provides anonymity, conditional privacy, mutual authentication, and perfect forward secrecy.

7.1.1. Insider Attack

If an adversary $\mathcal{A}$ is a legitimate insider, $\mathcal{A}$ can authenticate RSUs and the TA. In Sibahee et al.’s scheme, an RSU communicates with the TA using the constant parameter $h(K_{R_{j}TA}|\left|I{D}_j\right||I{D}_{TA})$. However, our scheme uses timestamps $T_V,T_R,T_{TA}$, and $T_{RR}$ with the parameters to change with each session. This approach protects each session individually and prevents $\mathcal{A}$ from computing the secret parameter.

7.1.2. OBU Captured Attack

According to Section 3.1, $\mathcal{A}$ can capture an OBU of the legitimate vehicle $V_i$ and obtain parameters $\{PI{D}_i,V_{Li},A_i,C_i\}$ from the OBU’s memory. However, without knowing the vehicle’s $I{D}_i$ and $P{W}_i$, $\mathcal{A}$ cannot calculate the secret parameter $X_i$, which is shared between $V_i$ and the TA. Therefore, our scheme is secure against OBU captured attacks.

7.1.3. Privileged Insider Attack

If $\mathcal{A}$ is a privileged insider and intercepts the legal vehicle’s registration message $\left\{I{D}_i\right\}$, the next goal is that $\mathcal{A}$ tries to compute a session key $SK=h(r_2|\left|r_3\right||r_1\oplus x)$. To derive $r_2$ and $r_3$, $\mathcal{A}$ needs to know the secret parameter $X_i$, which is shared with the TA. $\mathcal{A}$ cannot compute $(x||X_i)=A_i\oplus h(P{W}_i\left|\right|I{D}_i\left|\right|a)$ without correctly guessing both $I{D}_i$ and $P{W}_i$. Consequently, the proposed scheme can defend against privileged insider attacks.

7.1.4. Offline Password Guessing Attack

We assume that $\mathcal{A}$ can extract stored parameters $\{PI{D}_i,V_{Li},A_i,C_i\}$ from $V_i$. In the proposed scheme, the password $P{W}_i$ is only used in parameters $A_i=h(x||X_i)\oplus h(P{W}_i\left|\right|I{D}_i\left|\right|a)$ and $V_{Li}=h(P{W}_i\left|\right|HI{D}_i\left|\right|X_i)$ and is encrypted by a hash function. Since $\mathcal{A}$ must correctly obtain both $I{D}_i$ and a, $\mathcal{A}$ cannot guess the $P{W}_i$.

7.1.5. Identity-Guessing Attack

According to Section 6.1, the real identity $I{D}_i$ is only known to $V_i$ and the TA. After receiving $I{D}_i$, the TA derives $HI{D}_i=I{D}_i\oplus h(K_{TA}\left|\right|I{D}_{TA})$, where $K_{TA}$ and $I{D}_{TA}$ are the secret parameters that only the TA knows. During the login and authentication phases, the exchanged messages never directly include $I{D}_i$. Here, $a=C_i\oplus h(I{D}_i\left|\right|A_i)$, $(x||X_i)=A_i\oplus h(P{W}_i\left|\right|I{D}_i\left|\right|a)$, $HI{D}_i=PI{D}_i\oplus x$, $V_{Li}=h(P{W}_i\left|\right|HI{D}_i\left|\right|X_i)$. For similar explanations in Section 7.1.4, the proposed scheme has resistance to identity-guessing attacks.

7.1.6. Vehicle Impersonation Attack

Suppose that $\mathcal{A}$ attempts to impersonate a legitimate vehicle. $\mathcal{A}$ tries to construct the authentication request message $\{PI{D}_i,M_1,V_1,T_V\}$. However, $\mathcal{A}$ cannot compute $M_1=r_1\oplus h(X_i\left|\right|x\left|\right|T_V)$ and $V_1=h(PI{D}_i\left|\right|r_1\left|\right|X_i\left|\right|T_V)$. Based on Section 7.1.4 and Section 7.1.5, $\mathcal{A}$ cannot derive the parameters $X_i$ and x used for authentication, and hence, this attack fails.

7.1.7. ESL Attack

Assume that $\mathcal{A}$ obtains random nonces $r_1,r_2$, and $r_3$ and tries to compute the session key $SK=h(r_2|\left|r_3\right||r_1\oplus x)$. In spite of the leakage of all random nonces in a session, the security of $SK$ is still preserved. This is because the parameter x is derived using either $I{D}_i$ and $P{W}_i$ of $V_i$, or the master key $K_{TA}$. Specifically, x is computed as $(x||X_i)=A_i\oplus h(P{W}_i\left|\right|I{D}_i\left|\right|a)$ or $x=S_x\oplus h(PI{D}_i\left|\right|K_{TA})$. Similarly, the computation of $(r_1\oplus x)$ requires the parameter $K_{R_{j}TA}$, which is only shared between $RS{U}_j$ and the TA. Here, $(r_2\left|\right|r_1\oplus x)=M_2\oplus h(I{D}_j\left|\right|K_{R_{j}TA}\left|\right|T_{TA})$. For these reasons, the proposed scheme is secure against ESL attacks.

7.1.8. MitM Attack

$\mathcal{A}$ can intercept exchanged messages via an open channel. The next goal is to modify the login request message $\{PI{D}_i,M_1,V_1,T_V\}$. Although $\mathcal{A}$ obtains $PI{D}_i$ from the message, $\mathcal{A}$ still needs $HI{D}_i$ to compute $V_{Li}=h(P{W}_i$$\left|\right|$ $HI{D}_i$$\left|\right|X_i)$, which is used to calculate $M_1=r_1\oplus h(X_i\left|\right|x\left|\right|T_V)$ and $V_1=h(PI{D}_i\left|\right|r_1\left|\right|X_i\left|\right|T_V)$. The TA can easily detect a tampered $HI{D}_i$ because $HI{D}_i$ is derived from the parameter $S_x$ related to $PI{D}_i$, which is stored in the secure database of TA. In addition, modifying all messages is impossible because they include random parameters that change with each session. Similarly, it is difficult to modify the message $\{PI{D}_i,I{D}_j,M_1,V_2,T_V,T_R\}$ sent from the $RS{U}_j$ to the TA, as the parameters $V_2$ are masked with the shared secret key $K_{R_{j}TA}$ between $RS{U}_j$ and the TA. Accordingly, these messages are unavailable to $\mathcal{A}$, preventing the implementation of MitM attacks. Therefore, the proposed scheme is resistant to MitM attacks.

7.1.9. Forgery Attack

We assume that $\mathcal{A}$ tries to forge authentication messages such as $\{PI{D}_i,I{D}_j,M_1,V_2,T_V,$ $T_R\}$, $\{M_2,V_R,V_V,T_{TA}\}$, and $\{M_3,V_3,T_{TA},T_{RR}\}$. According to Section 7.1.8, $\mathcal{A}$ cannot obtain the secret keys $K_{R_{j}TA}$ to forge these messages. In addition, it is difficult for $\mathcal{A}$ to validate using forged messages because all random nonces and secret parameters are required to compute $V_2=h(V_1\left|\right|M_1\left|\right|I{D}_j\left|\right|K_{R_{j}TA}\left|\right|T_R),V_R=h(r_2\left|\right|I{D}_j\left|\right|K_{R_{j}TA}\left|\right|T_{TA})$, and $V_3=h(V_V\left|\right|SK\left|\right|r_3\left|\right|T_{RR})$ for validation. These parameters are secure and protected by their hash value. Without correctly guessing all at once, it is impossible to forge the messages. Thus, $\mathcal{A}$ cannot forge valid authentication messages.

7.1.10. Desynchronization Attack

In each session, the TA and $V_i$ update $PI{D}_i$ and related parameters, $A_i$, $C_i$ and $S_x$. This update is confirmed only after the authentication phase is successfully completed. There is no need to transmit the new parameter $PI{D}_i^{new}$ from the TA to $V_i$. According to Section 6.1, the TA derives $r_1$ and verifies whether the received message is legitimate. After $V_i$ and $RS{U}_j$ establish the correct session key $SK$, the TA and $V_i$ update $PI{D}_i^{new}=PI{D}_i\oplus h(r_1\left|\right|HI{D}_i)$ and other parameters, respectively. If the authentication is terminated, they do not update parameters until the synchronization is successful. In conclusion, the proposed scheme can resist desynchronization issues with pseudo-identity.

7.1.11. Replay Attack

In our scheme, all exchanged messages include timestamps and random nonces that are changed every session. If $\mathcal{A}$ obtains messages $\{PI{D}_i,M_1,V_1,T_V\}$ and $\{PI{D}_i,I{D}_j,M_1,$$V_2,T_V,T_R\}$ on a public channel, $\mathcal{A}$ may try to process authentication by resending previous messages. However, $\mathcal{A}$ cannot obtain the messages at the previous session because it fails to check the freshness of random nonces $r_1,r_2$, and $r_3$, and timestamps $T_V,T_R,T_{TA}$, and $T_{RR}$. Therefore, the proposed scheme is secure against replay attacks.

7.1.12. DoS Attack

To make TA unusable, $\mathcal{A}$ can continuously attempt to issue fake request messages. However, according to Section 7.1.4 and Section 7.1.5, $\mathcal{A}$ has failed login attempts without knowing the vehicle’s real identity and password. If $\mathcal{A}$ constructs and sends message $\{PI{D}_i,I{D}_j,M_1,$$V_2,$$T_V,T_R\}$, TA firstly checks the verification of $V_2$ before performing further computations. According to Section 3.1, $\mathcal{A}$ can register as a legal user and send superfluous request message $\{PI{D}_i,M_1,V_1,T_V\}$. However, RSUs can detect it at the beginning of the authentication phase by checking the revocation list with $PI{D}_i$. Therefore, the proposed scheme prevents TA from performing cumbrous computation in such situations and reduces the chance of a DoS attack.

7.1.13. Anonymity

$I{D}_i$ is masked in parameters $HI{D}_i=I{D}_i\oplus h(K_{TA}\left|\right|I{D}_{TA})$, $A_i=(x||X_i)\oplus h(P{W}_i\left|\right|I{D}_i$$\left|\right|a)$, and $C_i=h(I{D}_i\left|\right|A_i)\oplus a$. In addition, the parameters $HI{D}_i$ is masked in parameters $PI{D}_i=HI{D}_i\oplus x$, $X_i=h(HI{D}_i\left|\right|K_{TA})$, and $V_{Li}=h(P{W}_i\left|\right|HI{D}_i\left|\right|X_i)$. Similarly, pseudo-identity $PI{D}_i$ is updated in each session: $PI{D}_i^{new}=PI{D}_i\oplus h(r_1\left|\right|HI{D}_i)$. Since $\mathcal{A}$ cannot calculate these parameters, our scheme provides anonymity.

7.1.14. Conditional Privacy

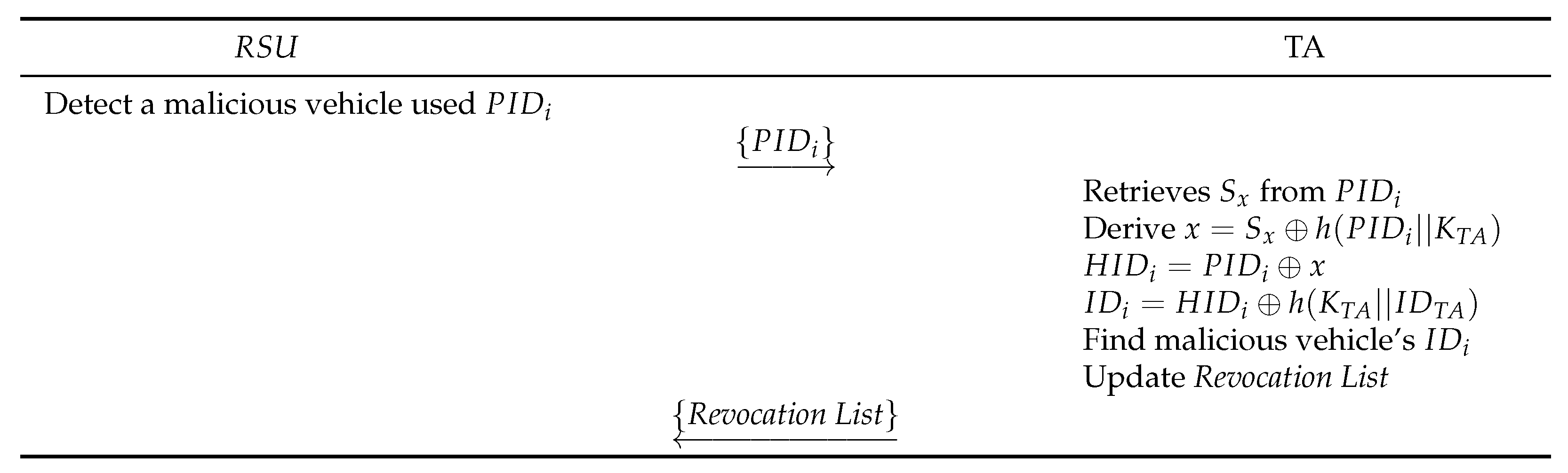
Only the TA can detect real $I{D}_i$ from $PI{D}_i$ when vehicles are involved in illegal activities. During the registration phase, the TA stores $PI{D}_i$ with secret parameter x. If a malicious vehicle used $PI{D}_i$, the TA retrieves $(S_x,PI{D}_i)$ in its secret database. To find the malicious vehicle’s real $I{D}_i$, the TA computes parameters $x=S_x\oplus h(PI{D}_i\left|\right|K_{TA})$, $HI{D}_i=PI{D}_i\oplus x$, and $I{D}_i=HI{D}_i\oplus h(K_{TA}\left|\right|I{D}_{TA})$. Due to the master key $K_{TA}$, only the TA can calculate these. Finally, the TA reveals the malicious vehicle’s real $I{D}_i$ and updates the revocation list. Thus, our scheme provides conditional privacy.

7.1.15. Mutual Authentication

To establish the authentication, our scheme performs a verification process. After $V_i$ inputs $I{D}_i$ and $P{W}_i$ into the OBU, the vehicle checks the equality of $V_{Li}^{\prime }=h(P{W}_i\left|\right|HI{D}_i\left|\right|X_i)$ and $V_{Li}$. If it is not equal, the login phase is terminated. The login request over the RSU is validated at the TA by checking if $V_2^{\prime }\stackrel{?}{=}{V}_2$. On the other hand, the RSU verifies $V_R^{\prime }\stackrel{?}{=}{V}_R$ and the vehicle checks $V_3^{\prime }\stackrel{?}{=}{V}_3$. In every verification process, the session is terminated immediately if a validation fails.

7.1.16. Perfect Forward Secrecy

If $\mathcal{A}$ obtains $K_{TA}$, $\mathcal{A}$ attempts to compute $SK=h(r_2|\left|r_3\right||r_1\oplus x)$ of a legitimate $V_i$. However, $K_{TA}$ is only used in the parameter $X_i=h(HI{D}_i\left|\right|K_{TA}),K_{R_{j}TA}=h(k_r\left|\right|I{D}_{TA}\left|\right|K_{TA})$. Moreover, $X_i$ and $K_{R_{j}TA}$ are not utilized indirectly, such as $V_2=h(V_1\left|\right|M_1\left|\right|I{D}_j\left|\right|K_{R_{j}TA}\left|\right|T_R)$, $V_V=h(r_2\left|\right|X_i\left|\right|r_1\left|\right|T_{TA})$ and $V_R=h(r_2\left|\right|I{D}_j\left|\right|K_{R_{j}TA}\left|\right|T_{TA})$. Even if $K_{TA}$ is leaked, $\mathcal{A}$ cannot obtain $SK$ without the shared secret parameters $HI{D}_i$ or $k_r$. Thus, the proposed scheme can achieve perfect forward secrecy.

7.2. BAN Logic

We utilize BAN logic [18], which is a logic proof method to ensure mutual authentication of the proposed scheme. Notations of BAN logic are presented in

Table 4. Notations of BAN logic.

Notations	Descriptions
$P_1,P_2$	Principals
$M_1,M_2$	Statements
$SK$	Session key
$P_1\mid \sim M_1$	$P_1$ once said $M_1$
$P_1\mid \equiv M_1$	$P_1$ believes $M_1$
$P_1⊲M_1$	$P_1$ receives $M_1$
$P_1\Rightarrow M_1$	$P_1$ controls $M_1$
$P_1\stackrel{K}{⟷}{P}_2$	$P_1$ and $P_2$ have shared key K
${\left\{M_1\right\}}_K$	$M_1$ is encrypted with K
$\#M_1$	$M_1$ is fresh

.

7.2.1. Rules

The five basic logical rules of BAN logic are summarized as follows.

1. Message meaning rule (MMR):

$${\displaystyle \frac{P_1\mid \equiv P_1\stackrel{K}{⟷}{P}_2,P_1⊲{\left\{M_1\right\}}_K}{P_1\mid \equiv P_2\mid \sim M_1}}$$

2. Nonce verification rule (NVR):

$${\displaystyle \frac{P_1\mid \equiv \#(M_1),P_1\mid \equiv P_2\mid \sim M_1}{P_1\mid \equiv P_2\mid \equiv M_1}}$$

3. Jurisdiction rule (JR):

$${\displaystyle \frac{P_1\mid \equiv P_2\Rightarrow M_1,P_1\mid \equiv P_2\mid \equiv M_1}{P_1\mid \equiv M_1}}$$

4. Belief rule (BR):

$${\displaystyle \frac{P_1\mid \equiv (M_1,M_2)}{P_1\mid \equiv M_1}}$$

5. Freshness rule (FR):

$${\displaystyle \frac{P_1\mid \equiv \#(M_1)}{P_1\mid \equiv \#(M_1,M_2)}}$$

7.2.2. Goals

We denote that principals of the vehicle, RSU, and TA are $V_i$, $RS{U}_j$, and $TA$, respectively. The goals of the proposed scheme describe $V_i$ and $RS{U}_j$ establish a session key, as shown as below:

$Goal1$:

$V_i\mid \equiv V_i\stackrel{SK}{⟷}RS{U}_j$

$Goal2$:

$V_i\mid \equiv RS{U}_j\mid \equiv V_i\stackrel{SK}{⟷}RS{U}_j$

$Goal3$:

$RS{U}_j\mid \equiv V_i\stackrel{SK}{⟷}RS{U}_j$

$Goal4$:

$RS{U}_j\mid \equiv V_i\mid \equiv V_i\stackrel{SK}{⟷}RS{U}_j$

7.2.3. Idealized Forms

Messages of the proposed scheme are formed to show the logical properties of BAN logic. The idealized forms are as follows:

$Ms{g}_1$:

$V_i\to RS{U}_j:{\{r_1,T_V\}}_x$

$Ms{g}_2$:

$RS{U}_j\to TA:{\{V_i\mid \sim {\{r_1,T_V\}}_x,T_R\}}_{K_{R_{j}TA}}$

$Ms{g}_3$:

$TA\to RS{U}_j:{\{r_1\oplus x,r_2,T_{TA}\}}_{K_{R_{j}TA}}$

$Ms{g}_4$:

$RS{U}_j\to V_i:{\{r_2,r_3,T_{RR}\}}_{r_1\oplus x}$

7.2.4. Assumptions

Each principal trusts that secret keys are shared and that timestamps are fresh. The proposed scheme applies the following assumptions in BAN logic proof:

$A_1$:

$V_i\mid \equiv \#(T_{RR})$

$A_2$:

$TA\mid \equiv \#(T_V)$

$A_3$:

$TA\mid \equiv \#(T_R)$

$A_4$:

$RS{U}_j\mid \equiv \#(T_{TA})$

$A_5$:

$TA\mid \equiv TA\stackrel{K_{R_{j}TA}}{⟷}RS{U}_j$

$A_6$:

$RS{U}_j\mid \equiv TA\stackrel{K_{R_{j}TA}}{⟷}RS{U}_j$

$A_7$:

$V_i\mid \equiv TA\stackrel{x}{⟷}{V}_i$

$A_8$:

$TA\mid \equiv TA\stackrel{x}{⟷}{V}_i$

$A_9$:

$V_i\mid \equiv RS{U}_j\Rightarrow (V_i\stackrel{SK}{⟷}RS{U}_j)$

$A_{10}$:

$RS{U}_j\mid \equiv V_i\Rightarrow (V_i\stackrel{SK}{⟷}RS{U}_j)$

$A_{11}$:

$V_i\mid \equiv V_i\stackrel{r_1\oplus x}{⟷}RS{U}_j$

7.2.5. BAN Logic Proof

The proceedings of BAN logic analysis to the proposed scheme are as follows:

Step 1:

According to $Ms{g}_2$, we can obtain $S_1$.

$$S_1:TA⊲{\{V_i\mid \sim {\{r_1,T_V\}}_x,T_R\}}_{K_{R_{j}TA}}$$

Step 2:

From the MMR using $A_5$ and $S_1$, we can obtain $S_2$.

$$S_2:TA\mid \equiv RS{U}_j\mid \sim (V_i\mid \sim {\{r_1,T_V\}}_x,T_R)$$

Step 3:

From $Ms{g}_1$, $TA$ believes that ${\{r_1,T_V\}}_x$ is sent from $V_i$ in $S_2$. Then, we can obtain $S_3$.

$$S_3:TA⊲{\{r_1,T_V\}}_x$$

Step 4:

From the MMR using $A_8$ and $S_3$, we can obtain $S_4$.

$$S_4:TA\mid \equiv V_i\mid \sim (r_1,T_V)$$

Step 5:

From the FR using $A_2$ and $S_4$, we can obtain $S_5$.

$$S_5:TA\mid \equiv \#(r_1,T_V)$$

Step 6:

From the NVR using $S_4$ and $S_5$, we can obtain $S_6$.

$$S_6:TA\mid \equiv V_i\mid \equiv (r_1,T_V)$$

Step 7:

According to $Ms{g}_3$, we can obtain $S_7$.

$$S_7:RS{U}_j⊲{\{r_1\oplus x,r_2,T_{TA}\}}_{K_{R_{j}TA}}$$

Step 8:

From the MMR using $A_6$ and $S_7$, we can obtain $S_8$.

$$S_8:RS{U}_j\mid \equiv TA\mid \sim (r_1\oplus x,r_2,T_{TA})$$

Step 9:

From the FR using $A_4$ and $S_8$, we can obtain $S_9$.

$$S_9:RS{U}_j\mid \equiv \#(r_1\oplus x,r_2,T_{TA})$$

Step 10:

From the NVR, we can obtain $S_{10}$.

$$S_{10}:RS{U}_j\mid \equiv TA\mid \equiv (r_1\oplus x,r_2,T_{TA})$$

Step 11:

According to $Ms{g}_4$, we can obtain $S_{11}$.

$$S_{11}:V_i⊲{\{r_2,r_3,T_{RR}\}}_{r_1\oplus x}$$

Step 12:

From the MMR using $A_{11}$, we can obtain $S_{12}$.

$$S_{12}:V_i\mid \equiv RS{U}_j\mid \sim (r_2,r_3,T_{RR})$$

Step 13:

From the FR using $A_1$, we can obtain $S_{13}$.

$$S_{13}:V_i\mid \equiv \#(r_2,r_3,T_{RR})$$

Step 14:

From the NVR using $S_{12}$ and $S_{13}$, we can obtain $S_{14}$.

$$S_{14}:V_i\mid \equiv RS{U}_j\mid \equiv (r_2,r_3,T_{RR})$$

Step 15:

$V_i$ and $RS{U}_j$ believe that they can compute the session key $SK=h(r_2|\left|r_3\right||r_1\oplus x)$ using the shared values with each other. Therefore, we can obtain $S_{15}$ and $S_{16}$ from $S_{10}$ and $S_{14}$.

$$\begin{array}{c}\hfill S_{15}:V_i\mid \equiv RS{U}_j\mid \equiv V_i\stackrel{SK}{⟷}RS{U}_j\mathbf{(}\mathbf{Goal}\mathbf{2}\mathbf{)}\\ \hfill S_{16}:RS{U}_j\mid \equiv V_i\mid \equiv V_i\stackrel{SK}{⟷}RS{U}_j(\mathbf{Goal}\mathbf{4})\end{array}$$

Step 16:

From the JR using $A_9$, $A_{10}$, $S_{15}$, and $S_{16}$, we can obtain $S_{17}$ and $S_{18}$.

$$\begin{array}{c}\hfill S_{17}:V_i\mid \equiv V_i\stackrel{SK}{⟷}RS{U}_j(\mathbf{Goal}\mathbf{1})\\ \hfill S_{18}:RS{U}_j\mid \equiv V_i\stackrel{SK}{⟷}RS{U}_j(\mathbf{Goal}\mathbf{3})\end{array}$$

7.3. ROR Model

We utilize the ROR model [19] to analyze the semantic security of the proposed scheme. In this model, we denote ${\mathcal{P}}^t$ as the $t^{th}$ instances of participants. There are three participants in the proposed scheme, which are vehicle ${\mathcal{P}}_V^{t_1}$, RSU ${\mathcal{P}}_{RSU}^{t_2}$, and TA ${\mathcal{P}}_{TA}^{t_3}$. The ROR model assumes that an adversary $\mathcal{A}$ can perform various attacks to disclose the session key by executing queries, such as Execute, CorruptOBU, Send, and Test. Moreover, all participants, including $\mathcal{A}$, can access a collision-resistant cryptographic one-way hash function $H(·)$, which is said as $Hash$ [38]. The detailed description of queries is as below.

• Execute(${\mathcal{P}}_V^{t_1}$, ${\mathcal{P}}_{RSU}^{t_2}$, ${\mathcal{P}}_{TA}^{t_3}$): $\mathcal{A}$ can eavesdrop the transmitted messages between ${\mathcal{P}}_V^{t_1}$, ${\mathcal{P}}_{RSU}^{t_2}$, and ${\mathcal{P}}_{TA}^{t_3}$ via public channel. This query represents the eavesdropping attack by $\mathcal{A}$.
• CorruptOBU(${\mathcal{P}}^t$): $\mathcal{A}$ performs this query to extract the stored data from the OBU of $V_i$.
• Send(${\mathcal{P}}^t$, Msg): Using this query, $\mathcal{A}$ can send a message $Msg$ to the participant ${\mathcal{P}}^t$ and receive a reply.
• Test(${\mathcal{P}}^t$): $\mathcal{A}$ uses this query to verify the semantic security of the session key. By executing this query, $\mathcal{A}$ can obtain a coin flip test, where $c=0$ represents the tail of a coin and $c=1$ represents the head of a coin. Based on the result, $\mathcal{A}$ receives a random string when $c=0$ and the session key when $c=1$ from ${\mathcal{P}}^t$. Otherwise, $\mathcal{A}$ receives a $NULL$ value. If $\mathcal{A}$ cannot distinguish the result between a random string and the session key, the session key is secure.

Theorem 1.

Suppose that $\mathcal{A}$ attempts to distinguish the session key and a random number. We denote $Ad{v}_{\mathcal{A}}$ as the advantage of $\mathcal{A}$ in the model. Then, $q_h$ and $q_s$ denote the number of $Hash$ and $Send$ queries executed by $\mathcal{A}$, and $\left|Hash\right|$ is the range of the $Hash$. $D_1$ and $D_2$ are the distributed identity and password dictionaries, and $|D_1|$ and $|D_2|$ are the size of each dictionary.

$$Ad{v}_{\mathcal{A}}\le {\displaystyle \frac{q_h^2}{\left|Hash\right|}}+{\displaystyle \frac{2q_s}{|D_1|·|D_2|}}$$

(1)

Proof. 

$\mathcal{A}$ can perform the attack procedures through four games $G_i(i=0,1,2,3)$. $Pr\left[Suc{c}_i\right]$ denotes the probability that $\mathcal{A}$ guesses the correct result c in $G_i$. The proof processes of $G_i$ and $Suc{c}_i$ are described as follows:

$G_0$: This game represents that $\mathcal{A}$ attempts the actual attack on the proposed authentication schemes. Then, $\mathcal{A}$ can guess a random bit c at the beginning of the game and hence the outcome is the following Equation (2).

$$Ad{v}_{\mathcal{A}}=|2Pr\left[Suc{c}_0\right]-1|$$

(2)

$G_1$: $\mathcal{A}$ performs $Execute$ query to attempt the eavesdropping attack. After that, $\mathcal{A}$ verifies whether the obtained session key $SK$ and a random number are real by executing $Test$ query. However, $\mathcal{A}$ cannot obtain meaningful parameters using an eavesdropping attack to calculate the session key $SK=h(r_2|\left|r_3\right||r_1\oplus x)$. This means $\mathcal{A}$ cannot obtain any advantage from winning $G_1$. Therefore, $G_1$ and $G_0$ are indistinguishable, and we obtain the following:

$$Pr\left[Suc{c}_1\right]=Pr\left[Suc{c}_0\right]$$

(3)

$G_2$: In this game, $\mathcal{A}$ performs $Send$ and $Hash$ queries to obtain the session key. $\mathcal{A}$ can attempt to modify transmitted messages. However, deriving secret parameters from the intercepted messages is a computationally infeasible task. It’s because all exchanged messages in our scheme are encrypted with one-way hash function $H(·)$, which has collision-resistant properties. According to [39], the birthday paradox represents the probability of hash collision as $(q_h^2/2^{l_h+1})$, where $l_h$ is the length of a hash result. Thus, we can obtain the advantage of $\mathcal{A}$ in $G_2$ as below.

$$|Pr\left[Suc{c}_2\right]-Pr\left[Suc{c}_1\right]|\le {\displaystyle \frac{q_h^2}{2\left|Hash\right|}}$$

(4)

$G_3$: $\mathcal{A}$ can try to obtain $SK=h(r_2|\left|r_3\right||r_1\oplus x)$ with $CorruptOBU$. $\mathcal{A}$ can obtain the information $\{PI{D}_i,XP{W}_i,V_i,A_i,C_i\}$. However, $\mathcal{A}$ needs $X_i$ which is masked with $I{D}_i$ and $P{W}_i$. Therefore, $\mathcal{A}$ can try to guess the values from identity and password dictionaries. Basically, the length of identity is 160 bits. As the length of a password increases, the probability that $\mathcal{A}$ correctly guesses both identity and password decreases exponentially. The whole combinations of dictionaries $|D_1|·|D_2|$ are roughly $2^{160}·2^{l_{PW}}$, where $l_{PW}$ is the length of the password. Then, we can obtain the following:

$$|Pr\left[Suc{c}_3\right]-Pr\left[Suc{c}_2\right]|\le {\displaystyle \frac{q_s}{|D_1|·|D_2|}}$$

(5)

As all the games are executed, $\mathcal{A}$ must guess the exact bit c. However, $\mathcal{A}$ has no advantage to guess c; then, we can obtain the below equation.

$$Pr\left[Suc{c}_3\right]={\displaystyle \frac{1}{2}}$$

(6)

Using Equations (2), (3), and (6), we can obtain the result as below:

$$\begin{array}{cc}\hfill \phantom{{\displaystyle \frac{1}{2}}Ad{v}_{\mathcal{A}}}& \begin{array}{cc}\hfill {\displaystyle \frac{1}{2}}Ad{v}_{\mathcal{A}}& =|Pr\left[Suc{c}_0\right]-{\displaystyle \frac{1}{2}}|\hfill \\ \hfill & =|Pr\left[Suc{c}_1\right]-Pr\left[Suc{c}_3\right]|\hfill \end{array}\hfill \end{array}$$

(7)

We obtain the following result by applying the triangular inequality to Equation (7):

$$\begin{array}{cc}\hfill \phantom{{\displaystyle \frac{1}{2}}Ad{v}_{\mathcal{A}}}& \begin{array}{cc}\hfill {\displaystyle \frac{1}{2}}Ad{v}_{\mathcal{A}}& =|Pr\left[Suc{c}_1\right]-Pr\left[Suc{c}_3\right]|\hfill \\ \hfill & \le |Pr\left[Suc{c}_1\right]-Pr\left[Suc{c}_2\right]|+|Pr\left[Suc{c}_2\right]-Pr\left[Suc{c}_3\right]|\hfill \\ \hfill & \le {\displaystyle \frac{q_h^2}{2\left|Hash\right|}}+{\displaystyle \frac{q_s}{|D_1|·|D_2|}}\hfill \end{array}\hfill \end{array}$$

(8)

Finally, we obtain the required result by multiplying both sides of Equation (8) by 2.

$$Ad{v}_{\mathcal{A}}\le {\displaystyle \frac{q_h^2}{\left|Hash\right|}}+{\displaystyle \frac{2q_s}{|D_1|·|D_2|}}$$

(9)

Therefore, we prove Theorem 1.

□

7.4. AVISPA Simulation

In this section, we analyze the security of the proposed scheme using the AVISPA simulation tool [20,21]. AVISPA has been widely accepted to evaluate the resistance against MitM and replay attacks [40,41]. To conduct an AVISPA analysis, the proposed scheme needs to be written in “High-Level Protocol Specification Language (HLPSL)”. To implement a protocol, HLPSL codes are converted to “Intermediate Format (IF)” by the translator. From the IF code, through the backends model, the outputs come out in “Output Format (OF)”. There are four backend modela, “On-the-Fly Model Checker (OFMC)”, “Constraint Logic-based Attack Searcher (CL-AtSe)”, “Tree Automata based on Automatic Approximations for Analysis of Security Protocol (TA4SP)”, and “SAT-based Model Checker (SATMC)”. In this analysis, we use the OFMC and CL-AtSe models, which supply XOR operation. If the summary of OF is safe, we demonstrate that the proposed scheme resists MitM and replay attacks.

7.4.1. HLPSL Specification

Based on HLPSL, the proposed scheme is divided into three roles: $V_i$, $RS{U}_j$, and the $TA$. “V” denotes a vehicle $V_i$, “R” denotes a roadside unit $RS{U}_j$, and “TA” denotes a trusted authority $TA$. Figure 9 comprises the environment and session of our scheme, which represents the security goals. Figure 10 describes the role of $V_i$ and the detailed descriptions are as follows.

At first, $V_i$ initializes the state (State = 0) and receives the start signal. During the registration phase, $V_i$ sends the registration request message $\left\{I{D}_i\right\}$ to the TA securely. Then, $V_i$ receives the reply from the TA through secure channel $(SKvta)$ and updates its state from 1 to 2. After the registration phase, $V_i$ generates random nonce $R{1}^{\prime }$ and timestamps $T{v}^{\prime }$, and calculates parameters to send the authentication request message via public $channel(dy)$. Then, $V_i$ declares $witness(V,TA,v\_ta\_r1,R{1}^{\prime })$, which means that $V_i$ generates random nonce $R1$ for TA. Finally, $V_i$ computes a session key and completes authentication with $RS{U}_j$ in state 3. Similarly, the specification roles of $RS{U}_j$ and the TA are like that of $V_i$. Their registration and authentication phases are defined as shown in Figure 11 and Figure 12.

7.4.2. AVISPA Simulation Result

Figure 13 shows the AVISPA simulation results under OFMC and CL-AtSe models. In OFMC, the search time takes 2.78 s to visit 1168 nodes. On the other hand, the CL-AtSe analyzed two states with 0.04 s to translate. The summary of results is safe; therefore, the proposed scheme is verified regarding the security resistance to replay and MitM attacks.

8. Performance Evaluations

This section discusses the performance of our scheme in terms of security properties, computational costs, communication costs, and energy consumption. We demonstrated that our scheme provides overall better results of performance analyses compared with other related schemes.

8.1. Security Properties

This section presents the security properties of our scheme compared with these related schemes, [17,25,26,27,28,31,32]. We consider security properties such as $S1$: “resistance to insider attack”, $S2$: “resistance to OBU captured attack”, $S3$: “resistance to privileged insider attack”, $S4$: “resistance to offline password guessing attack”, $S5$: "resistance to identity-guessing attack”, $S6$: “resistance to vehicle impersonation attack”, $S7$: “resistance to ESL attack”, $S8$: “resistance to MitM attack”, $S9$: “resistance to forgery attack”, $S10$: “resistance to desynchronization attack”, $S11$: “resistance to replay attack”, $S12$: “resistance to DoS attack”, $S13$: “anonymity”, $S14$: “conditional privacy”, $S15$: “mutual authentication”, and $S16$: “perfect forward secrecy”. Compared with the related schemes [17,25,26,27,28,31,32], the proposed scheme provides robust security and functional properties. As seen in

Table 5. Security properties.

	[25]	[26]	[27]	[28]	[31]	[32]	[17]	Proposed
$S1$	×	-	-	-	-	-	×	∘
$S2$	×	×	×	-	-	-	∘	∘
$S3$	×	∘	-	-	-	-	∘	∘
$S4$	-	-	×	∘	-	-	∘	∘
$S5$	-	×	-	-	×	-	∘	∘
$S6$	×	×	∘	×	-	∘	∘	∘
$S7$	-	∘	×	-	×	-	×	∘
$S8$	-	-	×	×	-	∘	∘	∘
$S9$	-	-	∘	-	-	-	∘	∘
$S10$	×	∘	-	-	-	-	∘	∘
$S11$	∘	∘	-	×	×	∘	∘	∘
$S12$	-	∘	-	-	∘	∘	-	∘
$S13$	∘	∘	∘	∘	-	∘	∘	∘
$S14$	-	-	-	∘	×	-	×	∘
$S15$	-	∘	-	∘	∘	∘	∘	∘
$S16$	×	×	-	×	-	-	×	∘

-: not considered; ×: Not supported; ∘: Supported.

, the proposed scheme is secure against various attacks and possesses a higher level of security.

8.2. Computational Costs

We analyze the computational costs of our scheme and related schemes [17,25,26,27,28,29,30,31,32]. According to [17], we approximate the execution time of each cryptographic operation. The implementation environment was Windows 10, Professional with an Intel (R) Core (TM) i5-4210U 64-bit, 8 GB DDR4, @4.1 GHz. Moreover, the programming language and library are Python and Pycryptodome cryptographic library, respectively.

The execution times of operations are summarized in

Table 6. Cryptographic execution time (ms).

Operation	Time (ms)
$T_B$: Bilinear pairing	33.75
$T_M$: Elliptic curve point multiplication	15.65
$T_A$: Elliptic curve point addition	4.26
$T_H$: One-way hash function	0.35
$T_S$: Symmetric encryption/decryption	1.27
$T_E$: Modular exponential	18.78

. We estimate that $T_B$, $T_M$, $T_A$, $T_H$, $T_S$, and $T_E$ are the time durations of bilinear pairing (33.75 ms), elliptic curve point (ECP) multiplication (15.65 ms), ECP addition (4.26 ms), one-way hashing (0.35 ms), symmetric key encryption/decryption (1.27 ms), and modular exponential (18.78 ms). Since the execution time of XOR operations is very small and negligible, we do not consider the computational cost of XOR operations.

In IoV networks, it is important to reduce overloads during the authentication phase. We calculate the costs required for each entity, such as $V_i$, $RS{U}_j$, and the TA.

Table 7. Total computational costs.

Scheme	Operations	Total Cost (ms)
Xu et al. [25]	$28T_H$	9.80
Kumar et al. [26]	$26T_H+4T_S$	14.18
Zhong et al. [27]	$8T_M+23T_H$	133.25
Cui et al. [28]	$8T_M+25T_H$	133.95
Awais et al. [29]	$15T_M+20T_H$	241.75
Kumar et al. [30]	$12T_M+20T_H+6T_S$	202.42
Chen et al. [31]	$12T_H+2T_S+6T_E$	119.42
Chaudhry [32]	$11T_H+12T_S$	19.09
Sibahee et al. [17]	$30T_H$	10.50
Proposed	$28T_H$	9.80

represents that our scheme has the lowest computational costs compared with related schemes. Consequently, the proposed scheme ensures high efficiency in IoV networks compared with the related schemes [17,25,26,27,28,31,32]. Moreover, the proposed scheme can provide lower computational overheads than recent studies [29,30] due to using only hash functions and XOR operators.

8.3. Communication Costs

According to [17], we assume that the communication costs of the elliptic curve point, hash function, random nonces, real identity, and timestamp are 320, 160, 160, 32, and 32 bits, respectively. Since the registration phase occurs once for new registrants, we only consider the costs of exchanged messages during the authentication phase. In our scheme, four messages are exchanged in total during the authentication phases, which are $\{PI{D}_i,M_1,V_1,T_V\}$, $\{PI{D}_i,I{D}_j,M_1,V_2,T_V,T_R\}$, $\{M_2,V_R,V_V,T_{TA}\}$, and $\{M_3,V_3,T_{TA},T_{RR}\}$. The costs of the four messages are 512, 576, 672, and 544 bits. On the other hand, the costs are 576, 544, 512, and 512 bits, respectively, in Sibahee et al.’s scheme. The overall communication cost of Sibahee et al.’s scheme [17] is 2144 bits, while ours is 2304, which is 160 bits more. However, our scheme provides better security properties and computational costs than [17]. Moreover, the communication cost of our scheme is still lower compared with the other schemes [25,26,27,28,29,30,31,32]. Based on the values in

Table 8. Total communication costs.

Scheme	No. of Messages	Total Cost (bits)
Xu et al. [25]	6	3328
Kumar et al. [26]	4	4224
Zhong et al. [27]	4	3840
Cui et al. [28]	5	3328
Awais et al. [29]	4	4320
Kumar et al. [30]	5	3488
Chen et al. [31]	4	2336
Chaudhry [32]	4	2912
Sibahee et al. [17]	4	2144
Proposed	4	2304

, the communication cost analysis of each scheme is as follows:

8.4. Energy Consumption

During the message exchange, some energy is consumed to communicate between vehicles and RSUs. Since vehicles equipped with OBUs have limited resources, the high energy consumption has the potential to affect low performance. As explained in [17], energy consumption is the product of total computational costs ($TC$) and maximum processing power ($MP$). Therefore, the equation of energy consumption $E_C$ can be represented as follows:

$$\begin{array}{c}\hfill E_C=TC\times MP\end{array}$$

According to [17], this maximum processing power is 10.88 W in wireless communication systems. Therefore, the total energy consumption of our scheme is 106.62 mJ, rounding to the nearest hundredth. The results of the energy consumption comparison are shown in

Table 9. Comparison study of energy consumption.

Scheme	Energy Consumption (mJ)
Xu et al. [25]	106.62
Kumar et al. [26]	154.28
Zhong et al. [27]	1449.76
Cui et al. [28]	1457.38
Awais et al. [29]	2630.24
Kumar et al. [30]	2202.33
Chen et al. [31]	1299.29
Chaudhry [32]	207.70
Sibahee et al. [17]	114.24
Proposed	106.62

. Compared with the related schemes [25,26,27,28,29,30,31,32], we can demonstrate that the proposed scheme has the lowest energy consumption. Therefore, the proposed scheme can extend the battery life of vehicles when deployed in IoV.

9. Conclusions

In this paper, we analyzed the scheme proposed by Sibahee et al. [17] and then proved its security weaknesses, such as insider and ESL attacks. Furthermore, we demonstrated that their scheme fails to ensure perfect forward secrecy. To address these security issues, we designed an anonymous and efficient authentication scheme with conditional privacy-preserving features. The proposed scheme effectively resists various attacks, such as OBU capture, privileged insider attacks, offline password guessing, and impersonation attacks. By using BAN logic and the ROR model, which is a formal analysis, we proved the mutual authentication and session key security of our scheme. Moreover, we executed an AVISPA simulation to show the resistance against replay and MitM attacks in our scheme. The performance evaluation demonstrated that our scheme offers better security properties than existing schemes. In terms of computational costs, our scheme is lightweight and uses only the XOR operations and hash functions. Furthermore, the proposed scheme guarantees a conditional privacy-preserving feature that allows the identification and revocation of malicious vehicles without exposing the privacy of legitimate users. Thus, the proposed scheme is applicable for practical IoV networks because it is more secure and efficient than existing related schemes. For instance, the proposed scheme enables secure communications between vehicles and infrastructure, exchanging real-time data such as traffic light statuses and road conditions from the traffic management center. This can improve traffic flow, optimize signal timing, and provide instant emergency alerts, enhancing overall road safety and efficiency. In future work, we will develop an architectural framework and authentication mechanisms that extend the proposed scheme to support V2V communications within IoV networks.