Iterative Optimization RCO: A “Ruler & Compass” Deterministic Method
Abstract
1. Introduction
| Algorithm | Stochastic | Evaluations/Run | Success Rate |
|---|---|---|---|
| CMA-ES [3] | yes | 10,000 | 0.12 |
| DE [4] | yes | 10,000 | 0.73 |
| ACO [5] | yes | 410 | 0.80 |
| 4010 | 0.94 | ||
| Jaya [6] | yes | 1000 | 0.985 |
| SPSO [7] | yes | 180 | 0 |
| 190 | 1 | ||
| GA-MPC [8] | yes | 80 | 0 |
| 90 | 1 | ||
| RCO | no | 20 | 1 |
2. RCO Principle
- If its position lies outside the search space (possibly at infinity), then the new position is determined by a barycenter of the previous positions. For the calculation of the barycenter, the weight of each position is inversely proportional to the value of the function at that position. See the detail in Appendix A.2.
- If its position is within the search space, then it is kept as the new position.
3. Examples
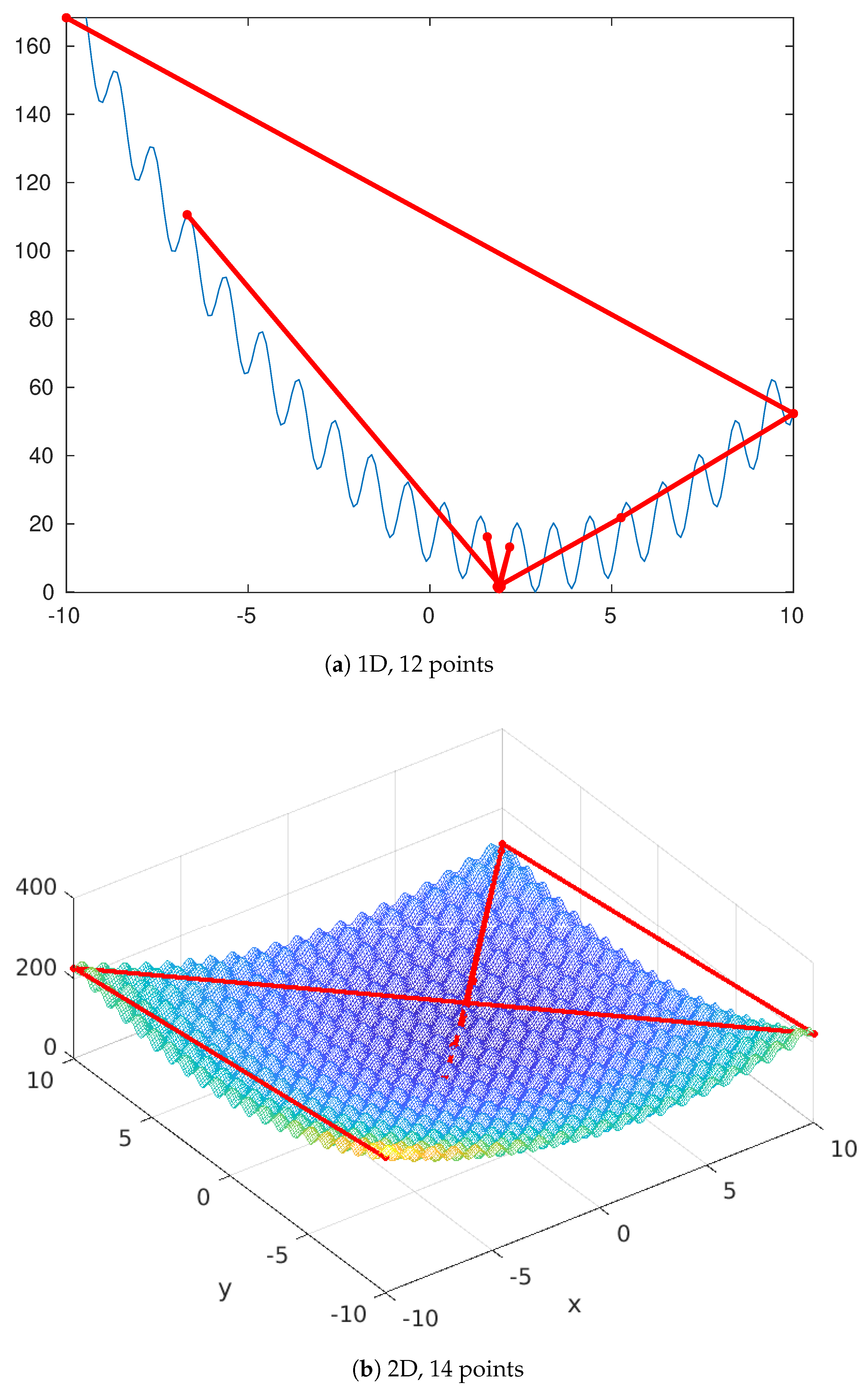
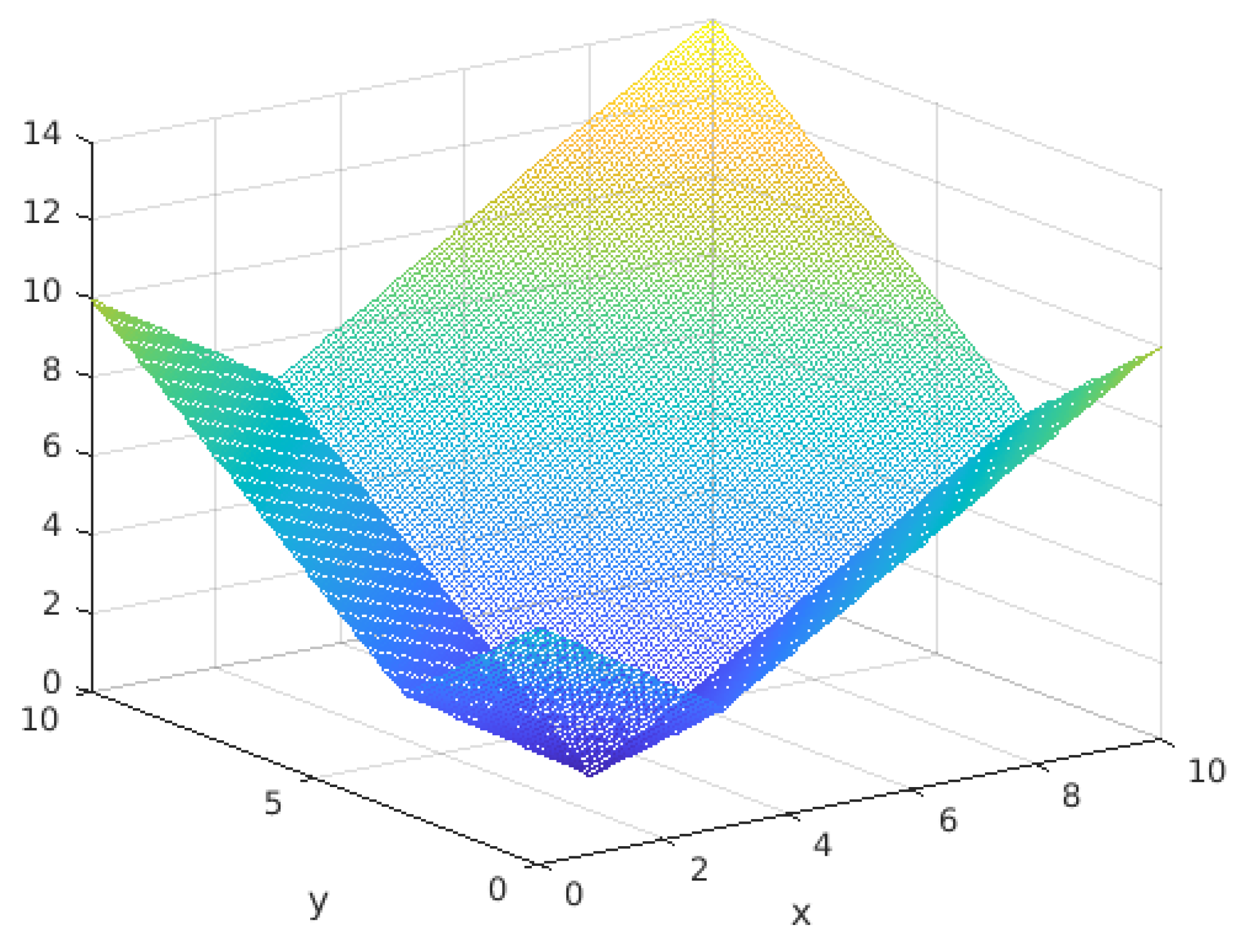
3.1. Six Hump Camel Back (Appendix A.7)
3.2. Shifted Rastrigin
3.3. Rosenbrock
3.4. Pressure Vessel
3.5. Gear Train
4. Comparison
5. Complexities
- Solving a linear system of D equations to determine a new position with D coordinates. The required space is , with a time complexity of .
- Computing a linear combination of positions, each with D coordinates. The required space is , and the number of multiplications is .
6. A Problem That RCO Cannot Solve
7. Conclusions and Future Works
- It requires a reasonably good lower bound. That said, compared to most other methods, this is the only user-defined parameter. In practice, for real-world problems, such a bound is often known. Moreover RCO is able to automatically define an adaptive lower bound (see Appendix A.5).
- It performs poorly on some problems, even in low dimensions, when the landscape is highly chaotic.
- It does not perform well on discrete problems, particularly when all variables are discrete. However, it still appears to be usable when only some of the variables are discrete.
- Its computation time per iteration increases exponentially with the dimension of the search space. Although it does not grow as quickly as theoretically predicted, in practice, it can still be challenging to use on a laptop for high-dimensional problems.
- As with many initial presentations of iterative optimization algorithms, such as Genetic Algorithm [13], Ant Colony Optimization [14], Particle Swarm Optimization [15], and Differential Evolution [16], among others, a formal convergence analysis has not yet been provided. Specifically, while it is clear that there is no explosion effect, as seen in the original PSO version [17], it would be beneficial to more precisely identify in which cases stagnation occurs and how it can be avoided. There is, in fact, an experimental RCO version that attempts to address the issue of stagnation, though it is not particularly convincing. For instance, in the case of the 10D Rosenbrock function (see Table 12), it finds a value of 2.3 instead of 8.996, which is still significantly worse than PSO ().
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. A Bit of Geometry
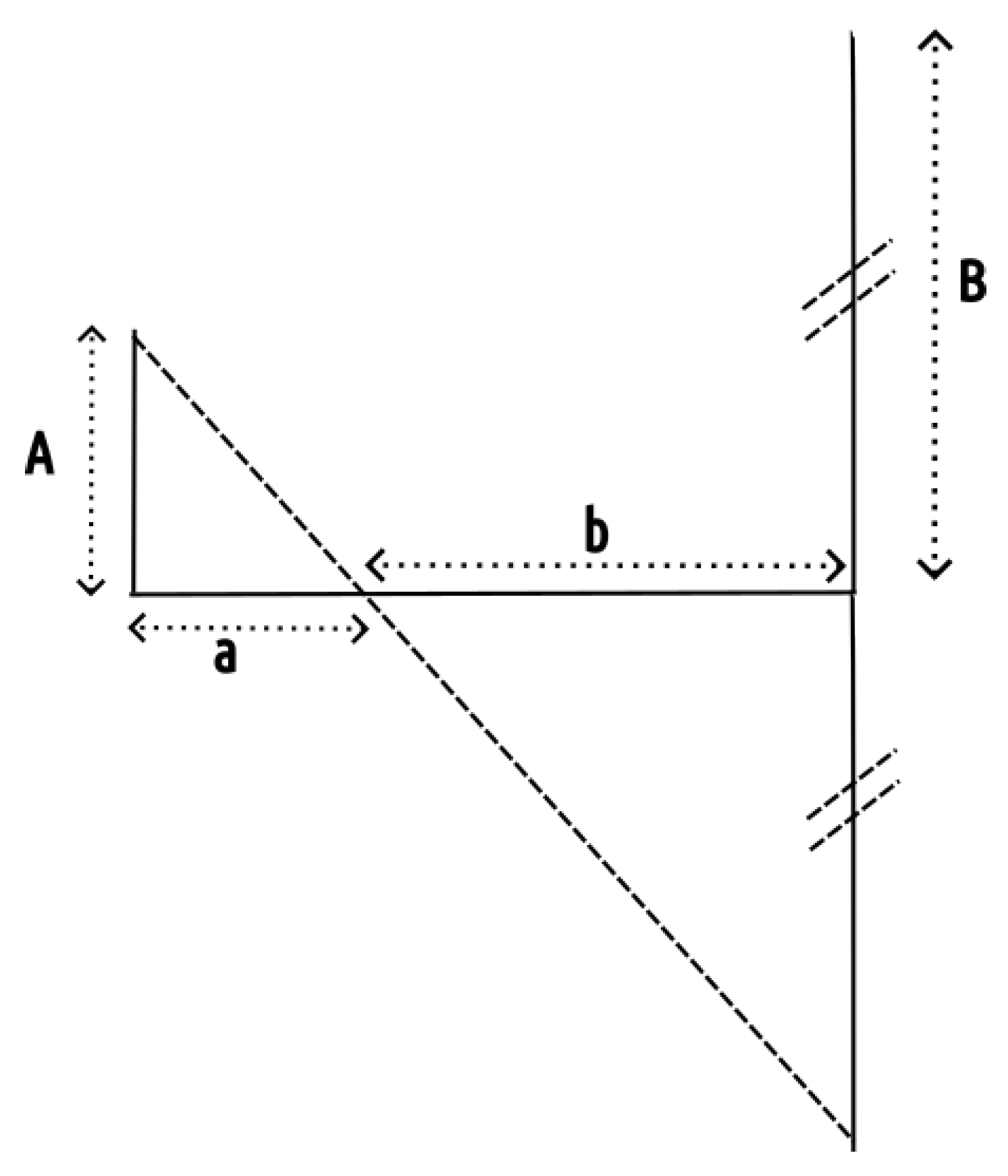
Appendix A.2. Barycenter
Appendix A.3. Number of Minima
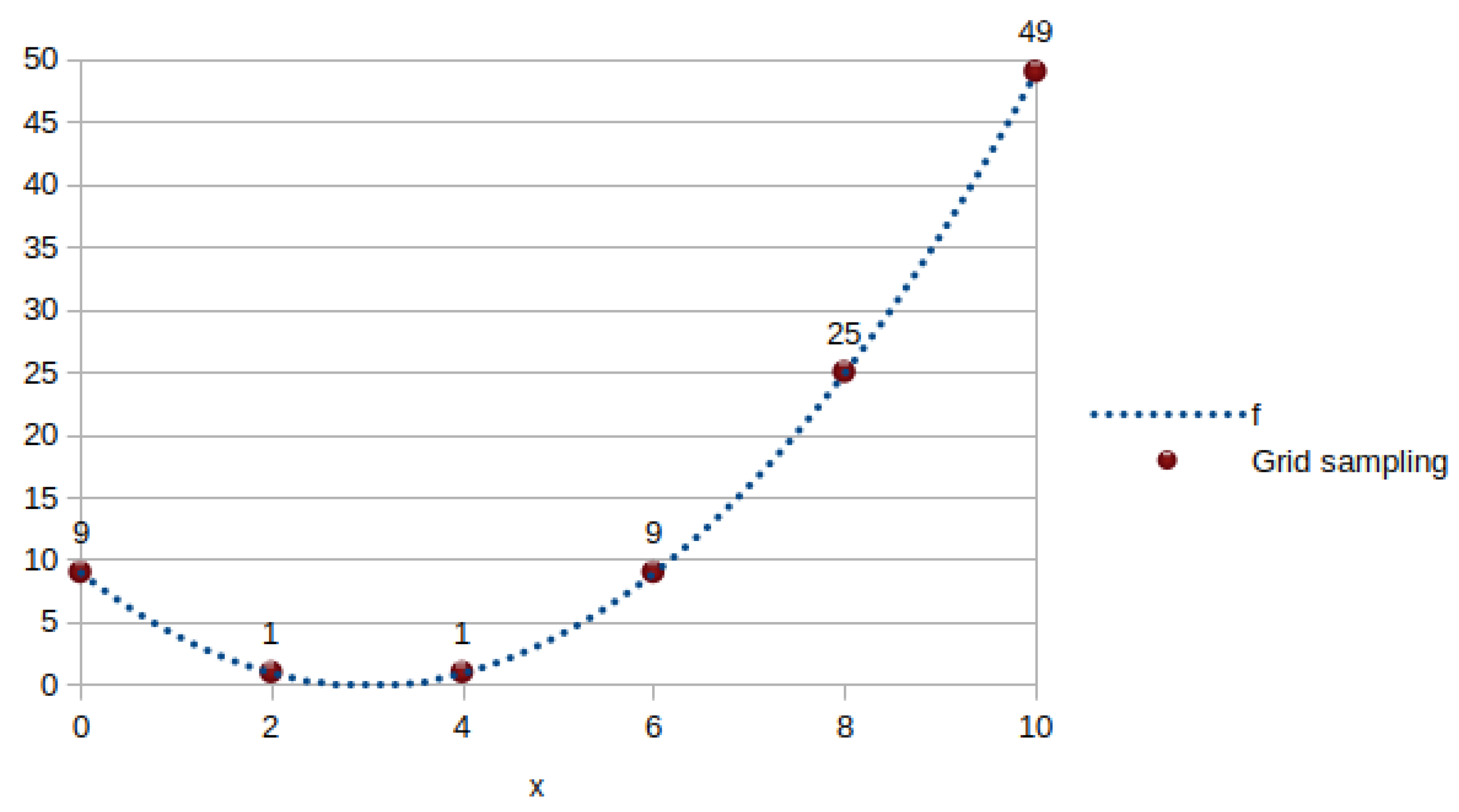
Appendix A.4. Difficulty Measures
| sinCos15 | Parabola | Six Hump Camel Back | Frequency Modulated Sound Waves | |
|---|---|---|---|---|
| Normalized roughness | 0.9643 | 0 | 0.3333 | >0.9999 |
| Tolerance threshold | 0.9996 | 0.9972 | 0.99997 | 1.0 |
| 0.4706 | 0.0711 | 0.6258 | 0.5263 |
Appendix A.5. About the Lower Bound
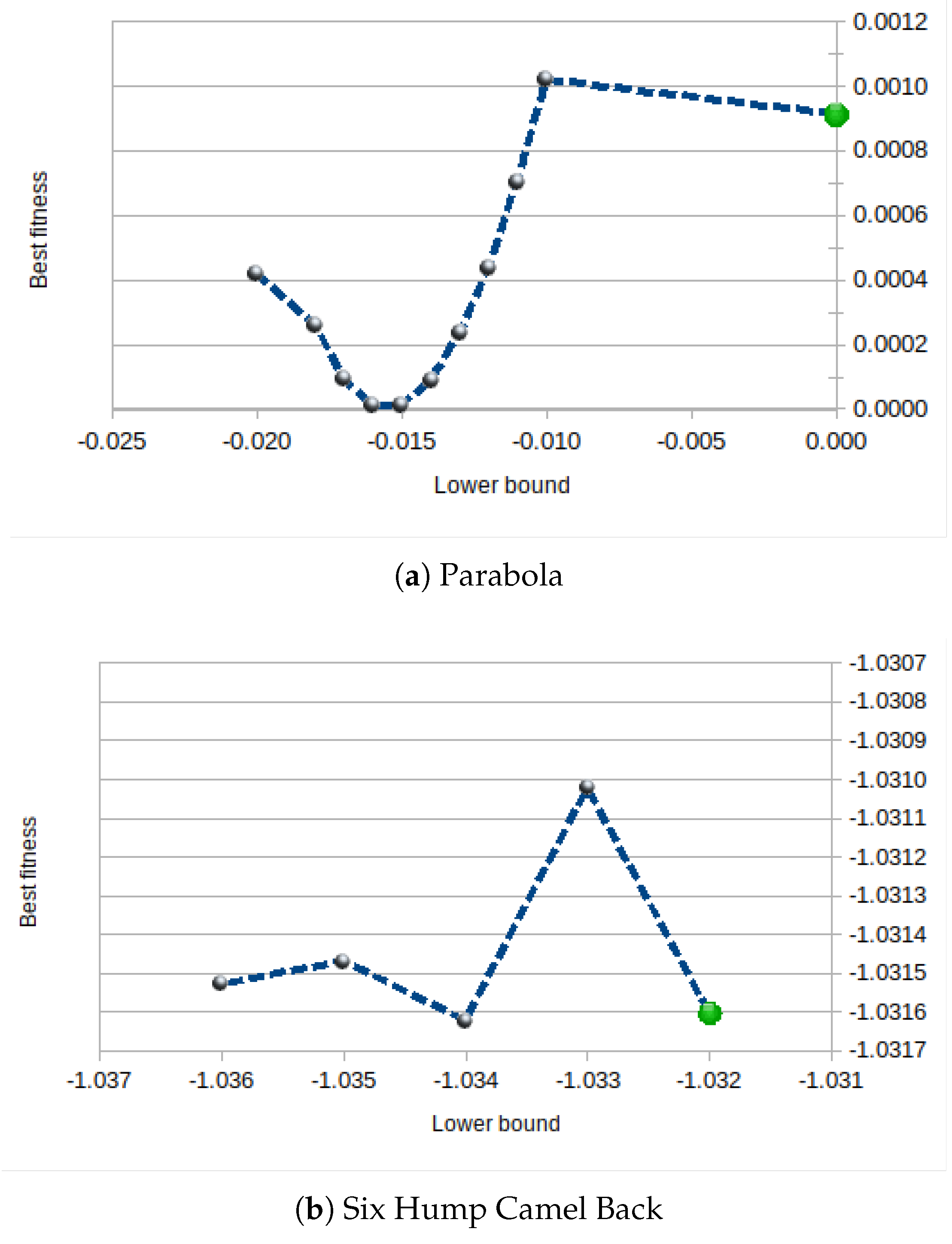
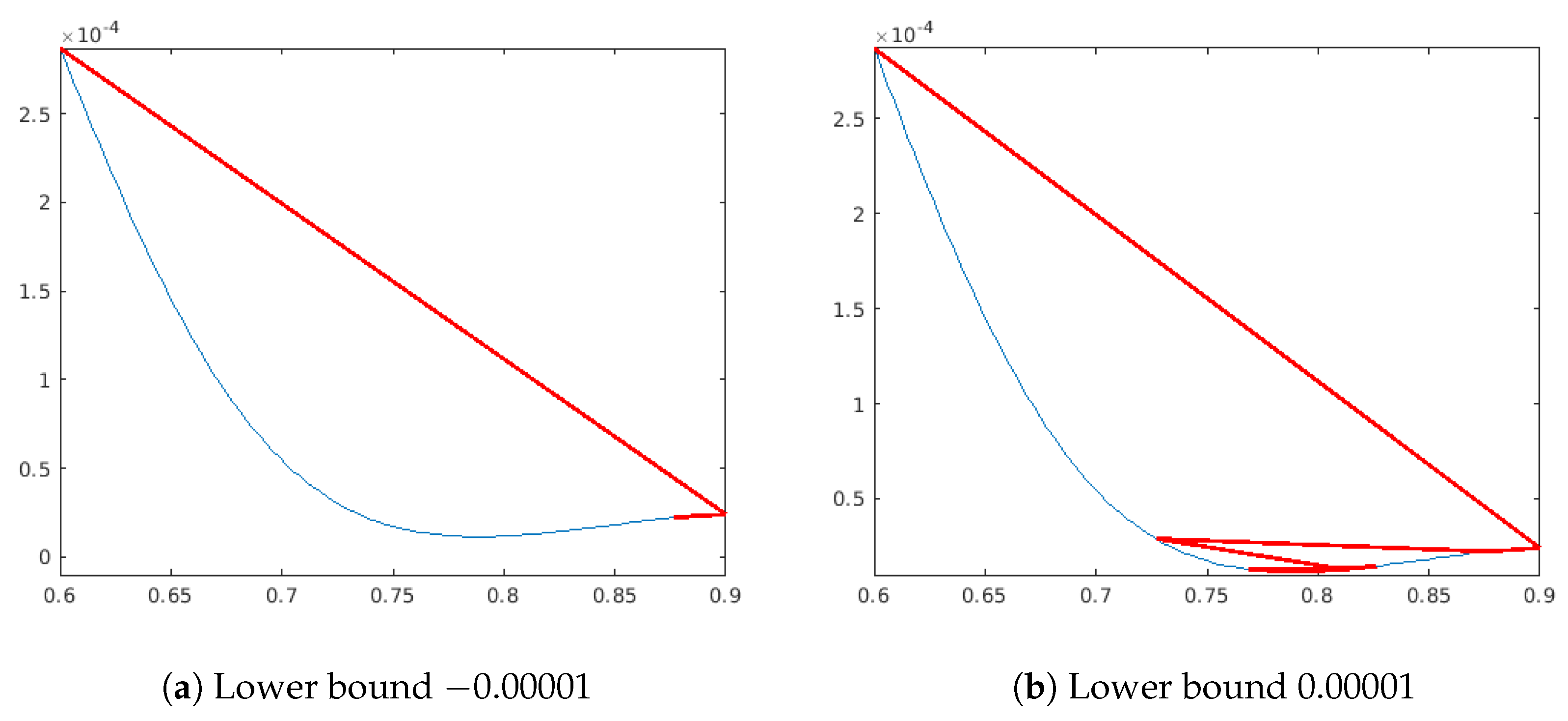
- if min_f>0 lower_bound=min_f*coeff; else lower_bound=min_f*(2-coeff);
| Dimension | Evaluations | Lower Bound | Non Adaptive | Adaptive Coeff. 0.5 | Adaptive Coeff. 0.1 | |
|---|---|---|---|---|---|---|
| Six Hump Camel Back | 2 | 104 | −1.1 | −1.031473 | −1.03157 | −0.947 |
| Shifted Rastrigin | 3 | 1508 | −0.1 | 0.002548 | 0.06729 | |
| 4 | 50,016 | −0.1 | 0.00173 | 0 | ||
| Rosenbrock | 3 | 1508 | −0.1 | 0.001 | 0.1866 | 0.238 |
| 4 | 10,016 | −0.1 | 0.003756 | |||
| Pressure Vessel | 4 | 6076 | 6000 | 6592 | 6955 | |
| Gear Train | 4 | 1753 | 0 |
Appendix A.6. More Examples

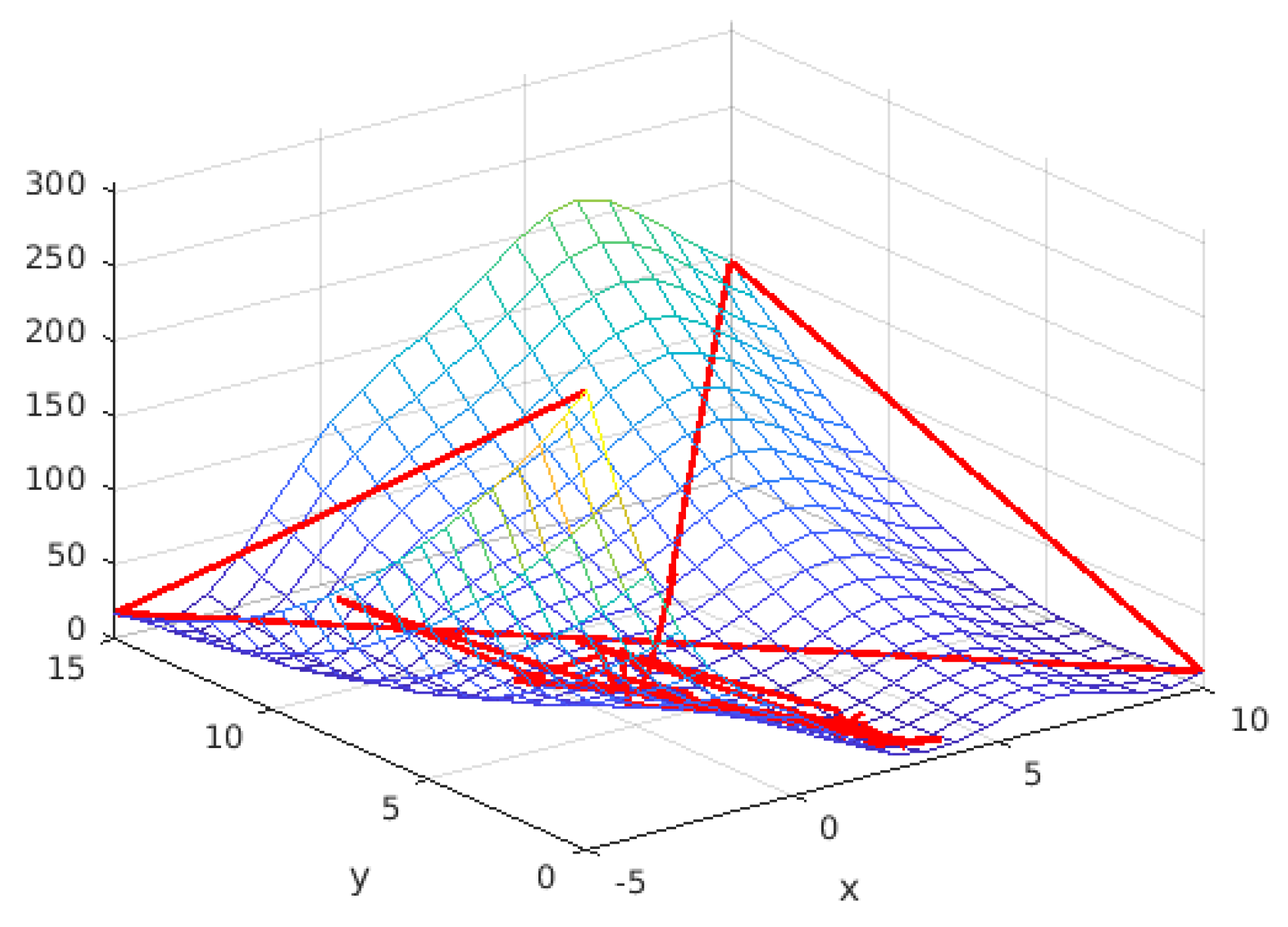
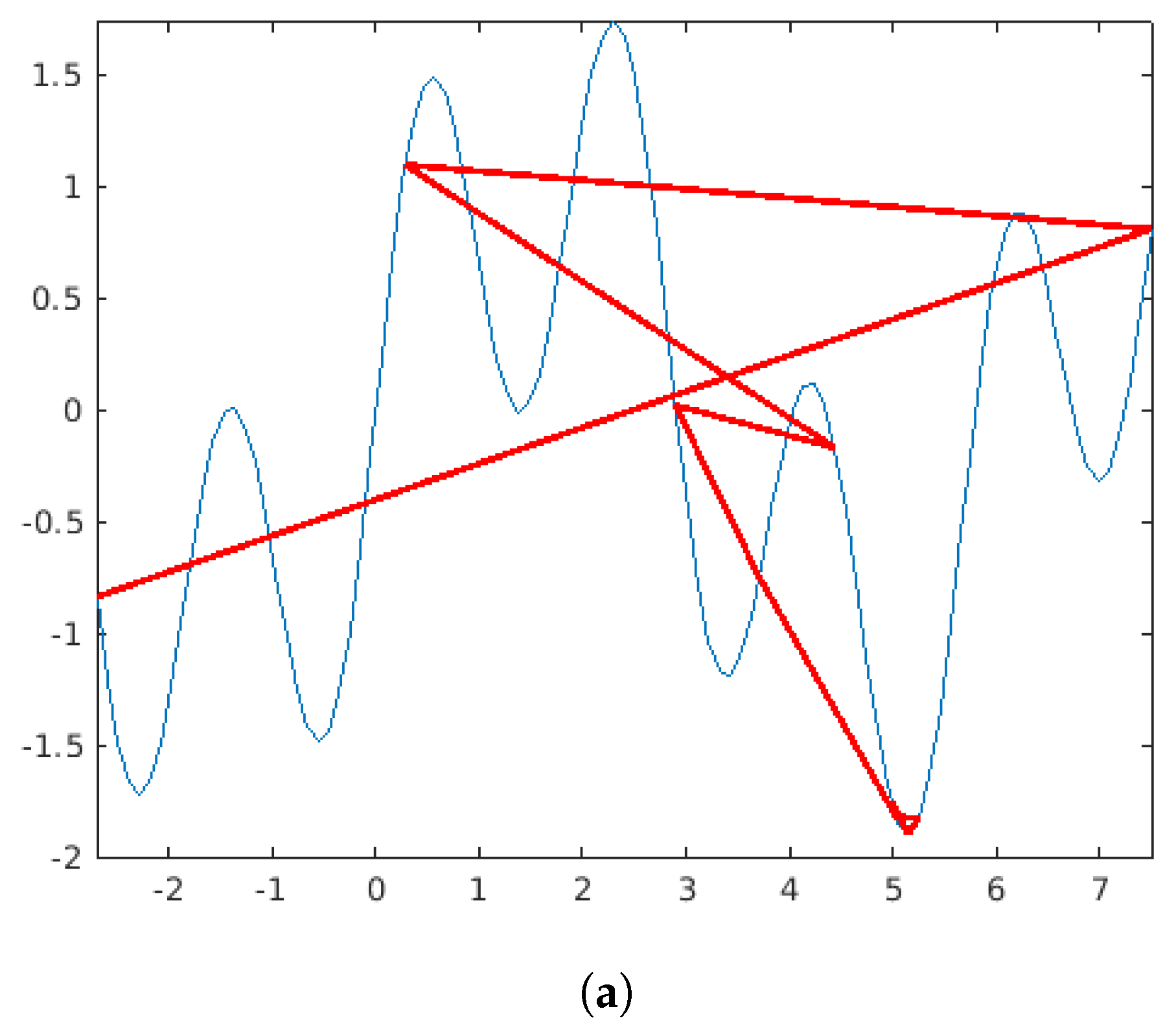
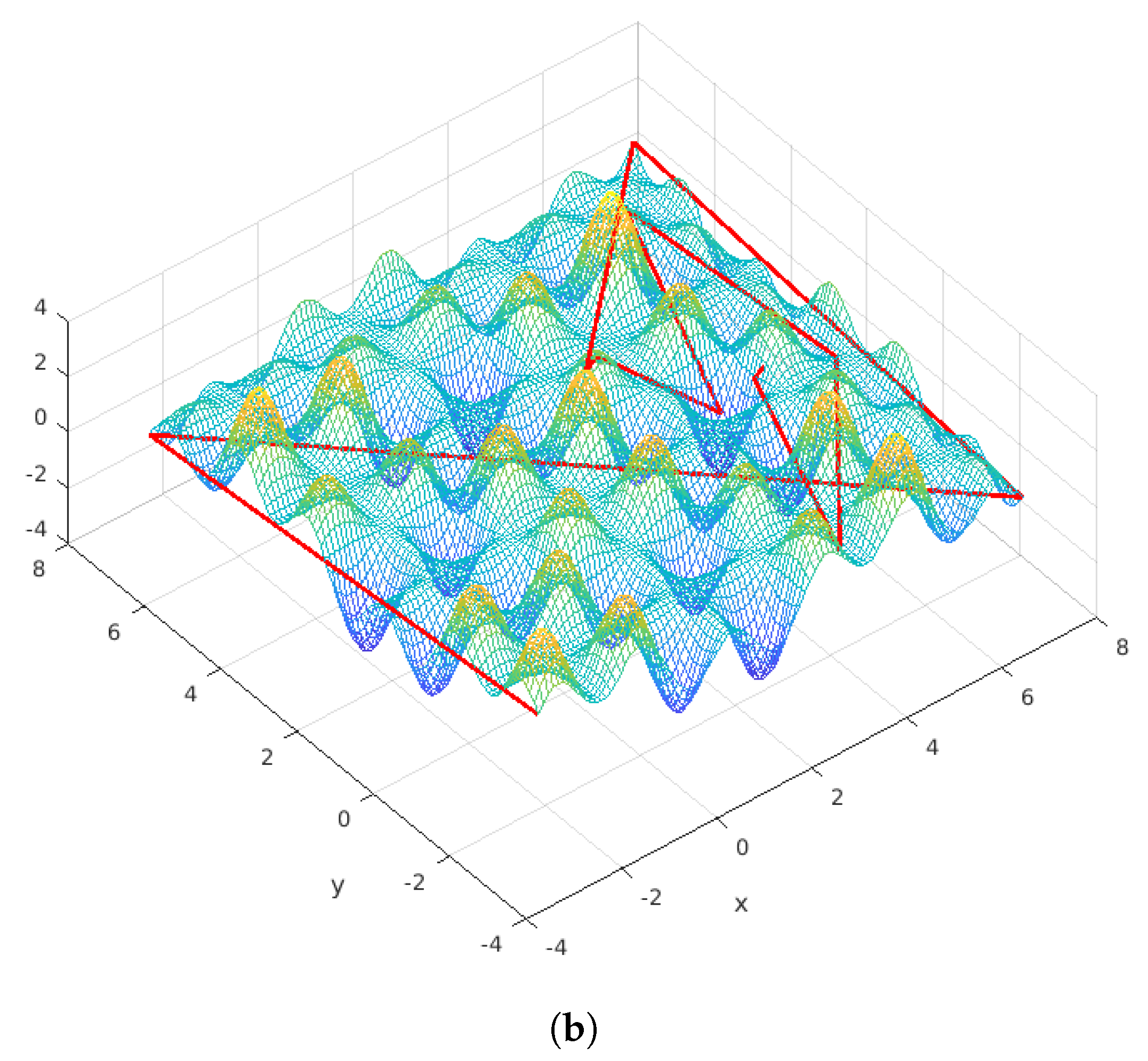
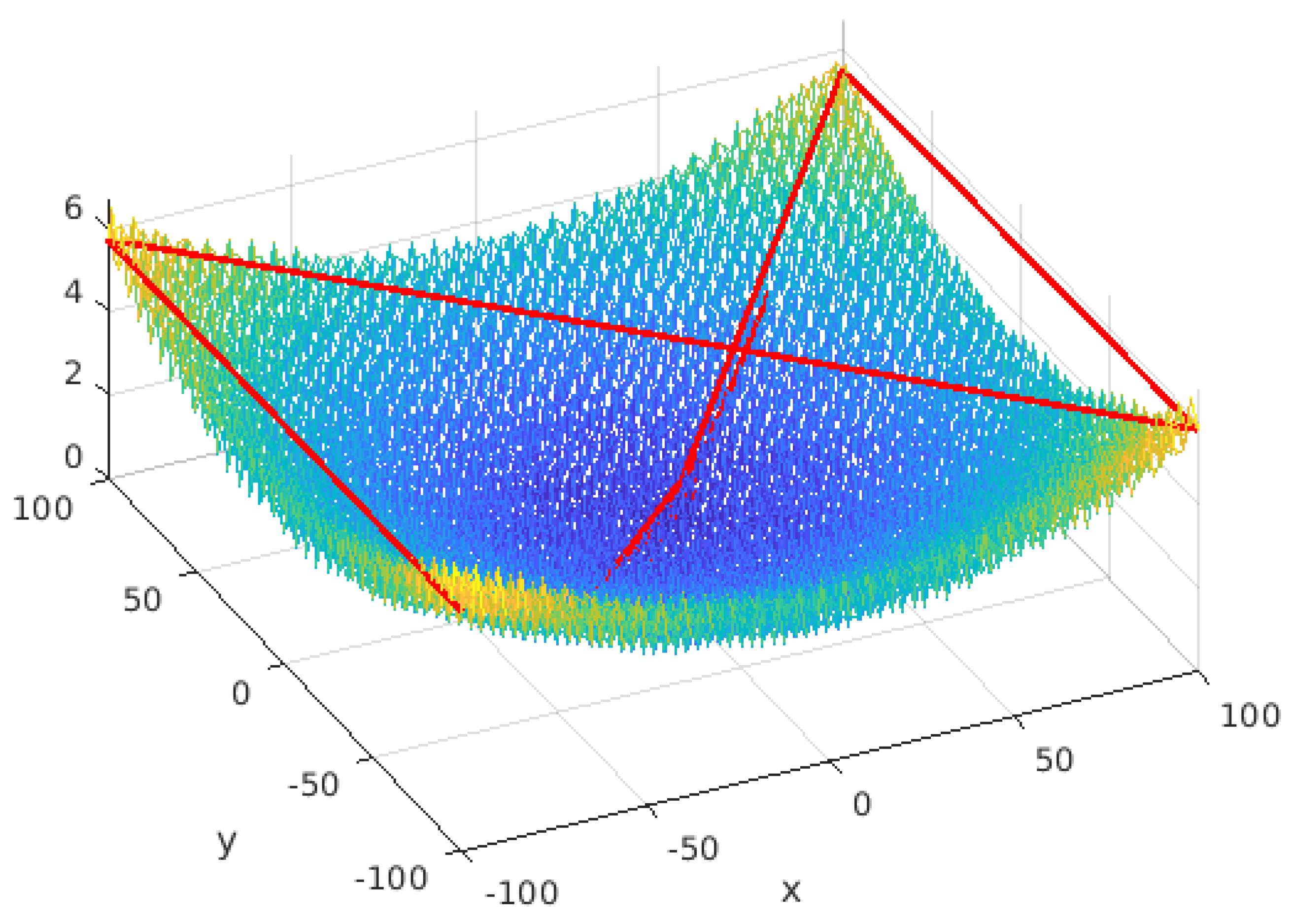
Appendix A.7. Problem Definitions
| Name | Definition | Search Space | Minimum |
| sinCos15 | 0.999507 for | ||
| Six Hump Camel Back | —1.031628453489877 | ||
| Shifted Rastrigin | 0 | ||
| Rosenbrock | 0 | ||
| Pressure Vessel | 6059.714335048436 | ||
| Gear Train | |||
| Frequency Modulated Sound Waves | 0 |
References
- Clerc, M. Iterative Optimizers—Difficulty Measures and Benchmarks; Wiley: Hoboken, NJ, USA, 2019. [Google Scholar]
- Wolpert, D.H.; Macready, W.G. No Free Lunch Theorems for Optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Hansen, N. The CMA Evolution Strategy: A Tutorial. arXiv 2023, arXiv:1604.00772. [Google Scholar] [CrossRef]
- Lampinen, J.; Storn, R. Differential Evolution. In New Optimization Techniques in Engineering; Springer: Berlin/Heidelberg, Germany, 2004; pp. 124–166. [Google Scholar]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant Colony Optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Da Silva, L.S.A.; Lúcio, Y.L.S.; Coelho, L.d.S.; Mariani, V.C.; Rao, R.V. A comprehensive review on Jaya optimization algorithm. Artif. Intell. Rev. 2023, 56, 4329–4361. [Google Scholar] [CrossRef]
- PSC. Particle Swarm Central. Available online: http://particleswarm.info (accessed on 1 November 2024).
- Elsayed, S.M.; Sarker, R.A.; Essam, D.L. GA with a New Multi-Parent Crossover for Solving IEEE-CEC2011 Competition Problems. In Proceedings of the 2011 IEEE Congress of Evolutionary Computation (CEC), New Orleans, LA, USA, 5–8 June 2011. [Google Scholar]
- Yang, X.S.; Huyck, C.; Karamanoglu, M.; Khan, N. True global optimality of the pressure vessel design problem: A benchmark for bio-inspired optimisation algorithms. Int. J. Bio-Inspired Comput. 2013, 5, 329–335. [Google Scholar] [CrossRef]
- Clerc, M. PSO Technical Site. Available online: http://clerc.maurice.free.fr/pso/ (accessed on 1 November 2024).
- Clerc, M. Iterative optimization-Complexity and Efficiency are not antinomic [Unpublished manuscript]. [CrossRef]
- Das, S.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for CEC 2011 Competition on Testing Evolutionary Algorithms on Real World Optimization Problems; Technical Report; Jadavpur University: Kolkata, West Bengal, India; Nanyang Technological University: Singapore, 2011; pp. 341–359. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Colorni, A.; Dorigo, M.; Maniezzo, V. Distributed Optimization by Ant Colonies. In Proceedings of the First European Conference on Artificial Life, Paris, France, 11–13 December 1991; pp. 134–142. [Google Scholar]
- Eberhart, R.C.; Kennedy, J. A New Optimizer Using Particle Swarm Theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Adaptive Scheme for Global Optimization over Continuous Spaces; Technical Report TR 95-012; International Computer Science Institute: Berkeley, CA, USA, 1995. [Google Scholar]
- Clerc, M.; Kennedy, J. The particle swarm—Explosion, stability, and convergence in a multidimensional complex space. IEEE Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef]
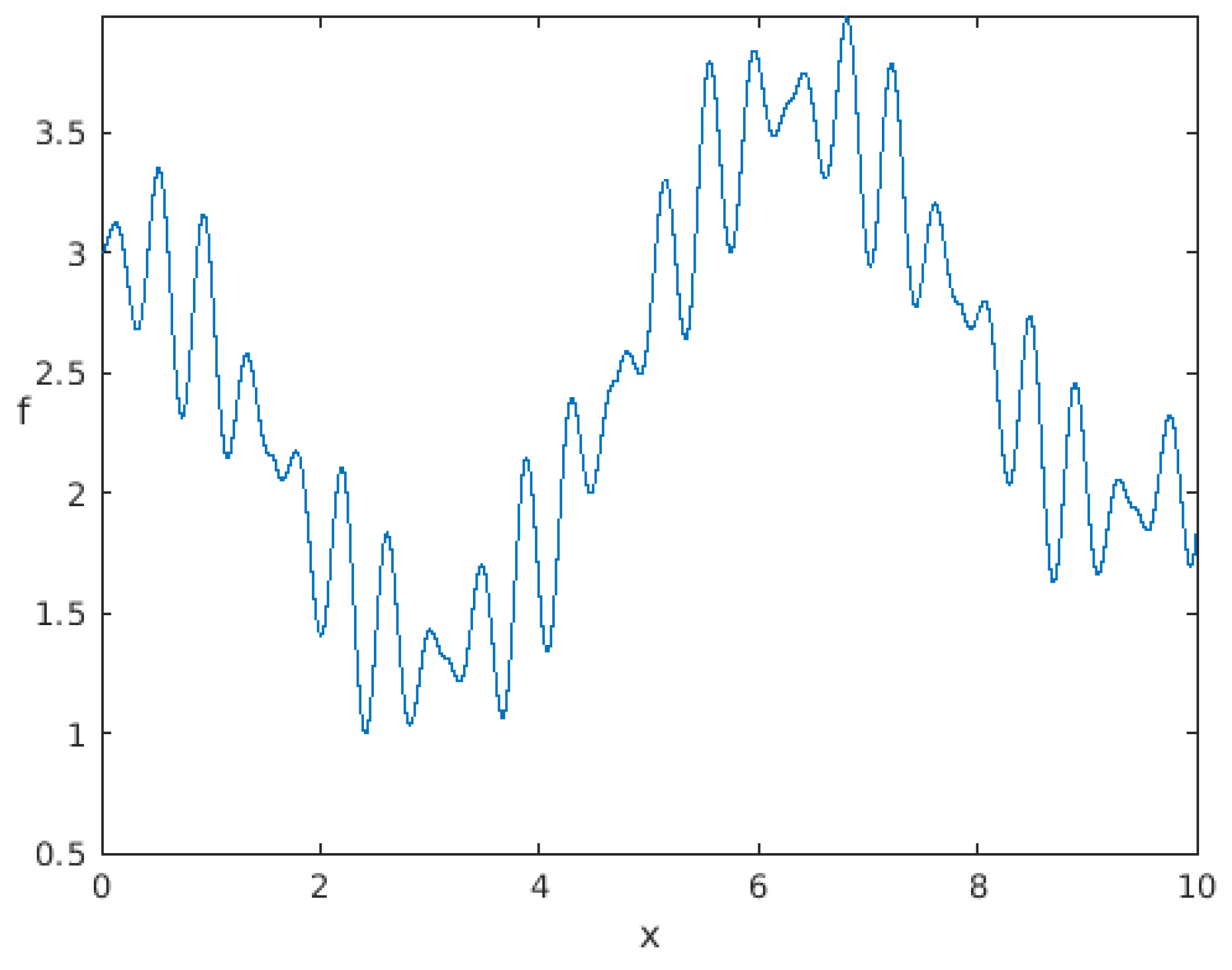
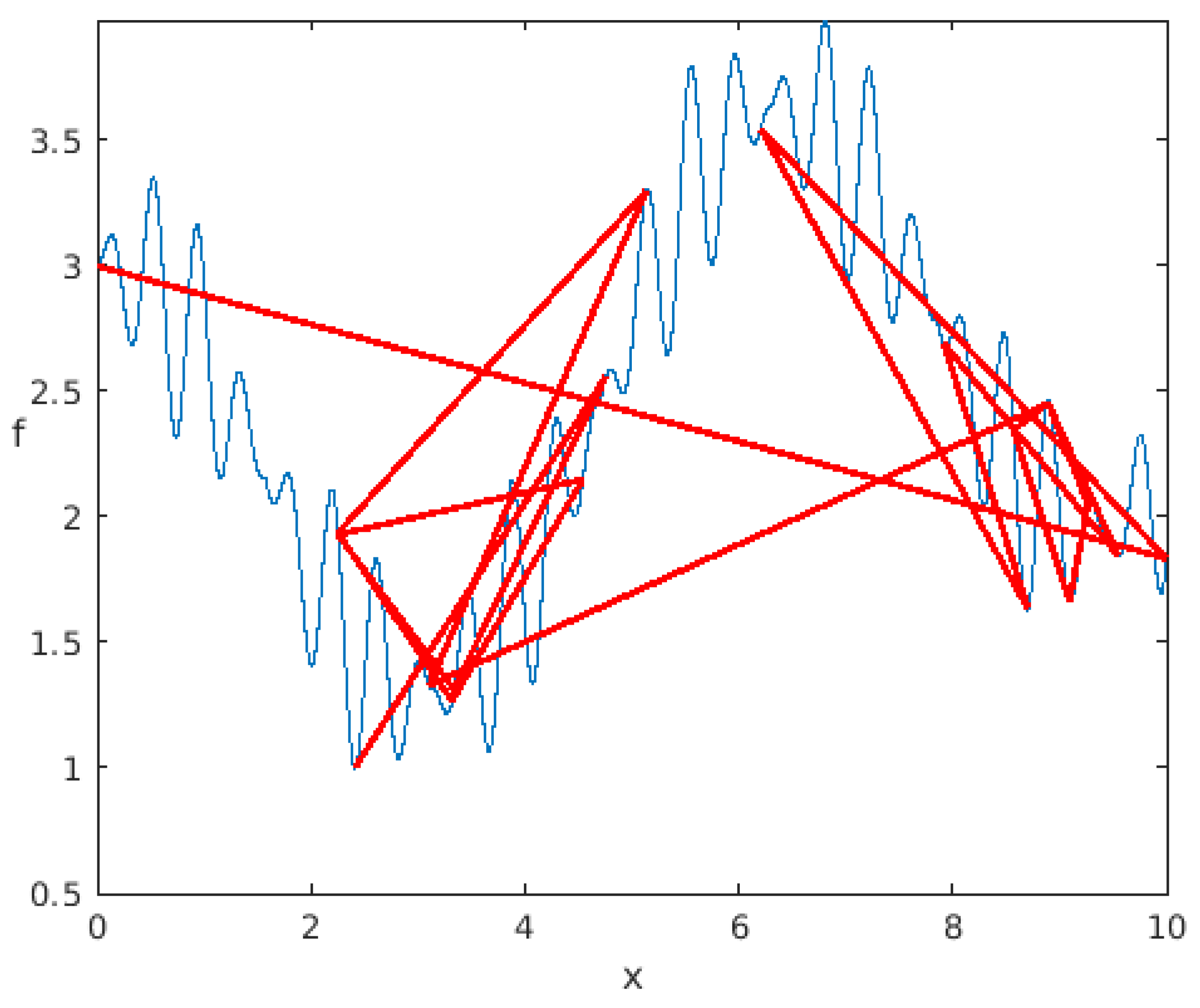

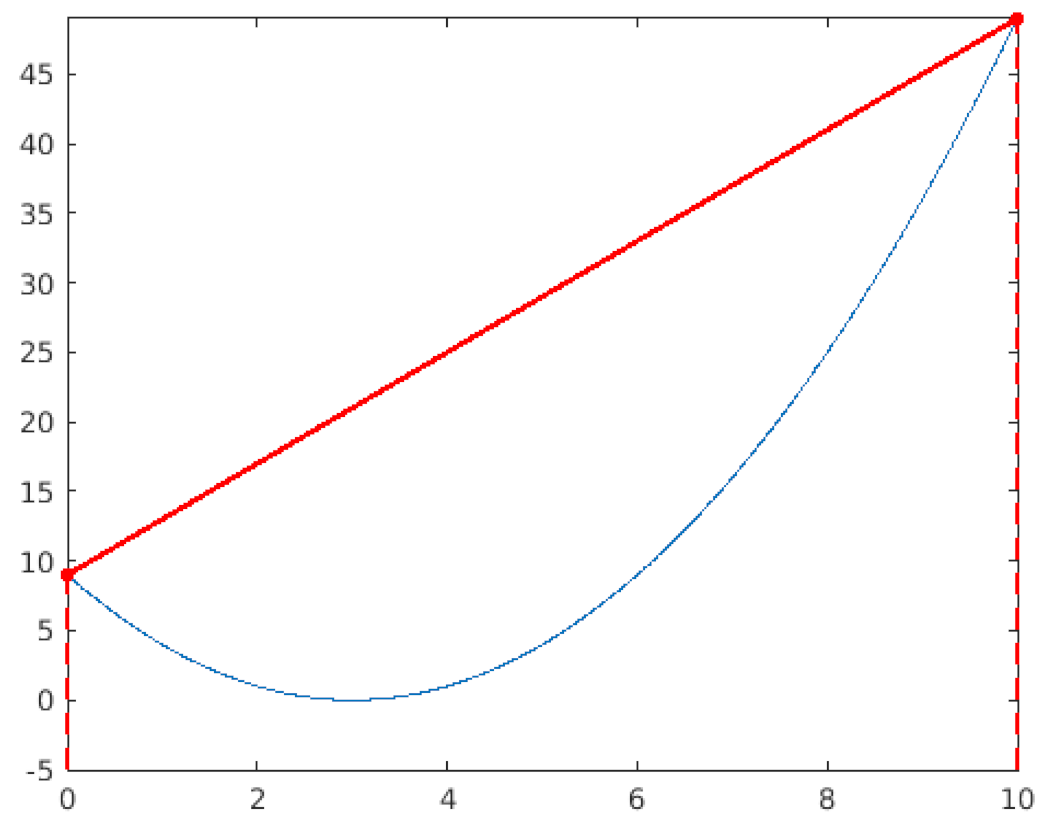
| An horizontal lower bound is defined. The “corners” are evaluated. The line connecting them intersects the lower bound beyond the search space, this intersection point is rejected and will be replaced with another one (step 2). |
 |
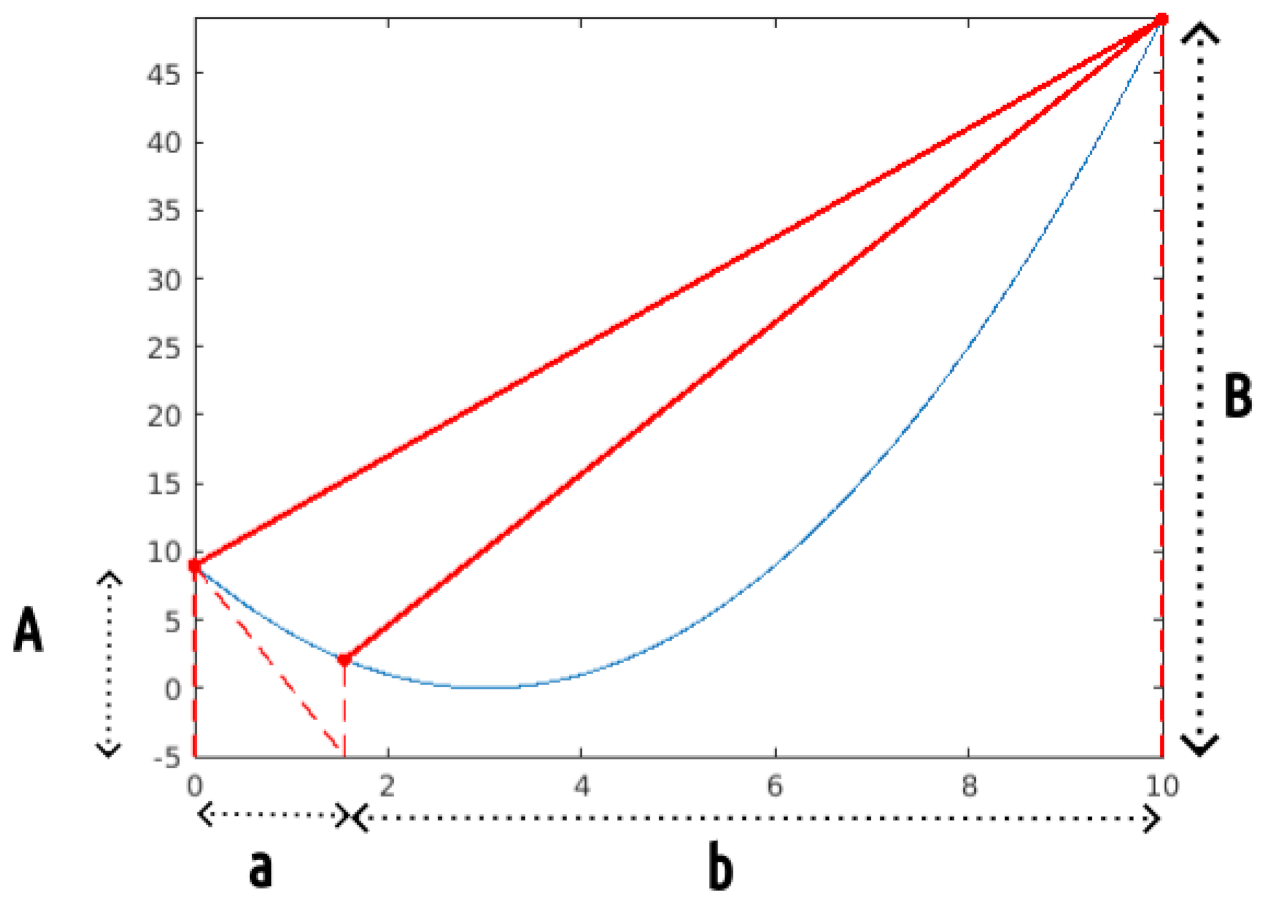
| The new position is defined so that . As the dimension is 1, this can be achieved thanks to a “Ruler & Compass” construction. Then, the position is evaluated to define the third point. |
 |
| Now the line joining the two last points does intersect the lower bound on a point whose position is inside the search space. This position is then maintained and evaluated. The same process is repeated, again. |
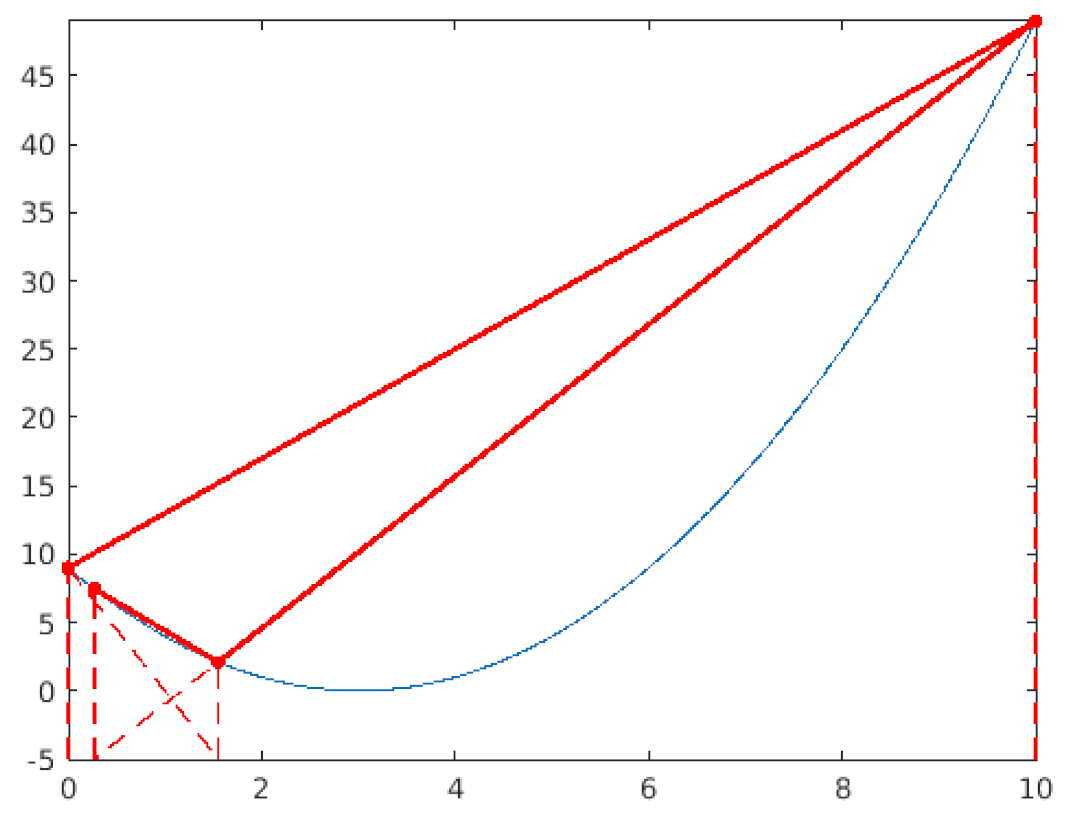 |
| … and again. |
 |
| After Step 9, the line connecting the last two points is nearly horizontal and intersects the lower boundary outside of the search space. Consequently, we generate a new position using the same method as in Step 2. This occurrence becomes increasingly frequent as the positions approach the solution. Hence, the new position often approximates the mean of the last two positions, which is a favorable behavior for better approaching the solution. |
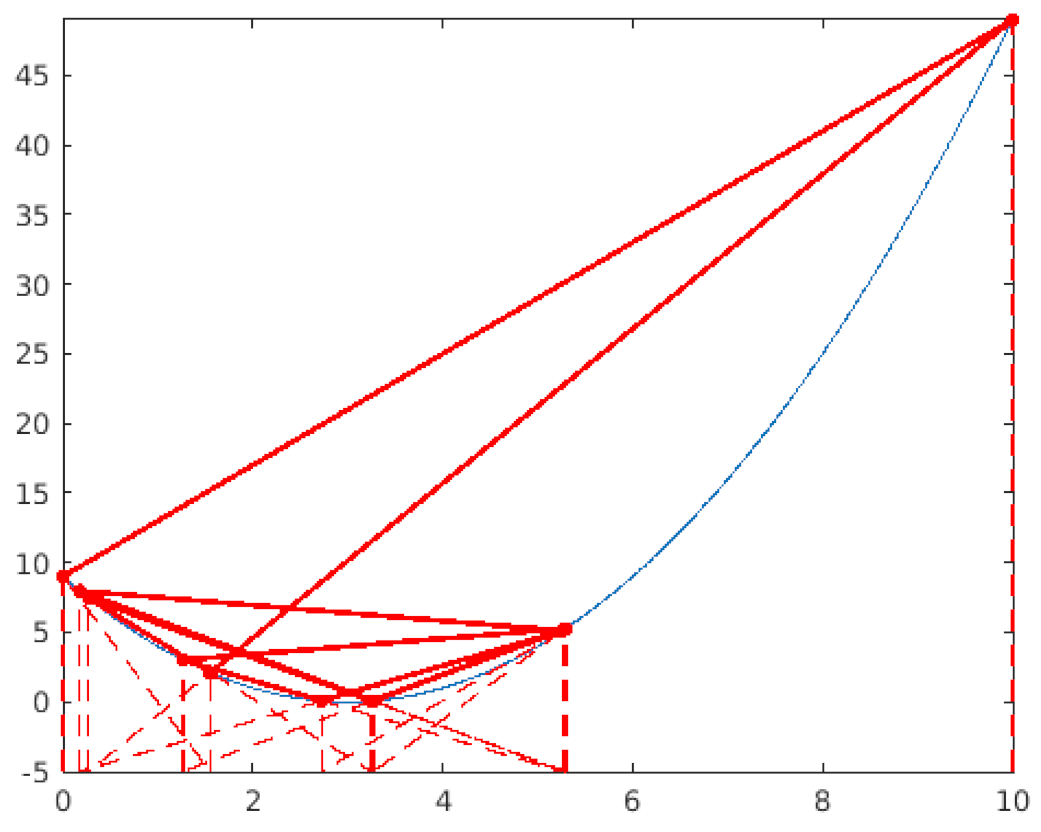 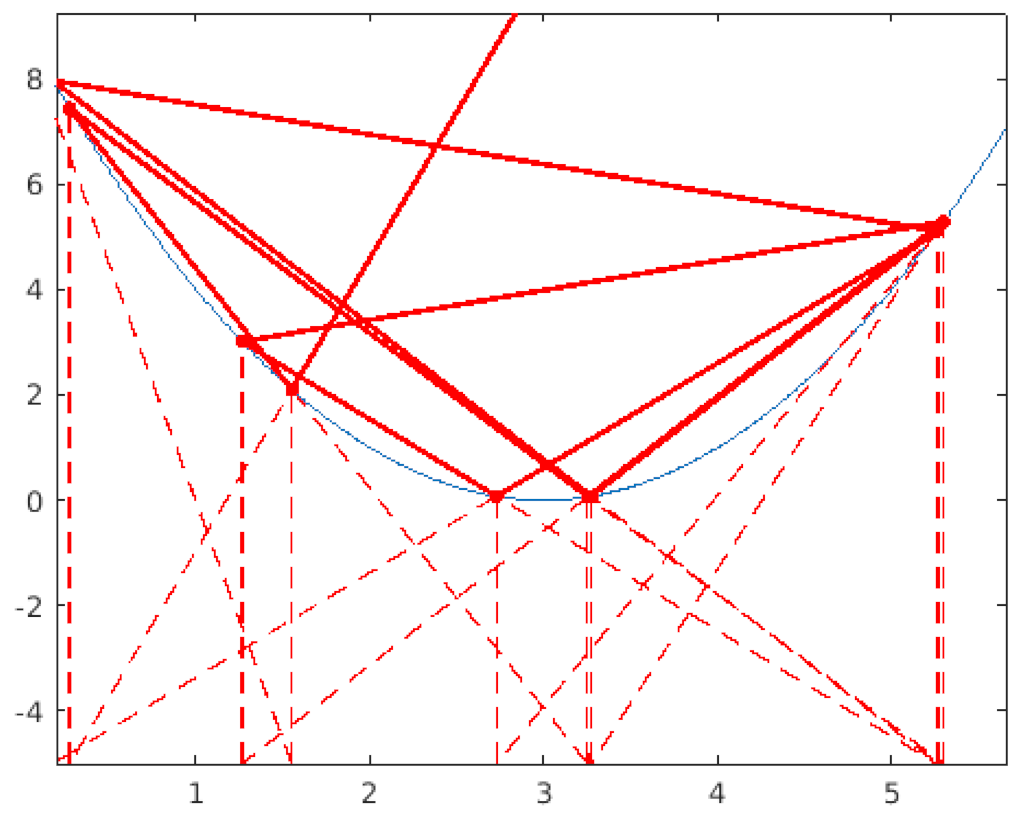 |
| Constructed Points (Evaluations) | Best Fitness |
|---|---|
| 14 | −0.957541 |
| 24 | −1.030227 |
| 34 | −1.030227 |
| 44 | −1.031227 |
| 54 | −1.031227 |
| 64 | −1.031473 |
| 74 | −1.031473 |
| 84 | −1.031473 |
| 94 | −1.031473 |
| 104 | −1.031473 |
| Dimension | Constructed Points (Evaluations) | Best Fitness |
|---|---|---|
| 1 | 52 | 0.000557 |
| 2 | 1004 | 0.001511 |
| 3 | 1508 | 0.002548 |
| 4 | 50,016 | 0.001735 |
| 5 | 250,032 | 0.004518 |
| Dimension | Evaluations | Best Fitness |
|---|---|---|
| 2 | 252 | 0.002788 |
| 3 | 1508 | 0.001003 |
| 4 | 10,016 | 0.003756 |
| 5 | 15,032 | 0.005719 |
| Evaluations | Best Fitness |
|---|---|
| 1052 | 11,056.81 |
| 2049 | 6646.71 |
| 3074 | 6615.977 |
| 4074 | 6615.977 |
| 5074 | 6615.977 |
| 6076 | 6592.011 |
| Evaluations | Best Fitness |
|---|---|
| 116 | |
| 130 | |
| 173 | |
| 223 | |
| 1753 |
| Problem | Dimension | Evaluations | RCO | PSO |
|---|---|---|---|---|
| Six Hump Camel Back | 2 | 54 | −1.031227 | −1.011030 |
| Shifted Rastrigin | 1 | 52 | 0.000557 | 0.510724 |
| 2 | 1004 | 0.001511 | 0.4397499 | |
| 5 | 250,032 | 0.004578 | 0.994959 | |
| 10 | 251,024 | 35.246 | 1.9899 | |
| Rosenbrock | 2 | 252 | 0.002788 | 266.94 |
| 5 | 15,032 | 0.005719 | 0.0864 | |
| 10 | 101,024 | 8.996 | ||
| Pressure Vessel | 4 | 3074 | 6615.977 | 6890.347 |
| 5074 | 6615.977 | 6821.931 | ||
| 20,074 | 6583.75 | 6820.410 | ||
| Gear Train | 4 | 173 | ||
| 1154 | ||||
| 199,752 |
| Dimension | Planes | Shifted Rastrigin |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| 11 | ||
| 12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clerc, M. Iterative Optimization RCO: A “Ruler & Compass” Deterministic Method. Mathematics 2024, 12, 3755. https://doi.org/10.3390/math12233755
Clerc M. Iterative Optimization RCO: A “Ruler & Compass” Deterministic Method. Mathematics. 2024; 12(23):3755. https://doi.org/10.3390/math12233755
Chicago/Turabian StyleClerc, Maurice. 2024. "Iterative Optimization RCO: A “Ruler & Compass” Deterministic Method" Mathematics 12, no. 23: 3755. https://doi.org/10.3390/math12233755
APA StyleClerc, M. (2024). Iterative Optimization RCO: A “Ruler & Compass” Deterministic Method. Mathematics, 12(23), 3755. https://doi.org/10.3390/math12233755






