One Class of Ideally Secret Autonomous Symmetric Ciphering Systems Based on Wiretap Polar Codes

Abstract

This paper introduces a class of symmetric ciphering systems with a finite secret key, which provides ideal secrecy, autonomy in key generation and distribution, and robustness against the probabilistic structure of messages (the Ideally Secret Autonomous Robust (ISAR) system). The ISAR system is based on wiretap polar codes constructed over an artificial wiretap channel with a maximum secrecy capacity of 0.5. The system autonomously maintains a minimum level of key equivocation by continuously refreshing secret keys without additional key generation and distribution infrastructure. Moreover, it can transform any stream ciphering system with a finite secret key of known length into an ISAR system without knowing and/or changing its algorithm. Therefore, this class of system strongly supports privacy, a critical requirement for contemporary security systems. The ISAR system’s reliance on wiretap polar coding for strong secrecy ensures resistance to passive known plaintext attacks. Furthermore, resistance to passive attacks on generated refreshing keys follows directly from ideal secrecy and autonomy. The results presented offer an efficient methodology for synthesizing this class of systems with predetermined security margins and a complexity of the order of $n\log n$, where $n$ is the block length of the applied polar code.

1. Introduction

The notion of unconditional secrecy was introduced by Claude Shannon in [1] to describe an encryption system that is resistant to any passive attack on messages based on ciphertext. However, he showed, in the same paper, that the necessary condition for unconditional secrecy is that the secret key’s length must be at least as long as the message, which is impractical for most applications. To address this, various approaches have been developed to create secure ciphers with shorter keys. Shannon himself suggested the so-called ideal and strongly ideal cipher systems, where an adversary is left with many equally probable decryption options, rather than a unique solution.

In this paper, we address two main questions.

• Is it possible to develop a general procedure for constructing ideal cipher systems with a predetermined minimum value of key equivocation, independent of the telecommunication environment or the probabilistic structure of the messages, and without additional infrastructure for generating and distributing secret keys?
• Is it possible to apply this solution to any existing symmetric stream ciphering system without modifying it or knowing the key stream generation algorithm, except for the length of the applied secret key?

If feasible, such a system would possess the following properties:

• Ideal secrecy—a guaranteed minimum value of key equivocation, regardless of the length of the ciphertext used by the adversary;
• Autonomy—the autonomous ability to maintain a given minimum value of key equivocation by continuously refreshing secret keys without additional infrastructure for key generation and distribution;
• Robustness—it retains the guaranteed properties regardless of the probabilistic structure of the messages.

We refer to this system as the ISAR (Ideally Secret Autonomous Robust) ciphering system. This paper presents a class of ISAR systems based on wiretap polar codes.

1.1. Related Works

Since key equivocation depends directly on the entropy of messages, the first group of works on ideal ciphering systems focuses on preprocessing messages before encryption to reduce redundancies (or, equivalently, to increase entropy). In this way, the minimum key equivocation available to a system attacker could be controlled. Compression and randomization techniques are standard for this approach and have a long tradition in cryptography [1,2,3,4,5]. Unlike other works [1,2,3,4], the study in [5] directly addressed the problem of constructing an ideal cipher system, not in terms of key equivocation, but rather message equivocation. In the first step, messages are transformed using Elias’s procedure for constructing unbiased random sequences into two subsets. The first, larger subset consists of independent and equiprobable symbols. The secret key is used in the form of a Vernam cipher to encrypt the second, smaller subset. The author demonstrated that, in this way, the message equivocation cannot fall below the threshold determined by the ratio of the cardinality of the second subset to the message length. It is important to note that this threshold depends on the probabilistic properties of the messages, as well as their length. Therefore, it is difficult to envision an operational procedure for synthesizing a symmetric cipher system with a given minimum value of key equivocation without prior knowledge of these values.

The homophonic coding technique, which transforms a sequence of message symbols into a uniquely decodable sequence where all symbols have the same frequency, also belongs to this approach [2,6,7,8]. The effectiveness of this approach depends on knowledge of the probabilistic properties of the message source being encrypted and reliable estimates of its statistical properties [3].

Another approach, not much different from the first, is entropic security [4,9,10,11]. The main difference lies in the security metrics used as a criterion. The goal of this metric is that any function of the original message is unattainable by passive adversaries. In the limiting case, when the so-called leakage parameter is equal to zero, this criterion aligns with Shannon’s definition of a perfect ciphering system. However, all the obtained results for the length of the secret key then become practically unusable or give lengths equal to the length of the messages, reducing these procedures to the Vernam cipher.

The honey cipher, introduced in [12], is similar to the concept of ideal cipher. The main goal of this approach is that an adversary is left with many highly probable hypotheses about the secret keys or messages. In [13], the authors combined the ideas of honey ciphers and entropic security to create practically implementable short-key ciphering systems. The dependence of the efficiency of these systems on the knowledge of the probabilistic properties of the source being encrypted is even more critical than in previous approaches. This is a consequence of the very idea of the system that, in the process of brute force attacks, hypothetical messages are generated that are difficult to distinguish from the true ones. However, the future development of these systems will likely enhance an understanding of the relationship between the probabilistic properties of the source and the minimum length of secret keys that is sufficient to prevent brute force attacks by an unbounded adversary, which brings us back to Shannon’s original ideas about the meaning of non-zero equivocation values of secret keys.

The final group of methods, relevant to the construction of ideally secret systems, comes from the broad research domain of combining the methods of error correcting codes, especially wiretap codes and cryptography [6,14,15,16,17,18,19]. In [6], a system based on wiretap codes was proposed, which proved to improve the performance of an arbitrary stream cyphering system in the regime of short messages, but whose key equivocation drops to zero for sufficiently long messages. In one paper [20], the authors integrated wiretap polar coding in encryption schemes based on learning with the problem of errors and showed that with appropriate refreshing of the secret key procedures, they achieved non-zero equivocation of the keys. In another paper [21], the connection between ideal secrecy and the wiretap coding approach was clarified. The same authors, in [22], proposed an encryption system over the MIMO wiretap channel, which, for an infinite lattice input alphabet, guarantees perfect security, while for finite constellations, it guarantees ideal secrecy with high probability. In [23], the authors proposed a polar coding scheme which achieves maximal secrecy capacity for a secret key of an arbitrary non-zero rate, shared between the transmitter and legitimate receiver. In [24], an encrypted secure polar coding scheme for general two-way wiretap channels is presented. To achieve strong security and reliability criteria, without any key pre-sharing, it is necessary to apply a complex cooperative jamming strategy.

On the basis of the presented analysis of the relevant published results, we can conclude the following.

• Wiretap coding provides a promising environment for implementing cryptographic systems with increased security.
• Works in which ideal secrecy has been proven are always related to a specific ciphering system, such as in [20], or are limited to a particular physical model of the wiretap channel, as in [22,24].

According to this analysis, which includes all four approaches, we conclude that there is no example of an ISAR system in the available literature. Namely, all techniques of compression, randomization, and homophonic encoding of message sources, as well as honey ciphering techniques, do not meet our first specified requirement. Furthermore, techniques based on wiretap coding fail to satisfy the same requirement regarding independence from the means of telecommunication used for transmission of the ciphertext.

The paper is organized into the following sections. Section 2 provides a basic conceptual and theoretical basis for understanding ISAR systems, particularly in the domain of wiretap channels, polar coding, privacy amplification techniques, and Shannon’s notion of ideal and strongly ideal systems. Section 3 describes the system’s architecture and the security properties of the ISAR ciphering system. Section 4 provides a security analysis of the ISAR ciphering system, including its resistance to passive attacks both on secret keys and messages. Section 5 summarizes the practical aspects of the implementation and application of the ISAR system in the contemporary information and communication infrastructure. Section 6 concludes the paper with a summary of the findings and suggestions for future research directions.

1.2. Notation

We define the integer interval $\left[a,b\right]$ as the integer set between $a$ and $b$. We denote $X,Y,Z,\dots$ as random variables taking values in the alphabets $\mathcal{X},\mathcal{Y},\mathcal{Z},\dots$ and their realization is denoted as $x,y,z,\dots$ respectively. Also, we denote a $n$-size vector $X^n=\left(X_1,X_2,\dots ,X_n\right)$ and denote $X_a^b=\left(X_a,X_{a+1},\dots ,X_b\right)$. Further, for any index set $A\subseteq \left[1,n\right]$, we define $X_A={\left\{X_i\right\}}_{i\in A}.$ $H(·)$ denotes entropy, and $I(·)$ denotes mutual information.

Table 1. Notation.

Notation	Description
$W_m$	Main channel of the wiretap model
$W_e$	Wiretap channel of the wiretap model
$C_s$	Secrecy capacity
$C\left(\mathrm{*}\right)$	$\mathrm{Capacity} \mathrm{of} *$
$W$	Binary-input symmetric memoryless discrete channel
$Z(*)$	Bhattacharrya parameter of $*$
$G_n$	Arikan’s generator matrix
$I(*)$	Mutual information of $*$
$H(*)$	Entropy of $*$

presents the significant notation, along with the respective meanings.

2. Preliminaries

In order make it easier to understand the operation of the proposed system, in this section, we will present the basic concepts from the domain of wiretap channel models, polar coding, and privacy amplification, since these three elements are its basic building blocks. In the final part of the section, the definition of an ideal autonomous ciphering system is given as a kind of generalization of Shannon’s notions of ideal and strongly ideal ciphering systems [25].

2.1. Wiretap Channel Model

The wiretap model consists of two channels $W_m:X\to Y$ and $W_e:X\to Z$, which are the main and wiretap channels, respectively, that were first introduced by Wyner [14]. With the help of random bits, the encoder maps the $k$-bit message $M$ into a sequence $X$ of $n$-bit channel symbols. This sequence is sent on the main and wiretap channels, giving the corresponding channel outputs $Y$ and $Z$. On the legitimate user’s side, the decoder maps $Y$ into an estimate $\widehat{M}$ of the original message. The basic purpose of wiretap coding is the design of encoders and decoders that provide the legitimate users (Alice and Bob) with reliability and security at the same time when the message length $k=\left|M\right|$ tends to infinity. The largest transmission rate at which both the reliability and secrecy conditions are simultaneously satisfied is commonly referred to as the secrecy capacity $C_s$. In the case when the main and wiretap channels are binary symmetric channels (BSC) and the wiretap channel is degraded with respect to the main channel, $C_s$ was given by [26] as

$$C_s=C\left(W_m\right)-C\left(W_e\right)=H\left(X|Z\right)-H\left(X|Y\right) ,$$

(1)

where the random variable $X$ at the input to the channel is uniform over $\mathcal{X}$, while $C$($W_m) \mathrm{a}\mathrm{n}\mathrm{d} C\left(W_e\right)$ denote the capacities of the main and wiretap channels, respectively.

2.2. Wiretap Polar Coding

Polar codes, introduced by Erdal Arikan [27,28], are a class of error-correcting codes that achieve the capacity of binary-input symmetric memoryless (BSM) discrete channels. The key idea behind polar coding is to transform a set of $n=2^b$ communication channels into a set of polarized channels, where a subset of channels becomes nearly perfect (noiseless) and the others become completely noisy. If, with $W$, we denote the BSM channel as $〈\left\{\mathrm{0,1}\right\},Y,W〉$, the Bhattacharyya parameter of $W$ is

$$\underset{k\to \infty }{Z(W)\triangleq {\sum }_{y\in Y}\sqrt{W\left(y\right|0\left)W\right(y\left|1\right)}}=0 .$$

(2)

Value (2) is equal to the upper bound probability of error of maximum likelihood (ML) decoding of a single use of the channel. It was shown that $Z\left(W\right)$ takes values from the interval [0,1]. Channels with small $Z\left(W\right)$ values are almost noiseless, while channels with $Z\left(W\right)$ values close to 1 are almost purely noise channels [28]. The essence of wiretap polar coding is the transformation of n instances of $W_m$ and $W_e$ into the n-input channels $W_m^{\left(i\right)}$ and $W_e^{\left(i\right)},i\in \left[1,n\right]$, which are polarized either as good or bad channels depending on their Bhattacharyya parameters, $Z\left(W_m^{\left(i\right)}\right)$ and $Z\left(W_e^{\left(i\right)}\right)$, respectively, and/or symmetric capacity $C\left(W_m^{\left(i\right)}\right),C\left(W_e^{\left(i\right)}\right)$. In order to achieve strong secrecy, the authors of [17,18] proposed the following definition of good and bad polarized channels

$$P_n\left(W_e,{\delta }_n\right)=\left\{i\in \left[1,n\right]:C\left(W_e^{\left(i\right)}\right)\le {\delta }_n\right\} , {\mathsf{\delta }}_{\mathrm{n}}-\mathrm{poor} \mathrm{bit} \mathrm{channels} \mathrm{for} \mathrm{Eve},$$

(3)

$$G_n\left(W_m,\beta \right)=\left\{i\in \left[1,n\right]:Z\left(W_m^{\left(i\right)}\right)<2^{-n^{\beta }}/n\right\}, \mathrm{good} \mathrm{for} \mathrm{Bob},$$

(4)

$$B_n\left(W_m,\beta \right)=\left\{i\in \left[1,n\right]:Z\left(W_m^{\left(i\right)}\right)\ge 2^{-n^{\beta }}/n\right\}, \mathrm{bad} \mathrm{for} \mathrm{Bob},$$

(5)

using the security function ${\delta }_n$ and a parameter $\beta \in \left(\mathrm{0,1}/2\right)$. For a fixed $\beta$, we can define next partition of $\left[1,n\right]$ as follows.

$$\mathcal{R}=\left[1,n\right]\setminus P_n\left(W_e,{\delta }_n\right) ,$$

(6)

$$\mathcal{A}=P_n\left(W_e,{\delta }_n\right) \bigcap G_n\left(W_m,\beta \right) ,$$

(7)

$$\mathcal{B}=P_n\left(W_e,{\delta }_n\right)\setminus G_n\left(W_m,\beta \right) .$$

(8)

Next, let us partition the set $\mathcal{R}$ into two subsets ${\mathcal{R}}_1$ and ${\mathcal{R}}_2$ ($\mathcal{R}={\mathcal{R}}_1\bigcup {\mathcal{R}}_2$)

$${\mathcal{R}}_1=\mathcal{R}\bigcap B_n\left(W_m,\beta \right) ,$$

(9)

$${\mathcal{R}}_2=\mathcal{R}\bigcap G_n\left(W_m,\beta \right) .$$

(10)

This process obtained subsets of the polarized channels, and their meanings in terms of transmission quality in the main and wiretap channels are shown in

Table 2. Partition of the index of the polarized channels $W_m^{\left(i\right)}$ and $W_e^{\left(i\right)},i\in \left[1,n\right]$, according to (3)–(10), ensuring strong secrecy.

	${\mathbf{N}\mathbf{o}\mathbf{t} \mathsf{\delta }}_{\mathbf{n}}$—$\mathbf{p}\mathbf{o}\mathbf{o}\mathbf{r} \mathbf{b}\mathbf{i}\mathbf{t} \mathbf{c}\mathbf{h}\mathbf{a}\mathbf{n}\mathbf{n}\mathbf{e}\mathbf{l}\mathbf{s} \mathbf{f}\mathbf{o}\mathbf{r} \mathbf{E}\mathbf{v}\mathbf{e}$		${\mathsf{\delta }}_{\mathbf{n}}$—$\mathbf{p}\mathbf{o}\mathbf{o}\mathbf{r} \mathbf{b}\mathbf{i}\mathbf{t} \mathbf{c}\mathbf{h}\mathbf{a}\mathbf{n}\mathbf{n}\mathbf{e}\mathbf{l}\mathbf{s} \mathbf{f}\mathbf{o}\mathbf{r} \mathbf{E}\mathbf{v}\mathbf{e}$
Good for Bob	$\mathcal{R}$	${\mathcal{R}}_2$—random bits	$\mathcal{A}$—message bits
Bad for Bob		${\mathcal{R}}_1$—random bits	$\mathcal{B}$—frozen bits (zeros)

.

A polar wiretap encoder performs a 1-1 transformation of the original input vector $V_1^n$ into an $n$-dimensional code vector $X_1^n$

$$X_1^n=V_1^n·G_n ,$$

(11)

where $G_n$ is Arikan’s generator matrix, given by

$$G_n=P_n·F^{\otimes b} ,$$

(12)

$P_n$ is the $n\times n$ bit-reversal permutation matrix defined in [28], while $F^{\otimes b}$ is the b-fold tensor product of $F\triangleq \left[\begin{array}{cc}1& 0\\ 1& 1\end{array}\right]$ with itself. The input vector $V$ has the following structure

$$V_1^n=\left[V_{\mathcal{R}},V_{\mathcal{A}},V_{\mathcal{B}}\right] .$$

(13)

The corresponding components of the input vector $V$ are set to the following values

$$V_{\mathcal{R}}=e, V_{\mathcal{A}}=M, V_{\mathcal{B}}=0,$$

(14)

where $e$ is a random vector, selected by Alice uniformly at random from {0, 1}. The vector of frozen bits $V_{\mathcal{B}}$ is set to the 0 vector of dimension $\left|V_{\mathcal{B}}\right|=n-\left|V_{\mathcal{B}}^C\right|=n-\left|V_{\mathcal{R}}\cup V_{\mathcal{A}}\right|$, where $V_{\mathcal{B}}^C$ is the complement of $V_{\mathcal{B}}$ in $\left[1,n\right]$. As was mentioned in [28], in the case of symmetric channels, any choice of frozen values is as good as another. From now on, we will assume that it is

$$k=\left|M\right|, m=\left|R\right|.$$

(15)

For the coding scheme described, Proposition 16 in [17] is proven to hold:

$$I\left(M_k;Z_1^n\right)\le \left|P_n\left(W_e,{\delta }_n\right)\right|{\delta }_n .$$

(16)

From here, the conclusion follows that by choosing the security function ${\delta }_n$, we can bound the mutual information leaked to Eve for any message distribution. Specifically, according to [17] (see Theorem 17), for any security function such that

$${\delta }_n=o\left(1/n\right) ,$$

(17)

the described wiretap coding scheme guarantees strong security.

As for achieving reliability conditions, since, in the general case,

$${\mathcal{R}}_1=\mathcal{R}\bigcap B_n\left(W_m,\beta \right)\ne \varnothing ,$$

(18)

it is necessary to apply involving chaining construction [18] over multiple blocks to ensure reliability. Namely, since non-frozen channels in a strong security coding scheme are given by

$$\mathcal{A}\cup \mathcal{R}=G_n\left(W_m,\beta \right)\bigcup {\mathcal{R}}_1 ,$$

(19)

it is necessary to ensure reliable transmission in the channels indexed in the index set ${\mathcal{R}}_1$. This is exactly what chaining construction achieves by taking a subset of indices from the set $\mathcal{A}$, i.e., $\mathcal{H}\subset \mathcal{A}$, such that $\left|\mathcal{H}\right|=\left|{\mathcal{R}}_1\right|$. Random bits that are placed in $\mathcal{H}$ in the $j$-th block are used in $\mathcal{H}$ in the $(j+1)$-th block for $j=1, 2, 3,$… In the first block, random bits are used that were distributed to Alice and Bob before starting communication. In this way, the Successive Cancellation (SC) decoder on Bob’s side in each block can successfully decode the contents in the channels with indices from (19), and therefore $V_{\mathcal{A}}=M.$

The corresponding secrecy capacity is provided by Theorem 1 in [17].

2.3. Privacy Amplification (PA)

Privacy amplification is a technique used in cryptography to enhance the security of a shared secret key between two parties. The primary goal is to convert a partially secure or somewhat compromised key into a highly secure key, even in the presence of an eavesdropper who may have some knowledge about the original key [19,29]. In terms of practical application, hash functions called universal families have a special role [30].

Definition 1.

The family of $G$ functions $g:A\to B$, where $A$ and $B$ are two final sets, is 2—universal, or in short—universal, if the following holds

$$\forall x_1,x_2\in A , x_1\ne x_2⟹P_G\left\{G\left(x_1\right)=G\left(x_2\right)\right\}\le {\displaystyle \frac{1}{\left|B\right|}} .$$

(20)

where $G$ is a random variable that represents a random choice of a function $g\in G$ uniformly at random in $G$.

An example of a frequently used class of universal hash functions is given by

$$H_M=\left\{h_M\left(x\right)=M·x, x\in GF{\left(2\right)}^k, M\in GF{\left(2\right)}^{k\times r}\right\} .$$

(21)

In applications, a random choice of a hash function from a given set is implemented using a seeded pseudo-random generator. To emphasize this fact, we explicitly introduce seed notation. Therefore, a hash function from the class $H_M$, is denoted as

$$h_M\left(x,K_h\right) .$$

(22)

where $K_h$ denotes a seed of adequate length. If $K_h$ is available only to legitimate users, the hash functions are typically known as cryptographic hash functions.

Definition 2.

The difference between the dimensions of the domain and codomain of a given class of hash functions will be referred to as its compression rate $∆R$.

The compression rate of class $H_M$, defined in (21), is $∆R=r-k.$

2.4. Ideal and Ideal Autonomous Cipher Systems

Consider a general symmetric cipher system $(X,Z,K)$, where $X$ is the input plaintext, $Z$ is the ciphertext, and $K$ is the secret key.

According to Shannon, an ideal ciphering system is one in which the key equivocation, i.e., $H\left(K|{\mathrm{Z}}_1^n\right)$, remains non-zero even as the number of ciphertext symbols $n$ approaches infinity [25]. This means that the uncertainty about the key does not reduce to zero, regardless of how much ciphertext is available to an attacker. Important properties of ideal encryption systems are as follows.

• Non-zero key equivocation: the key remains partially unknown, no matter the length of the intercepted ciphertext.
• Security over time: the security of the system does not degrade with the amount of data encrypted and transmitted.
• Practical key length: the key length can be shorter than the message length, unlike a one-time pad, but must be sufficient to maintain key equivocation.

A strongly ideal system has a key equivocation constant at the entropy of the secret key, i.e., $H\left(K|{\mathrm{Z}}_1^n\right)=H\left(K\right).$ This implies an even higher level of security, ensuring that the key’s uncertainty remains unchanged from its a priori value, regardless of the volume of ciphertext available. The key characteristics are as follows.

• Constant key equivocation: the amount of information about the key that remains unknown does not diminish with increasing ciphertext.
• Enhanced security: it offers superior protection against extensive ciphertext analysis, maintaining key secrecy over an indefinite amount of encrypted data.
• Robust design: it typically requires more sophisticated cryptographic techniques to ensure that key equivocation remains constant.

By distinguishing these two concepts, Shannon’s theories provide a framework for evaluating and designing cryptographic systems based on the desired level of security and practical constraints.

Starting from these foundational Shannon definitions, we will define a new term—the ideally secret autonomous robust ciphering system.

Definition 3.

An ideally secret autonomous robust (ISAR) ciphering system is one which can maintain minimal key equivocation at a predefined value ${∆}_K$, i.e.,

$${H\left(K|Z_1^n\right)\ge ∆}_K,$$

(23)

independently of the message’s probability distribution and without an additional secret key distribution system.

If several different secret keys are used during operation of one cipher system, ${ K}_{1, }{K}_{2, }\dots K_{t, }$ which correspond to ciphertexts${ Z}_{1, }{Z}_{2, }\dots Z_{t, }$, we say that the system is ideally secret autonomous and robust if it is able to maintain a predetermined minimum value of equivocation for each of the applied keys, i.e.,

$$H\left(K_i|Z_i\right)\ge {∆}_K, \forall i\in \left[1,t\right],$$

(24)

independently of the message’s probability distribution and without additional secret key distribution system.

Remark 1.

In Shannon’s definition of an ideal system, it is important that the key equivocation is not reduced to zero with an unlimited increase in the available ciphertext. On the other hand, a strongly ideal cipher system requires constant maintenance of key equivocation at the entropy level of the secret key. An ideally secret autonomous robust cipher system is, in a certain sense, between these two extremes. It maintains the minimum value of key equivocation at a predetermined value, which, in general, belongs to the open interval $\left(0,H\left(K\right)\right)$.

Remark 2.

Since $H\left(K|Z_1^n\right)$ is a non-increasing function of the number of observed ciphertext symbols n, the minimum in (23) is always reached at the maximum available n.

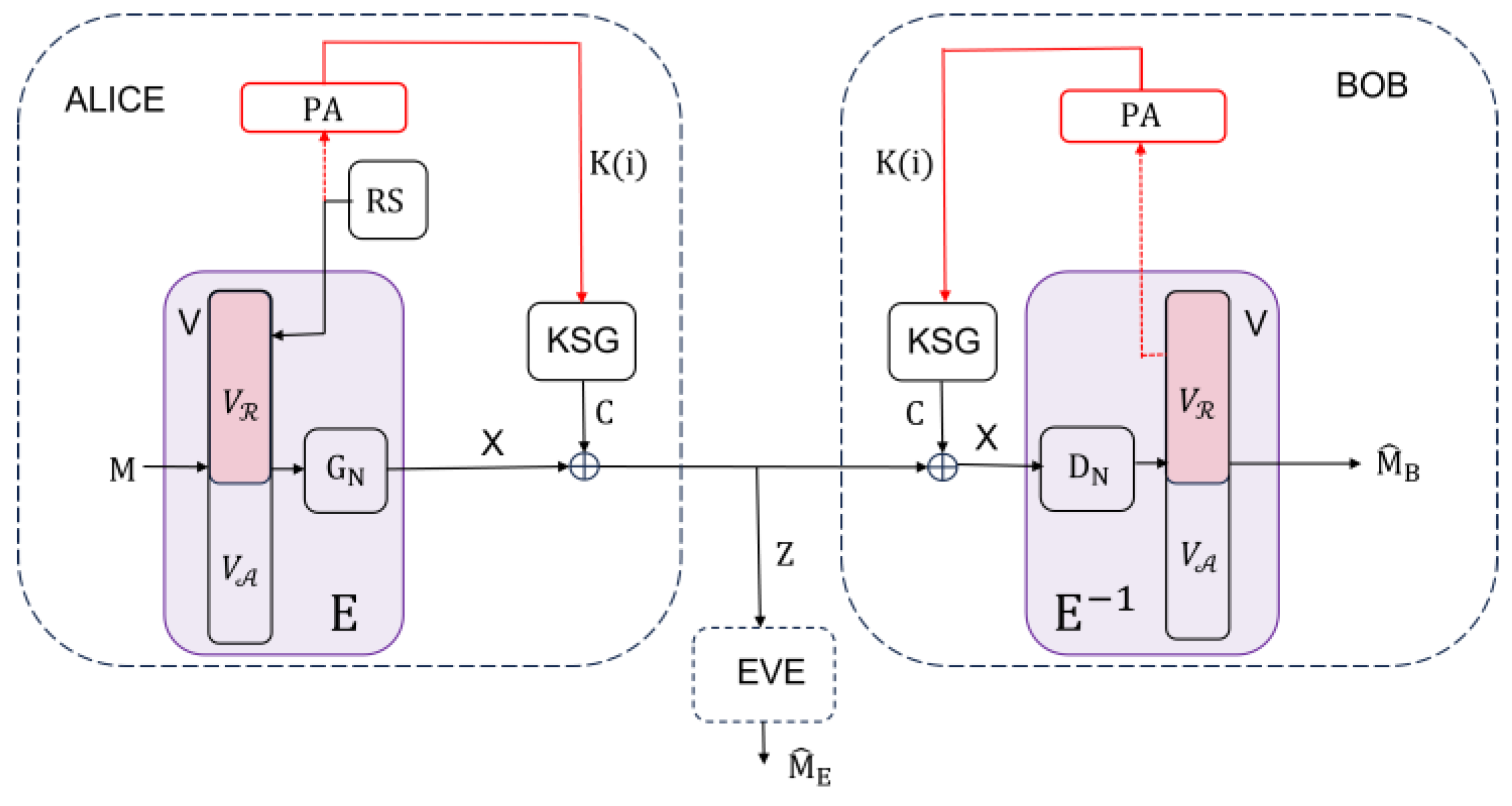
3. System Architecture and Security Properties of the ISAR Cyphering System

In this section, it will be shown that the ISAR cyphering system is equivalent to a wiretap model, whose main channel is error-free, while the wiretap channel is equivalent to an embedded symmetric stream cyphering system. In Theorem 1, it is shown how wiretap coding should be constructed in order to achieve strong secrecy and reliability. Theorem 3 gives the capacity of the wiretap channel, which turns out to decrease linearly with the length of the secret key. Theorem 4 gives the equivocation of secret key, while Theorem 5 gives the secrecy capacity of the proposed ISAR as a function of the polar code length and security margins for equivocation and privacy amplification. Then it is shown that for an arbitrary cipher system to be ideal with the same lower bound of key equivocation as the ISAR system, its secret key must be $t$ times greater than that of ISAR, where $t$ is proportional to message length. Thus, the superiority of the ISAR system increases with the length of the messages. The section concludes with a demonstration of how any symmetric stream ciphering system can be transformed into an ISAR.

Let the protected communication between the legitimate parties Alice and Bob take place in the successive exchange of messages $M$, which were previously divided into a series of blocks of length $k$. At their disposal is a symmetric stream cyphering system based on a key stream generator KSG($K$) with a short secret key $K$ that produces the key stream $C$ (see Figure 1). As is known [1], such systems cannot provide strong security, and practical secrecy is measured by the amount of computer resources spent by the adversary (Eve) in arriving either at the message (partial system cracking) or the secret key (total system cracking). Block $E$ denotes a polar coder, which performs a 1-1 transformation of message $M$ into an $n$-dimensional codeword vector $X$, while the block $E^{-1}$ performs an inverse transformation of vector $X$ into message $M$. Alice and Bob have local sources of randomness (denoted by RS on Alice’s side), as well as privacy amplification (PA) blocks, which, based on the input random string obtained in block $i-1$, generate a shorter random string that serves as a new secret key $K\left(i\right)$ for encrypting the vector $X$ in block $i$. We will assume that the system uses a cryptographic hash function $h_M\left(x,K_h\right)$ from the class of universal hash functions, as well as that the seed $K_h$ was previously exchanged between Alice and Bob. In the initial block, $K\left(1\right)=S$, i.e., the initial secret key of the given KSG($S$).

Remark 3.

Additionally, we assume that the cipher system based on KSG($K$) is semi-injective with respect to $K$, i.e., that the knowledge of ciphers and messages uniquely determines $K$, i.e., $H\left(K\right|X, Z)=0$holds.

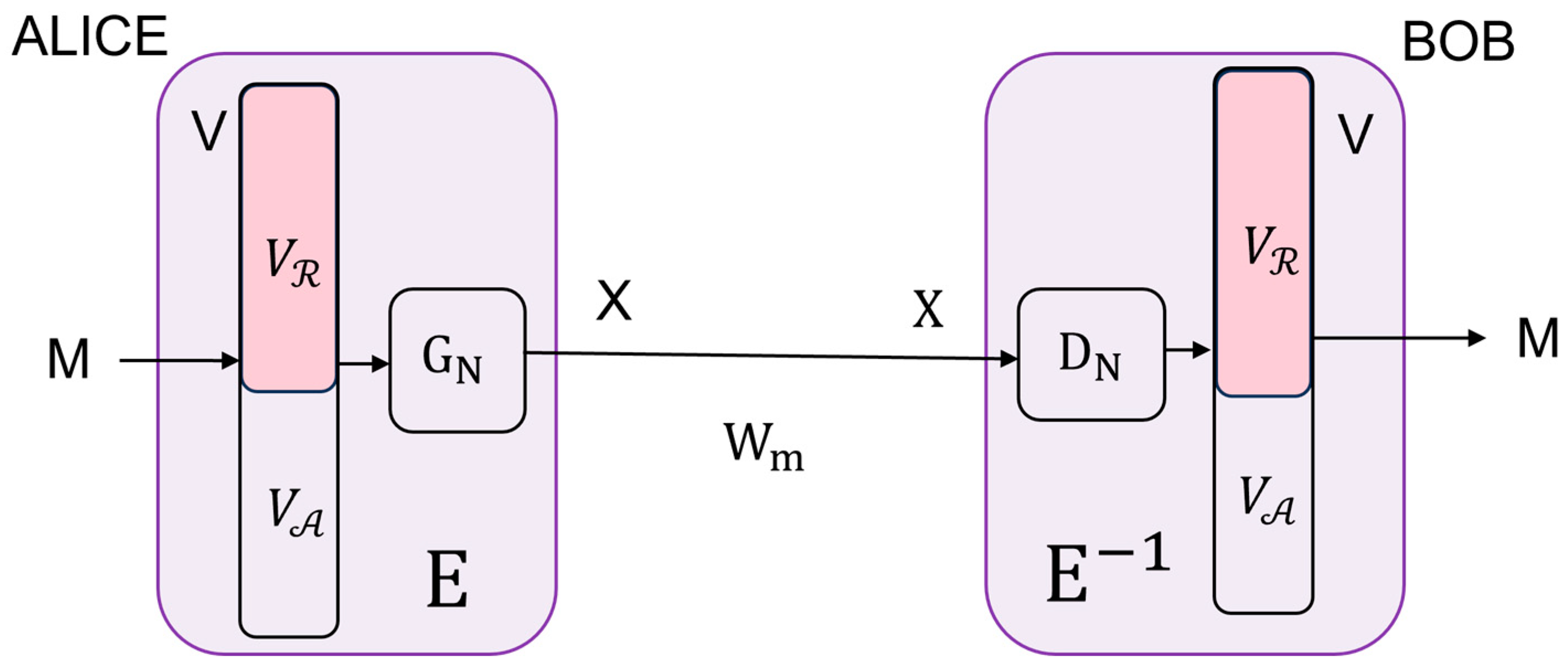
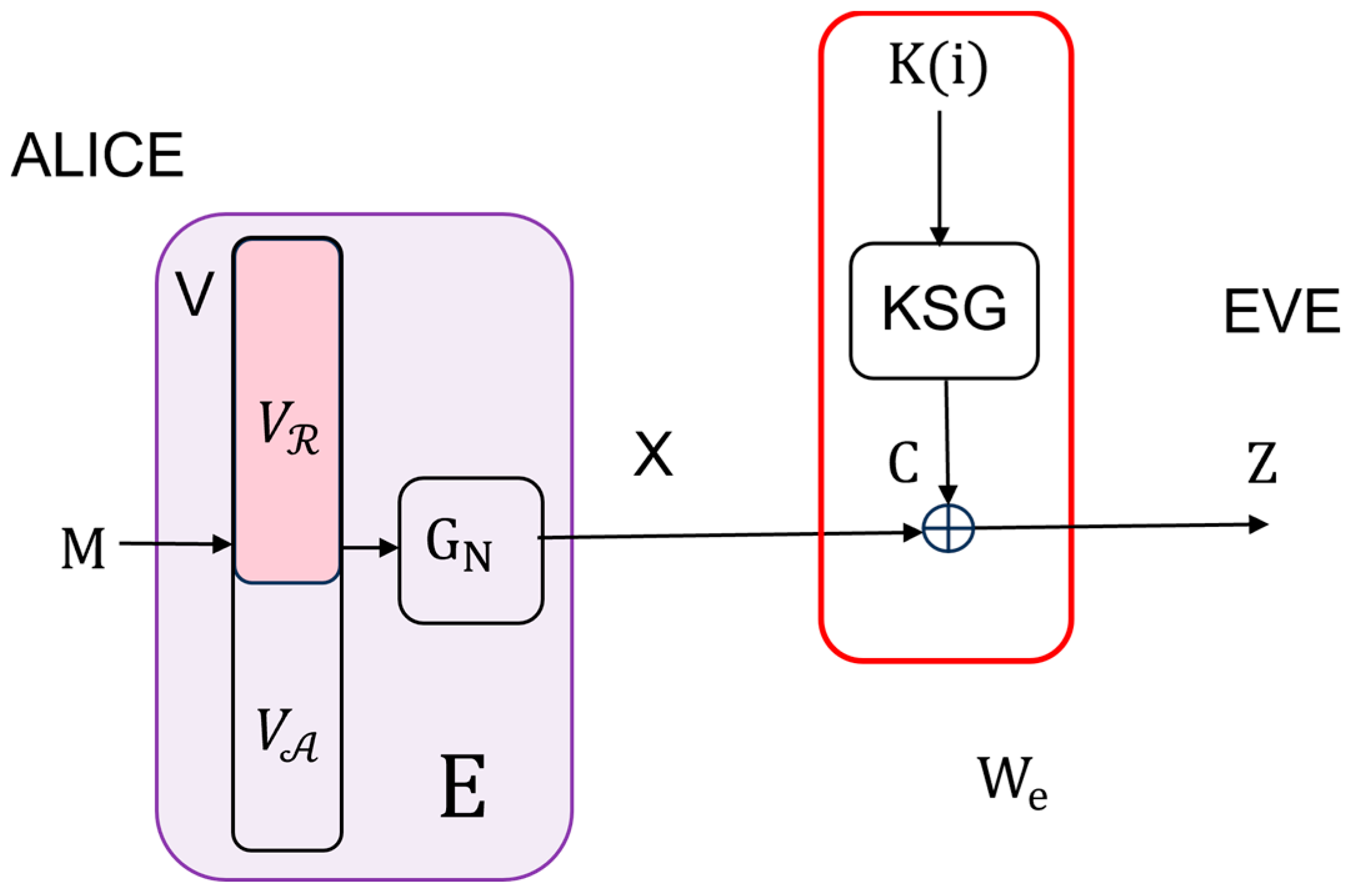
A system conceived of in this way can also be viewed as a kind of wiretap model. The legitimate users Alice and Bob are communicating over an equivalent noiseless main channel $〈M,X,W_m〉=〈\left\{\mathrm{0,1}\right\},\left\{\mathrm{0,1}\right\},I〉$, where $I$ is the identity matrix (see Figure 2). An eavesdropper, Eve, is wiretapping over an equivalent wiretap channel $〈M,Z,W_e〉=〈\left\{\mathrm{0,1}\right\},\left\{\mathrm{0,1}\right\},W_e〉$, where $W_e$ is an $\left|M\right|\times \left|Z\right|$ matrix, with $W_e\left(z|m\right)$ being the probability of receiving $z\in Z$, given that $m\in M$ was sent (see Figure 3). In order to be able to apply the results presented in Section 2, we have to prove that the equivalent wiretap channel is a BSC.

Lemma 1.

The equivalent wiretap channel $〈M,Z,W_e〉$ is a BSC.

Proof. 

According to the proposed scheme (Figure 1),

$$Z=C ⨁ X.$$

(25)

Since $C$ is independent of $X$, (25) is equivalent to BSC ($\sigma ),$ where the crossover probability is given by $\sigma =Pr\left\{C=1\right\}$. □

We can now formulate the main result of this part of the work.

Theorem 1.

Let ${\delta }_n$ be an arbitrary security function that satisfies Condition (17). Let the index sets $\mathcal{A}$ and $\mathcal{R}$ be given by $\mathcal{A}$$=P_n\left(W_e,{\delta }_n\right)$ and $\mathcal{R}$$=[1,n]\setminus P_n\left(W_e,{\delta }_n\right)$, while$e$ is a random vector, selected by Alice uniformly at random from {0, 1}. If, in the ISAR system, the input vector is structured as follows

$$V_1^n=\left[V_{\mathcal{R}},V_{\mathcal{A}}\right], V_{\mathcal{R}}=e, V_{\mathcal{A}}=M.$$

(26)

then it satisfies both the reliability and strong security criteria precisely.

$$Pr\left\{M\ne \widehat{M_B}\right\}=0 ,$$

(27)

$$\underset{\left|M\right|\to \infty }{\mathit{lim}}I(M;Z)=0 .$$

(28)

Proof. 

Bearing in mind that the equivalent main channel for the ISAR system is noiseless, the wiretap coding scheme for strong secrecy is determined by the sets of polarized channel indices found by (3)–(10), which now have the following values

$$P_n\left(W_e,{\delta }_n\right)=\left\{i\in \left[1,n\right]:C\left(W_e^{\left(i\right)}\right)\le {\delta }_n\right\} ,$$

(29)

$$G_n\left(W_m,\beta \right)=\left[1,n\right] ,$$

(30)

$$B_n\left(W_m,\beta \right)=\varnothing ,$$

(31)

$$\mathcal{R}=\left[1,n\right]\setminus P_n\left(W_e,{\delta }_n\right) ,$$

(32)

$$\mathcal{A}=P_n\left(W_e,{\delta }_n\right) \bigcap G_n\left(W_m,\beta \right)=P_n\left(W_e,{\delta }_n\right) ,$$

(33)

$$\mathcal{B}=P_n\left(W_e,{\delta }_n\right)\setminus G_n\left(W_m,\beta \right)=P_n\left(W_e,{\delta }_n\right)\setminus \left[1,n\right]=\varnothing ,$$

(34)

$${\mathcal{R}}_1=\mathcal{R}\bigcap B_n\left(W_m,\beta \right)=[1,n]\setminus P_n\left(W_e,{\delta }_n\right)\cap \varnothing =\varnothing ,$$

(35)

$${\mathcal{R}}_2=\mathcal{R}\bigcap G_n\left(W_m,\beta \right)=\mathcal{R}\bigcap \left[1,n\right]=\mathcal{R}.$$

(36)

According to (35), the problematic set of indices ${\mathcal{R}}_1$ is an empty set; therefore, it is not necessary to apply the chaining scheme. By structuring the input vector $V$ according to (26), where the sets of indices $\mathcal{R}$ and $\mathcal{A}$ are given by (32) and (33), respectively, we conclude that the proposed polar coding scheme is merely an instantiation of the general polar wiretap coding scheme from Section 2.2, which, under the assumptions of Theorem 1, ensures both reliability and strong secrecy. Since the main channel is noiseless, decoding on Bob’s side is not performed using the SC decoder, but rather by a simple inverse operation with respect to the encoding, i.e.,

$$X{G}_n^{-1}=\left(V{G}_n\right)G_n^{-1}=\left(V{G}_n\right)G_n=V ,$$

(37)

given that Arikan’s generator matrix $G_n$ is its own inverse over the Galois field $GF\left(2\right)$. Therefore, the reliability condition expressed by (27) is actually deterministically satisfied. This completes the proof. □

Theorem 2.

For any security function ${\delta }_n$ and the constants $\beta , c_1, c_2$ that satisfies Condition (17), $c_1{2}^{{-n}^{\beta }}\le {\delta }_n\le 1-c_2$, $\beta \in \left(\mathrm{0,1}/2\right)$, and $c_1, c_2>0$, the rate of the coding scheme of the proposed system from Figure 1 approaches the secrecy capacity, namely

$$\underset{n\to \infty }{\mathit{lim}}{R}_n=\underset{n\to \infty }{lim}{\displaystyle \frac{\left|\mathcal{A}\right|}{n}}=1-C\left(W_e\right) ,$$

(38)

Proof. 

The proof follows directly from Theorem 1 of [17], and the fact that the capacity of main channel is $C\left(W_m\right)=1$. □

Remark 4.

Eve’s optimal strategy is to attempt to decode the wiretapped $Z$ using the SC decoder after receiving it [28]. The average block error probability on Eve’s side can be lower-bounded, applying Lemma 2.9 of [31] by Korada

$$P_e\left(A\right)\ge \underset{i\in A}{\mathit{max}}{\displaystyle \frac{1}{2}}\left(1-\sqrt{1-{Z\left(W_n^i\right)}^2}\right) ,$$

(39)

where $A$ is the information set. Considering that Eve does not know the frozen bits on her side, the information set includes all indices, i.e., $A=\left[1,n\right],$ and the polar code applied is of rate 1; see the similar argumentation in [32]. The maximum value of $Z\left(W_n^i\right)$ is very close to 1, bearing in mind that $A$ includes bad channels as well. Therefore, according to (39), it follows that

$$P_e\left(A\right)\ge {\displaystyle \frac{1}{2}}-\delta , \delta ={\displaystyle \frac{1}{2}}\sqrt{1-\underset{i\in A}{max}\left\{{Z\left(W_n^i\right)}^2\right\}} ,$$

(40)

where $\delta$ is small. From this, we conclude that Eve’s optimal decoding strategy of using the SC decoder results in the maximum decoding error, preventing her from obtaining both the message $M$ and the purely random sequence $e$.

It is evident that the key properties of the proposed system depend on the capacity of the wiretap channel $C\left(W_e\right)$. The following theorem determines the value of this quantity, depending on the length of the polar code $n$ and the length of the secret key $k_C$.

Theorem 3.

The capacity of Eve’s channel in the proposed system in Figure 1 is given by

$$C\left(W_e\right)=1-{\displaystyle \frac{k_C}{n}} ,$$

(41)

where $k_C=\left|K\right|$ is the length of the secret key of the given symmetric stream cyphering system based on KSG($K$), while $n$ is the length of the polar code.

Proof. 

For a discrete memoryless symmetric channel $W_e$ with the input $X$ and the output $Z$, the channel capacity is defined as

$$C\left(W_e\right)=\underset{p\left(x\right)}{\mathit{max}}I\left(X;Z\right) ,$$

(42)

where the maximum is taken over all possible input distributions $p\left(x\right)$ [33]. Furthermore, we have

$$I\left(X_1^n;Z_1^n\right)=H\left(X_1^n\right)-H\left(X_1^n|Z_1^n\right) .$$

(43)

The input to the wiretap channel $W_e$ is also the input (messages) to the symmetric stream ciphering system based on KSG($K$). Message equivocation is equal to key equivocation

$$H\left(X_1^n|Z_1^n\right)=H\left(K|Z_1^n\right) ,$$

(44)

for every symmetric ciphering system, semi-injective with respect to $K$ (see Theorem 1 in [34]). On the other hand, it well known that (see, for example, [25])

$$H\left(K|Z_1^n\right)=H\left(K\right)+H\left(X_1^n\right)-H\left(Z_1^n\right) ,$$

(45)

which, by substituting into (44) and then into (43), gives

$$I\left(X_1^n;Z_1^n\right)=H\left(Z_1^n\right)-H\left(K\right) .$$

(46)

One of the primary goals in designing any cipher system is for the ciphertext to appear to be totally random for as long as possible, i.e.,

$$H\left(Z_1^n\right)\approx n ,$$

(47)

This holds for larger values of $n$. The assumption in (47) is referred to by Massey in [35] as the “total randomness” assumption, and it is shown to be valid as long as

$$n\le n_u ,$$

(48)

where $n_u$ is the unicity distance of a given cipher system [1]. Considering (47) and the fact that $H\left(K\right)=k_C,$ since the secret keys are chosen as purely random sequences, from (46), we obtain $I\left(X_1^n;{\mathrm{Z}}_1^n\right)=n-k_C$ or, normalized per bit,

$$C\left(W_e\right)=\underset{p\left(x\right)}{\mathit{max}}I\left(X;Z\right)={\displaystyle \frac{1}{n}}\left(n-k_C\right)=1-{\displaystyle \frac{k_C}{n}},$$

(49)

which had to be proven. □

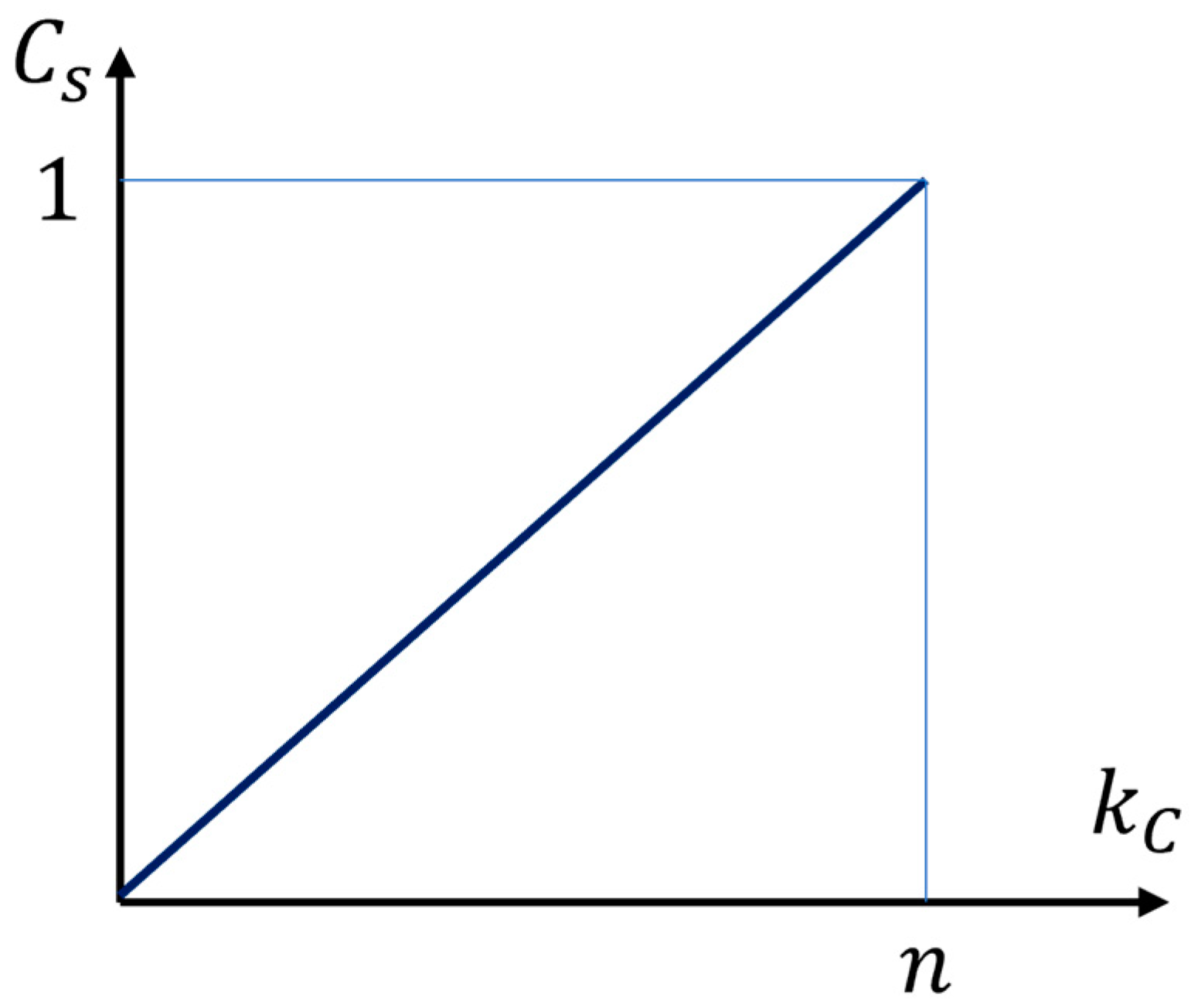
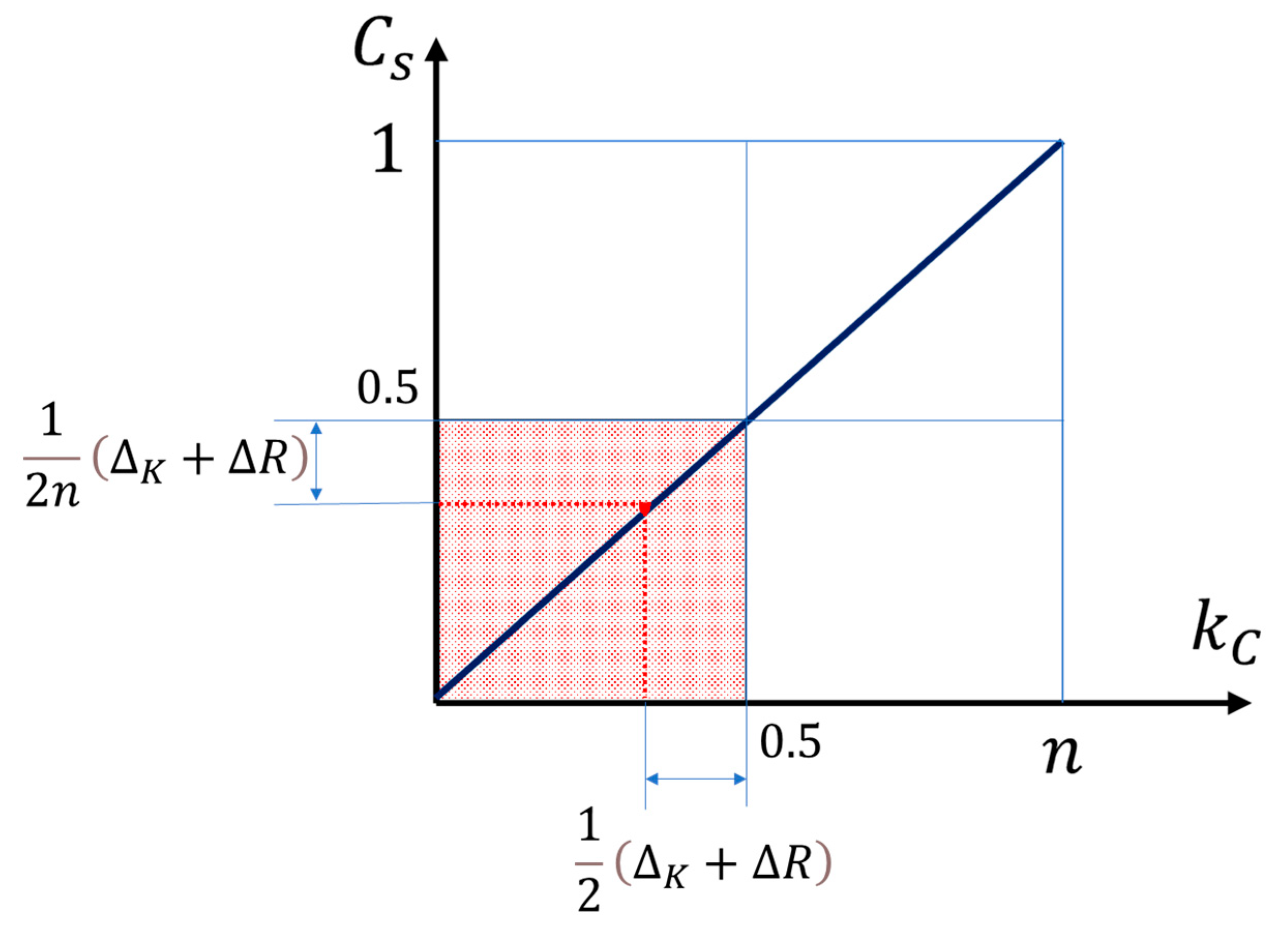
Remark 5.

Given Theorems 2 and 3, the secrecy capacity of the proposed system is

$$C_s=1-C\left(W_e\right)={\displaystyle \frac{k_C}{n}},$$

(50)

From this, the fundamental impact of the secret key length is clearly evident (see Figure 4). For $k_C=0$, the system does not provide any security, while for $k_C=n$, $C_s=1$. This means that in the latter case, we can choose all n bits of polar code for secure transmission of n message bits.

In order to examine the properties of ideally secret autonomous cipher systems, we need the following theorem, which provides a lower bound on the equivocation of the system’s secret keys.

Theorem 4.

The equivocation of the secret keys $K$ of KSG($K$), when the ciphertext is known, satisfies the inequality

$$H\left(K|Z_1^n\right)\ge H\left(K\right)+H\left(V_{\mathcal{R}}\right)-n ,$$

(51)

where n is the length of the polar code, $H\left(K\right)$ is the entropy of the secret key, and $V_{\mathcal{R}}=e$ is a purely random vector of dimension $\left|V_{\mathcal{R}}\right|=\left|\mathcal{R}\right|=\left|[1,n]\setminus P_n\left(W_e,{\delta }_n\right)\right|$.

Proof. 

Generally, according to [25], for any cipher system with a secret key $K$, the input $X_1^n$, and the ciphertext (output) $Z_1^n$, it holds that $H\left(K|Z_1^n\right)=H\left(K\right)+H\left(X_1^n\right)-H\left(Z_1^n\right)$. On the basis of (11), the output vector $X_1^n$ can be written in the form

$$X_1^n=V_{\mathcal{R}}{G}_{\mathcal{R}}\oplus V_{\mathcal{A}}{G}_{\mathcal{A}}=e_1^{n-k}{G}_{\mathcal{R}}\oplus m_1^k{G}_{\mathcal{A}}$$

(52)

where $G_{\mathcal{R}}$ and $G_{\mathcal{A}}$ are submatrices of the polar code generator matrix $G_n,$ consisting of the corresponding rows in $G_n$.

The ranks of the matrices $G_{\mathcal{R}}$ and $G_{\mathcal{A}}$ are $n-k$ and $k$, respectively, because the generator matrix $G_n$ has the full rank $n$. Therefore, $e_1^{n-k}{G}_{\mathcal{R}}$ and $m_1^k{G}_{\mathcal{A}}$ can be uniquely represented by a set of basis vectors of dimensions $n-k$ and $k$. These base vectors are some of the column vectors of the matrices $G_{\mathcal{R}}$ and $G_{\mathcal{A}}$. We will denote these sets of column indices as ${\mathcal{T}}_{\mathcal{R}}$ and ${\mathcal{T}}_{\mathcal{A}}$. Then there exists a one-to-one correspondence between $e_1^{n-k}$ and $X_{{\mathcal{T}}_{\mathcal{R}}}$, and between $m_1^k$ and $X_{{\mathcal{T}}_{\mathcal{A}}}$. Hence

$$H\left(V_{\mathcal{R}}{G}_{\mathcal{R}}\right)=H\left(V_{\mathcal{R}}\right) ,$$

(53)

$$H\left(V_{\mathcal{A}}{G}_{\mathcal{A}}\right)=H\left(V_{\mathcal{A}}\right) .$$

(54)

According to the data processing properties of entropy [35], we conclude that in the PA procedure, there is a limitation, ${n{C}_s=k}_c\le H\left(V_{\mathcal{R}}\right)=n-k=n-n{C}_s$, from which it follows that the secrecy capacity in the ISAR system must be $C_s<{\displaystyle \frac{1}{2}}.$ Thus, it holds that

$$H\left(X_1^n\right)=V_{\mathcal{R}}{G}_{\mathcal{R}}\oplus V_{\mathcal{A}}{G}_{\mathcal{A}}\ge max\left\{H\left(V_{\mathcal{R}}\right),H\left(V_{\mathcal{A}}\right)\right\}=H\left(V_{\mathcal{R}}\right) ,$$

(55)

given the condition $C_s<{\displaystyle \frac{1}{2}}$ and the fact that $V_{\mathcal{R}}$ is a purely random vector with the maximum entropy equal to $H\left(V_{\mathcal{R}}\right)=\left|V_{\mathcal{R}}\right|=n-k.$ Since it is always true that

$$H\left(Z_1^n\right)\le n ,$$

(56)

we finally obtain

$$H\left(K|Z_1^n\right)=H\left(K\right)+H\left(X_1^n\right)-H\left(Z_1^n\right)\ge H\left(K\right)+H\left(V_{\mathcal{R}}\right)-n ,$$

(57)

which had to be proven. □

To ensure that the system has autonomy in generating secret keys, we need to limit the polar code rate, because some of the polar code bits must be used for generating and distributing secret keys. Additionally, for the system to be ideal and autonomous, a further reduction in secrecy capacity is necessary to maintain the desired minimum level of key equivocation. These facts are summarized in Theorem 5 below.

Theorem 5.

The proposed system is ideally secret, autonomous, and robust, with the maximal secrecy capacity

$$C_s={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2n}}\left({∆}_K+∆R\right) ,$$

(58)

where ${∆}_K\in \left(0,k_C\right)$ is a given minimum value of key equivocation and $∆R$ is the compression rate of the applied class of universal hash functions. The length of the secret key of the given symmetric stream cyphering system is $k_C=\left|K\right|$, while $n$ is the length of the polar code.

Proof. 

To prove that the proposed system is ideal, it is necessary to show that for given ${∆}_K,$ (23) and (24) hold. Consider the general case where Alice sends a message $M$ of arbitrary length ${\left|M\right|=n}_M$ to Bob. The message $M$ will be divided into blocks of length $k=\left|\mathcal{A}\right|=\left|P_n\left(W_e,{\delta }_n\right)\right|.$ The total number of blocks will be $t=⌈{\displaystyle \frac{n_M}{n}}⌉$, where $n$ is the length of the polar code, so $M=\left[m_1\left|m_2\right|\dots |m_t\right].$ The last block, if it is not of length $k$, can be padded with arbitrary content. According to the proposed coding scheme that provides strong security, $n-k=\left|\mathcal{R}\right|=n-\left|\mathcal{A}\right|=n-\left|P_n\left(W_e,{\delta }_n\right)\right|$. According to (37), in addition to the transmitted message $m_i$, Bob decodes, without error, a purely random vector $e_i$, which is of length $n-k$, which was written on the indices from the set $\mathcal{R}$ given in (32) during the encoding process on Alice’s side. Thus, Alice and Bob, after decoding, possess identical random sequences $\left\{{e_1,e_2,\dots ,e}_t\right\}$ in each of the $t$ transmitted blocks of the polar code. Eve’s optimal strategy is to decode her received signal at the output of the wiretap channel using the SC decoder. Eve knows the parameters of the applied polar code, such as the length $n$ and the index sets $\mathcal{A}$ and $\mathcal{R}$, but does not know the values of the bits at those positions. This situation is equivalent to the SC decoder operating in the mode of unknown so-called frozen bits. As noted in Remark 4, Eve’s error in optimal decoding is close to the maximum, so it can be said that Eve’s information about the sequence $\left\{{e_1,e_2,\dots ,e}_t\right\}$ is close to zero. By applying PA to the common random sequences $\left\{e_i\right\}$, Alice and Bob can further reduce Eve’s residual information about these sequences. In each current block, a secret key of length $k_C$ is generated for the next block using some chosen PA algorithm

$$K_i=PA\left(e_{i-1}\right), e_0=S, \left|K_i\right|=k_C, i=\mathrm{1,2},\dots ,t.$$

(59)

Given that $∆R$ is the compression rate of the class of universal hash functions applied in the PA process, it follows that

$$\left|K_i\right|=\left|e_{i-1}\right|-∆R, i=\mathrm{1,2},\dots ,t.$$

(60)

Having in mind that $\left|e_{i-1}\right|=n-k, i=\mathrm{1,2},\dots ,t.$ from (59) and (60), it follows that

$$k_C=n-k-∆R.$$

(61)

For the system to be ideal, it is sufficient to ensure that the right-hand side of (57) equals a predetermined minimum value of key equivocation ${∆}_K>0$ in each block, i.e.,

$$H\left(K_i\right)+H\left(V_{\mathcal{R}}\right)-n={∆}_K, i=\mathrm{1,2},\dots ,t,$$

(62)

That is, assuming that the ergodicity of the local randomness source, i.e., $H\left(e_{i-1}\right)=n-k,$ $i=\mathrm{1,2},\dots ,t$, it follows that

$$k_C+n-k-n=k_C-k{=∆}_K .$$

(63)

By substituting (61) into (63), it is obtained that

$$C_s={\displaystyle \frac{k}{n}}={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2n}}\left({∆}_K+∆R\right) ,$$

(64)

which had to be proven. □

Figure 5 gives a graphical presentation of the interdependence of the quantities $k_C$, $n$, $C_s$, ${∆}_K$, and $∆R$ from Theorem 5. If we compare Figure 4 and Figure 5, the restrictions imposed by ideality and autonomy on the possible values of secrecy capacity, secret key length, and polar code length can be clearly seen.

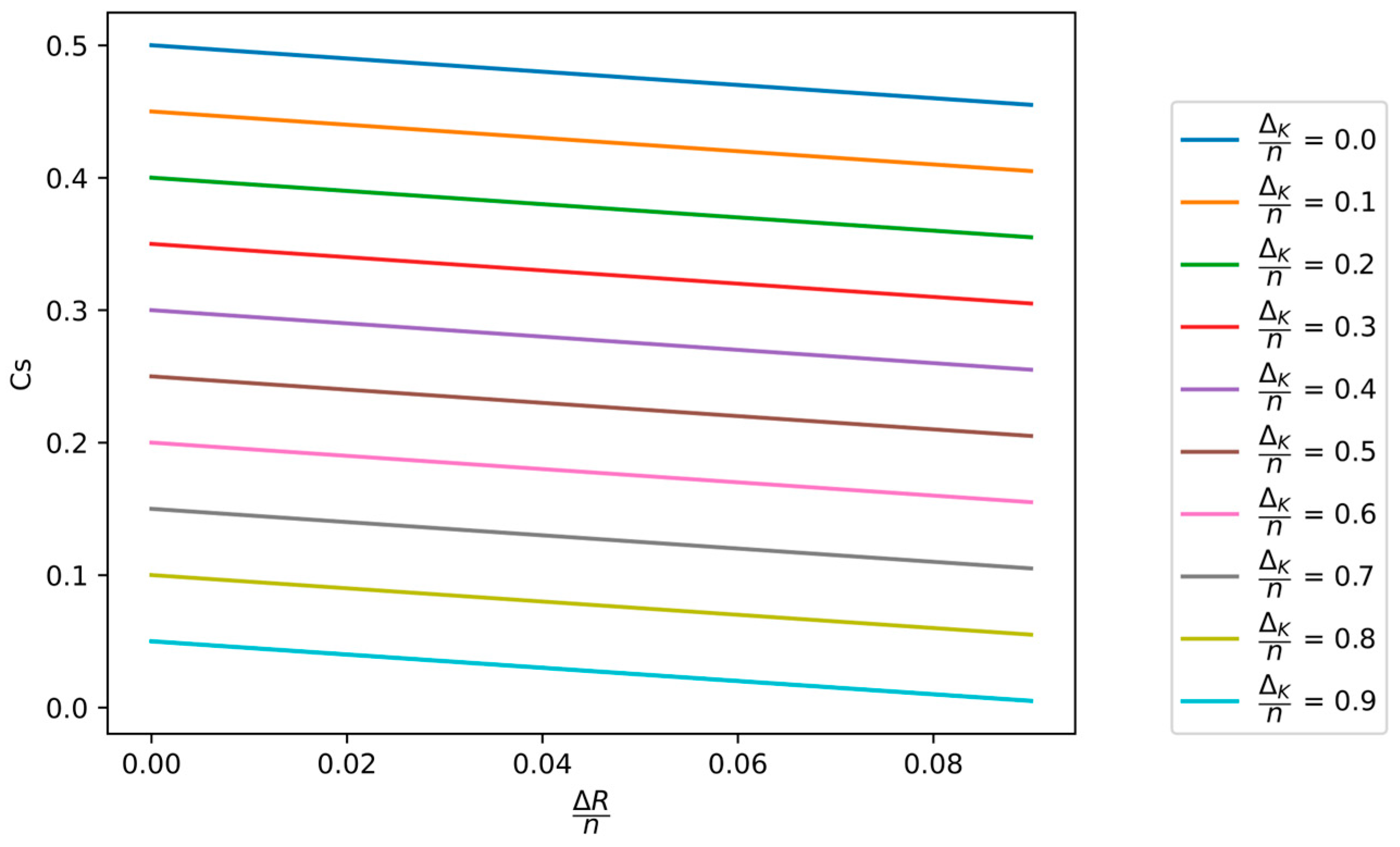
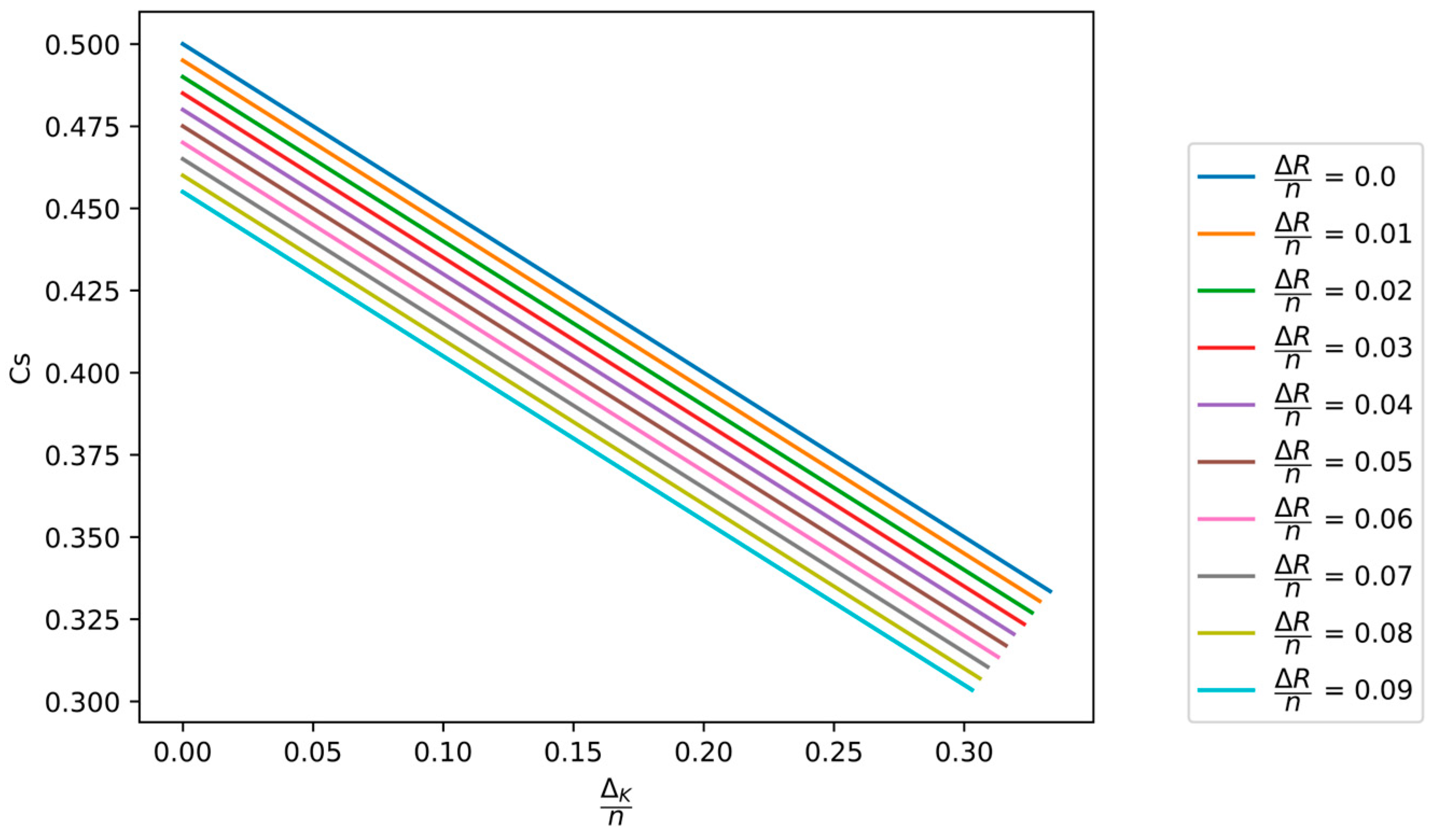
In Figure 6 and Figure 7, the dependence of the secrecy capacity $C_s$ on the normalized minimum value of key equivocation ${\displaystyle \frac{{∆}_K}{n}}$ and the normalized compression rate ${\displaystyle \frac{∆R}{n}}$ of the hash function applied in the PA process is shown.

Note that if the security margins ${∆}_K$ and $∆R$ are fixed constants, then, on the basis of Theorem 5, we conclude that ${\lim }_{n\to \infty }{C}_s={\displaystyle \frac{1}{2}}$ holds, which is the maximum possible value of the secret capacity of the ISAR system.

The presented theory offers an effective methodology for synthesizing this class of systems with predetermined security margins. The algorithms for configuring the ISAR system and for enciphering/deciphering messages of arbitrary length are described below. On the basis of the initial values of parameters ${∆}_K$ and $∆R$, the secrecy capacity $C_s$ and the length of the secret key $k_C$ are determined. If these parameters are acceptable, the synthesis of the corresponding wiretap polar code proceeds. Identifying the index sets $\mathcal{A}$$=P_n\left(W_e,{\delta }_n\right)$ and $\mathcal{R}$$=\left[1,n\right]\setminus P_n\left(W_e,{\delta }_n\right)$ requires the polarization of the wiretap channel. For practical purposes, it is simpler to replace this channel with an equivalent $BSC\left(\epsilon \right)$ channel of the same capacity. Consequently, the crossover probability must satisfy the condition

$$\epsilon =h_b^{-1}\left({\displaystyle \frac{k_C}{n}}\right) ,$$

(65)

where

$$h_b\left(a\right)=-a\mathit{log}a-(1-a)\mathit{log}1-a), 0<a<1, h_b(0)=h_b(1)=0 ,$$

(66)

is the binary entropy function, and $h_b^{-1}$ is its inverse. The polarization procedure under SC decoding can be performed using various methods, such as Monte Carlo [28], density evolution (DE) [36,37], and DE with Gaussian approximation (GA) [38], among others. In the ISAR system, where the wiretap channel is designed by the system developer, all essential parameters for the wiretap channel are much more accessible and accurately estimated compared with a scenario involving real wiretap channels. For instance, in determining the Bhattacharyya parameters $Z\left(W_e^{\left(i\right)}\right)$ using the Monte Carlo method for polarization, generating an ensemble of wiretap channel output samples is manageable. This process is facilitated by the precise knowledge of the crossover probability (65), allowing for an accurate assessment of the results.

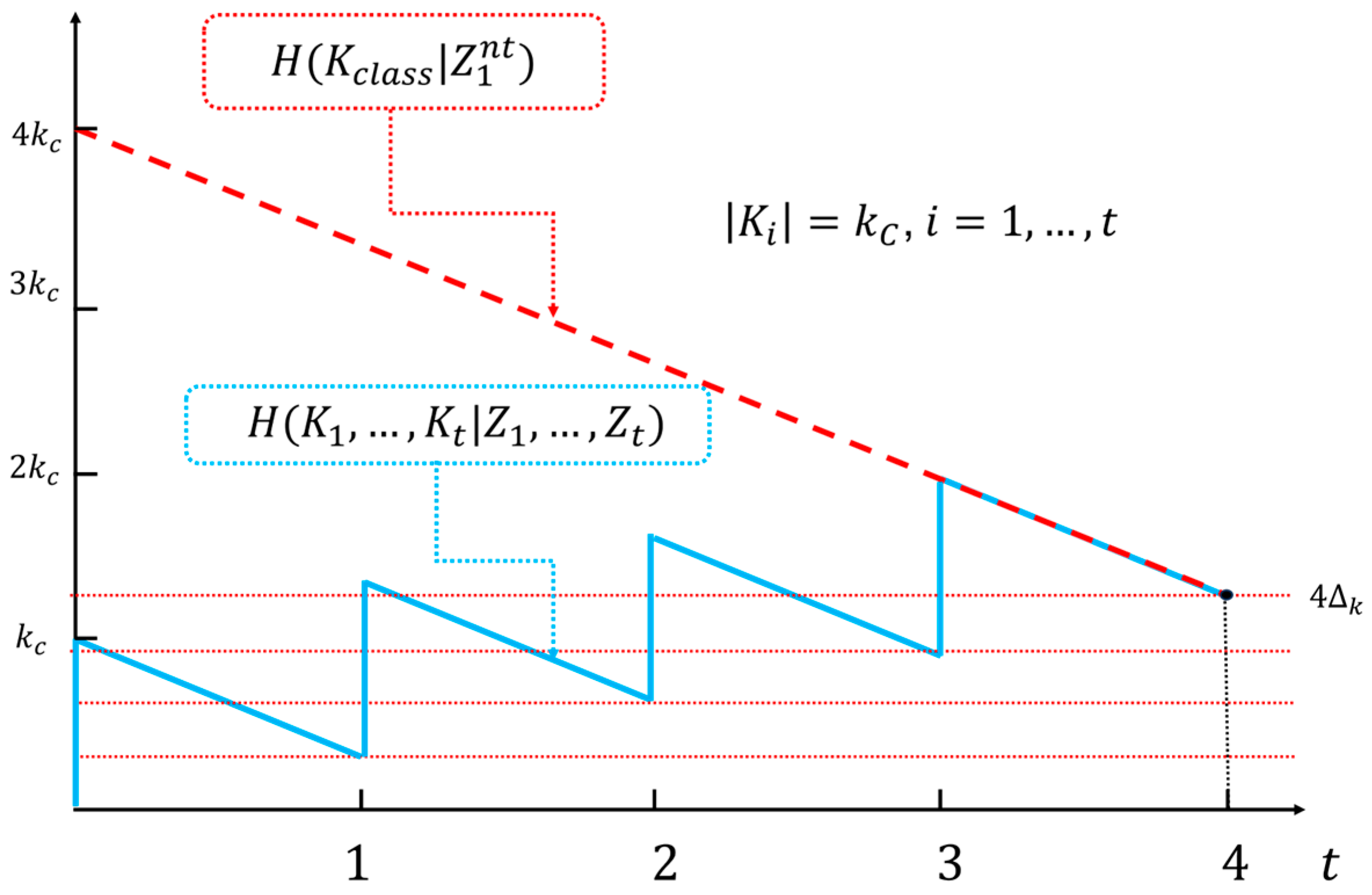
Remark 6.

Let us compare the proposed ISAR system with a classic ideal cipher system that has the same minimal key equivocation value for the same length of observed ciphertext. To ensure a fair comparison, we assume that the entropy of the input messages is identical in both systems. After encrypting t blocks of messages, and assuming that the blocks are independent, the ISAR system has a total equivocation of all applied keys equal to

$$H(K_1,\dots ,K_t|Z_1,\dots ,Z_t)={\sum }_{i=1}^{t}H\left(K_i|Z_i\right)\ge tH\left(K\right)+tH\left(V_{\mathcal{R}}\right)-nt=t{∆}_k ,$$

(67)

since the formation of each block in the polar code is independent of the previously formed blocks. A classic ideal cipher system with the secret key $K_{class}$ under the same conditions and for the same length of ciphertext has an equivocation given by

$$H\left(K_{class}|Z_1^{nt}\right)\ge H\left(K_{class}\right)+tH\left(V_{\mathcal{R}}\right)-nt=t{∆}_k .$$

(68)

Equating the same lower bounds in (67) and (68) yields the condition that

$$H\left(K_{class}\right)=tH\left(K\right) .$$

(69)

That is

$$\left|K_{class}\right|=t\left|K\right| .$$

(70)

assuming that all secret keys in both systems have maximum entropy.

To ensure that a classic encryption system achieves the same lower bound on key equivocation as the ISAR system for the same observed ciphertext length, it would need a secret key t times longer than the key length of the KSG($K$) (see Figure 8). Additionally, $K_{class}$ must be pre-distributed to legitimate parties. The length of this key scales linearly with the message length $\left|M\right|$, specifically with $t=⌈{\displaystyle \frac{\left|M\right|}{n}}⌉$. In contrast, the proposed ideal autonomous system requires only a fixed-length secret key K, independent of the message length, and requires only an initial exchange of the key values $K_1=S$. Therefore, the benefits of the ISAR system become more significant as the length of the messages increases.

Remark 7.

The ISAR system can be obtained by a suitable transformation of any given stream ciphering system based on KSG($K$) with a known secret key length $\left|K\right|=k_C$. The procedure includes the following steps.

• On the basis of the expression in (58) for the given value of the length of the secret key $k_C$, we can directly obtain the required length of the polar code, i.e.,

$$n=2k_C{+∆}_K+∆R .$$

(71)

Since the length of the polar code must be a power of 2, it is necessary to correct (71) to the value

$$\tilde{n}=2^{⌈{\mathit{log}}_{2}n⌉} .$$

(72)

• The corrected value of the length of the polar code block (72) allows the eventual correction of the total security margin to the new value

$${\widetilde{∆}}_K+\widetilde{∆}R=\tilde{n}-2k_C ,$$

(73)

bearing in mind the limitation

$${\widetilde{∆}}_K\le k_C .$$

(74)

• Since all elements for the ISAR system’s setup are available at this step, i.e., $\tilde{n},{\widetilde{∆}}_K, \widetilde{∆}R, {\delta }_{\tilde{n}}$, further operation of the system takes place according to Algorithms 1–3.

Algorithm 1 System setup

Choose $n,{∆}_K,\Delta R,{\delta }_n$. Calculate $C_s$ and $k_C=n·C_s$ based on (58). Form the corresponding equivalent $BSC\left(\mathsf{\epsilon }\right)$ wiretap channel, $\epsilon =h_b^{-1}\left({\displaystyle \frac{k_C}{n}}\right)$, and perform polarization. Determine the set of indices $P_n(W_e,{\delta }_n)=\left\{iϵ\right[1,n], C(W_e\left(i\right))\le {\delta }_n\}$. Determine the set of indices $\mathcal{A}$$=P_n(W_e,{\delta }_n)$ and $\mathcal{R}$$=[1: n] \backslash P_n(W_e,{\delta }_n)$. Agree on initial secret key $S$, and seed of hash function $K_h$.

Algorithm 2 Enciphering

Split message $M$ into $t$ blocks so that $t=⌈{\displaystyle \frac{\left|M\right|}{N}}⌉$, $M=\left[m_1\right|m_2 \dots \left|m_n\right]$, with padding of the last block with random bits if necessary. Creation of ciphertext, $z_i$.    For $i=1, \dots , t$       $e_i$                                      // generate random sequence of length $\left|e_i\right|=\left|\mathcal{A}\right|$       If $i=1$ then          $K=S$       else          $K_i=h_M(e_i-1, K_h)$       end       $c_i=$ KSG$\left(K_i\right)$                    // generate stream ciphering sequence of length $n$       $V_{\mathcal{R}}=e_i$       $V_{\mathcal{A}}=m_i$       $x_i=[V_{\mathcal{R}}, V_{\mathcal{A}}]·G_n$           // polar coding       $z_i=c_i\oplus x_i$                        // enciphering end

Algorithm 3 Deciphering

$M_d=\{ 0 \}$                          // empty set at the beginning of the algorithm For $i=1, \dots , t$       If $i=1$ then          $K=S$       else          $K_i=h_M(e_i-1, K_h)$       end       $c_i=$ KSG$\left(K_i\right)$                  // generate stream ciphering sequence of length $n$       $[V_{\mathcal{R}}, V_{\mathcal{A}}]=x_i·G_n$         // deciphering       $e_i=V_{\mathcal{R}}$                          // deciphered random sequence       $m_i=V_{\mathcal{A}}$                         // deciphered message       $M_d=\left[M_d\right|m_i]$                 // completly deciphered message    end

4. Security Analysis of the ISAR Ciphering System

The standard assumptions common in cryptography were used in the analysis of the ISAR system. The Kirchhoff principle dictates that the attacker knows the entire system operation algorithm, except for the initial secret key K of KSG(K). Further, the security integrity of cyphering and deciphering devices is an obvious assumption in cryptography. Therefore, the computation processes on the side of the legitimate sender (the dot-framed square named Alice) are inaccessible to the attacker during the execution of the polar coding and encryption operations. Otherwise, the attacker would have direct access to the messages and/or the key stream $C$. The same applies to the computation processes on the side of the legitimate recipient (the dot-framed square named Bob) during polar code decoding and decryption.

In the following analysis, we focus on the examination of passive attacks on the system. This implies that the attacker has access to the output of the wiretap channel and all information related to the architecture and operation of the system, except for the initial value $K_1=S$ and the seed of the chosen hash function $K_h.$ According to the primary objective of the attack, we can distinguish three types: message attacks, attacks on locally generated random sequences, and attacks on the secret key.

4.1. Attacks on Messages

In this type of attack, Eve attempts to obtain the message $m_i$ in each block, based on the observation of the wiretap channel output $Z_i$. According to Theorem 1, the proposed system satisfies the strong security criterion (28), which means that, asymptotically, with an increase in the codeword length $n$, Eve can only acquire a negligible amount of information about the messages $m_i$. In the case of codewords of final lengths n, the amount of information leaking to the attacker is not only limited in quantity but is also not localized to specific bit positions in the ciphertext, which further complicates potential cryptanalysis.

4.2. Attacks on Locally Generated Random Sequences

In this type of attack, Eve first tries to obtain one of the random sequences $\left\{{e_1,e_2,\dots ,e}_t\right\}$ locally generated by Alice based on the observation of the wiretap channel outputs $\left\{Z_1,\dots ,Z_t\right\}$. In the second step, using some obtained value $e_{i^{*}}, i^{*}\in \left[1,t-1\right]$, Alice could potentially generate the correct secret key for the next block $i^{*}+1$. Knowing the secret key for block $i^{*}+1$, Eve could successfully decode all subsequent blocks, thereby obtaining all messages in the sequence $\left\{m_{i^{*}+1}, m_{i^{*}+2},\dots ,m_t\right\}$. However, this scenario is not feasible. The first step cannot be realized efficiently since, according to Remark 4, the average block error probability on Eve’s side is close to maximal (see (40)). Of course, in this step, Eve can apply a brute force attack, which requires $2^{\left|e_i\right|}$ attempts. This means that this number of active hypotheses for $e_i$ will proceed to the next step. The second step is not possible without knowing the seed of the chosen hash function $K_h.$ As the success of this attack depends on the success of both steps, this type of attack is practically unfeasible because the overall difficulty of the attack is equal to the product of the difficulties of both steps.

4.3. Attacks on the Secret Key KSG($K$)

A far more powerful cryptanalytic attack than an attack on individual messages is an attack on the secret key $K$ of the KSG. If Eve were to obtain the secret key $K_{i^{*}}$ in block $i^{*}$ where $i^{*}\in \left[1,t-1\right]$, she would be able to access message $m_{i^{*}}$, the random sequence $e_{i^{*}}$, and, consequently, the secret key $K_{i^{*}+1}$ for the next block. This would allow her to repeat the same process for each subsequent block, thereby gaining access to all subsequent transmitted messages $\left\{m_{i^{*}+1}, m_{i^{*}+2},\dots ,m_t\right\}$, the random sequence $\left\{e_{i^{*}+1}, e_{i^{*}+2},\dots ,e_t\right\}$, and the generated secret keys $\left\{K_{i^{*}+1}, K_{i^{*}+2},\dots ,K_t\right\}.$ From the system designer’s perspective, it is crucial to prevent this scenario. The information-theoretic quantity that quantifies the likelihood of such an attack is the equivocation of the secret keys for a given wiretap channel’s output. As the ISAR system is ideally secret, its secret key equivocation, according to (62), never falls below the value ${∆}_k$, which is the security parameter in the synthesis process of the ISAR. It is important to mention that, from the cryptanalyst’s point of view, $2^{{∆}_k}$ possible values for keys/messages exist with equal probabilities. Therefore, the system’s designer can render this attack unsuccessful with any chosen margin of security. It is important to note that increasing the margin of security leads to a reduction in the secrecy capacity of ISAR (see Theorem 5 and Figure 7).

Remark 8.

An attack on the secret key of KSG(K), both as an independent entity and as part of an ISAR system, requires additional clarification. It is logical to assume that doubling the length m of the secret key increases the cryptanalyst’s effort by $2^m$ times in a brute force attack if a ciphertext of length $\left|Z\right|$ greater than the unicity point $k_C+H\left(M\right)$ is available. The outcome of this attack is a unique secret key, given that $H\left(K\right|Z)=0$. In the case of an ISAR system, however, key equivocation never falls below the value ${∆}_K$, meaning the cryptanalyst is left with $2^{{∆}_K}$ equally likely hypotheses, regardless of the ciphertext length. Additionally, according to (71), for any secret key length (including a doubled one), it is possible, by increasing the length of the polar code n, to independently select a security margin ${∆}_K$.

From this brief analysis, we can conclude that classic cryptographic systems with a finite secret key and the ISAR system must be carefully compared, since the work of the cryptanalyst in the case of the ISAR system does not lead to a unique solution.

Example 1.

To understand the order of magnitude of the difficulty of executing this attack, let us consider a typical example of an ISAR with the parameters (expressed in bits) $n=4096, {∆}_k=100, ∆R=40$. According to (58), $C_s=0.4829$, and the key length is $k_c=n{C}_s=1978$ bits. Let us assume that Eve’s optimal strategy for each block of the polar wiretap code reaches the lower bound of equivocation of 100 bits of the key. This means that Eve cannot resolve this uncertainty in any way. Recall that in a brute force attack examining all $2^{100}$ possible keys, all decrypted messages would be equally likely and valid as potential final solutions.

The example above shows that for the polar code length n of order $2^b$, the key length of KSG($K$) is of order $2^{b-1}$. These lengths are not common for commercial stream ciphering systems. However, this does not mean that such systems cannot be relatively easily upgraded to the required key lengths. As an example, we cite a generic model of a pseudo-random generator described in [39]. If the address and selection sequences are chosen so that they are the outputs of two multiple linear shift registers, then the lengths of the equivalent secret key of this pseudo-random generator can easily be set in ranges of order $2^{b-1}$.

The cryptanalysis presented here may cause some doubt regarding the level of security of the ISAR system. Specifically, wiretap polar encoding enables perfect secrecy of the messages, while the ISAR, on the other hand, guarantees only ideal secrecy. The explanation is simple. The security of the entire system is equal to the security of the weakest link in the chain. In this case, it is KSG(K), which can only provide ideal security.

To confirm this, let us show that the ISAR cannot be perfectly secret. For perfect secrecy, it is necessary for the following to be valid

$$H\left(m_i\right|Z_i)=H(Z_i), \mathrm{for} \mathrm{all} i ,$$

(75)

That is, in the case of symmetrical semi-injective systems

$$H\left(K_i\right|Z_i)=H(K_i),\mathrm{for} \mathrm{all} i .$$

(76)

According to (57), it follows that

$$H\left(K_i\right|Z_i)=H\left(K_i\right)+H\left(X_i\right)-H\left(Z_i\right)=H\left(K_i\right) ,$$

(77)

or

$$H\left(X_i\right)=H\left(Z_i\right) ⟹ H\left(X_i\right)=H\left(X_i⨁C_i\right) .$$

(78)

The last equality holds if and only if $X_i$ is a binary symmetric source (BSS) with maximum entropy. Taking (11) into account, as well as the fact that Arikan’s generator matrix $G_n$ is nonsingular, it follows that

$$H\left(X_i\right)=H\left(\left[V_{R_i} V_{A_i}\right]{\cdot G}_n\right)=H\left(\left[V_{R_i} V_{A_i}\right]\right) ,$$

(79)

In other words, $\left[V_{R_i}{V}_{A_i}\right]$ must be a BSS, and, therefore, $V_{A_i}$ must also be a BSS. Considering that, according to (14), $V_{A_i}=m_i$, we conclude that the message must be a BSS. This contradicts the robustness of the ISAR, which requires that its properties must be independent of the probability distribution of the messages. In addition to this difficulty, perfect secrecy of the ISAR would require that the entropy rate of the secret keys must be greater than or equal to the entropy rate of the input sequence $X_i$ in KSG($K_i)$, or

$$R_{X_i}={\displaystyle \frac{H\left(X_i\right)}{n}}\le R_{K_i}={\displaystyle \frac{H\left(K_i\right)}{n}}=C_s .$$

(80)

According to (50) in Remark 5, for $R_{X_i}=1$, which corresponds to the fact that $\left[V_{R_i}{V}_{A_i}\right]$ must be a BSS, it follows that, in this case, $C_s=1$ would have to hold. This contradicts the property of the ISAR stated in Theorem 5, namely that $C_s\le {\displaystyle \frac{1}{2}}$.

5. Practical Aspects

This section shows that the complexity of the system is $O\left(n\mathit{log}n\right)$, where n is the length of the polar code. For point-to-point protection, the initial exchange of the secret key and the hash function seed is performed only once, regardless of the number of sessions or communication disruptions.

5.1. Complexity of the ISAR

The computational complexity of the ISAR system includes the total complexity of polar coding and decoding, as well as the complexity of the PA block.

Polar codes are attractive in practice due to their relatively low complexity compared with other coding schemes, especially when considering the powerful error-correcting capabilities they offer. The complexity of encoding a polar code of block size n is $O\left(n\log n\right)$. This efficient complexity is due to the structured way in which the polar transform combines inputs, leveraging the recursive nature of the polar code’s construction, and can be performed using the Fast Fourier Transform (FFT) approach. To be precise, let $\mathcal{X}\left(n\right)$ denotes the worst-case complexity over all polar codes with the given block length $n$. Arikan, in [28], showed that $\mathcal{X}\left(n\right)\le {\displaystyle \frac{n}{2}}+n+2\mathcal{X}\left({\displaystyle \frac{n}{2}}\right)$. Starting with the initial value $\mathcal{X}\left(2\right)=3$, by induction, it is obtained that $\mathcal{X}\left(n\right)\le {\displaystyle \frac{3}{2}}n\log n$ for all $n=2^b$, where $b\ge 1$. Thus, the encoding complexity is indeed $O\left(n\log n\right)$.

In general, the decoding complexity depends on the applied decoding algorithm. However, in the ISAR system, decoding is a deterministic procedure identical to encoding since Arikan’s generator matrix is involutory. Therefore, the complexity of decoding is identical to the complexity of encoding, i.e., $O\left(n\log n\right)$ [28].

The PA block was implemented using random binary matrices of dimension n × $k_c$, which have the Toeplitz structure. It is known that this class of hash functions belongs to the universal family of hash functions (see [40,41]). The Toeplitz hash functions are particularly suitable for typical values for n in polar coding (in the order of $2^{10}-2^{16}$). Namely, the PA block can be efficiently implemented with a complexity of $O\left(n\log n\right)$, instead of O($n^2$), in the case of hash functions in the form of random binary matrices without the Toeplitz structure. The choice of ΔR is closely related to the leakage of the secret key to Eve. Practical methodologies for selecting this parameter, based on the estimation of a conditional Renyi entropy of order 2, have been developed in other works [42,43].

Consequently, we can say that the complexity of the ISAR system, without taking the complexity of KSG($K$) into account, is of the order of $O\left(n\log n\right)$, which indicates that the implementation of the proposed algorithm does not require special memory and computational resources. This makes it very attractive for practical implementation and use.

5.2. Integration of the ISAR Ciphering System in Contemporary Information and Communication Infrastructure

When applying the ISAR in modern information and communication infrastructure, one should keep in mind the two most important advantages of this system:

• Guaranteed security margins in terms of key equivocation (ideality);
• Independence of the length of the keys from the length of the messages.

The ideal position of the ISAR system is within the framework of permanent point-to-point protection of large-capacity information flows. That is when ideality and the independence of the length of the keys from the length of the messages come into play. As already mentioned, the start of communication requires the exchange of the secret key of KSG($K$) and the seed of the applied crypto hash function. It is interesting to note that the disruption of protected communication or its regular termination does not require an additional exchange of these values for subsequent communication. Namely, the decoded random sequences of the last block of polar code can be memorized and used to generate the initial key for subsequent communication. This raises the autonomy of the ISAR system to an even higher level.

The ISAR can also be viewed as an autonomous key generation and distribution system based on a local source of pure randomness (denoted by RS in Figure 1). In such an application, the decoded random sequences $e$ can be accumulated, stored, and then used independently of the ISAR, for the purposes of any legitimate party’s cyphering system which requires previously exchanged secret keys.

6. Conclusions

In this paper, we introduced a class of symmetric ciphering systems termed ISAR (Ideally Secret Autonomous Robust) systems. These systems are designed to provide ideal secrecy, autonomy in key generation and distribution, and robustness to the probabilistic structure of messages. These systems address the longstanding challenge in cryptography of balancing security with practicality, particularly by eliminating the need for lengthy secret keys and additional key distribution infrastructure. By ensuring a predetermined minimum value of key equivocation and continuous key refreshing, ISAR systems provide robust security against passive attacks on both keys and messages.

Our work demonstrates that ISAR systems can be applied to any existing symmetric stream ciphering system without requiring changes to the original encryption algorithm, thus offering a versatile and efficient solution for enhancing the security of current cryptographic practices. This transformation greatly supports privacy, a critical requirement for modern security systems. Overall, the ISAR system represents an advancement in cryptographic security, offering an efficient methodology for creating ciphering systems with predetermined security margins.

The main limitation of the ISAR system is its dependence on the encoding and decoding of the chosen polar code. Particularly, the constraint that the block length $n$ must be of the form $2^b$ may cause some practical problems. Although recent advancements have proposed efficient modifications for polar codes of arbitrary block lengths, their application within the ISAR system requires more careful analysis and assessment of potential security breaches. Another potential limitation of the ISAR system is its current applicability to symmetric stream ciphering systems only.

Future research directions include exploring optimizations in the ISAR architecture, extending its applicability to a broader range of cryptographic scenarios, and investigating additional techniques for enhancing its resistance to more sophisticated attack vectors. Also, the potential extension to block cipher systems is of great practical and theoretical significance. The continued development of ISAR systems holds the promise of ensuring stronger privacy and security measures in an increasingly digital world.