Abstract
The analysis of aggregate data has received increasing attention in the statistical discipline over the past 20 years, with the ongoing development of a suite of techniques that are classified as ecological inference. Much of its development has been focused solely on estimating the cell frequencies in a 2 × 2 contingency table where only the marginal totals are given; an approach that has been received with mixed reviews. More recently, the focus has shifted toward analyzing the overall association structure, rather than on the estimation of cell frequencies. This article provides some insight into how informative the aggregate data in a single 2 × 2 contingency table are for assessing the association between the variables. This is achieved through the development of a new index, the aggregate informative index. This new index quantifies how much information, on a [0, 100] scale, is needed in the marginal information in a 2 × 2 contingency table to conclude that a statistically significant association exists between the variables. It is established that, unlike Pearson’s (and other forms of the) chi-squared statistic, this new index is immune to changes in the sample size. It is also shown that the new index remains stable when the 2 × 2 contingency table consists of extreme marginal information.
Keywords:
aggregate data; aggregate association index; ecological inference; Pearson’s chi-squared statistic MSC:
62H17; 62H20; 62P10
1. Introduction
This study will focus on the case of two dichotomous categorical variables that are cross-classified to form a 2 × 2 contingency table. We shall confine our attention to when only the aggregate, or marginal, totals in this table are known. The issues arising from the analysis of aggregated categorical data (especially those from a 2 × 2 contingency table) have attracted considerable attention in the statistical and allied literature. Fisher [1] was the first to consider the problem, stating:
“Let us blot out the contents of the table, leaving only the marginal frequencies. If it be admitted that these marginal frequencies by themselves supply no information on the point at issue, namely, as to the proportionality of the frequencies in the body of the table, we may recognize that we are concerned only with the relative probabilities of occurrence of the different ways in which the table can be filled in, subject to these marginal frequencies.”
Yates [2] agreed with Fisher’s comments noting that there are exceptions “in extreme cases and in repeated sampling”. Others who have discussed their agreement with Fisher’s comments can also be found in [3,4,5]. To help provide further context on the estimation of the “frequencies in the body of the table”, Goodman [6,7] developed a simple linear equation. He referred to this equation as an “ecological regression” and used it to estimate the cell frequencies of a 2 × 2 contingency table; a technique designed to undertake such inferences of the cell frequencies would be referred to as an ecological inference (EI) technique. Goodman built his model around the known marginal information in G stratified 2 × 2 contingency tables and the unknowns, and ; these quantities are the parameters to be estimated for the gth strata, where g = 1, 2, …, G. Here, is the conditional probability of an individual/unit being classified into “Column 1”, given that it has been classified into “Row 1”, while is the conditional probability of an individual/unit being classified into the same column, given that it has been classified into “Row 2”. While Goodman’s model is simple and intuitive, it suffers from two key flaws. Firstly, there are 2G unknowns, but only G equations leading to the indeterminacy problem. Secondly, to avoid this problem, Goodman assumed that each of the unknowns are homogeneous across the G strata, so that and . These assumptions have proved to be unrealistic in most practical situations. As a result, the EI literature has focused on the estimation of and , which relies heavily on a range of Bayesian assumptions and strategies. Of special note is the book by King [8]; he put forward a suite of EI techniques that center on the assumption that and can be modelled using a truncated bivariate normal distribution. King [8] was careful to note that his approach meant that “aggregation bias” is not present in his approach and that it is assumed that each strata behaves independently; both aspects being generally unrealistic and discussed in detail by Cho [9]. Further advances to EI methodologies were proposed by King [10], wherein he used Markov chain Monte Carlo methods to extend his EI approach. Steel et al. [11] introduced their homogeneous model, which overcame most of the assumptions in the approach put forward by Goodman [6,7] and King [8], while also addressing assumptions made in terms of other EI techniques. Rather than assuming anything about the underlying behavior of and , they assumed that the (1, 1)th cell frequency of the gth strata 2 × 2 table is a binomial random variable, with the parameters being the marginal total of the first row of the gth strata and P(Column 1|Row 1). They also assumed that the (2, 1)th cell frequency is a binomial random variable, where its parameters are the marginal total of the gth strata’s second row, so that P(Column 2|Row 1). To deal with the indeterminacy problem, Steel et al. [11] assumes that and . Hudson et al. [12] showed the utility of the EI method by Steel et al. [11], when analyzing early gendered New Zealand voting data (between 1893 and 1919, inclusive). The data that Hudson et al. [12] analyzed consisted of known cell frequencies and, therefore, they were able to compare the predictions made for and using a variety of EI techniques, including King’s [8] technique and that of Steel et al. [11], with the known values, to assess their practicality and utility. Hudson et al. [12] (pp. 198–199) pointed out that:
“Choosing the method that is appropriate to a particular data set involves several considerations. Firstly, do the assumptions fit the data? All EI methods make assumptions about the data to compensate for the loss of information due to aggregation. Secondly, statistical evaluations of models can point to theoretically better alternatives…Thirdly, [the] plausibility and consistency of results are, in themselves, important indicators for success. Fourthly, testing EI methods relies on using empirical evaluation on a range of data sets.”
Furthermore, in the context of epidemiological studies, Greenland and Robins [13] (p. 747) note that estimating and can be subject to biases that are not present in the estimation methods used, since individual level covariate information is often not used to estimate these parameters. Cho [9] (p. 163) issues a warning about using EI techniques, saying:
“As with any model, EI is built on assumptions, and these can be far off or right on target. The estimates therefore may also be far off or right on the true parameters. Substantive discussions of the results of EI should thus always include a discussion of the assumptions, how reasonable they are for the problem at hand, and how these assumptions drive the results. Excitement about the advances to ecological inference provided by EI should not be allowed to lead to insufficient attention to the strong and potentially inappropriate assumptions at the heart of the model. The model is useful if and only if the assumptions fit.”
More recently, Barreto et al. [14] (p. 298) concedes that “claims about the superiority of one method [of EI] over the other should not be made without clear and convincing evidence” and that this evidence comes from knowledge about the data and the strength and weaknesses of the EI method being used. Additionally, Papalia and Vazquez [15] (p. 1) warn that “in many [EI] situations…the accuracy of any predicted value cannot be verified”. Roumeliotis et al. [16] are far more cautious about using EI, showing that it can impact on six practical research questions posed in the context of health disciplines; these questions are centered on the assumption that conclusions at the aggregate level transfer to the individual level (the ecological fallacy). They conclude their discussion by saying (p. 504):
“The conclusions of an ecological study should be carefully evaluated in order to assess whether they are biologically plausible, whether alternative explanations exist to interpret the results and whether all potential confounders were taken into account in the data analysis. When reading an ecological study, we should always be aware of the possibility of an ecological fallacy whereby potentially misleading causal inferences might be generated.”
Kim and Lee [17] also warn against the use of EI when analyzing voting behavior data, while Geissbühler et al. [18] raise similar concerns to those made by Roumeliotis et al. [16], but from the perspective of meta-analyses of aggregated data in clinical studies. They highlighted that such analyses could lead to at least one of three “pitfalls”: committing the ecological fallacy, the models used can lead to overfitting of the data, especially if too few confounding variables are considered, and models that involve regressions to the mean are inappropriate when analyzing aggregated data.
Despite seeing the concerns and caveats raised in the last three decades over the development and refinement of EI techniques and the assumptions they make, new techniques and applications are being developed. For example, Barreto et al. [14] have used EI to study voting differences across elections that include the involvement of more than two racial groups, while Pavía and Romero [19] have studied voting behavior when an individual is asked to choose a party and a candidate. Papalia and Vazquez [15] proposed two entropy-based EI techniques, which they showed “have the potential to obtain disaggregated estimates based on minimal assumptions about the data-generating process” (p. 10), and Fisher and Wakefield [20] built a series of models to study aggregated surveillance data in order to study the effectiveness of vaccines for treating the transmission of infectious diseases. Their EI method relies on the assumption that the unknown parameters are binomial random variables and then various assumptions are made to help simplify the estimation procedure, ultimately finding that their method performs “reasonably well” (p. 233). While the development of EI techniques continues, concerns about the choice of EI model and the assumptions that are made persist.
The last 20 years has also seen an a lot of attention given to the development of EI strategies to study stratified R × C tables; see, for example, the work by Ferree [21], Greiner and Quinn [22], Collingwood et al. [23], Plescia and De Sio [24], Greiner et al. [25], Barreto et al. [14], Pavía and Thomsen [26], and Pavía and Romero [19,27,28], who propose a range of methods, each involving different ways to model aggregate data and using different assumptions for the unknown quantities. Some of these contributions also present R packages that aid in the computation of EI, as does the work by Imai et al. [29], King and Roberts [30], Lau et al. [31], Forcina and Pavía [32], and Pavía and Romero [33]. Despite this recent growth in attention, most EI strategies generally only involve the analysis of stratified 2 × 2 contingency tables. It is also the case that none of the EI strategies developed are designed to analyze a single table of any size. Therefore, rather than focusing on the estimation of cell values in 2 × 2 tables, the focus can be and has been redirected to determining the association structure between the two relevant dichotomous variables, using the marginal (aggregated) information only. In doing so, Beh [34,35] developed an index that does exactly this and referred to it as the aggregated association index or the AAI. The AAI quantifies, on a [0, 100] scale, the extent of association that may be present in the table, based only on marginal information. It does this by identifying those cell values that lead to a statistically significant association between the variables, keeping in mind that the permissible cell values are constrained by a special set of Fréchet [36] bounds.
Further development of the AAI has since been undertaken by [37,38,39]. See Tran et al. [40] for an application of the AAI to the 1893 election data from New Zealand, the first country to permit voting by females. We also refer the interested reader to Beh et al. [41], who presented a novel application of the AAI for the clustering of stratified aggregated data using voter turnout data from New Zealand (1893–1919). These applications and developments were reported in the work by Fairburn and Olssen [42] and were elaborated on in the work by Moore [43].
While the AAI helps to determine whether there is evidence of a statistically significant association between the variables in a 2 × 2 table when only the marginal information is given, it does not help to answer the following question:
“How informative is the marginal information for determining whether there exists a statistically significant association between the variables?”
Answering this question becomes important, since a statistically significant association between the variables in all contingency tables is a function of the sample size. For example, doubling the sample size will double the chi-squared statistic, so that there is always a sample size where a statistically significant association will be detected (even if the underlying proportions in the cells and margins remain unchanged). Therefore, the aim of this paper is to answer the above question by developing a new index, the aggregate informative index (AII). This new index quantifies how much information, on a [0, 100] scale, there is in the row and column totals of a 2 × 2 contingency table in order to conclude that a statistically significant association exists between the variables. It is established that, unlike Pearson’s (and other forms of the) chi-squared statistic and the AAI, the new index, the AII, is immune to changes in the sample size. The applicability of the AII is demonstrated in the Results Section by using real-life classic data sets, namely R.A. Fisher’s criminal twin data [1] and Irving Selikoff’s asbestosis data [44].
2. Methods
2.1. The 2 × 2 Contingency Table
Consider a 2 × 2 contingency table, N, with a sample size, n. Denote to be the joint frequency of the cell, so that its relative joint frequency is for and . Define the row and column marginal frequency according to and , respectively, such that is the total sample size. We shall also denote the row and column relative marginal frequency according to and , respectively. Table 1 provides a description of the notations used in this paper.

Table 1.
A general 2 × 2 contingency table.
For the purpose of investigating how informative the marginal frequencies of N are for analyzing the association between the row and column variables, we consider the conditional probability and . Here, is the conditional probability of the classification of an individual/unit into “Column 1”, given that it has been classified into “Row 1”. Similarly, is the conditional probability of an individual/unit being classified into “Column 1”, given that it has been classified into “Row 2”. According to the hypothesis of independence between two dichotomous variables, the expected value of is denoted by . We shall also consider the overall mean cell frequency of the four cells in Table 1, which we denote according to . Therefore, the overall mean cell proportion for the cell is 0.25.
When the cell values in Table 1 are not known, then lies within the Fréchet bounds:
These bounds have been considered for the analysis of a 2 × 2 contingency table, especially in the EI literature; see, for example, King [8] and Duncan and Davis [45]. By considering (1), is therefore bounded by:
Using only the marginal information of the row and column in a 2 × 2 table, Beh et al. [39] showed that when a test of the association between the variables is made at the level of significance, the bounds of are narrowed to:
Here, is the 1—α percentile of the chi-squared distribution, with one degree of freedom.
2.2. The Aggregate Association Index
By considering only the marginal information in a single 2 × 2 table, Beh [34,35] developed the AAI. The AAI is bounded by [0, 100] and quantifies, for a given level of significance α, how likely a particular set of fixed marginal frequencies will enable the analyst to conclude that there exists a statistically significant association between the two dichotomous variables. An AAI close to zero indicates that there is virtually no information in the margins to suggest that such an association might exist, while an AAI close to 100 reflects that such an association is very likely to exist. This section briefly outlines the AAI and shows the impact that the sample size, n, and extreme margins have on its magnitude.
When the four cell frequencies of N are unknown, is also unknown, but bounded by (2). Therefore, we may consider Pearson’s chi-squared statistic as a function of , such that:
See, for example, Beh [34] (Equation (16)). Therefore, by graphically depicting the relationship between (4) and , we obtain a parabolic curve, with positive concavity. This curve is referred to as the AAI curve and is depicted Figure 1. Since we are interested in detecting where there exists a statistically significant association between the row and column variables in Table 1, this can then be assessed by observing those values that exceed the critical value of , but lie under the AAI curve. This region is represented by the shaded area in Figure 1. Therefore, the proportion of this shaded area, when compared with the total area under the curve, is:
and is the AAI of N. Beh [35] showed that (5) can be alternatively and equivalently expressed free of integrals, so that:
where:
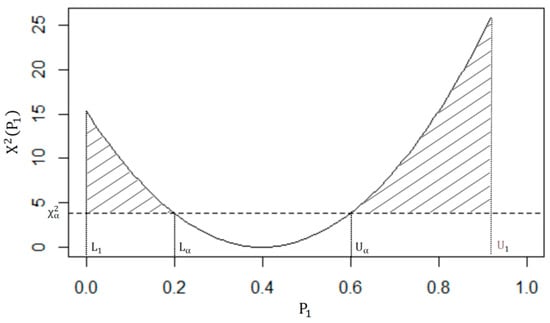
Figure 1.
The shaded region depicts the aggregate association index (AAI).
The maximum value that the AAI can attain is 100, when the extent of association between both variables is very high. Similarly, the minimum possible value of the AAI is zero and indicates that, based only on the marginal information in Table 1, the likelihood of a statistically significant association existing between the variables, at the α level of significance, is very low. Beh [35] (Section 4) showed that the AAI can also be partitioned as follows:
where is the aggregate positive association index and is that part of that reflects the extent to which the marginal information of N reflects a statistically significant positive association at the a level of significance. Similarly, is the aggregate negative association index and reflects a statistically significant negative association at this value of α.
An important issue that needs to be considered when calculating an AAI is that the sample size of N, n, has an impact on its magnitude. One can see that Pearson’s chi-squared statistic, (4), is greatly influenced by the magnitude of the sample size n; see also Everitt [46] (p. 56). As the sample size increases, so does Pearson’s chi-squared statistic, a feature described by Mosteller [47]. Therefore, for a fixed level of significance, α, the AAI will also increase; so that doubling, say, the original sample size, will double the magnitude of the chi-squared statistic. Like Pearson’s chi-squared statistic, this can create problems when assessing the association structure of the variables when only the marginal information is given. To help reduce the impact that the sample size has on the magnitude of the AAI, Beh et al. [38] derives alternative definitions of the AAI, (5). We will not describe these alternatives here.
2.3. The Aggregate Informative Index
To accommodate the feature that any change in the sample size of N impacts on the magnitude of Pearson’s chi-squared statistic and, therefore the AAI, this section introduces a new index that assesses how informative, on a scale from 0 to 100, the marginal frequencies in a 2 × 2 contingency table are for concluding whether a statistically significant association exists between the variables in the table. This index is referred to as the aggregate informative index, or the AII, and its mathematical foundations are the same foundations on which the AAI rest; see Equations (1)–(4). To develop this index, we first need to establish a “benchmark” quantity that reflects no information in the marginal totals of N.
2.3.1. The Benchmark Situation (No Information)
For any given sample size, n, in a 2 × 2 contingency table, the individuals/units can be classified into each of the two row and two column categories in a variety of ways. Here, we will define the benchmark situation to be the case where the sample size is equally distributed between the two row categories and the two column categories. For example, in the case where n is even, the benchmark situation arises when . With no further information on the classifications made in the contingency table and assuming that the individuals/units are uniformly distributed between the two categories, this benchmark situation is considered to be the most conservative option. Allocations based on other criteria may also be considered to define the benchmark situation, but to keep the description in our new index simple, we will not consider them here.
As described by Beh [35], when only marginal information is available, the benchmark situation is also the situation where the least amount of information on the association structure exists. Then, it is also equally likely that the dichotomous variables are positively or negatively associated. As one moves closer to the case where the allocation of the sample size amongst the categories is deemed to be “extreme” (for example, when or ), the information contained in the margins for establishing whether a statistically significant association exists between the variables becomes more apparent. Based on the underlying structure of the AAI, we shall now quantify how informative the marginal information is by comparing it with the benchmark situation.
In the benchmark situation, the expected cell frequency of the cell, in terms of the null hypothesis of independence between the two dichotomous variables, is identical to the overall mean cell value of the cells. That is, . Therefore, in the benchmark situation, is bounded by:
while Pearson’s chi-squared statistic is a parabolic function of with positive concavity, such that:
Therefore, the AAI curve that describes this relationship is symmetrical around and this is also where attains its minimum value of zero. The AAI curve depicted using (7) is referred to as the benchmark curve. In this benchmark case, the maximum value of will be equal to the sample size, n, and this situation arises at the bounds of (6).
Figure 2 provides a visual comparison of the benchmark and AAI curves, given the margins of an unspecified 2 × 2 contingency table. The shaded region reflects how much information there is in the row and column totals to conclude that the association between the dichotomous variables is statistically significant at the α level of significance. We now describe how to quantify the area of this shaded region.
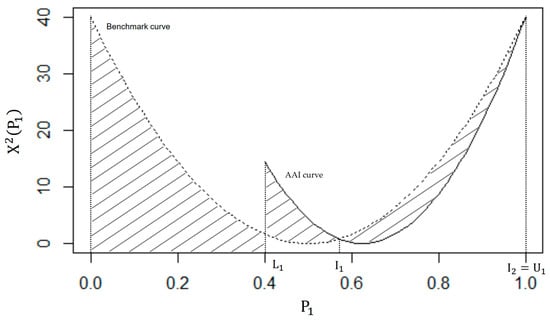
Figure 2.
A graphical interpretation of the AAI curve and the benchmark curve for n = 40, yielding the AII (the shaded region); .
2.3.2. The New Index
The rationale underlying the AII is to quantify the area arising from any deviation in the AAI curve from the benchmark situation. This area is quantified relative to the maximum possible area between the benchmark and the AAI curve and is defined by:
so that . For (8), the numerator (denoted as ) is the area under the curve specified by the difference between the benchmark curve and the AAI curve and is dependent on the range of possible values. The denominator of (8) (denoted as ) is the maximum possible area under the AAI or benchmark curve.
If the AII is close to 100, then the features of the AAI curve are as different to the benchmark curve as they can be. Thus, the marginal information in the 2 × 2 contingency table varies considerably from the benchmark situation. Hence, the marginal information is deemed to be informative for determining the statistical significance of the association between the variables. Conversely, an AII close to (or equal) to zero shows that the marginal information is consistent with the benchmark situation. Therefore, the marginal information in the 2 × 2 contingency table is deemed to be not very informative for determining the association between the variables.
We can simplify the AII of (8) by removing the integrals in the expression. In doing so:
and
where:
Therefore, can be alternatively and equivalently expressed as:
Similarly:
Therefore, the AII, (8), may be alternatively and equivalently expressed without the need for the integrals, so that:
Since the magnitude of , , and do not depend on the sample size, n, the magnitude of the AII is independent of n. Therefore, unlike the AAI and Pearson’s chi-squared statistic, any change in the sample size of the 2 × 2 contingency table does not impact the magnitude of the AII. This feature is shown in the two applications discussed in detail in Section 3.
When visualizing the AII, identifying the points where the benchmark curve and the AAI curve intersect is important. Since both curves are parabolic, there will be either a single or two points of intersection. Suppose we consider the case where there are two points of intersection, denoted by and , they can be derived by solving when . Doing so yields:
Depending on the configuration of the marginal information, there may also be a single point of intersection between the benchmark curve and the AII curve.
3. Results
3.1. Analysis of Fisher’s Criminal Twin Data
3.1.1. The Data
Consider R.A. Fisher’s [1] (p. 48) classic data, summarized in Table 2. These data are based on a study of 30 criminal twins who have been classified according to whether they are a monozygotic or dizygotic twin and whether their same sex twin sibling has been convicted for criminal activity or not. This data set was also discussed by Beh [34,35] and recently by Beh et al. [39] in their discussion on the AAI. Therefore, we will consider the data here, with a view to demonstrating the applicability of the AII.

Table 2.
R.A. Fisher’s [1] classic criminal twin data.
In the case where the cell frequencies in Table 2 are assumed to be known, Pearson’s test of independence results in a p-value of 0.0012. Therefore, there is ample evidence to conclude that there is a statistically significant association between the two variables in Table 2. A more practical interpretation of this conclusion is that the type of twin and the conviction status of their twin sibling (of the same sex) are related. By just observing the cell frequencies in Table 2, this relationship is defined by the dominance that a monozygotic twin has a twin sibling (of the same sex) that is more likely to be convicted of a crime than not, while there is a dominance in terms of dizygotic twins and their twin sibling who are not likely to be convicted of a crime. If we now “blot out” the cells, as Fisher [1] (p. 48) originally considered, or are faced with the situation where the cell frequencies are not known, ; here, is defined as the proportion of convicted twins that are monozygotic twins with their sibling (of the same sex). When a test of the association is performed using the 5% level of significance, there is a statistically significant association between the dichotomous variables in Table 2 when and Also, when using (5), the AAI is . The magnitude of this index shows that, using only the marginal information in Table 2, there is strong evidence to conclude that the variables are significantly statistically associated at the 5% level of significance. In fact, by partitioning the AAI, we have and . Therefore, the marginal information in Table 2 shows that if there is a statistically significant association between the variables, it is about three times more likely to be positive than negative. This is indeed reflected in the cell frequencies in Table 2; recall that there is a dominant link between monozygotic twins with their convicted twin sibling and dizygotic twins with their twin sibling, who has not been convicted of a crime.
Now that we have determined that the marginal information in Table 2 indicates the likely strength and direction of the association between the row and column variables, we can now determine how informative this information is for making such a conclusion. It is apparent that the two row totals are relatively similar and the two column totals are relatively similar. If the difference between the marginal frequency of each row and the marginal frequency of each column were greater, the AAI of 61.83 may indeed be closer to 100, yielding marginal data that is more informative (when compared with the benchmark situation of “no information”) than what is summarized in Table 2.
To calculate the AII, we first note that the overall mean frequency of the four cells is 30/4 = 7.5, so that in the benchmark situation each row total and column total is 15. Then, any deviation in the row and column totals from this value provides better quality information for identifying the nature of the association that may exist in Table 2. Now, consider Pearson’s chi-squared statistic (4). Based on Table 2, this statistic can be expressed as a function of , so that:
Similarly, in the benchmark case, this relationship is expressed as:
A graphical comparison of (11) and (12) is given in Figure 3. By using (10), the points of intersection of the two curves exist at the values of and and ; note that is the only valid intersection between the benchmark and AAI curves based on the data in Table 2. We can also see that the maximum area under the curve, for , is , so that the AII for Table 2 is:
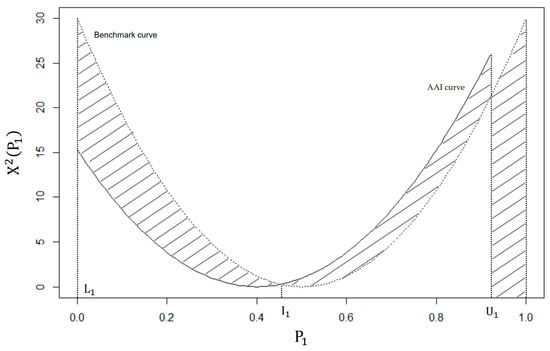
Figure 3.
A graphical interpretation of the AII for Table 1.
Therefore, the marginal information in Table 2 is not very informative for assessing the association between the variables.
3.1.2. On the Robustness of the New Index
The relatively small value of the AII arises because there is only a 20% difference between the two column totals in Table 2 and less than 15% difference between the row totals; here, and . Therefore, even if the sample size was doubled (say), and the relative marginal frequencies remained unchanged, the AII will remain unchanged. Note that, unlike the AAI, the magnitude of the AII is independent of the sample size, as (9) shows.
3.1.3. Concerning Extreme Marginal Information
It is also interesting to study the impact on the AII when altering the marginal configuration given a particular sample size, say n = 30. Suppose a more extreme allocation of the marginal frequencies is made, such that for all the values of n. In this case, using (2), is bounded by , and the relationship between Pearson’s chi-squared statistic and , as defined by (4), is:
Therefore, in this case, the AII can be written solely in terms of n, so that:
Table 3 summarizes, to two decimal places, the behavior of the AII when the sample size of Table 2 has an extreme marginal relative frequency allocation of for various values of n; when n = 30 (as it is for Table 2), this configuration of marginal information means that there are only two valid assignments of the cell frequencies, which are and . In this case, we can see that the AII changes from 33.0063 (for Table 2) to 54.9261 (when and ). This change in the AII demonstrates the responsiveness of the AII to shifts in the marginal frequencies. It also shows that, in the case of extreme marginal information, the AII remains relatively stable as the sample size increases. Table 3 also summarizes the AAI for and as n → ; recall that the AAI for Table 2 is 61.83, while, for and , the AAI is 69.4. Table 3 also shows the increase in the AAI in the case of our extreme marginal information configuration, as the sample size of Fisher’s crime data increases to n = 5000. Refer to Beh [34,35] and Beh et al. [38] for a detailed description of the impact of the sample size on the magnitude of the AAI, (5).

Table 3.
The behavior of the AAI and AII for and different values of n.
3.2. Analysis of Selikoff’s Asbestosis Data
In 1963, a study was conducted that involved collecting data from 1117 insulation workers in New York. This landmark epidemiological study, and its findings published by Irving Selikoff in 1981 [44], established the link between long-term occupational exposure to asbestos fibers and the severity of the asbestosis that the workers were diagnosed with. These data, summarized in Table 4, have also been a topic of statistical discussion by Beh and Smith [48] and Tran et al. [49], where the latter studied the asbestosis data in terms of the AAI. Based on Table 4, and , so that, unlike the columns, the marginal relative frequencies of the rows are notably different from when compared with the marginal relative frequencies for Table 2.

Table 4.
Irving Selikoff’s asbestosis data [44].
A study of the data in Table 4 shows that, when the cell frequencies are known, the chi-squared test of independence yields a p-value that is less 0.0001. Therefore, the association between the two dichotomous variables in Table 4 is statistically significant. In fact, this association is positive (confirmed by testing the correlation between the variables), a conclusion which helps to confirm Selikoff’s [44] (p. 948) now famous “20-year rule”; this “rule” reflects the finding that workers who were exposed to asbestos fibers for at least 20 years were at a higher risk of being diagnosed with asbestosis than workers who were exposed to the fibers for less than 20 years.
Suppose that the joint cell frequencies in Table 4 are assumed to be unknown, given the marginal information on the data, the AAI is (at the 5% level of significance), with and showing that the association is slightly more likely to be positive than negative, given the marginal information in Table 4. This is reflected in Table 4, with those exposed to asbestos fibers for less than 20 years being likely to not be diagnosed with asbestosis, while those exposed to such fibers for more than 20 years being likely to be diagnosed with asbestosis. Such a very high AAI value indicates that, given only the marginal information, it is highly likely that the association between the years of occupational exposure and whether a worker is diagnosed with asbestosis is statistically significant at the 5% level of significance. The magnitude of the AAI may in fact be due to the large sample size. However, it is also possible that the distribution of the marginal information is also very informative when making a conclusion about the association based solely on this information. To investigate how informative the marginal information is, we shall determine the AII for Table 4.
By considering (4) and (7) in regard to Table 4, the AAI and benchmark curves are defined by Pearson’s chi-squared statistic, respectively:
and
Figure 4 provides a graphical depiction of the benchmark and AAI curves. Using (2), the bounds of for the AAI curve is and the points of intersection between the AAI curve and the benchmark curve exist at = 0.51 and = 0.56. It is apparent from Figure 4 that the area under the AAI curve, based on the marginal information in Table 2, is vastly different from the area under the benchmark. In fact, D = 262.44, while M = 371.67, resulting in an AII of:
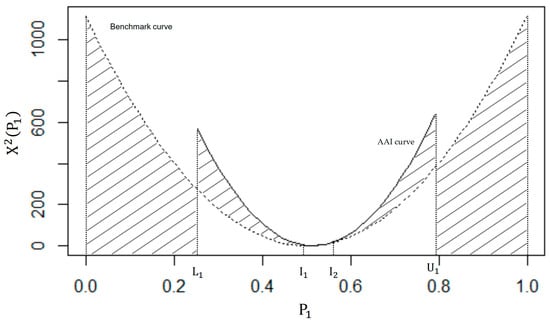
Figure 4.
A graphical interpretation of the AII for Table 4.
Therefore, the configuration of the marginal information in Table 4 suggests that the data are informative for helping to detect the association structure of the two dichotomous variables when the cell frequencies are unknown.
4. Discussion
The analysis of 2 × 2 contingency tables, when only the aggregate data are available, has traditionally been based on a large array of EI techniques. However, the use of EI across a broad range of disciplines has been placed under increasing scrutiny due, primarily, to the untestable and unreliable assumptions that are made. The AAI makes no assumptions about the data and, as such, is a sensible alternative to EI, which does not focus on estimating the cell frequencies (or some function of them) in a 2 × 2 contingency table, but instead focuses on the association structure between the variables. This paper goes further and shows how the AII can be used to examine how informative the marginal information in a 2 × 2 contingency table is for making inferences about the statistical significance of this association structure. The calculation of the AII is shown to depend only on the relative marginal frequencies and is independent of the sample size; the analysis of the two data sets in Section 3 confirms this feature of the AII. We have also shown that the AII is highly responsive to changes in the configuration of the relative marginal frequencies.
While there are clear practical benefits to the AII, there are also ways in which the index can be further refined and developed. For example, while the focus of this paper has been on the development, interpretation, and practical demonstration of the AII in regard to a 2 × 2 contingency table, a limitation is that it is not yet applicable to contingency tables consisting of more than two row categories and/or two column categories. Formalizing the mathematical links between the AII and the AAI also requires attention. At present, the AII is expressed only in terms of the conditional proportion, , although we see no reason why other measures cannot be considered to quantify the index. These include the classic odds ratio or a more general linear transformation of . Such extensions would supplement the work on the AAI, where Beh et al. [37] showed how the AAI can be expressed in terms of the odds ratio of a 2 × 2 contingency table and where Beh et al. [39] showed how the AAI can be extended to cater to a family of measures of association that are a linear transformation of . While the development of the AII (and AAI) is centered on the hypothesis of independence between the row and column variables, further amendments can be made that center on the hypothesis of perfect symmetry between the variables. For example, Haber [50] (p. 154) put forward a procedure for testing the statistical significance of the symmetry given only marginal information using Bowker’s chi-squared statistic [51] and, thus, there is scope for investigating whether the AII (and AAI) can be expressed in terms of this statistic, a measure that (interestingly) relies solely on the cell frequencies in a 2 × 2 contingency table. We shall leave these avenues of research for future consideration.
Author Contributions
Conceptualization, S.C.; methodology, S.C., E.J.B. and I.L.H.; software, E.J.B.; validation, S.C., E.J.B. and I.L.H.; formal analysis, S.C. and E.J.B.; investigation, E.J.B. and I.L.H.; writing—original draft preparation, S.C.; writing—review and editing, E.J.B. and I.L.H.; visualization, E.J.B.; supervision, E.J.B. and I.L.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Conflicts of Interest
The authors declare that there are no conflicts of interest.
References
- Fisher, R.A. The logic of inductive inference (with discussion). J. R. Stat. Assoc. Ser. A 1935, 98, 39–82. [Google Scholar] [CrossRef]
- Yates, F. Tests of significance for 2 × 2 contingency tables (with discussion). J. R. Stat. Soc. Ser. A 1984, 147, 426–463. [Google Scholar] [CrossRef]
- Plackett, R.L. The marginal totals of a 2 × 2 table. Biometrika 1977, 64, 37–42. [Google Scholar]
- Aitkin, M.; Hind, J.P. Comments to Yates’ “Tests of significance for 2 × 2 contingency tables”. J. R. Stat. Soc. Ser. A 1984, 147, 453–454. [Google Scholar]
- Barnard, G.A. Comments to Yates’ “Tests of significance for 2 × 2 contingency tables”. J. R. Stat. Soc. Ser. A 1984, 147, 449–450. [Google Scholar]
- Goodman, L.A. Ecological regressions and behaviour of individuals. Am. Sociol. Rev. 1953, 18, 663–664. [Google Scholar] [CrossRef]
- Goodman, L.A. Some alternatives to ecological correlation. Am. J. Sociol. 1959, 64, 610–625. [Google Scholar] [CrossRef]
- King, G. A Solution to Ecological Inference Problem; Princeton University Press: Princeton, NJ, USA, 1997. [Google Scholar]
- Cho, W.K.T. Iff the assumption fits. A comment on the King ecological inference solution. Political Anal. 1998, 7, 143–163. [Google Scholar]
- King, G. EI: A program for ecological inference. J. Stat. Softw. 2004, 11, 41. [Google Scholar] [CrossRef]
- Steel, D.G.; Beh, E.J.; Chambers, R.L. The information in aggregate data. In Ecological Inference: New Methodological Strategies; King, G., Rosen, O., Tanner, M., Eds.; Cambridge University Press: New York, NY, USA, 2004; pp. 51–68. [Google Scholar]
- Hudson, I.L.; Moore, L.; Beh, E.J.; Steel, D.G. Ecological inference techniques: An empirical evaluation using data describing gender and voter turnout at New Zealand elections 1893–1919. J. R. Stat. Soc. Ser. A 2010, 173, 185–213. [Google Scholar] [CrossRef]
- Greenland, S.; Robins, J. Ecologic studies–biases, misconceptions, and counterexamples. Am. J. Epidemiol. 1994, 8, 747–760. [Google Scholar] [CrossRef]
- Barreto, M.; Collingwood, L.; Garcia-Rios, S.; Oskooii, K.A.R. Estimating candidate support in voting rights act cases: Comparing iterative EI and EI-RxC methods. Sociol. Methods Res. 2022, 51, 271–304. [Google Scholar] [CrossRef]
- Papalia, R.B.; Vazquez, E.F. Entropy-based solutions for ecological inference problems: A composite estimator. Entropy 2020, 22, 781. [Google Scholar] [CrossRef]
- Roumeliotis, S.; ElHafeez, S.A.; Jager, K.J.; Dekker, F.W.; Stel, V.S.; Pitino, A.; Zoccali, C.; Tripepi, G. Be careful with ecological associations. Nephrology 2021, 26, 501–505. [Google Scholar] [CrossRef]
- Kim, S.; Lee, W. Discovering hidden statistical issues through individual-level models in ecological inference. J. Appl. Stat. 2019, 46, 2540–2552. [Google Scholar] [CrossRef]
- Geissbühler, M.; Hincapié, C.A.; Aghlmandi, S.; Zwahlen, M.; Jüni, P.; da Costa, B.R. Most published meta-regression analyses based on aggregate data suffer from methodological pitfalls: A meta-epidemiological study. BMC Med. Res. Methodol. 2021, 21, 123. [Google Scholar] [CrossRef]
- Pavía, J.M.; Romero, R. Improving estimates accuracy of voter transitions. Two new algorithms for ecological inference based on linear programming. Sociol. Methods Res. 2024, 53, 1491–1533. [Google Scholar] [CrossRef]
- Fisher, L.H.; Wakefield, J. Ecological inference for infectious disease data, with application to vaccination strategies. Stat. Med. 2020, 39, 220–238. [Google Scholar] [CrossRef]
- Ferree, K.E. Iterative approaches to R×C ecological inference problems: Where they can go wrong and one quick fix. Political Anal. 2004, 12, 143–159. [Google Scholar] [CrossRef]
- Greiner, D.J.; Quinn, K.M. R×C ecological inference: Bounds, correlations, flexibility and transparency of assumptions. J. R. Stat. Soc. Ser. A 2009, 172, 67–81. [Google Scholar] [CrossRef]
- Collingwood, L.; Oskooii, K.; Garcia-Rios, S.; Barreto, M. eiCompare: Comparing ecological inference estimates across EI and EI:R×C. R J. 2016, 8, 92–101. [Google Scholar] [CrossRef]
- Plescia, C.; De Sio, L. An evaluation of the performance and suitability of R×C methods for ecological inference with known true values. Qual. Quant. 2018, 52, 669–683. [Google Scholar] [CrossRef]
- Greiner, D.J.; Baines, P.; Quinn, K.M. R×CEcoInf: R×C Ecological Inference with Optional Incorporation of Survey Information (R Package Version 0.1-5). 2021. Available online: https://cran.r-project.org/web/packages/RxCEcolInf/index.html (accessed on 13 November 2024).
- Pavía, J.M.; Thomsen, S.R. ecolRxC: Ecological inference estimation of R×C tables using latent structure approaches. Political Sci. Res. Methods 2024, in press. [Google Scholar] [CrossRef]
- Pavía, J.M.; Romero, R. Data wrangling, computational burden, automation, robustness and accuracy in ecological inference forecasting of R×C tables. SORT 2023, 47, 151–186. [Google Scholar]
- Pavía, J.M.; Romero, R. Symmetry estimating R×C vote transfer matrices from aggregate data. J. R. Stat. Soc. Ser. A 2024, 187, 919–943. [Google Scholar] [CrossRef]
- Imai, K.; Lu, Y.; Strauss, A. eco: R package for ecological inference in 2 × 2 tables. J. Stat. Softw. 2011, 42, 23. [Google Scholar] [CrossRef]
- King, G.; Roberts, M. ei: Ecological Inference (R Package Version 1.3-3). 2016. Available online: https://cran.r-project.org/web/packages/ei/index.html (accessed on 13 November 2024).
- Lau, O.; Moore, R.T.; Kellerman, M. eiPack: Ecological Inference and Higher-Dimension Data Management (R Package Version 0.2-2). 2023. Available online: https://cran.r-project.org/web/packages/eiPack/index.html (accessed on 13 November 2024).
- Forcina, A.; Pavía, J.M. eiCircles: Ecological Inference of R×C Tables by Overdispersed-Multinomial Models (R Package Version 0.0.1-7). 2024. Available online: https://cran.r-project.org/web/packages/eiCircles/index.html (accessed on 13 November 2024).
- Pavía, J.M.; Romero, R. lphom: Ecological Inference by Linear Programming Under Homogeneity (R Package Version 0.3.5-5). 2024. Available online: https://cran.r-project.org/web/packages/lphom/index.html (accessed on 13 November 2024).
- Beh, E.J. Correspondence analysis of aggregate data: The 2 × 2 table. J. Stat. Plan. Inference 2008, 138, 2941–2952. [Google Scholar] [CrossRef]
- Beh, E.J. The aggregate association index. Comput. Stat. Data Anal. 2010, 54, 1570–1580. [Google Scholar] [CrossRef]
- Fréchet, M. Sur les tableaux de corrélation dont les marges sont données. Ann. Univ. Lyon Sect. A Sér. 3 1951, 14, 53–77. [Google Scholar]
- Beh, E.J.; Tran, D.; Hudson, I.L. A reformulation of the aggregate association index using the odds ratio. Comput. Stat. Data Anal. 2013, 68, 52–65. [Google Scholar] [CrossRef]
- Beh, E.J.; Cheema, S.A.; Tran, D.; Hudson, I.L. Adjustment to the aggregate association index to minimize the impact of large samples. In Advances in Latent Variables; Carpita, M., Brentari, E., Qannari, E.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 241–251. [Google Scholar]
- Beh, E.J.; Tran, D.; Hudson, I.L. A generalization of the aggregate association index (AAI): Incorporating a linear transformation of the cells of a 2 × 2 table. Metrika 2024, 87, 499–531. [Google Scholar] [CrossRef]
- Tran, D.; Beh, E.J.; Hudson, I.L. The aggregate association index applied to stratified 2 × 2 tables: Application to the 1893 election data in New Zealand. Stat. J. IAOS 2018, 34, 379–394. [Google Scholar] [CrossRef]
- Beh, E.J.; Tran, D.; Hudson, I.L.; Moore, L. Clustering of stratified aggregated data using the aggregate association index: Analysis of New Zealand voter turnout (1893–1919). In Analysis and Modeling Complex Data in Behavioral and Social Sciences; Vicari, D., Okada, A., Ragozini, G., Weihs, C., Eds.; Springer: Cham, Switzerland, 2014; pp. 21–28. [Google Scholar]
- Fairburn, M.; Olssen, E. Class, Gender and the Vote: Historical Perspectives from New Zealand; University of Otago Press: Dunedin, New Zealand, 2013. [Google Scholar]
- Moore, L. Gender Counts: Men, Women and Electoral Politics in New Zealand, 1893–1919. Unpublished Master’s Thesis, University of Canterbury, Christchurch, New Zealand, 2004. Available online: https://ir.canterbury.ac.nz/items/6cbad7e6-bf0f-4eb6-bf27-6c4c0cc29367/full (accessed on 13 November 2024).
- Selikoff, I.J. Household risk with inorganic fibers. Bull. N. Y. Acad. Med. 1981, 57, 947–961. [Google Scholar]
- Duncan, O.D.; Davis, B. An alternative to ecological correlation. Am. Sociol. Rev. 1953, 18, 665–666. [Google Scholar] [CrossRef]
- Everitt, B.S. The Analysis of Contingency Tables, 2nd ed.; Chapman & Hall: London, UK, 1992. [Google Scholar]
- Mosteller, F. Association and estimation in contingency tables. J. Am. Stat. Assoc. 1968, 63, 1–28. [Google Scholar] [CrossRef]
- Beh, E.J.; Smith, D.R. Real world occupational epidemiology, Part 1: Odds ratios, relative risk, and asbestosis. Arch. Environ. Occup. Health 2011, 66, 119–123. [Google Scholar] [CrossRef]
- Tran, D.; Beh, E.J.; Smith, D.R. Real-world occupational epidemiology, Part 3: An aggregate data analysis of Selikoff’s “20-year rule”. Arch. Environ. Occup. Health 2012, 67, 243–248. [Google Scholar] [CrossRef]
- Haber, M. Do the marginal total of a 2 × 2 contingency table contain information regarding the table proportion? Commun. Stat. Theory Methods 1989, 18, 147–156. [Google Scholar] [CrossRef]
- Bowker, A.H. A test for symmetry in contingency tables. J. Am. Stat. Assoc. 1948, 43, 572–598. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).