Enhanced Carbon Price Forecasting Using Extended Sliding Window Decomposition with LSTM and SVR
Abstract
1. Introduction
- An ESWD strategy is proposed to address information leakage in carbon price forecasting. By incorporating an extended window on the left side, left-side boundary effects are mitigated, which enhances data decomposition quality.
- Multivariate empirical mode decomposition (MEMD) is utilized for preprocessing multivariate data, which reduces prediction bias by preserving the intrinsic relationships between variables. Issues with inconsistent modal quantities are addressed through partial decomposition techniques.
- A hybrid framework integrating MEMD and ESWD with SVR and LSTM models is developed to capture multi-scale features in carbon price data.
2. Methodology
2.1. Multivariate Empirical Mode Decomposition (MEMD)
2.2. Support Vector Regressions (SVR)
2.3. Long Short-Term Memory Network (LSTM)
3. The Proposed Model
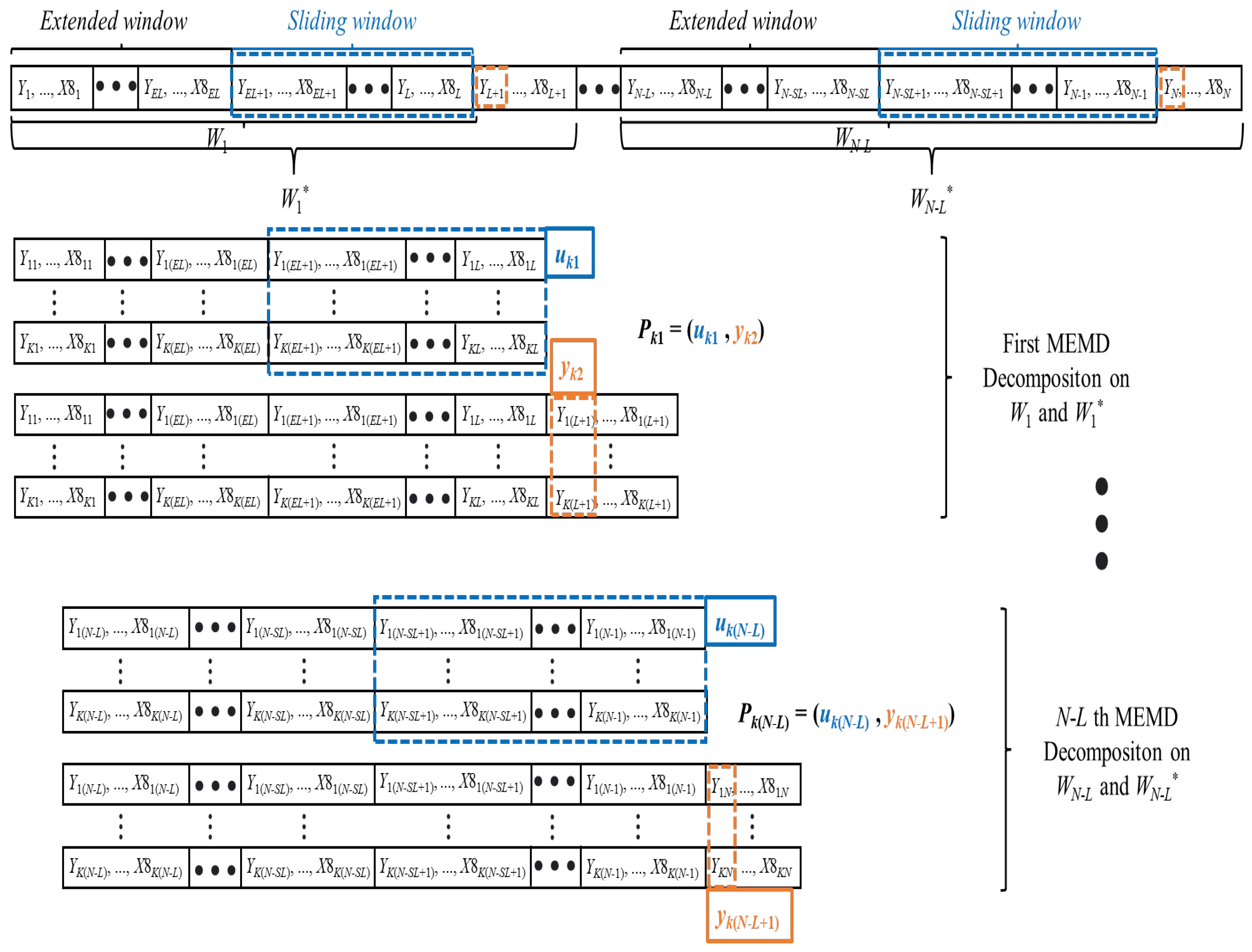
3.1. Extended Sliding Window Decomposition (ESWD) Mechanism
3.2. Mode Number Selection Strategy
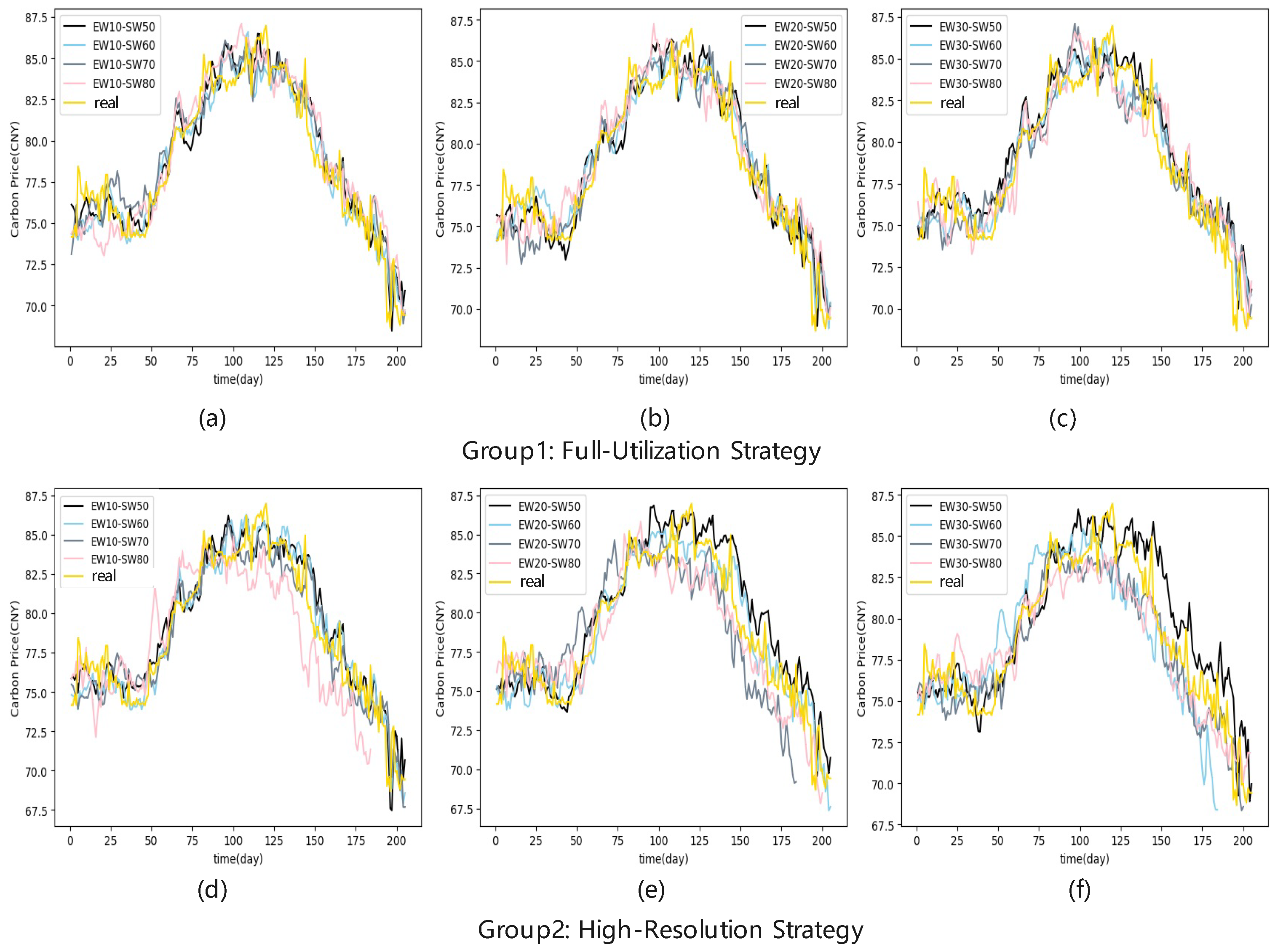
- High-resolution strategy: This strategy maintains a higher multi-scale resolution by discarding decomposition results that produce fewer than K modes. For example, if the minimum mode number standard is set to 6, then only windows that produce at least six IMFs are retained, with fewer-mode windows excluded from the model. This helps preserve finer details by focusing on windows with richer frequency content.
- Full-utilization strategy: This strategy accepts a lower minimum mode number to maximize the use of available data, even if it means a slight reduction in multi-scale resolution. For example, if , all windows with at least five IMFs are included. This strategy sacrifices some high-resolution detail but fully utilizes the information from all windows.
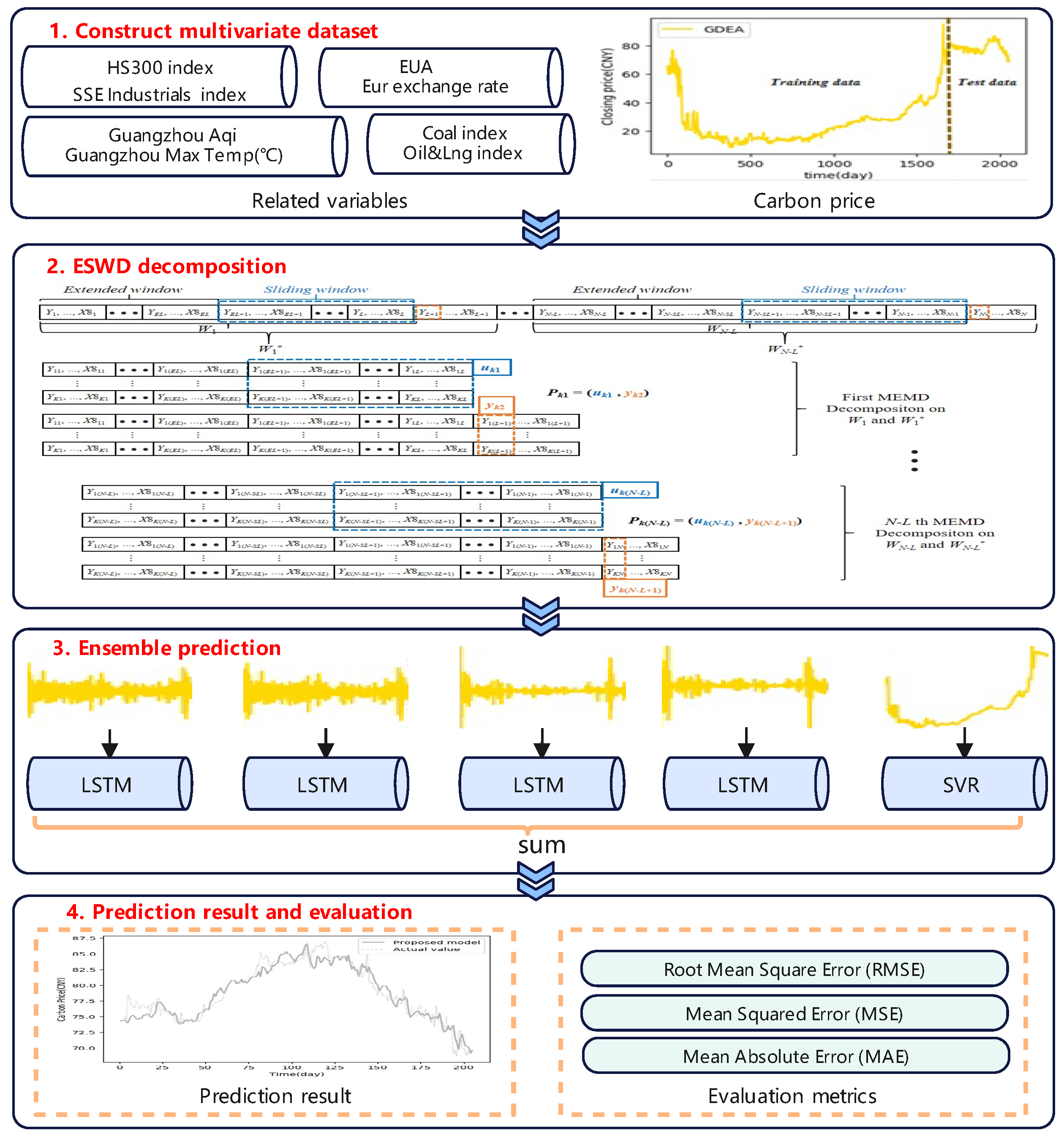
3.3. The Process of Carbon Price Forecasting
4. Case Studies
4.1. Study Object
4.2. Experimental Setup and Evaluation Metrics
4.3. Discussion of Results
4.3.1. Expanded and Sliding Window Length Analysis
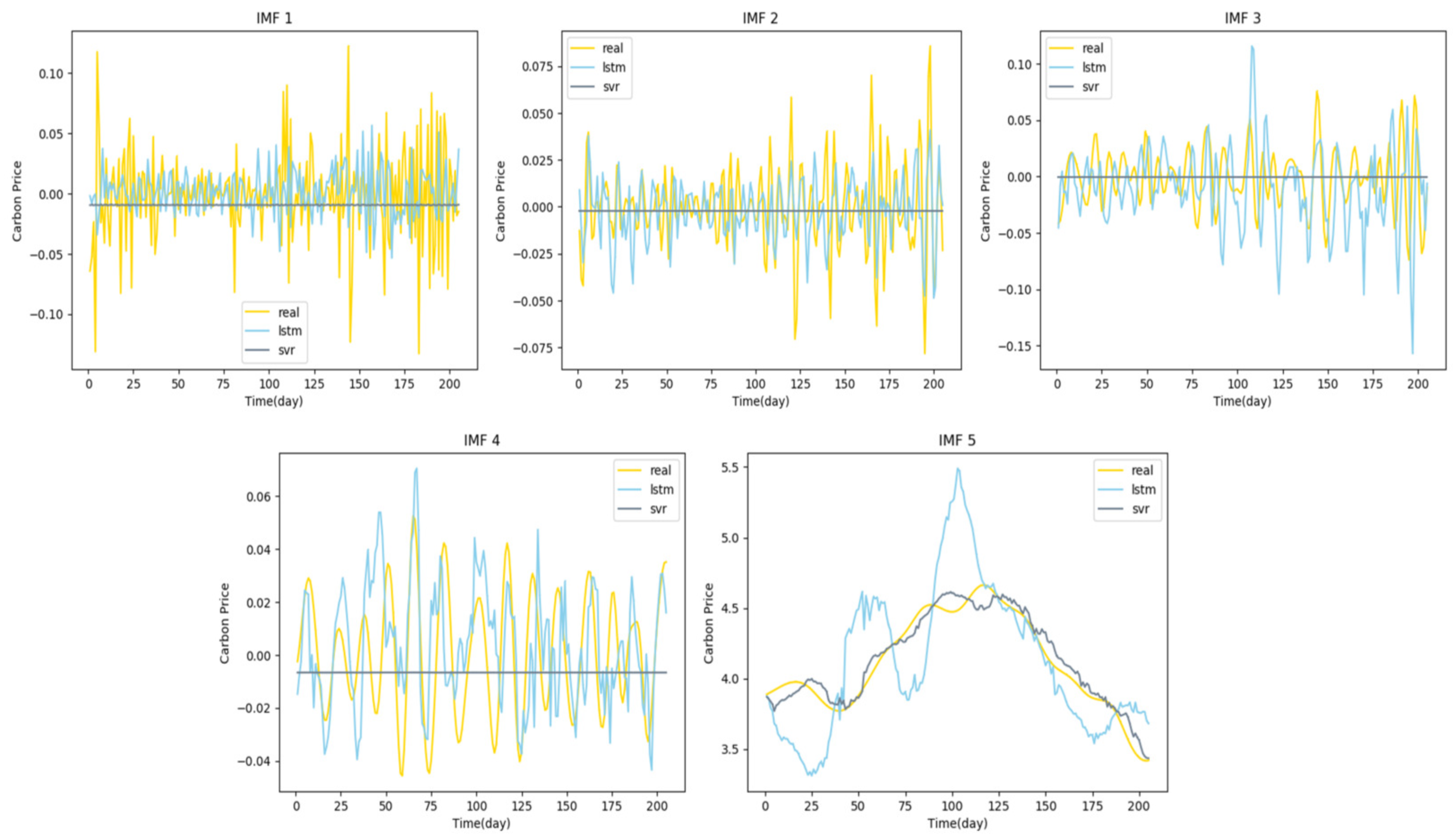
4.3.2. Decomposition Comparative Analysis
4.3.3. Model Configuration Impact Analysis
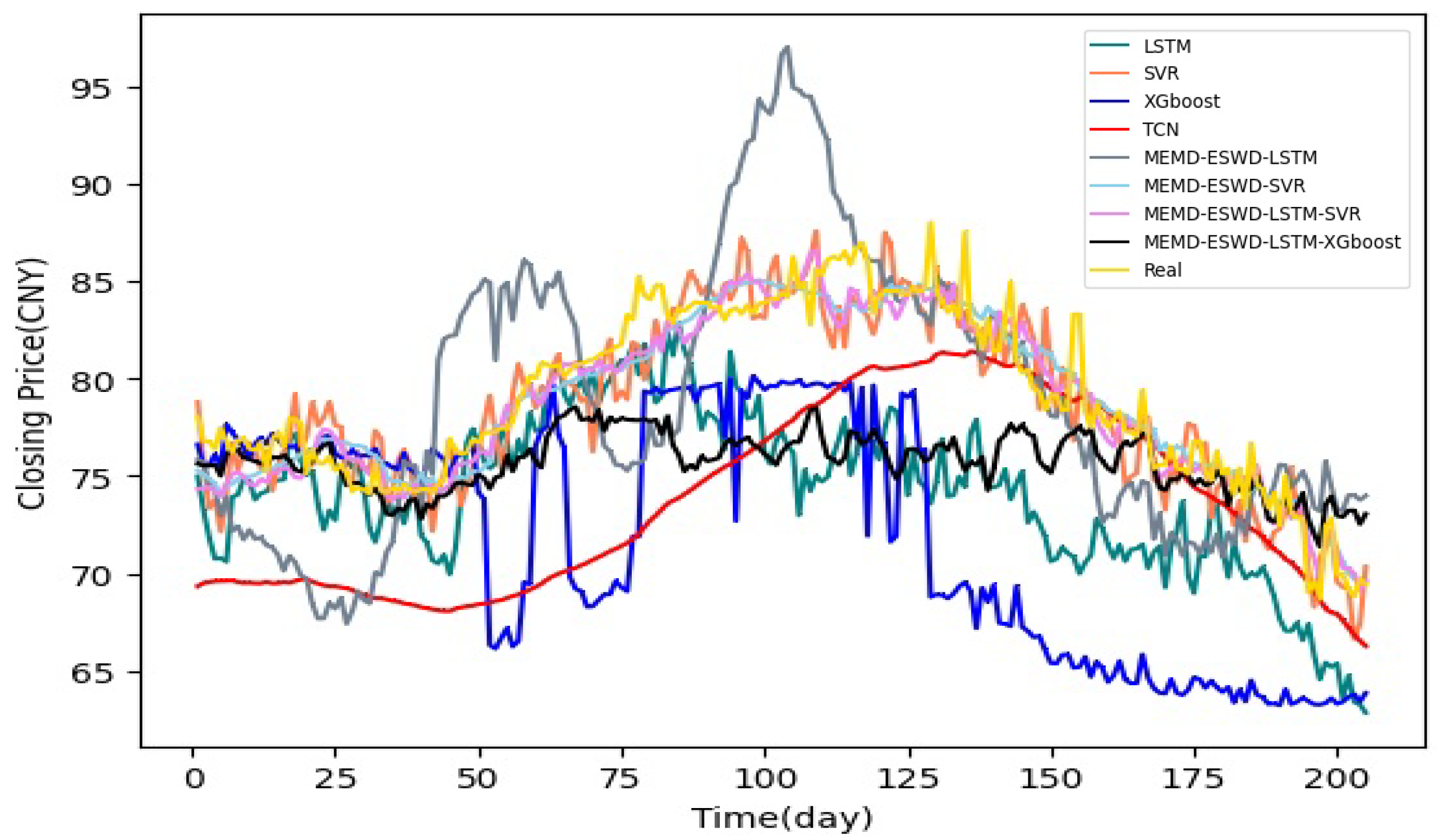
4.3.4. Prediction Performance Evaluation and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wara, M. Is the global carbon market working? Nature 2007, 445, 595–596. [Google Scholar] [CrossRef] [PubMed]
- Boyce, J.K. Carbon pricing: Effectiveness and equity. Ecol. Econ. 2018, 150, 52–61. [Google Scholar] [CrossRef]
- Farouq, I.S.; Sambo, N.U.; Ahmad, A.U.; Jakada, A.H.; Danmaraya, I. Does financial globalization uncertainty affect CO2 emissions? Empirical evidence from some selected SSA countries. Quant. Financ. Econ 2021, 5, 247–263. [Google Scholar] [CrossRef]
- Savaresi, A. The Paris Agreement: A new beginning? J. Energy Nat. Resour. Law 2016, 34, 16–26. [Google Scholar] [CrossRef]
- Narassimhan, E.; Gallagher, K.S.; Koester, S.; Alejo, J.R. Carbon pricing in practice: A review of existing emissions trading systems. Clim. Policy 2018, 18, 967–991. [Google Scholar] [CrossRef]
- Zhu, B.; Chevallier, J.; Zhu, B.; Chevallier, J. Carbon price forecasting with a hybrid Arima and least squares support vector machines methodology. In Pricing and Forecasting Carbon Markets: Models and Empirical Analyses; Springer: Berlin/Heidelberg, Germany, 2017; pp. 87–107. [Google Scholar]
- Zhu, B.; Wang, P.; Chevallier, J.; Wei, Y.M.; Xie, R. Enriching the VaR framework to EEMD with an application to the European carbon market. Int. J. Financ. Econ. 2018, 23, 315–328. [Google Scholar] [CrossRef]
- Paolella, M.S.; Taschini, L. An econometric analysis of emission allowance prices. J. Bank. Financ. 2008, 32, 2022–2032. [Google Scholar] [CrossRef]
- Segnon, M.; Lux, T.; Gupta, R. Modeling and forecasting the volatility of carbon dioxide emission allowance prices: A review and comparison of modern volatility models. Renew. Sustain. Energy Rev. 2017, 69, 692–704. [Google Scholar] [CrossRef]
- Tsai, M.T.; Kuo, Y.T. A forecasting system of carbon price in the carbon trading markets using artificial neural network. Int. J. Environ. Sci. Dev. 2013, 4, 163. [Google Scholar] [CrossRef]
- Zou, Y.; Lin, Z.; Li, D.; Liu, Z. Advancements in Artificial Neural Networks for health management of energy storage lithium-ion batteries: A comprehensive review. J. Energy Storage 2023, 73, 109069. [Google Scholar] [CrossRef]
- Zhu, B.; Ye, S.; Wang, P.; Chevallier, J.; Wei, Y.M. Forecasting carbon price using a multi-objective least squares support vector machine with mixture kernels. J. Forecast. 2022, 41, 100–117. [Google Scholar] [CrossRef]
- Cai, X.; Luo, S. Prediction of Spot Price of Iron Ore Based on PSR-WA-LSSVM Combined Model. J. Comput. Inf. Technol. 2021, 29, 27–38. [Google Scholar] [CrossRef]
- Xu, H.; Wang, M.; Jiang, S.; Yang, W. Carbon price forecasting with complex network and extreme learning machine. Phys. A Stat. Mech. Its Appl. 2020, 545, 122830. [Google Scholar] [CrossRef]
- Huang, Y.; Shen, L.; Liu, H. Grey relational analysis, principal component analysis and forecasting of carbon emissions based on long short-term memory in China. J. Clean. Prod. 2019, 209, 415–423. [Google Scholar] [CrossRef]
- Nasiri, H.; Ebadzadeh, M.M. MFRFNN: Multi-functional recurrent fuzzy neural network for chaotic time series prediction. Neurocomputing 2022, 507, 292–310. [Google Scholar] [CrossRef]
- Lazcano, A.; Herrera, P.J.; Monge, M. A combined model based on recurrent neural networks and graph convolutional networks for financial time series forecasting. Mathematics 2023, 11, 224. [Google Scholar] [CrossRef]
- Wang, J.; Cui, Q.; He, M. Hybrid intelligent framework for carbon price prediction using improved variational mode decomposition and optimal extreme learning machine. Chaos Solitons Fractals 2022, 156, 111783. [Google Scholar] [CrossRef]
- Nasiri, H.; Ebadzadeh, M.M. Multi-step-ahead stock price prediction using recurrent fuzzy neural network and variational mode decomposition. Appl. Soft Comput. 2023, 148, 110867. [Google Scholar] [CrossRef]
- Zhu, B.; Han, D.; Wang, P.; Wu, Z.; Zhang, T.; Wei, Y.M. Forecasting carbon price using empirical mode decomposition and evolutionary least squares support vector regression. Appl. Energy 2017, 191, 521–530. [Google Scholar] [CrossRef]
- Sun, W.; Xu, C. Carbon price prediction based on modified wavelet least square support vector machine. Sci. Total Environ. 2021, 754, 142052. [Google Scholar] [CrossRef]
- Cheng, M.; Xu, K.; Geng, G.; Liu, H.; Wang, H. Carbon price prediction based on advanced decomposition and long short-term memory hybrid model. J. Clean. Prod. 2024, 451, 142101. [Google Scholar] [CrossRef]
- Huan-ying, C.; Xiang-sheng, D. Carbon price forecasts in Chinese carbon trading market based on EMD-GA-BP and EMD-PSO-LSSVM. Oper. Res. Manag. Sci. 2018, 27, 133. [Google Scholar]
- Yun, P.; Huang, X.; Wu, Y.; Yang, X. Forecasting carbon dioxide emission price using a novel mode decomposition machine learning hybrid model of CEEMDAN-LSTM. Energy Sci. Eng. 2023, 11, 79–96. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, Z. Optimal hybrid framework for carbon price forecasting using time series analysis and least squares support vector machine. J. Forecast. 2022, 41, 615–632. [Google Scholar] [CrossRef]
- Zhu, J.; Wu, P.; Chen, H.; Liu, J.; Zhou, L. Carbon price forecasting with variational mode decomposition and optimal combined model. Phys. A Stat. Mech. Its Appl. 2019, 519, 140–158. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Zhang, J.L. Volatility forecasting of crude oil market: A new hybrid method. J. Forecast. 2018, 37, 781–789. [Google Scholar] [CrossRef]
- Zhu, B.; Yuan, L.; Ye, S. Examining the multi-timescales of European carbon market with grey relational analysis and empirical mode decomposition. Phys. A Stat. Mech. Its Appl. 2019, 517, 392–399. [Google Scholar] [CrossRef]
- Zhang, J.; Wei, Y.M.; Li, D.; Tan, Z.; Zhou, J. Short term electricity load forecasting using a hybrid model. Energy 2018, 158, 774–781. [Google Scholar] [CrossRef]
- Cai, X.; Li, D. M-EDEM: A MNN-based Empirical Decomposition Ensemble Method for improved time series forecasting. Knowl.-Based Syst. 2024, 283, 111157. [Google Scholar] [CrossRef]
- Wu, F.; Li, D.; Zhao, J.; Jiang, H.; Luo, X. SDIPPWV: A novel hybrid prediction model based on stepwise decomposition-integration-prediction avoids future information leakage to predict precipitable water vapor from GNSS observations. Sci. Total Environ. 2024, 933, 173116. [Google Scholar] [CrossRef]
- Liu, T.; Ma, X.; Li, S.; Li, X.; Zhang, C. A stock price prediction method based on meta-learning and variational mode decomposition. Knowl.-Based Syst. 2022, 252, 109324. [Google Scholar] [CrossRef]
- Huang, Y.; Deng, Y. A new crude oil price forecasting model based on variational mode decomposition. Knowl.-Based Syst. 2021, 213, 106669. [Google Scholar] [CrossRef]
- He, M.; Wu, S.f.; Kang, C.x.; Xu, X.; Liu, X.f.; Tang, M.; Huang, B.b. Can sampling techniques improve the performance of decomposition-based hydrological prediction models? Exploration of some comparative experiments. Appl. Water Sci. 2022, 12, 175. [Google Scholar] [CrossRef]
- Yu, L.; Ma, Y.; Ma, M. An effective rolling decomposition-ensemble model for gasoline consumption forecasting. Energy 2021, 222, 119869. [Google Scholar] [CrossRef]
- Quilty, J.; Adamowski, J. Addressing the incorrect usage of wavelet-based hydrological and water resources forecasting models for real-world applications with best practices and a new forecasting framework. J. Hydrol. 2018, 563, 336–353. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, S.; Tian, X.; Zhang, F.; Zhao, F.; Zhang, C. A stock series prediction model based on variational mode decomposition and dual-channel attention network. Expert Syst. Appl. 2024, 238, 121708. [Google Scholar] [CrossRef]
- He, K.; Zha, R.; Wu, J.; Lai, K.K. Multivariate EMD-based modeling and forecasting of crude oil price. Sustainability 2016, 8, 387. [Google Scholar] [CrossRef]
- Ghazani, M.M. Analyzing the drivers of CO2 allowance prices in EU ETS under the COVID-19 pandemic: Considering MEMD approach with a novel filtering procedure. J. Clean. Prod. 2023, 427, 139043. [Google Scholar]
- Rehman, N.; Mandic, D.P. Multivariate empirical mode decomposition. Proc. R. Soc. A Math. Phys. Eng. Sci. 2010, 466, 1291–1302. [Google Scholar] [CrossRef]
- Fan, G.F.; Peng, L.L.; Hong, W.C.; Sun, F. Electric load forecasting by the SVR model with differential empirical mode decomposition and auto regression. Neurocomputing 2016, 173, 958–970. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]






| Variable | Symbol | Description | Reasons for Choosing Variables |
|---|---|---|---|
| GDEA | Y | carbon price | Regional carbon market allocates and trades quotas. |
| Coal index | X1 | energy price | Raw material prices impact energy producers and various sectors. |
| Oil&Lng index | X2 | energy price | |
| HS300 index | X3 | macroeconomics | Macroeconomic changes reflect total social consumption and demand. |
| SSE Industrials index | X4 | macroeconomics | Macroeconomics affects carbon prices via industry and electricity, reflected by the SSE Industrials index. |
| EUA | X5 | international market | Imperfect pricing and trading affect international carbon market prices. |
| EUR exchange rate | X6 | international market | Used as a reference for pricing. |
| Guangzhou Aqi | X7 | climate | AQI reflects greenhouse gas levels. |
| Guangzhou Max Temp (°C) | X8 | climate | Temperature affects residential and commercial energy consumption. |
| Variables | Max | Min | Mean | Std | Skewness |
|---|---|---|---|---|---|
| Y | 35.41 | 95.26 | 8.10 | 24.45 | 0.91 |
| X1 | 2749.69 | 5136.80 | 1587.81 | 796.19 | 1.00 |
| X2 | 2432.52 | 4415.32 | 1595.59 | 462.32 | 0.75 |
| X3 | 3801.72 | 5807.72 | 2086.97 | 765.25 | −0.11 |
| X4 | 2336.24 | 4837.49 | 1263.07 | 524.68 | 0.88 |
| X5 | 29.55 | 97.67 | 3.93 | 29.12 | 1.04 |
| X6 | 7.58 | 8.58 | 6.49 | 0.41 | −0.14 |
| X7 | 67.84 | 205.00 | 13.00 | 30.46 | 1.17 |
| X8 | 27.12 | 38.00 | 6.00 | 6.35 | −0.62 |
| Models | Parameter Setting Method | Parameter Setting and Search Range |
|---|---|---|
| SVR | Grid Search | Grid search with RBF and linear kernels. ‘gamma’: [, ,], ‘C’: [0.001, 0.01, 1, 100, 10,000], |
| LSTM | Empirical setting | LSTM layer with 60 units, Optimized using SGD with momentum, trained for 60 epochs. |
| XGboost | Empirical setting | maximum depth of 3, learning rate = 0.2 and 100 boosting rounds. |
| TCN | Empirical setting | Three Conv1D layers with 128 filters, kernel size 2, and increasing dilation rates (1, 2, 4). Final fully connected layer for prediction. |
| Window Length | High-Resolution Strategy | Full-Utilization Strategy | ||||||
|---|---|---|---|---|---|---|---|---|
| SW-50 | SW-60 | SW-70 | SW-80 | SW-50 | SW-60 | SW-70 | SW-80 | |
| EW-10 | 6 | 6 | 6 | 7 | 5 | 5 | 5 | 6 |
| EW-20 | 6 | 6 | 7 | 7 | 5 | 5 | 6 | 6 |
| EW-30 | 6 | 7 | 7 | 7 | 5 | 6 | 6 | 6 |
| Window Length | Metrics | High-Resolution Strategy | Full-Utilization Strategy | ||||||
|---|---|---|---|---|---|---|---|---|---|
| SW-50 | SW-60 | SW-70 | SW-80 | SW-50 | SW-60 | SW-70 | SW-80 | ||
| EW-10 | RMSE | 2.665 | 2.567 | 2.934 | 3.496 | 2.518 | 2.469 | 2.885 | 3.178 |
| MSE | 7.171 | 6.574 | 8.367 | 11.952 | 6.574 | 5.976 | 8.367 | 10.160 | |
| MAE | 2.078 | 2.029 | 2.371 | 2.860 | 1.956 | 1.858 | 2.396 | 2.567 | |
| EW-20 | RMSE | 3.325 | 2.811 | 3.031 | 3.202 | 2.738 | 2.616 | 2.909 | 3.129 |
| MSE | 11.355 | 7.769 | 8.964 | 10.160 | 7.769 | 6.574 | 8.367 | 9.562 | |
| MAE | 2.567 | 2.225 | 2.445 | 2.616 | 2.151 | 2.078 | 2.298 | 2.469 | |
| EW-30 | RMSE | 3.422 | 2.860 | 3.105 | 3.545 | 2.934 | 2.738 | 3.202 | 3.276 |
| MSE | 11.952 | 8.367 | 9.562 | 12.550 | 8.367 | 7.769 | 10.160 | 10.757 | |
| MAE | 2.640 | 2.322 | 2.591 | 2.909 | 2.322 | 2.200 | 2.591 | 2.665 | |
| Models | RMSE | MSE | MAE | Dstat | TIME (s) |
|---|---|---|---|---|---|
| LSTM(SW60) | 4.497 | 20.976 | 3.346 | 50.7% | 50.21 |
| SVR(SW60) | 1.965 | 3.859 | 1.551 | 53.6% | 22.43 |
| XGboost(SW60) | 5.018 | 25.181 | 4.135 | 51.1% | 1.13 |
| TCN(SW60) | 6.895 | 47.545 | 6.565 | 47.8% | 100.35 |
| MEMD-ESWD-LSTM(EW10-SW60) | 8.996 | 80.929 | 7.434 | 48.8% | 28,887.455 |
| MEMD-ESWD-SVR(EW10-SW60) | 1.537 | 2.341 | 1.279 | 53.2% | 50,264.21 |
| MEMD-ESWD-LSTM-XGboost(EW10-SW60) | 4.897 | 23.976 | 3.746 | 52.7% | 28,845.557 |
| MEMD-ESWD-LSTM-SVR(EW10-SW60) | 1.503 | 2.259 | 1.165 | 56.6% | 49,607.601 |
| Models | RMSE | MSE | MAE | Dstat | TIME (s) |
|---|---|---|---|---|---|
| LSTM(SW60) | 6.12 | 45.241 | 5.82 | 50.6% | 30.786 |
| SVR(SW60) | 1.794 | 3.217 | 1.437 | 55.5% | 66.324 |
| XGboost(SW60) | 4.891 | 23.921 | 3.762 | 49.8% | 1.197 |
| TCN(SW60) | 2.56 | 6.556 | 2.238 | 49.3% | 134.21 |
| MEMD-ESWD-LSTM(EW10-SW60) | 7.301 | 53.308 | 6.401 | 54.6% | 21,863.3 |
| MEMD-ESWD-SVR(EW10-SW60) | 1.677 | 2.813 | 1.348 | 54.1% | 49,881.365 |
| MEMD-ESWD-LSTM-XGboost(EW10-SW60) | 3.433 | 11.788 | 2.74 | 49.8% | 21,809.668 |
| MEMD-ESWD-LSTM-SVR(EW10-SW60) | 1.601 | 2.562 | 1.306 | 59.5% | 47,240.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, X.; Li, D.; Feng, L. Enhanced Carbon Price Forecasting Using Extended Sliding Window Decomposition with LSTM and SVR. Mathematics 2024, 12, 3713. https://doi.org/10.3390/math12233713
Cai X, Li D, Feng L. Enhanced Carbon Price Forecasting Using Extended Sliding Window Decomposition with LSTM and SVR. Mathematics. 2024; 12(23):3713. https://doi.org/10.3390/math12233713
Chicago/Turabian StyleCai, Xiangjun, Dagang Li, and Li Feng. 2024. "Enhanced Carbon Price Forecasting Using Extended Sliding Window Decomposition with LSTM and SVR" Mathematics 12, no. 23: 3713. https://doi.org/10.3390/math12233713
APA StyleCai, X., Li, D., & Feng, L. (2024). Enhanced Carbon Price Forecasting Using Extended Sliding Window Decomposition with LSTM and SVR. Mathematics, 12(23), 3713. https://doi.org/10.3390/math12233713








