1. Introduction
Over the past decade, machine learning techniques based on deep neural networks, commonly referred to as
deep learning [
1], have achieved significant breakthroughs across a wide range of fields, including image recognition [
2,
3], speech recognition [
4], language translation [
5,
6], and game playing [
7], among others. These advancements are largely driven by the availability of increasingly large training datasets and greater computational resources. Another important factor is the development of specialized neural network architectures, including convolutional neural networks [
2], residual networks [
3], recurrent networks (notably LSTMs [
5]), and transformer networks [
6].
A common theme in the design of neural network architectures is the necessity to respect the symmetries inherent in the task at hand. For instance, in image classification, the classification result should remain invariant under small translations of the input image, making convolutional neural networks a suitable choice. Likewise, in audio classification [
8], the classification result should be invariant to shifts in time or changes in pitch. In principle, a fully connected neural network can learn to respect such symmetries provided that training data are sufficiently given. Nevertheless, architectures that are inherently aligned with these symmetries tend to exhibit improved generalization and thus show better performance.
In mathematical terms, symmetries can be expressed as follows. Let V be a vector space and let be the general linear group of V. For a group G and a map , we say that a map is equivariant under group actions of G (or simply G-equivariant) if for all , and invariant under group actions of G (or simply G-invariant) if for all . We will be focusing on the case where V is a Hilbert space and is a unitary operator for all . (A Hilbert space is a vector space equipped with an inner product that induces a distance function, making it a complete metric space. Examples of Hilbert spaces include and , and Hilbert spaces are often regarded as natural generalizations of signal spaces.)
A particularly important and well-studied example of equivariance involves translations. It is well known that translation-equivariant linear operators are exactly the convolution operators (see, e.g., Section 2.3 of [
9], Theorem 4.12 of [
10], and Theorem 2.17 of [
11]), and that convolutional neural networks (CNNs) are well-suited for approximating these operators. As a natural generalization of CNNs, Cohen and Welling [
12] introduced the so-called group equivariant convolutional neural networks (GCNNs), which can handle more general symmetry groups than just translations. Later, Cohen et al. [
13] developed a general framework for GCNNs on homogeneous spaces such as
and
, and Yarotsky [
14] investigated the approximation of equivariant operators using equivariant neural networks. More recently, Cahill et al. [
15] introduced the so-called group-invariant max filters, which are particularly useful for classification tasks involving symmetries, and Balan and Tsoukanis [
16,
17] constructed stable embeddings on quotient space modulo group action, yielding group-invariant representations via coorbits. Further advances include the work of Huang et al. [
18], who designed approximately group-equivariant graph neural networks by focusing on active symmetries, and Blum-Smith and Villar [
19], who introduced a method for parameterizing invariant and equivariant functions based on invariant theory. In addition, Wang et al. [
20] provided a theoretical analysis of data augmentation and equivariant neural networks applied to non-stationary dynamics forecasting.
In this paper, we are particularly interested in the setting of finite-dimensional time-frequency analysis, which provides a versatile framework for a wide range of signal processing applications, see, e.g., [
21,
22]. It is known that every
linear map from
to
can be expressed as a linear combination of compositions of translations and modulations (see (
3) below). We consider maps
that are generally
nonlinear and are Λ-
equivariant for a given subgroup
of
, that is,
for all
. Here,
represents the time-frequency shift by
, where
are the translation and modulation operators defined as
and
,
, for
, respectively (see
Section 2.1 for further details). For any
and any nonzero
, we define
by
,
. For any
, we say that a function
is Ω-
phase homogeneous if
for all
and
.
We first address the properties of the mapping from the space of -equivariant functions to the space of certain phase homogeneous functions.
Theorem 1 (see Theorem 3 below)
. Assume that for some subgroup Λ of and some vector . Then, the mapping is an injective map from the space of Λ-equivariant functions to the space of -phase homogeneous functions , where . Moreover, if is a dual frame of in , then a Λ-equivariant function can be expressed asIf , then the mapping is a bijective map from the space of Λ-equivariant functions to the space of -phase homogeneous functions . We then consider the approximation of -equivariant maps. In particular, we show that if is a cyclic subgroup of order N in , then every -equivariant map can be easily approximated by a shallow neural network whose affine linear maps consist of linear combinations of time-frequency shifts by .
Theorem 2 (see Theorem 5 below)
. Assume that is shallow universal and satisfies for all . Let for some . Then, any continuous Λ-equivariant map can be approximated (uniformly on compact sets) by a shallow neural networkwhere , for , and satisfies for all . Moreover, every map of this form is Λ-equivariant. In the case , i.e., , the -equivariant maps are precisely those that are translation equivariant, meaning that . Furthermore, if F is linear, then F is just a convolutional map, which can be expressed as a linear combination of , , or simply as an circulant matrix. If F is nonlinear, then Theorem 2 shows that F can be approximated by a shallow neural network whose affine linear maps are convolutional maps, i.e., by a shallow convolutional neural network. This agrees with the well-established fact that convolutional neural networks (CNNs) are particularly well-suited for applications involving translation equivariance, especially in image and signal processing.
Organization of the Paper
In
Section 2, we begin by reviewing some basic properties of time-frequency shift operators, followed by a discussion on time-frequency group equivariant maps, and then prove our first main result, Theorem 1, which establishes a 1:1 correspondence between
-equivariant maps and certain phase-homogeneous functions.
Section 3 is devoted to the approximation of
-equivariant maps. We first discuss the embedding of
into the Weyl–Heisenberg group, which allows for the use of tools from group representation theory. (The finite Weyl–Heisenberg group
is the set
equipped with group operation
. The noncommutativity of
plays an important role in finite-dimensional time-frequency analysis; see, e.g., [
21,
23].) After reviewing key concepts from group representation theory, we consider the case of cyclic subgroups of
, where group representations can be defined directly without embedding into the Weyl–Heisenberg group.
Section 3 concludes with the proof of our second main result, Theorem 2, which establishes the approximation of
-equivariant maps by a shallow neural network whose affine linear maps consist of linear combinations of time-frequency shifts by
.
3. Approximation of -Equivariant Maps
In this section, we consider an approximation of continuous
-equivariant maps
that are generally nonlinear, where
is a subgroup of
and the
-equivariance is defined by (
5). For instance, the map
given by
with
, is a nonlinear continuous
-equivariant map.
As seen in
Section 2.2 (particularly in Theorem 3 and its proof), working with the time-frequency shift operators
,
, usually requires careful bookkeeping of extra multiplicative phase factors due to the non-commutativity of
T and
M. (The non-commutativity of
T and
M can often be frustrating. However, it is precisely this non-commutativity that has given rise to the deep and rich theory of time-frequency analysis [
23].) In fact, the map
is generally not a group homomorphism; indeed,
is equal to
only if
is a multiple of
N (see Proposition 1). (Although
is not a group homomorphism and thus not a group representation, it is often referred to as a
projective group representation of
G on
. In general, a map
is called a
projective group representation of
G on
if for each pair of
, there exists a unimodular
such that
; see, e.g., [
25].) Obviously, the computations involved would be simplified significantly if
were a group homomorphism in general. Note that, as mentioned in
Section 1, a group homomorphism
whose images are unitary operators on
is called a
(unitary) group representation of G on , where
G is a group and
is a separable Hilbert space. Therefore, the map
would be a unitary representation if it were a group homomorphism.
In the following, we first discuss a systematic method of avoiding such extra multiplicative phase factors by embedding into the Weyl–Heisenberg group. After briefly reviewing essential concepts on group representations and neural networks, we consider cyclic subgroups of , in which case the map can be replaced by a unitary group representation. We show that if is a cyclic subgroup of , then any -equivariant map can be approximated with shallow neural networks involving the adjoint group , which has significantly fewer degrees of freedom compared with standard shallow neural networks.
3.1. Embedding of into the Weyl–Heisenberg Group
To avoid the bookkeeping of extra multiplicative phase factors, we can simply embed the subgroups of
into the finite Weyl–Heisenberg group
, on which group representations can be defined. There exists a group representation
, known as the
Schrödinger representation, which satisfies
for all
. In fact, for any subgroup
of
and any subgroup
of
containing
, the map
is a group representation of
on
, with the group operation on
G given by
Clearly, we have
for all
.
It is clear that a map
is
-equivariance in the sense of (
5) if and only if it is
-equivariant in the sense of Definition 4. Moreover, in this case, Proposition 2 implies that
F is
-phase homogeneous, which is equivalent to
for all
. Consequently, we have the following proposition.
Proposition 3. For any subgroup Λ of and any , the following are equivalent.
- (i)
F is Λ-equivariant;
- (ii)
F is -equivariant;
- (iii)
F is -equivariant.
Using the true group representation instead of allows us to avoid the tedious bookkeeping of extra multiplicative phase factors. Note, however, that requires three input parameters, while involves only two. In fact, the description of the extra phase factors is simply transferred to the third parameter of . Nevertheless, an important advantage of using instead of is that it allows for the use of tools from group representation theory.
3.2. Group Representations and Neural Networks
In this section, we review some concepts and tools from group representation theory and introduce the so-called ♮-transform and its inverse transform for later use. We also review the basic structure of neural networks and the universal approximation theorem.
We assume that G is a finite group, and consider maps of the form , where is a finite-dimensional Hilbert spaces on which a unitary representation of G is defined. This means that for each , the map is a linear unitary operator, and that is a group homomorphism, i.e., for all . Let us formally state the definition of equivariance and invariance in this setting.
Definition 4 (Equivariance and Invariance). For a group G and a unitary representation ρ of G on a Hilbert space , we say that a map is
-equivariant if for all ;
-invariant if for all .
Note that a -equivariant/invariant map is not necessarily linear or bounded.
Definition 5. For a group G, the left translation
of a vector by is given by In fact, the map is a group homomorphism from G to , that is, for all , and therefore, it induces a group representation of G on . We say that a map is left G-translation equivariant if for all .
Definition 6. Let G be a group and let ρ be a unitary representation of G on a Hilbert space . Given a window , the set is called the orbit of
g under
for
. The map defined byis called the analysis operator of
, and its adjoint operator given byis called the synthesis operator of
.
We are particularly interested in the case where the orbit of
g spans
, that is,
. Since
is finite-dimensional, this implies that
is a frame for
and the associated frame operator
is a positive, self-adjoint bounded operator on
. It follows from (
10) that
and thus
for all
. For any
, we have
where
. This shows that
is the identity operator on
, i.e.,
and correspondingly,
is the canonical dual frame of
.
In light of (
11), we newly introduce a transform which lifts a map
to a map
, and also its inverse transform.
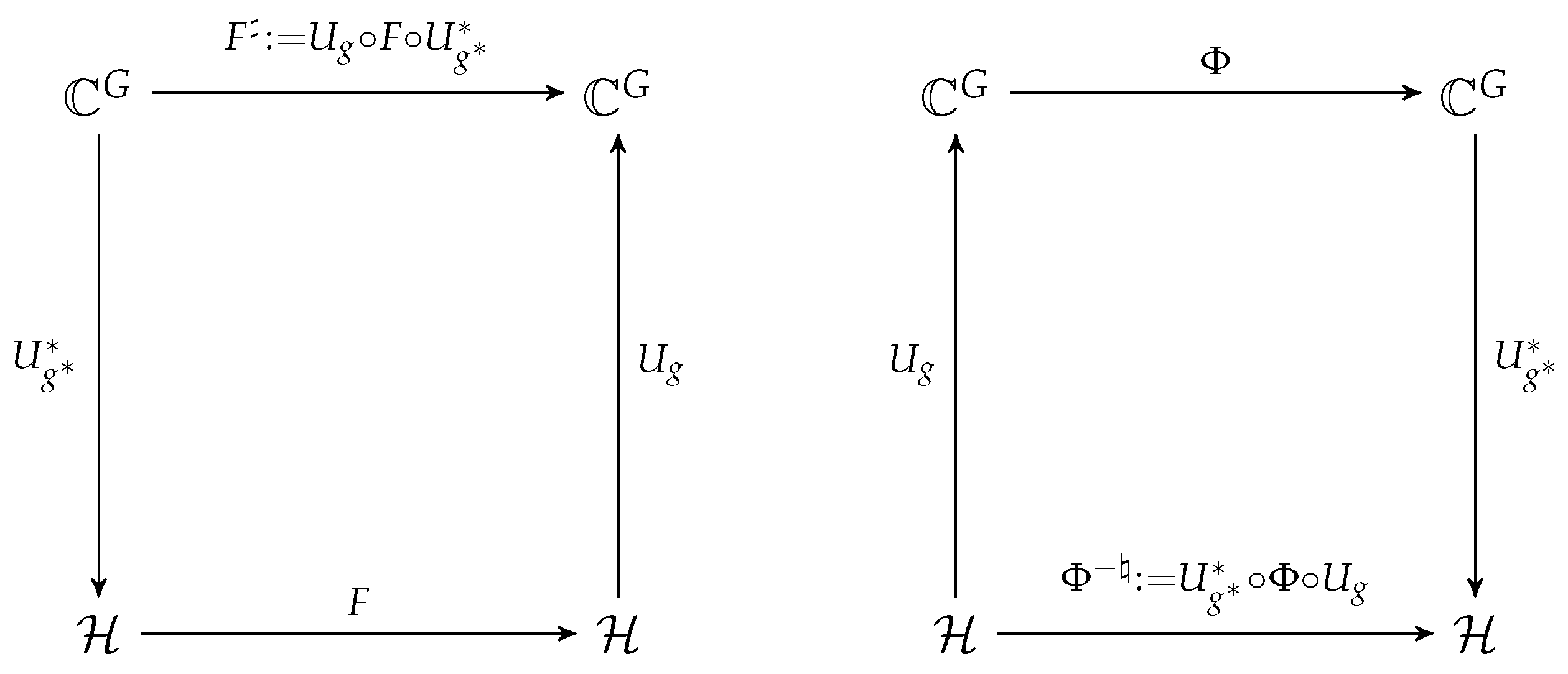
Definition 7. Let G be a finite group and let ρ be a unitary representation of G on a finite-dimensional Hilbert space . Assume that , and let and . For any map , the ♮-transform
of F is defined byFor any map , the inverse ♮-transform
of Φ is defined by As shown in
Figure 1, the ♮-transform converts a map
into a map
, and the inverse ♮-transform converts a map
into a map
.
Proposition 4. Let G be a finite group, and let ρ be a unitary representation of G on a finite-dimensional Hilbert space . Assume that , and let and . Then, the following hold.
- (i)
for any map .
- (ii)
A map is continuous if and only if is continuous.
- (iii)
A map is -equivariant if and only if is left G-translation equivariant.
Proof. (i) It follows from (
11) that
for any
.
(ii) Since the maps and are bounded linear operators, the continuity of F implies the continuity of . Similarly, the continuity of implies the continuity of .
(iii) It follows from (
10) that the
G-equivariance of
F implies the left
G-translation equivariance of
. Similarly, the left
G-translation equivariance of
implies the
G-equivariance of
. □
We now provide a brief review of neural networks and the universal approximation theorem.
Let be either or . An activation function is a function that acts componentwise on vectors; that is, for any .
A fully connected feedforward neural network with
P hidden layers is given by
where
,
is affine-linear with
and
. Such a function
is often called a
neural network, but we will call it a
σ-neural network to specify the activation function employed.
A
shallow neural network is a neural network with a single (
) hidden layer. In particular, a shallow neural network with output dimension
is given by
Definition 8. A function is called shallow universal if the set of -valued shallow σ-networks is dense in the set of all continuous functions , with respect to locally uniform convergence.
The following theorem, known as the universal approximation theorem, is a fundamental result in the theory of neural networks.
Theorem 4 (The universal approximation theorem; see [
27,
28,
29,
30,
31] for
, and [
32] for
)
. Let .A function is shallow universal if and only if σ is not a polynomial.
A function is shallow universal if and only if σ is not a polyharmonic. Here, a function is called polyharmonic if there exists such that in the sense of real variables and , where is the usual Laplace operator on .
In 1996, Mhaskar [
33] obtained a quantitative result for approximation of
functions using shallow networks with smooth activation functions. More recently, Yarotsky [
34] derived a quantitative approximation result for deep ReLU networks, where ReLU networks are given by (
12) with
and the ReLU activation function
,
, and “deep” refers to having a large
in (
12). For the case of complex-valued deep neural networks, we refer to [
35].
3.3. Cyclic Subgroups of
We now consider the case of cyclic subgroups of
, where group representations can be defined directly without embedding into the Weyl–Heisenberg group. The cyclic subgroups of order
N in
are given by
If
N is prime, these are the only nontrivial proper subgroups of
, but if
N is composite, there exist noncyclic subgroups of order
N in
; for instance,
is a noncyclic subgroup of order 6 in
. It is easily seen that the adjoint group of
in
is
itself; that is,
(see
Section 2.1).
We define the map
by
Setting
, we may simply write
For any
, we have
where we used the fact that
for all
. This shows that
is a group homomorphism and thus a unitary group representation of
on
. Due the symmetry in (
14),
is called the
symmetric representation of
on
.
Note that for any
and
, we have
if and only if
, where we used the relation
from (
14). This implies that a map
is
-equivariant in the sense of Definition 1 if and only if it is
-equivariant in the sense of Definition 4. Importantly, employing
-equivariance in place of
-equivariance will allow us to apply the tools from group representation theory described in
Section 3.2.
We are interested in approximating
-equivariant (or
-equivariant) maps
by neural networks. For this, we need to choose a complex-valued activation function
(see
Section 3.2) for the neural networks. Since
acts componentwise on its input, i.e.,
, it clearly commutes with all translations, i.e.,
; however,
does not commute with modulations in general. As shown in (
14), the representation
includes the multiplicative phase factor
, so we will assume that
is
-phase homogeneous (see Definition 2):
which ensures that
commutes with all
and all modulations.
We first need the following lemma. Below, we denote by the vector whose entries are all equal to 1.
Lemma 1. Assume that is shallow-universal. If a map satisfies , then there exists a shallow convolutional neural networkwhere and for , which approximates F uniformly on compact sets in . Proof. Using the universal approximation theorem (see Theorem 4), the first output component map
,
, can be approximated by a shallow network
with some
,
,
. Note that since
and since
is the identity map on
, we have
for all
. This condition provides approximations for other component maps
,
, with
, in terms of
. In fact, we have
Consequently, the map
,
, is approximated by the map
defined by
for
. For
, let
be the circular convolution of
a and
b defined by
, where
x and
y are understood as
N-periodic sequences on the integers. Then, for any
and
, we have
and therefore, we may write
It is easily seen that every convolutional map
,
, is a linear map, and in fact, a linear combination of
,
. Hence, the map
can be rewritten as
where
for
. The fact that
approximates
F uniformly on compact sets in
follows from the uniform approximation of
by
on compact sets in
. Finally, we note that
expressed above is a shallow convolutional neural network described in
Section 3.2. This completes the proof. □
Theorem 5. Assume that is shallow universal and satisfies for all . Let for some . Then, any continuous -equivariant (or Λ-equivariant) map can be approximated (uniformly on compact sets) by a shallow neural networkwhere and for , and satisfies for all . Moreover, every map of this form is -equivariant (or Λ-equivariant). Remark 4. Since by (14), we have for any . On the other hand, the vectors satisfying can be significantly different from those satisfying . Proof. Since
is cyclic, we order its elements as
, and treat
as
, since
. Then, the operators
and
, given in Definition 6, can be represented as the
matrices
respectively, where
denotes the conjugate transpose. Setting
, we have
so that
and
. As a result, the set
forms an orthonormal basis for
.
Note that for any continuous
-equivariant
, the map
is continuous and left
-translation equivariant (see Proposition 4). If
F is
linear, then
is also linear and can be represented as a circulant matrix, equivalently,
for some
, so that
Therefore, the commutant of
is given by
On the other hand, since
by (
14), the commutant of
coincides with that of
, i.e.,
Since the adjoint group of
is itself, i.e.,
(see
Section 2.1), we obtain
Now, we consider the general case where
is possibly
nonlinear. If
F is nonlinear, then
is a nonlinear left
-translation equivariant map. Since
is an additive group and since
and
, the map
can be viewed as a map from
to
. For simplicity, we will abuse notation and write
instead of
; thus, the first component of
will be simply denoted by
instead of
. Then, the left
-translation equivariance of
can be expressed as
. By applying Lemma 1 to
, we obtain a shallow convolutional neural network
where
, and
for
, which approximates
uniformly on compact sets in
; that is,
By the continuity of the operators
and
, we obtain
Note that since
for all
, the function
commutes with
given by (
15), that is,
. Therefore, we have
where
by (
16), and the vector
satisfies
Finally, we note that for any
,
where we used that
is a linear (unitary) operator commuting with
, and that
by (
16) and
by (
17). Therefore, every map of the form
is
-equivariant. □
Remark 5. The proof relies on observing (16) and choosing such that . To obtain , we have chosen so that is a diagonal matrix with exponential entries, and required an appropriate phase-homogeneity on σ so that σ commutes with those exponentials. This technique does not work for because cannot be expressed as a diagonal matrix for any in that case. Example 1. Let and , so that . In this case, we have , , and . Then,and for all . With , we haveIt is easy to check that v is invariant under , , , ; that is, for all . Theorem 5 shows that any Λ-equivariant map can be approximated (uniformly on compact sets) by functions of the formwhere and for . It is worth noting that while ρ is a unitary group representation of on , the map given by for is not a group representation of Λ on , since by (8). 4. Discussion
In this paper, we used finite-dimensional time-frequency analysis to investigate the properties of time-frequency shift equivariant maps that are generally nonlinear.
First, we established a one-to-one correspondence between -equivariant maps and certain phase-homogeneous functions, accompanied by a reconstruction formula expressing -equivariant maps in terms of these functions. This deepens our understanding of the structure of -equivariant maps by connecting them to their corresponding phase-homogeneous functions.
Next, we considered the approximation of -equivariant maps by neural networks. When is a cyclic subgroup of order N in , we proved that every -equivariant map can be approximated by a shallow neural network with affine linear maps formed as linear combinations of time-frequency shifts by . For the subgroup , the -equivariance corresponds to translation equivariance, and our result shows that every translation equivariant map can be approximated by a shallow convolutional neural network, which aligns well with the established effectiveness of convolutional neural networks (CNNs) for applications involving translation equivariance. In this context, our result extends the approximation of translation equivariant maps to general -equivariant maps, with potential applications in signal processing.
Finally, we note that the tools used to prove the approximation result (Theorem 2) are applicable in a more general setting than the one described in
Section 3.3. In particular, Definitions 6 and 7, and Proposition 4 apply to general unitary representations of arbitrary groups. Therefore, our approach can be adapted to derive similar results for general group-equivariant maps, which we leave as a direction for future research.