A Parallel-GPU DGTD Algorithm with a Third-Order LTS Scheme for Solving Multi-Scale Electromagnetic Problems
Abstract
1. Introduction
2. The DGTD Method for Maxwell’s Equations
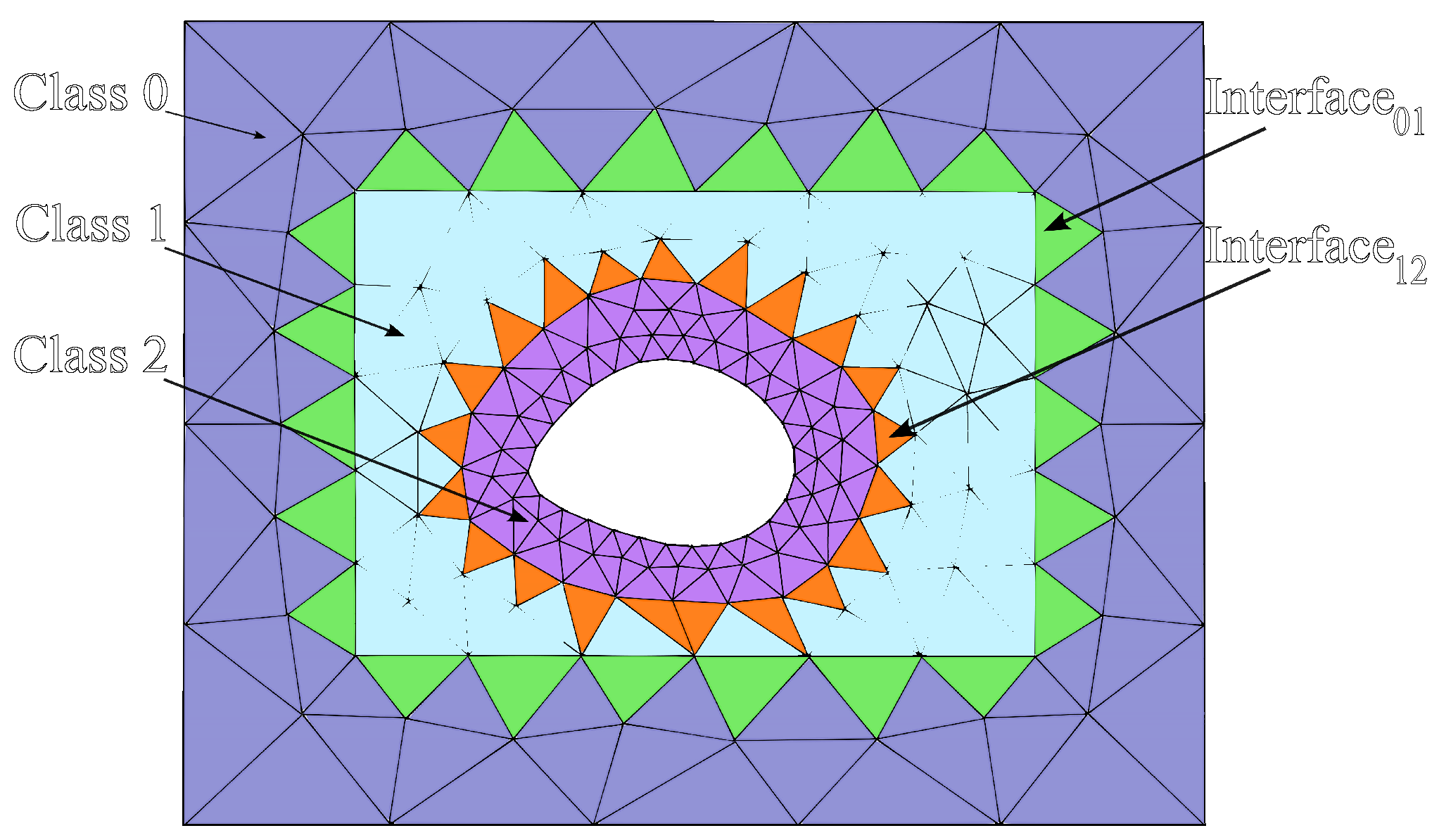
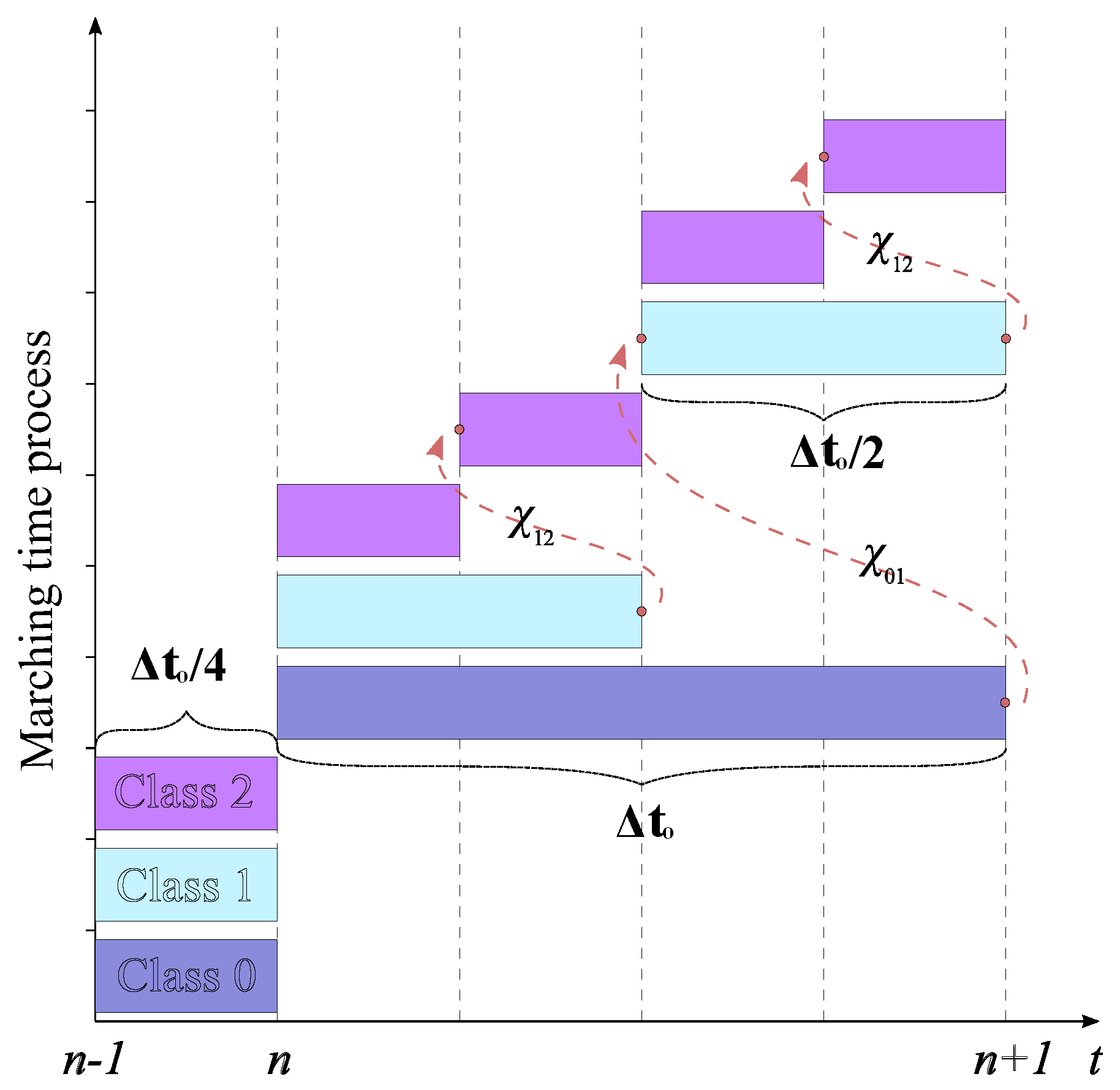
3. The Local Time Stepping Scheme
| Algorithm 1 LTS RK3 procedure for multiple levels of refinement |
| Step 1: Update the fields in all classes and store appropriate data to calculate at the interfaces between different classes. Step 2: Advance all class elements in time by using their own locally stable time step, starting with class 0 until class 2. Step 3: Calculate the interpolating polynomial, , at the interface between class 1 and class 2. Then, use it to advance class 2 in one local time step . Now, class 1 and class 2 are at the same time level. Step 4: Advance the elements in classes 1 and 2 with the local time steps and , respectively. To do this, calculate the interpolating polynomial, , at the interface between class 0 and class 1. Now, class 0 and class 1 are at the same time level. Step 5: Repeat step 3 and store the appropriate data to calculate at the interfaces between different classes. Now, all classes are at the same time level. Step 6: Repeat steps 2–5. |
4. Parallel-GPU Implementation
4.1. The DGTD on Graphic Processors
| Algorithm 2 The GPU-DGTD-GTS method | |
| procedure PAR_MAXWELL (q,, , LIFT, , ) | |
| Initialize all variables and create update matrices Pq, rhsq Calculate the time step value | |
| Copy data from the CPU to the GPU | |
| Define the number of time steps | |
| for k = 0 until Nts do | //time loop |
| for l = 0 until 2 do | //RK 3 stages |
| <surface_integral_Kernel> {Calculate } | |
| <volume_integral_Kernel> {Calculate } | |
| <time_integration_Kernel> {Update q} | |
| endfor | |
| Copy data from the GPU to the CPU | |
| endfor | |
| return q | |
| end | |
4.1.1. The Surface Integral Kernel
| Algorithm 3 Surface integral kernel |
| procedure SUR_KERNEL (q,, , ) for each block of elements do Calculate using and Apply boundary conditions to terms Use and to calculate Equation (11) Store the values in endfor return end |
4.1.2. The Volume Integral Kernel
4.1.3. The Time Integration Kernel
4.2. The GPU-DGTD-LTS Method
| Algorithm 4 Volume integral kernel |
| procedure VOL_KERNEL (q,, , LIFT, , ) for each block of elements , do Send arrays to shared memory for each element of each block , do Load geometric factor from Load field components from Load differentiation matrices from Calculate field derivatives and store in endfor Obtain from shared memory and store in global memory Send arrays to shared memory for each element of each block , do Load flux vectors from Load the matrix Load Multiply and store in a temporal array Update using temporal array endfor Obtain from shared memory and store in global memory endfor return end |
| Algorithm 5 Time integration kernel |
| procedure TIME_KERNEL (q, , ) for each block of elements do Define the RK3 constant coefficients of stage [4] Update term q using endfor return end |
| Algorithm 6 GPU-DGTD-LTS method | |
| procedure PAR_LTS_MAXWELL (q, , , LIFT, , ) | |
| Extract class(0) information {Calculate q0,,,} | |
| Extract class(1) information {Calculate q1,,,} | |
| Initialize update matrices {, , , } | |
| Calculate the time step values for class(0), , and class(1), | |
| Copy data from the CPU to the GPU | |
| Define the number of time steps {calculated using } | |
| Advance by one global time step and store the appropriate data | |
| for k = 0 until Nts, do | //time loop |
| for l = 0 until 2, do | //RK3 for class(0) |
| <surface_integral_Kernel_C0> {Calculate } | |
| <volume_integral_Kernel_C0> {Calculate } | |
| <time_integration_Kernel_C0> {Update q0} | |
| endfor | |
| Update q using q0 | |
| Calculate the interpolating polynomial to advance in class(1) | |
| for j = 0 until 1, do | //two refinement levels |
| for l = 0 until 2, do | //RK3 for class(1) |
| <surface_integral_Kernel_C1> {Calculate } | |
| <volume_integral_Kernel_C1> {Calculate } | |
| <time_integration_Kernel_C1> {Update q1} | |
| endfor | |
| endfor | |
| Update q using q1 | |
| Copy data from the GPU to the CPU | |
| endfor | |
| return q | |
| end | |
5. Numerical Results
5.1. A Metallic Cavity Benchmark Problem
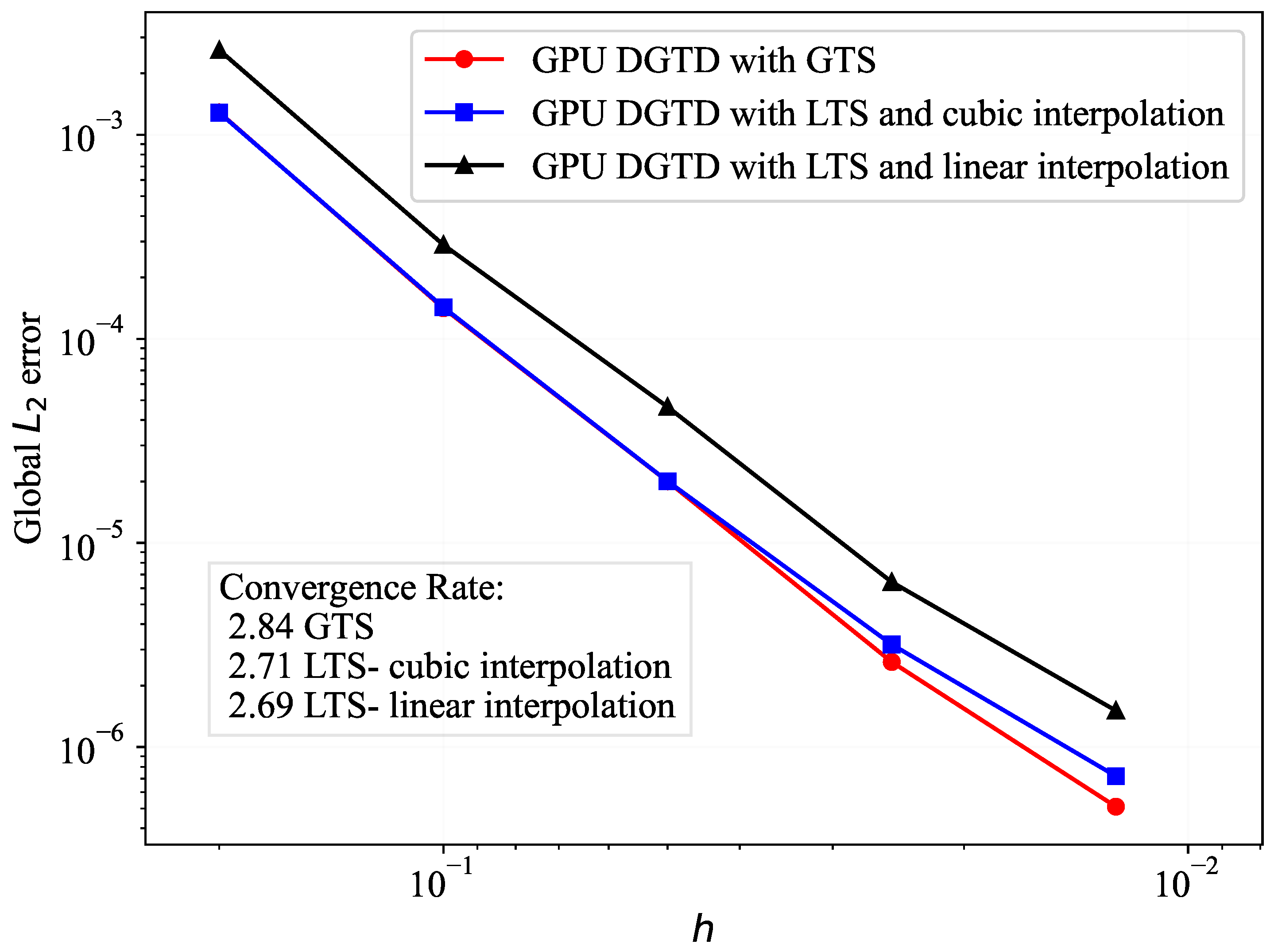
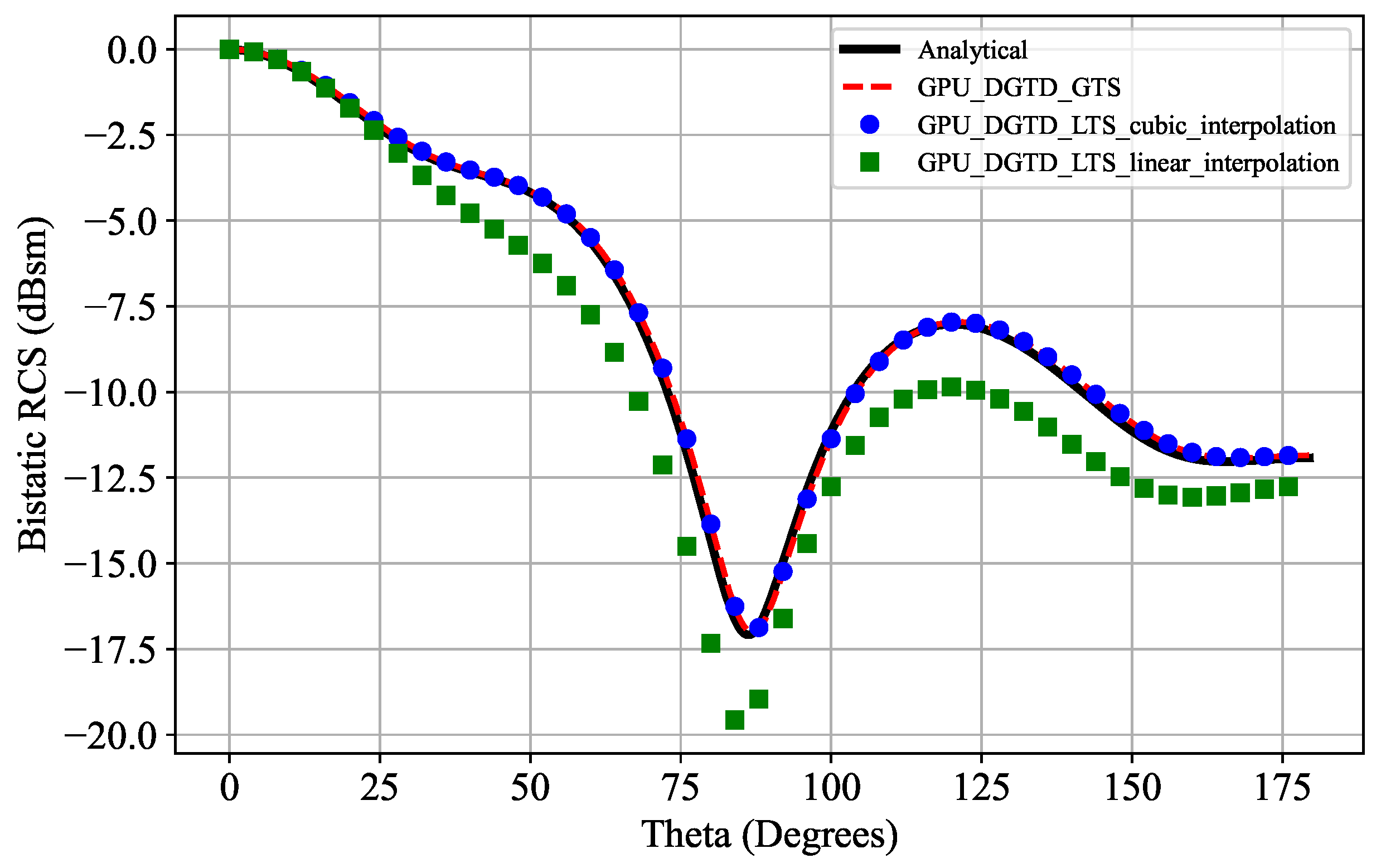
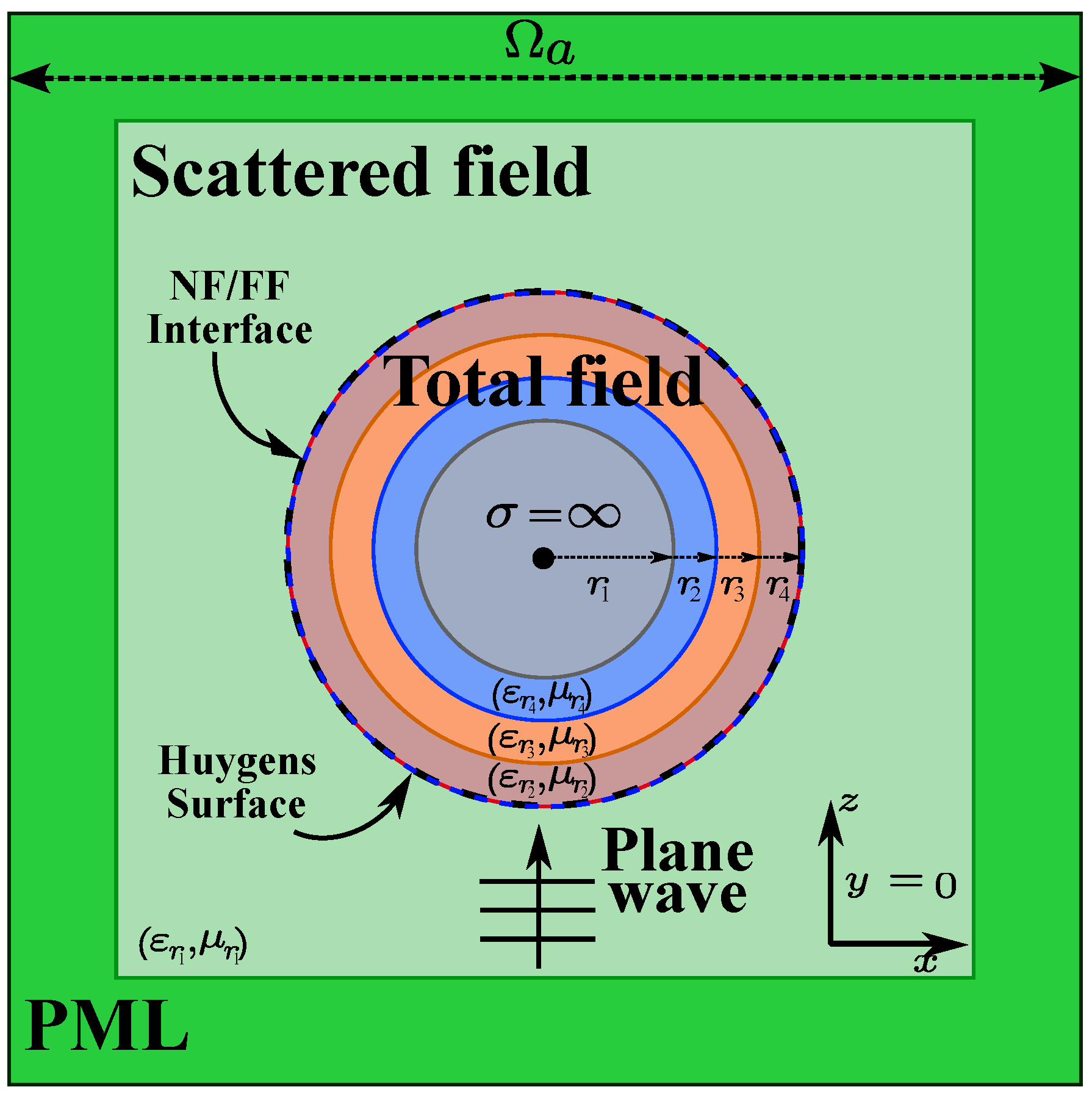
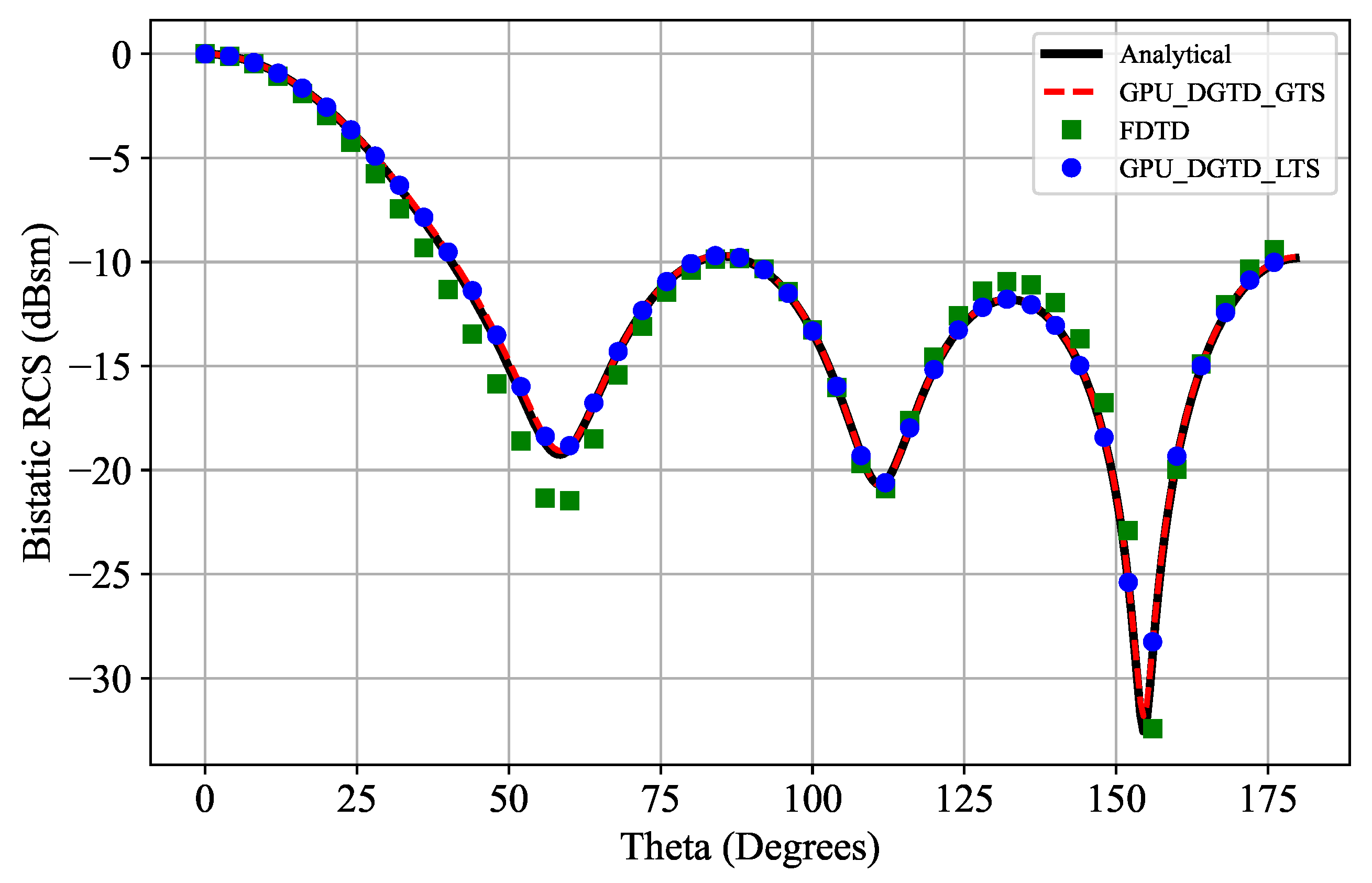
5.2. Scattering by a PEC Sphere
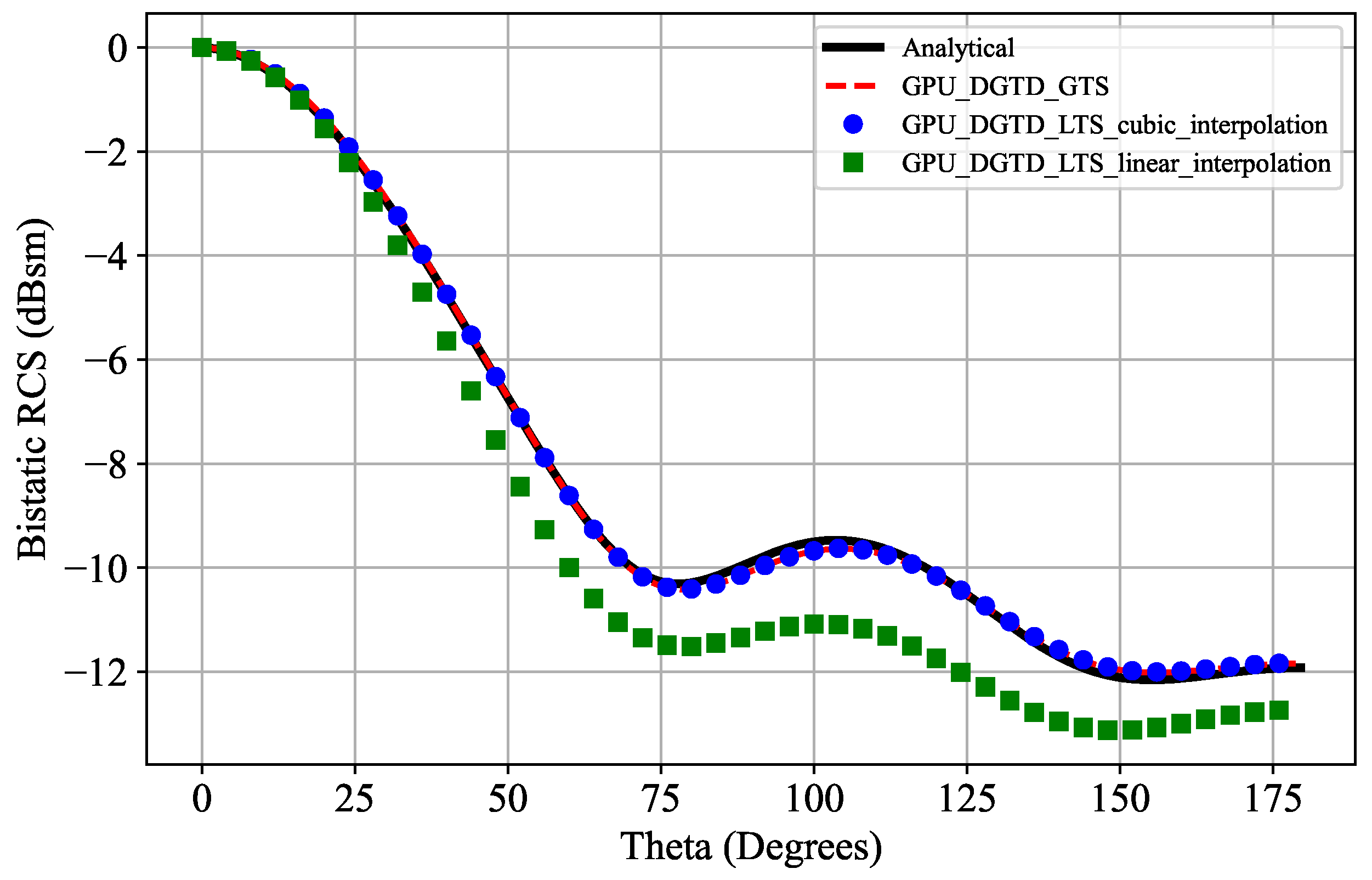
5.3. Scattering by a Multilayer Dielectric Sphere
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, J. Development of discontinuous galerkin methods for maxwell’s equations in metamaterials and perfectly matched layers. J. Comput. Appl. Math. 2011, 236, 950–961. [Google Scholar] [CrossRef][Green Version]
- Mi, J.; Ren, Q.; Su, D. Parallel subdomain-level dgtd method with automatic load balancing scheme with tetrahedral and hexahedral elements. IEEE Trans. Antennas Propag. 2021, 69, 2230–2241. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, R.; Huang, Z.; Wu, X. A verlet time-stepping nodal dgtd method for electromagnetic scattering and radiation. In Proceedings of the 2019 IEEE International Conference on Computational Electromagnetics (ICCEM), Shanghai, China, 20–22 March 2019; pp. 1–3. [Google Scholar] [CrossRef]
- Hesthaven, J.S.; Warburton, T. Nodal Discontinuous Galerkin Methods: Algorithms, Analysis, and Applications; Springer: New York, NY, USA, 2008. [Google Scholar]
- Ban, Z.G.; Shi, Y.; Wang, P. Advanced Parallelism of DGTD Method with Local Time Stepping Based on Novel MPI + MPI Unified Parallel Algorithm. IEEE Trans. Antennas Propag. 2022, 70, 3916–3921. [Google Scholar] [CrossRef]
- Wen, P.; Kong, W.; Hu, N.; Wang, X. Efficient Analysis of Radio Wave Propagation for Complex Network Environments Using Improved DGTD Method. IEEE Trans. Antennas Propag. 2024, 72, 5923–5934. [Google Scholar] [CrossRef]
- Yáñez-Casas, G.A.; Couder-Castañeda, C.; Hernández-Gómez, J.J.; Enciso-Aguilar, M.A. Scattering and Attenuation in 5G Electromagnetic Propagation (5 GHz and 25 GHz) in the Presence of Rainfall: A Numerical Study. Mathematics 2023, 11, 4074. [Google Scholar] [CrossRef]
- Fang, X.; Zhang, W.; Zhao, M. A Non-Traditional Finite Element Method for Scattering by Partly Covered Grooves with Multiple Media. Mathematics 2024, 12, 254. [Google Scholar] [CrossRef]
- Sheng, Y.; Zhang, T. A Finite Volume Method to Solve the Ill-Posed Elliptic Problems. Mathematics 2022, 10, 4220. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, P.; Ban, Z.G.; Zhu, S.C. Application of Hybridized Discontinuous Galerkin Time Domain Method into the Solution of Multiscale Electromagnetic Problems. In Proceedings of the 2019 Photonics & Electromagnetics Research Symposium-Fall (PIERS-Fall), Xiamen, China, 17–20 December 2019; pp. 2325–2329. [Google Scholar] [CrossRef]
- Piperno, S. Symplectic local time-stepping in non-dissipative dgtd methods applied to wave propagation problems. ESAIM Math. Model. Numer. Anal. 2006, 40, 815–841. [Google Scholar] [CrossRef]
- Montseny, E.; Pernet, S.; Ferrieres, X.; Cohen, G. Dissipative terms and local time-stepping improvements in a spatial high order discontinuous galerkin scheme for the time-domain maxwell’s equations. J. Comput. Phys. 2008, 227, 6795–6820. [Google Scholar] [CrossRef]
- Cui, X.; Yang, F.; Gao, M. Improved local time-stepping algorithm for leap-frog discontinuous galerkin time-domain method. IET Microw. Antennas Propag. 2018, 12, 963–971. [Google Scholar] [CrossRef]
- Trahan, C.J.; Dawson, C. Local time-stepping in runge–kutta discontinuous galerkin finite element methods applied to the shallow-water equations. Comput. Methods Appl. Mech. Eng. 2012, 217–220, 139–152. [Google Scholar] [CrossRef]
- Angulo, L.; Alvarez, J.; Teixeira, F.; Pantoja, M.; Garcia, S. Causal-path local time-stepping in the discontinuous galerkin method for maxwells equations. J. Comput. Phys. 2014, 256, 678–695. [Google Scholar] [CrossRef]
- Li, M.; Li, X.; Xu, P.; Zhang, Y.; Shi, Y.; Wang, G. A Multi-scale Domain Decomposition Strategy for the Hybrid Time Integration Scheme of DGTD Method. In Proceedings of the 2024 International Applied Computational Electromagnetics Society Symposium (ACES-China), Xi’an, China, 16–19 August 2024; pp. 1–3. [Google Scholar] [CrossRef]
- Reuter, B.; Aizinger, V.; Kostler, H. A multi-platform scaling study for an OpenMP parallelization of a discontinuous Galerkin ocean model. Comput. Fluids 2015, 117, 325–335. [Google Scholar] [CrossRef]
- Zhao, L.; Chen, G.; Yu, W. GPU Accelerated Discontinuous Galerkin Time Domain Algorithm for Electromagnetic Problems of Electrically Large Objects. Prog. Electromagn. Res. B 2016, 67, 137–151. [Google Scholar] [CrossRef]
- Chen, H.; Zhao, L.; Yu, W. GPU Accelerated DGTD Method for EM Scattering Problem from Electrically Large Objects. In Proceedings of the 2018 Cross Strait Quad-Regional Radio Science and Wireless Technology Conference (CSQRWC), Xuzhou, China, 21–24 July 2018; pp. 1–2. [Google Scholar] [CrossRef]
- Feng, D.; Liu, S.; Wang, X.; Wang, X.; Li, G. High-order GPU-DGTD method based on unstructured grids for gpr simulation. J. Appl. Geophys. 2022, 202, 104666. [Google Scholar] [CrossRef]
- Einkemmer, L.; Moriggl, A. A Semi-Lagrangian Discontinuous Galerkin Method for Drift-Kinetic Simulations on GPUs. SIAM J. Sci. Comput. 2024, 46, B33–B55. [Google Scholar] [CrossRef]
- Ban, Z.G.; Shi, Y.; Yang, Q.; Wang, P.; Zhu, S.C.; Li, L. Gpu-accelerated hybrid discontinuous galerkin time domain algorithm with universal matrices and local time stepping method. IEEE Trans. Antennas Propag. 2020, 68, 4738–4752. [Google Scholar] [CrossRef]
- Li, M.; Wu, Q.; Lin, Z.; Zhang, Y.; Zhao, X. Novel parallelization of discontinuous galerkin method for transient electromagnetics simulation based on sunway supercomputers. Appl. Comput. Electromagn. Soc. J. 2022, 37, 795–804. [Google Scholar] [CrossRef]
- Li, M.; Wu, Q.; Lin, Z.; Zhang, Y.; Zhao, X. A minimal round-trip strategy based on graph matching for parallel dgtd method with local time-stepping. IEEE Antennas Wirel. Propag. Lett. 2023, 22, 243–247. [Google Scholar] [CrossRef]
- Cheng, J.; Grossman, M.; Mckercher, T. Professional CUDA C Programming; Wrox: Indianapolis, IN, USA, 2014. [Google Scholar]
- Ashbourne, A. Efficient Runge-Kutta Based Local Time-Stepping Methods. Master’s Dissertation, Department of Applied Mathematics, University of Waterloo, Ontario, CA, USA, 2016. [Google Scholar]
- Klockner, A. High-Performance High-Order Simulation of Wave and Plasma Phenomena. Ph.D. Thesis, Department of Applied Mathematics, Brown University, Providence, RI, USA, 2010. [Google Scholar]
- Elsherbeni, A.Z.; Demir, V. The Finite-Difference Time-Domain Method for Electromagnetics with MATLAB Simulations; SciTech Pub: Sydney, Australia, 2009. [Google Scholar]
- Jin, J.-M. The Finite Element Method in Electromagnetics; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]



| Array | Dimension | Description |
|---|---|---|
| Field components | ||
| Volume geometric factors | ||
| Surface geometric factors | ||
| Surface integration matrix | ||
| Differentiation matrices | ||
| Global element indexes + and − |
| Mesh Number | M1 | M2 | M3 | M4 | M5 |
|---|---|---|---|---|---|
| Max edge size—h (m) | 0.2 | 0.1 | 0.05 | 0.025 | 0.0125 |
| No. of elements | 368 | 1352 | 4822 | 18,358 | 73,516 |
| No. of vertices | 205 | 717 | 2492 | 9340 | 37,079 |
| Elements in class 0 | 312 | 1224 | 4356 | 16,676 | 66,936 |
| Elements in class 1 | 56 | 128 | 466 | 1682 | 6580 |
| Large interface elements | 16 | 28 | 32 | 64 | 124 |
| —Class 0 (ps) | 41.52 | 21.64 | 11.12 | 5.68 | 2.78 |
| —Class 1 (ps) | 20.76 | 10.82 | 5.56 | 2.84 | 1.39 |
| DGTD Simulations | |||
|---|---|---|---|
| GPU-LTS-Cubic | 2.4 × | 3.6 × | 3.8 × |
| GPU-LTS-Linear | 6.5 × | 7.9 × | 1.3 × |
| DGTD Simulations | Execution Time (s) | E-Planeerror | H-Planeerror | Speed-Up |
|---|---|---|---|---|
| GPU-GTS | 822 | 0.0054 | 0.0025 | - |
| GPU-LTS-Cubic | 339 | 0.0056 | 0.00259 | 2.42 |
| GPU-LTS-Linear | 334 | 0.0271 | 0.042 | 2.46 |
| Numerical Method | Execution Time (s) | E-Planeerror | H-Planeerror | Speedup |
|---|---|---|---|---|
| GPU-DGTD-GTS | 18,780 | 0.0049 | 0.0044 | - |
| GPU-DGTD-LTS | 4150 | 0.0051 | 0.0047 | 4.52 |
| FDTD | - | 0.011 | 0.0081 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lizarazo, M.J.; Silva, E.J. A Parallel-GPU DGTD Algorithm with a Third-Order LTS Scheme for Solving Multi-Scale Electromagnetic Problems. Mathematics 2024, 12, 3663. https://doi.org/10.3390/math12233663
Lizarazo MJ, Silva EJ. A Parallel-GPU DGTD Algorithm with a Third-Order LTS Scheme for Solving Multi-Scale Electromagnetic Problems. Mathematics. 2024; 12(23):3663. https://doi.org/10.3390/math12233663
Chicago/Turabian StyleLizarazo, Marlon J., and Elson J. Silva. 2024. "A Parallel-GPU DGTD Algorithm with a Third-Order LTS Scheme for Solving Multi-Scale Electromagnetic Problems" Mathematics 12, no. 23: 3663. https://doi.org/10.3390/math12233663
APA StyleLizarazo, M. J., & Silva, E. J. (2024). A Parallel-GPU DGTD Algorithm with a Third-Order LTS Scheme for Solving Multi-Scale Electromagnetic Problems. Mathematics, 12(23), 3663. https://doi.org/10.3390/math12233663







