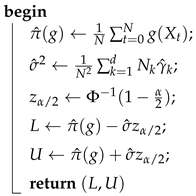Confidence Regions for Steady-State Probabilities and Additive Functionals Based on a Single Sample Path of an Ergodic Markov Chain

Abstract

Discrete, finite-state Markov chains are applied in many different fields. When a system is modeled as a discrete, finite-state Markov chain, the asymptotic properties of the system, such as the steady-state distribution, are often estimated based on a single, empirically observable sample path of the system, whereas the actual steady-state distribution is unknown. A question that arises is: how close is the empirically estimated steady-state distribution to the actual steady-state distribution? In this paper, we propose a method to numerically determine asymptotically exact confidence regions for the steady-state probabilities and confidence intervals for additive functionals of an ergodic Markov chain based on a single sample path.

1. Introduction

Consider the following problem. Let $P=\left[p_{ij}\right]\in {[0,1]}^{d\times d}$ be the unknown transition matrix of an ergodic Markov chain on a finite, discrete state-space $\mathsf{\Omega }$ of size d. Let $\pi$ be the unknown stationary distribution vector associated with P. Assume that we are interested in approximating $\pi$ based on a single sample path characterized by a sequence of observed states ${\left(X_t\right)}_{t=0}^N$, where N is a positive integer. Assume that $\widehat{P}=\left[{\widehat{p}}_{ij}\right]\in {[0,1]}^{d\times d}$ is the maximum likelihood estimate of P based on ${\left(X_t\right)}_{t=0}^N$ and that $\widehat{P}$ admits the unique stationary distribution vector $\widehat{\pi }$.

A question that naturally arises is: how close is $\widehat{\pi }$ to $\pi$? This question is likely to occur in many applications where a process is assumed to follow a Markov chain; we are interested in the steady-state value of a quantity of interest, which can be expressed as a function g, where $g:\mathsf{\Omega }\to \mathbb{R}$. More specifically, in this context we are interested in

$$\pi \left(g\right):=\sum _{i=1}^d{\pi }_{i}g\left({\omega }_i\right),$$

where $\pi$ is unknown.

This paradigm is likely to arise in areas as diverse as computational physics [1,2], social and environmental sciences [3], and Markov decision processes (MDPs), particularly in the case of infinite-horizon undiscounted MDPs, also called average reward processes [4].

Depending on the exact context, it may be useful to derive confidence regions for $\pi$ and/or confidence intervals for $\pi \left(g\right)$. In this paper, we propose an approach to this effect that, to the best of our knowledge, has not been previously suggested in the literature.

There is a vast statistical literature on Markov chain estimation. With regards to research that is relevant to the previously mentioned context, the research can be divided into two main categories.

The first category comprises asymptotic results (e.g., [5,6]) that are useful to understand the limiting behavior of $\widehat{\pi }$ but are not suitable for finite-time, non-asymptotic analysis, as is required for the context we described. For instance, it is known that the sample mean $\widehat{\pi }\left(g\right):={\displaystyle \frac{1}{N}}{\sum }_{t=0}^{N}g\left(X_t\right)$ converges almost surely to $\pi \left(g\right)$ for $N\to \infty$ [6]. Moreover, it is also known that, under certain conditions, for $N\to \infty$ the distribution of $\sqrt{N}\left(\widehat{\pi }\left(g\right)-\pi \left(g\right)\right)$ converges toward a normal distribution with mean 0 and asymptotic variance ${lim}_{N\to \infty }N\mathbf{Var}\left(\widehat{\pi }\left(g\right)\right)$ [5].

The second category includes results that are appropriate for non-asymptotic analysis (e.g., [7,8,9,10,11]) but assumes that some of the key properties of the Markov chain are known, such as the mixing time (see [12] for more details on this concept), the spectral gap, or even P itself.

Our work adds to the existing literature in that our main result in Section 2 is suitable for non-asymptotic analysis whilst making no assumptions about the properties of P beyond what can be inferred from ${\left(X_t\right)}_{t=0}^n$. To achieve this, we expand on the results in [11].

Despite not strictly falling within the statistical domain, we deem it relevant to mention a third category of results due to the wealth of available literature. This category of results revolves around deriving so-called perturbation bounds for $\pi$ and analyzing the sensitivity of $\widehat{\pi }$ (see [13,14,15,16,17,18,19]). By and large, the existing literature revolves around absolute bounds of the following form:

$$\parallel \widehat{\pi }{-\pi \parallel }_p\le k{\parallel P-\widehat{P}\parallel }_q,$$

(1)

where k is derived in a variety of ways; $\widehat{P}$ is a perturbation of P; and $p=q=\infty$ or, alternatively, $p=1$ and $q=\infty$. Much of the focus of the existing literature is on ways to derive k, whereby k is commonly expressed in terms of either the fundamental matrix of the underlying Markov chain; the mean first passage times; or the group inverse of $I-P$, where I is the identity matrix. While inequalities of the form of (1) are useful when $\parallel P-\widehat{P}{\parallel }_q$ is known, in the setting that we described in the introduction, $\parallel P-\widehat{P}{\parallel }_q$ is unknown.

Given the rich available literature on bounds of the form (1), a natural place to start for our purposes is to derive a confidence bound on $\parallel P-\widehat{P}{\parallel }_{\infty }$, which can then be plugged into a suitable variation of inequality (1). However, numerical experiments revealed that the realized coverage ratios obtained with this approach far exceeded the level of confidence. A major challenge with this kind of approach is that worst-case assumptions need to be made in order to derive inequalities of form (1), which are absolute bounds. We found that confidence regions based on such inequalities therefore tend to be exceedingly conservative. By contrast, our proposed approach relies on asymptotically exact relationships and therefore is not affected by the same shortcoming.

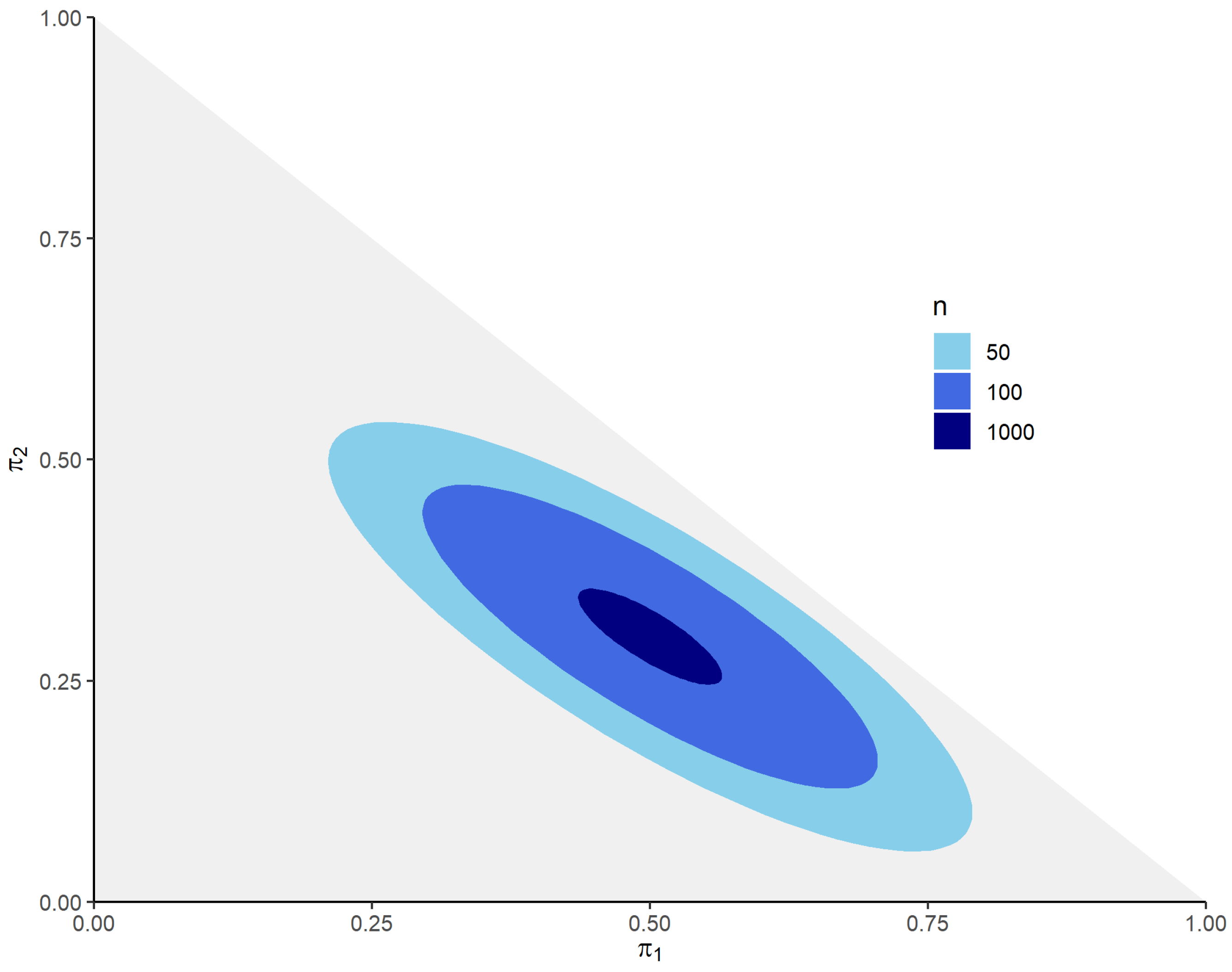
The rest of this paper proceeds as follows. Section 2 presents the results underpinning the proposed approach as well as the proofs of these results. Section 3 presents the proposed approach. Section 4 illustrates the proposed approach with examples and presents numerical experiments to analyze the coverage characteristics of the approach. Section 5 concludes this work and discusses potential future directions of research.

2. Results Underpinning the Proposed Approach and Proofs

2.1. Results Underpinning the Proposed Approach

Let $\left\{X_t\right\}$ be an irreducible Markov chain with finite and discrete state-space $\mathsf{\Omega }:=\{{\omega }_k:k\in \left[d\right]\}$. Throughout this paper, for any integer n we denote $\left[n\right]$ as the set of indices from 1 to n. Let P be the transition matrix, and assume that P admits the unique stationary distribution vector $\pi$.

Let $\widehat{\pi }\left(g\right)=:{\displaystyle \frac{1}{N}}{\sum }_{t=1}^{N}g\left(X_t\right)$ be based on a sample path ${\left(X_t\right)}_{t=0}^N$ of this Markov chain, and let $\widehat{P}$ be the maximum likelihood estimate of P based on this sample path. Assume that $\widehat{P}$ admits the unique stationary distribution vector $\widehat{\pi }$. Furthermore, $\forall k\in \left[d\right]$, let $N_k=\left|\{t\in [N-1]:X_t={\omega }_k\}\right|$. Assume that $\forall k\in \left[d\right]$, $N_k\ge 1$.

Theorem 1. 

$\forall (i,j)\in {\left[d\right]}^2,$

$$\underset{N\to \infty }{lim}\left[N\mathbf{Cov}\right({\pi }_i-{\widehat{\pi }}_i,{\pi }_j-{\widehat{\pi }}_j|{\left\{N_k\right\}}_{k\in \left[d\right]})-{\displaystyle \frac{1}{N}}\sum _{k=1}^d{N}_k{\widehat{h}}_i^T{\widehat{\mathbf{\Sigma }}}_k{\widehat{h}}_j]=0,$$

(2)

and

$$\underset{N\to \infty }{lim}\left[N\mathbf{Var}\right(\widehat{\pi }\left(g\right)|{\left\{N_k\right\}}_{k\in \left[d\right]})-{\displaystyle \frac{1}{N}}\sum _{k=1}^d{N}_k{\widehat{\gamma }}_k]=0,$$

(3)

where ${\widehat{\mathbf{\Sigma }}}_k$ is a symmetric matrix that depends on the kth row of $\widehat{P}$; $\forall i\in \left[d\right],{\widehat{h}}_i$ is a column vector that depends on the $ith$ column of a one-condition g-inverse of $\widehat{P}$; and $\forall k\in \left[d\right]$,

$${\widehat{\gamma }}_k=\sum _{i=1}^d\sum _{j=1}^{d}g\left({\omega }_i\right){\widehat{h}}_i^T{\widehat{\mathbf{\Sigma }}}_k{\widehat{h}}_{j}g\left({\omega }_j\right).$$

The definition of a one-condition g-inverse is given in Section 2.2. We then expose the proof of Theorem 1 in Section 2.3. The proof of Equation (3) is similar to that of Theorem 3.1 in [11]. The key difference between Equation (3) and Theorem 3.1 in [11] is that Equation (3) only involves inputs that can be inferred from ${\left(X_t\right)}_{t=0}^N$.

2.2. Core Concepts Underlying the Proof of Theorem 1

The following definition and Equation (4) are drawn from [19].

Definition 1 

(One-condition g-inverse). A one-condition g-inverse (or one-condition generalized inverse) of a matrix A is any matrix $A^{-}$ such that $A{A}^{-}A=A.$

Let $P=\left[p_{ij}\right]\in {[0,1]}^{d\times d}$ be the transition matrix of a finite irreducible Markov chain, which is assumed to have the associated steady-state distribution vector $\pi$. Let $\tilde{P}=\left[{\tilde{p}}_{ij}\right]=P+E$ be the transition matrix of the perturbed Markov chain, where $E=\left[{ϵ}_{ij}\right]$ is the matrix of perturbations. Notice that $\forall (i,j)\in {\left[d\right]}^2,\left|{ϵ}_{ij}\right|\le 1$, and $\forall i\in \left[d\right],{\sum }_{j=1}^d{ϵ}_{ij}=0$. $\tilde{P}$ is assumed to admit the unique steady-state distribution vector $\tilde{\pi }$. Then, according to Theorem 2.1 in [19],

$${\tilde{\pi }}^T-{\pi }^T={\tilde{\pi }}^{T}EH,$$

(4)

where $H=G(I-e{\pi }^T)$, $e^T=(1,\dots ,1)$, I is the identity matrix, and G is a one-condition g-inverse of $I-P$.

An exhaustive review of the different ways to compute matrix G (and therefore matrix H) is beyond the scope of this work. For the purposes of the examples in Section 4, we computed G as the so-called group inverse (see [20]) of $I-\widehat{P}$. This choice is mainly motivated by ease of computation for the transition matrix of an ergodic Markov chain (Theorem 5.2 in [20]). Indeed, the most computationally intensive step is the calculation of the inverse of a ${(d-1)}^2$ principal submatrix of $I-\widehat{P}$.

It bears mentioning that H can also be derived based on the matrix of mean first passage times and the steady-state distribution vector (see [19]), which can enhance interpretability.

For a sample path of length N characterized by the sequence of observed states ${\left(X_i\right)}_{i=0}^N$ of a discrete ergodic Markov chain with transition matrix P, let $N_i=:\left|\{t\in [N-1]:X_t={\omega }_i\}\right|$. For any pair of states $({\omega }_i,{\omega }_j)\in {\mathsf{\Omega }}^2$, let $N_{ij}$ be the number of transitions from ${\omega }_i$ to ${\omega }_j$ in the sample path ${\left(X_t\right)}_{t=0}^N$, or more formally $N_{ij}:=\left|\{t\in [n-1]:(X_t,X_{t+1})=({\omega }_i,{\omega }_j)\}\right|,(i,j)\in {\left[d\right]}^2$. We will refer to $M=\left[N_{ij}\right]\in {\mathbb{N}}^{d\times d}$ as the sequence matrix. Also, throughout this work, we will assume that $\forall i\in \left[d\right],N_i\ge 1$.

Lemma 1. 

Conditional on $\left\{N_i\right|i\in \left[d\right]\}$, the rows of M are mutually independent and respectively follow multinomial distributions with $N_i$ trials and unknown event probabilities $p_{i1},\dots ,p_{id}$.

Proof. 

Conditional on $N_i$, the joint outcome of $N_{i1},\dots ,N_{id}$ can be equated to $N_i$ independent trials (independence follows from the Markov property) where the outcome of each trial has a categorical distribution with fixed success probabilities $p_{i1},\dots ,p_{id}$. In other words, conditional on $N_i$, $N_{i1},\dots ,N_{id}$ jointly follow a multinomial distribution with $N_i$ trials and event probabilities $p_{i1},\dots ,p_{id}$.

Also, for $\forall i\in \left[d\right]$ let $N_{i·}$ be a vector corresponding to row i of the sequence matrix M and let $P_{i·}$ be a vector corresponding to row i of the unknown transition matrix P. Given known $\left\{N_i\right|i\in \left[d\right]\}$ and unknown $\left\{P_{i·}\right|i\in \left[d\right]\}$, for $j\ne k$:

$$\begin{array}{c}\mathbf{P}(N_{j·}=x\cap N_{k·}=y|\left\{N_i\right|i\in \left[d\right]\},\left\{P_{i·}\right|i\in \left[d\right]\})\hfill \\ =\mathbf{P}(N_{j·}=x|N_{k·}=y,\left\{N_i\right|i\in \left[d\right]\},\left\{P_{i·}\right|i\in \left[d\right]\})\mathbf{P}(N_{k·}=y|\left\{N_i\right|i\in \left[d\right]\},\left\{P_{i·}\right|i\in \left[d\right]\})\hfill \\ =\mathbf{P}(N_{j·}=x|N_j,P_{j·})\mathbf{P}(N_{k·}=y|N_k,P_{k·})\hfill \\ =\mathbf{P}(N_{j·}=x|\left\{N_i\right|i\in \left[d\right]\},\left\{P_{i·}\right|i\in \left[d\right]\})\mathbf{P}(N_{k·}=y|\left\{N_i\right|i\in \left[d\right]\},\left\{P_{i·}\right|i\in \left[d\right]\}).\hfill \end{array}$$

□

Importantly, independence between the rows only holds conditional on the knowledge of $\left\{N_i\right|i\in \left[d\right]\}$. Otherwise, the rows of M are of course not independent since crucially $\forall i\in \left[d\right],N_i$ depends on ${\sum }_{j\in \left[d\right]}{N}_{ji}$.

2.3. Proof of Theorem 1

Notice that for a sample path ${\left(X_t\right)}_{t=0}^N$ of an irreducible Markov chain with discrete and finite state-space $\mathsf{\Omega }$, transition matrix P, and unique steady-state distribution vector $\pi$, we can build the maximum likelihood estimate $\widehat{P}=\left[{\widehat{p}}_{ij}\right]=[N_{ij}/N_i]$ of P based on the sequence matrix. Moreover, $\widehat{P}$ can be viewed as a perturbation of P (and vice versa).

Assume that $\widehat{P}$ admits the unique steady-state distribution vector $\widehat{\pi }$. Let $E=\left[{ϵ}_{ij}\right]=P-\widehat{P}$ and $H=G(I-e{\widehat{\pi }}^T)$, where $e^T=(1,\dots ,1)$, I is the identity matrix, and G is a one-condition g-inverse of $I-\widehat{P}$. In this context, the following lemmas apply.

Lemma 2. 

$\forall (i,j)\in {\left[d\right]}^2,$

$$\begin{array}{c}\hfill \mathbf{Cov}({\pi }_i-{\widehat{\pi }}_i,{\pi }_j-{\widehat{\pi }}_j|{\left\{N_k\right\}}_{k\in \left[d\right]})=\sum _{k=1}^d{\pi }_k^2\mathbf{Cov}\left(\sum _{l=1}^d{h}_{li}{ϵ}_{kl},\sum _{m=1}^d{h}_{mj}{ϵ}_{km}|N_k\right).\end{array}$$

Proof. 

By matrix multiplication and following Equation (4), $\forall (i,j)\in {\left[d\right]}^2,$

$${\pi }_i-{\widehat{\pi }}_i=\sum _{k=1}^d{\pi }_k\sum _{l=1}^d{h}_{li}{ϵ}_{kl},$$

$${\pi }_j-{\widehat{\pi }}_j=\sum _{k=1}^d{\pi }_k\sum _{m=1}^d{h}_{mj}{ϵ}_{km}.$$

Hence,

$$\begin{array}{cc}& \mathbf{Cov}({\pi }_i-{\widehat{\pi }}_i,{\pi }_j-{\widehat{\pi }}_j|{\left\{N_k\right\}}_{k\in \left[d\right]})\hfill \\ & =\mathbf{Cov}\left(\sum _{k=1}^d{\pi }_k\sum _{l=1}^d{h}_{li}{ϵ}_{kl},\sum _{k=1}^d{\pi }_k\sum _{m=1}^d{h}_{mj}{ϵ}_{km}|{\left\{N_k\right\}}_{k\in \left[d\right]}\right)\hfill \\ & =\sum _{k=1}^d{\pi }_k^2\mathbf{Cov}\left(\sum _{l=1}^d{h}_{li}{ϵ}_{kl},\sum _{m=1}^d{h}_{mj}{ϵ}_{km}|N_k\right).\hfill \end{array}$$

The second equality follows from conditional independence between the rows of the sequence matrix (Lemma 1).    □

The following three lemmas are corollaries of Lemmas 3.4–3.6 in [11], except that here $E=\left[{ϵ}_{ij}\right]=P-\widehat{P}$ and $H=G(I-e{\widehat{\pi }}^T)$, whereby $e^T=(1,\dots ,1)$, I is the identity matrix, and G is a one-condition g-inverse of $I-\widehat{P}$. For the sake of brevity, we refer the reader to [11] for the respective proofs.

Lemma 3. 

$$\begin{array}{c}\hfill \widehat{\pi }\left(g\right)-\pi \left(g\right)=\sum _{k=1}^d{\pi }_k\sum _{i=1}^{d}g\left({\omega }_i\right)\sum _{l=1}^d{h}_{li}{ϵ}_{kl}.\end{array}$$

Lemma 4. 

$$\mathbf{Var}\left(\widehat{\pi }\left(g\right)-\pi \left(g\right)|{\left\{N_k\right\}}_{k\in \left[d\right]}\right)=\sum _{k=1}^d{\pi }_k^2\sum _{i=1}^d\sum _{j=1}^{d}g\left({\omega }_i\right)g\left({\omega }_j\right)\mathbf{Cov}\left(\sum _{l=1}^d{h}_{li}{ϵ}_{kl},\sum _{m=1}^d{h}_{mj}{ϵ}_{km}|N_k\right).$$

Lemma 5. 

Without a loss of generality, assume that the row vector $P_{k·}$ has only nonzero elements. $\forall (i,j,k)\in {\mathbb{N}}^3$,

$$\mathbf{Cov}\left(\sum _{l=1}^d{h}_{li}{ϵ}_{kl},\sum _{m=1}^d{h}_{mj}{ϵ}_{km}|N_k\right)={\displaystyle \frac{1}{N_k}}{\widehat{h}}_i^T{\mathbf{\Sigma }}_k{\widehat{h}}_j,$$

where

$${\widehat{h}}_i=\left[\begin{array}{c}{h}_{1i}\\ ⋮\\ h_{di}\end{array}\right]-h_{di}\left[\begin{array}{c}1\\ ⋮\\ 1\end{array}\right],$$

$${\widehat{h}}_j=\left[\begin{array}{c}{h}_{1j}\\ ⋮\\ h_{dj}\end{array}\right]-h_{dj}\left[\begin{array}{c}1\\ ⋮\\ 1\end{array}\right],$$

and

$${\mathbf{\Sigma }}_k=\left(\begin{array}{cccc}{p}_{k1}(1-p_{k1})& -p_{k1}{p}_{k2}& \cdots & -p_{k1}{p}_{kd}\\ -p_{k1}{p}_{k2}& p_{k2}(1-p_{k2})& \cdots & -p_{k2}{p}_{kd}\\ ⋮& ⋮& \ddots & ⋮\\ -p_{k1}{p}_{kd}& -p_{k2}{p}_{kd}& \cdots & p_{kd}(1-p_{kd})\end{array}\right).$$

Notice that $\forall k\in \left[d\right],$

$$\underset{N\to \infty }{lim}{\displaystyle \frac{N_k}{N}}=\underset{N\to \infty }{lim}{\widehat{\pi }}_k={\pi }_k,$$

$$\underset{N\to \infty }{lim}{\widehat{P}}_{k·}=P_{k·},\mathrm{and}\mathrm{hence}$$

$$\underset{N\to \infty }{lim}{\widehat{\mathbf{\Sigma }}}_k={\mathbf{\Sigma }}_k.$$

From these equalities and Lemma 5

$$\underset{N\to \infty }{lim}{\displaystyle \frac{1}{N}}\sum _{k=1}^d{N}_k{\widehat{h}}_i^T{\widehat{\mathbf{\Sigma }}}_k{\widehat{h}}_j=\underset{N\to \infty }{lim}\sum _{k=1}^d{\pi }_k{\widehat{h}}_i^T{\mathbf{\Sigma }}_k{\widehat{h}}_j,$$

and

$$\underset{N\to \infty }{lim}{\displaystyle \frac{1}{N}}\sum _{k=1}^d{N}_k\sum _{i=1}^d\sum _{j=1}^{d}g\left({\omega }_i\right)g\left({\omega }_j\right){\widehat{h}}_i^T{\widehat{\mathbf{\Sigma }}}_k{\widehat{h}}_j=\underset{N\to \infty }{lim}\sum _{k=1}^d{\pi }_k\sum _{i=1}^d\sum _{j=1}^{d}g\left({\omega }_i\right)g\left({\omega }_j\right){\widehat{h}}_i^T{\mathbf{\Sigma }}_k{\widehat{h}}_j.$$

Additionally, given Lemmas 2 and 4, respectively,

$$\underset{N\to \infty }{lim}N\mathbf{Cov}({\pi }_i-{\widehat{\pi }}_i,{\pi }_j-{\widehat{\pi }}_j|{\left\{N_k\right\}}_{k\in \left[d\right]})=\underset{N\to \infty }{lim}\sum _{k=1}^d{\pi }_k{\widehat{h}}_i^T{\mathbf{\Sigma }}_k{\widehat{h}}_j$$

and

$$\underset{N\to \infty }{lim}N\mathbf{Var}\left(\widehat{\pi }\left(g\right)-\pi \left(g\right)|{\left\{N_k\right\}}_{k\in \left[d\right]}\right)=\underset{N\to \infty }{lim}\sum _{k=1}^d{\pi }_k\sum _{i=1}^d\sum _{j=1}^{d}g\left({\omega }_i\right)g\left({\omega }_j\right){\widehat{h}}_i^T{\mathbf{\Sigma }}_k{\widehat{h}}_j,$$

which proves Theorem 1.

3. Proposed Approach

3.1. Deriving a Confidence Interval for $\pi \left(g\right)$

The Markov chain Central Limit Theorem (MCCLT) states that, under certain conditions (see [21] for more details),

$$\sqrt{N}\left(\widehat{\pi }\left(g\right)-\pi \left(g\right)\right)\stackrel{\mathcal{D}}{\to }\mathcal{N}\left(0,{\sigma }^2\right),$$

where ${\sigma }^2={lim}_{N\to \infty }N\mathbf{Var}\left(\widehat{\pi }\left(g\right)\right)$. We note that given the assumptions made in Theorem 1, the MCCLT applies. Equation (3) therefore lends itself to the computation of a normal confidence interval for $\pi \left(g\right)$ based on a single sample path of a Markov chain using the non-asymptotic variance estimate

$${\widehat{\sigma }}^2={\displaystyle \frac{1}{N^2}}\sum _{k=1}^d{N}_k{\widehat{\gamma }}_k.$$

(5)

The steps can be summarized in Algorithm 1 as follows.

Algorithm 1: Compute confidence interval for $\pi \left(g\right)$

Data: Sample path ${\left(X_t\right)}_{t=0}^N$, confidence level $1-\alpha$  Result: Confidence interval lower and upper bound

Here, ${\mathsf{\Phi }}^{-1}:[0,1]\to \mathbb{R}$ is the inverse of the cumulative distribution function of the standard normal distribution. We exemplify Algorithm 1 in Section 4.2.

3.2. Deriving a Confidence Region for $\pi$

A corollary of the MCCLT is that $\forall i\in \left[d\right],$

$$\sqrt{N}\left({\widehat{\pi }}_i-{\pi }_i\right)\stackrel{\mathcal{D}}{\to }\mathcal{N}\left(0,{\sigma }_{ii}\right),$$

where ${\sigma }_{ii}={lim}_{N\to \infty }N\mathbf{Var}\left({\widehat{\pi }}_i-{\pi }_i\right)$. To see this, let $g\left(x\right)=\mathbb{1}(x={\omega }_i)$. Equation (2) therefore lends itself to the computation of a normal confidence interval for ${\pi }_i$ based on a single sample path of a Markov chain using the non-asymptotic variance estimate

$${\widehat{\sigma }}_{ii}={\displaystyle \frac{1}{N^2}}\sum _{k=1}^d{N}_k{\widehat{h}}_i^T{\mathbf{\Sigma }}_k{\widehat{h}}_i.$$

By the same corollary and Equation (2), for large N the joint distribution of ${\widehat{\pi }}_1-{\pi }_1,\dots ,{\widehat{\pi }}_{d-1}-{\pi }_{d-1}$ converges towards a multivariate normal distribution with covariance matrix ${\mathbf{\Sigma }}_{*}=\left[{\widehat{\sigma }}_{ij}\right]$ whereby $\forall (i,j)\in {[d-1]}^2$,

$${\widehat{\sigma }}_{ij}={\displaystyle \frac{1}{N^2}}\sum _{k=1}^d{N}_k{\widehat{h}}_i^T{\widehat{\mathbf{\Sigma }}}_k{\widehat{h}}_j.$$

(6)

The full covariance matrix over $(i,j)\in {\left[d\right]}^2$ is rank-deficient as ${\sum }_{i=1}^N{\widehat{\pi }}_i={\sum }_{i=1}^N{\pi }_i=1$.

We can leverage the convergence towards a multivariate normal distribution to derive confidence regions for $\pi$. Let ${\widehat{\pi }}_{*}:={\left[{\widehat{\pi }}_i\right]}_{i\in [d-1]}$ and ${\Delta }_{d-1}:=\{x\in {[0,1]}^{d-1}:{\sum }_{i=1}^{d-1}{x}_i\le 1\}$. By the well-known properties of the multivariate normal distribution (see textbooks such as [22] for more details), the set of vectors in ${\Delta }_{d-1}$ that satisfy the inequality

$${(x-{\widehat{\pi }}_{*})}^T{\mathbf{\Sigma }}_{*}^{-1}(x-{\widehat{\pi }}_{*})\le {\chi }_{d-1,\alpha }^2$$

(7)

form a $1-\alpha$ confidence region for ${\left[{\pi }_i\right]}_{i\in [d-1]}$ and therefore also for $\pi$. Here, ${\chi }_{d-1,\alpha }^2$ denotes the $1-\alpha$ cumulative probability quantile of a chi-squared distribution with $d-1$ degrees of freedom. This confidence region takes the form of an ellipsoid in ${\Delta }_{d-1}$. The steps can be summarized in Algorithm 2 as follows.

Algorithm 2: Compute confidence region for $\pi$

Data: Sample path ${\left(X_t\right)}_{t=0}^N$, confidence level $1-\alpha$  Result: Parameters of ellipsoidal confidence region

In two-dimensional space (i.e., for $d=3$), the boundary set of the ellipse is described by the parametric curve

$$x\left(\theta \right)={\widehat{\pi }}_{*}+\sqrt{{\chi }_{d-1,\alpha }^2}\mathit{C}\left[\begin{array}{c}cos\left(\theta \right)\\ sin\left(\theta \right)\end{array}\right]$$

for $0<\theta <2\pi$, where $\mathit{C}$ is the cholesky factor of ${\mathbf{\Sigma }}_{*}$. We exemplify Algorithm 2 in Section 4.1.

4. Examples

4.1. Example 1: Ellipsoidal Confidence Regions for $\pi$

In this section, we illustrate the approach suggested in Section 3.2 with an example. Assume that an observed sample path is characterized by the $3\times 3$ sequence matrix (defined in Section 2.2)

$$M_n=\left(\begin{array}{ccc}4n& n& 0\\ 0& 2n& n\\ n& 0& n\end{array}\right).$$

Hence, ${\left\{N_k\right\}}_{k\in \left[3\right]}=\{5n,3n,2n\}$, and therefore the maximum likelihood transition matrix estimate is

$$\widehat{P}=\left(\begin{array}{ccc}{\displaystyle \frac{4}{5}}& {\displaystyle \frac{1}{5}}& 0\\ 0& {\displaystyle \frac{2}{3}}& {\displaystyle \frac{1}{3}}\\ {\displaystyle \frac{1}{2}}& 0& {\displaystyle \frac{1}{2}}\end{array}\right),$$

and the estimated steady-state distribution vector is $\widehat{\pi }=(0.5,0.3,0.2)$.

As was discussed in Section 3.2, Equations (6) and (7) can be leveraged to derive an ellipsoidal confidence region for $\pi$ based on $\widehat{P}$, $\widehat{\pi }$. Figure 1 represents this confidence region at confidence level $1-\alpha =0.9$ for various values of n.

4.2. Example 2: Normal Confidence Interval for $\pi \left(g\right)$

Suppose that ${\left(X_t\right)}_{t=0}^N$ is a sample path of a birth-death chain on ${\mathbb{N}}_d=\{0,1,\dots ,d\}$ with transition probabilities

$$\left\{\begin{array}{c}\mathbf{P}(X_{t+1}=i+1|X_t=i)=p,\forall i\le d-1,\hfill \\ \mathbf{P}(X_{t+1}=i-1|X_t=i)=q,\forall i\ge 1,\hfill \end{array}\right.$$

whereby $0<p\le q<1$ and $q+p<1$. It can easily be shown that the elements of the steady-state distribution vector are

$${\pi }_i={\displaystyle \frac{{(p/q)}^i(1-p/q)}{1-{(p/q)}^{d+1}}},i\in {\mathbb{N}}_d.$$

Assume that p and q are unknown and that we want to derive a confidence interval for the mean population in equilibrium, i.e., $\pi \left(g\right)={\sum }_{i\in {\mathbb{N}}_d}i{\pi }_i$, based on ${\left(X_t\right)}_{t=0}^N$.

To evaluate the coverage performance of a normal confidence interval based on Theorem 1, we fix $d=4,p=0.4,q=0.5$ and proceed as follows. We generate 5000 random ergodic sample paths with fixed length N of this Markov chain. For every sample path, we compute $\widehat{\pi }\left(g\right)$ as well as ${\widehat{\sigma }}^2$ (Equation (5)). The realized coverage ratio corresponds to the proportion of sample paths for which $|\pi \left(g\right)-\widehat{\pi }\left(g\right)|\le \widehat{\sigma }{\mathsf{\Phi }}^{-1}(1-{\displaystyle \frac{\alpha }{2}})$, where ${\mathsf{\Phi }}^{-1}:[0,1]\to \mathbb{R}$ is the inverse of $\mathsf{\Phi }$, the cumulative distribution function of a standard normal distribution, and $1-\alpha$ is the desired level of confidence.

We repeat this experiment for different values of N and different values of $\alpha$. The random sample paths were generated using an R library (see [23]). The results of these experiments are summarized below in

Table 1. Realized coverage levels for different values of N and $\alpha$.

$\mathit{N}$	Realized Coverage Level			Shapiro–Wilk Test p-Value
	$\mathit{\alpha }$ = 0.1	$\mathit{\alpha }$ = 0.05	$\mathit{\alpha }$ = 0.01
250	0.8834	0.9324	0.9806	5.796 × ${10}^{-5}$
500	0.8884	0.9368	0.9826	0.03163
1000	0.8968	0.9458	0.9872	0.1535
2000	0.8994	0.9524	0.9892	0.9101

. In all cases, the realized coverage ratio is very close to 1 −$\alpha$, indicating that the confidence intervals perform well.

Moreover, the coverage levels converge toward the respective confidence levels as N increases. We ascribe this to the fact that the confidence interval becomes increasingly precise as the sample distribution converges towards a normal distribution. To see this, notice how the Shapiro–Wilk normality test p-value inceases from 5.796 × ${10}^{-5}$ at $N=250$ to 0.9101 at $N=2000$.

Another likely reason why coverage levels improve as N increases is that the numerical stability of ${\widehat{\sigma }}^2$ increases with N. To illustrate this, Figure 2 represents estimates of $N{\widehat{\sigma }}^2$ for 25 randomly sampled paths whose length we progressively extend until $N=2000$. These sample paths are based on the same birth-death chain we used for the numerical experiment summarized in Table 1. For $N<250$, the values of $N{\widehat{\sigma }}^2$ clearly seem prone to numerical instability.

The premise of this paper is that nothing is known about the Markov chain beyond what can be inferred from ${\left(X_t\right)}_{t=0}^N$. Under this premise, it may be difficult to ascertain that N is high enough for ${\widehat{\sigma }}^2$ to be a reliable estimate. One way to alleviate this difficulty could be to verify whether $N{\widehat{\sigma }}^2$ seems to have converged for a given value of N. This could be done through visual inspection of plots like Figure 2 or by determining convergence based on the differences between successive iterations of $N{\widehat{\sigma }}^2$.

Another aspect to consider is bias, i.e., $\mathbf{E}\left[\widehat{\pi }\left(g\right)-\pi \left(g\right)\right]$. In order for the confidence intervals to yield reliable results, we need to be able to assume that $\mathbf{E}\left[\widehat{\pi }\left(g\right)-\pi \left(g\right)\right]\approx 0$ (or at least that $|\mathbf{E}\left[\widehat{\pi }\left(g\right)-\pi \left(g\right)\right]|<<\widehat{\sigma }$). For the Markov chain we discussed in this section, bias shrinks to the order of ${10}^{-10}$ for $N=70$ (no matter which state the simulation is initialized in). This suggests that for this particular Markov chain, bias is negligible relative to $\widehat{\sigma }$ even for small values of N.

5. Conclusions

In this paper, we proposed a method to numerically determine confidence regions for the steady-state probabilities and confidence intervals for additive functionals of an ergodic finite-state Markov chain. The novelty of our method stems from the fact that it simultaneously fulfills three conditions. First, our method is asymptotically exact. Second, our method requires only a single sample path ${\left(X_t\right)}_{t=0}^N$ as an input. Third, our method does not require any inputs beyond what can be inferred from ${\left(X_t\right)}_{t=0}^N$. To the best of our knowledge, no method that satisfies all three conditions has previously been proposed in the literature.

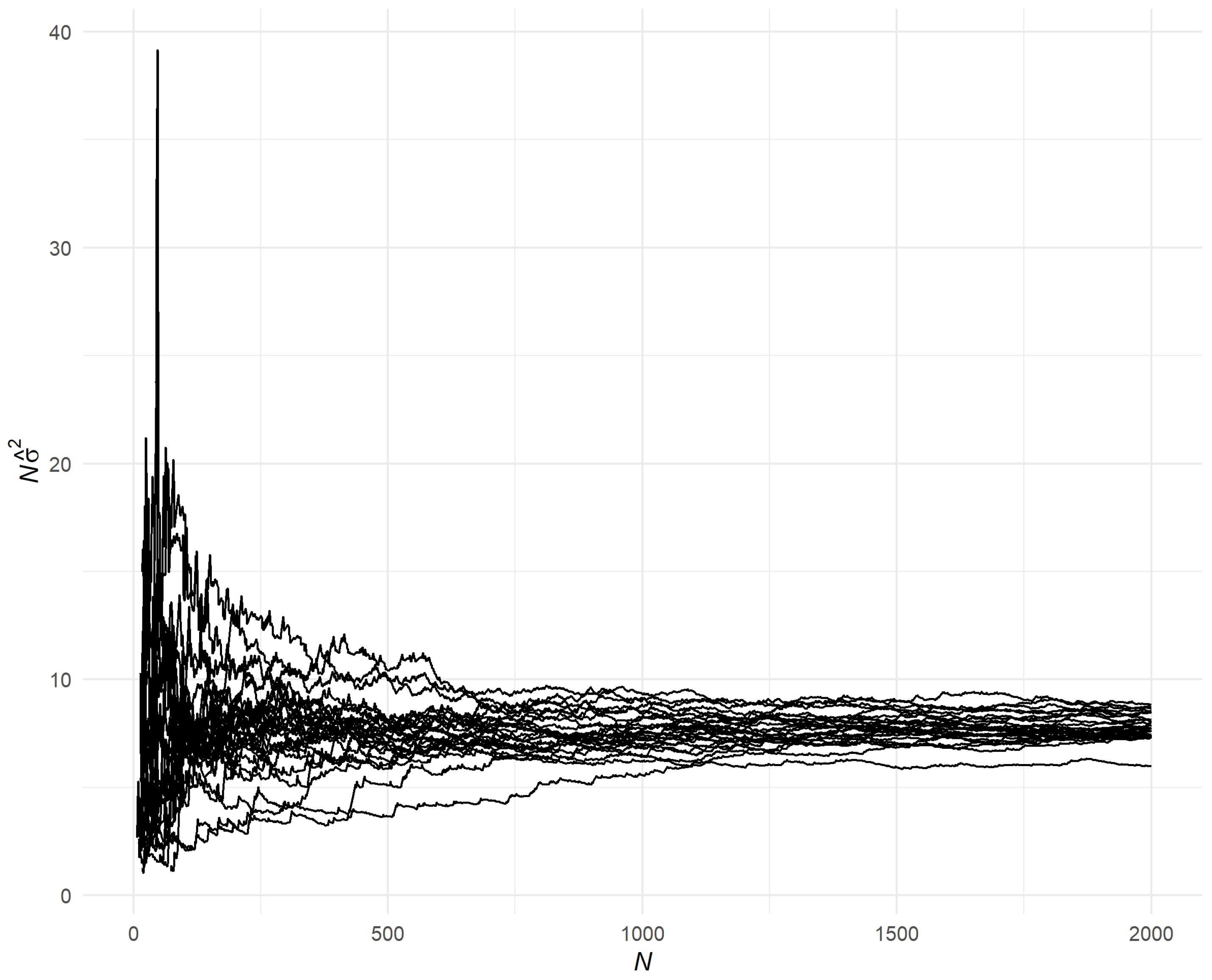
Since our method relies on asymptotically exact results, we expect it to work well for large enough values of N, as exemplified by the numerical experiment in Section 4.2. However, since the premise of this paper is that nothing is known about the Markov chain beyond what can be inferred from ${\left(X_t\right)}_{t=0}^N$, what constitutes a large enough value of N cannot be known with certainty. If N is too small, the variance estimate ${\widehat{\sigma }}^2$ may become numerically unstable, as illustrated in Section 4.2. In this case, the confidence interval’s realized coverage level could undershoot the desired confidence level. One way to mitigate this risk could be to analyze the convergence of $N{\widehat{\sigma }}^2$ as N is increased to include the entire sample path (see Section 4.2 and in particular Figure 2).

Another aspect to consider is bias, which could be a potential concern for small values of N. In order for the confidence intervals discussed in Section 3 to be valid, we need to be able to assume that $\mathbf{E}\left[\widehat{\pi }\left(g\right)-\pi \left(g\right)\right]\approx 0$ (or at least that $|\mathbf{E}\left[\widehat{\pi }\left(g\right)-\pi \left(g\right)\right]|<<\widehat{\sigma }$). This is not a strong assumption for large N since $\widehat{\pi }\left(g\right)$ is an unbiased estimator of $\pi \left(g\right)$, assuming the initial state is sampled from $\pi$. However, given the premise that nothing is known beyond what can be inferred from ${\left(X_t\right)}_{t=0}^N$, it may be difficult to determine with certainty whether ${\left(X_t\right)}_{t=0}^N$ is large enough to make this assumption. One way to address this issue could be through the lens of mixing time (see [12] for more details). If N exceeds the mixing time, then bias is likely close to 0. An approach to estimating mixing time based on a single sample path was proposed in [24].

Lastly, an open question is how one might extend our proposed approach to infinite state-space Markov chains.