Abstract
The paper studies a nonlinear equation including both fractional and ordinary derivatives. The singular Cauchy problem is considered. The theorem of the existence of uniqueness of a solution in the neighborhood of a fixed singular point of algebraic type is proved. An analytical approximate solution is built, an a priori estimate is obtained. A formula for calculating the area where the proven theorem works is obtained. The theoretical results are confirmed by a numerical experiment in both digital and graphical versions. The technology of optimizing an a priori error using an a posteriori error is demonstrated.
Keywords:
nonlinear differential equation; fractional derivative; singular points; analytical approximate solution; a priori estimate MSC:
34G20; 35A05
1. Introduction
A large number of problems in various fields lead to mathematical models based on differential equations. Thus, we encounter linear ordinary differential equations when solving the problem of body motion around a fixed point (Euler’s dynamic equation) [1], in describing the dependence of a body’s acceleration on the resultant of all applied forces (Newton’s equations on a straight line), and when finding a curve of uniform descent (Jacob Bernoulli equation) [2]. Problems in fields such as control and optimization theory [3], quantum field theory [4], as well as the simplest liquid nonlinear oscillations, lead to the nonlinear differential equations of Ricatti. Abel’s equations arise in problems of nonlinear optics when describing a superradiant avalanche [5], the theory of finite elasticity [6], nonlinear diffusion [7], and the nonlinear thermal conductivity of a steady state [8].
Moving algebraic-type singular points play an important role in nonlinear differential equations. Such equations belong to the class of equations that are generally not solvable in quadratures. The solution region is approached in two domains, the neighborhood of singular points and the analyticity area.
At the moment, based on publications, two approaches to solving nonlinear differential equations can be noted.
The first approach involves special substitutions of variables that, with certain parameter values, allow for the resolution of nonlinear differential equations in quadratures. This approach allows us to resolve nonlinear differential equations only in special cases [9,10,11,12,13,14,15,16,17,18,19].
The second approach is related to the search for an analytical approximate solution presented in the author’s works. Theorems of existence and uniqueness of solutions are proved both in the area of analyticity and in the neighborhood of moving singular points. Analytical approximate solutions are constructed in these specified regions, with techniques presented for optimizing a priori estimates through the use of a posteriori estimates [20,21,22,23,24,25]. The proposed idea has been successfully implemented for other classes of nonlinear differential equations [26,27,28].
Up to now, only linear equations have been considered for equations with fractional derivatives and the features of methods for solving explicit and implicit schemes combining types of Riemann–Liouville and Caputo derivatives have been investigated.
At the moment, there are no works devoted to the study of nonlinear differential equations with fractional derivative. It is necessary to note the features of the theory for ordinary differential equations (ODE) and equations with a fractional derivative (EFD). The theorem of the existence and uniqueness of the solution to the ODE has a local character, and for the EFD—a global character.
In this work, the idea of the author’s analytical approximate solution method [25] for a nonlinear equation with a fractional derivative is implemented.
Taking into account Fuchs’ classification of singular points into fixed and moving [29], the problem of solving a nonlinear differential equation divides the search area for a solution into two parts. The first part concerns the analyticity region of the solution, and the second part concerns the neighborhood of singular points.
It should be noted that the classical theory of existence and uniqueness of solutions to linear equations with fractional derivatives does not work in this case.
The article contains a review of sources on the topic under consideration with an analysis of research solution options. The research methods section includes the implementation of the author’s approach to finding an analytical approximate solution in the neighborhood of a fixed singular point [25] for a nonlinear differential equation with fractional derivatives for the case of an equation with fractional derivatives. The theorem of the existence and uniqueness of a solution in the neighborhood of a fixed singular point of the equation under consideration is proved. At the first stage of the proof, the uniqueness of the solution structure is substantiated, and at the second stage, the convergence of the correct part of the constructed series is proved. An analytical approximate solution in the neighborhood of a fixed singular point is built. A formula for calculating the region in which the theorem works is obtained. A numerical experiment is presented in the results discussion section. The calculation results are presented both numerically and graphically. The calculations were performed in Excel. The conclusion lists the obtained results and prospective problems for subsequent research.
2. Research Method: Statement of the Singular Cauchy Problem
The movement of fluid in fractured reservoirs is described by the following formula [30]:
here, —is the pressure gradient; —dynamic viscosity of the liquid; v—filtration rate, k—permeability of the medium; —coefficient depending on the geometry of the fractured medium and on the micro roughness, which is determined empirically [31].
A continuity equation for an incompressible fluid, with radial filtration to a vertical cylindrical well, can be written as follows:
Equation (2) in a cylindrical coordinate system has the following form:
where .
For an axisymmetric and planar problem, Equation (3) takes the following form:
Obviously, there exists a constant such that
We find the integration constant under the condition and, knowing the flow rate of a well with a radius of , we open a layer with a thickness of H:
Substituting expression (5) into (6), we obtain Q, the value of the volume of liquid over a certain period of time. The flow goes in one direction:
In the work [32] a plane axisymmetric problem of steady fluid flow in the vicinity of a well was considered, revealing a purely fractured dependence of the effective thickness of the formation on the pressure gradient and was approximated by the following dependence:
where H is the thickness of the formation, h—is the thickness of the formation at ; is a pressure gradient; —is an empirical coefficient characterizing the change in the effective thickness of the formation from the pressure gradient.
Having performed a number of transformations in Equation (9), we arrive at the following form:
where
, is the well radius, is the supply contour radius (formation boundary).
Let us introduce the following notations:
where and are constants, respectively, are equal to the expressions:
Let us consider the singular Cauchy problem:
We proceed to search for a solution to problem (10), (11) in the way
where , are the parameters to be determined.
Let us determine :
For a fractional derivative we will have the following:
where
Let us define
Let us expand the right side of Equation (10):
For the identity in the obtained Equation (19), equality of coefficients at the same powers «r» is necessary.
When , the equality of degrees on the left and right sides is fulfilled when
Since the structure of solution (12) implies , therefore
When , we will have . When the equality of degrees «r» on the left and right sides is (19) determined by a ratio
from which we obtain
Assuming , then . Thus, for we obtain
The requirement of identity in equality (19) implies the equality of the coefficients at the corresponding powers. Due to the complexity of the structure of relation (19), all subsequent stages of the proof require fixing the values of , , . Let us carry out the subsequent steps with the specified values of the parameters , ,
For the specified values of the parameters, relation (19) is reduced to a form in which the expressions of the sums contain powers of «r» of the same sign for the simplicity of obtaining recurrence relations for finding
With the least degree of the left and the right side of the Equation (20) we obtain
from which we obtain
Analysis of the left-hand side of expression (20) indicates the following degree . Taking into account this degree in the right-hand side of Equation (20), we obtain
Or, after transforming the expression, we have
The last one implies .
We continue this process for subsequent degrees «r» and find expressions for the coefficients . We present non-zero expressions for the coefficients :
Thus, we obtain unambiguous expressions of the coefficients .
Table 1 provides information on the values of the coefficients .

Table 1.
Degrees «r» and numbers of coefficients .
Non-zero values of the coefficients are indicated in Table 1 (third line). The arrow, line 3, points to the next non-zero coefficient in the second line of Table 1. Table 1 clearly illustrates the pattern of non-zero values.
Based on the analysis of the expressions of the coefficients , the expression (21), an assessment hypothesis is constructed:
To prove the estimate in the general case, it is necessary to compile a recurrence relation for the coefficient according to Equation (20). To perform this, we determine the degree «r» by the index of the coefficient and then, according to the value of this degree from Equation (20), we assemble an expression for determining Thus we obtain
At the next stage, we discard expressions with zero values , including even index values. Equation (23) is simplified:
Or, after removing the zero values of the terms on the right side of the last equation, we obtain
An extended expression of the Formula (24) is presented afterwards. Taking into consideration the rules established in Table 1 as well as the number of zero and non-zero coefficients, the number of terms in the right side of the Equation (25) in the expression under round brackets will contain no more than terms. Taking into consideration that each term will contain the expression is raised to the power .
This estimate can be verified using Formula (15) for calculating , given above. So from (25), taking into account (22) and the value we will have
Let us consider the series
which, by virtue of (26), is a majorant for the regular part of the series (12).
Based on the sufficient criterion for the convergence of power series, we obtain the region of convergence for the series (27)
Therefore, the correct part of the series (12) also converges in this region.
Thus, we complete the proof of Theorem 1, the existence and uniqueness of the solution in the neighborhood of a fixed singular point.
Theorem 1.
when , ,
The proven theorem allows us to construct an analytical approximate solution to problem (10) and (11) in the form
and obtain its a priori error estimate.
3. Results Discussion
According to Formula (28), we determine , , falls within the domain for Theorem 2.
The calculations are given in Table 2.

Table 2.
Numerical experiment calculations.
In this case, is an analytical approximate solution (29); is an a priori estimate of the error ; —is an a posteriori estimate of the error .
For the an analytical approximate solution specified in the structure (29) is required . The sum from the 27th to the 33rd terms in the structure (29) does not exceed the value 1.1138 × . Therefore, the a priori error estimate does not exceed the value .
A graphical interpretation of the analytical approximate solution (29) in the vicinity of a fixed singular point is given in Figure 1.
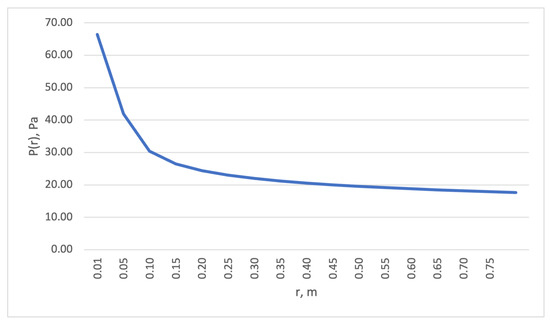
Figure 1.
Graphical interpretation of the analytical approximate solution (31).
4. Conclusions
The paper presents a proof of the existence and uniqueness theorem for a solution to the singular Cauchy problem (10) and (11) for a nonlinear fractional differential equation in the neighborhood of a fixed singular point. An analytical approximate solution is constructed, and an a priori error estimate is obtained. A formula is obtained for calculating the region in which the proven theorem 1 works. A technology for optimizing an a priori error using an a posteriori error is demonstrated. The results presented in the paper are the first stage of the study of nonlinear differential equations with fractional derivative. The next stage involves the study of an analytical approximate solution in the region of analyticity of the solution, and then in the vicinity of a moving singular point.
Funding
This research received no external funding.
Data Availability Statement
The statistical data presented in the article does not require copyright. They are freely available and are listed at the reference address in the bibliography.
Acknowledgments
The author expresses gratitude to the reviewers for valuable comments that helped improve the content of the article, as well as to the editors of the journal for their positive attitude towards the work.
Conflicts of Interest
The author declare no conflicts of interests.
References
- Kolesnikov, K.S. Course of Theoretical Mechanics; Bauman Moscow State Technical University Publishing House: Moscow, Russia, 2005. [Google Scholar]
- Bufetov, A.I.; Goncharuk, N.B.; Ilyashenko, Y.S. Ordinary Differential Equations; Publishing House of the Board of Trustees of the Faculty of Mechanics and Mathematics of Moscow State University: Moscow, Russia, 2012; p. 120. [Google Scholar]
- Lewis, F.L. Optimal Control; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; p. 540. [Google Scholar]
- Matveev, N.M. Lectures on the Analytical Theory of Differential Equations; St. Petersburg State University Publishing House: St. Petersburg, Russia, 2008; p. 336. [Google Scholar]
- Chudnovsky, V.M.; Kholodkevich, E.D. Theory of Superradiant Avalanches of the Radio Wave Range. FTT 1982, 24, 1118–1123. [Google Scholar]
- Hill, J.M. Radial Deflections of Thin Precompressed Cylindrical Rubber Bush Mountings. Internat. J. Solids Struct. 1977, 13, 93–104. [Google Scholar] [CrossRef]
- Ockendon, J.R. Numerical and Analytical Solutions of Moving Boundary Problems. In Proceedings of the Symposium and Moving Boundary Problems, Gatlinburg, TN, USA, 26–28 September 1977; Wilson, D.G., Solomon, A.D., Boggs, P.T., Eds.; Academic Press: New York, NY, USA, 1978; pp. 129–145. [Google Scholar]
- Axford, R.A. Non-linear Thermal Instability Phenomena in Plates and Rods. In Proceedings of the A.S.M.E. Nuclear Engineering Division Winter Annual Meeting, Detroit, MI, USA, 11–15 November 1973; pp. 1–12. [Google Scholar]
- Conte, R.; Musette, M. The Painlevé Handbook; Springer: Dordrecht, The Netherlands, 2008. [Google Scholar]
- Filipuk, G.; Chichurin, A. The Properties of Certain Linear and Nonlinear Differential Equations. Adv. Mech. Math. 2019, 41, 193–200. [Google Scholar] [CrossRef]
- Chichurin, A.; Shvychkina, H.N. Computer Simulation of Two Chemostat Models for One Nutrient Resource. Math. Biosci. 2016, 278, 30–36. [Google Scholar] [CrossRef] [PubMed]
- Evtushenko, S.A. Nonlinear System of Differential Equations in Supercritical Flow Spread Problem and Its Solution Technique. Axioms 2023, 12, 11. [Google Scholar] [CrossRef]
- Dukhnovskii, S. Global Existence Theorems of a Solution of the Cauchy Problem for Systems of the Kinetic Carleman and Godunov—Sultangazin Equations. Eurasian Math. J. 2021, 12, 97–102. [Google Scholar] [CrossRef]
- Dukhnovsky, S. New Exact Solutions for the Time Fractional Broadwell System. Adv. Stud. Euro-Tbil. Math. J. 2022, 15, 53–66. [Google Scholar] [CrossRef]
- Dukhnovsky, S. A Self-Similar Solution and the Tanh–Function Method for the Kinetic Carleman System. Bul. Acad. Ştiinţe Repub. Mold. Mat. 2022, 98, 99–110. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, Y.; Martynov, I.P. First Integrals and Rational Solutions of Differential Equations with a Moving Singular Line. PFMT 2019, 38, 72–77. [Google Scholar]
- Martynov, I.; Chichurin, A. On the Solution of the Chazy System of Equations. Nonlinear Oscil. 2009, 12, 94–100. [Google Scholar] [CrossRef]
- Kudryashov, N. Exact Solutions and Integrability of the Duffing–Van der Pol Equation. Regul. Chaotic Dyn. 2018, 23, 471–479. [Google Scholar] [CrossRef]
- Kudryashov, N. One Method for Finding Exact Solutions of Nonlinear Differential Equations. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 2248–2253. [Google Scholar] [CrossRef]
- Orlov, V.; Chichurin, A. On the Theory of Constructing a Numerical-Analytical Solution of a Cantilever Beam Bend Nonlinear Differential Equation of the First Order. J. Phys. Conf. Ser. 2020, 1425, 012129. [Google Scholar] [CrossRef]
- Orlov, V.; Gasanov, M. Research of a Third-Order Nonlinear Differential Equation in the Vicinity of a Moving Singular Point for a Complex Plane. E3S Web Conf. 2021, 263, 03019. [Google Scholar] [CrossRef]
- Orlov, V.; Leont’eva, T. On the Expansion of the Domain for an Analytical Approximate Solution of a Class of Second-Order Nonlinear Differential Equations in the Complex Domain. Bull. Samara State. Tech. Univ. Ser. Phys. Mat. Sci. 2020, 24, 174–186. [Google Scholar] [CrossRef]
- Orlov, V.; Gasanov, M. Analytic Approximate Solution in the Neighborhood of a Moving Singular Point of a Class of Nonlinear Equations. Axioms 2022, 11, 637. [Google Scholar] [CrossRef]
- Orlov, V.; Gasanov, M. Technology for Obtaining the Approximate Value of Moving Singular Points for a Class of Nonlinear Differential Equations in a Complex Domain. Mathematics 2022, 10, 3984. [Google Scholar] [CrossRef]
- Orlov, V. Moving Singular Points and the Van der Pol Equation, as Well as the Uniqueness of Its Solution. Mathematics 2023, 11, 873. [Google Scholar] [CrossRef]
- Leont’eva, T. Influence of Perturbation of Moving Singular Point on the Approximate Solution of a Nonlinear Second Order Differential Equation in the Complex Region. Bull. Yakovlev Chuvash State Pedagog. Univ. Ser. Mech. Limit State 2015, 24, 109–118. (In Russian) [Google Scholar]
- Pchelova, A.; Kudryashova, N. Existence Theorem for a Solution to a Third-Order Nonlinear Differential Equation with a Third-Degree Polynomial Right-Hand Side in the Domain of Analyticity. In Proceedings of the All-Russian Scientific Conference “Mechanics of the Limit State and Related Matters”, Dedicated to the 85th Anniversary of Prof. D. D. Ivlev, Cheboksary, Russia, 15–18 September 2015; pp. 215–220, Part 2. [Google Scholar]
- Pchelova, A.; Kolle, K. Existence Theorem for a Solution to a Third-Order Nonlinear Differential Equation with a Third-Degree Polynomial Right-Hand Side in a Neighborhood of a Moving Singular Point. In Proceedings of the All-Russian Scientific Conference “Mechanics of the Limit State and Related Matters”, Dedicated to the 85th Anniversary of Prof. D. D. Ivlev, Cheboksary, Russia, 15–18 September 2015; pp. 221–226, Part 2. [Google Scholar]
- Fuchs, L. Zur Theorie der linearen Differentialgleichungen mit veränderlichen Coefficienten. J. Die Reine Angew. Math. 1873, 76, 177–213. [Google Scholar]
- Shaimuratov, R.V. Hydrodynamics of a Fractured Oil Reservoir; Nedra: Moscow, Russia, 1980; p. 223. [Google Scholar]
- Nakaznaya, L. Filtration of Liquid and Gas in Fractured Reservoirs; Nedra: Moscow, Russia, 1972; p. 183. [Google Scholar]
- Aleroev, T.S.; Aleroeva, H.T.; Tang, Y.; Zhang, S. Features of Seepage of a Liquid to a Chink in the Cracked Deformable Layer. Int. J. Model. Simul. Sci. Comput. 2010, 1, 333–347. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).