Partition Differential Equations and Some Combinatorial Algebraic Structures

Abstract

Let $\mathrm{\Lambda }$ be the algebra of symmetric functions. We introduce Stirling partitions, factorial partition polynomials, partition differential equations and their corresponding partitions, and partition primitive functions. Most importantly, this investigation provides a new combinatorial coalgebra structure on $\mathrm{\Lambda }$, and it characterizes the primitive elements in $\mathrm{\Lambda }$ using the Jacobian determinants of partition primitive functions.

1. Introduction

Throughout this paper, $\mathbf{k}$ is a commutative ring, and all unadorned tensor products are over $\mathbf{k}$. Let $\mathrm{\Lambda }$ be the algebra of symmetric functions. It is well known that $\mathrm{\Lambda }$ is a graded $\mathbf{k}$-algebra since $\mathrm{\Lambda }={⨁}_{n\ge 0}{\mathrm{\Lambda }}_n$, where ${\mathrm{\Lambda }}_n$ are the homogeneous symmetric functions of degree n, and ⨁ denotes the usual direct sum of modules [1].

For any partition $\lambda$, the monomial symmetric function

$m_{\lambda }$ is given by

$$m_{\lambda }:=\sum _{\alpha \in {\mathfrak{S}}_{(\infty )}\lambda }{\mathbf{x}}^{\alpha },$$

(1)

where ${\mathfrak{S}}_{(\infty )}\lambda$ is the group of all permutations of the set $\left\{1,2,3,\dots \right\}$ which leave all but finite elements invariant [1]. Letting $\lambda$ run through the set $Par$ of all partitions, this gives the monomial $\mathbf{k}$-basis $\left\{m_{\lambda }\right\}$ of $\mathrm{\Lambda }$ [1,2]. Letting $\lambda$ run only through the set $Pa{r}_n$ of partitions of n gives the monomial $\mathbf{k}$-basis for ${\mathrm{\Lambda }}_n$ [1,2].

We have $(\mathrm{\Lambda },\tilde{m},\tilde{u},\tilde{\Delta },\widetilde{ϵ})$, which is a Hopf algebra [1,2], where

• The multiplication is the map

  $$\mathrm{\Lambda }\otimes \mathrm{\Lambda }\stackrel{\tilde{m}}{⟶}\mathrm{\Lambda },m_{\mu }\otimes m_{\nu }\mapsto m_{\mu }{m}_{\nu }.$$
• The unit is the inclusion map

  $$\mathbf{k}={\mathrm{\Lambda }}_0\stackrel{\tilde{u}}{⟶}\mathrm{\Lambda }.$$
• The comultiplication is the map

  $$\mathrm{\Lambda }\stackrel{\tilde{\Delta }}{⟶}\mathrm{\Lambda }\otimes \mathrm{\Lambda },m_{\lambda }\mapsto \sum _{\begin{array}{c}(\mu ,\nu ):\\ \mu \bigsqcup \nu =\lambda \end{array}}{m}_{\mu }\otimes m_{\nu },$$

  in which $\mu \bigsqcup \nu$ is the partition obtained by taking the multiset union of the parts of $\mu$ and $\nu$, and then reordering them to make them weakly decreasing.
• The counit is the $\mathbf{k}$-linear map

  $$\mathbf{k}={\mathrm{\Lambda }}_0\stackrel{\widetilde{ϵ}}{⟶}\mathrm{\Lambda }$$

  with $\widetilde{ϵ}{|}_{{\mathrm{\Lambda }}_0=\mathbf{k}}=i{d}_{\mathbf{k}}$ and $\widetilde{ϵ}{|}_{I={⨁}_{n>0}{\mathrm{\Lambda }}_n}=0$.

For the basic notions of symmetric functions, the reader is referred to [1,2,3,4,5,6,7].

Let $\lambda =⟨1^{m_1},2^{m_2},\cdots ,k^{m_k}⟩$ denote the (nonempty) partition $\lambda$, where $m_i$ is the multiplicity of part i in partition $\lambda$ and k is the largest part of $\lambda$, as opposed to the traditional additive notation. This notation is called the multiplicative notation or the frequency notation for $\lambda$ [8].

Let $\lambda =⟨1^{m_1},2^{m_2},\cdots ,k^{m_k}⟩$ be a partition written in frequency notation. Following [9], the partition polynomial$f_{\lambda }$ is defined by

$$f_{\lambda }\left(x\right)=\sum _{i=1}^k{m}_i{x}^i.$$

(2)

If we define the partition $\lambda ={\lambda }^{\left(0\right)}=⟨1^{m_1},2^{m_2},\cdots ,k^{m_k}⟩$, then $f_{\lambda }^{\left(1\right)}\left(x\right)$ is the partition polynomial of the new partition ${\lambda }^{\left(1\right)}$ defined by ${\lambda }^{\left(1\right)}=⟨1^{2m_2},2^{3m_3},\cdots ,{(k-1)}^{k{m}_k}⟩$. Continuing in this way, we obtain the following (finite) sequence of partitions ${\left({\lambda }^{\left(d\right)}\right)}_{0\le d<k}$ whose partition polynomials are related by differentiation [9]:

$$\begin{array}{cc}\hfill {\lambda }^{\left(d\right)}& =⟨1^{(d+1)!m_{d+1}/1!},2^{(d+2)!m_{d+2}/2!},\cdots ,{(k-d)}^{k!m_k/(k-d)!}⟩\mathrm{for}\mathrm{all}0\le d<k.\hfill \end{array}$$

(3)

Explicitly, one has

$$f_{\lambda }^{\prime }\left(x\right)={\displaystyle \frac{d}{dx}}{f}_{\lambda }\left(x\right)=\sum _{i=1}^{k}i{m}_i{x}^{i-1}.$$

(4)

$$\begin{array}{cc}\hfill f_{\lambda }^{\left(1\right)}\left(x\right)& =f_{\lambda }^{\prime }\left(x\right)\hfill \\ \hfill & ={\displaystyle \frac{d}{dx}}{f}_{\lambda }\left(x\right)\hfill \\ \hfill & ={\displaystyle \frac{d}{dx}}\sum _{i=1}^k{m}_i{x}^i\hfill \\ \hfill & =\sum _{i=1}^k{m}_i{\displaystyle \frac{d}{dx}}{x}^i\hfill \\ \hfill & =\sum _{i=1}^{(k-1)}i{m}_i{x}^{i-1}\hfill \\ \hfill & =m_1+\sum _{i=1}^{(k-1)}(i+1)m_{i+1}{x}^i\hfill \\ \hfill & =1!m_1+f_{{\lambda }^{\left(1\right)}}\left(x\right),\hfill \end{array}$$

where ${\lambda }^{\left(1\right)}=⟨1^{2\times m_2},2^{3\times m_3},\cdots ,{(k-1)}^{k\times m_k}⟩$.

$$\begin{array}{cc}\hfill f_{\lambda }^{\left(2\right)}\left(x\right)& =f_{\lambda }^{″}\left(x\right)\hfill \\ \hfill & ={\displaystyle \frac{d^2}{d{x}^2}}{f}_{\lambda }\left(x\right)\hfill \\ \hfill & =\sum _{i=1}^{(k-1)}i(i+1)m_{i+1}{x}^{i-1}\hfill \\ \hfill & =2m_2+\sum _{i=1}^{(k-2)}(i+1)(i+2)m_{i+2}{x}^i\hfill \\ \hfill & =2!m_2+f_{{\lambda }^{\left(2\right)}}\left(x\right),\hfill \end{array}$$

where ${\lambda }^{\left(2\right)}=⟨1^{3\times 2\times m_3},2^{4\times 3\times m_4},\cdots ,{(k-2)}^{k\times (k-1)\times m_k}⟩$.

$$\begin{array}{cc}\hfill f_{\lambda }^{\left(d\right)}\left(x\right)& ={\displaystyle \frac{d^d}{d{x}^d}}{f}_{\lambda }\left(x\right)\hfill \\ \hfill & =\sum _{i=1}^{(k-(d-1\left)\right)}i(i+1)\cdots (i+(d-1))m_{i+(d-1)}{x}^{i-1}\hfill \\ \hfill & =d!m_d+\sum _{i=1}^{(k-d)}(i+1)(i+2)\cdots (i+d)m_{i+d}{x}^i\hfill \\ \hfill & =d!m_d+f_{{\lambda }^{\left(d\right)}}\left(x\right),\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill {\lambda }^{\left(d\right)}& =⟨1^{(d+1)!m_{d+1}/1!},2^{(d+2)!m_{d+2}/2!},\cdots ,{(k-d)}^{k!m_k/(k-d)!}⟩\mathrm{for}\mathrm{all}0\le d<k.\hfill \end{array}$$

(5)

The main goal of this paper is to use partition polynomials to define new combinatorial structures on $\mathrm{\Lambda }$. Explicitly, the paper is organized as follows. In Section 2, we introduce Stirling partitions and factorial partition polynomials, and we show that every partition polynomial of a partition $\lambda$ is a factorial partition polynomial of a unique Stirling partition $\overline{\lambda }$. Section 3 is devoted to introducing partition differential equations and their corresponding partitions using integration as well as giving explicit examples. Section 4 explores new combinatorial operations on $\mathrm{\Lambda }$ and investigates an alternative characterization for primitive elements in $\mathrm{\Lambda }$ using partition polynomials and calculus tools. The last section of this paper summarizes the most important consequences and gives some potential future directions that offer some paths for the next investigation.

2. Stirling Partitions and Factorial Partition Polynomials

Recall that factorial polynomials are defined by

$$x^{\left(n\right)}=x(x-1)\cdots (x-n+1),$$

where n is a non-negative integer ($x^{\left(0\right)}=1$ by convention).

Definition 1. 

Let $\lambda =⟨1^{m_1},2^{m_2},\cdots ,k^{m_k}⟩\in Par$ be a partition.

(i)

The factorial partition polynomial of λ is defined by

$$h_{\lambda }\left(x\right)=\sum _{i=1}^k{m}_i{x}^{\left(i\right)}.$$

(6)

(ii)

λ is called a Stirling partition of the second kind (or simply a Stirling partition) if

$$m_i=\sum _{j=i}^k{n}_j\left\{{\displaystyle \genfrac{}{}{0pt}{}{j}{i}}\right\},$$

(7)

where $n_i$s are non-negative integers, and the numbers $\left\{{\displaystyle \genfrac{}{}{0pt}{}{j}{i}}\right\}$ are the Stirling number of the second kind.

Notice that the above definition implies that if $\lambda \ne \varnothing$, then $n_k>0$.

Theorem 1. 

Let $\lambda =⟨1^{m_1},2^{m_2},\cdots ,k^{m_k}⟩$ be a partition.

(i)

There exists a unique Stirling partition $\overline{\lambda }$ with $f_{\lambda }=h_{\overline{\lambda }}$.

(ii)

Conversely, if λ is a Stirling partition, then it gives rise to a unique partition $\widehat{\lambda }$ with $h_{\lambda }=f_{\widehat{\lambda }}$. Furthermore, $\overline{\widehat{\lambda }}=\widehat{\overline{\lambda }}=\lambda$.

Proof. 

(i)

$$\begin{array}{cc}\hfill f_{\lambda }\left(x\right)& =\sum _{i=1}^k{m}_i{x}^i\hfill \\ \hfill & =\sum _{i=1}^k{m}_i\sum _{j=1}^i\left\{{\displaystyle \genfrac{}{}{0pt}{}{j}{i}}\right\}{x}^{\left(i\right)}\hfill \\ \hfill & =m_1\left\{{\displaystyle \genfrac{}{}{0pt}{}{1}{1}}\right\}{x}^{\left(1\right)}+m_2(\left\{{\displaystyle \genfrac{}{}{0pt}{}{2}{1}}\right\}{x}^{\left(1\right)}+\left\{{\displaystyle \genfrac{}{}{0pt}{}{2}{2}}\right\}{x}^{\left(2\right)})\hfill \\ \hfill & +\cdots +m_k(\left\{{\displaystyle \genfrac{}{}{0pt}{}{k}{1}}\right\}{x}^{\left(1\right)}+\left\{{\displaystyle \genfrac{}{}{0pt}{}{k}{2}}\right\}{x}^{\left(2\right)}+\cdots +\left\{{\displaystyle \genfrac{}{}{0pt}{}{k}{k}}\right\}{x}^{\left(k\right)})\hfill \\ \hfill & =\left(\sum _{j=1}^k{m}_j\left\{{\displaystyle \genfrac{}{}{0pt}{}{j}{1}}\right\}\right)x^{\left(1\right)}+\left(\sum _{j=2}^k{m}_j\left\{{\displaystyle \genfrac{}{}{0pt}{}{j}{2}}\right\}\right)x^{\left(2\right)}\hfill \\ \hfill & +\cdots +\left(\sum _{j=k-1}^k{m}_j\left\{{\displaystyle \genfrac{}{}{0pt}{}{j}{k-1}}\right\}\right)x^{(k-1)}+\left(\sum _{j=k}^k{m}_j\left\{{\displaystyle \genfrac{}{}{0pt}{}{j}{k}}\right\}\right)x^{\left(k\right)}\hfill \\ \hfill & =\left(\sum _{j=1}^k{m}_j\left\{{\displaystyle \genfrac{}{}{0pt}{}{j}{1}}\right\}\right)x^{\left(1\right)}+\left(\sum _{j=2}^k{m}_j\left\{{\displaystyle \genfrac{}{}{0pt}{}{j}{2}}\right\}\right)x^{\left(2\right)}\hfill \\ \hfill & +\cdots +\left(\sum _{j=k-1}^k{m}_j\left\{{\displaystyle \genfrac{}{}{0pt}{}{j}{k-1}}\right\}\right)x^{(k-1)}+\left(\sum _{j=k}^k{m}_j\left\{{\displaystyle \genfrac{}{}{0pt}{}{j}{k}}\right\}\right)x^{\left(k\right)}\hfill \\ \hfill & =\sum _{i=1}^k{t}_i{x}^{\left(i\right)}\hfill \\ \hfill & =h_{\overline{\lambda }}\left(x\right),\hfill \end{array}$$

where $\overline{\lambda }=⟨1^{t_1},2^{t_2},\cdots ,k^{t_k}⟩$ and

$$t_i=\sum _{j=i}^k{m}_j\left\{{\displaystyle \genfrac{}{}{0pt}{}{j}{i}}\right\}.$$

(8)

(ii)

If $\lambda$ is a Stirling partition, then

$$m_i=\sum _{j=i}^k{n}_j\left\{{\displaystyle \genfrac{}{}{0pt}{}{j}{i}}\right\},$$

(9)

where $n_i$s are non-negative integers and the numbers $\left\{{\displaystyle \genfrac{}{}{0pt}{}{j}{i}}\right\}$ are the Stirling number of the second kind. Set $\widehat{\lambda }=⟨1^{n_1},2^{n_2},\cdots ,k^{n_k}⟩$. Then, it is quite obvious that $h_{\lambda }=f_{\widehat{\lambda }}$ and $\overline{\widehat{\lambda }}=\widehat{\overline{\lambda }}=\lambda$. The uniqueness follows directly from the fact that the set of ordinary powers of x and the set of factorial powers of x both form a basis for the vector space of polynomials, and the numbers $\left\{{\displaystyle \genfrac{}{}{0pt}{}{j}{i}}\right\}$ are simply a “change in basis coefficients” for these bases.

□

The partition $\overline{\lambda }$ defined in Theorem (1) is called the Stirling partition of $\lambda$. It is well known that $\left\{{\displaystyle \genfrac{}{}{0pt}{}{j}{1}}\right\}=1$ for any positive integer j. Thus, the following proposition is an obvious consequence.

Proposition 1. 

Let $\lambda =⟨1^{m_1},2^{m_2},\cdots ,k^{m_k}⟩$ be a partition, and let $\overline{\lambda }=⟨1^{t_1},2^{t_2},\cdots ,k^{t_k}⟩$ be the Stirling partition of λ. Then,

(i)

If $m_i=i$ for $i=1,2\cdots ,k$, then

$$t_1={\displaystyle \frac{k(k+1)}{2}}.$$

(ii)

If $m_i=i^2$ for $i=1,2\cdots ,k$, then

$$t_1={\displaystyle \frac{k(k+1)(2k+1)}{6}}.$$

(iii)

If $m_i=i^3$ for $i=1,2\cdots ,k$, then

$$t_1={\left({\displaystyle \frac{k(k+1)}{2}}\right)}^2.$$

Example 1. 

(i)

Let $\lambda =⟨1^2,2^0,3^4,4^0,5^1⟩$. Then,

$$\begin{array}{cc}\hfill \overline{\lambda }& =\overline{⟨1^2,2^0,3^4,4^0,5^1⟩}\hfill \\ \hfill & =⟨1^{{\sum }_{j=1}^5{m}_j\left\{{\displaystyle \genfrac{}{}{0pt}{}{j}{1}}\right\}},2^{{\sum }_{j=2}^5{m}_j\left\{{\displaystyle \genfrac{}{}{0pt}{}{j}{2}}\right\}},3^{{\sum }_{j=3}^5{m}_j\left\{{\displaystyle \genfrac{}{}{0pt}{}{j}{3}}\right\}},4^{{\sum }_{j=4}^5{m}_j\left\{{\displaystyle \genfrac{}{}{0pt}{}{j}{4}}\right\}},5^{{\sum }_{j=5}^5{m}_j\left\{{\displaystyle \genfrac{}{}{0pt}{}{j}{5}}\right\}}⟩\hfill \\ \hfill & =⟨1^{2\left(1\right)+0\left(1\right)+4\left(1\right)+0\left(1\right)+1\left(1\right)},2^{0\left(1\right)+4\left(3\right)+0\left(7\right)+1\left(15\right)},3^{4\left(1\right)+0\left(6\right)+1\left(25\right)},4^{0\left(1\right)+1\left(10\right)},5^{1\left(1\right)}⟩\hfill \\ \hfill & =⟨1^7,2^{27},3^{29},4^{10},5^1⟩.\hfill \end{array}$$

(ii)

To illustrate Proposition (1), let $\lambda =⟨1^1,2^8,3^{27}⟩$. Then,

$$\begin{array}{cc}\hfill \overline{\lambda }& =\overline{⟨1^1,2^8,3^{27}⟩}\hfill \\ \hfill & =⟨1^{{\sum }_{j=1}^3{m}_j\left\{{\displaystyle \genfrac{}{}{0pt}{}{j}{1}}\right\}},2^{{\sum }_{j=2}^3{m}_j\left\{{\displaystyle \genfrac{}{}{0pt}{}{j}{2}}\right\}},3^{{\sum }_{j=3}^3{m}_j\left\{{\displaystyle \genfrac{}{}{0pt}{}{j}{3}}\right\}}⟩\hfill \\ \hfill & =⟨1^{{\sum }_{j=1}^3{j}^3\left\{{\displaystyle \genfrac{}{}{0pt}{}{j}{1}}\right\}},2^{{\sum }_{j=2}^3{j}^3\left\{{\displaystyle \genfrac{}{}{0pt}{}{j}{2}}\right\}},3^{{\sum }_{j=3}^3{j}^3\left\{{\displaystyle \genfrac{}{}{0pt}{}{j}{3}}\right\}}⟩\hfill \\ \hfill & =⟨1^{{\sum }_{j=1}^3{j}^3},2^{{\sum }_{j=2}^3{j}^3\left\{{\displaystyle \genfrac{}{}{0pt}{}{j}{2}}\right\}},3^{{\sum }_{j=3}^3{j}^3\left\{{\displaystyle \genfrac{}{}{0pt}{}{j}{3}}\right\}}⟩\hfill \\ \hfill & =⟨1^{{\left({\displaystyle \frac{3(3+1)}{2}}\right)}^2},2^{8\left(1\right)+27\left(3\right)},3^{1\left(27\right)}⟩\hfill \\ \hfill & =⟨1^{36},2^{89},3^{27}⟩.\hfill \end{array}$$

3. Partition Differential Equations

Definition 2. 

Let $\lambda =⟨1^{m_1},2^{m_2},\cdots ,k^{m_k}⟩\in Par$ and fix an integer d, where $0\le d\le k$. A $(\lambda ,(\ast \left)\right)$-partition differential equation is a differential equation of the form

$$\begin{array}{cc}\hfill y^{\left(d\right)}& =M{f}_{\lambda }\left(x\right)=M\sum _{i=1}^k{m}_i{x}^i,\hfill \end{array}$$

(10)

subject to the initial conditions

$$(\ast ).......\left\{\begin{array}{cc}{y}^{(d-1)}\left(x_0\right)\hfill & =M_{d-1},\hfill \\ y^{(d-2)}\left(x_0\right)\hfill & =M_{d-2},\hfill \\ .\hfill & .\hfill \\ .\hfill & .\hfill \\ .\hfill & .\hfill \\ y^{\left(1\right)}\left(x_0\right)\hfill & =M_1,\hfill \\ y^{\left(0\right)}\left(x_0\right)\hfill & =M_0,\hfill \end{array}\right.$$

where $M>0$, $x_0,M_0,M_1,\cdots ,M_{d-1}$ and the coefficients of each polynomial of the polynomials $y^{(d-1)},\cdots ,y^{\left(1\right)},y^{\left(0\right)}$ are non-negative integers. Unless confusion is possible, we will simply say that $(\lambda ,\ast )$ is a partition differential equation.

The solutions are completely determined by the given partition $\lambda$ and by the initial conditions $(\ast )$.

Remark 1. 

(i)

In the above definition, $y^{\left(0\right)}=y,y^{\left(1\right)}={\displaystyle \frac{dy}{dx}},\cdots ,y^{\left(t\right)}={\displaystyle \frac{d^{t}y}{d{x}^t}}$.

(ii)

If $d=x_0=0$ and $M=1$, then $M_1=0$ and $y=f_{\lambda }\left(x\right)={\sum }_{i=1}^k{m}_i{x}^i$.

Let

$$\begin{array}{cc}\hfill y^{\left(d\right)}& =M{f}_{\lambda }\left(x\right)=M\sum _{i=1}^k{m}_i{x}^i,\hfill \end{array}$$

$$(\ast ).......\left\{\begin{array}{cc}{y}^{(d-1)}\left(x_0\right)\hfill & =M_{d-1},\hfill \\ y^{(d-2)}\left(x_0\right)\hfill & =M_{d-2},\hfill \\ .\hfill & .\hfill \\ .\hfill & .\hfill \\ .\hfill & .\hfill \\ y^{\left(1\right)}\left(x_0\right)\hfill & =M_1,\hfill \\ y^{\left(0\right)}\left(x_0\right)\hfill & =M_0,\hfill \end{array}\right.$$

be a $(\lambda ,(\ast \left)\right)$-partition differential equation. We have

$$\begin{array}{cc}\hfill y^{(d-1)}& =\int M\sum _{i=1}^k{m}_i{x}^{i}dx\hfill \\ \hfill & =M\int \sum _{i=1}^k{m}_i{x}^{i}dx\hfill \\ \hfill & =M\sum _{i=1}^k{m}_i\int x^{i}dx\hfill \\ \hfill & =M\sum _{i=1}^k{m}_i{\displaystyle \frac{x^{i+1}}{i+1}}+C_{d-1}\hfill \\ \hfill & =M\sum _{i=1}^k{m}_i{\displaystyle \frac{x^{i+1}}{(i+1)!/i!}}+C_{d-1}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill y^{(d-2)}& =\int y^{(d-1)}dx\hfill \\ \hfill & =M\int \sum _{i=1}^k{m}_i{\displaystyle \frac{x^{i+1}}{(i+1)!/i!}}dx+\int C_{d-1}dx\hfill \\ \hfill & =M\sum _{i=1}^k{\displaystyle \frac{m_i}{(i+1)!/i!}}\int x^{i+1}dx+\int C_{d-1}dx\hfill \\ \hfill & =M\sum _{i=1}^k{m}_i{\displaystyle \frac{x^{i+2}}{(i+2)(i+1)}}+C_{d-1}x+C_{d-2}\hfill \\ \hfill & =M\sum _{i=1}^k{m}_i{\displaystyle \frac{x^{i+2}}{(i+2)!/i!}}+C_{d-1}x+C_{d-2}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill y^{(d-3)}& =\int y^{(d-2)}dx\hfill \\ \hfill & =M\int \sum _{i=1}^k{m}_i{\displaystyle \frac{x^{i+2}}{(i+2)!/i!}}dx+\int C_{d-1}xdx+\int C_{d-2}dx\hfill \\ \hfill & =M\sum _{i=1}^k{\displaystyle \frac{m_i}{(i+2)!/i!}}\int x^{i+1}dx+\int C_{d-1}xdx+\int C_{d-2}dx\hfill \\ \hfill & =M\sum _{i=1}^k{m}_i{\displaystyle \frac{x^{i+3}}{(i+3)(i+2)(i+1)}}+C_{d-1}{\displaystyle \frac{x^2}{2!}}+C_{d-2}x+C_{d-3}\hfill \\ \hfill & =M\sum _{i=1}^k{m}_i{\displaystyle \frac{x^{i+3}}{(i+3)!/i!}}+C_{d-1}{\displaystyle \frac{x^2}{2!}}+C_{d-2}{\displaystyle \frac{x}{1!}}+C_{d-3}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill y^{\left(1\right)}& =\int y^{\left(2\right)}dx\hfill \\ \hfill & =M\int (\sum _{i=1}^k{m}_i{\displaystyle \frac{x^{i+d-2}}{(i+d-2)!/i!}}+C_{d-1}{\displaystyle \frac{x^{d-3}}{(d-3)!}}+C_{d-2}{\displaystyle \frac{x^{d-4}}{(d-4)!}}\hfill \\ \hfill & +\cdots +C_3{\displaystyle \frac{x}{1!}}+C_2)dx\hfill \\ \hfill & =M\sum _{i=1}^k\int m_i{\displaystyle \frac{x^{i+d-2}}{(i+d-2)!/i!}}dx+\int C_{d-1}{\displaystyle \frac{x^{d-3}}{(d-3)!}}dx\hfill \\ \hfill & +\cdots +\int C_3{\displaystyle \frac{x}{1!}}dx+\int C_{2}dx\hfill \\ \hfill & =M\sum _{i=1}^k{m}_i{\displaystyle \frac{x^{i+d-1}}{(i+d-1)!/i!}}+C_{d-1}{\displaystyle \frac{x^{d-2}}{(d-2)!}}+C_{d-2}{\displaystyle \frac{x^{d-3}}{(d-3)!}}\hfill \\ \hfill & +\cdots +C_3{\displaystyle \frac{x^2}{2!}}+C_2{\displaystyle \frac{x}{1!}}+C_1.\hfill \end{array}$$

$$\begin{array}{cc}\hfill y^{\left(0\right)}& =\int y^{\left(1\right)}dx\hfill \\ \hfill & =\int (M\sum _{i=1}^k{m}_i{\displaystyle \frac{x^{i+d-1}}{(i+d-1)!/i!}}+C_{d-1}{\displaystyle \frac{x^{d-2}}{(d-2)!}}+C_{d-2}{\displaystyle \frac{x^{d-3}}{(d-3)!}}\hfill \\ \hfill & +\cdots +C_3{\displaystyle \frac{x^2}{2!}}+C_2{\displaystyle \frac{x}{1!}}+C_1)dx\hfill \\ \hfill & =M\sum _{i=1}^k{m}_i{\displaystyle \frac{x^{i+d}}{(i+d)!/i!}}+C_{d-1}{\displaystyle \frac{x^{d-1}}{(d-1)!}}+C_{d-2}{\displaystyle \frac{x^{d-2}}{(d-2)!}}\hfill \\ \hfill & +\cdots +C_3{\displaystyle \frac{x^3}{3!}}+C_2{\displaystyle \frac{x^2}{2!}}+C_1{\displaystyle \frac{x}{1!}}+C_0.\hfill \end{array}$$

Applying the initial conditions, we have

$$\begin{array}{cc}\hfill y^{\left(0\right)}& =\sum _{i=1}^k{\displaystyle \frac{M{m}_i}{(i+d)!/i!}}{x}^{i+d}+{\displaystyle \frac{M_{d-1}}{(d-1)!}}{x}^{d-1}+{\displaystyle \frac{M_{d-2}}{(d-2)!}}{x}^{d-2}\hfill \\ \hfill & +\cdots +{\displaystyle \frac{M_2}{2!}}{x}^2+{\displaystyle \frac{M_1}{1!}}x+M_0\hfill \\ \hfill & =\sum _{i=1}^k{\displaystyle \frac{i!M{m}_i}{(i+d)!}}{x}^{i+d}+{\displaystyle \frac{M_{d-1}}{(d-1)!}}{x}^{d-1}+{\displaystyle \frac{M_{d-2}}{(d-2)!}}{x}^{d-2}\hfill \\ \hfill & +\cdots +{\displaystyle \frac{M_2}{2!}}{x}^2+{\displaystyle \frac{M_1}{1!}}x+M_0.\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill {\int }_{(\ast )}^{\left(d\right)}\left(\lambda \right)& =⟨1^{{\displaystyle \frac{M_1}{1!}}},2^{{\displaystyle \frac{M_2}{2!}}},\cdots ,{(d-1)}^{{\displaystyle \frac{M_{d-1}}{(d-1)!}}},d^0,{(d+1)}^{{\displaystyle \frac{1!M{m}_1}{(1+d)!}}},\hfill \\ \hfill & \cdots ,{(k+d)}^{{\displaystyle \frac{k!M{m}_k}{(k+d)!}}}⟩.\hfill \end{array}$$

(12)

Theorem 2. 

Let $\lambda =⟨1^{m_1},2^{m_2},\cdots ,k^{m_k}⟩$ be a partition, and let

$$\begin{array}{cc}\hfill y^{\left(d\right)}& =M{f}_{\lambda }\left(x\right)=M\sum _{i=1}^k{m}_i{x}^i,\hfill \end{array}$$

(13)

be a $(\lambda ,(\ast \left)\right)$-partition differential equation subject to the initial conditions

$$(\ast ).......\left\{\begin{array}{cc}{y}^{(d-1)}\left(x_0\right)\hfill & =M_{d-1},\hfill \\ y^{(d-2)}\left(x_0\right)\hfill & =M_{d-2},\hfill \\ .\hfill & .\hfill \\ .\hfill & .\hfill \\ .\hfill & .\hfill \\ y^{\left(1\right)}\left(x_0\right)\hfill & =M_1,\hfill \\ y^{\left(0\right)}\left(x_0\right)\hfill & =M_0.\hfill \end{array}\right.$$

Then,

$$\begin{array}{cc}\hfill {\left({\int }_{(\ast )}^{\left(d\right)}\left(\lambda \right)\right)}^{\left(t\right)}& ={\int }_{(\ast )}^{(d-t)}\left(\lambda \right),\hfill \end{array}$$

(14)

for all $1\le t\le d$.

Proof. 

Using (11), we have

$$\begin{array}{cc}\hfill {\displaystyle \frac{d^t}{d{x}^t}}{y}^{\left(0\right)}& ={\displaystyle \frac{d^t}{d{x}^t}}(\sum _{i=1}^k{\displaystyle \frac{i!M{m}_i}{(i+d)!}}{x}^{i+d}+{\displaystyle \frac{M_{d-1}}{(d-1)!}}{x}^{d-1}+\hfill \\ \hfill & +\cdots +{\displaystyle \frac{M_2}{2!}}{x}^2+{\displaystyle \frac{M_1}{1!}}x+M_0)\hfill \\ \hfill & =\sum _{i=1}^k{\displaystyle \frac{i!M{m}_i}{(i+d-t)!}}{x}^{i+d-t}+{\displaystyle \frac{M_{d-1}}{(d-t-1)!}}{x}^{d-t-1}\hfill \\ \hfill & +\cdots +{\displaystyle \frac{M_{t+2}}{2!}}{x}^2+{\displaystyle \frac{M_{t+1}}{1!}}x+M_t\hfill \\ \hfill & =\sum _{i=1}^k{\displaystyle \frac{i!M{m}_i}{(i+d-t)!}}{x}^{i+d-t}+{\displaystyle \frac{M_{d-1}}{(d-(t+1\left)\right)!}}{x}^{d-(t+1)}\hfill \\ \hfill & +\cdots +{\displaystyle \frac{M_{t+2}}{2!}}{x}^2+{\displaystyle \frac{M_{t+1}}{1!}}x+M_t\hfill \\ \hfill & =y^{\left(t\right)},\hfill \end{array}$$

(15)

which is the solution of the $(\lambda ,(\ast \left)\right)$-partition differential equation

$$\begin{array}{cc}\hfill z^{(d-t)}& =M{f}_{\lambda }\left(x\right)=M\sum _{i=1}^k{m}_i{x}^i,\hfill \end{array}$$

(16)

satisfying the initial conditions

$$(\ast ).......\left\{\begin{array}{cc}{z}^{(d-t-1)}\left(x_0\right)\hfill & =M_{d-1},\hfill \\ z^{(d-t-2)}\left(x_0\right)\hfill & =M_{d-2},\hfill \\ .\hfill & .\hfill \\ .\hfill & .\hfill \\ .\hfill & .\hfill \\ z^{\left(1\right)}\left(x_0\right)\hfill & =M_{t+1},\hfill \\ z^{\left(0\right)}\left(x_0\right)\hfill & =M_t,\hfill \end{array}\right.$$

for $\lambda =⟨1^{m_1},2^{m_2},\cdots ,k^{m_k}⟩$, where

$$z^{\left(0\right)}=y^{\left(t\right)},z^{\left(1\right)}=y^{(t+1)},\cdots ,z^{(d-t)}=y^{\left(d\right)}.$$

Thus,

$$\begin{array}{cc}\hfill {\left({\int }_{(\ast )}^{\left(d\right)}\left(\lambda \right)\right)}^{\left(t\right)}& ={\int }_{(\ast )}^{(d-t)}\left(\lambda \right).\hfill \end{array}$$

(17)

□

Theorem 3. 

Let λ be a partition, and let

$$\begin{array}{cc}\hfill y^{\left(d\right)}& =M{f}_{\lambda }\left(x\right)\hfill \end{array}$$

(18)

be a $(\lambda ,(\ast \left)\right)$-partition differential equation subject to the initial conditions

$$(\ast ).......\left\{\begin{array}{cc}{y}^{(d-1)}\left(0\right)\hfill & ={\displaystyle \frac{(k+d-1)!}{k!}},\hfill \\ y^{(d-2)}\left(0\right)\hfill & ={\displaystyle \frac{(k+d-2)!}{k!}},\hfill \\ .\hfill & .\hfill \\ .\hfill & .\hfill \\ .\hfill & .\hfill \\ y^{\left(1\right)}\left(0\right)\hfill & ={\displaystyle \frac{(k+1)!}{k!}},\hfill \\ y^{\left(0\right)}\left(0\right)\hfill & =0.\hfill \end{array}\right.$$

(i)

If $\lambda =⟨1^{m_1},2^{m_2},\cdots ,k^{m_k}⟩$ and $M=(k+d)!$, then

$$\begin{array}{cc}\hfill {\int }_{(\ast )}^{\left(d\right)}\left(\lambda \right)& =⟨1^{\left({\displaystyle \genfrac{}{}{0pt}{}{k+1}{1}}\right)},2^{\left({\displaystyle \genfrac{}{}{0pt}{}{k+2}{2}}\right)},\cdots ,{(d-1)}^{\left({\displaystyle \genfrac{}{}{0pt}{}{k+d-1}{d-1}}\right)},d^0,{(d+1)}^{{\displaystyle \frac{m_{1}1!(k+d)!}{(1+d)!}}},\hfill \\ \hfill & \cdots ,{(d+k)}^{{\displaystyle \frac{m_{k}k!(k+d)!}{(k+d)!}}}⟩.\hfill \end{array}$$

(ii)

If $\lambda =⟨1^{m_1},2^{m_2},\cdots ,k^{m_k}⟩$ and $M={\displaystyle \frac{\left(kd\right)!(k+d)!}{d!k!}}$, then

$$\begin{array}{cc}\hfill {\int }_{(\ast )}^{\left(d\right)}\left(\lambda \right)& =⟨1^{\left({\displaystyle \genfrac{}{}{0pt}{}{k+1}{1}}\right)},2^{\left({\displaystyle \genfrac{}{}{0pt}{}{k+2}{2}}\right)},\cdots ,{(d-1)}^{\left({\displaystyle \genfrac{}{}{0pt}{}{k+d-1}{d-1}}\right)},d^0,{(d+1)}^{{\displaystyle \frac{m_1\left(kd\right)!\left(\genfrac{}{}{0pt}{}{k+d}{d}\right)}{d!\left(\genfrac{}{}{0pt}{}{1+d}{d}\right)}}},\hfill \\ \hfill & \cdots ,{(d+k)}^{{\displaystyle \frac{m_k\left(kd\right)!\left(\genfrac{}{}{0pt}{}{k+d}{d}\right)}{d!\left(\genfrac{}{}{0pt}{}{k+d}{d}\right)}}}⟩.\hfill \end{array}$$

(iii)

If $\lambda =⟨1^{m_1{k}^{(k-1)}},2^{m_2{k}^{(k-2)}},\cdots ,k^{m_k{k}^{(k-k)}}⟩$ and $M={\displaystyle \frac{(k+d)!}{k!}}$, then we have

$$\begin{array}{cc}\hfill {\int }_{(\ast )}^{\left(d\right)}\left(\lambda \right)& =⟨1^{\left({\displaystyle \genfrac{}{}{0pt}{}{k+1}{1}}\right)},2^{\left({\displaystyle \genfrac{}{}{0pt}{}{k+2}{2}}\right)},\cdots ,{(d-1)}^{\left({\displaystyle \genfrac{}{}{0pt}{}{k+d-1}{d-1}}\right)},d^0,{(d+1)}^{{\displaystyle \frac{m_1(k+d)!}{(1+d)!}}},\hfill \\ \hfill & \cdots ,{(d+k)}^{{\displaystyle \frac{m_k(k+d)!}{(k+d)!}}}⟩.\hfill \end{array}$$

Proof. 

(i)

We have a $(\lambda ,(\ast \left)\right)$-partition differential equation

$$\begin{array}{cc}\hfill y^{\left(d\right)}& =M{f}_{\lambda }\left(x\right),\hfill \end{array}$$

(19)

$$(\ast ).......\left\{\begin{array}{cc}{y}^{(d-1)}\left(x_0\right)\hfill & =M_{d-1},\hfill \\ y^{(d-2)}\left(x_0\right)\hfill & =M_{d-2},\hfill \\ .\hfill & .\hfill \\ .\hfill & .\hfill \\ .\hfill & .\hfill \\ y^{\left(1\right)}\left(x_0\right)\hfill & =M_1,\hfill \\ y^{\left(0\right)}\left(x_0\right)\hfill & =M_0.\hfill \end{array}\right.$$

where

$$\lambda =⟨1^{m_1},2^{m_2},\cdots ,k^{m_k}⟩,x_0=M_0=0,M=(k+d)!,$$

$$M_1={\displaystyle \frac{(k+1)!}{k!}},\cdots ,M_{d-2}={\displaystyle \frac{(k+d-2)!}{k!}},M_{d-1}={\displaystyle \frac{(k+d-1)!}{k!}}.$$

Using (11), we have

$$\begin{array}{cc}\hfill y^{\left(0\right)}& =\sum _{i=1}^k{m}_i(k+d)!{\displaystyle \frac{x^{i+d}}{(i+d)!/i!}}+{\displaystyle \frac{(k+d-1)!x^{d-1}}{k!(d-1)!}}+{\displaystyle \frac{(k+d-2)!x^{d-2}}{k!(d-2)!}}\hfill \\ \hfill & +\cdots +{\displaystyle \frac{(k+2)!x^2}{k!2!}}+{\displaystyle \frac{(k+1)!x}{k!1!}}\hfill \\ \hfill & =\sum _{i=1}^k{\displaystyle \frac{m_{i}i!(k+d)!}{(i+d)!}}{x}^{i+d}+{\displaystyle \frac{(k+d-1)!}{k!(d-1)!}}{x}^{d-1}+{\displaystyle \frac{(k+d-2)!}{k!(d-2)!}}{x}^{d-2}\hfill \\ \hfill & +\cdots +{\displaystyle \frac{(k+2)!}{k!2!}}{x}^2+{\displaystyle \frac{(k+1)!}{k!1!}}x\hfill \\ \hfill & =\sum _{i=1}^k,{\displaystyle \frac{m_{i}i!(k+d)!}{(i+d)!}}{x}^{i+d}+\left({\displaystyle \genfrac{}{}{0pt}{}{k+d-1}{d-1}}\right)x^{d-1}+\left({\displaystyle \genfrac{}{}{0pt}{}{k+d-2}{d-2}}\right)x^{d-2}\hfill \\ \hfill & +\cdots +\left({\displaystyle \genfrac{}{}{0pt}{}{k+2}{2}}\right)x^2+\left({\displaystyle \genfrac{}{}{0pt}{}{k+1}{1}}\right)x.\hfill \end{array}$$

Consequently, we have

$$\begin{array}{cc}\hfill {\int }_{(\ast )}^{\left(d\right)}\left(\lambda \right)& =⟨1^{\left({\displaystyle \genfrac{}{}{0pt}{}{k+1}{1}}\right)},2^{\left({\displaystyle \genfrac{}{}{0pt}{}{k+2}{2}}\right)},\cdots ,{(d-1)}^{\left({\displaystyle \genfrac{}{}{0pt}{}{k+d-1}{d-1}}\right)},d^0,{(d+1)}^{{\displaystyle \frac{m_{1}1!(k+d)!}{(1+d)!}}},\hfill \\ \hfill & \cdots ,{(d+k)}^{{\displaystyle \frac{m_{k}k!(k+d)!}{(k+d)!}}}⟩.\hfill \end{array}$$

(ii)

We have a $(\lambda ,(\ast \left)\right)$-partition differential equation

$$\begin{array}{cc}\hfill y^{\left(d\right)}& =M{f}_{\lambda }\left(x\right),\hfill \end{array}$$

(20)

$$(\ast ).......\left\{\begin{array}{cc}{y}^{(d-1)}\left(x_0\right)\hfill & =M_{d-1},\hfill \\ y^{(d-2)}\left(x_0\right)\hfill & =M_{d-2},\hfill \\ .\hfill & .\hfill \\ .\hfill & .\hfill \\ .\hfill & .\hfill \\ y^{\left(1\right)}\left(x_0\right)\hfill & =M_1,\hfill \\ y^{\left(0\right)}\left(x_0\right)\hfill & =M_0.\hfill \end{array}\right.$$

where $\lambda =⟨1^{m_1},2^{m_2},\cdots ,k^{m_k}⟩$, $M={\displaystyle \frac{\left(kd\right)!(k+d)!}{d!k!}}$, $x_0=M_0=0$, and

$$M_1={\displaystyle \frac{(k+1)!}{k!}},\cdots ,M_{d-2}={\displaystyle \frac{(k+d-2)!}{k!}},M_{d-1}={\displaystyle \frac{(k+d-1)!}{k!}}.$$

Using (11), we have

$$\begin{array}{cc}\hfill y^{\left(0\right)}& =\sum _{i=1}^k{\displaystyle \frac{m_i\left(kd\right)!(k+d)!}{d!k!}}{\displaystyle \frac{x^{i+d}}{(i+d)!/i!}}+{\displaystyle \frac{(k+d-1)!x^{d-1}}{k!(d-1)!}}+{\displaystyle \frac{(k+d-2)!x^{d-2}}{k!(d-2)!}}\hfill \\ \hfill & +\cdots +{\displaystyle \frac{(k+2)!x^2}{k!2!}}+{\displaystyle \frac{(k+1)!x}{k!1!}}\hfill \\ \hfill & =\sum _{i=1}^k{\displaystyle \frac{m_i\left(kd\right)!(k+d)!}{d!d!k!}}{\displaystyle \frac{x^{i+d}}{(i+d)!/d!i!}}+{\displaystyle \frac{(k+d-1)!x^{d-1}}{k!(d-1)!}}+{\displaystyle \frac{(k+d-2)!x^{d-2}}{k!(d-2)!}}\hfill \\ \hfill & +\cdots +{\displaystyle \frac{(k+2)!x^2}{k!2!}}+{\displaystyle \frac{(k+1)!x}{k!1!}}\hfill \\ \hfill & =\sum _{i=1}^k{\displaystyle \frac{m_i\left(kd\right)!\left(\genfrac{}{}{0pt}{}{k+d}{d}\right)}{d!\left(\genfrac{}{}{0pt}{}{i+d}{d}\right)}}{x}^{i+d}+{\displaystyle \frac{(k+d-1)!x^{d-1}}{k!(d-1)!}}+{\displaystyle \frac{(k+d-2)!x^{d-2}}{k!(d-2)!}}\hfill \\ \hfill & +\cdots +{\displaystyle \frac{(k+2)!x^2}{k!2!}}+{\displaystyle \frac{(k+1)!x}{k!1!}}\hfill \\ \hfill & =\sum _{i=1}^k{\displaystyle \frac{m_i\left(kd\right)!\left(\genfrac{}{}{0pt}{}{k+d}{d}\right)}{d!\left(\genfrac{}{}{0pt}{}{i+d}{d}\right)}}{x}^{i+d}+\left({\displaystyle \genfrac{}{}{0pt}{}{k+d-1}{d-1}}\right)x^{d-1}+\left({\displaystyle \genfrac{}{}{0pt}{}{k+d-2}{d-2}}\right)x^{d-2}\hfill \\ \hfill & +\cdots +\left({\displaystyle \genfrac{}{}{0pt}{}{k+2}{2}}\right)x^2+\left({\displaystyle \genfrac{}{}{0pt}{}{k+1}{1}}\right)x.\hfill \end{array}$$

Consequently, we have

$$\begin{array}{cc}\hfill {\int }_{(\ast )}^{\left(d\right)}\left(\lambda \right)& =⟨1^{\left({\displaystyle \genfrac{}{}{0pt}{}{k+1}{1}}\right)},2^{\left({\displaystyle \genfrac{}{}{0pt}{}{k+2}{2}}\right)},\cdots ,{(d-1)}^{\left({\displaystyle \genfrac{}{}{0pt}{}{k+d-1}{d-1}}\right)},d^0,{(d+1)}^{{\displaystyle \frac{m_1\left(kd\right)!\left(\genfrac{}{}{0pt}{}{k+d}{d}\right)}{d!\left(\genfrac{}{}{0pt}{}{1+d}{d}\right)}}},\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill & \cdots ,{(d+k)}^{{\displaystyle \frac{m_k\left(kd\right)!\left(\genfrac{}{}{0pt}{}{k+d}{d}\right)}{d!\left(\genfrac{}{}{0pt}{}{k+d}{d}\right)}}}⟩.\hfill \end{array}$$

(22)

(iii)

We have a $(\lambda ,(\ast \left)\right)$-partition differential equation

$$\begin{array}{cc}\hfill y^{\left(d\right)}& =M{f}_{\lambda }\left(x\right).\hfill \end{array}$$

(23)

$$(\ast ).......\left\{\begin{array}{cc}{y}^{(d-1)}\left(x_0\right)\hfill & =M_{d-1},\hfill \\ y^{(d-2)}\left(x_0\right)\hfill & =M_{d-2},\hfill \\ .\hfill & .\hfill \\ .\hfill & .\hfill \\ .\hfill & .\hfill \\ y^{\left(1\right)}\left(x_0\right)\hfill & =M_1,\hfill \\ y^{\left(0\right)}\left(x_0\right)\hfill & =M_0.\hfill \end{array}\right.$$

where $\lambda =⟨1^{m_1{k}^{(k-1)}},2^{m_2{k}^{(k-2)}},\cdots ,k^{m_k{k}^{(k-k)}}⟩$, $M={\displaystyle \frac{(k+d)!}{k!}}$, $x_0=M_0=0$ and

$$M_1={\displaystyle \frac{(k+1)!}{k!}},\cdots ,M_{d-2}={\displaystyle \frac{(k+d-2)!}{k!}},M_{d-1}={\displaystyle \frac{(k+d-1)!}{k!}}.$$

Using (11), we have

$$\begin{array}{cc}\hfill y^{\left(0\right)}& =\sum _{i=1}^k{\displaystyle \frac{m_i{k}^{(k-i)}(k+d)!}{k!}}{\displaystyle \frac{x^{i+d}}{(i+d)!/i!}}+{\displaystyle \frac{(k+d-1)!x^{d-1}}{k!(d-1)!}}+{\displaystyle \frac{(k+d-2)!x^{d-2}}{k!(d-2)!}}\hfill \\ \hfill & +\cdots +{\displaystyle \frac{(k+2)!x^2}{k!2!}}+{\displaystyle \frac{(k+1)!x}{k!1!}}\hfill \\ \hfill & =\sum _{i=1}^k{\displaystyle \frac{m_i{k}^{(k-i)}i!(k+d)!}{k!}}{\displaystyle \frac{x^{i+d}}{(i+d)!}}+{\displaystyle \frac{(k+d-1)!x^{d-1}}{k!(d-1)!}}+{\displaystyle \frac{(k+d-2)!x^{d-2}}{k!(d-2)!}}\hfill \\ \hfill & +\cdots +{\displaystyle \frac{(k+2)!x^2}{k!2!}}+{\displaystyle \frac{(k+1)!x}{k!1!}}\hfill \\ \hfill & =\sum _{i=1}^k{\displaystyle \frac{m_{i}k!(k+d)!}{k!}}{\displaystyle \frac{x^{i+d}}{(i+d)!}}+{\displaystyle \frac{(k+d-1)!x^{d-1}}{k!(d-1)!}}+{\displaystyle \frac{(k+d-2)!x^{d-2}}{k!(d-2)!}}\hfill \\ \hfill & +\cdots +{\displaystyle \frac{(k+2)!x^2}{k!2!}}+{\displaystyle \frac{(k+1)!x}{k!1!}}\hfill \\ \hfill & =\sum _{i=1}^k{\displaystyle \frac{m_i(k+d)!}{(i+d)!}}{x}^{i+d}+\left({\displaystyle \genfrac{}{}{0pt}{}{k+d-1}{d-1}}\right)x^{d-1}+\left({\displaystyle \genfrac{}{}{0pt}{}{k+d-2}{d-2}}\right)x^{d-2}\hfill \\ \hfill & +\cdots +\left({\displaystyle \genfrac{}{}{0pt}{}{k+2}{2}}\right)x^2+\left({\displaystyle \genfrac{}{}{0pt}{}{k+1}{1}}\right)x.\hfill \end{array}$$

Therefore,

$$\begin{array}{cc}\hfill {\int }_{(\ast )}^{\left(d\right)}\left(\lambda \right)& =⟨1^{\left({\displaystyle \genfrac{}{}{0pt}{}{k+1}{1}}\right)},2^{\left({\displaystyle \genfrac{}{}{0pt}{}{k+2}{2}}\right)},\cdots ,{(d-1)}^{\left({\displaystyle \genfrac{}{}{0pt}{}{k+d-1}{d-1}}\right)},d^0,{(d+1)}^{{\displaystyle \frac{m_1(k+d)!}{(1+d)!}}},\hfill \\ \hfill & \cdots ,{(d+k)}^{{\displaystyle \frac{m_k(k+d)!}{(k+d)!}}}⟩.\hfill \end{array}$$

□

4. New Algebraic and Coalgebraic Structures for the Algebra of Symmetric Functions

Definition 3. 

Let $\mu =⟨1^{a_1},2^{a_2},\cdots ,k^{a_k}⟩$ and $\nu =⟨1^{b_1},2^{b_2},\cdots ,t^{b_t}⟩$ be partitions. Then,

(i)

$f_{\mu }{f}_{\nu }=f_{\mu \odot \nu }$, where $\mu \odot \nu$ is the partition

$$\begin{array}{cc}\hfill \mu \odot \nu & =⟨1^{c_1},2^{c_2},\cdots ,{(k+t)}^{c_{k+t}}⟩\hfill \end{array}$$

(24)

where

$$\begin{array}{cc}\hfill c_i& =\sum _{j=1}^i{a}_j{b}_{i-j},i=1,2,\cdots ,k+t.\hfill \end{array}$$

(25)

(ii)

$f_{\mu }+f_{\nu }=f_{\mu ⊞\nu }$, where $\mu +\nu$ is the partition

$$\begin{array}{cc}\hfill \mu ⊞\nu & =⟨1^{c_1},2^{c_2},\cdots ,s^{c_s}⟩\hfill \end{array}$$

(26)

where

$$\begin{array}{cc}\hfill s& =max(k,t)\hfill \end{array}$$

(27)

and

$$\begin{array}{cc}\hfill c_i& =a_i+b_i,i=1,2,\cdots ,s.\hfill \end{array}$$

(28)

We have the following theorem:

Theorem 4. 

Let $\lambda ,{\lambda }^{\prime },{\lambda }^{″}\in Par$. Then,

(i)

$$\begin{array}{cc}\hfill \lambda ⊞{\lambda }^{\prime }& =\lambda \bigsqcup {\lambda }^{\prime }.\hfill \end{array}$$

(ii)

The operation ⊙ is associative.

(iii)

$$\begin{array}{cc}\hfill {(\lambda \odot {\lambda }^{\prime })}^{\left(1\right)}& =\lambda \odot {\lambda }^{\prime \left(1\right)}⊞{\lambda }^{\prime }\odot {\lambda }^{\left(1\right)}\hfill \end{array}$$

(iv)

For any partition differential equations $(\lambda ,(\ast \left)\right)$ and $({\lambda }^{\prime },(\ast ))$, one has

$$\begin{array}{cc}\hfill {\int }_{(\ast )}^{\left(d\right)}(\lambda ⊞{\lambda }^{\prime })& ={\int }_{(\ast )}^{\left(d\right)}\left(\lambda \right)⊞{\int }_{(\ast )}^{\left(d\right)}\left({\lambda }^{\prime }\right).\hfill \end{array}$$

(v)

For any partition differential equations $(\lambda ,(\ast \left)\right)$, $({\lambda }^{\prime },(\ast ))$, and $({\lambda }^{″},(\ast ))$, one has

$$\begin{array}{cc}\hfill {\int }_{(\ast )}^{\left(d\right)}(\lambda ⊞{\lambda }^{\prime })\odot {\lambda }^{″}& ={\int }_{(\ast )}^{\left(d\right)}(\lambda \odot {\lambda }^{″})⊞{\int }_{(\ast )}^{\left(d\right)}({\lambda }^{\prime }\odot {\lambda }^{″}).\hfill \end{array}$$

(vi)

$$\begin{array}{cc}\hfill \overline{\lambda ⊞{\lambda }^{\prime }}& =\overline{(\lambda }⊞\overline{{\lambda }^{\prime })}.\hfill \end{array}$$

(vii)

$$\begin{array}{cc}\hfill \overline{(\lambda ⊞{\lambda }^{\prime })\odot {\lambda }^{″}}& =\overline{\lambda \odot {\lambda }^{″}}⊞\overline{{\lambda }^{\prime }\odot {\lambda }^{″}}).\hfill \end{array}$$

(viii)

$$\begin{array}{cc}\hfill \overline{{(\lambda \odot {\lambda }^{\prime })}^{\left(1\right)}}& =\overline{\lambda \odot {\lambda }^{\prime \left(1\right)}}⊞\overline{{\lambda }^{\prime }\odot {\lambda }^{\left(1\right)}}\hfill \end{array}$$

(ix)

For any partition differential equations $(\lambda ,(\ast \left)\right)$ and $({\lambda }^{\prime },(\ast ))$, one has

$$\begin{array}{cc}\hfill \overline{{\int }_{(\ast )}^{\left(d\right)}(\lambda ⊞{\lambda }^{\prime })}& =\overline{{\int }_{(\ast )}^{\left(d\right)}\left(\lambda \right)}⊞\overline{{\int }_{(\ast )}^{\left(d\right)}\left({\lambda }^{\prime }\right)}.\hfill \end{array}$$

(x)

For any partition differential equations $(\lambda ,(\ast \left)\right)$, $({\lambda }^{\prime },(\ast ))$, and $({\lambda }^{″},(\ast ))$, one has

$$\begin{array}{cc}\hfill \overline{{\int }_{(\ast )}^{\left(d\right)}(\lambda ⊞{\lambda }^{\prime })\odot {\lambda }^{″}}& =\overline{{\int }_{(\ast )}^{\left(d\right)}(\lambda \odot {\lambda }^{″})}⊞\overline{{\int }_{(\ast )}^{\left(d\right)}({\lambda }^{\prime }\odot {\lambda }^{″})}.\hfill \end{array}$$

Proof. 

(i)

This is obvious.

(ii)

For any $\lambda ,{\lambda }^{\prime },{\lambda }^{″}\in Par$, we have $\left(f_{\lambda }{f}_{{\lambda }^{\prime }}\right)f_{{\lambda }^{″}}=f_{\lambda }\left(f_{{\lambda }^{\prime }}{f}_{{\lambda }^{″}}\right)$. Thus,

$$\begin{array}{cc}\hfill (\lambda \odot {\lambda }^{\prime })\odot {\lambda }^{″}& =\lambda \odot ({\lambda }^{\prime }\odot {\lambda }^{″}).\hfill \end{array}$$

(iii)

This follows directly from $(f_{\lambda }+f_{{\lambda }^{\prime }})f_{{\lambda }^{″}}=f_{\lambda }{f}_{{\lambda }^{″}}+f_{{\lambda }^{\prime }}{f}_{{\lambda }^{″}}$.

(iv)

This comes immediately from the fact that

$$\begin{array}{cc}\hfill {\displaystyle \frac{d}{dx}}\left(f_{\lambda }{f}_{{\lambda }^{\prime }}\right)& =f_{\lambda }{\displaystyle \frac{d}{dx}}{f}_{{\lambda }^{\prime }}+f_{{\lambda }^{\prime }}{\displaystyle \frac{d}{dx}}{f}_{\lambda }.\hfill \end{array}$$

and Definition (3).

(v)

For any $\lambda ,{\lambda }^{\prime }\in Par$, we have

$$\begin{array}{cc}\hfill \int (f_{\lambda }+f_{{\lambda }^{\prime }})dx& =\int f_{\lambda }dx+\int f_{{\lambda }^{\prime }}dx.\hfill \end{array}$$

Therefore, we have

$$\begin{array}{cc}\hfill {\int }_{(\ast )}^{\left(d\right)}(\lambda ⊞{\lambda }^{\prime })& ={\int }_{(\ast )}^{\left(d\right)}\left(\lambda \right)⊞{\int }_{(\ast )}^{\left(d\right)}\left({\lambda }^{\prime }\right).\hfill \end{array}$$

(vi)

For any $\lambda ,{\lambda }^{\prime },{\lambda }^{″}\in Par$, we have

$$\begin{array}{cc}\hfill \int (f_{\lambda }+f_{{\lambda }^{\prime }})f_{{\lambda }^{″}}dx& =\int f_{\lambda }{f}_{{\lambda }^{″}}dx+\int f_{{\lambda }^{\prime }}{f}_{{\lambda }^{″}}dx.\hfill \end{array}$$

Accordingly, we have

$$\begin{array}{cc}\hfill (\lambda ⊞{\lambda }^{\prime })\odot {\lambda }^{″}& =\lambda \odot {\lambda }^{″}⊞{\lambda }^{\prime }\odot {\lambda }^{″}).\hfill \end{array}$$

(vii)

This follows directly from Theorem (1) and Definition (3).

Parts (vii)-(x) are immediate consequences of parts (ii)–(vi).

□

Using the convention $f_{\varnothing }=1$ (the constant polynomial $f\left(x\right)=1$), we have

$$\begin{array}{cc}\hfill \lambda \odot \varnothing & =\varnothing \odot \lambda =\lambda .\hfill \end{array}$$

Using Theorem (4), we have the following theorem.

Theorem 5. 

(i)

The triple $(\mathrm{\Lambda },\eta ,u$) is a $\mathbf{k}$-algebra, where the multiplication is the map

$$\mathrm{\Lambda }\otimes \mathrm{\Lambda }\stackrel{\eta }{⟶}\mathrm{\Lambda },m_{\mu }\otimes m_{\nu }\mapsto m_{\mu \odot \nu },$$

and the unit is the inclusion map

$$\mathbf{k}={\mathrm{\Lambda }}_0\stackrel{u}{⟶}\mathrm{\Lambda }.$$

(ii)

The triple $(\mathrm{\Lambda },\mathrm{{\rm Y}},ϵ$) is a $\mathbf{k}$-coalgebra, where the comultiplication is the map

$$\mathrm{\Lambda }\stackrel{\mathrm{{\rm Y}}}{⟶}\mathrm{\Lambda }\otimes \mathrm{\Lambda },m_{\lambda }\mapsto \sum _{\begin{array}{c}(\mu ,\nu )\in Par\times Par:\\ \mu \odot \nu =\lambda \end{array}}{m}_{\mu }\otimes m_{\nu },$$

and the counit is the $\mathbf{k}$-linear map

$$\mathbf{k}={\mathrm{\Lambda }}_0\stackrel{ϵ}{⟶}\mathrm{\Lambda }$$

with ${ϵ|}_{{\mathrm{\Lambda }}_0=\mathbf{k}}=i{d}_{\mathbf{k}}$ and ${ϵ|}_{I={⨁}_{n>0}{\mathrm{\Lambda }}_n}=0$.

Proof. 

The proof of $\left(i\right)$ follows directly from Theorem (4). To prove part $\left(ii\right)$, we have to show that the following diagrams are commutative:

(29)

(30)

Here, $\mathrm{\Phi }$ and $\mathrm{\Psi }$ are the isomorphisms $\mathrm{\Phi }:\mathrm{\Lambda }\otimes \mathbf{k}\to \mathrm{\Lambda },m_{\lambda }\otimes 1\mapsto m_{\lambda }$ and $\mathrm{\Psi }:\mathbf{k}\otimes \mathrm{\Lambda }\to \mathrm{\Lambda },1\otimes m_{\lambda }\mapsto m_{\lambda }$. For any $\lambda \in Par$, we have

$$\begin{array}{cc}\hfill (\mathrm{{\rm Y}}\otimes id)\mathrm{{\rm Y}}{m}_{\lambda }& =(\mathrm{{\rm Y}}\otimes id)(\sum _{\begin{array}{c}(\mu ,{\mu }^{\prime })\in Par\times Par:\\ \mu \odot {\mu }^{\prime }=\lambda \end{array}}{m}_{\mu }\otimes m_{{\mu }^{\prime }})\hfill \\ \hfill & =\sum _{\begin{array}{c}(\mu ,{\mu }^{\prime })\in Par\times Par:\\ \mu \odot {\mu }^{\prime }=\lambda \end{array}}\mathrm{{\rm Y}}{m}_{\mu }\otimes m_{{\mu }^{\prime }}\hfill \\ \hfill & =\sum _{\begin{array}{c}(\mu ,{\mu }^{\prime })\in Par\times Par:\\ \mu \odot {\mu }^{\prime }=\lambda \end{array}}\sum _{\begin{array}{c}(\nu ,{\nu }^{\prime })\in Par\times Par:\\ \nu \odot {\nu }^{\prime }=\mu ,\end{array}}(m_{\nu }\otimes m_{{\nu }^{\prime }})\otimes m_{{\mu }^{\prime }}\hfill \\ \hfill & =\sum _{\begin{array}{c}(\nu ,{\nu }^{\prime },{\mu }^{\prime })\in Par\times Par\times Par:\\ \nu \odot {\nu }^{\prime }\odot {\mu }^{\prime }=\lambda \end{array}}{m}_{\nu }\otimes m_{{\nu }^{\prime }}\otimes m_{{\mu }^{\prime }}\hfill \\ \hfill & =\sum _{\begin{array}{c}(\mu ,{\mu }^{\prime })\in Par\times Par:\\ \mu \odot {\mu }^{\prime }=\lambda \end{array}}\sum _{\begin{array}{c}(\nu ,{\nu }^{\prime })\in Par\times Par:\\ \nu \odot {\nu }^{\prime }={\mu }^{\prime }\end{array}}{m}_{\mu }\otimes (m_{\nu }\otimes m_{{\nu }^{\prime }})\hfill \\ \hfill & =\sum _{\begin{array}{c}(\mu ,{\mu }^{\prime })\in Par\times Par:\\ \mu \odot {\mu }^{\prime }=\lambda \end{array}}{m}_{\mu }\otimes \sum _{\begin{array}{c}(\nu ,{\nu }^{\prime })\in Par\times Par:\\ \nu \odot {\nu }^{\prime }={\mu }^{\prime }\end{array}}(m_{\nu }\otimes m_{{\nu }^{\prime }})\hfill \\ \hfill & =\sum _{\begin{array}{c}(\mu ,{\mu }^{\prime })\in Par\times Par:\\ \mu \odot {\mu }^{\prime }=\lambda \end{array}}{m}_{\mu }\otimes \mathrm{{\rm Y}}{m}_{{\mu }^{\prime }}\hfill \\ \hfill & =(id\otimes \mathrm{{\rm Y}})(\sum _{\begin{array}{c}(\mu ,{\mu }^{\prime })\in Par\times Par:\\ \mu \odot {\mu }^{\prime }=\lambda \end{array}}{m}_{\mu }\otimes m_{{\mu }^{\prime }})\hfill \\ \hfill & =(id\otimes \mathrm{{\rm Y}})\mathrm{{\rm Y}}{m}_{\lambda }.\hfill \end{array}$$

Therefore, the commutativity of the associativity diagram follows. Checking the commutativity of the unity diagram can be performed as follows:

$$\begin{array}{cc}\hfill \mathrm{\Psi }(ϵ\otimes id)\mathrm{{\rm Y}}{m}_{\lambda }& =\mathrm{\Psi }(ϵ\otimes id)(\sum _{\begin{array}{c}(\mu ,{\mu }^{\prime })\in Par\times Par:\\ \mu \odot {\mu }^{\prime }=\lambda \end{array}}{m}_{\mu }\otimes m_{{\mu }^{\prime }})\hfill \\ \hfill & =\mathrm{\Psi }(\sum _{\begin{array}{c}(\mu ,{\mu }^{\prime })\in Par\times Par:\\ \mu \odot {\mu }^{\prime }=\lambda \end{array}}ϵ\left(m_{\mu }\right)\otimes m_{{\mu }^{\prime }})\hfill \\ \hfill & =\sum _{\begin{array}{c}(\mu ,{\mu }^{\prime })\in Par\times Par:\\ \mu \odot {\mu }^{\prime }\odot =\lambda \end{array}}ϵ\left(m_{\mu }\right)m_{{\mu }^{\prime }}\hfill \\ \hfill & =m_{\lambda }{(\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{e} ϵ|}_{\mathbf{k}}=i{d}_{\mathbf{k}} \mathrm{and} ϵ{|}_{I={⨁}_{n>0}{\mathrm{\Lambda }}_n}=0).\hfill \\ \hfill & =id\left(m_{\lambda }\right)\hfill \\ \hfill & =\sum _{\begin{array}{c}(\mu ,{\mu }^{\prime })\in Par\times Par:\\ \mu \odot {\mu }^{\prime }=\lambda \end{array}}{m}_{\mu }ϵ\left(m_{{\mu }^{\prime }}\right)\hfill \\ \hfill & =\mathrm{\Phi }(\sum _{\begin{array}{c}(\mu ,{\mu }^{\prime })\in Par\times Par:\\ \mu \odot {\mu }^{\prime }=\lambda \end{array}}{m}_{\mu }\otimes ϵ\left(m_{{\mu }^{\prime }}\right))\hfill \\ \hfill & =\mathrm{\Phi }(id\otimes ϵ)(\sum _{\begin{array}{c}(\mu ,{\mu }^{\prime })\in Par\times Par:\\ \mu \odot {\mu }^{\prime }=\lambda \end{array}}{m}_{\mu }\otimes m_{{\mu }^{\prime }})\hfill \\ \hfill & =\mathrm{\Phi }(id\otimes ϵ)\mathrm{{\rm Y}}{m}_{\lambda }.\hfill \end{array}$$

It follows that $(\mathrm{\Lambda },\mathrm{{\rm Y}},ϵ)$ is a $\mathbf{k}$-coalgebra. □

Example 2. 

Let $\lambda =⟨1^0,2^2,3^7,4^5,5^1⟩$ be a partition. Then,

$$\begin{array}{cc}\hfill \mathrm{{\rm Y}}{m}_{\lambda }& =m_{⟨1^0,2^2,3^7,4^5,5^1⟩}\otimes 1+m_{⟨1^2,2^1⟩}\otimes m_{⟨1^1,2^3,3^1⟩}+m_{⟨1^1,2^3,3^1⟩}\otimes m_{⟨1^2,2^1⟩}\hfill \\ \hfill & +m_{⟨1^2,2^7,3^5,4^1⟩}\otimes m_{⟨1^1⟩}+m_{⟨1^1⟩}\otimes m_{⟨1^2,2^7,3^5,4^1⟩}+1\otimes m_{⟨1^0,2^2,3^7,4^5,5^1⟩}.\hfill \end{array}$$

Using the definitions of the polynomials $f_{\lambda }$ and the map $\Delta$, we end the paper by giving an explicit description for the primitive elements in the $\mathbf{k}$-coalgebra $(\mathrm{\Lambda },\mathrm{{\rm Y}},ϵ)$.

Theorem 6. 

Let $\lambda =⟨1^{m_1},2^{m_2},\cdots ,k^{m_k}⟩$ be a nonempty partition. Then, $m_{\lambda }$ is a primitive element in $(\mathrm{\Lambda },\mathrm{{\rm Y}},ϵ)$ if and only if $m_1\ne 0$.

Proof. 

The case is obvious when the length of $\lambda$ equals 1. If $k\ge 2$ and $m_1=0$, then $x^2$ divides $f_{\lambda }$. Consequently, we have $f_{\lambda }=x{f}_{\mu }$, where $\mu =⟨1^{m_1},2^{m_2},\cdots ,{(k-1)}^{m_{k-1}}⟩$, and this completes the proof. □

Definition 4. 

Let

$$F_{\lambda }\left(\left[\begin{array}{c}x\\ y\end{array}\right]\right)=\left[\begin{array}{c}{f}_{\lambda }\left(x\right)\\ f_{\overline{\lambda }}\left(y\right)\end{array}\right],$$

where $\overline{\lambda }$ is defined in Theorem (1). Then, $F_{\lambda }$ is called the partition primitive function of λ.

Let

$$J_{F_{\lambda }}(x,y)={\nabla }^{T}F=\left[\begin{array}{c}{\nabla }^T{f}_{\lambda }\\ {\nabla }^T{f}_{\overline{\lambda }}\end{array}\right]=\left[\begin{array}{cc}{\displaystyle \frac{\partial f_{\lambda }}{\partial x}}& {\displaystyle \frac{\partial f_{\lambda }}{\partial y}}\\ {\displaystyle \frac{\partial f_{\overline{\lambda }}}{\partial x}}& {\displaystyle \frac{\partial f_{\overline{\lambda }}}{\partial y}}\end{array}\right].$$

be the Jacobian matrix of $F_{\lambda }$, where ${\nabla }^T{f}_{\lambda }$ and ${\nabla }^T{f}_{\overline{\lambda }}$ are the transpose of the gradient of the first and second component, respectively. The following theorem shows that the partition primitive functions can be used to characterize the primitive elements in $(\mathrm{\Lambda },\mathrm{{\rm Y}},ϵ)$.

Theorem 7. 

Let $\lambda =⟨1^{m_1},2^{m_2},\cdots ,k^{m_k}⟩$ be a nonempty partition, and write $\overline{\lambda }=⟨1^{n_1},2^{n_2},\cdots ,k^{n_k}⟩$. Then,

(i)

$m_{\lambda }$ and $m_{\overline{\lambda }}$ are primitive elements in $(\mathrm{\Lambda },\mathrm{{\rm Y}},ϵ)$ if and only if $det\left(J_{F_{\lambda }}(0,0)\right)\ne 0$.

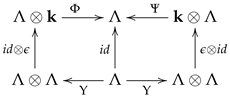
(ii)

For any $k\ge 2$ and $1\le d<k$, let $J_{F_{\lambda }}^{\left(d\right)}(x,y)={{\nabla }^d}^{T}F(x,y)$, where ${\nabla }^d=\nabla {\nabla }^{d-1}$. Then, $m_{{\lambda }^{\left(d\right)}}$ and $m_{{\overline{\lambda }}^{\left(d\right)}}$ are primitive elements in $(\mathrm{\Lambda },\mathrm{{\rm Y}},ϵ)$ if and only if $det\left(J_{F_{\lambda }}^{\left(d\right)}(0,0)\right)\ne 0$.

Proof. 

We note that the Jacobian matrix of $F_{\lambda }$ is given by

$$J_{F_{\lambda }}(x,y)=\left[\begin{array}{cc}{\displaystyle \frac{\partial f_{\lambda }}{\partial x}}& {\displaystyle \frac{\partial f_{\lambda }}{\partial y}}\\ {\displaystyle \frac{\partial f_{\overline{\lambda }}}{\partial x}}& {\displaystyle \frac{\partial f_{\overline{\lambda }}}{\partial y}}\end{array}\right]=\left[\begin{array}{cc}{m}_1+f_{{\lambda }^{\left(1\right)}}\left(x\right)& 0\\ 0& n_1+f_{{\overline{\lambda }}^{\left(1\right)}}\left(y\right)\end{array}\right].$$

So,

$$J_{F_{\lambda }}(0,0)=\left[\begin{array}{cc}{m}_1+f_{{\lambda }^{\left(1\right)}}\left(0\right)& 0\\ 0& n_1+f_{{\overline{\lambda }}^{\left(1\right)}}\left(0\right)\end{array}\right]=\left[\begin{array}{cc}{m}_1+0& 0\\ 0& n_1+0\end{array}\right]=\left[\begin{array}{cc}{m}_1& 0\\ 0& n_1\end{array}\right].$$

Thus, $det\left(J_{F_{\lambda }}(0,0)\right)=m_1{n}_1$, and $m_1{n}_1\ne 0$ if and only if $m_1\ne 0$ and $n_1\ne 0$. It follows from Theorem (6) that $m_{\lambda }$ is a primitive element in $(\mathrm{\Lambda },\mathrm{{\rm Y}},ϵ)$ if and only if $det\left(J_{F_{\lambda }}(0,0)\right)\ne 0$. The proof of the other part follows directly from the fact that

$$J_{F_{\lambda }}^{\left(d\right)}(x,y)=\left[\begin{array}{cc}{\displaystyle \frac{{\partial }^d{f}_{\lambda }}{\partial x^d}}& {\displaystyle \frac{{\partial }^d{f}_{\lambda }}{\partial y^d}}\\ {\displaystyle \frac{\partial f_{\overline{\lambda }}}{\partial x}}& {\displaystyle \frac{\partial f_{\overline{\lambda }}}{\partial y}}\end{array}\right]=\left[\begin{array}{cc}d!m_d+f_{{\lambda }^{\left(d\right)}}\left(x\right)& 0\\ 0& d!n_d+f_{{\overline{\lambda }}^{\left(d\right)}}\left(y\right)\end{array}\right].$$

So,

$$J_{F_{\lambda }}^{\left(d\right)}(0,0)=\left[\begin{array}{cc}d!m_d& 0\\ 0& d!n_d\end{array}\right],$$

and $det\left(J_{F_{\lambda }}^{\left(d\right)}(0,0)\right)={(d!)}^2{m}_d{n}_d$. □

5. Brief Conclusions and Future Directions

5.1. Brief Conclusions

(i)

Every partition corresponds uniquely to a Stirling partition.

(ii)

While partitions behave well with integration, the integrand partitions are completely determined by the initial conditions of the partition differential equations.

(iii)

Partition polynomials can be used as extremely useful tools to establish combinatorial structures on the algebra of symmetric functions.

(iv)

Partition primitive functions play a central role in our investigation of characterizing primitive elements in $\mathrm{\Lambda }$.

5.2. Future Directions

A Bayer pattern array can be seen in (Figure 1):

Figure 1. Bayer Filter Mosaic.

Every image can be seen as a basic element for a certain free module generated by a basis indexed by the set of all partitions or compositions (based on the shape of its pixels) [10,11]. Consequently, we can apply some digital image processing tools, such as Bayer’s filter, to define coalgebraic structures in terms of colors using [10]. We can also extend our research to define composition polynomials and use that to introduce combinatorial algebraic or coalgebraic structures using [11]. One can also think of developing partition primitive functions and using the integral of partitions to define new structures on the algebra of symmetric functions.