Polarization Division Multiplexing CV-QKD with Pilot-Aided Polarization-State Sensing

Abstract

Continuous-variable quantum key distribution (CV-QKD) with local local oscillator (LLO) is well-studied for its security and simplicity, but enhancing performance and interference resistance remains challenging. In this paper, we utilize polarization division multiplexing (PDM) to enhance spectral efficiency and significantly increase the key rate of the CV-QKD system. To address dynamic changes in the state of polarization (SOP) in Gaussian modulated coherent states (GMCS) signals due to polarization impairment effects, we designed a time-division multiplexing pilot scheme to sense and recover changes in SOP in GMCS signals, along with other digital signal processing methods. Experiments over 20 km show that our scheme maintains low excess noise levels (0.062 and 0.043 in shot noise units) and achieves secret key rates of 4.65 Mbps and 5.66 Mbps for the two polarization orientations, totaling 10.31 Mbps. This work confirms the effectiveness of PDM GMCS-CV-QKD and offers technical guidance for high-rate QKD within metropolitan areas.

1. Introduction

Quantum key distribution (QKD), a well-known application in the field of quantum cryptography, is favored by researchers because it adopts quantum mechanisms and thus can guarantee the unconditional security of the key distribution process [1,2]. Continuous-variable quantum key distribution (CV-QKD) has become an important research element in the field of QKD due to factors such as low realization cost and better integration with classical optical communication [3]; its security against collective attacks [4,5,6] and coherent attacks [7,8] has been well proved in the Gaussian modulated coherent states (GMCS) format.

Fiber-based QKD has progressed in a number of ways, and its ability to generate keys stably and at high speeds over fiber-optic links provides a more advanced extension of QKD [9,10,11,12]. Up to now, research on CV-QKD has mainly focused on improving performance and diversification, including high-rate and long-distance, as well as network expansion and chip integration. To improve the performance of CV-QKD, it is generally necessary to employ a higher repetition frequency while controlling noise to achieve a higher key rate [13,14]. Increasing the repetition frequency implies the need for more bandwidth. However, the repetition frequency cannot be infinitely increased due to limitations such as the detection bandwidth of balanced detectors, the bandwidth of modulation modules, and the sampling rate limits of DAC and ADC chips. The scheme with frequency-division multiplexed (FDM) pilots [15] can separate the pilot and signal while providing a real-time phase reference. However, the scheme requires the pilot to occupy an additional bandwidth equal to that of the signal, thereby reducing spectral efficiency. In this context, polarization division multiplexing (PDM) is an advantageous method. It allows different signals to be modulated in the orthogonal polarization orientations of an optical carrier, thus doubling the spectral efficiency of the system, thereby achieving a theoretical key rate that is double that of the single-channel scheme.

The use of PDM technology in CV-QKD systems should address polarization-related impairments, as misalignment to the local oscillator (LO) and changes in the state of polarization (SOP) can lead to signal power loss, increased noise, and degraded key distribution performance. While most CV-QKD experiments use manual or dynamic polarization controllers for SOP control, recent years have seen researchers considering digital signal processing (DSP) for SOP tracking and compensation, such as the Kalman filter (KF) algorithm [16] and its variants. The Stokes space technique is also suitable for short frame data due to its fast convergence [17] and has been applied in the CV-QKD field [18]. The implementation of the single-frequency pilot has shown promising performance, including assisting the KF algorithm for phase recovery [19], joint polarization and phase compensation [20], as well as a polarization state tracking algorithm based on orthogonal pilots [21]. In these SOP recovery methods, quantum signals are modulated on one polarization while pilot tones are on the other, or their bands are separated via FDM, but without improving spectral efficiency.

In this paper, we enhance the spectral efficiency of CV-QKD by utilizing PDM technology, which is commonly employed in optical communication systems to increase transmission rates. Additionally, we tackle the challenges posed by polarization-related impairments on GMCS signals within PDM CV-QKD systems. To address this, we design a time-division multiplexing pilot scheme specifically for GMCS signals, which facilitates the sensing and recovery of the SOP. This approach not only improves the robustness of the communication system but also contributes to the overall efficiency of quantum key distribution.

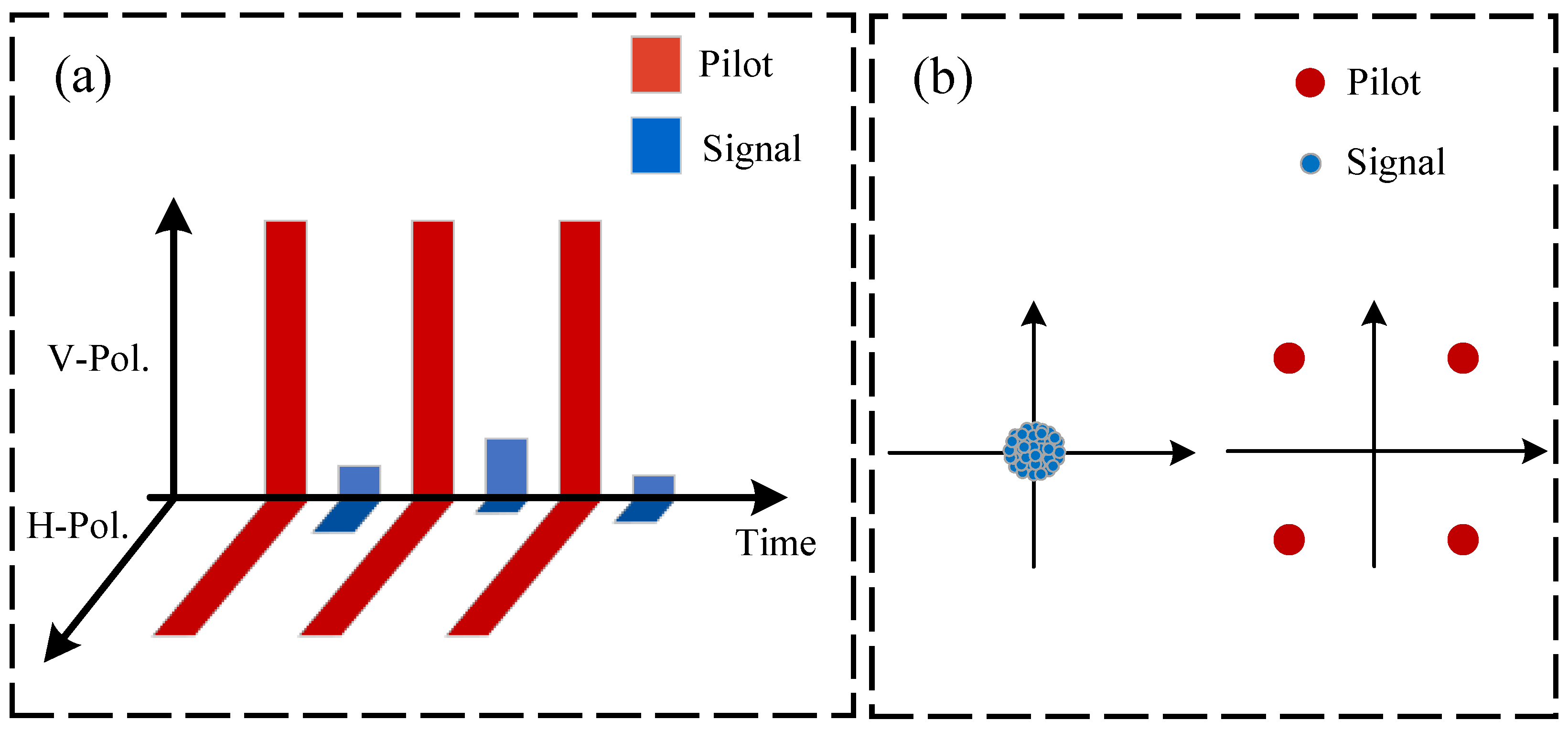
2. Scheme Description

2.1. Scheme of the Dual-Channel CV-QKD

There are three primary polarization impairment effects that significantly impact optical communication systems: rotation of the state of polarization (RSOP), polarization mode dispersion (PMD), and polarization-dependent loss (PDL) [22]. These effects not only degrade the performance of classical optical communication systems but also have a more pronounced impact on weak quantum signals in continuous-variable quantum key distribution (CV-QKD) systems, making receiver-side processing essential. In our approach, we employ a polarization multiplexing technique, which is a central focus of this paper. Among the aforementioned impairments, RSOP is particularly critical for the accurate demultiplexing of polarization-division multiplexing (PDM) signals in optical communications [23]. This importance is magnified in PDM CV-QKD systems, where maintaining the integrity of quantum states is paramount. Consequently, this work specifically addresses the RSOP challenge within PDM CV-QKD systems. By investigating effective methods to mitigate RSOP, we aim to enhance the reliability and security of quantum communication protocols. This focus not only contributes to the theoretical understanding of polarization effects in quantum systems but also has practical implications for the design and implementation of future quantum communication networks.

The impact of RSOP can be described using the Jones matrix $\mathit{J}\left(t\right)$, which is mathematically expressed as

$$\mathit{J}\left(t\right)=\left[\begin{array}{cc}cos\alpha \left(t\right)e^{j{\displaystyle \frac{\theta \left(t\right)}{2}}}& -sin\alpha \left(t\right)e^{j{\displaystyle \frac{\theta \left(t\right)}{2}}}\\ sin\alpha \left(t\right)e^{-j{\displaystyle \frac{\theta \left(t\right)}{2}}}& cos\alpha \left(t\right)e^{-j{\displaystyle \frac{\theta \left(t\right)}{2}}}\end{array}\right],$$

(1)

where $\alpha \left(t\right)$ is the polarization rotation angle and $\theta \left(t\right)$ denotes the phase angles between two signals in different orientations. According to Equation (1), the SOP rotation directly leads to signal power aliasing in two mutually orthogonal polarization orientations and the associated phase angle changes.

For our PDM CV-QKD system, the transmission of signals through the optical fiber channel is affected not only by RSOP due to birefringence in the single-mode fiber, but also by other factors such as phase drift and frequency offset. According to Ref. [16], the whole process can be described as

$${\mathit{Z}}_{\mathit{B}}\left(t\right)=\sqrt{\eta T}{e}^{j(\Delta \omega t+{\theta }_n\left(t\right))}\mathit{J}\left(t\right){\mathit{Z}}_{\mathit{A}}\left(t\right)+\mathit{\xi }\left(t\right),$$

(2)

where $\eta$, T and $\mathit{\xi }$ denote the quantum efficiency of the receiver, channel transmittance and the additive white Gaussian noise in dual-polarization, respectively. The $\Delta \omega$ is the frequency difference between the signal laser and the local oscillator (LO), which is zero in our experiment because the LO is derived from the signal laser. ${\theta }_n\left(t\right)$ is the carrier phase noise, caused by the optical path length difference and the laser linewidth. $\mathit{J}\left(t\right)$ is the Jones matrix, which is the mathematical model causing RSOP. ${\mathit{Z}}_A\left(t\right)$ and ${\mathit{Z}}_B\left(t\right)$ denote Alice’s transmitted signal and Bob’s received signal, respectively. The Jones matrix $J\left(t\right)$ of Equation (1) can be expanded as

$$\mathit{J}\left(t\right)=\left[\begin{array}{cc}{e}^{j{\displaystyle \frac{\theta \left(t\right)}{2}}}& 0\\ 0& e^{-j{\displaystyle \frac{\theta \left(t\right)}{2}}}\end{array}\right]\left[\begin{array}{cc}cos\alpha \left(t\right)& -sin\alpha \left(t\right)\\ sin\alpha \left(t\right)& cos\alpha \left(t\right)\end{array}\right]=\mathbf{\Phi }\left(t\right)\mathit{A}\left(t\right),$$

(3)

where $\alpha \left(t\right)$ is the polarization rotation angle and $\theta \left(t\right)$ denotes the phase angles between two signals in the different orientations. Since we adopt the PDM scheme, both $X\left(t\right)$ and $R\left(t\right)$ are two-dimensional data containing components in the vertical (V) and horizontal (H) polarization orientations, i.e., ${\mathit{Z}}_{\mathit{A}}\left(t\right)={\left[Z_{VA}\left(t\right)Z_{HA}\left(t\right)\right]}^T$ and ${\mathit{Z}}_{\mathit{B}}\left(t\right)={\left[Z_{VB}\left(t\right)Z_{HB}\left(t\right)\right]}^T$, where ${(·)}^T$ denotes the transpose operation. According to Equation (3), under the consideration of only RSOP, the relationship between the received signal and the transmitted signal at a particular time can be derived as

$$\begin{array}{c}\hfill Z_{VB}=[(X_{VA}+i{P}_{VA})cos\alpha -(X_{HA}+i{P}_{HA})sin\alpha ]e^{j{\displaystyle \frac{\theta }{2}}}+{\xi }_V,\end{array}$$

(4)

$$\begin{array}{c}\hfill Z_{HB}=[(X_{VA}+i{P}_{VA})sin\alpha +(X_{HA}+i{P}_{HA})cos\alpha ]e^{-j{\displaystyle \frac{\theta }{2}}}+{\xi }_H,\end{array}$$

(5)

where $X_{(·)}$ and $P_{(·)}$ represent the X and P quadrature components in the V and H polarization orientations for Alice (A) and Bob (B), respectively. Additionally, ${\xi }_H$ and $x{i}_V$ are the components of the Gaussian noise $\mathit{\xi }\left(t\right)$ at a given time in the H and V polarization orientations, and they are uncorrelated. Based on Equations (4) and (5) we can see that the received $Z_{VB}$ and $Z_{HB}$ each contain a mix of $Z_{VA}$ and $Z_{HA}$ due to $\mathit{A}\left(t\right)$. Additionally, there is a phase change in each polarization orientation caused by $\mathbf{\Phi }\left(t\right)$. The phase drift in LLO CV-QKD caused by frequency offset and carrier phase noise is generally compensated for with pilot tone, which serves as a reference to track the phase change [14,24]. In addition, due to the weak power of the quantum signal, direct signal processing is challenging, necessitating pilot tone to assist the DSP algorithms. Additionally, since GMCS has a non-constant modulus, directly applying DSP algorithms to recover the original modulus is infeasible. In this context, we proposed a pilot-aided SOP recovery algorithm based on the constant modulus algorithm (CMA) to equalize the received GMCS signals modulated in two polarization orientations. In our scheme, pilot tone is used to sense changes in SOP. By using adjacent pilots in the time domain, we can track the SOP of the quantum signals, assisting CMA with the SOP recovery of the quantum signals.

The modulation format of the pilot-aided scheme is depicted in Figure 1, which consists of a time-division multiplexed sequence of pilot and signal based on PDM. Specifically, the modulation techniques used here include GMCS modulation for the quantum signals and QPSK-modulated pilots with constant modulus properties. For simplicity, we illustrate the signal formats for one polarization. The entire modulation sequence containing $2n$ elements can be described by the following process

$$Seq\left(j\right)=\left\{\begin{array}{c}A{e}^{{\theta }_d\left(k\right)},j=2k-1,\hfill \\ |{\alpha }_{G_k}\rangle ,j=2k,\hfill \end{array}k\in \{1,2,...,n\},\right.$$

(6)

where ${\theta }_d\left(k\right)={\displaystyle \frac{m\pi }{4}},m\in \{1,2,3,4\}$, A is the amplitude of the pilot tone and $|{\alpha }_{G_k}\rangle$ is the coherent state of GMCS.

2.2. Noise Model of the PDM CV-QKD System

Due to experimental imperfections in our system, in addition to shot noise, there are other sources of noise in the system, which is called excess noise. Excess noise can originate from the transmitter, channel, or receiver. For instance, the transmitter may introduce noise due to laser intensity fluctuations or imperfect modulation, while the receiver might experience noise detection or quantization noise. Additionally, scattering in the fiber contributes to excess noise. These noise sources are typically assumed to be statistically independent, allowing their variances to be combined. The total excess noise of the PDM CV-QKD scheme can be expressed as

$${\epsilon }_{tot}={\epsilon }_{Pol}+{\epsilon }_{PR}+{\epsilon }_{mod}+{\epsilon }_{rest},$$

(7)

where ${\epsilon }_{Pol}$ and ${\epsilon }_{PR}$ are the residual polarization crosstalk noise, and phase recovery noise. The ${\epsilon }_{mod}$ includes not only the noise described in [25] but also the modulation noise introduced by the AWG precision limitations mentioned in the main text. ${\epsilon }_{rest}$ represents the excess noise present in other typical CV-QKD systems. According to [25], it mainly includes ${\epsilon }_{RIN,sig}$, ${\epsilon }_{RIN,LO}$, ${\epsilon }_{det}$, and ${\epsilon }_{ADC}$.

The ${\epsilon }_{PR}$ arises partly from the low signal-to-noise ratio (SNR) of the pilot tone, which leads to insufficient recovery accuracy, and partly from the rapid phase jitter occurring during the modulation of the pilot tones and quantum signals. The ${\epsilon }_{Pol}$ also stems from the insufficient accuracy in SOP sensing due to the low SNR of the pilot tone, as well as from the limited convergence precision of the CMA algorithm. Additionally, it arises from a discrepancy in the SOP between the pilot tones and quantum signals caused by their temporal separation.

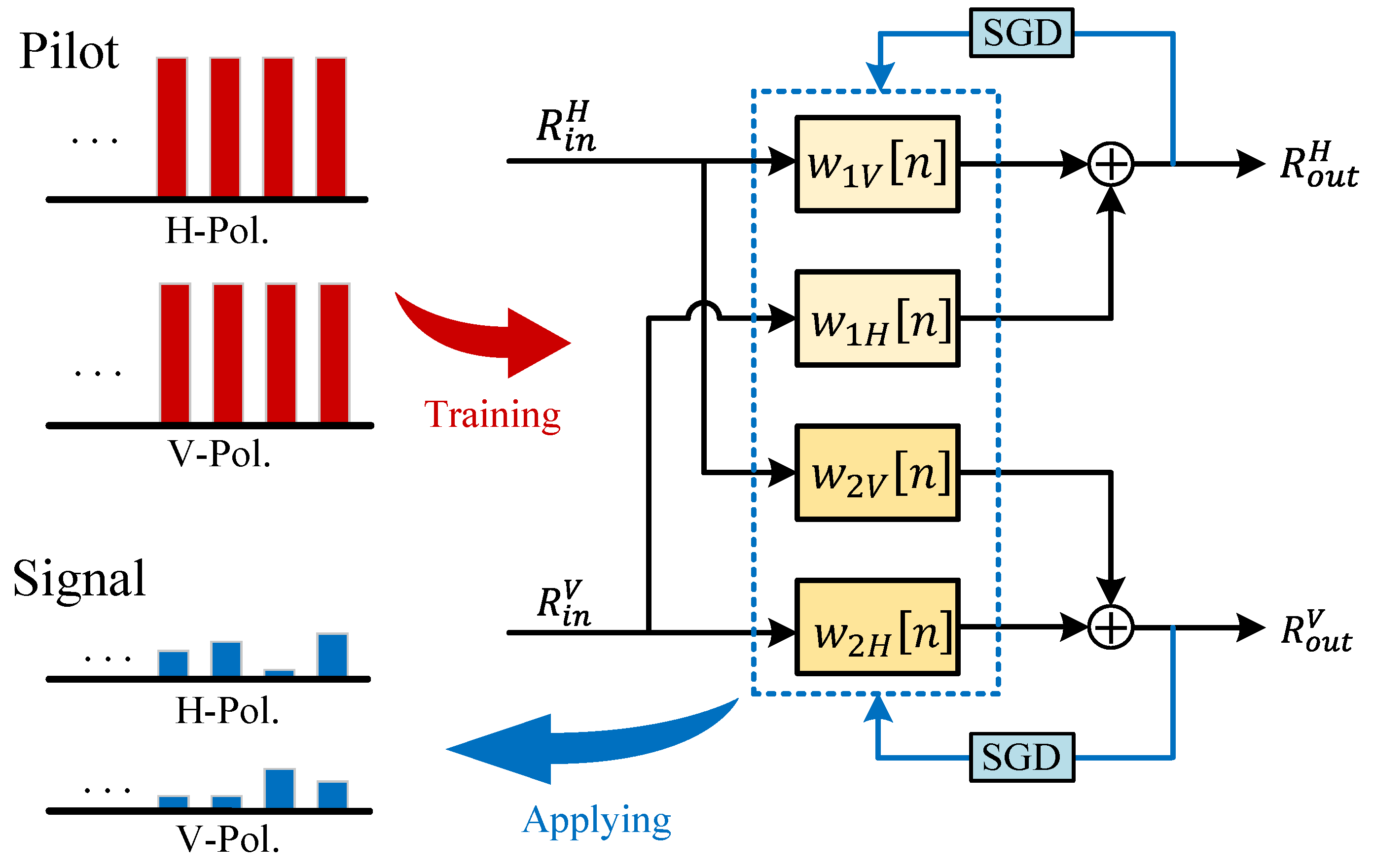
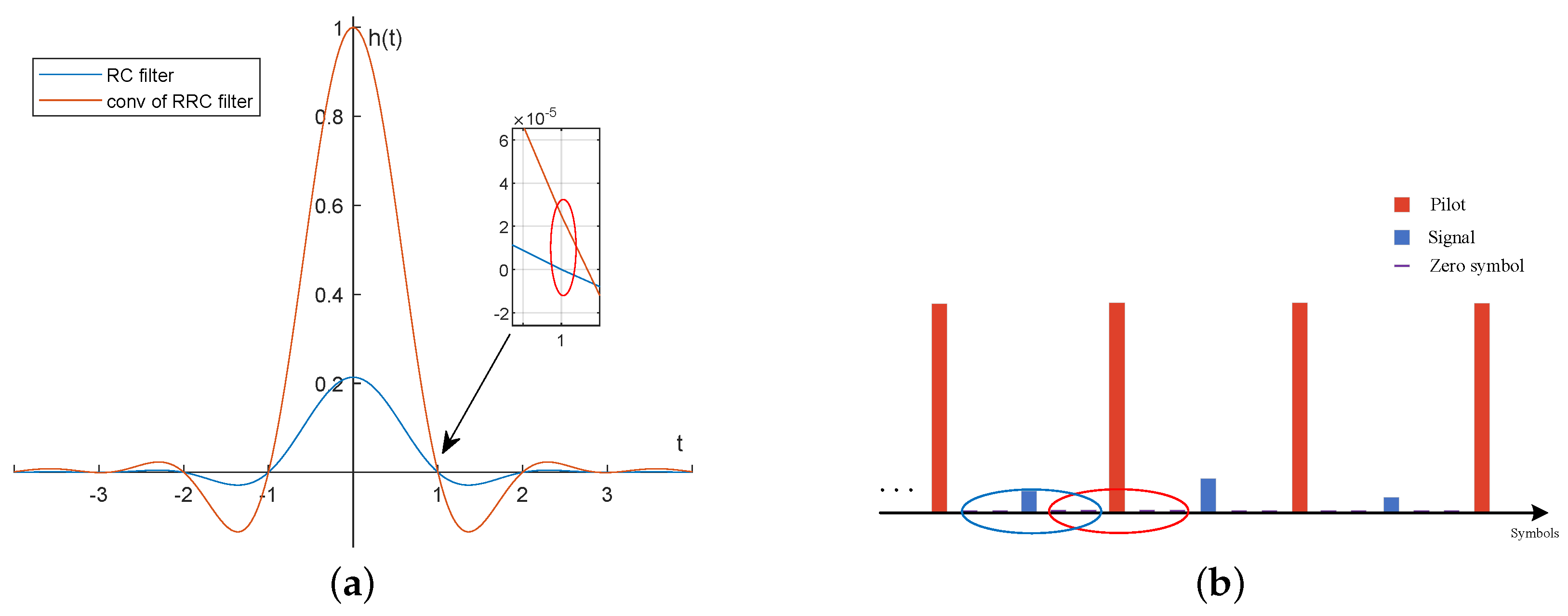
2.3. Noise-Suppression Based on Pilot-Aided CMA

CMA offers another advantage in its resistance to phase noise since the algorithm is primarily based on the signal’s modulus while disregarding its phase. Therefore, in our SOP recovery algorithm, we only need to focus on the recovery of the signal’s amplitude. The phase changes introduced by RSOP can be recovered in the subsequent phase compensation stage. Assuming the received raw sequence is represented in the digital domain as $R_{in}\left(n\right)$, and the equalized sequence is $R_{out}\left(n\right)$. The filter coefficient vector of the CMA adaptive equalizer is denoted as $\mathit{W}\left(n\right)$. To simplify the presentation, we only describe the signal sequence and filter coefficients in one polarization. Here, we introduce a cost function of CMA with respect to filter ${\mathit{W}}_n$,

$$J_{CMA}\left({\mathit{W}}_n\right)=E\left\{\left[\right|R_{out}\left(n\right){{|}^2-R_0]}^2\right\},$$

(8)

where $R_0$ is the expected modulus of the signal $R_{in}\left(n\right)$ with constant modulus, and $R_{out}\left(n\right)$ is the convolution of $R_{in}\left(n\right)$ and the filter $\mathit{W}\left(n\right)={[w_1\left(n\right),w_2\left(n\right),...,w_N\left(n\right)]}^T$ of length N. The purpose of CMA is to minimize the error function $J_{CMA}$, with the goal of discovering the optimal filter $\mathit{W}\left(n\right)$,

$$\mathit{W}\left(n\right)=arg\underset{\mathit{W}\left(n\right)}{min}{J}_{CMA}\left(\mathit{W}\left(n\right)\right).$$

(9)

Typically, this process is achieved through the stochastic gradient descent method. Specifically, the filter update process in the digital domain is as follows.

Consider an FIR filter $\mathit{W}\left(n\right)={[w_1\left(n\right),w_2\left(n\right),...,w_N\left(n\right)]}^T$ of length N, representing one of the filters (within ${\mathit{W}}_{1V}\left(n\right)$, ${\mathit{W}}_{1H}\left(n\right)$, ${\mathit{W}}_{2V}\left(n\right)$ and ${\mathit{W}}_{2H}\left(n\right)$) in our 2×2 MIMO structure. Denote the input signal vector as ${\mathit{R}}_{in}\left(n\right)={[s\left(n\right),s(n-1),...,s(n-N+1)]}^T$. Then, the ouput signal ${\mathit{R}}_{out}\left(n\right)$ can be expressed as

$$R_{out}\left(n\right)={\mathit{R}}_{in}{\left(n\right)}^T\mathit{W}\left(n\right).$$

(10)

The cost function of CMA with respect to ${\mathit{W}}_n$ can be expressed as

$$J_{CMA}\left({\mathit{W}}_n\right)=E\left\{\left[\right|R_{out}\left(n\right){{|}^2-R_0]}^2\right\},$$

(11)

where R is the real-valued constant depends on the ideal symbols $x_{s}ym$ according to Ref. [26], and given by $R_0={\displaystyle \frac{E\left\{\right|x_{sym}{|}^4\}}{E\left\{\right|x_{sym}{|}^2\}}}$. In our scheme, after normalizing the pilot magnitude, we set the $R_0=1$. The process of updating filter tap coefficients to find extremum using stochastic gradient descent can be expressed as

$$\mathit{W}(n+1)=\mathit{W}\left(n\right)-\mu \nabla J_{CMA}\left(\mathit{W}\left(n\right)\right),$$

(12)

where $\nabla J_{CMA}\left(\mathit{W}\left(n\right)\right)={\displaystyle \frac{\partial J_e\left(\mathit{W}\left(n\right)\right)}{\partial \mathit{W}\left(n\right)}}$ represents the gradient of the cost function $J_e$ with respect to the weight vector $\mathit{W}\left(n\right)$. The parameter $\mu$, known as the iteration step size, plays a crucial role in controlling both the convergence speed and the accuracy of the algorithm. In general, $\mu$ is set to a small value to ensure stable convergence and prevent overshooting during the optimization process. Choosing an appropriate value for $\mu$ requires balancing faster convergence and achieving a high level of precision in the final solution. Based on Equation (11), then we can obtain

$${\displaystyle \frac{\partial J_e\left(\mathit{W}\left(n\right)\right)}{\partial \mathit{W}\left(n\right)}}=2E\left\{\left[\right|R_{out}\left(n\right){|}^2-R_0]{\displaystyle \frac{\partial |R_{out}{|}^2}{\partial \mathit{W}\left(n\right)}}\right\}.$$

(13)

Based on Equation (10), we can obtain

$${\displaystyle \frac{\partial |R_{out}{|}^2}{\partial \mathit{W}\left(n\right)}}=2{\mathit{R}}_{in}^{*}\left(n\right)R_{out}\left(n\right),$$

(14)

where ${(·)}^{*}$ denotes the conjugate operation. Substituting Equation (14) into Equation (13), we can obtain

$${\displaystyle \frac{\partial J_e\left(\mathit{W}\left(n\right)\right)}{\partial \mathit{W}\left(n\right)}}=4E\left\{\left[\right|R_{out}\left(n\right){|}^2-R_0]{\mathit{R}}_{in}^{*}\left(n\right)R_{out}\left(n\right)\right\}.$$

(15)

By replacing the expected value with stochastic gradients, the digital domain iterative update formula for CMA is given as

$$\mathit{W}(n+1)=\mathit{W}\left(n\right)+\mu R_{out}\left(n\right)[R_0-|R_{out}\left(n\right){|}^2]{\mathit{R}}_{in}^{*}\left(n\right).$$

(16)

Based on the abovementioned CMA process, our pilot-aided CMA scheme can be described as Algorithm 1. In our scheme, we set a threshold parameter to determine whether to update the filter tap coefficients. The purpose of this approach is to allow the algorithm to tolerate a certain level of noise in the pilot tone. When employing CMA to recover PDM signals, a 2 × 2 MIMO finite impulse response filtering system is utilized, as depicted in Figure 2. For simplification of mathematical expressions, consider that $R_{in}=[R_{in}^H;R_{in}^V]$ and $R_{out}=[R_{out}^H;R_{out}^V]$. In the pilot-aided CMA scheme, demultiplexed pilot tone is first input into the MIMO structure until the filter converges, during which $R_{in}=A{e}^{{\theta }_d}$. The converged tap weights are then used to recover the quantum signal, during which $R_{in}=|{\alpha }_G\rangle$.

Algorithm 1 Pilot−aided CMA

Input:  Received signals $R_{in}$ and raw filter taps $W\left(n\right)$; Output:  $R_{out}$ which includes equalized pilot tone and GMCS quantum signals; 1: for $\mathit{P}\left(n\right)$ in pilots sequence and $\mathit{Q}\left(n\right)$ in signals sequence do 2:  if $\mathit{W}{\left(\mathit{n}\right)}^T\mathit{P}\left(n\right)$> Threshold then 3:     Update $\mathit{W}\left(\mathit{n}\right)$ using Equation (16); 4:  else 5:     Calculate $\mathit{W}{\left(\mathit{n}\right)}^T\mathit{Q}\left(n\right)$; 6:  end if 7: end for 8: return  $R_{out}$;

We simulated the proposed scheme and evaluated the linear relationship between the transmitted and received signals before and after SOP recovery, as shown in Figure 3. In our simulation, the pilot-to-signal ratio was set to 26 dB, the SNR of the pilot was set to 29.5 dB, and a Jones matrix with $\alpha \left(t\right)=1$ krad/s and $\theta \left(t\right)={\displaystyle \frac{\pi }{12}}$ was applied to the modulated signal sequence to simulate SOP rotation. Simulation results show that our scheme performs effectively under a polarization state rotation of 1 krad/s.

2.4. Phase Compensation

Considering the received sequence at Bob’s end, obtained after down sampling the measured signal, can be described as

$$Se{q}_B\left(j\right)=\left\{\begin{array}{c}A\left(j\right)e^{{\theta }_d\left(j\right)},j=2k-1,\hfill \\ |{\alpha }_{G_j}\rangle ,j=2k,\hfill \end{array}k\in \{1,2,...,n\},\right.$$

(17)

where $A\left(j\right)$ and ${\theta }_d\left(j\right)$ are the amplitude and phase of k-th received pilot tone. Then, we use two adjacent pilot tones to recover the phase of the k-th quantum signal. The phase compensation algorithm can be expressed as

$$\Delta {\phi }_P^k={\displaystyle \frac{U_P^k\left|U_{ref}^k\right|}{U_{ref}^k}},$$

(18)

$$\Delta {\phi }_Q^k={\displaystyle \frac{\Delta {\phi }_P^k+\Delta {\phi }_P^{k+1}}{2}},$$

(19)

where $U_P$ and $U_{ref}$ are the received pilot tone at Bob’end and the reference pilot tone sent by Alice, respectively, and $\Delta {\phi }_P$ is the phase difference between them. We calculate the phase change $\Delta {\phi }_Q$ of the quantum signal by averaging the phase differences of adjacent pilots. Then, we can recover the phase of the quantum signal by rotating its phase by $-\Delta {\phi }_Q$. Considering the coherent states of GMCS is $|X+iP\rangle$, the process of phase compensation can be expressed as

$$\begin{array}{c}\hfill X_{Q,k}^{\prime }=X_{Q,k}cos\Delta {\phi }_Q-P_{Q,k}sin\Delta {\phi }_Q,\\ \hfill P_{Q,k}^{\prime }=X_{Q,k}sin\Delta {\phi }_Q+P_{Q,k}cos\Delta {\phi }_Q,\end{array}$$

(20)

where $X^{\prime }$ and $P^{\prime }$ denote the recovered X and P quadrature components, respectively.

3. Experiment and Results

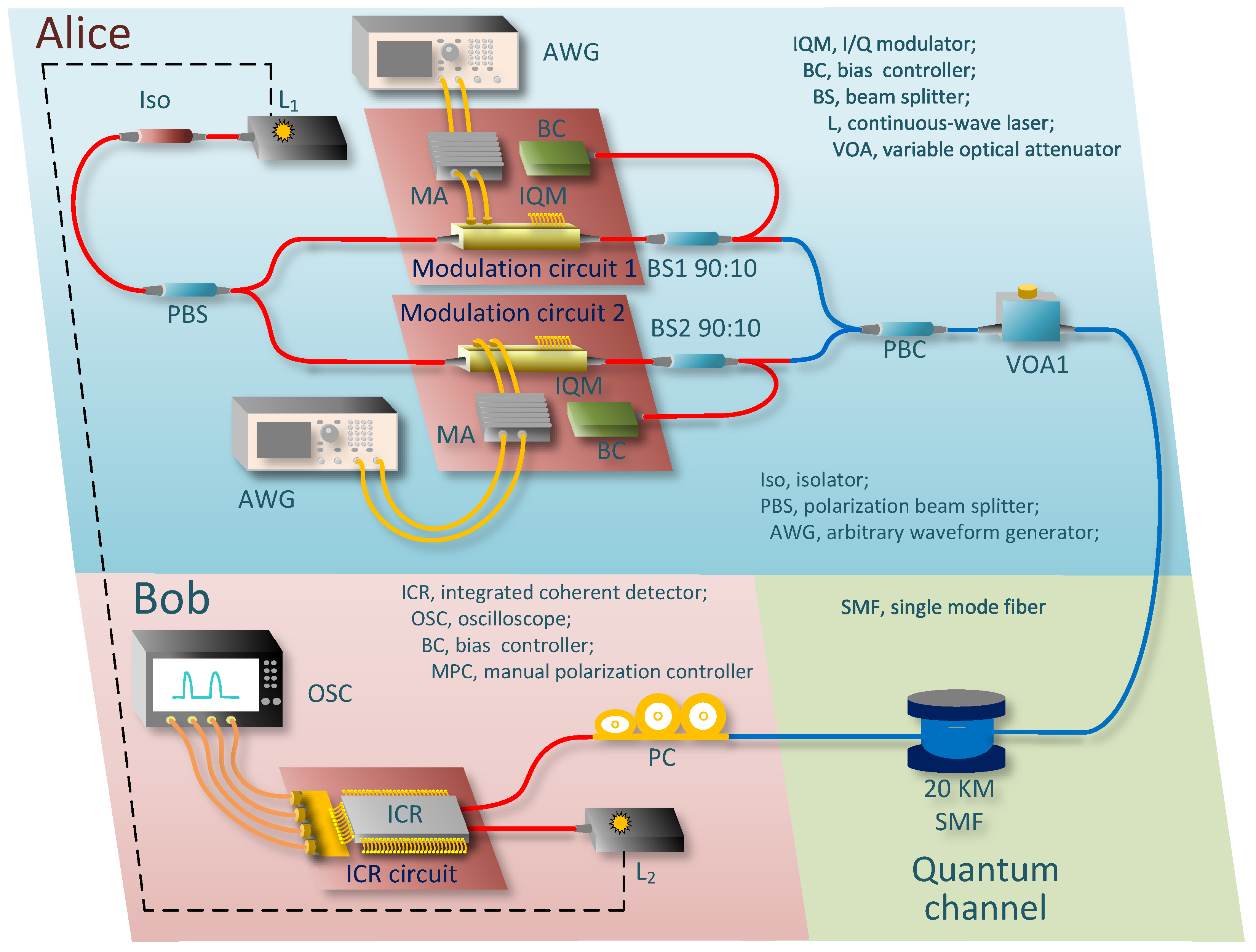
3.1. Experimental Setup

We conducted experiments based on the implementation of local local oscillator (LLO) scheme to verify the effectiveness of our scheme. The experimental setup is illustrated in Figure 4.

At Alice’s side, a commercial narrow linewidth laser (continuous wave) serves as the coherent state source, operating at a wavelength of 1550.12 nm. It is followed by a polarization beam splitter that divides the source into two orthogonally polarized beams. These beams are directed into two optical IQ modulators to modulate quantum and pilot signals. A four-channel high-speed arbitrary waveform generator (AWG) with a 5 GS/s sampling rate and 16-bit depth loads data for modulation. Channels 1 and 2 of the AWG output signals for the I and Q branches of IQM1, while channels 3 and 4 do the same for IQM2. A bias controller (BC) maintains bias voltages in the linear region via automatic feedback control [27]. The orthogonally polarized signals from the IQMs are combined into a PDM signal by a polarization beam combiner (PBC). A manual variable optical attenuator (VOA) controls the modulation variance, and the signal is transmitted through a 20 km single-mode fiber quantum channel. At Bob’s side, an MPC is used to pre-correct the SOP to ensure proper reception of the orthogonal component. In our experiment, Bob’s LO is generated by Alice’s laser. A 50:50 beam splitter divides Alice’s light source into two beams: one for Alice’s signal and the other for Bob’s LO. The signal is then fed into the polarization diversity receiver module, integrated within an integrated coherent receiver (ICR) consisting of two ${90}^{\circ }$ optical hybrids and four coherent detectors. Each detector detects one of the four orthogonal components of the two polarizations. The detected optical signals are converted to electrical signals, sampled at 5 GS/s by an oscilloscope, and then transmitted to a personal computer.

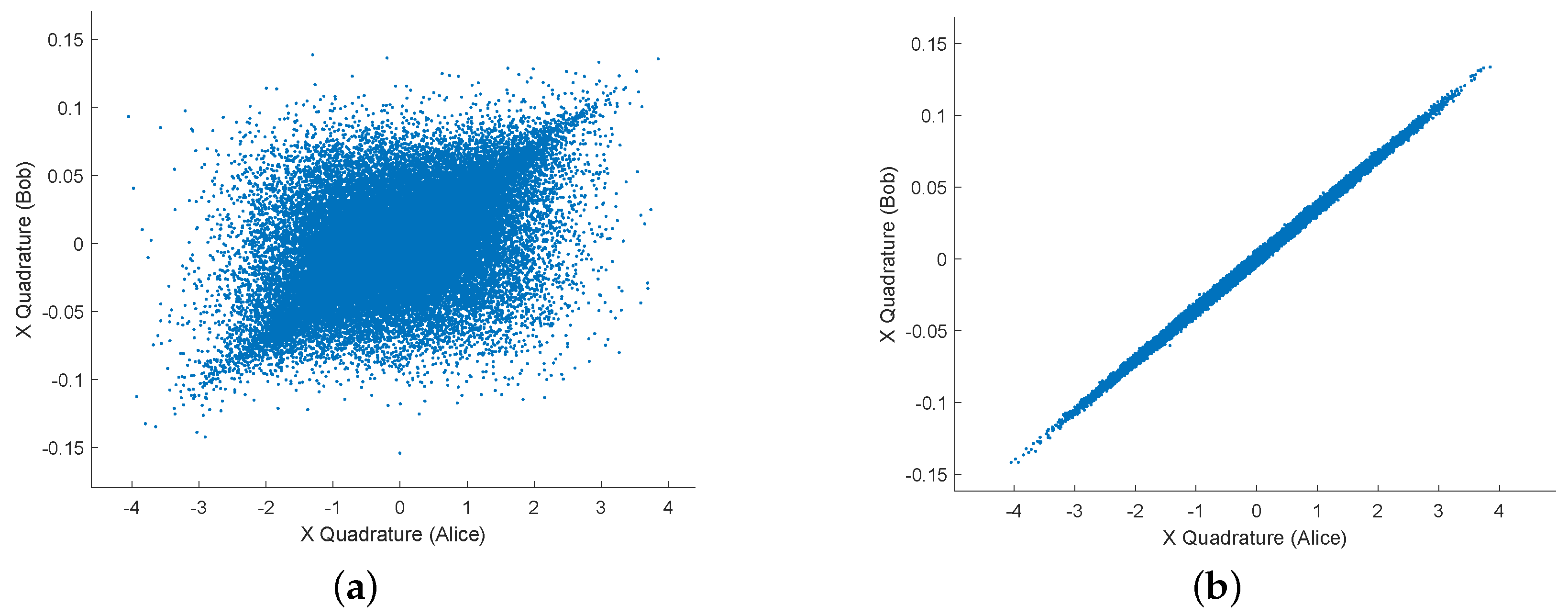
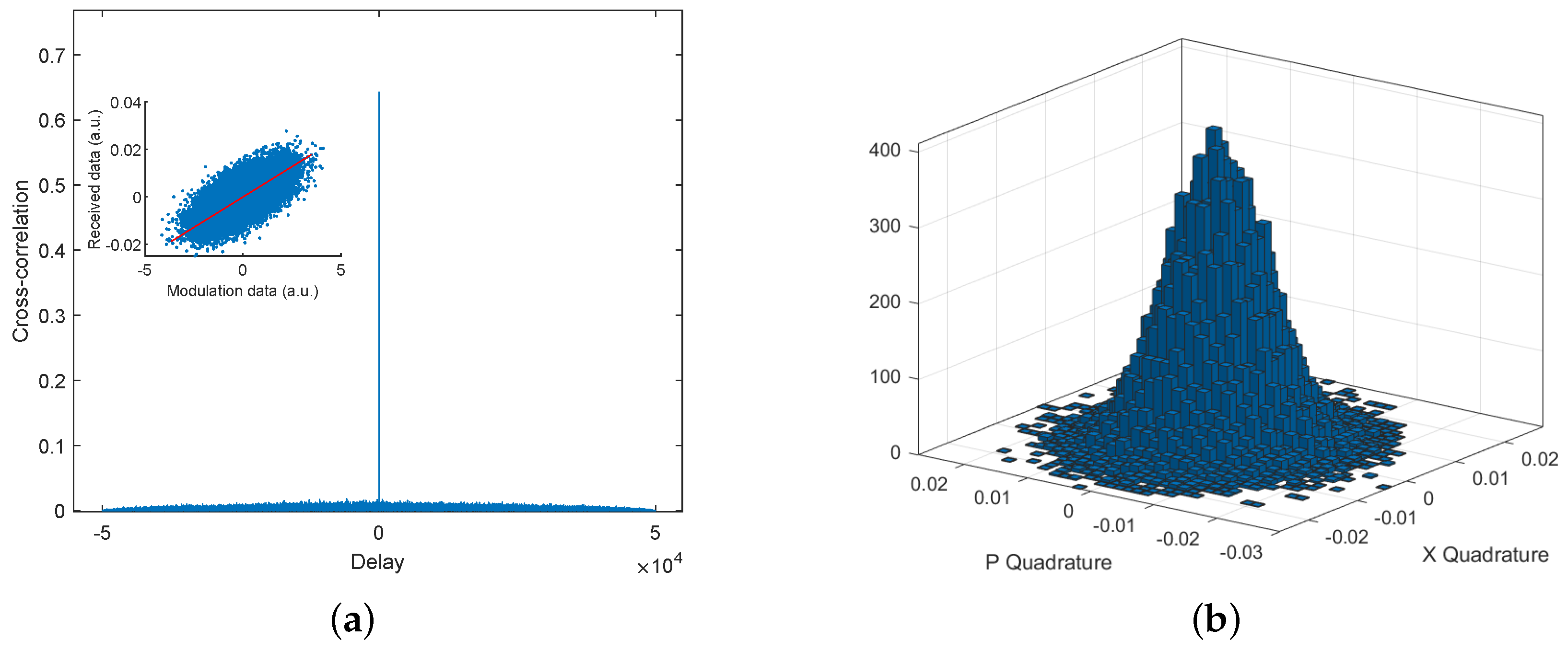
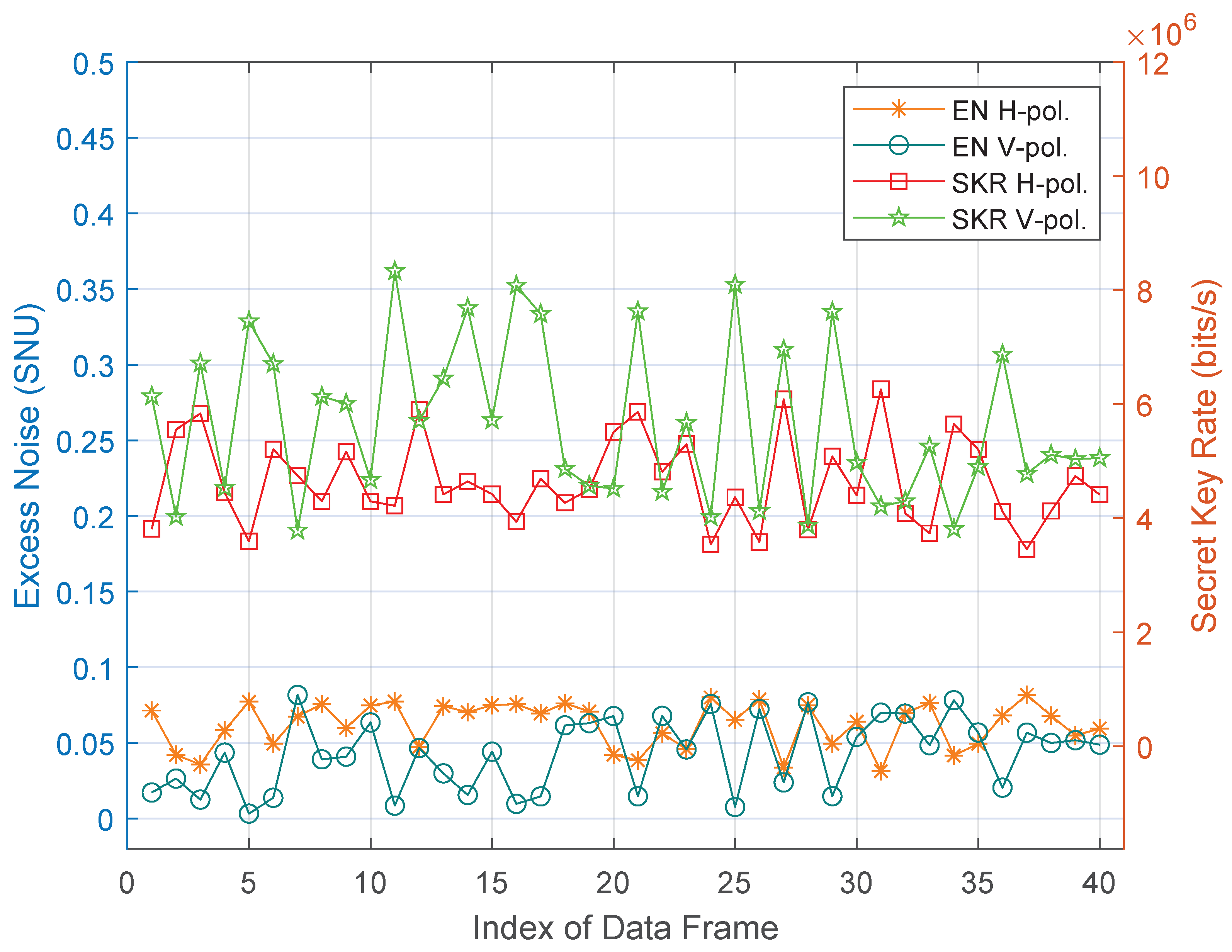
3.2. Noise-Suppression in Experiment

In our experiment, we employed double sideband suppressed carrier modulation to upconversion the baseband GMCS and pilot signals. At the receiving end, coherent demodulation and low-pass filtering were used to receive the signals. The primary purpose of this approach was to filter out the inherent $1/f$ noise [28] of the ICR and other low-frequency noise. Since both the IQM and ICR are bandwidth-limited devices, we performed pulse shaping on the square-wave baseband signals to suppress sidelobes in the signal spectrum, ensuring that no signal components are lost during filtering.

To effectively limit the signal bandwidth, Nyquist pulse shaping is essential. In extreme cases, this shaping can produce a nearly rectangular spectrum. Typically, raised cosine (RC) spectral shaping is employed to satisfy the Nyquist criterion, thereby achieving zero intersymbol interference (ISI) [29]. The RC filter response is defined as follows:

$$H_{RC}\left(\omega \right)=\left\{\begin{array}{cc}{T}_s,& 0\le \left|\omega \right|<\pi \left(1-\beta \right)/T_s\\ {\displaystyle \frac{T_s}{2}}\left(1-sin\left[{\displaystyle \frac{T_s}{2\beta }}\left(\left|\omega \right|-{\displaystyle \frac{\pi }{T_s}}\right)\right]\right),& {\displaystyle \frac{\pi (1-\beta )}{T_s}}\le \left|\omega \right|<{\displaystyle \frac{\pi (1+\beta )}{T_s}}\\ 0,& \left|\omega \right|\ge \pi \left(1+\beta \right)/T_s\end{array}\right.,$$

(21)

where $\beta$ is the roll-off factor. To maximize the SNR, RC filters can be used at both the transmitter and receiver [26]. Therefore, in our experiment, we used root-raised cosine (RRC) pulse shaping at the transmitter and a second RRC filter at the receiver as a matched filter, with the RRC filter response given by $H_{RRC}\left(\omega \right)=\sqrt{H_{RC}\left(\omega \right)}$.

Utilizing RRC filters for pulse shaping offers the advantage of minimizing bandwidth while enhancing SNR at the sampling points through matched filtering. By employing an RRC filter at both ends, we ensure that the convolution of these filters results in an RC filter. This configuration effectively eliminates ISI at optimal sampling points, addressing issues often encountered with square wave or pulse signals. Consequently, our approach not only optimizes bandwidth usage but also significantly improves the overall integrity and reliability of the transmitted signal.

However, achieving ISI free in practical experiments is often challenging. This difficulty typically arises from two factors: the challenge of precisely sampling the signal at the optimal point and the finite duration of the RRC filter’s impulse response, where the convolution of two finite impulse response (FIR) RRC filters does not exactly equal a single raised cosine (RC) filter. This discrepancy means the impulse response at symbol points is not zero, failing to ensure ISI free at the optimal sampling points, as depicted in Figure 5a.

From the inset, it can be seen that at the first symbol sampling point, the value of the RC filter’s FIR differs from the convolution of two RRC filter’s FIR. The former is zero at the symbol sampling point, while the latter deviates significantly from zero. This discrepancy is also observed at other sampling points. To address this issue, we modified the original Alice modulation sequence by inserting two zero symbols between the pilot and GMCS signals, as shown in Figure 5b. We then adjusted the impulse response length of the RRC filter to four symbols (i.e., $span=4$) and set the roll-off factor $\beta =0.5$. We extracted the residual noise from the quantum signals at the receiver after signal processing and observed the noise power spectral density (PSD) of the scheme before and after the improvement, as shown in Figure 6. Before the improvement, i.e., without inserting zero symbols and with an RRC filter impulse response length $span=6$, the PSD of the noise was non-stationary. It is evident that certain components were present in the noise, likely due to pilot crosstalk introduced by the non-zero characteristics of the FIR RRC at the sampling points during pulse shaping. This crosstalk could not be eliminated by digital signal processing, and therefore, appeared in the noise. After the improvement, the scheme exhibited a stationary noise PSD, indicating that the crosstalk had been removed.

Although the convolution of two FIR RRC filters does not result in ISI free at the optimal sampling points, this issue does not significantly impact the performance of traditional optical communication systems, due to the presence of decision processes. However, for a CV-QKD system employing interleaved pilot and quantum signals, the high-intensity pilot can cause interference with the weak quantum signal, leading to significant performance degradation and increased excess noise in the CV-QKD system. To address this problem, we interleaved two empty symbols between the pilot and GMCS symbols in our experiment and set the impulse response length of the RRC filter to four symbols. This approach ensures that during pulse shaping, the pilot signal does not introduce interference to the GMCS signal while effectively suppressing the signal bandwidth.

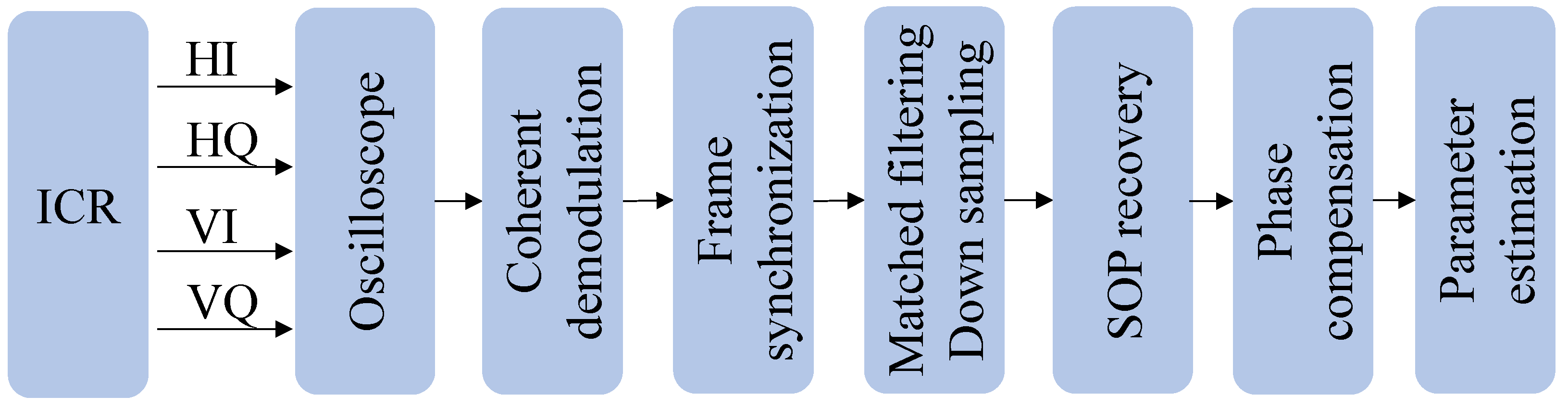
3.3. Data Acquisition and Offline Signal Processing

Finally, we collected a total of 40 frames of data over a period of 3 h under laboratory conditions. The block size used in the experiment was $1\times {10}^5$, and offline digital signal processing was performed to suppress noise and obtain the raw key. Our data processing mainly consists of the following processes: coherent demodulation, frame synchronization, matched filtering and downsampling, SOP recovery, phase compensation, and parameter estimation, as depicted in Figure 7.

For the data collected at Bob’s end, we used coherent demodulation with a low pass filter to obtain the baseband signal and filter out the $1/f$ noise and other low-frequency noise. During the frame synchronization process, we disclose Alice’s pilot as the reference signal and determine the lag value of the received signal by calculating the cross-correlation between Bob’s received pilot and the reference signal. We then applied the same RRC filter as Alice’s end to achieve matched filtering. After downsampling, we obtained the unprocessed sequence including the pilot and GMCS signal. We first used the pilot-aided CMA algorithm mentioned in the Section 2.3 for the SOP compensation, and then applied a phase compensation algorithm in Section 2.4 for phase compensation. The cross−correlation result between Bob’s measurement and Alice’s modulation is shown in Figure 8. Additionally, the measurements at Bob’s end exhibit pronounced Gaussian characteristics.

When the intensity ratio between the pilot and quantum signals is too large, part of the precision of the GMCS signal is lost. Conversely, when the intensity ratio is too small, the pilot signal’s SNR is low due to noise interference, making it difficult to accurately track changes in phase and SOP. In our experiment, we set the ratio of the pilot tone intensity to the variance of the Gaussian data to 24 dB, ensuring that the AWG quantization noise is minimized while maintaining a high SNR for the pilot signal, thus improving its ability to track phase and SOP variations. We calculated the excess noise via parameter estimation. As shown in Figure 9, the excess noise of the GMCS signals in both polarization orientations was measured at approximately 0.062 (H) and 0.043 (V) in shot noise units (SNUs). The achievable secret key rate (SKR) of the system is calculated according to Ref. [30], which is asymptotic and does not take into account the finite-size effects. The formula of SKR can be expressed as

$$R=f_{rep}\times (\beta I_{AB}-{\chi }_{BE}).$$

(22)

One can see Appendix A for the calculating formula of the secret key rate. Due to the variations in the intensities of the signal light and the LO, the modulation variance of our signal also changes. We record the modulation variance of each frame of the signal. The modulation variance $V_A$ of the signals in the H and V polarization are distributed between [2.5, 3.5] and [1.5, 3] in SNUs, with mean values $V_{A_H}=2.93$ and $V_{A_V}=2.76$. According to the parameter estimation calculation formula Equation (22), we obtain the average achievable SKR in the H and V polarization as 4.65 Mbps and 5.66 Mbps, respectively, with a total average SKR of 10.31 Mbps. The results indicate that the SKR of our system is nearly doubled compared to single-channel CV-QKD.

4. Discussion

Our analysis identifies that the primary source of excess noise is the insufficient quantization precision of the AWG, which is limited to 16 bits. This limitation introduces additional noise during modulation. Additionally, the low SNR of the pilot tone degrades the accuracy of phase and SOP recovery, leading to residual phase noise and polarization crosstalk. Excessive noise jitter is primarily caused by variable channel noise, low SNR of the pilot signal affecting recovery quality, and shot noise variations due to fluctuations in LLO intensity.

In addition, our system employs the PDM technique to realize a dual-channel CV-QKD with SOP sensing, which has some theoretical and experimental safety. Among the theoretical security, the security of GMCS is proven to be complete. In terms of experimental security, we add an additional test of security through the pilot-aided PDM.

Our system has the following advantages:

Privacy Protection Advantages:

• Two orthogonal polarizations can simultaneously carry both key and monitoring information.
• It is difficult for an attacker to precisely access information from both polarizations at the same time.
• Additional security checks are provided through the relative polarization relationship.
• The functions of key distribution and environmental monitoring can be decoupled.

Attack Resistance Capabilities:

• Real-time monitoring of channel fluctuations is possible.
• Quick response to abnormal polarization changes can be achieved.
• Interference can be identified by comparing the correlation between the two polarizations.
• Environmental noise and active attacks can be distinguished.

Specific Defense Mechanisms:

• Against intercept-resend attacks: Detection of polarization correlation.
• Against Trojan horse attacks: Real-time monitoring of channel anomalies.
• Against phase attacks: Utilizing the relative phase between the two polarizations.
• Against collective attacks: increasing the technical difficulty for attackers.

Sensor Feedback Advantages:

• Provides real-time feedback on channel status.
• Protocol parameters can be dynamically adjusted based on environmental changes.
• Enhances system adaptability and robustness.
• Optimizes the balance between key generation rate and security.

5. Conclusions

This work successfully implements GMCS-CV-QKD via PDM and verifies the feasibility of the proposed SOP sensing and recovery scheme. We sensed the SOP changes and reduced polarization crosstalk via a pilot-aided CMA scheme and applied matched filtering to improve tracking accuracy and suppress excess noise. Additionally, we used RRC to limit bandwidth while enhancing spectral efficiency and optimized the RRC filter application to eliminate ISI between the pilot and GMCS signals. Our scheme can be implemented in hardware and fully inherits the existing coherent optical communication modules and algorithms, making it applicable to future quantum optical communication modules.